| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Теория активированного комплекса
Теория активированного комплекса, без сомнения, является развитием идей Аррениуса. Согласно этой теории, элементарная реакция протекает непрерывно от начального до конечного состояния и проходит через переходное состояние, характеризующееся максимальной энергией. Говорят, что соответствующий этому состоянию комплекс является активированным комплексом. Изменение энергии в ходе реакции может быть представлено диаграммой энергии, как на рис. 5-1. В такой диаграмме по оси ординат можно откладывать различные величины энергии. Поскольку мы рассматриваем реакции в растворах, где разность энергий измеряется при постоянном давлении, разумно использовать энтальпию. Тогда разность молярных энтальпий начального и конечного состояний является энтальпией реакции  а соответствующая разность для начального и переходного состояний — энтальпией активации
а соответствующая разность для начального и переходного состояний — энтальпией активации  (Для обозначения величин, относящихся к активированному комплексу, используют надстрочный индекс в виде двойного крестика.) Абсцисса соответствует координате реакции, представляющей собой глубину протекания реакции. Следует заметить, что имеется несколько проблем, связанных с физическим смыслом таких диаграмм энергий. Проблема возникает из-за смешения микроскопического и макроскопического поведения вещества. Очевидно, координата реакции соответствует пути отдельной молекулы, а не совокупному поведению всех частиц, присутствующих в реакционном сосуде. Если бы все реагирующие частицы одновременно преодолевали энергетический барьер, это было бы несовместимо со вторым законом термодинамики. В то же время
(Для обозначения величин, относящихся к активированному комплексу, используют надстрочный индекс в виде двойного крестика.) Абсцисса соответствует координате реакции, представляющей собой глубину протекания реакции. Следует заметить, что имеется несколько проблем, связанных с физическим смыслом таких диаграмм энергий. Проблема возникает из-за смешения микроскопического и макроскопического поведения вещества. Очевидно, координата реакции соответствует пути отдельной молекулы, а не совокупному поведению всех частиц, присутствующих в реакционном сосуде. Если бы все реагирующие частицы одновременно преодолевали энергетический барьер, это было бы несовместимо со вторым законом термодинамики. В то же время

Рис. 5-1. Диаграмма энергии для эндотермической элементарной реакции.
координата энергии отражает термодинамические свойства реагирующей системы, т.е. средние изменения энергии больших скоплений частиц. Однако эта проблема довольно формальна. К примеру, ее можно обойти, рассматривая «пограничное» число частиц, скажем  которое, с одной стороны, так малб, что второй закон термодинамики не нарушается, поскольку отклонения от термодинамического равновесия, так называемые флуктуации, более вероятны, когда число наблюдаемых частиц уменьшается. С другой стороны, это число частиц оказывается достаточным для применения термодинамических величин.
которое, с одной стороны, так малб, что второй закон термодинамики не нарушается, поскольку отклонения от термодинамического равновесия, так называемые флуктуации, более вероятны, когда число наблюдаемых частиц уменьшается. С другой стороны, это число частиц оказывается достаточным для применения термодинамических величин.
Предполагается, что активированный комплекс находится в равновесии с исходными реагентами, и уравнение элементарной реакции второго порядка

можно представить в виде

Тогда по аналогии с уравнением  константу скорости реакции можно записать как
константу скорости реакции можно записать как

где К — константа равновесия,  Константу скорости к можно рассматривать как частоту распада активированного комплекса, благодаря которой образуется продукт. Эйринг предложил считать к равной
Константу скорости к можно рассматривать как частоту распада активированного комплекса, благодаря которой образуется продукт. Эйринг предложил считать к равной  Отсюда
Отсюда

где  — постоянные Больцмана и Планка соответственно. Константа равновесия связана с изменением свободной энергии Гиббса:
— постоянные Больцмана и Планка соответственно. Константа равновесия связана с изменением свободной энергии Гиббса:

Гиббсову свободную энергию активации  можно выразить через энтальпию активации и энтропию активации, т.е.
можно выразить через энтальпию активации и энтропию активации, т.е.

Подстановка (5-11) и (5-10) в  приводит к уравнению Эйринга
приводит к уравнению Эйринга

или, в логарифмической форме,

которую удобно преобразовать к виду

Соответственно на диаграмме Эйринга строят зависимость  от
от  при этом получают прямую с наклоном, равным —
при этом получают прямую с наклоном, равным —  Зная эту величину, из уравнения (5-14) выводят
Зная эту величину, из уравнения (5-14) выводят  используя различные наборы значений
используя различные наборы значений  Нужно отметить, что константа скорости в уравнении Эйринга имеет размерность
Нужно отметить, что константа скорости в уравнении Эйринга имеет размерность  Поэтому, строго говоря, энтропию активации можно вычислить только для реакций первого порядка. [Размерность концентрации теряется при переходе от
Поэтому, строго говоря, энтропию активации можно вычислить только для реакций первого порядка. [Размерность концентрации теряется при переходе от  к (5-10), поскольку измеряется в
к (5-10), поскольку измеряется в  тогда как величина
тогда как величина  Конечно, уравнение Эйринга можно применить к реакциям любого порядка, но следует иметь в виду, что абсолютные величины
Конечно, уравнение Эйринга можно применить к реакциям любого порядка, но следует иметь в виду, что абсолютные величины  сильно зависят от выбора стандартных состояний. Поэтому необходима осторожность при сравнении энтропий активации реакций, имеющих различный порядок. Как показал Мелвин-Хьюз [91], согласно теории столкновений, энтропия активации бимолекулярной реакции при
сильно зависят от выбора стандартных состояний. Поэтому необходима осторожность при сравнении энтропий активации реакций, имеющих различный порядок. Как показал Мелвин-Хьюз [91], согласно теории столкновений, энтропия активации бимолекулярной реакции при  на
на  более положительна, чем энтропия активации, вычисленная по формуле Эйринга. Нужно еще доказать, связано ли это с тем наблюдением, что только указанная разница в энтропиях активации была экспериментально найдена для двух реакций, из которых одна первого, а другая второго порядка; в противном случае остается предположить, что эти реакции происходят по одному и тому же «внутреннему механизму» [138].
более положительна, чем энтропия активации, вычисленная по формуле Эйринга. Нужно еще доказать, связано ли это с тем наблюдением, что только указанная разница в энтропиях активации была экспериментально найдена для двух реакций, из которых одна первого, а другая второго порядка; в противном случае остается предположить, что эти реакции происходят по одному и тому же «внутреннему механизму» [138].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
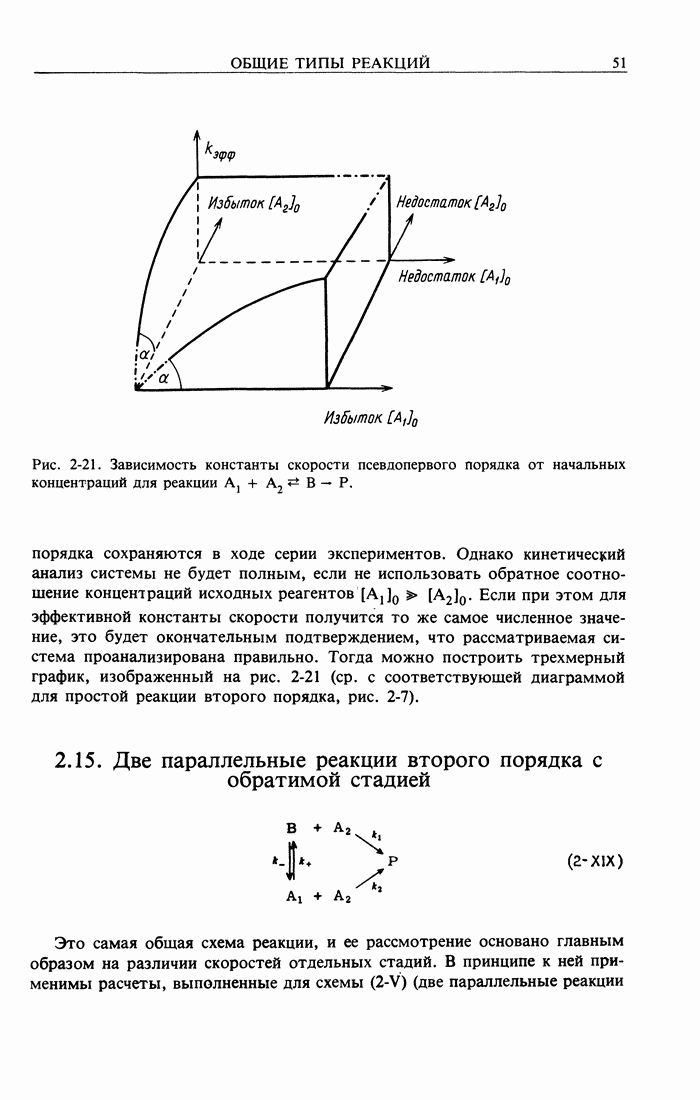
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
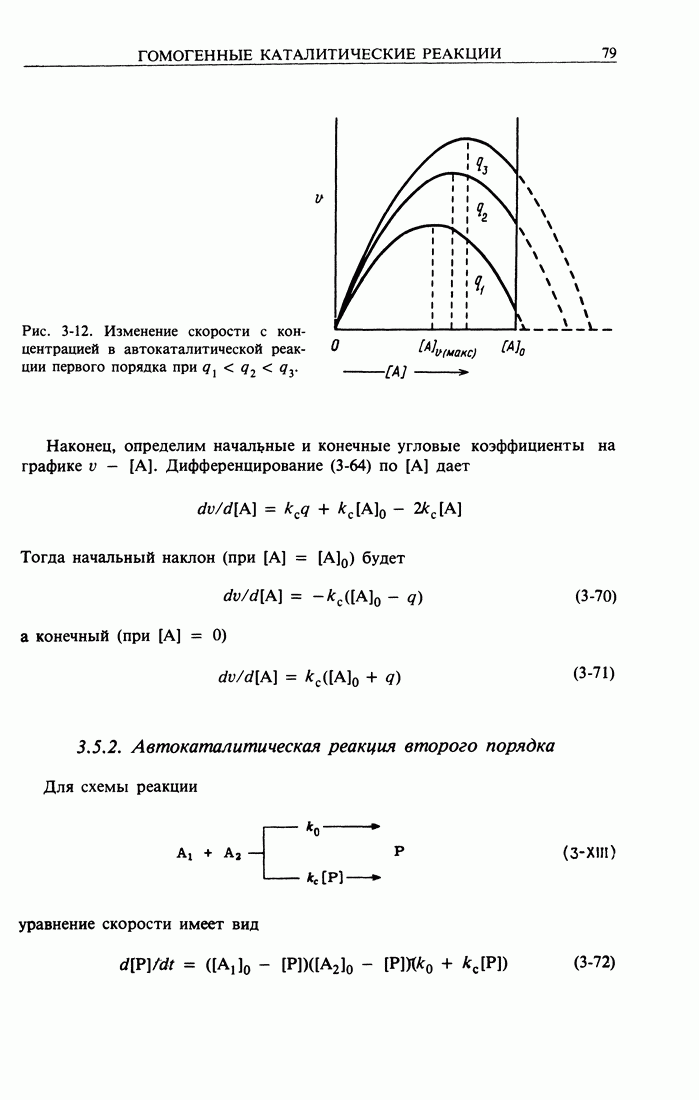
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
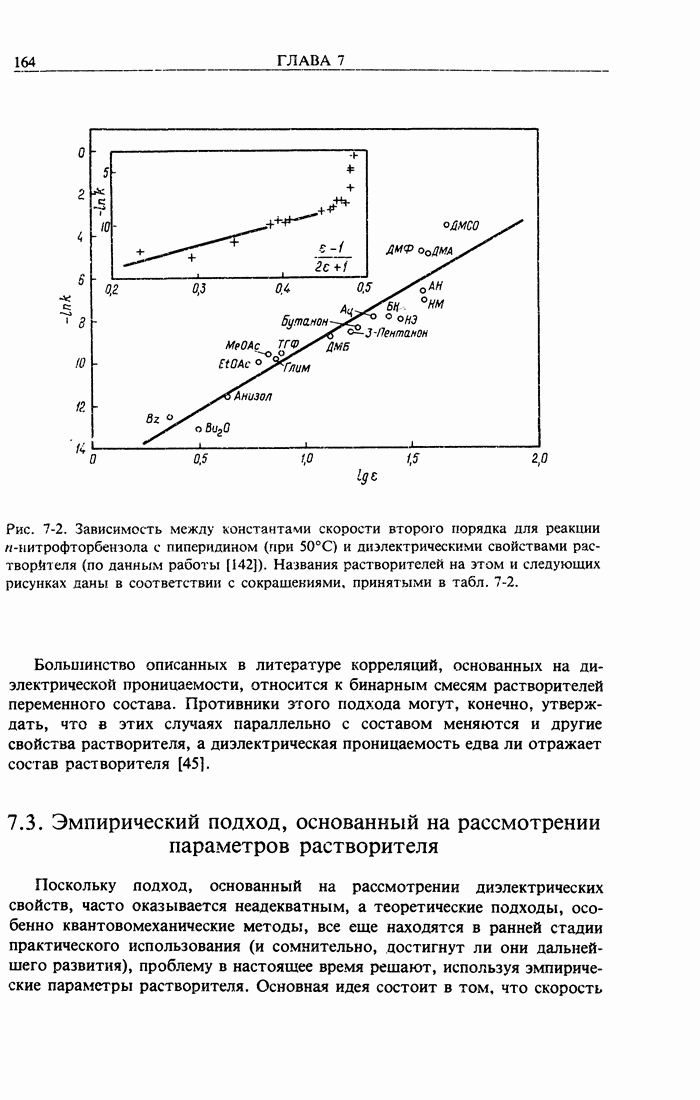
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
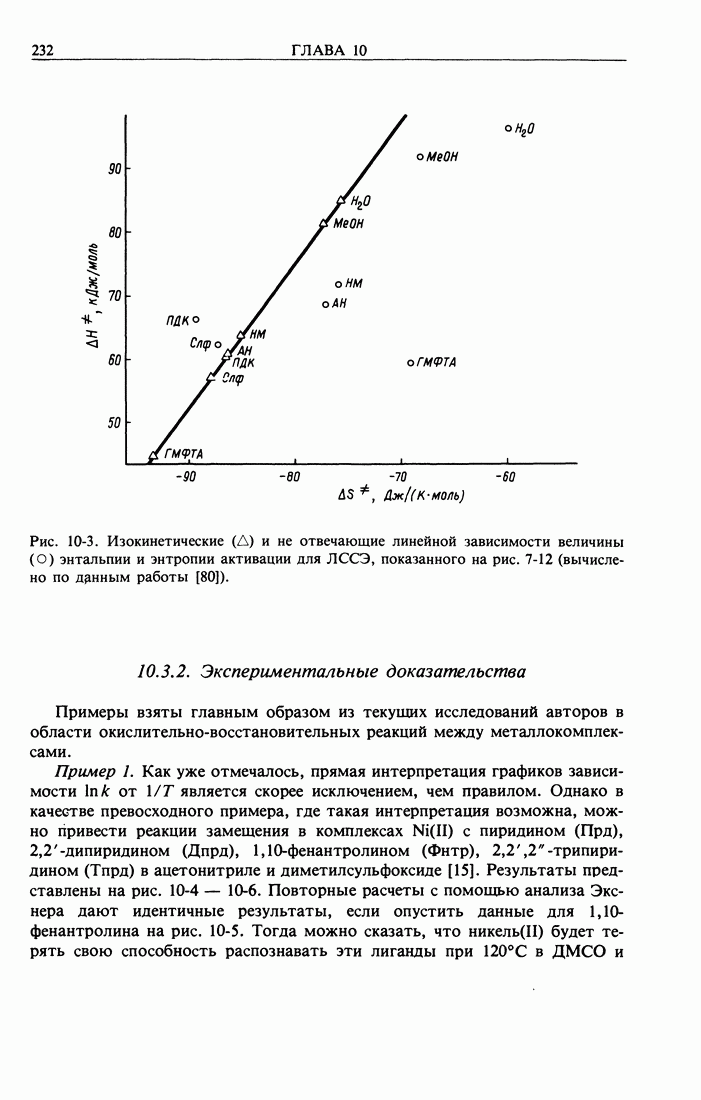
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений