| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. ВВЕДЕНИЕ
Когда начинают изучать кинетику какой-либо реакции, то делают это по крайней мере по двум причинам: а) чтобы иметь возможность моделировать промышленные химико-технологические процессы и б) чтобы выяснить механизмы реакций.
История предмета свидетельствует о том, что кинетические методы развивались применительно к обеим вышеназванным целям в более или менее равной мере. Однако традиционные кинетические методы оказываются довольно ограниченным средством для изучения механизмов реакций. Чтобы выяснить этот вопрос детально, мы хотели бы начать с описания в общих чертах основных стадий кинетического анализа.
Первичные данные кинетических экспериментов представляют собой набор концентраций химических компонентов реагирующей системы (или некоторых пропорциональных им величин) при разных значениях времени реакции. По этим данным графически строят кривую зависимости концентрации от времени (график  как, например, показано на рис. 1-1 для уменьшения концентрации реагента А. После получения таких кривых для серий с различными начальными концентрациями реагентсэв, так называемых экспериментальных серий, переходят к следующей стадии — выводу уравнения, описывающего зависимость между переменными. Используют два типа уравнений. Первый — это дифференциальное уравнение скорости, выражающее скорость реакции как функцию концентрации:
как, например, показано на рис. 1-1 для уменьшения концентрации реагента А. После получения таких кривых для серий с различными начальными концентрациями реагентсэв, так называемых экспериментальных серий, переходят к следующей стадии — выводу уравнения, описывающего зависимость между переменными. Используют два типа уравнений. Первый — это дифференциальное уравнение скорости, выражающее скорость реакции как функцию концентрации:

Скорость реакции в данный момент времени  дается тангенсом угла наклона кривой в этот момент времени:
дается тангенсом угла наклона кривой в этот момент времени:

Знак «минус» показывает, что в ходе реакции концентрация реагента уменьшается. В то же время реакция может сопровождаться увеличением во времени концентрации продукта, и тогда скорость реакции выражается дифференциалом 

Рис. 1-1. Кривая зависимости концентрации реагента А от времени.
Другой тип уравнения — это интегральное уравнение скорости, представляющее концентрацию как функцию времени:
Концентрация  (время)
(время) 
Каждое из используемых уравнений имеет и свои преимущества, и свои недостатки, которые будут обсуждаться в разд. 4.3.
При выводе экспериментального уравнения скорости было разработано исключительно полезное понятие порядка реакции. Часто уравнение скорости можно выразить в виде

где  скорость реакции, а
скорость реакции, а  величины, от которых зависит скорость. Показатели степени
величины, от которых зависит скорость. Показатели степени  называют парциальными порядками реакции: порядок а по компоненту А, порядок
называют парциальными порядками реакции: порядок а по компоненту А, порядок  по компоненту В. Сумма парциальных порядков
по компоненту В. Сумма парциальных порядков  дает полный, или общий, порядок реакции. Константа к называется удельной скоростью или константой скорости.
дает полный, или общий, порядок реакции. Константа к называется удельной скоростью или константой скорости.
На практике парциальные порядки получают с помощью метода изоляции, согласно которому все реагенты, кроме одного (например, А), берутся в таком большом избытке, что концентрации избыточных реагентов (или реагента) остаются практически постоянными в ходе реакции и поэтому могут быть включены в константу скорости; это дает новую, эффективную константу скорости к:

Тогда говорят, что реакция происходит в условиях псевдо-а-порядка. Существует несколько методов для получения численного значения а. Например, уравнение  представляют в логарифмической форме:
представляют в логарифмической форме:

Построив график зависимости  от
от  получают прямую, тангенс угла наклона которой соответствует а. Точно так же можно найти порядок реакции по всем остальным реагентам, делая каждый из них по очереди тем компонентом, который присутствует в низкой концентрации.
получают прямую, тангенс угла наклона которой соответствует а. Точно так же можно найти порядок реакции по всем остальным реагентам, делая каждый из них по очереди тем компонентом, который присутствует в низкой концентрации.
Посмотрим теперь, какую информацию мы хотели бы получить из экспериментального уравнения скорости. Прежде всего подход к уравнению будет различным в зависимости от целей — должен ли быть оптимизирован процесс или выяснен механизм реакции. Если в первом случае требуется просто найти аналитическую зависимость скорости от концентрации, то во втором случае уравнение скорости должно дать представление о реакции на молекулярном уровне. Это подразумевает выяснение отдельных элементарных стадий или элементарных реакций, которые происходят одновременно и последовательно внутри общей реакции. Элементарные реакции бывают реакциями первого порядка, например внутримолекулярные перегруппировки или реакции разложения, а чаще всего реакциями второго порядка, когда молекулярное взаимодействие между двумя частицами прямо приводит к продукту. Большинство химических реакций можно представить как те или иные комбинации элементарных реакций. Обычно различают следующие простые комбинации: 1) параллельные реакции (конкурирующие, одновременные); 2) последовательные реакции или последовательность реакций; 3) обратимые реакции.
Реакцию, в которой реагент подвергается превращению по двум или нескольким путям независимо и одновременно, называют параллельной, В последовательной реакции продукт, образующийся в одной стадии, является реагентом в другой. Если две стадии реакции противоположного направления происходят с соизмеримой вероятностью, то такую реакцию называют обратимой. Наконец, существуют сложные реакции, сочетающие в себе два или все  названных типа, например последовательно-параллельная реакция. Вопрос заключается в том, возможно ли распознать различные типы реакций с помощью экспериментального уравнения скорости.
названных типа, например последовательно-параллельная реакция. Вопрос заключается в том, возможно ли распознать различные типы реакций с помощью экспериментального уравнения скорости.
Из вышеизложенного можцо заключить, что экспериментальные уравнения скорости типа  могут иметь физический смысл при условии, что парциальные порядки — простые положительные целые числа. Законы скорости реакций первого и второго порядков могут указывать на наличие элементарных процессов, однако это необязательно, поскольку вполне вероятно, что в реакции участвуют также молекулы растворителя. По выражению скорости нельзя сделать вывод о таком участии, так как растворитель обычно присутствует в большом избытке, а, как уже говорилось, в выражение скорости должны входить только те реагенты, концентрации которых меняются в ходе эксперимента. С другой стороны если парциальные порядки представляют собой дробные или отрицательные числа, невозможно сделать однозначных и имеющих физический смысл выводов, за исключением вывода о том, что реакция достаточно сложная. Например,
могут иметь физический смысл при условии, что парциальные порядки — простые положительные целые числа. Законы скорости реакций первого и второго порядков могут указывать на наличие элементарных процессов, однако это необязательно, поскольку вполне вероятно, что в реакции участвуют также молекулы растворителя. По выражению скорости нельзя сделать вывод о таком участии, так как растворитель обычно присутствует в большом избытке, а, как уже говорилось, в выражение скорости должны входить только те реагенты, концентрации которых меняются в ходе эксперимента. С другой стороны если парциальные порядки представляют собой дробные или отрицательные числа, невозможно сделать однозначных и имеющих физический смысл выводов, за исключением вывода о том, что реакция достаточно сложная. Например,
уравнение скорости газофазной реакции водорода с бромом в определенных условиях эксперимента можно записать в виде

Одной из причин получения дробной величины парциальных порядков может быть тот факт, что реакция идет по нескольким путям. Хорошо изученным примером такого случая служит катализируемая кислотой бензидиновая перегруппировка  -диарил гидразинов [132]. Сообщалось, что закон скорости, по которому происходит исчезновение
-диарил гидразинов [132]. Сообщалось, что закон скорости, по которому происходит исчезновение  -гидразотолуола
-гидразотолуола  имеет вид
имеет вид

Однако более подробное исследование показало, что дробный порядок по отношению к иону водорода связан с тем, что  -гидразотолуол перегруппировывается в кислой среде одновременно по двум путям, один из которых соответствует реакции первого порядка, а другой — реакции второго порядка:
-гидразотолуол перегруппировывается в кислой среде одновременно по двум путям, один из которых соответствует реакции первого порядка, а другой — реакции второго порядка:

Поэтому порядок, равный 1,6 в уравнении  является общим, или усредненным, порядком, отражающим относительный вклад каждого из двух путей. Как будет подробнее рассмотрено в разд. 4.7, два члена в правой части уравнения
является общим, или усредненным, порядком, отражающим относительный вклад каждого из двух путей. Как будет подробнее рассмотрено в разд. 4.7, два члена в правой части уравнения  можно связать с внутримолекулярными перегруппировками моно- и дипротонированных частиц соответственно. Этот вывод следует из более детального рассмотрения констант скоростей
можно связать с внутримолекулярными перегруппировками моно- и дипротонированных частиц соответственно. Этот вывод следует из более детального рассмотрения констант скоростей 
Сообщалось также, что дробные порядки появляются в тех случаях, когда фактическая концентрация компонента, фигурирующая в уравнении скорости, отличается от аналитически определяемой концентрации. Например, имеется равновесие между частицами мономера и димера, и при разных скоростях в реакции участвуют либо только одна, либо обе частицы. Время от времени парциальные порядки обнаруживаются по отношению к  в катализируемых кислотами реакциях. Причина заключается в том, что не все водородные ионы принимают участие в реакции. В этом случае вместо концентрации ионов водорода следует использовать функцию кислотности (см., например, [11, 49]).
в катализируемых кислотами реакциях. Причина заключается в том, что не все водородные ионы принимают участие в реакции. В этом случае вместо концентрации ионов водорода следует использовать функцию кислотности (см., например, [11, 49]).
Помимо дробных порядков реакций существуют случаи, когда зависимость скорости от концентрации в начале реакции отличается от зависимости на более поздних стадиях. Для таких случаев введены представления о порядке относительно концентрации («концентрационный» порядок) и порядке относительно времени («временной» порядок).  наконец, известны
наконец, известны
реакции переменного порядка, т.е. реакции, общий порядок которых изменяется в ходе процесса.
Имеются разнообразные типы математических приближений для описания взаимозависимостей переменных. Сравнение уравнений (1-8) и (1-9) показывает, что данные о зависимости концентрации от времени могут быть представлены совершенно различными формами выражений скорости. Некоторые выражения, как, например, (1-9), содержат указания о молекулярном механизме реакции. Это наблюдение позволило нам провести различие между формальной и неформальной кинетикой.
До сих пор мы рассматривали различные моменты, относящиеся к формальной кинетике, характерные признаки которой можно суммировать следующим образом. Формальная кинетика способна дать уравнения скорости, имеющие физический смысл, только для простых случаев, а не для сложных реакций. Дробные порядки оказываются «кажущимися», т.е. формальными, порядками, которые лишены физического смысла и не могут быть однозначно интерпретированы. В тех случаях, когда зависимость скорости от концентрации меняется в ходе реакции, понятие формального порядка реакции вообще неприменимо. Для сложных реакций формальная кинетика ищет прежде всего набор приемлемых для какого-либо механизма стадий реакции. Затем для этого предполагаемого механизма выводится выражение скорости. Далее это соотношение сверяется с экспериментальными данными. Если эти данные не воспроизводятся выражением скорости, процедуру повторяют с другим набором предполагаемых стадий реакции и т.д. Таким образом, когда речь идет о книге по формальной кинетике, то, как правило, имеется в виду книга, содержащая множество выводов формул для постулированных типов реакций, цель которой — помочь вывести формулы для новых типов реакций. Или же, в лучшем случае, в такой книге можно найти готовую схему, пригодную для исследуемой реакции. Однако зачастую экспериментальным данным отвечает несколько мыслимых механизмов, поэтому успешная интерпретация данных основывается не только на эксперименте, но и на интуиции.
Несомненно, что химическая кинетика должна развиваться на базе формальной кинетики, если удается разработать математический аппарат, который дает имеющие физический смысл кинетические уравнения даже для сложных реакций.
В этом и состоит задача неформальной кинетики. В неформальном смысле понятие порядка реакции применимо: а) к реакциям, скорость которых можно выразить уравнением (1-4), где показатели степени — простые положительные целые числа; б) к отдельной стадии сложной реакции (в терминах формального порядка реакции это называется молекулярностью, т.е. числом частиц, вовлеченных в элементарный процесс); в) к лимитирующей стадии реакции в определенных условиях эксперимента.
Здесь следует также заметить, что лишь дифференциальное уравнение скорости, а не интегральная его форма может иметь физический смысл, поскольку последний может передать выражение скорости реакции в дифференциальном уравнении, а не время в интегральном уравнении. Имеющие физический смысл уравнения скорости будут рассмотрены как математические модели реакции.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
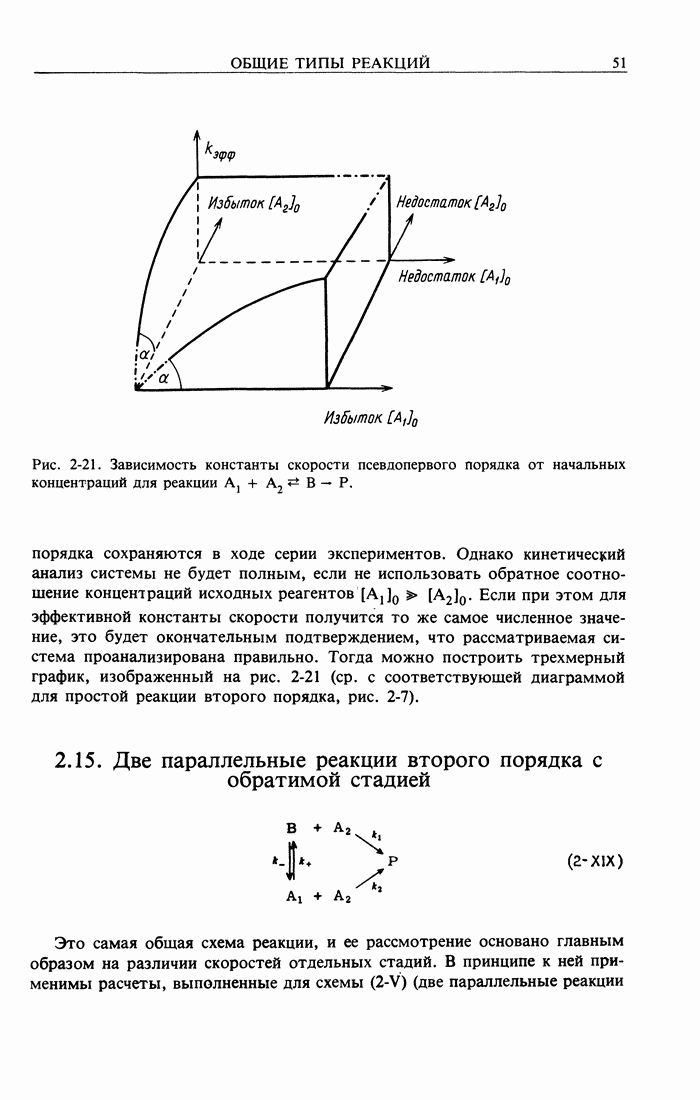
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
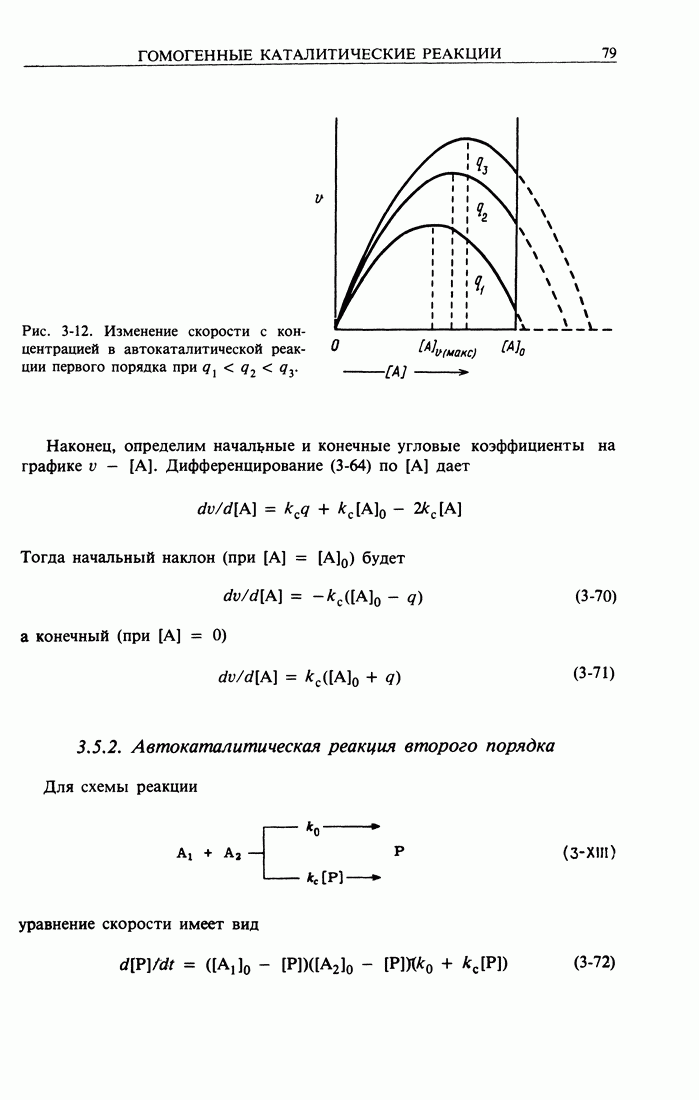
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
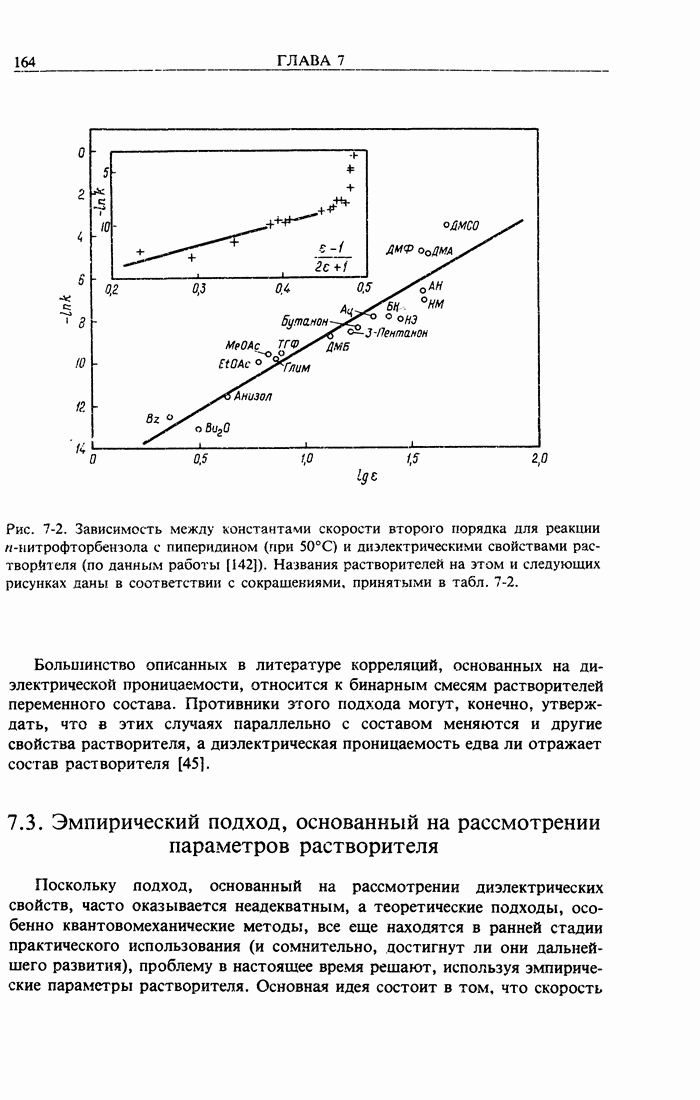
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
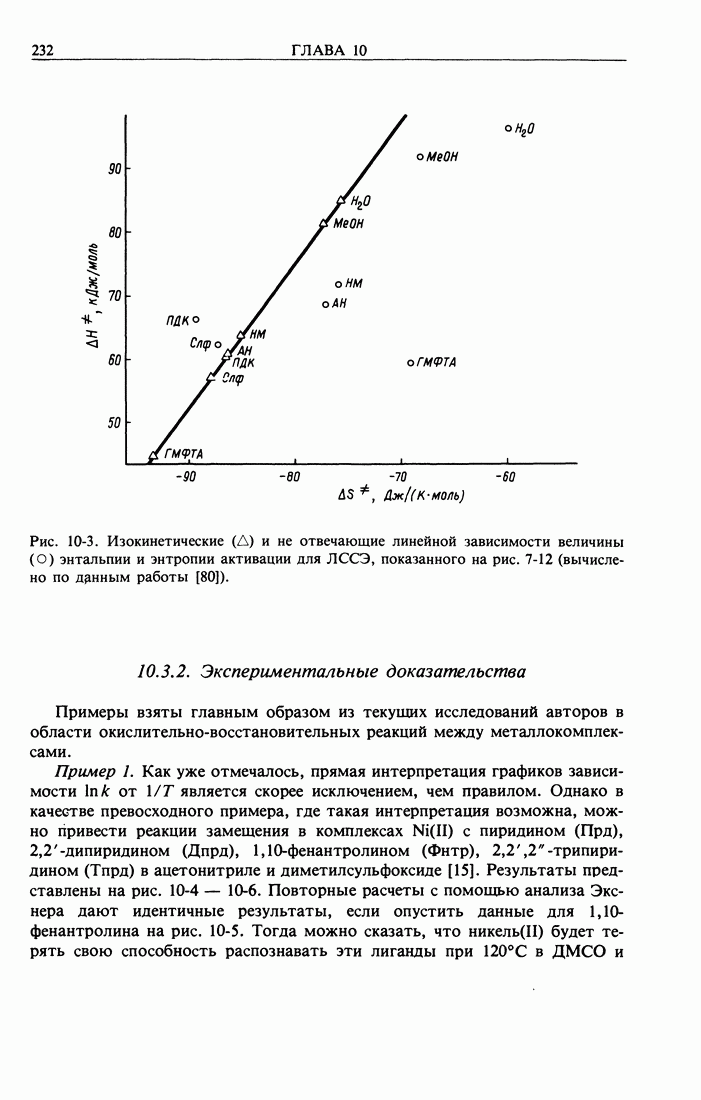
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений