| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.1. Обратимое ингибирование
Тип 1: конкурентное ингибирование. Молекулы ингибитора, которыми могут быть чужеродные частицы I или обычно продукт реакции  и молекулы субстрата
и молекулы субстрата  конкурируют между собой за присоединение к активному центру катализатора.
конкурируют между собой за присоединение к активному центру катализатора.
Тип  ингибитором является чужеродная частица, концентрация которой не зависит от времени:
ингибитором является чужеродная частица, концентрация которой не зависит от времени:

Тогда

Графики зависимостей  от
от  от
от  представляют собой идентичные прямые, тангенсы угла наклона которых увеличиваются с ростом
представляют собой идентичные прямые, тангенсы угла наклона которых увеличиваются с ростом  Все прямые, отвечающие различным концентрациям ингибитора, пересекаются с ординатой в одной точке
Все прямые, отвечающие различным концентрациям ингибитора, пересекаются с ординатой в одной точке  Эти прямые пересекают абсциссу в точках
Эти прямые пересекают абсциссу в точках  (рис. 3-4).
(рис. 3-4).
Тип 1б: ингибитором является продукт реакции:


Рис. 3-4. График Лайнуивера — Берка для конкурентного ингибирования чужеродной частицей I при 
Поскольку  , уравнение (3-33) принимает вид
, уравнение (3-33) принимает вид

Естественно, при  такое ингибирование отсутствует и потому не определяется на графике зависимости
такое ингибирование отсутствует и потому не определяется на графике зависимости  от
от  (тонкая пунктирная линия на рис. 3-5). Наклон графика, построенного в координатах
(тонкая пунктирная линия на рис. 3-5). Наклон графика, построенного в координатах  зависит от
зависит от  так как
так как  Все прямые, каждая из которых отвечает определенной величине
Все прямые, каждая из которых отвечает определенной величине  пересекают ординату в одной точке, положение которой зависит от отношения
пересекают ординату в одной точке, положение которой зависит от отношения  (рис. 3-5). Если
(рис. 3-5). Если  эта точка лежит ниже абсциссы.
эта точка лежит ниже абсциссы.
Тип 2: неконкурентное ингибирование. Катализатор имеет не один, а несколько центров, способных к комплексообразованию. Активный интермедиат сам может присоединиться к молекуле ингибитора, давая неактивный комплекс:

Следовательно,


Рис. 3-5. График Лайнуивера — Берка для конкурентного ингибирования продуктом при 
Тип 2а: ингибитором является чужеродная частица. Тогда

Графики зависимости  от
от  от
от  представляют собой идентичные прямые, которые пересекают ординату в точке
представляют собой идентичные прямые, которые пересекают ординату в точке  а абсциссу в точке —К
а абсциссу в точке —К  Поэтому при использовании различных концентраций ингибитора получаются параллельные прямые.
Поэтому при использовании различных концентраций ингибитора получаются параллельные прямые.
Тип 2б: ингибитором является продукт реакции. Здесь

Нетрудно заметить, что график Лайнуивера-Берка нелинеен, но становится линейным на последних стадиях реакции, т.е. когда практически весь реагент  израсходован. Прямые части графиков для различных величин
израсходован. Прямые части графиков для различных величин  параллельны, их угловой коэффициент равен
параллельны, их угловой коэффициент равен  Как видно из рис. 3-6, это тот же самый угловой коэффициент, что и у зависимости
Как видно из рис. 3-6, это тот же самый угловой коэффициент, что и у зависимости  от
от 
Чисто неконкурентное игибирование наблюдается очень редко, так как сам ингибитор может присоединяться к активному центру катализатора. Это приводит к комбинации конкурентного и неконкурентного ингибирования, так называемому «перекрестному ингибированию».

Рис. 3-6. График Лайнуивера — Берка для неконкурентного ингибирования продуктом при 
Тип 3: перекрестное ингибирование. Этот тип ингибирования, как упоминалось выше, объединяет типы 1 и 2. Различают три ситуации, в которых ингибитором является чужеродная частица, продукт реакции или сам субстрат. Последний случай так и называют «ингибирование субстратом». Тип за: ингибитором является чужеродная частица. Тогда

Таким образом, график Лайнуивера-Берка представляет собой прямую, наклон которой соответствует  эта прямая пересекает ординату в точке
эта прямая пересекает ординату в точке  а абсциссу в точке
а абсциссу в точке  Все прямые, отвечающие разным концентрациям ингибитора, должны пересекаться в одной точке, лежащей либо в третьем, либо в четвертом квадранте в зависимости от отношения
Все прямые, отвечающие разным концентрациям ингибитора, должны пересекаться в одной точке, лежащей либо в третьем, либо в четвертом квадранте в зависимости от отношения  В частном случае, когда константы К равны, точка пересечения находится на абсциссе, отсекая отрезок, равный
В частном случае, когда константы К равны, точка пересечения находится на абсциссе, отсекая отрезок, равный 
Тип 3б: продукт реакции действует как ингибитор. Здесь


Рис. 3-7. График Лайнуивера — Берка для перекрестного ингибирования продуктами при 
Комбинация типов 16 и 26 приводит к такому графику, как на рис. 3-7.
Тип 3в: ингибирование субстратом. Активный интермедиат связывает еще одну молекулу субстрата, что приводит к образованию неактивного комплекса:

В этом случае

С учетом последнего выражения уравнение скорости принимает вид

или, через обратные величины,

Благодаря квадратичному члену в знаменателе уравнения (3-42) кривая скорости может проходить через максимум во время уменьшения  от начального значения до нуля (рис. 3-8,а). Дальнейший ход кривой зависит от того, ложатся ли экспериментальные точки на восходящую ветвь кривой,
от начального значения до нуля (рис. 3-8,а). Дальнейший ход кривой зависит от того, ложатся ли экспериментальные точки на восходящую ветвь кривой,

Рис. 3-8. Ингибирование субстратом. Пунктирная линия в части а относится к реакции без ингибирования субстратом.
как обычно (т.е. слева от пика на рисунке), или на нисходящую. Имеются две возможности построения графика по уравнению (3-43) — зависимость  от
от  или от
или от  Оба графика представляют собой кривые, переходящие в прямую, как показано на рис.
Оба графика представляют собой кривые, переходящие в прямую, как показано на рис.  График зависимости двух обратных величин линеен до тех пор, пока
График зависимости двух обратных величин линеен до тех пор, пока  тогда как график зависимости
тогда как график зависимости  от
от  сохраняет линейность в области, где
сохраняет линейность в области, где 
Приложение. До сих пор мы рассматривали различные типы обратимого ингибирования с помощью дифференциального метода. Однако (3-30) можно свести к стандартному уравнению

которое легко интегрируется, давая

Входящие в это уравнение коэффициенты можно вычислить путем обработки кинетических кривых, полученных в разных сериях экспериментов. В случае когда  уравнение (3-45) преобразуется в уже упоминавшееся уравнение Генри [ср. с (3-21)]
уравнение (3-45) преобразуется в уже упоминавшееся уравнение Генри [ср. с (3-21)]

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
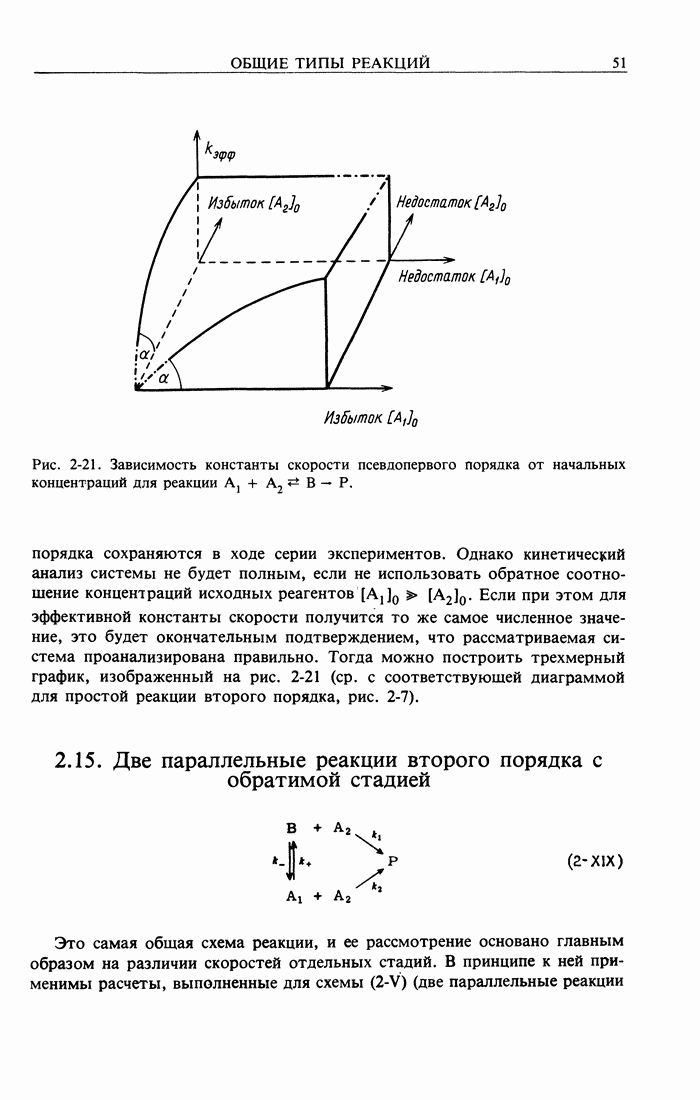
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
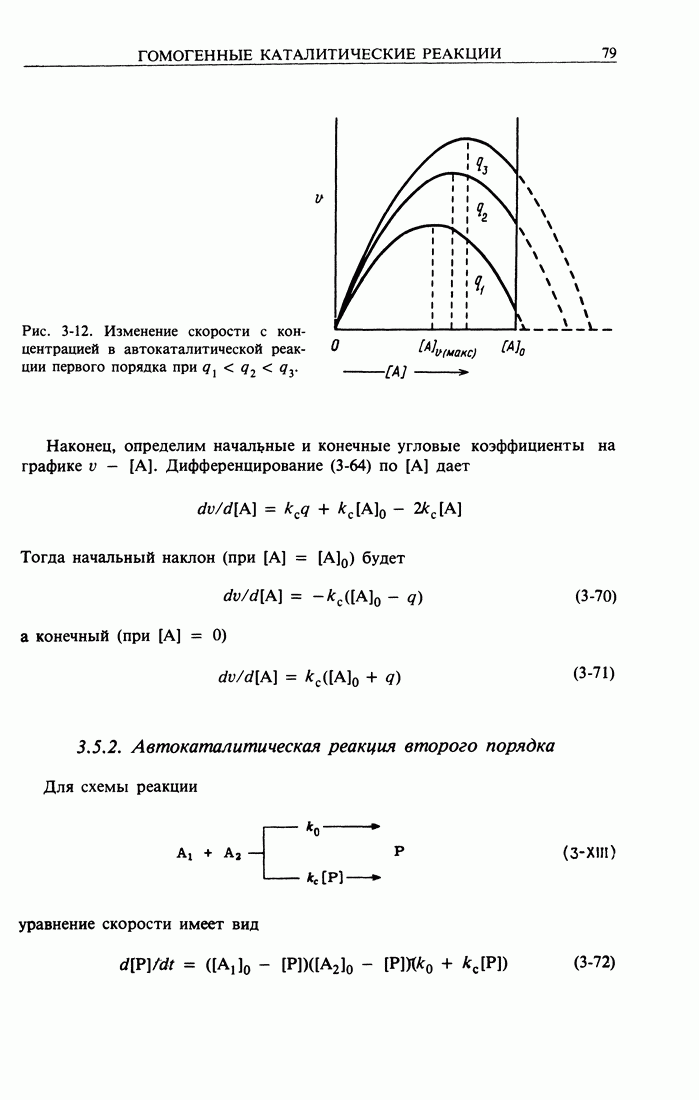
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
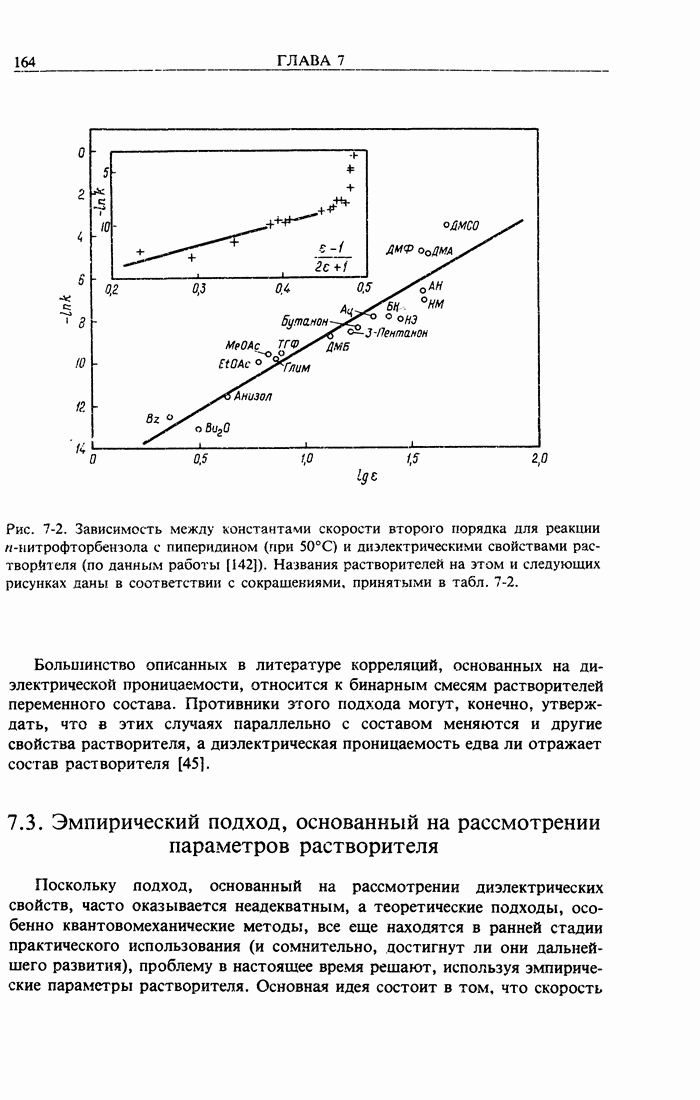
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
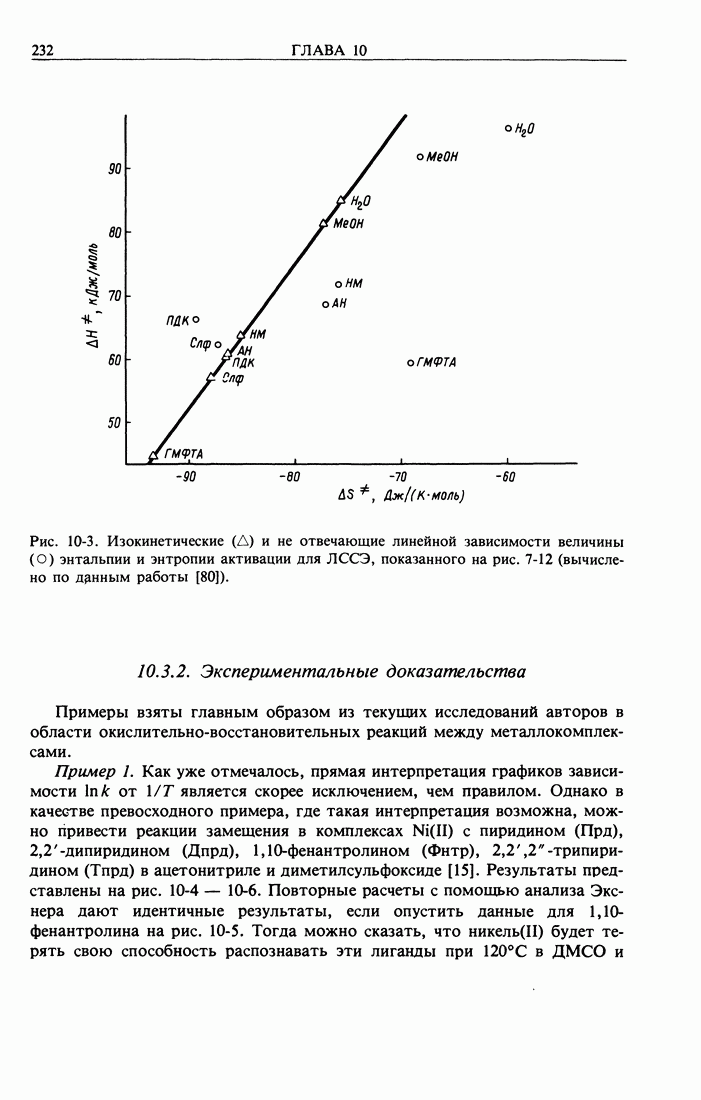
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений