| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
Как хорошо известно, скорость химической реакции обычно резко возрастает с увеличением температуры. Эмпирическое правило, предложенное еще Вант-Гоффрм, гласит, что скорость реакции возрастает в 2—3 раза при повышении температуры на 10 °С. Поскольку в уравнении скорости член, отвечающий концентрации, практически нечувствителен к изменению температуры, особенно для реакций в растворах, температурная зависимость скорости должна сводиться к температурной зависимости константы скорости. Иногда эту зависимость характеризуют температурным коэффициентом  который определяют как возрастание скорости реакции или константы скорости при повышении температуры на
который определяют как возрастание скорости реакции или константы скорости при повышении температуры на  Однако температурный коэффициент сам является функцией температуры.
Однако температурный коэффициент сам является функцией температуры.
5.1. Уравнение Аррениуса
Существует несколько уравнений, пригодных для количественного описания температурной зависимости констант скоростей элементарных реакций. Выведем сначала известное уравнение Аррениуса. Влияние температуры на элементарную реакцию первого порядка

интерпретируется в терминах первичного эндотермического равновесия между А и активированной частицей А, которая затем превращается в продукт:

В частном случае, когда  уравнение скорости, согласно разд. 2.11 (случай 2), имеет вид
уравнение скорости, согласно разд. 2.11 (случай 2), имеет вид

Подстрочный индекс  для константы равновесия указывает, что это концентрационная константа. Подстановка
для константы равновесия указывает, что это концентрационная константа. Подстановка  в
в  дает выражение
дает выражение

которое логарифмируют и дифференцируют по температуре (считая, что  не зависит от температуры):
не зависит от температуры):

Применяя изохору Вант-Гоффа, т.е. соотношение между константой равновесия и температурой, получают уравнение

где  количество энергии, требующееся для образования А из А, называемое аррениусовской энергией активации. Интегрирование
количество энергии, требующееся для образования А из А, называемое аррениусовской энергией активации. Интегрирование  приводит к уравнению Аррениуса
приводит к уравнению Аррениуса

или, в экспоненциальной форме,

где А — константа, называемая частотным фактором, предэкспоненциальным множителем или аррениусовским множителем. Если построить зависимость А: от  в аррениусовских координатах, т.е.
в аррениусовских координатах, т.е.  то получится прямая с отрицательным наклоном, равным
то получится прямая с отрицательным наклоном, равным  отсекающая от оси отрезок, равный
отсекающая от оси отрезок, равный  Однако на практике А таким путем не определяют, поскольку экстраполяция к бесконечной температуре слишком долгая для того, чтобы получить точную величину. Поэтому А вычисляют по известному значению
Однако на практике А таким путем не определяют, поскольку экстраполяция к бесконечной температуре слишком долгая для того, чтобы получить точную величину. Поэтому А вычисляют по известному значению  и наборам значений
и наборам значений  подставляя их в уравнение
подставляя их в уравнение 
Хотя для объяснения температурной зависимости скорости реакции разработано несколько более совершенных теорий (см., например, [73, 92]), при выяснении механизмов реакций первостепенный интерес представляют аррениусовский график и его физическая интерпретация. Прежде всего важно выяснить, линейный это график или нелинейный. Далее, определенную информацию о рассматриваемой реакции могут дать аррениусовские параметры  Начнем со второго вопроса и выясним физический смысл этих параметров. С этой целью используются две основные теории — теория активированного комплекса и теория столкновений.
Начнем со второго вопроса и выясним физический смысл этих параметров. С этой целью используются две основные теории — теория активированного комплекса и теория столкновений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
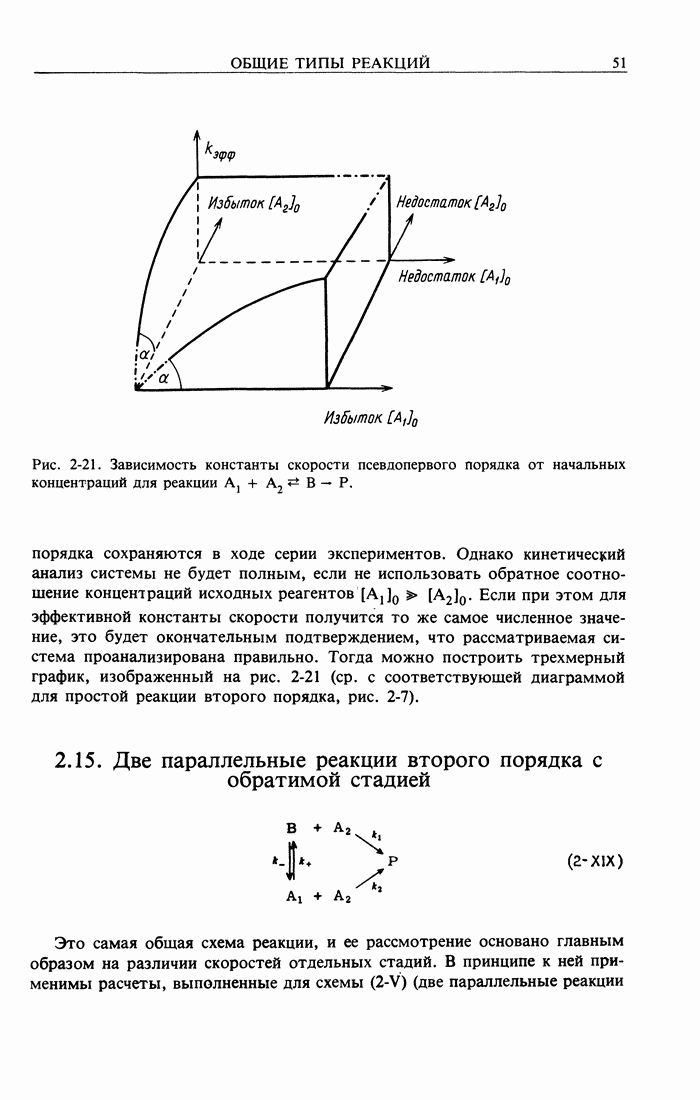
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
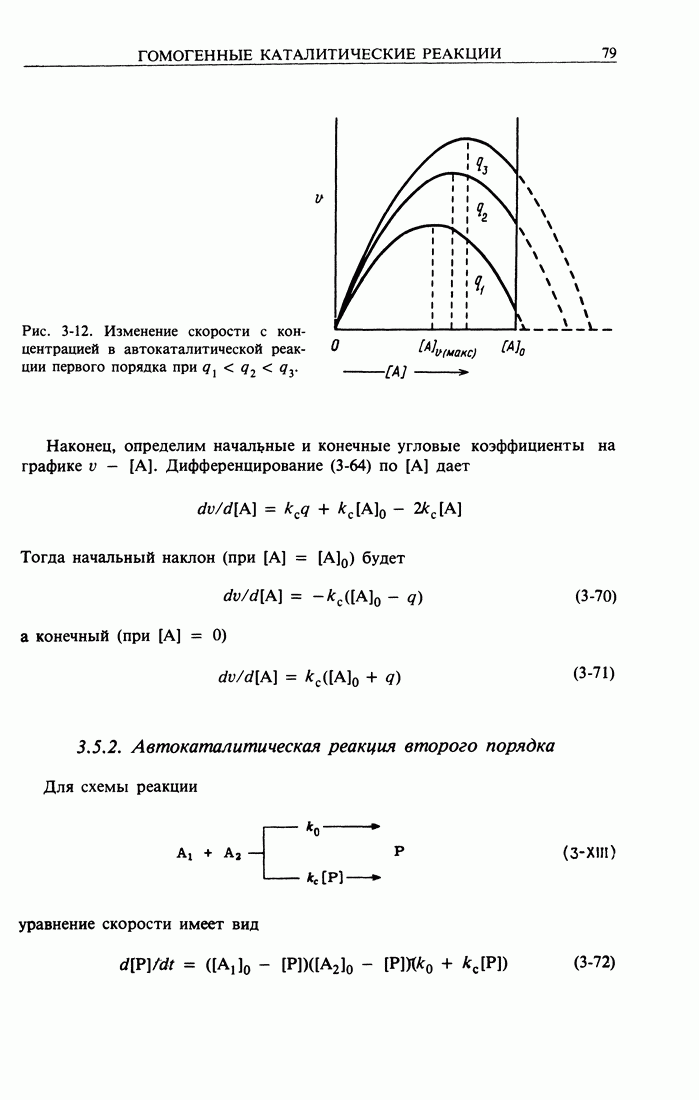
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
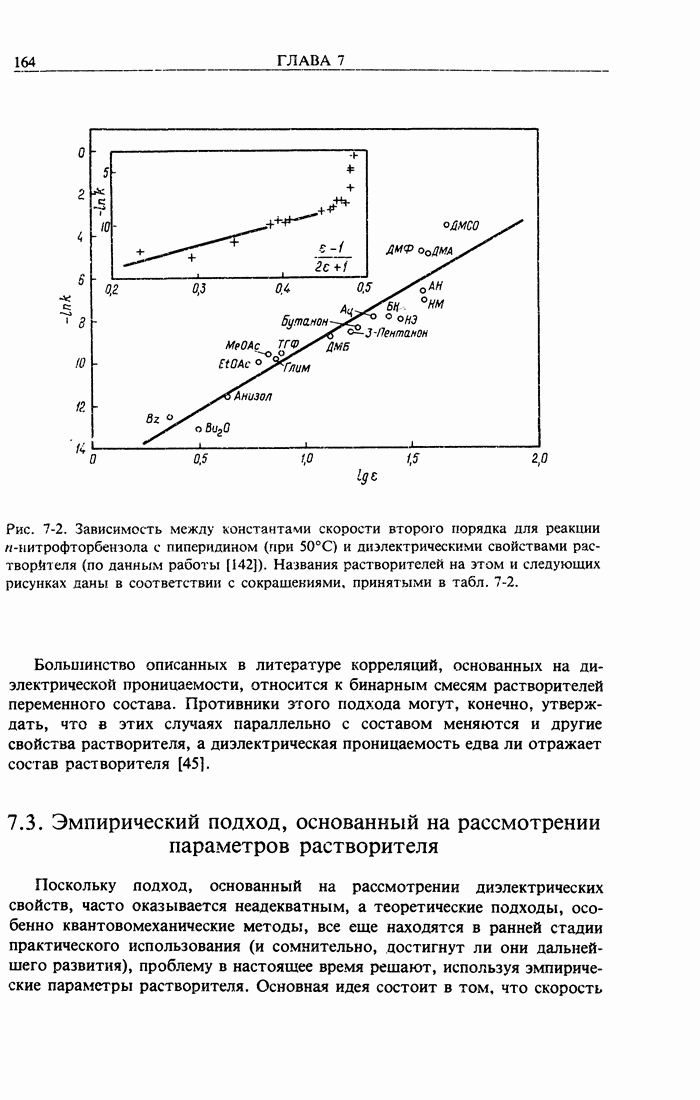
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
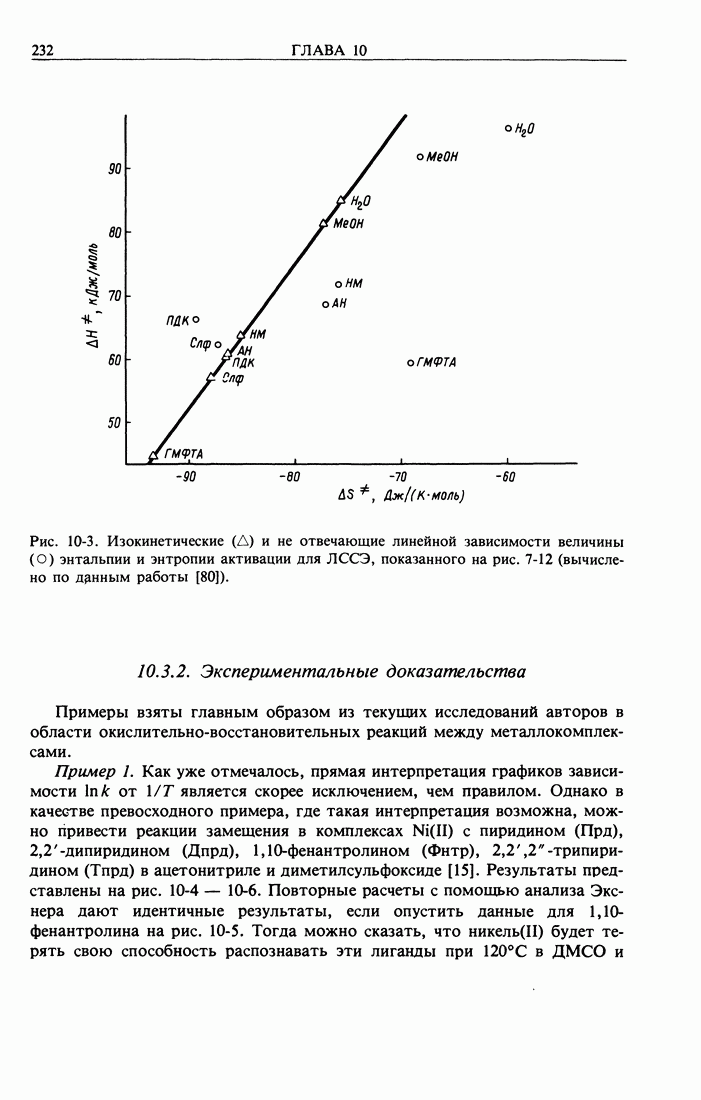
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений