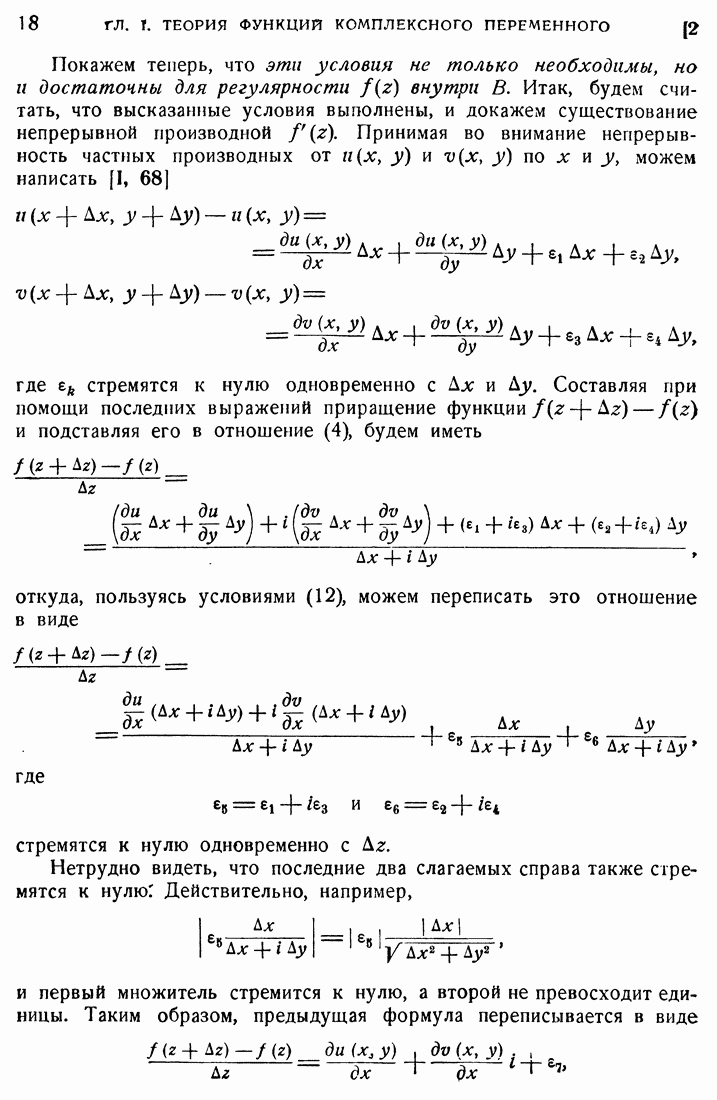| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Теорема Коши.
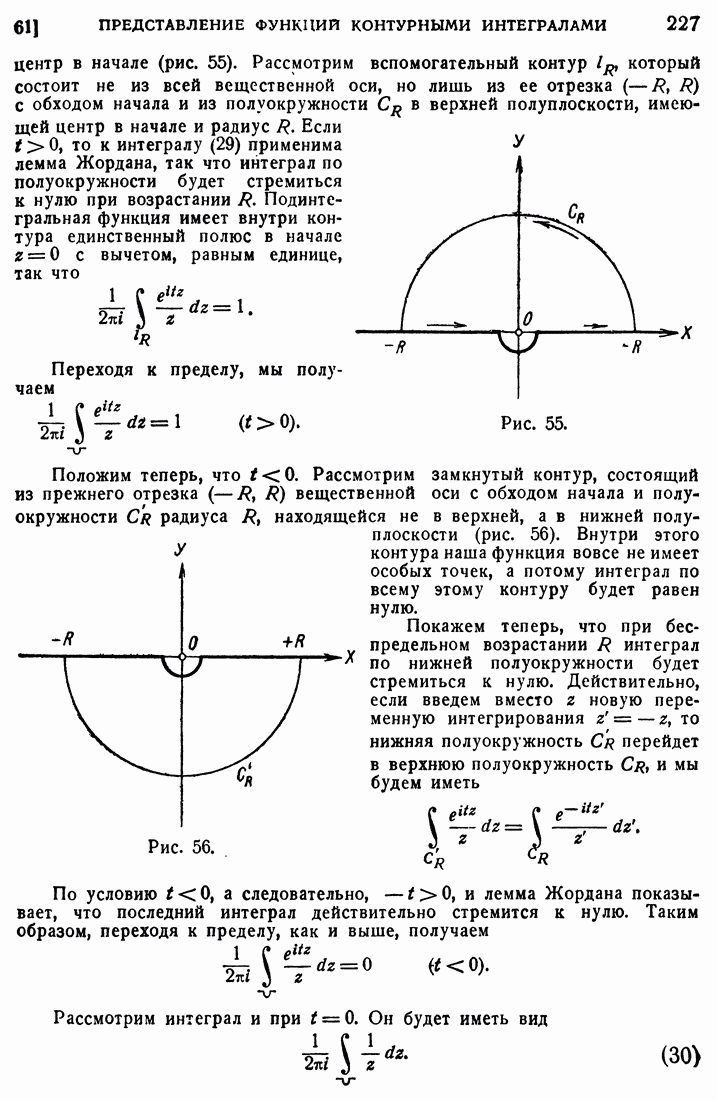
В дальнейшем мы постоянно будем иметь дело с функциями, регулярными в некоторых областях. Границей области может быть весьма сложное множество. Мы в дальнейшем будем предполагать, если не оговорено особо, что граница области состоит из одной или нескольких простых замкнутых кривых, гладких или кусочно гладких [4]. Определим точно понятие простой замкнутой кривой. Пусть замкнутой кривой I соответствует параметрическое представление  при котором параметр t меняется на промежутке
при котором параметр t меняется на промежутке  причем
причем  Кривая называется простой, если ни для какой пары различных значений
Кривая называется простой, если ни для какой пары различных значений  (кроме концов
(кроме концов  ) точки
) точки  и
и  не совпадают. В некоторых случаях, которые будут оговариваться особо, замкнутая кривая может вырождаться в точку. Например, если область есть круг
не совпадают. В некоторых случаях, которые будут оговариваться особо, замкнутая кривая может вырождаться в точку. Например, если область есть круг  с исключенной точкой
с исключенной точкой  граница состоит из окружности
граница состоит из окружности  и точки
и точки 
Поставим теперь основной вопрос о том, при каких условиях контурный интеграл (16) не зависит от пути. Для этого, очевидно, необходимо и достаточно, чтобы оба криволинейных интеграла, стоящих в правой части и дающих вещественную и мнимую части контурного интеграла, не зависели от пути. Применяя указанный в [II, 74] критерий независимости криволинейного интеграла от пути, приходим к уравнениям

а это суть в точности условия (12) из [2]. Итак, окончательно, условие независимости контурного интеграла от пути совпадает с условием регулярности f(z). Это является основным фактом интегрального исчисления теории функций комплексного переменного.
Отметим, что при выводе условий независимости криволинейного интеграла от пути мы пользовались формулой

При выводе этой формулы мы предполагали непрерывность не только самих функций  но и их частных производных, поскольку они входят под знак двойного интеграла. В данном случае это будет иметь место, так как для регулярной функции
но и их частных производных, поскольку они входят под знак двойного интеграла. В данном случае это будет иметь место, так как для регулярной функции  функции и
функции и  имеют непрерывные частные производные первого порядка. В дальнейшем мы будем применять интегрирование и по самому контуру области В. Это будет вполне законным, если предположить, что
имеют непрерывные частные производные первого порядка. В дальнейшем мы будем применять интегрирование и по самому контуру области В. Это будет вполне законным, если предположить, что  регулярна в замкнутой области В. Мы понимаем под этим, что
регулярна в замкнутой области В. Мы понимаем под этим, что  регулярна в несколько более широкой области, содержащей область В вместе с ее контуром внутри себя, т. е.
регулярна в несколько более широкой области, содержащей область В вместе с ее контуром внутри себя, т. е.  называется регулярной в замкнутой области В, если она регулярна внутри некоторой области, содержащей В вместе с ее контуром внутри себя.
называется регулярной в замкнутой области В, если она регулярна внутри некоторой области, содержащей В вместе с ее контуром внутри себя.
Для более подробного исследования вопроса необходимо принять во внимание вид области, в которой функция  регулярна, а именно существенную роль играет здесь, так же как и при исследовании вещественных контурных интегралов, то обстоятельство, является ли область односвязной или многосвязной. Напомним относящиеся сюда основные определения и сформулируем результаты, которые совершенно аналогичны соответствующим результатам для вещественных контурных интегралов
регулярна, а именно существенную роль играет здесь, так же как и при исследовании вещественных контурных интегралов, то обстоятельство, является ли область односвязной или многосвязной. Напомним относящиеся сюда основные определения и сформулируем результаты, которые совершенно аналогичны соответствующим результатам для вещественных контурных интегралов 
Если ограниченная область плоскости z имеет контуром одну замкнутую кривую (иначе говоря, область не имеет дыр), то область называется односвязной.
Если при этом  регулярная функция в такой области и
регулярная функция в такой области и  некоторая точка этой области, то интеграл
некоторая точка этой области, то интеграл

{через  обозначена переменная интегрирования), взятый по любой кривой внутри этой области, не зависит от пути и дает однозначную функцию своего верхнего предела z. При этом, конечно, величина интеграла по любому замкнутому контуру внутри области будет равна нулю. Если наша функция
обозначена переменная интегрирования), взятый по любой кривой внутри этой области, не зависит от пути и дает однозначную функцию своего верхнего предела z. При этом, конечно, величина интеграла по любому замкнутому контуру внутри области будет равна нулю. Если наша функция  регулярна в замкнутой области, то мы можем интегрировать и по самому контуру области
регулярна в замкнутой области, то мы можем интегрировать и по самому контуру области  и результатом интегрирования будет нуль.
и результатом интегрирования будет нуль.
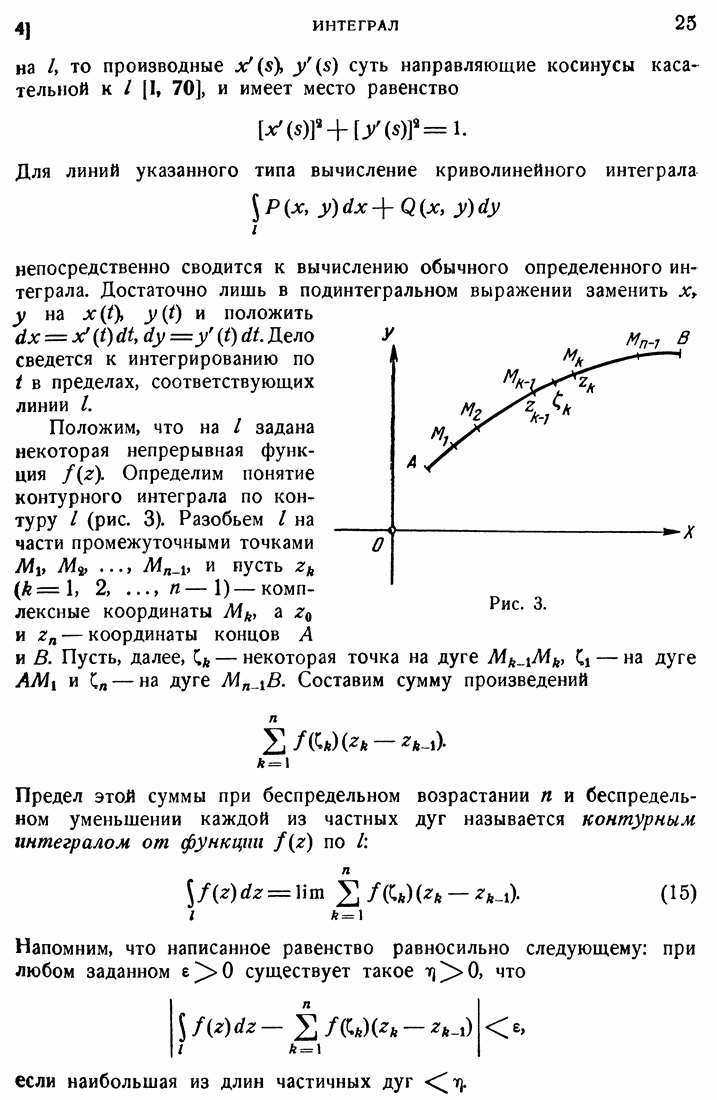
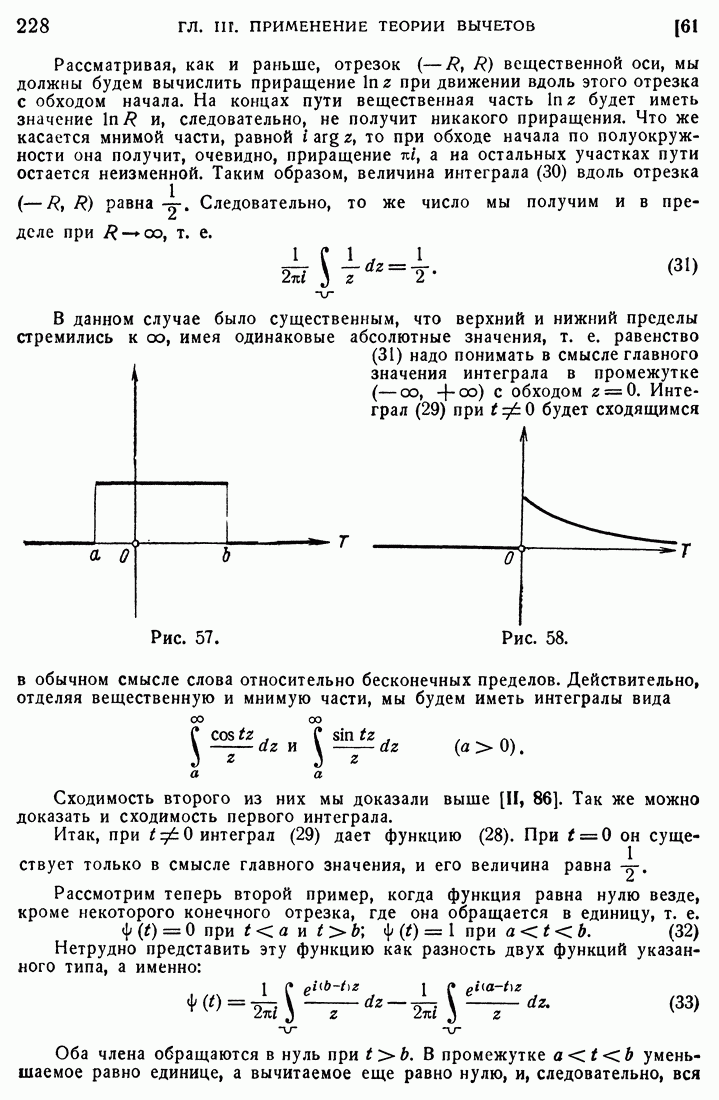
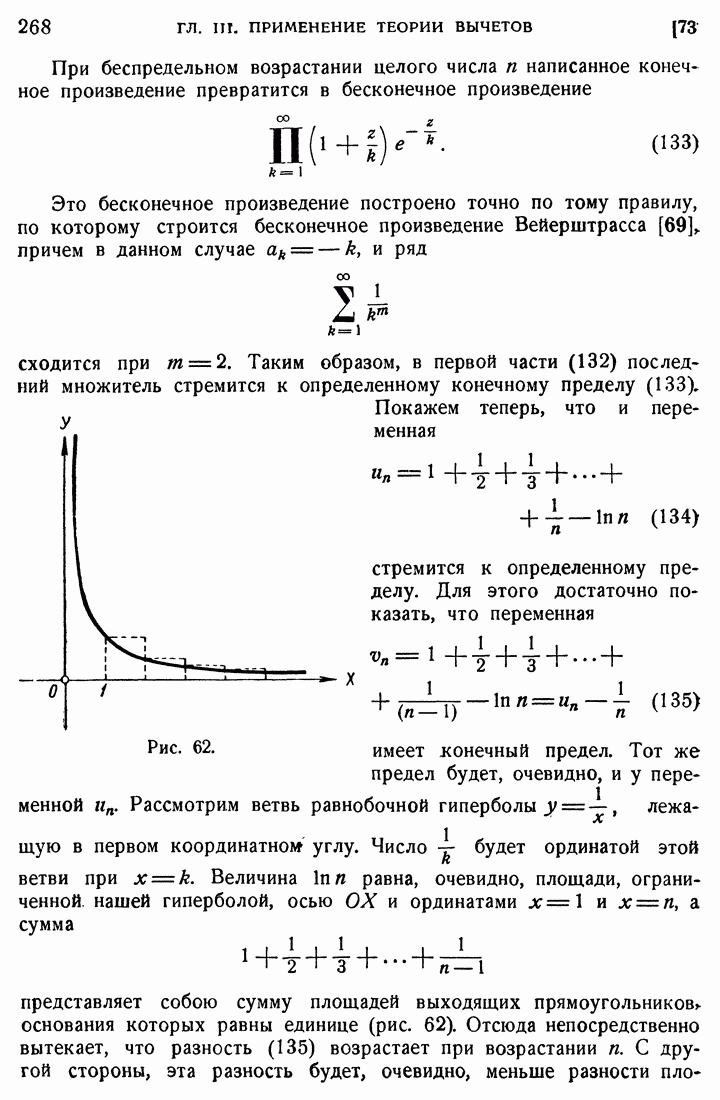
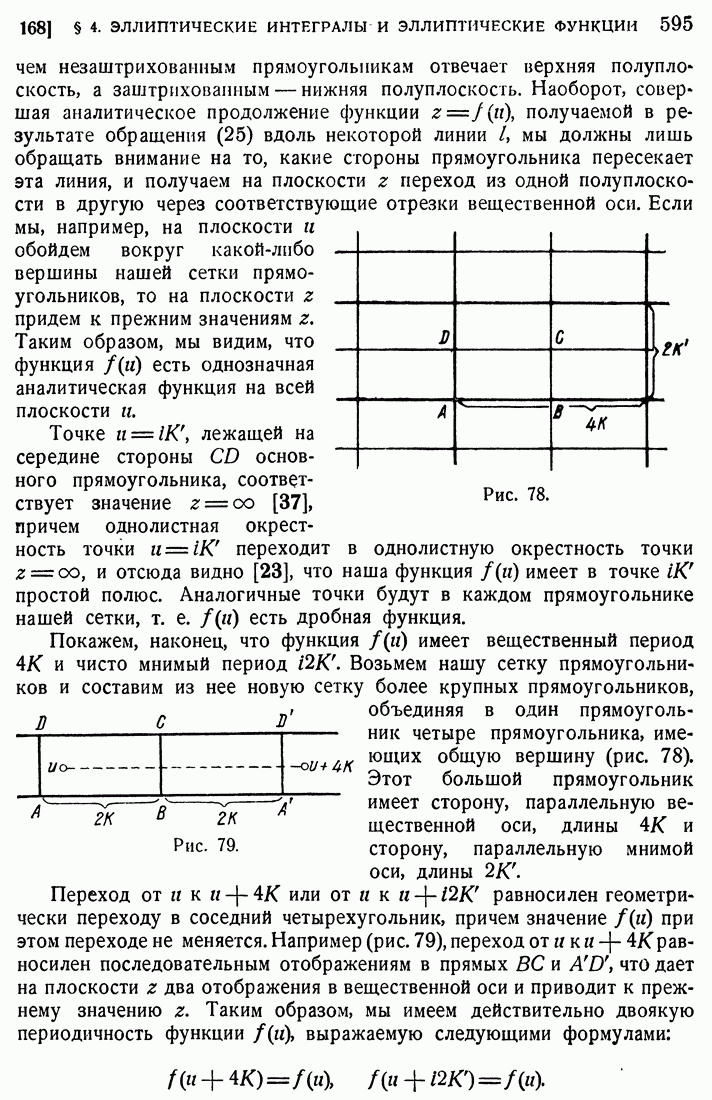
Положим теперь, что наша область В многосвязна и ограничена одним замкнутым внешним контуром и несколькими замкнутыми внутренними контурами. Положим для определенности, что имеется лишь один внутренний контур [область двусвязна (рис. 4)].
Проведем в нашей области разрез X, соединяющий внешний контур с внутренним.

Рис. 4.
Таким образом разрезанная область  будет уже односвязной, и выражение (20) будет давать однозначную функцию от
будет уже односвязной, и выражение (20) будет давать однозначную функцию от  в
в 
Если предположить, что  регулярна в замкнутой области, то можно интегрировать и по самому контуру области. Мы можем при этом утверждать, что интеграл по всему контуру односвязной области
регулярна в замкнутой области, то можно интегрировать и по самому контуру области. Мы можем при этом утверждать, что интеграл по всему контуру односвязной области  должен равняться нулю. При этом, как указано на рисунке, нам придется интегрировать по внешнему контуру против часовой стрелки, по внутреннему контуру — по часовой стрелке и по разрезу X — два раза в противоположных направлениях. Интегралы по разрезу взаимно уничтожатся, и мы будем, следовательно, иметь
должен равняться нулю. При этом, как указано на рисунке, нам придется интегрировать по внешнему контуру против часовой стрелки, по внутреннему контуру — по часовой стрелке и по разрезу X — два раза в противоположных направлениях. Интегралы по разрезу взаимно уничтожатся, и мы будем, следовательно, иметь

где  внешний контур, — внутренний и стрелками обозначено направление интегрирования. Как непосредственно следует из чертежа, это направление для обоих контуров можно определить из одного и того же условия, а именно из того условия, что при обходе контура область остается слева. Такое направление назовем положительным относительно области. Пользуясь равенством (21), можем сказать, что и для случая многосвязной области интеграл по контуру будет равняться нулю, если интегрировать везде в положительном относительно области направлении.
внешний контур, — внутренний и стрелками обозначено направление интегрирования. Как непосредственно следует из чертежа, это направление для обоих контуров можно определить из одного и того же условия, а именно из того условия, что при обходе контура область остается слева. Такое направление назовем положительным относительно области. Пользуясь равенством (21), можем сказать, что и для случая многосвязной области интеграл по контуру будет равняться нулю, если интегрировать везде в положительном относительно области направлении.
Если изменить направление интегрирования по внутреннему контуру, то вместо формулы (21) мы можем написать

т. е. интеграл по внешнему контуру равен сумме интегралов по внутренним контурам (здесь только один), если согласиться интегрировать по всем контурам против часовой стрелки.
Полученные нами результаты составляют основную для теории функций комплексного переменного теорему, которая называется обычно теоремой Коши. Мы ее формулируем несколькими различными способами.
Теорема Коши I. Если функция регулярна в замкнутой односвязной области, то интеграл от нее по контуру этой области равен нулю.
Теорема Коши II. Если функция регулярна в замкнутой многосвязной области, то интеграл от нее по всему контуру этой области в положительном направлении равен нулю.
Теорема Коши III. Если функция регулярна в замкнутой многосвязной области, то интеграл от нее по внешнему контуру равен сумме интегралов по всем внутренним контурам при условии, что интегрирование по всем контурам производится против часовой стрелки.
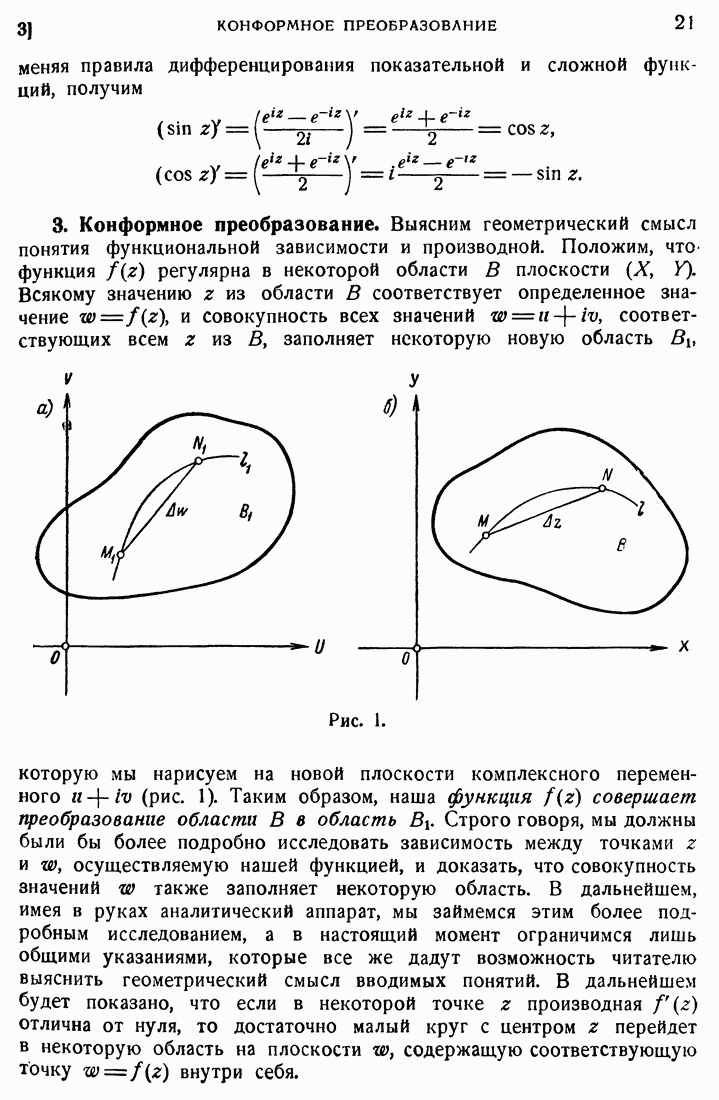
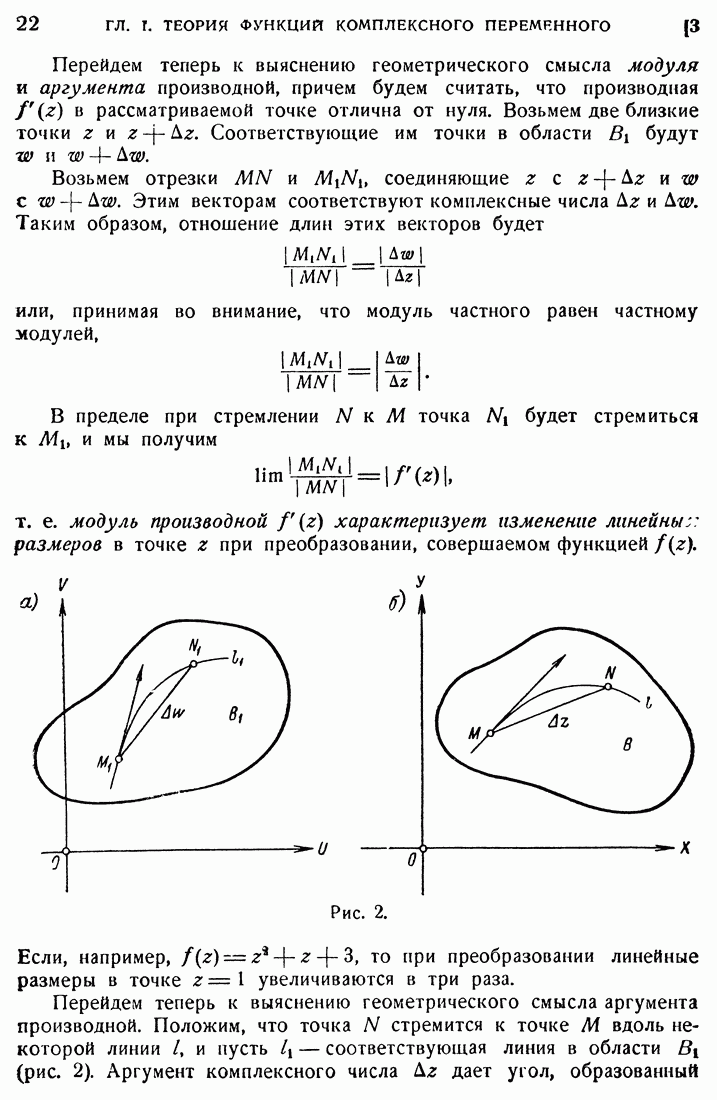
Выясним одно практически важное следствие теоремы Коши. Пусть два разных контура  имеют одни и те же концы А и В. Положим, что V можно непрерывной деформацией перевести в не покидая области, где
имеют одни и те же концы А и В. Положим, что V можно непрерывной деформацией перевести в не покидая области, где  регулярна, и сохраняя неизменными концы А и В. Из теоремы Коши непосредственно вытекает, что при этом величина интеграла от
регулярна, и сохраняя неизменными концы А и В. Из теоремы Коши непосредственно вытекает, что при этом величина интеграла от  не будет меняться, т. е. если некоторый контур при закрепленных концах непрерывно деформируется и при этом не выходит из области регулярности функции
не будет меняться, т. е. если некоторый контур при закрепленных концах непрерывно деформируется и при этом не выходит из области регулярности функции  то при такой деформации величина интеграла от функции
то при такой деформации величина интеграла от функции  по контуру не меняется. То же самое имеет место и при деформировании замкнутого контура, если при этом он все время остается замкнутым.
по контуру не меняется. То же самое имеет место и при деформировании замкнутого контура, если при этом он все время остается замкнутым.
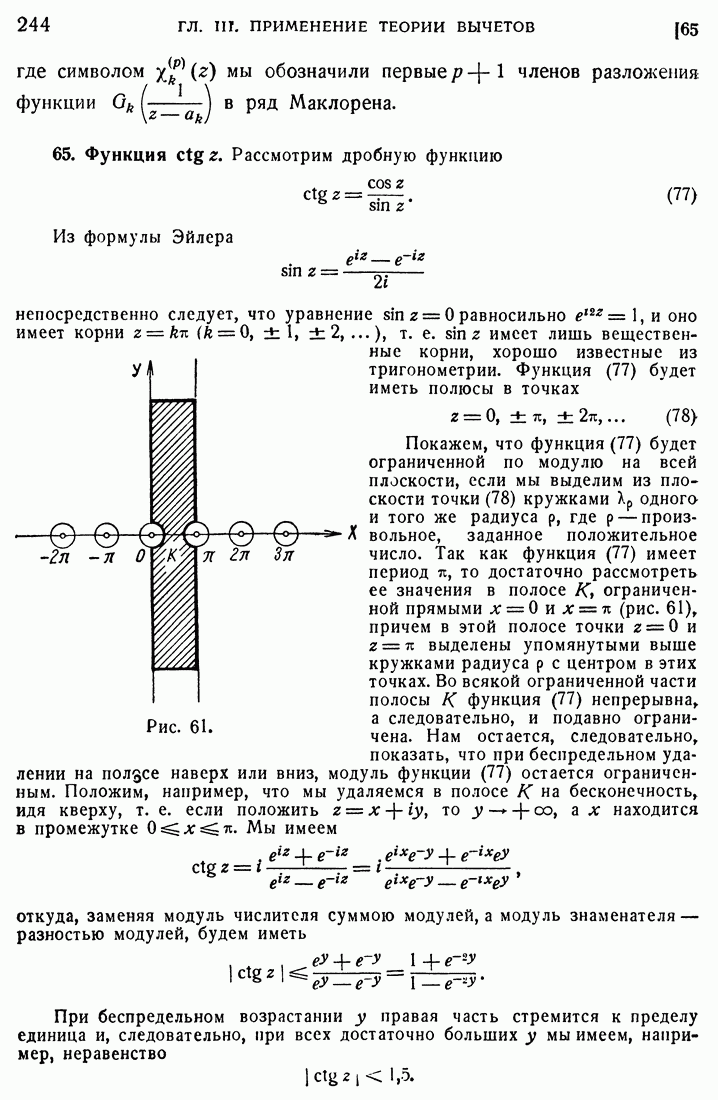
В заключение сделаем одно замечание, имеющее принципиальное значение. При выводе теоремы Коши мы пользовались, как указывалось, не только существованием, но и непрерывностью производной  Эта непрерывность входит в определение регулярной функции. Применяя другой метод доказательства, можно доказать теорему Коши, пользуясь только существованием
Эта непрерывность входит в определение регулярной функции. Применяя другой метод доказательства, можно доказать теорему Коши, пользуясь только существованием  но не ее непрерывностью. Но в дальнейшем мы увидим, что из теоремы Коши вытекает, что
но не ее непрерывностью. Но в дальнейшем мы увидим, что из теоремы Коши вытекает, что  имеет производные всех порядков, откуда сразу следует, что
имеет производные всех порядков, откуда сразу следует, что  непрерывна.
непрерывна.
Таким образом, второе доказательство теоремы Коши, которое мы не приводим, имеет то принципиально важное значение, что оно не пользуется непрерывностью  но из него, как следствие, вытекает, что из наличия производной
но из него, как следствие, вытекает, что из наличия производной  следует и ее непрерывность.
следует и ее непрерывность.
В дальнейшем, если не будет оговорено особо, мы будем всегда считать, что при интегрировании по замкнутому контуру направление обхода берется против часовой стрелки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- 1. Функции комплексного переменного.
- 2. Производная.
- 3. Конформное преобразование.
- 4. Интеграл.
- 5. Теорема Коши.
- 6. Основная формула интегрального исчисления.
- 7. Формула Коши.
- 8. Интегралы типа Коши.
- 9. Следствия формулы Коши.
- 10. Изолированные особые точки.
- 11. Бесконечные ряды с комплексными членами.
- 12. Теорема Вейерштрасса.
- 13. Степенные ряды.
- 14. Ряд Тейлора.
- 15. Ряд Лорана.
- 16. Примеры.
- 17. Изолированные особые точки. Бесконечно далекая точка.
- 18. Аналитическое продолжение.
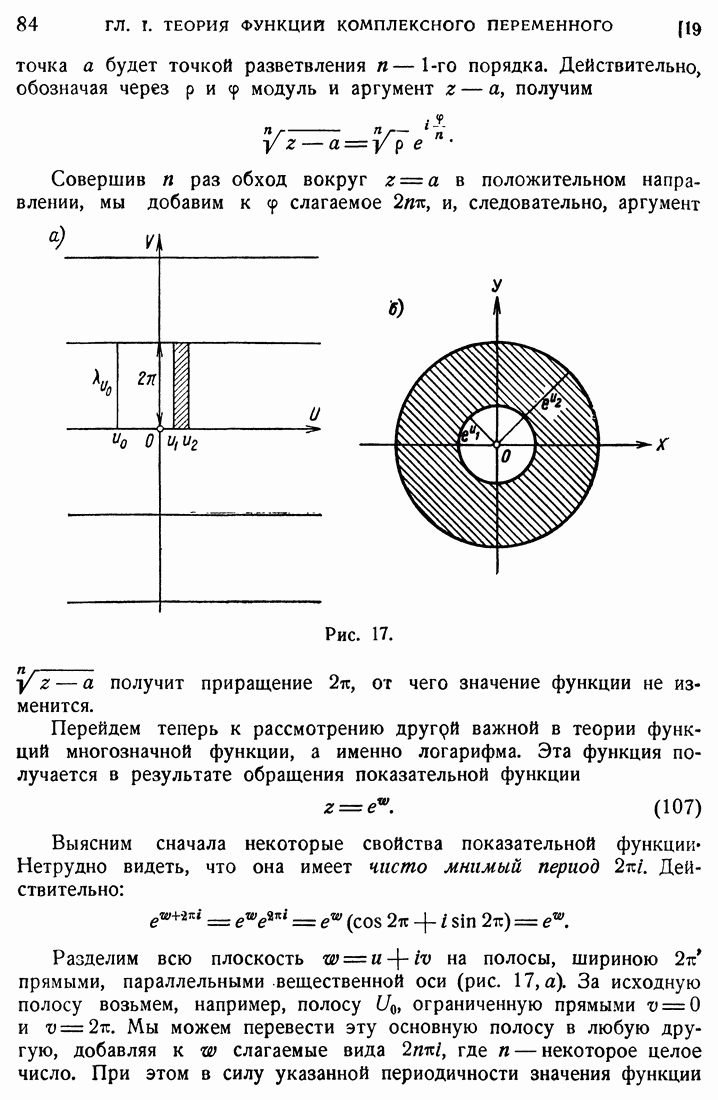
- 19. Примеры многозначных функций.
- 20. Особые точки аналитических функций и римановы поверхности.
- 21. Теорема вычетов.
- 22. Теоремы о числе корней.
- 23. Обращение степенного ряда.
- 24. Принцип симметрии.
- 25. Ряд Тейлора на окружности круга сходимости.
- 26. Дополнительные сведения о формуле Коши.
- 27. Главное значение интеграла.
- 28. Главное значение интеграла (продолжение).
- 29. Интегралы типа Коши.
- 30. Интегралы типа Коши (продолжение).
- ГЛАВА II. КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ И ПЛОСКОЕ ПОЛЕ
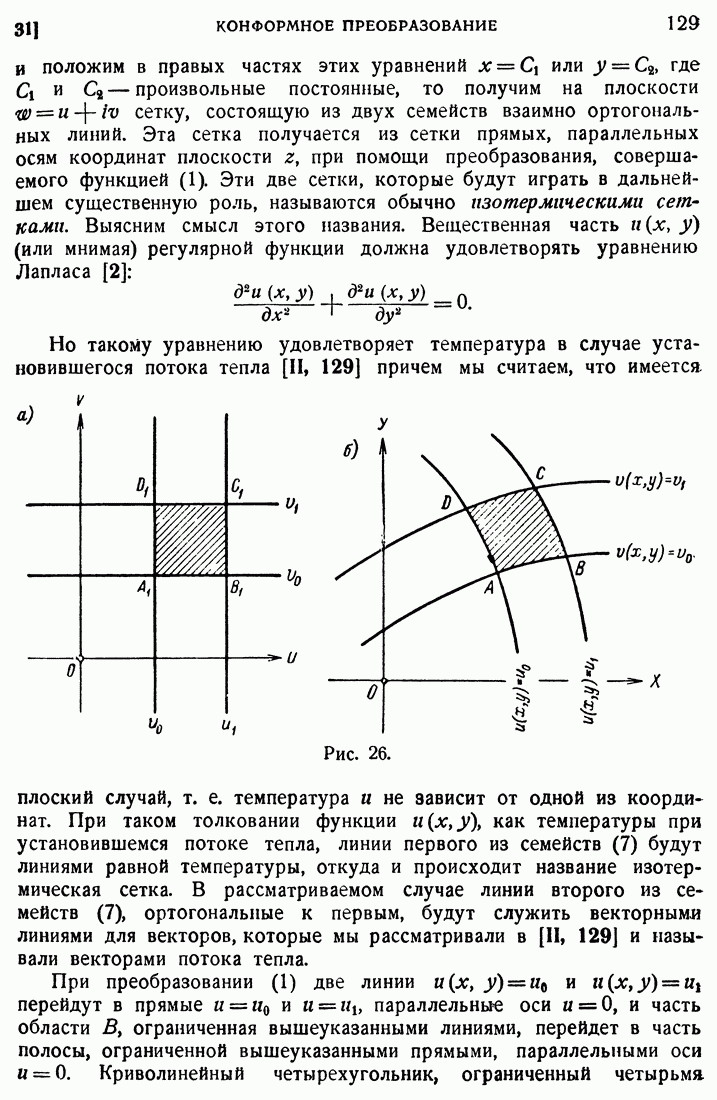
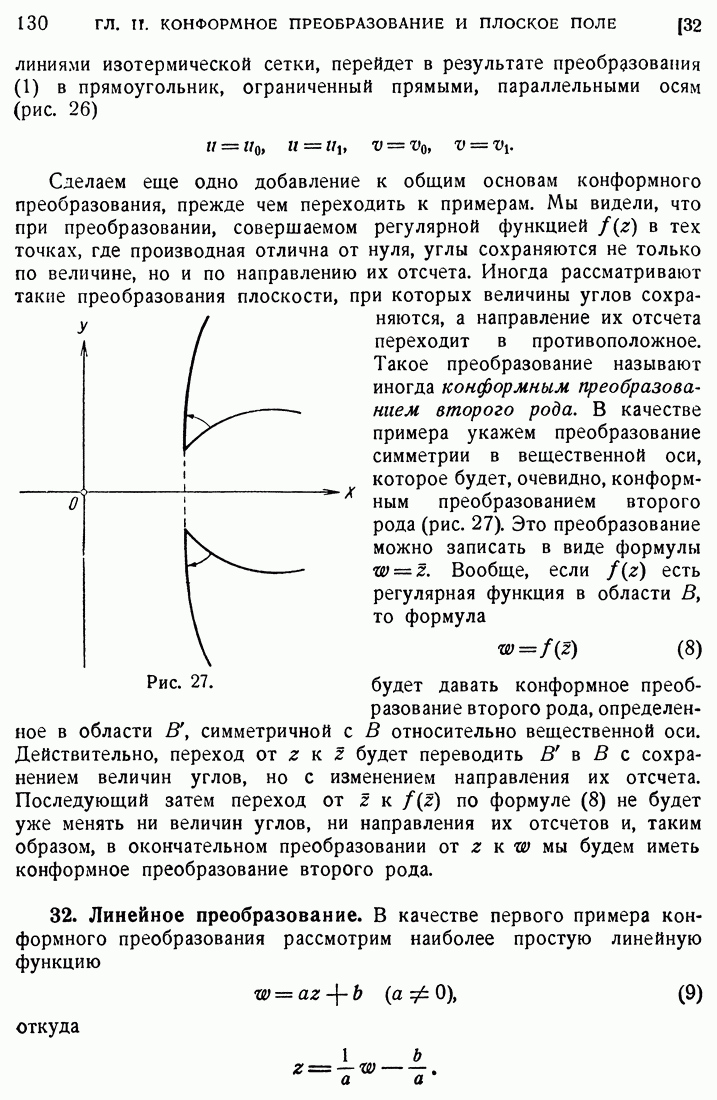
- 31. Конформное преобразование.
- 32. Линейное преобразование.
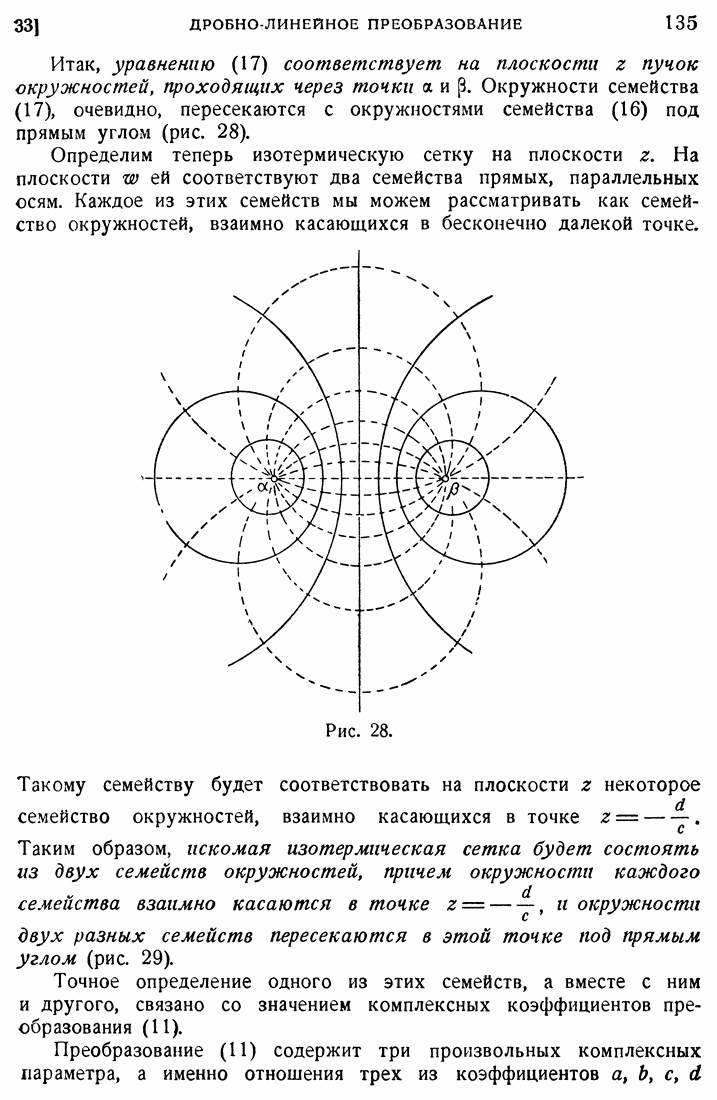
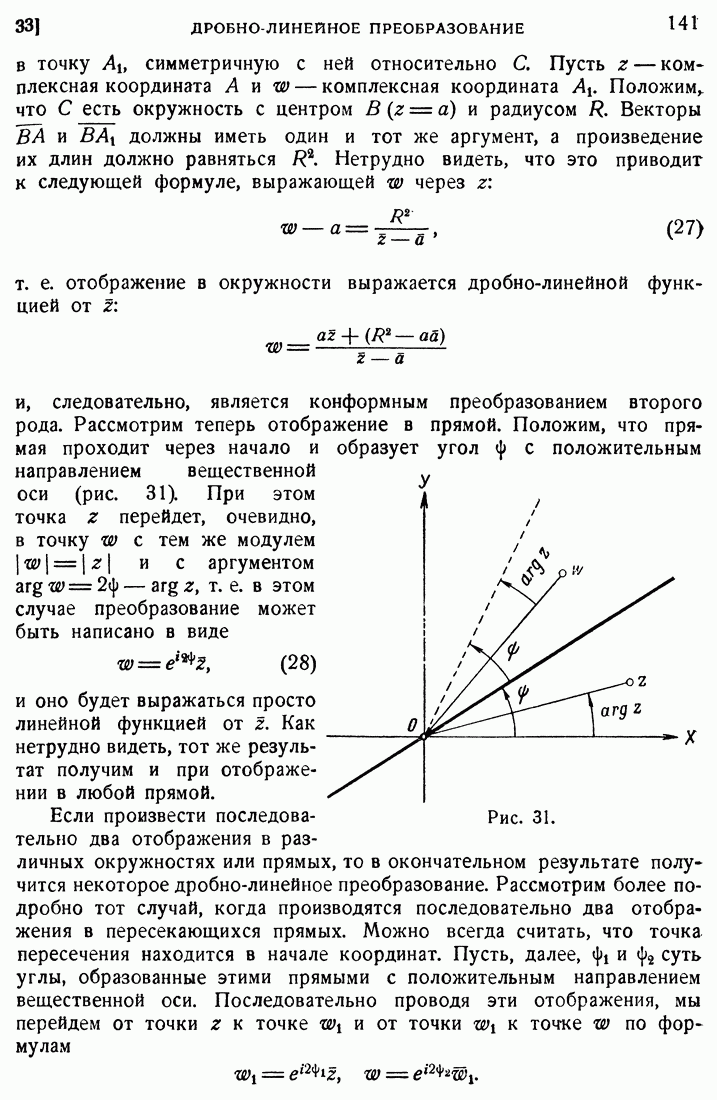
- 33. Дробно-линейное преобразование.
- 34. Функция w = z^2.
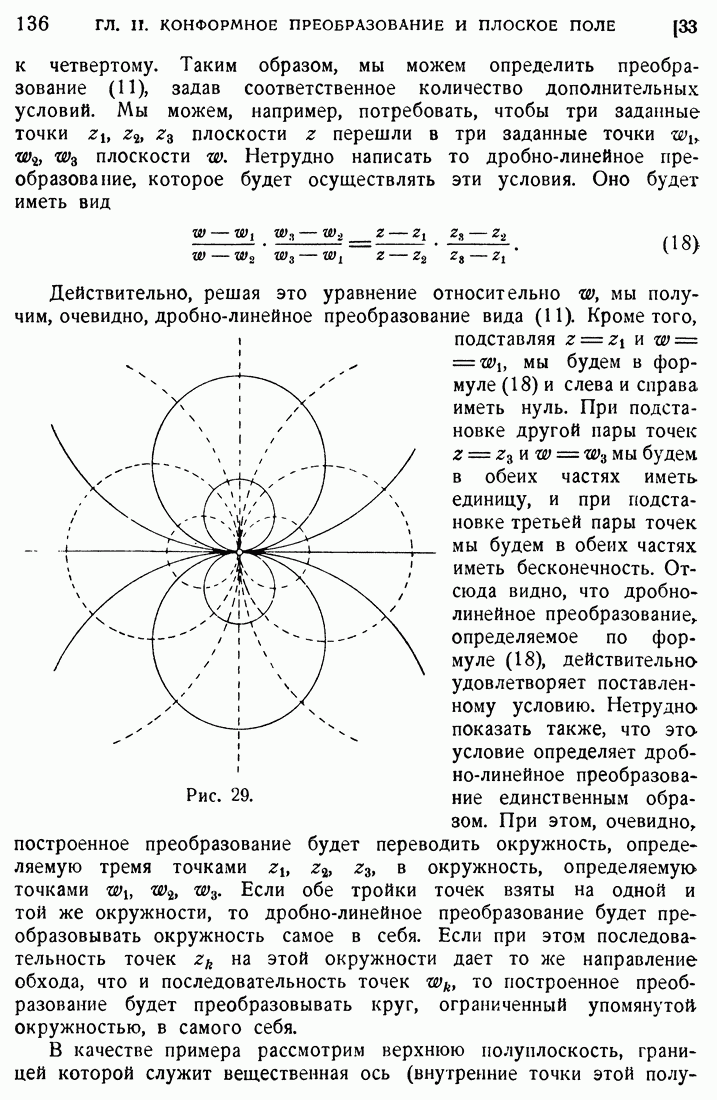
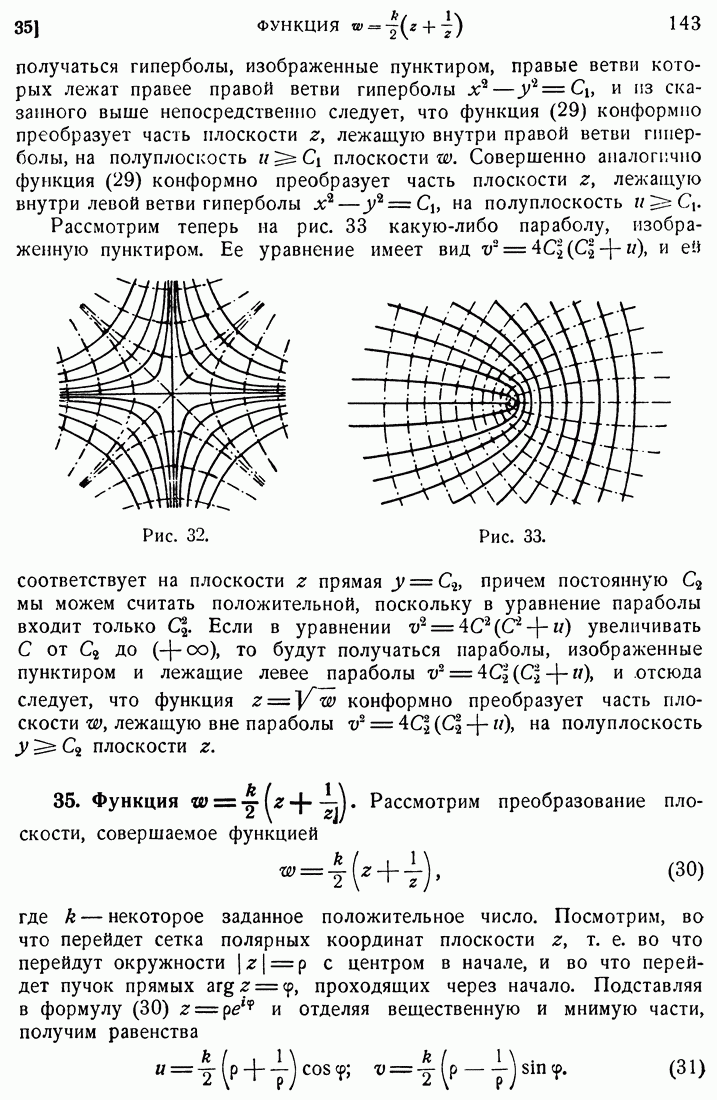
- 35. Функция …
- 36. Двуугольник и полоса.
- 37. Основная теорема.
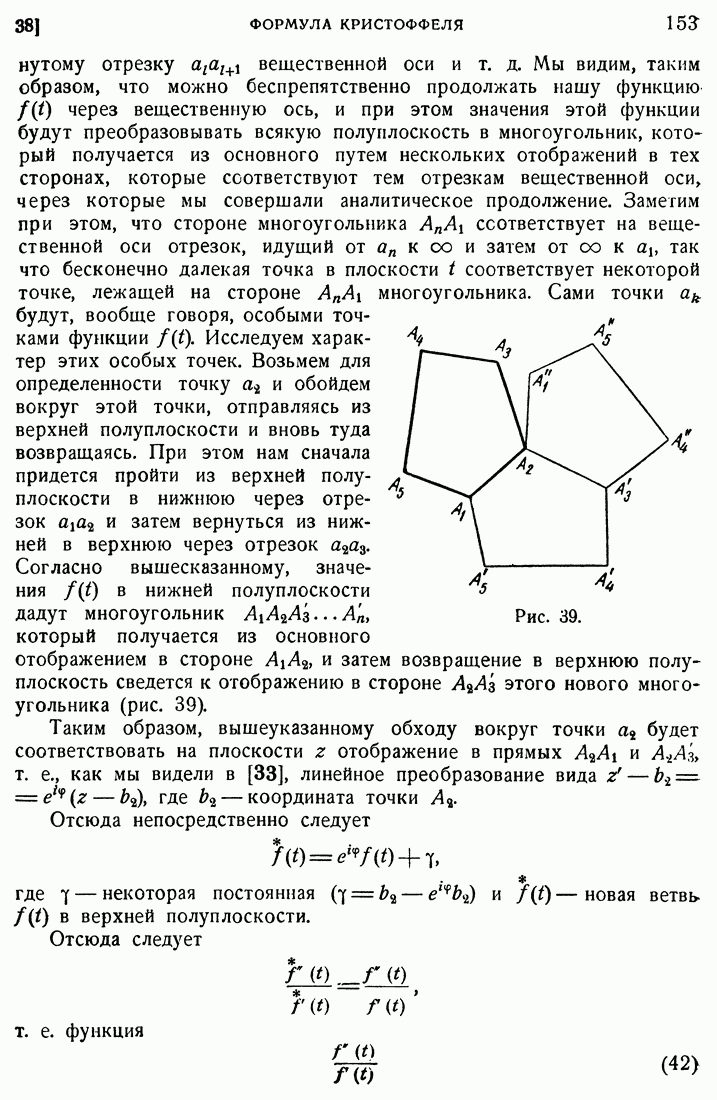
- 38. Формула Кристоффеля.
- 39. Частные случаи.
- 40. Случай внешности многоугольника.
- 41. Минимальное свойство преобразования на круг.
- 42. Способ сопряженных тригонометрических рядов.
- 43. Плоское установившееся течение жидкости.
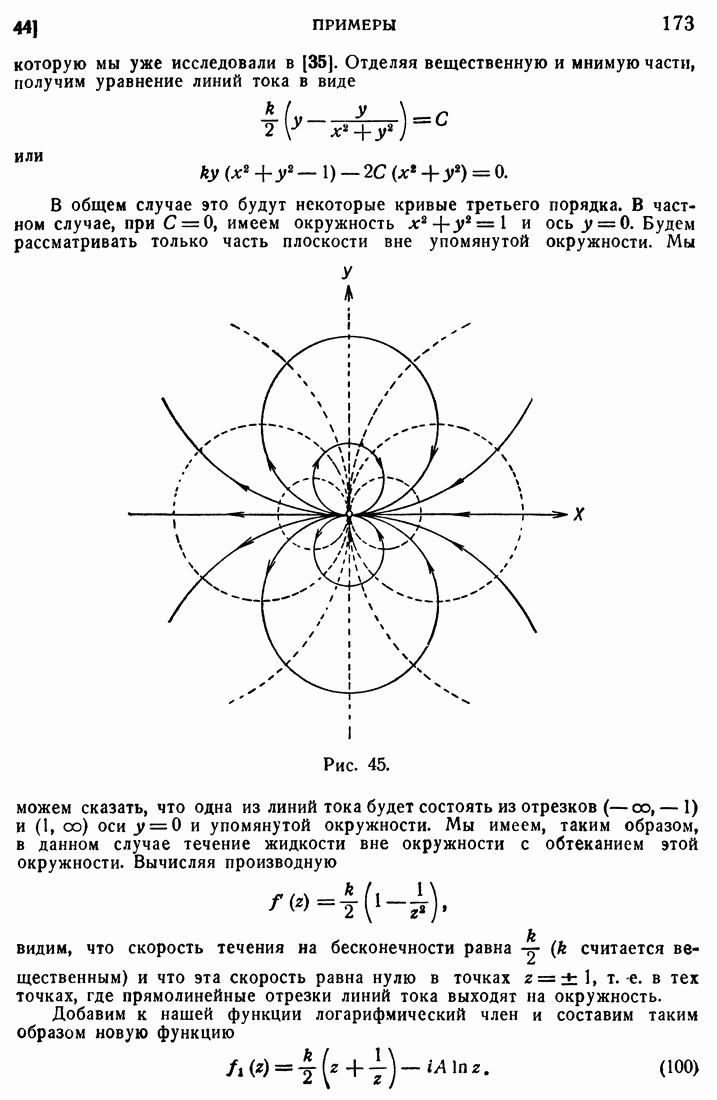
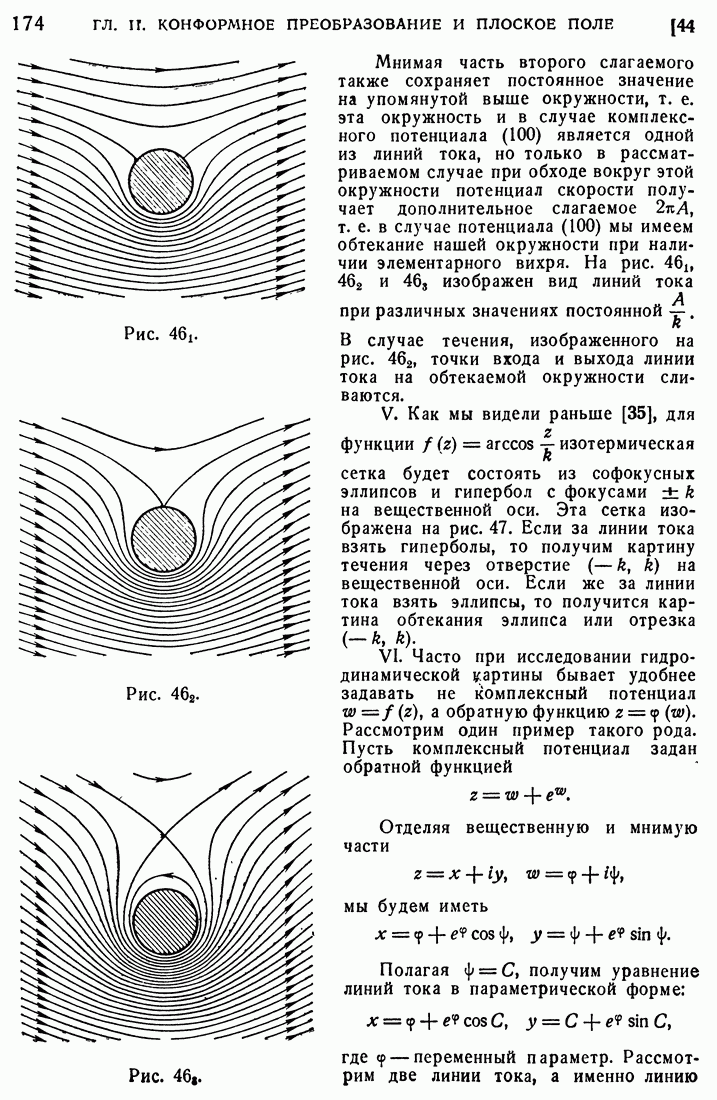
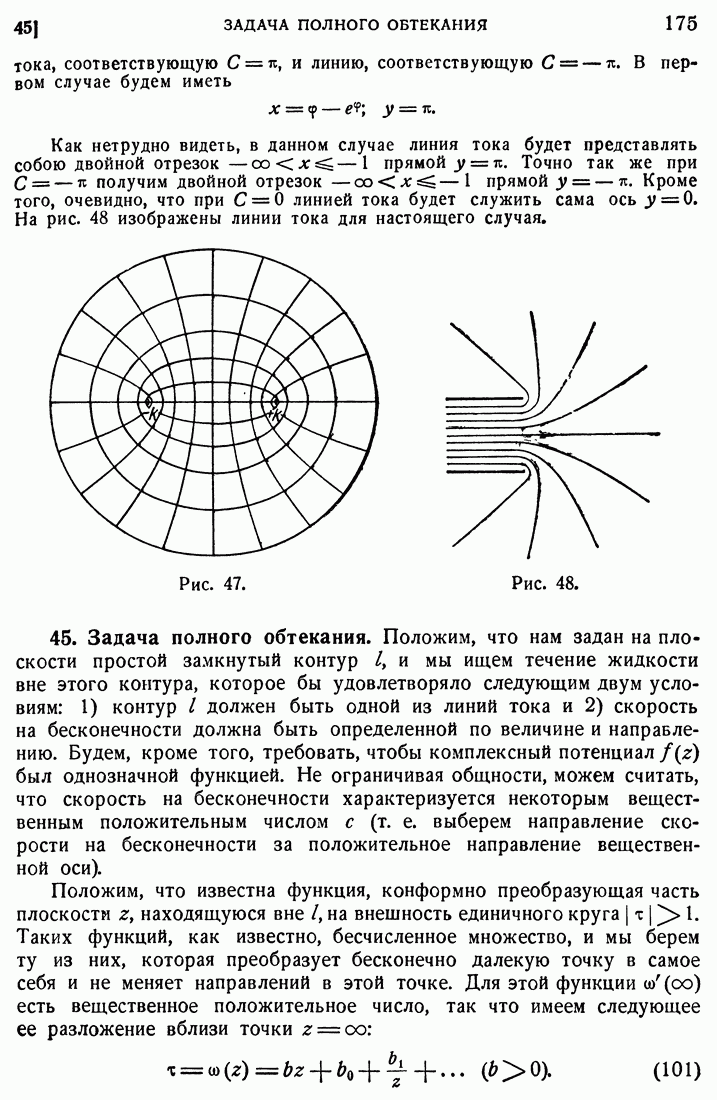
- 44. Примеры.
- 45. Задача полного обтекания.
- 46. Формула Н. Е. Жуковского.
- 47. Плоская электростатическая задача.
- 48. Формула Шварца.
- 49. Ядро ctg((s-t)/2).
- 50. Предельные задачи.
- 51. Бигармоническое уравнение.
- 52. Волновое уравнение и аналитические функции.
- 53. Основная теорема.
- 54. Дифракция плоской волны.
- 55. Отражение упругих волн от прямолинейной границы.
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ ВЫЧЕТОВ, ЦЕЛЫЕ И ДРОБНЫЕ ФУНКЦИИ
- 56. Интеграл Френеля.
- 57. Интегрирование выражений с тригонометрическими функциями.
- 58. Интегрирование рациональной дроби.
- 59. Некоторые новые типы интегралов с тригонометрическими функциями.
- 60. Лемма Жордана.
- 61. Представление некоторых функций контурными интегралами.
- 62. Примеры интегралов от многозначных функций.
- 63. Интегрирование системы линейных уравнений с постоянными коэффициентами.
- 64. Разложение дробной функции на простейшие дроби.
- 66. Построение мероморфной функции.
- 67. Целые функции.
- 68. Бесконечные произведения.
- 69. Построение целой функции по ее корням.
- 70. Интегралы, зависящие от параметра.
- 71. Эйлеров интеграл второго рода.
- 72. Эйлеров интеграл первого рода.
- 73. Бесконечное произведение для функции …
- 74. Представление Г(z) контурным интегралом.
- 75. Формула Стирлинга.
- 76. Формула суммирования Эйлера.
- 77. Числа Бернулли.
- 78. Метод скорейшего спуска.
- 79. Асимптотическое разложение интеграла.
- 80. Примеры.
- 81. Метод стационарной фазы.
- ГЛАВА IV. АНАЛИТИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ И ФУНКЦИИ МАТРИЦ
- 82. Регулярные функции многих переменных.
- 83. Двойной интеграл и формула Коши.
- 84. Степенные ряды.
- 85. Аналитическое продолжение.
- 86. Функции матриц. Предварительные понятия.
- 87. Степенные ряды от одной матрицы.
- 88. Умножение степенных рядов. Обращение степенного ряда.
- 89. Дальнейшее исследование сходимости.
- 90. Интерполяционные полиномы.
- 91. Тождество Кейли. Формула Сильвестра.
- 92. Определение функций одной матрицы формулой Коши.
- 93. Аналитическое продолжение.
- 94. Логарифм матриц.
- 95. Обращение целой функции от матрицы в случае матриц второго порядка.
- 96. Системы линейных уравнений с постоянными коэффициентами.
- 97. Функции нескольких матриц.
- ГЛАВА V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 98. Разложение решения в степенной ряд.
- 99. Аналитическое продолжение решения.
- 100. Окрестность особой точки.
- 101. Регулярная особая точка.
- 102. Уравнения класса Фукса.
- 103. Уравнение Гаусса.
- 104. Гипергеометрический ряд.
- 105. Полиномы Лежандра.
- 106. Полиномы Якоби.
- 107. Конформное преобразование и уравнение Гаусса.
- 108. Преобразование Лапласа.
- 109. Различный выбор решений.
- 110. Уравнение Бесселя.
- 111. Функции Ханкеля и интегральное представление решений уравнения Бесселя.
- 112. Асимптотические разложения.
- 113. Асимптотические разложения решений, полученных преобразованием Лапласа.
- 114. Асимптотические разложения решений уравнения Бесселя.
- 115. Вырождение уравнения Гаусса.
- 116. Формальные ряды в окрестности иррегулярной особой точки.
- 117. Построение асимптотических разложений методом после довательных приближений.
- 118. Функции Эйри.
- 119. Асимптотика при большом значении параметра.
- 120. Уравнения с периодическими коэффициентами.
- 121. Условия устойчивости и неустойчивости для уравнения Хилла.
- 122. Системы линейных дифференциальных уравнений.
- 123. Регулярная особая точка.
- 124. Регулярные системы.
- 125. Представление решения в окрестности особой точки.
- 126. Канонические решения.
- 127. Связь с регулярными решениями типа Фукса.
- 128. Случай любых Us.
- 129. Формальные разложения в окрестности иррегулярной особой точки.
- ГЛАВА VI. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- 130. Определение сферических функций.
- 131. Явные выражения сферических функций.
- 132. Свойство ортогональности.
- 133. Полиномы Лежандра.
- 134. Разложение по сферическим функциям.
- 135. Доказательство сходимости.
- 136. Связь сферических функций с предельными задачами.
- 137. Задачи Дирихле и Неймана.
- 138. Потенциал объемных масс.
- 139. Потенциал сферического слоя.
- 140. Электрон в центральном поле.
- 141. Шаровые функции и линейные представления группы вращения.
- 142. Функция Лежандра.
- 143. Функция Лежандра второго рода.
- § 2. ФУНКЦИИ БЕССЕЛЯ
- 144. Определение функций Бесселя.
- 145. Соотношения между функциями Бесселя.
- 146. Ортогональность функций Бесселя и их корни.
- 147. Производящая функция и интегральное представление.
- 148. Формула Фурье — Бесселя.
- 150. Разложение функций Неймана с целым значком.
- 151. Случай чисто мнимого аргумента.
- 152. Новые интегральные представления.
- 153. Асимптотические представления.
- 154. Функции Бесселя и уравнение Лапласа.
- 155. Волновое уравнение в цилиндрических координатах.
- 156. Волновое уравнение в сферических координатах.
- § 3. ПОЛИНОМЫ ЭРМИТА И ЛАГЕРРА
- 157. Линейный осциллятор и полиномы Эрмита.
- 158. Свойство ортогональности.
- 159. Производящая функция.
- 160. Параболические координаты и функции Эрмита.
- 161. Полиномы Лагерра.
- 162. Связь полиномов Эрмита и Лагерра.
- 163. Асимптотическое выражение полиномов Эрмита.
- 164. Асимптотическое выражение полиномов Лежандра.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ И ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
- 165. Приведение эллиптических интегралов к нормальному виду.
- 166. Приведение интегралов к тригонометрической форме.
- 167. Примеры.
- 168. Обращение эллиптического интеграла.
- 169. Общие свойства эллиптических функций.
- 170. Основная лемма.
- 171. Функции Вейерштрасса.
- 172. Дифференциальное уравнение для …
- 173. Функции …
- 174. Разложение целой периодической функции.
- 175. Новые обозначения.
- 176. Функция …
- 177. Функции …
- 178. Свойства функций тэта.
- 179. Выражение чисел … через …
- 180. Эллиптические функции Якоби.
- 181. Основные свойства функций Якоби.
- 182. Дифференциальные уравнения для функций Якоби.
- 183. Формулы сложения.
- 184. Связь функций p(u) и sn(u).
- 185. Эллиптические координаты.
- 186. Введение эллиптических функций.
- 187. Уравнение Лямэ.
- 188. Простой маятник.
- 189. Пример конформного преобразования.
- ДОБАВЛЕНИЕ. ПРИВЕДЕНИЕ МАТРИЦ К КАНОНИЧЕСКОЙ ФОРМЕ
- 191. Случай простых корней.
- 192. Первый этап преобразований в случае кратных корней.
- 193. Приведение к канонической форме.
- 194. Определение структуры канонической формы.
- 196. Пример.