Глава II. ПОПОЛНЕНИЯ

В этой главе вводятся пополнения числовых полей относительно -адических топологий, а также топологий, индуцированных вложениями числового поля в поле вещественных или комплексных чисел.

В книге [7] этот вопрос изучался с точки зрения теории нормирований и был изложен в законченном виде.

В § 3 мы изучим грубую структуру полных полей. В § 4 и 5 изложены основные сведения относительно неразветвленных и слабо разветвленных расширений. По поводу теории высшего ветвления мы отсылаем читателя к книге Артина-Тейта [3]. В § 4 и 5 мы занимаемся полными дедекиндовыми кольцами. Мы вводим понятия неразветвленного, слабо разветвленного и вполне разветвленного идеала над Эти понятия можно определить и глобально, так как они зависят лишь от индекса ветвления и степени поля классов вычетов. Однако в локальном случае они применимы также к расширениям полей, потому что в каждом конечном расширении основного поля К имеется лишь один простой идеал лежащий над

§ 1. Определения и пополнения

Пусть К — поле. Нормированием поля К называется вещественнозначная функция на К, удовлетворяющая следующим трем условиям:

Если нормирование вместо условия удовлетворяет более сильному требованию

то оно называется неархимедовым.

Нормирование, для которого при всех называется тривиальным. В дальнейшем мы будем считать, что все рассматриваемые нормирования нетривиальны.

Так как всякое нормирование поля определяет в нем метрику и тем самым топологию, мы обычно будем писать или просто вместо

Мы будем заниматься в основном следующими примерами.

Пусть — поле рациональных чисел. Обычная абсолютная величина является нормированием.

Для каждого простого числа определено -адическое нормирование

где - любое целое число, -целые числа, не делящиеся на

Пусть — дискретно нормированное кольцо с максимальным идеалом порожденным элементом . Всякий ненулевой элемент а поля частных К кольца о представляется в виде яги, где целое число, а — единица кольца . Число называется порядком а. Пусть с — положительное вещественное число, Положив

мы определим некоторое нормирование поля К (проверка тривиальна), которое оказывается неархимедовым.

В выборе константы с, конечно, имеется значительный произвол. В числовых полях мы будем иметь дело с двумя возможными вариантами выбора этой константы.

Пусть А — целое замыкание кольца целых чисел в поле алгебраических чисел К, и пусть — простой идеал. Пусть элемент имеет порядок 1 относительно и пусть — простое число, порождающее идеал Тогда Для некоторого целого числа и некоторой - единицы и. Пусть -степень поля над

Поле классов вычетов состоит из элементов: это число мы обозначаем символом Идеал однозначно определяет следующие два нормирования: то, для которого

и то, для которого

Для всякого элемента а имеем

Пусть -конечное расширение поля лежит над в кольце алгебраических чисел В поля —элемент, имеющий порядок 1 относительно Тогда

и

Мультипликативность индексов ветвления и степеней полей классов вычетов при расширениях обеспечивает согласованность этих определений при переходе к расширениям конечной степени.

Всякое продолжение -адического нормирования поля на числовое поле К определяется некоторым простым идеалом в целом замыкании А кольца Действительно, пусть -кольцо данного нормирования, — его максимальный идеал: пересечение не может сводиться к нулю и, следовательно, представляет собой некоторый максимальный идеал Тривиальная проверка тогда показывает, что Таким способом получаются все нормирования поля К, индуцирующие -адические нормирования на исходя из принятых нами в качестве основных понятий дедекиндова кольца и целого замыкания.

Пусть К—числовое поле. Всякое вложение К в поле вещественных или комплексных чисел определяет некоторое нормирование на К, которое называется соответственно вещественным или комплексным.

Множество нормирований поля К, состоящее из -адических нормирований описанных выше, а также вещественных и комплексных нормирований, называется канонической системой и обозначается символом Вещественные и комплексные нормирования из системы называются также архимедовыми.

Очевидно, любые два разных нормирования из канонической системы независимы в том смысле, что они определяют различные топологии поля . Следующая теорема о приближении является аналогом китайской теоремы об остатках для нормирований.

Теорема 1. Пусть К — поле, -нетривиальные попарно независимые нормирования К? Пусть произвольные элементы поля Существует такой элемент что

Доказательство. Прежде всего отметим, что для любых двух нормирований нашей системы, скажем существует такой элемент что . В самом деле, поскольку эти нормирования определяют разные и недискретные топологии, существует такая последовательность элементов поля К, что при всех

Если существует индекс такой, что то утверждение справедливо; в противном случае и для достаточно большого имеем для всех Элемент для удовлетворяет требуемым условиям.

Теперь индукцией по покажем, что можно найти элемент удовлетворяющий неравенствам для всех Случай уже разобран. Пусть элемент с условиями для всех уже найден. Если то для любого элемента и для достаточно больших элемент удовлетворяет всем требованиям. Если же то, полагая имеем при

так что можно положить для достаточно большого

Для всякого элемента удовлетворяющего неравенствам при имеем при при Следовательно, для всякого индекса можно найти элемент сколь угодно близкий к единице в метрике и к нулю — в остальных метриках. Тогда элемент близок к в метрике что доказывает теорему.

Пусть К — числовое поле, а — некоторое нормирование (в дальнейшем все рассматриваемые нормирования будут принадлежать канонической системе). Так же, как вещественные числа строятся исходя из рациональных, вводится пополнение поля К относительно Рассмотрим последовательности Коши элементов поля К. Они образуют кольцо. Последовательности, сходящиеся к нулю, образуют максимальный идеал, факторкольцо по которому является полем . Поле К естественно вкладывается в (элементу сопоставляется класс последовательности, все члены которой равны этому элементу). Нормирование поля К продолжается на поле по непрерывности. Обычно мы отождествляем поле К с его образом в поле и называем Ко пополнением поля К.

Если архимедово нормирование, то — поле вещественных или комплексных чисел.

Если неархимедово нормирование, соответствующее некоторому простому идеалу кольца алгебраических чисел поля К, то вместо К мы иногда будем писать и называть его полем -адических чисел. Сейчас мы подробнее изучим случай -адического нормирования

Пусть целое замыкание кольца в поле К, т. е. кольцо целых алгебраических чисел поля К. Обозначим символом замыкание кольца в поле Пусть Выберем такой элемент для которого

Тогда потому что наше нормирование неархимедово. Так как -адическая норма любого элемента кольца А не превосходит 1, то же верно для элементов кольца Это же рассуждение показывает, что замыкание идеала состоит из элементов с нормой меньше 1 и что элемент не принадлежащий кольцу имеет норму больше 1. В частности, нормирование на поле и на поле К имеет одну и ту же бесконечную циклическую группу значений. Для любого элемента имеющего порядок 1 относительно число порождает эту группу.

Пусть локальное кольцо идеала -адическая норма всех элементов кольца о не превосходит единицы, потому что порядки этих элементов относительно неотрицательны. Следовательно, кольцо о лежит в замыкании кольца А и, больше того, замыкания колец о и в поле совпадают. Это общее замыкание называется кольцом целых -адических чисел поля Пусть максимальный идеал кольца -замыкание идеала в кольце Имеют место канонические изоморфизмы

В силу сказанного всякий ненулевой элемент представляется в виде

где так что и является единицей в замыкании кольца Тем самым -область с однозначным разложением на множители, имеющая единственный простой элемент и потому представляющая собой дискретно нормированное кольцо.

Пусть — конечное расширение поля целое замыкание кольца в поле - простой идеал кольца В, лежащий над Пусть каноническое нормирование, соответствующее идеалу Имеет место коммутативная диаграмма

в которой стрелки вверху, внизу и слева означают вложения, а правая вертикальная стрелка отображает на замыкание кольца А в кольце Аналогичная коммутативная диаграмма для полей классов вычетов выглядит так:

здесь вертикальные стрелки—вложения, а горизонтальные — изоморфизмы.

Пусть замыкание поля К в поле Композит является конечным расширением поля содержащимся в

Пусть базис линейного пространства над К? Покажем, что индуцированная нормированием топология поля совпадает с топологией -пространства Для этого следует проверить, что для любой последовательности Коши в поле

последовательности коэффициентов сходятся в Проведем индукцию по При утверждение очевидно; пусть Достаточно разобрать случай, когда о (если это не так, можно рассмотреть последовательность ). Предположим, что последовательность не сходится к нулю. Тогда для некоторого числа и для бесконечно многих будем иметь Переходя к подпоследовательности, мы можем считать это неравенство выполненным для всех Последовательность сходится к нулю. Кроме того,

Последовательность правых частей сходится; из индуктивного предположения следует, что пределы существуют при всех Поэтому

что противоречит линейной независимости элементов Отсюда вытекает, что поле полно.

Следовательно, поле замкнуто и, стало быть, совпадает с Это же рассуждение, разумеется, применимо к случаю, когда индуцированы вложениями в поле вещественных и комплексных чисел.

Предложение 0. Пусть К — числовое поле, одно из его канонических нормирований, -конечное расширение поля К. Два вложения поля над К индуцируют одно и то же нормирование поля в том и только том случае, когда они сопряжены над

(Сопряженность над означает существование изоморфизма Я поля на поле тождественного на

Доказательство. Если вложения сопряжены над то на они индуцируют одинаковые нормирования, потому что нормирование с на продолжается однозначно.

Докажем обратное утверждение. Пусть некоторый -изоморфизм. Покажем, что его можно продолжить до -изоморфизма полей Поскольку множество плотно всякий элемент представляется в виде

Поскольку нормирования на индуцированные а и совпадают, последовательность сходится. Обозначим ее предел символом Легко проверить, что не зависит от выбора последовательности и что отображение представляет собой изоморфизм. Очевидно, он оставляет поле инвариантным.

Это предложение дает ясную картину строения продолжений нормирования и на поле включая архимедовы нормирования.

Пусть К — числовое поле конечной степени над полем - некоторое нормирование поля Символом обозначим локальную степень

Имеем

где сумма берется по всем продолжениям фиксированного нормирования поля

Из предложения 0 и определения нормы вытекает

Следствие. Пусть К — числовое поле, -некоторое нормирование из системы Для любого элемента

Пусть А — дедекиндово кольцо. Группа его дробных идеалов изоморфна свободной абелевой группе, порожденной простыми идеалами. Пусть простой идеал, соответствующее локальное кольцо. Группа его дробных идеалов — бесконечная циклическая. Она порождена максимальным идеалом кольца Пусть -нормирование, соответствующее идеалу пополнение кольца Тогда — также дедекиндово кольцо, а его группа дробных идеалов — бесконечная циклическая группа, порожденная идеалом Тем самым определены естественные отображения

первое из которых — изоморфизм, а второе — вложение. Для краткости удобно иногда отождествлять обозначая символом любой из этих идеалов. Произведение

в котором — целые числа, все, кроме конечного числа, равные нулю, можно назвать формальным идеалом и в зависимости от контекста интерпретировать как элемент любой из групп Идеал называется -компонентой формального идеала и обозначается символом Число называется порядком идеала

относительно и обозначается так:

Для любого ненулевого элемента а поля частных одного из колец можно образовать главные дробные идеалы а А, а или порядки которых относительно 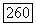совпадают с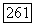

Для любых двух элементов 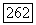запись

означает, что 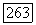Если 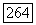принадлежат полю частных кольца А, а 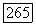рассматривается как дробный идеал, то это — обычное сравнение, означающее, что разность а 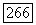принадлежит 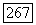Если 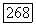удобно рассматривать это сравнение как относящееся одновременно ко всем трем кольцам.

Пусть А — дедекиндово кольцо, 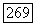некоторый простой идеал, 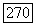соответствующее нормирование. Пусть 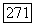замыкание кольца А в пополнении 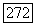его поля частных, 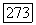-замыкание идеала 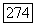в кольце 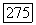Тогда 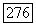-дискретно нормированное кольцо. Для любого дробного идеала а кольца А имеем тривиальное соотношение

где 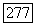Обратно,

если 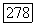Замыкание дробного идеала а в поле частных кольца 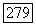равно 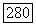Все эти утверждения проверяются тривиально, и мы оставляем эту проверку читателю.