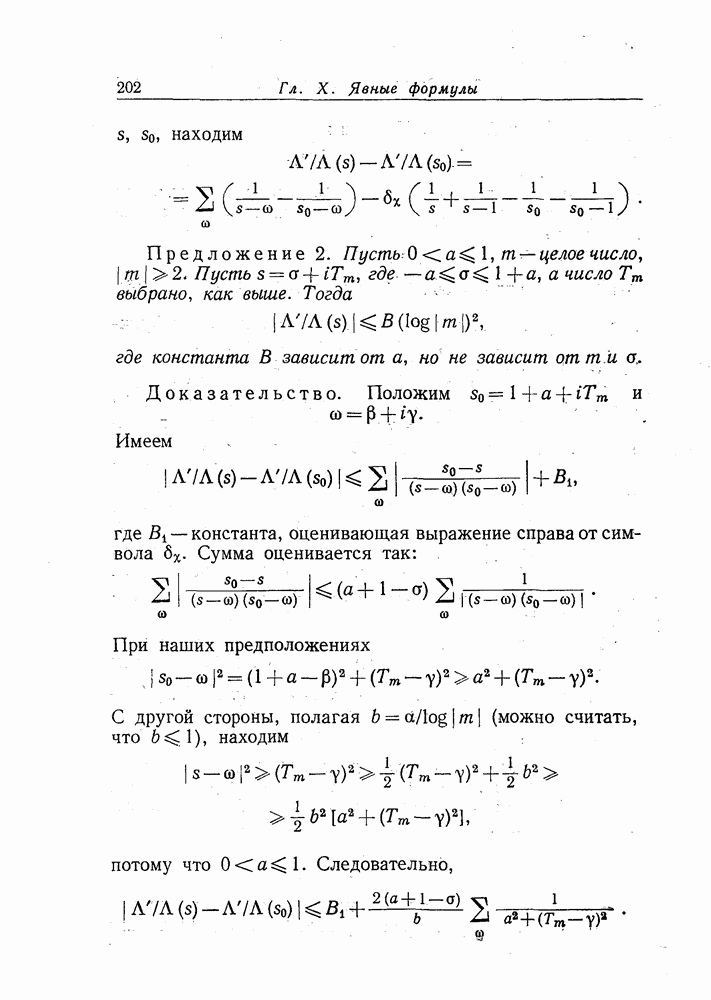| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Нижняя оценка для вычета
Лемма 3. Пусть  вещественное число,
вещественное число,  Предположим, что
Предположим, что  (или, что то же самое,
(или, что то же самое,  . Тогда
. Тогда

Доказательство. В силу теоремы 15 гл. VII, § 8, имеем

Уменьшим область интегрирования до  где
где  множество единиц
множество единиц  для неархимедовых
для неархимедовых  и область
и область

для архимедовых  Значение интеграла при этом уменьшится; интеграл по
Значение интеграла при этом уменьшится; интеграл по  равен произведению локальных интегралов, которые мы сейчас вычислим.
равен произведению локальных интегралов, которые мы сейчас вычислим.
Пусть  есть
есть  -адическое нормирование. Тогда
-адическое нормирование. Тогда  значит,
значит,  есть
есть  -кратная характеристическая функция множества
-кратная характеристическая функция множества  Поэтому в этом случае интересующий нас локальный интеграл равен
Поэтому в этом случае интересующий нас локальный интеграл равен

Пусть теперь и  — архимедово. Воспользуемся предложением 9 гл. VII, § 8, чтобы выразить
— архимедово. Воспользуемся предложением 9 гл. VII, § 8, чтобы выразить  через
через  Замена переменной
Замена переменной  превращает интеграл по
превращает интеграл по  в
в

где область интегрирования имеет вид  Заменим
Заменим  нижней гранью этой функции в области интегрирования, именно числом
нижней гранью этой функции в области интегрирования, именно числом  в вещественном случае и
в вещественном случае и  — в комплексном. Мера области равна
— в комплексном. Мера области равна  соответственно. Это дает для интеграла оценку снизу вида
соответственно. Это дает для интеграла оценку снизу вида

Произведение по всем нормированиям приводит к неравенству

где мы пользуемся числом  вместо
вместо  Оценка в формулировке леммы является некоторым ослаблением этого неравенства.
Оценка в формулировке леммы является некоторым ослаблением этого неравенства.
Наша цель состоит в доказательстве следующей теоремы.
Теорема 1. Пусть  Существует такое число
Существует такое число  что для всех полей
что для всех полей  нормальных над
нормальных над  имеет место неравенство
имеет место неравенство

Доказательство. Пользуясь гипотезой Римана, мы могли бы избавиться от условия нормальности. В самом деле, в рассуждениях приходится различать два случая.
Случай 1. Для всех нормальных полей  функция
функция  не обращается в нуль для вещественных
не обращается в нуль для вещественных  в интервале
в интервале

Из интегрального представления тогда следует, что дзета-функция отрицательна вблизи от 1 слева. Следовательно,  и, полагая,
и, полагая, 
в лемме 3, находим требуемое. Это же рассуждение проходит и для полей  не являющихся нормальными.
не являющихся нормальными.
Случай 2. Существует такое нормальное расширение  поля
поля  степени
степени  что
что  для некоторого вещественного значения
для некоторого вещественного значения  удовлетворяющего неравенствам
удовлетворяющего неравенствам 
Чтобы справиться с этим случаем, нам придется предпринять обходной путь через теорию  -рядов. В следующем параграфе мы докажем такой результат.
-рядов. В следующем параграфе мы докажем такой результат.
Теорема 2. Существует такая константа  что для всех числовых полей
что для всех числовых полей  и нормальных расширений К поля
и нормальных расширений К поля  имеет место неравенство
имеет место неравенство

для любых 
Примем пока эту теорему. Нам понадобится еще следующая фундаментальная лемма Брауэра, доказательство которой приведено в приложении.
Лемма. Пусть  конечная группа,
конечная группа,  характер ее регулярного представления. Существуют такие циклические подгруппы
характер ее регулярного представления. Существуют такие циклические подгруппы  положительные рациональные числа
положительные рациональные числа  и одномерные характеры
и одномерные характеры  групп
групп  что
что

где звездочка означает индуцированный характер.
Мы воспользуемся этой леммой несколько раз. Для начала отметим, что если поле К нормально над  для некоторого
для некоторого  то также
то также  (Для расширений, не являющихся нормальными, вопрос остается открытым. Конечно, ответ следовал бы из гипотез Артина.) Мы используем формулу Артина
(Для расширений, не являющихся нормальными, вопрос остается открытым. Конечно, ответ следовал бы из гипотез Артина.) Мы используем формулу Артина

входящие в нее  -ряды являются абелевыми
-ряды являются абелевыми  -рядами типа, изученного в гл. VII.
-рядами типа, изученного в гл. VII.
Теперь приступим к разбору второго случая. Число  нуль дзета-функции между
нуль дзета-функции между  и 1 и дискриминант поля
и 1 и дискриминант поля  можно считать функциями только от
можно считать функциями только от  Пусть
Пусть  нормальное расширение поля
нормальное расширение поля  Положим
Положим  Тогда поле К нормально над
Тогда поле К нормально над  следовательно,
следовательно, 
По лемме 3,

Элементарная оценка дает

откуда

и мы получаем

В силу теоремы 2, связывающей вычеты в полях  полагая
полагая  получаем неравенство
получаем неравенство

Из последних двух неравенств следует теорема 1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДВАРИТЕЛЬНЫЕ ТРЕБОВАНИЯ
- Глава I. ЦЕЛЫЕ АЛГЕБРАИЧЕСКИЕ ЧИСЛА
- § 2. Целое замыкание
- § 3. Простые идеалы
- § 4. Китайская теорема об остатках
- § 5. Расширения Галуа
- § 6. Дедекиндовы кольца
- 7. Дискретно нормированные кольца
- Глава II. ПОПОЛНЕНИЯ
- § 2. Многочлены над полными полями
- § 3. Некоторые фильтрации
- § 4. Неразветвленные расширения
- § 5. Слабо разветвленные расширения
- Глава III. ДИФФЕРЕНТА И ДИСКРИМИНАНТ
- § 2. Дифферента и ветвление
- § 3 Дискриминант
- Глава IV. КРУГОВЫЕ ПОЛЯ
- § 2. Квадратичные поля
- § 3. Символ Артина
- § 4. Лемма Артина
- Глава V. ПАРАЛЛЕЛОТОПЫ
- § 2. Точки решетки в параллелотопах
- § 3. Вычисление одного объема
- § 4. Константа Минковского
- Глава VI. ИДЕЛИ И АДЕЛИ
- § 2. Адели
- § 3. Идели
- Глава VII. ФУНКЦИОНАЛЬНОЕ УРАВНЕНИЕ
- § 1. Локальная аддитивная двойственность
- § 2. Локальная мультипликативная теория
- § 3. Локальное функциональное уравнение
- § 4. Локальные вычисления
- § 5. Ограниченные прямые произведения
- § 6. Глобальная аддитивная двойственность. Теорема Римана-Роха
- § 7. Глобальное функциональное уравнение
- § 8. Глобальные вычисления
- Глава VIII. ПЛОТНОСТЬ ПРОСТЫХ ИДЕАЛОВ И ТАУБЕРОВА ТЕОРЕМА
- § 1. Интеграл Дирихле
- § 2. Тауберова теорема Икеара
- § 3. Тауберова теорема для рядов Дирихле
- § 4. Некоторые теоремы о сходимости
- § 5. Плотности
- Глава IX. ТЕОРЕМА БРАУЭРА—ЗИГЕЛЯ
- § 1. Верхняя оценка для вычета
- § 2. Нижняя оценка для вычета
- § 3. Сравнение вычетов в нормальных расширениях
- § 4. Окончание доказательства
- Приложение — лемма Брауэра
- Глава Х. ЯВНЫЕ ФОРМУЛЫ
- § 1. Вейерштрассово разложение L-ряда
- § 2. Оценка функции …
- § 3. Основная сумма
- § 4. Вычисление суммы: первая часть
- § 5. Вычисление суммы: вторая часть