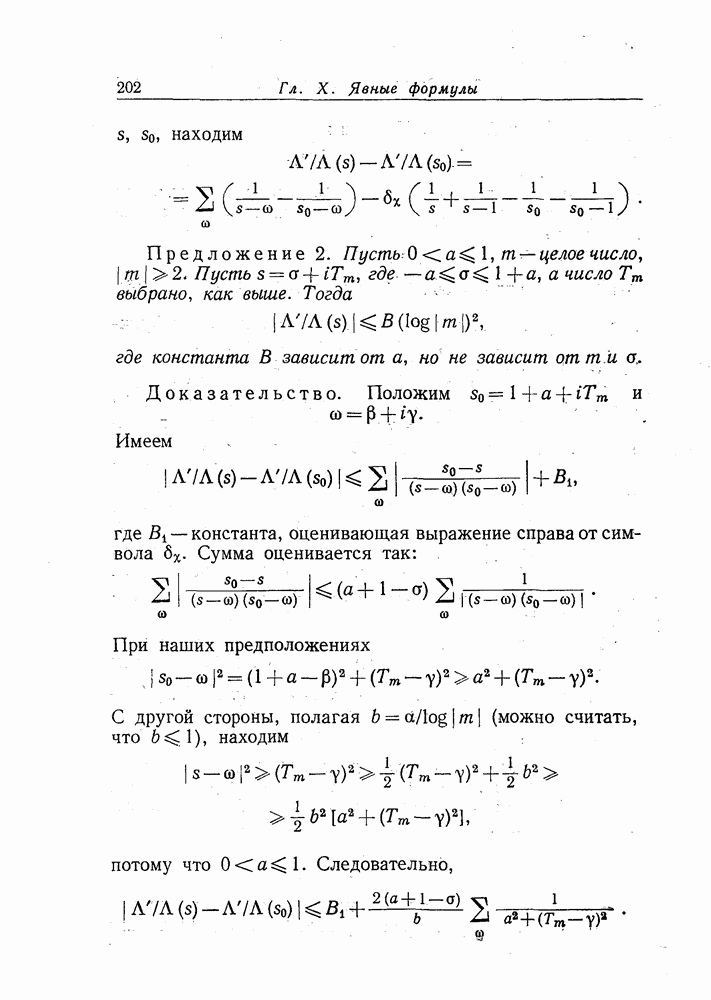§ 7. Глобальное функциональное уравнение

В мультипликативной теории мы рассматриваем группу иделей как ограниченное прямое произведение локальных мультипликативных групп относительно подгрупп единиц и применяем § 5. Квазихарактеры, интересующие нас, будут тривиальны для почти всех т. е. неразветвлены для почти всех

Нам будет удобно рассматривать как некоторое прямое произведение (топологическое и алгебраическое). Вложим в группу положительных вещественных чисел с помощью отображения

(компонента для каждого архимедова нормирования и - для всех остальных). Это отображение сохраняет норму, так как

Очевидно, что

т. е. всякий идель а можно единственным способом представить в виде произведения

где и это разложение непрерывно. На группе существует однозначно определенная мера такая, что формально

Введем одно ограничение на квазихарактеры, которыми мы будем пользоваться в дальнейшем. Будем считать, что они тривиальны на Тогда их можно, рассматривать как квазихарактеры группы классов иделей Такие характеры называются характерами Гекке. Поскольку группа компактна, ограничение любого квазихарактера на нее является характером. Тем самым ситуация похожа на локальную (архимедову). Если квазихарактер с тривиален на то

где некоторое комплексное число, однозначно определенное квазихарактером. Для произвольного квазихарактера с существует единственное вещественное число , такое, что Оно называется вещественной частью квазихарактера с и обозначается символом Для любого характера группы произведение представляет собой квазихарактер, и обратно, любой квазихарактер можно представить в таком виде (характер однако, определен не однозначно, а с точностью до множителя вида

Иногда удобно нормализовать характеры группы потребовав, чтобы они были тривиальны на подгруппе (выше было определено ее каноническое вложение). Очевидно, это условие равносильно формуле

Всякий квазихарактер с однозначно определяет так нормализованный характер, для которого с

Как и в локальной теории, положим так что описанной нормализации).

Мы дополним конструкцию, предшествовавшую формулировке теоремы 6 гл. VI, § 3, вычислением меры.

Как прежде, фиксируем архимедово нормирование и полагаем

Пусть такие единицы, что векторы порождают всю решетку. Эти единицы называются фундаментальными. Они порождают группу единиц по

модулю подгруппы корней из единицы. Определитель

в котором с точностью до знака равен объему фундаментального параллелотопа в евклидовом пространстве. Его абсолютная величина называется регулятором поля и обозначается символом Через мы обозначаем абсолютную величину дискриминанта.

Предложение 8. Мера множества равна

(отображение I определено в доказательстве теоремы 6 гл. VI, § 3).

Доказательство. Пусть — единичный куб в -мерном пространстве. Так как гомоморфизм, имеем

Поэтому достаточно вычислить меру мы оставляем это в качестве нетрудного упражнения читателю (воспользоваться определением мультипликативной меры).

Предложение 9. Мера фундаментальной области для факторгруппы равна

(обозначения, как в теореме 6 гл. VI, § 3).

Доказательство. Тривиальное следствие предложения 8.

Мы приближаемся к концу нашего путешествия. Для определения глобальной дзета-функции рассмотрим функции на группе аделей, удовлетворяющие следующим условиям:

Л1. непрерывны и принадлежат т. е.

Л2. Суммы сходятся абсолютно и равномерно, когда меняются в компактных подмножествах групп иделей и аделей соответственно.

ЛЗ. Функции при принадлежат пространству

Отметим, что выполнение первых двух условий обеспечивает применимость теоремы Римана-Роха к функциям такого типа. Третье условие необходимо нам для определения дзета-функции. Каждой функции соответствует дзета-функция на множестве квазихарактеров с с

где интеграл берется по группе иделей. Пусть тогда

(Мы все время предполагаем, что рассматриваемые квазихарактеры и характеры тривиальны на Когда характер х фиксирован, дзета-функция становится функцией одного параметра из условия следует, что она голоморфна в области

Теорема 12. Всякую дзета-функцию можно аналитически продолжить на область всех квазихарактеров группы Продолженная функция однозначна и голоморфна всюду, кроме где она имеет простые полюсы с вычетами соответственно; здесь k — объем фундаментальной области для Кроме того, имеет место функциональное уравнение

где

Доказательство. Имеем

Второй интеграл, очевидно, сходится для любого вещественного значения потому что он сходится при где некоторое число, и тем более сходится при Займемся преобразованием первого интеграла; докажем следующий результат.

Теорема 13. Пусть при имеем с и пусть -характер группы индуцированный квазихарактером с. Тогда

где или 1 в зависимости от того, тривиален или нет характер индуцированный квазихарактером с на подгруппе Оба интеграла сходятся при всех с равномерно в каждой полосе

Равномерная сходимость интегралов в полосе очевидна из сделанных выше замечаний. Далее, покажем, как из этой формулы следует функциональное уравнение. Заменим на в выражении справа. Учтем, что Замена переменной во втором интеграле выделяет множитель но с тривиален на Следовательно, замена на не меняет выражения справа — это и есть функциональное уравнение.

Остается преобразовать интеграл по так, чтобы получить требуемое выражение. Запишем группу иделей в качестве произведения:

Будем, кроме того, считать характер нормализованным так, чтобы Для всякого фиксированного значения имеем

Пользуясь инвариантностью меры относительно мультипликативных сдвигов и тем, что с при а преобразуем это выражение так:

Свойство Л2 позволяет менять местами суммирование и интегрирование; пользуясь затем теоремой Римана—Роха, находим

Если бы мы начали с выражения

сделали замену переменной сохраняющую меру, и затем произвели те же преобразования, что и выше, в результате получилось бы то же самое выражение. Иначе говоря, имеет место тождество

Заметим теперь, что откуда

(Мы снова пользуемся тем, что интеграл по компактной группе от нетривиального характера равен нулю, а от тривиального характера — мере группы.)

Теперь следует проинтегрировать наше тождество по от 0 до 1 и заменить справа на а пределы интегрирования — на Это даст формулу теоремы 13, чем и заканчивается доказательство.