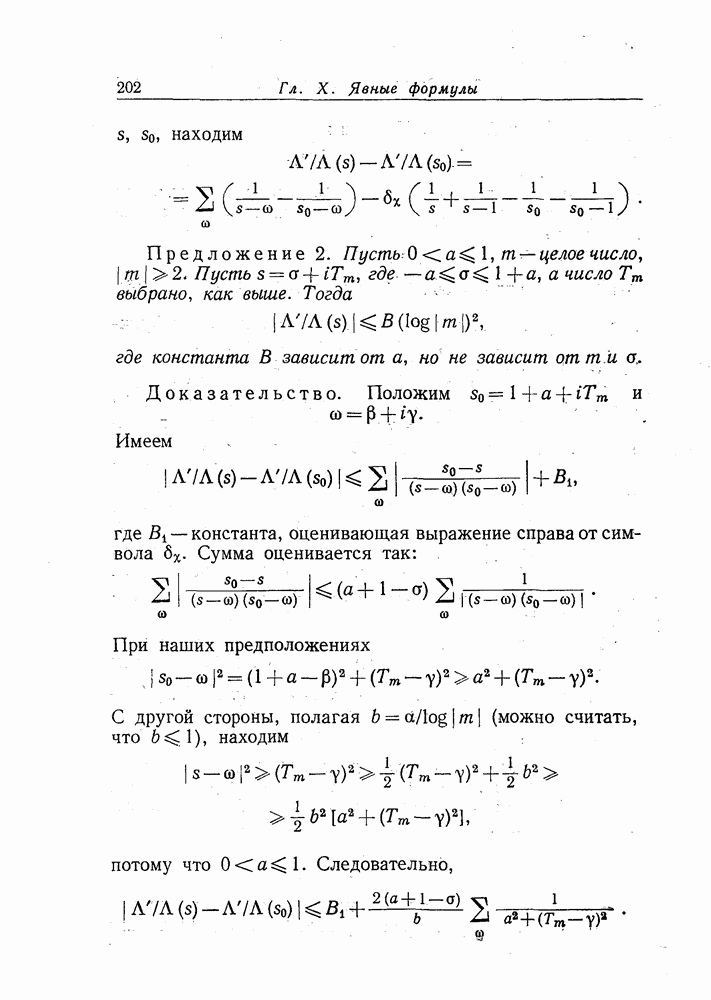| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Плотности
Пусть  характер Гекке, т. е. характер группы классов иделей поля
характер Гекке, т. е. характер группы классов иделей поля  Если он неразветвлен в конечном простом идеале
Если он неразветвлен в конечном простом идеале  т. е. обращается в нуль на группе локальных единиц
т. е. обращается в нуль на группе локальных единиц  то
то  представляет собой функцию только от
представляет собой функцию только от  и мы можем ввести функцию
и мы можем ввести функцию

где произведение распространено на все  в которых характер
в которых характер  неразветвлен. Из результатов гл. VII следует, что такой
неразветвлен. Из результатов гл. VII следует, что такой  -ряд удовлетворяет условиям, сформулированным в предыдущем параграфе, и условиям применимости тауберовой теоремы.
-ряд удовлетворяет условиям, сформулированным в предыдущем параграфе, и условиям применимости тауберовой теоремы.
Пусть  символом
символом  обозначим множество простых идеалов с условием а символом
обозначим множество простых идеалов с условием а символом  множество целых идеалов с условием
множество целых идеалов с условием  Для всякого конечного множества простых иделов
Для всякого конечного множества простых иделов  обозначим символом
обозначим символом  множество тех целых идеалов
множество тех целых идеалов  , которые взаимно просты с
, которые взаимно просты с  и для которых аналогичный смысл имеет
и для которых аналогичный смысл имеет 
В качестве частного случая тауберовой теоремы получаем:
Теорема 4. Пусть а — вычет дзета-функции  в точке 1. Пусть
в точке 1. Пусть  число элементов множеств
число элементов множеств  соответственно. Имеют место следующие асимптотические формулы.
соответственно. Имеют место следующие асимптотические формулы.

где 
В самом деле, вычет в точке 1 функции, которая получается из  опусканием множителей, относящихся к элементам
опусканием множителей, относящихся к элементам  равен
равен  Отсюда следует первое утверждение. Для доказательства второго применим тауберову теорему к логарифмической производной дзета-функции
Отсюда следует первое утверждение. Для доказательства второго применим тауберову теорему к логарифмической производной дзета-функции

Разобьем эту сумму, как обычно, на две: одну по всем  другую — по
другую — по  Вторая сумма не вносит вклада в вычет в точке 1, а первая сумма
Вторая сумма не вносит вклада в вычет в точке 1, а первая сумма

представляет собой ряд Дирихле  где
где  если
если  не является степенью простого числа. Для каждого целого числа
не является степенью простого числа. Для каждого целого числа  обозначим символом
обозначим символом  число идеалов
число идеалов  для которых
для которых  Тогда
Тогда  Вычет логарифмической производной функции
Вычет логарифмической производной функции  в точке
в точке  равен 1. В силу теоремы 1 получаем
равен 1. В силу теоремы 1 получаем

Для завершения доказательства остается применить предложение 1.
Займемся теперь вопросом о равномерности распределения простых идеалов.
Пусть  компактная коммутативная группа. Пусть
компактная коммутативная группа. Пусть  объединение конечных подмножеств
объединение конечных подмножеств  Рассмотрим некоторое отображение
Рассмотрим некоторое отображение  Мы будем говорить, что множество
Мы будем говорить, что множество  -равномерно распределено в группе
-равномерно распределено в группе  если для всякого характера
если для всякого характера  этой группы
этой группы

Напомним, что  если
если  и если
и если 
Мы примем без доказательства, что всякая непрерывная функция на компактной группе допускает равномерное приближение линейными комбинациями характеров с комплексными коэффициентами.
Назовем вещественную функцию  на
на  допустимой, если существуют такие последовательности вещественных непрерывных функций
допустимой, если существуют такие последовательности вещественных непрерывных функций  что
что

 сходятся к
сходятся к  соответственно монотонно возрастая и убывая, и, кроме того,
соответственно монотонно возрастая и убывая, и, кроме того,

при
Комплексная функция называется допустимой, если ее вещественная и мнимая части допустимы.
Если множество  - равномерно распределено в группе
- равномерно распределено в группе  любая допустимая функция на
любая допустимая функция на  то
то

Это немедленно следует из рассмотрения равномерных приближений функции  линейными комбинациями характеров. На практике в качестве
линейными комбинациями характеров. На практике в качестве  берется характеристическая функция подходящих подмножеств группы
берется характеристическая функция подходящих подмножеств группы  Если, например,
Если, например,  конечна, рассмотрим характеристическую функцию
конечна, рассмотрим характеристическую функцию  одного элемента; тогда
одного элемента; тогда 
Все интересующие нас теоремы о равномерном распределении вытекают из следующего результата.
Теорема 5. Пусть  нормализованный характер Гекке,
нормализованный характер Гекке,  конечное множество простых идеалов, содержащее все идеалы, где х разветвлен. Тогда
конечное множество простых идеалов, содержащее все идеалы, где х разветвлен. Тогда

Доказательство. Результат получается немедленно. В самом деле, мы знаем, что  -ряд голоморфен в точке 1 и не обращается в ней в нуль. Следовательно, вычеты
-ряд голоморфен в точке 1 и не обращается в ней в нуль. Следовательно, вычеты  -ряда и его производной равны нулю и наше утверждение следует из теоремы 1 и предложения 1 соответственно.
-ряда и его производной равны нулю и наше утверждение следует из теоремы 1 и предложения 1 соответственно.
Пусть  группа иделей поля
группа иделей поля  Пусть
Пусть  — конечное множество нормирований, содержащее архимедовы нормирования, — подгруппа группы
— конечное множество нормирований, содержащее архимедовы нормирования, — подгруппа группы  состоящая из иделей, компоненты которых являются единицами вне
состоящая из иделей, компоненты которых являются единицами вне  Не следует смешивать эту подгруппу с подгруппой
Не следует смешивать эту подгруппу с подгруппой  элементы которой имеют компонентами единицы вне
элементы которой имеют компонентами единицы вне  и что угодно
и что угодно  . По непрерывности, всякий характер группы классов иделей становится тривиальным на одной из подгрупп
. По непрерывности, всякий характер группы классов иделей становится тривиальным на одной из подгрупп  кроме того, он тривиален на мультипликативной группе
кроме того, он тривиален на мультипликативной группе  поля
поля  вложенной в
вложенной в  Пусть
Пусть  компактная группа,
компактная группа,  непрерывный гомоморфизм. Тогда для любого характера х группы
непрерывный гомоморфизм. Тогда для любого характера х группы  функция
функция  является характером группы классов иделей, т. е. характером Гекке. Множество
является характером группы классов иделей, т. е. характером Гекке. Множество  простых идеалов, не принадлежащих
простых идеалов, не принадлежащих  можно следующим образом погрузить в
можно следующим образом погрузить в  Пусть
Пусть  — элемент первого порядка относительно идеала
— элемент первого порядка относительно идеала  Этому элементу соответствует идель, у которого
Этому элементу соответствует идель, у которого  -компонента равна
-компонента равна  , а остальные — 1. Класс
, а остальные — 1. Класс  по модулю
по модулю  не зависит от выбора простого элемента; отображение, ставящее в соответствие идеалу
не зависит от выбора простого элемента; отображение, ставящее в соответствие идеалу  этот класс, определяет интересующее
этот класс, определяет интересующее
нас вложение  можем также поставить в соответствие идеалу
можем также поставить в соответствие идеалу  идель
идель  Это и будет сделано в последующих примерах, чтобы не расходиться с классическим описанием для архимедовых нормирований.)
Это и будет сделано в последующих примерах, чтобы не расходиться с классическим описанием для архимедовых нормирований.)
Гомоморфизм X индуцирует некоторое отображение  и из предыдущей теоремы следует, что множество
и из предыдущей теоремы следует, что множество  Я-равномерно распределено в группе
Я-равномерно распределено в группе 
Подведем итоги этого обсуждения.
Теорема 6. Пусть  множество простых идеалов,
множество простых идеалов,  отображение, которое определяется так. Для каждого идеала
отображение, которое определяется так. Для каждого идеала  выберем простой элемент
выберем простой элемент  и обозначим символом
и обозначим символом  идель, все компоненты которого, кроме
идель, все компоненты которого, кроме  равны 1, а
равны 1, а  равна
равна  Множество
Множество  представим как объединение подмножеств
представим как объединение подмножеств  состоящих из тех
состоящих из тех  для которых
для которых  Пусть
Пусть  компактная коммутативная группа,
компактная коммутативная группа,  непрерывный эпиморфизм, ядро которого содержит
непрерывный эпиморфизм, ядро которого содержит  но не содержит
но не содержит  Тогда множество
Тогда множество  -равномерно распределено в группе
-равномерно распределено в группе 
Можно, например, положить  (это — конечная группа), а в качестве X взять канонический гомоморфизм. Это даст равномерное распределение простых идеалов в
(это — конечная группа), а в качестве X взять канонический гомоморфизм. Это даст равномерное распределение простых идеалов в  -классах идеалов. Оставляем читателю в качестве упражнения вывод равномерного распределения простых идеалов в обычных арифметических прогрессиях (теорема Дирихле).
-классах идеалов. Оставляем читателю в качестве упражнения вывод равномерного распределения простых идеалов в обычных арифметических прогрессиях (теорема Дирихле).
Рассмотрим, наконец, гауссово поле  Пусть
Пусть  состоит из архимедова нормирования. Имеем
состоит из архимедова нормирования. Имеем

где  мультипликативная группа комплексных чисел. Идеалы можно рассматривать как точки первого квадранта гауссовой плоскости. Беря в качестве X радиальную проекцию на единичную окружность, получим равномерное распределение идеалов и простых идеалов в секторах.
мультипликативная группа комплексных чисел. Идеалы можно рассматривать как точки первого квадранта гауссовой плоскости. Беря в качестве X радиальную проекцию на единичную окружность, получим равномерное распределение идеалов и простых идеалов в секторах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДВАРИТЕЛЬНЫЕ ТРЕБОВАНИЯ
- Глава I. ЦЕЛЫЕ АЛГЕБРАИЧЕСКИЕ ЧИСЛА
- § 2. Целое замыкание
- § 3. Простые идеалы
- § 4. Китайская теорема об остатках
- § 5. Расширения Галуа
- § 6. Дедекиндовы кольца
- 7. Дискретно нормированные кольца
- Глава II. ПОПОЛНЕНИЯ
- § 2. Многочлены над полными полями
- § 3. Некоторые фильтрации
- § 4. Неразветвленные расширения
- § 5. Слабо разветвленные расширения
- Глава III. ДИФФЕРЕНТА И ДИСКРИМИНАНТ
- § 2. Дифферента и ветвление
- § 3 Дискриминант
- Глава IV. КРУГОВЫЕ ПОЛЯ
- § 2. Квадратичные поля
- § 3. Символ Артина
- § 4. Лемма Артина
- Глава V. ПАРАЛЛЕЛОТОПЫ
- § 2. Точки решетки в параллелотопах
- § 3. Вычисление одного объема
- § 4. Константа Минковского
- Глава VI. ИДЕЛИ И АДЕЛИ
- § 2. Адели
- § 3. Идели
- Глава VII. ФУНКЦИОНАЛЬНОЕ УРАВНЕНИЕ
- § 1. Локальная аддитивная двойственность
- § 2. Локальная мультипликативная теория
- § 3. Локальное функциональное уравнение
- § 4. Локальные вычисления
- § 5. Ограниченные прямые произведения
- § 6. Глобальная аддитивная двойственность. Теорема Римана-Роха
- § 7. Глобальное функциональное уравнение
- § 8. Глобальные вычисления
- Глава VIII. ПЛОТНОСТЬ ПРОСТЫХ ИДЕАЛОВ И ТАУБЕРОВА ТЕОРЕМА
- § 1. Интеграл Дирихле
- § 2. Тауберова теорема Икеара
- § 3. Тауберова теорема для рядов Дирихле
- § 4. Некоторые теоремы о сходимости
- § 5. Плотности
- Глава IX. ТЕОРЕМА БРАУЭРА—ЗИГЕЛЯ
- § 1. Верхняя оценка для вычета
- § 2. Нижняя оценка для вычета
- § 3. Сравнение вычетов в нормальных расширениях
- § 4. Окончание доказательства
- Приложение — лемма Брауэра
- Глава Х. ЯВНЫЕ ФОРМУЛЫ
- § 1. Вейерштрассово разложение L-ряда
- § 2. Оценка функции …
- § 3. Основная сумма
- § 4. Вычисление суммы: первая часть
- § 5. Вычисление суммы: вторая часть