| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. Математические обозначения
В механике твердого тела векторы играют важную роль. Векторная величина обозначается буквой жирного шрифта. Вектор  можно представить как линейную комбинацию трех взаимно ортогональных единичных векторов
можно представить как линейную комбинацию трех взаимно ортогональных единичных векторов 

Единичные векторы являются базисными векторами векторного базиса (называемого также базисом отсчета или просто базисом), который обозначается символом е. Везде в книге предполагается, что базисные векторы векторных базисов образуют правые системы. Скалярные величины  в уравнении (1.1) являются координатами вектора
в уравнении (1.1) являются координатами вектора  в базисе
в базисе  или, короче, координатами
или, короче, координатами  . Отметим, что термин вектор употребляется только для величины
. Отметим, что термин вектор употребляется только для величины  а не как сокращенное название для координатной тройки величин
а не как сокращенное название для координатной тройки величин  , как это обычно делается в тензорном исчислении
, как это обычно делается в тензорном исчислении  .
.
В механике твердого тела обычно приходится рассматривать несколько векторных базисов. В дальнейшем у базисов ставится верхний индекс в скобках. Например  Базисные векторы базиса
Базисные векторы базиса  обладают тем свойством, что скалярное произведение любых двух из них равно дельте Кронекера:
обладают тем свойством, что скалярное произведение любых двух из них равно дельте Кронекера:

Базисный вектор  базиса
базиса  можно представить как линейную комбинацию базисных векторов другого базиса
можно представить как линейную комбинацию базисных векторов другого базиса 

Все три уравнения можно записать в виде одного матричного уравнения:

Символ  который до сих пор использовался просто для обозначения базиса, благодаря этому уравнению определяется как матрица-столбец
который до сих пор использовался просто для обозначения базиса, благодаря этому уравнению определяется как матрица-столбец  базисных векторов. Показатель Т обозначает транспонирование. Величина
базисных векторов. Показатель Т обозначает транспонирование. Величина  есть
есть  -матрица, составленная из координат
-матрица, составленная из координат  векторов (а — индекс строки).
векторов (а — индекс строки).
Все матрицы отмечаются чертой под символом. Употребление буквы жирного шрифта для  указывает на то, что элементами этой матрицы являются векторы. Уравнение (1.3) показывает, что матричное произведение
указывает на то, что элементами этой матрицы являются векторы. Уравнение (1.3) показывает, что матричное произведение  вычисляется по общему правилу умножения матричной алгебры, хотя один множитель составлен из скаляров, а другой — из векторов.
вычисляется по общему правилу умножения матричной алгебры, хотя один множитель составлен из скаляров, а другой — из векторов.
Скалярное произведение  двух базисных векторов, принадлежащих различным базисам, равно косинусу угла между этими векторами. В силу уравнений (1.3) и (1.2), оно также равно
двух базисных векторов, принадлежащих различным базисам, равно косинусу угла между этими векторами. В силу уравнений (1.3) и (1.2), оно также равно  . Это тождество объясняет название матрицы направляющих косинусов для
. Это тождество объясняет название матрицы направляющих косинусов для  Заменим в уравнении
Заменим в уравнении  выражением (1.3) и
выражением (1.3) и  аналогичным выражением с индексом
аналогичным выражением с индексом  вместо а. Из этого уравнения видно, что скалярное произведение строк а и
вместо а. Из этого уравнения видно, что скалярное произведение строк а и  равно
равно  . Отсюда следует,
. Отсюда следует,  представляет собой единичную матрицу, так как каждый элемент произведения матриц равен скалярному произведению двух строк матрицы
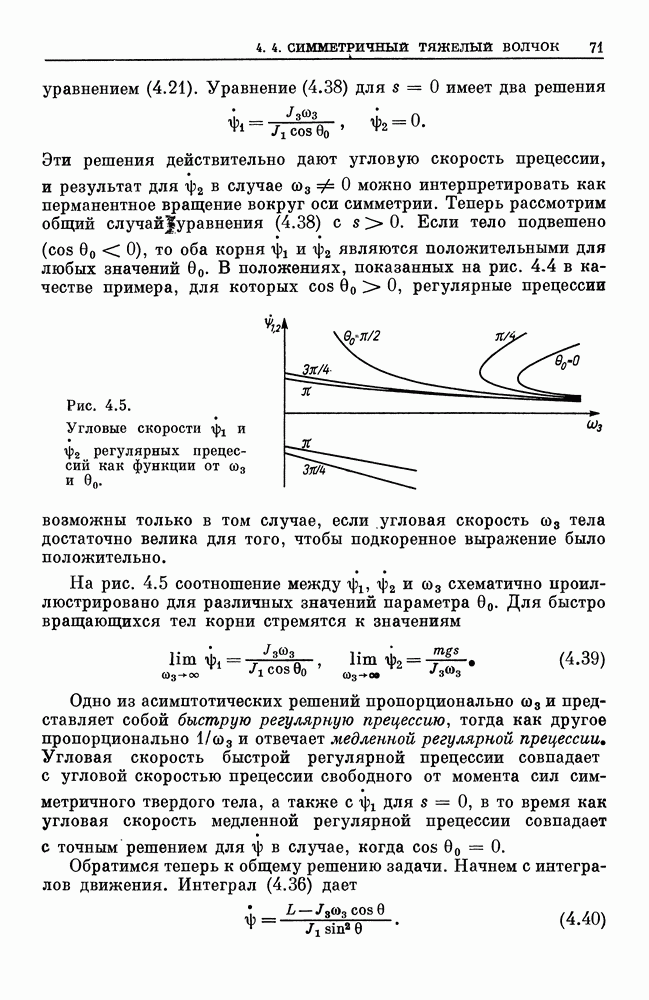
представляет собой единичную матрицу, так как каждый элемент произведения матриц равен скалярному произведению двух строк матрицы  Из этого тождества вытекают два важных свойства матрицы
Из этого тождества вытекают два важных свойства матрицы  . Первое: матрица, обратная
. Первое: матрица, обратная  равна транспонированной,
равна транспонированной,  . Отсюда следует, что обращение уравнения (1.4) есть
. Отсюда следует, что обращение уравнения (1.4) есть

Второе: детерминант матрицы  равен +1 или —1. Случай —1 имеет место только тогда, когда один из двух базисов
равен +1 или —1. Случай —1 имеет место только тогда, когда один из двух базисов  образует правую систему, а другой — левую. В нашем случае это не имеет места, так что
образует правую систему, а другой — левую. В нашем случае это не имеет места, так что

Правую часть равенства (1.1) можно представить в форме матричного произведения. Для этого введем в рассмотрение матрицу-столбец  составленную из координат
составленную из координат  в базисе
в базисе  (более короткое название для
(более короткое название для  — матрица координат
— матрица координат  в
в  ). Тогда уравнение (1.1) примет вид
). Тогда уравнение (1.1) примет вид

или

В двух разных базисах  вектор
вектор  имеет разные матрицы координат. Они обозначаются соответственно через и
имеет разные матрицы координат. Они обозначаются соответственно через и  . Уравнение (1.7) приводит к тождеству
. Уравнение (1.7) приводит к тождеству

Подставим вместо  правую часть соотношения (1.5). Тогда получим
правую часть соотношения (1.5). Тогда получим

или

Это соотношение представляет собой правило преобразования координат вектора. Оно показывает, что матрица направляющих косинусов служит также матрицей преобразования координат. Отметим удобное для запоминания расположение верхних индексов  и
и 
Скалярное произведение двух векторов a и b можно записать в виде матричного произведения. Обозначим через  матрицы координат векторов a и b соответственно в некотором векторном базисе
матрицы координат векторов a и b соответственно в некотором векторном базисе  . Тогда
. Тогда  Часто матрицы координат двух векторов
Часто матрицы координат двух векторов  известны в двух разных базисах, скажем
известны в двух разных базисах, скажем  . Тогда
. Тогда 
Рассмотрим далее задачу на собственные значения  для данной матрицы
для данной матрицы  направляющих косинусов, связывающей два базиса
направляющих косинусов, связывающей два базиса  Это уравнение является частным случаем уравнения (1.9), когда
Это уравнение является частным случаем уравнения (1.9), когда  Поскольку длина вектора одна и та же в обоих базисах, суммы квадратов элементов
Поскольку длина вектора одна и та же в обоих базисах, суммы квадратов элементов  должны быть равными. Отсюда следует, что абсолютные значения всех (вещественных или комплексных) собственных значений X равны единице. Характеристический полином
должны быть равными. Отсюда следует, что абсолютные значения всех (вещественных или комплексных) собственных значений X равны единице. Характеристический полином  с единичной матрицей Е представляет собой уравнение третьей степени. Следовательно, существует по крайней мере одно вещественное собственное значение с
с единичной матрицей Е представляет собой уравнение третьей степени. Следовательно, существует по крайней мере одно вещественное собственное значение с  . То, что это собственное значение есть
. То, что это собственное значение есть  следует из факта, что три собственных значения
следует из факта, что три собственных значения  удовлетворяют уравнению
удовлетворяют уравнению  Координаты вещественного собственного вектора и, отвечающего собственному значению
Координаты вещественного собственного вектора и, отвечающего собственному значению  определяются из уравнения
определяются из уравнения

Это уравнение показывает, что для любой матрицы  направляющих косинусов существует (по крайней мере) один вещественный
направляющих косинусов существует (по крайней мере) один вещественный
вектор  координаты которого являются одними и теми же в обоих базисах
координаты которого являются одними и теми же в обоих базисах  Отсюда следует
Отсюда следует
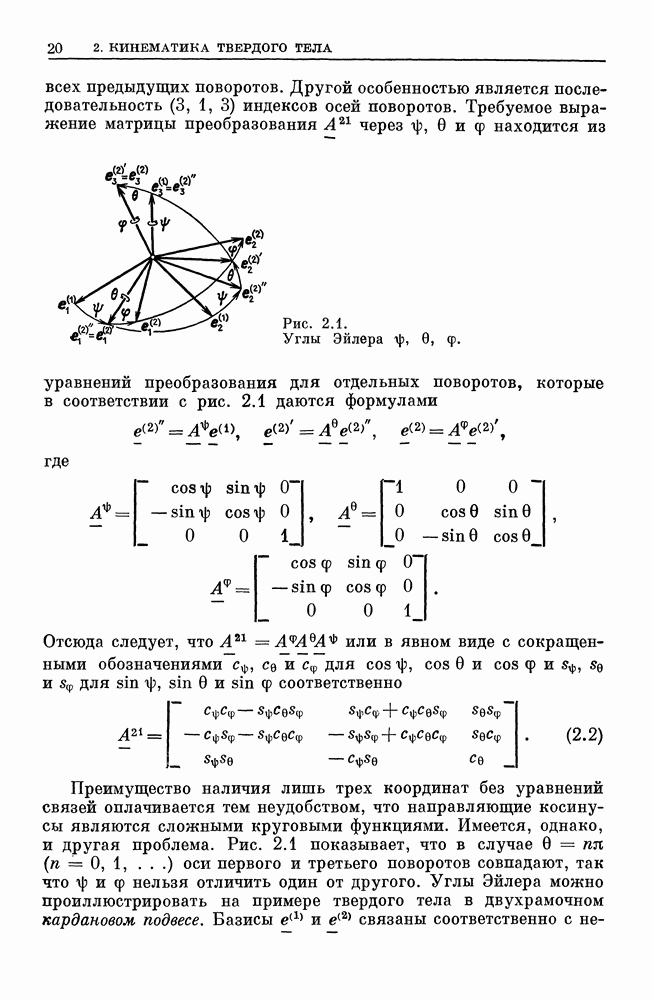
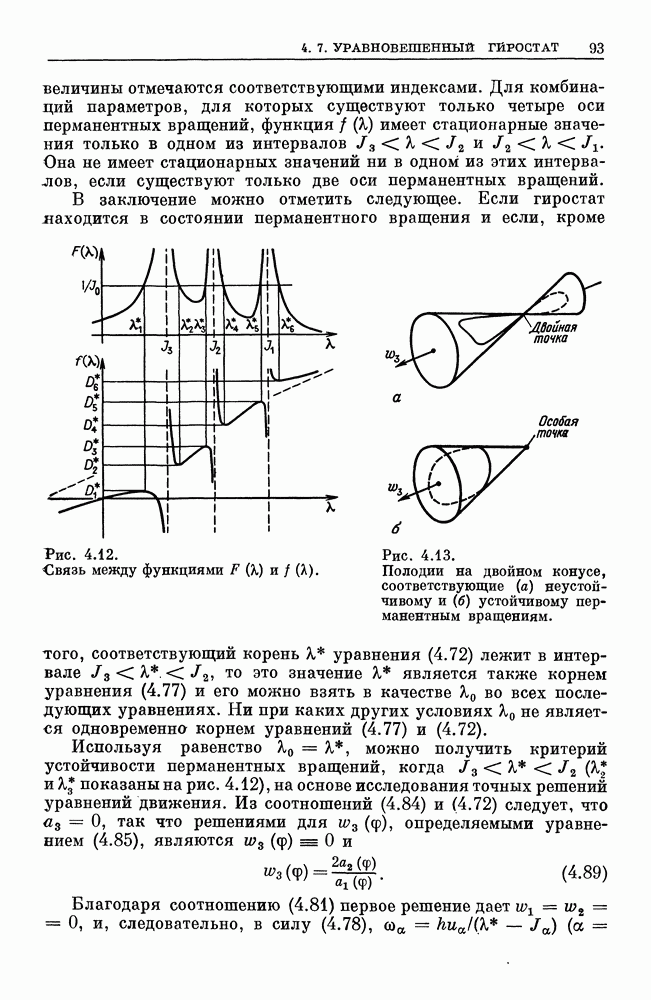
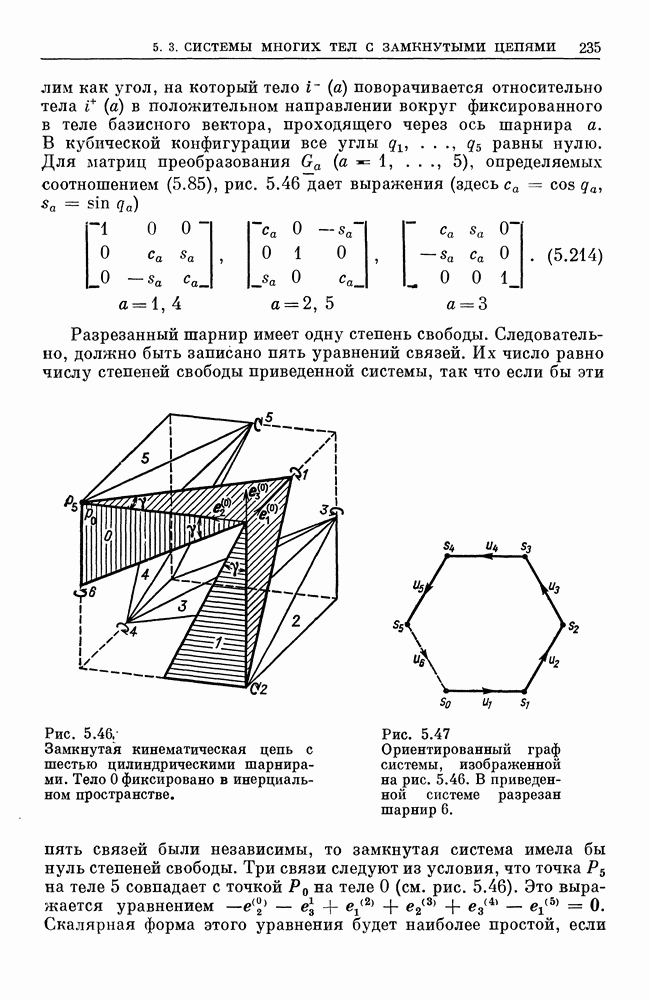
Теорема Эйлера. Два произвольно ориентированных базиса  с общим началом Р могут быть приведены в совпадение один с другим в результате поворота одного из них на некоторый угол вокруг оси, которая проходит через Р и имеет направление собственного вектора и, определяемого уравнением (1.10).
с общим началом Р могут быть приведены в совпадение один с другим в результате поворота одного из них на некоторый угол вокруг оси, которая проходит через Р и имеет направление собственного вектора и, определяемого уравнением (1.10).
Наряду с векторами важную роль в динамике твердого тела играют тензоры второго порядка. В его наиболее общей форме тензор  есть сумма диадных произведений двух векторов:
есть сумма диадных произведений двух векторов:

Тензор представляет собой оператор. Его скалярное произведение на вектор  справа определяется как вектор:
справа определяется как вектор:

Аналогично скалярное произведение тензора  на вектор
на вектор  слева определяется как вектор
слева определяется как вектор

Если во всех диадных произведениях, составляющих тензор  порядок множителей изменить на обратный, то получим новый тензор. Он называется тензором, сопряженным с
порядок множителей изменить на обратный, то получим новый тензор. Он называется тензором, сопряженным с  и обозначается символом
и обозначается символом 

В векторной алгебре справедлив дистрибутивный закон:

Следовательно, диадные произведения в тензоре также дистрибутивны:

Поэтому можно в правой части соотношения (1.11) все векторы разложить в некотором базисе  и получить выражение
и получить выражение

Девять скаляров  называются координатами тензора
называются координатами тензора  в базисе
в базисе  (отметим, что под тензором понимается не эта совокупность координат, а только величина
(отметим, что под тензором понимается не эта совокупность координат, а только величина  Они образуют
Они образуют  -матрицу
-матрицу
координат  . С помощью этой матрицы тензор примет вид
. С помощью этой матрицы тензор примет вид

Соотношение (1.15) дает непосредственный способ построения матрицы  из матриц координат векторов
из матриц координат векторов  . Пусть эти последние матрицы будут
. Пусть эти последние матрицы будут  . Подстановка соотношений (1.7) и (1.8) в (1.11) дает
. Подстановка соотношений (1.7) и (1.8) в (1.11) дает

Сравнение с соотношением (1.15) показывает, что

Отсюда и из соотношения (1.13) следует, что матрица координат тензора, сопряженного с  получается из матрицы координат тензора
получается из матрицы координат тензора  в результате транспонирования. С учетом соотношений (1.14) и (1.1) вектор
в результате транспонирования. С учетом соотношений (1.14) и (1.1) вектор  примет вид
примет вид

Его матрица координат в базисе  равна поэтому произведению
равна поэтому произведению  матриц координат
матриц координат  и
и  в е. Тот же самый результат получается более формальным путем при подстановке соотношений (1.15) и (1.7) для
в е. Тот же самый результат получается более формальным путем при подстановке соотношений (1.15) и (1.7) для  и
и  соответственно:
соответственно:

В этом выражении появляется новый тип матричного произведения, а именно скалярное произведение  двух матриц, элементами которых являются векторы. Далее нам встретится еще другое матричное произведение, называемое векторным произведением двух векторных матриц. Эти два произведения определяются следующим образом. Пусть Р есть
двух матриц, элементами которых являются векторы. Далее нам встретится еще другое матричное произведение, называемое векторным произведением двух векторных матриц. Эти два произведения определяются следующим образом. Пусть Р есть 
 -матрица, элементами которой являются векторы
-матрица, элементами которой являются векторы 
 -матрица с векторными элементами
-матрица с векторными элементами  . Тогда скалярное произяедение
. Тогда скалярное произяедение  есть
есть 
 -матрица с элементами
-матрица с элементами

а векторное произведение  есть векторная
есть векторная  -матрица с элементами
-матрица с элементами

Эти определения являются обобщением общего правила умножения матриц. Вернемся теперь к соотношению (1.17). Согласно только что приведенному определению, скалярное произведение  есть единичная матрица, так что в соответствии с соотношением
есть единичная матрица, так что в соответствии с соотношением 
Особый интерес представляет тензор

матрицей координат которого служит единичная матрица. Если этот тензор умножить скалярно на произвольный вектор  то в результате получим сам вектор
то в результате получим сам вектор  По этой причине Е называется единичным тензором.
По этой причине Е называется единичным тензором.
При помощи соотношения (1.5) не представляет труда установить закон преобразования матрицы координат тензора, когда вместо базиса  используется для разложения другой базис
используется для разложения другой базис  . Пусть
. Пусть  — матрицы координат
— матрицы координат  в двух базисах; тогда, согласно соотношению (1.15), справедливо тождество
в двух базисах; тогда, согласно соотношению (1.15), справедливо тождество

Подставим в правую часть вместо  значение (1.5). Это дает
значение (1.5). Это дает

или

Обратим внимание и здесь на удобное для запоминания расположение верхних индексов.
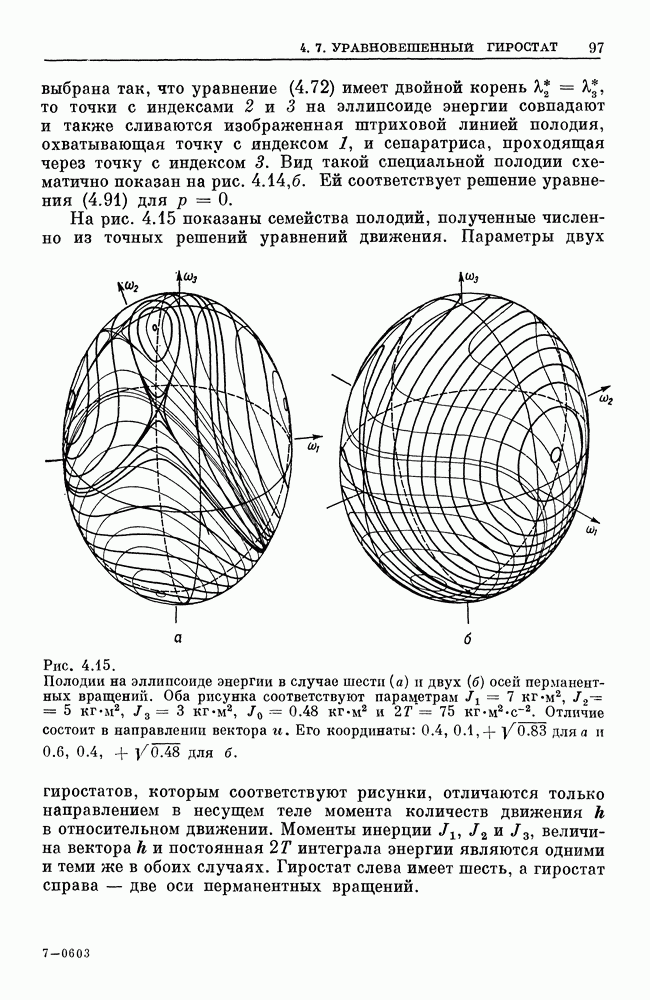
В механике твердого тела встречаются тензоры с симметрическими и кососимметрическими матрицами координат. Тензор инерции, который будет определен в разд. 3.1, и единичный тензор Е имеют симметрические матрицы координат. Тензоры с несимметрическими матрицами координат связаны с векторными произведениями. Рассмотрим сначала двойное векторное произведение  . Его можно записать в форме
. Его можно записать в форме

т. е. в форме скалярного произведения тензора  на вектор
на вектор  Если
Если  суть матрицы координат
суть матрицы координат  соответственно
соответственно
в некотором векторном базисе, то матрица координат тензора в этом базисе представляет собой кососимметрическую матрицу:

Вектор, равный векторному произведению с  также можно представить как скалярное произведение тензора на вектор
также можно представить как скалярное произведение тензора на вектор  . Для этого построим два вектора a и b, удовлетворяющих уравнению
. Для этого построим два вектора a и b, удовлетворяющих уравнению  Тогда искомый тензор снова определяется выражением
Тогда искомый тензор снова определяется выражением  , а его матрица координат дается соотношением (1.21). Эта матрица совпадает с матрицей
, а его матрица координат дается соотношением (1.21). Эта матрица совпадает с матрицей

где  — координаты вектора с в том же базисе, в котором вычисляются а и
— координаты вектора с в том же базисе, в котором вычисляются а и  Для этой матрицы введем символ с (читается — с с тильдой), так что вектор с
Для этой матрицы введем символ с (читается — с с тильдой), так что вектор с  имеет матрицу координат
имеет матрицу координат  Это обозначение упрощает переход от символических векторных уравнений к скалярным координатным уравнениям
Это обозначение упрощает переход от символических векторных уравнений к скалярным координатным уравнениям  Для преобразования матричных уравнений в координатной форме нам потребуются следующие основные правила. Если к — скаляр, то
Для преобразования матричных уравнений в координатной форме нам потребуются следующие основные правила. Если к — скаляр, то

Более того.

Из  следует, что
следует, что  . Тождество
. Тождество  а дает
а дает

а для частного случая  имеем
имеем

При помощи единичного тензора Е вектор двойного векторного произведения  можно записать в форме
можно записать в форме

Соответствующее уравнение в координатной форме имеет вид  , где Е — единичная матрица. Так как это соотношение выполняется для любого
, где Е — единичная матрица. Так как это соотношение выполняется для любого  , то справедливо тождество
, то справедливо тождество

В соответствии с соотношением (1.20) матрица координат  есть
есть  . Ее можно также записать в форме
. Ее можно также записать в форме  Так как обе формы тождественны для любого
Так как обе формы тождественны для любого  то справедливо тождество
то справедливо тождество

Наконец, правило преобразования координат тензора (соотношение (1.19)) показывает, что

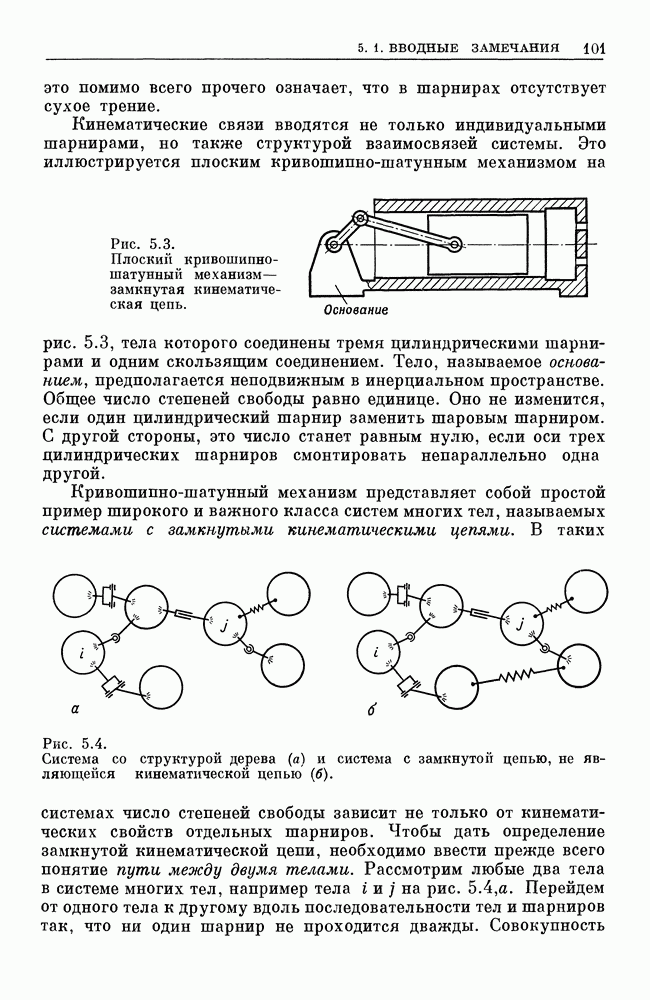
Системы линейных векторных уравнений можно записать в очень компактной форме, если наряду с матрицами с векторными элементами использовать матрицы с тензорными элементами. Такие матрицы обозначаются прописными буквами жирного шрифта с чертой под буквами. Они имеют общий вид

с произвольным числом строк и столбцов. Скалярное произведение 
 -матрицы
-матрицы  справа на векторную матрицу
справа на векторную матрицу  , элементы которой суть
, элементы которой суть  определяется как
определяется как 
 -матрица с элементами
-матрица с элементами

Аналогичное определение справедливо для скалярного произведения  слева на
слева на 
 -матрицу с элементами
-матрицу с элементами  . Следующий пример иллюстрирует практическое использование этих понятий. Допустим, что желательно записать скаляр
. Следующий пример иллюстрирует практическое использование этих понятий. Допустим, что желательно записать скаляр

в виде матричного произведения. Это можно сделать в символической форме  с множителями
с множителями

Если желательно вычислить с, то более удобно следующее выражение, составленное из матриц координат. Пусть  суть матрицы координат
суть матрицы координат  соответственно в некотором общем векторном базисе. Тогда
соответственно в некотором общем векторном базисе. Тогда

Это выражение в свою очередь можно записать в виде матричного произведения  , где
, где

суть блочные скалярные матрицы с субматрицами  и соответственно.
и соответственно.
Задачи
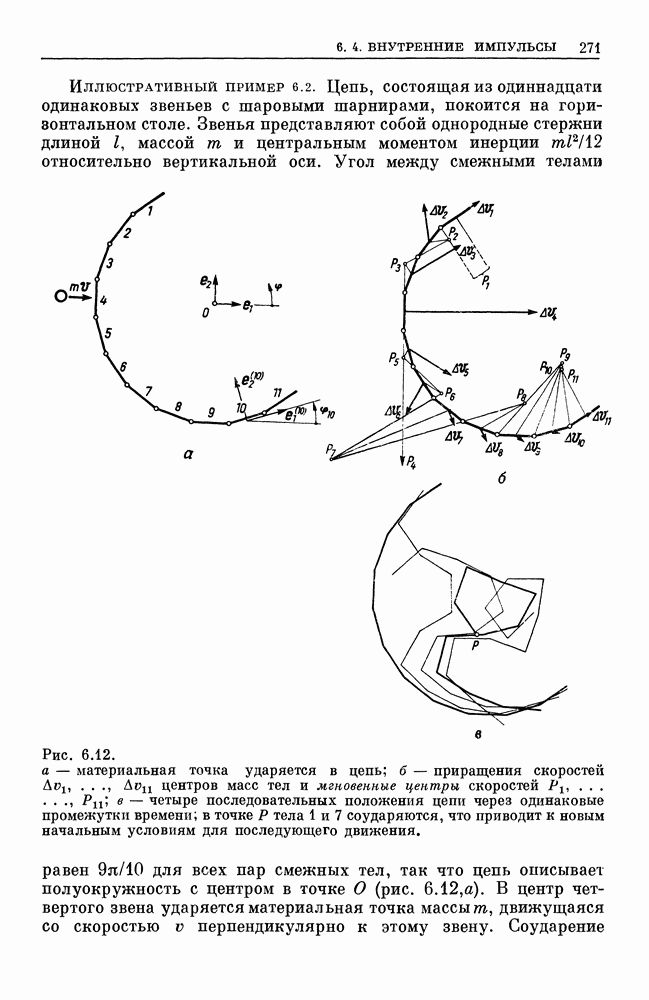
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- От редактора перевода
- Предисловие
- 1. Математические обозначения
- 2. Кинематика твердого тела
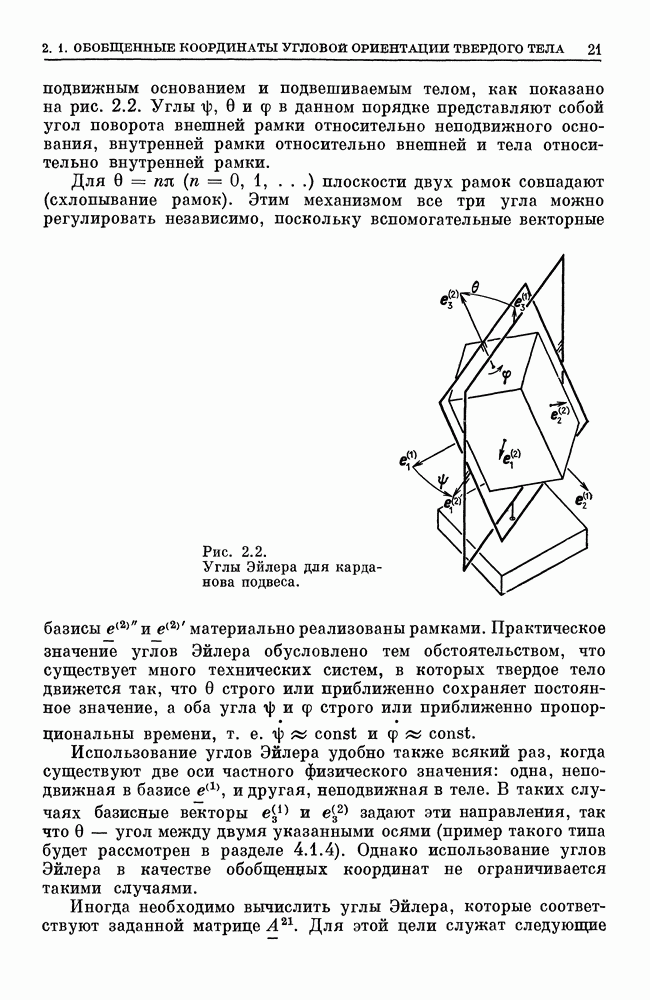
- 2.1. Обобщенные координаты угловой ориентации твердого тела
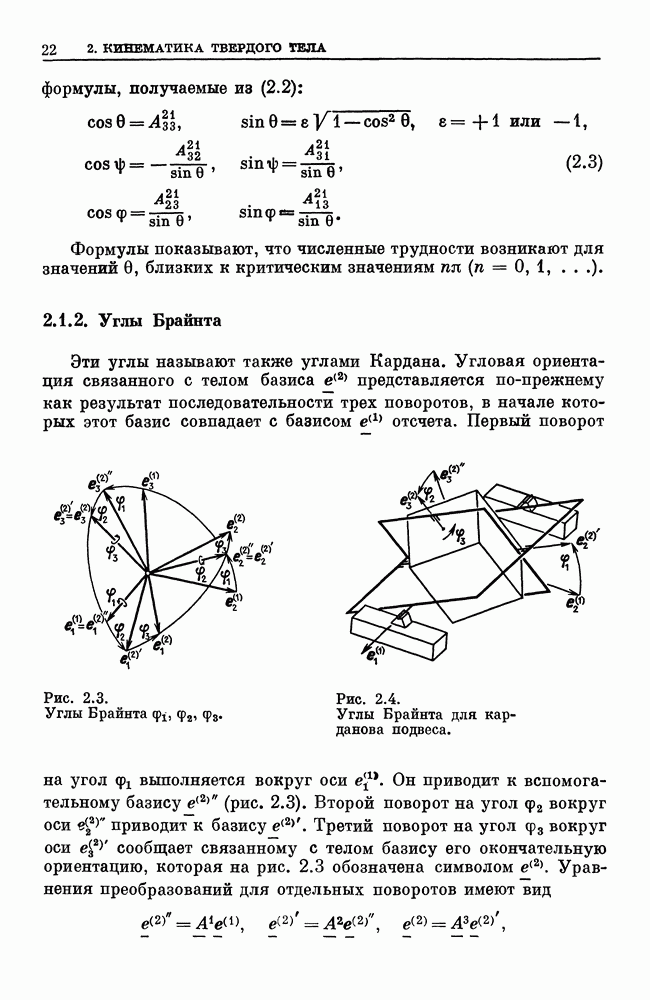
- 2.1.2. Углы Брайнта
- 2.1.3. Параметры Эйлера
- 2.2. Понятие угловой скорости
- 2.3. Соотношения между угловой скоростью тела и обобщенными координатами, описывающими угловую ориентацию тела
- 3.1. Кинетическая энергия
- 3.2. Момент количеств движения
- 3.3. Свойства моментов и произведений инерции
- 3.3.2. Переход к другому базису отсчета без изменения полюса
- 3.3.3. Главные оси и главные моменты инерции
- 3.3.4. Инварианты и неравенства для моментов и произведений инерции
- 3.4. Теорема об изменении момента количеств движения
- 3.5. Принцип Даламбера в применении к твердому телу
- 4. Классические задачи механики твердого тела
- 4.1. Движение по инерции несимметричного твердого тела
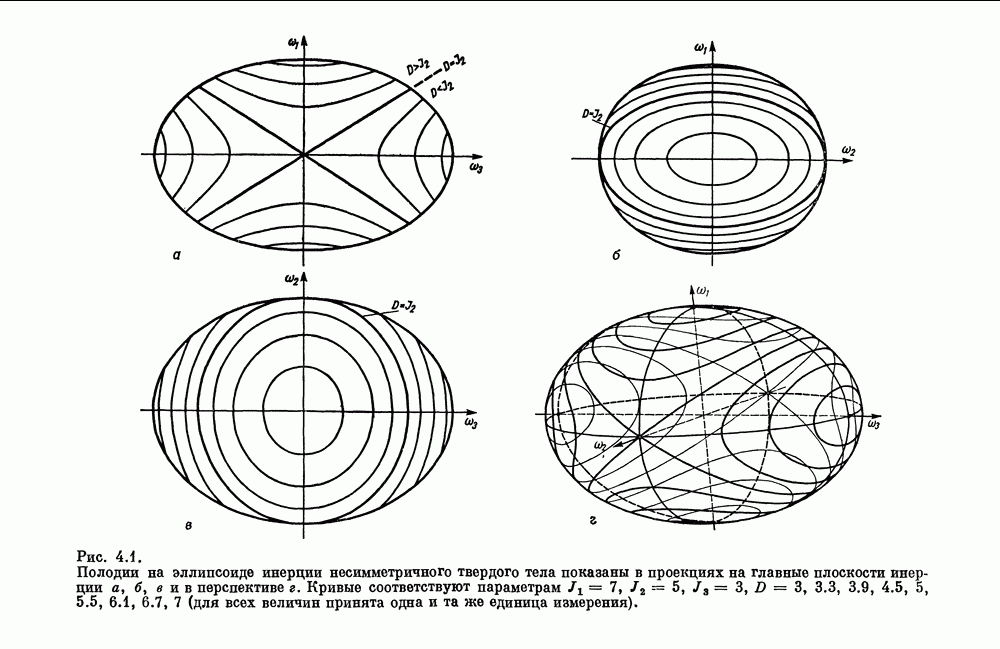
- 4.1.1. Полодии и перманентные вращения
- 4.1.2. Геометрическая интерпретация движения Пуансо
- 4.1.3. Решение уравнений движения Эйлера
- 4.1.4. Решение кинематических дифференциальных уравнений
- 4.2. Симметричное твердое тело в отсутствие момента сил
- 4.3. Самовозбуждаемое симметричное твердое тело
- 4.4. Симметричный тяжелый волчок
- 4.5. Симметричное тяжелое тело в кардановом подвесе
- 4.6. Гиростат. Общий анализ
- 4.7. Уравновешенный гиростат
- 4.7.2. Решение динамических уравнений движения
- 5. Общие системы многих тел
- 5.2. Уравнения движения для систем со структурой дерева
- 5.2.2. Системы с шаровыми шарнирами. Одно тело соединено с внешним телом, совершающим заданное движение
- 5.2.3. Частный случай плоских движений
- 5.2.4. Системы с шаровыми шарнирами, не связанные с внешним телом, совершающим заданное движение
- 5.2.5. Частный случай спутника на круговой орбите, состоящего из многих тел
- 5.2.6. Системы с шаровыми, универсальными и цилиндрическими шарнирами
- 5.2.6.2. Кинематика движения тел относительно инерциального пространства
- 5.2.6.3. Исключение моментов сил реакций связей
- 5.2.6.4. Случай управляемых переменных
- 5.2.7. Инструкции для программирования
- 5.2.8. Системы с произвольными голономными связями в шарнирах
- 5.2.8.1. Составление уравнения принципа Даламбера
- 5.2.8.2. Кинематика движения смежных тел относительно друг друга
- 5.2.8.3. Кинематика движения тел относительно инерциального пространства
- 5.2.8.4. Возможная работа, совершаемая в шарнирах
- 5.2.8.5. Уравнения движения
- 5.2.9. Внутренние силы и моменты в шарнирах системы с произвольными голономными связями
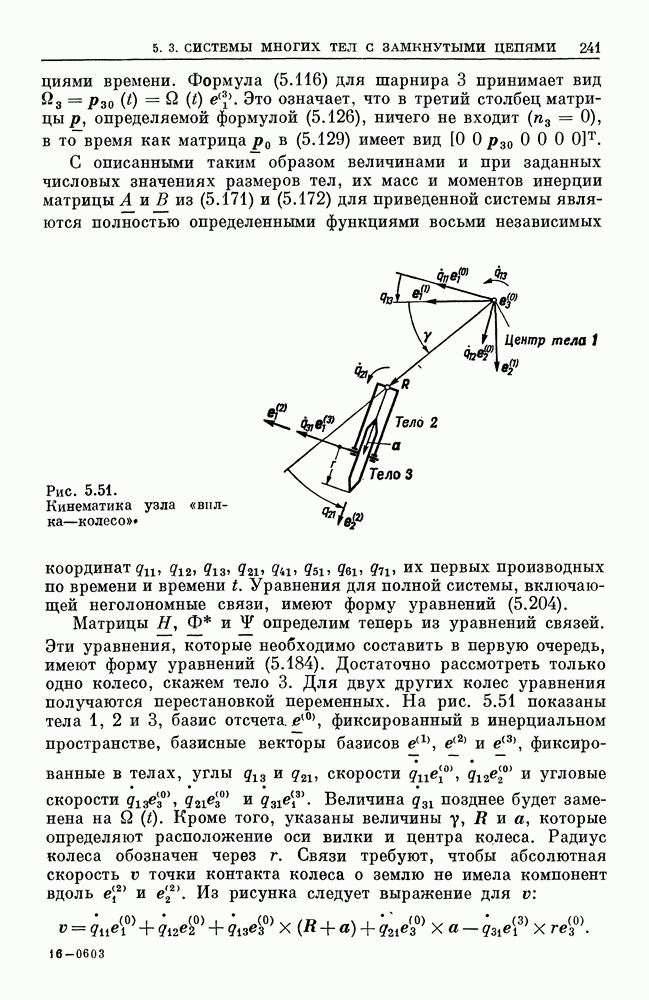
- 5.3. Системы многих тел с замкнутыми цепями и произвольными связями
- 5.3.1. Математическое описание структуры взаимосвязей. Обобщение раздела 5.2.1
- 5.3.2. Уравнения движения
- 5.3.2.2. Возможная работа в разрезанных шарнирах
- 5.3.2.3. Критерии выбора приведенной системы
- 5.4. Заключительные замечания
- 6. Задачи удара в голономных системах многих тел
- 6.2. Мгновенные приращения скоростей
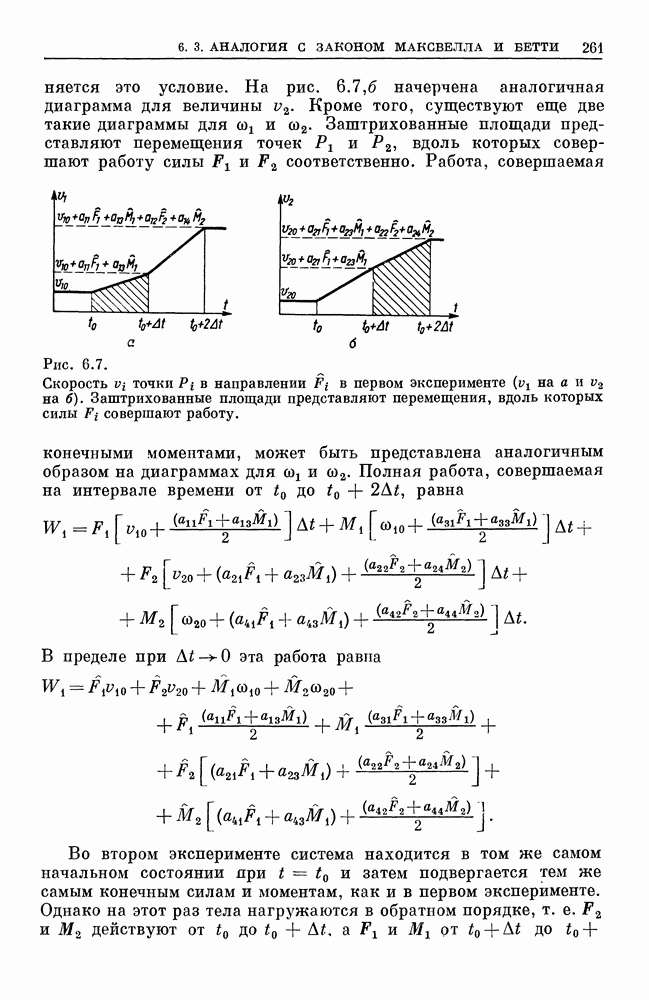
- 6.3. Аналогия с законом Максвелла и Бетти
- 6.4. Внутренние импульсы и импульсные пары в шарнирах
- Ответы на задачи
- Список литературы
- Список обозначений