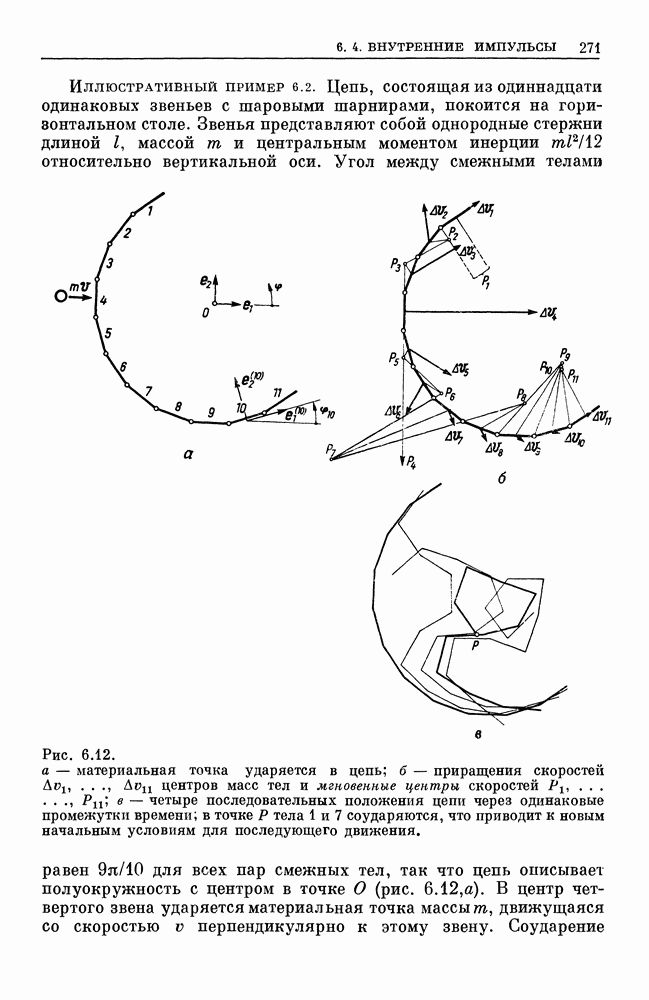
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4. Симметричный тяжелый волчок
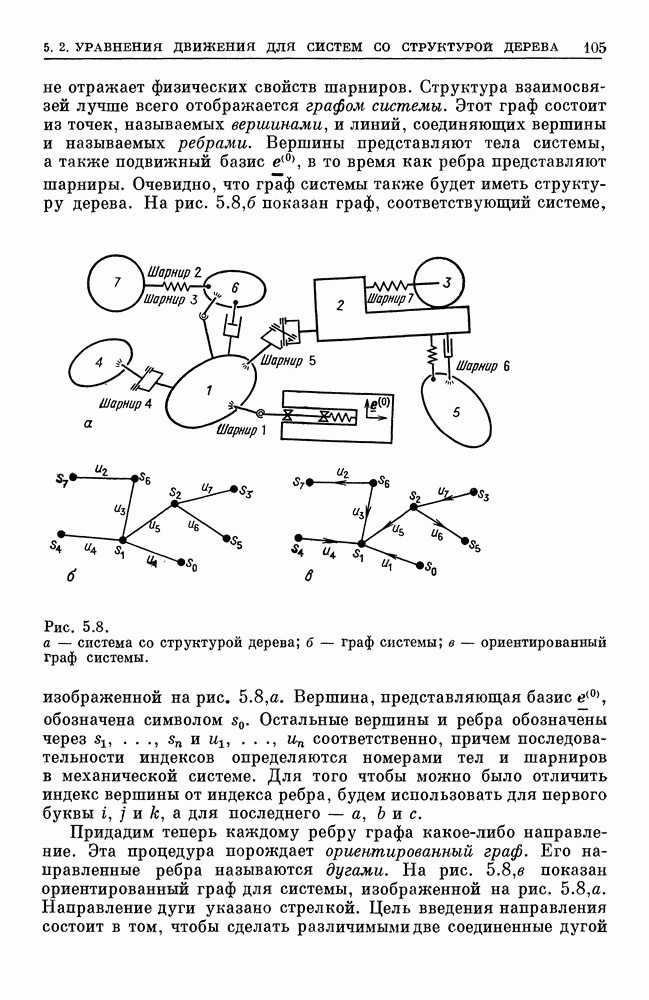
Рассматривается твердое тело, которое в инерциальном пространстве оперто в одной точке, не совпадающей с центром масс тела. На тело действует только сила тяжести. В литературе эта система известна как тяжелый волчок. Общее решение его уравнений движения неизвестно. Оно известно только для частного случая, когда распределение масс тела обладает осевой симметрией и, кроме того, точка опоры находится на оси симметрии. На рис. 4.4 изображен такой симметричный тяжелый волчок в положении, когда точка опоры расположена ниже центра масс. Эта система, решение для которой было найдено Лагранжем, служит предметом последующего рассмотрения.

Рис. 4.4. Симметричный тяжелый волчок и его координаты 
Момент силы тяжести зависит от ориентации тела в инерциальном пространстве. Следствием этой функциональной зависимости является то обстоятельство, что уравнения движения Эйлера связаны с кинематическими дифференциальными уравнениями, которыми определяется  через обобщенные координаты. По этой причине мы не будем использовать уравнения Эйлера. Вместо них лучше составить дифференциальные уравнения второго порядка для соответствующим образом выбранных обобщенных координат и решать эти уравнения.
через обобщенные координаты. По этой причине мы не будем использовать уравнения Эйлера. Вместо них лучше составить дифференциальные уравнения второго порядка для соответствующим образом выбранных обобщенных координат и решать эти уравнения.
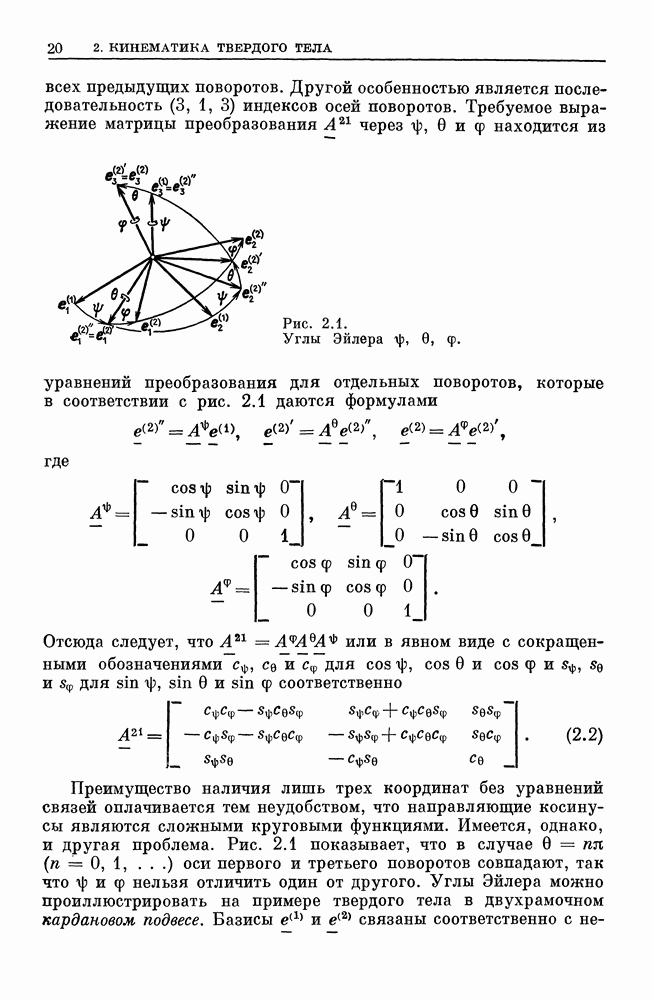
В теле, а также в инерциальном пространстве существуют важные с физической точки зрения направления, а именно ось симметрии в теле и вертикальная линия действия силы тяжести в инерциальном пространстве. Это наводит на мысль использовать в качестве обобщенных координат углы Эйлера, из которых  — угол между этими двумя направлениями. Углы Эйлера
— угол между этими двумя направлениями. Углы Эйлера  определим, как показано на рис. 2.1. Они связывают базис, неподвижный в теле, с базисом, неподвижным в инерциальном пространстве.
определим, как показано на рис. 2.1. Они связывают базис, неподвижный в теле, с базисом, неподвижным в инерциальном пространстве.
На рис. 4.4 связанный с телом базис не показан. Показаны базис  неподвижный в инерциальном пространстве, и базис
неподвижный в инерциальном пространстве, и базис  который не является неподвижным ни в теле, ни в инерциальном пространстве. Его базисный вектор
который не является неподвижным ни в теле, ни в инерциальном пространстве. Его базисный вектор  лежит на оси симметрии, а
лежит на оси симметрии, а  всегда перпендикулярен вертикали
всегда перпендикулярен вертикали  Этот базис совпадает с базисом
Этот базис совпадает с базисом  на рис. 2.1. Его абсолютная угловая скорость отличается от абсолютной угловой скорости
на рис. 2.1. Его абсолютная угловая скорость отличается от абсолютной угловой скорости  тела на составляющую» которая направлена вдоль оси симметрии и равна
тела на составляющую» которая направлена вдоль оси симметрии и равна  . В силу симметрии моменты инерции тела постоянны в
. В силу симметрии моменты инерции тела постоянны в  несмотря на движение этого базиса относительно тела.
несмотря на движение этого базиса относительно тела.
Уравнения движения получим из теоремы о кинетическом моменте в общей форме (3.15). Возьмем точку опоры О тела за начало отсчета в инерциальном пространстве. Абсолютная производная по времени  выражается через производную по времени
выражается через производную по времени  в базисе
в базисе  Согласно уравнению (2.23), две производные связаны соотношением
Согласно уравнению (2.23), две производные связаны соотношением

где  — абсолютная угловая скорость базиса
— абсолютная угловая скорость базиса  Используя рис. 4.4, находим
Используя рис. 4.4, находим

Подстановка в уравнения (4.26) и (3.15) приводит к искомым скалярным дифференциальным уравнениям движения

В последнем уравнении выражение в левой части равно

откуда следует первый интеграл

Его можно получить также непосредственно из третьего уравнения Эйлера, которое для  сводится к
сводится к  .
.
С учетом этого интеграла уравнения (4.29) и (4.30) принимают вид 

Эти уравнения дают еще два алгебраических интеграла. Если второе уравнение умножить на  то его можно переписать в форме
то его можно переписать в форме

С другой стороны, если уравнение (4.32) умножить на  , а уравнение (4.33) — на
, а уравнение (4.33) — на  и оба уравнения сложить, то найдем, что
и оба уравнения сложить, то найдем, что

Эти два интеграла можно также найти непосредственно, не обращаясь к уравнениям движения. Поскольку момент силы тяжести относительно вертикали  равен нулю, составляющая кинетического момента на это направление должна быть постоянной. Принимая во внимание соотношение (4.27) и геометрию системы, показанной на рис. 4.4, для величины
равен нулю, составляющая кинетического момента на это направление должна быть постоянной. Принимая во внимание соотношение (4.27) и геометрию системы, показанной на рис. 4.4, для величины  этой составляющей имеем выражение
этой составляющей имеем выражение

Это уравнение эквивалентно уравнению (4.34). Рассматриваемая система консервативна, так что ее полная энергия Е сохраняет
постоянное значение. Это дает

или, используя выражения для  из (4.28),
из (4.28),

Оно эквивалентно уравнению (4.35).
Перед изложением общего решения задачи рассмотрим два частных типа движений, которые могут быть реализованы при соответствующем выборе начальных условий. Одно из них представляет собой произвольное плоское движение маятника с  для которого единственной изменяющейся со временем координатой является угол
для которого единственной изменяющейся со временем координатой является угол  . В этом случае уравнения движения приводятся к уравнению
. В этом случае уравнения движения приводятся к уравнению  , а из трех интегралов движения оказывается нетривиальным только интеграл энергии
, а из трех интегралов движения оказывается нетривиальным только интеграл энергии  .
.
Эти два уравнения действительно представляют собой дифференциальное уравнение и интеграл энергии соответственно плоского физического маятника (отметим, что обычно в качестве независимой переменной используется  ). Второй частный тип движения характеризуется постоянным значением угла
). Второй частный тип движения характеризуется постоянным значением угла  .
.
При этом условии уравнение (4.33) дает  , кроме того, уравнение (4.31) приводится к
, кроме того, уравнение (4.31) приводится к  Эта геометрически простая форма движения известна под названием регулярной прецессии. Ось симметрии тела движется с постоянной угловой скоростью прецессии
Эта геометрически простая форма движения известна под названием регулярной прецессии. Ось симметрии тела движется с постоянной угловой скоростью прецессии  по круговому конусу с вертикальной осью
по круговому конусу с вертикальной осью  . Уравнение (4.32) при
. Уравнение (4.32) при  представляет собой квадратное уравнению относительно
представляет собой квадратное уравнению относительно  , которое имеет решения
, которое имеет решения

Следует отметить, что все полученные до сих пор результаты справедливы также для частного случая, когда  равно нулю, т. е. для симметричного тела, опертого в его центре масс, и на которое, следовательно, не действует момент сил. Из разд. 4.2 известно, что при этих условиях возможны только два типа движений, а именно перманентное вращение вокруг оси симметрии и прецессия с угловой скоростью прецессии
равно нулю, т. е. для симметричного тела, опертого в его центре масс, и на которое, следовательно, не действует момент сил. Из разд. 4.2 известно, что при этих условиях возможны только два типа движений, а именно перманентное вращение вокруг оси симметрии и прецессия с угловой скоростью прецессии  , определяемой
, определяемой
уравнением (4.21). Уравнение (4.38) для  имеет два решения
имеет два решения

Эти решения действительно дают угловую скорость прецессии, и результат для  в случае
в случае  можно интерпретировать как перманентное вращение вокруг оси симметрии. Теперь рассмотрим общий случай уравнения (4.38)
можно интерпретировать как перманентное вращение вокруг оси симметрии. Теперь рассмотрим общий случай уравнения (4.38)  . Если тело подвешено
. Если тело подвешено  , то оба корня
, то оба корня  являются положительными для любых значений
являются положительными для любых значений  . В положениях, показанных на рис. 4.4 в качестве примера, для которых
. В положениях, показанных на рис. 4.4 в качестве примера, для которых  регулярные прецессии возможны только в том случае, если угловая скорость
регулярные прецессии возможны только в том случае, если угловая скорость  тела достаточно велика для того, чтобы подкоренное выражение было положительно.
тела достаточно велика для того, чтобы подкоренное выражение было положительно.
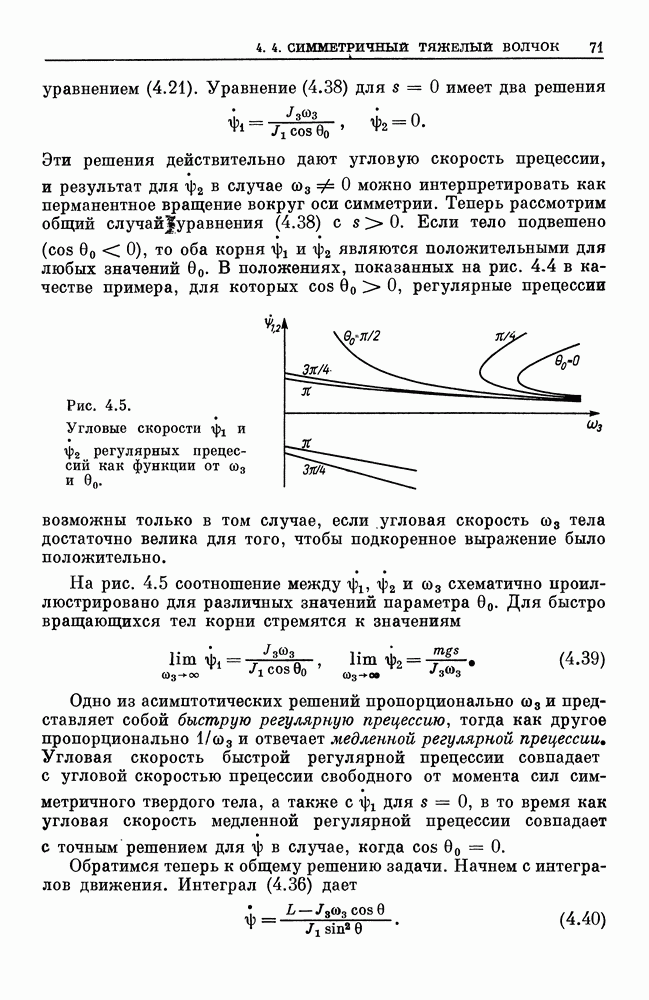
На рис. 4.5 соотношение между  схематично проиллюстрировано для различных значений параметра
схематично проиллюстрировано для различных значений параметра  . Для быстро вращающихся тел корни стремятся к значениям
. Для быстро вращающихся тел корни стремятся к значениям


Рис. 4.5. Угловые скорости и регулярных прецессий как функции от 
Одно из асимптотических решений пропорционально  и представляет собой быструю регулярную прецессию, тогда как другое пропорционально
и представляет собой быструю регулярную прецессию, тогда как другое пропорционально  и отвечает медленной регулярной прецессии. Угловая скорость быстрой регулярной прецессии совпадает с угловой скоростью прецессии свободного от момента сил симметричного твердого тела, а также с
и отвечает медленной регулярной прецессии. Угловая скорость быстрой регулярной прецессии совпадает с угловой скоростью прецессии свободного от момента сил симметричного твердого тела, а также с  для
для  в то время как угловая скорость медленной регулярной прецессии совпадает с точным решением для
в то время как угловая скорость медленной регулярной прецессии совпадает с точным решением для  в случае, когда
в случае, когда  .
.
Обратимся теперь к общему решению задачи. Начнем с интегралов движения. Интеграл (4.36) дает

Подстановка в интеграл (4.37) приводит к дифференциальному уравнению для  :
:

Как только известно решение  этого уравнения,
этого уравнения,  можно найти в виде квадратур из уравнений (4.40) и (4.31). С новой переменной
можно найти в виде квадратур из уравнений (4.40) и (4.31). С новой переменной

уравнение (4.41) после простых преобразований принимает вид

Выражение в правой части представляет собой кубический полином  . Относительно расположения его корней можно высказать следующие утверждения. Для
. Относительно расположения его корней можно высказать следующие утверждения. Для  , а также для и
, а также для и  этот полином принимает отрицательные значения. В пределе при
этот полином принимает отрицательные значения. В пределе при  он стремится к плюс бесконечности. Поэтому он имеет по крайней мере один вещественный корень
он стремится к плюс бесконечности. Поэтому он имеет по крайней мере один вещественный корень  . В силу соотношения (4.42) представляет интерес только интервал
. В силу соотношения (4.42) представляет интерес только интервал  .
.

Рис. 4.6. Схематичный вид функции  .
.
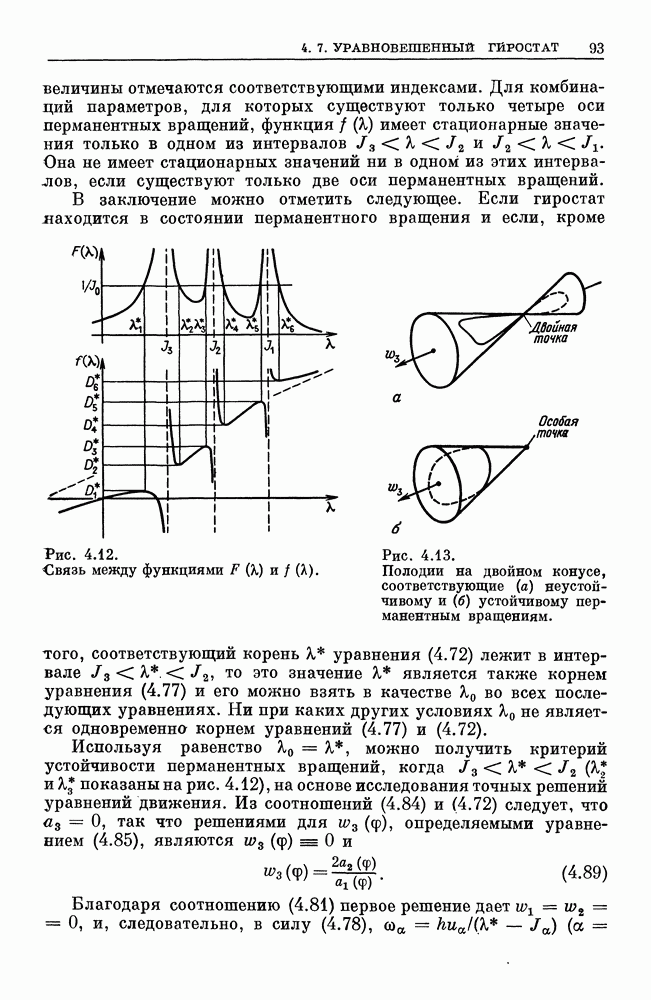
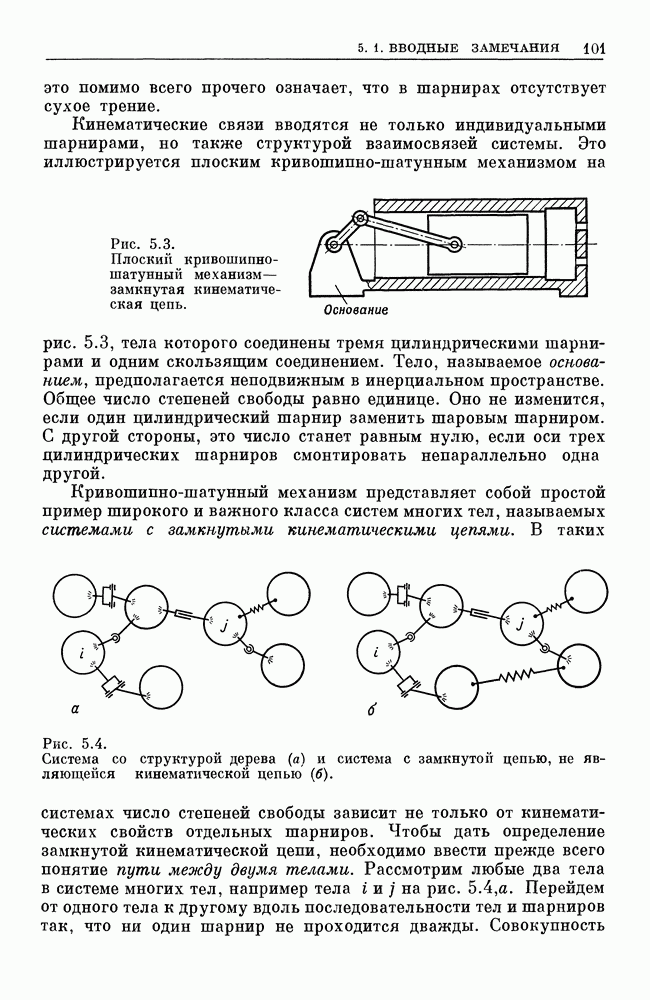
Поскольку для вещественных решений  должно быть неотрицательно, то где-то на этом интервале полином должен иметь или два вещественных корня, или один двойной вещественный корень. Поэтому для комбинаций параметров, соответствующих вещественным решениям, график функции
должно быть неотрицательно, то где-то на этом интервале полином должен иметь или два вещественных корня, или один двойной вещественный корень. Поэтому для комбинаций параметров, соответствующих вещественным решениям, график функции  имеет вид, схематично представленный на рис. 4.6. Корни
имеет вид, схематично представленный на рис. 4.6. Корни  имеют или одинаковые, или противоположные знаки. То, что оба случая физически реализуемы, можно показать на двух частных типах движения, исследованных ранее. Для маятниковых движений амплитуда 9 может быть выбрана так, что знак и
имеют или одинаковые, или противоположные знаки. То, что оба случая физически реализуемы, можно показать на двух частных типах движения, исследованных ранее. Для маятниковых движений амплитуда 9 может быть выбрана так, что знак и  всегда остается или отрицательным, или положительным. Для регулярной прецессии и постоянно. Предположим, что корни
всегда остается или отрицательным, или положительным. Для регулярной прецессии и постоянно. Предположим, что корни  занумерованы в порядке, указанном на рис. 4.6
занумерованы в порядке, указанном на рис. 4.6  . Используя эти корни, уравнение (4.43) приведем к виду
. Используя эти корни, уравнение (4.43) приведем к виду

Если и заменить новой переменной  определяемой уравнением
определяемой уравнением

то это уравнение после простых преобразований примет вид

где

Разделение переменных приводит к эллиптическому интегралу первого рода с модулем 

Он имеет решение  . Поэтому решением для
. Поэтому решением для  , в силу соотношений (4.44) и (4.42), будет
, в силу соотношений (4.44) и (4.42), будет

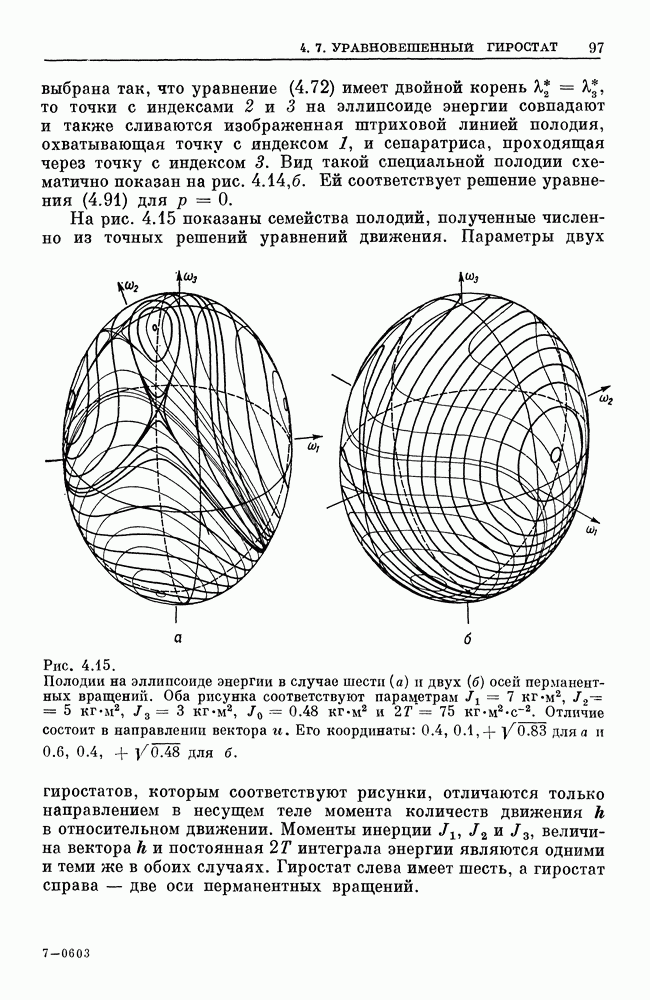
Постоянные  определяются из уравнений
определяются из уравнений  соответственно. Они равны минимальному и максимальному значениям
соответственно. Они равны минимальному и максимальному значениям  . Из уравнений (4.40) и (4.31) получаем также
. Из уравнений (4.40) и (4.31) получаем также  как функции
как функции 

Таким образом, все три величины  выражаются через эллиптические функции времени. Период этих функций равен половине периода
выражаются через эллиптические функции времени. Период этих функций равен половине периода  для переменной
для переменной  и
и

для переменной  есть полный эллиптический интеграл:
есть полный эллиптический интеграл:

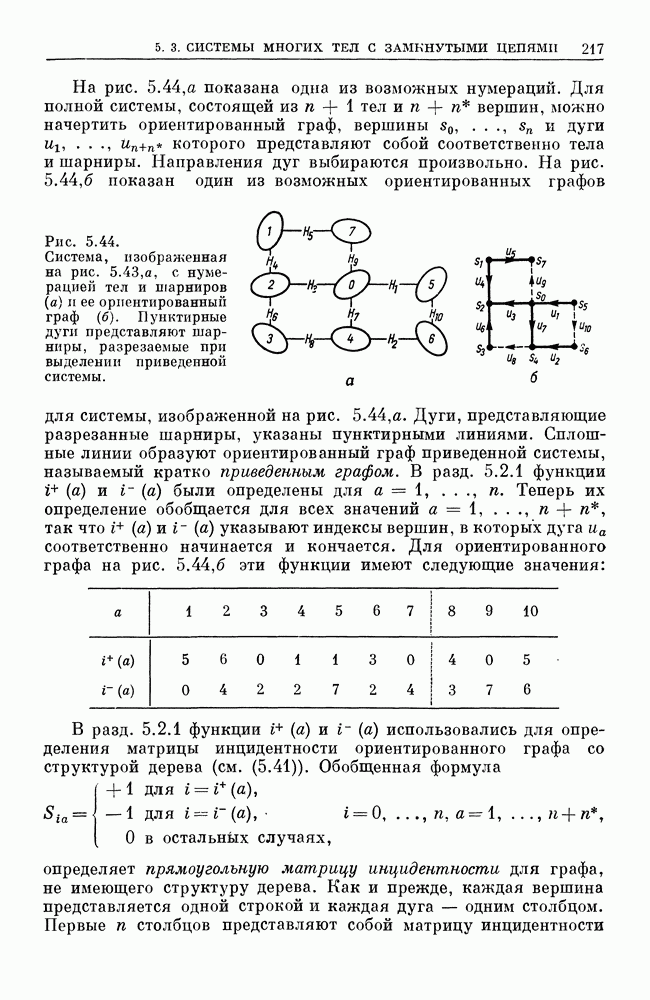
Наложение периодических изменений  в прецессии вокруг вертикали с (периодически изменяющейся) угловой скоростью
в прецессии вокруг вертикали с (периодически изменяющейся) угловой скоростью  лучше всего наблюдать следующим образом. Вообразим сферу с центром в точке опоры волчка. Точка пересечения оси симметрии тела с этой сферой вычерчивает кривые, которые дают наглядное представление о периодических изменениях
лучше всего наблюдать следующим образом. Вообразим сферу с центром в точке опоры волчка. Точка пересечения оси симметрии тела с этой сферой вычерчивает кривые, которые дают наглядное представление о периодических изменениях  , а также
, а также  . На рис. 4.7 схематически представлены характерные особенности всех физически возможных типов кривых. Две нижние кривые соответствуют частным типам движения: маятниковому движению
. На рис. 4.7 схематически представлены характерные особенности всех физически возможных типов кривых. Две нижние кривые соответствуют частным типам движения: маятниковому движению
и регулярной прецессии. Три верхние кривые соответствуют общим случаям движения, в которых  изменяется или между отрицательным и положительным значениями (кривая а), или между нулевым и положительным максимумом (кривая б), или между двумя положительными крайними значениями (кривая
изменяется или между отрицательным и положительным значениями (кривая а), или между нулевым и положительным максимумом (кривая б), или между двумя положительными крайними значениями (кривая  Периодические «кивающие» движения волчка, описываемые функцией
Периодические «кивающие» движения волчка, описываемые функцией  которые налагаются на прецессионное движение, называются нутацией. Более подробный анализ решений читатель может найти в монографиях Арнольда и Маундера [9] и Магнуса [6].
которые налагаются на прецессионное движение, называются нутацией. Более подробный анализ решений читатель может найти в монографиях Арнольда и Маундера [9] и Магнуса [6].

Рис. 4.7. Кривые, описываемые осью симметрии на сфере с началом в точке опоры тяжелого волчка.
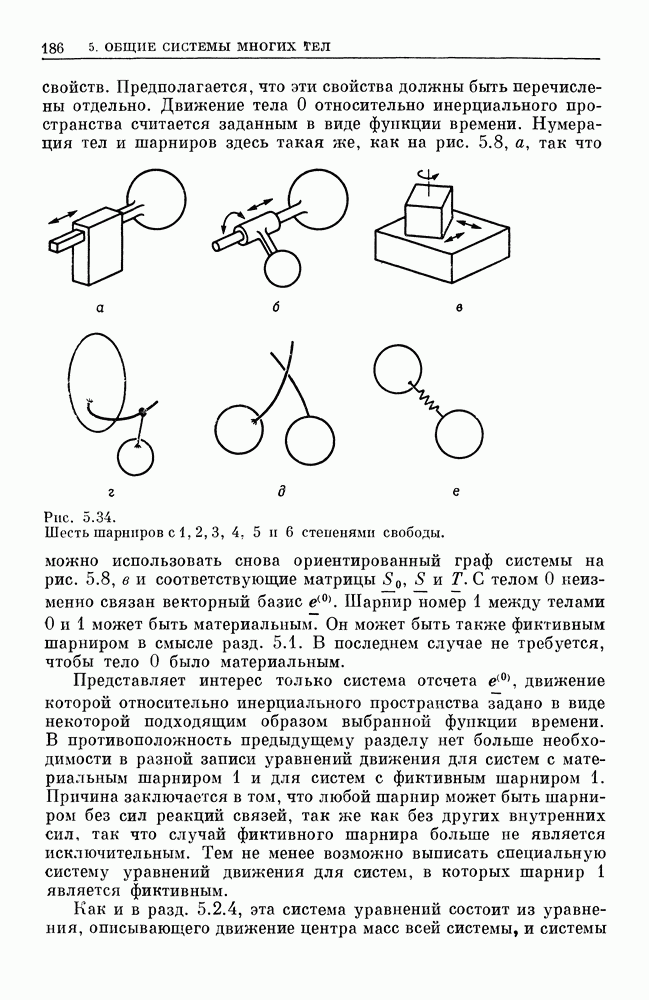
Многие технические гироскопические приборы, по существу, представляют собой симметричный тяжелый волчок (см. Магнус [6]). Такие приборы работают в специальных условиях. Во-первых, они находятся в быстром вращении. Это означает, что часть  кинетической энергии тела очень велика по сравнению с потенциальной энергией
кинетической энергии тела очень велика по сравнению с потенциальной энергией  Во-вторых, такие приборы приводятся в движение таким образом, что вначале угловая скорость прецессии очень мала по сравнению с
Во-вторых, такие приборы приводятся в движение таким образом, что вначале угловая скорость прецессии очень мала по сравнению с  (обычно
(обычно  и
и  удерживаются фиксированными до тех пор, пока тело не достигнет полного вращения; лишь после этого связи на
удерживаются фиксированными до тех пор, пока тело не достигнет полного вращения; лишь после этого связи на  удаляются так, чтобы начальные значения
удаляются так, чтобы начальные значения  были по возможности малыми).
были по возможности малыми).
Наблюдаемые при этих условиях движения можно лишь с трудом отличить от регулярных прецессий. В действительности они описываются уравнениями (4.46) и (4.47). Однако амплитуда нутации  чрезвычайно мала, и
чрезвычайно мала, и  быстро колеблется.
быстро колеблется.
Угловая скорость прецессии  очень мала и кажется постоянной, хотя она также подвержена быстрым колебаниям. Такие движения называются псевдорегулярными прецессиями. Их характерные свойства можно вывести из общего решения посредством приближенных формул. С этой целью предположим, что движение волчка соответствует начальным условиям
очень мала и кажется постоянной, хотя она также подвержена быстрым колебаниям. Такие движения называются псевдорегулярными прецессиями. Их характерные свойства можно вывести из общего решения посредством приближенных формул. С этой целью предположим, что движение волчка соответствует начальным условиям  (постоянная во все время движения). Интегралы момента
(постоянная во все время движения). Интегралы момента
количеств движения и энергии суть (уравнения (4.36) и (4.37))

Подставим эти выражения в кубическое уравнение (4.43). В силу начального условия  угол
угол  , является одним из двух крайних значений
, является одним из двух крайних значений  . Это означает, что
. Это означает, что  является корнем кубического уравнения. Деление на
является корнем кубического уравнения. Деление на  приводит после некоторых алгебраических преобразований к уравнению
приводит после некоторых алгебраических преобразований к уравнению

где  — безразмерные величины:
— безразмерные величины:

Квадратичная функция от  в фигурных скобках имеет корни
в фигурных скобках имеет корни

При сделанных предположениях величина а много больше единицы, а абсолютное значение  много меньше единицы. Отсюда приближенно получаем
много меньше единицы. Отсюда приближенно получаем

Разложения в ряды Тейлора (с точностью до членов второго порядка) дают

Принимая во внимание этот результат для  и формулу Тейлора
и формулу Тейлора  для амплитуды нутации
для амплитуды нутации  получаем приближенное значение
получаем приближенное значение

Действительно, это очень малая величина. Отметим, что она становится равной нулю, если начальное значение равно угловой скорости медленной регулярной прецессии (см. уравнение  Модуль к эллиптических функций, определяемый уравнением (4.45), очень мал по сравнению с единицей, как можно видеть из уравнений (4.50) и (4.49). Поэтому полный эллиптический интеграл
Модуль к эллиптических функций, определяемый уравнением (4.45), очень мал по сравнению с единицей, как можно видеть из уравнений (4.50) и (4.49). Поэтому полный эллиптический интеграл  приближенно равен
приближенно равен  . Отсюда для периода функций
. Отсюда для периода функций  получаем приближенное значение
получаем приближенное значение 

Соответствующая круговая частота  очень велика. Она равна угловой скорости прецессии симметричного тела при отсутствии момента сил в случае малых амплитуд нутации (см. уравнение (4.22)). Окончательно приближенную формулу для можно получить из уравнений (4.47) и (4.48):
очень велика. Она равна угловой скорости прецессии симметричного тела при отсутствии момента сил в случае малых амплитуд нутации (см. уравнение (4.22)). Окончательно приближенную формулу для можно получить из уравнений (4.47) и (4.48):

Для разности  уравнение (4.46) дает (с приближением
уравнение (4.46) дает (с приближением  справедливым для к
справедливым для к  . Для
. Для  воспользуемся уравнением (4.50). Оно приводит к выражению
воспользуемся уравнением (4.50). Оно приводит к выражению

и далее к

Этот результат указывает, что  колеблется около среднего значения
колеблется около среднего значения  равного угловой скорости медленной регулярной прецессии. Амплитуда колебания равна нулю, если начальное значение равно этому среднему значению. Только что установленная приближенная формула подтверждает сделанное ранее утверждение о том, что движение быстро вращающегося симметричного волчка мало отличается от регулярной прецессии. Это движение можно интерпретировать как суперпозицию быстрой нутации с очень малой амплитудой
равного угловой скорости медленной регулярной прецессии. Амплитуда колебания равна нулю, если начальное значение равно этому среднему значению. Только что установленная приближенная формула подтверждает сделанное ранее утверждение о том, что движение быстро вращающегося симметричного волчка мало отличается от регулярной прецессии. Это движение можно интерпретировать как суперпозицию быстрой нутации с очень малой амплитудой  и медленной регулярной прецессии.
и медленной регулярной прецессии.
| << Предыдущий параграф | Следующий параграф >> |
- От редактора перевода
- Предисловие
- 1. Математические обозначения
- 2. Кинематика твердого тела
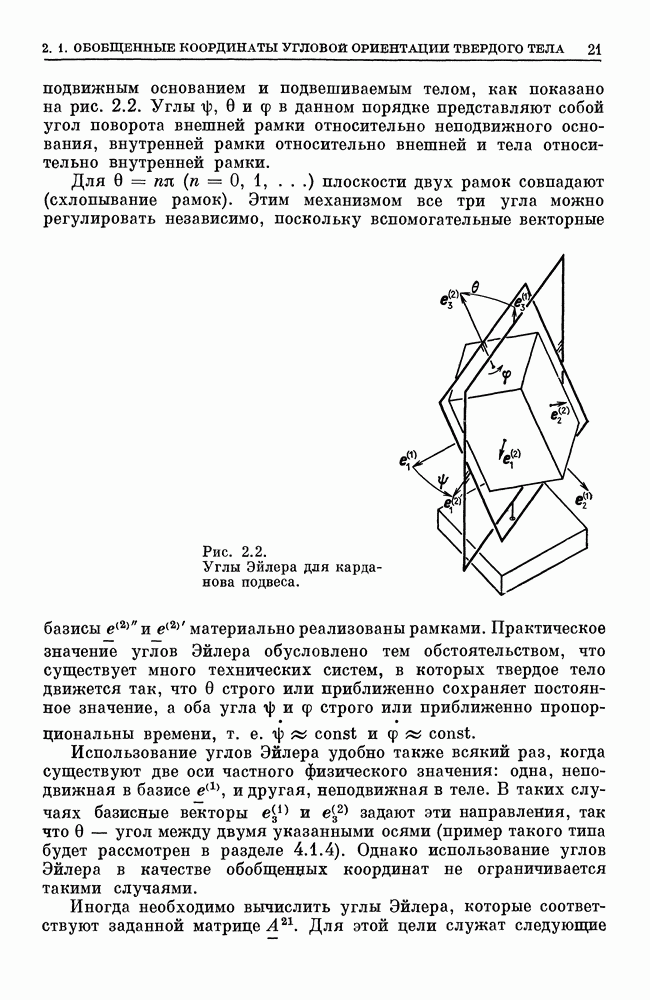
- 2.1. Обобщенные координаты угловой ориентации твердого тела
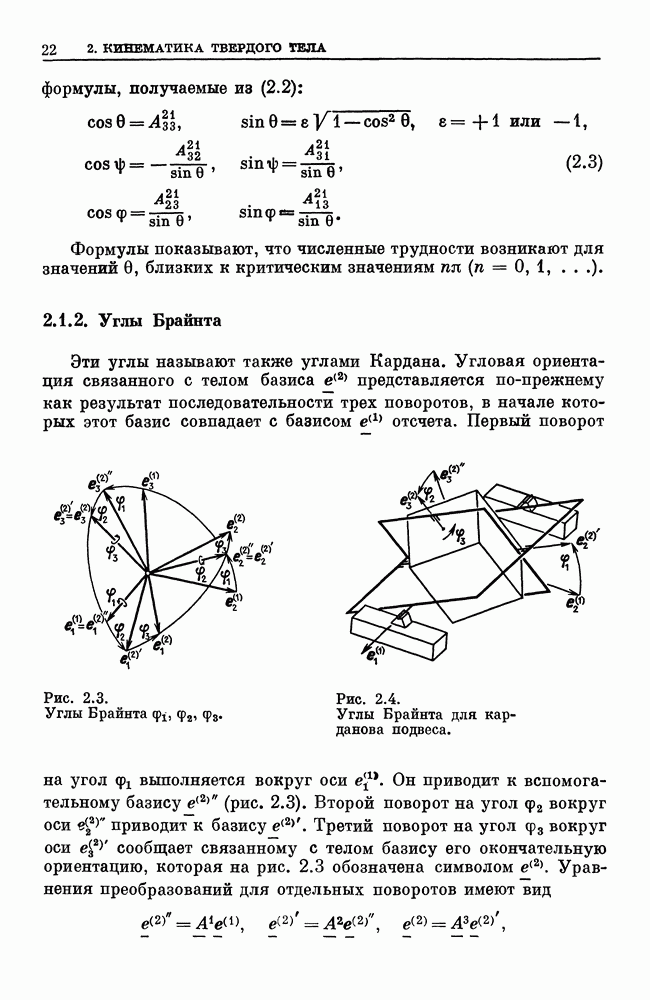
- 2.1.2. Углы Брайнта
- 2.1.3. Параметры Эйлера
- 2.2. Понятие угловой скорости
- 2.3. Соотношения между угловой скоростью тела и обобщенными координатами, описывающими угловую ориентацию тела
- 3.1. Кинетическая энергия
- 3.2. Момент количеств движения
- 3.3. Свойства моментов и произведений инерции
- 3.3.2. Переход к другому базису отсчета без изменения полюса
- 3.3.3. Главные оси и главные моменты инерции
- 3.3.4. Инварианты и неравенства для моментов и произведений инерции
- 3.4. Теорема об изменении момента количеств движения
- 3.5. Принцип Даламбера в применении к твердому телу
- 4. Классические задачи механики твердого тела
- 4.1. Движение по инерции несимметричного твердого тела
- 4.1.1. Полодии и перманентные вращения
- 4.1.2. Геометрическая интерпретация движения Пуансо
- 4.1.3. Решение уравнений движения Эйлера
- 4.1.4. Решение кинематических дифференциальных уравнений
- 4.2. Симметричное твердое тело в отсутствие момента сил
- 4.3. Самовозбуждаемое симметричное твердое тело
- 4.4. Симметричный тяжелый волчок
- 4.5. Симметричное тяжелое тело в кардановом подвесе
- 4.6. Гиростат. Общий анализ
- 4.7. Уравновешенный гиростат
- 4.7.2. Решение динамических уравнений движения
- 5. Общие системы многих тел
- 5.2. Уравнения движения для систем со структурой дерева
- 5.2.2. Системы с шаровыми шарнирами. Одно тело соединено с внешним телом, совершающим заданное движение
- 5.2.3. Частный случай плоских движений
- 5.2.4. Системы с шаровыми шарнирами, не связанные с внешним телом, совершающим заданное движение
- 5.2.5. Частный случай спутника на круговой орбите, состоящего из многих тел
- 5.2.6. Системы с шаровыми, универсальными и цилиндрическими шарнирами
- 5.2.6.2. Кинематика движения тел относительно инерциального пространства
- 5.2.6.3. Исключение моментов сил реакций связей
- 5.2.6.4. Случай управляемых переменных
- 5.2.7. Инструкции для программирования
- 5.2.8. Системы с произвольными голономными связями в шарнирах
- 5.2.8.1. Составление уравнения принципа Даламбера
- 5.2.8.2. Кинематика движения смежных тел относительно друг друга
- 5.2.8.3. Кинематика движения тел относительно инерциального пространства
- 5.2.8.4. Возможная работа, совершаемая в шарнирах
- 5.2.8.5. Уравнения движения
- 5.2.9. Внутренние силы и моменты в шарнирах системы с произвольными голономными связями
- 5.3. Системы многих тел с замкнутыми цепями и произвольными связями
- 5.3.1. Математическое описание структуры взаимосвязей. Обобщение раздела 5.2.1
- 5.3.2. Уравнения движения
- 5.3.2.2. Возможная работа в разрезанных шарнирах
- 5.3.2.3. Критерии выбора приведенной системы
- 5.4. Заключительные замечания
- 6. Задачи удара в голономных системах многих тел
- 6.2. Мгновенные приращения скоростей
- 6.3. Аналогия с законом Максвелла и Бетти
- 6.4. Внутренние импульсы и импульсные пары в шарнирах
- Ответы на задачи
- Список литературы
- Список обозначений