| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
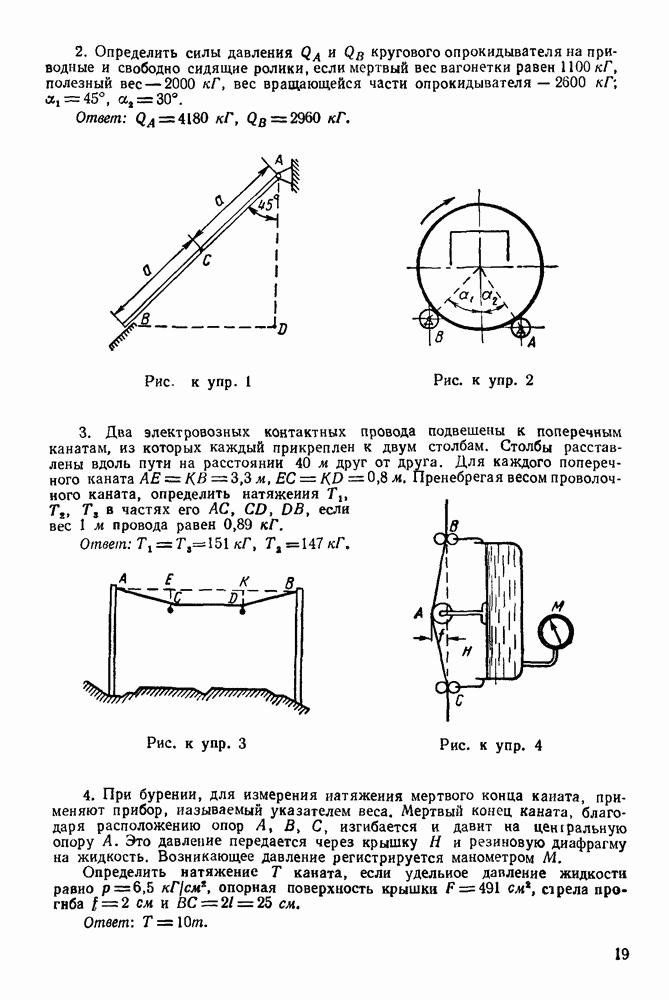
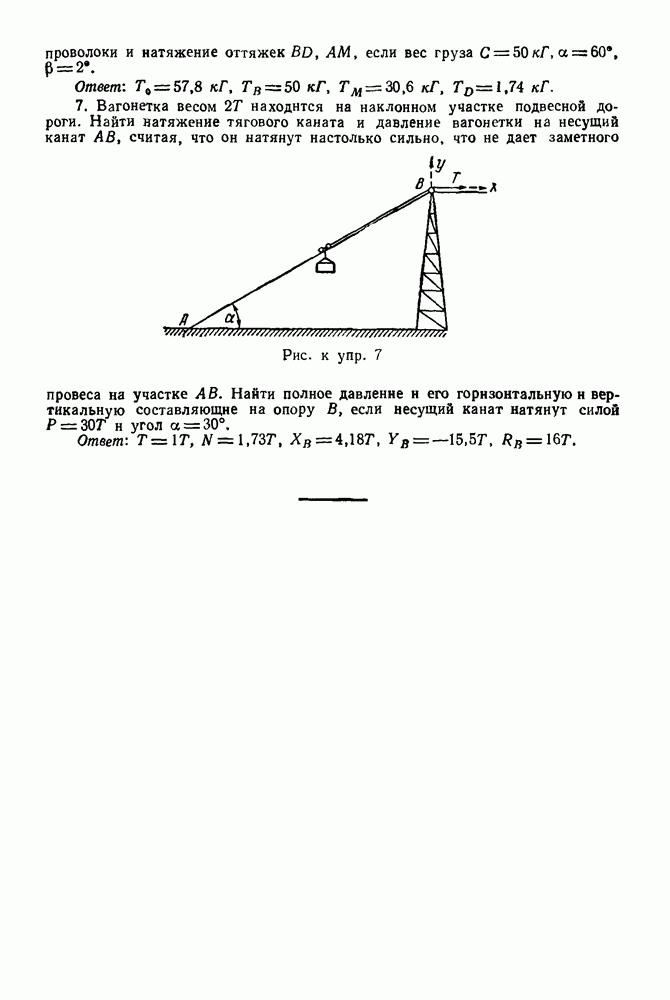
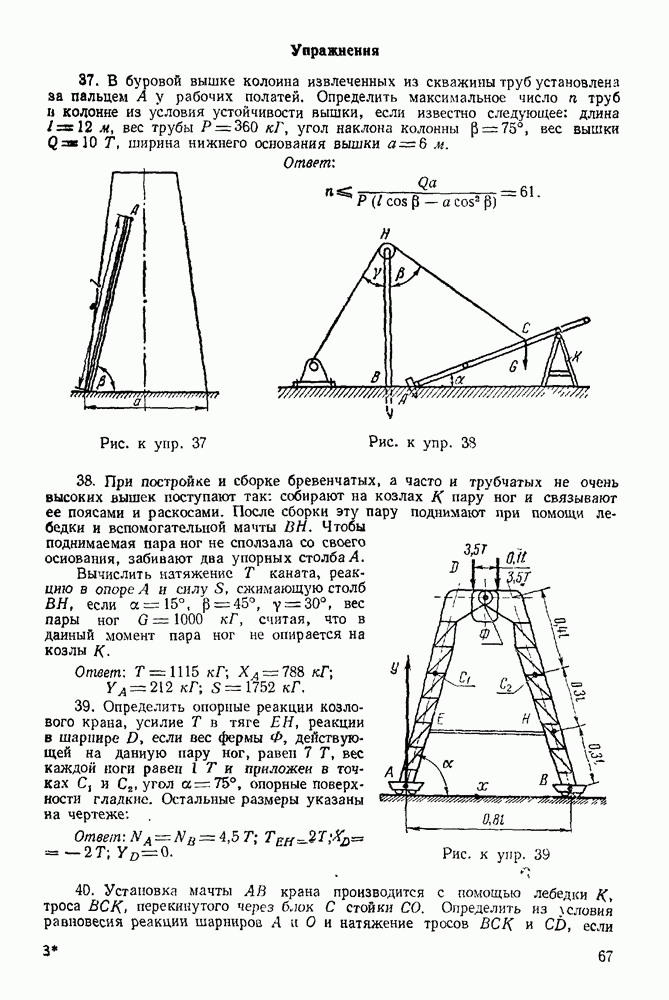
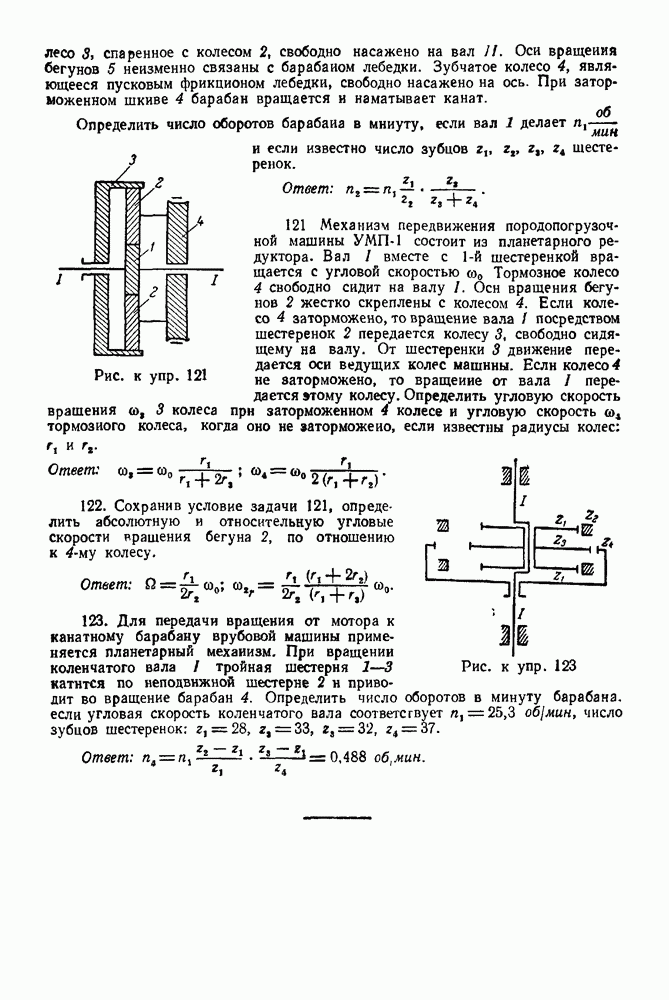
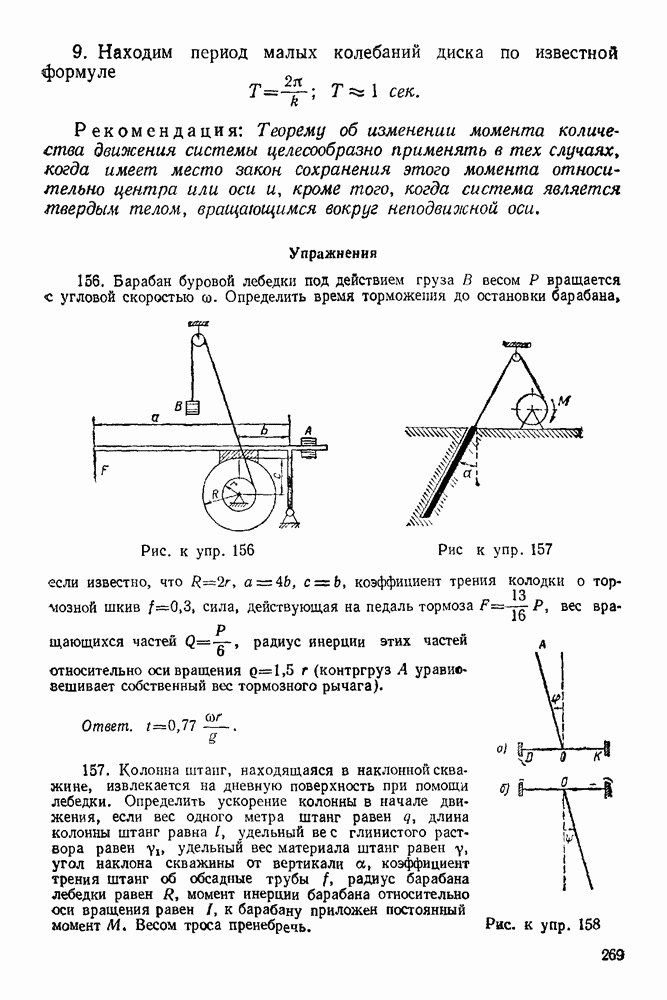
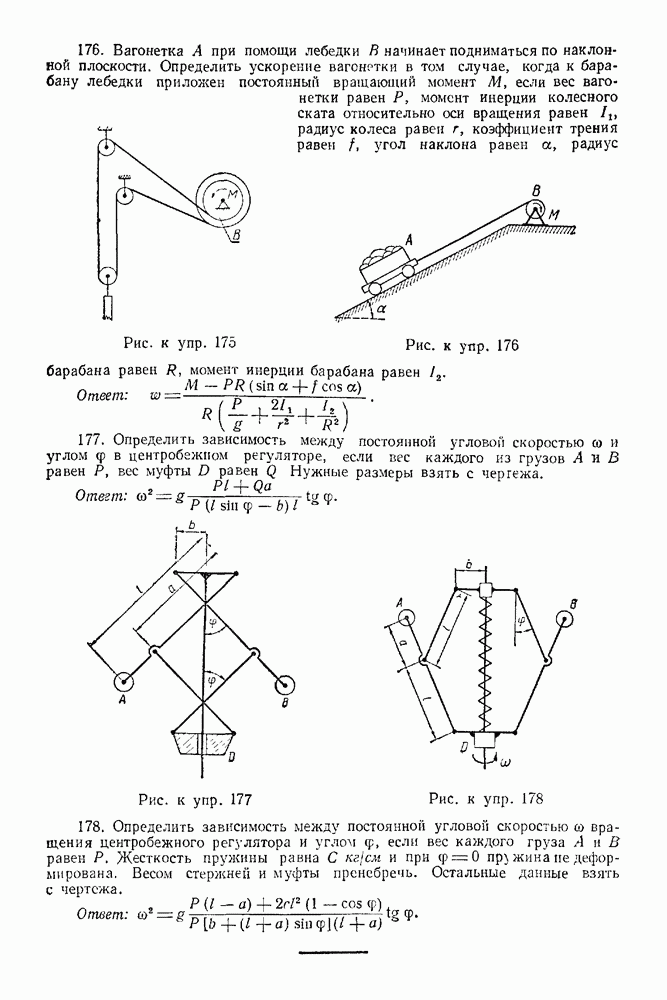
Задача 11. Однородная балка (рис. 39) весом  шарнирно закреплена на опоре А, а концом В она положена на катки. На балку, под углом
шарнирно закреплена на опоре А, а концом В она положена на катки. На балку, под углом  действует сила
действует сила  Определить реакции опор
Определить реакции опор  взяв размеры с чертежа, если
взяв размеры с чертежа, если 

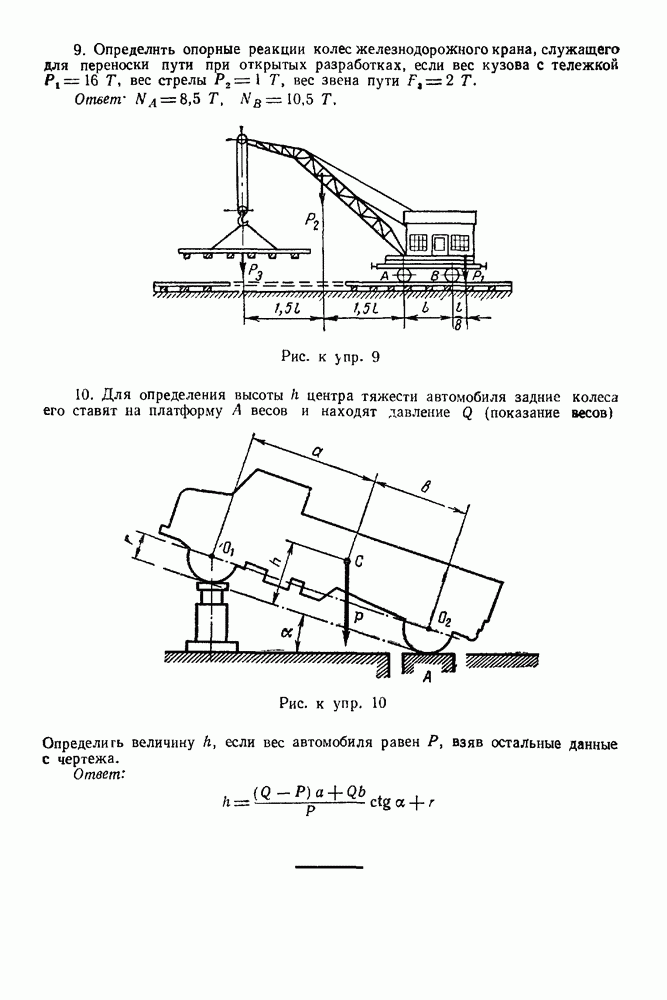
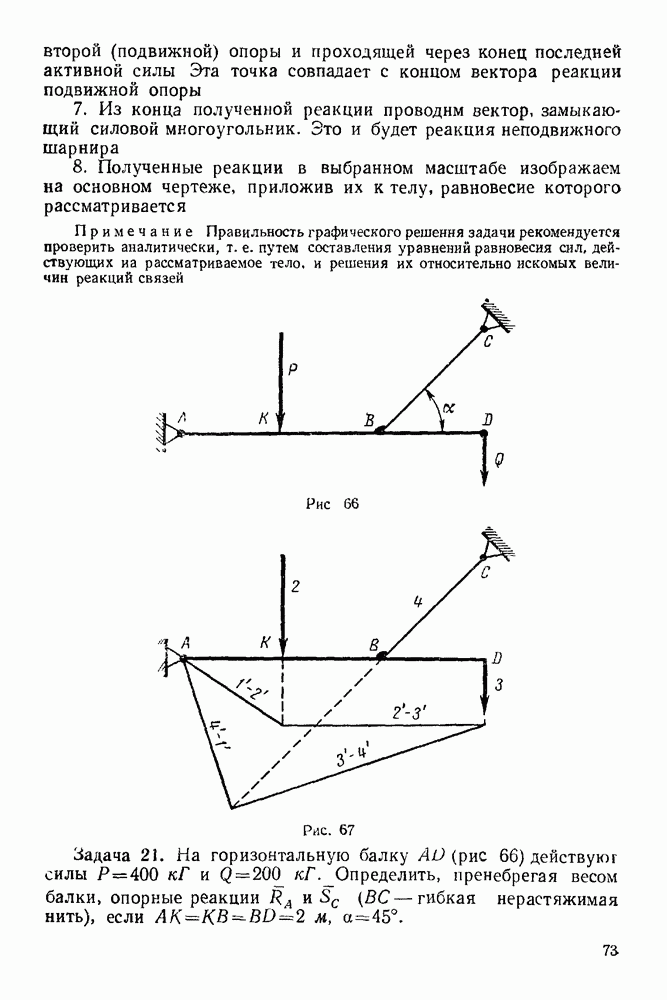
Рис. 39
Решение. 1. Рассматриваем равновесие балки  (рис. 40).
(рис. 40).
2. Изображаем силу  вес балки (эта сила приложена к середине балки, так как балка однородная и постоянного сечения) и силу К Это активные силы, действующие на балку.
вес балки (эта сила приложена к середине балки, так как балка однородная и постоянного сечения) и силу К Это активные силы, действующие на балку.
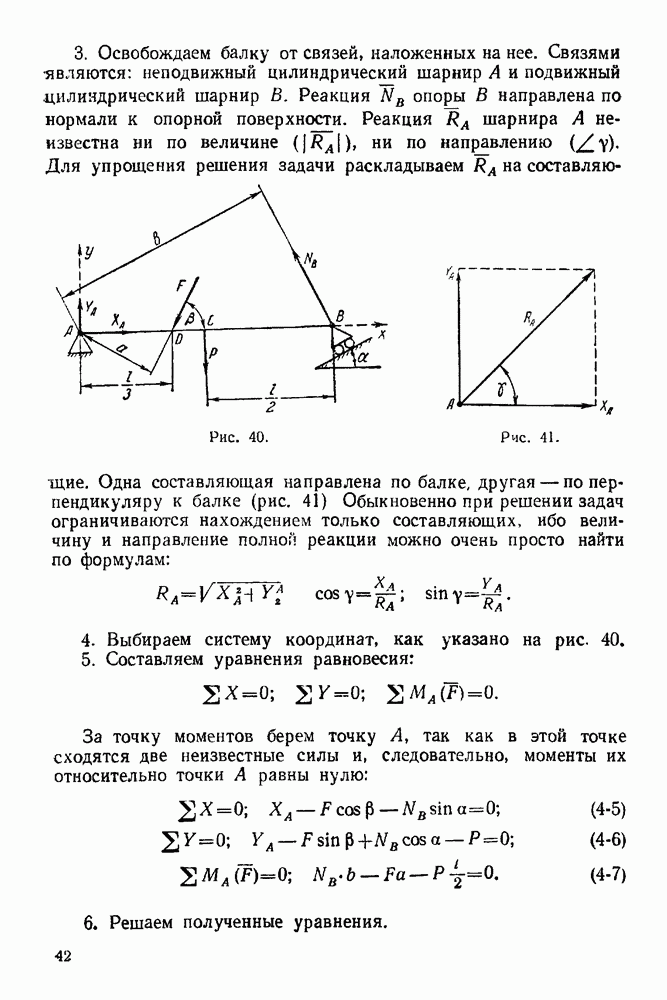
3. Освобождаем балку от связей, наложенных на нее. Связями являются: неподвижный цилиндрический шарнир А и подвижный цилиндрический шарнир В. Реакция  опоры В направлена по нормали к опорной поверхности. Реакция
опоры В направлена по нормали к опорной поверхности. Реакция  шарнира А неизвестна ни по величине
шарнира А неизвестна ни по величине  ни по направлению
ни по направлению  Для упрощения решения задачи раскладываем
Для упрощения решения задачи раскладываем  на составляющие.
на составляющие.

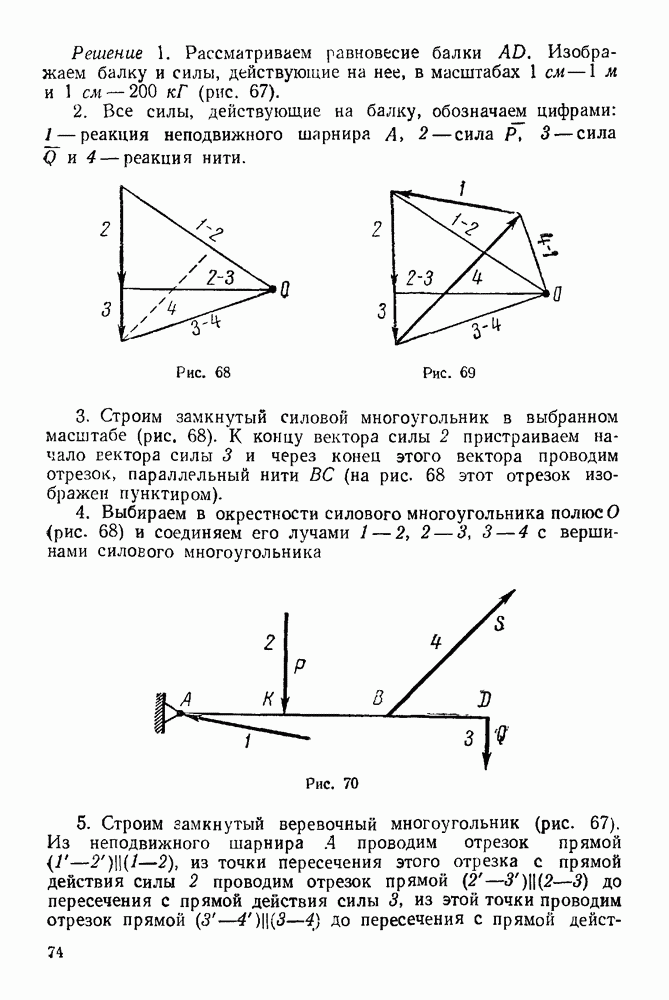
Рис. 40.

Рис. 41.
Одна составляющая направлена по балке, другая — по перпендикуляру к балке (рис. 41) Обыкновенно при решении задач ограничиваются нахождением только составляющих, ибо величину и направление полной реакции можно очень просто найти по формулам:

4. Выбираем систему координат, как указано на рис. 40.
5. Составляем уравнения равновесия:

За точку моментов берем точку А, так как в этой точке сходятся две неизвестные силы и, следовательно, моменты их относительно точки А равны нулю:

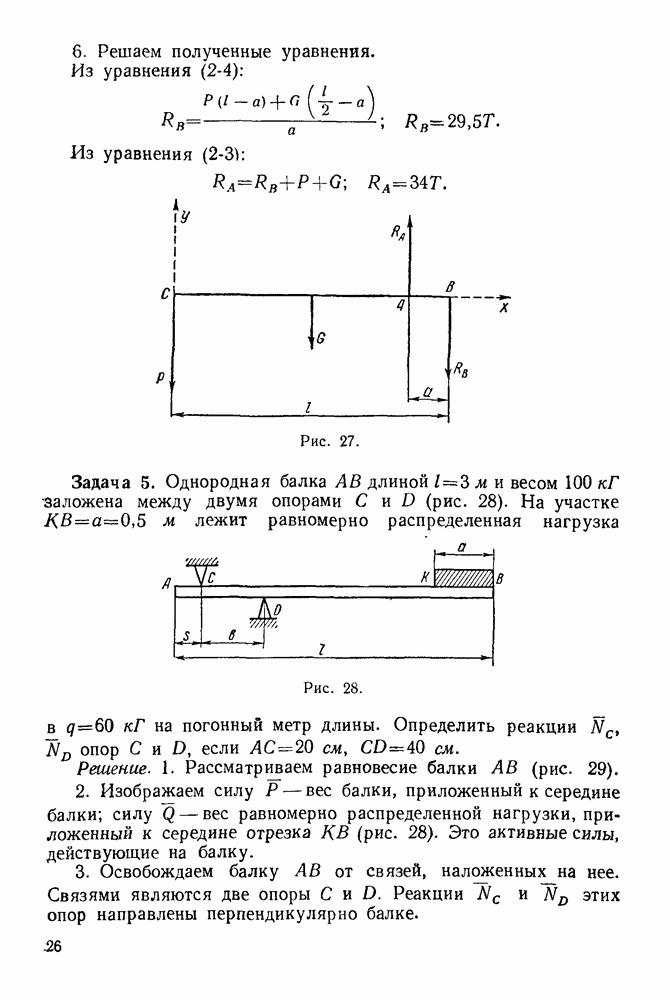
6. Решаем полученные уравнения.
Из уравнения (4-7):

Из уравнения (4-5):

Из уравнения (4-6):

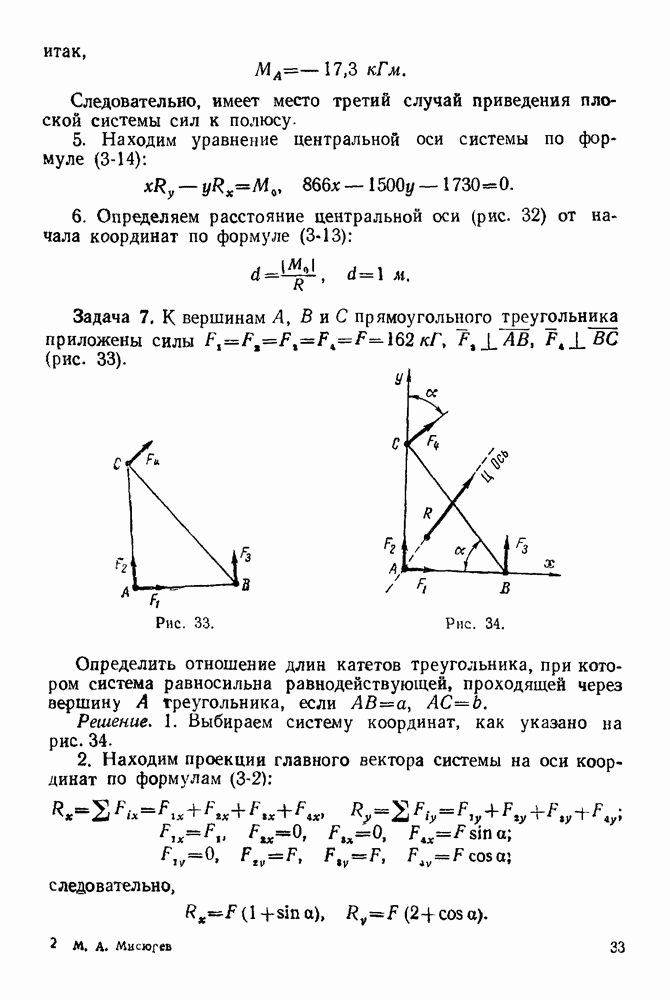
Итак

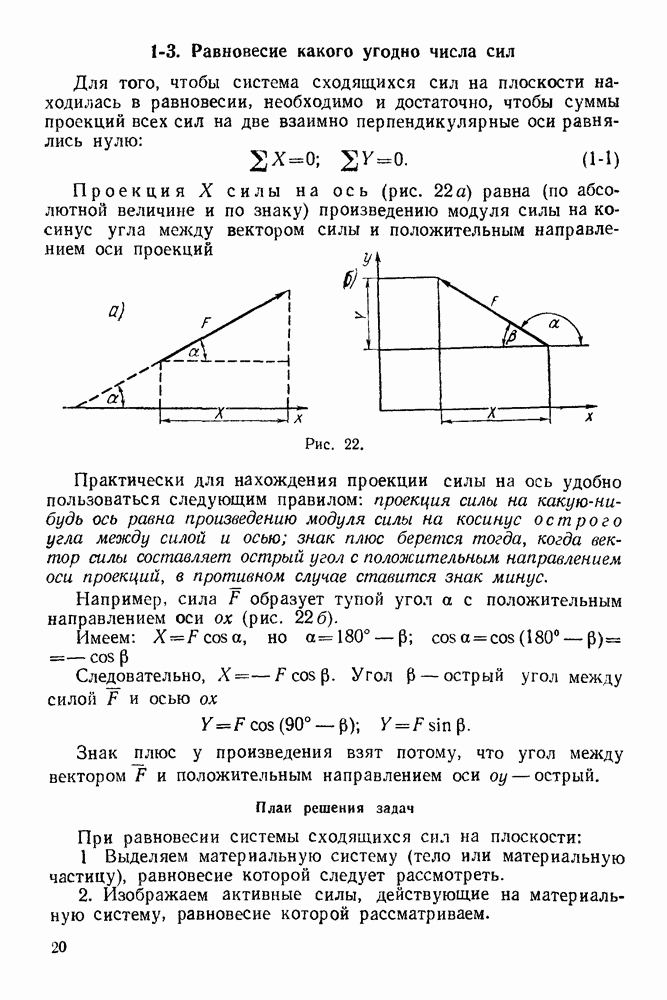
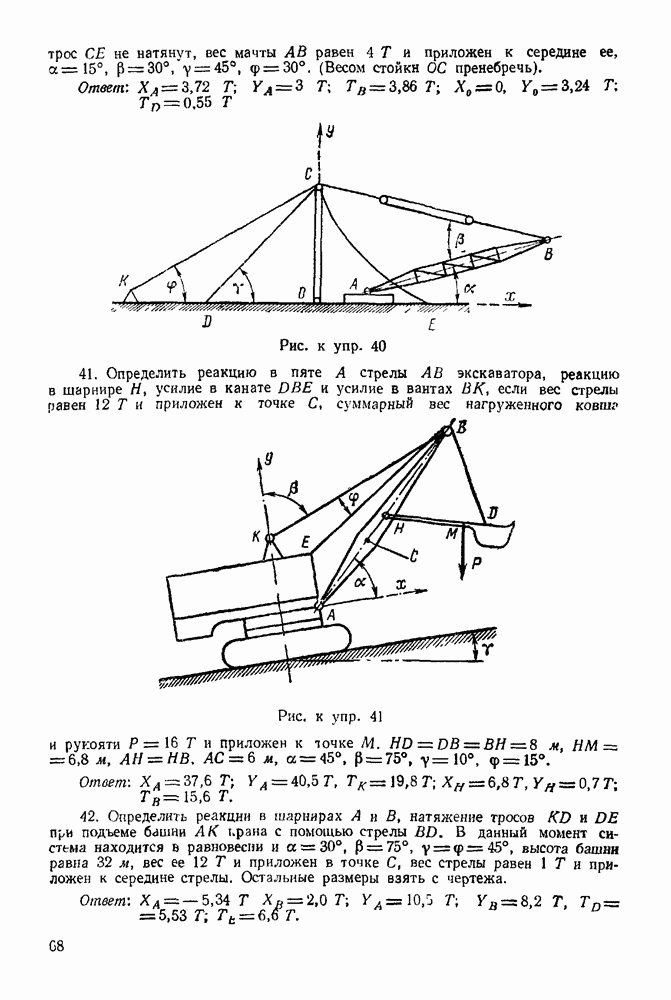
Задача 12. Вагонетка весом  удерживается на наклонной плоскости с углом наклона
удерживается на наклонной плоскости с углом наклона  канатом, перекинутым через блок и параллельным этой плоскости. Определить давление колес вагонетки на плоскость в точках
канатом, перекинутым через блок и параллельным этой плоскости. Определить давление колес вагонетки на плоскость в точках  и натяжение каната, если
и натяжение каната, если  и причем С обозначает центр тяжести вагонетки (рис. 42).
и причем С обозначает центр тяжести вагонетки (рис. 42).

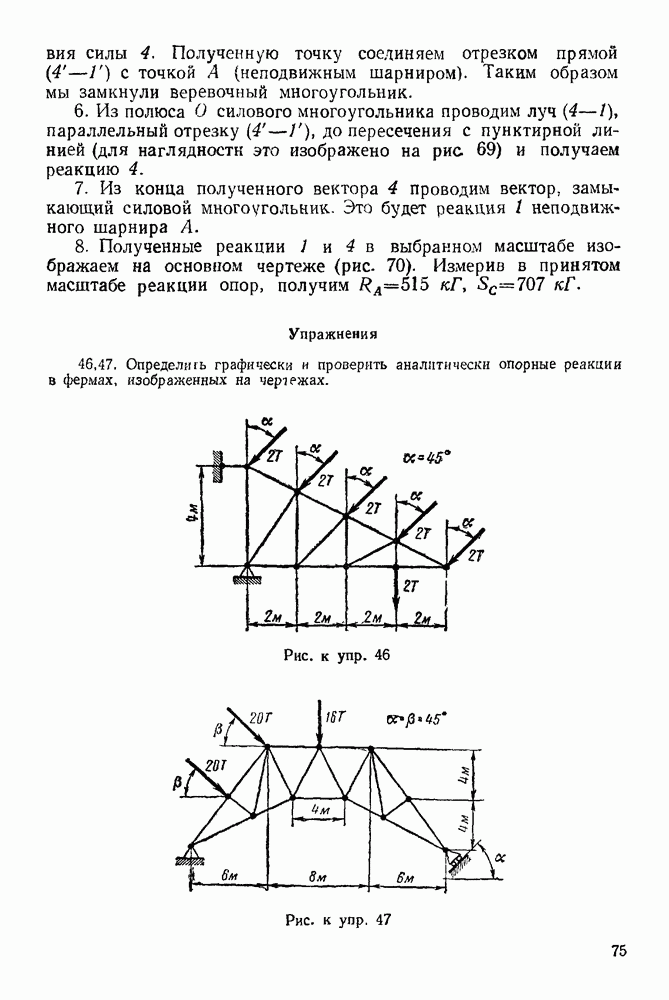
Рис. 42.
Решение. 1, Рассматриваем равновесие вагонетки (рис. 43).
2. Изображаем силу  вес вагонетки (активная сила, действующая на вагонетку).
вес вагонетки (активная сила, действующая на вагонетку).
3. Освобождаем вагонетку от связей, наложенных на нее. Связями являются гладкая наклонная плоскость (рельсы) и канат.
4. Выбираем осн координат, как указано на рис. 43.
5. Составляем уравнения равновесия:

Причем в уравнениях  и (4-10) для облегчения решения задачи при нахождении моментов силы
и (4-10) для облегчения решения задачи при нахождении моментов силы  относительно точек
относительно точек  применили первую теорему Вариньона, разложив силу
применили первую теорему Вариньона, разложив силу  на составляющие, величины которых равны
на составляющие, величины которых равны  по осям х и у — соответственно.
по осям х и у — соответственно.

Рис. 43.
6. Решаем полученные уравнения.
Подобрав соответствующим образом форму уравнений равновесия, получили три уравнения с разделенными неизвестными. Из уравнения 

Из уравнения  :
:

Из уравнения (4-10):

Давления вагонетки на наклонную плоскость в точках  равны по модулю реакциям
равны по модулю реакциям  но направлены в противоположные стороны.
но направлены в противоположные стороны.
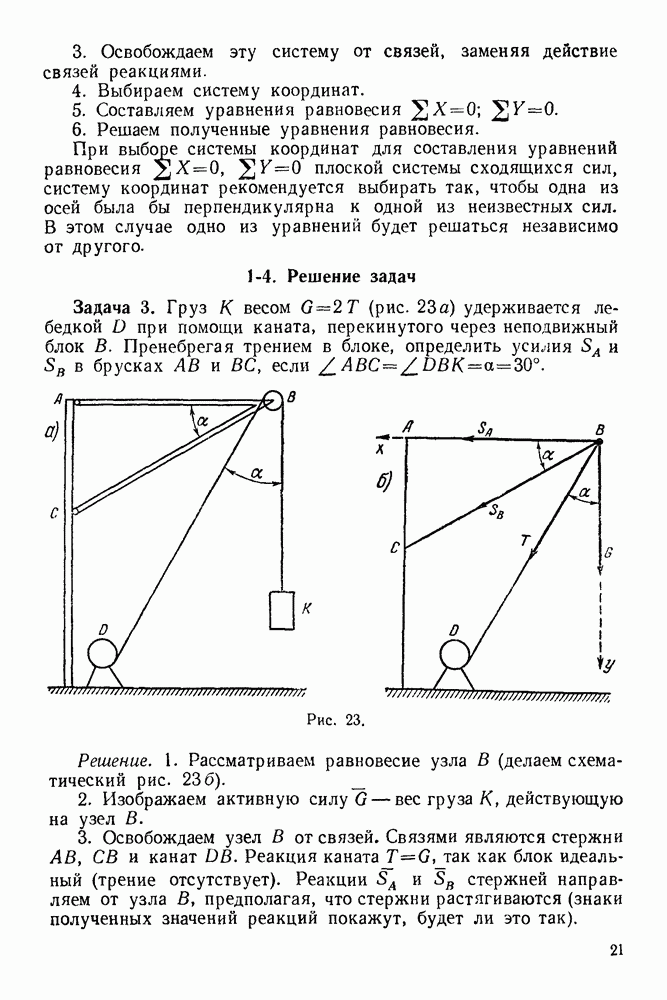
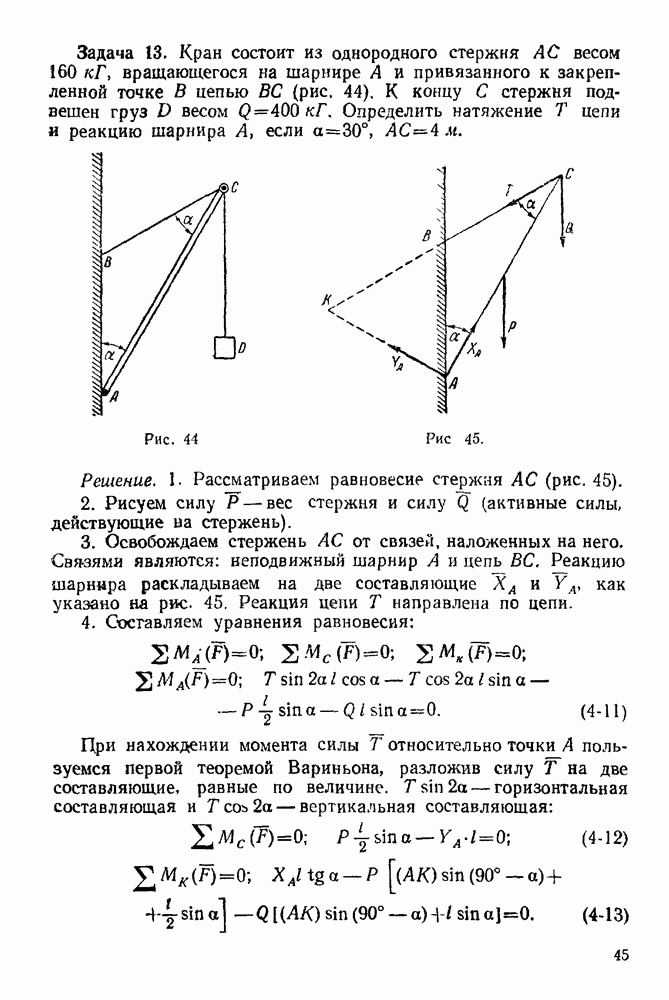
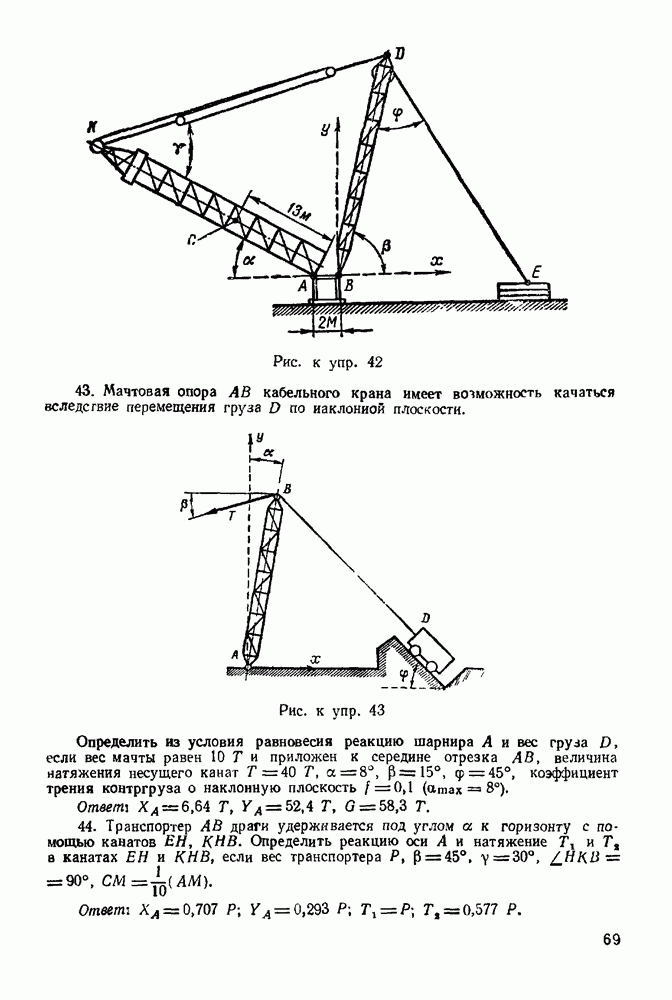
Задача 13. Кран состоит из однородного стержня  весом
весом  вращающегося на шарнире А и привязанного к закрепленной точке В цепью
вращающегося на шарнире А и привязанного к закрепленной точке В цепью  (рис. 44). К концу С стержня подвешен груз
(рис. 44). К концу С стержня подвешен груз  весом
весом  Определить натяжение
Определить натяжение  цепи и реакцию шарнира А, если
цепи и реакцию шарнира А, если 

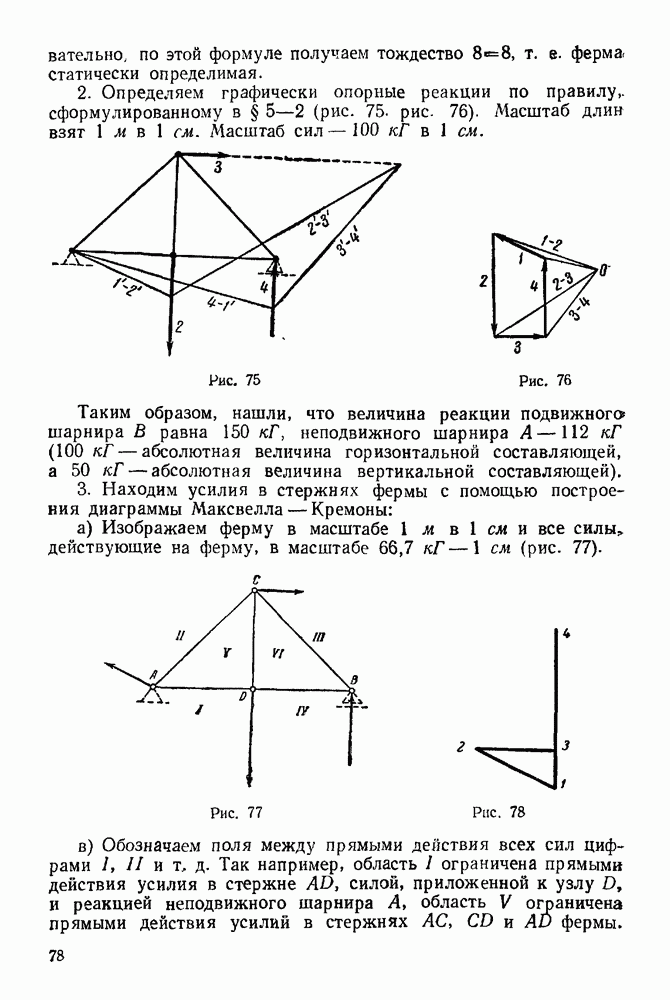
Рис. 44

Рис. 45.
Решение. 1. Рассматриваем равновесие стержня  (рис. 45).
(рис. 45).
2. Рисуем силу  вес стержня и силу
вес стержня и силу  (активные силы, действующие
(активные силы, действующие  стержень).
стержень).
3. Освобождаем стержень  от связей, наложенных на него. Связями являются: неподвижный шарнир А и цепь
от связей, наложенных на него. Связями являются: неподвижный шарнир А и цепь  Реакцию шарнира раскладываем на две составляющие
Реакцию шарнира раскладываем на две составляющие  и
и  как указано на рис. 45. Реакция цепи
как указано на рис. 45. Реакция цепи  направлена по цепи.
направлена по цепи.
4. Составляем уравнения равновесия:

При нахождении момента силы  относительно точки А пользуемся первой теоремой Вариньона, разложив силу
относительно точки А пользуемся первой теоремой Вариньона, разложив силу  на две составляющие, равные по величине.
на две составляющие, равные по величине.  — горизонтальная составляющая и
— горизонтальная составляющая и  вертикальная составляющая:
вертикальная составляющая:

5. Решаем полученные уравнения.
Благодаря надлежащему выбору формы уравнений равновесия и трех точек моментов получилась система трех уравнений с разделенными неизвестными.
Из уравнения (4-11):

Из уравнения (4-12):

Из уравнения (4-13):

Ответ: 
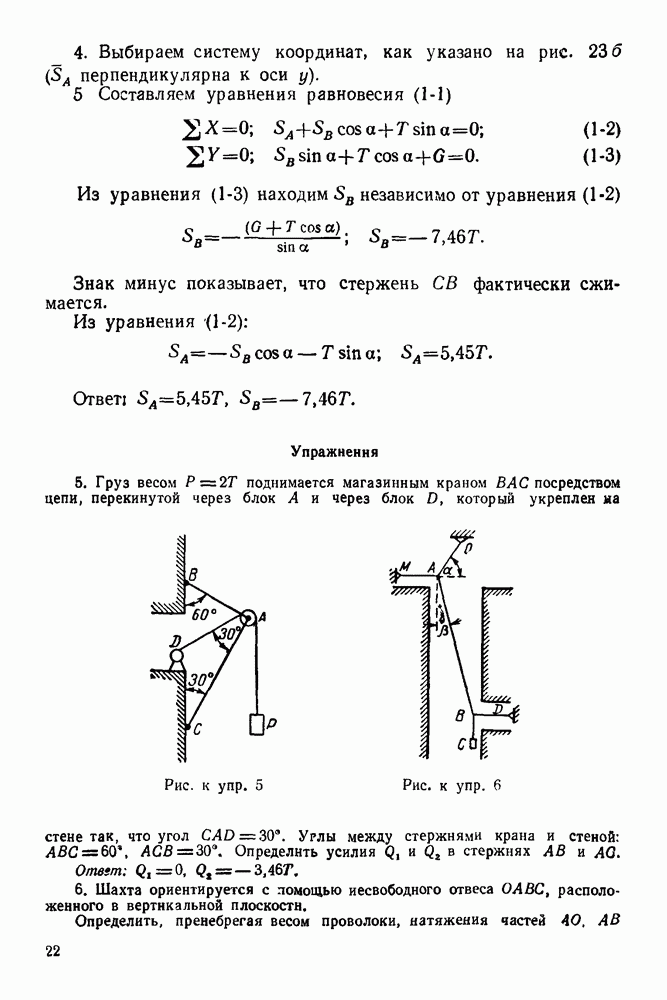
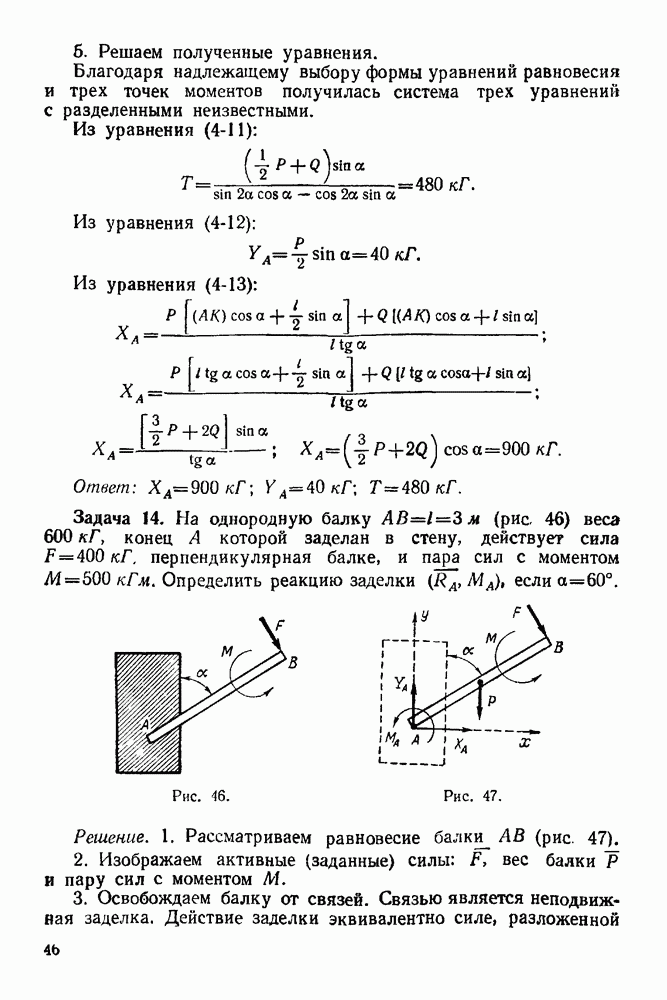
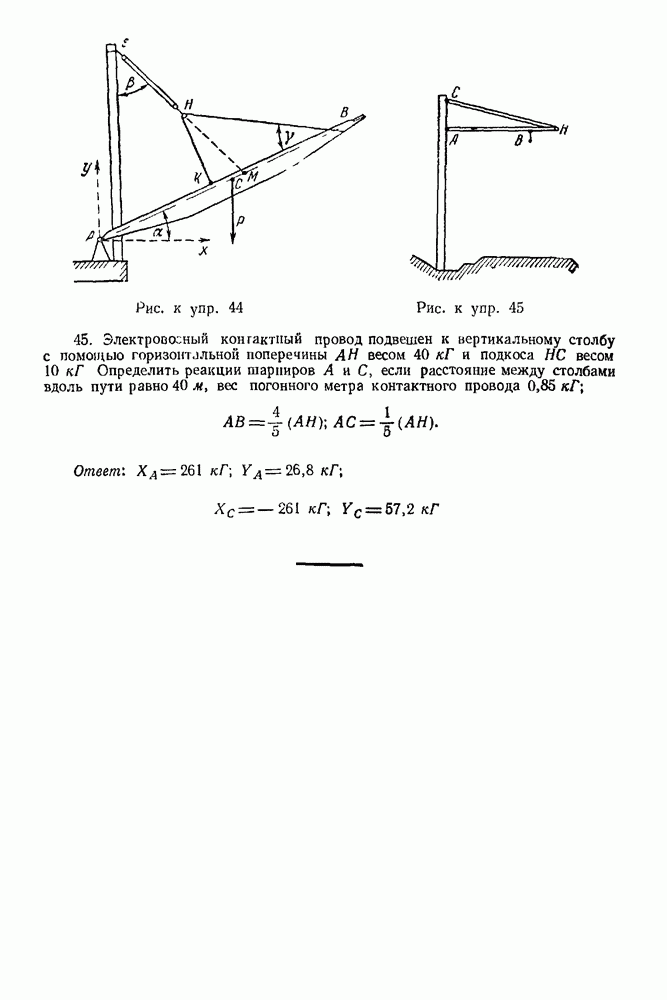
Задача 14. На однородную балку  (рис. 46) веса
(рис. 46) веса  конец А которой заделан в стену, действует сила
конец А которой заделан в стену, действует сила  перпендикулярная балке, и пара сил с моментом
перпендикулярная балке, и пара сил с моментом  Определить реакцию заделки
Определить реакцию заделки  если
если 

Рис. 46.

Рис. 47.
Решение. 1. Рассматриваем равновесие  (рис. 47).
(рис. 47).
2. Изображаем активные (заданные) силы:  вес балки
вес балки  и пару сил с моментом
и пару сил с моментом 
3. Освобождаем балку от связей. Связью является неподвижная заделка. Действие заделки эквивалентно силе, разложенной
на составляющие  и
и  и паре с моментом
и паре с моментом  Итак, имеем:
Итак, имеем:  пара с моментом
пара с моментом  и пара с моментом
и пара с моментом
4. Выбираем систему координат, как указано на рис. 47.
5. Составляем уравнения равновесия:

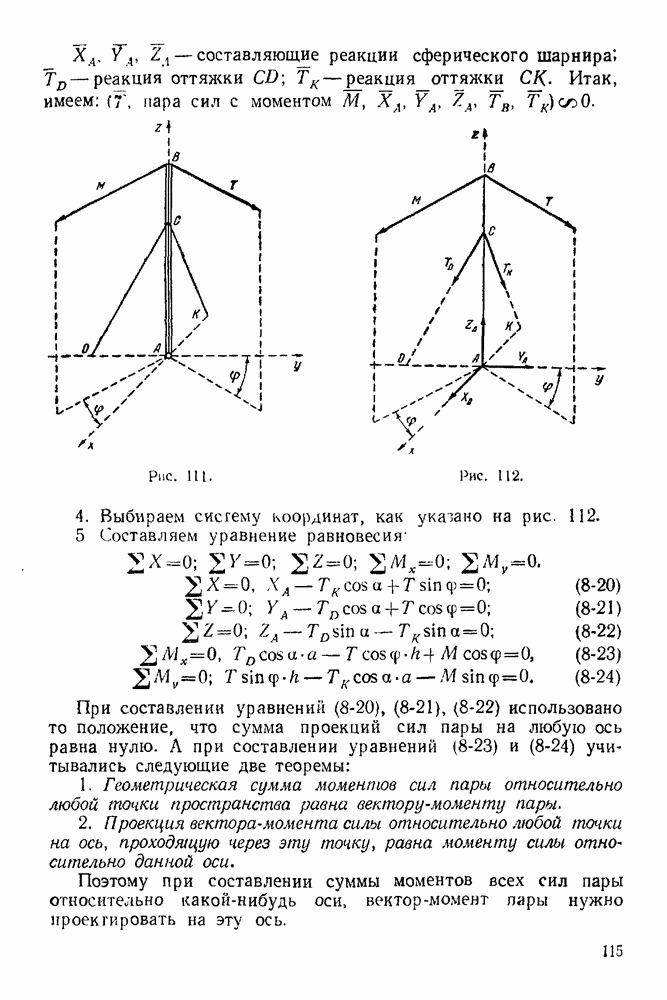
При составлении уравнений (4-14) и (4-15) использовано то положение, что сумма проекций сил пары на любую ось равна нулю. А при составлении уравнения (4-16) учитывалась теорема о том, что сумма моментов сил пары относительно любой точки плоскости равна моменту пары.
6. Решаем полученные уравнения.
Из уравнения (4-14):

Из уравнения (4-15):

Из уравнения (4-16):

7. Анализируем результаты решения задачи.
Знак минус  в ответе
в ответе  указывает, что в действительности составляющая
указывает, что в действительности составляющая  силы
силы  направлена в сторону отрицательного направления оси
направлена в сторону отрицательного направления оси 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
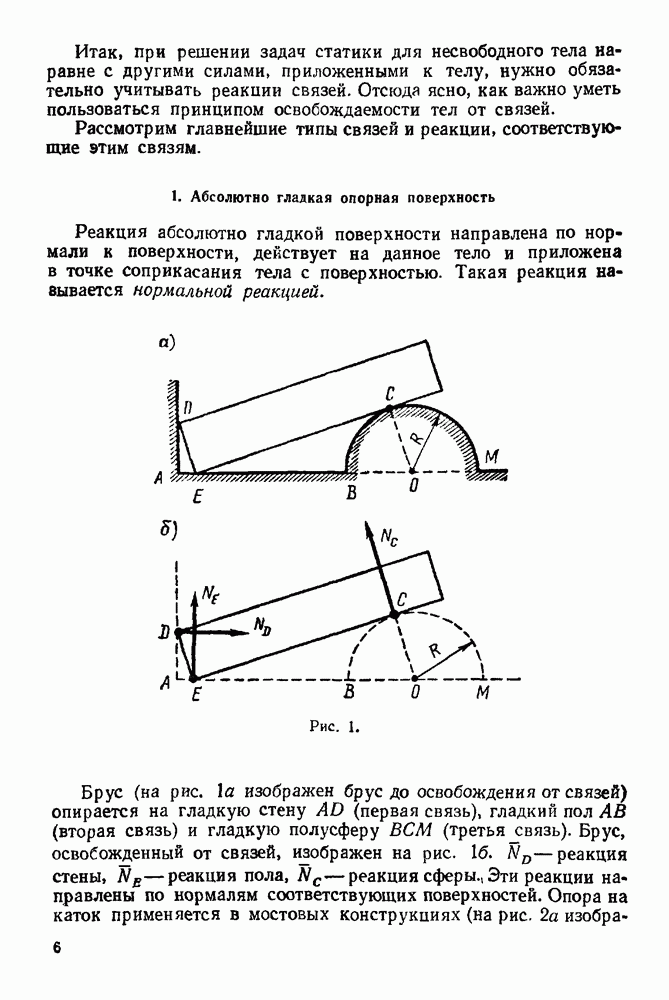
- 1. Абсолютно гладкая опорная поверхность
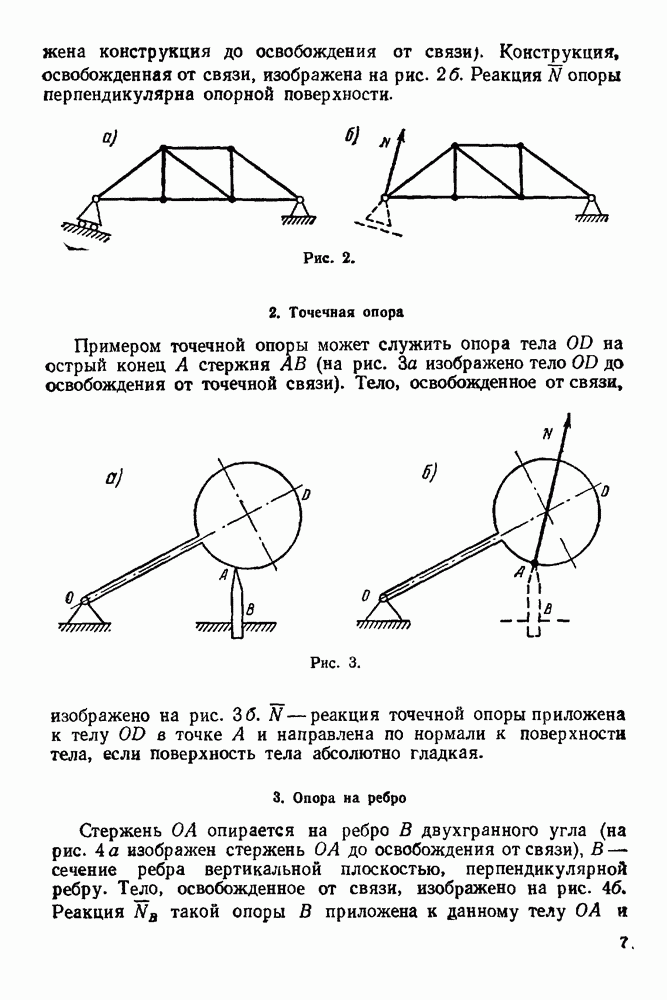
- 2. Точечная опора
- 3. Опора на ребро
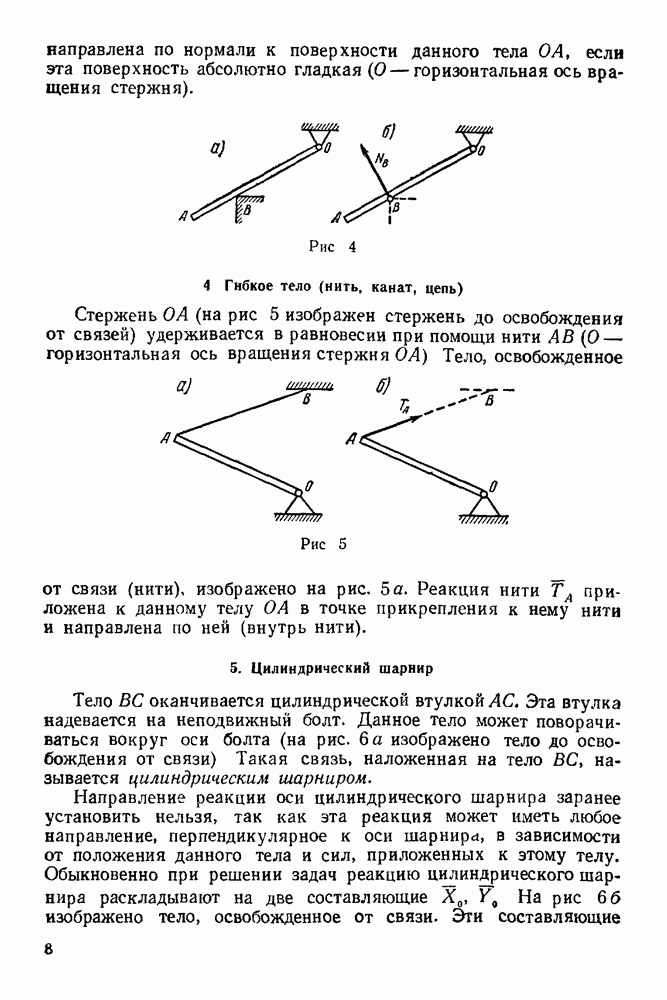
- 4. Гибкое тело (нить, канат, цепь)
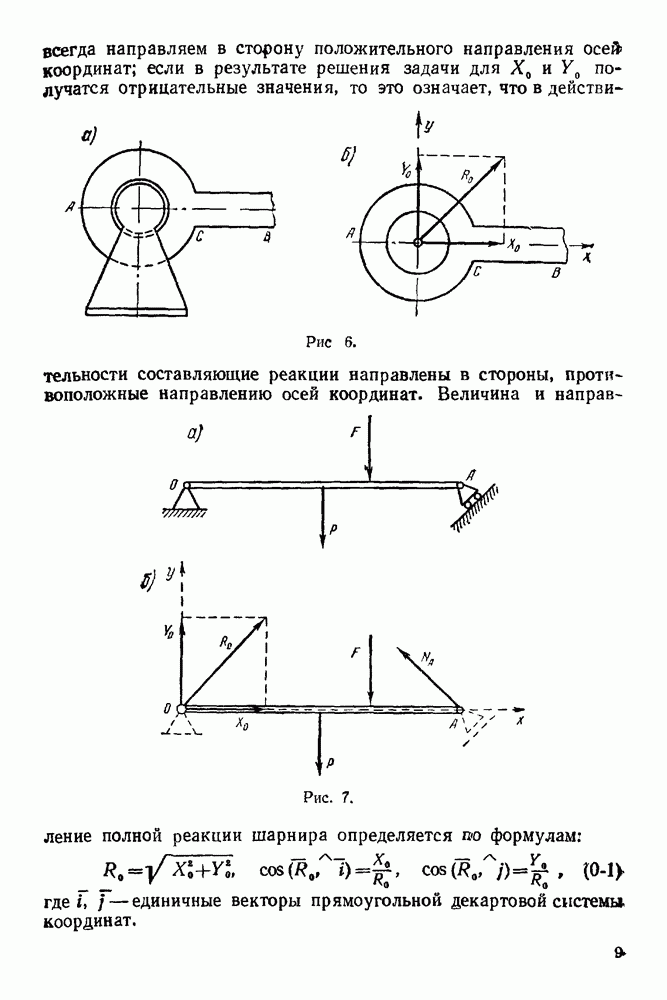
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
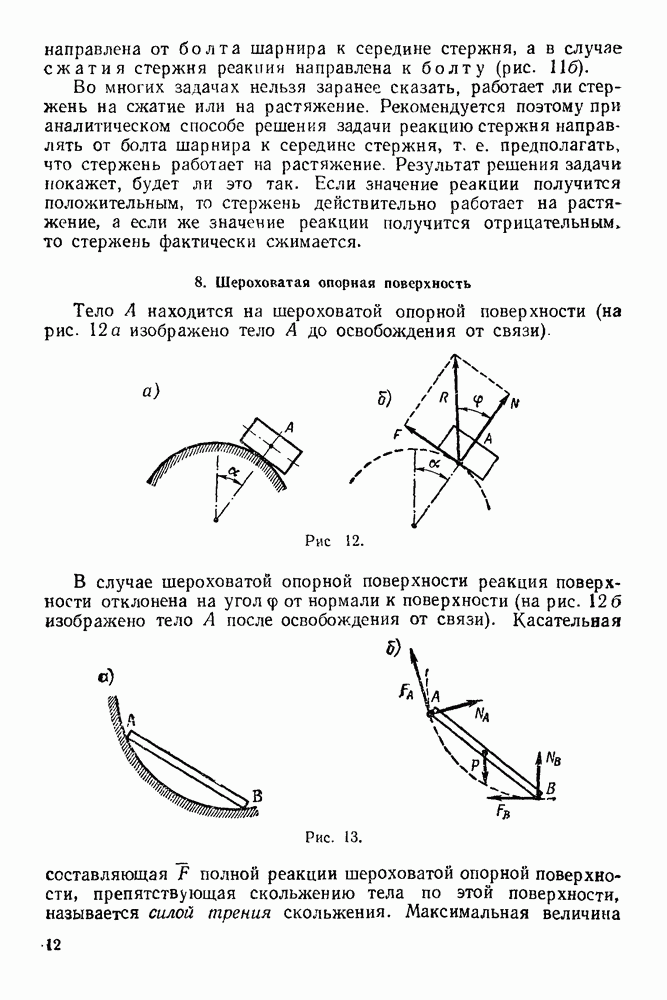
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
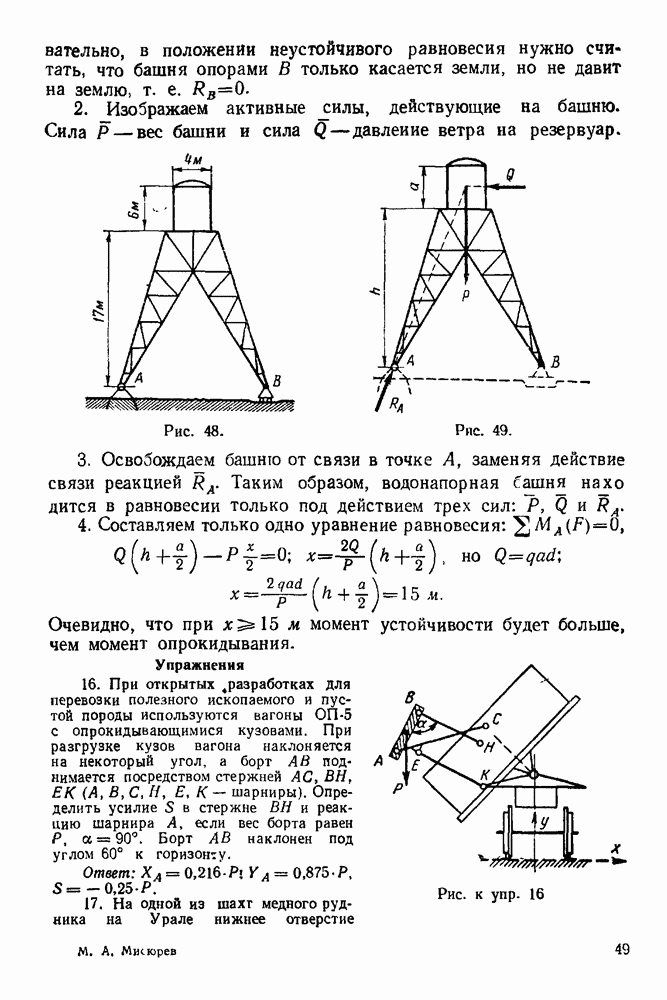
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
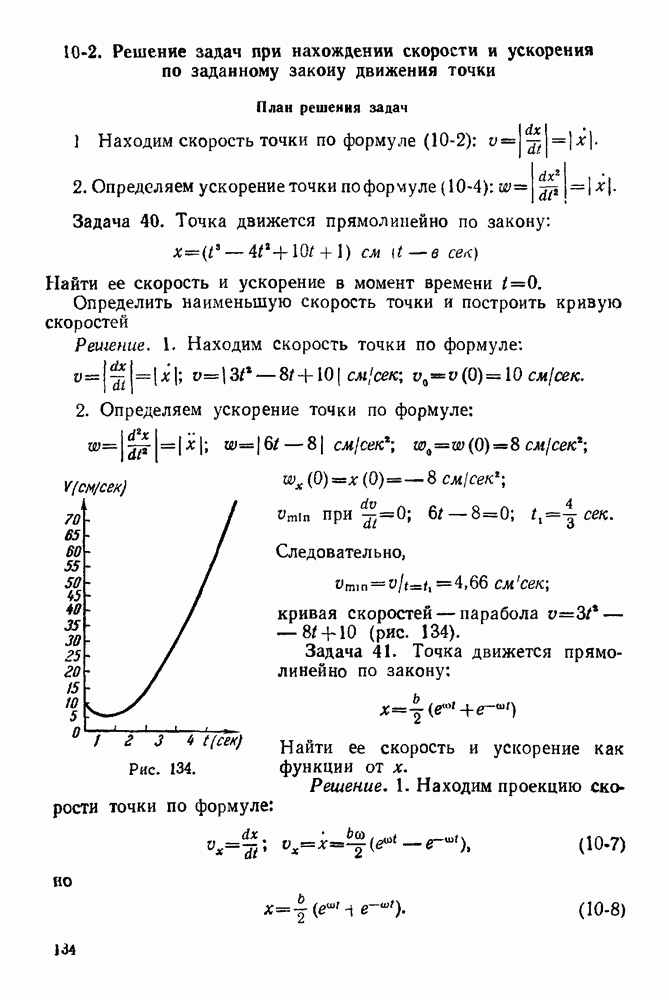
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
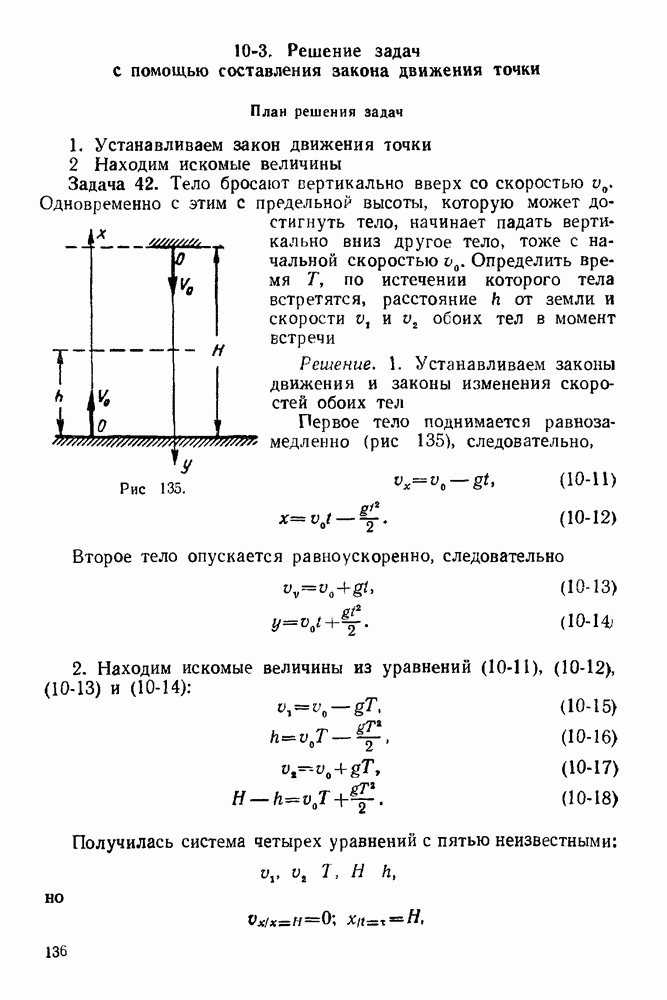
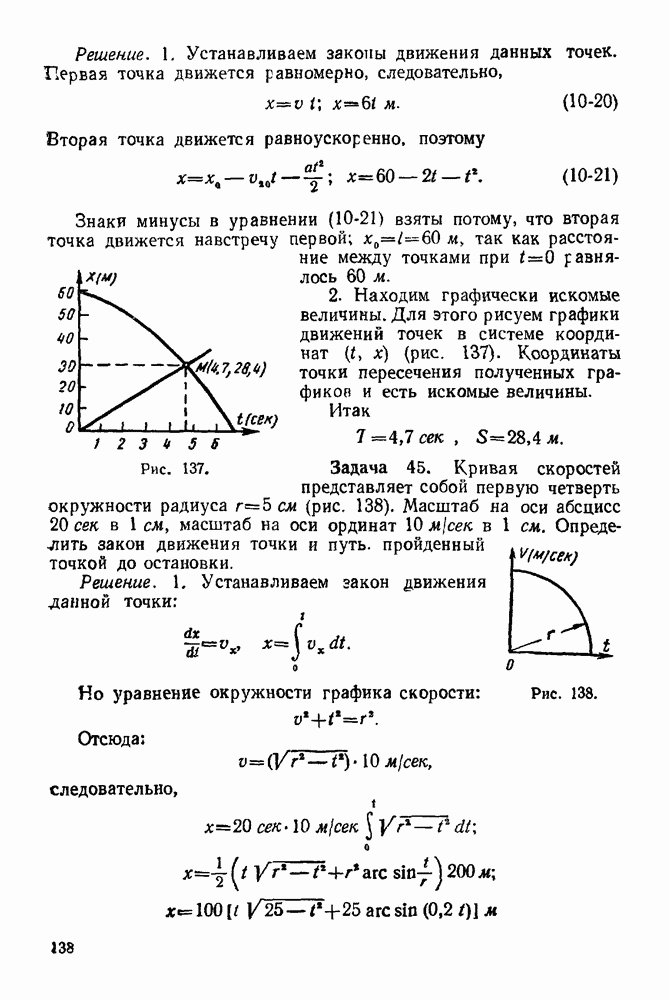
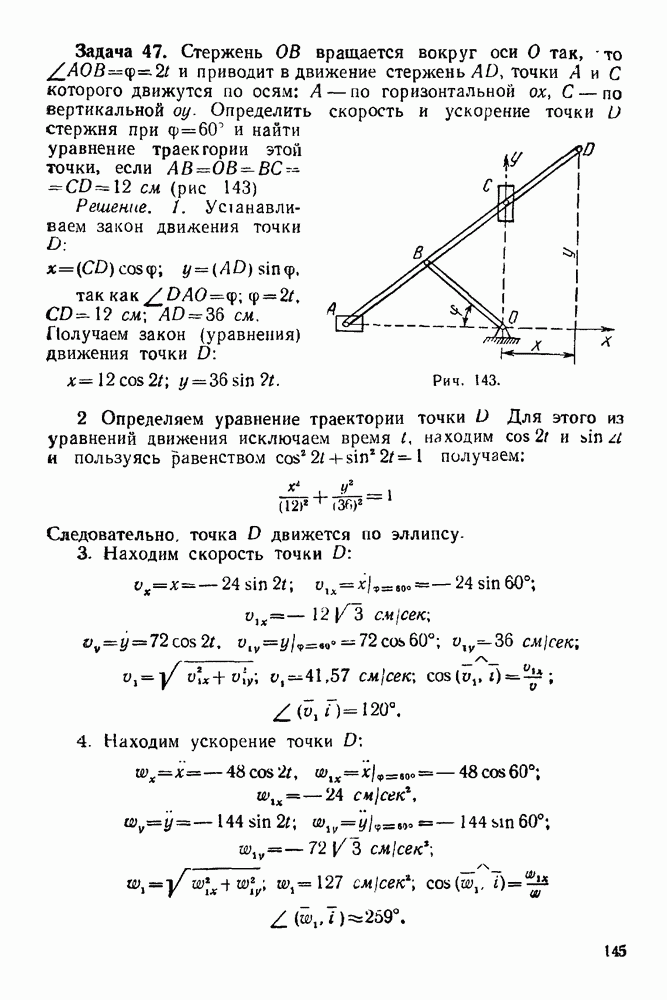
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
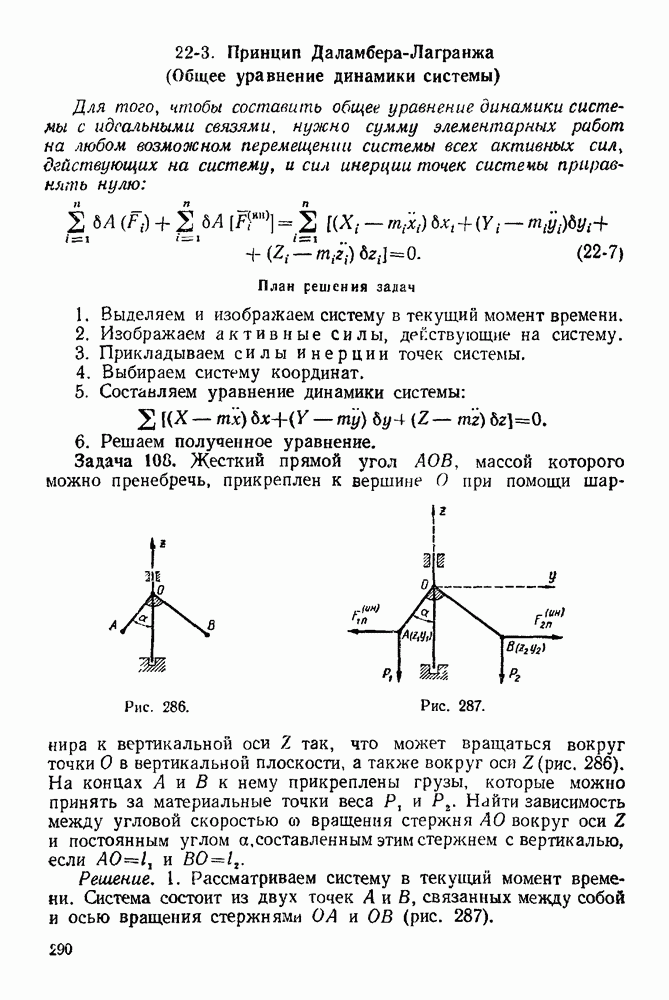
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР