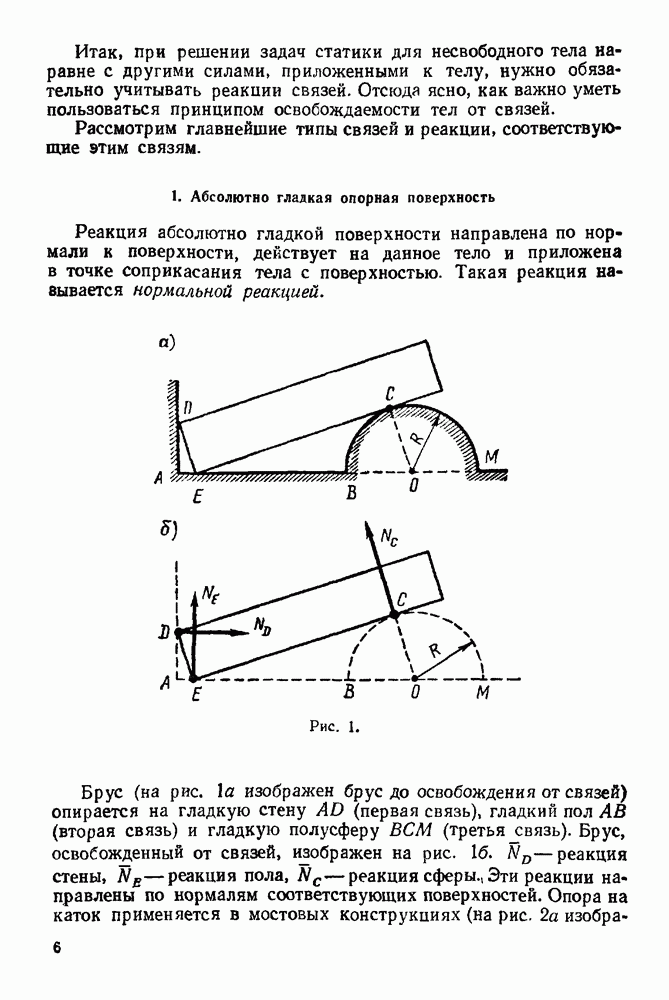
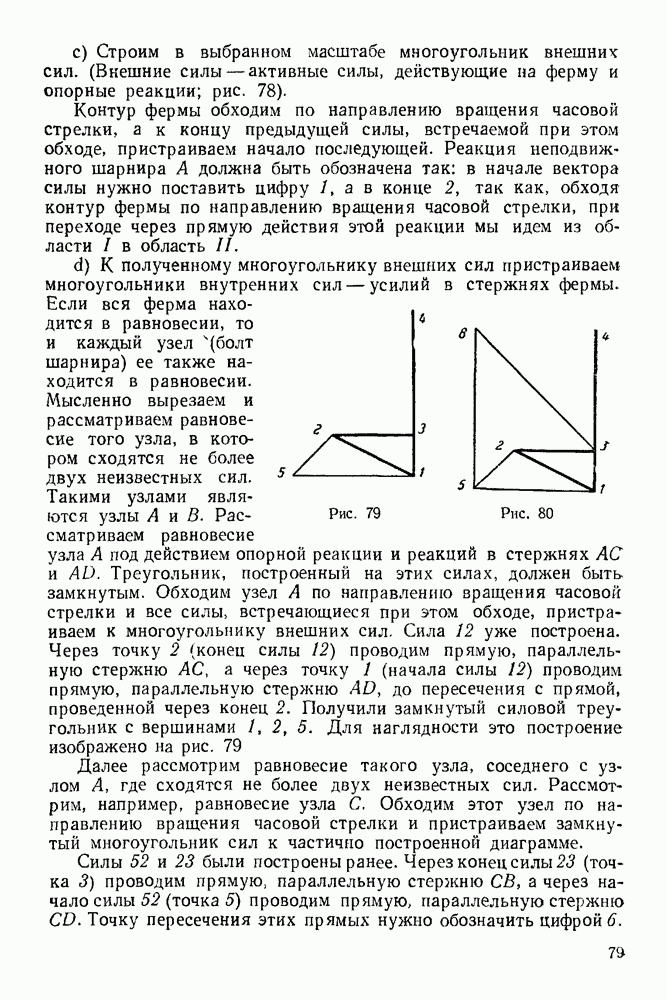
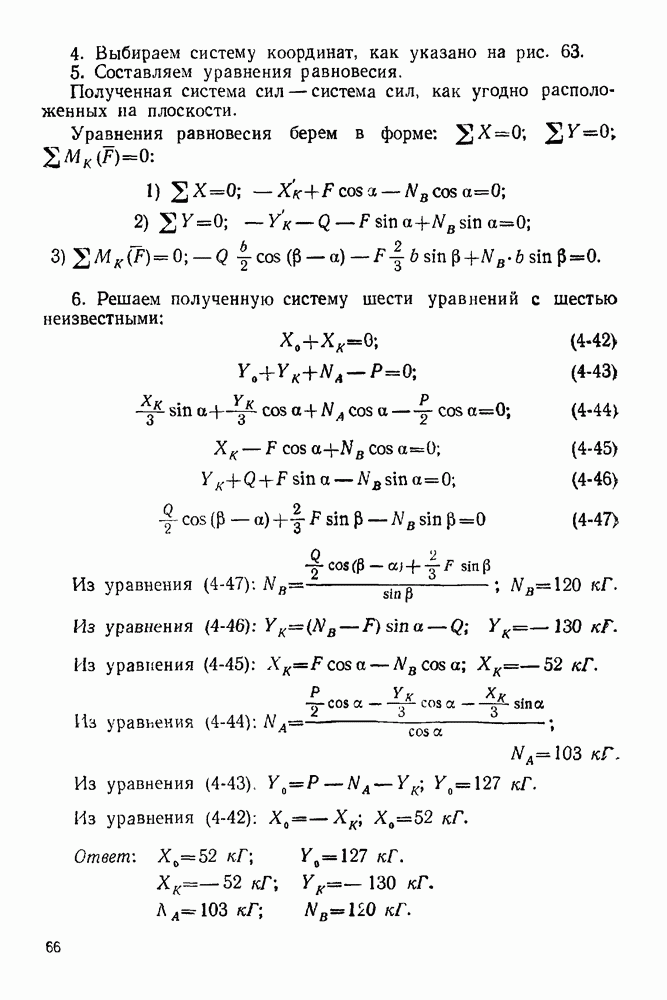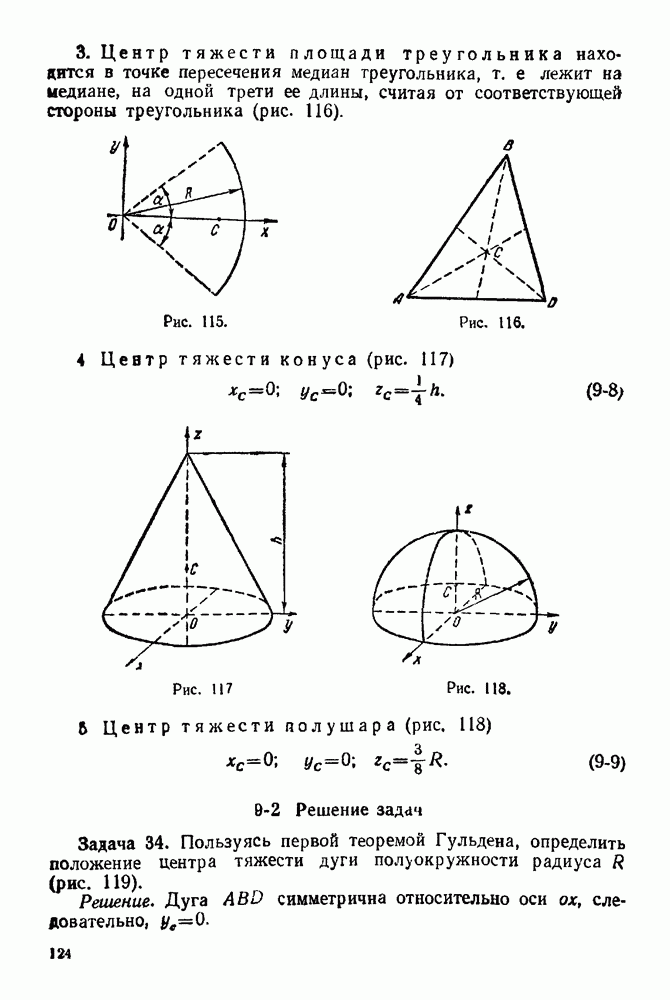| << Предыдущий параграф | Следующий параграф >> |
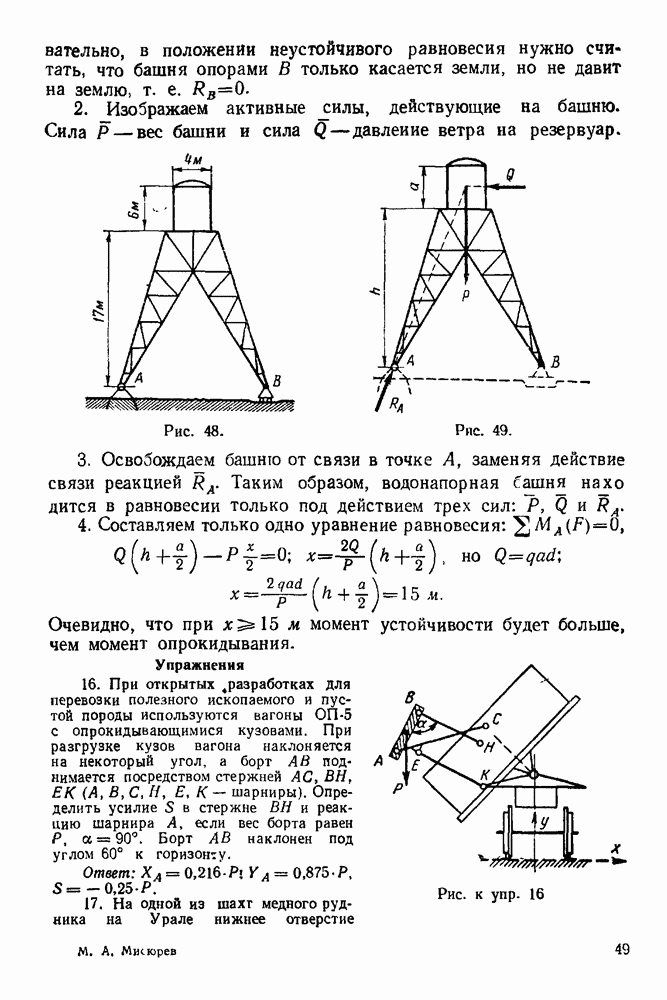
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
5.1. Основные положения
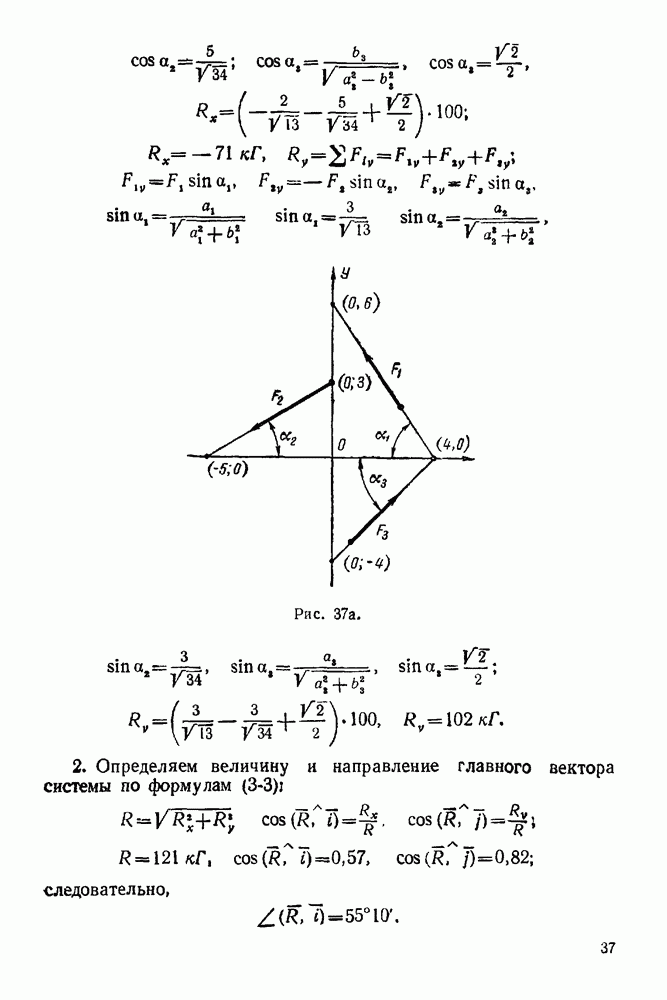
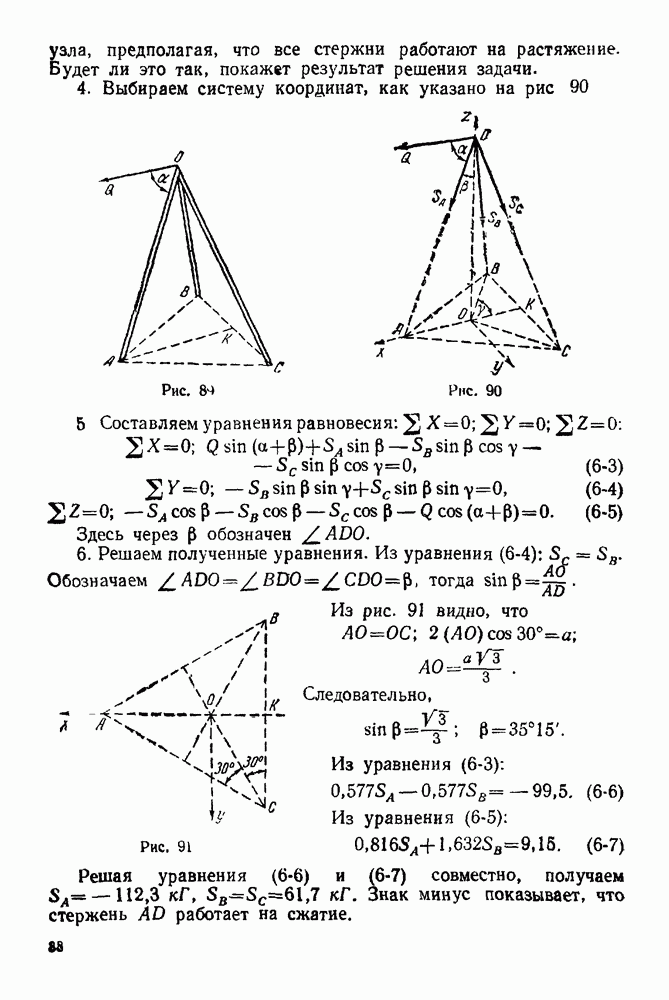
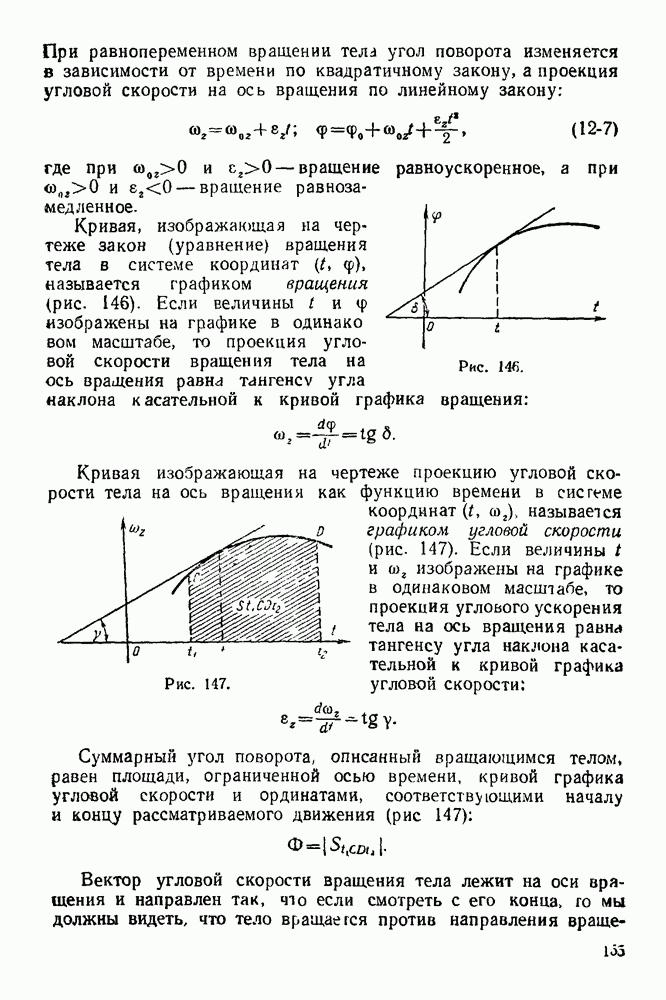
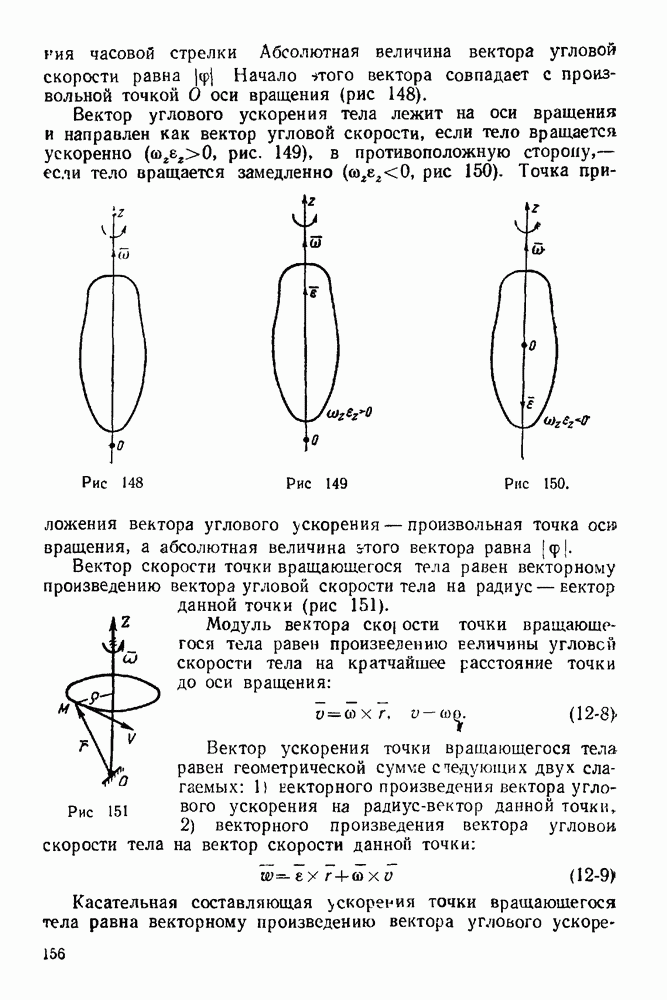
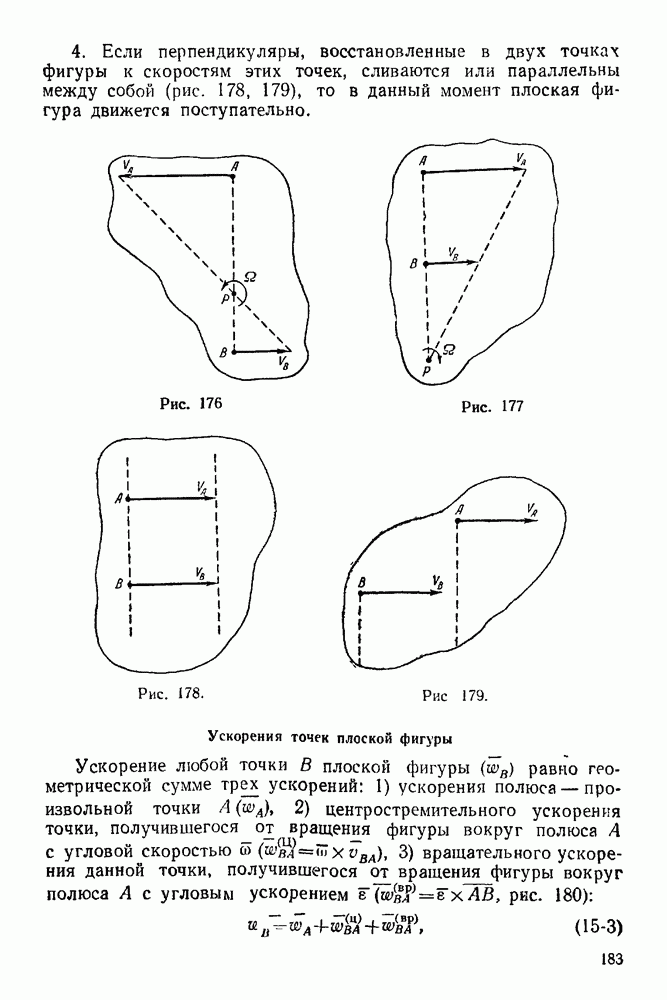
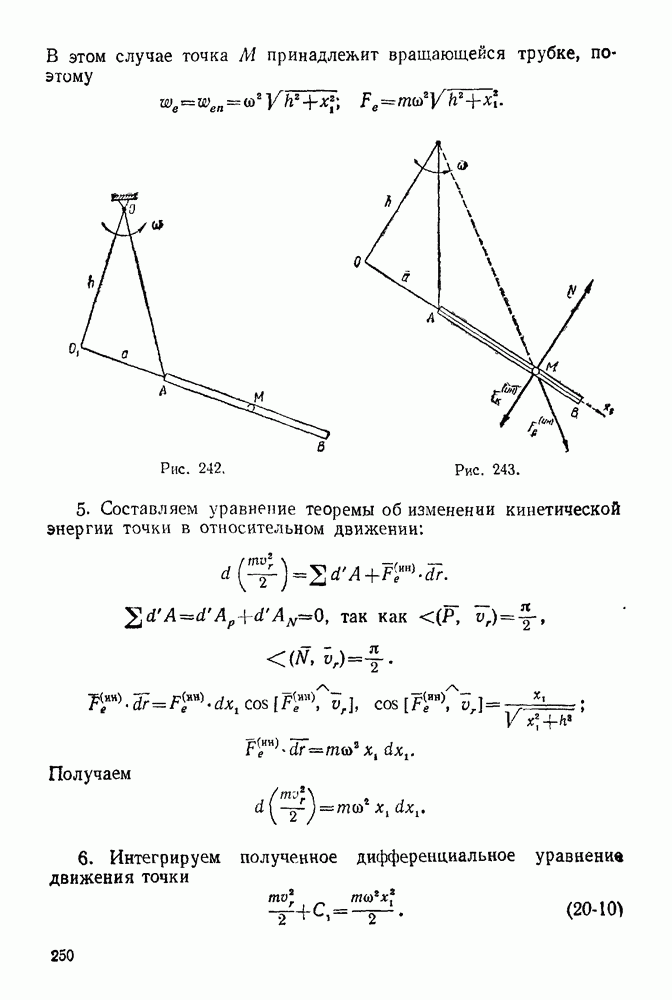
Графостатика — раздел статики, в котором решаются задачи о сложении и равновесии сил плоской системы методами графики. Для равновесия сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы силовой и веревочный многоугольники этой системы были замкнутыми.
Силовой многоугольник данной системы сил — такой многоугольник, стороны которого равны и параллельны силам этой системы.  (рис. 65) — силовой многоугольник системы сил
(рис. 65) — силовой многоугольник системы сил  изображенных на рис. 64.
изображенных на рис. 64.

Рис. 64

Рис. 65
Веревочный многоугольник данной системы сил — такой многоугольник, стороны которого параллельны соответствующим лучам силового многоугольника, а вершины его лежат на прямых действия сил системы а, 1—2, 2—3,  — веревочный многоугольник (рис. 64).
— веревочный многоугольник (рис. 64).  Причем точка О — полюс — произвольная точка плоскости (рис. 65). Лучи силового многоугольника соединяют полюс О с вершинами силового многоугольника. Так луч
Причем точка О — полюс — произвольная точка плоскости (рис. 65). Лучи силового многоугольника соединяют полюс О с вершинами силового многоугольника. Так луч  соединяет полюс О с вершиной, где сходятся силы
соединяет полюс О с вершиной, где сходятся силы  , поэтому этот луч обозначен 1—2. Первый луч обозначают буквой а, последний
, поэтому этот луч обозначен 1—2. Первый луч обозначают буквой а, последний  Соответствующая
Соответствующая
сторона веревочного многоугольника  начало этой стороны лежит на прямой действия силы 1, а конец — на прямой действия силы 2
начало этой стороны лежит на прямой действия силы 1, а конец — на прямой действия силы 2
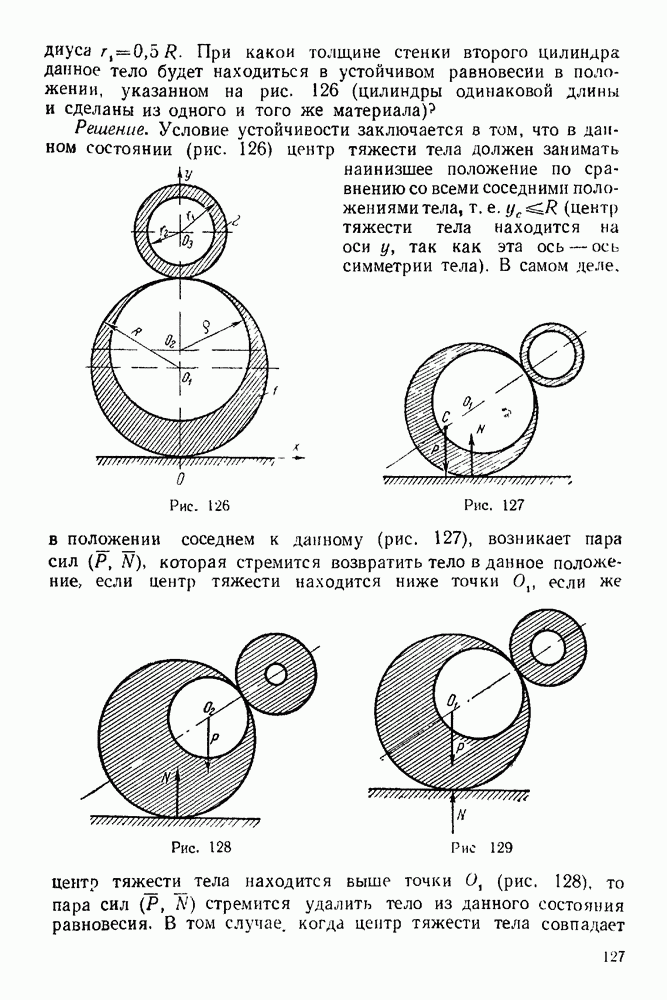
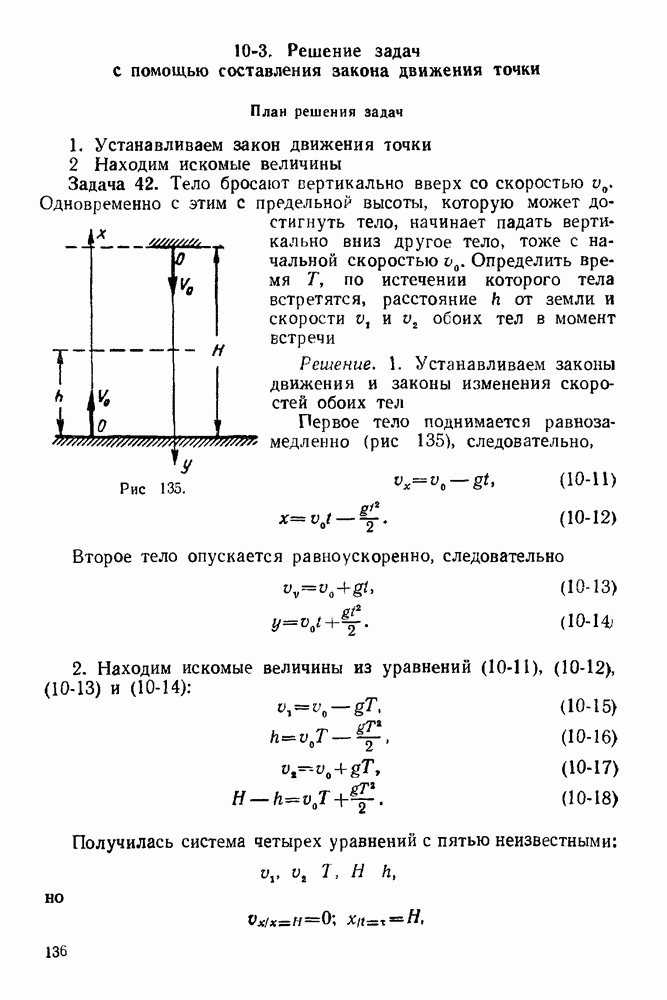
5-2. Определение опорных реакций.
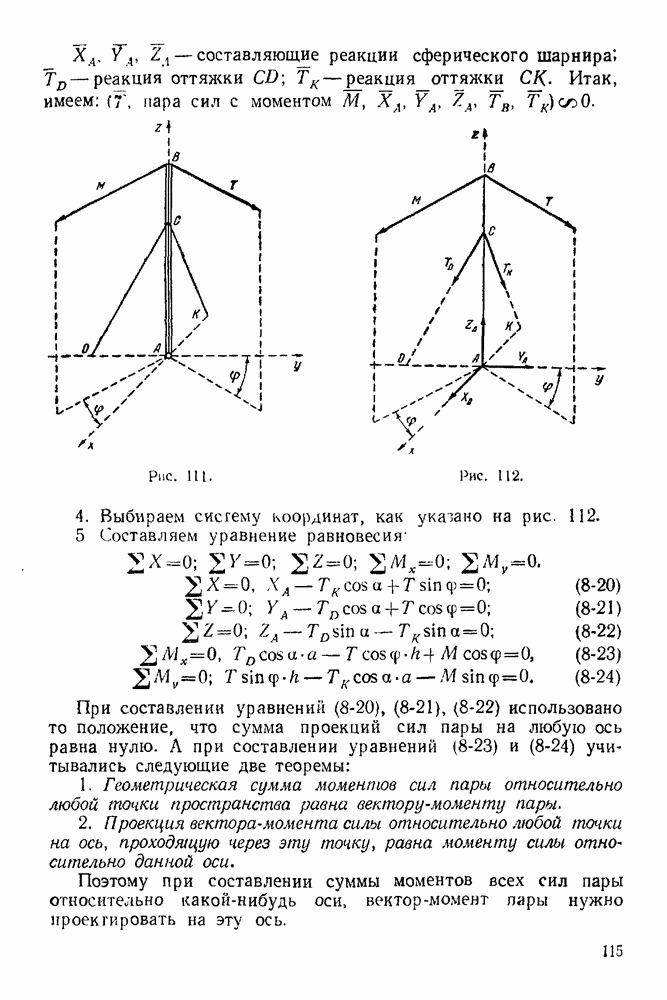
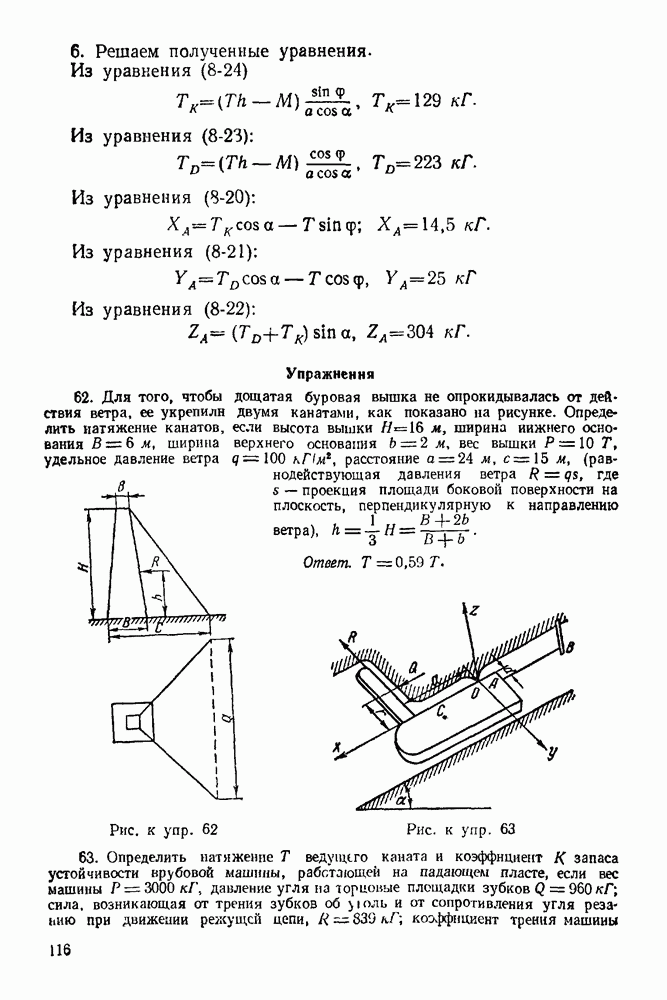
План решения задачи.
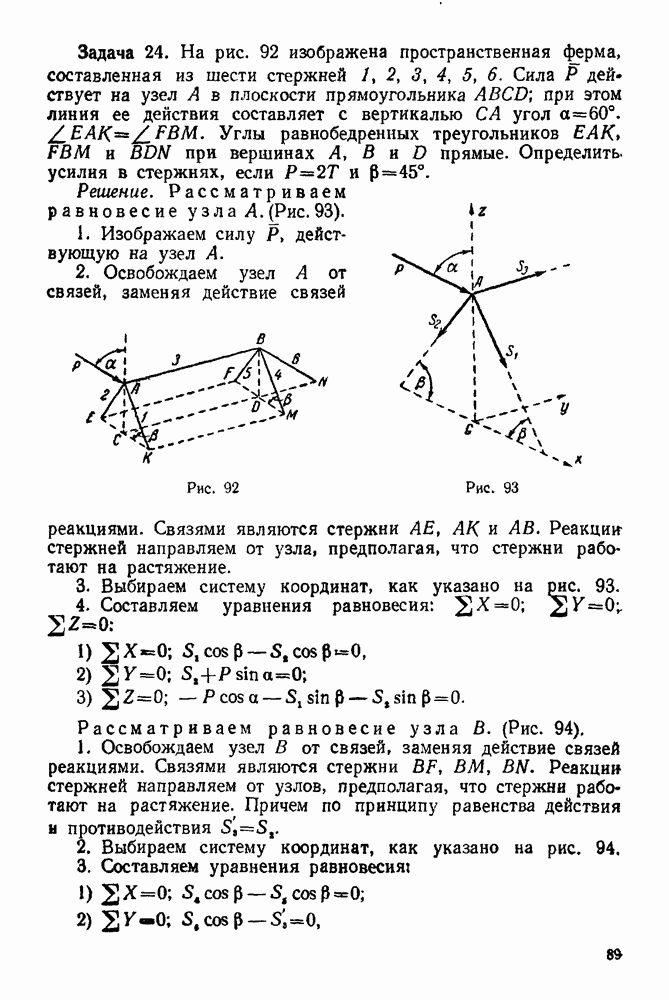
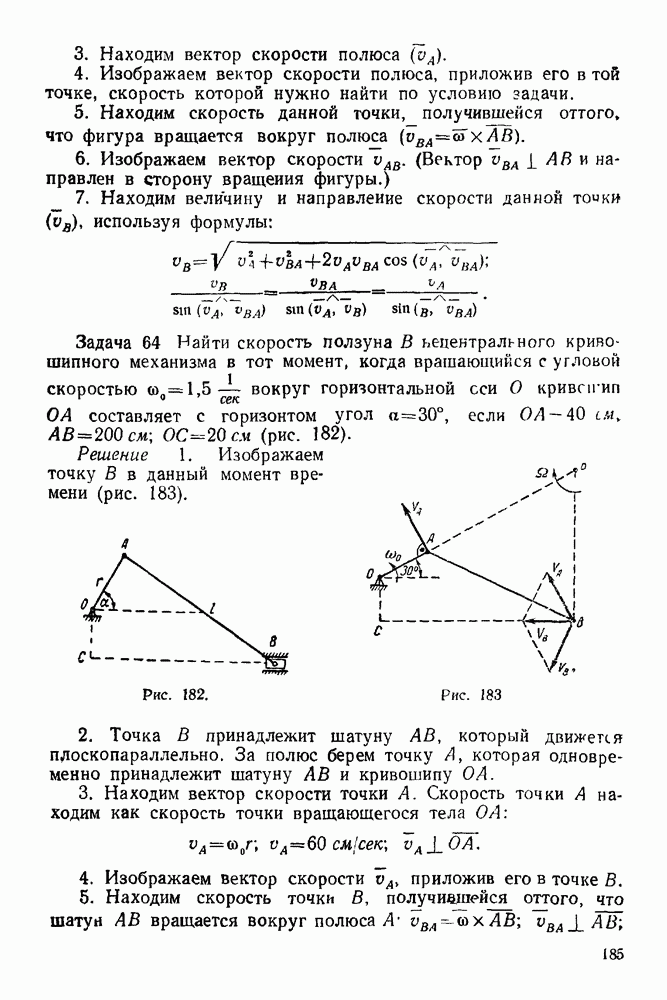
Если твердое тело, опорные реакции которого нужно найти, находится в равновесии, то силовой и веревочный многоугольники должны быть замкнутыми.
При решении задачи необходимо придерживаться следующего порядка:
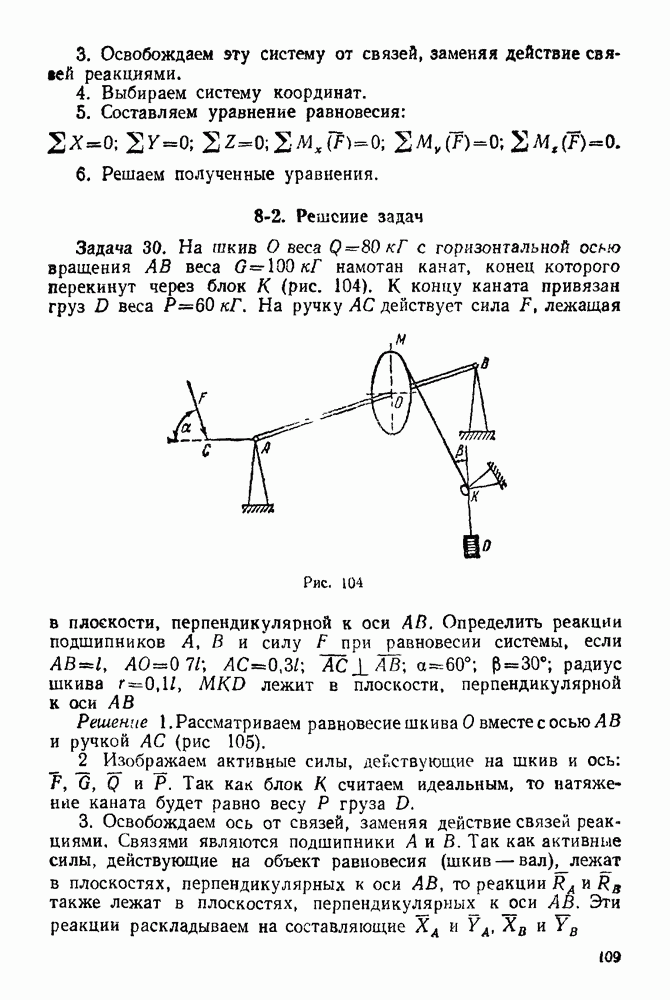
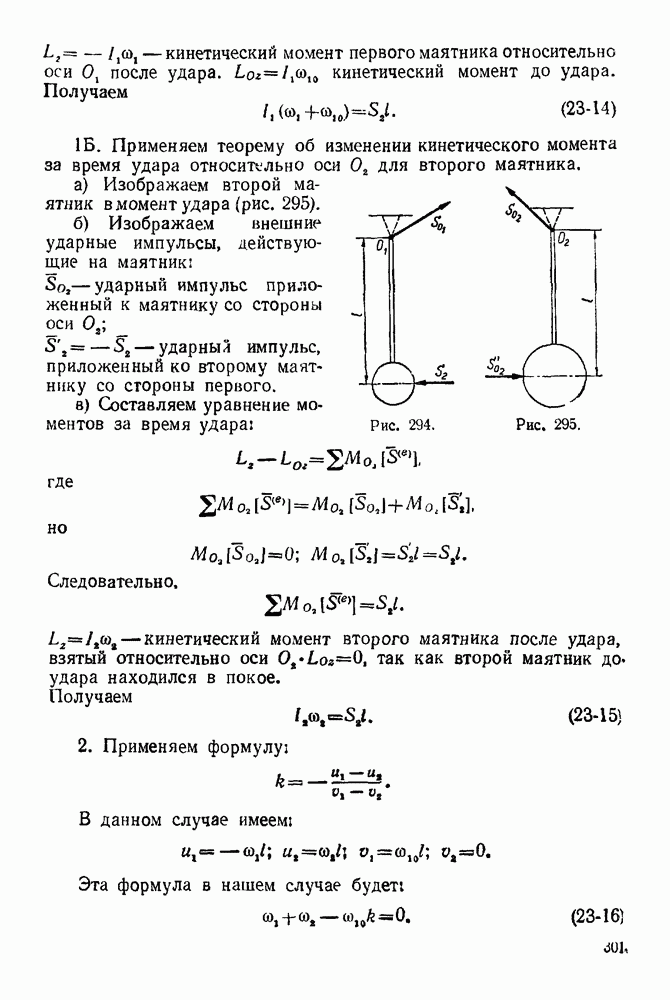
1 Изображаем тело, равновесие которого рассматриваем. Силы, действующие на него, следует рассмотреть в выбранных масштабах.
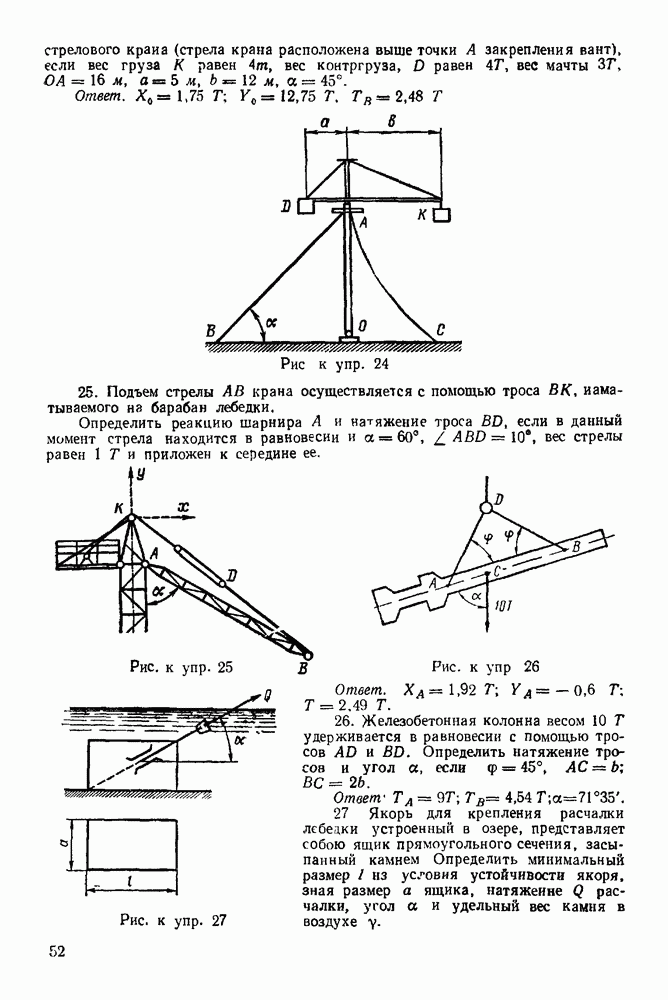
2. Все силы, действующие на это тело (включая и реакции связей), обозначим цифрами  Для удобства реакции неподвижного шарнира необходимо считать первой силой, а реакцию другой опоры — последней силой (
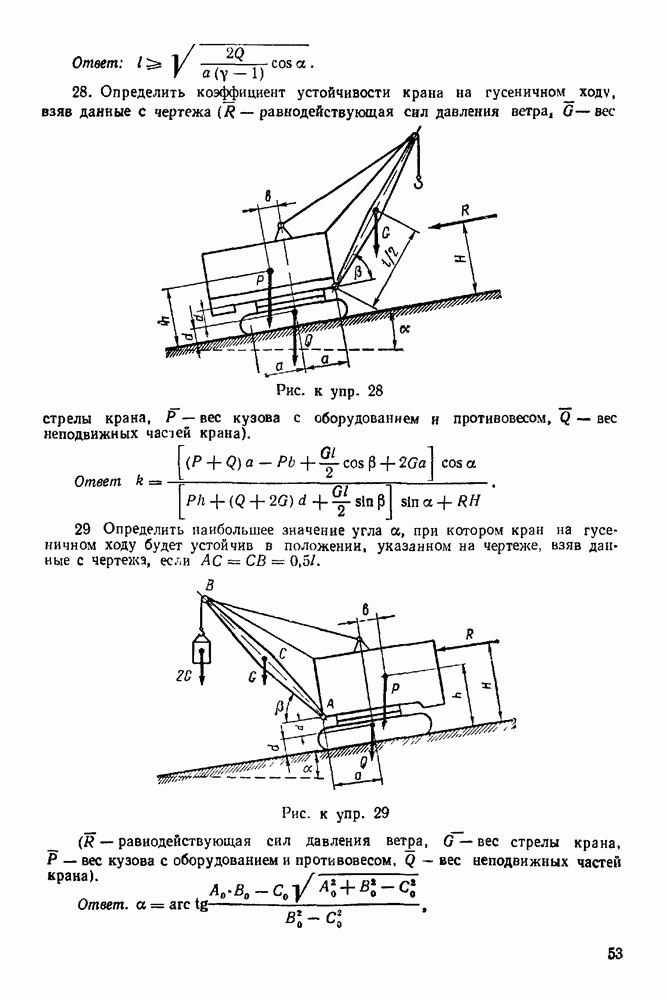
Для удобства реакции неподвижного шарнира необходимо считать первой силой, а реакцию другой опоры — последней силой ( -ной силой)
-ной силой)
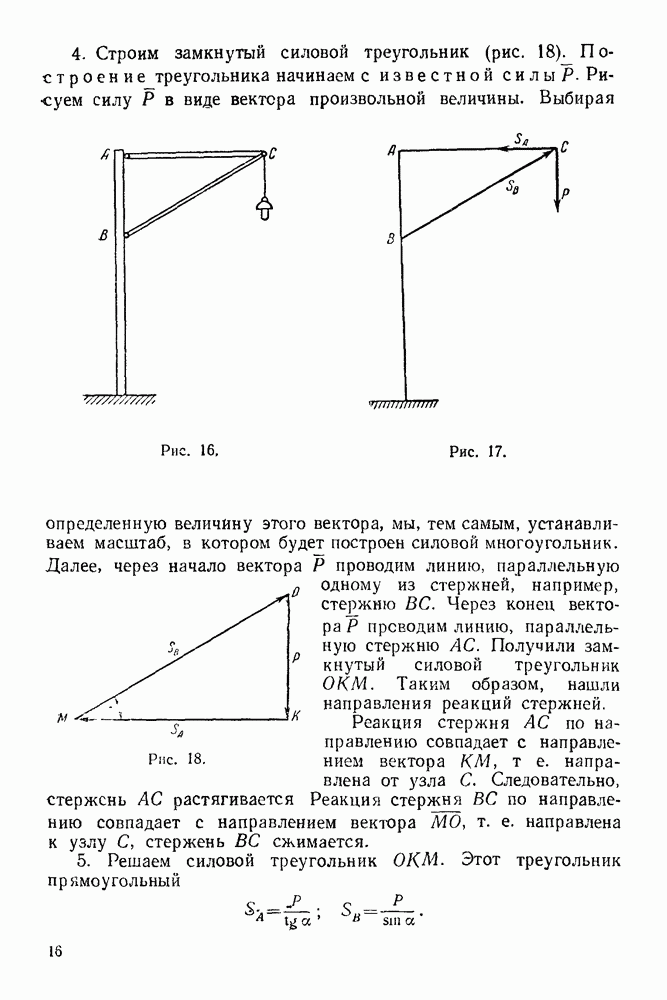
3 Строим в выбранном масштабе замкнутый силовой многоугольник При построении многоугольника силы изображаем последовательно в порядке принятой нумерации Построение временно заканчиваем на том, что проводим через конец последней активной силы  сила] прямую, параллельную реакции подвижной опоры (эта реакция известна только по направлению)
сила] прямую, параллельную реакции подвижной опоры (эта реакция известна только по направлению)
4. Выбираем в окрестности силового многоугольника полюс (полюс — произвольно выбранная точка, не лежащая на силах многоугольника) и соединяем его лучами с вершинами силового многоугольника. Если луч соединяет полюс с вершиной, образованной силами  и 2, то его обозначаем
и 2, то его обозначаем 
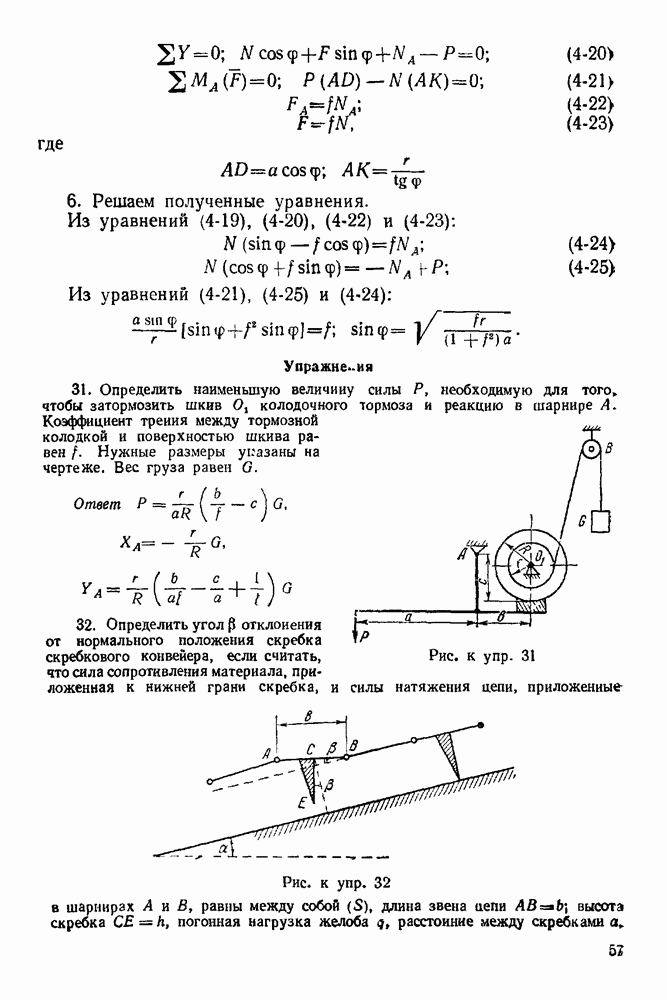
5 Строим замкнутый веревочный многоугольник. Построение его начинаем обязательно с неподвижного шарнира (если все силы, действующие на объект равновесия, — параллельные, то построение веревочного многоугольника можно начинать из любой точки, лежащей на прямой действия опорной реакции). Из неподвижного шарнира проводим отрезок прямой  до пересечения с прямой действия силы 2. Из ьтой точки проводим отрезок прямой
до пересечения с прямой действия силы 2. Из ьтой точки проводим отрезок прямой  до пересечения с прямой действия силы
до пересечения с прямой действия силы  наконец, точку пересечения отрезка прямой
наконец, точку пересечения отрезка прямой  с прямой действия силы
с прямой действия силы  (второй опорной реакции) соединяем отрезком прямой
(второй опорной реакции) соединяем отрезком прямой  с неподвижным шарниром и получаем замкнутый силовой многоугольник.
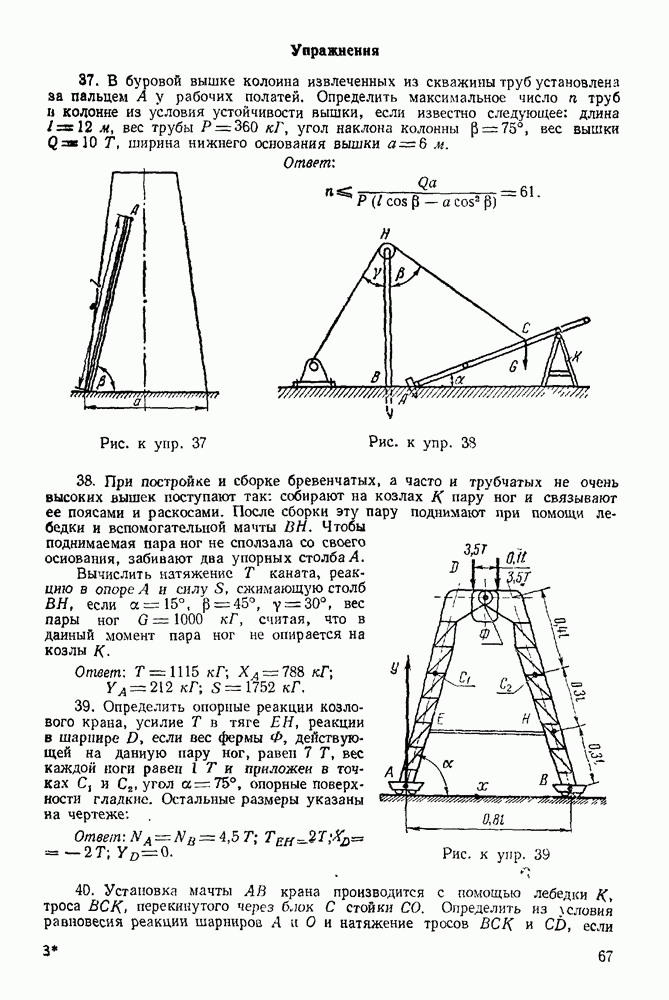
с неподвижным шарниром и получаем замкнутый силовой многоугольник.
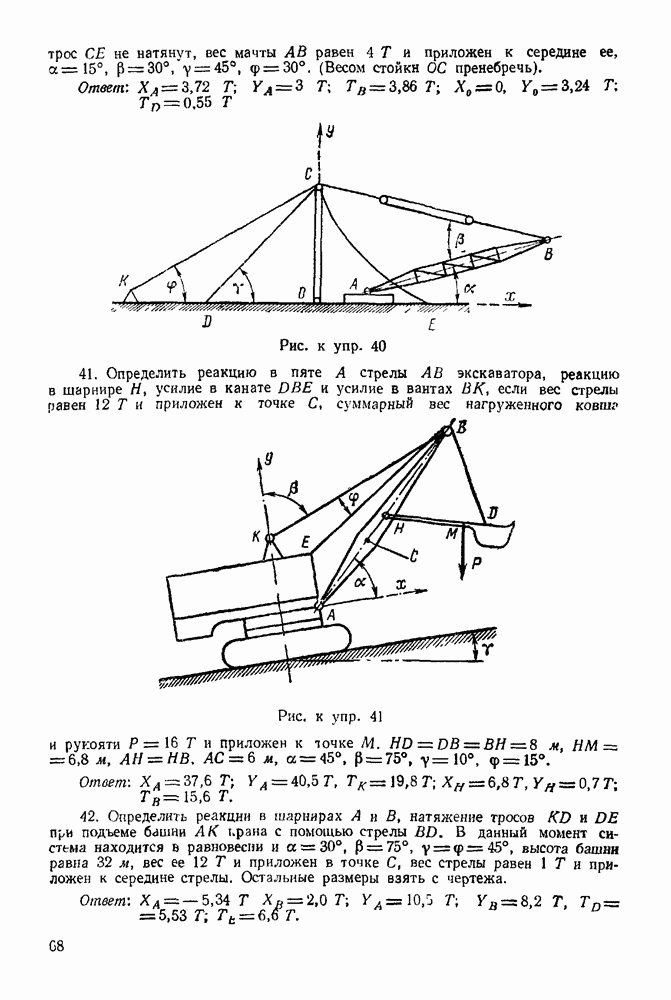
6 Из полюса силового многоугольника проводим луч  до пересечения с прямой, параллельной реакции
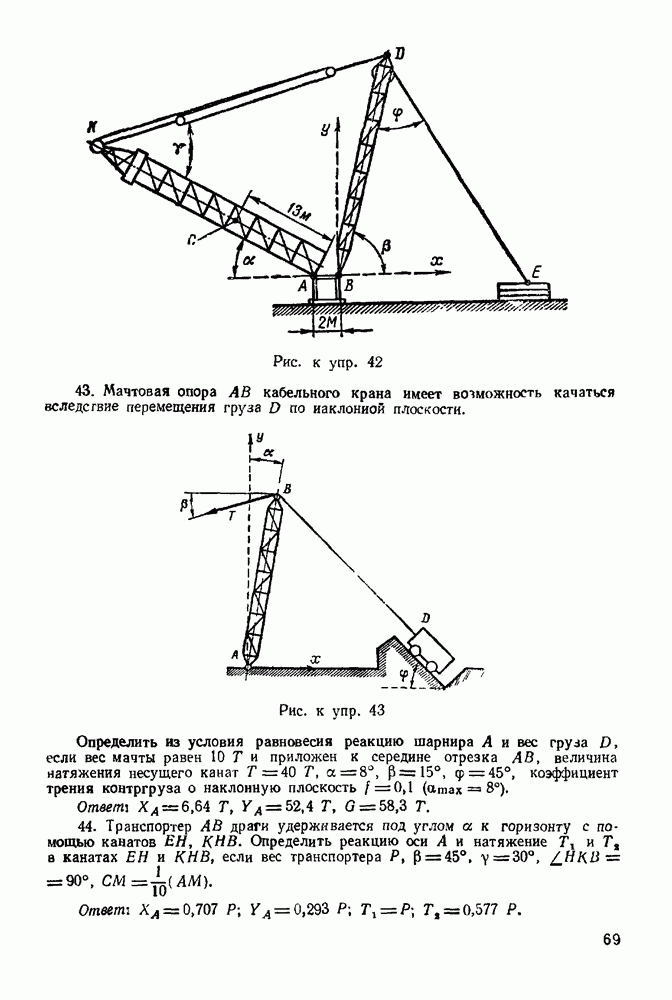
до пересечения с прямой, параллельной реакции
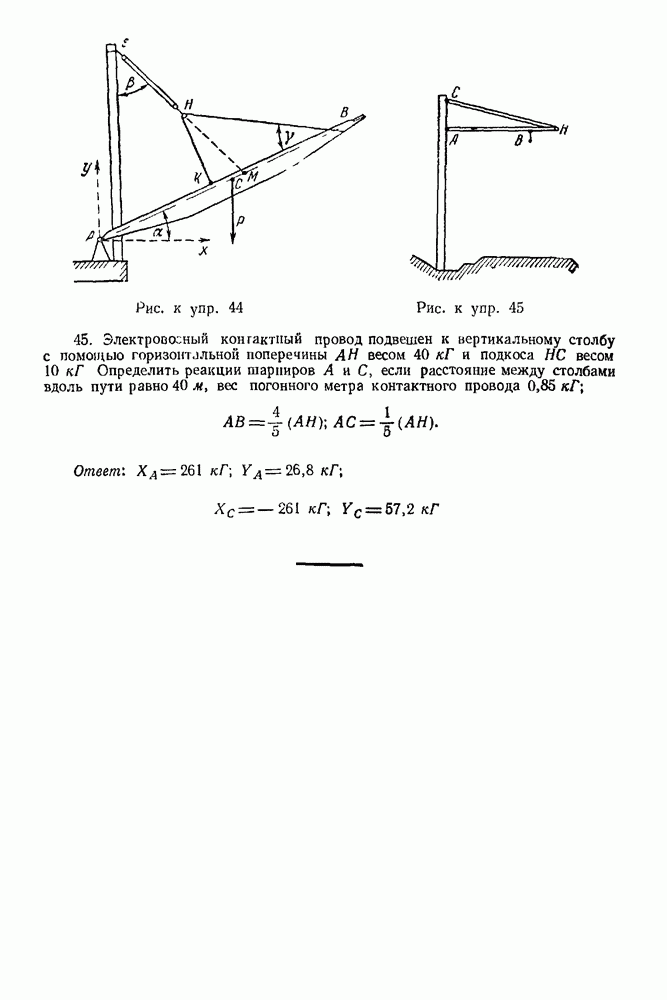
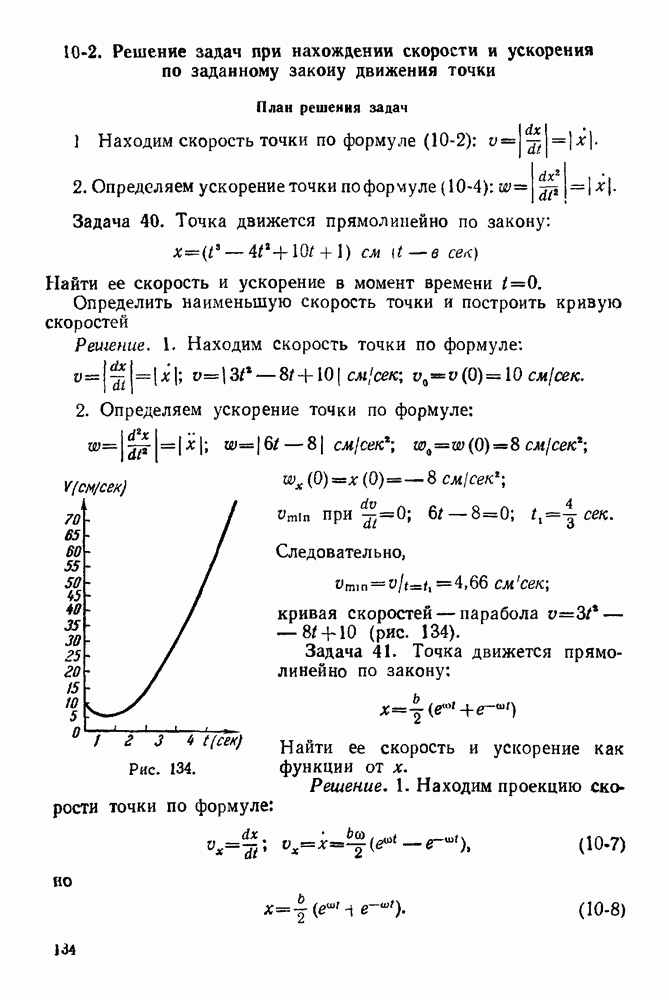
второй (подвижной) опоры и проходящей через конец последней активной силы Эта точка совпадает с концом вектора реакции подвижной опоры
7. Из конца полученной реакции проводим вектор, замыкающий силовой многоугольник. Это и будет реакция неподвижного шарнира
8. Полученные реакции в выбранном масштабе изображаем на основном чертеже, приложив их к телу, равновесие которого рассматривается
Примечание. Правильность графического решения задачи рекомендуется проверить аналитически, т. е. путем составления уравнений равновесия сил, действующих на рассматриваемое тело, и решения их относительно искомых величин реакций связей

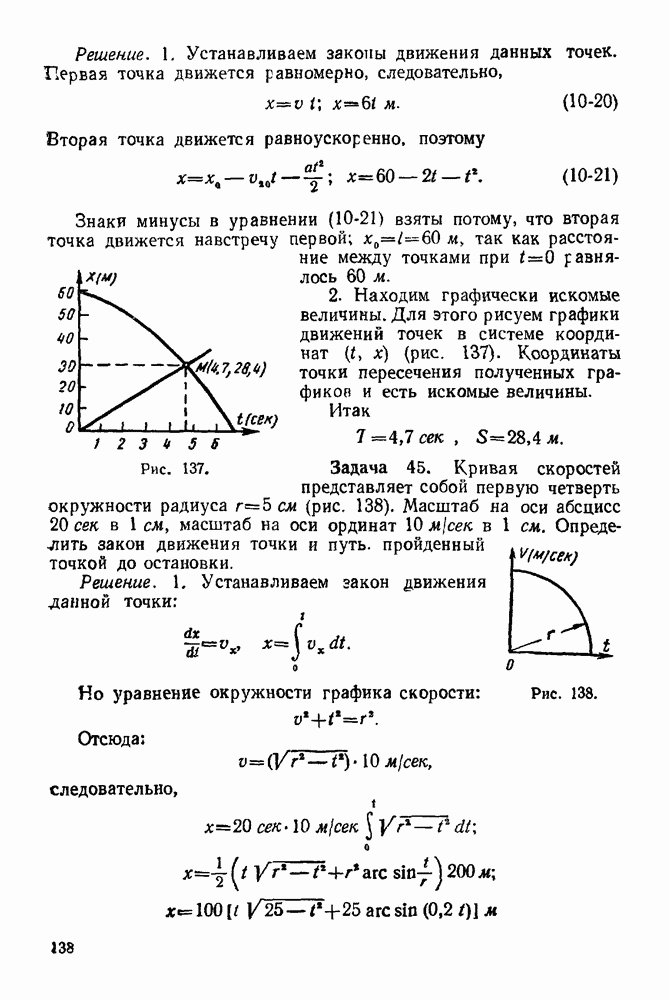
Рис. 66.

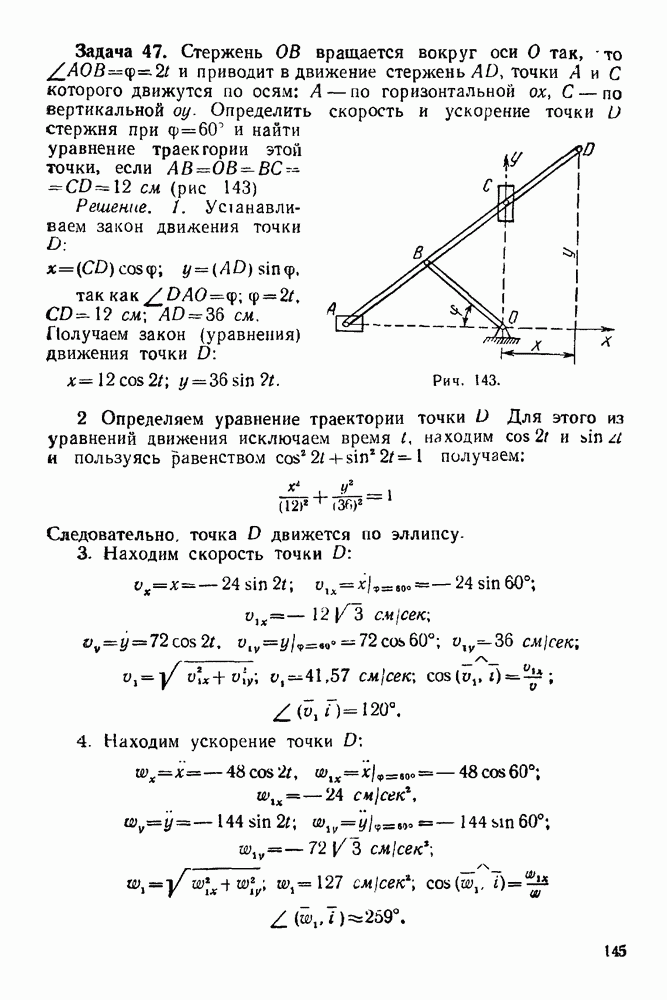
Рис. 67.
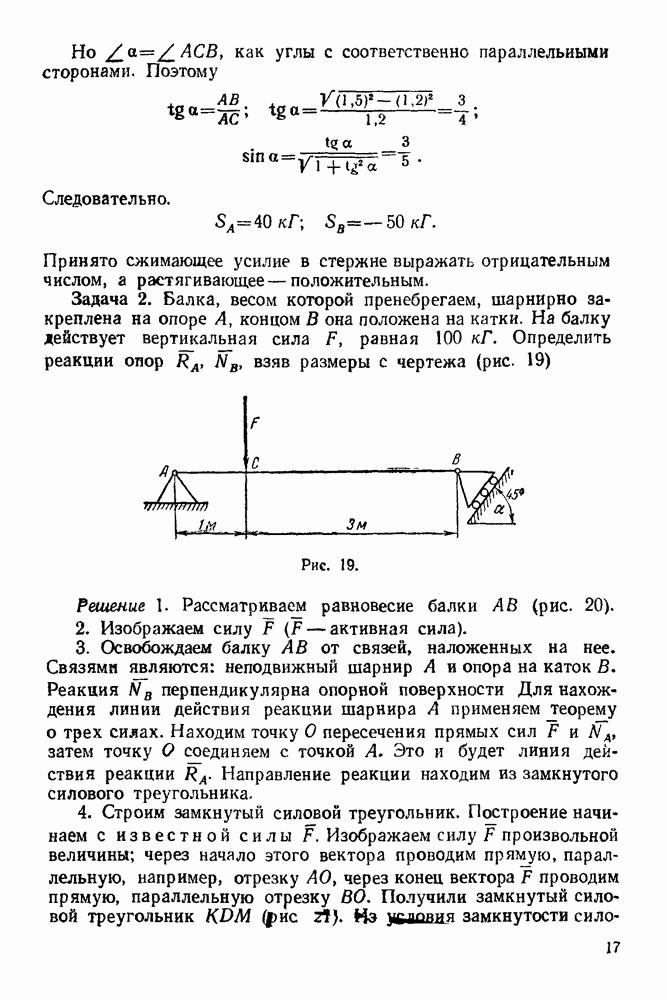
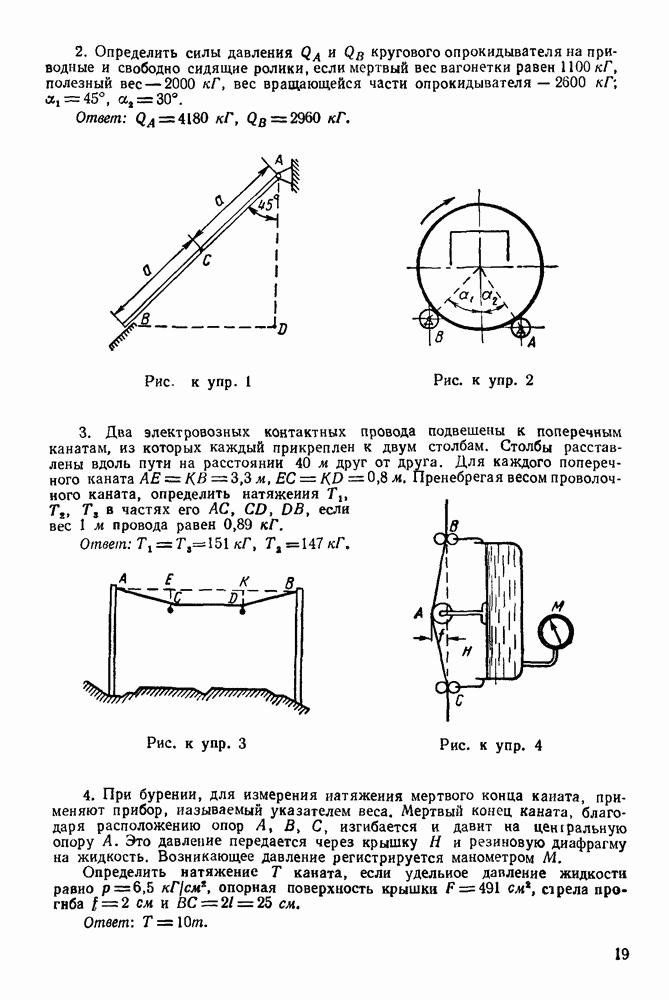
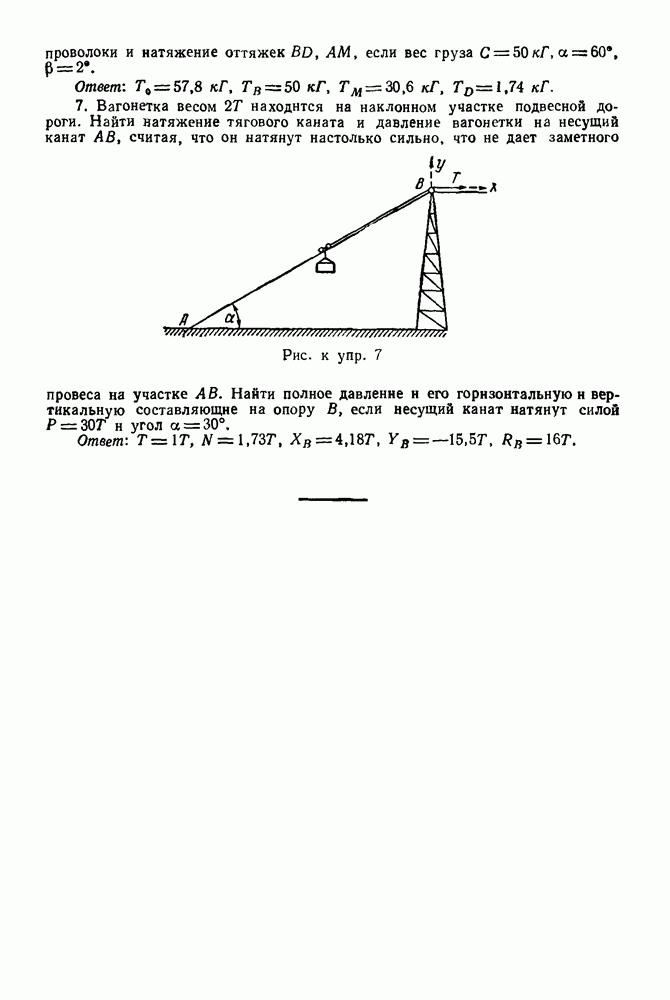
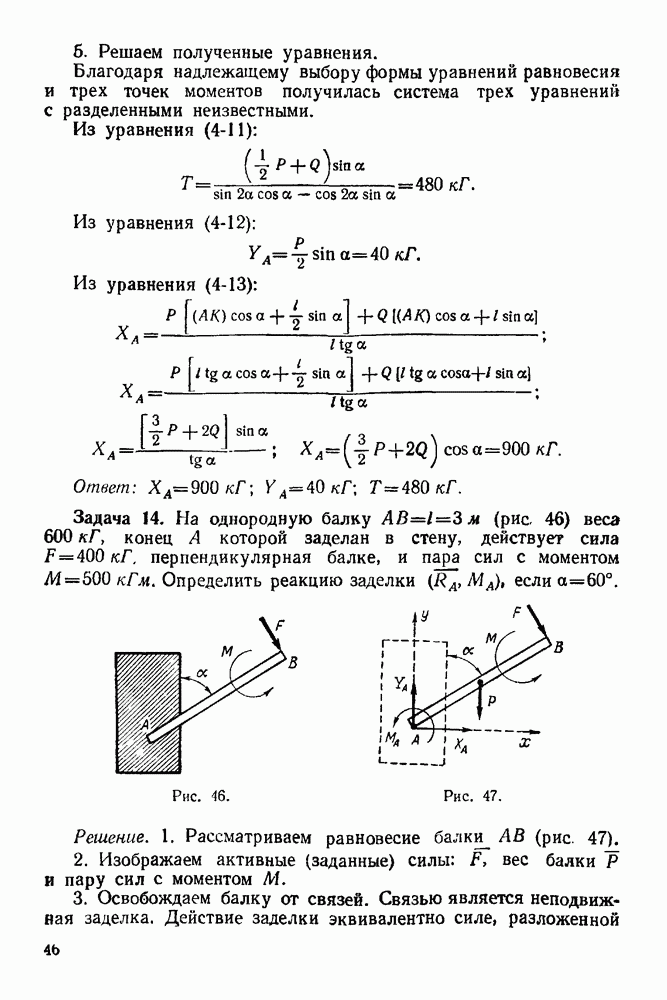
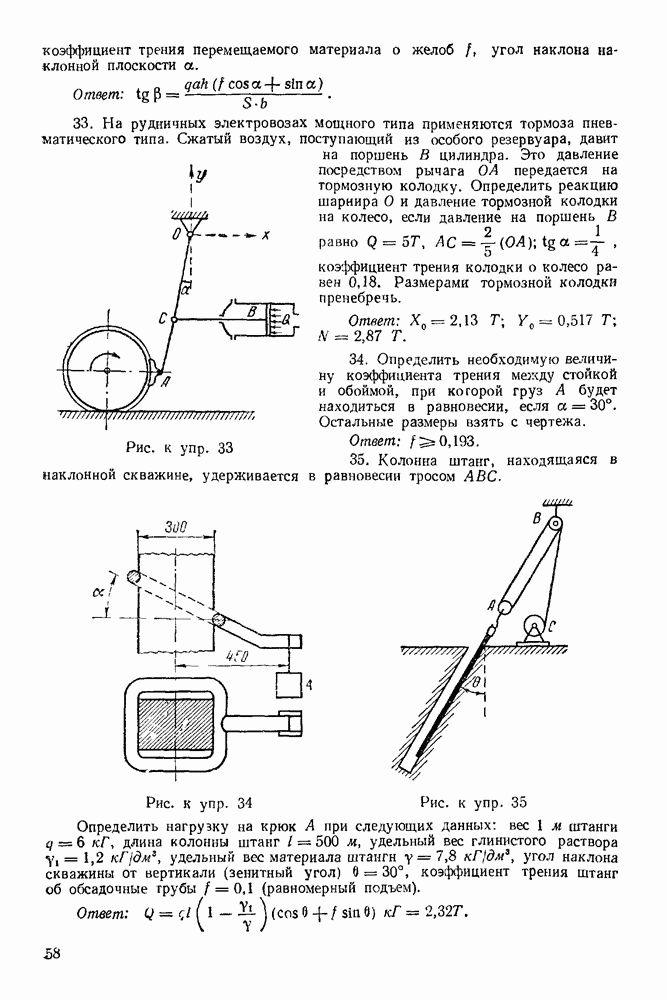
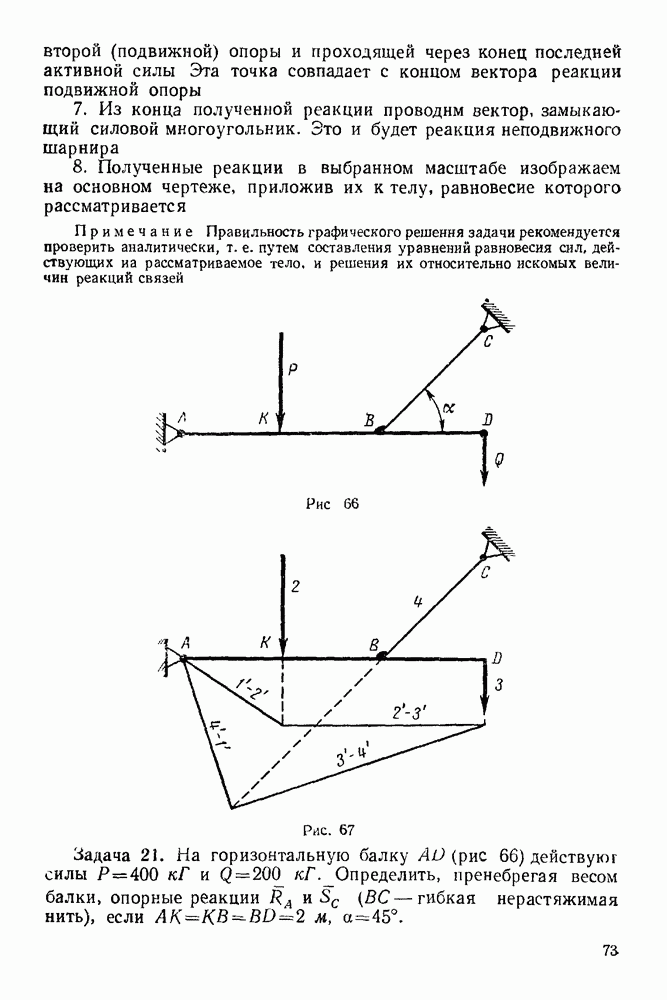
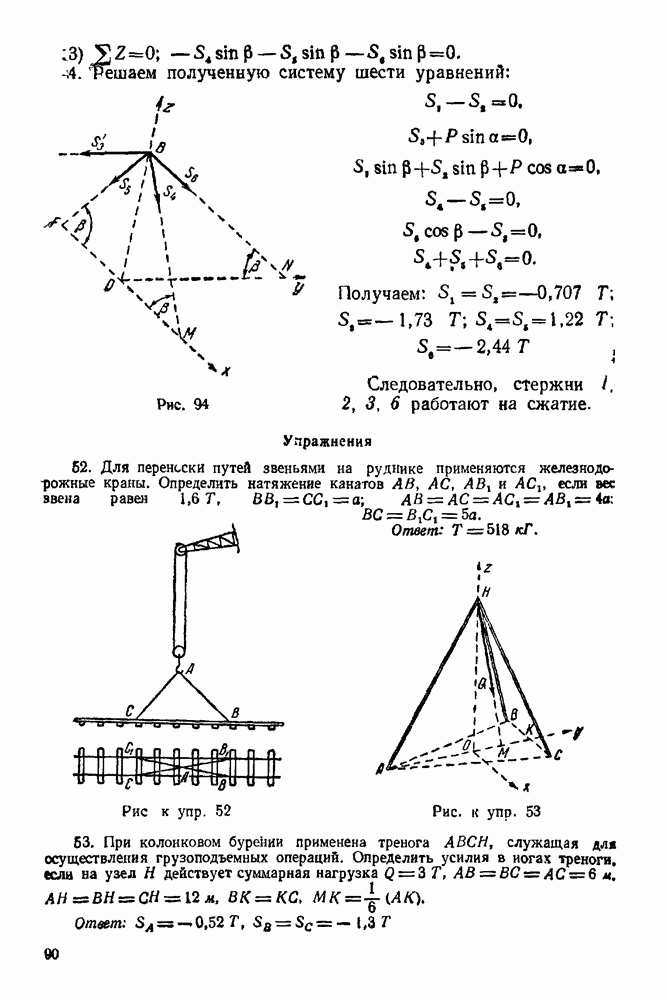
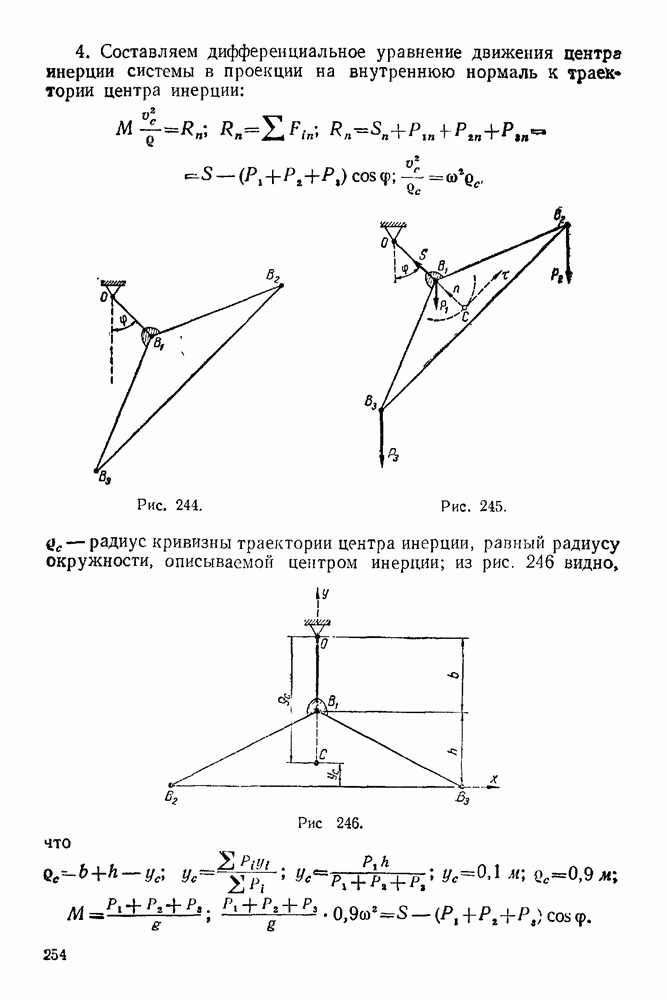
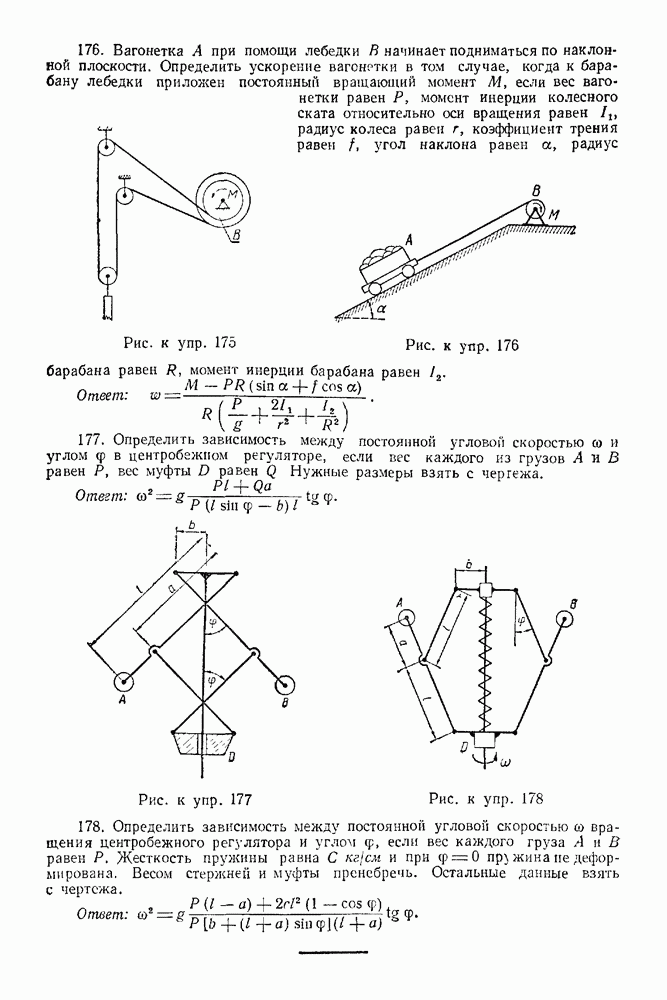
Задача 21. На горизонтальную балку  (рис 66) действуют силы
(рис 66) действуют силы  Определить, пренебрегая весом балки, опорные реакции
Определить, пренебрегая весом балки, опорные реакции  и
и  гибкая нерастяжимая нить), если
гибкая нерастяжимая нить), если 
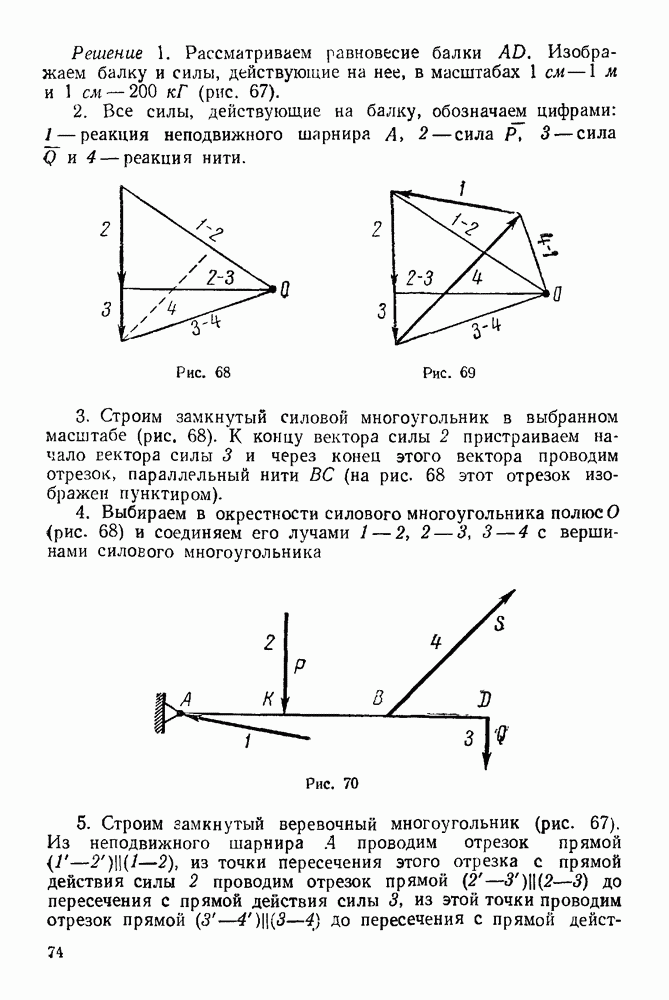
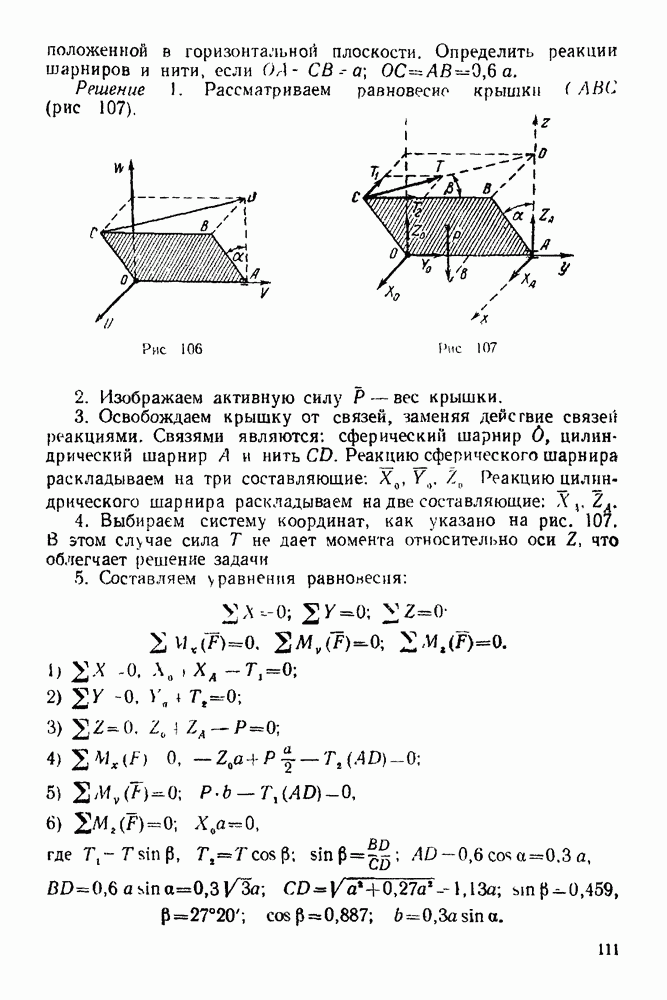
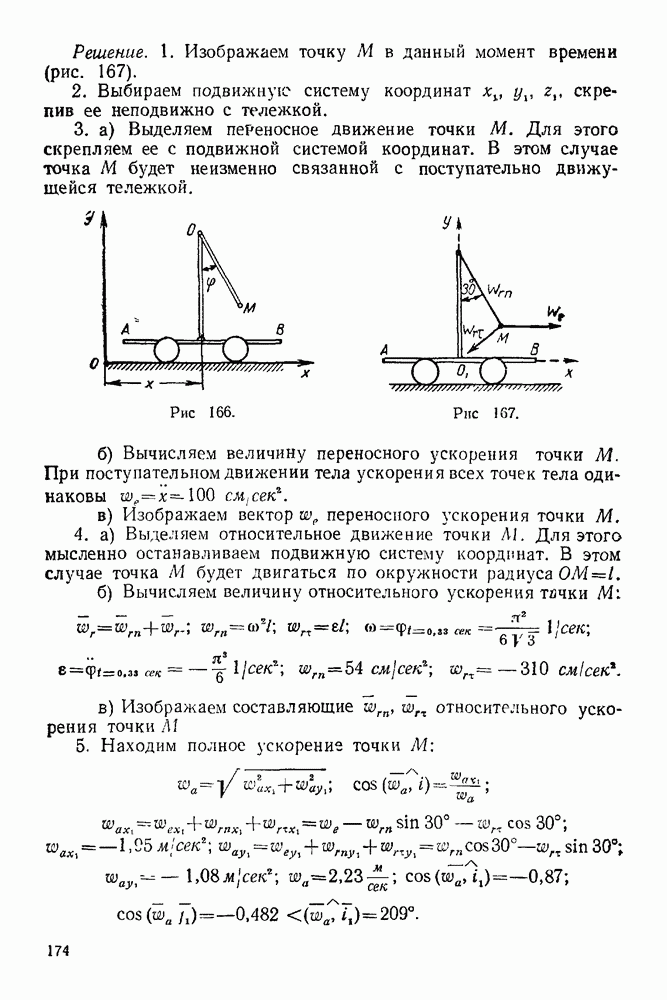
Решение 1. Рассматриваем равновесие балки  Изображаем балку и силы, действующие на нее, в масштабах
Изображаем балку и силы, действующие на нее, в масштабах  и
и 
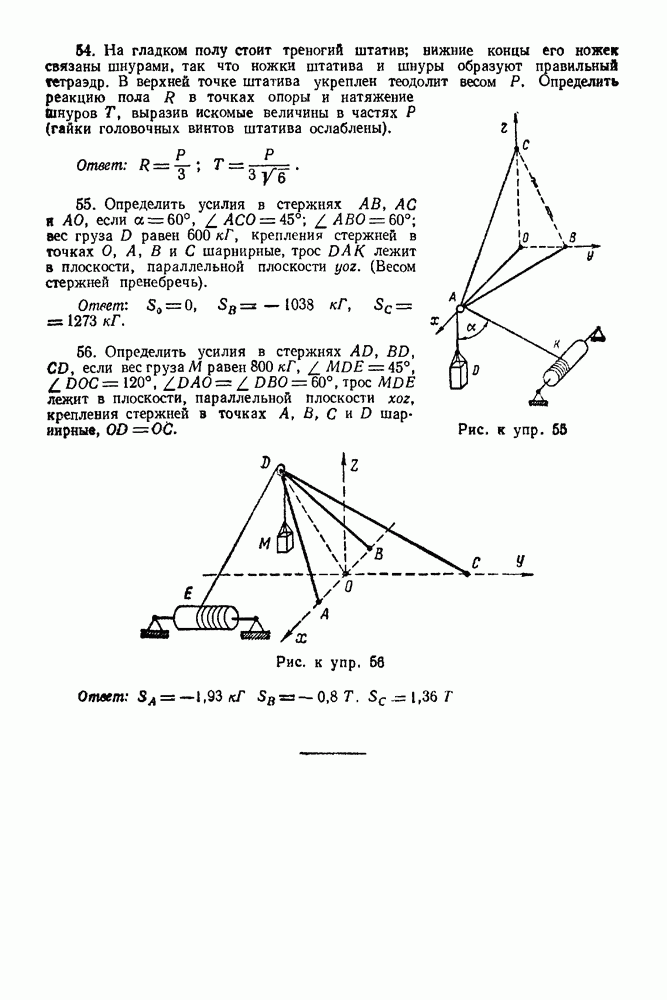
2. Все силы, действующие на балку, обозначаем цифрами: 1 — реакция неподвижного шарнира А, 2- сила Р, 3 — сила Q и 4 — реакция нити.

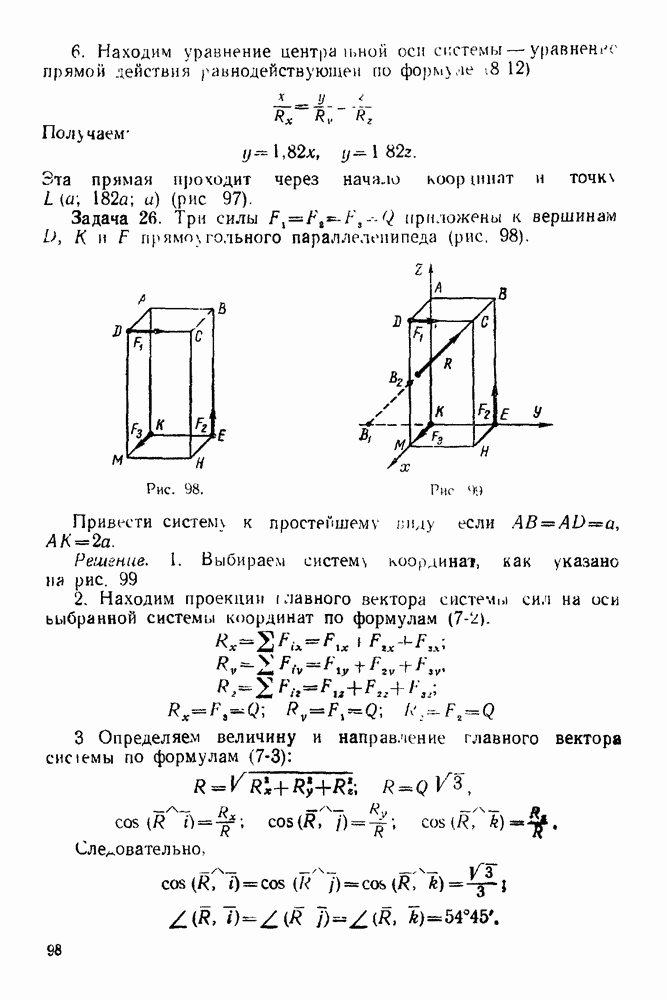
Рис. 68

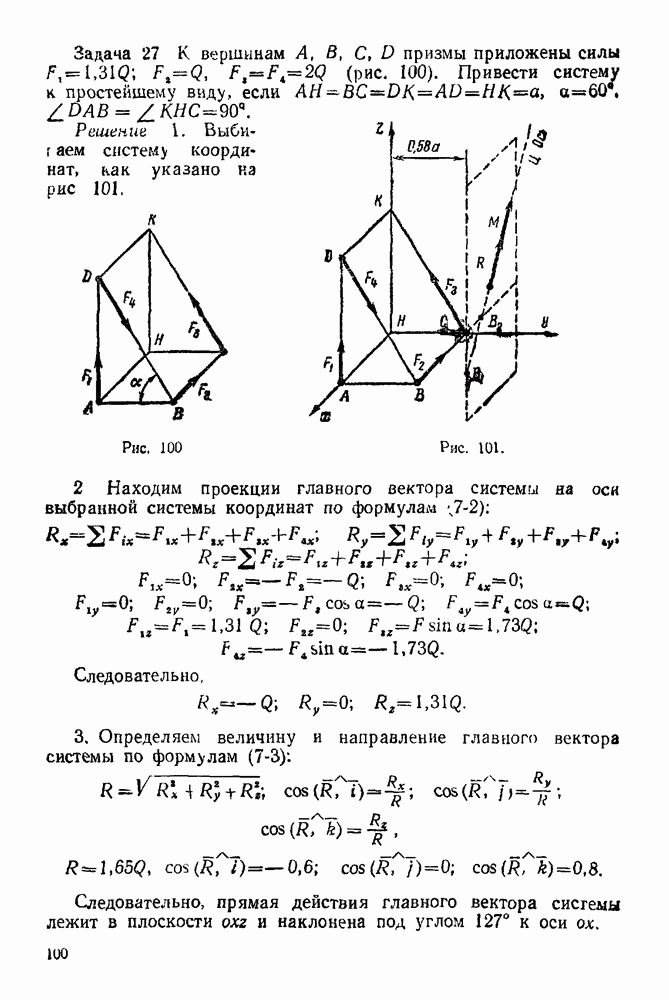
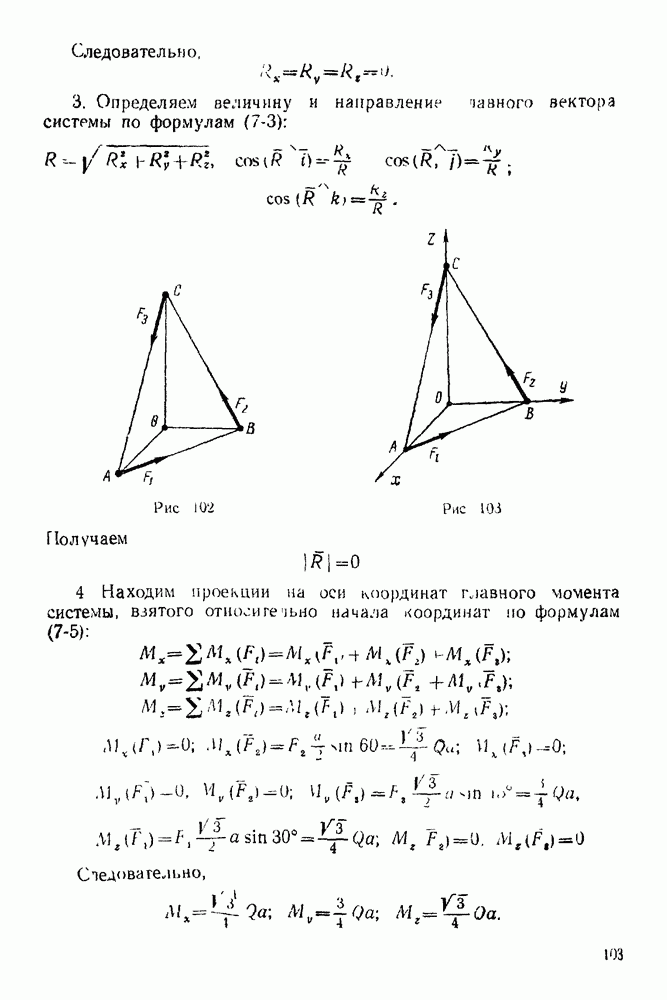
Рис. 69
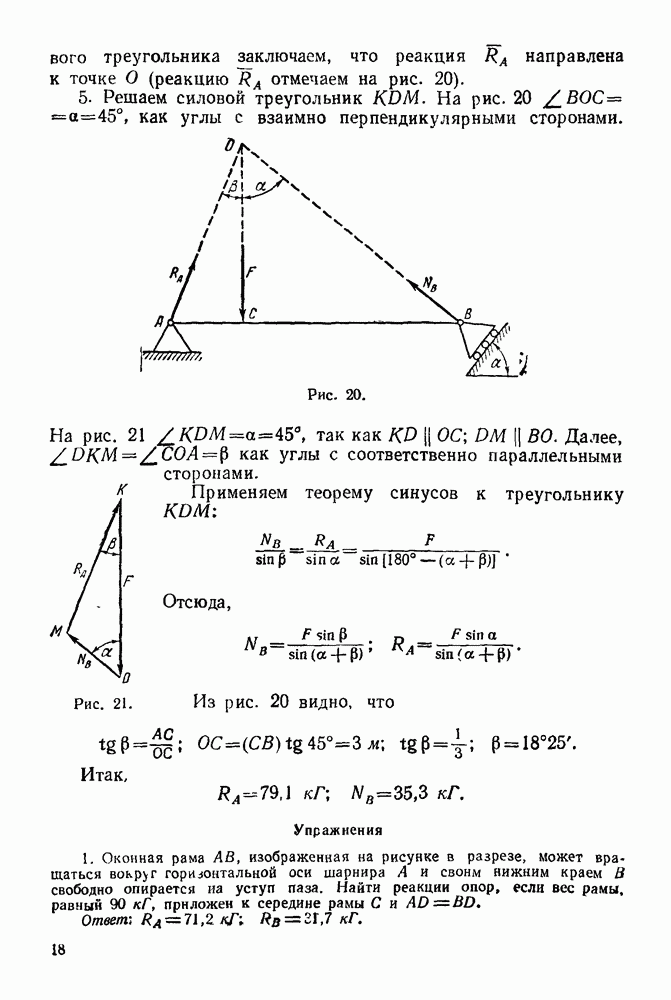
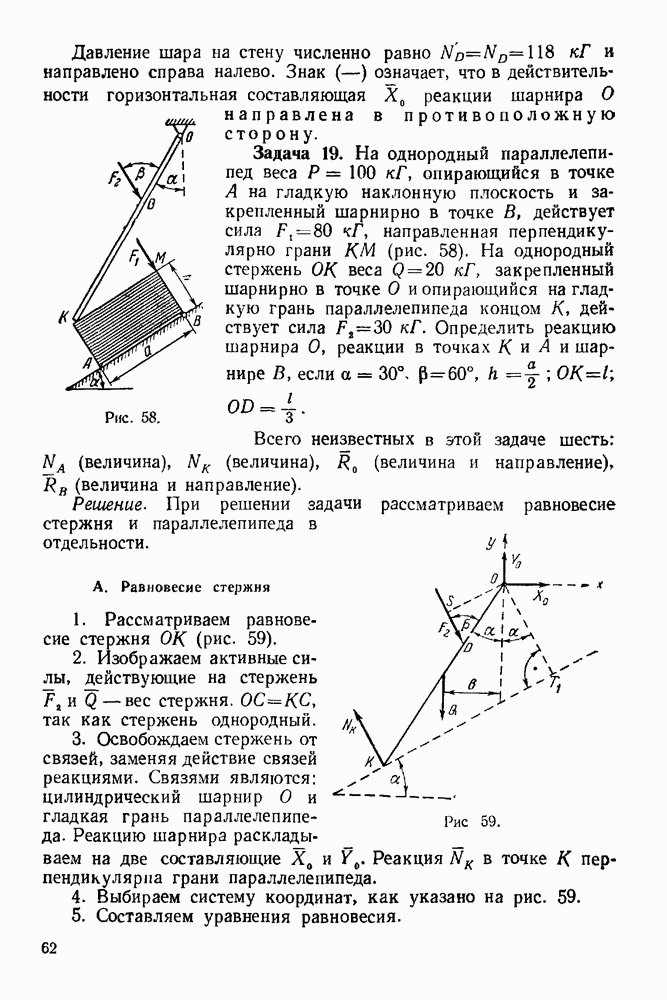
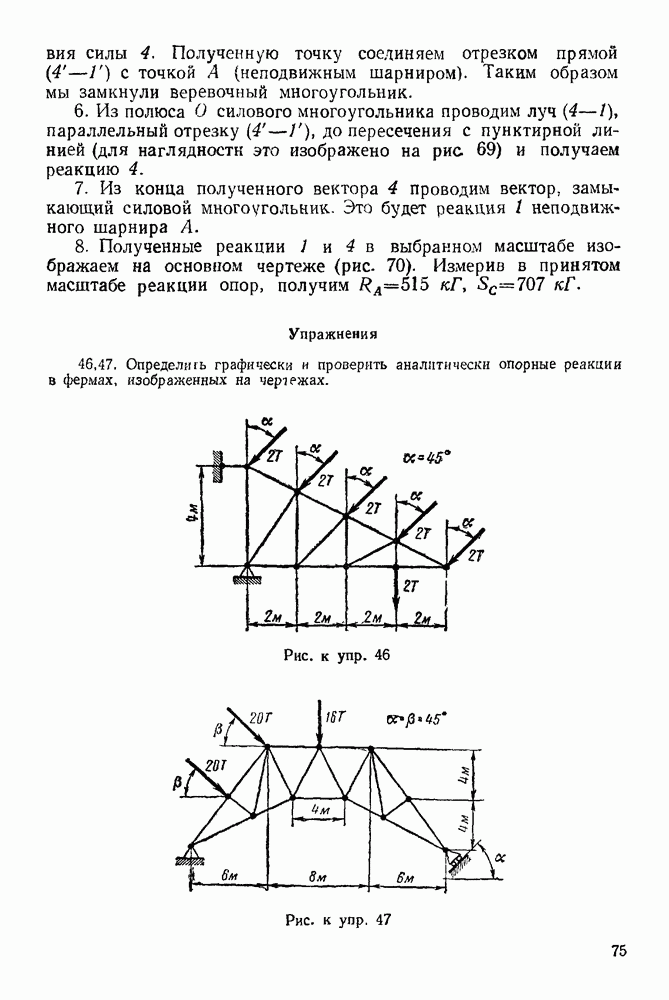
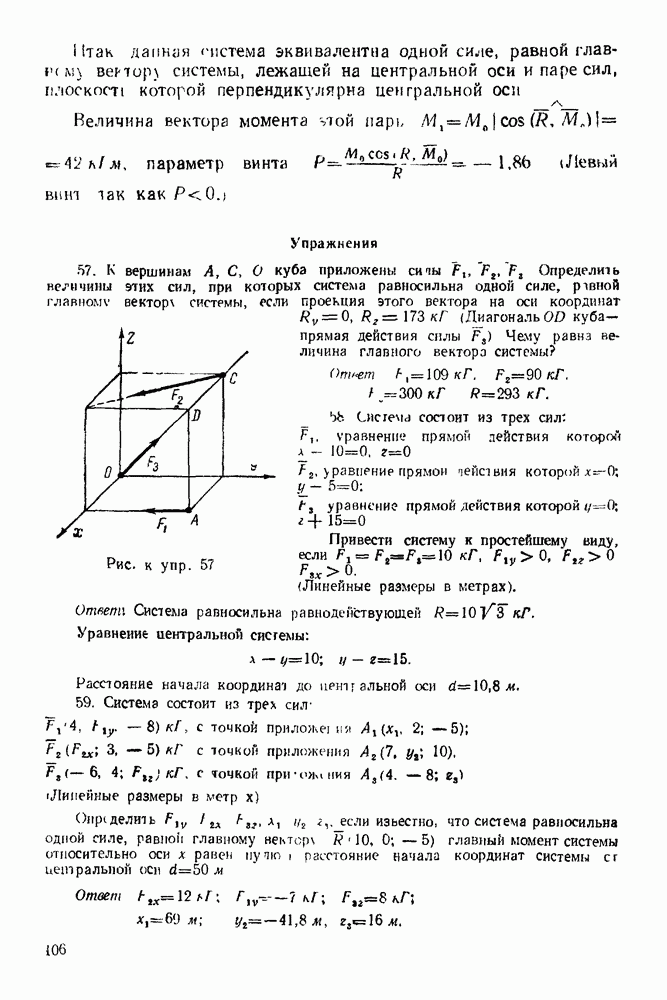
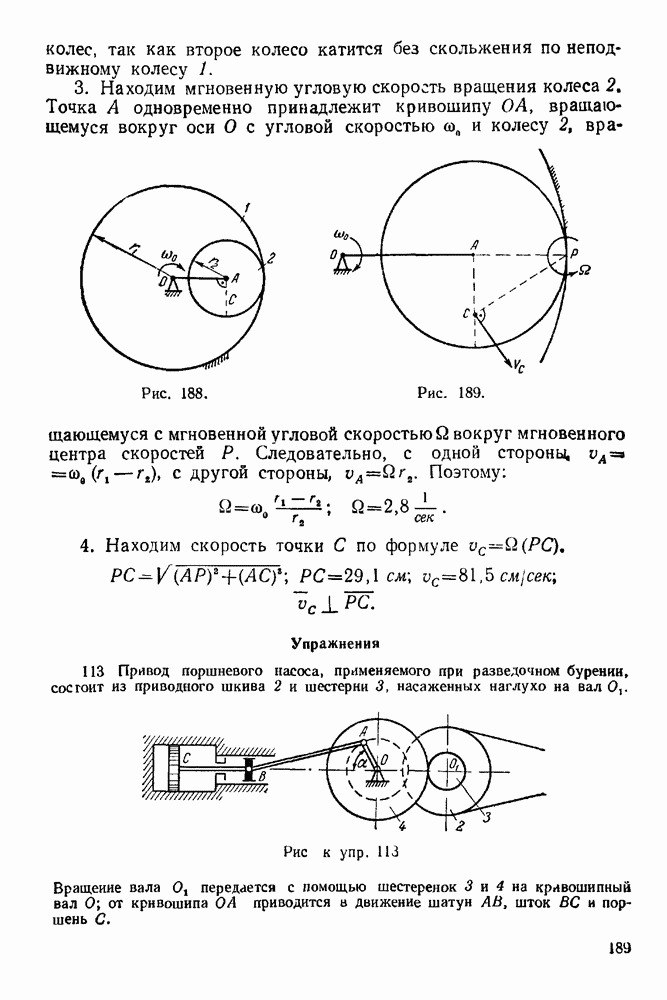
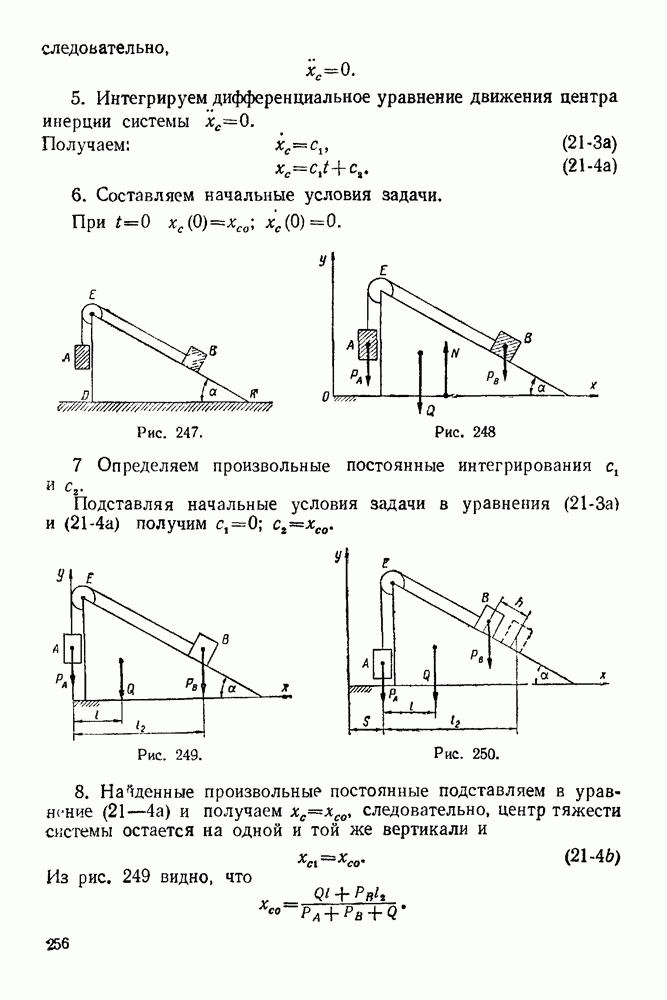
3. Строим замкнутый силовой многоугольник в выбранном масштабе (рис. 68). К концу вектора силы 2 пристраиваем начало Еектора силы 3 и через конец этого вектора проводим отрезок, параллельный нити  (на рис. 68 этот отрезок изображен пунктиром).
(на рис. 68 этот отрезок изображен пунктиром).
4. Выбираем в окрестности силового многоугольника полюс О <рис. 68) и соединяем его лучами  с вершинами силового многоугольника
с вершинами силового многоугольника

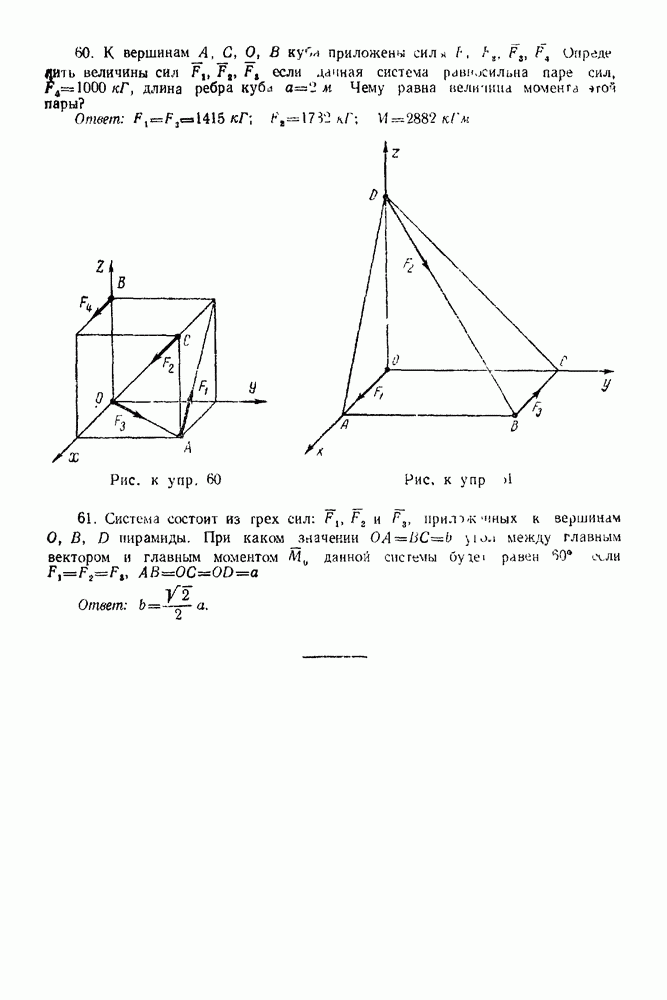
Рис. 70
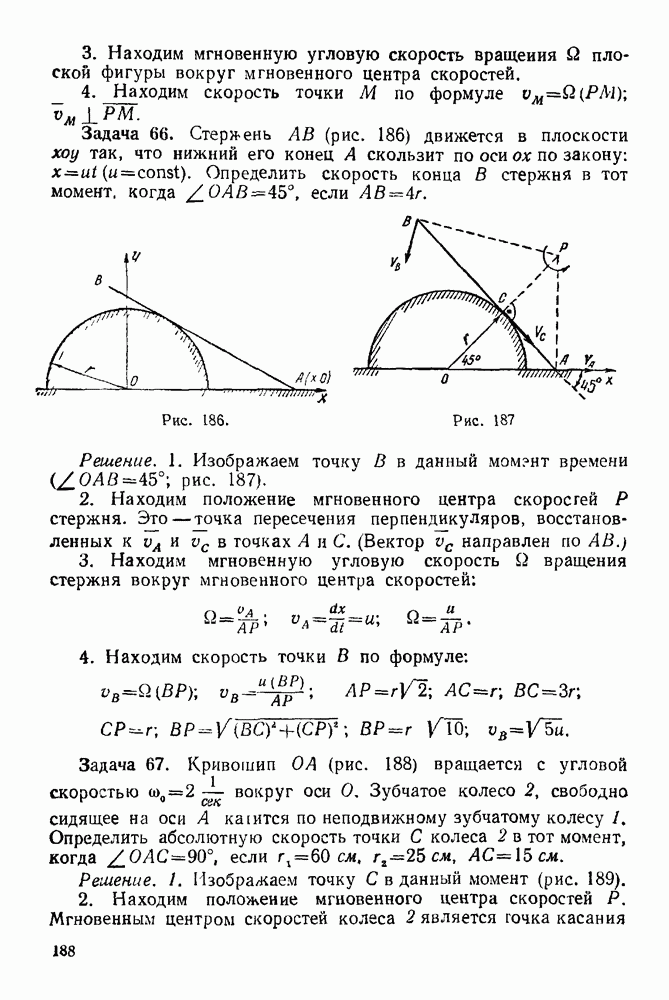
5. Строим замкнутый веревочный многоугольник (рис. 67). Из неподвижного шарнира 4 проводим отрезок прямой  из точки пересечения этого отрезка с прямой действия силы 2 проводим отрезок прямой
из точки пересечения этого отрезка с прямой действия силы 2 проводим отрезок прямой  до пересечения с прямой действия силы 3, из этой точки проводим отрезок прямой
до пересечения с прямой действия силы 3, из этой точки проводим отрезок прямой  до пересечения с прямой
до пересечения с прямой
действия силы 4. Полученную точку соединяем отрезком прямой  с точкой А (неподвижным шарниром). Таким образом мы замкнули веревочный многоугольник.
с точкой А (неподвижным шарниром). Таким образом мы замкнули веревочный многоугольник.
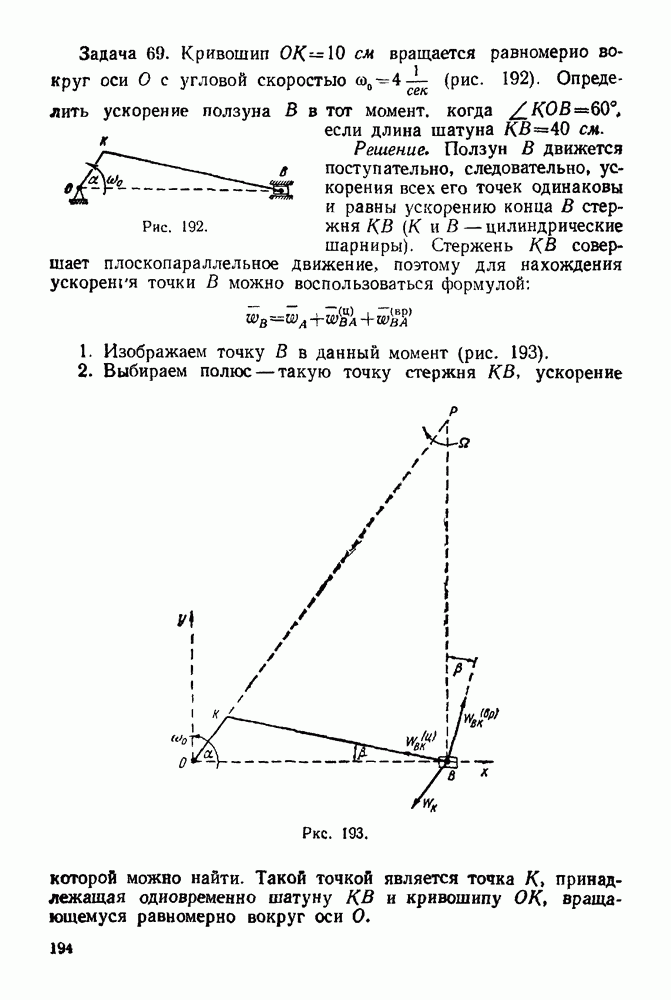
6. Из полюса О силового многоугольника проводим луч  параллельный отрезку
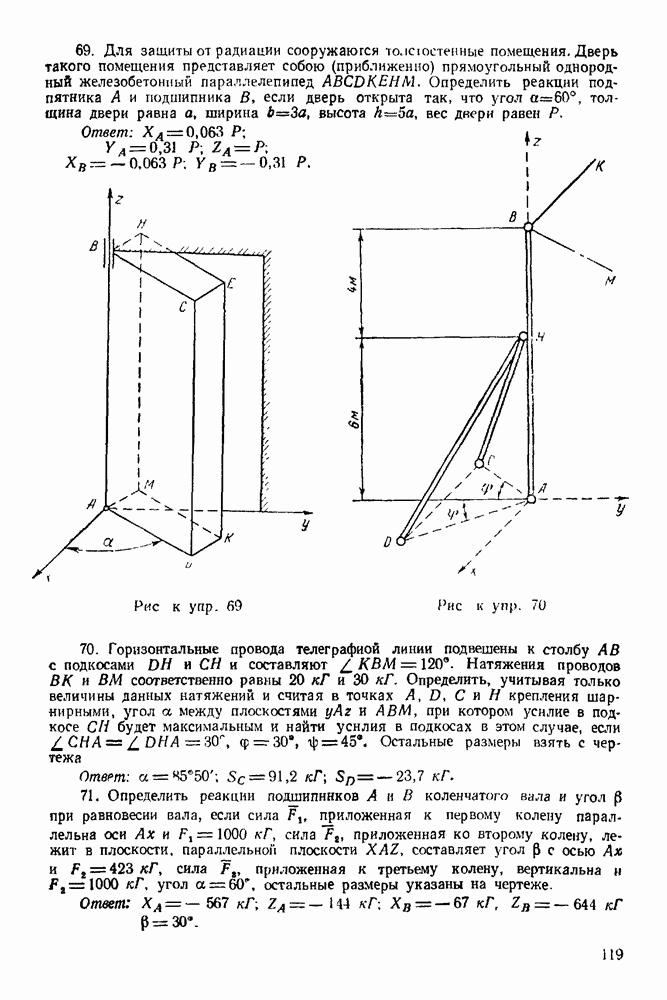
параллельный отрезку  до пересечения с пунктирной линией (для наглядности это изображено на рис. 69) и получаем реакцию 4.
до пересечения с пунктирной линией (для наглядности это изображено на рис. 69) и получаем реакцию 4.
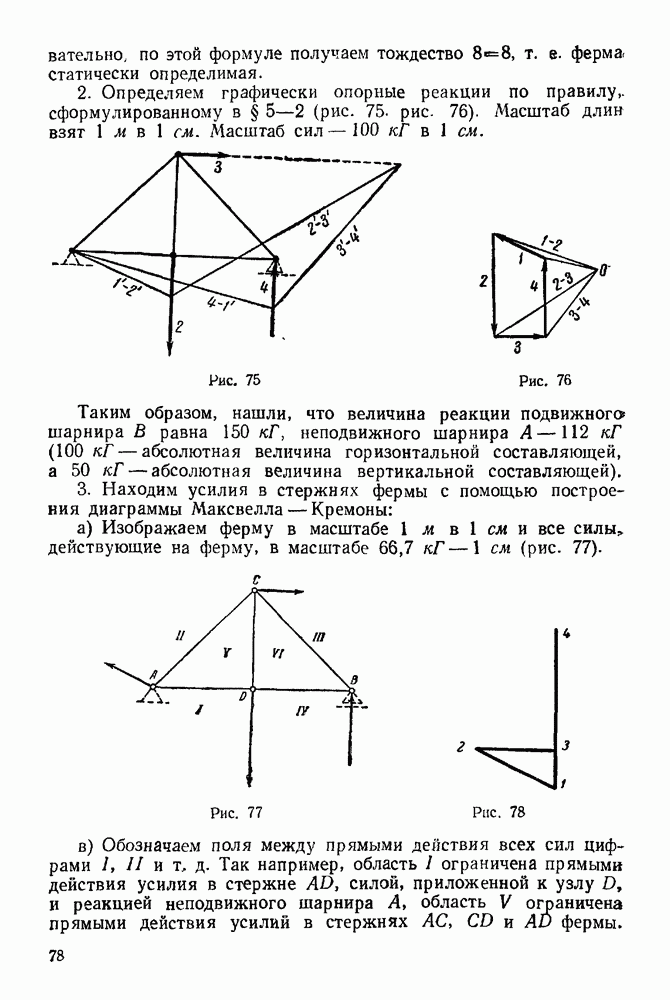
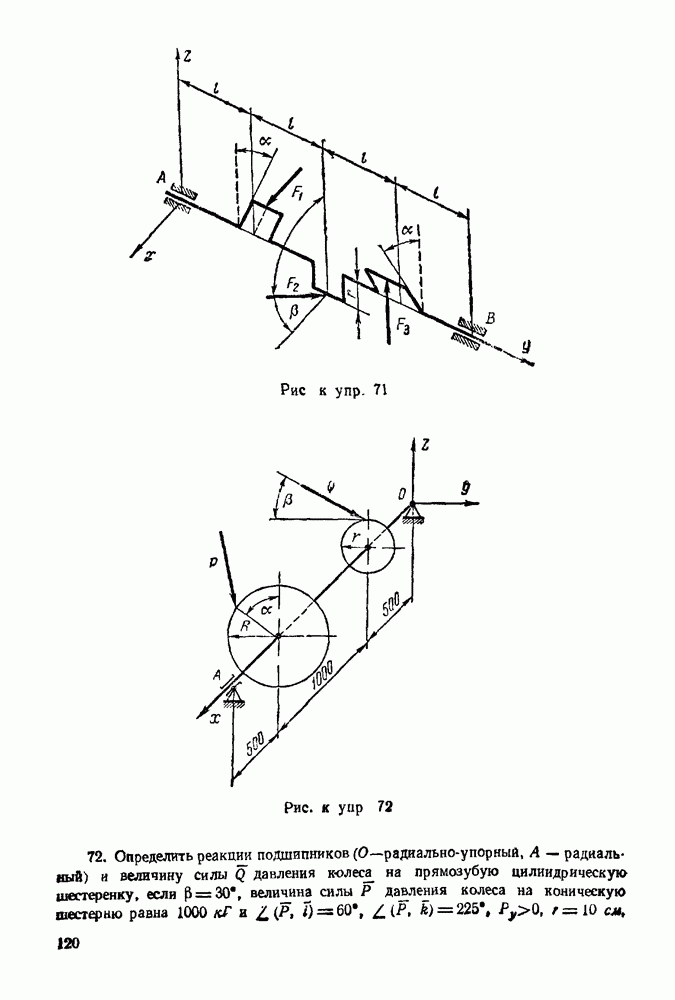
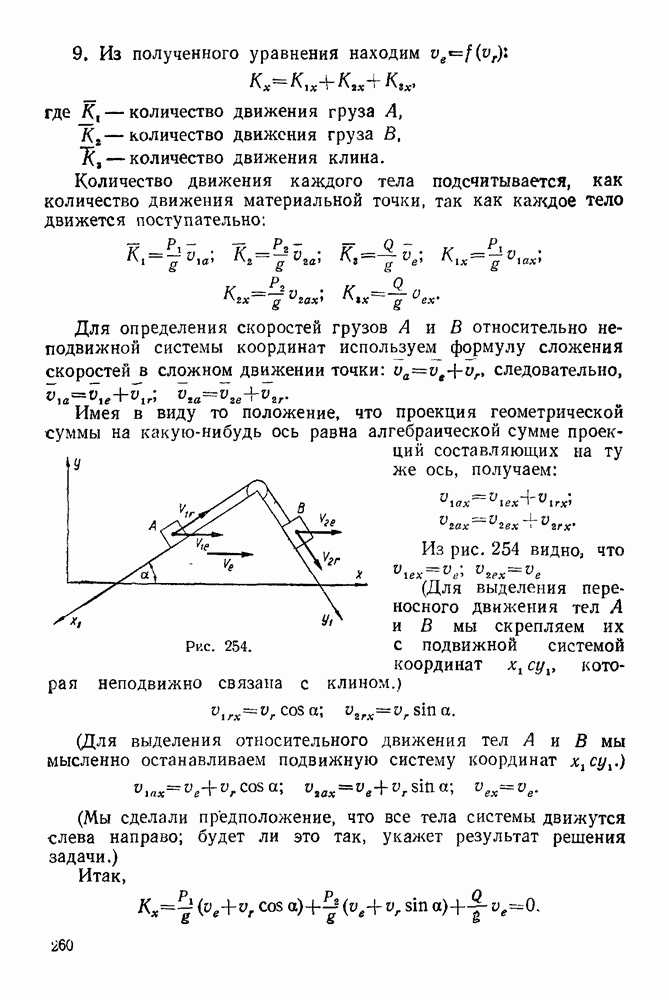
7. Из конца полученного вектора 4 проводим вектор, замыкающий силовой многоугольник. Это будет реакция I неподвижного шарнира А.
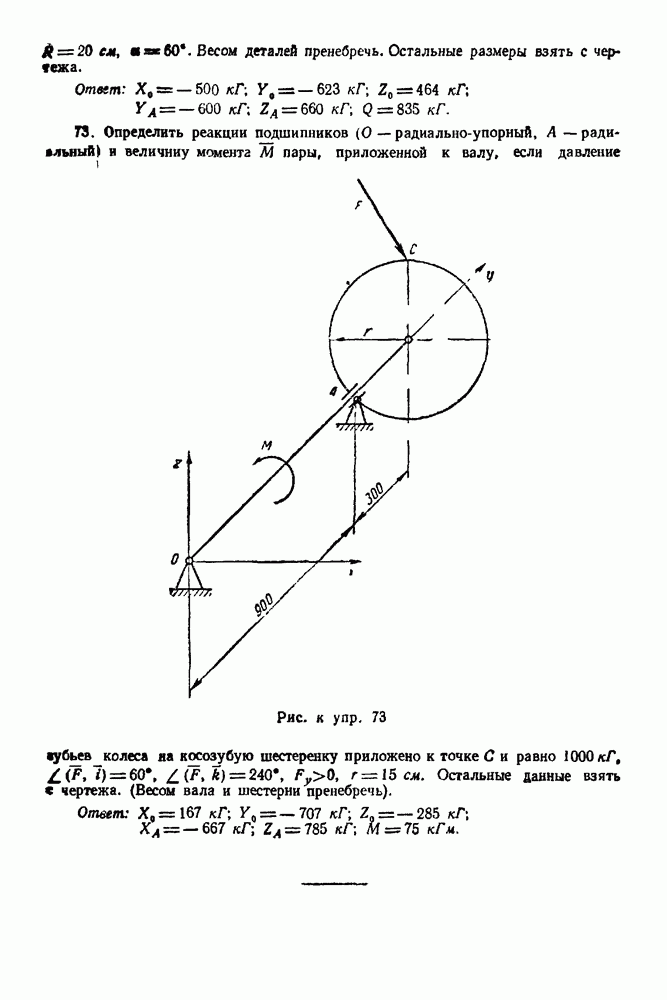
8. Полученные реакции 1 и 4 в выбранном масштабе изображаем на основном чертеже (рис. 70). Измерив в принятом масштабе реакции опор, получим 
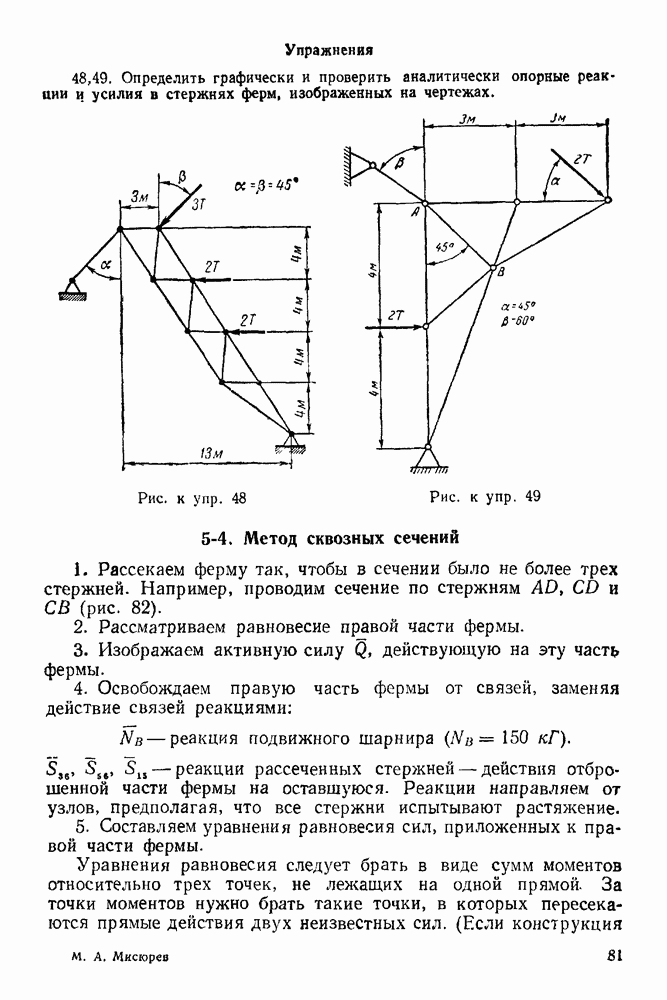
Упражнения
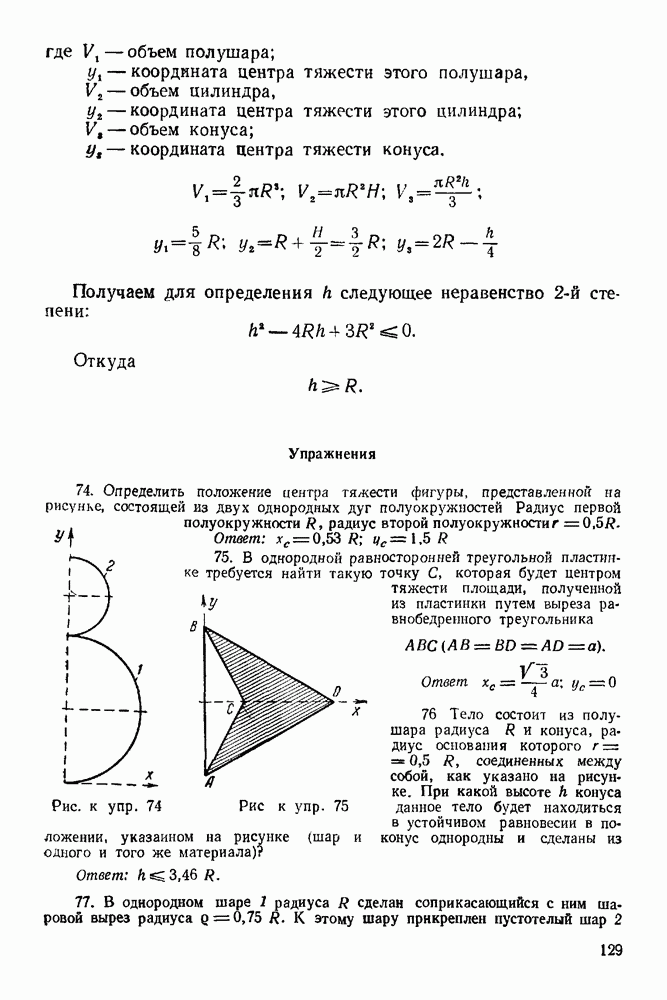
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
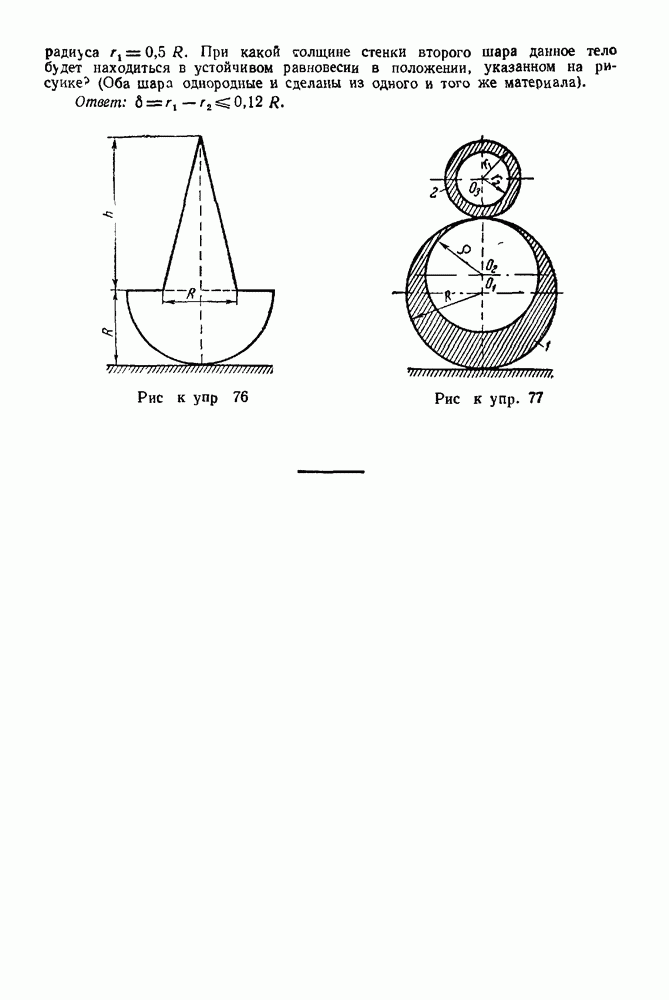
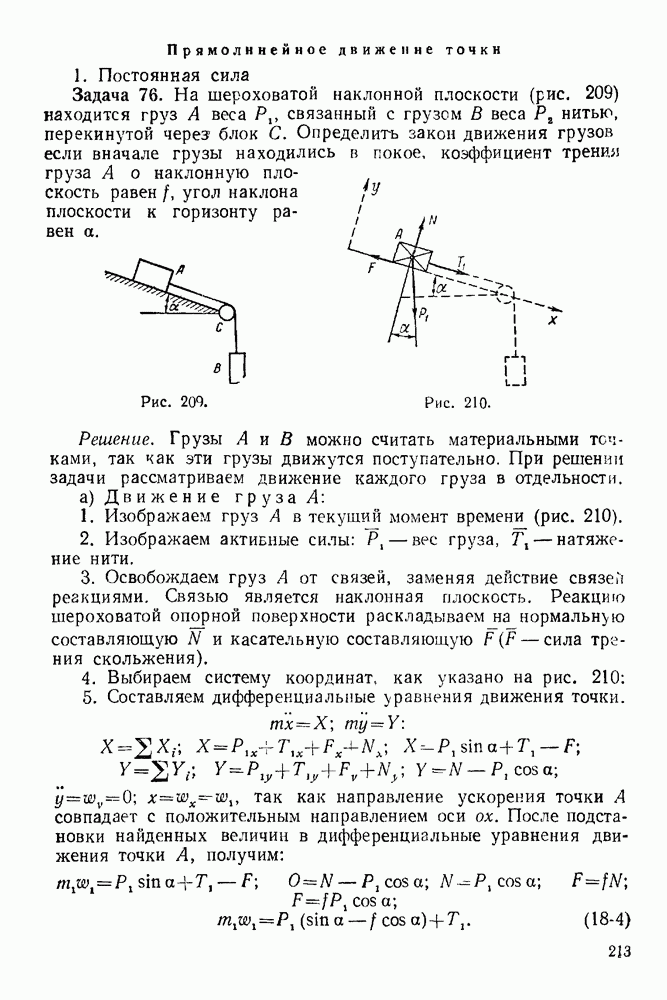
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
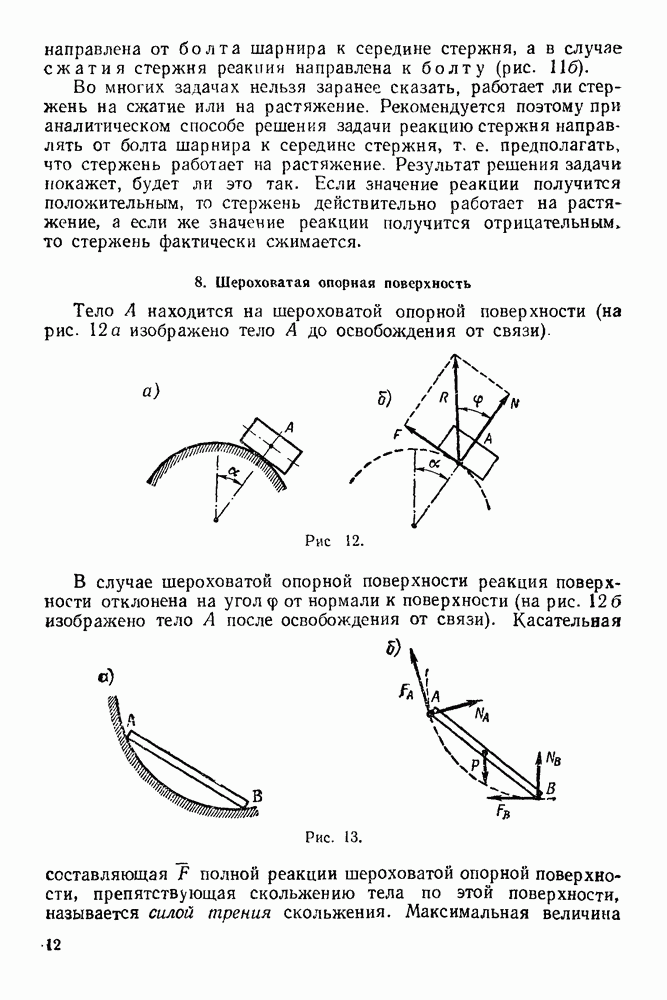
- 1. Абсолютно гладкая опорная поверхность
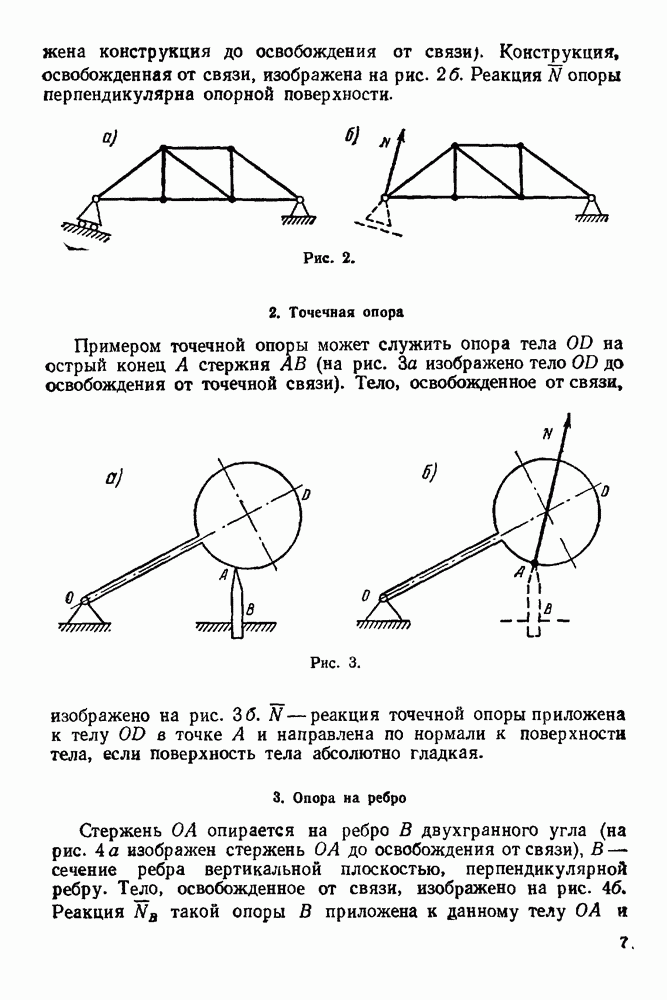
- 2. Точечная опора
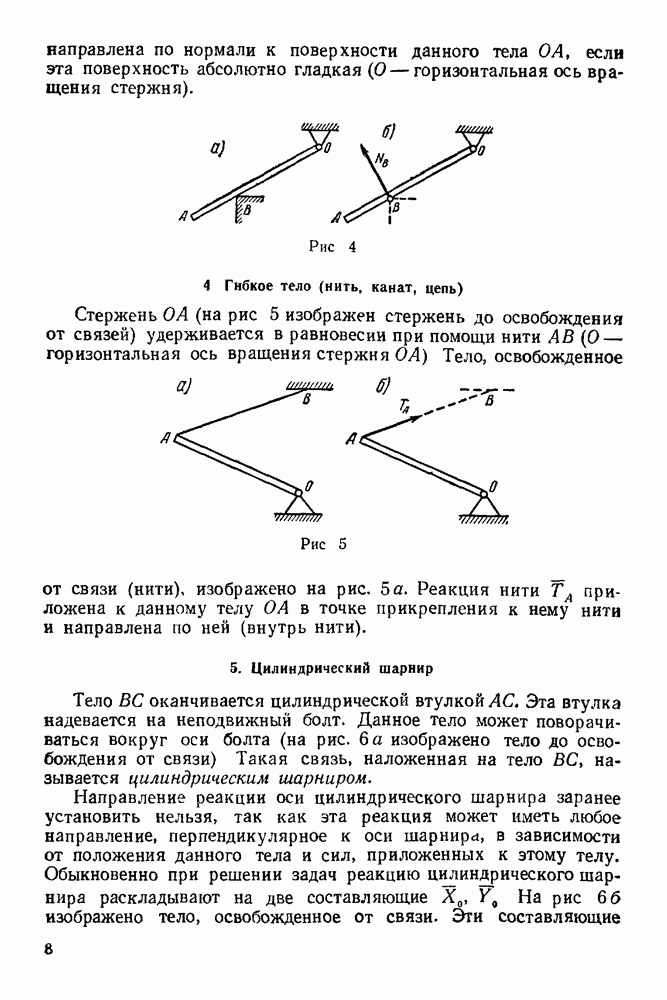
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
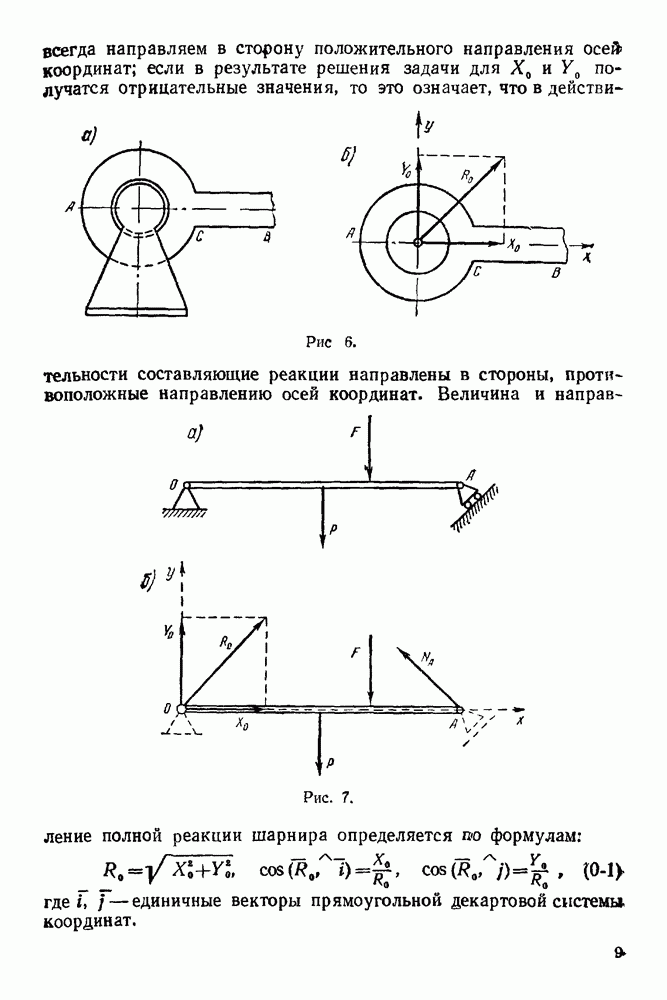
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
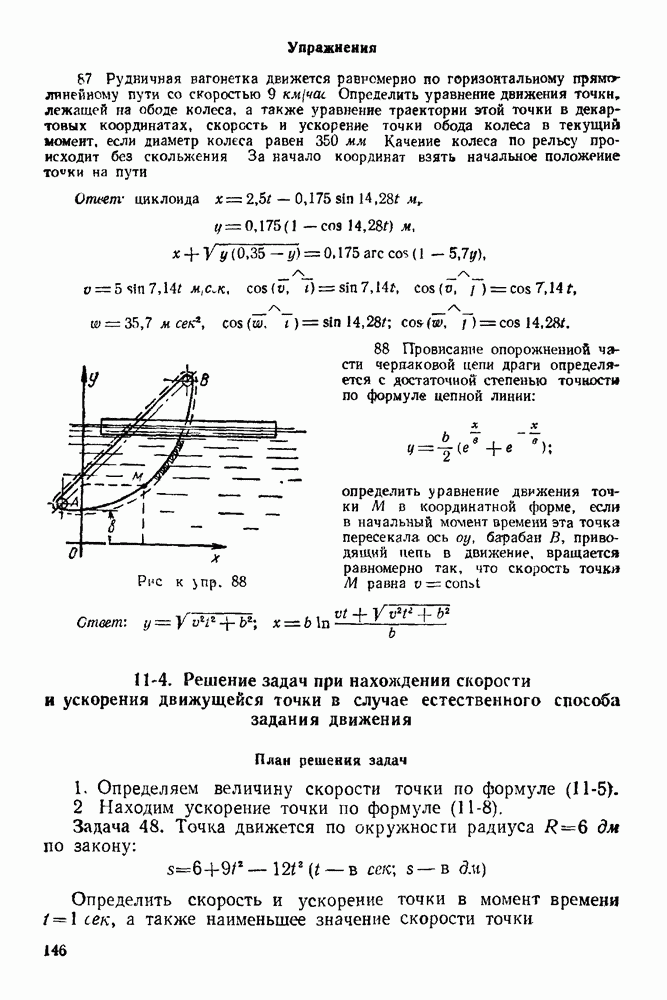
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
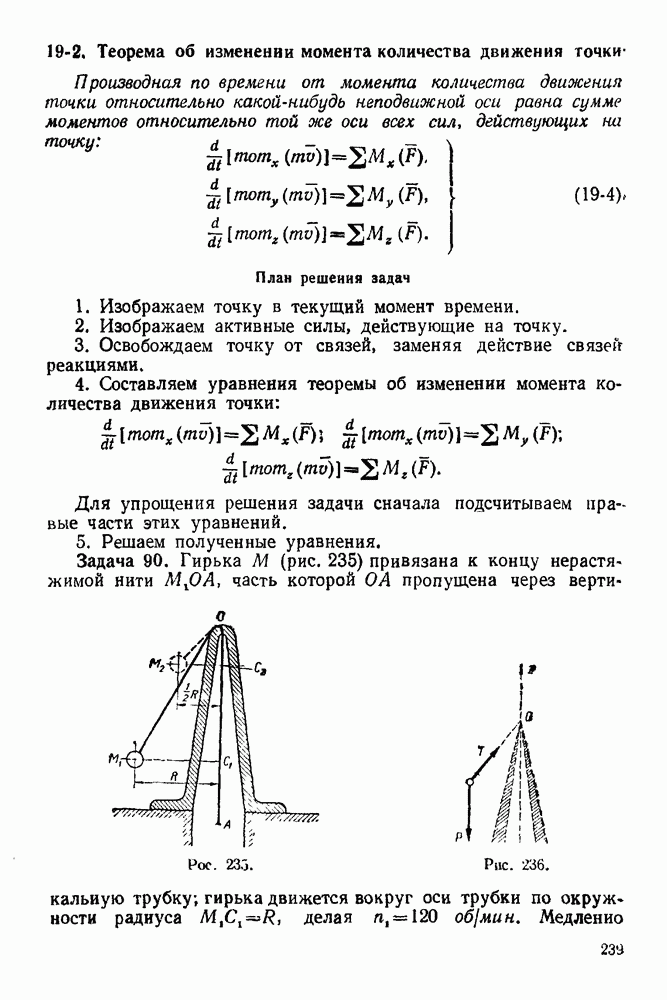
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
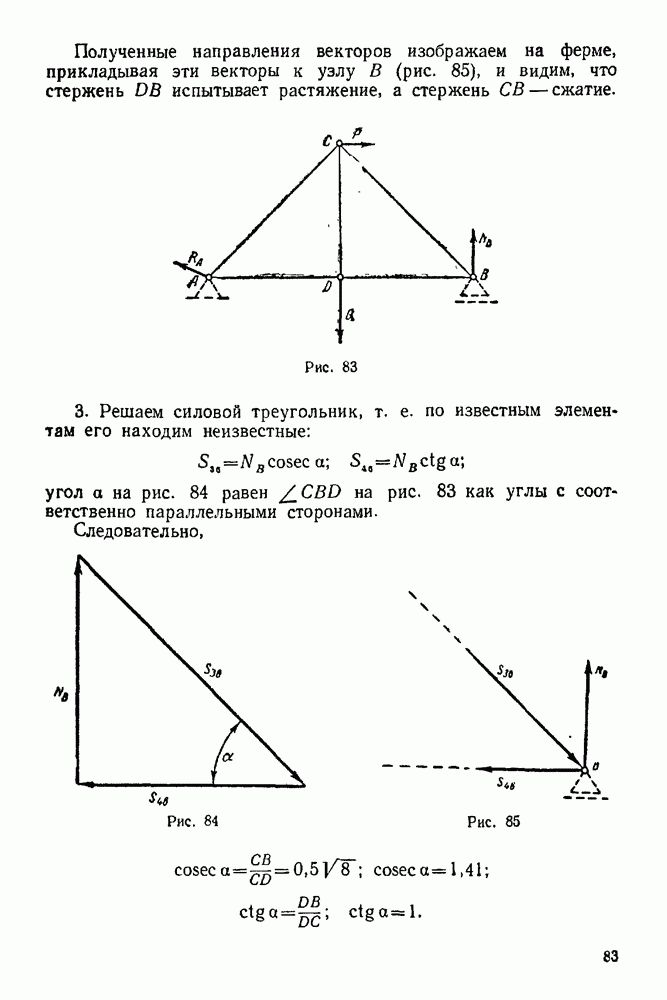
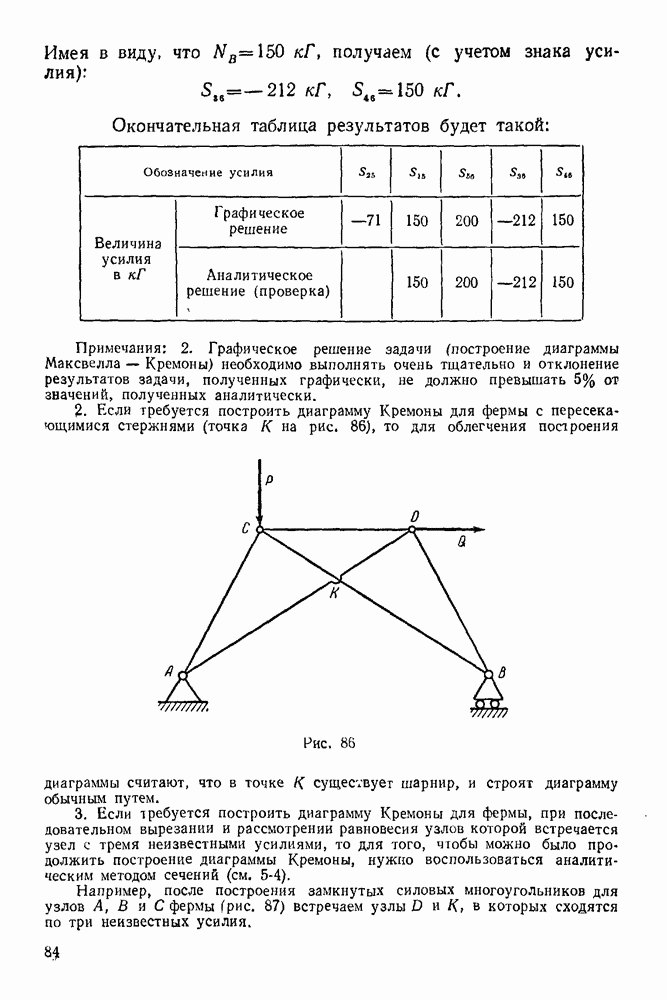
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
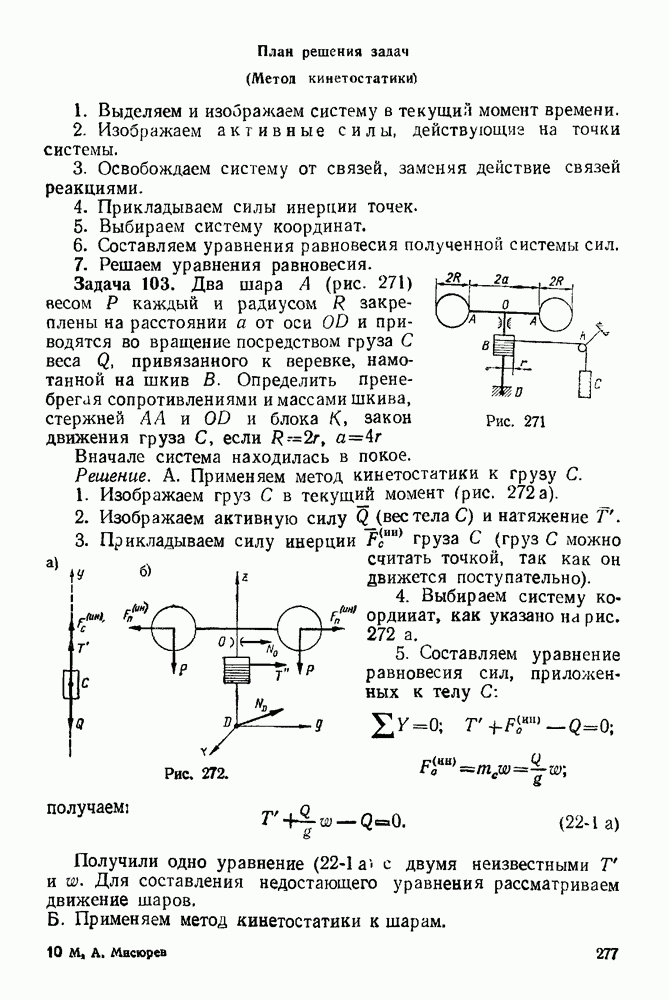
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
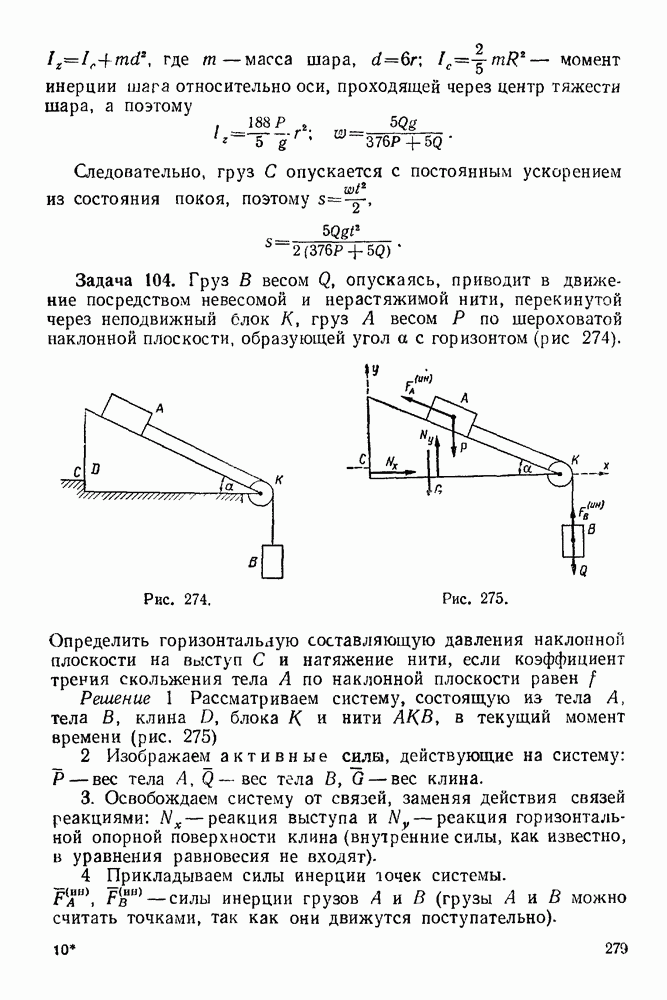
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
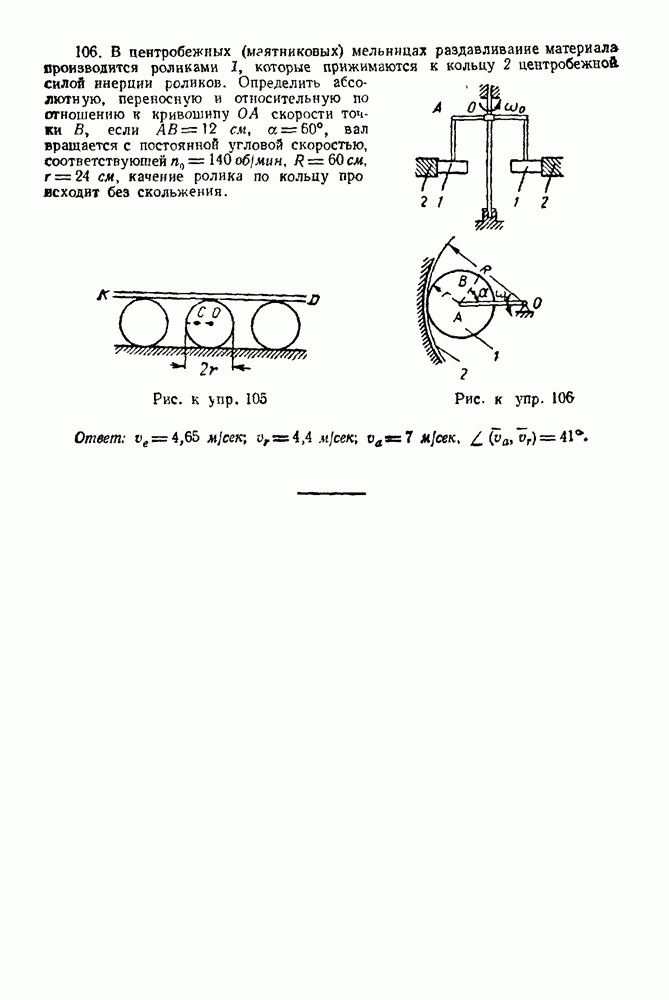
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
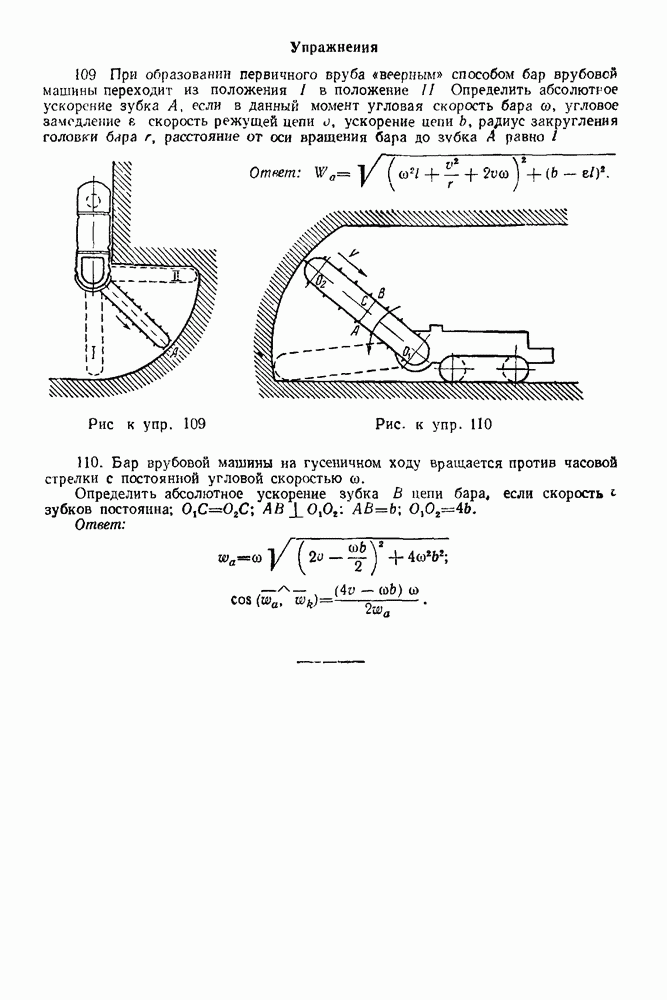
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
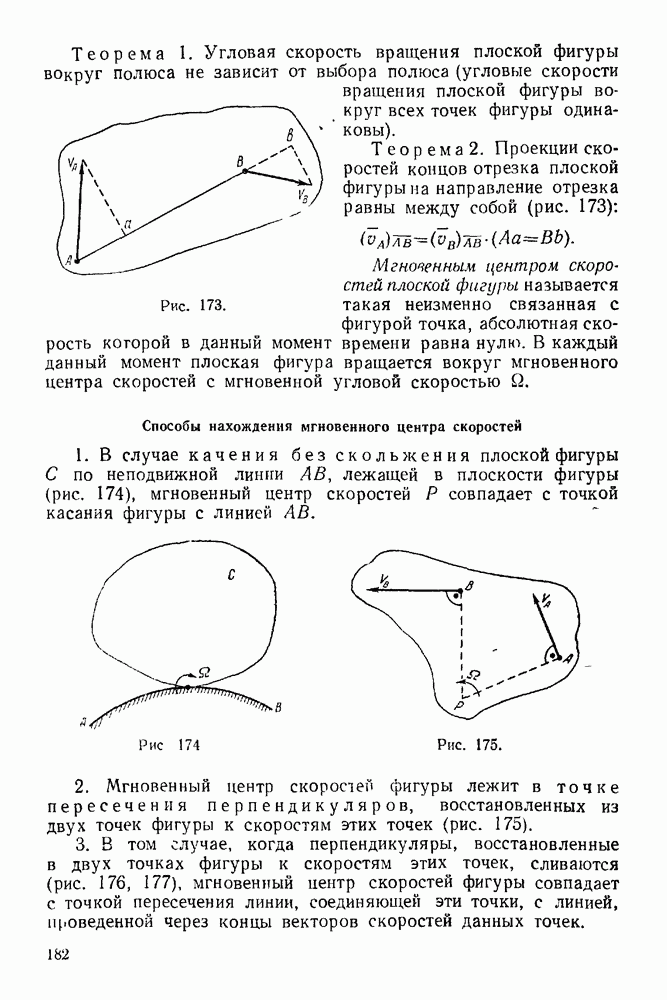
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
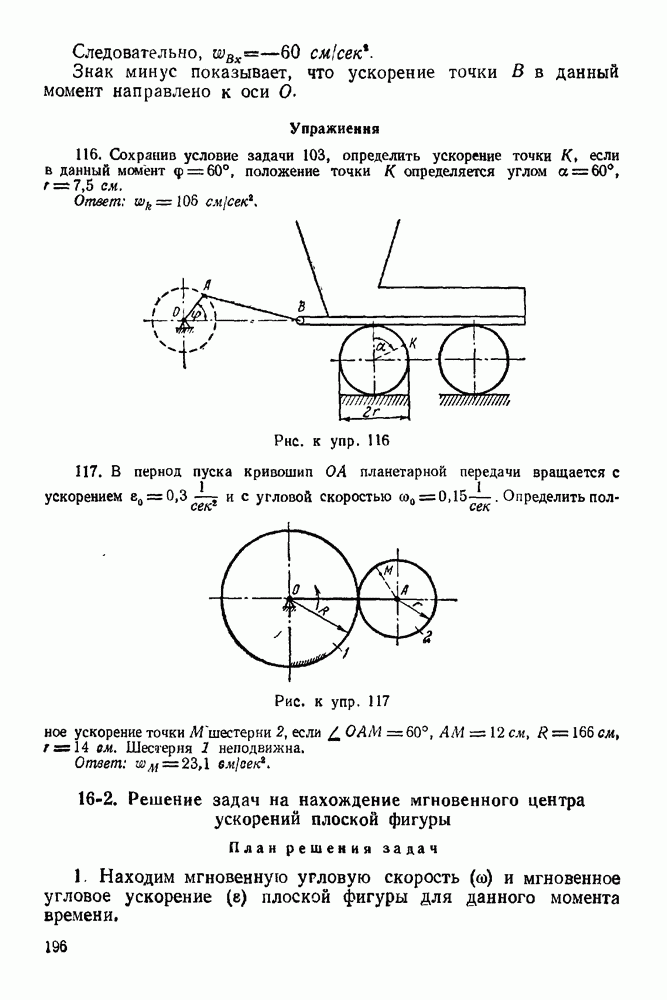
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
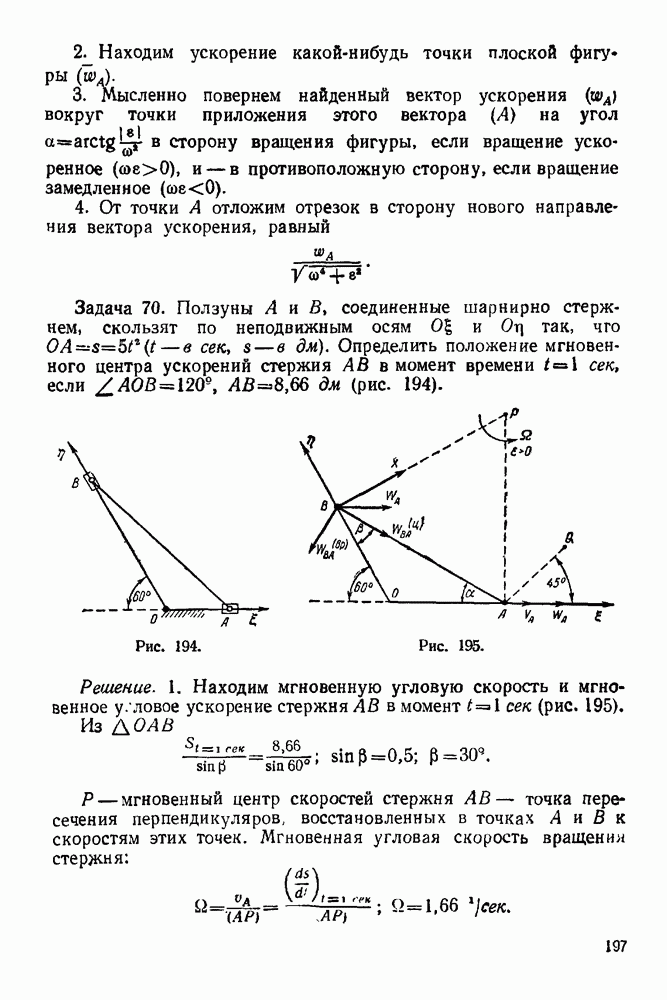
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
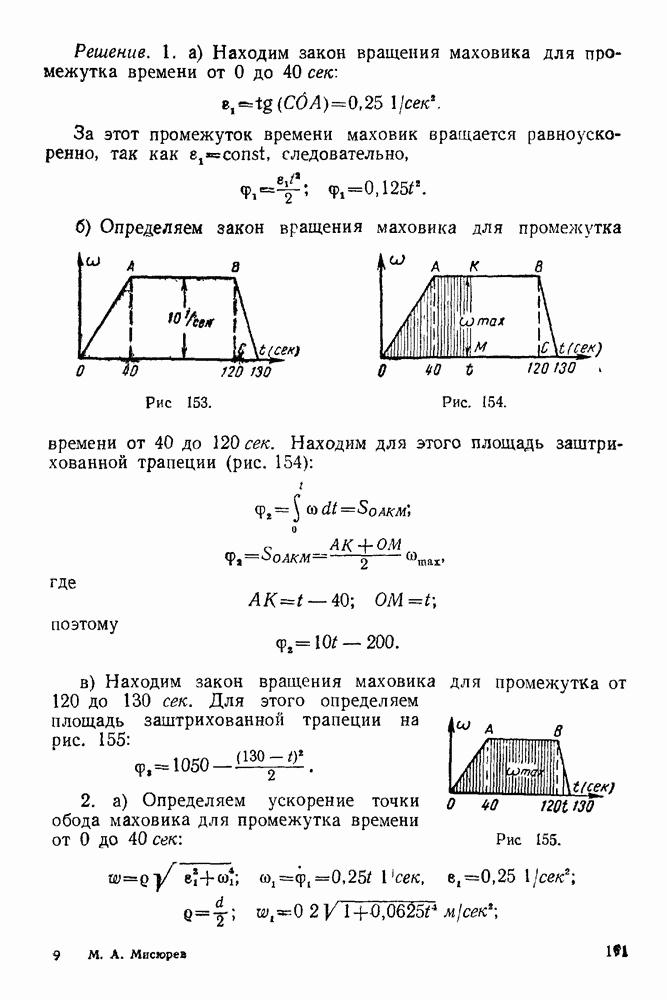
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
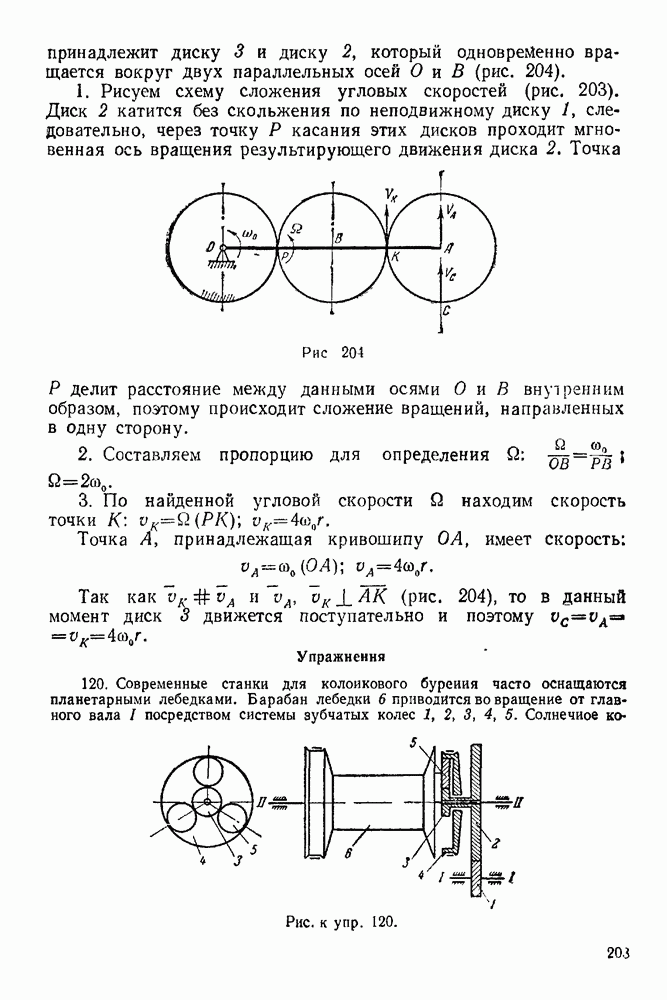
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
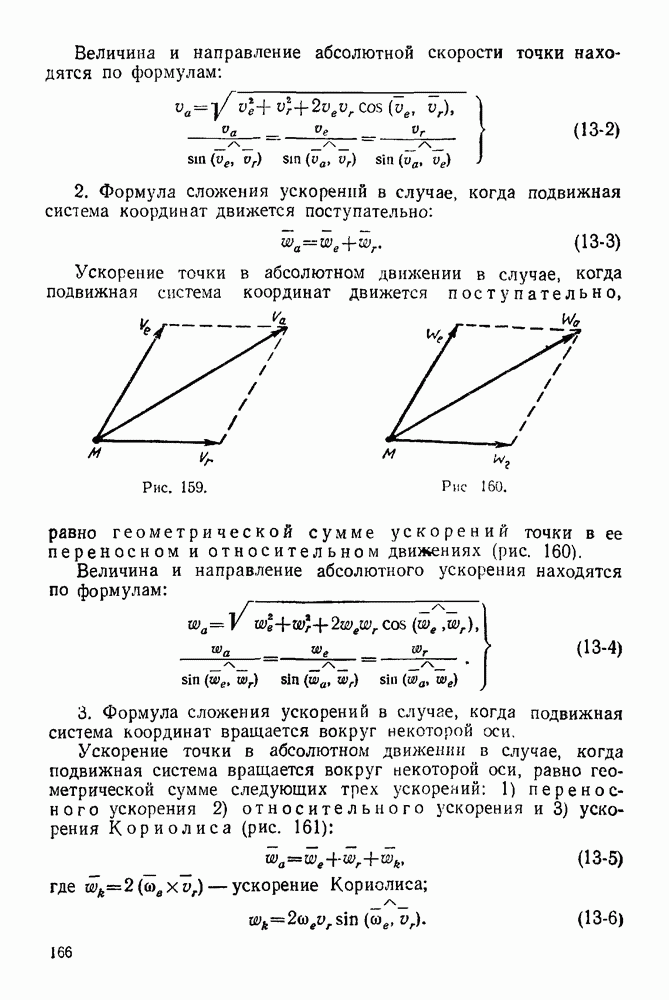
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
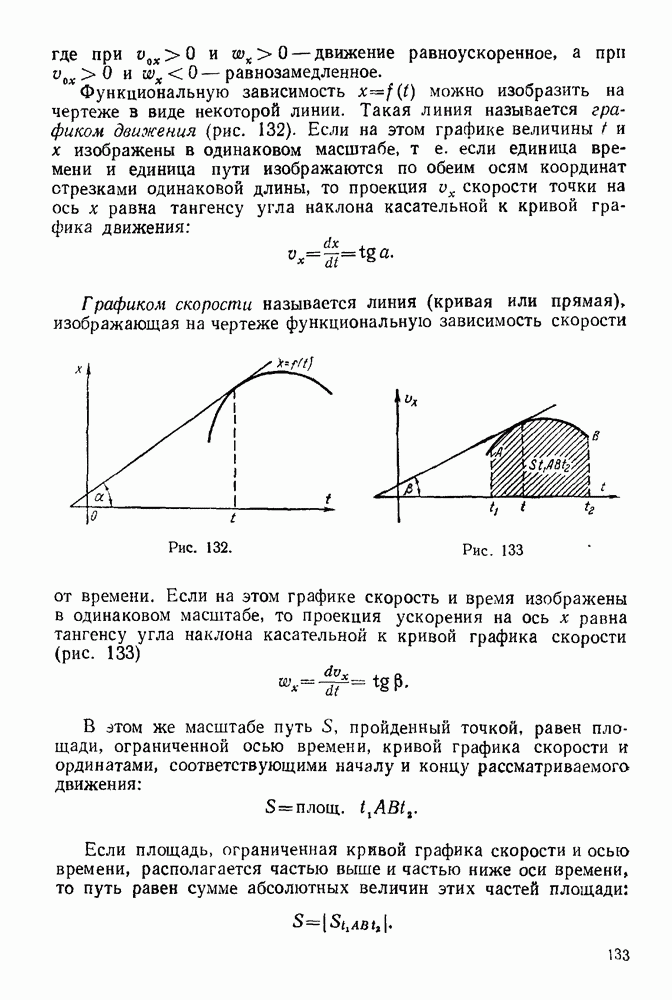
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
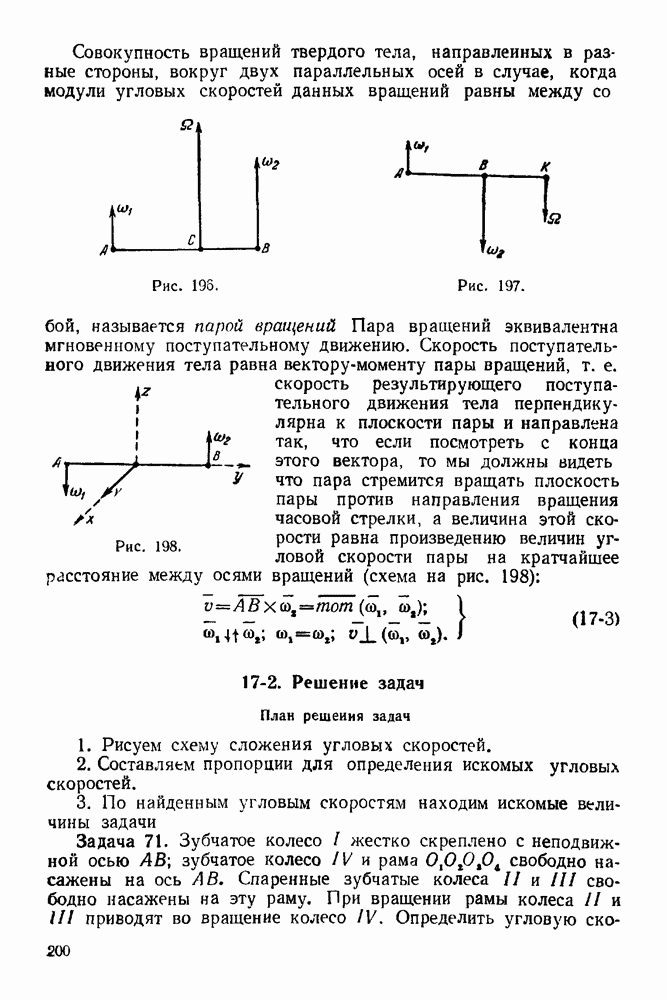
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР