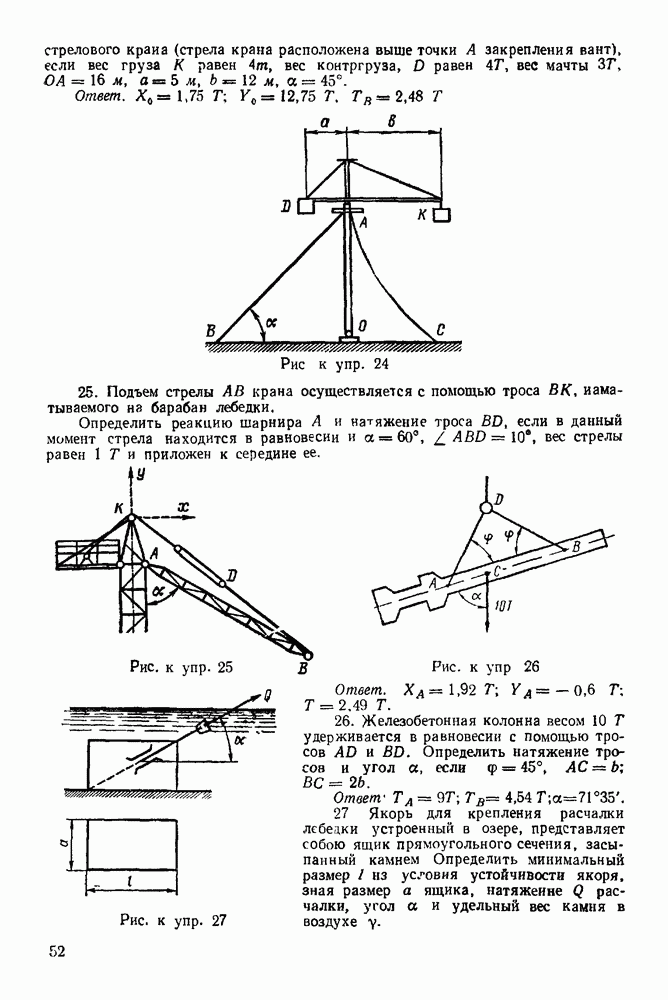
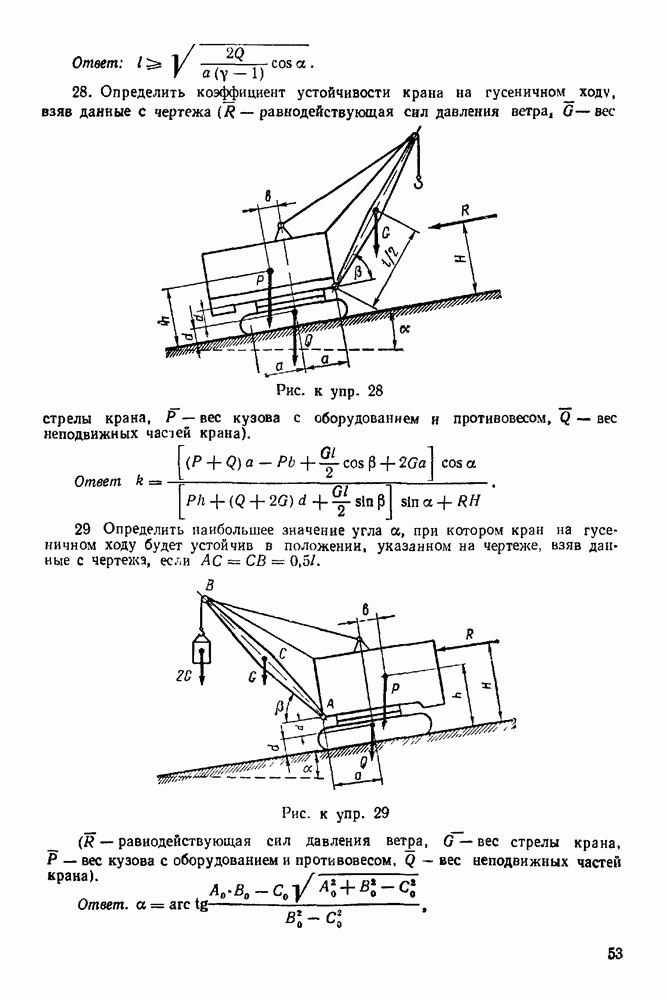
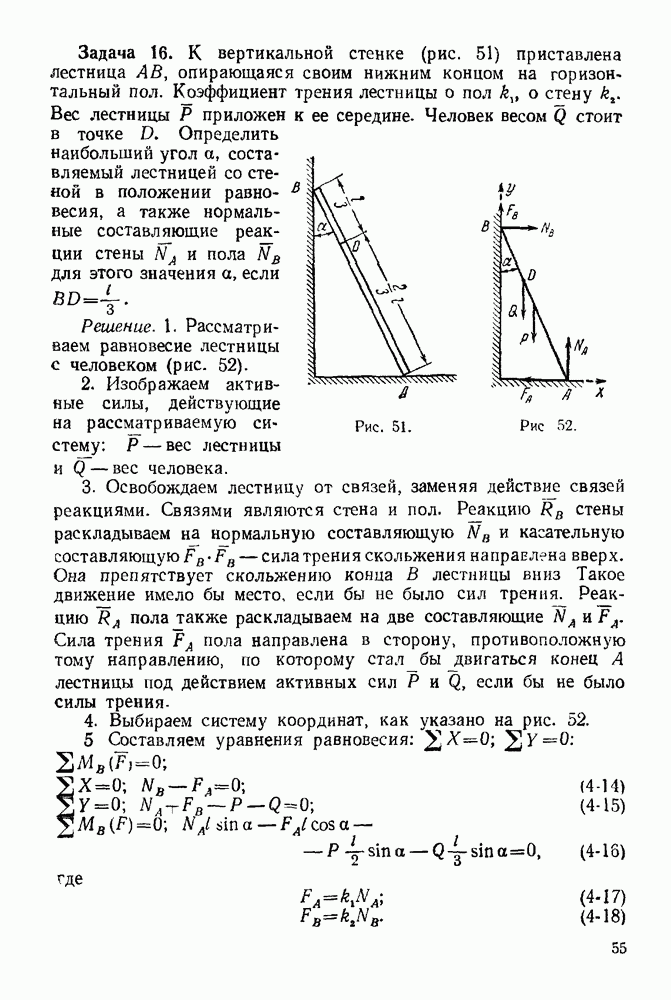
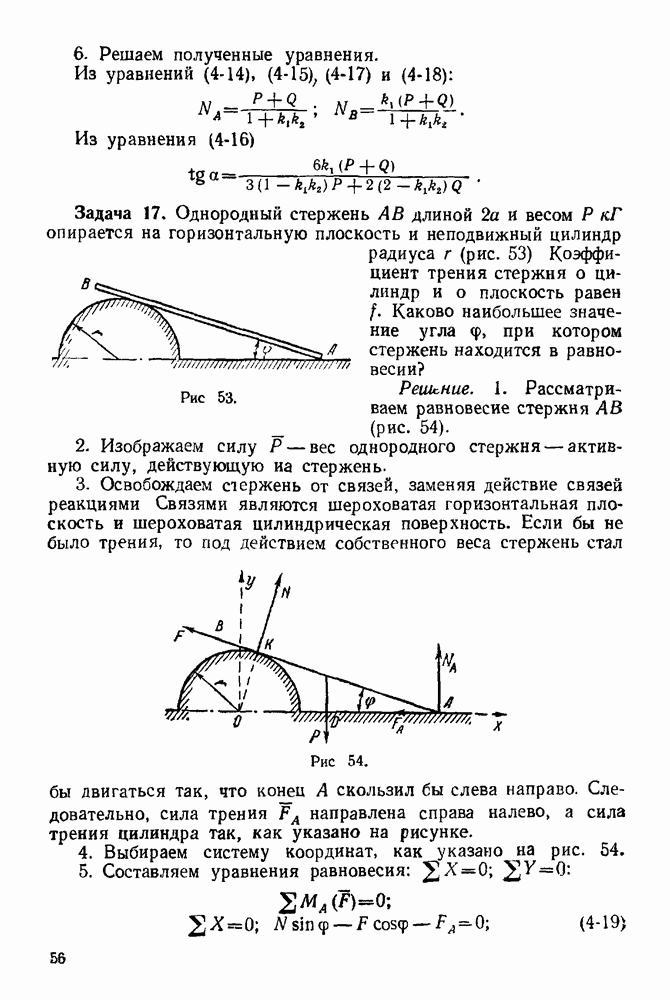
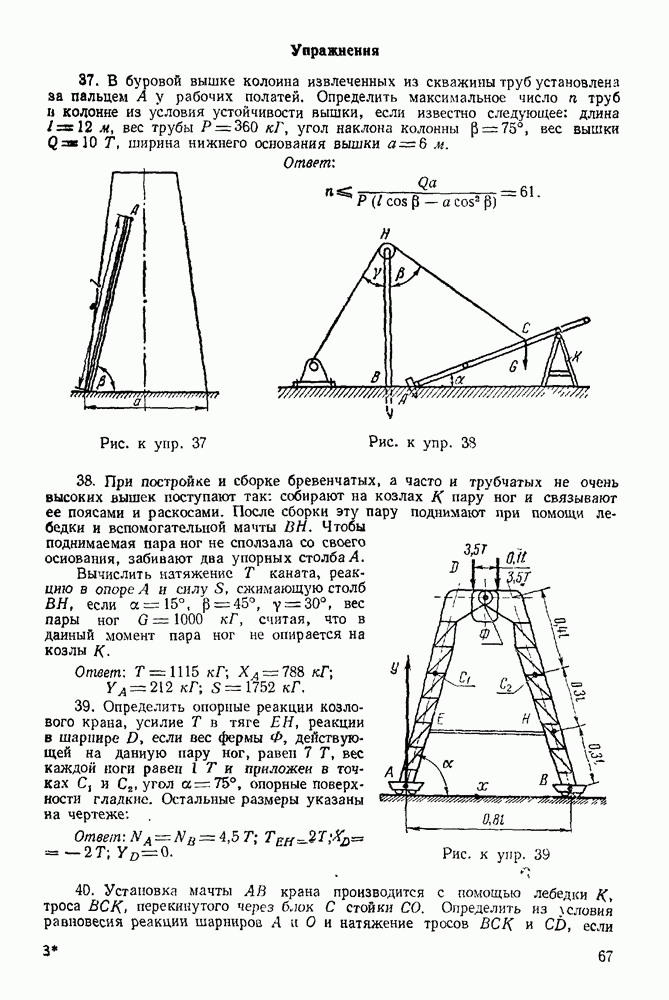
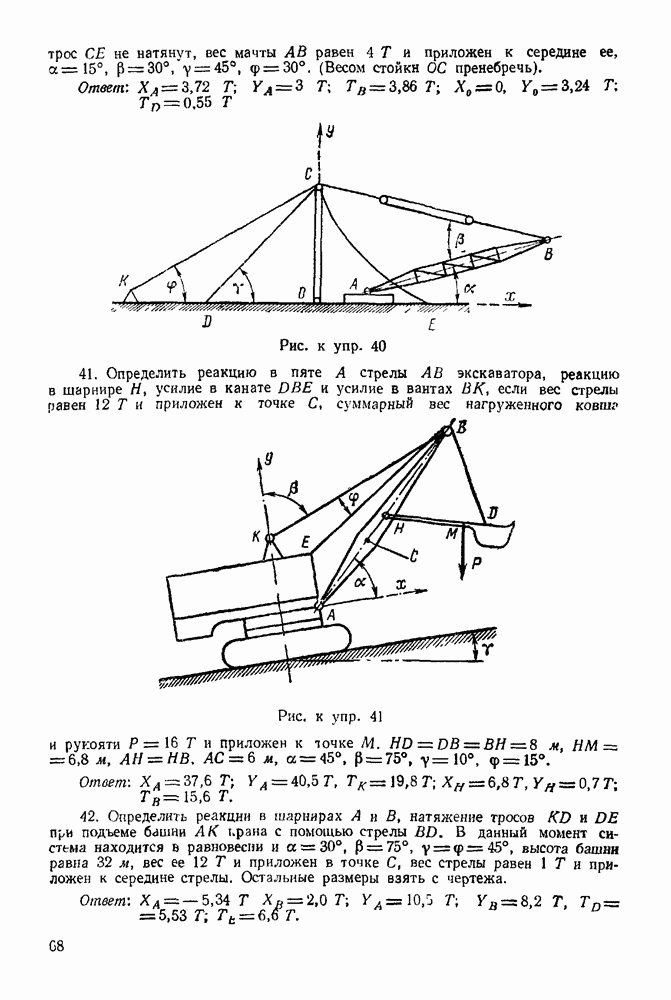
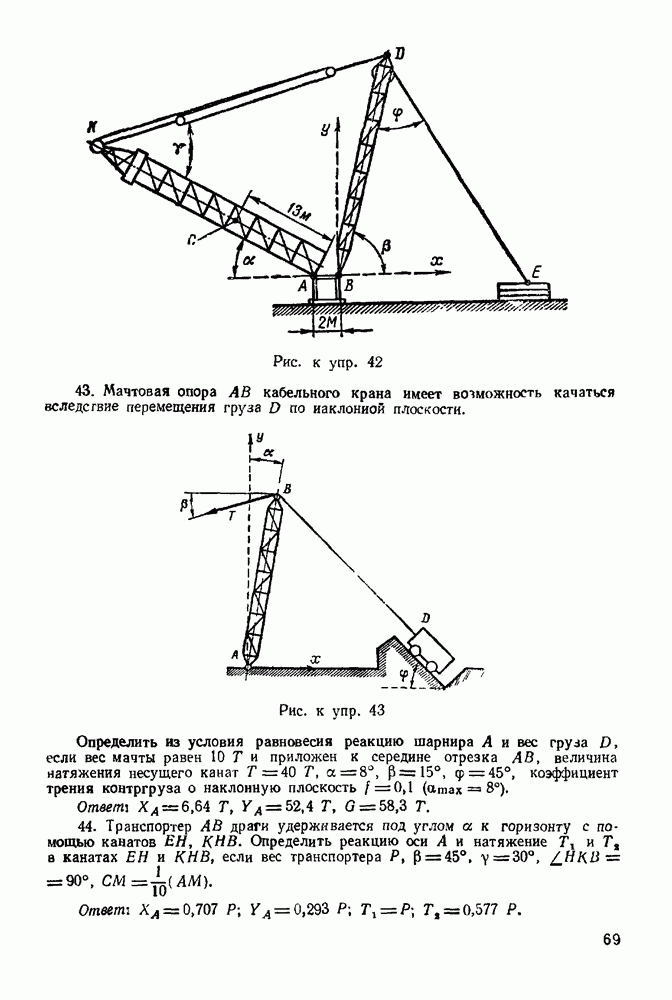
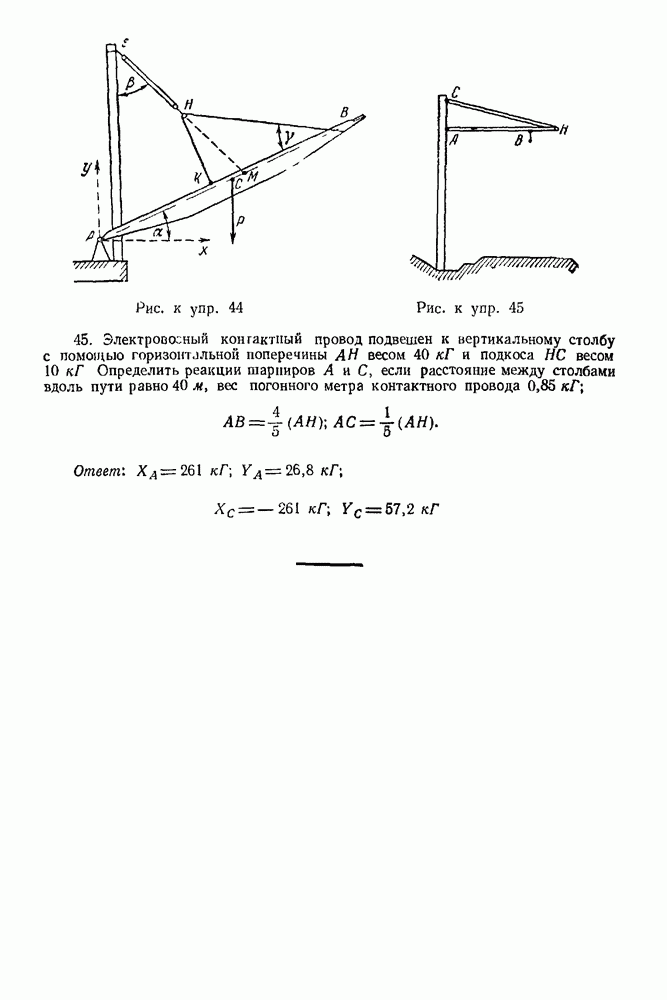
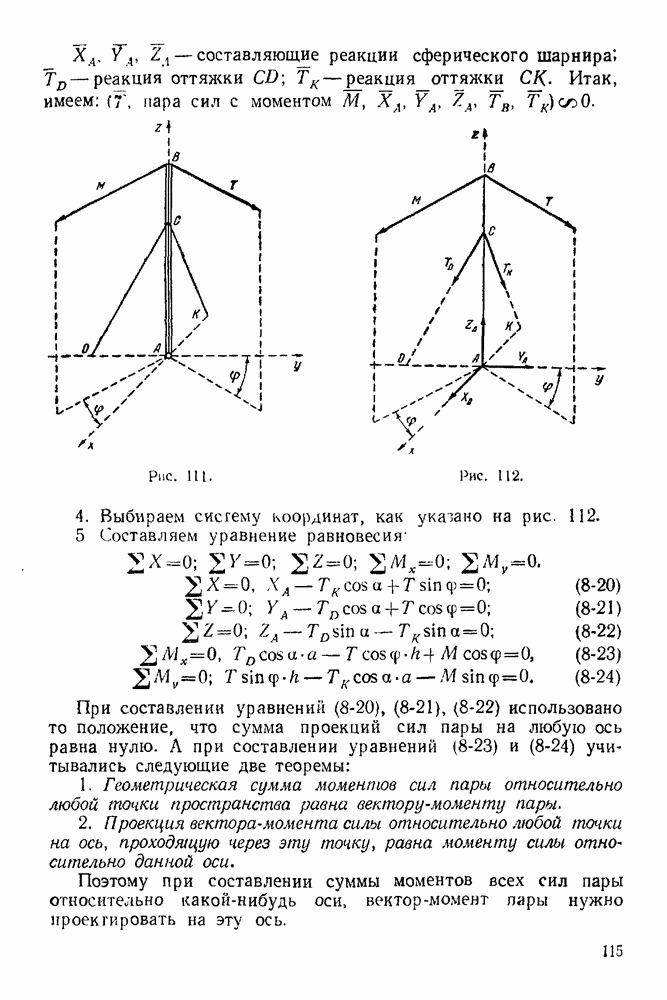
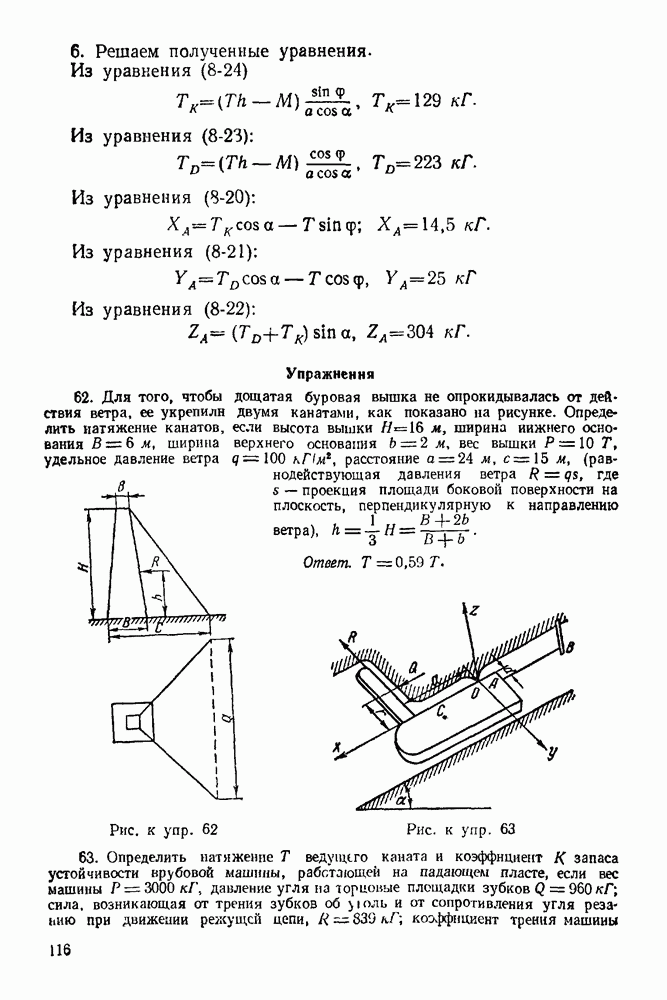
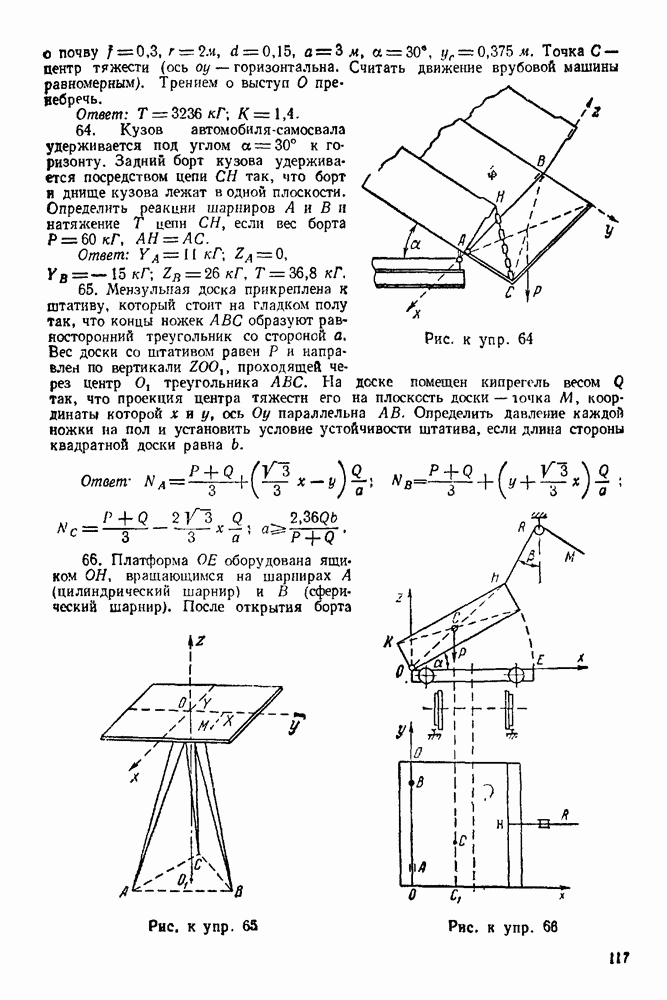
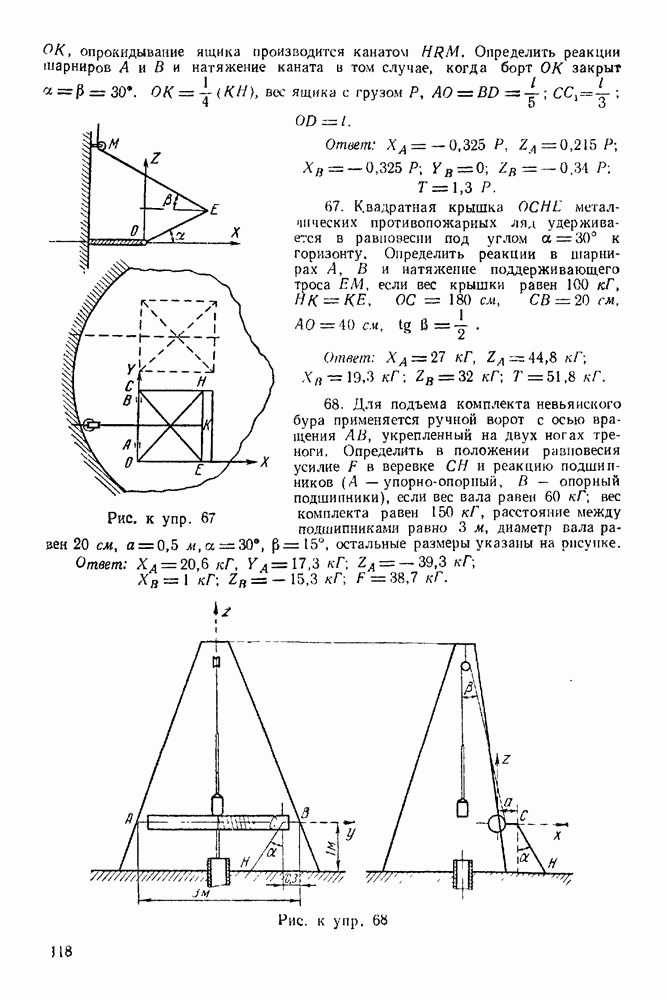
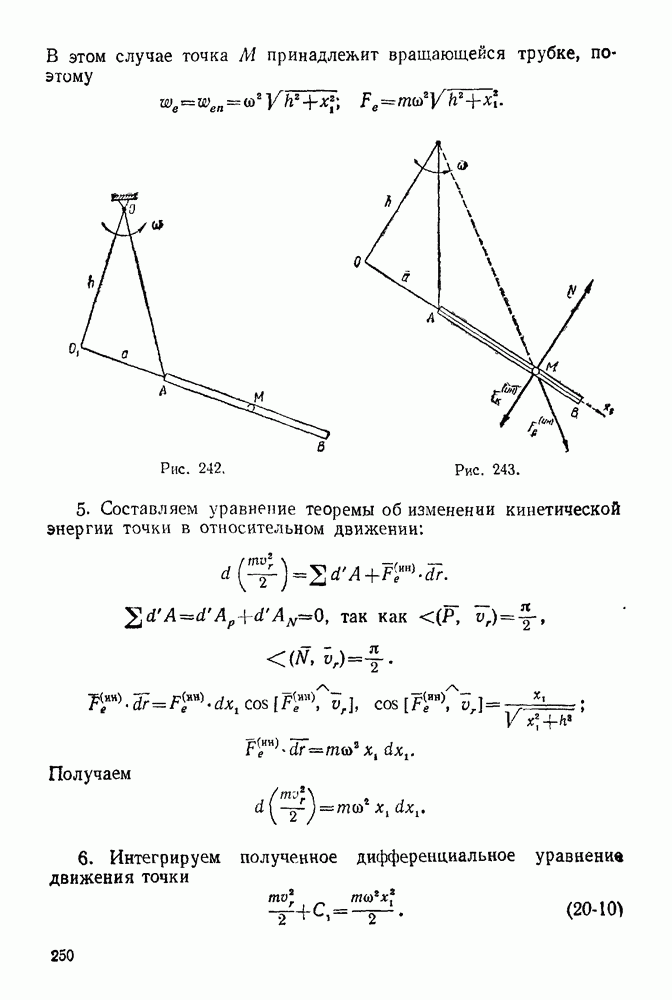
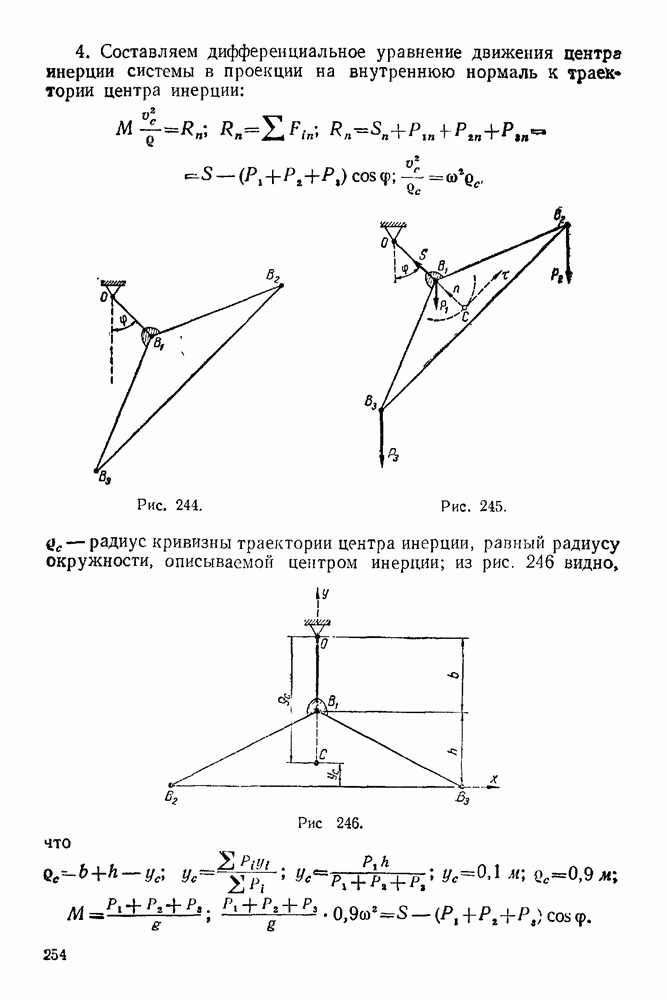
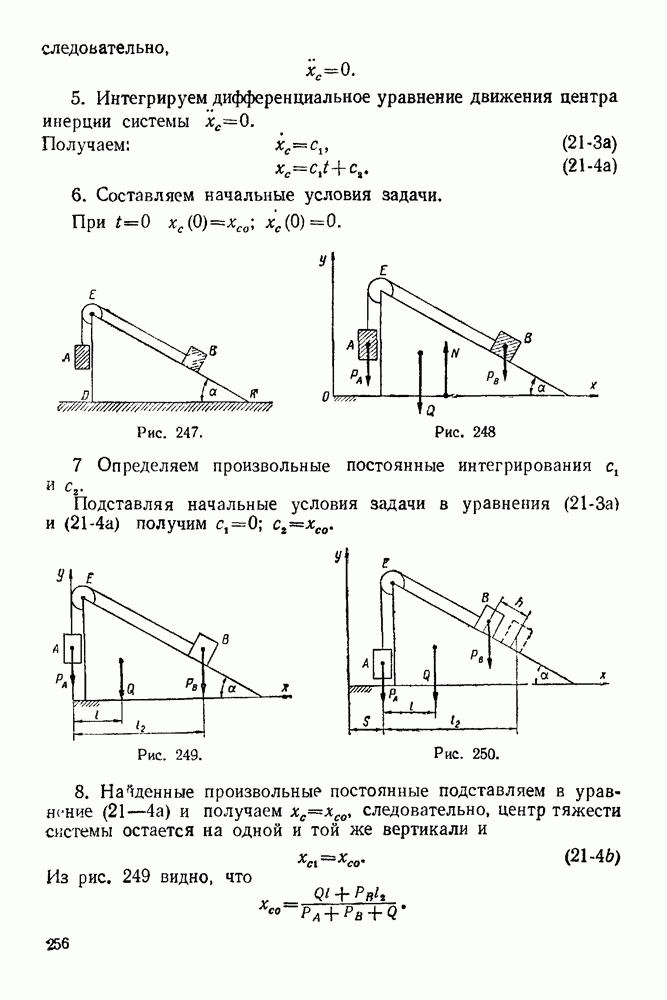
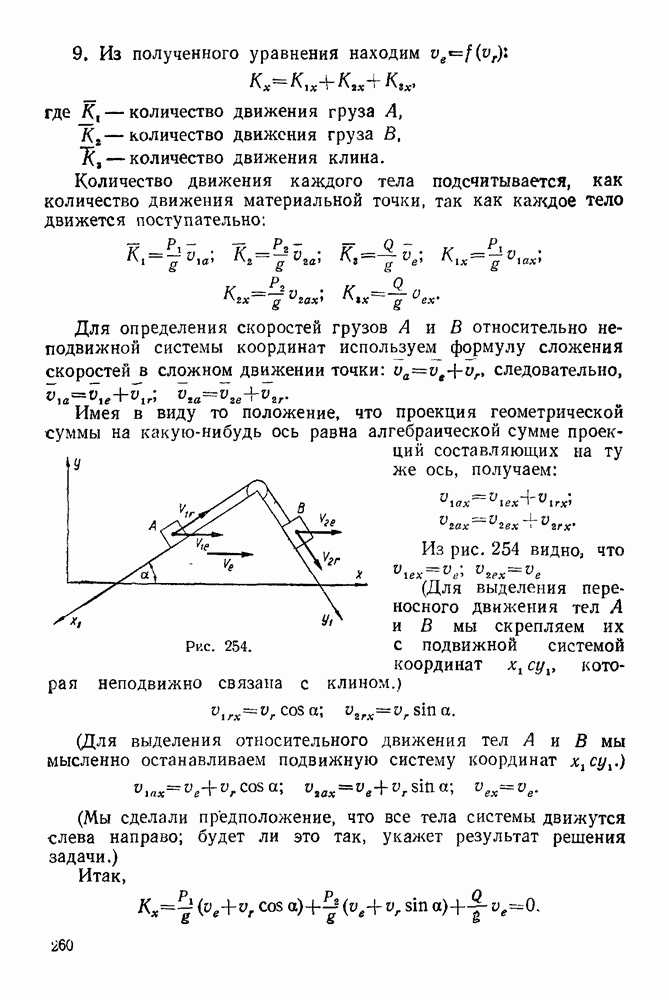
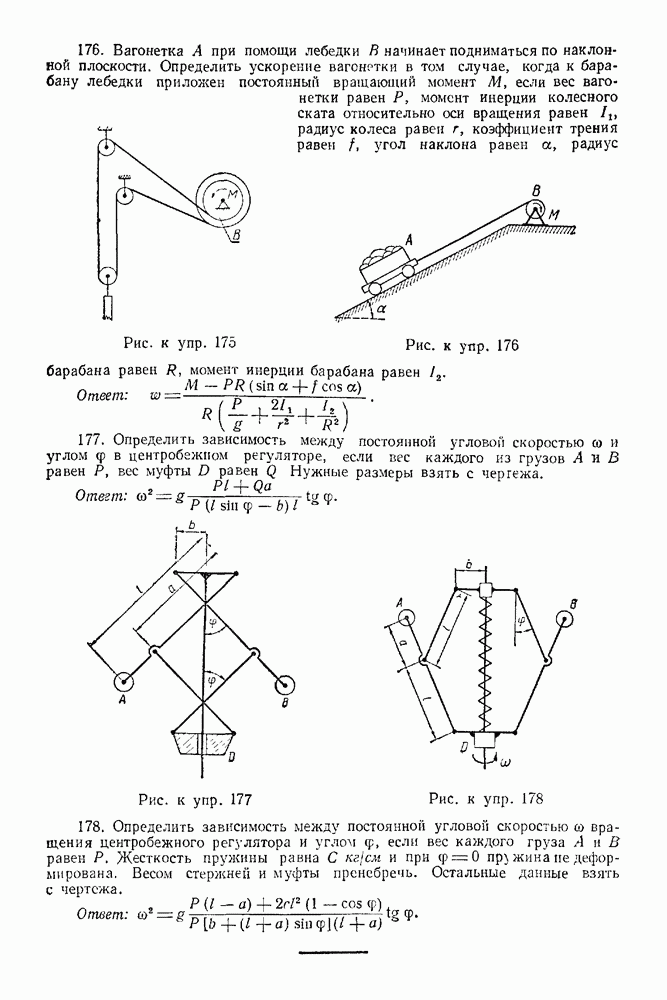
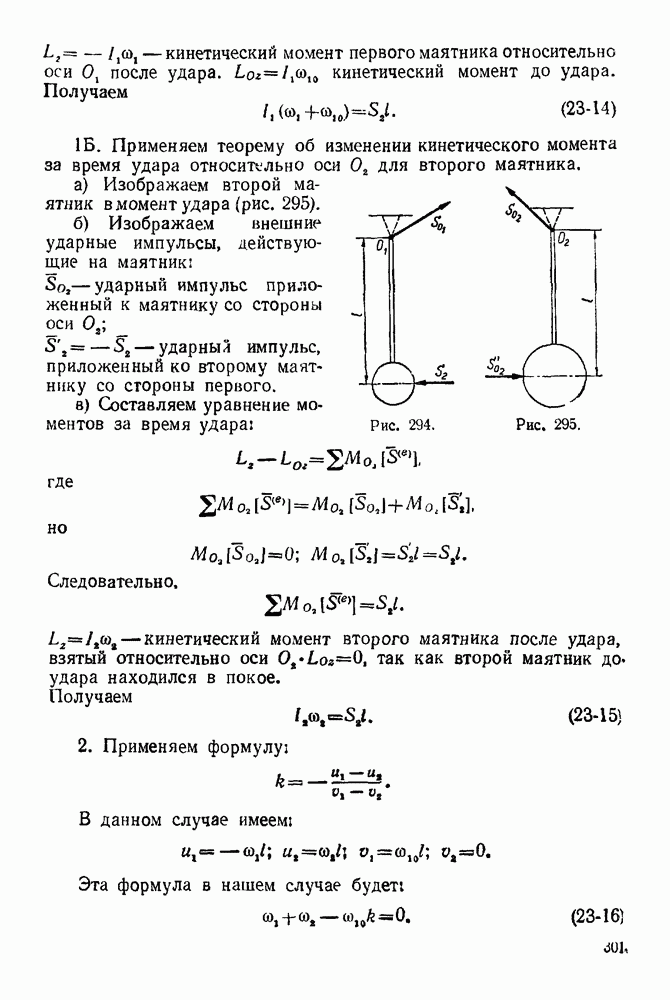
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть вторая. КИНЕМАТИКА
III. ДВИЖЕНИЕ ТОЧКИ
ГЛАВА X. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
10-1. Предмет кинематики. Основные положения
В разделе «кинематика» изучается механическое движение, рассматриваемое без учета сил, приложенных к движущимся объектам.
Механическое движение является одним из видов движения материи, выражающийся в изменении с течением времени взаимных положений тел или частей тела Кинематически определить движение тела — значит указать положение любой точки тела в любой момент времени относительно выбранной системы координат. Пространство, в котором происходят наблюдаемые движения материальных тел, в классической механике рассматривается как трехмерное евклидово пространство Время предполагается не зависящим от относительного движения систем отсчета, т. е. оно одинаково во всех системах отсчета. Время в кинематике, рассматриваемое как величина непрерывно изменяющаяся, с точки зрения математики играет роль независимого переменного и обозначается буквой  Под термином «момент времени
Под термином «момент времени  понимается число секунд, отделяющих данное мгновение от некоторого начала отсчета времени. Под термином тромежуток времени
понимается число секунд, отделяющих данное мгновение от некоторого начала отсчета времени. Под термином тромежуток времени  понимается число секунд
понимается число секунд  отделяющих два каких-нибудь последовательных момента времени. Для удобства изложения кинематика делится на кинематику точки и кинематику твердого тела. Траекторией точки называется линия, описываемая движущейся точкой в пространстве. Прямолинейное движение точки — такое движение, при котором траектория точки есть прямая линия. Равенство, выражающее абсциссу х движущейся точки, как функцию времени, называется законом (уравнением) движения
отделяющих два каких-нибудь последовательных момента времени. Для удобства изложения кинематика делится на кинематику точки и кинематику твердого тела. Траекторией точки называется линия, описываемая движущейся точкой в пространстве. Прямолинейное движение точки — такое движение, при котором траектория точки есть прямая линия. Равенство, выражающее абсциссу х движущейся точки, как функцию времени, называется законом (уравнением) движения
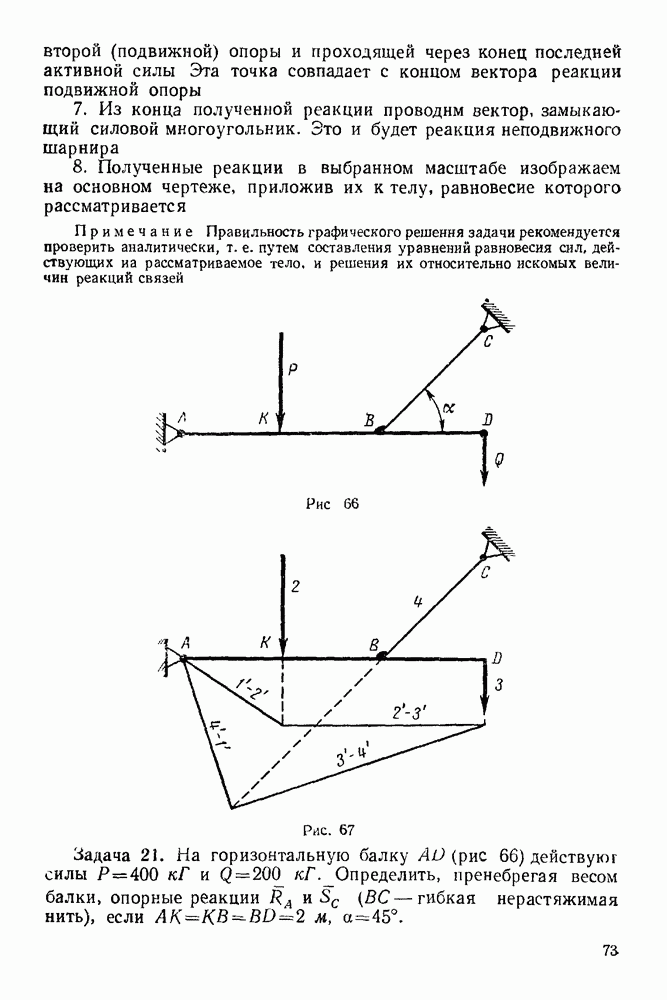
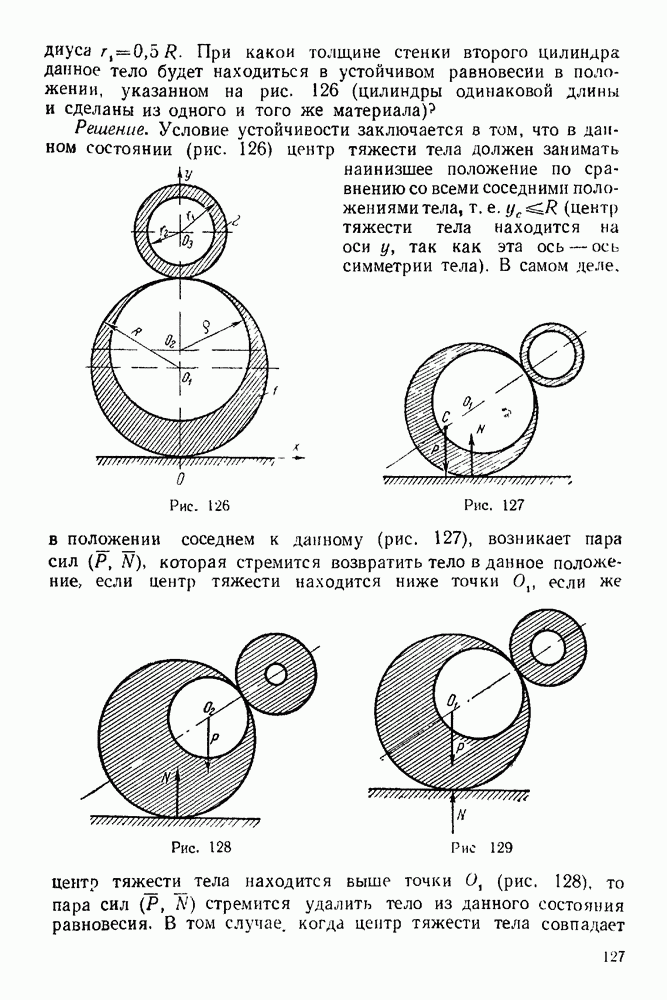
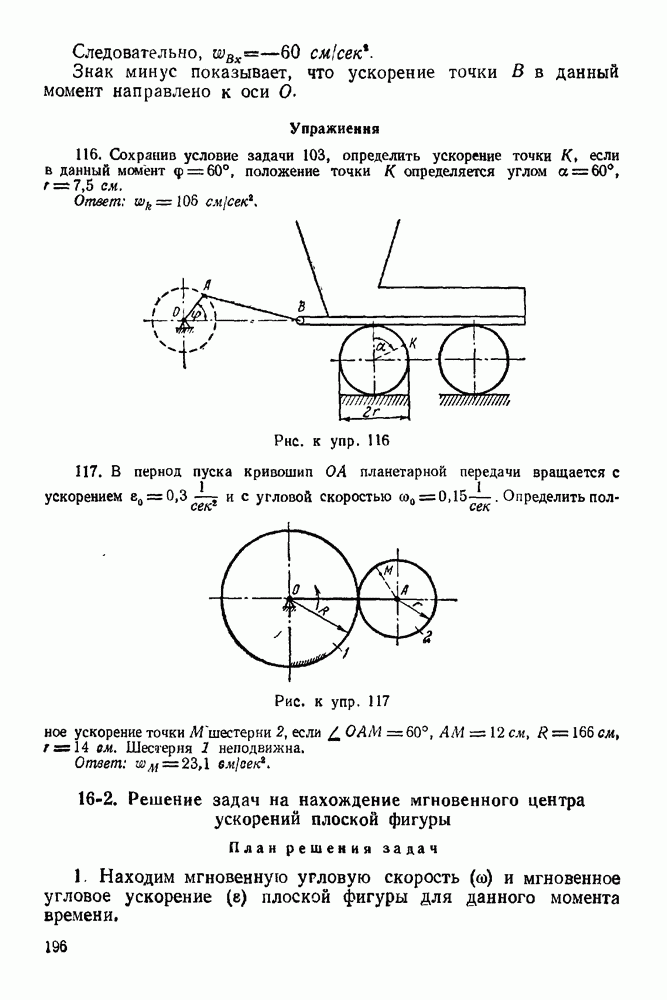
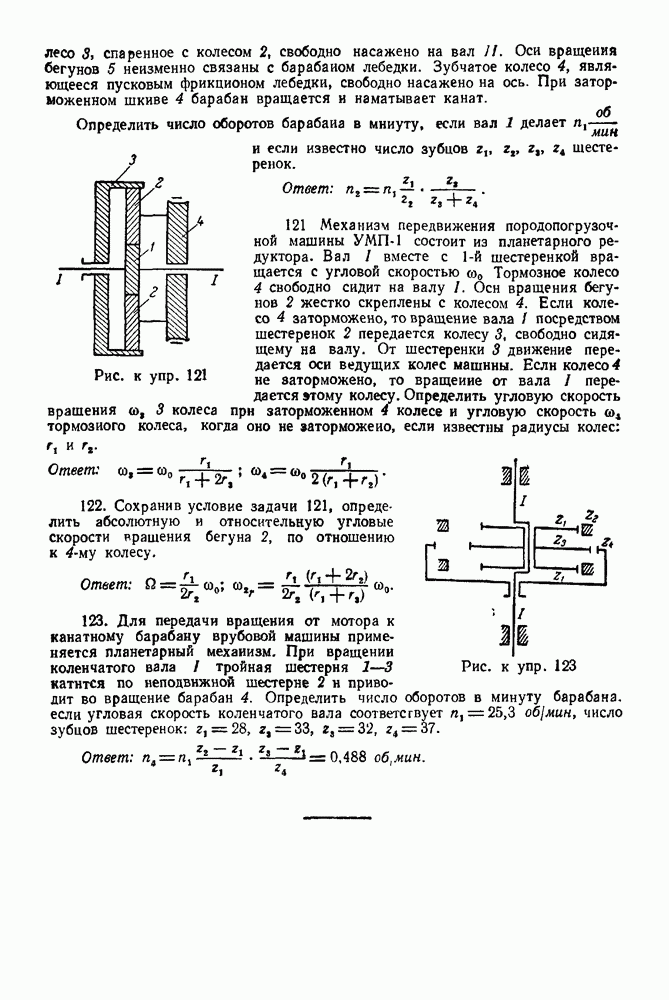
точки (рис. 131):

где  текущее положение точки.
текущее положение точки.
Проекция  вектора скорости точки на ось х равна первой производной по времени от абсциссы точки:
вектора скорости точки на ось х равна первой производной по времени от абсциссы точки:

Если  то движение происходит в положительном направлении оси х, в противном случае точка движется в отрицательном направлении.
то движение происходит в положительном направлении оси х, в противном случае точка движется в отрицательном направлении.
Модуль вектора скорости точки в прямолинейном движении по оси х равен абсолютной величине первой производной по времени от абсциссы точки:


Рис. 131.
Проекция  вектора ускорения точки на ось х равна второй производной по времени от абсциссы точки:
вектора ускорения точки на ось х равна второй производной по времени от абсциссы точки:

Модуль вектора ускорения точки в прямолинейном движении по оси х равен абсолютной величине второй производной по времени от абсциссы точки:

Прямолинейное движение точки называется равномерным, если проекция вектора скорости точки на ось  постоянная величина.
постоянная величина.
При равномерном движении точка перемещается по линейному закону:

Прямолинейное движение точки называется равнопеременным, если проекция вектора ускорения точки на ось х есть постоянная величина:

При равнопеременном движении точка движется по квадратичному закону, а проекция скорости точки на ось х изменяется по линейному закону:

где при  движение равноускоренное, а при
движение равноускоренное, а при  равнозамедленное.
равнозамедленное.
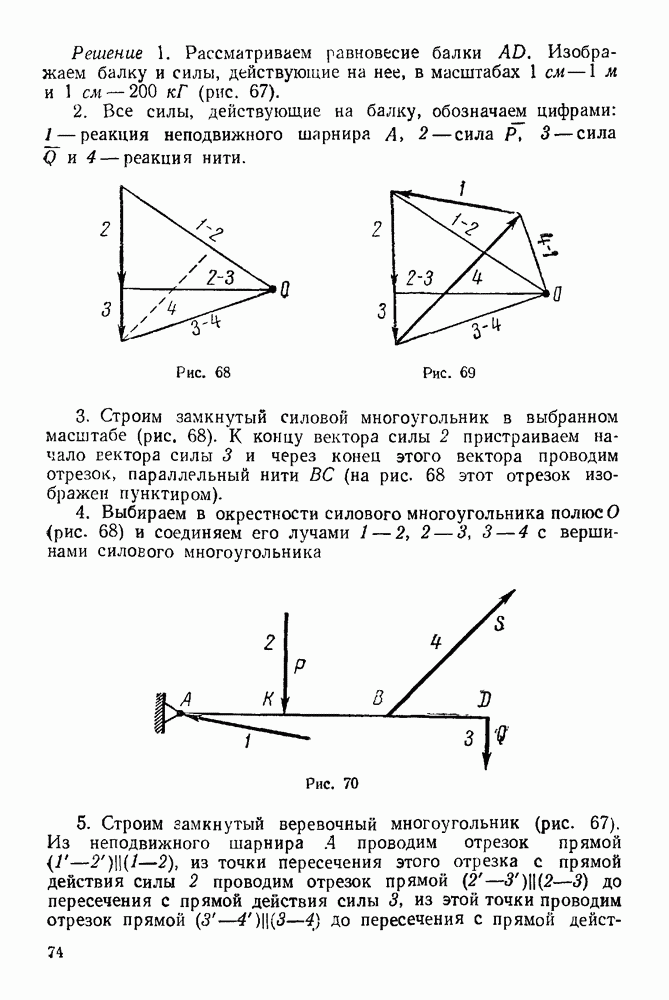
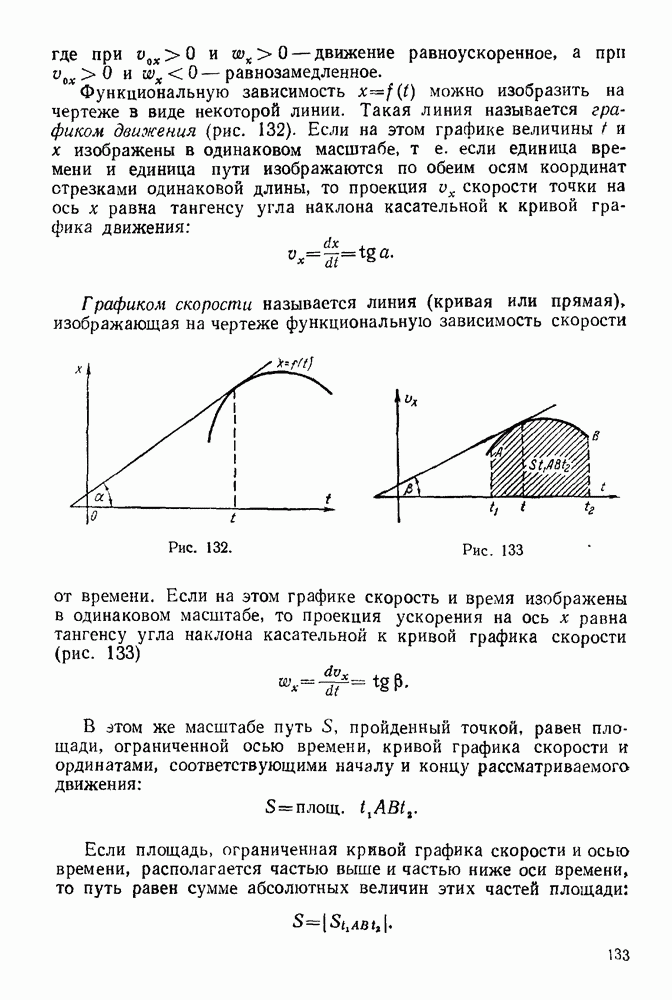
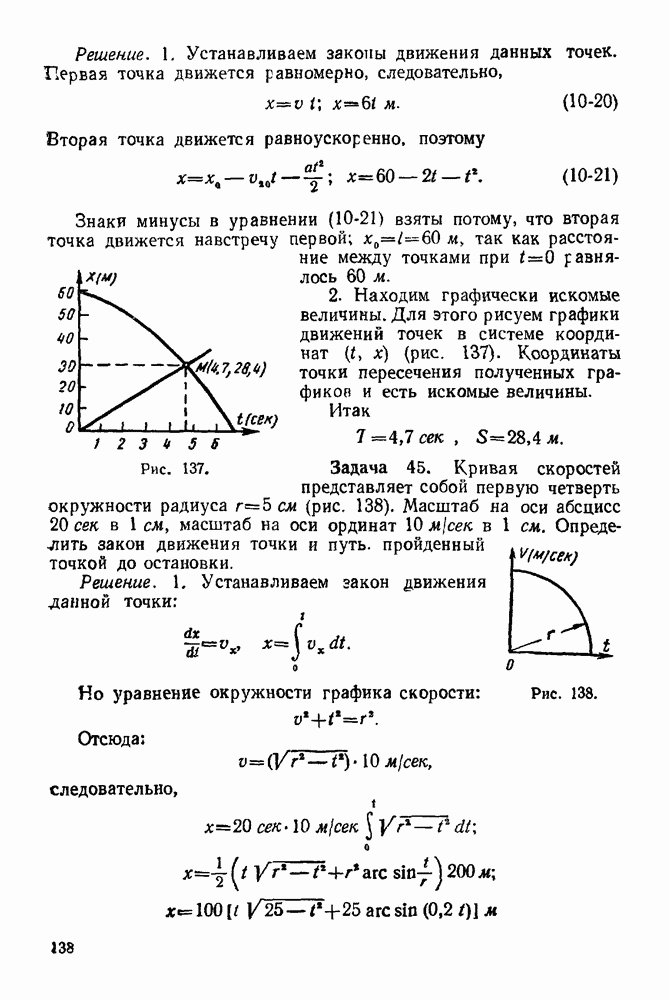
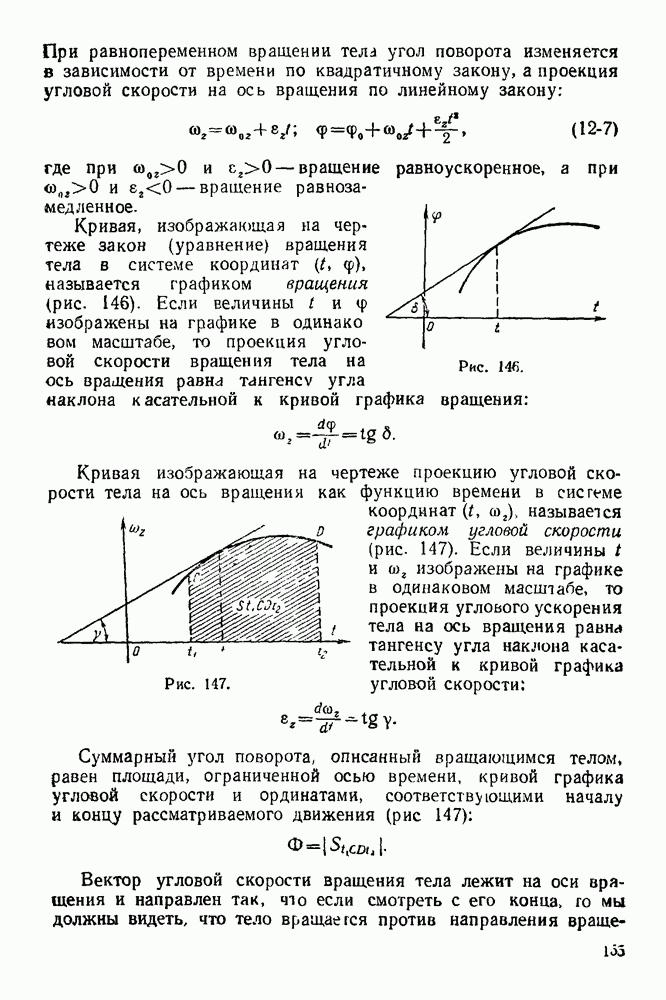
Функциональную зависимость  можно изобразить на чертеже в виде некоторой линии. Такая линия называется графиком движения (рис. 132). Если на этом графике величины
можно изобразить на чертеже в виде некоторой линии. Такая линия называется графиком движения (рис. 132). Если на этом графике величины  изображены в одинаковом масштабе, т. е. если единица времени и единица пути изображаются по обеим осям координат отрезками одинаковой длины, то проекция
изображены в одинаковом масштабе, т. е. если единица времени и единица пути изображаются по обеим осям координат отрезками одинаковой длины, то проекция  скорости точки на ось х равна тангенсу угла наклона касательной к кривой графика движения:
скорости точки на ось х равна тангенсу угла наклона касательной к кривой графика движения:

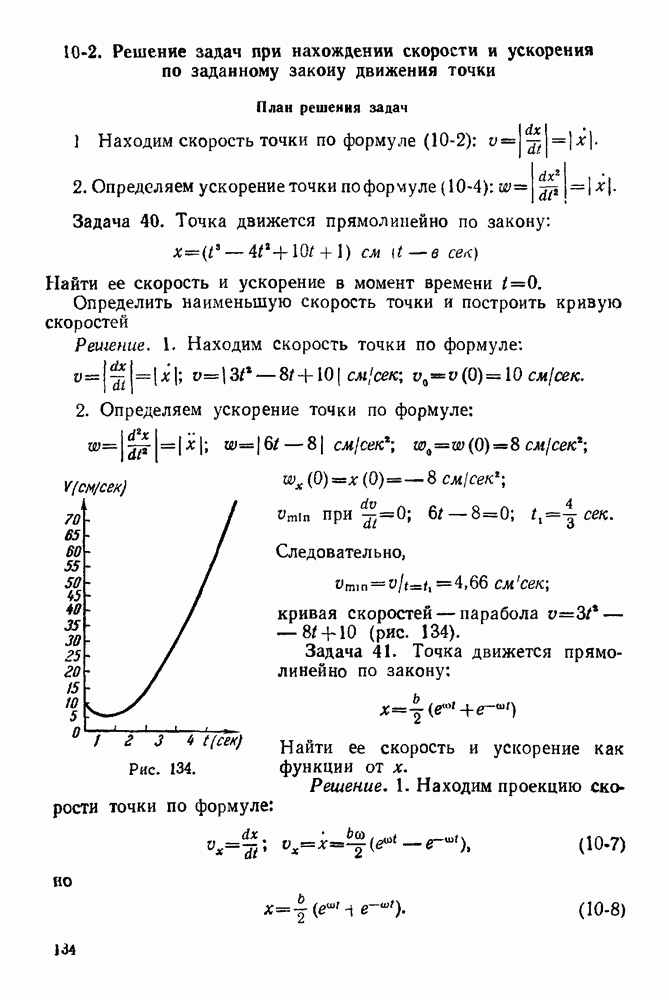
Графиком скорости называется линия (кривая или прямая), изображающая на чертеже функциональную зависимость скорости от времени.

Рис. 132.

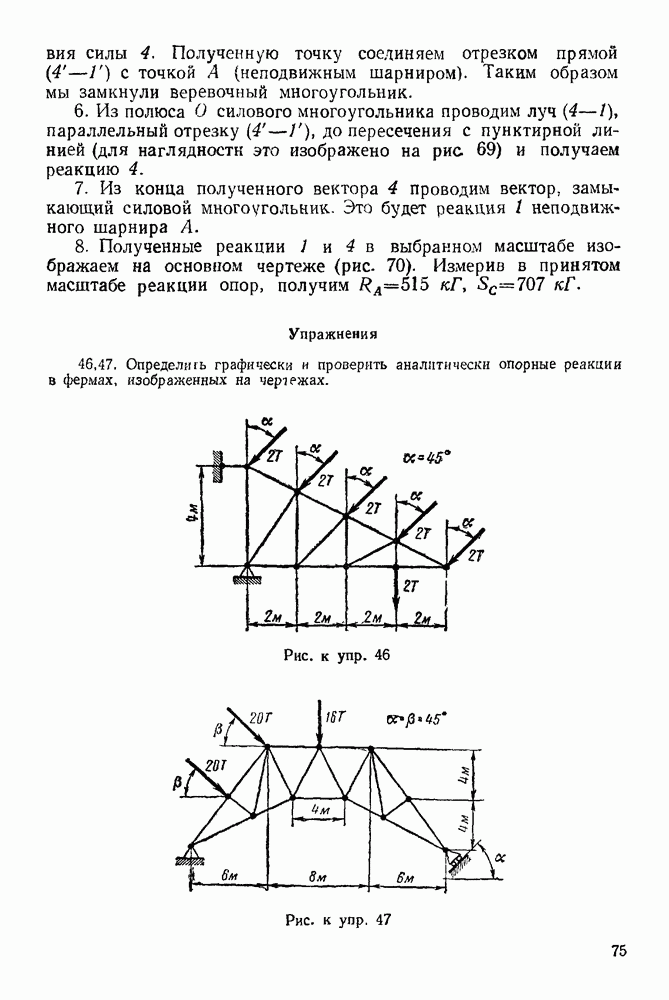
Рис. 133
Если на этом графике скорость и время изображены в одинаковом масштабе, то проекция ускорения на ось х равна тангенсу угла наклона касательной к кривой графика скорости (рис. 133)

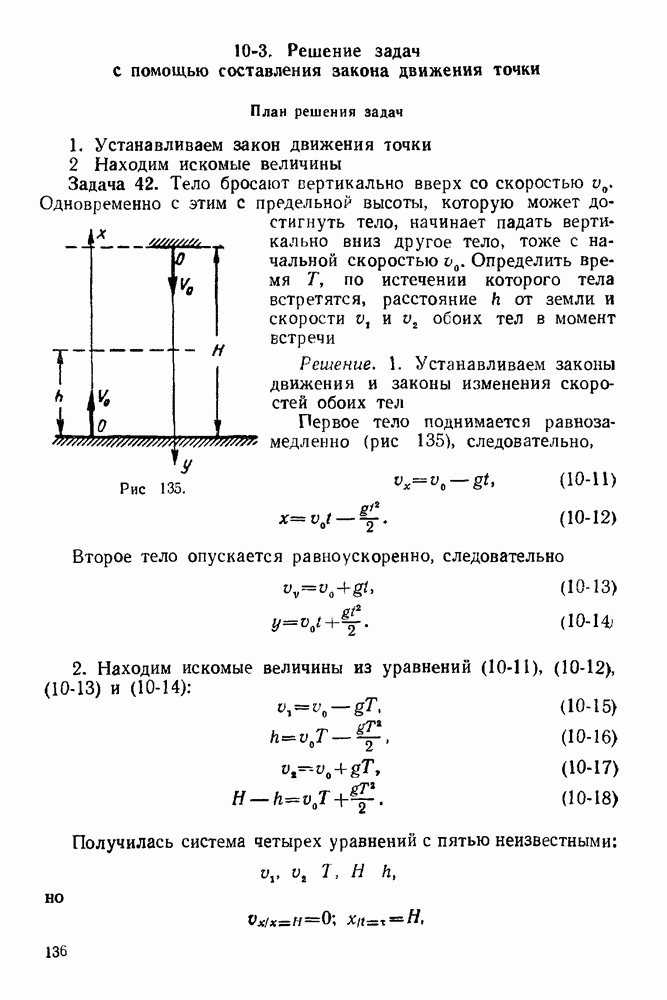
В сэтом же масштабе путь  пройденный точкой, равен площади, ограниченной осью времени, кривой графика скорости и ординатами, соответствующими началу и концу рассматриваемого движения:
пройденный точкой, равен площади, ограниченной осью времени, кривой графика скорости и ординатами, соответствующими началу и концу рассматриваемого движения:

Если площадь, ограниченная кривой графика скорости и осью времени, располагается частью выше и частью ниже оси времени, то путь равен сумме абсолютных величин этих частей площади:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
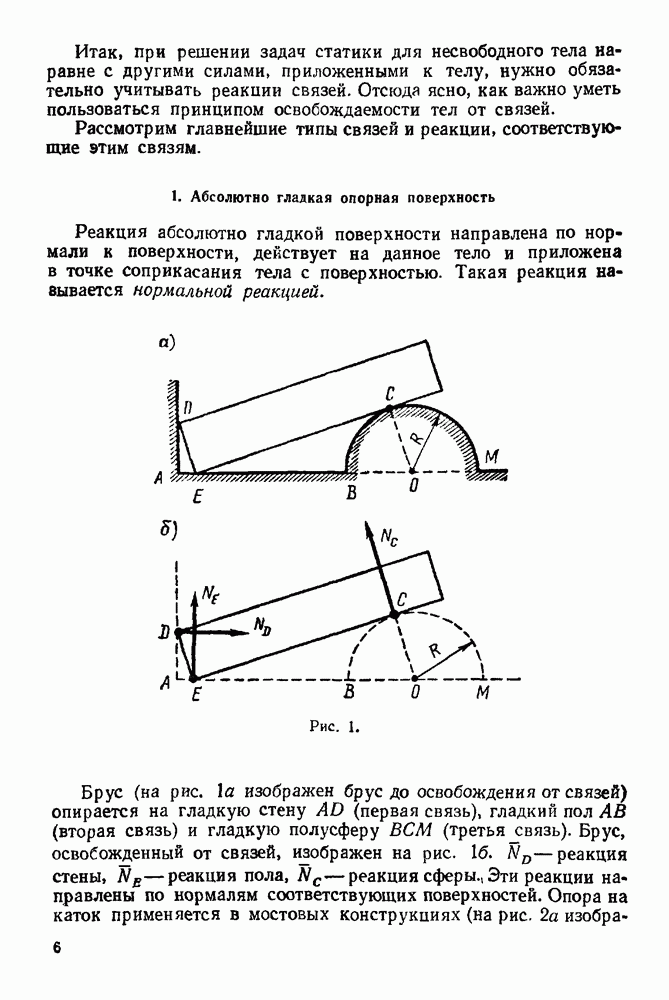
- 1. Абсолютно гладкая опорная поверхность
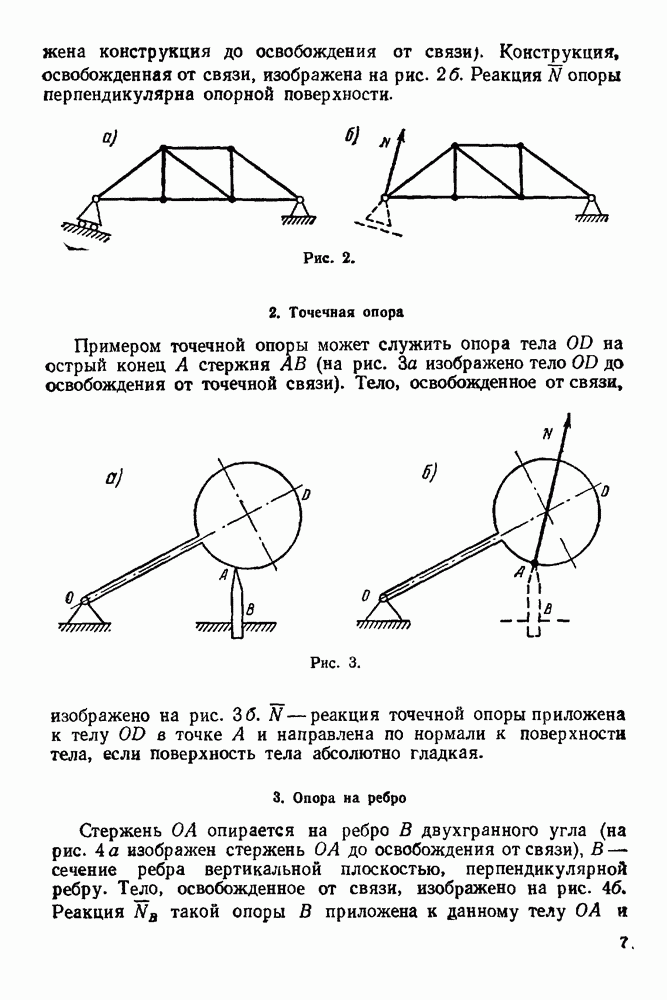
- 2. Точечная опора
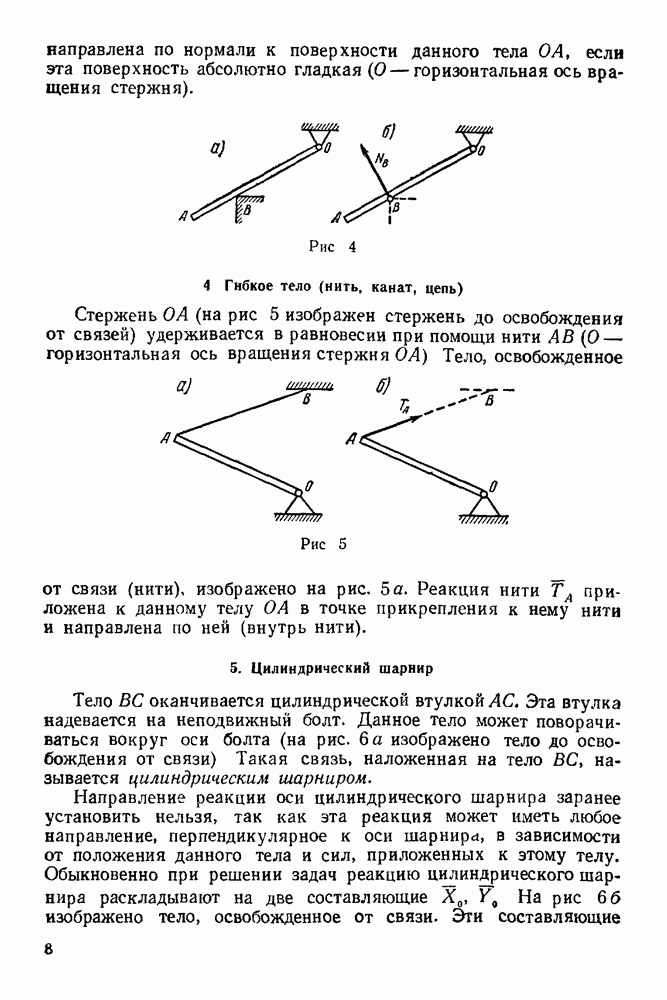
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
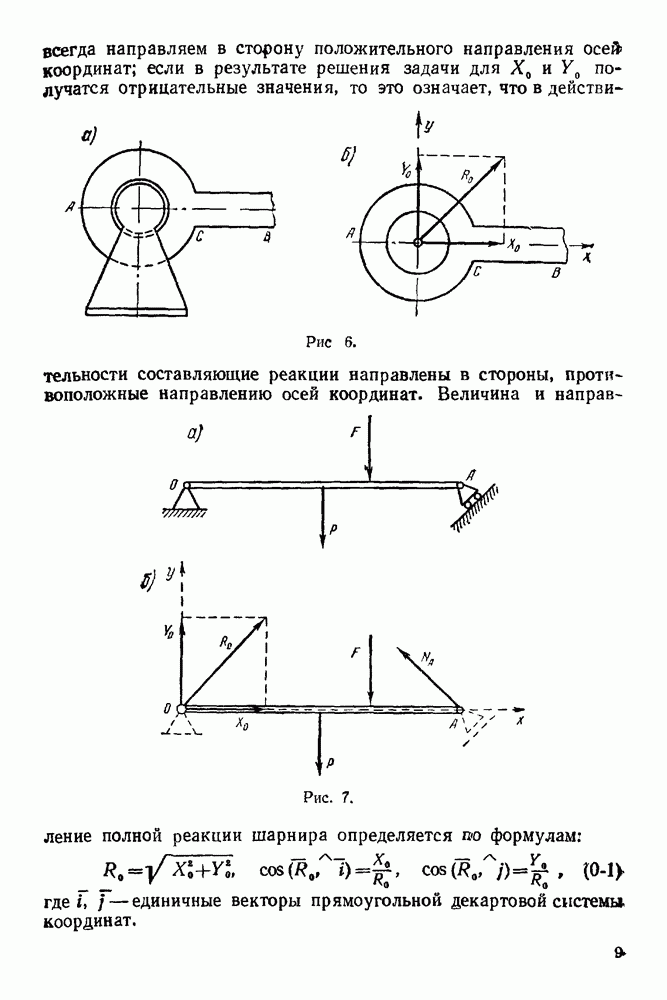
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
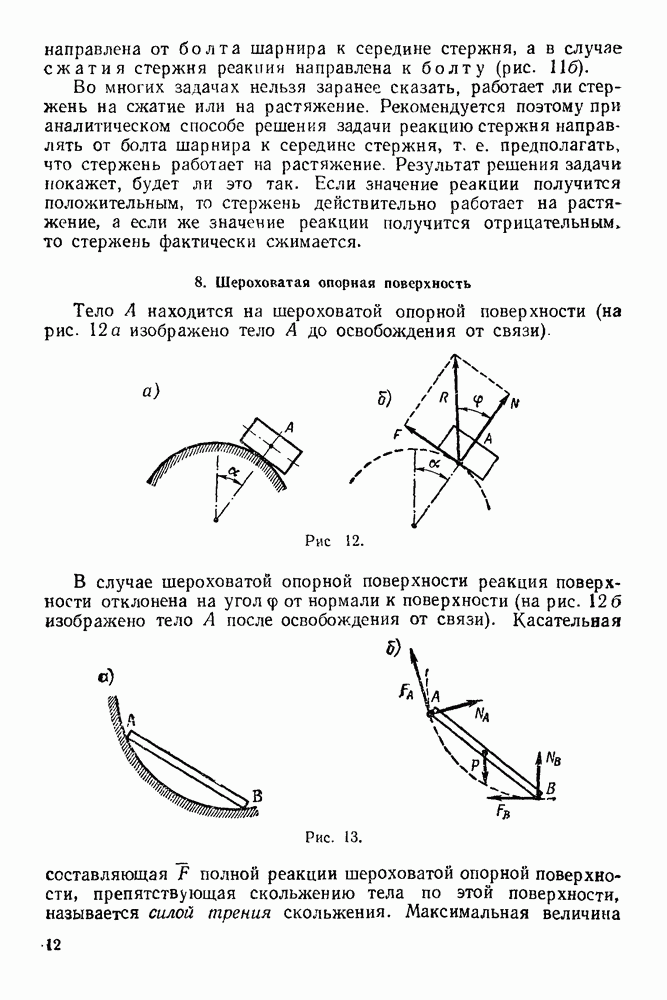
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
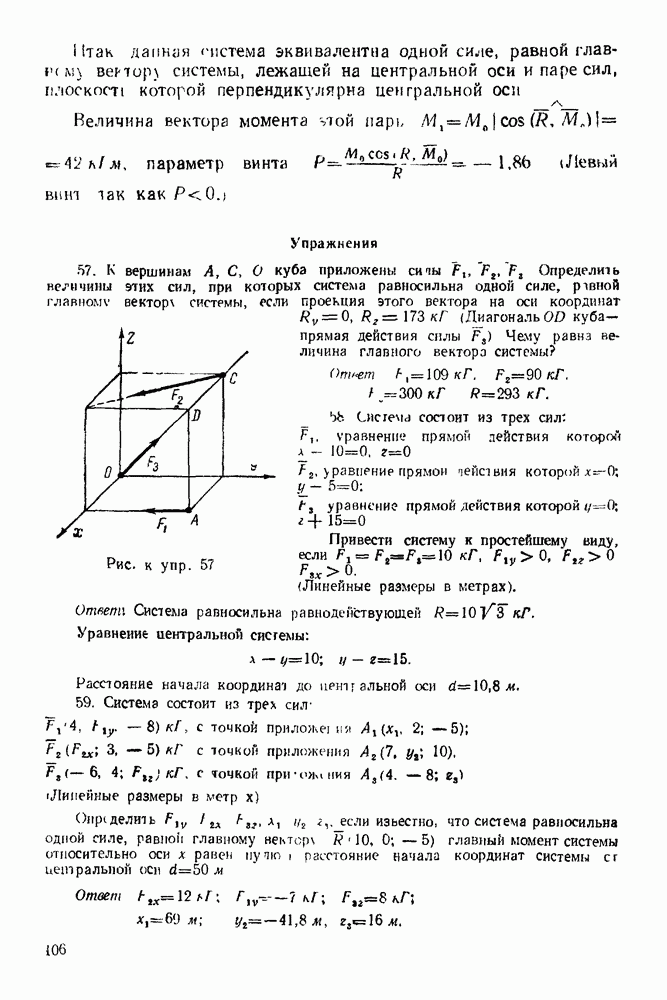
- I. ПЛОСКАЯ СИСТЕМА СИЛ
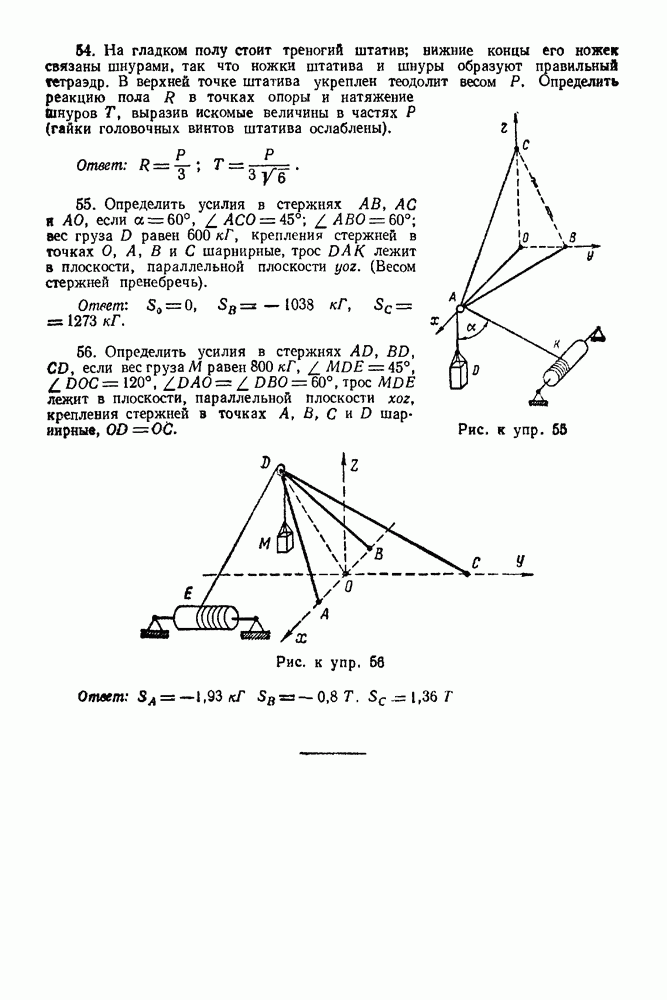
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
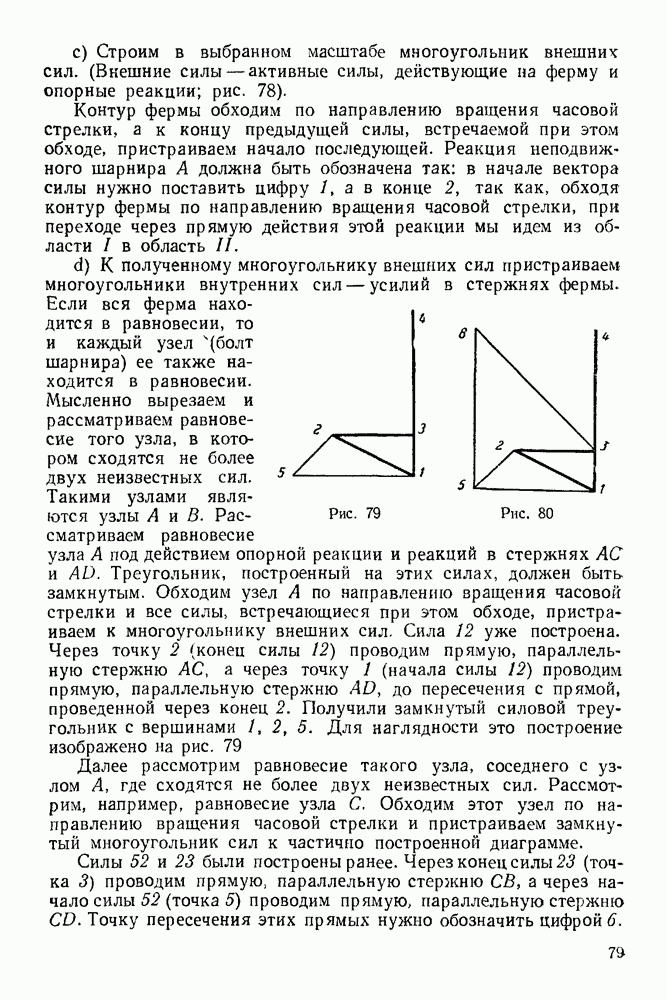
- 5-3. Определение усилий в стержнях фермы
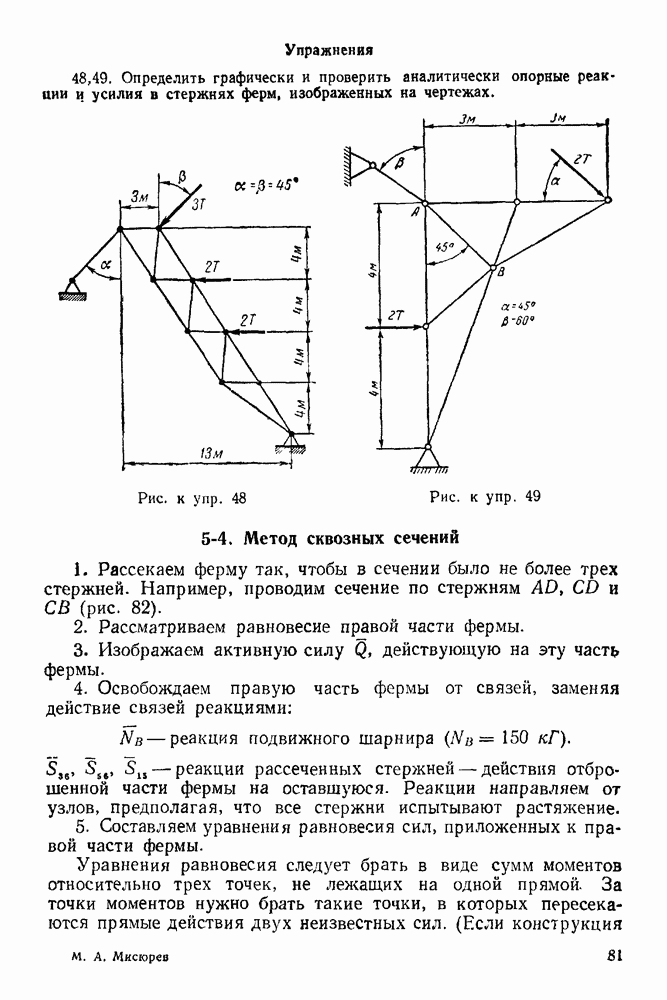
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
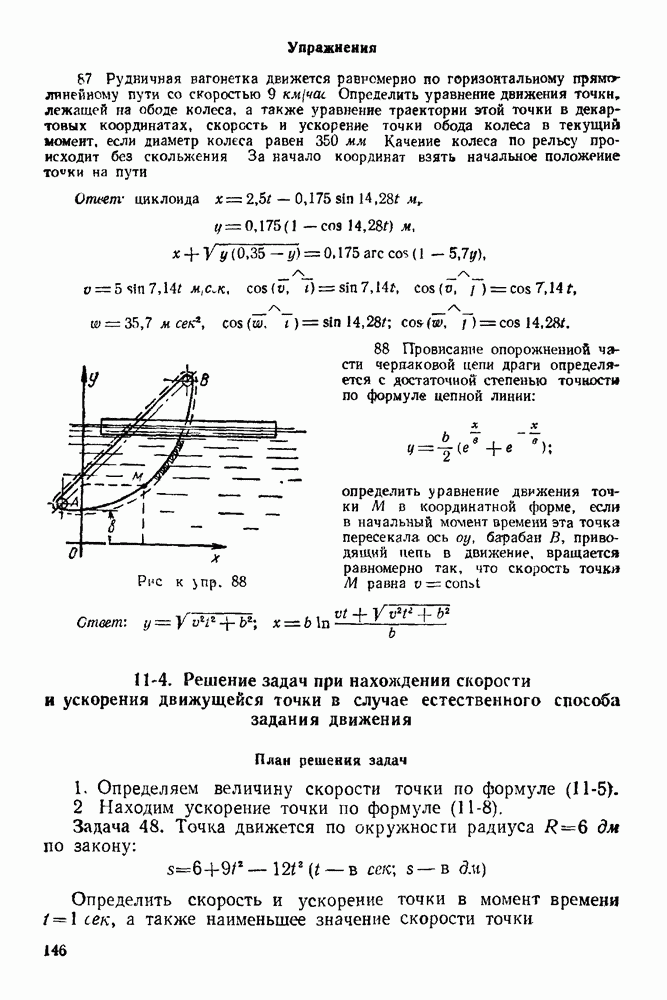
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
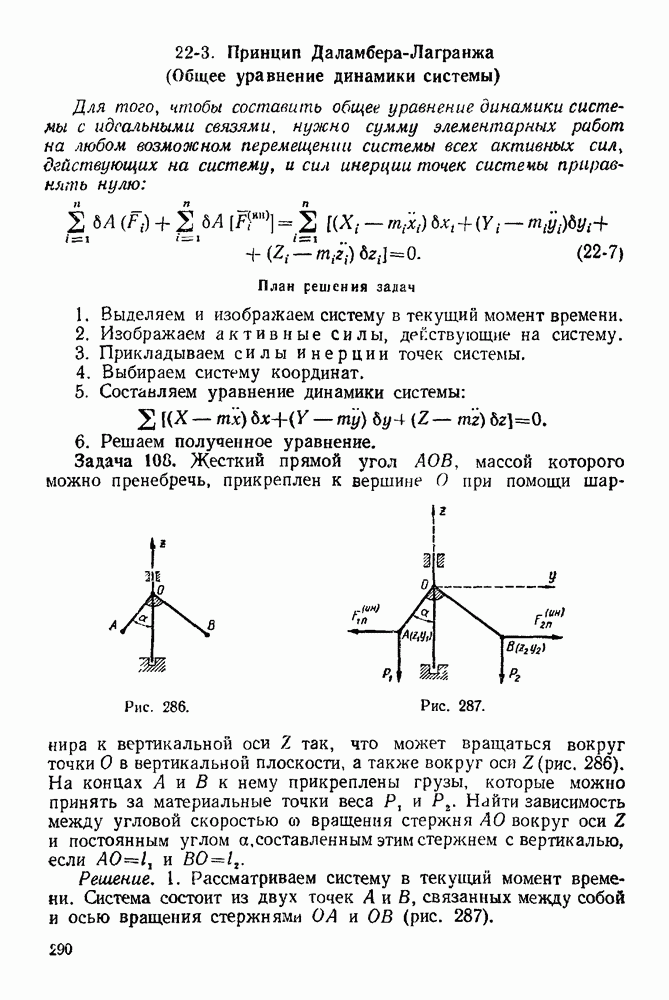
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР