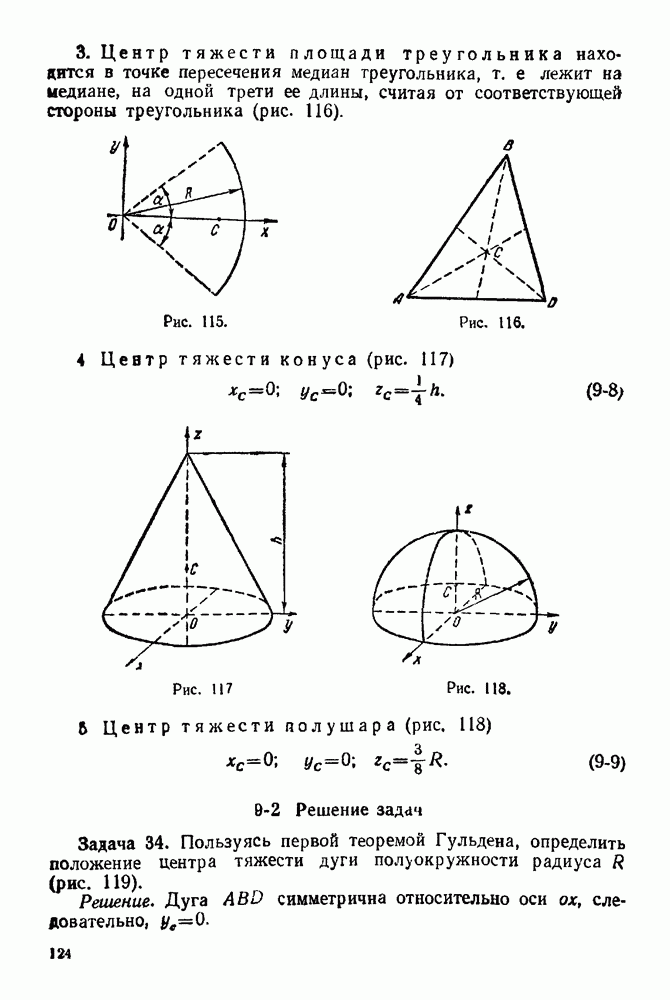| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
6-1. Основные положения
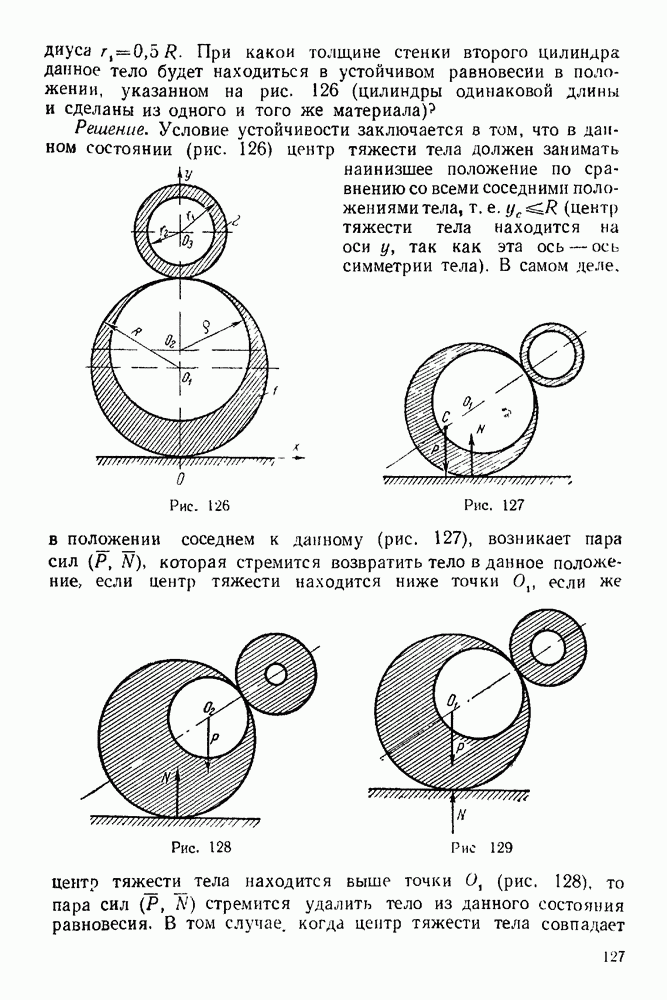
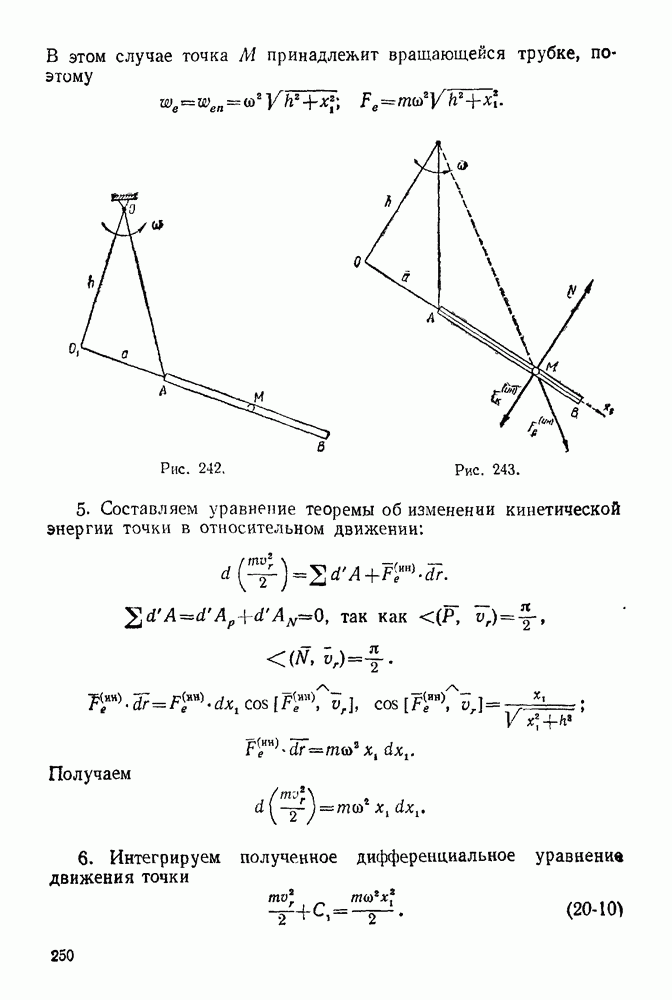
Совокупность сил, линии действия которых пересекаются в одной точке, называется сходящейся системой сил.
Для того, чтобы система сходящихся сил в пространстве находилась в равновесии, необходимо и достаточно, чтобы суммы проекций всех сил системы на три взаимно перпендикулярных оси равнялись нулю:

Проекция силы на ось
Из рис. 88 видно, что  где составляющая
где составляющая  параллельна оси
параллельна оси  составляющая
составляющая  параллельна плоскости
параллельна плоскости  Используем следующую теорему: проекция равнодействующей на какую-нибудь ось равна алгебраической сумме проекций составляющих на ту же ось:
Используем следующую теорему: проекция равнодействующей на какую-нибудь ось равна алгебраической сумме проекций составляющих на ту же ось:

но 
Обозначая  получаем
получаем

Но  проекция данной силы на одну из координатных
проекция данной силы на одну из координатных
плоскостей, проходящих через ось проекций. Следовательно, 

Таким образом, приходим к следующему правилу.
Для того, чтобы найти проекцию силы на какую-нибудь из координатных осей, нужно сначала эту силу спроектировать на одну из координатных плоскостей, проходящих через ось проекций, а затем полученную проекцию спроектировать на данную ось.

Рис. 88
Отсюда следует, что если:  перпендикулярна плоскости
перпендикулярна плоскости  то
то  перпендикулярна плоскости
перпендикулярна плоскости  то
то  перпендикулярна плоскости
перпендикулярна плоскости  то
то 
Решаем задачи, придерживаясь следующего плана:
1. Выделяем материальную систему (тело или материальную частицу), равновесие которой следует рассмотреть.
2. Изображаем активные силы, действующие на материальную систему, равновесие которой рассматриваем.
3. Освобождаем эту систему от связей, заменяя действие связей реакциями.
4. Выбираем систему координат.
5. Составляем уравнения равновесия:

6. Решаем полученные уравнения.
6-2. Решение задач.
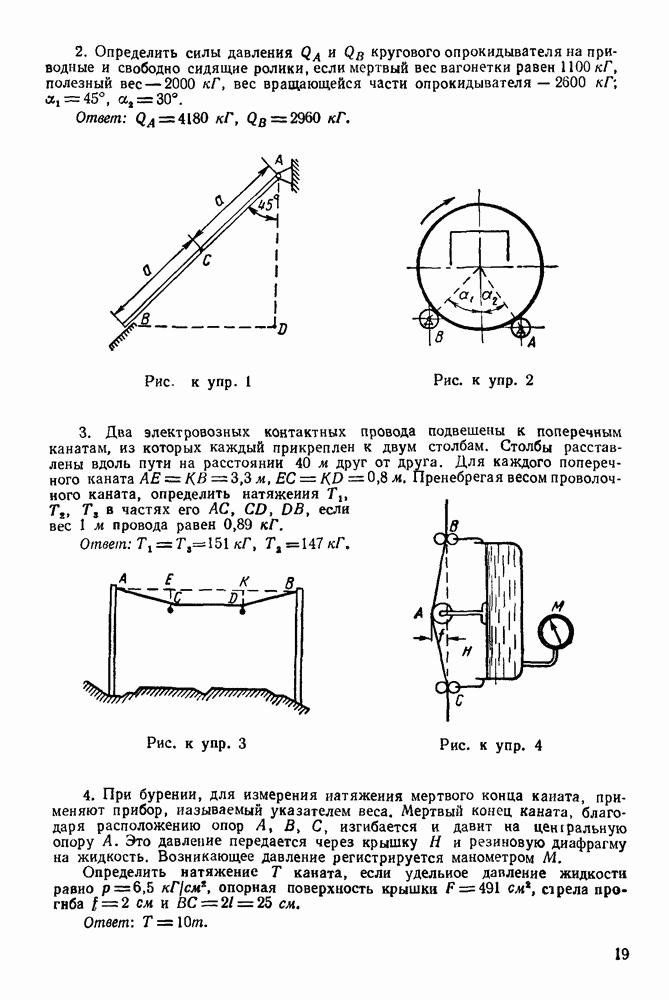
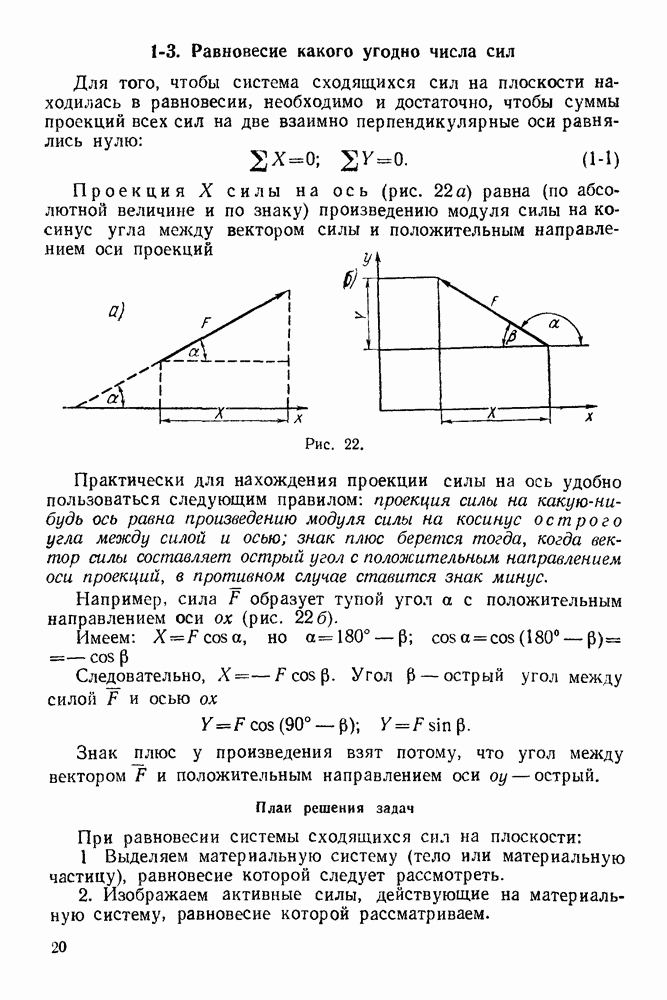
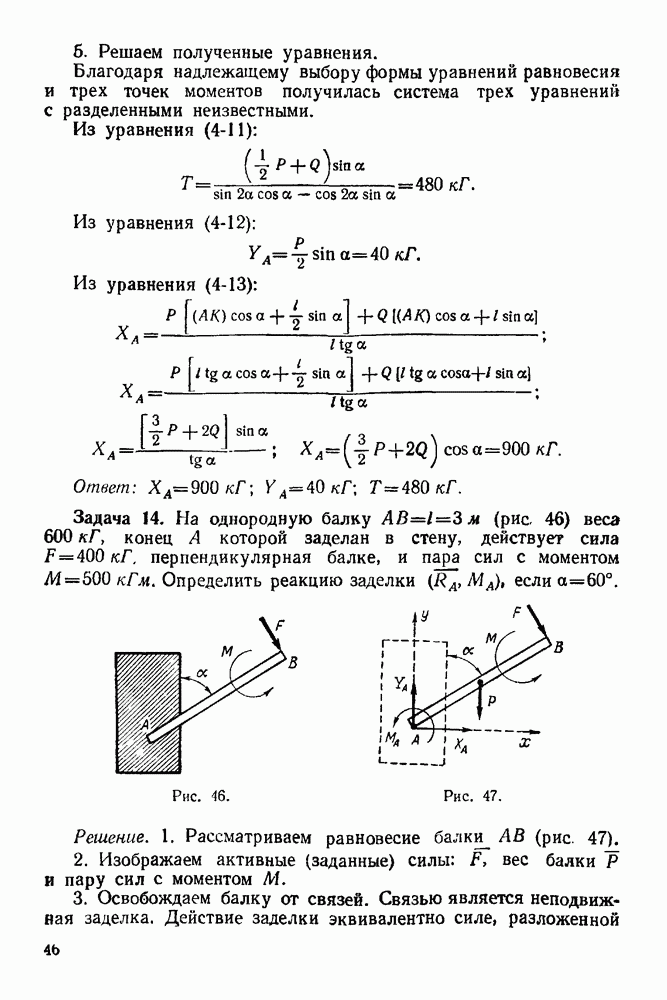
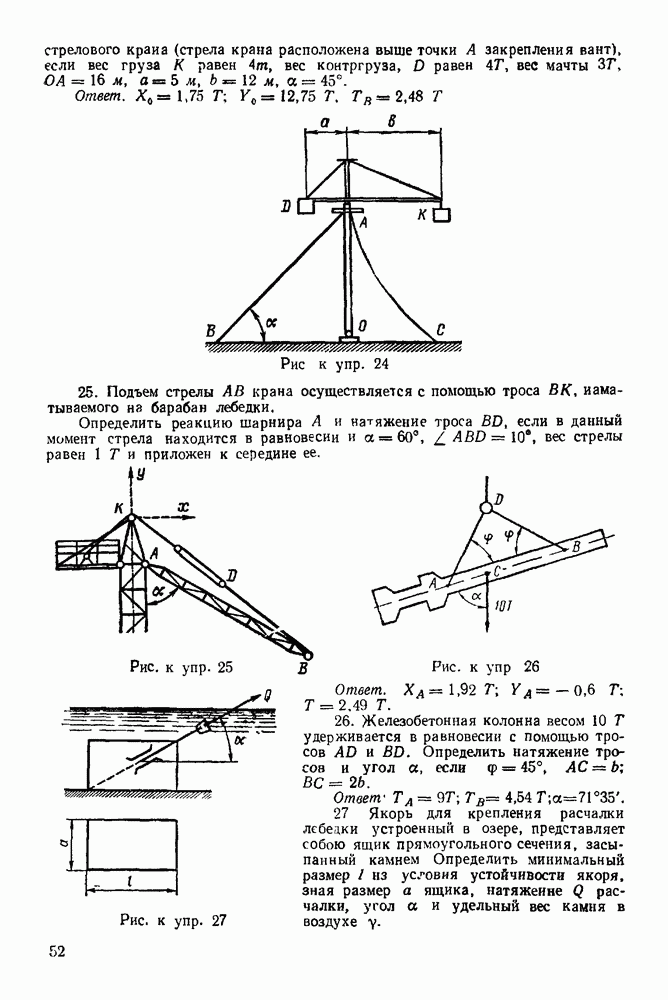
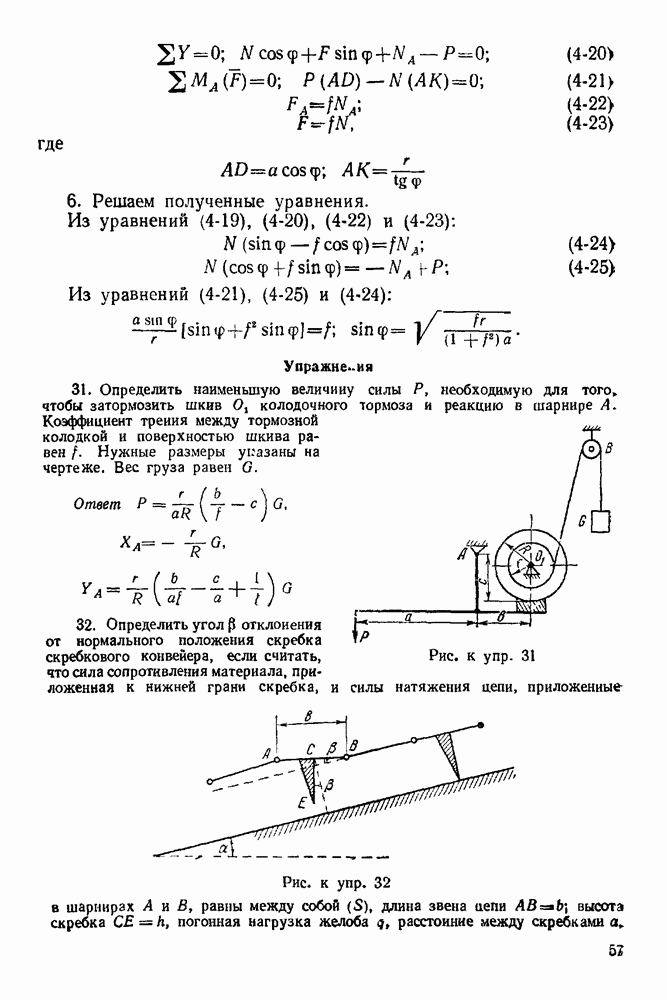
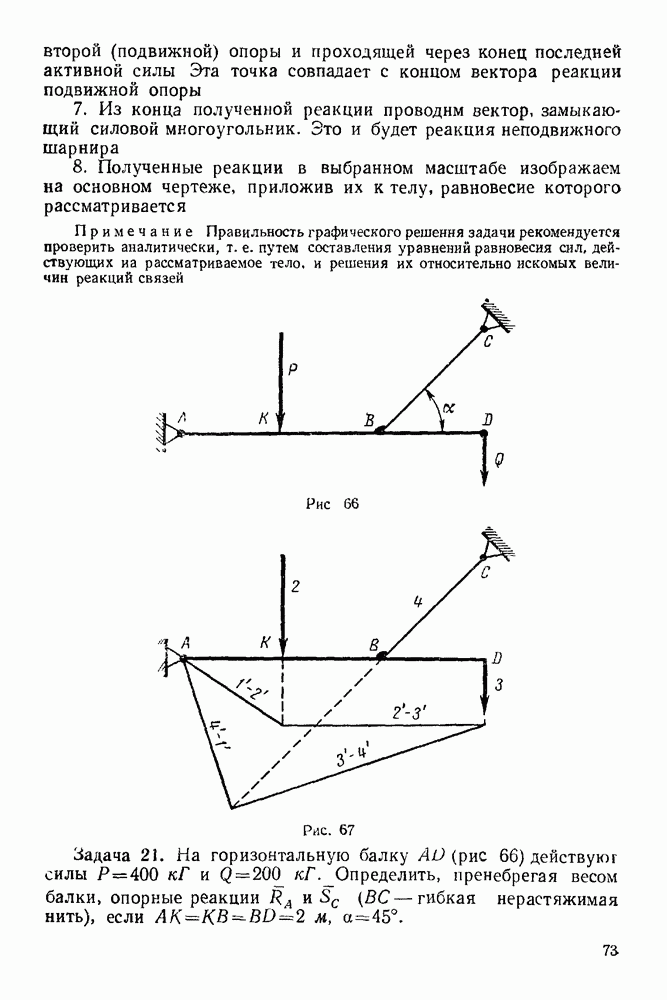
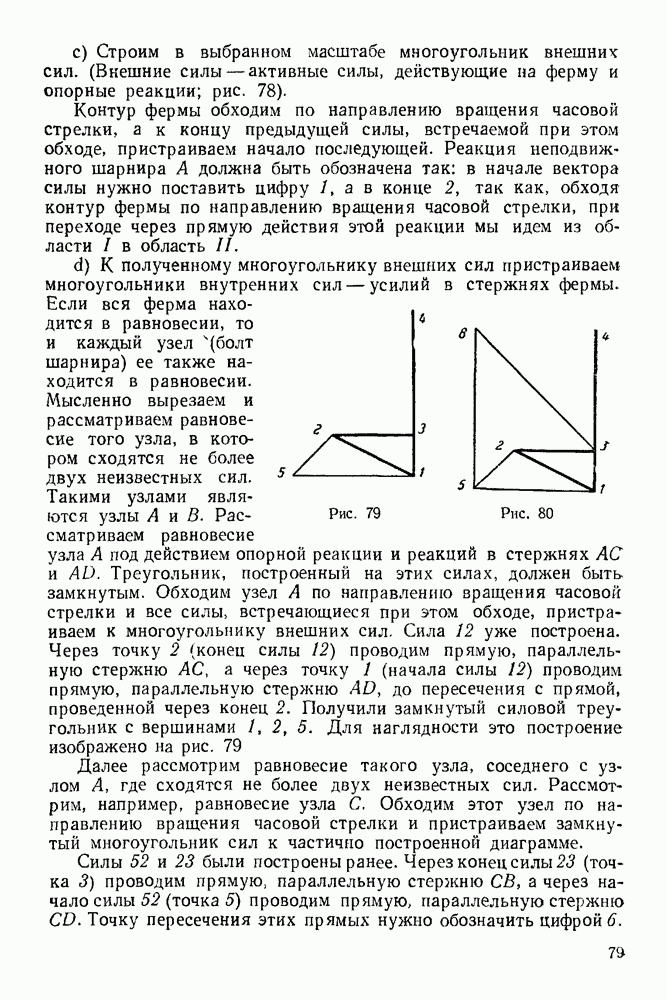
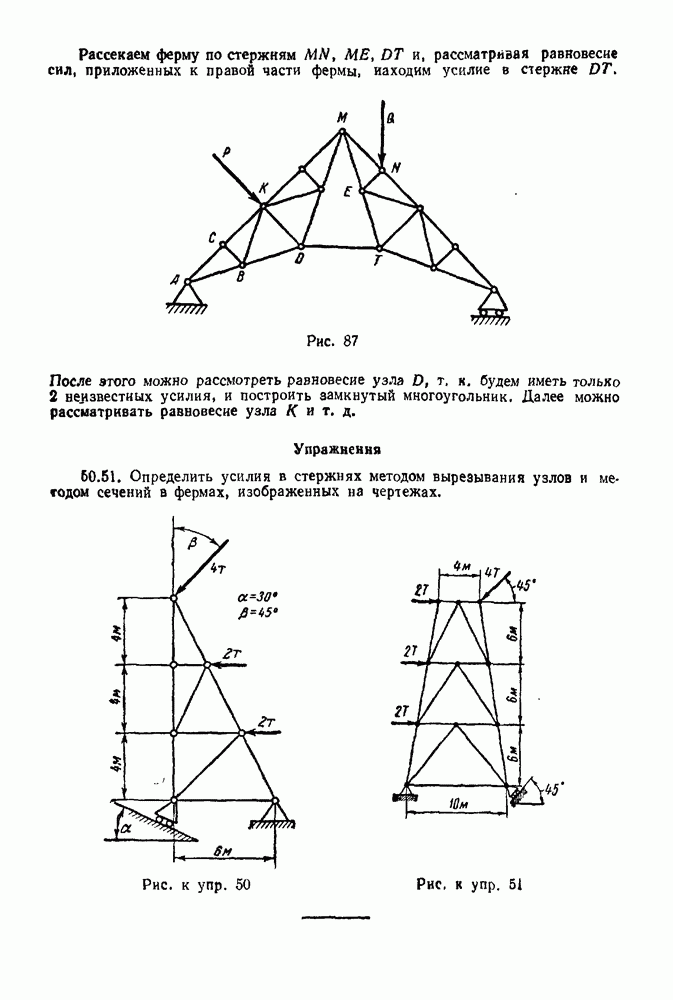
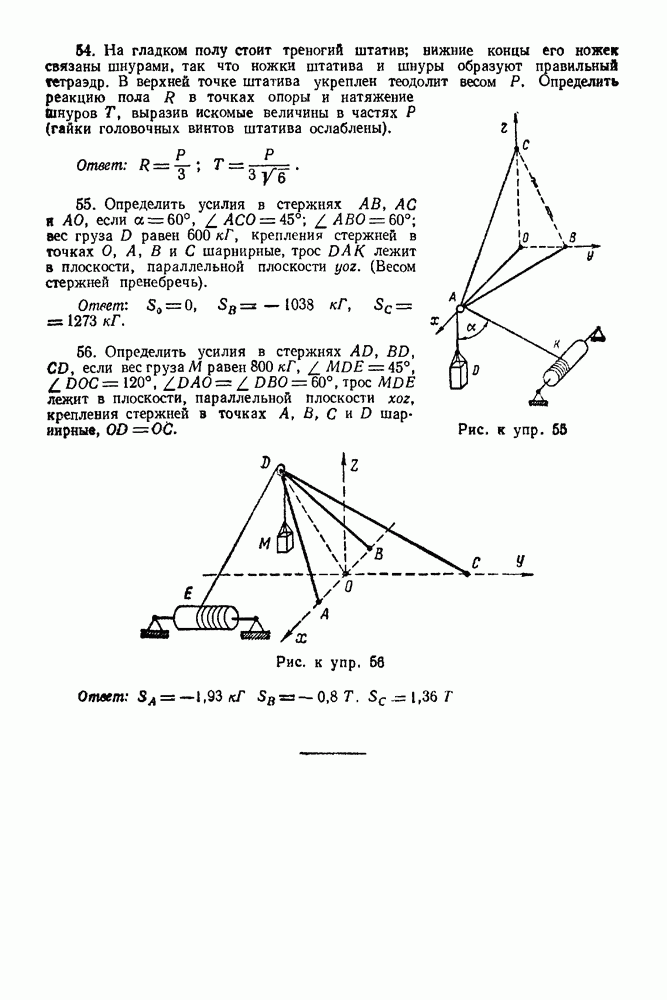
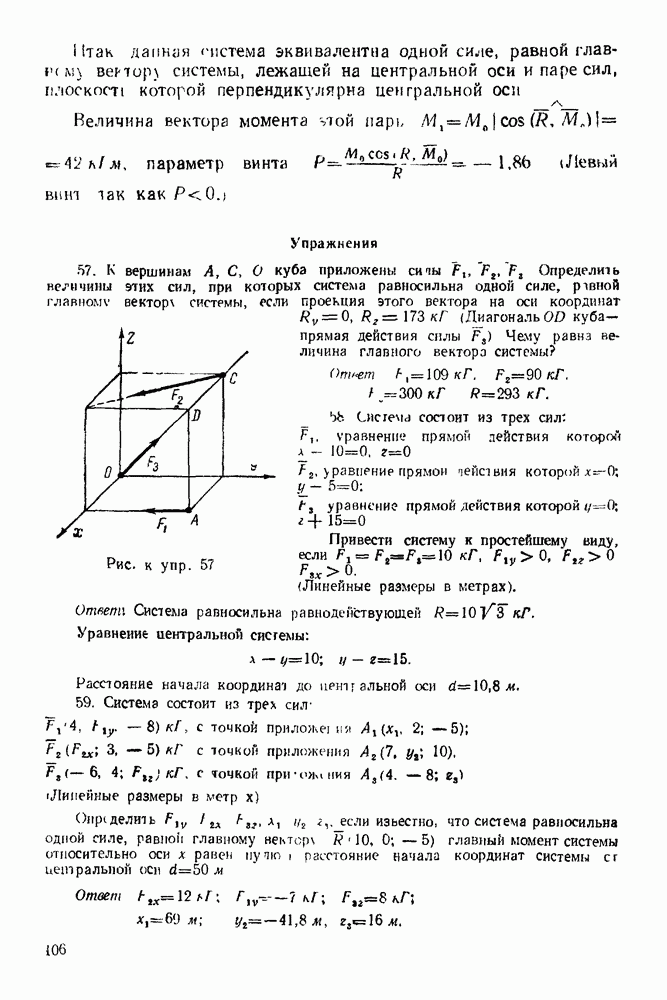
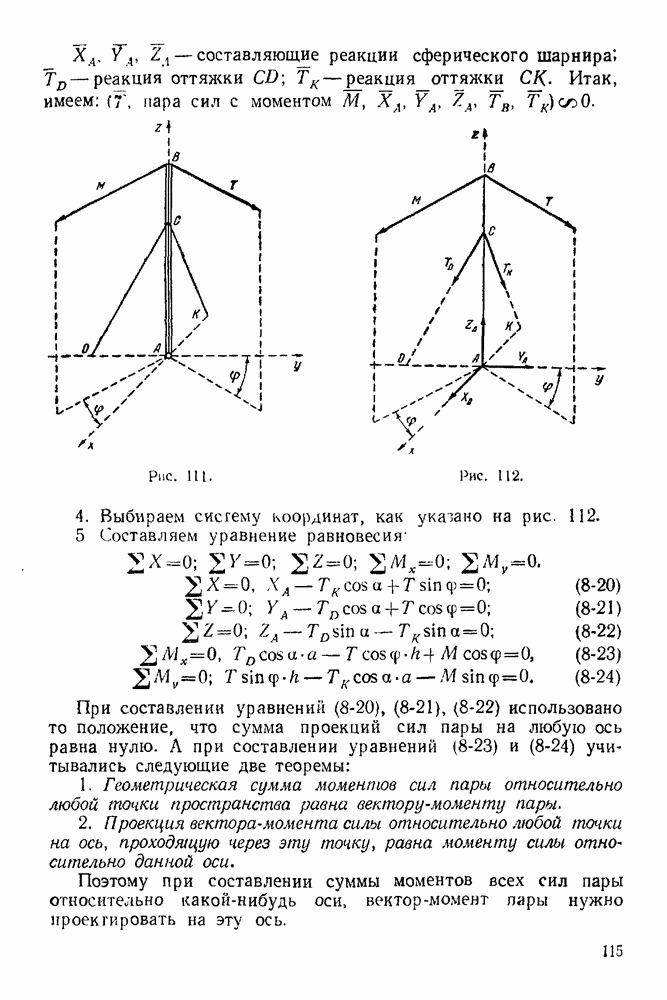
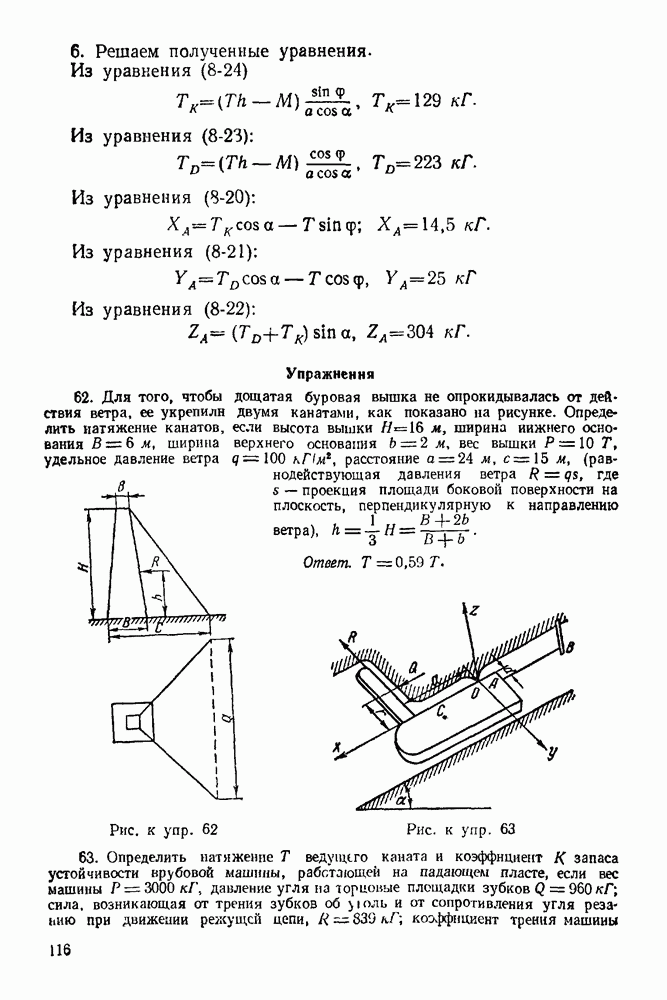
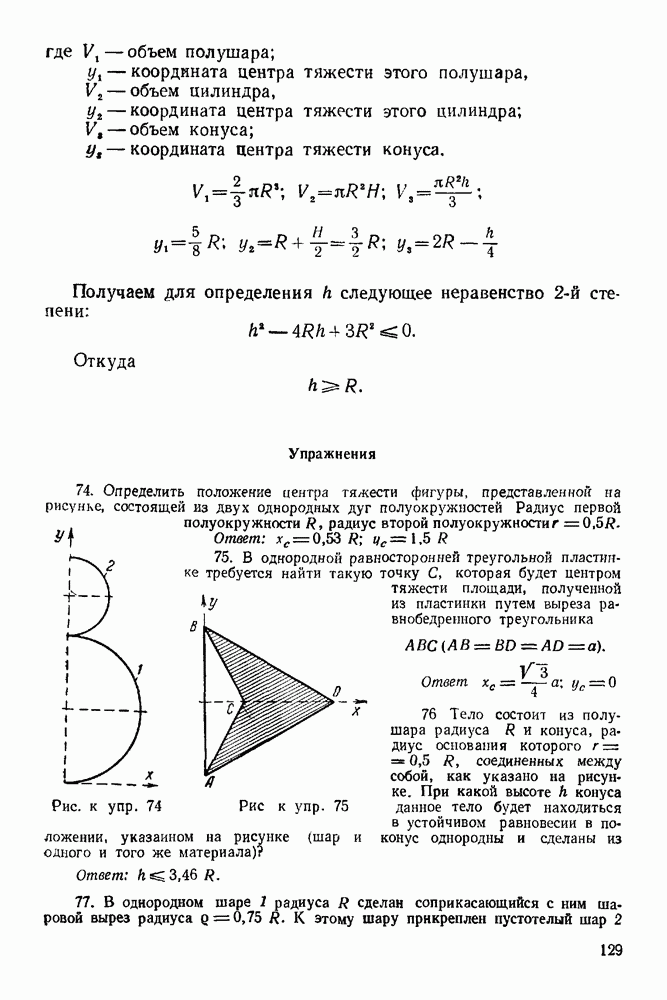
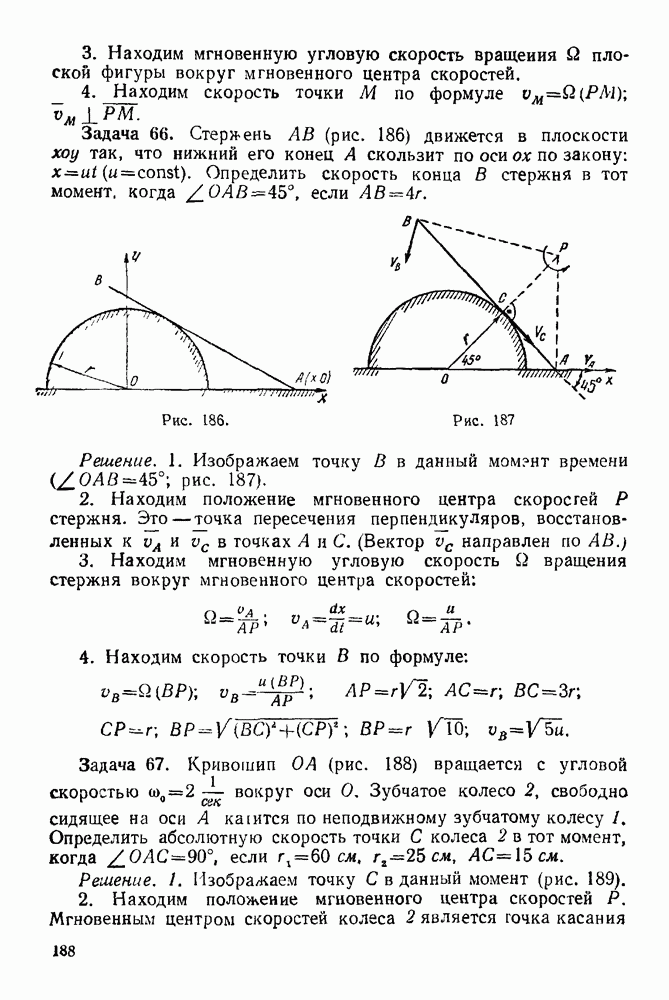
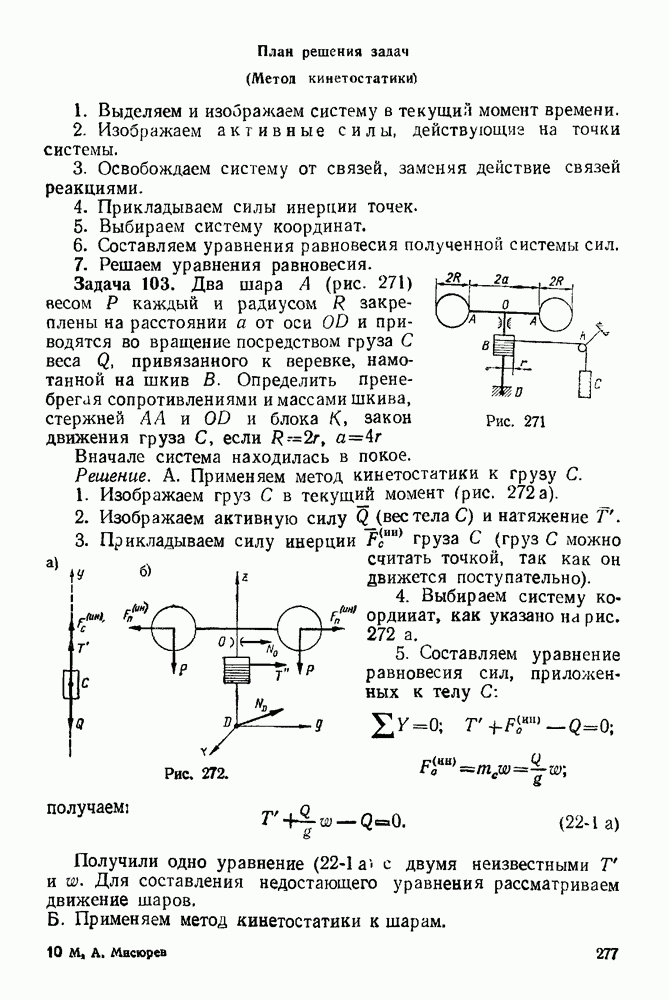
Задача 23. К узлу  треноги
треноги  (рис. 89) приложена сила
(рис. 89) приложена сила  лежащая в плоскости
лежащая в плоскости  симметрии треноги
симметрии треноги  и направленная под углом
и направленная под углом  к стержню
к стержню  Определить усилия в стержнях
Определить усилия в стержнях  и
и  если
если  правильный тетраэдр
правильный тетраэдр  шарниры. Весами стержней пренебречь.
шарниры. Весами стержней пренебречь.
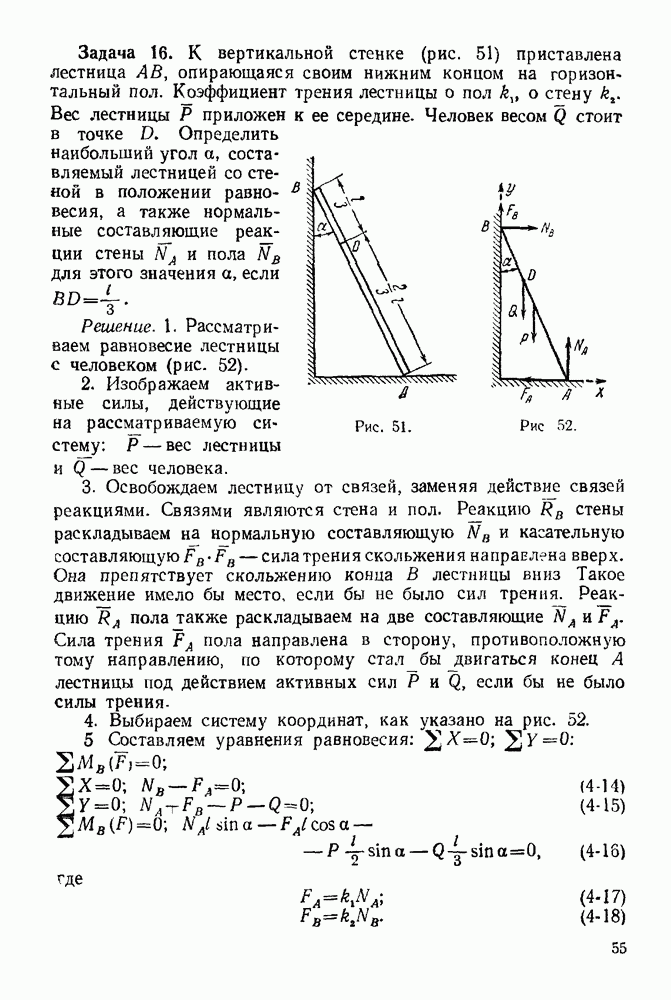
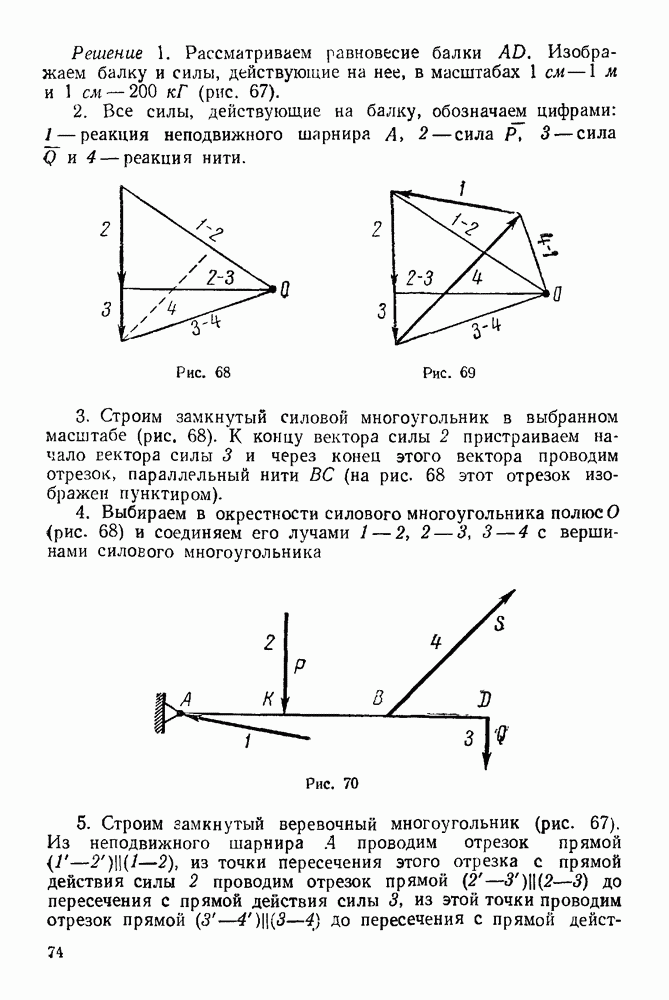
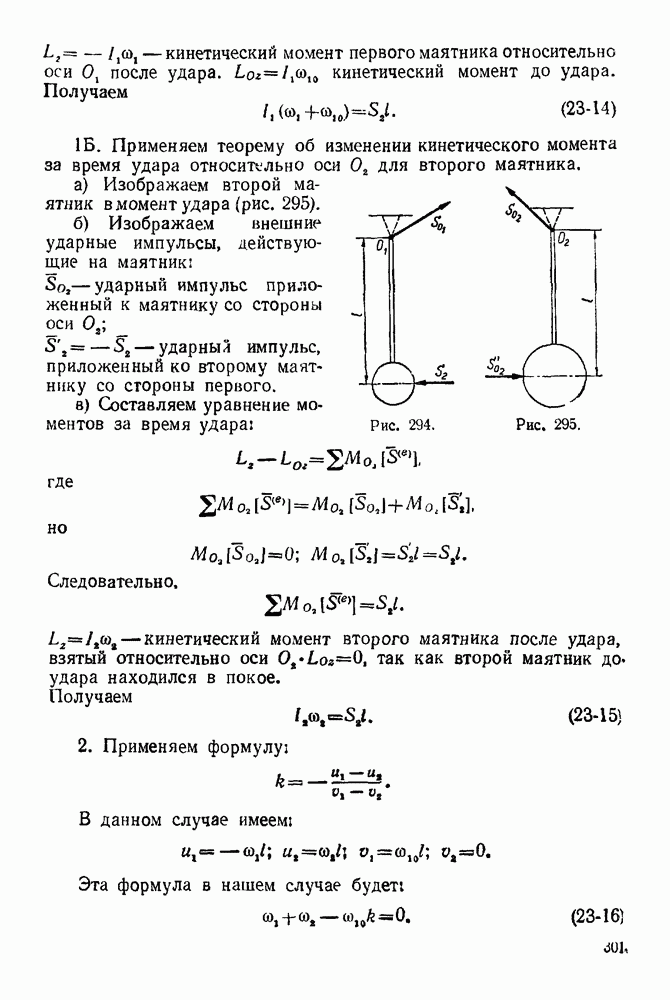
Решение. 1. Рассматриваем равновесие узла  (рис. 90).
(рис. 90).
2. На узел  действует активная сила
действует активная сила 
3. Освобождаем узел  от связей, заменяя действие связей реакциями. Связями являются стержни
от связей, заменяя действие связей реакциями. Связями являются стержни  и
и  Реакции стержней направлены по стержням. Направляем эти реакции от
Реакции стержней направлены по стержням. Направляем эти реакции от
узла, предполагая, что все стержни работают на растяжение. Будет ли это так, покажет результат решения задачи.
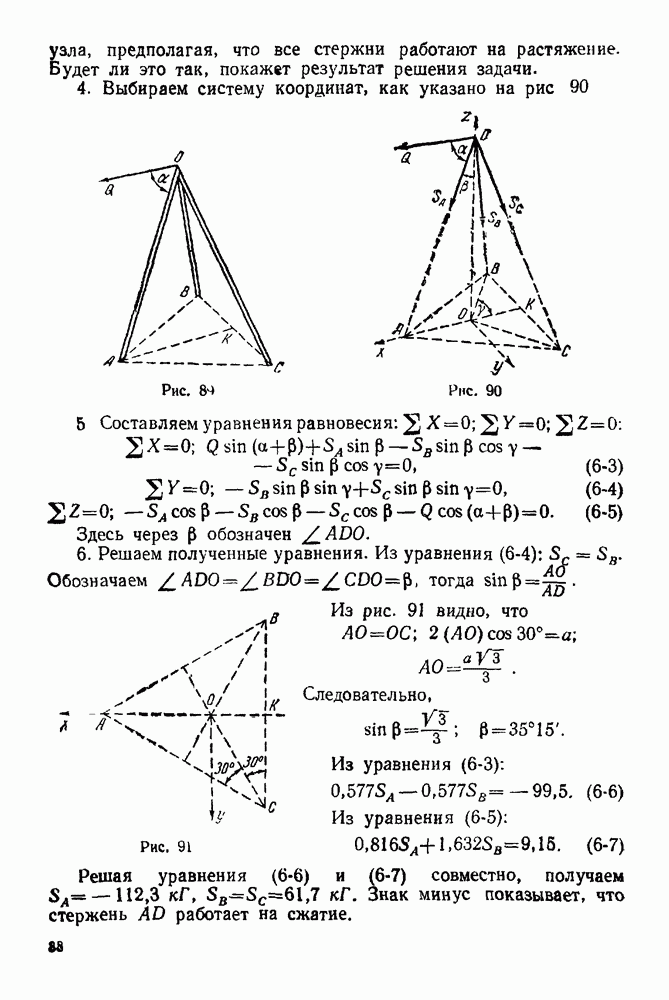
4. Выбираем систему координат, как указано на рис 90

Рис. 89

Рис. 90
5 Составляем уравнения равновесия:  —
—

 Здесь через
Здесь через  обозначен
обозначен 
6. Решаем полученные уравнения. Из уравнения  :
:  Обозначаем
Обозначаем  тогда
тогда 
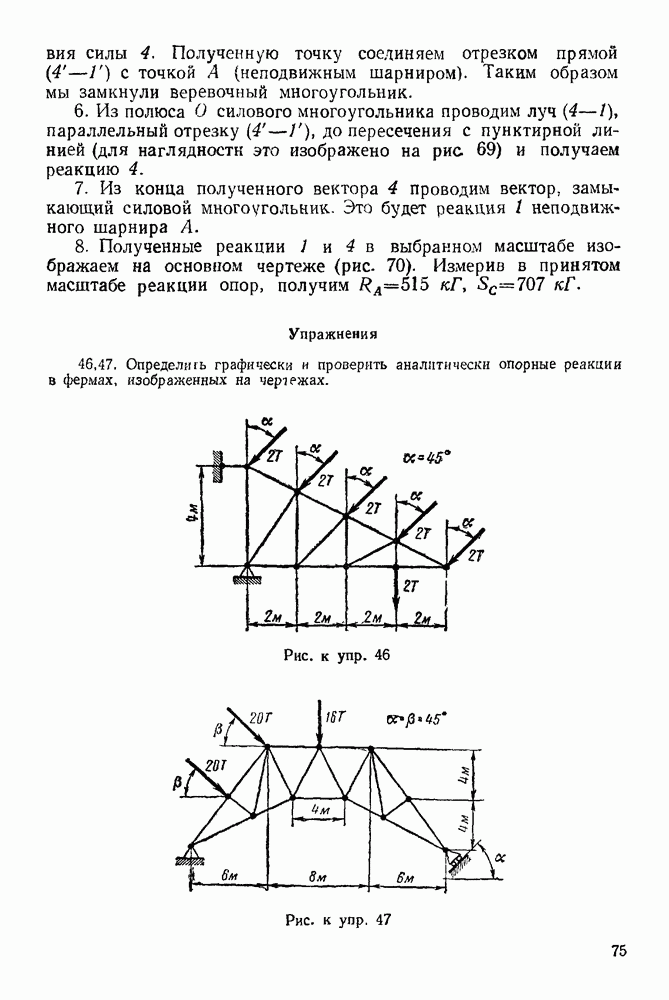
Из рис. 91 видно, что

Следовательно,

Из уравнения (6-3):

Из уравнения (6-5):


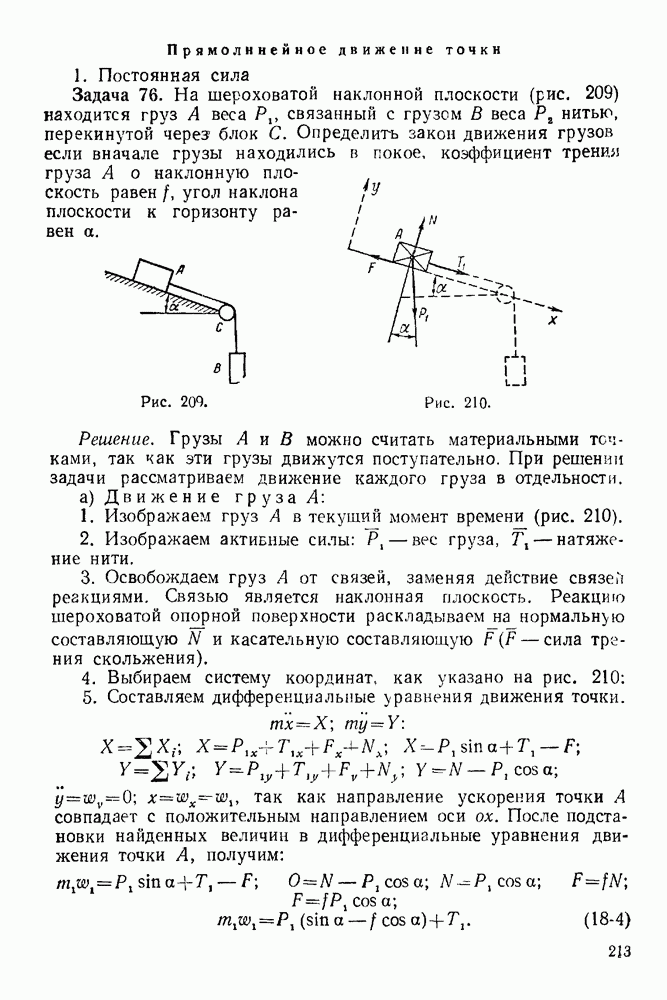
Рис. 91
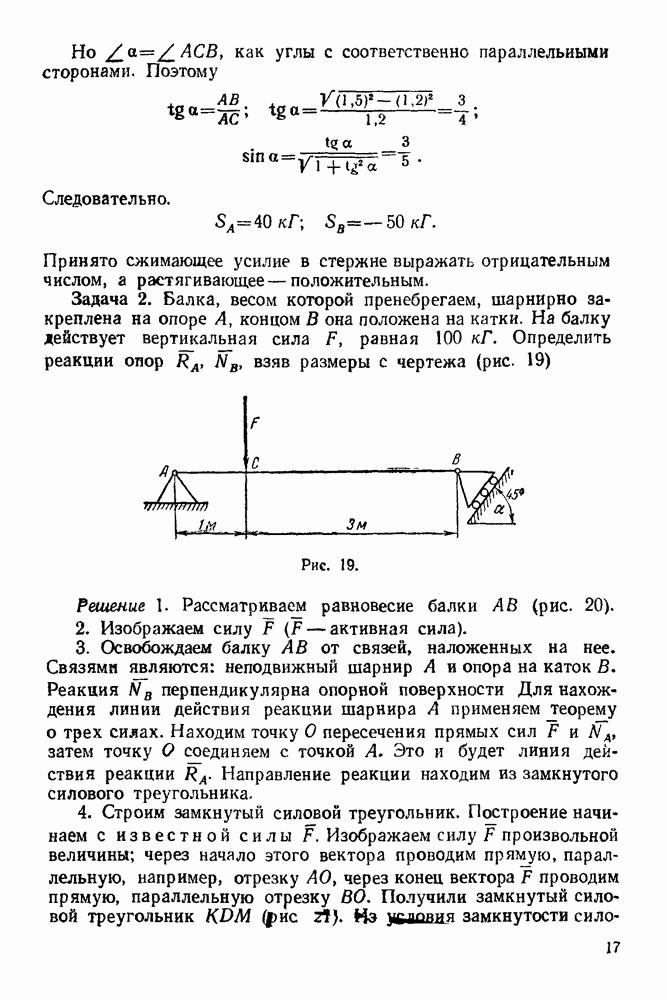
Решая уравнения  и
и  совместно, получаем —
совместно, получаем —  Знак минус показывает, что стержень
Знак минус показывает, что стержень  работает на сжатие.
работает на сжатие.
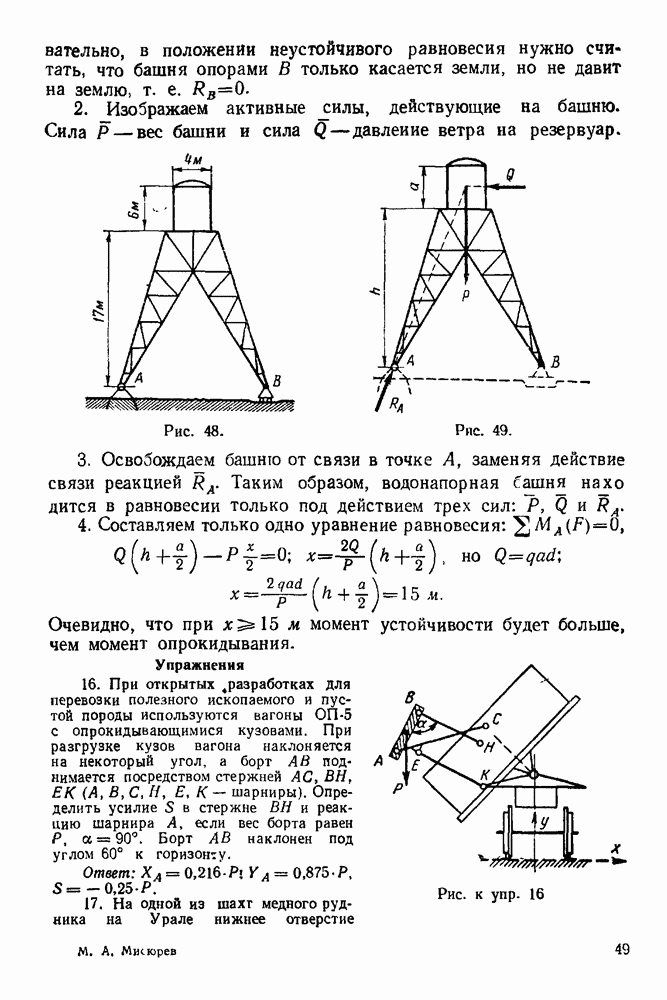
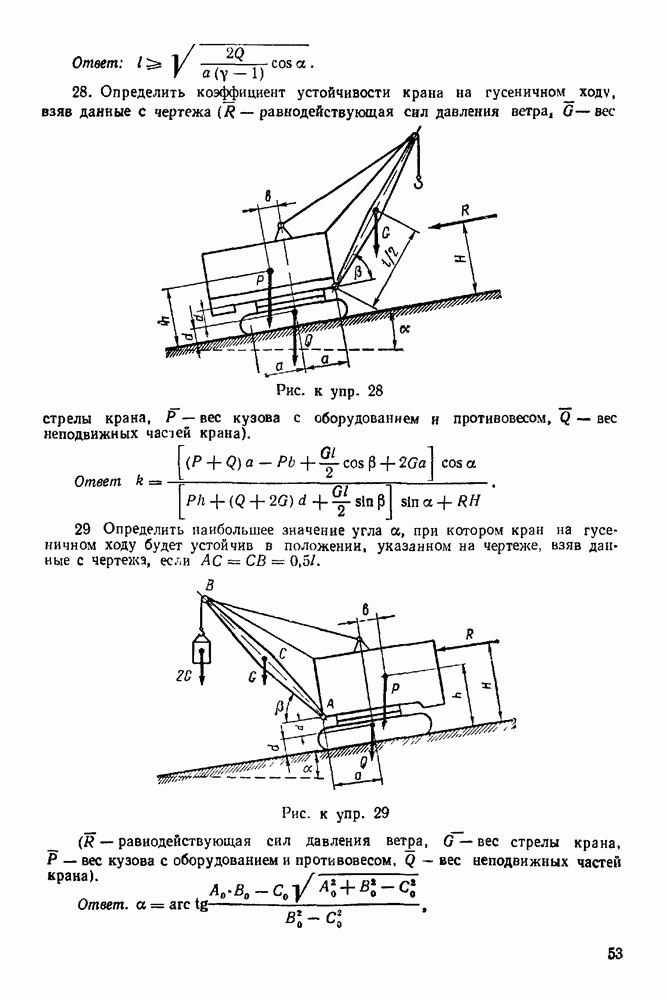
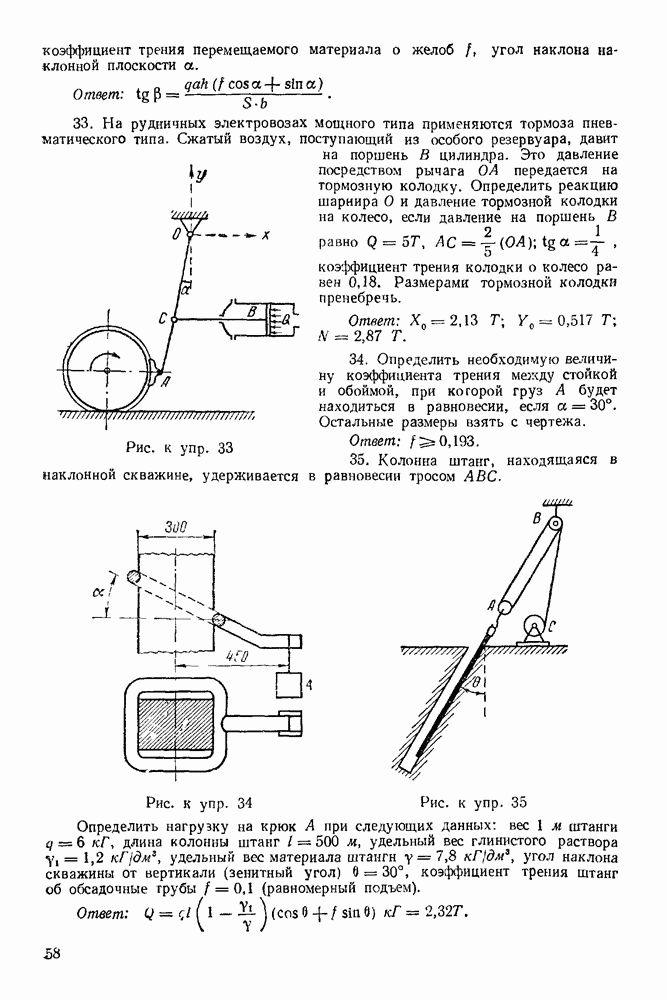
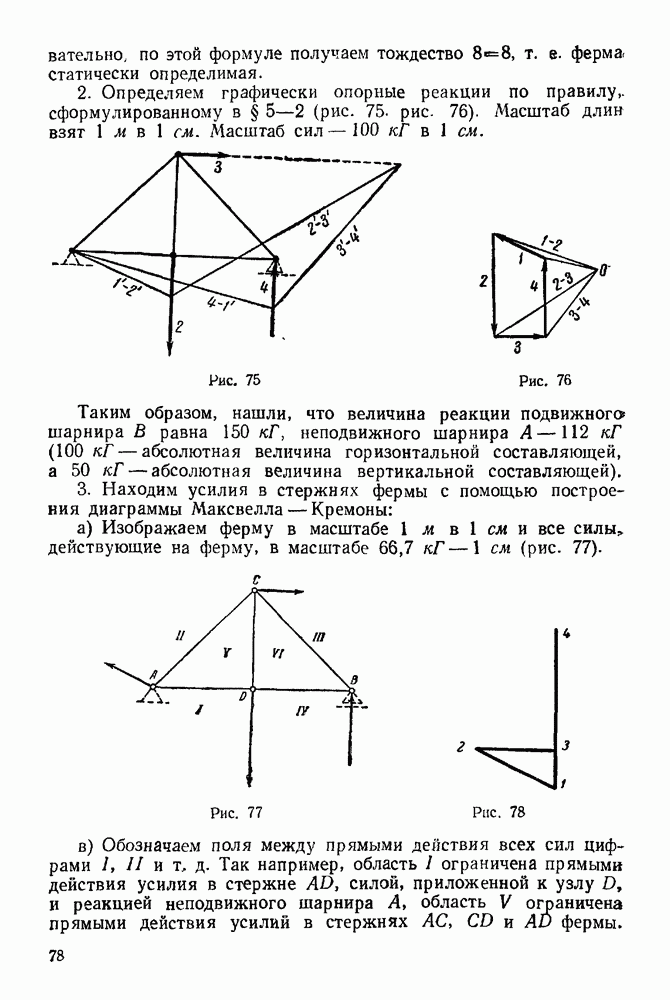
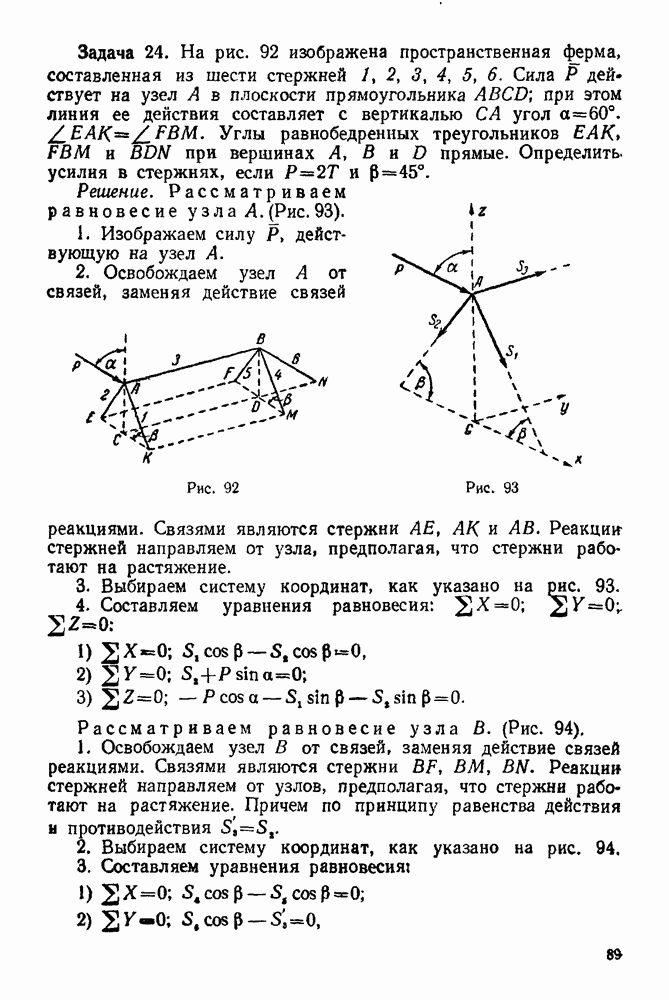
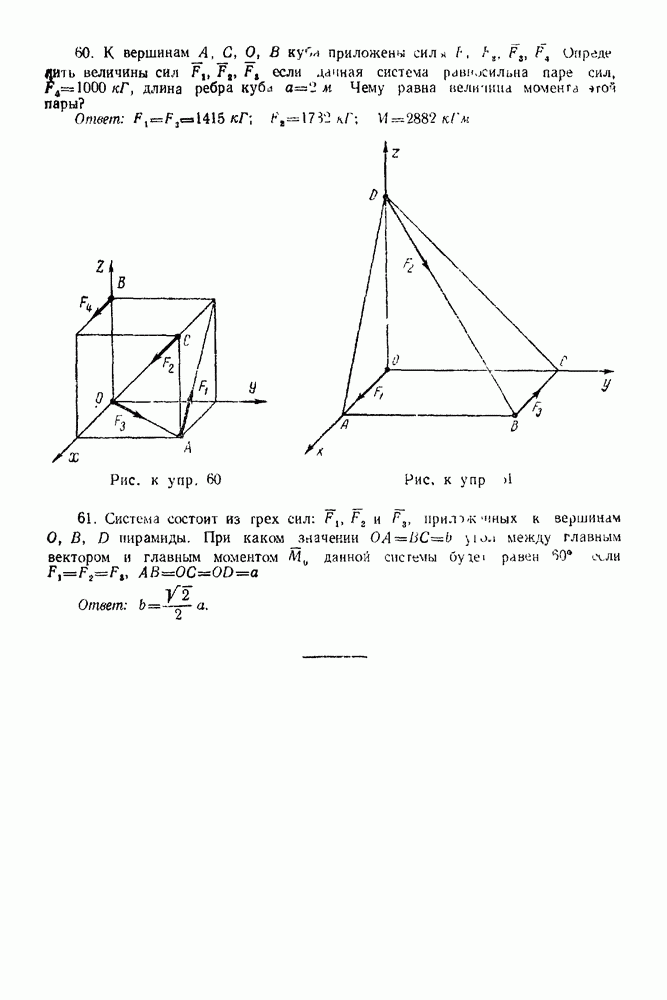
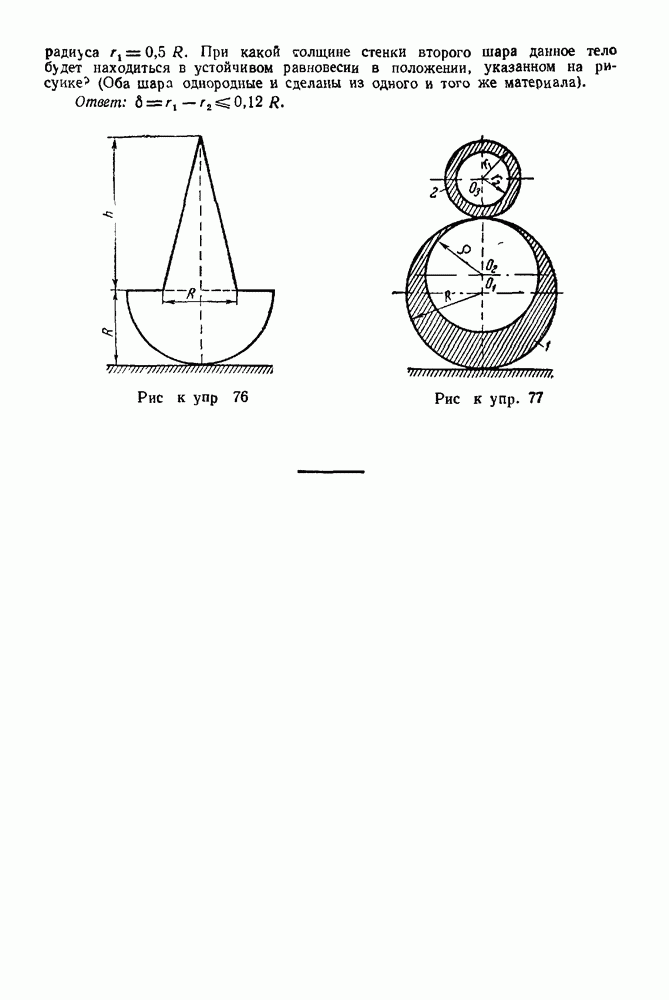
Задача 24. На рис. 92 изображена пространственная ферма, составленная из шести стержней  Сила
Сила  действует на узел А в плоскости прямоугольника
действует на узел А в плоскости прямоугольника  при этом линия ее действия составляет с вертикалью
при этом линия ее действия составляет с вертикалью  угол
угол 
Углы равнобедренных треугольников  и
и  при вершинах
при вершинах  прямые. Определить, усилия в стержнях, если
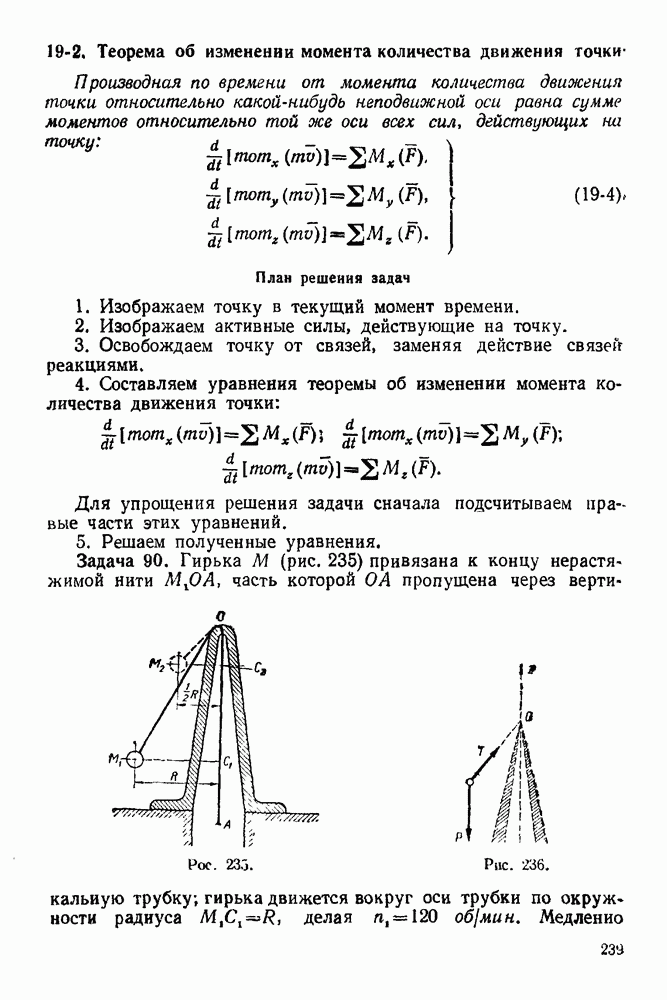
прямые. Определить, усилия в стержнях, если 
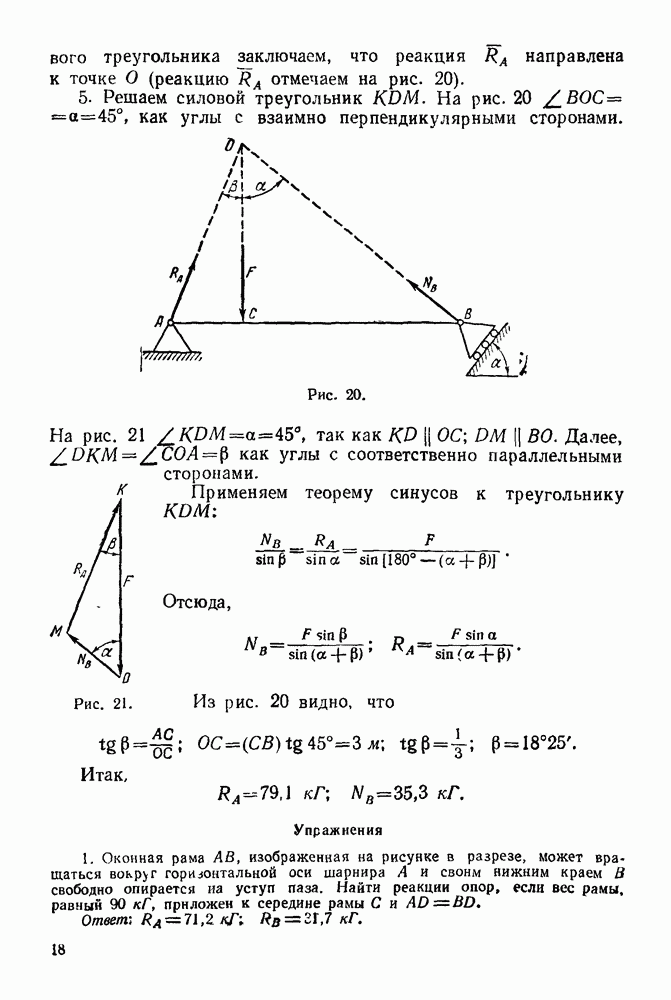
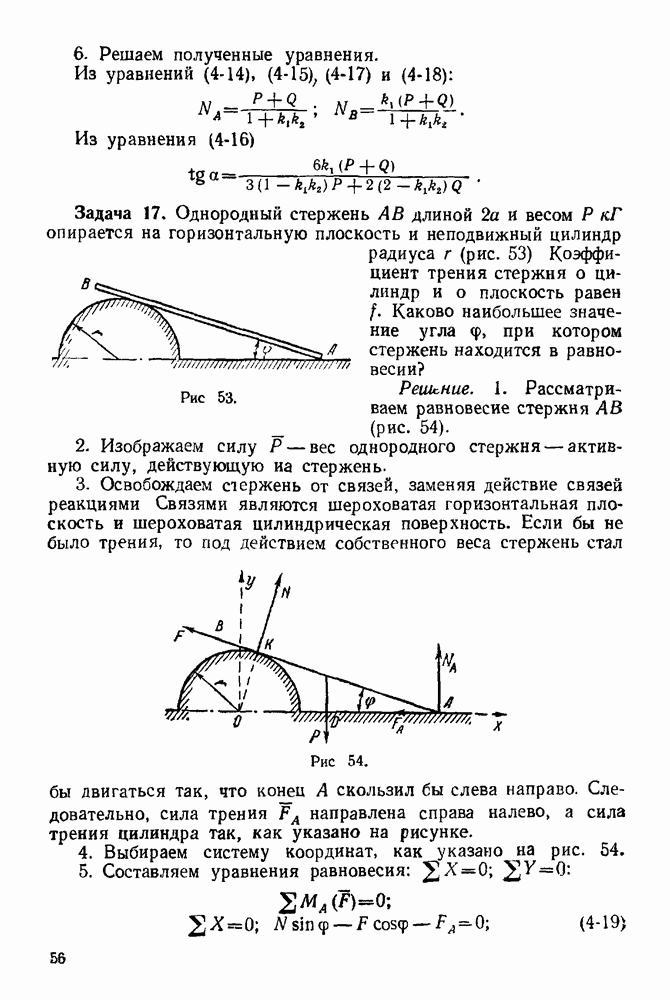
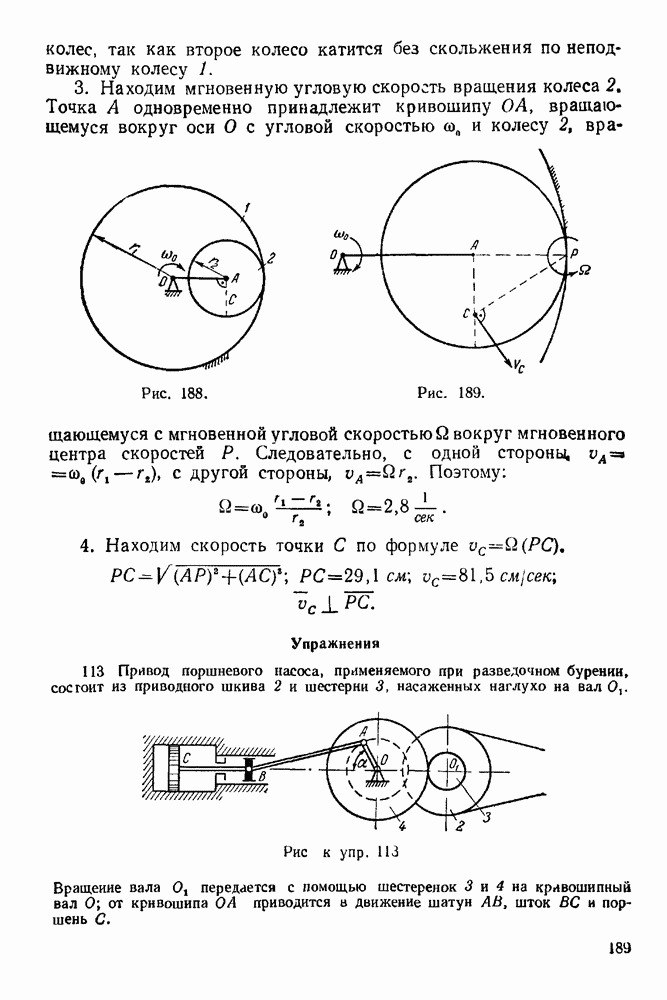
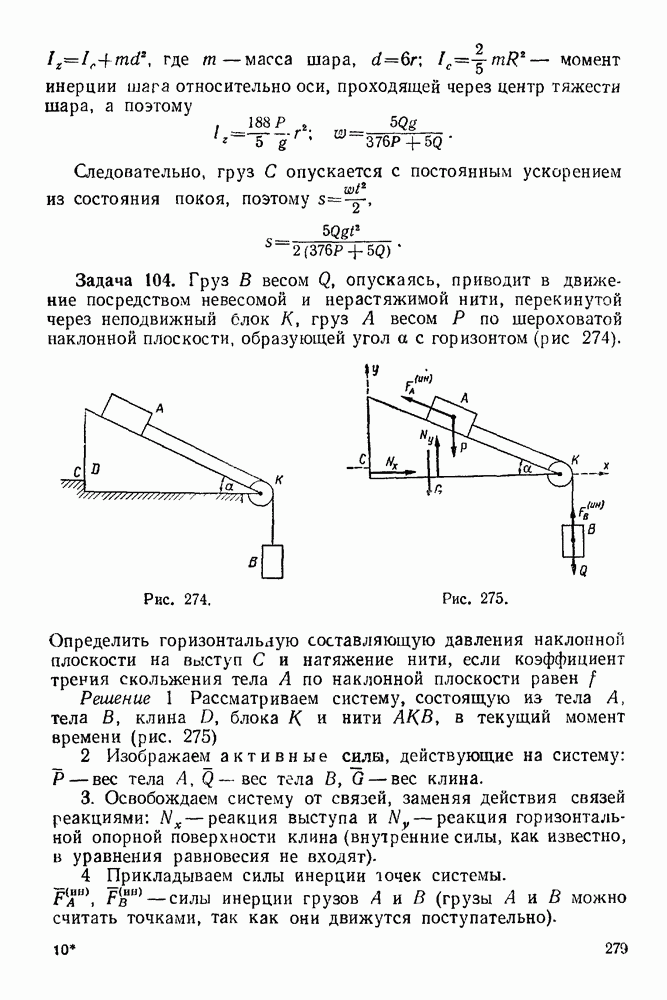
Решение. Рассматриваем равновесие у зла  (Рис. 93).
(Рис. 93).
1. Изображаем силу  действующую на узел
действующую на узел 
2. Освобождаем узел  от связей, заменяя действие связей реакциями.
от связей, заменяя действие связей реакциями.

Рис. 92

Рис. 93
Связями являются стержни  и
и  Реакции стержней направляем от узла, предполагая, что стержни работают на растяжение.
Реакции стержней направляем от узла, предполагая, что стержни работают на растяжение.
3. Выбираем систему координат, как указано на рис. 93.
4. Составляем уравнения равновесия: 

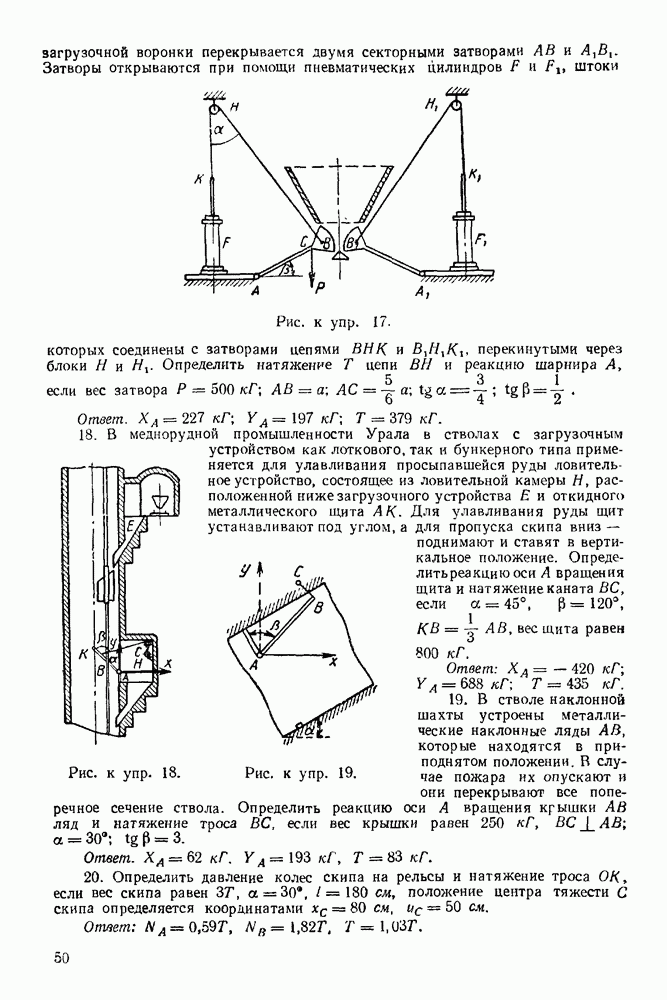
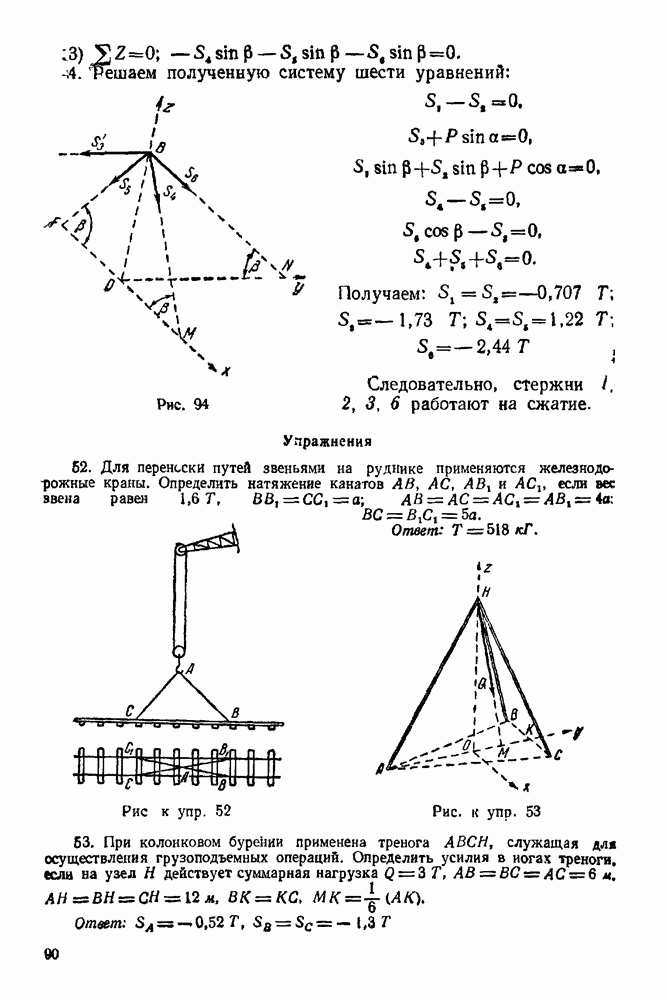
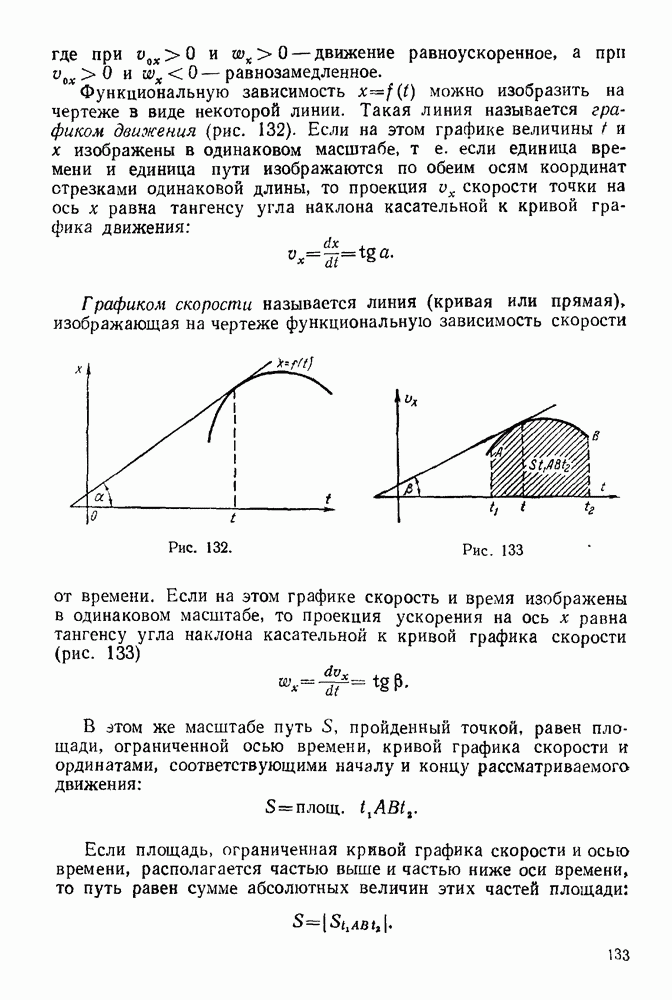
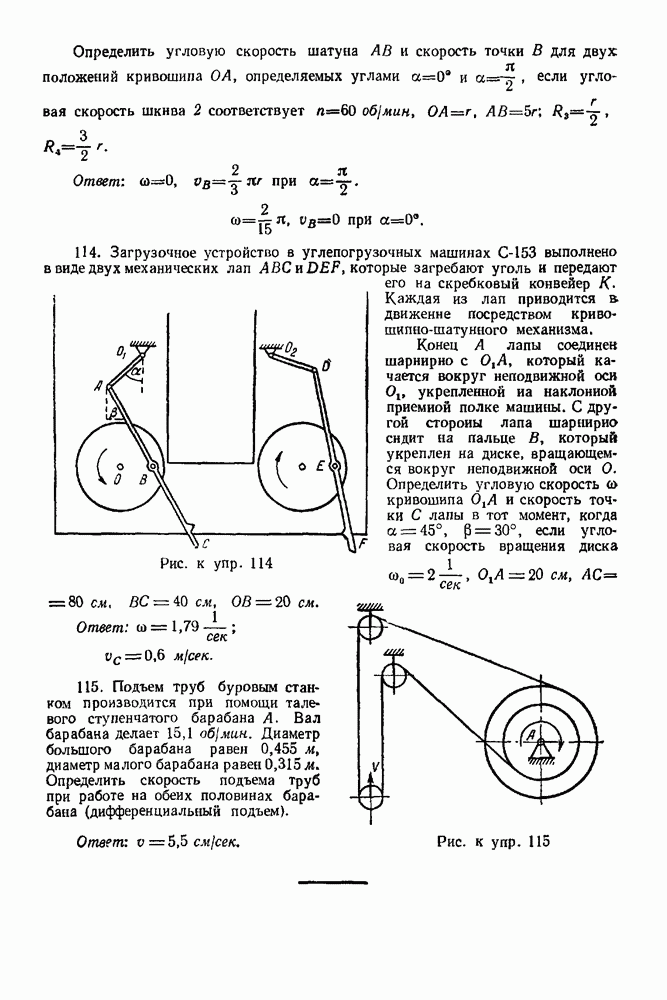
Рассматриваем равновесие узла В. (Рис. 94).
1. Освобождаем узел В от связей, заменяя действие связей реакциями. Связями являются стержни  Реакции стержней направляем от узлов, предполагая, что стержни работают на растяжение. Причем по принципу равенства действия и противодействия
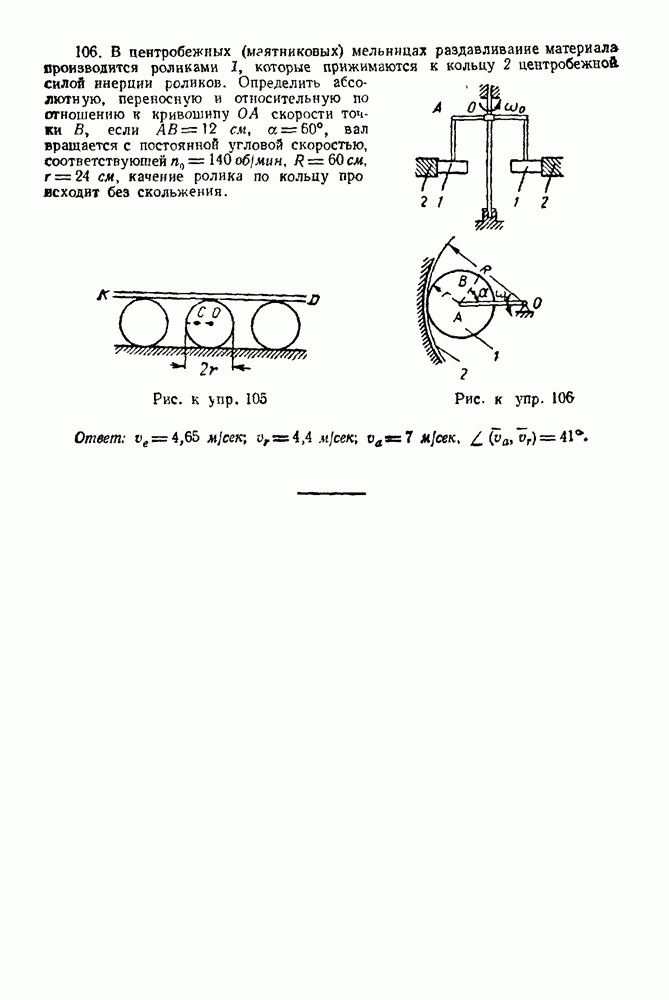
Реакции стержней направляем от узлов, предполагая, что стержни работают на растяжение. Причем по принципу равенства действия и противодействия
2. Выбираем систему координат, как указано на рис. 94.
3. Составляем уравнения равновесия:


4. Решаем полученную систему шести уравнений:

Получаем: 


Рис. 94
Следовательно, стержни I, 2, 3, 6 работают на сжатие.
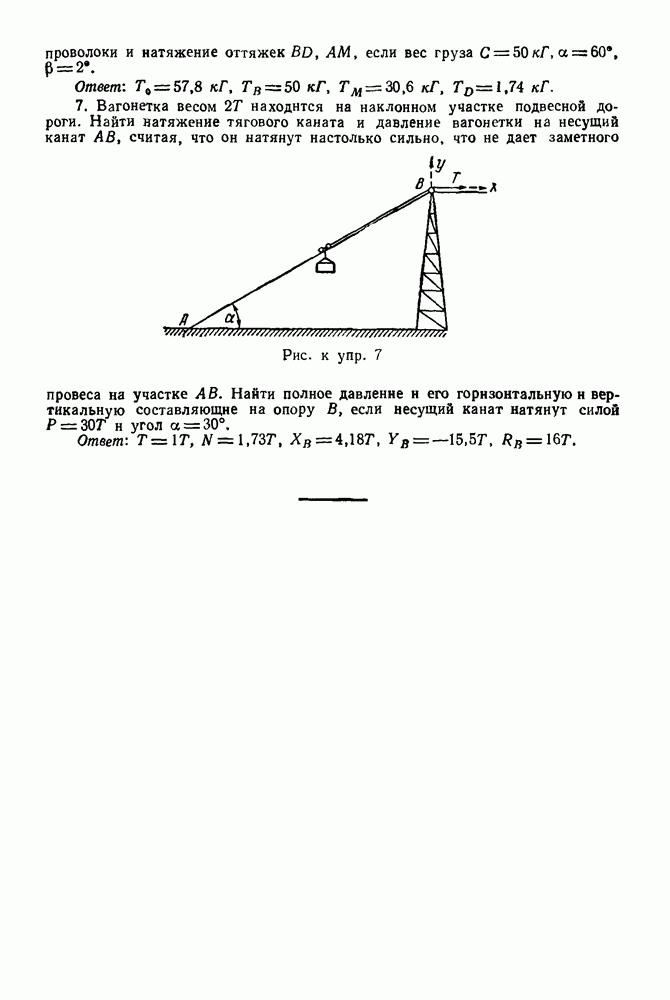
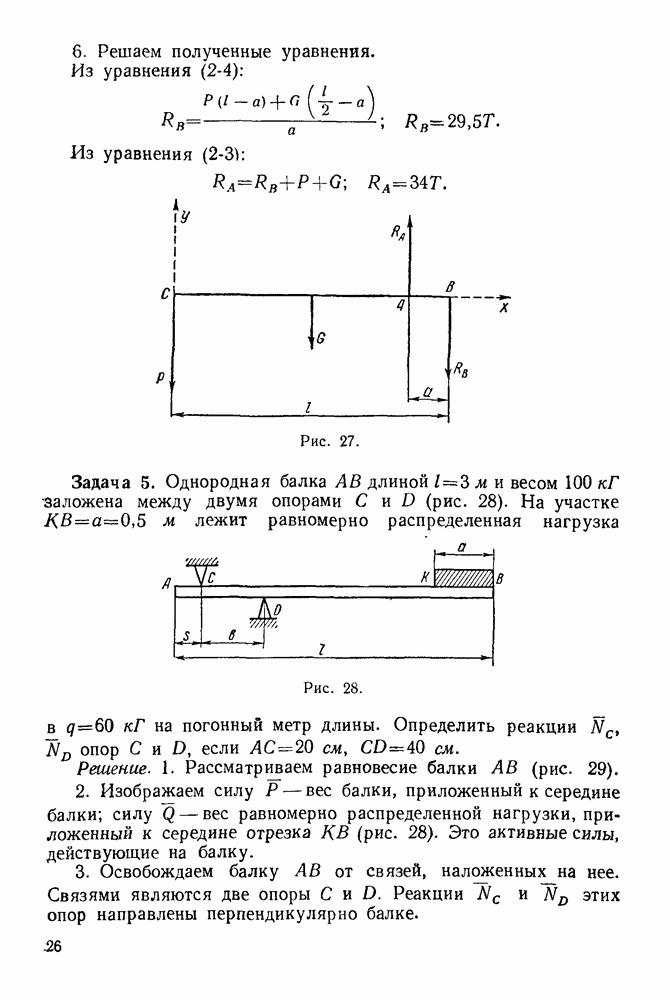
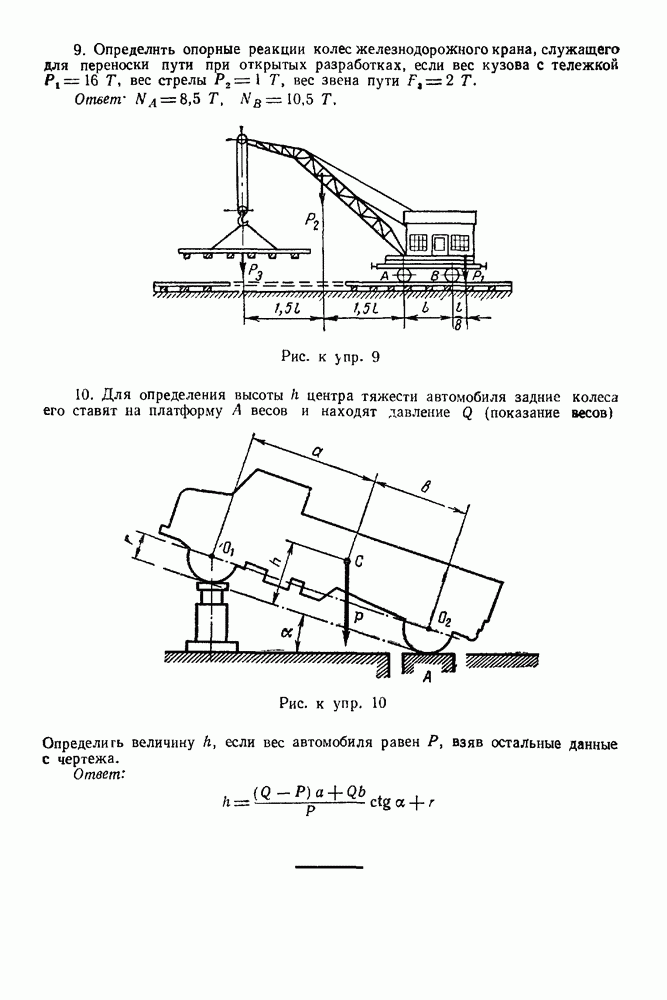
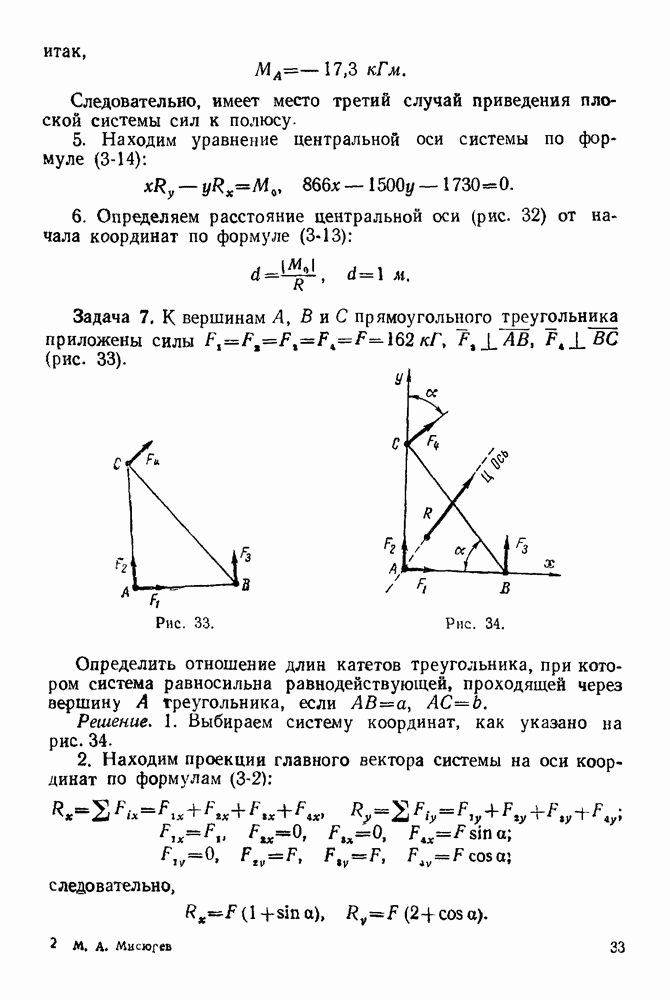
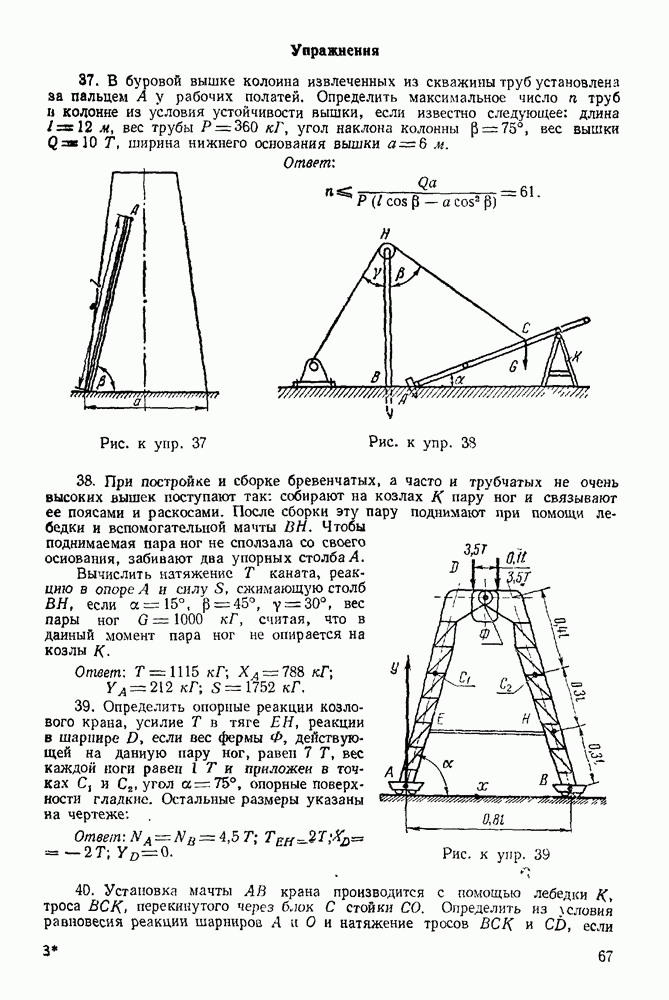
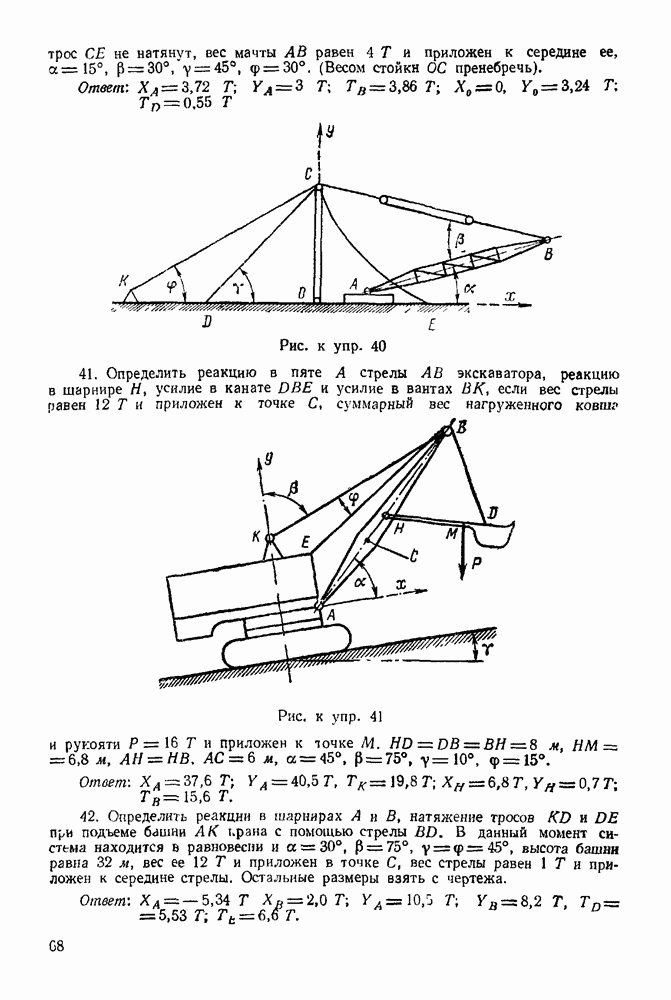
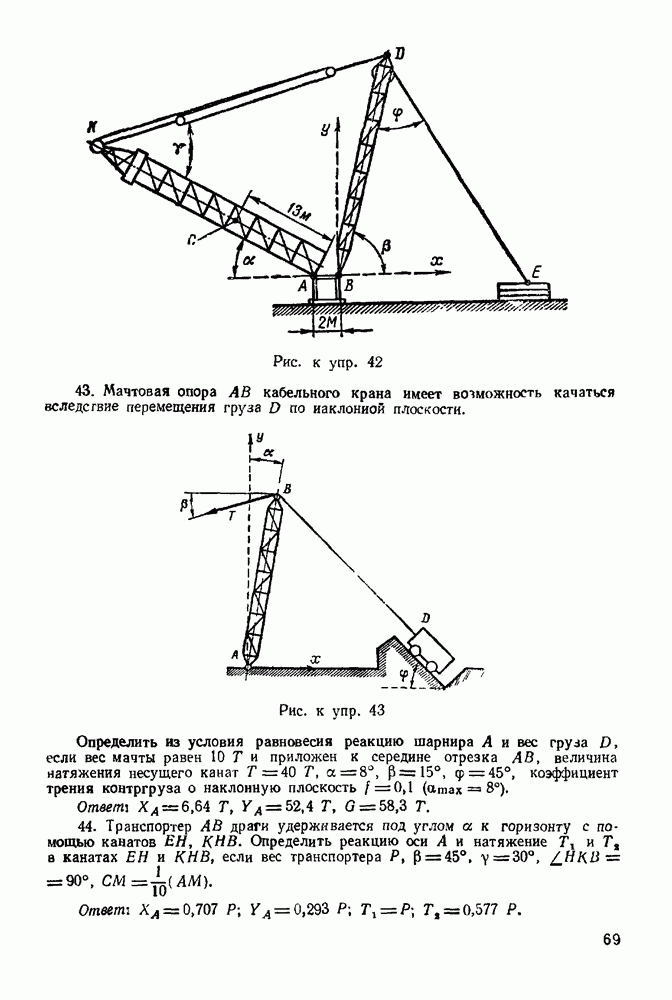
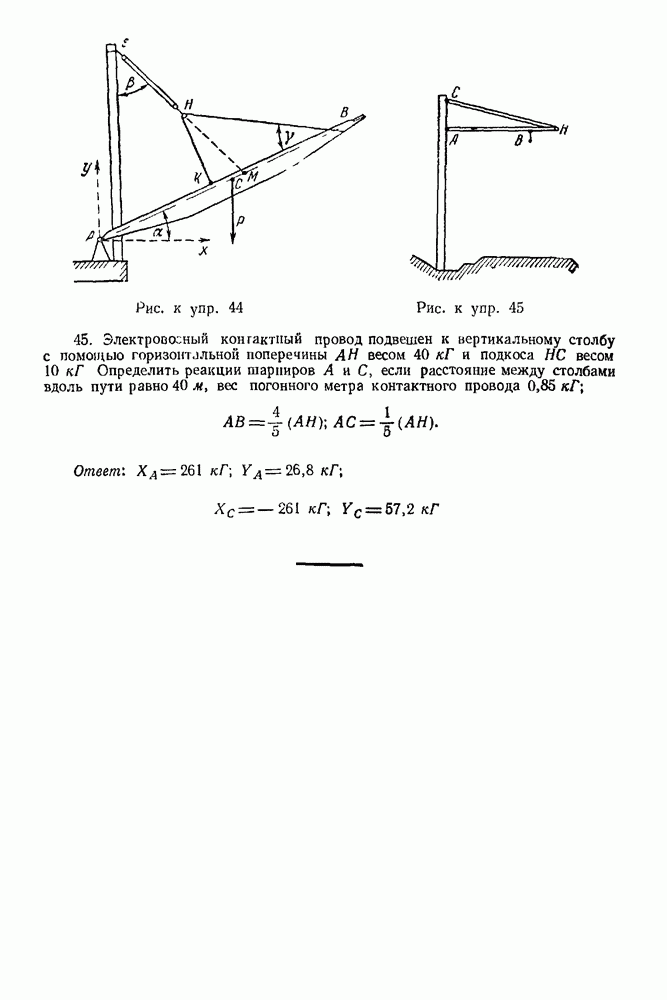
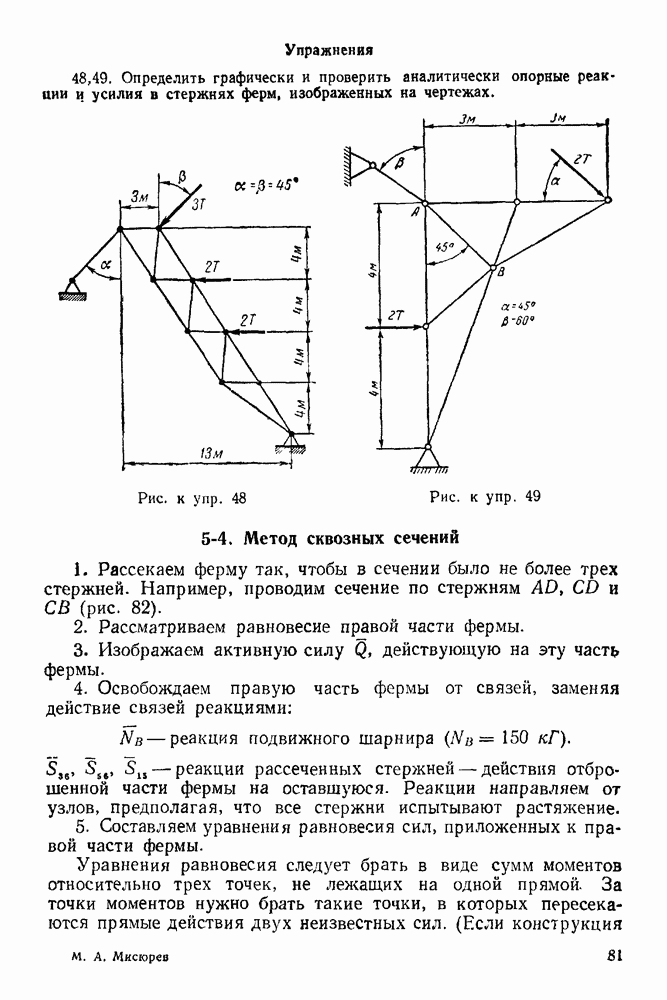
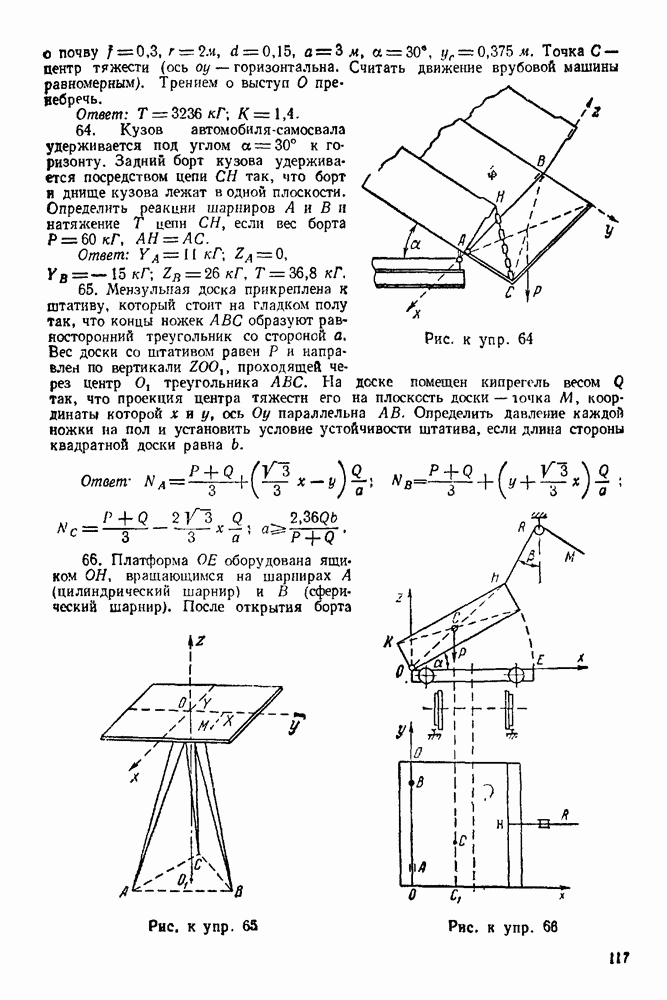
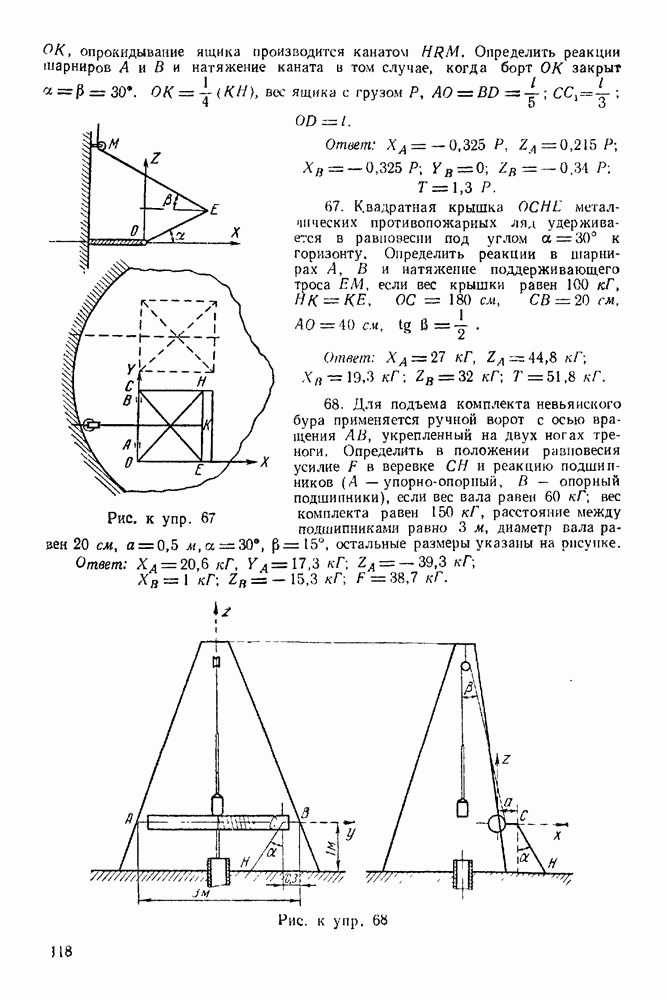
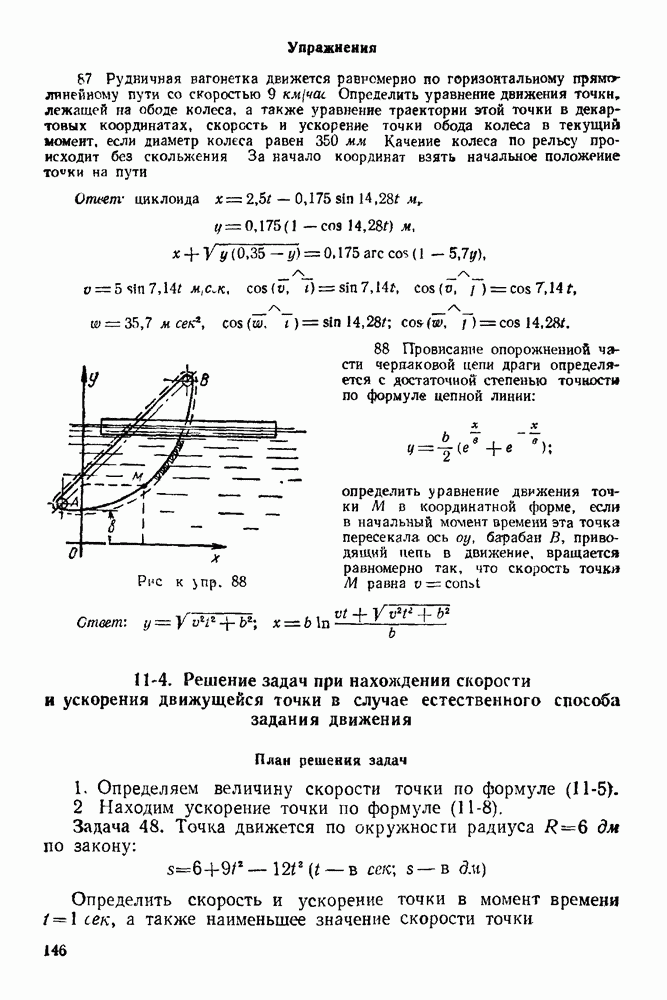
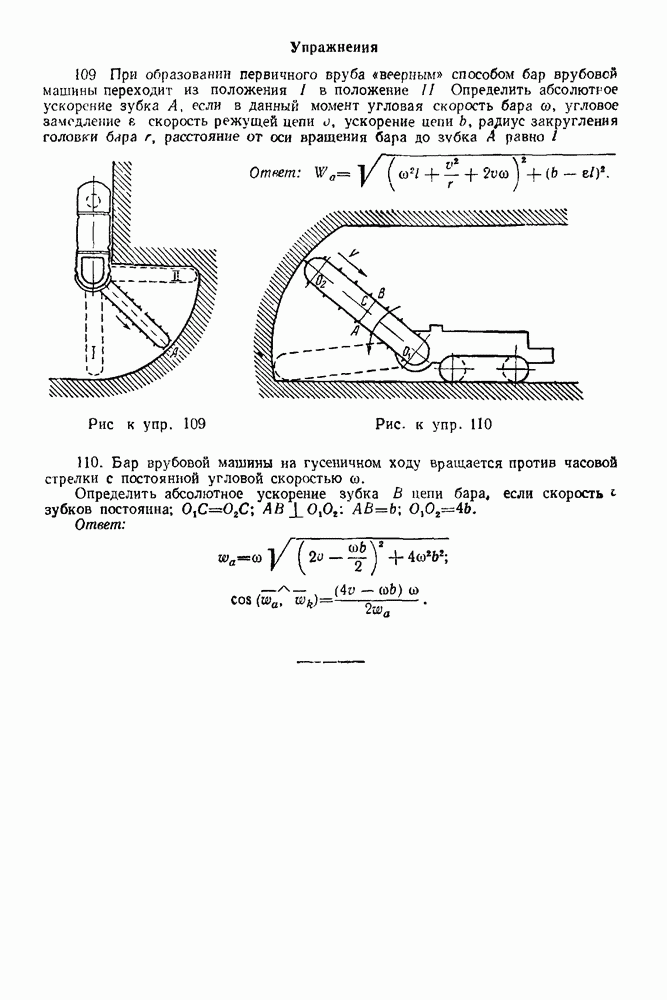
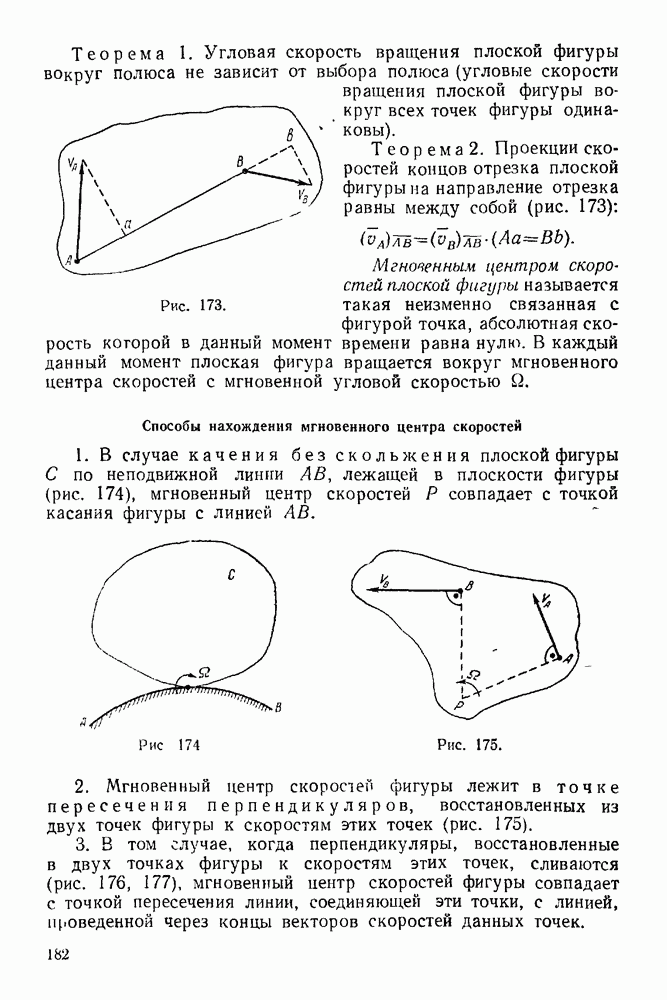
Упражнения
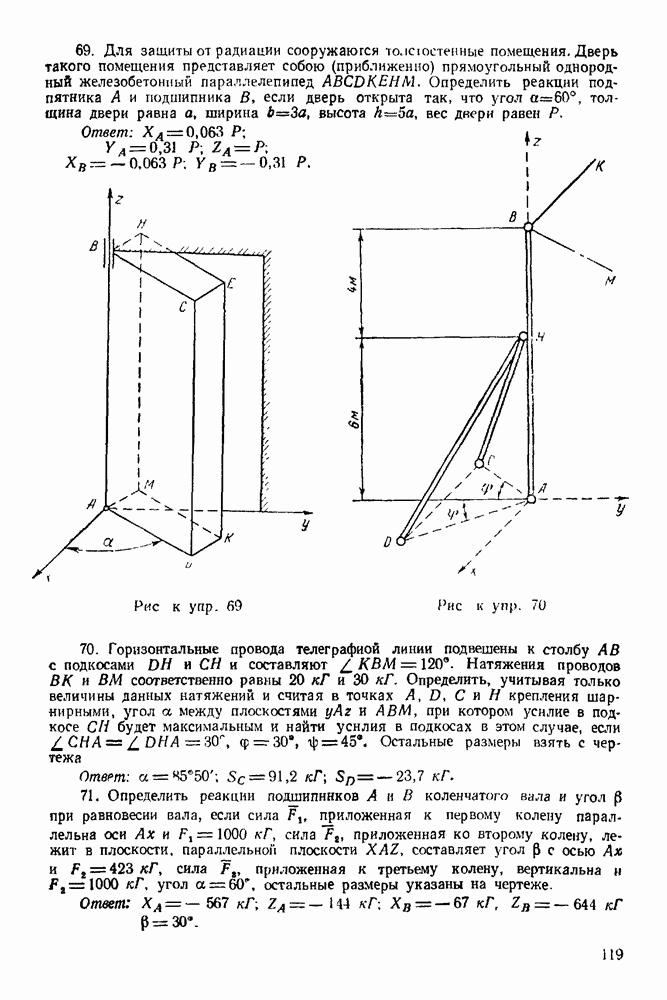
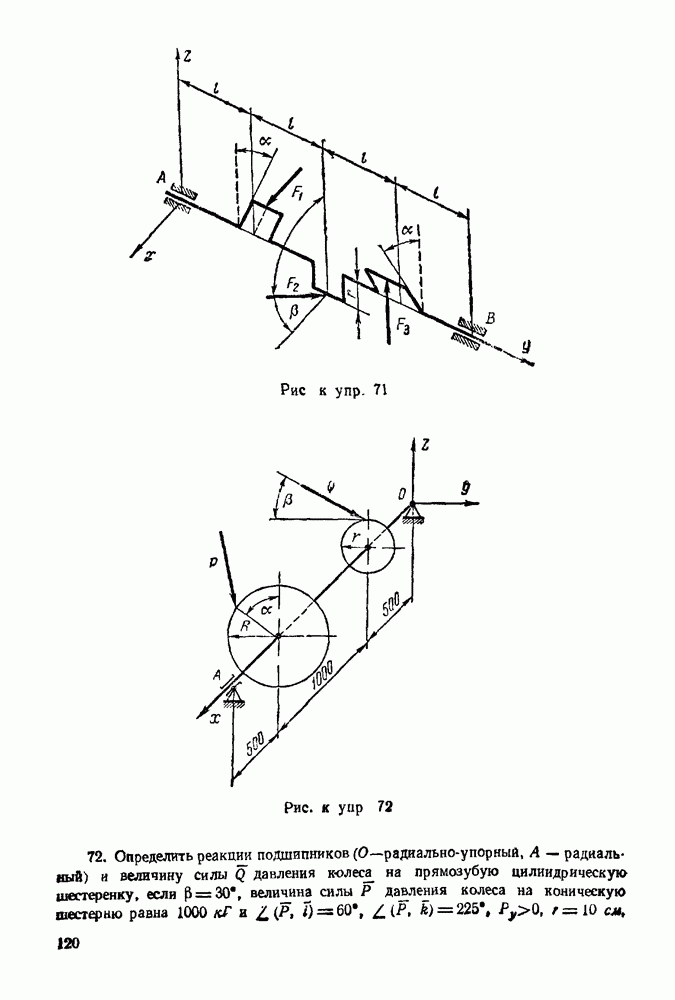
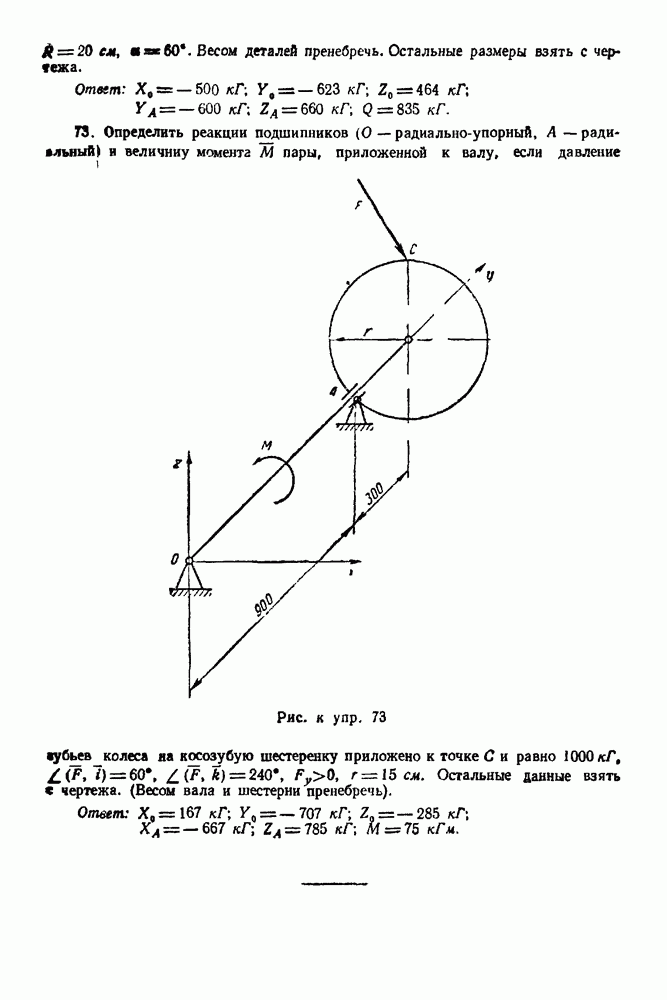
(см. скан)
(см. скан)
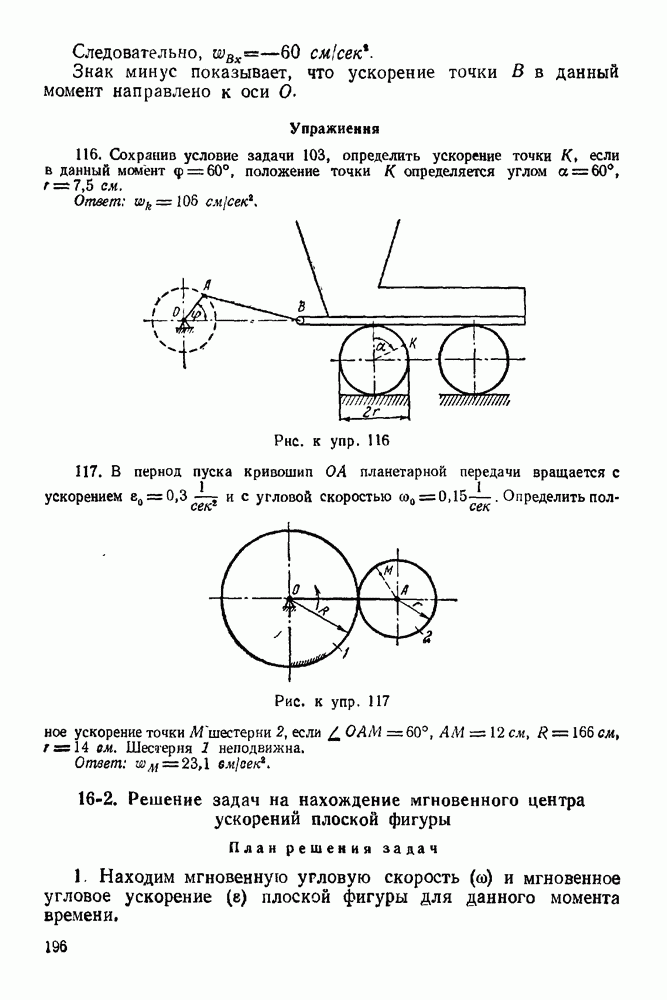
| << Предыдущий параграф | Следующий параграф >> |
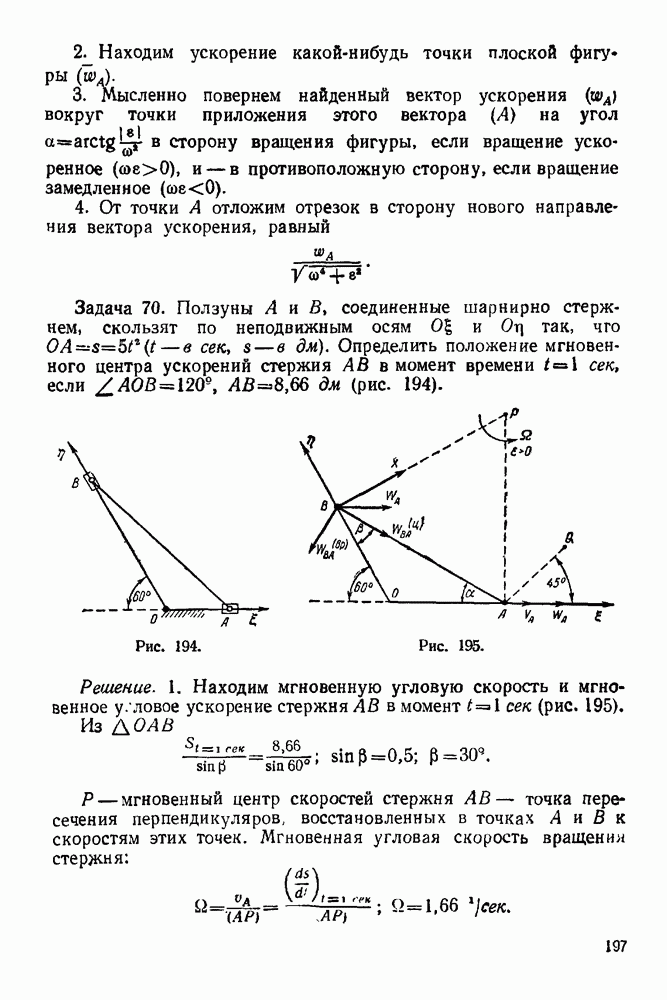
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
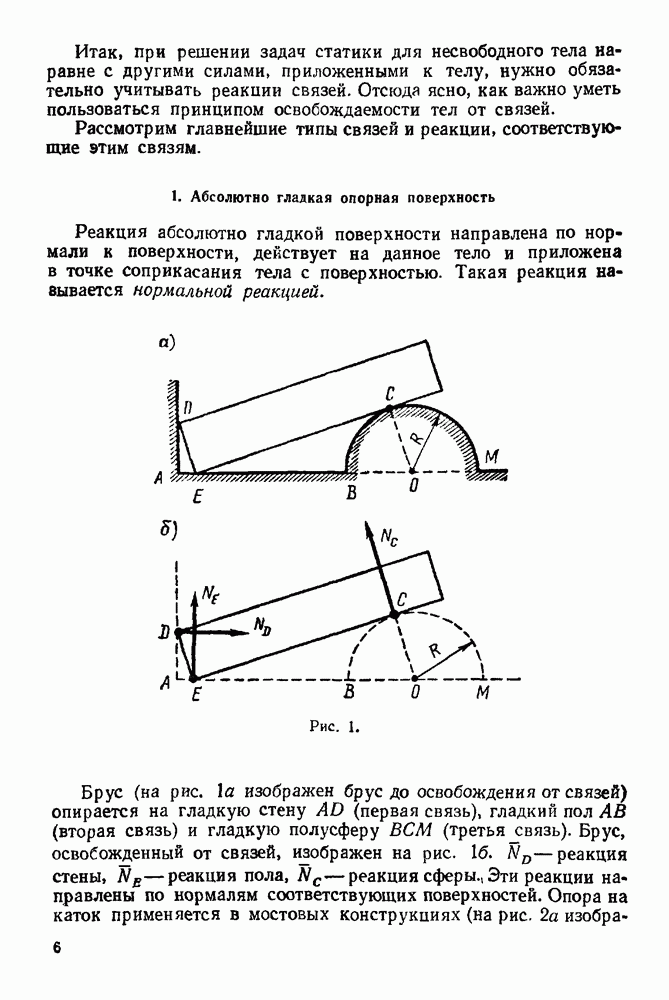
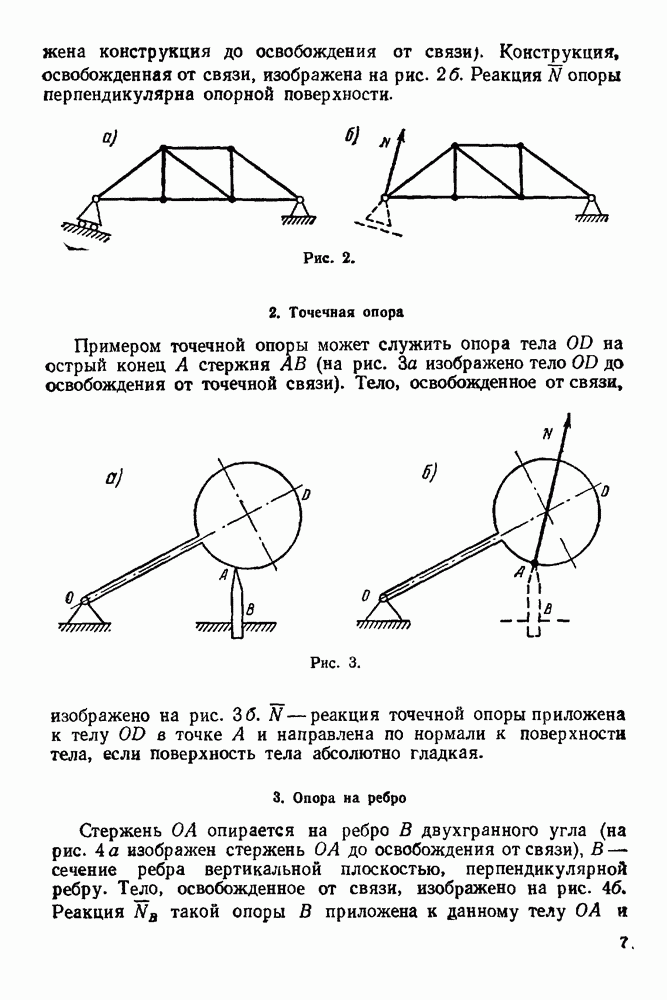
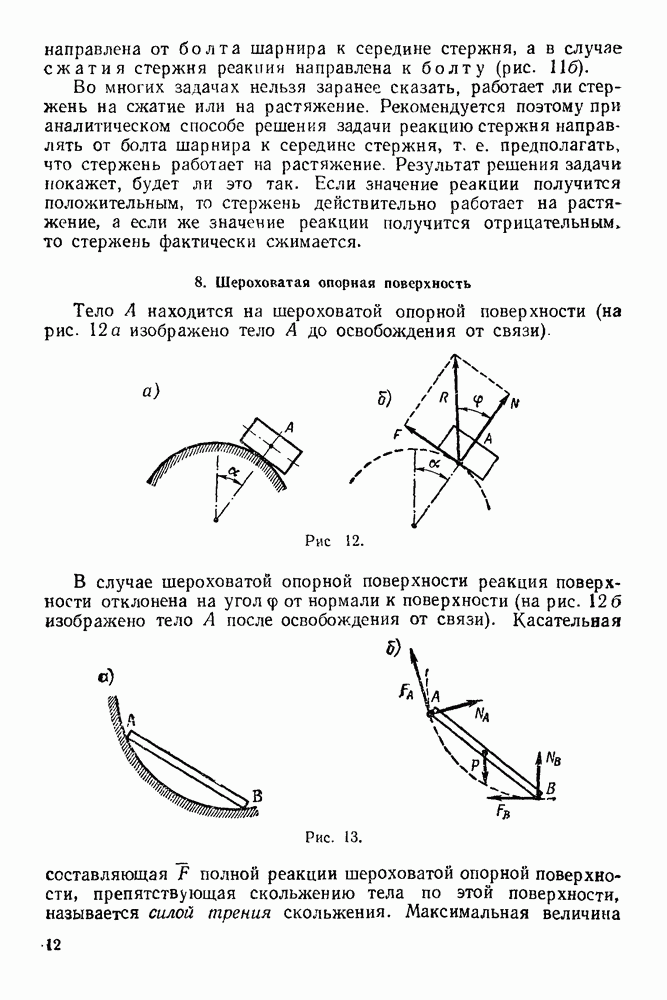
- 1. Абсолютно гладкая опорная поверхность
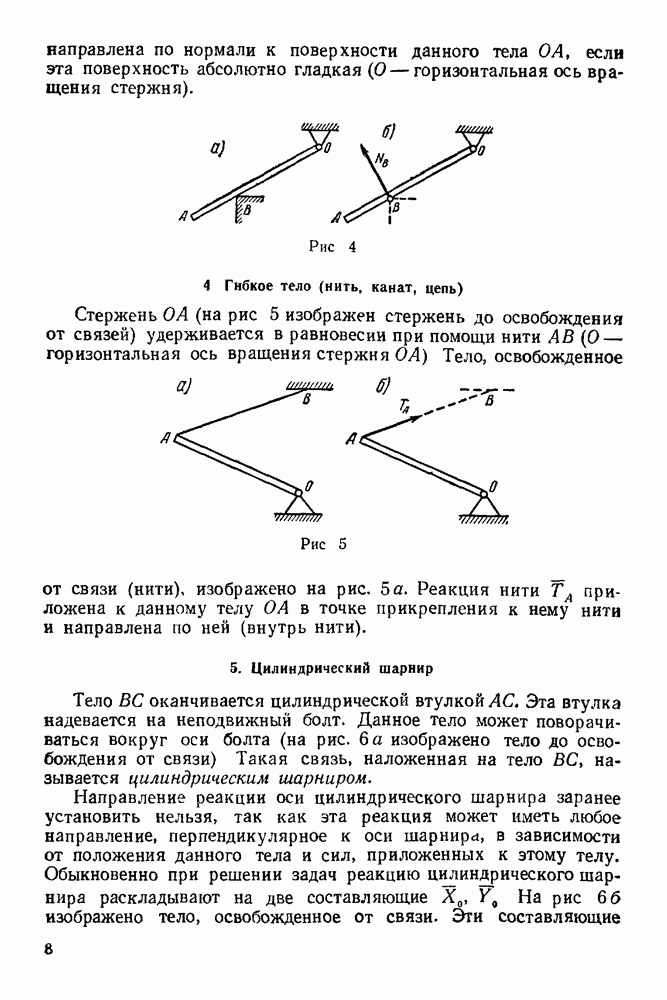
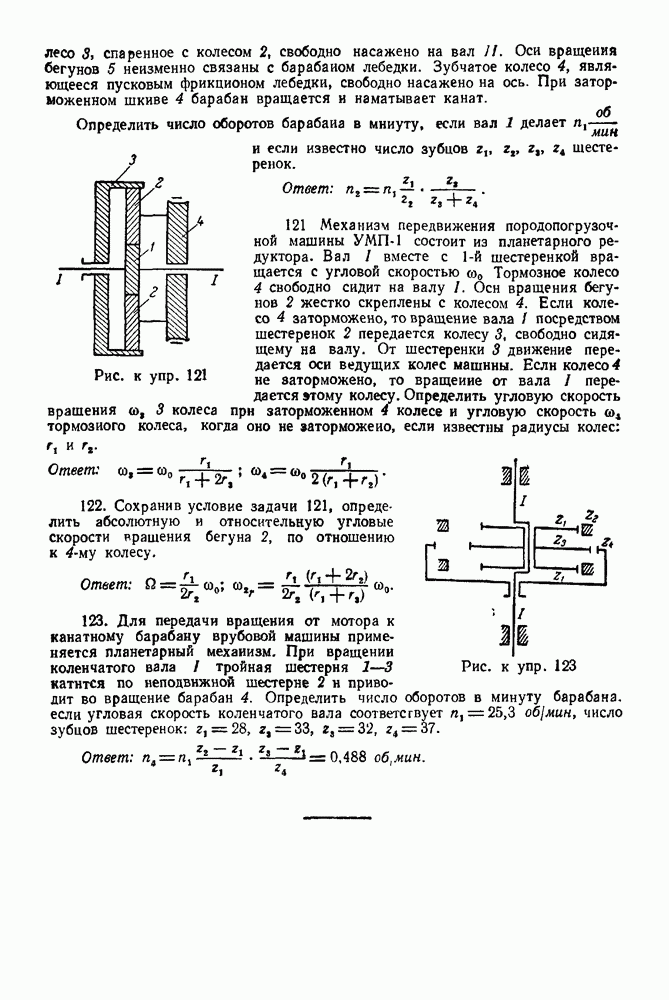
- 2. Точечная опора
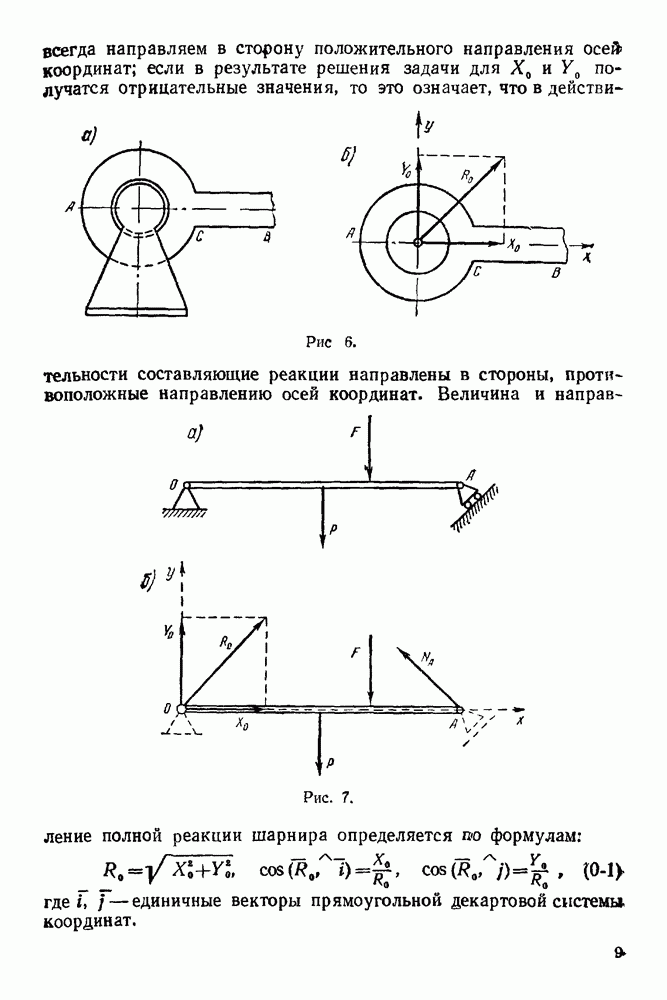
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
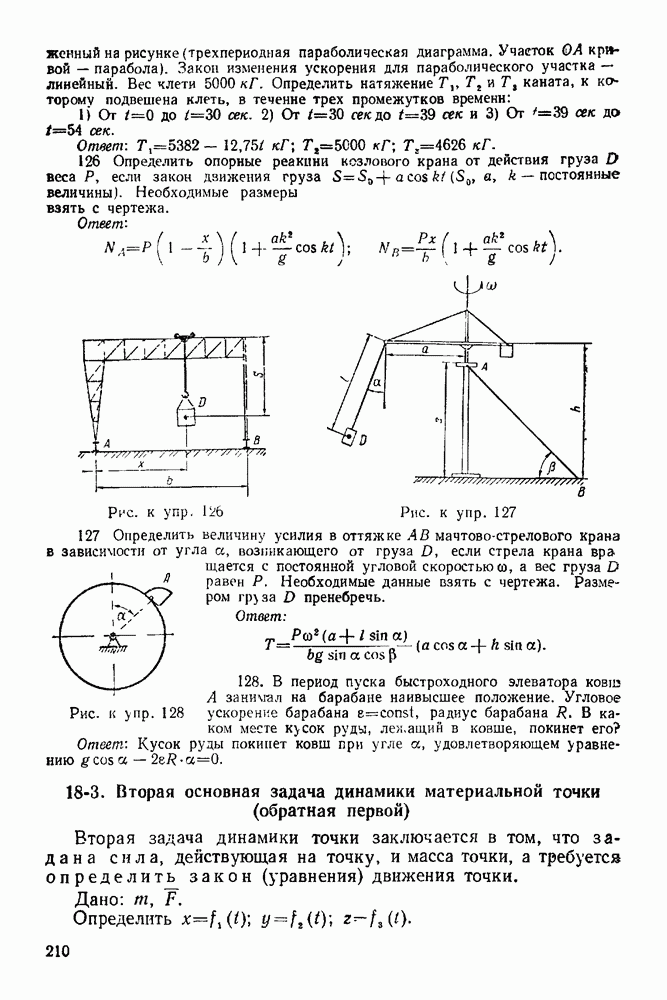
- 6. Сферический шарнир
- 7. Стержневая опора
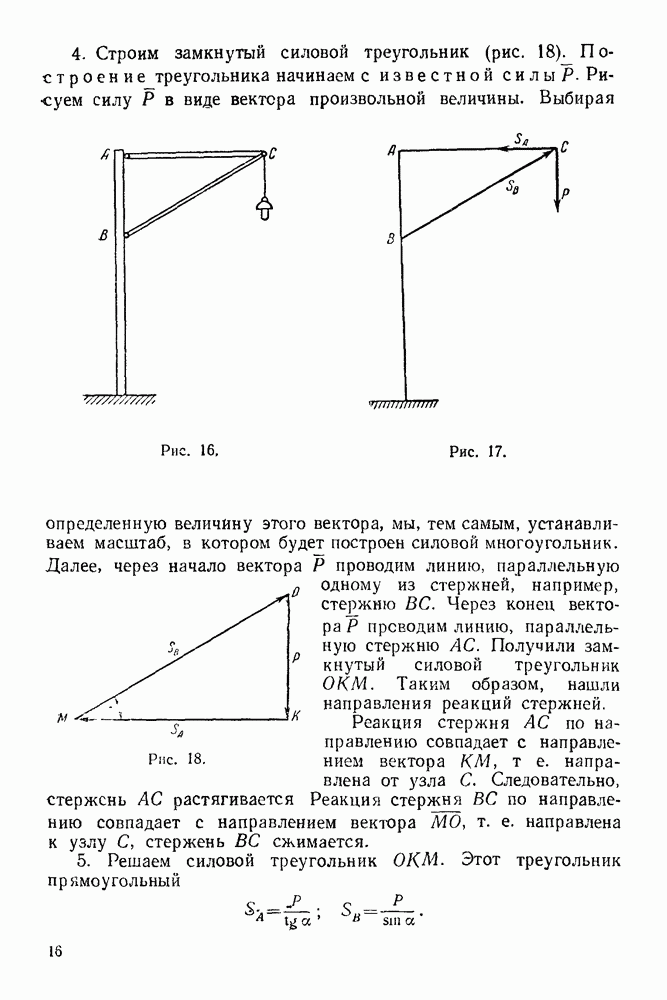
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
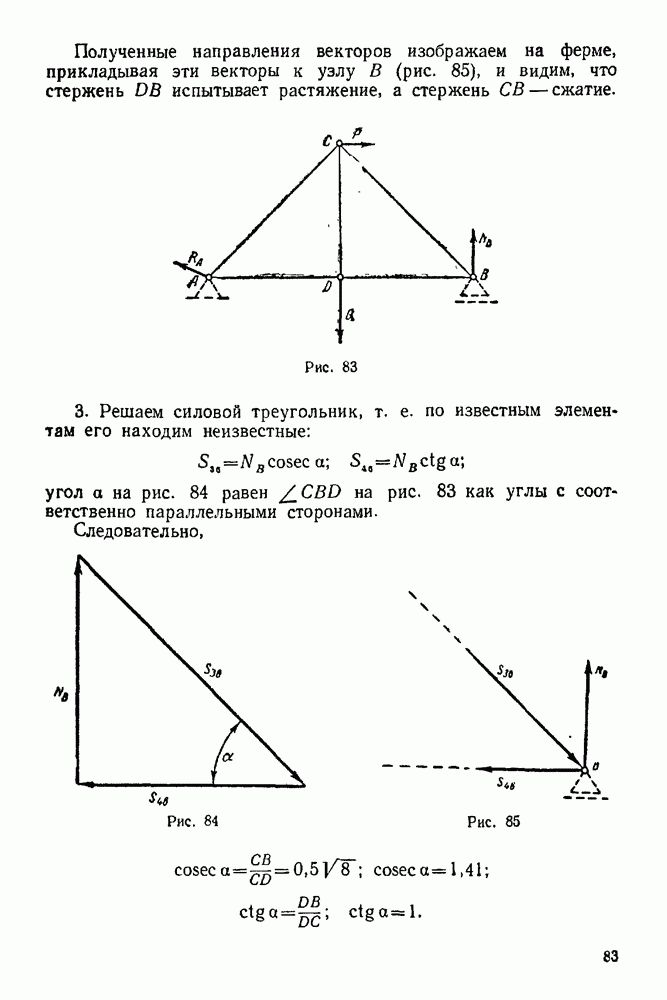
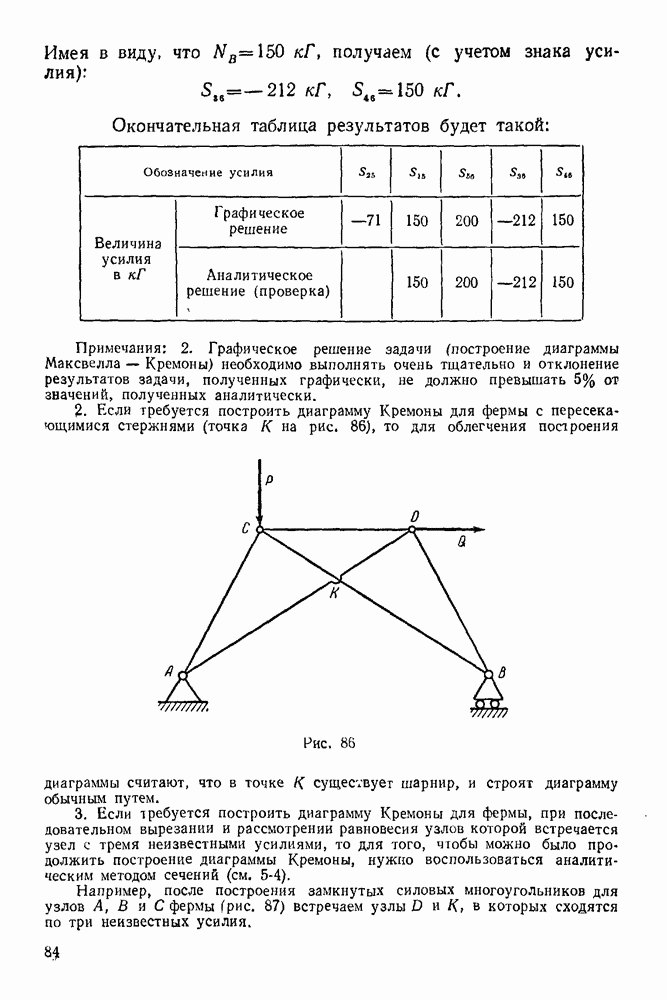
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
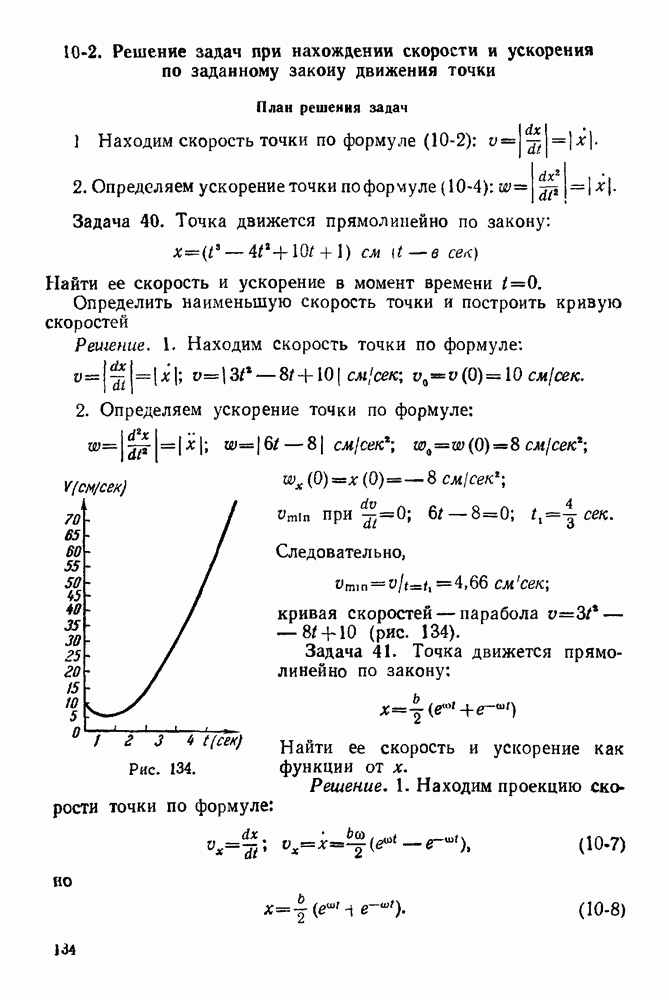
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
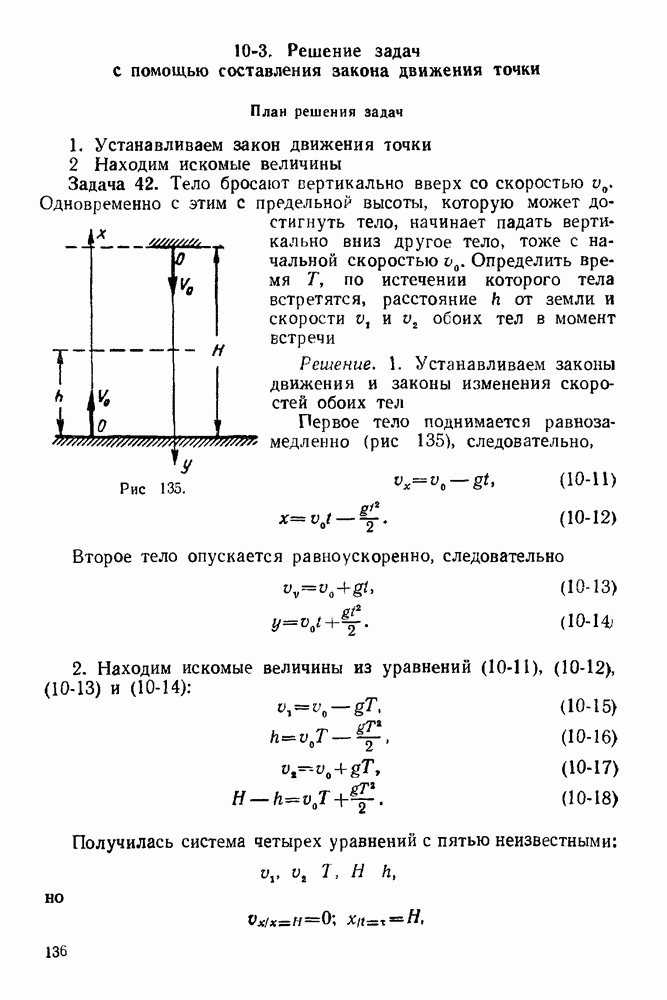
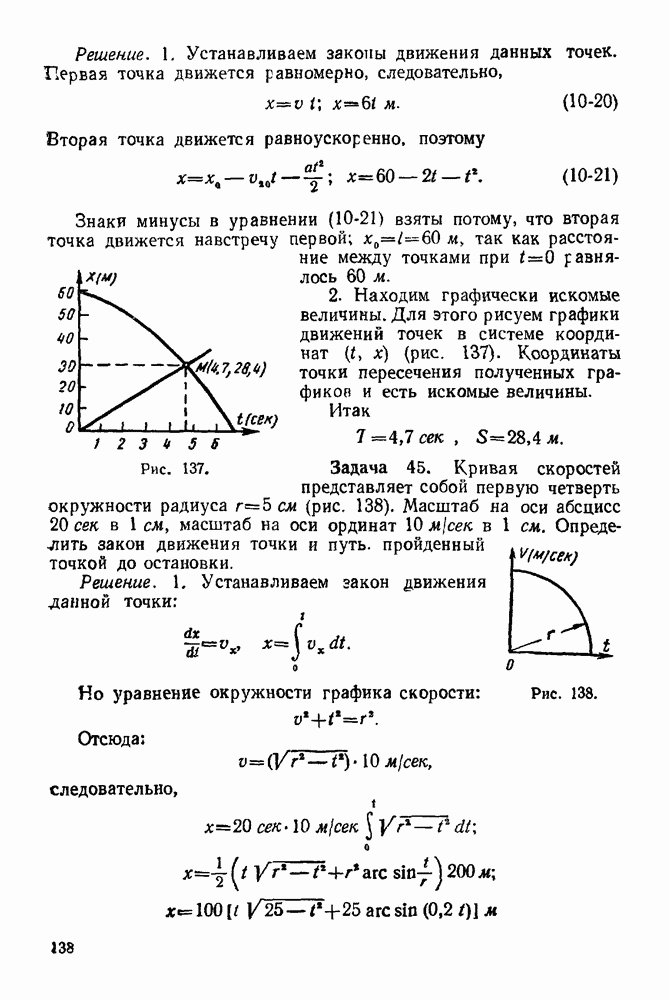
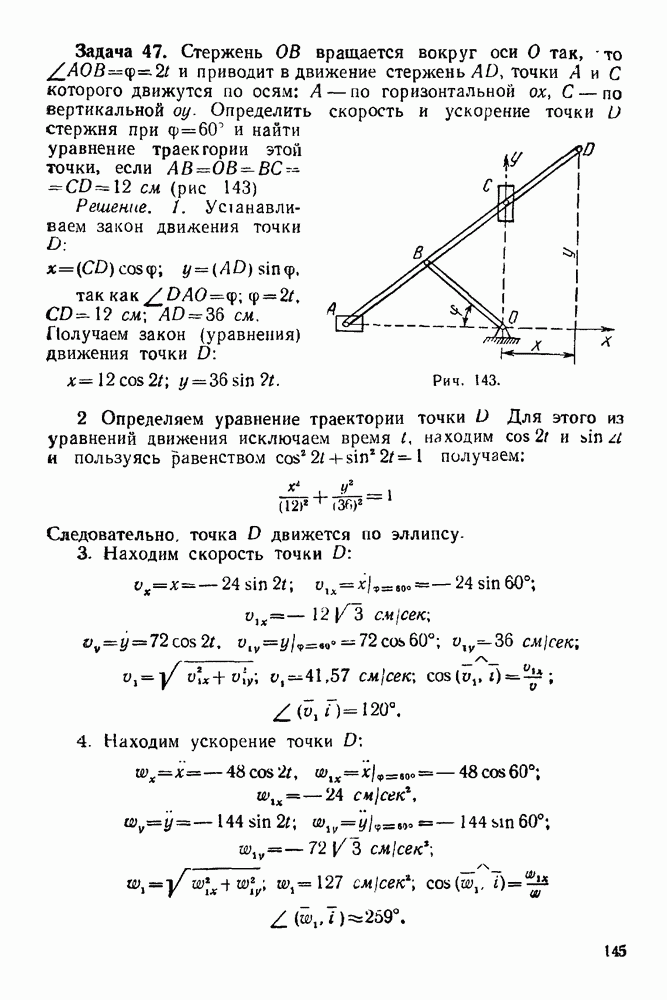
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
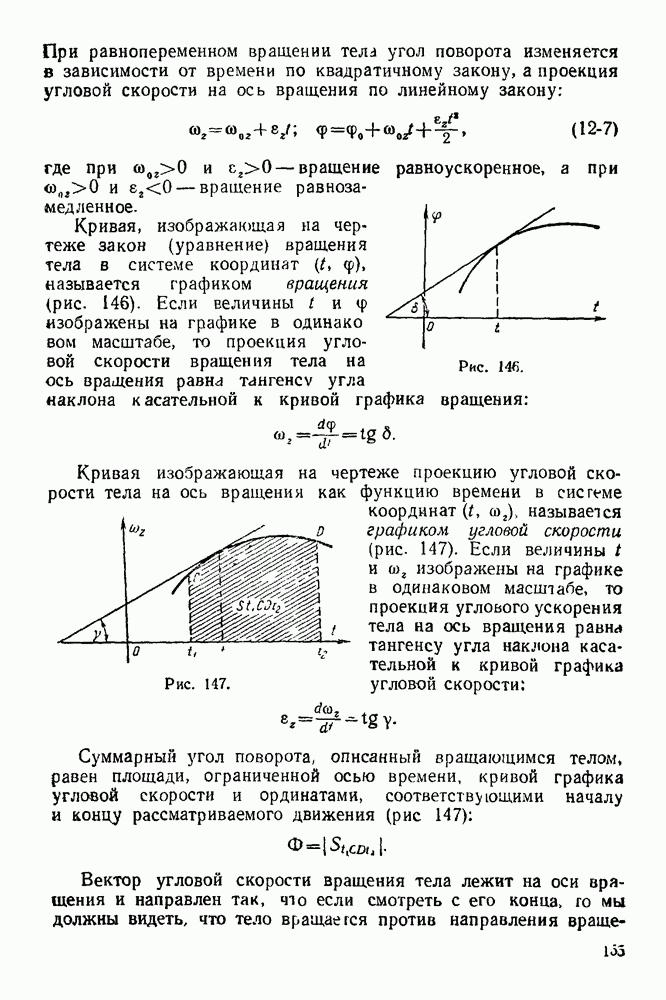
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
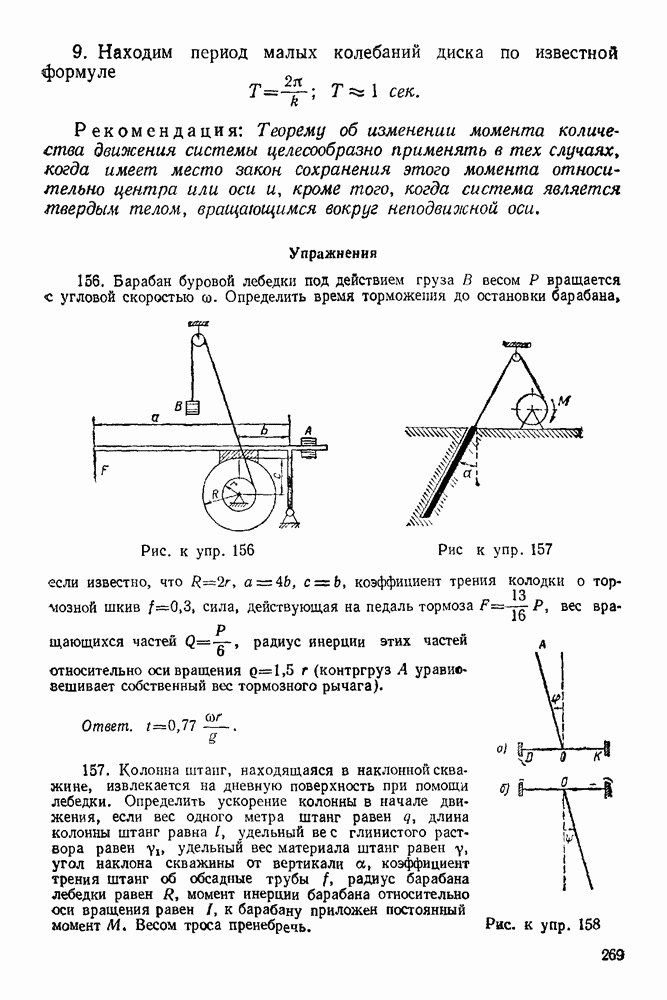
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
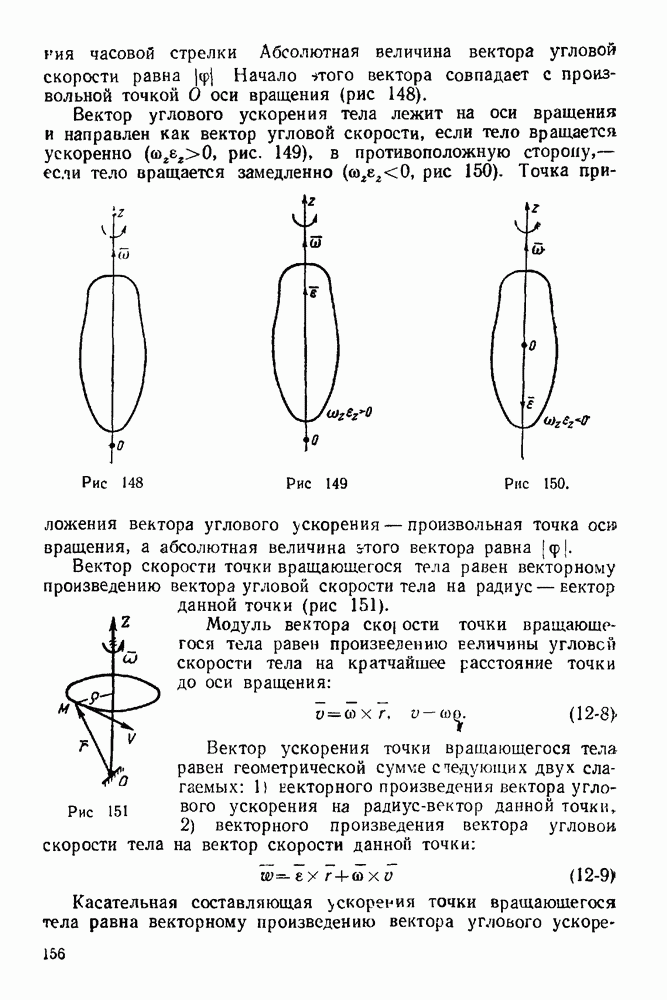
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
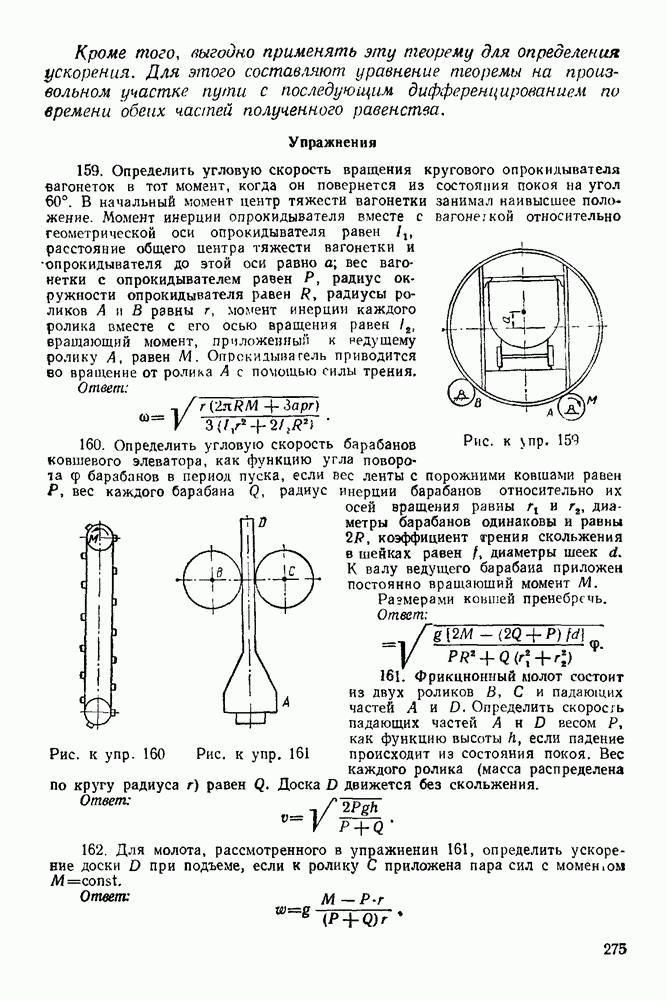
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
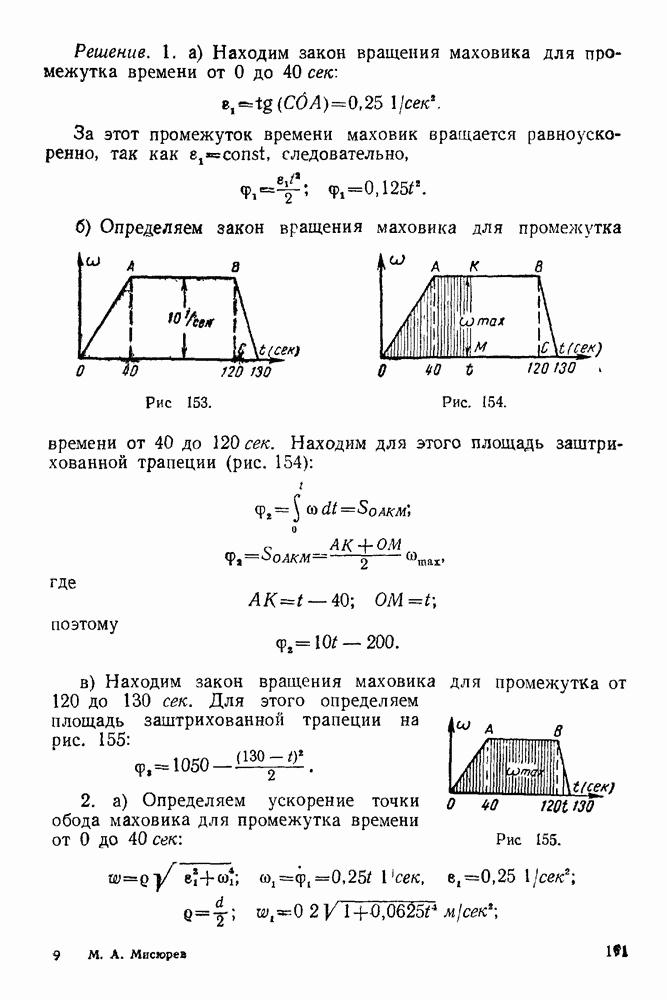
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
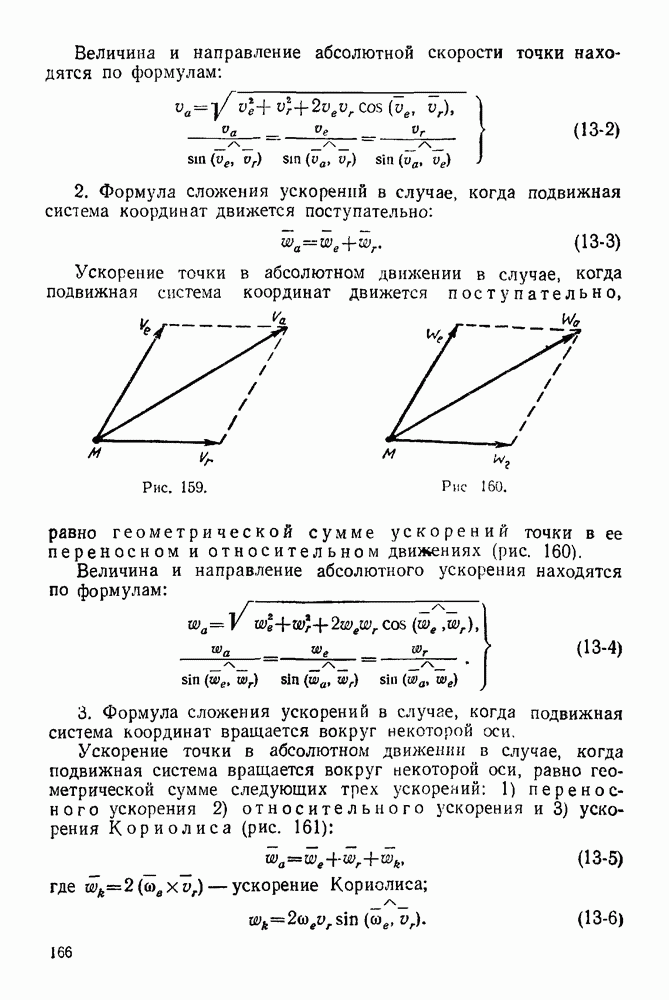
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
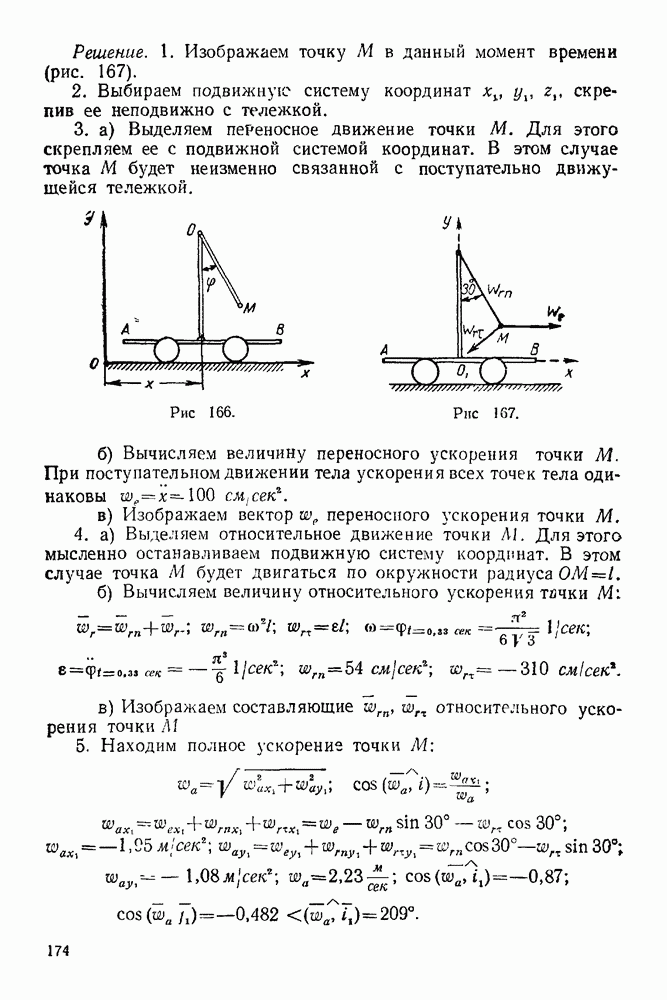
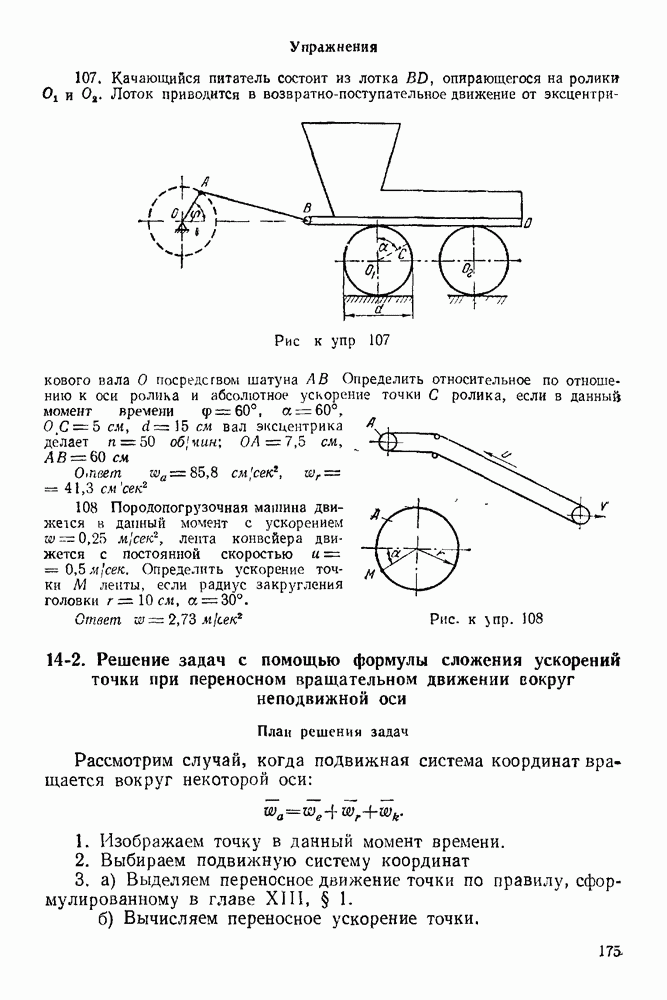
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
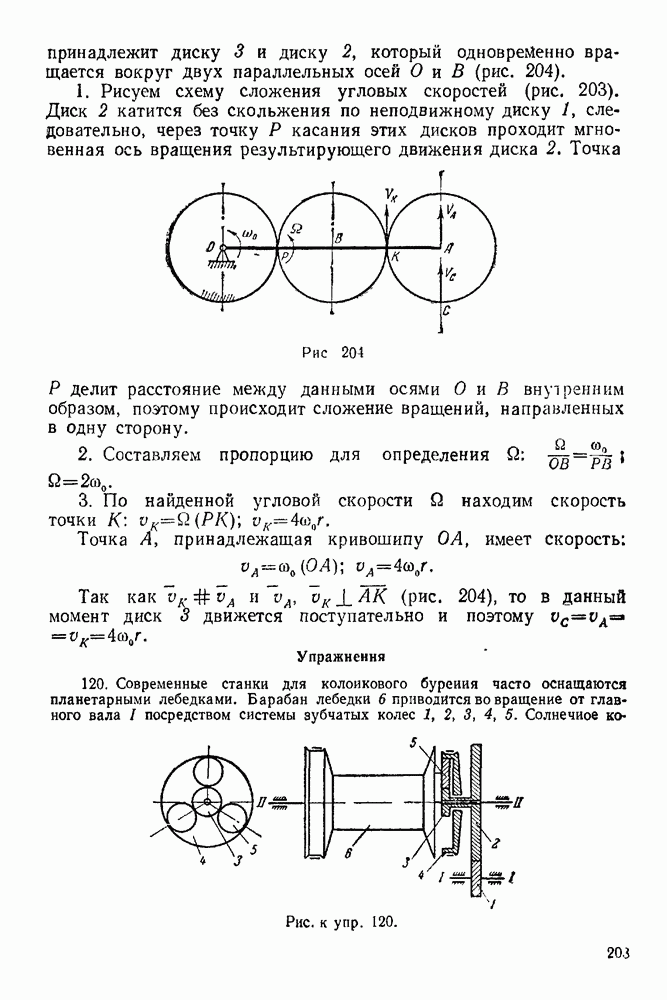
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
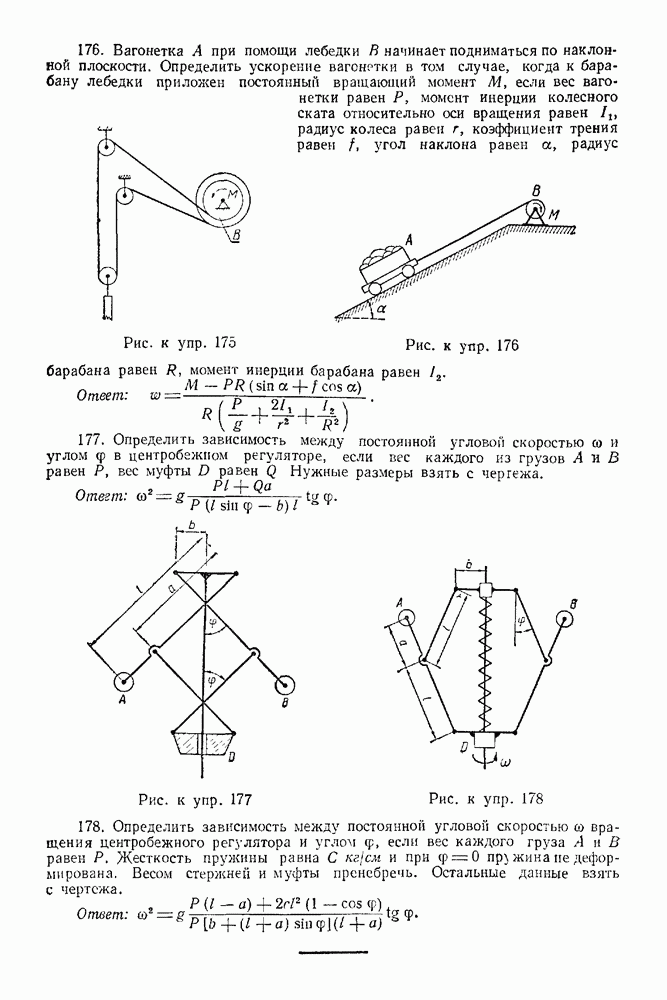
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР