| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
8-1. Основные положения
Для того, чтобы силы, как угодно расположенные в пространстве, находились в равновесии, необходимо и достаточно, чтобы суммы проекций на три взаимно перпендикулярные оси и суммы моментов всех сил системы относительно тех же осей равнялись нулю.

Для облегчения решения задачи рекомендуется так выбирать оси, чтобы линия действия той силы, момент которой вычисляется сложно, пересекала какую-нибудь ось. При нахождении момента силы относительно оси для таких сил выгодно применять третью теорему Вариньона: момент равнодействующей относительно какой-нибудь оси равен алгебраической сумме моментов составляющих относительно той же оси:

Данную силу следует разложить на такие составляющие, моменты которых легко вычисляются (см. решение задачи 32).
При решении задач будем придерживаться следующего плана:
1. Выделяем материальную систему (тело), равновесие которой следует рассмотреть.
2. Изображаем активные силы, действующие на материальную систему, равновесие которой рассматриваем.
3. Освобождаем эту систему от связей, заменяя действие связей реакциями.
4. Выбираем систему координат.
5. Составляем уравнение равновесия:

6. Решаем полученные уравнения.
8-2. Решение задач
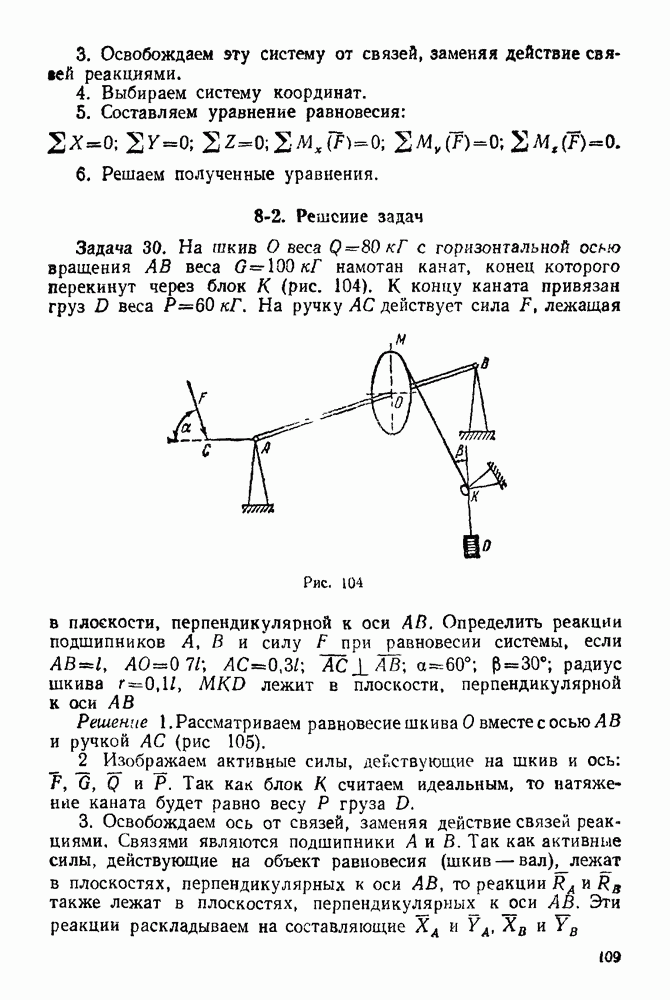
Задача 30. На шкив О веса  с горизонтальной осью вращения
с горизонтальной осью вращения  веса
веса  намотан канат, конец которого перекинут через блок К (рис. 104). К концу каната привязан груз
намотан канат, конец которого перекинут через блок К (рис. 104). К концу каната привязан груз  веса
веса 

Рис. 104
На ручку  действует сила
действует сила  лежащая в плоскости, перпендикулярной к оси
лежащая в плоскости, перпендикулярной к оси  Определить реакции подшипников
Определить реакции подшипников  и силу
и силу  при равновесии системы, если
при равновесии системы, если  радиус шкива
радиус шкива  лежит в плоскости, перпендикулярной к оси
лежит в плоскости, перпендикулярной к оси 
Решение 1. Рассматриваем равновесие шкива О вместе с осью  и ручкой
и ручкой  (рис 105).
(рис 105).
2 Изображаем активные силы, действующие на шкив и ось:  Так как блок К считаем идеальным, то натяжение каната будет равно весу
Так как блок К считаем идеальным, то натяжение каната будет равно весу  груза
груза 
3. Освобождаем ось от связей, заменяя действие связей реакциями, Связями являются подшипники  Так как активные силы, действующие на объект равновесия (шкив — вал), лежат в плоскостях, перпендикулярных к оси
Так как активные силы, действующие на объект равновесия (шкив — вал), лежат в плоскостях, перпендикулярных к оси  то реакции
то реакции  и
и  также лежат в плоскостях, перпендикулярных к оси
также лежат в плоскостях, перпендикулярных к оси  Эти реакции раскладываем на составляющие
Эти реакции раскладываем на составляющие  и
и 
4. Выбиргем систему координат, как указано на рис. 108.
5. Составляем уравнения равновесия:


Рис. 105
Уравнение  обращается к тождество
обращается к тождество 

6. Решаем полученные уравнения.
Из уравнения 
Из уравнения  Из уравнения
Из уравнения 
Из уравнения 
Из уравнения 
Ответ. 
Задача 31. Однородная прямоугольная крышка (рис. 106) веса  наклонена под углом
наклонена под углом  к вертикальной плоскости
к вертикальной плоскости  и удерживается в таком положении при помощи сферического шарнира О, цилиндрического шарнира А и нити CD,
и удерживается в таком положении при помощи сферического шарнира О, цилиндрического шарнира А и нити CD,
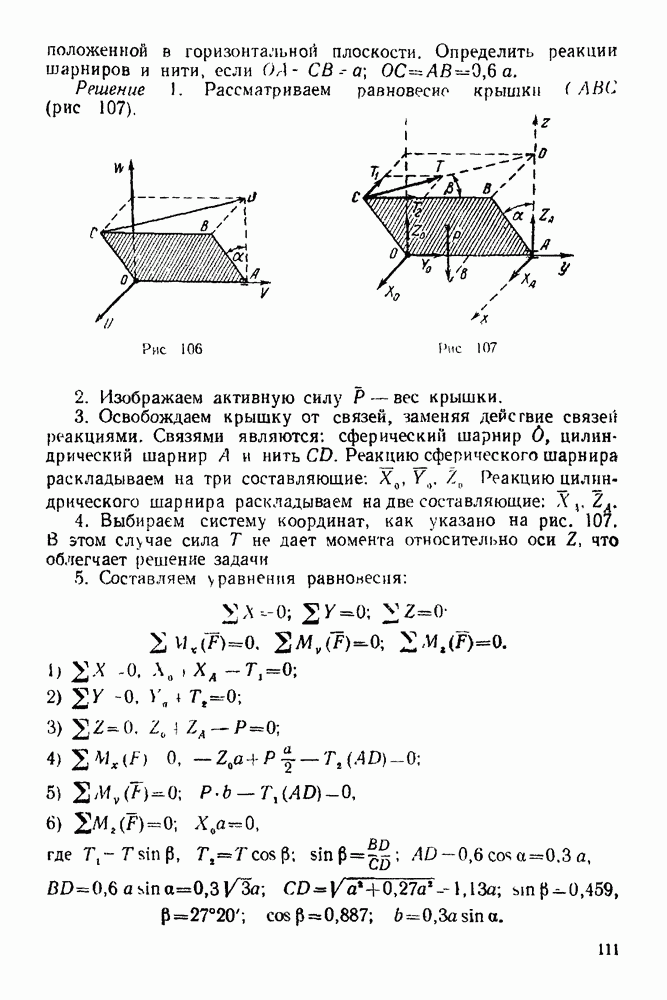
расположенной в горизонтальной плоскости. Определить реакции шарниров и нити, если 
Решение  Рассматриваем равновесие крышки
Рассматриваем равновесие крышки  (рис 107).
(рис 107).

Рис. 106

Рис. 107
2. Изображаем активную силу  вес крышки.
вес крышки.
3. Освобождаем крышку от связей, заменяя действие связей реакциями. Связями являются; сферический шарнир 0, цилиндрический шарнир  и нить
и нить  Реакцию сферического шарнира раскладываем на три составляющие:
Реакцию сферического шарнира раскладываем на три составляющие:  Реакцию цилиндрического шарнира раскладываем на две составляющие:
Реакцию цилиндрического шарнира раскладываем на две составляющие: 
4. Выбираем систему координат, как указано на рис. 107. В этом случае сила  не дает момента относительно оси
не дает момента относительно оси  что облегчает решение задачи
что облегчает решение задачи
5. Составляем уравнения равнонесня:

где 

6. Решаем полученную систему уравнений:

Из уравнения (8-13): 
Из уравнения (8-12): 
Из уравнения (8-11): 
Из уравнения (8-10):  Из уравнения
Из уравнения  :
: 
Из уравнения  :
: 
Ответ: 
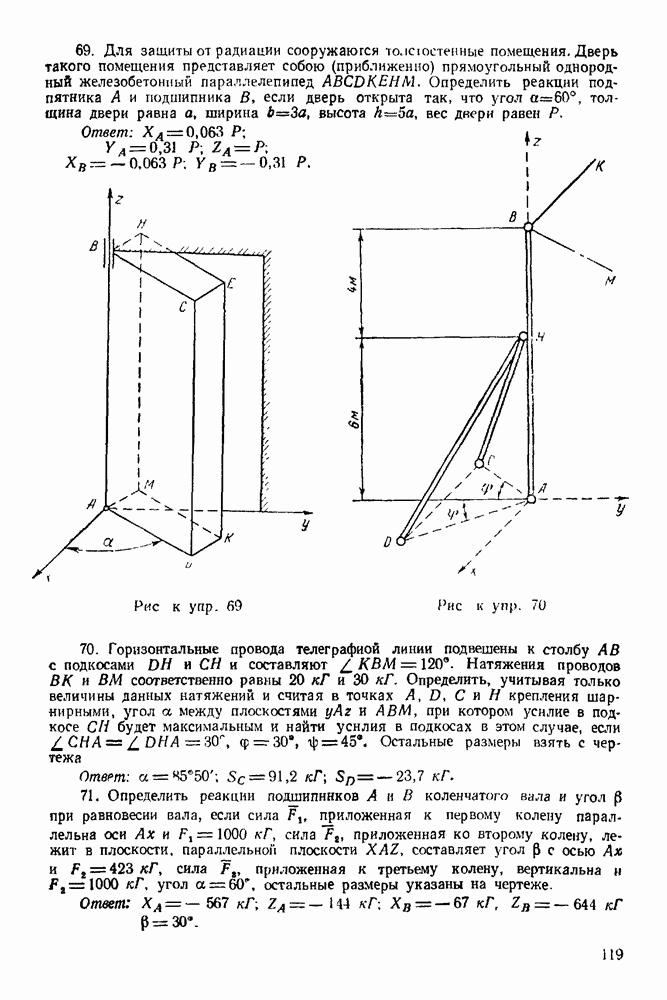
Задача 32. Дверь  веса
веса  затворяется при помощи груза
затворяется при помощи груза  веса
веса  подвешенного на веревке
подвешенного на веревке  перекинутой через блоки
перекинутой через блоки  (рис. 108).
(рис. 108).

Рис. 108.

Рис. 109.
Дверь, открытая на угол  удерживается в равновесии силой
удерживается в равновесии силой  приложенной в точке К. Эта сила лежит в плоскости, проходящей через
приложенной в точке К. Эта сила лежит в плоскости, проходящей через  перпендикулярно к плоскости двери, и направлена под углом
перпендикулярно к плоскости двери, и направлена под углом  к линии
к линии  Определить реакцию подпятника А, подшипника В и силу
Определить реакцию подпятника А, подшипника В и силу  если
если  ;
;
Решение. 1. Рассматриваем равновесие двери  (рис. 109).
(рис. 109).
2. Изображаем активные силы, действующие на дверь:  вес двери,
вес двери,  вес груза
вес груза  Так как
Так как  идеальные блоки, то натяжение веревки будет равно весу
идеальные блоки, то натяжение веревки будет равно весу  груза
груза 
3. Освобождаем дверь от связей, заменяя действие связей реакциями. Связями являются: а) подпятник  и б) подшипник В. Реакцию подпятника раскладываем на три взаимно перпендикулярные составляющие
и б) подшипник В. Реакцию подпятника раскладываем на три взаимно перпендикулярные составляющие  Реакцию подшипника раскладываем на две взаимно перпендикулярные составляющие
Реакцию подшипника раскладываем на две взаимно перпендикулярные составляющие 
4. Выбираем систему координат, как указано на рис.  Составляем уравнения равновесия:
Составляем уравнения равновесия:

При составлении уравнений используем рис. 110 (вид сверху):

При составлении четвертого уравнения все силы нужно проектировать на плоскость  и брать моменты этих проекций относительно точки А:
и брать моменты этих проекций относительно точки А:


Рис. 110.
При составлении пятого уравнения все силы нужно проектировать на плоскость  и брать моменты этих проекций относительно точки А:
и брать моменты этих проекций относительно точки А:

При составлении шестого уравнения все силы нужно проектировать на плоскость  и брать моменты этих проекций относительно точки А:
и брать моменты этих проекций относительно точки А:

При вычислении моментов силы  относительно осей использовали теорему Вариньона, разложив эту силу на составляющие
относительно осей использовали теорему Вариньона, разложив эту силу на составляющие  составляющая, перпендикулярная
составляющая, перпендикулярная 
и  составляющая, параллельная оси
составляющая, параллельная оси  причем
причем 
6. Решаем полученную систему уравнений:

Из уравнения (8-19): 
Из уравнения (8-18):

Из уравнения (8-17): 

Из уравнения (8-16): 
Из уравнения (8-15): 
Из уравнения (8-14):  Ответ
Ответ 
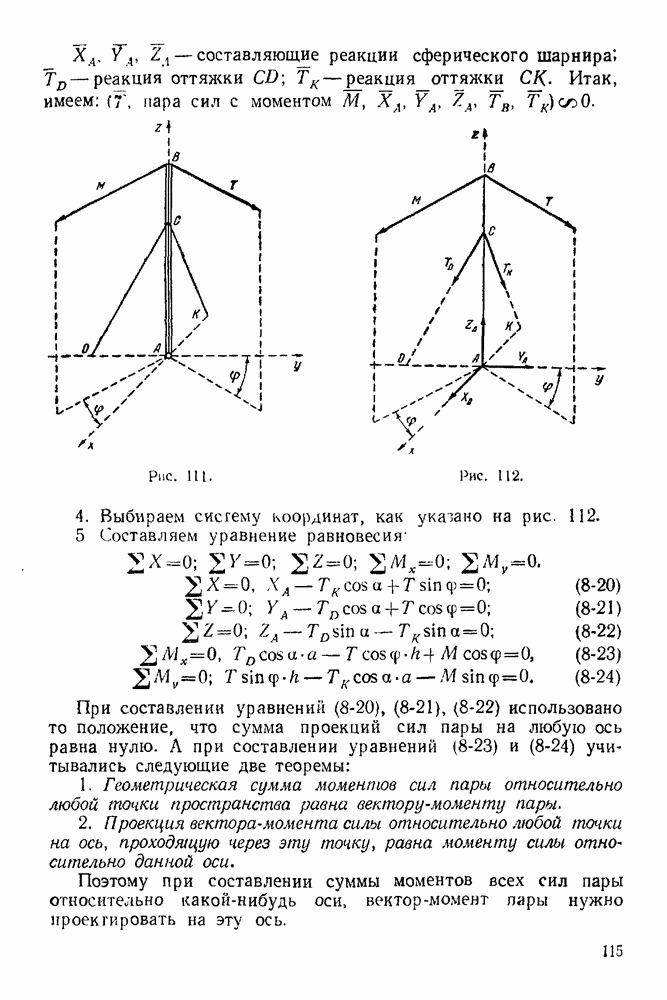
Задача 33. Определить реакцию сферического шарнира А и натяжение оттяжек  и
и  столба
столба  (рис. 111), вызываемые горизонтальной равнодействующей
(рис. 111), вызываемые горизонтальной равнодействующей  натяжений проводов и парой сил, вектор-момент которой лежит в горизонтальной плоскости и равен
натяжений проводов и парой сил, вектор-момент которой лежит в горизонтальной плоскости и равен  если
если 
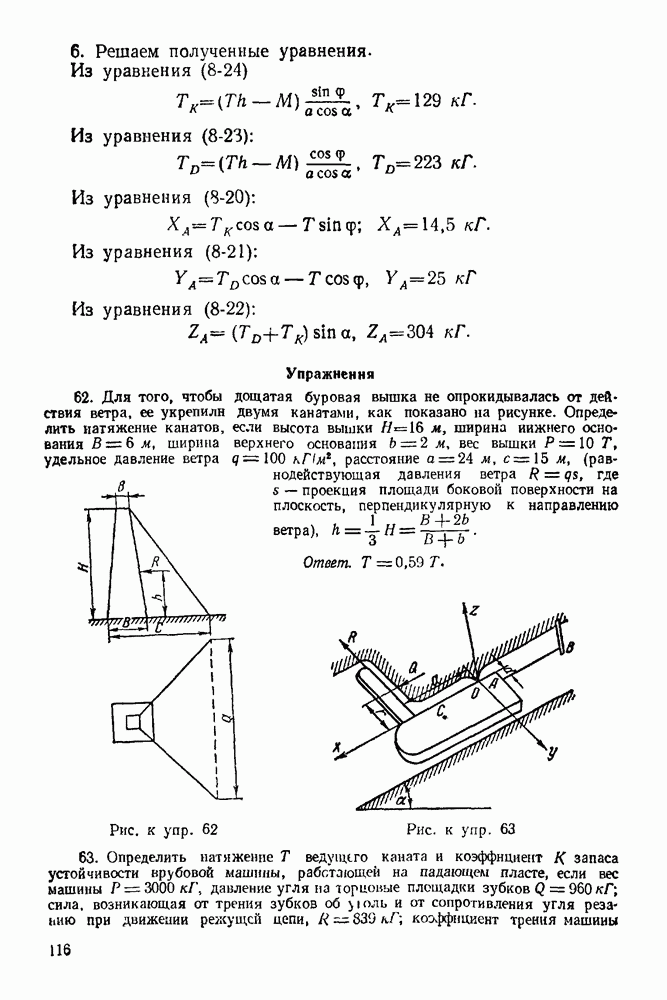
Решение. 1. Рассматриваем равновесие столба  (рис. 112)
(рис. 112)
2 Изображаем активные силы, действующие на столб:  и пара сил с моментом
и пара сил с моментом 
3 Освобождаем столб  связей, заменяя действие связей силами-реакциями связей.
связей, заменяя действие связей силами-реакциями связей.
 составляющие реакции сферического шарнира.
составляющие реакции сферического шарнира.  реакция оттяжки
реакция оттяжки  — реакция оттяжки
— реакция оттяжки  Итак, имеем:
Итак, имеем:  пара сил с моментом
пара сил с моментом 

Рис. 111.

Рис. 112.
4. Выбуграем систему координат, как указано на рис. 112.
5 Составляем уравнение равновесия

При составлении уравнений (8-20), (8-21), (8-22) использовано то положение, что сумма проекций сил пары на любую ось равна нулю. А при составлении уравнений (8-23) и (8-24) учитывались следующие две теоремы:
1. Геометрическая сумма моментов сил пары относительно любой точки пространства равна вектору-моменту пары.
2. Проекция вектора-момента силы относительно любой точки на ось, проходящую через эту точку, равна моменту силы относительно данной оси.
Поэтому при составлении суммы моментов всех сил пары относительно какой-нибудь оси, вектор-момент лары нужно проектировать на эту ось.
6. Решаем полученные уравнения. Из уравнения (8-24)

Из уравнения (8-23):

Из уравнения (8-20):

Из уравнения (8-21):

Из уравнения (8-22):

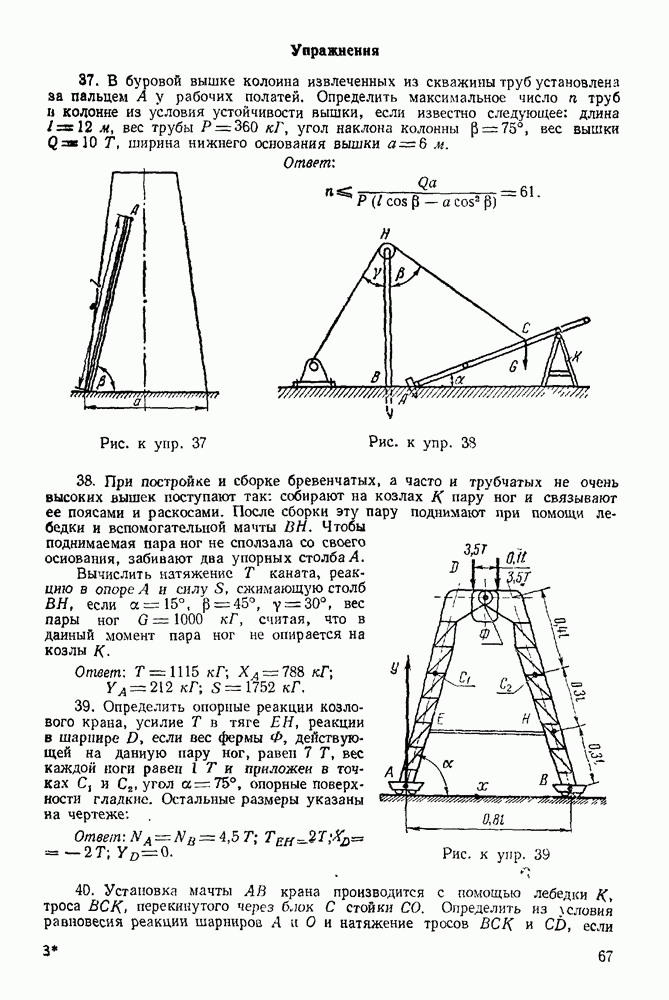
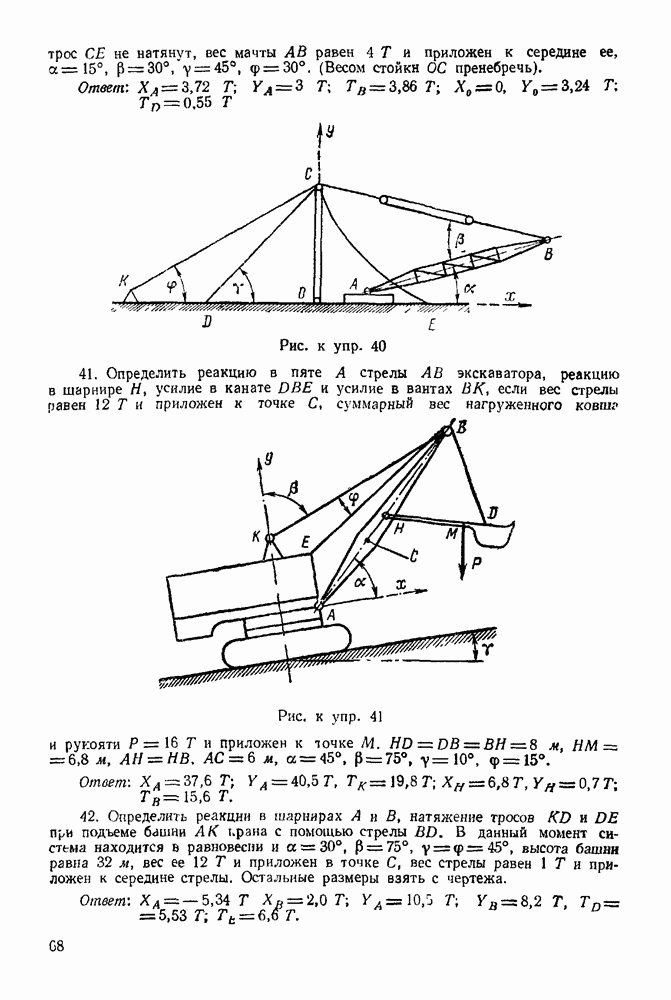
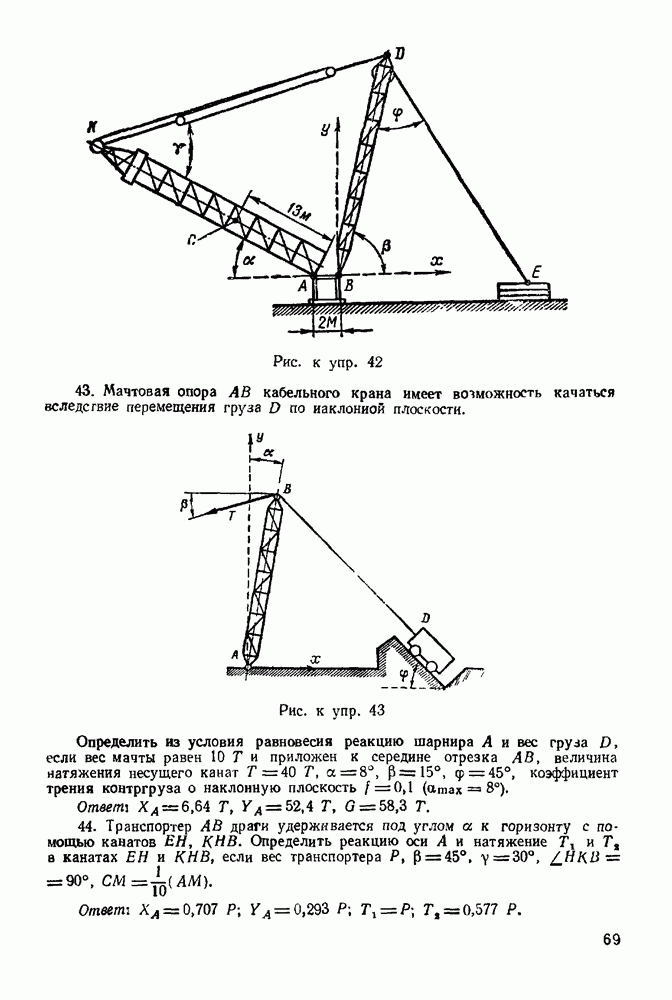
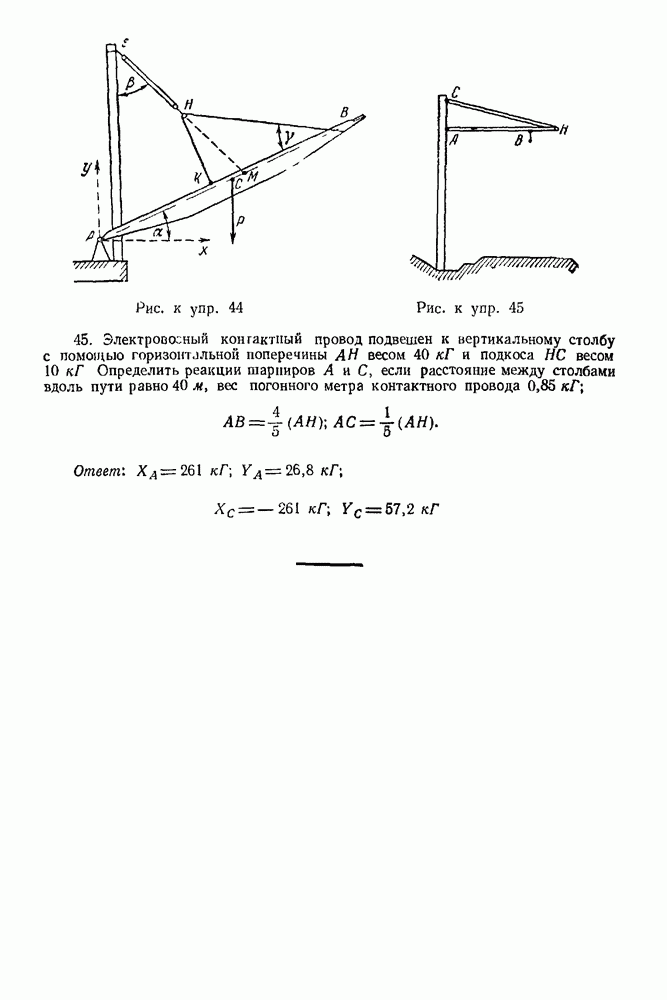
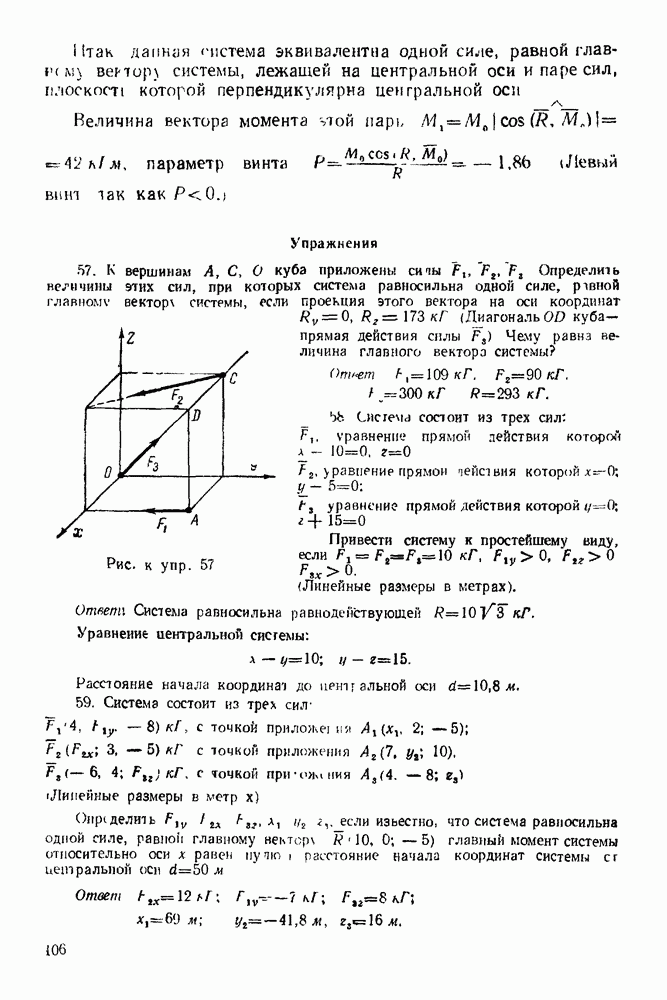
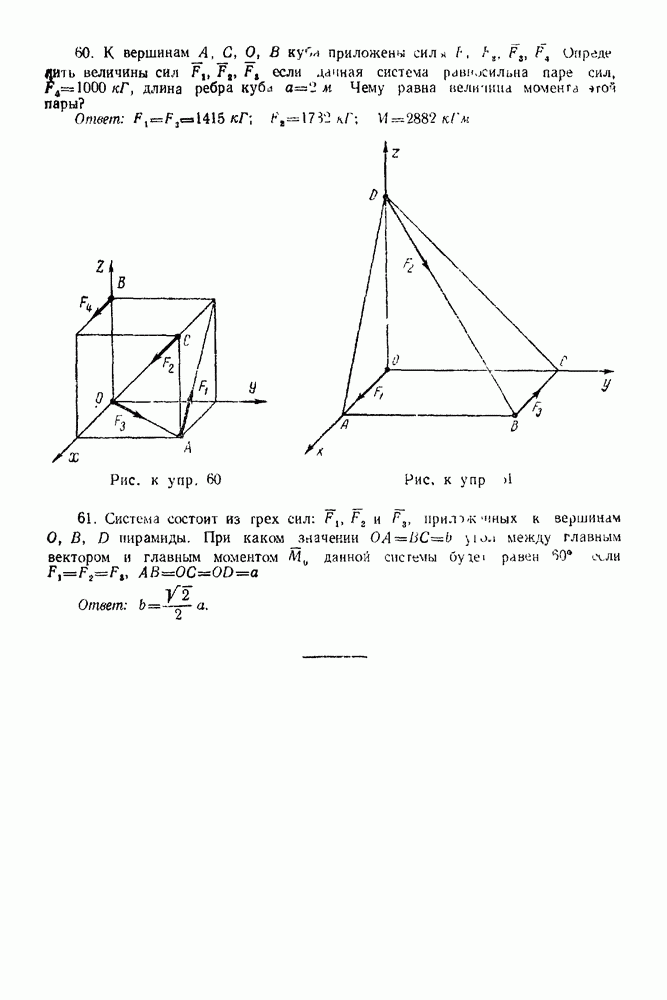
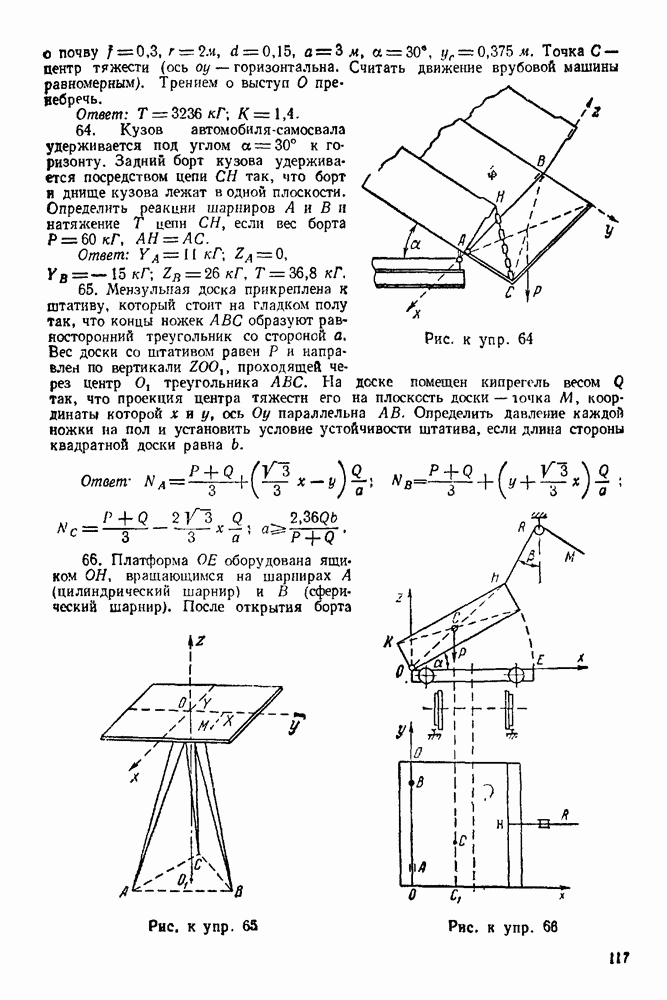
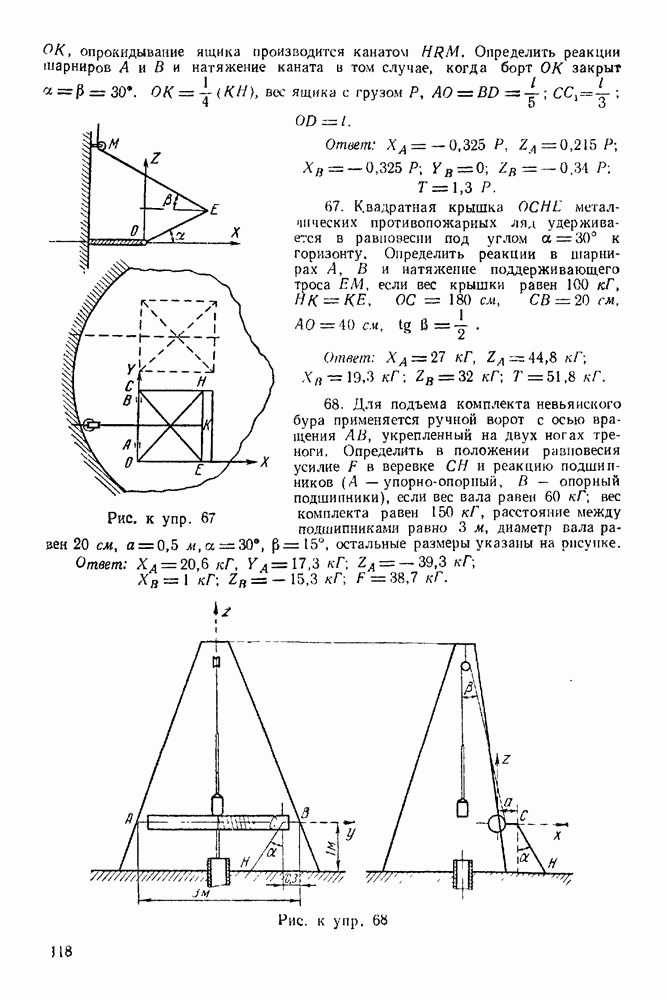
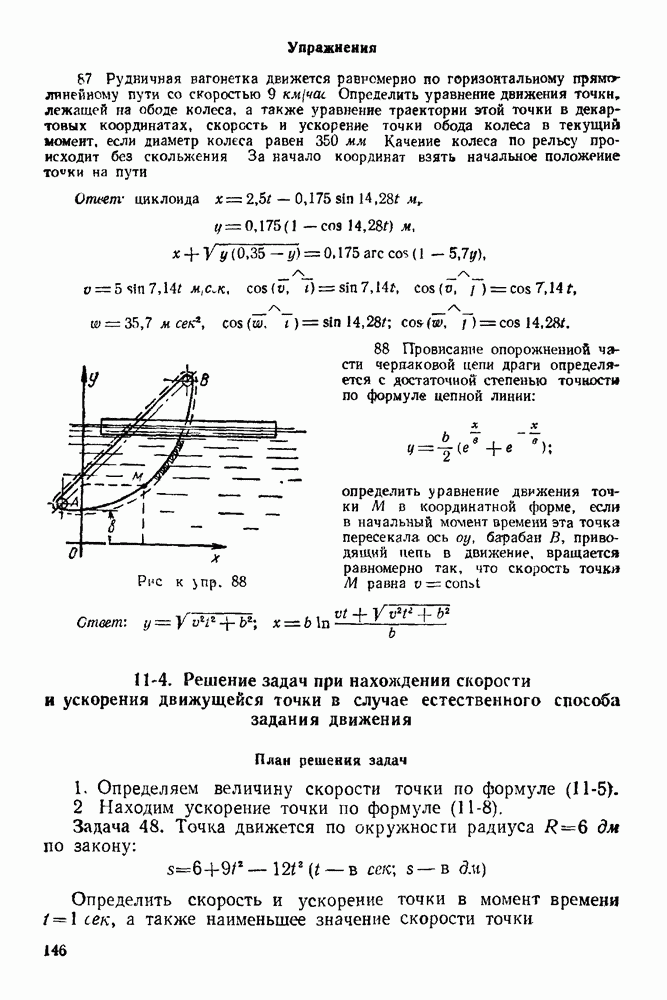
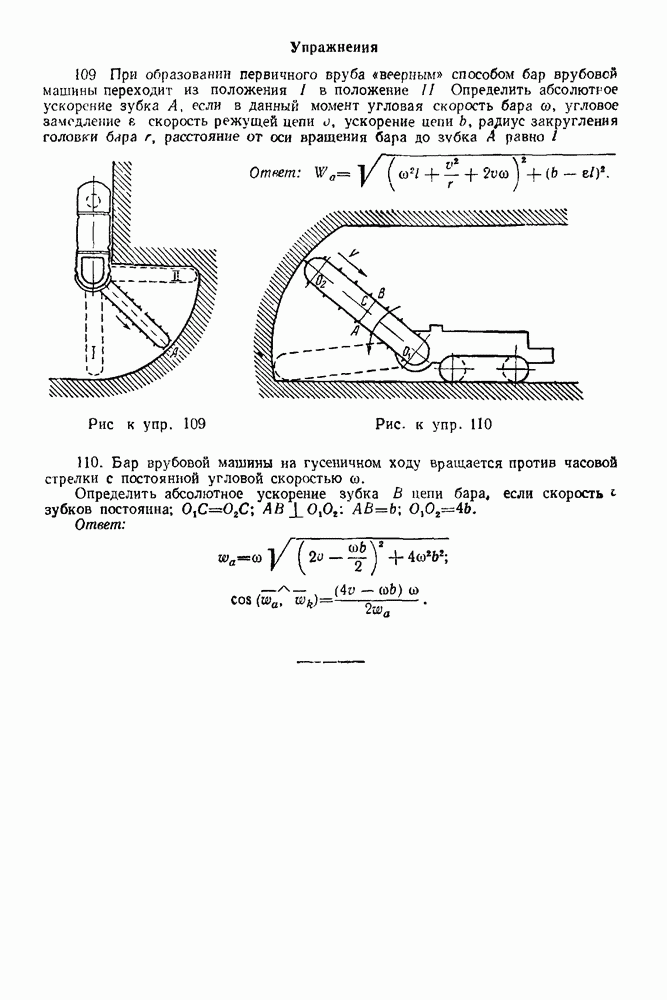
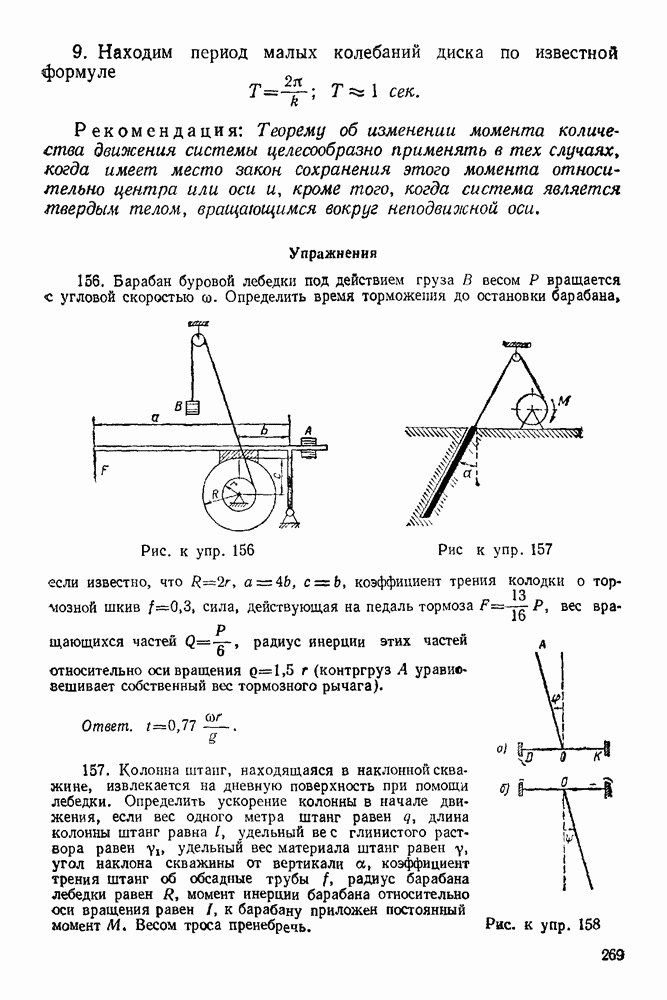
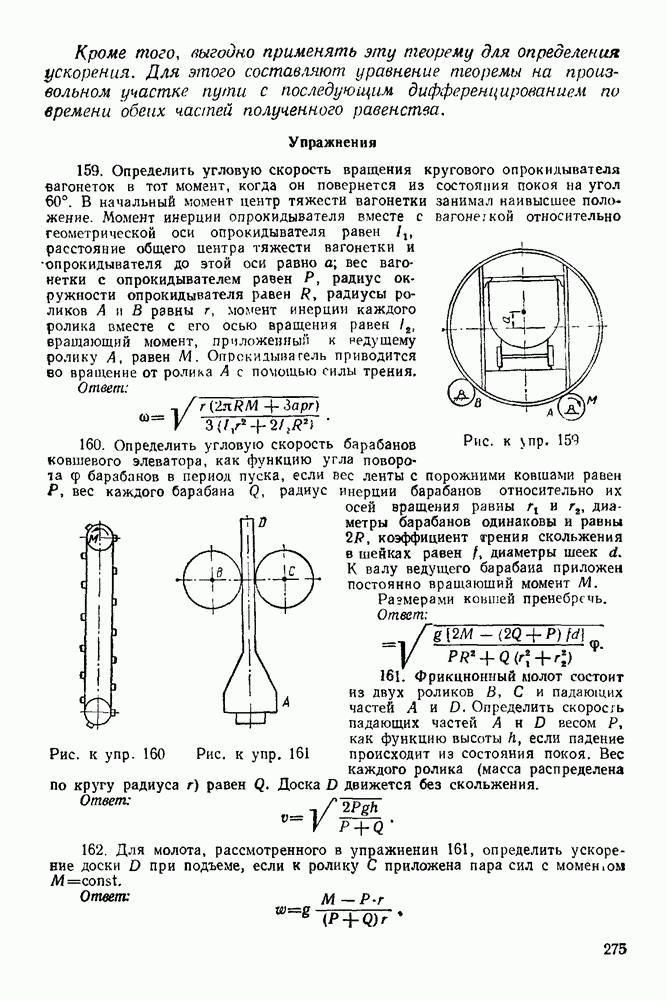
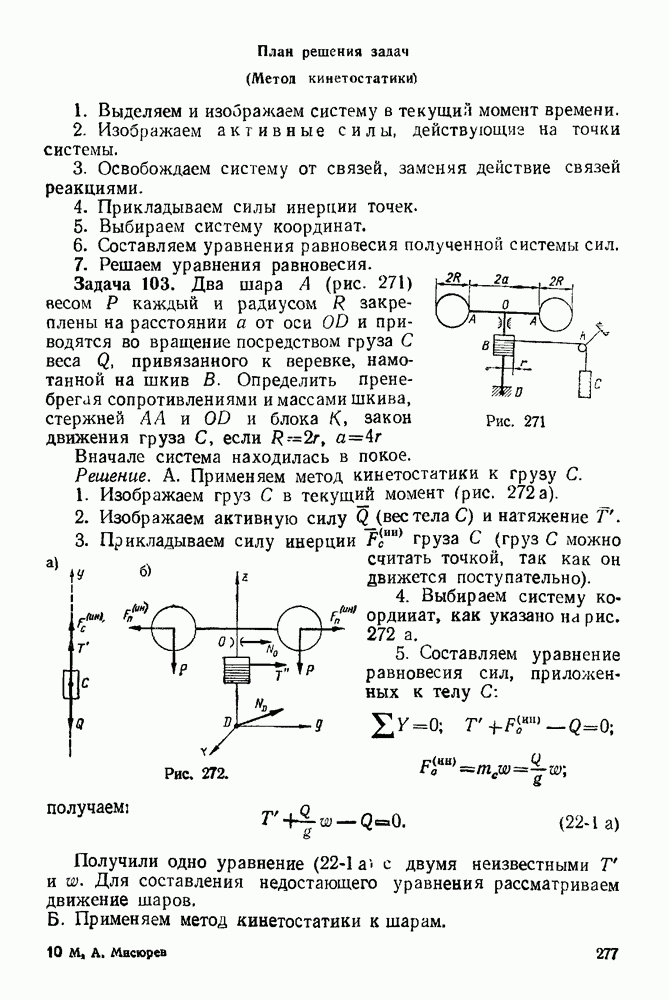
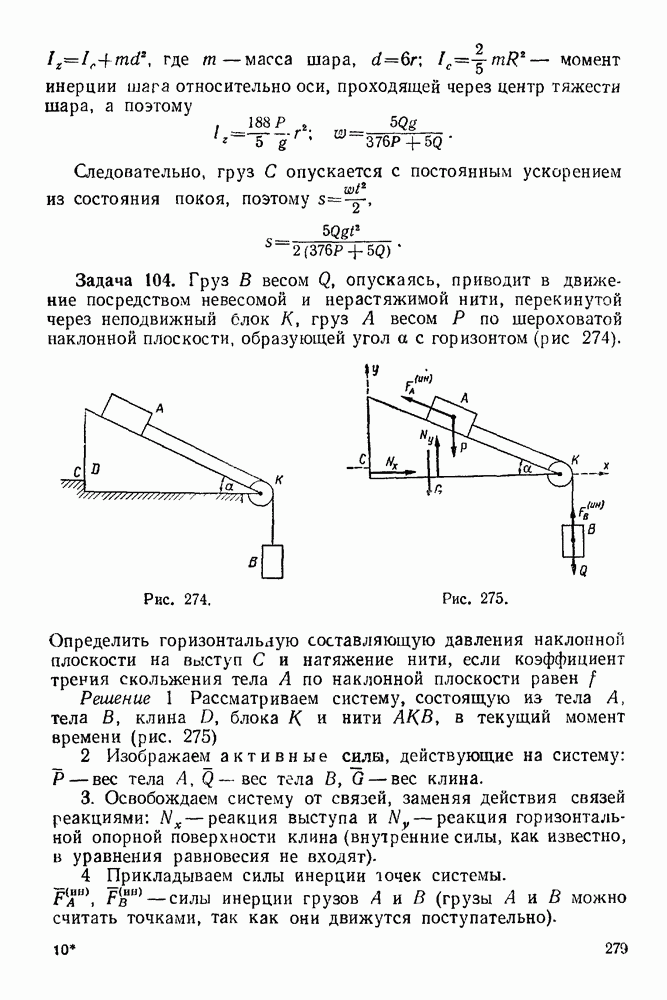
Упражнения
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
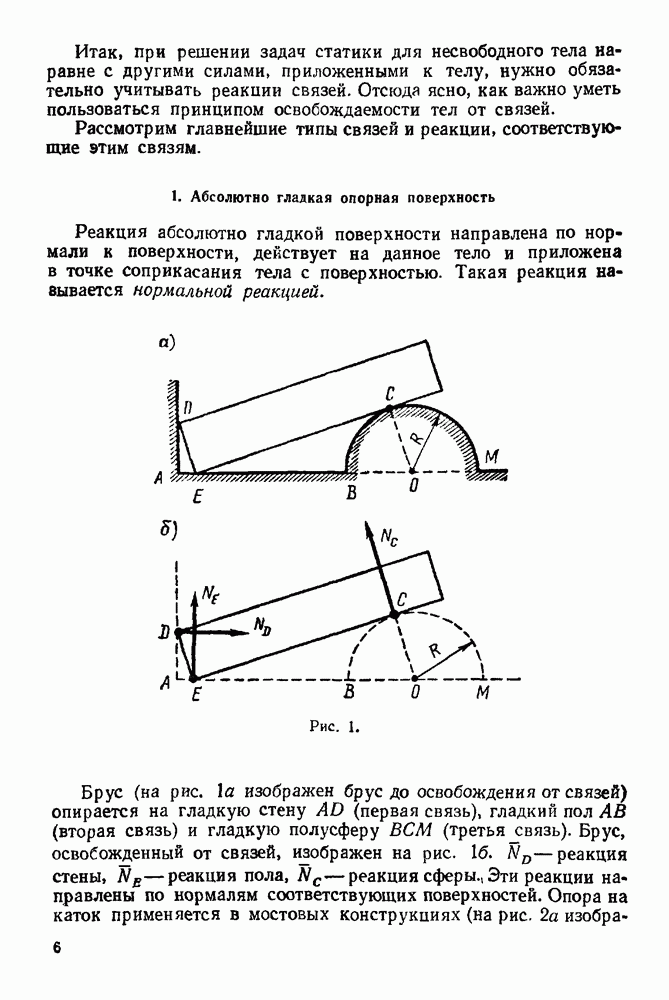
- 1. Абсолютно гладкая опорная поверхность
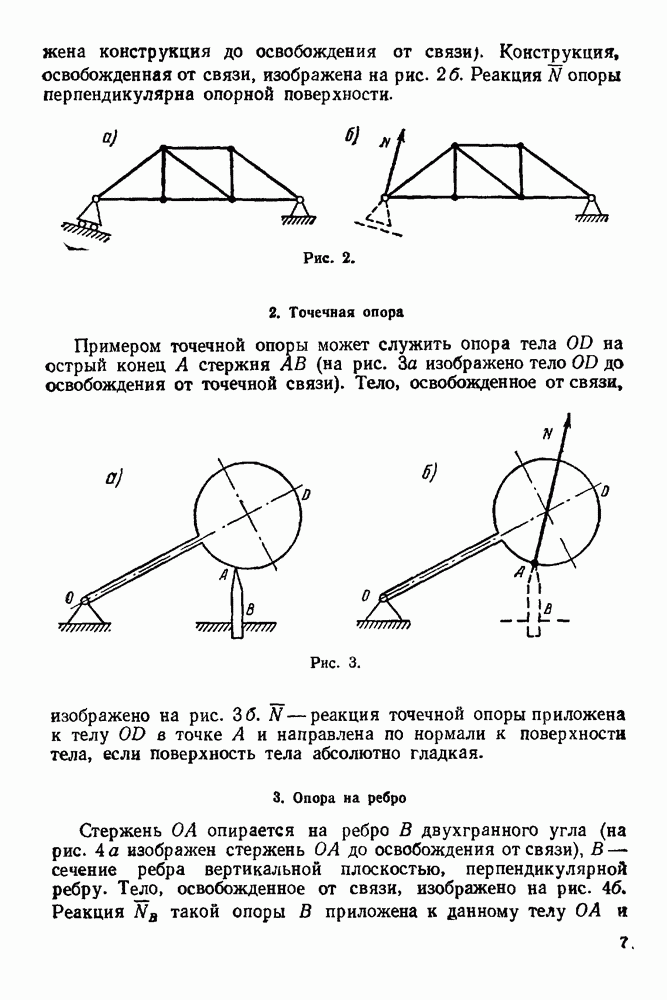
- 2. Точечная опора
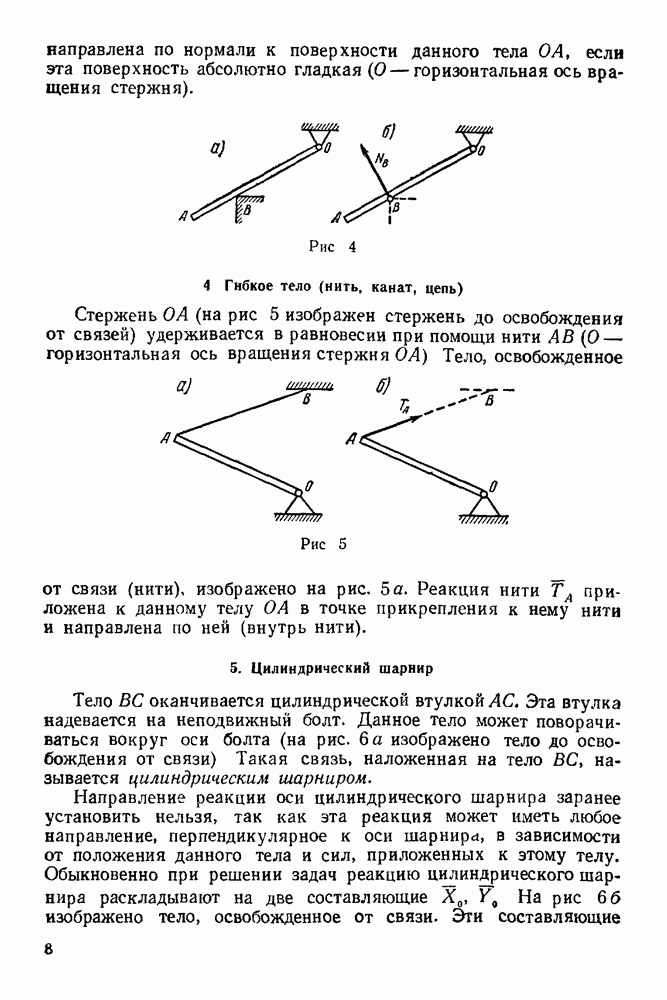
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
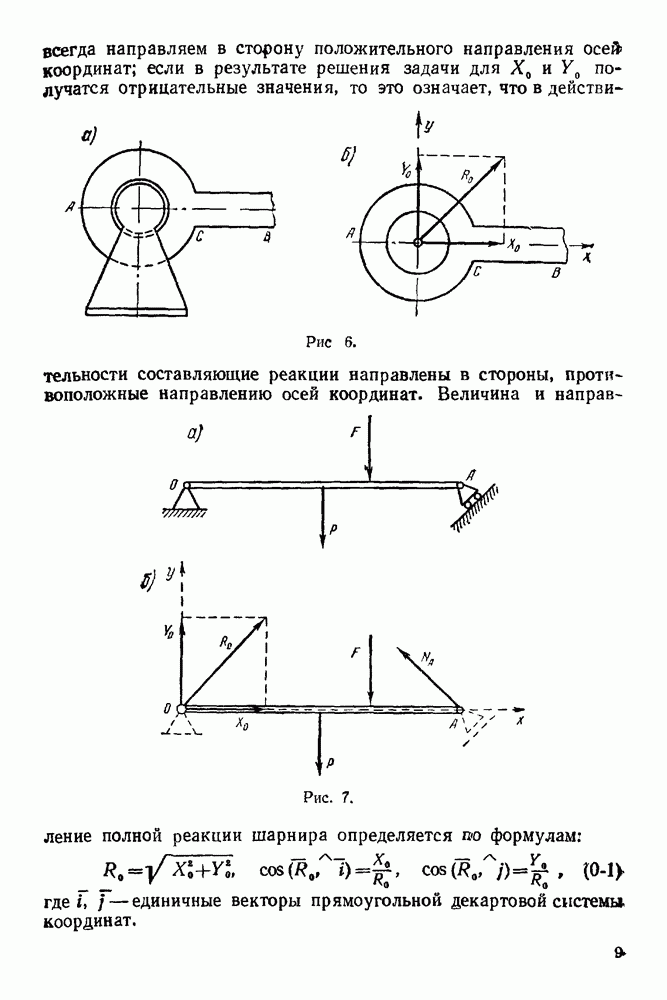
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
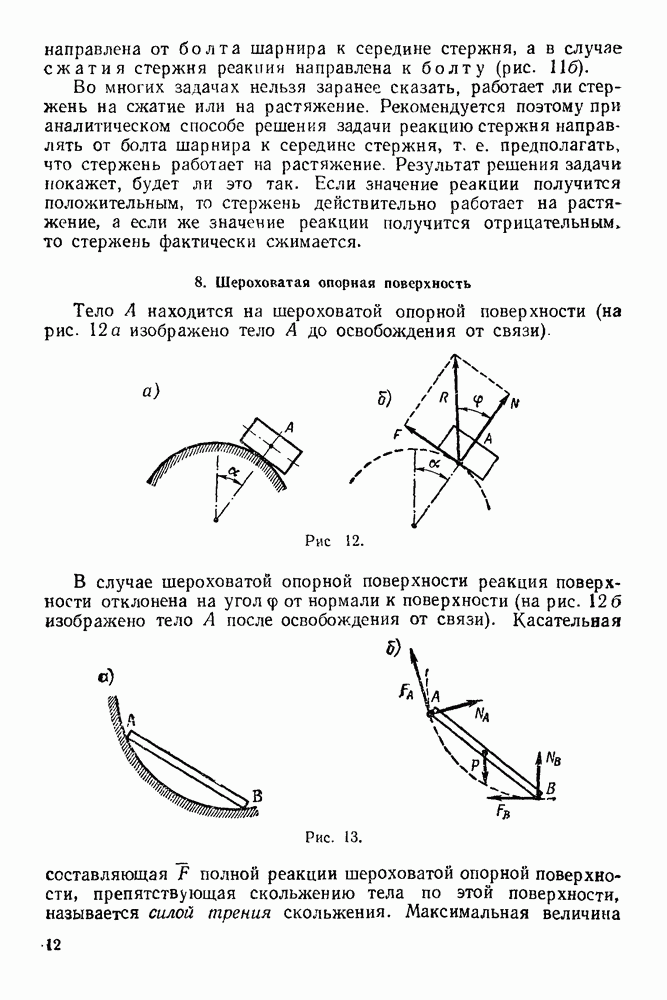
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
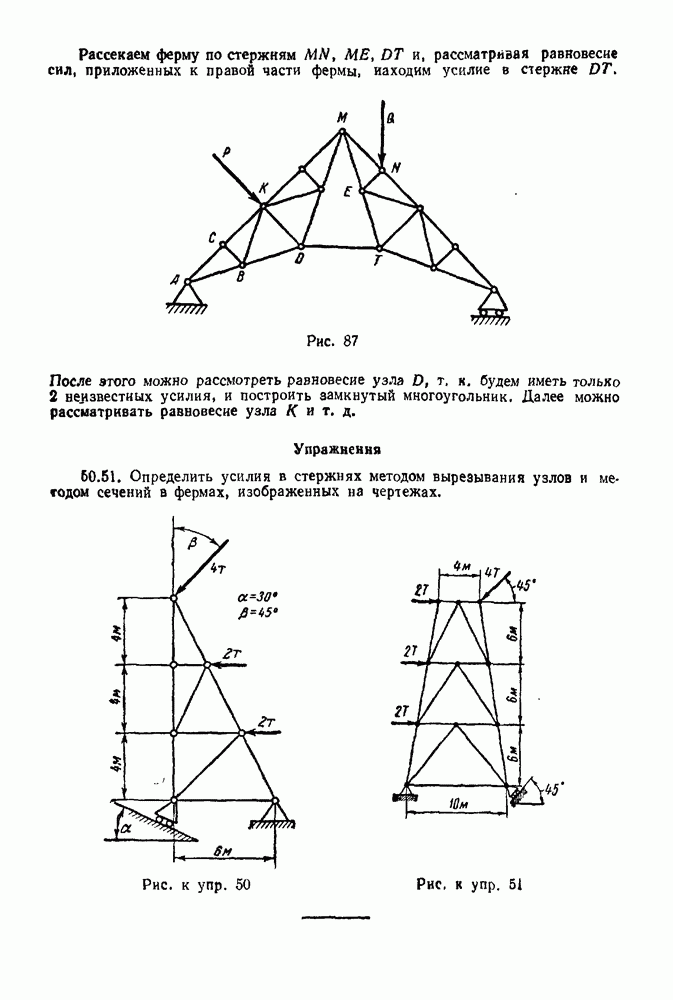
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
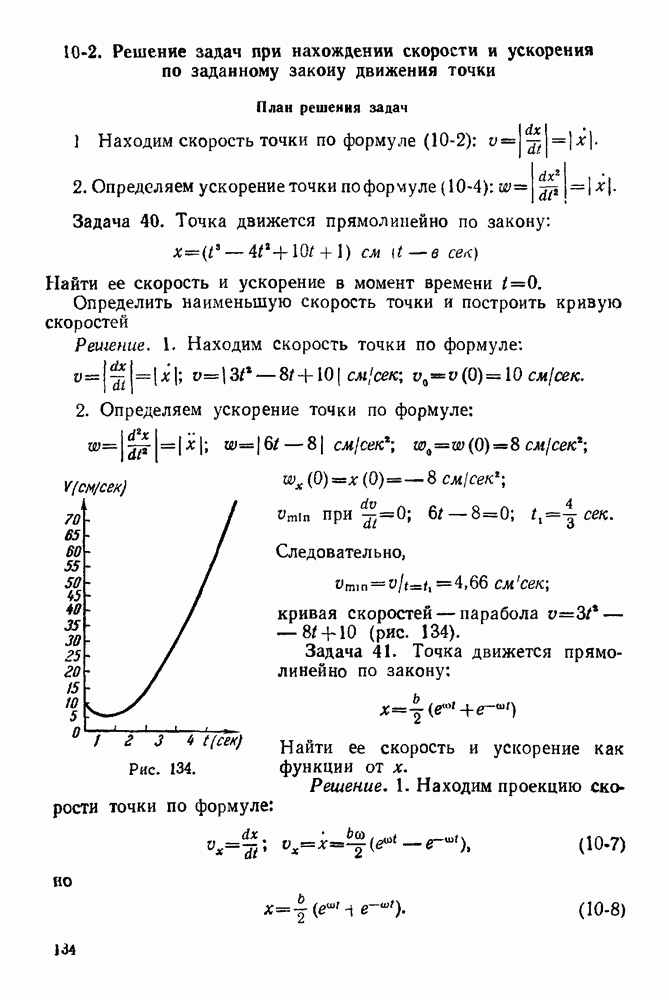
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
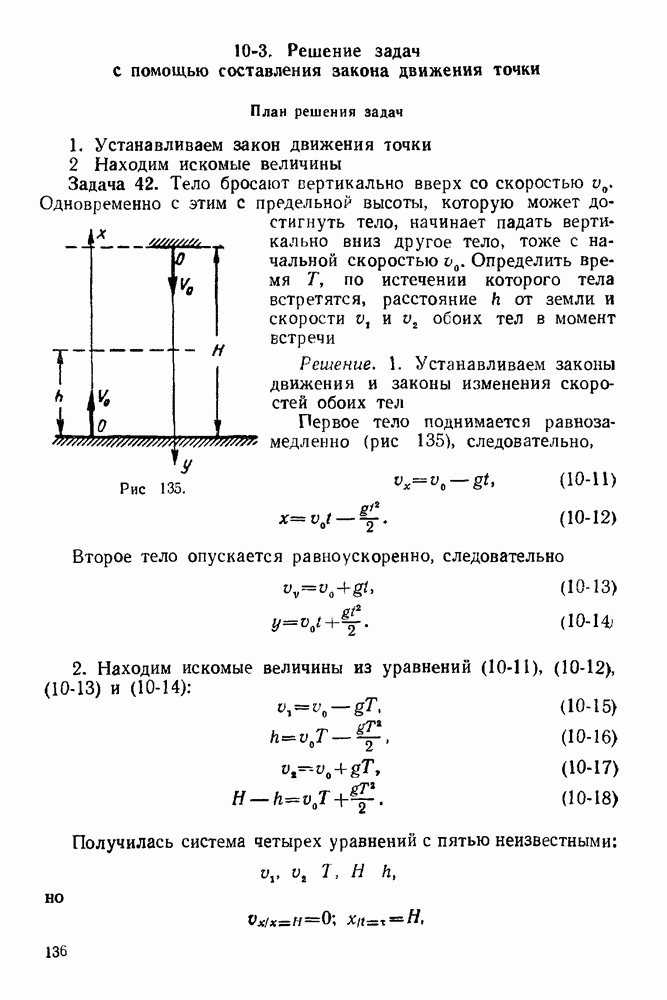
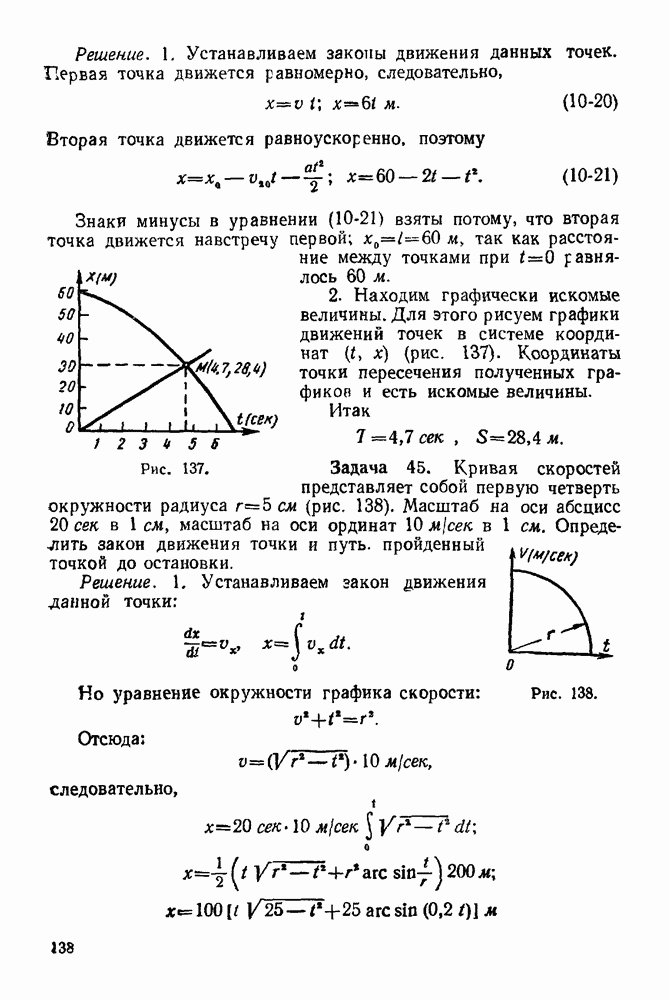
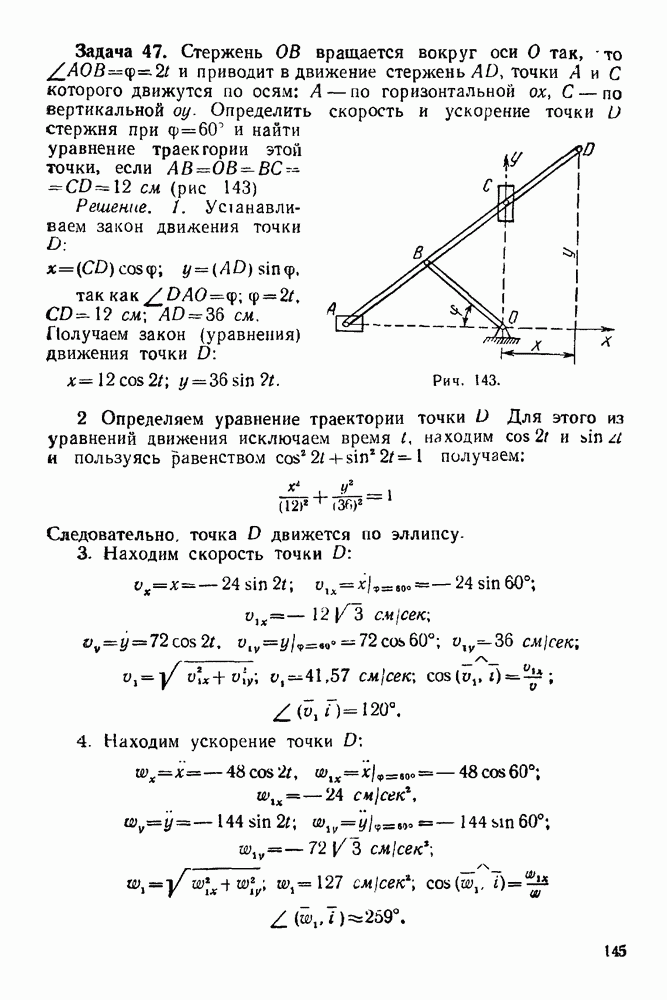
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР