| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
20-1. Общие положения
Для того, чтобы написать дифференциальные уравнения движения точки относительно движущейся системы координат, нужно к силам, действующим на точку, присоединить переносную и кориолисову силы инерции:

где  переносная сила инерции точки;
переносная сила инерции точки;  поворотная (кориолисова) сила инерции точки.
поворотная (кориолисова) сила инерции точки.
Дифференциал кинетической энергии материальной точки в относительном движении равен сумме элементарных работ всех сил, действующих на точку, плюс элементарная работа пеоеносной силы инерции точки:

Для того, чтобы выделить относительное движение точки, нужно мысленно остановить подвижную систему координат и посмотреть, как будет в этом случае двигаться точка. Для того, чтобы выделить переносное движение точки, нужно мысленно скрепить точку с подвижной системой координат и посмотреть, как будет в этом случае двигаться точка
План решения задач
1. Изображаем точку в текущий момент времени.
2. Изображаем активные силы, действующие на точку.
3 Освобождаем точку от связей, заменяя действие связей реакциями.
4. Изображаем переносную  и повторную
и повторную  силы инерции точки.
силы инерции точки.
5. Составляем дифференциальные уравнения движения точки в относительном движении.
6. Интегрируем дифференциальные уравнения движения.
7. Составляем начальные условия движения для определения произвольных постоянных.
8 Определяем произвольные постоянные интегрирования по начальным условиям задачи.
9. Найденные произвольные постоянные подставляем в результат интегрирования уравнений и получим закон движения точки Если задачу решить с помощью теоремы об изменении кинетической энергии в относительном движении точки, то первые три пункта плана остаются прежними, а далее нужно сделать следующее:
Нарисуем переносную силу инерции точки.
Составим уравнение теоремы об изменении кинетической энергии точки в относительном движении:

Из полученного уравнения находим неизвестную величину.
20-2. Решение задач
Задача 93. Материальная точка массы  может свободно двигаться без трения в плоскости
может свободно двигаться без трения в плоскости  вращающейся вокруг неподвижной вертикальной оси
вращающейся вокруг неподвижной вертикальной оси  с постоянной угловой скоростью
с постоянной угловой скоростью  Найти относительное движение этой точки, если она находится под действием силы тяжести и если ее начальные координаты равны
Найти относительное движение этой точки, если она находится под действием силы тяжести и если ее начальные координаты равны  а начальная относительная скорость равна нулю. Определить также реакцию
а начальная относительная скорость равна нулю. Определить также реакцию  вращающейся плоскости.
вращающейся плоскости.
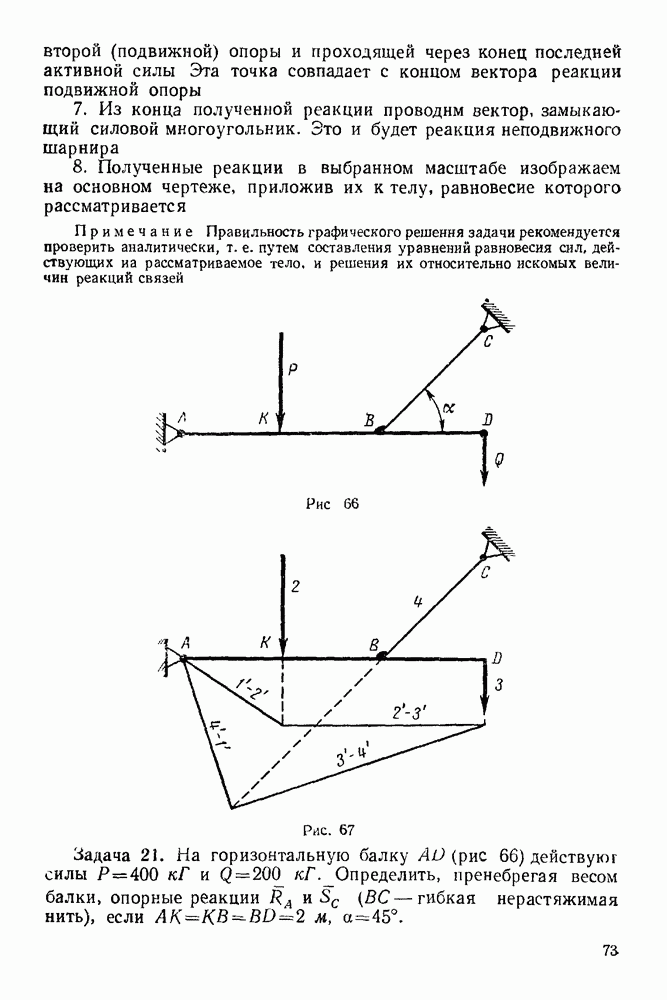
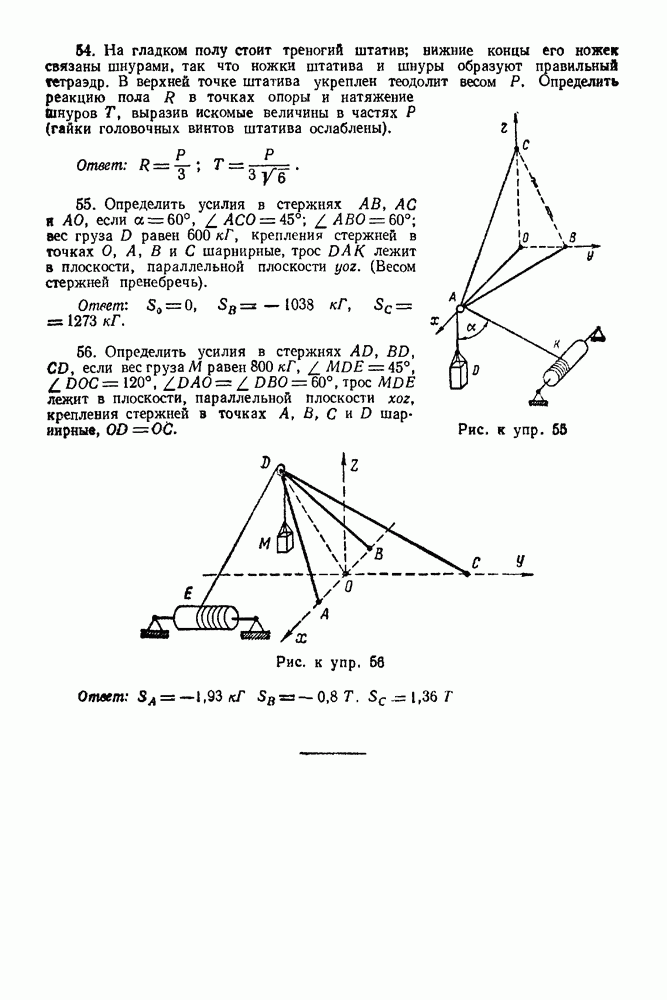
Решение 1 Изображаем точку  в текущий момент (рис. 241).
в текущий момент (рис. 241).
2 Изображаем активную силу  вес точки.
вес точки.
3. Освобождаем точку  от связи, заменяя действие связи реакцией. Связью является гладкая плоскость
от связи, заменяя действие связи реакцией. Связью является гладкая плоскость  Реакция
Реакция  плоскости направлена по нормали к плоскости.
плоскости направлена по нормали к плоскости.
4. Прикладываем переносную силу инерции  и поворотную
и поворотную  силу инерции течки. Для выделения переносного движения точки скрепляем ее с подвижной системой координат
силу инерции течки. Для выделения переносного движения точки скрепляем ее с подвижной системой координат  В этом случае точка будет принадлежать вращающейся плоскости, следовательно,
В этом случае точка будет принадлежать вращающейся плоскости, следовательно,  направлена в сторону, противоположную
направлена в сторону, противоположную  для выделения относительного движения мысленно останавливаем подвижную систему координат и приходим к заключению, что
для выделения относительного движения мысленно останавливаем подвижную систему координат и приходим к заключению, что  лежит в плоскости
лежит в плоскости  Векторы
Векторы  образуют правую систему координат, а вектор направлен в сторону, противоположную направлению вектора
образуют правую систему координат, а вектор направлен в сторону, противоположную направлению вектора  т. е.
т. е. 


Рис. 241.
5. Составляем дифференциальные уравнения движения точки в относительном движении:

Дифференциальные уравнения будут:

6. Интегрируем дифференциальные уравнения движения точки  характеристическое уравнение для данного линейного уравнения будет
характеристическое уравнение для данного линейного уравнения будет  корни этого уравнения
корни этого уравнения  следовательно, общее решение дифференциального уравнения (20-3) таково:
следовательно, общее решение дифференциального уравнения (20-3) таково:

Интегрируем уравнение (20-4):

7. Составляем начальные условия движения для определения произвольных постоянных 
При 

8. Определяем произвольные постоянные интегрирования. Для этого подставляем начальные условия движения в уравнения (20-6), (20-7), (20-8), (20-9) и получаем:

9. Найденные произвольные постоянные подставляем в уравнения (20-6) и (20-9) и получаем закон относительного движения точки:

Из уравнения (20-5) 
Следовательно,

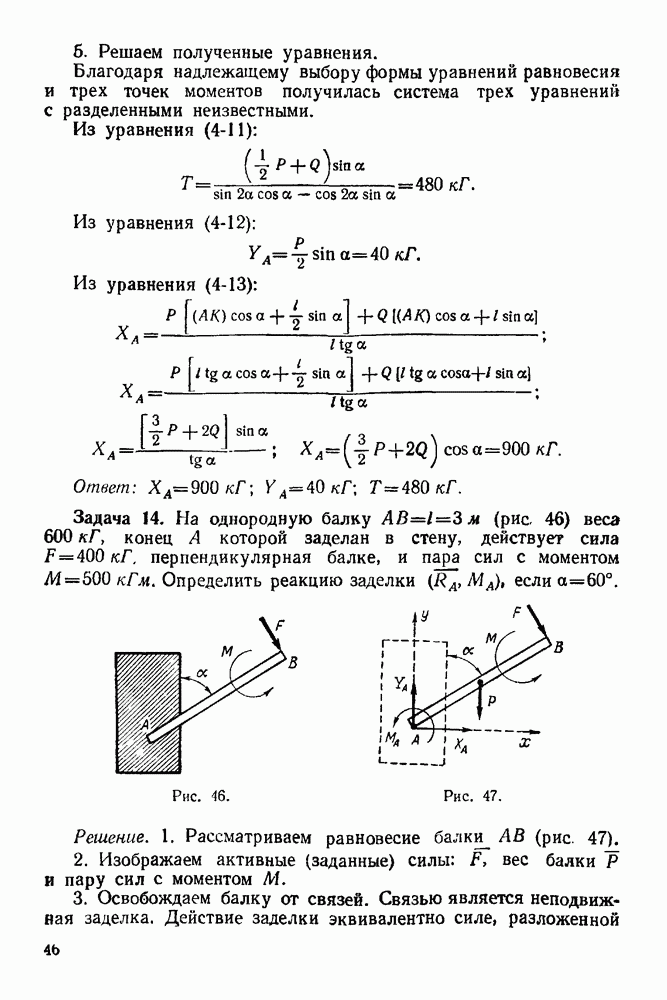
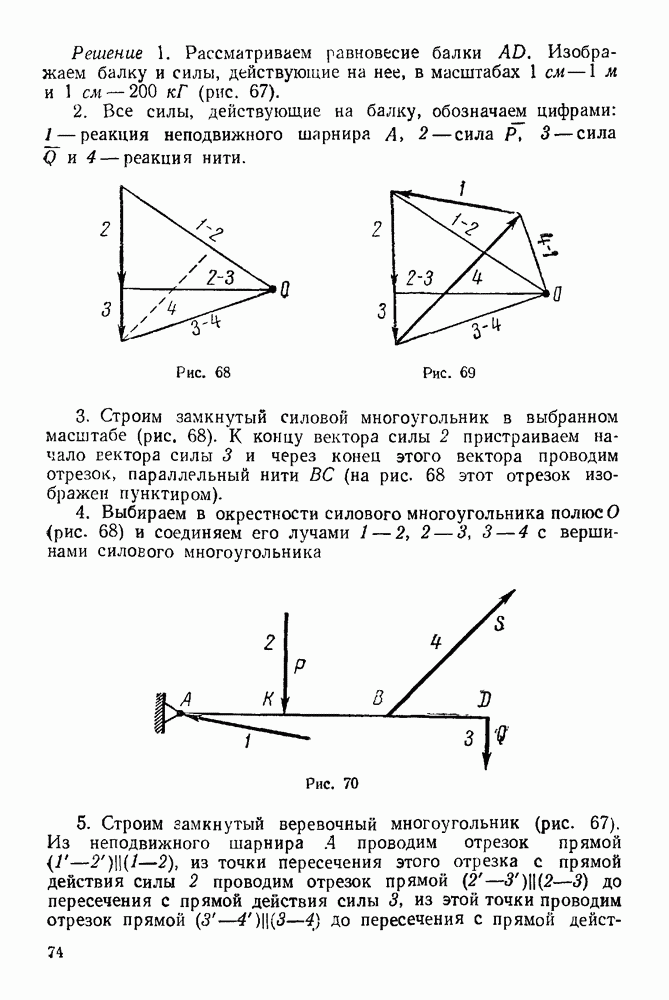
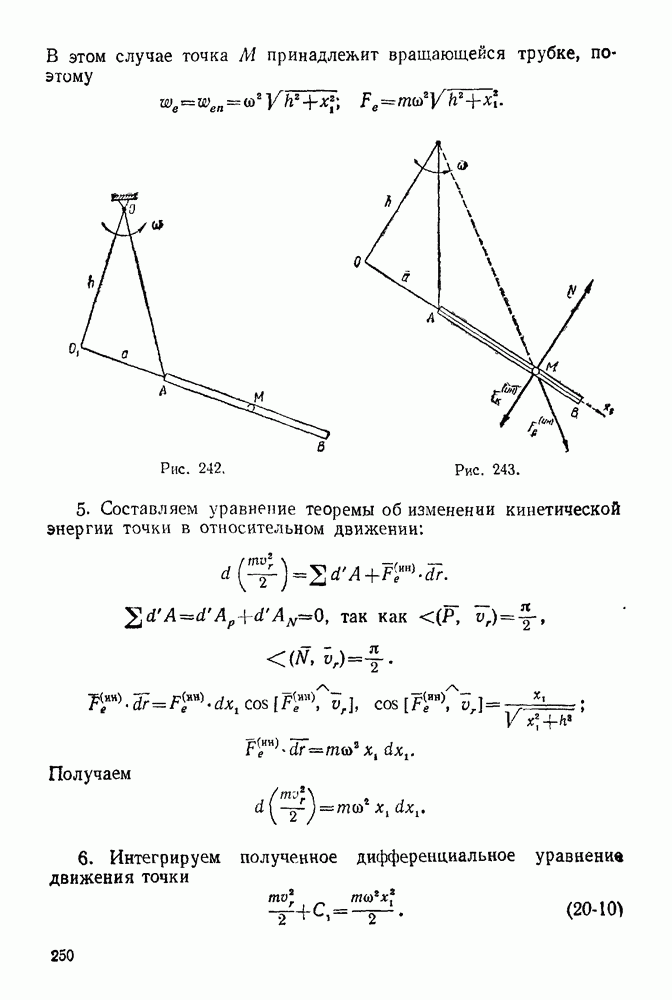
Задача 94. Прямолинейная трубка  (рис. 242) вращается в горизонтальной плоскости вокруг неподвижной точки О с постоянной угловой скоростью со. Внутри трубки может двигаться без трения шарик
(рис. 242) вращается в горизонтальной плоскости вокруг неподвижной точки О с постоянной угловой скоростью со. Внутри трубки может двигаться без трения шарик  массы
массы  Найти относительную по отношению к трубке скорость шарика в зависимости от расстояния, проходимого шариком, если в начальный момент он находился в точке А и его начальная относительная скорость равна нулю,
Найти относительную по отношению к трубке скорость шарика в зависимости от расстояния, проходимого шариком, если в начальный момент он находился в точке А и его начальная относительная скорость равна нулю, 
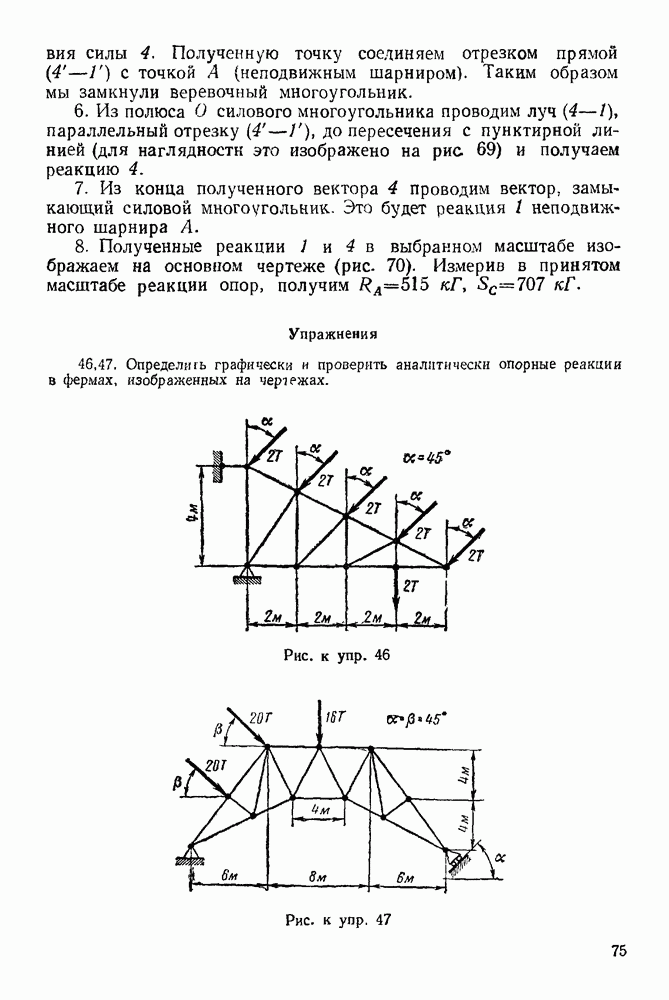
Решение. 1. Изображаем точку  в текущий момент времени (рис. 243).
в текущий момент времени (рис. 243).
2. Изображаем активную силу, действующую на точку,  -вес точки.
-вес точки.
3. Освобождаем точку от связи, заменяя действие связи реакцией, в Связью является гладкая трубка. Реакция трубки  направлена по нормали к трубке.
направлена по нормали к трубке. 
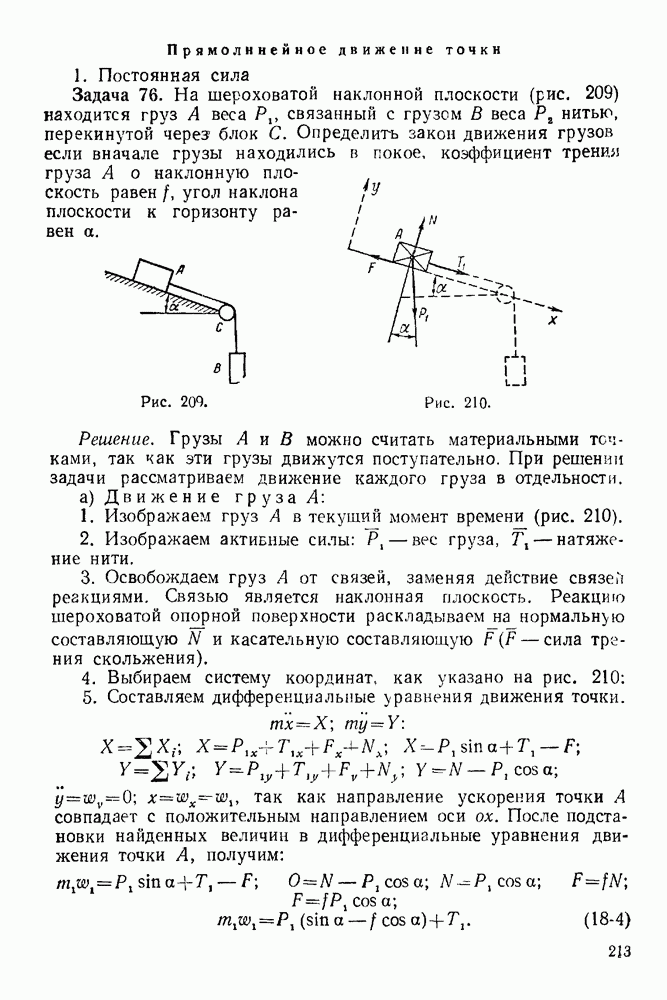
4. Прикладываем переносную силу инерции точки  Для выделения переносного движения точки, мысленно точку скрепляем с подвижной системой координат
Для выделения переносного движения точки, мысленно точку скрепляем с подвижной системой координат
В этом случае точка  принадлежит вращающейся трубке, поэтому
принадлежит вращающейся трубке, поэтому


Рис. 242.

Рис. 243.
5. Составляем уравнение теоремы об изменении кинетической энергии точки в относительном движении:

Получаем

6. Интегрируем полученное дифференциальное уравнение движения точки

7. Составляем начальные условия движения для определения произвольной постоянной интегрирования 

8. Определяем произвольную постоянную 
Начальные условия задачи подставляем в уравнение (20-10), получаем:

9. Подставляем найденную произвольную постоянную  в уравнение (20-10), находим относительную скорость точки как функцию
в уравнение (20-10), находим относительную скорость точки как функцию 

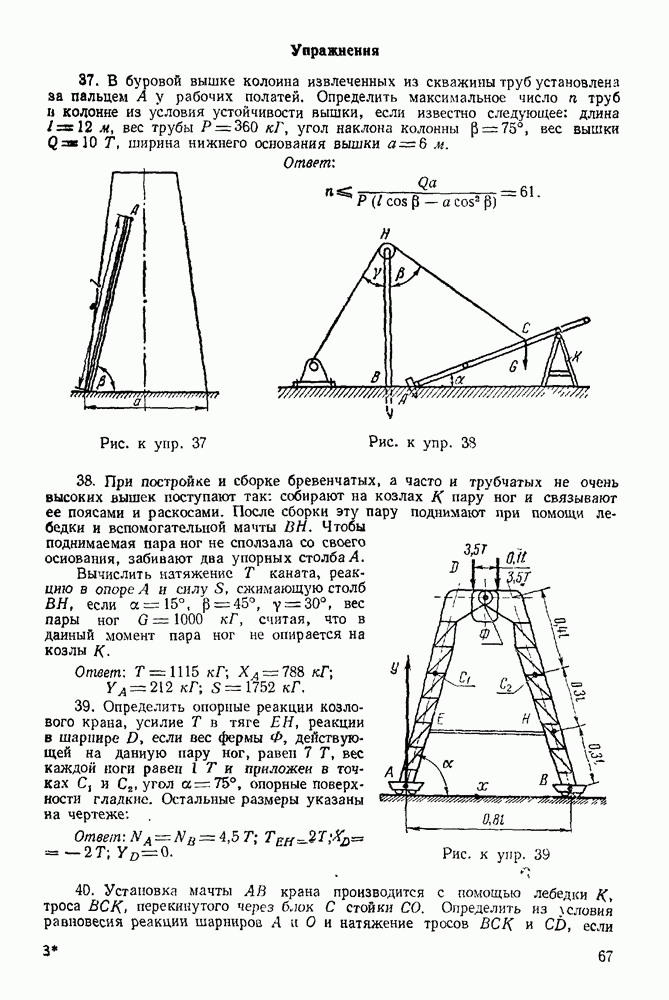
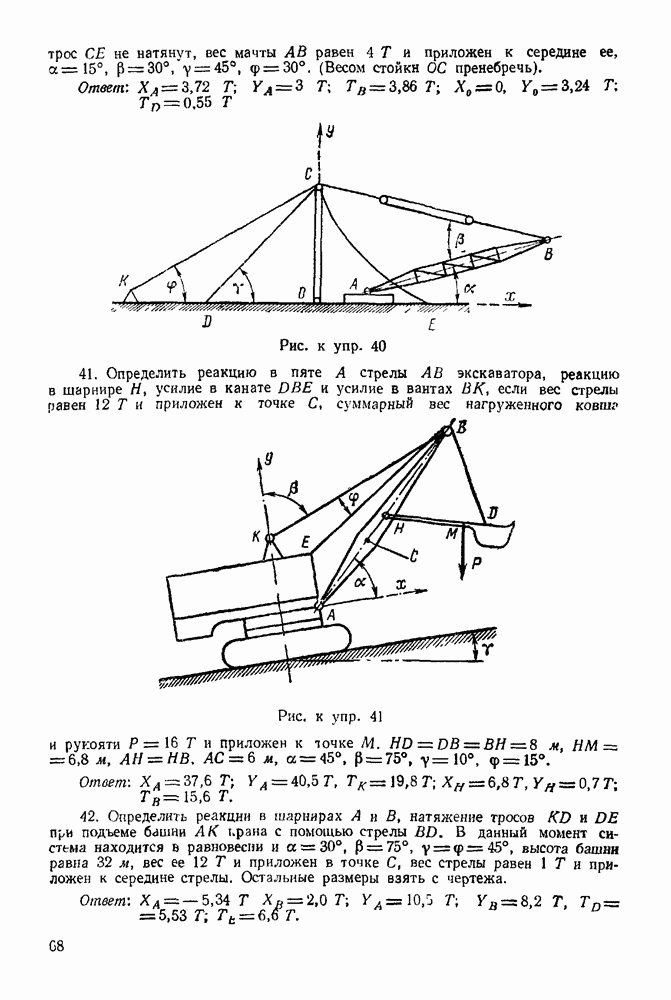
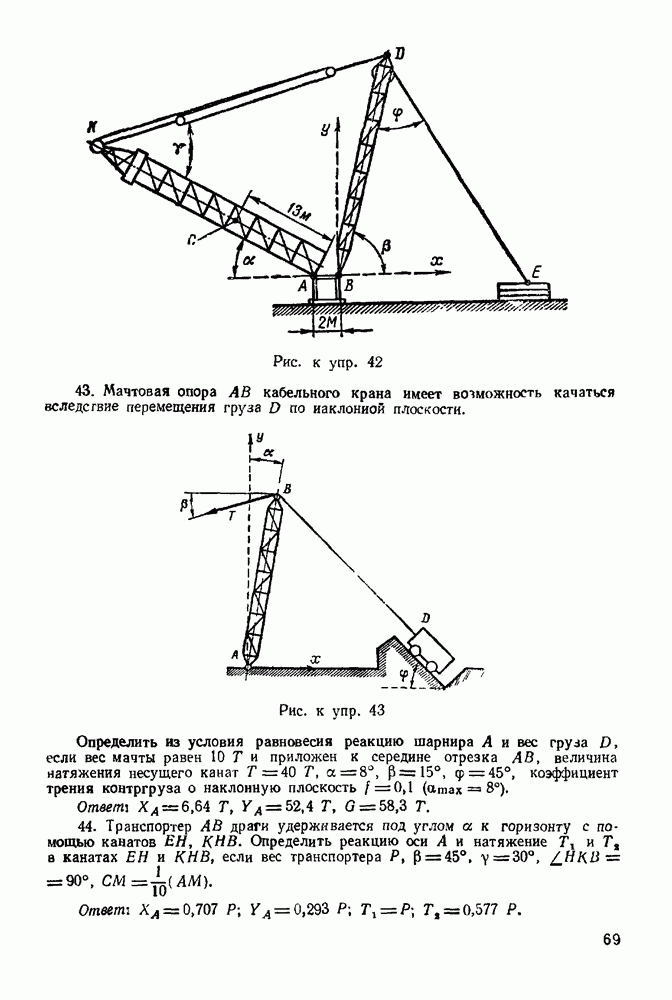
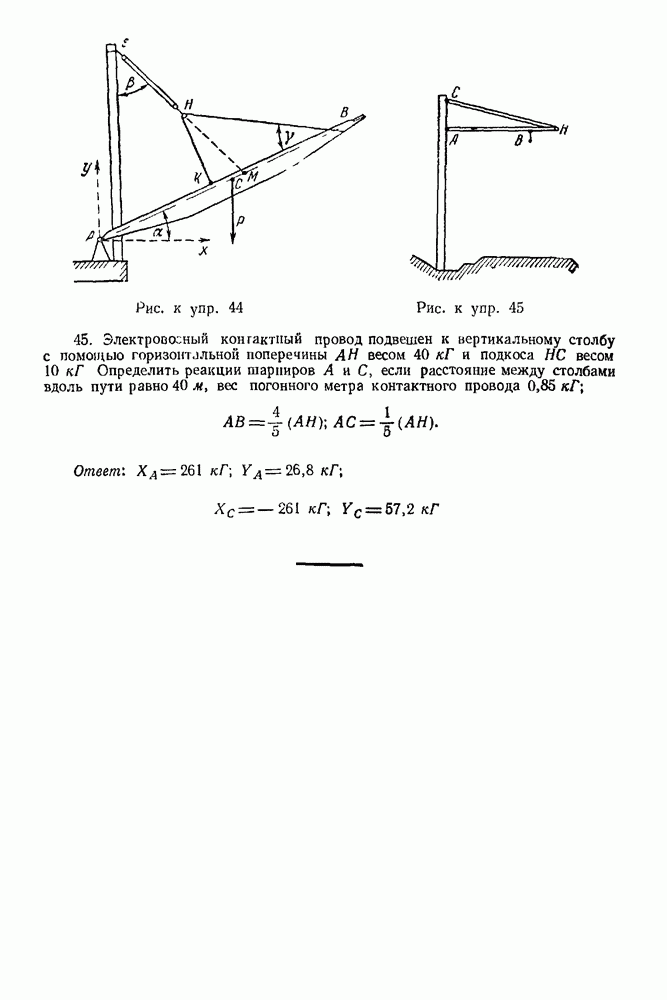
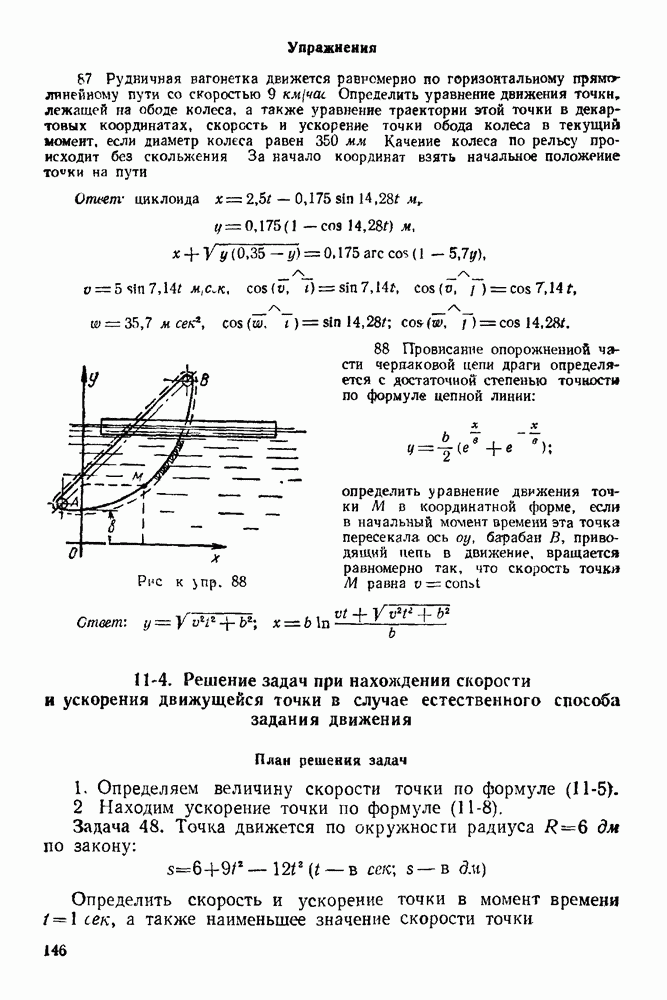
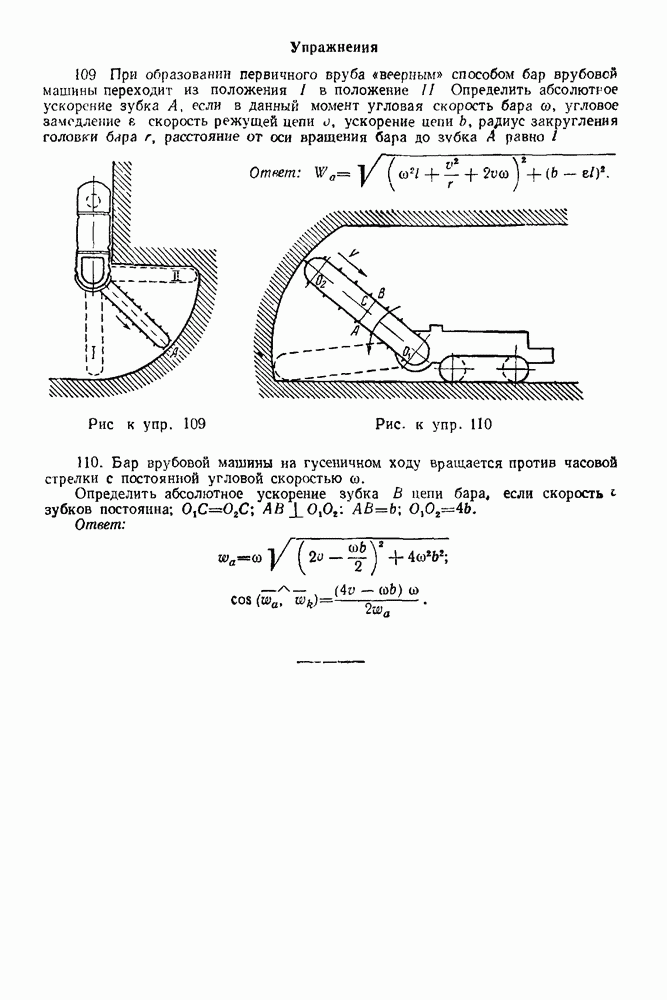
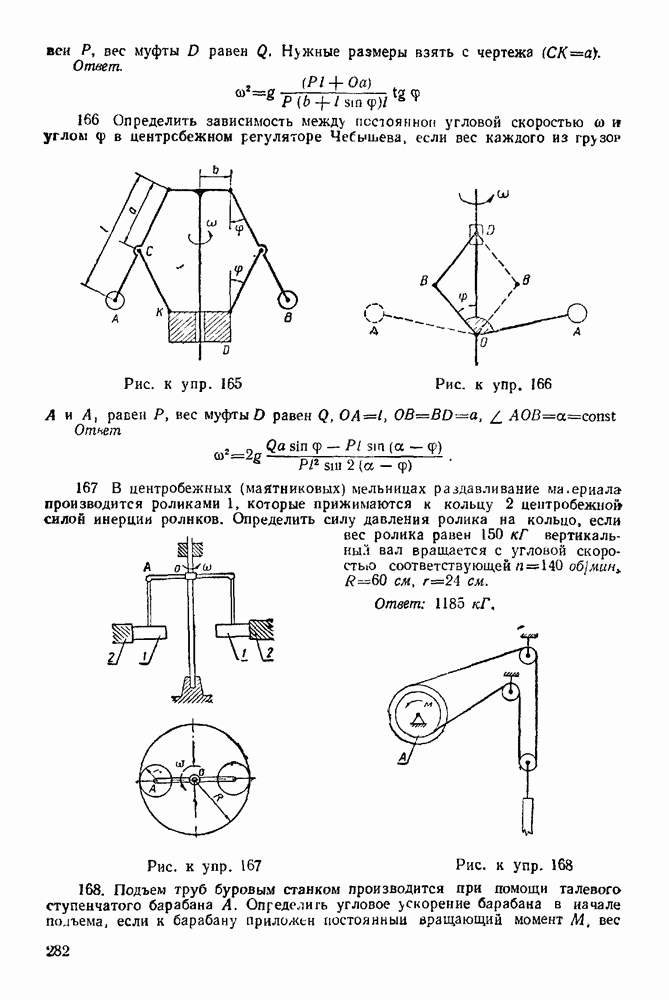
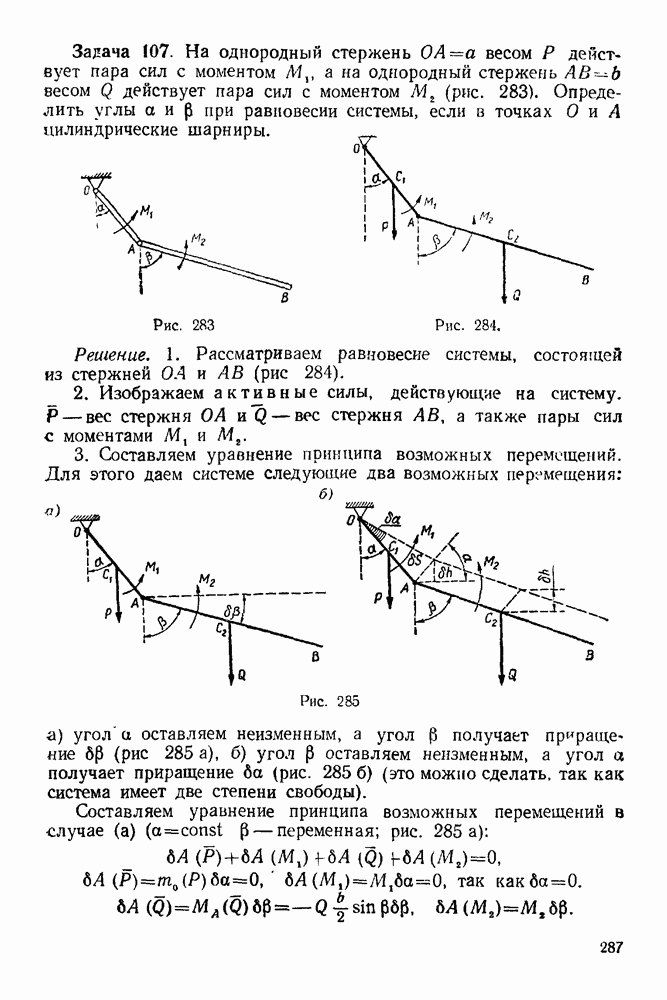
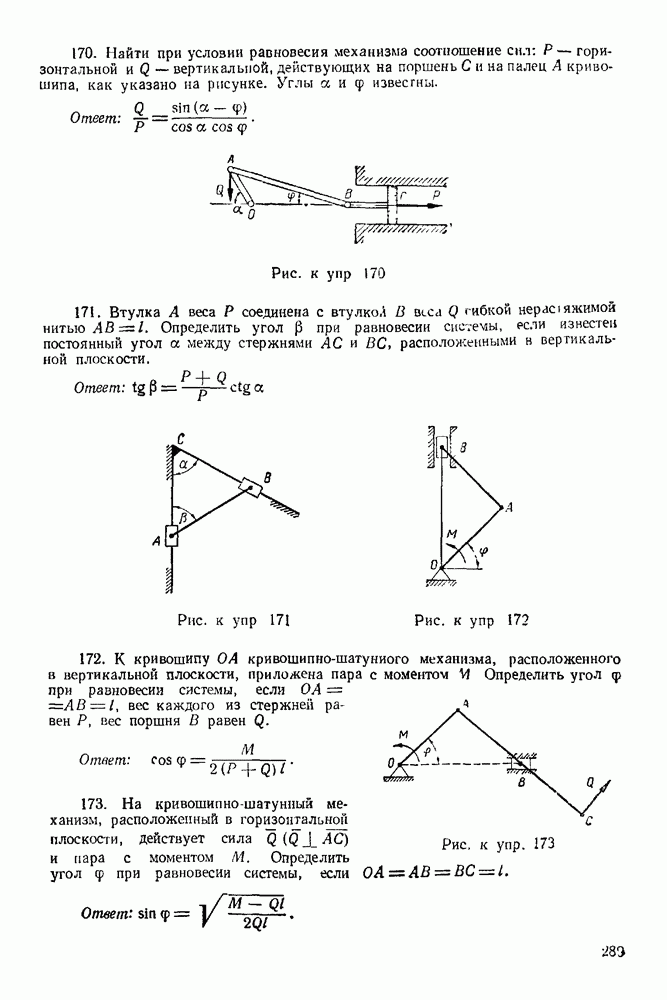
Упражнения
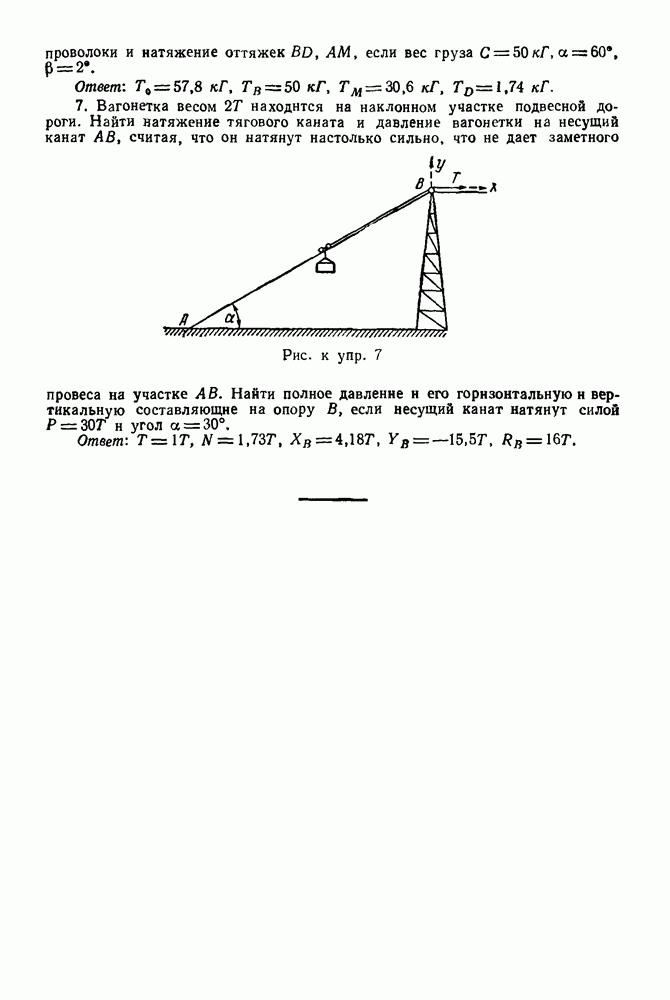
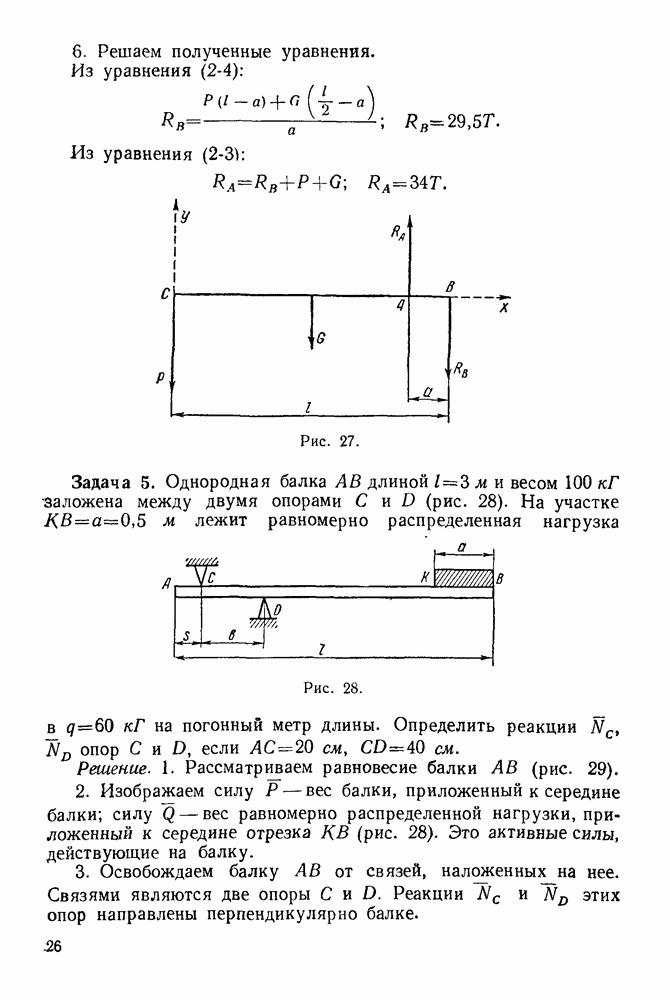
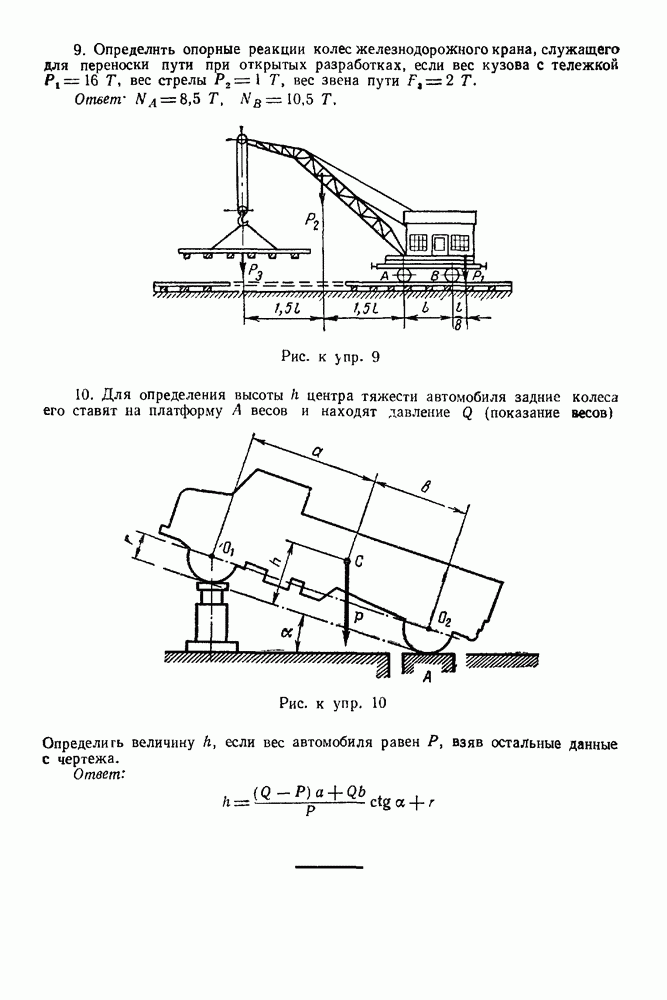
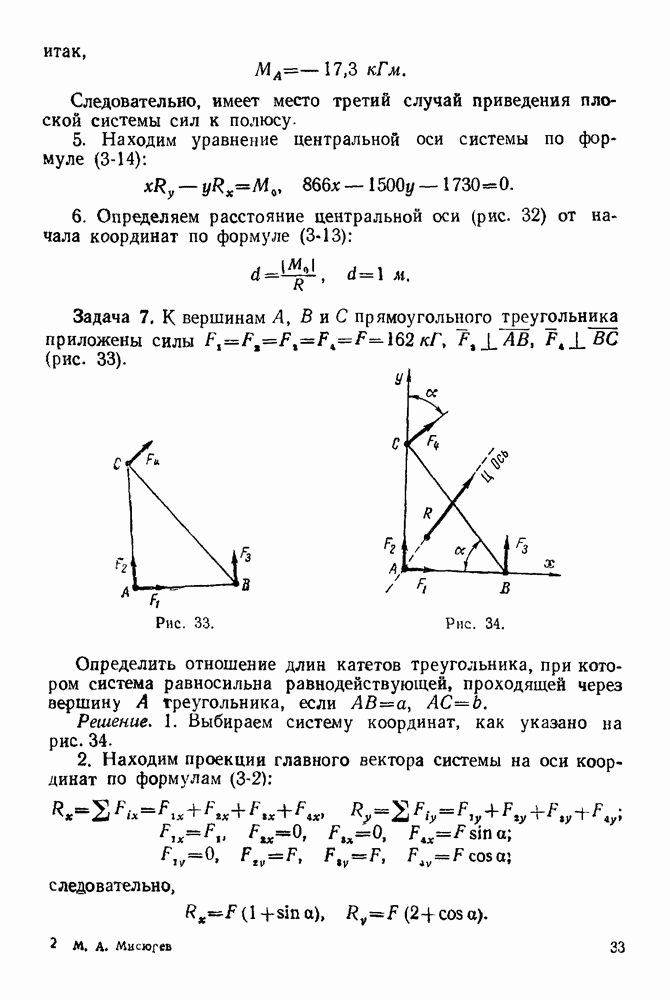
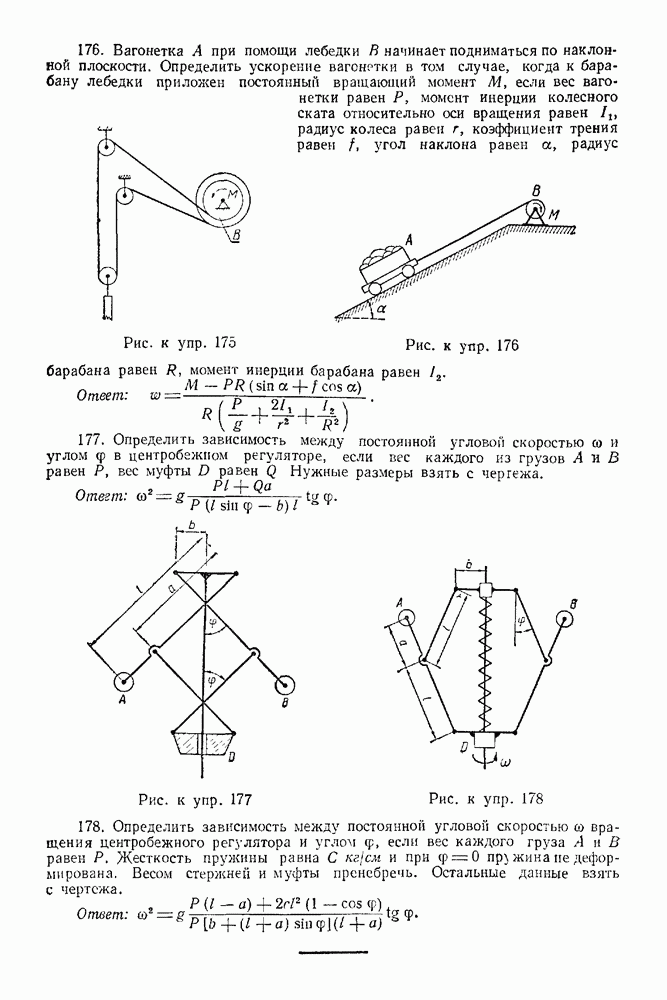
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
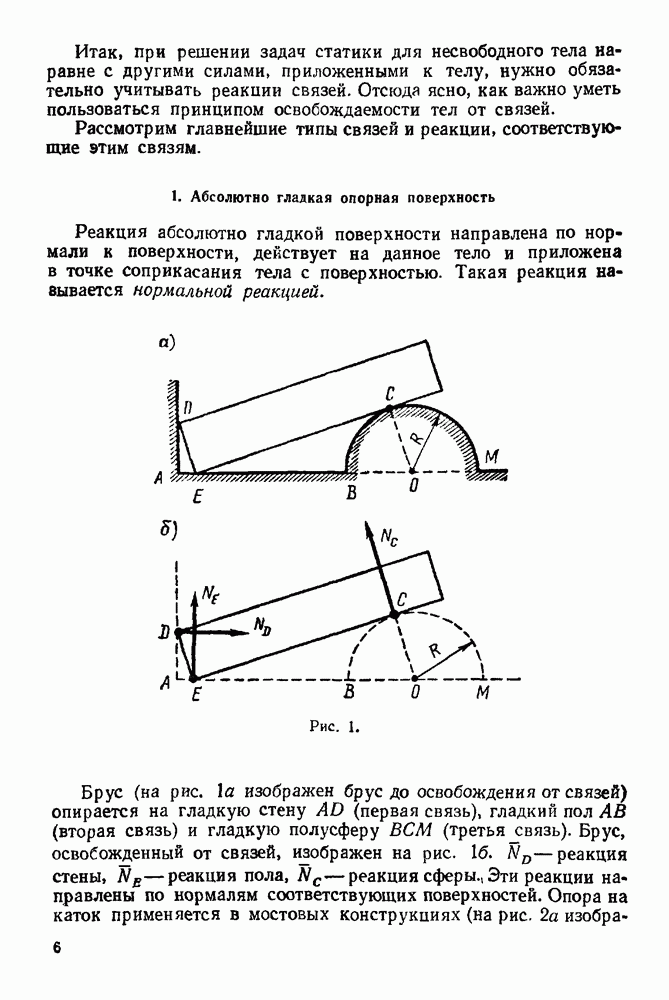
- 1. Абсолютно гладкая опорная поверхность
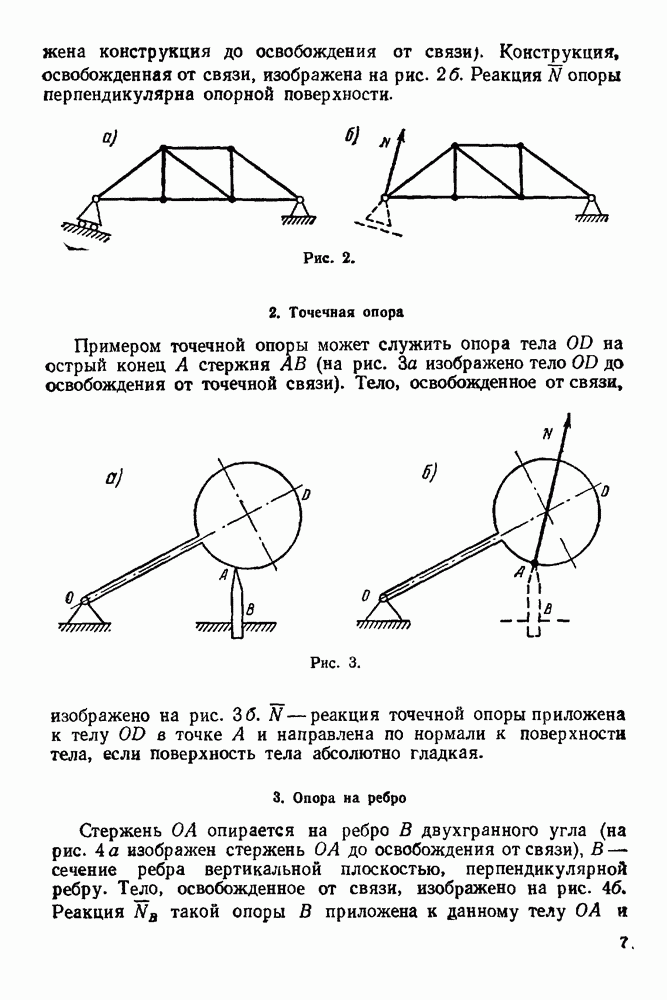
- 2. Точечная опора
- 3. Опора на ребро
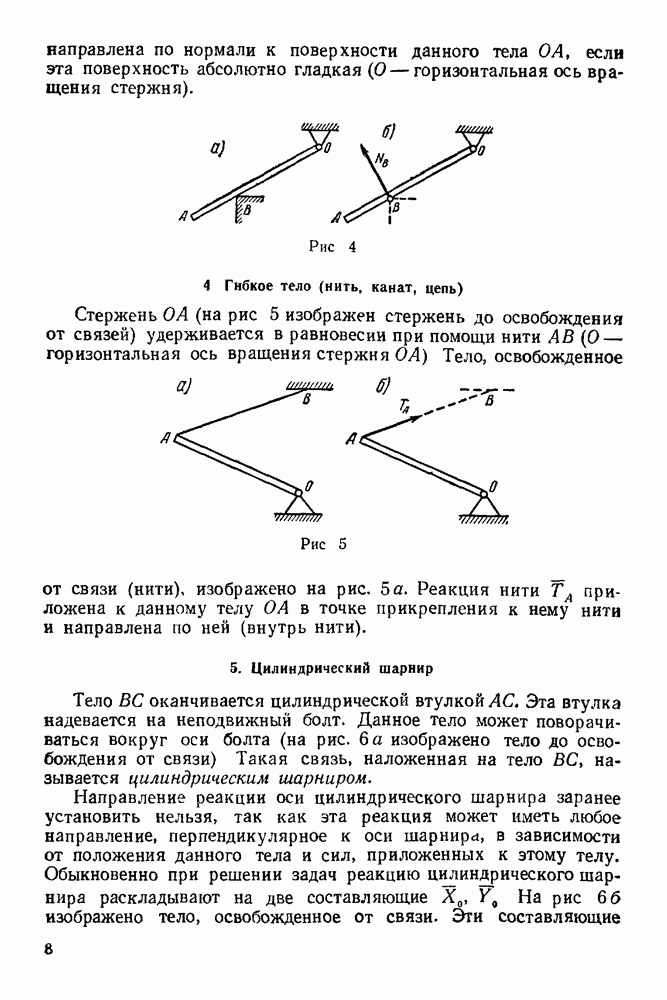
- 4. Гибкое тело (нить, канат, цепь)
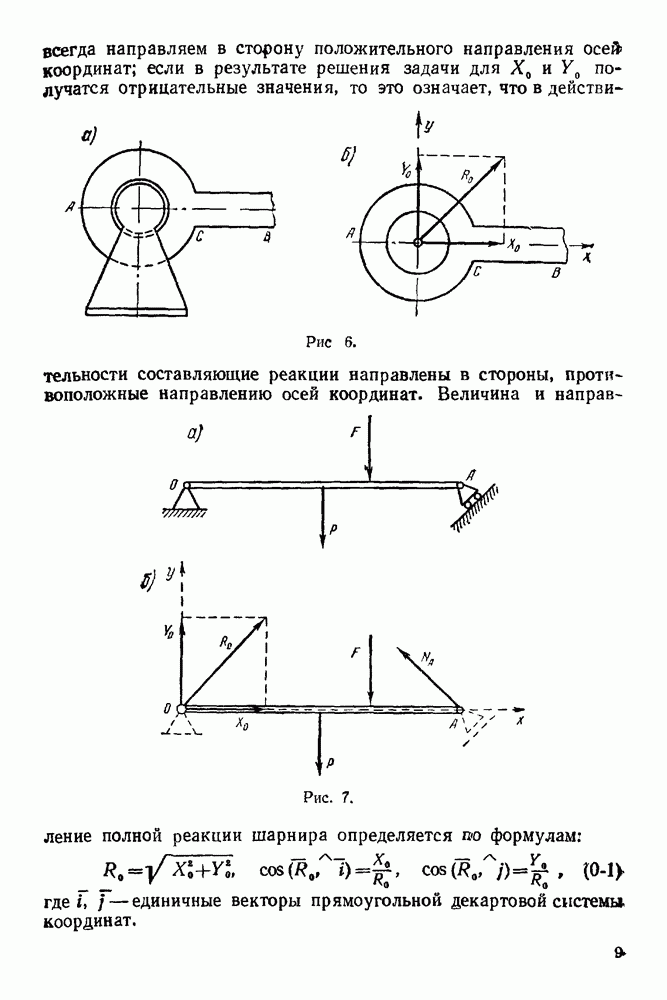
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
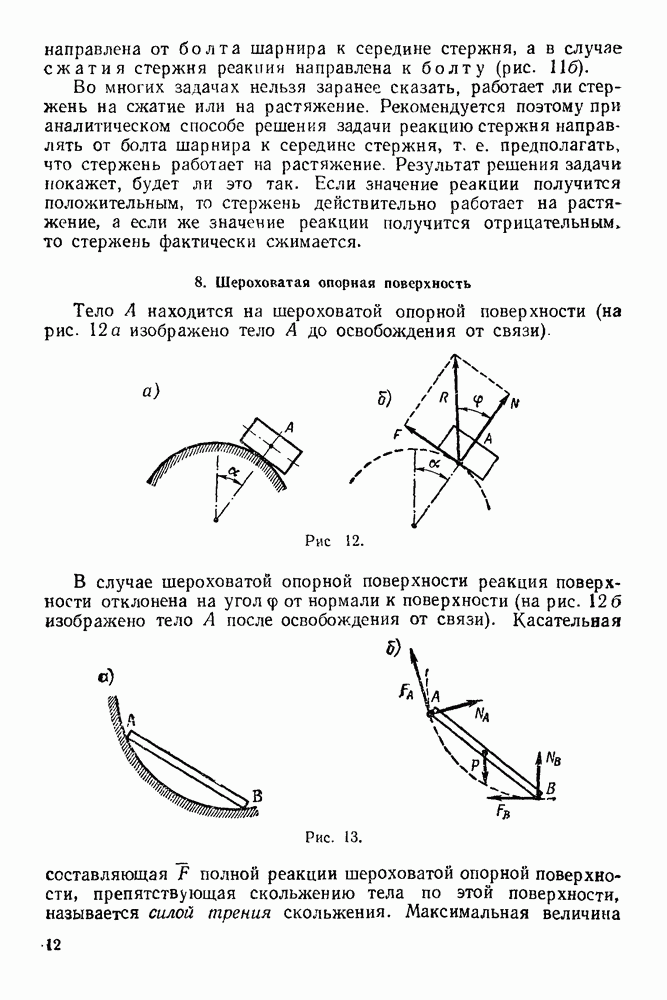
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
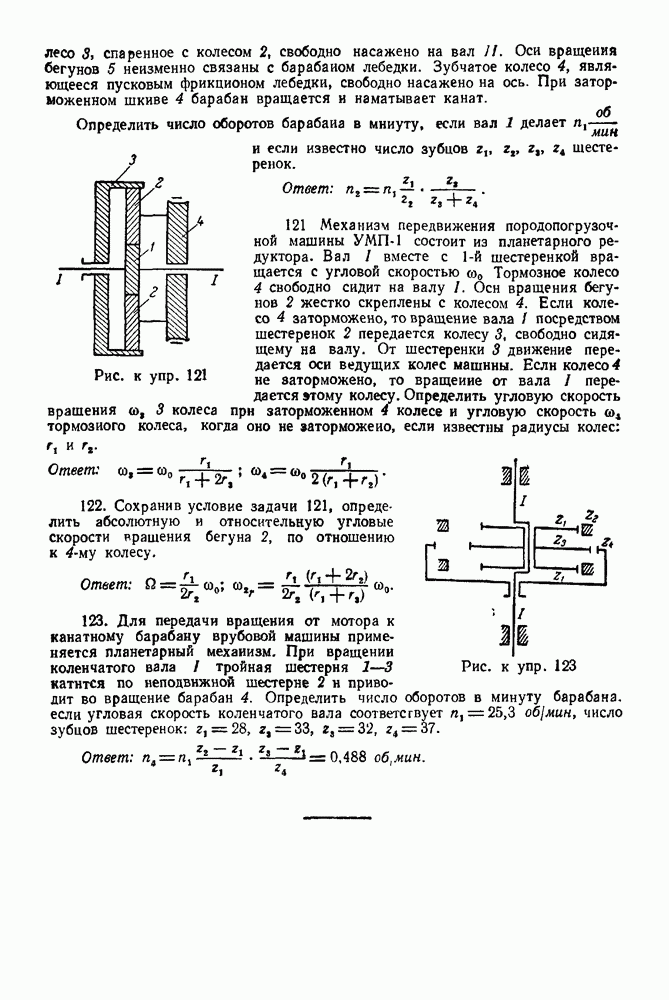
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
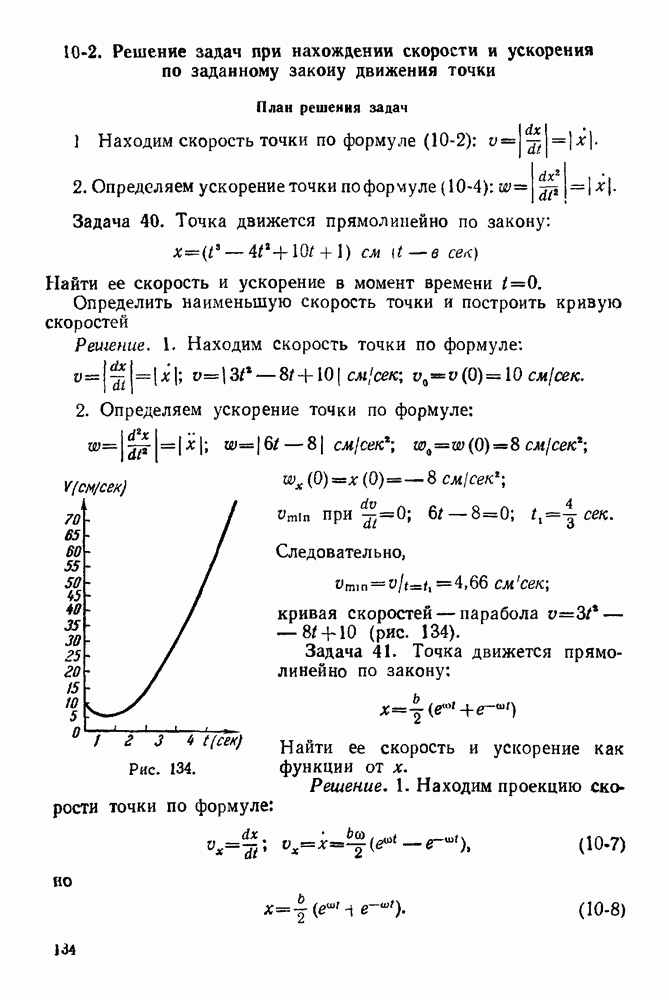
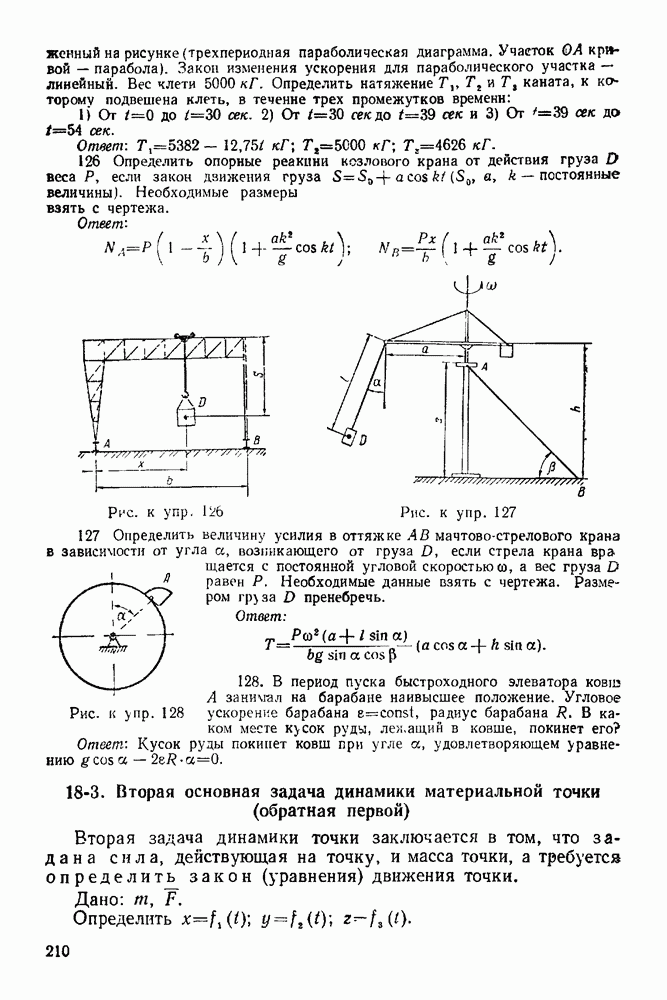
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
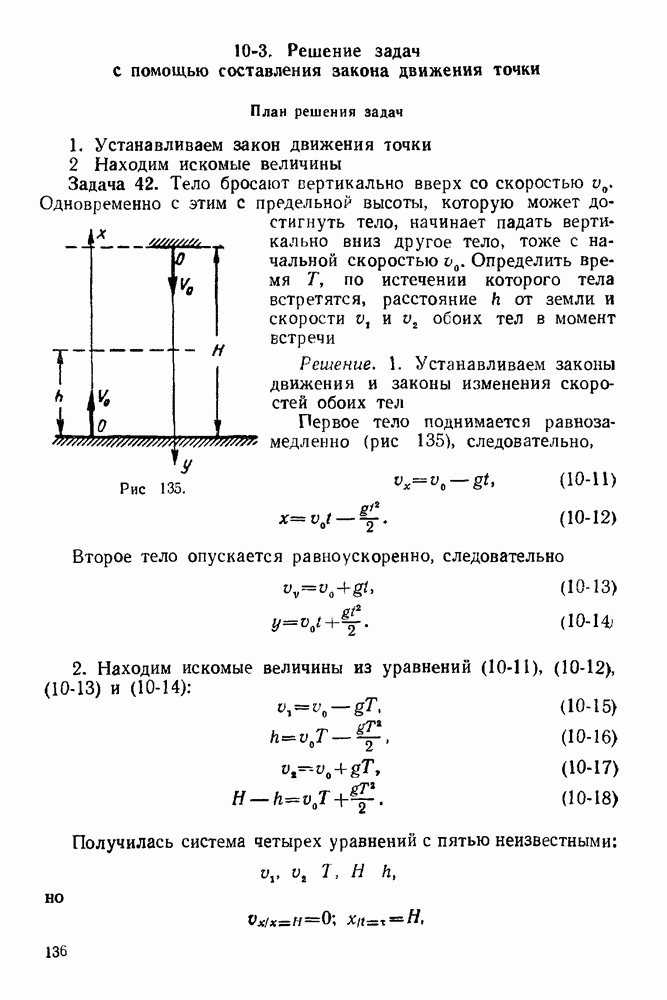
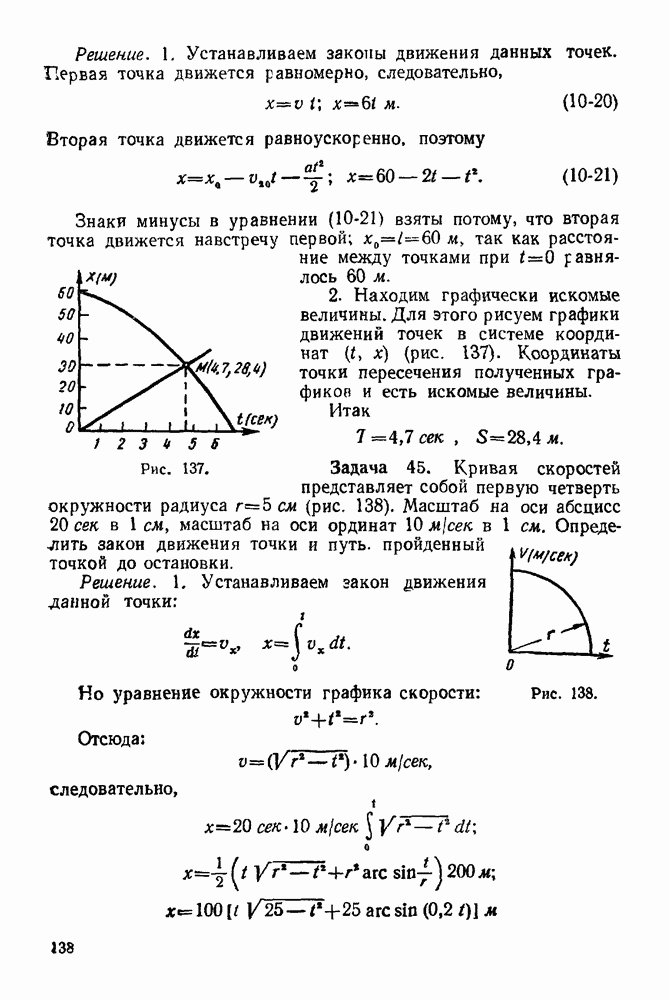
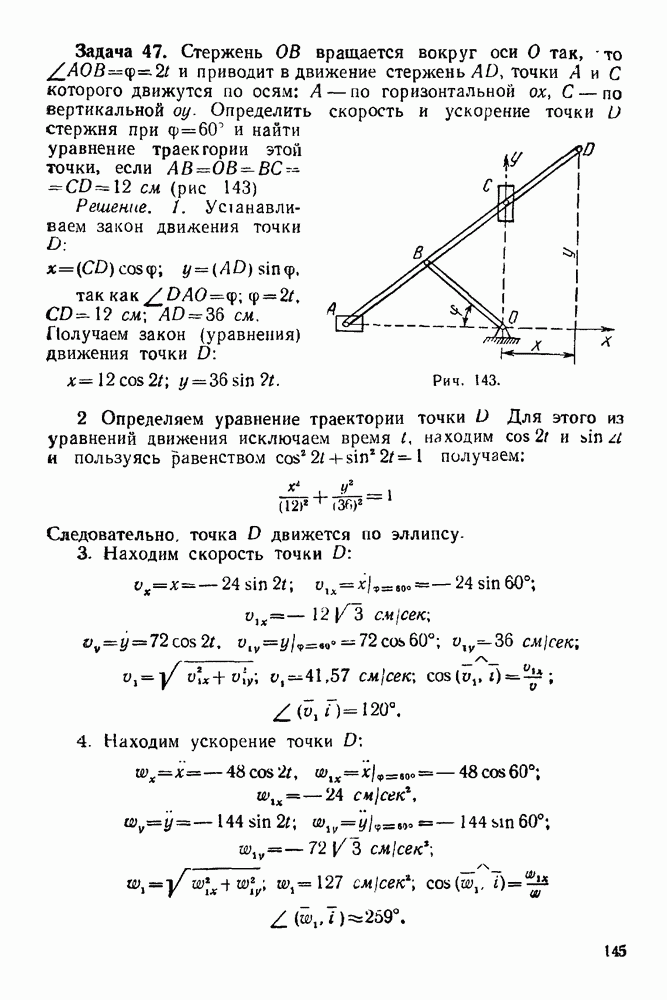
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
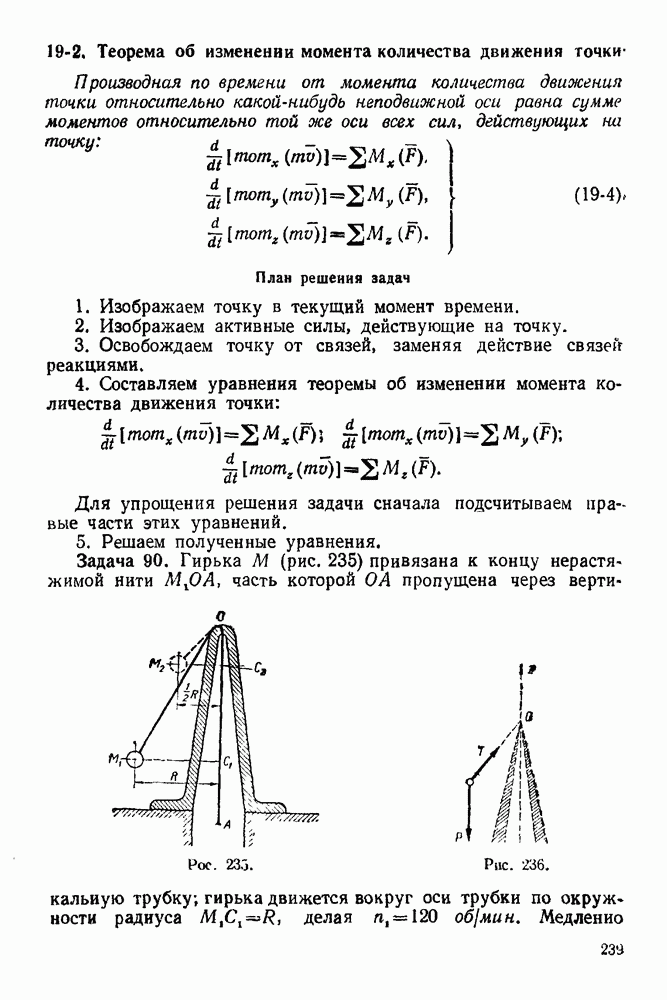
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
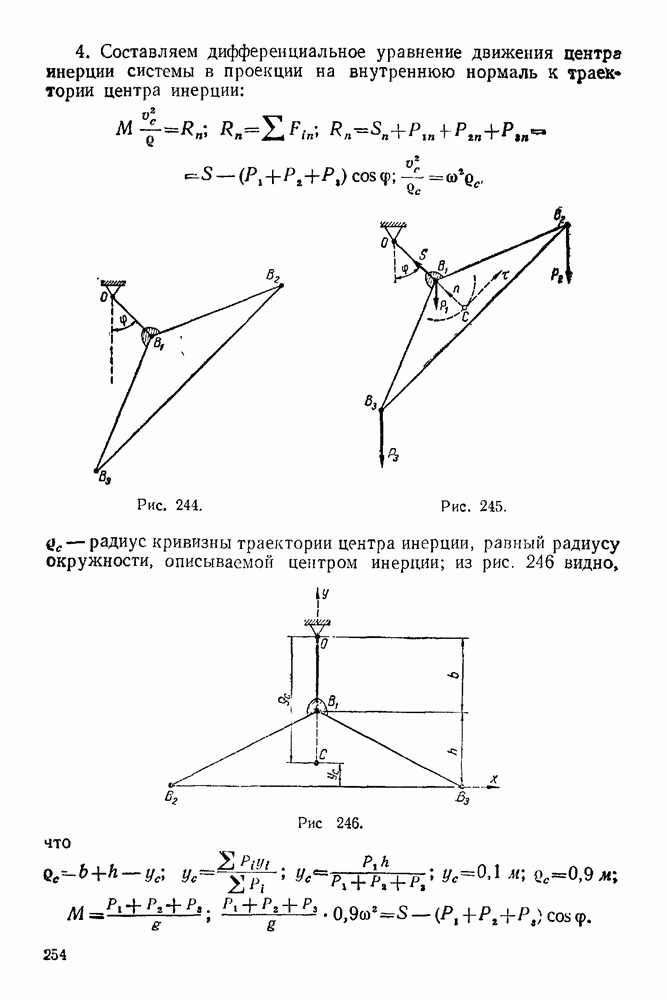
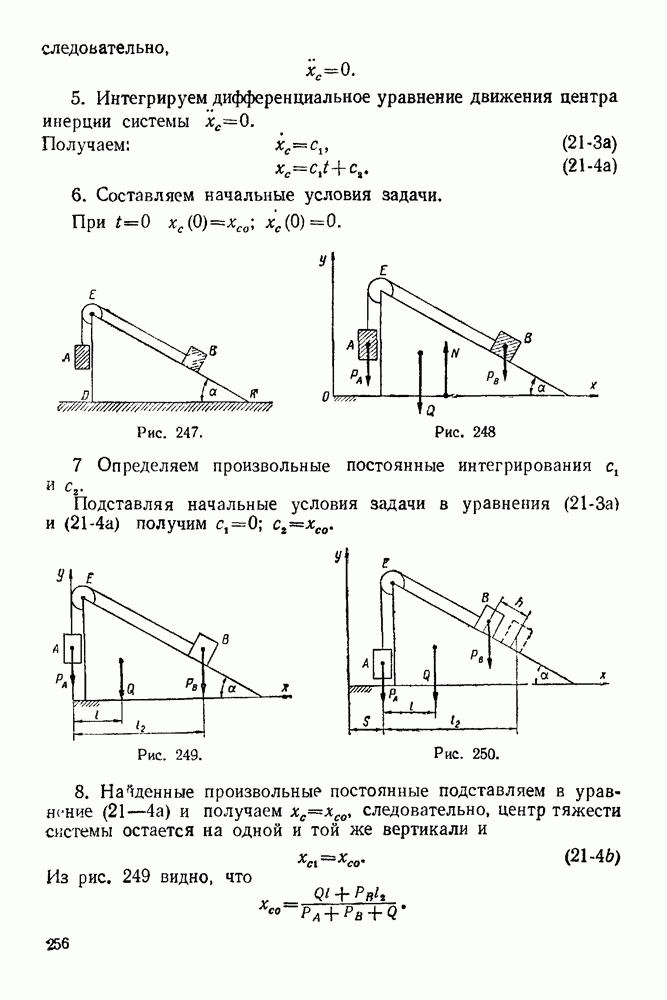
- 21-1. Теорема о движении центра инерции системы
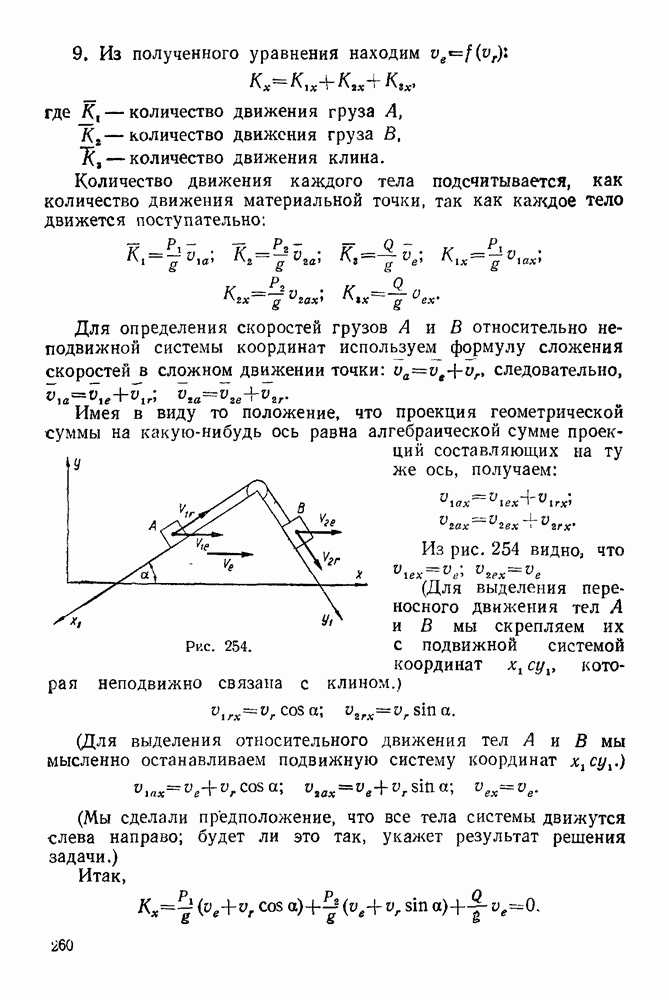
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
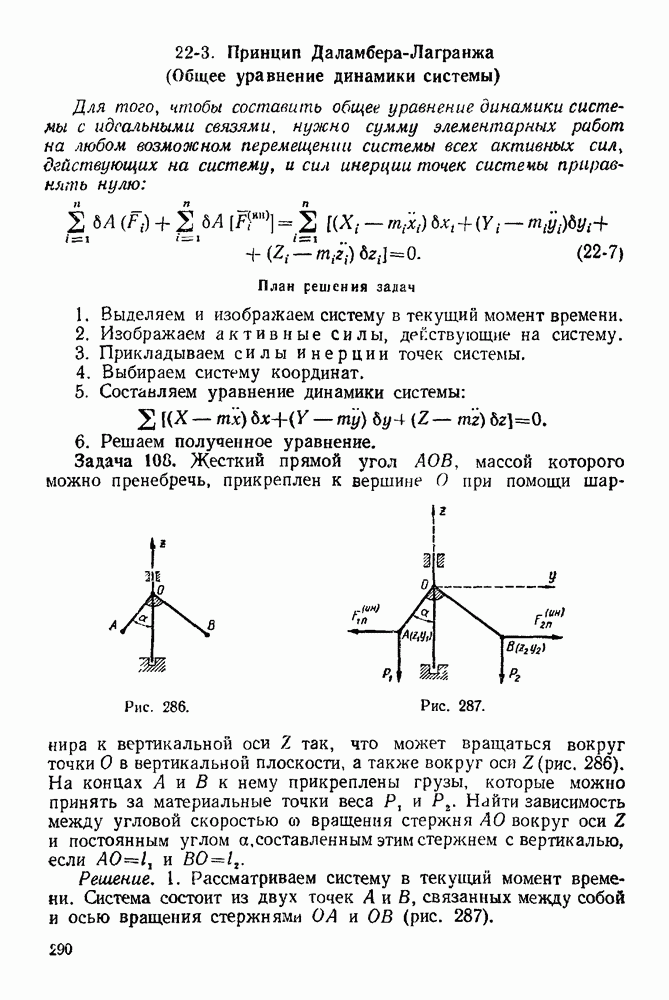
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР