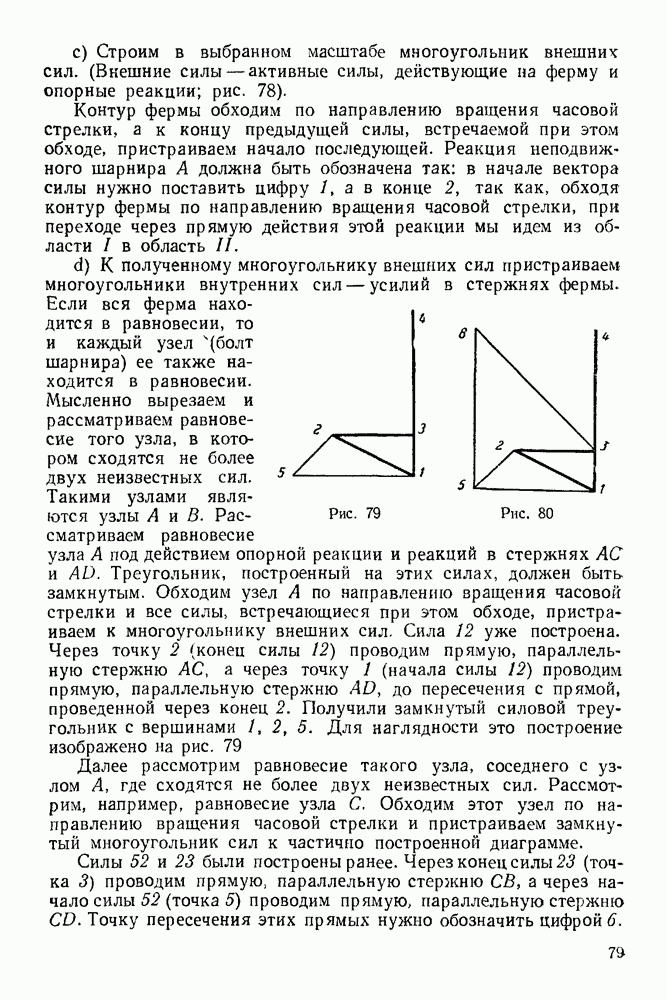
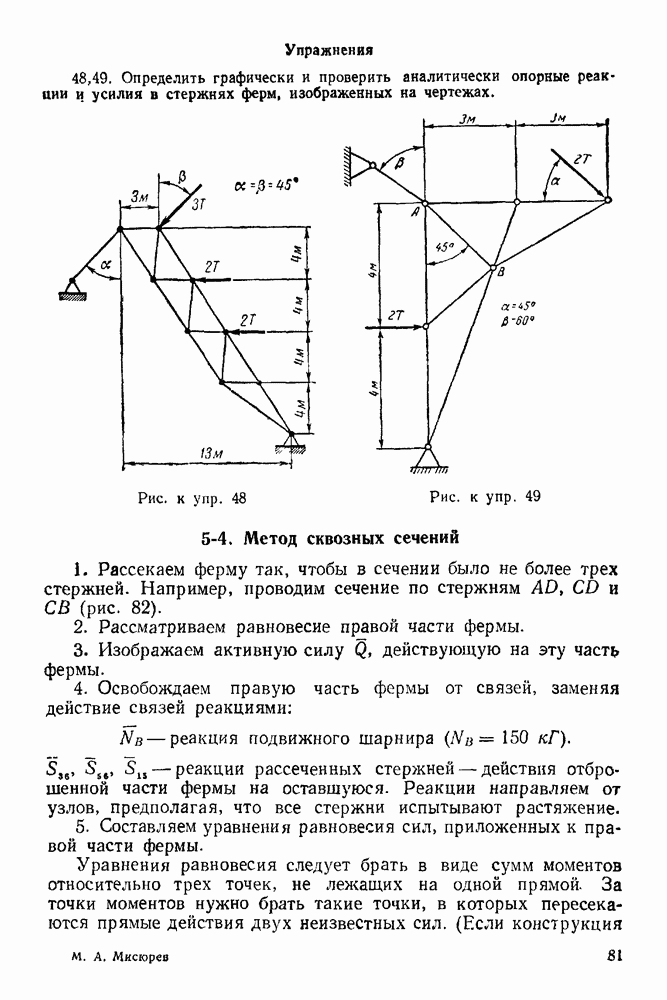
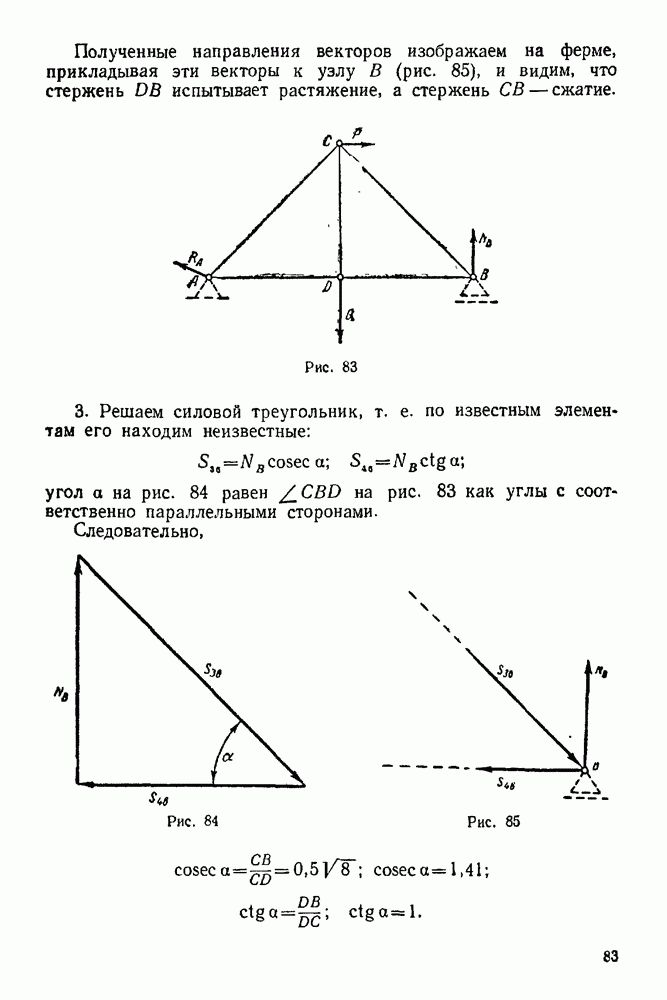
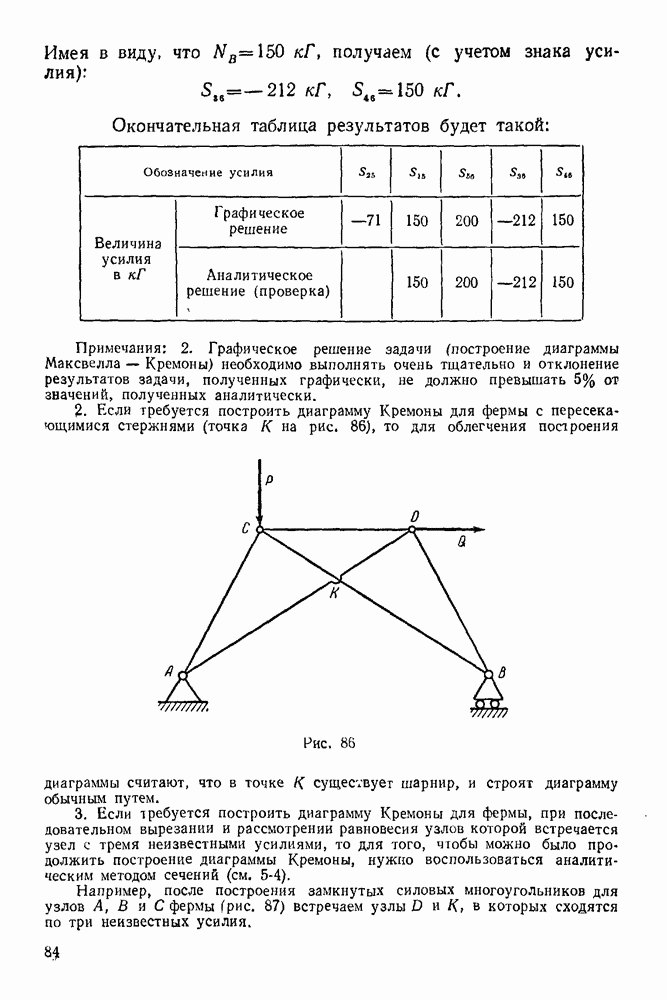
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
ГЛАВА XXI. ОБЩИЕ ТЕОРМЫ ДИНАМИКИ СИСТЕМЫ
21-1. Теорема о движении центра инерции системы
Центр инерции системы движется как материальная точка, масса которой равна массе всей системы и на которую действуют все внешние силы, приложенные к системе;

где  масса всей системы,
масса всей системы,  ускорение центра инерции,
ускорение центра инерции,  главный вектор внешних сил системы.
главный вектор внешних сил системы.
Центром инерции системы называется такая геометрическая точка, координаты которой определяются следующими формулами:

Внутренними силами системы  называются силы взаимодействия точек системы друг с другом. Внешними силами системы
называются силы взаимодействия точек системы друг с другом. Внешними силами системы  называются силы взаимодействия точек системы с точками и телами, не входящими в данную систему.
называются силы взаимодействия точек системы с точками и телами, не входящими в данную систему.
А. Дифференциальные уравнения движения центра инерции системы в декартовых координатах:

Б. Дифференциальные уравнения движения центра инерции системы в естественной форме:

где  - скорость центра инерции системы,
- скорость центра инерции системы,  радиус кривизны траектории центра инерции системы.
радиус кривизны траектории центра инерции системы.
Все задачи, решаемые с помощью теоремы о движении центра инерции системы, можно разделить, как и задачи динамики точки, на две группы.
К первой группе задач относятся такие задачи, в которых известен закон движения центра инерции системы, а нужно определить внешние силы, действующие на систему (первая задача динамики).
Ко второй группе задач относятся такие задачи, в которых известны внешние силы, действующие на систему, а нужно определить закон движения центра инерции системы (вторая задача динамики).
План решения первой группы задач
1. Выделяем систему и изображаем ее в текущий момент времени.
2. Изображаем внешние силы, действующие на систему.
3. Выбираем систему координат.
4. Составляем дифференциальные уравнения движения центра инерции системы в выбранной системе координат; уравнения (21-3) или (21-4).
5. По заданному закону движения центра инерции системы находим путем дифференцирования проекции ускорения центра на координатные оси.
6. Решаем полученные уравнения, найдем внешние силы, действующие на систему.
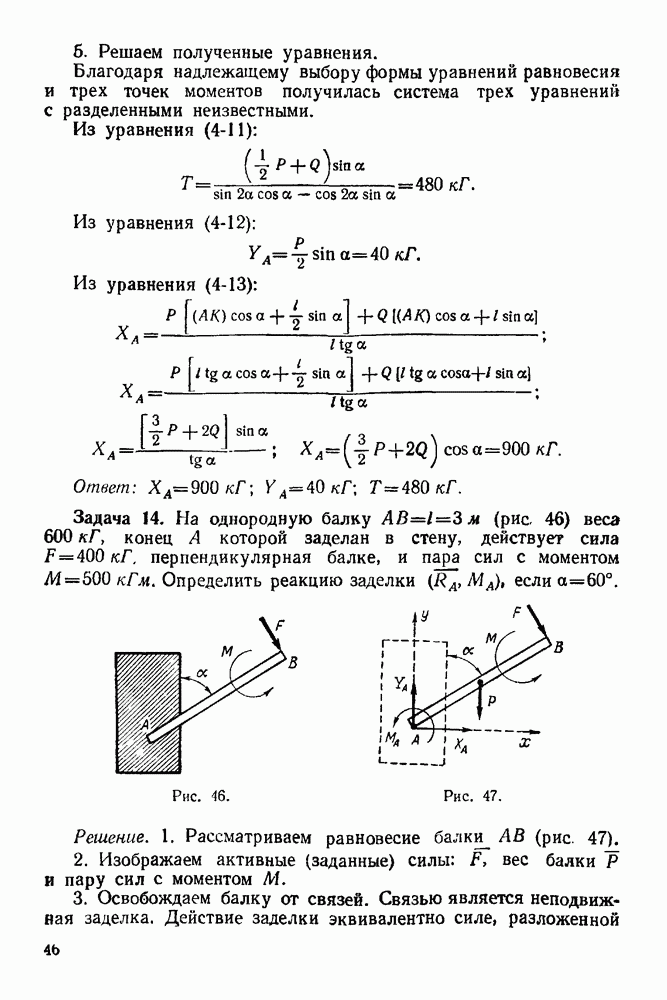
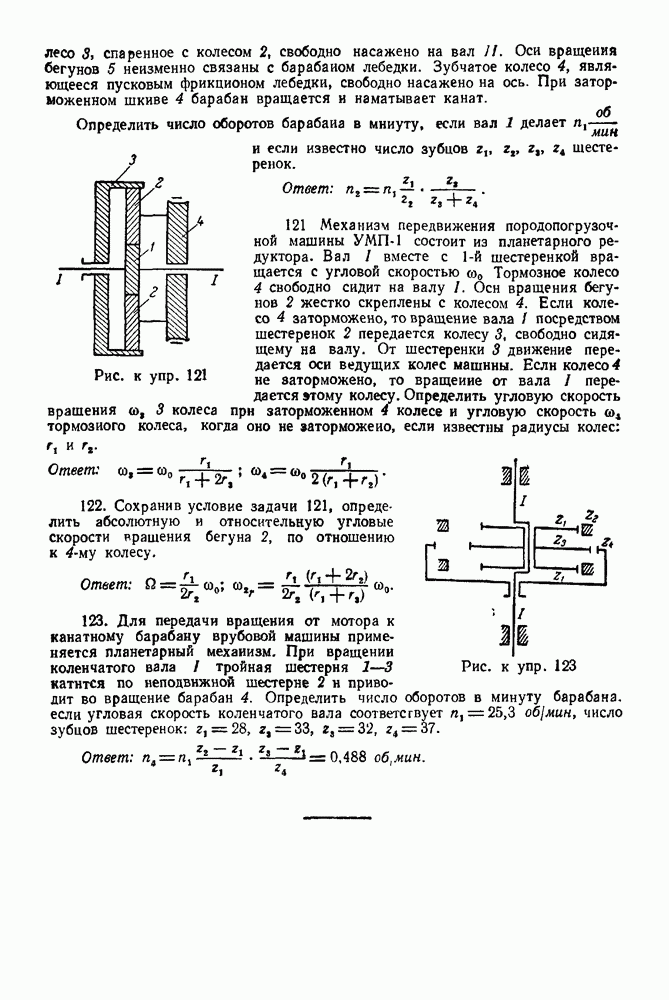
Задача 95. Материальная система состоит из трех точек  веса которых соответственно равны
веса которых соответственно равны 
Точки соединены между собой и с горизонтальной осью О вращения жесткими стержнями. Определить, пренебрегая массами стержней, усилие  в стержне
в стержне  в момент времени
в момент времени  сек, если
сек, если  (время
(время  измеряется в
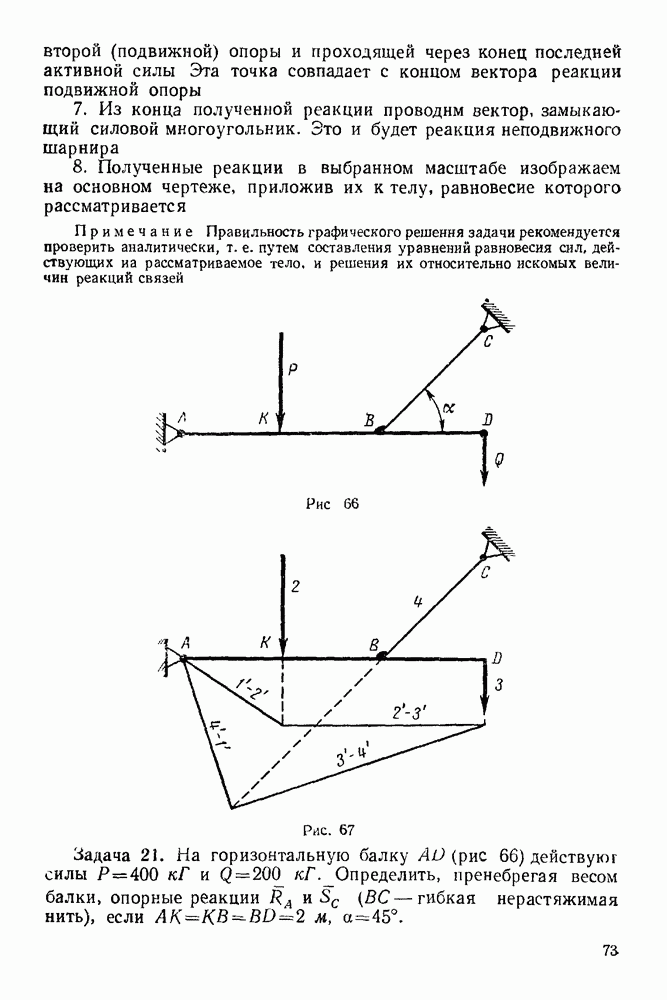
измеряется в  (рис. 244).
(рис. 244).
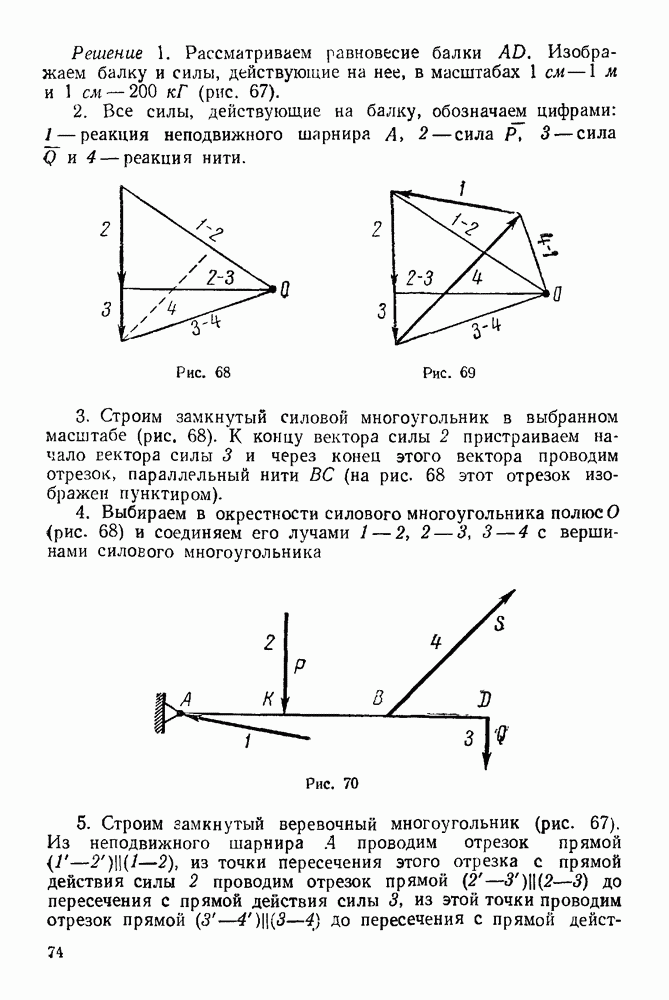
Решение. 1. Изображаем систему в текущий момент времени (рис. 245).
2. Изображаем внешние силы, действующие на систему. Система состоит из точек  связанных между собой стержнями; следовательно, внешними силами, действующими на систему, будут веса
связанных между собой стержнями; следовательно, внешними силами, действующими на систему, будут веса  и
и  точек и реакция
точек и реакция  стержня
стержня 
3. Выбираем систему координат  как указано на рис. 245. Начало координат помещаем в центре инерции системы.
как указано на рис. 245. Начало координат помещаем в центре инерции системы.
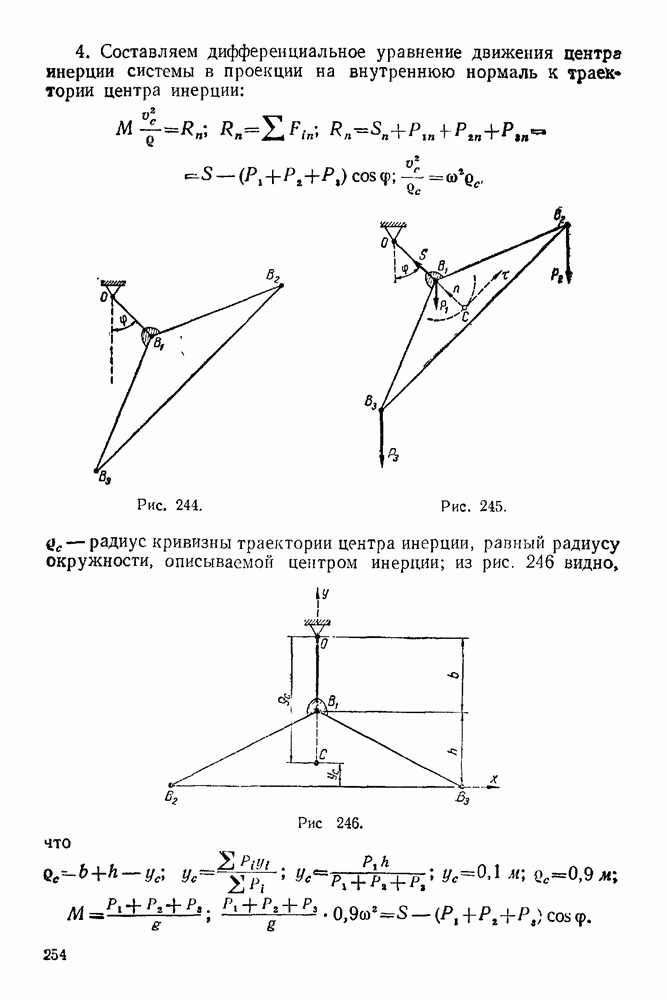
4. Составляем дифференциальное уравнение движения центра инерции системы в проекции на внутреннюю нормаль к траек» тории центра инерции:

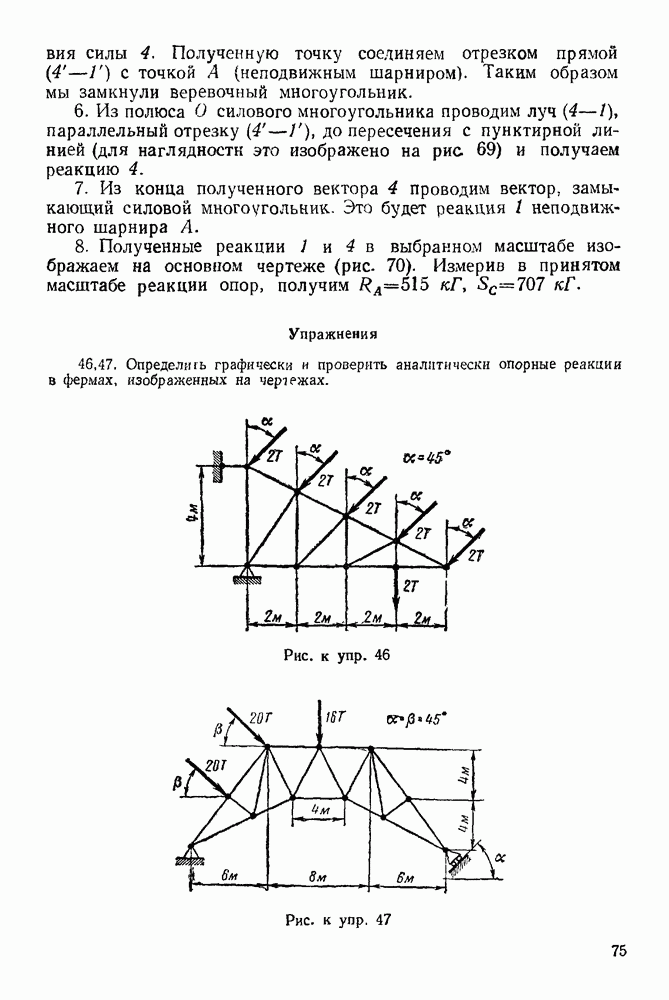
 радиус кривизны траектории центра инерции, равный радиусу окружности, описываемой центром инерции; из рис. 246 видно, что
радиус кривизны траектории центра инерции, равный радиусу окружности, описываемой центром инерции; из рис. 246 видно, что


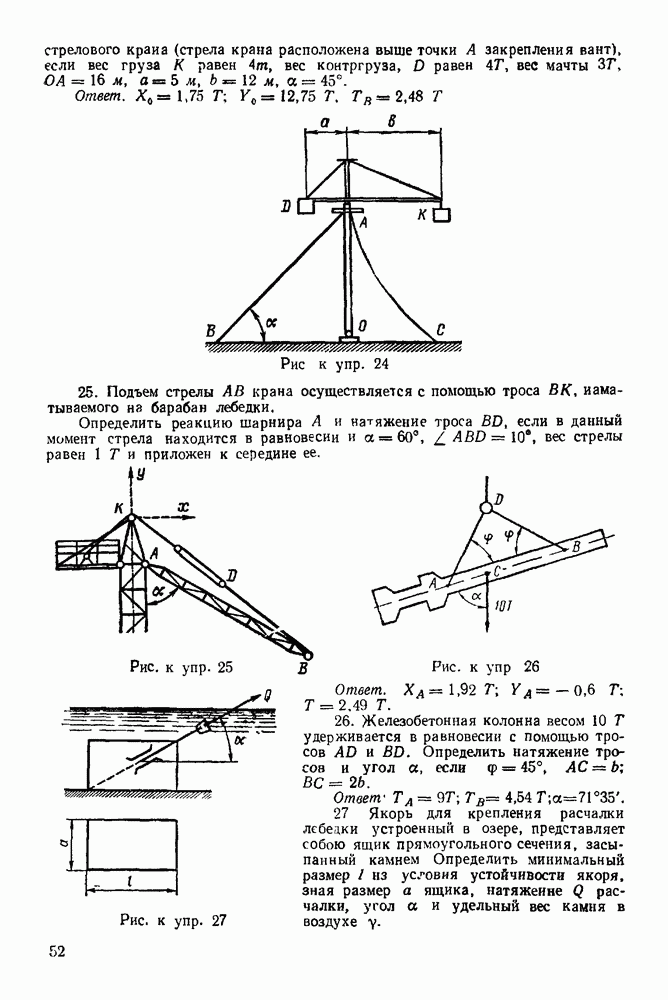
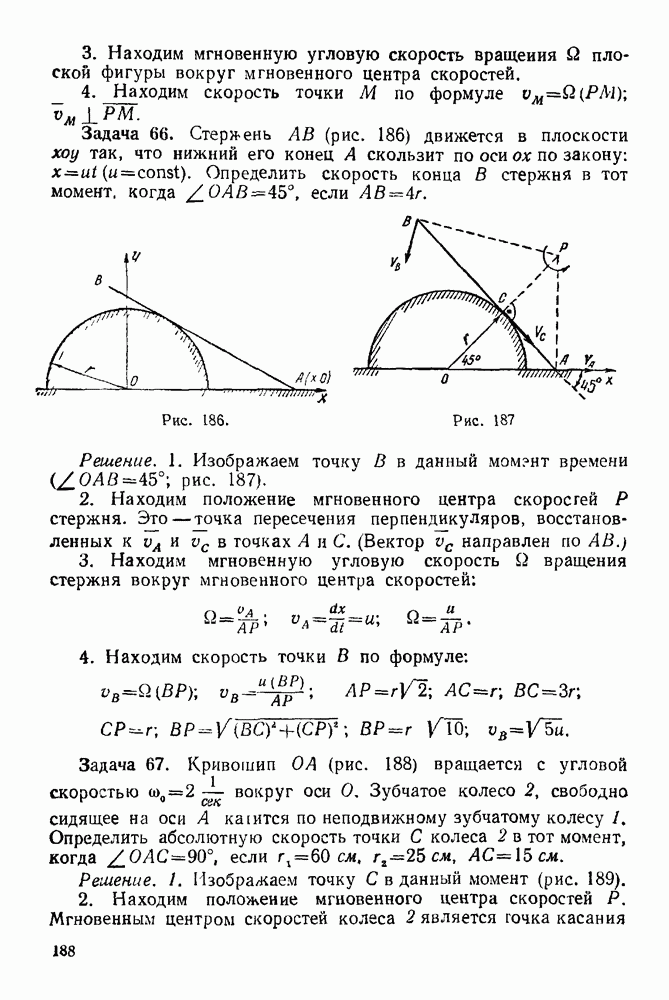
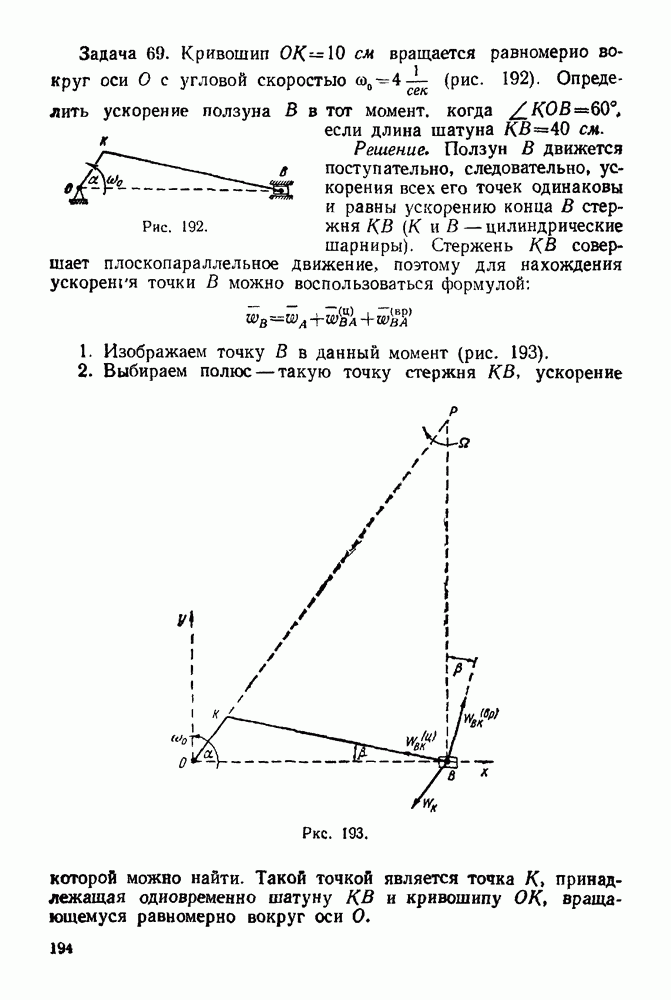
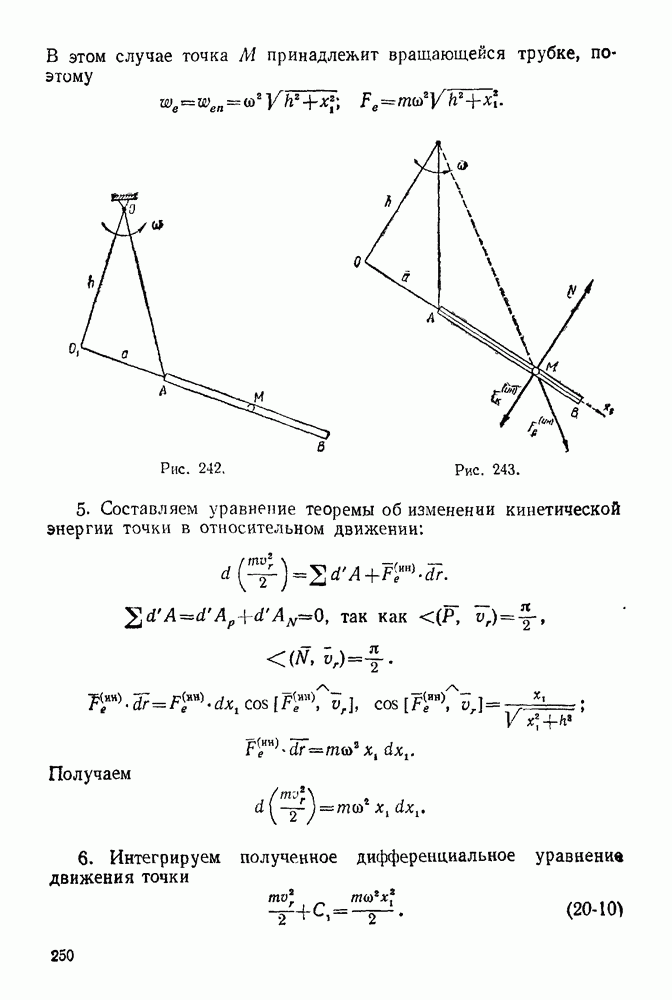
Рис. 244.

Рис. 245.

Рис. 246
5. По заданному закону движения центра инерции системы находим

6. Решаем полученное уравнение:

Получаем 
План решения второй группы задач
1. Выделяем и изображаем систему в произвольный момент времени.
2. Изображаем все внешние силы, действующие на систему.
3. Выбираем систему координат.
4. Составляем дифференциальные уравнения движения центра инерции системы в выбранной системе координат [уравнения (21-3) или (21-4)].
5. Интегрируем полученные дифференциальные уравнения.
6. Составляем начальные условия движения для определения произвольных постоянных интегрирования.
7. Определяем произвольные постоянные интегрирования по начальным условиям задачи.
8. Найденные произвольные постоянные подставляем в результат интегрирования дифференциальных уравнений движения центра инерции системы и найдем неизвестные величины задачи.
Задача 96. Грузы  веса
веса  и В веса
и В веса  соединен!
соединен!  нерастяжимой нитью, переброшенной через блок
нерастяжимой нитью, переброшенной через блок  Груз В скользит по боковой стороне клина, опирающегося основаниед)
Груз В скользит по боковой стороне клина, опирающегося основаниед)  на гладкую горизонтальную плоскость. Найти перемещение клина по горизонтальной плоскости при опускании груза
на гладкую горизонтальную плоскость. Найти перемещение клина по горизонтальной плоскости при опускании груза  на высоту
на высоту  если вес клина
если вес клина  массой нити и блока, а также отклонением нити
массой нити и блока, а также отклонением нити  от вертикали пренебречь, вначале система находилась в покое (рис. 247).
от вертикали пренебречь, вначале система находилась в покое (рис. 247).
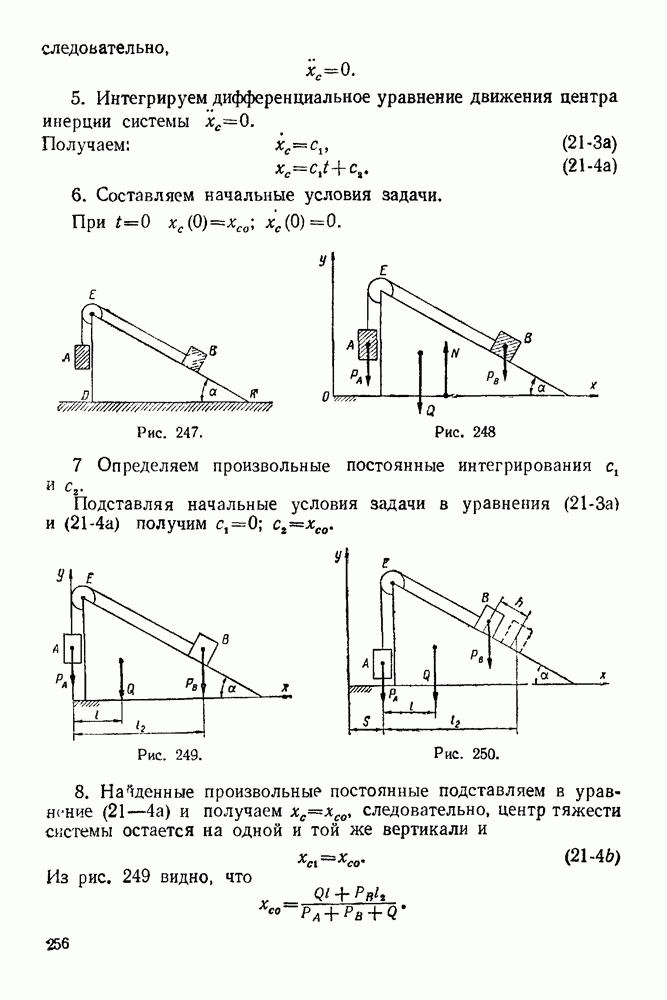
Решение. 1. Рассматриваем систему, состоящую из клина, грузов  нити и блока, в текущий момент (рис. 248).
нити и блока, в текущий момент (рис. 248).
2. Изображаем все внешние силы, действующие на систему:  вес клина,
вес клина,  вес груза
вес груза  вес груза
вес груза  нормальная реакция пола.
нормальная реакция пола.
3. Выбираем систему координат, как указано на рис. 248.
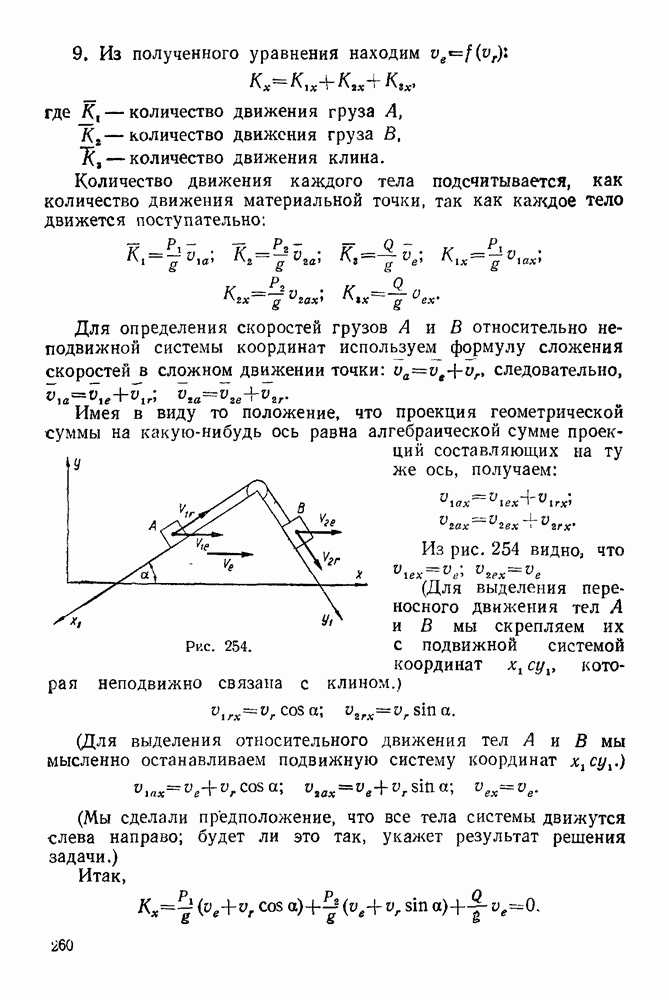
4. Составляем дифференциальное уравнение движения центра инерции в проекции на ось 

следовательно,

5. Интегрируем дифференциальное уравнение движения центра инерции системы 
Получаем:

6. Составляем начальные условия задачи.
При 

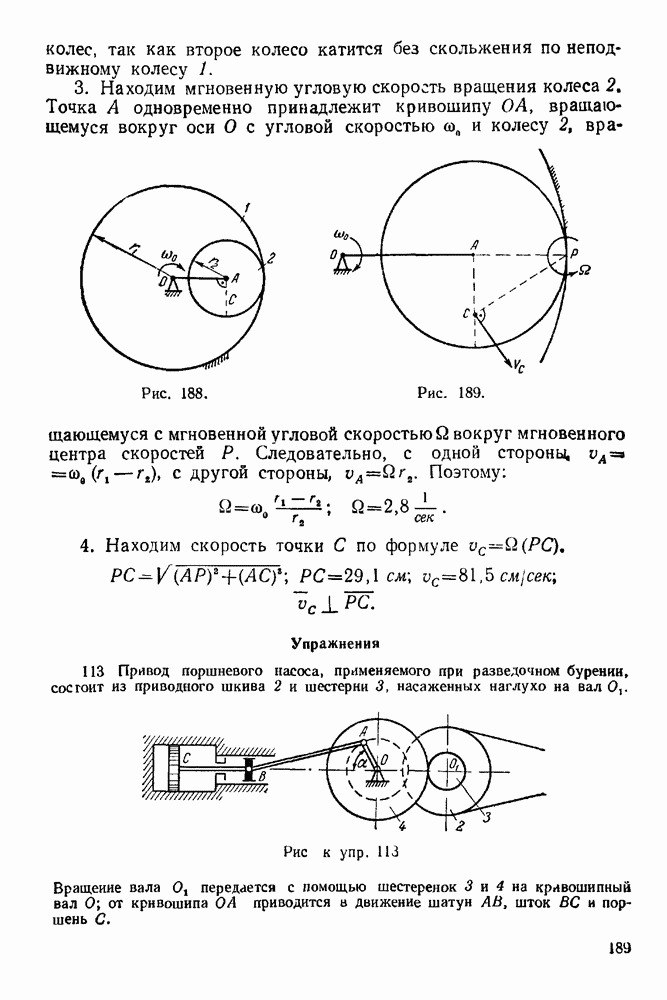
Рис. 247.

Рис. 248
7 Определяем произвольные постоянные интегрирования 
Подставляя начальные условия задачи в уравнения  и (21-4а) получим
и (21-4а) получим 

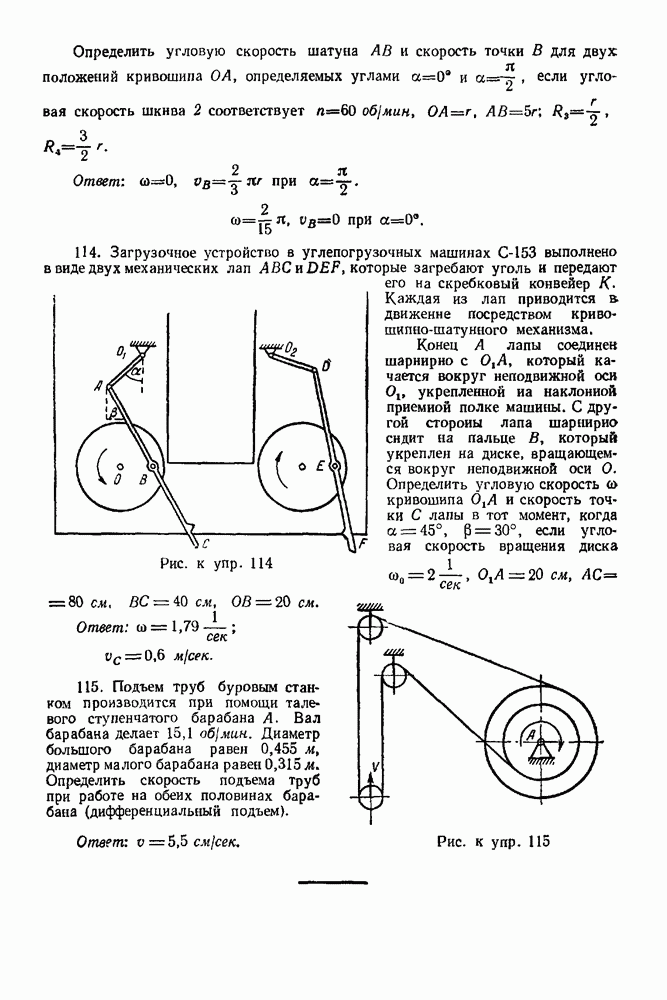
Рис. 249.

Рис. 250.
8. Наеденные произвольные постоянные подставляем в уравнение (21—4а) и получаем  следовательно, центр тяжести системы остается на одной и той же вертикали и
следовательно, центр тяжести системы остается на одной и той же вертикали и

Из рис. 249 видно, что

Из рис. 250 следует, что

После подстановки найденных величин в соотношение (21-46) и несложных преобразований получим:

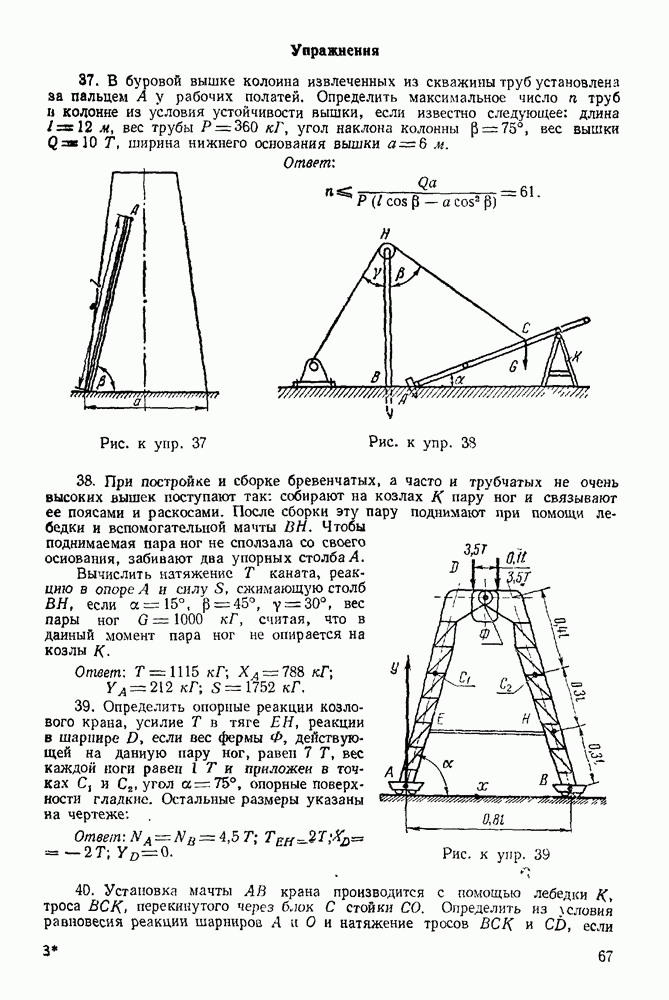
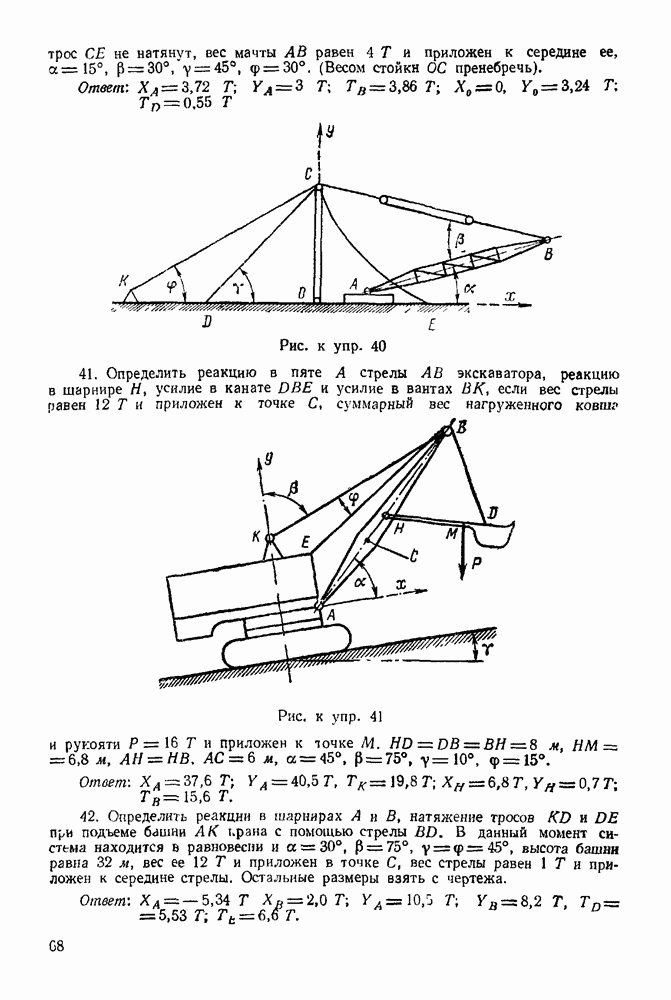
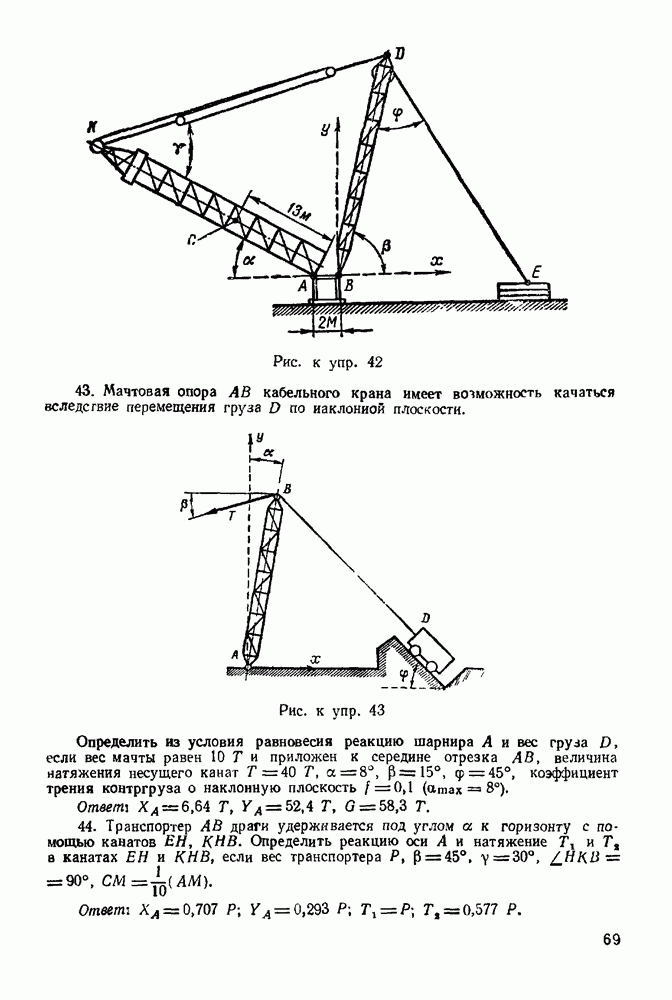
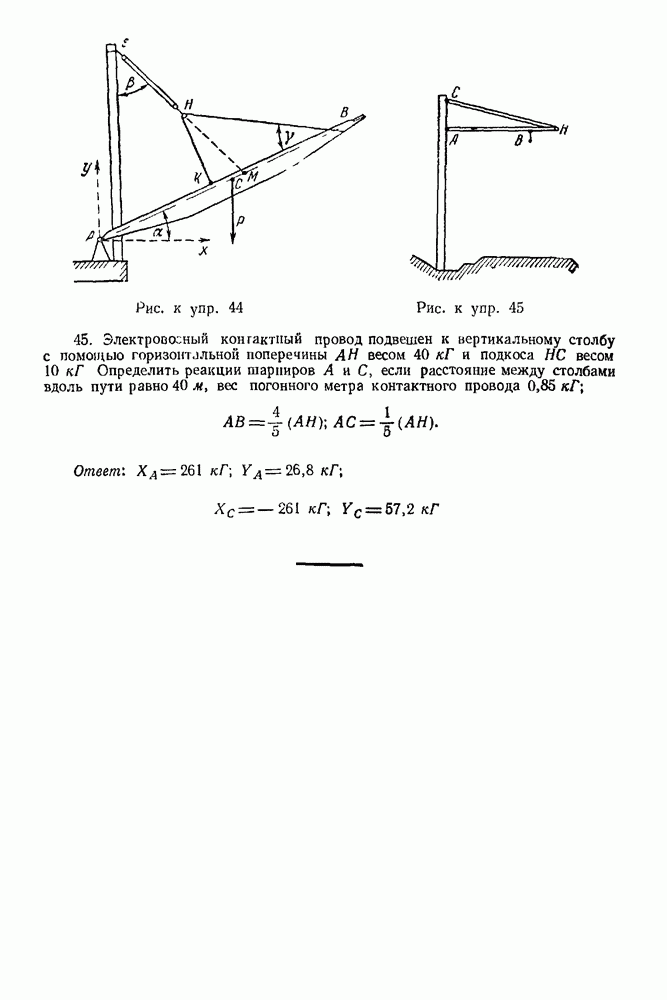
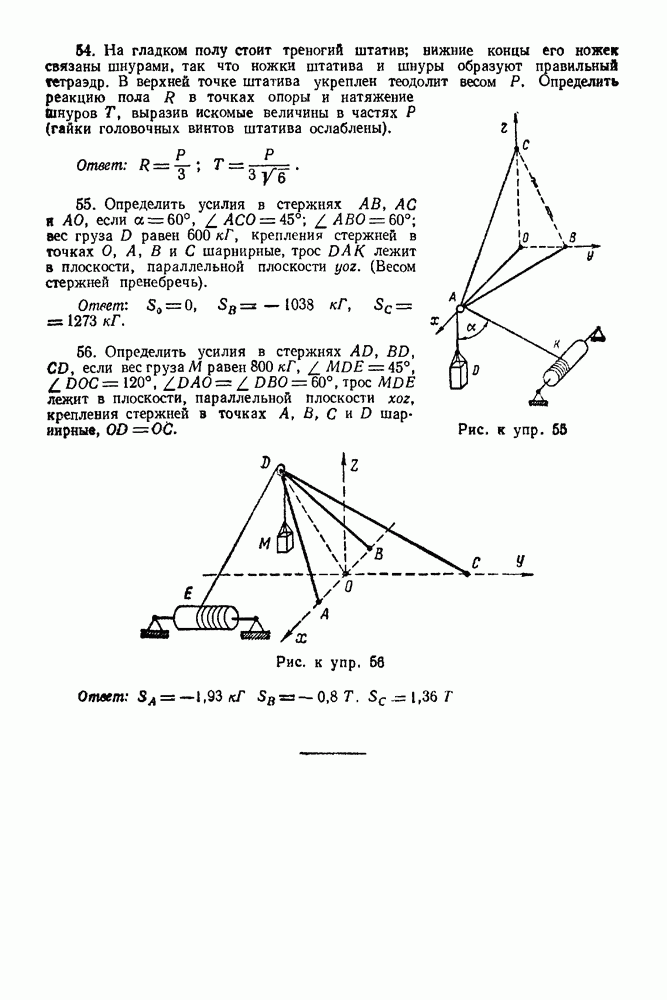
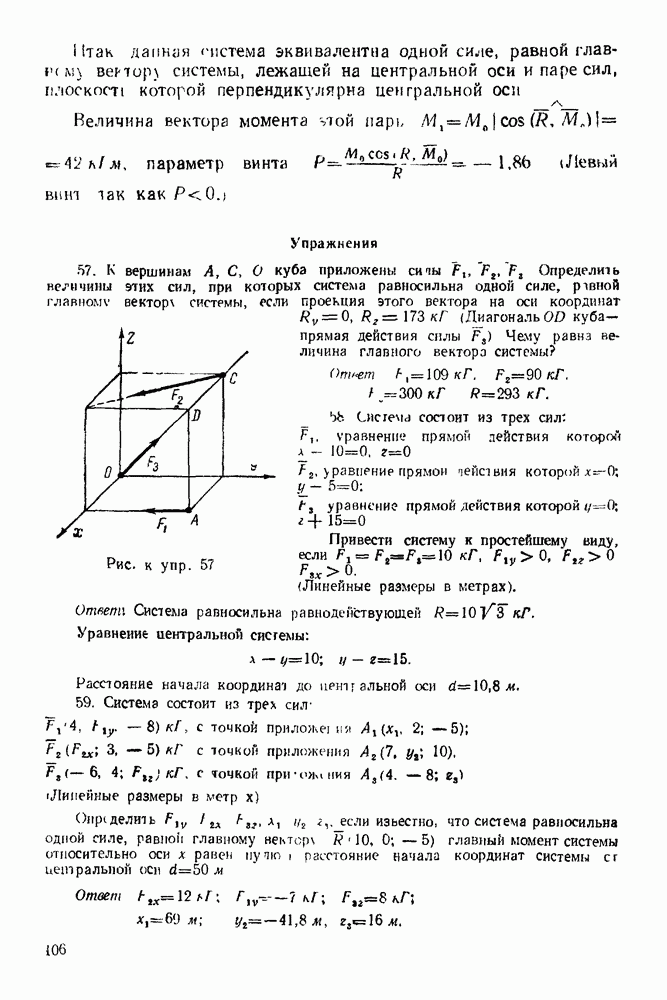
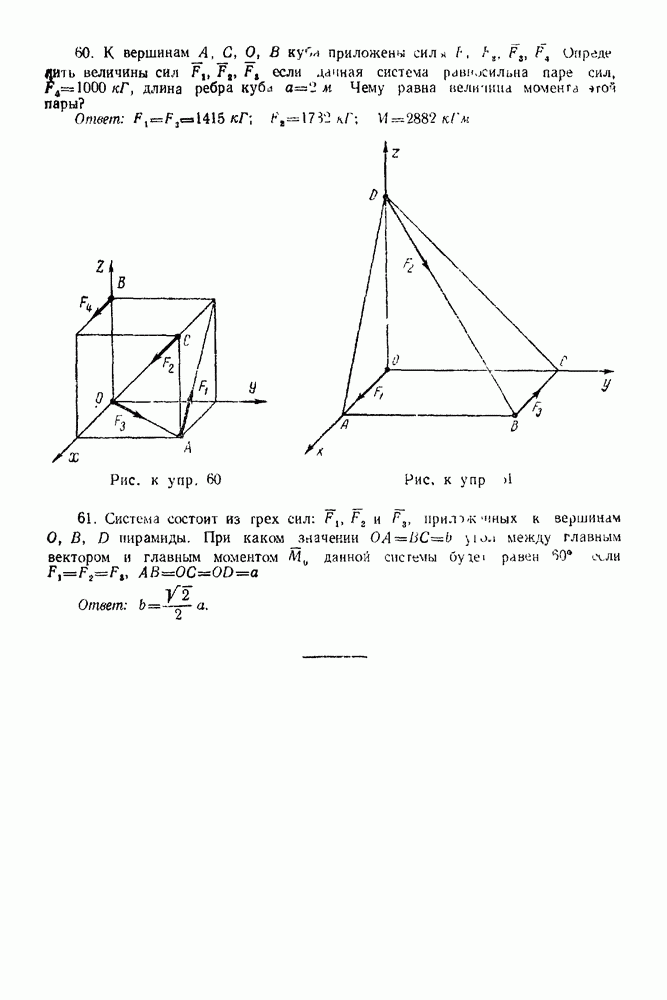
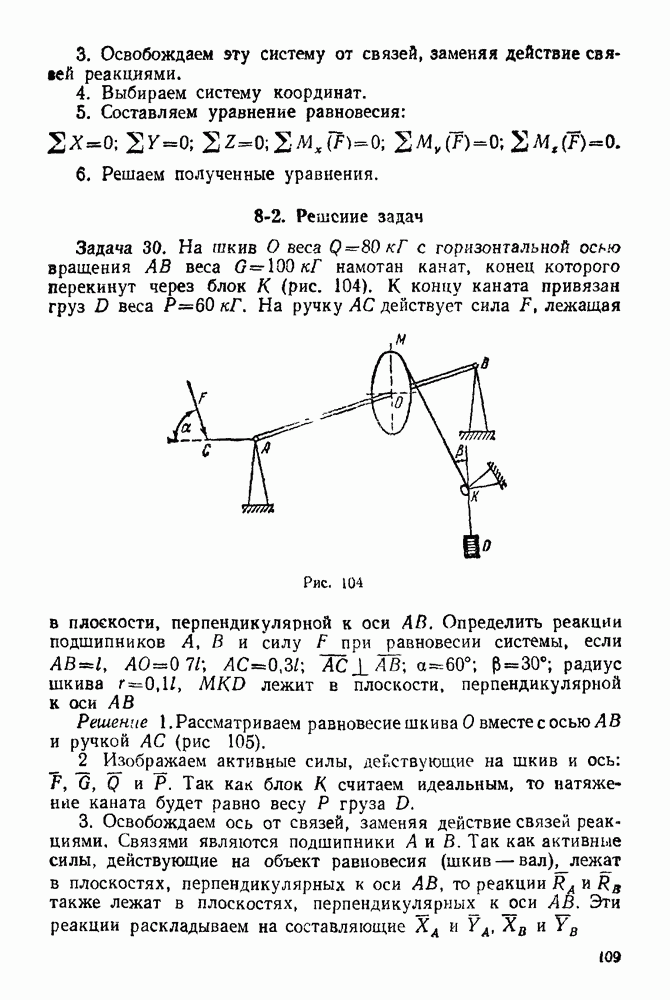
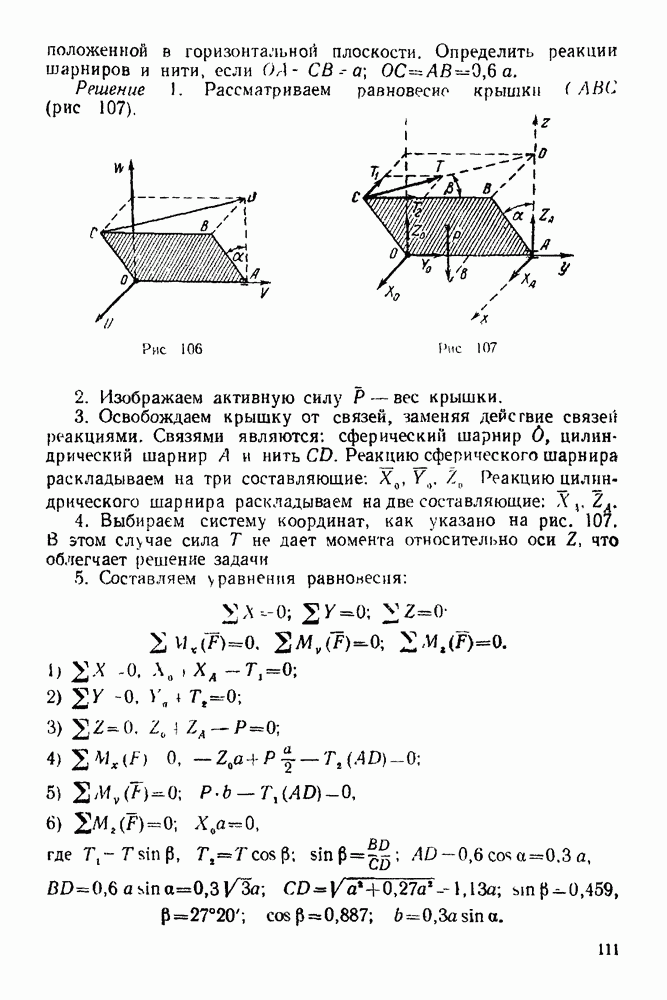
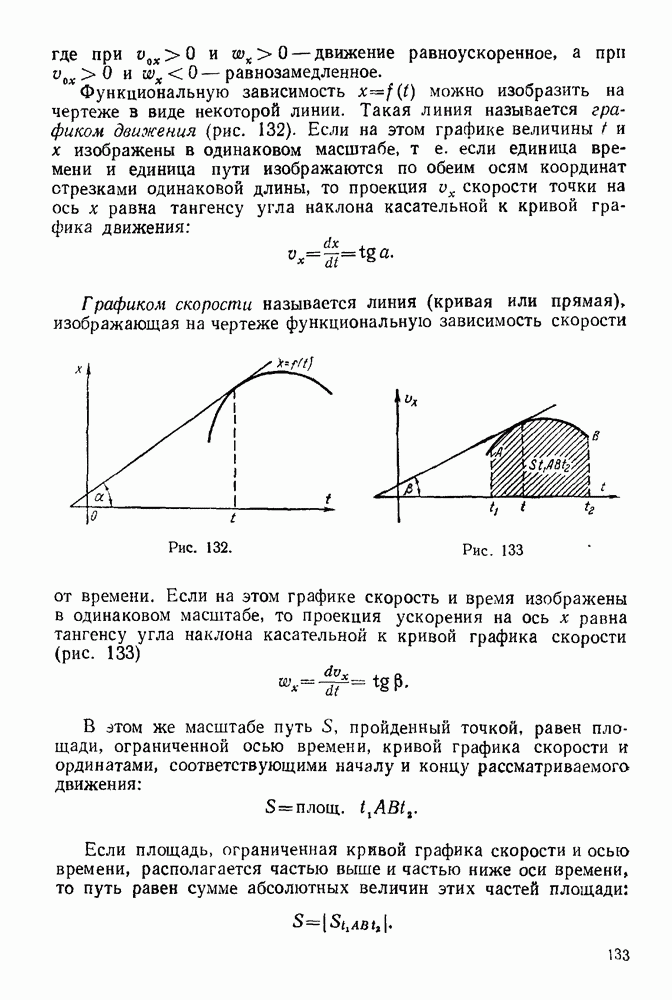
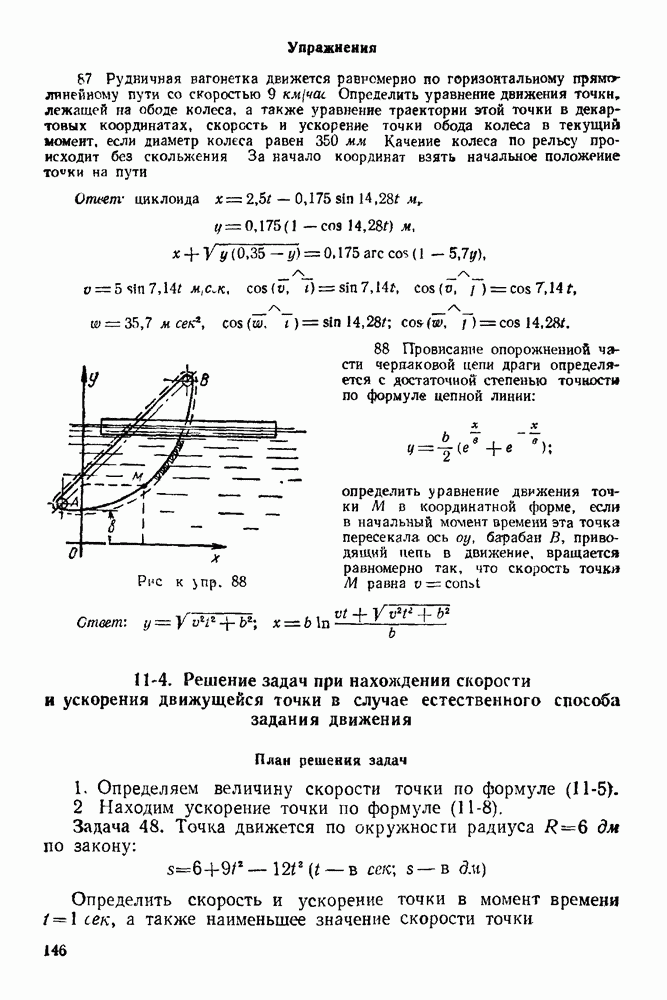
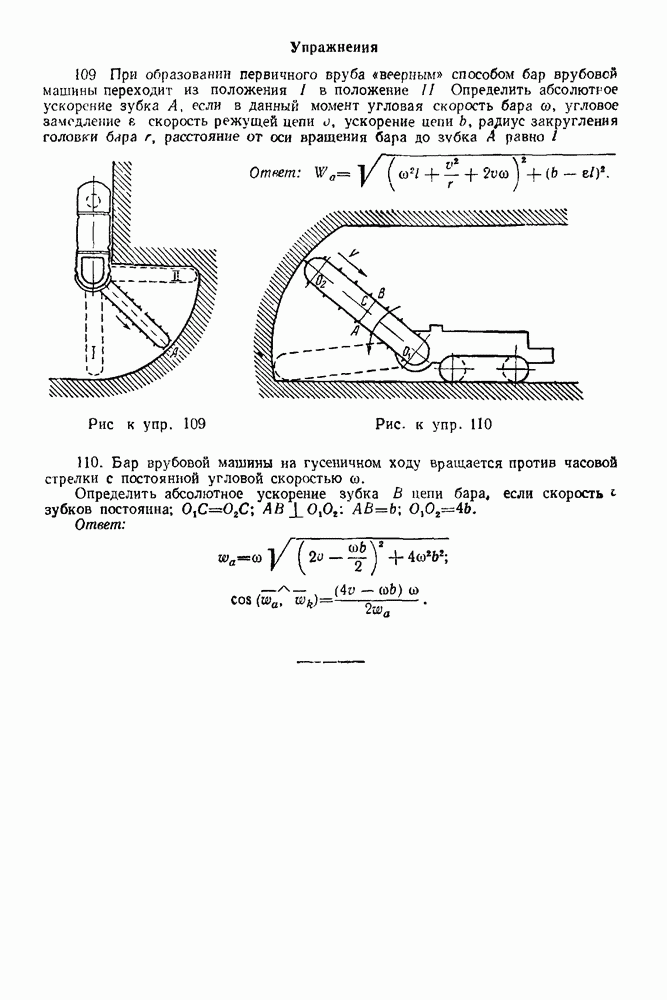
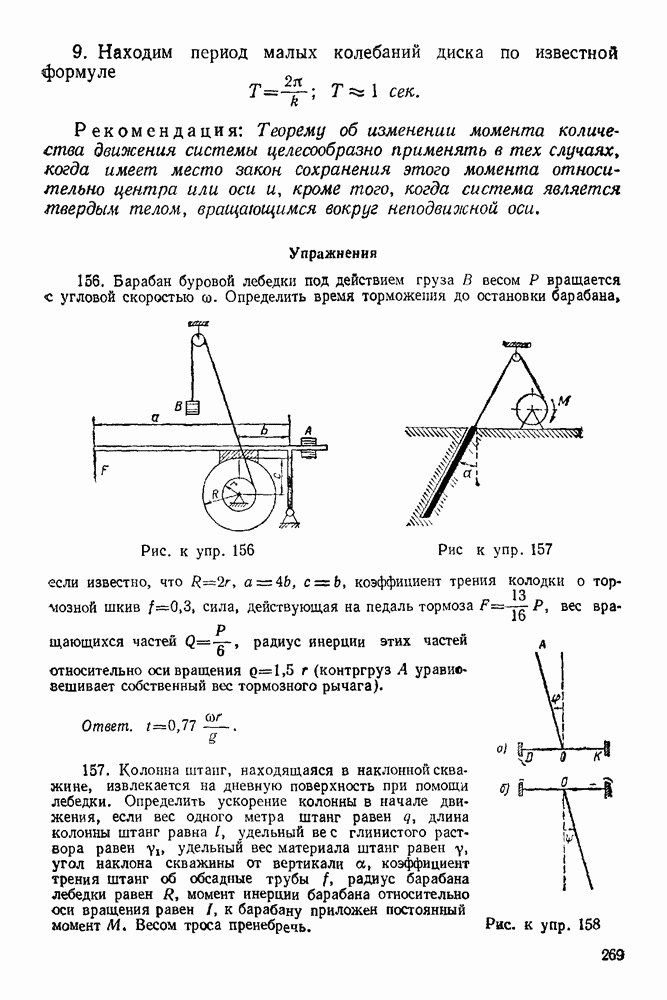
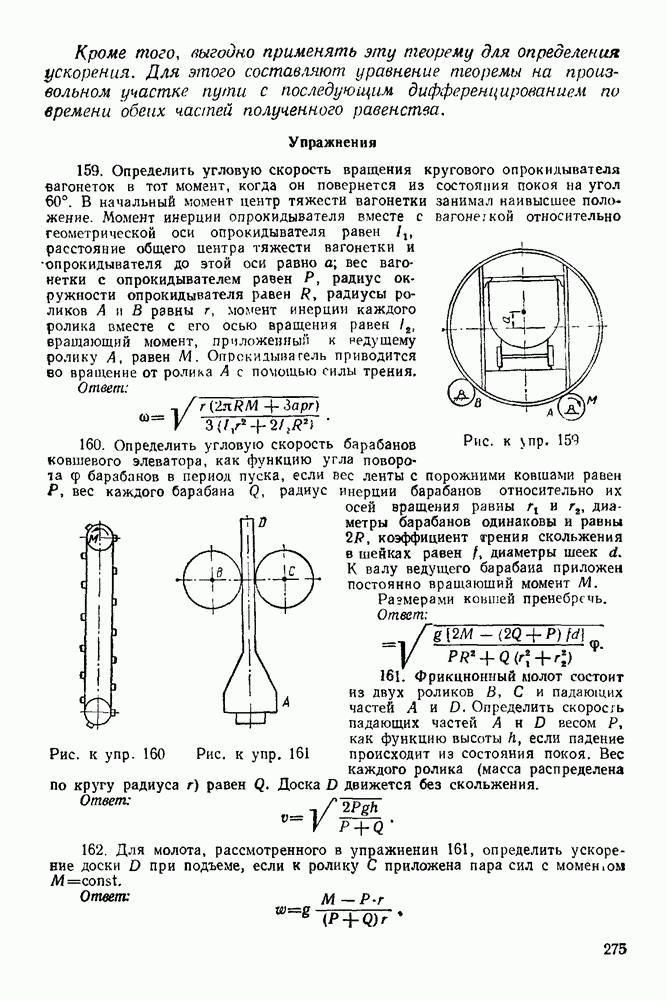
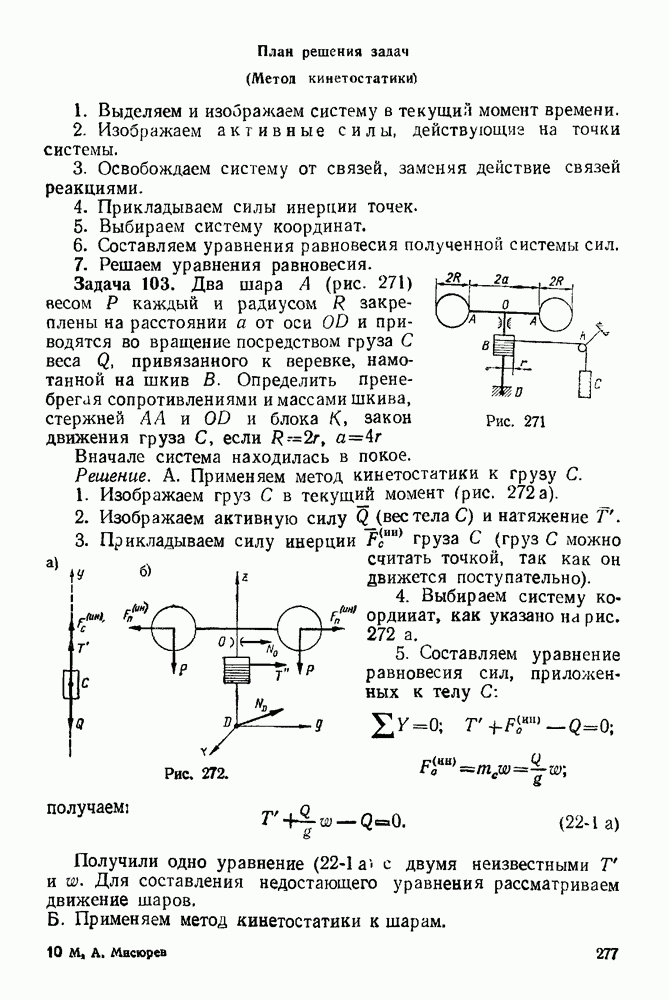
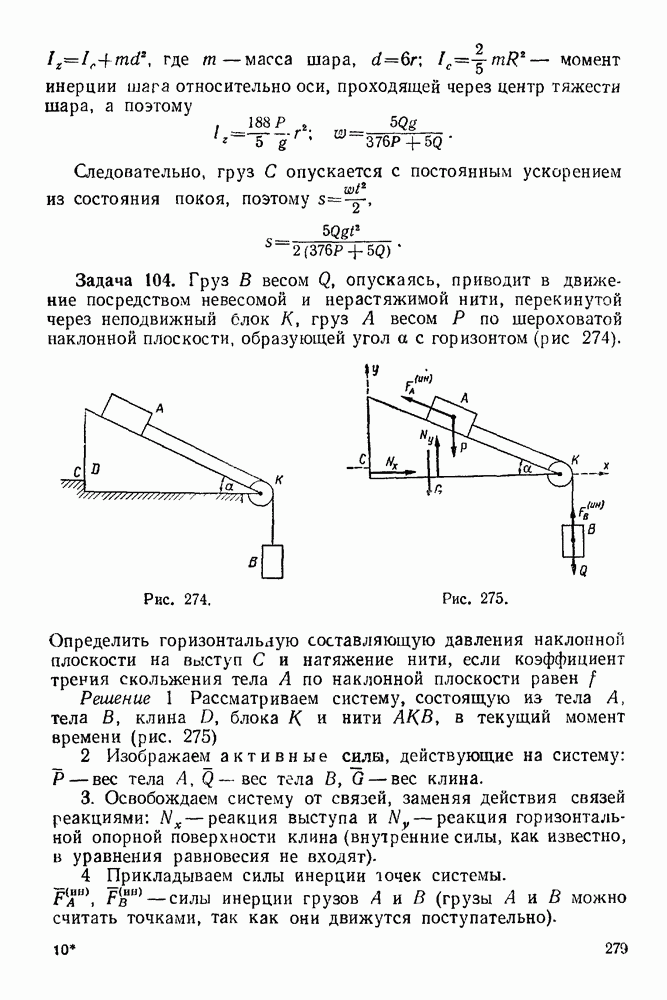
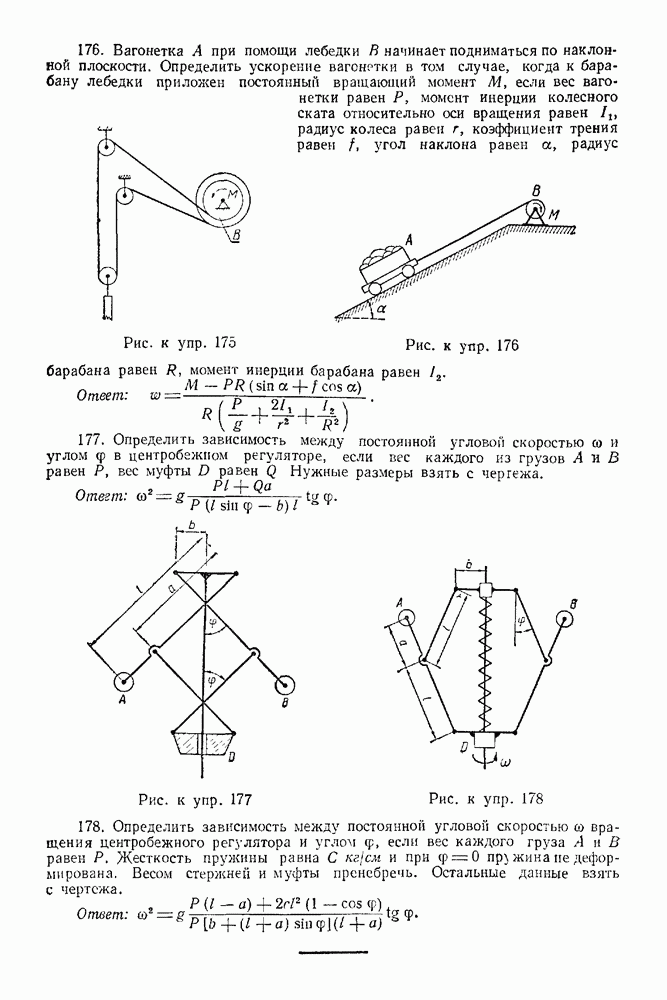
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
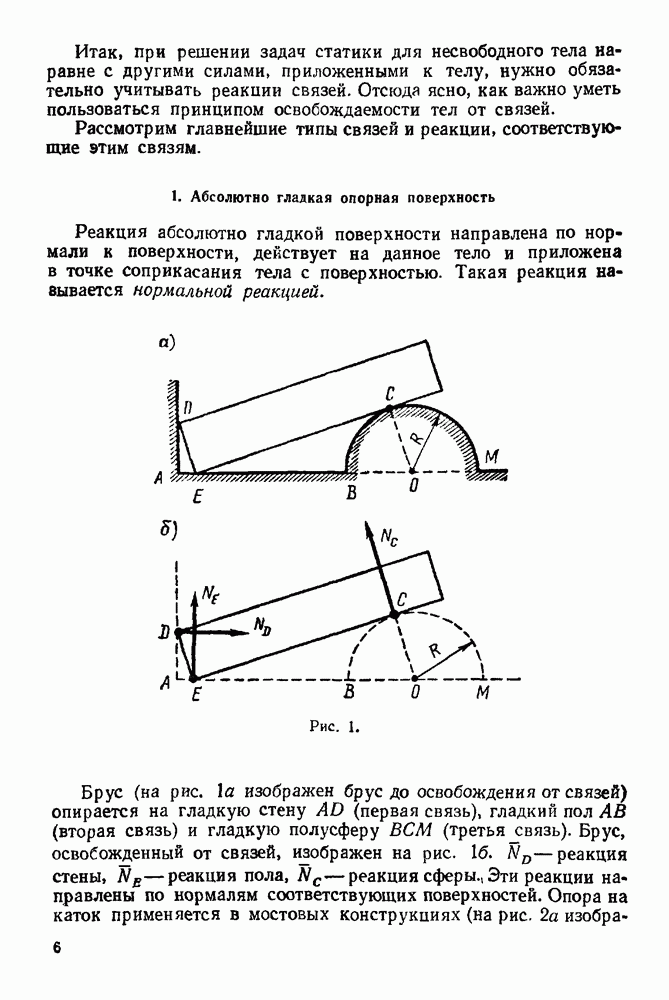
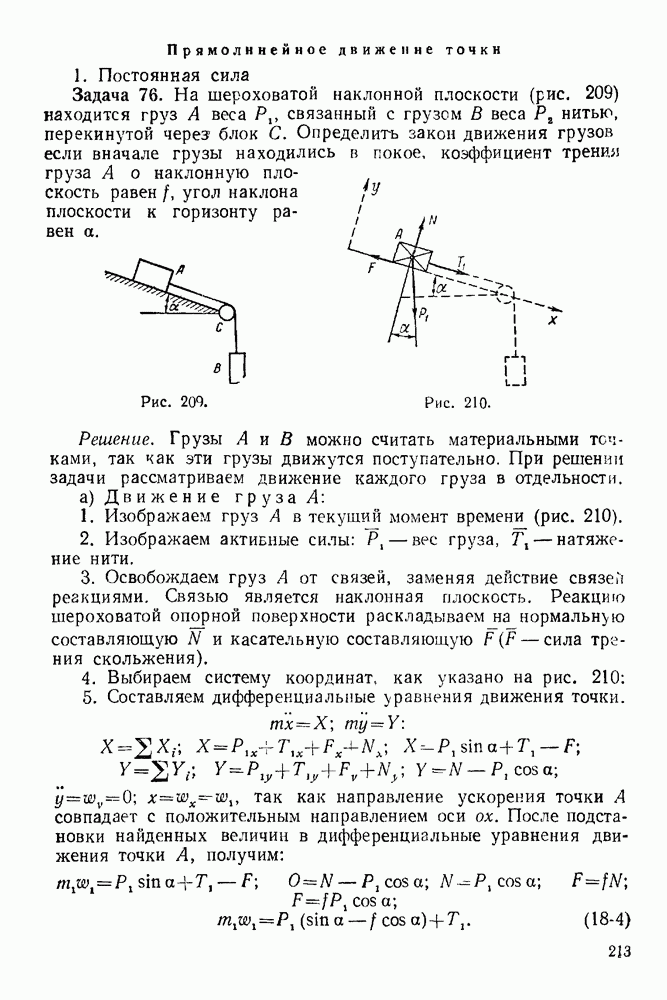
- 1. Абсолютно гладкая опорная поверхность
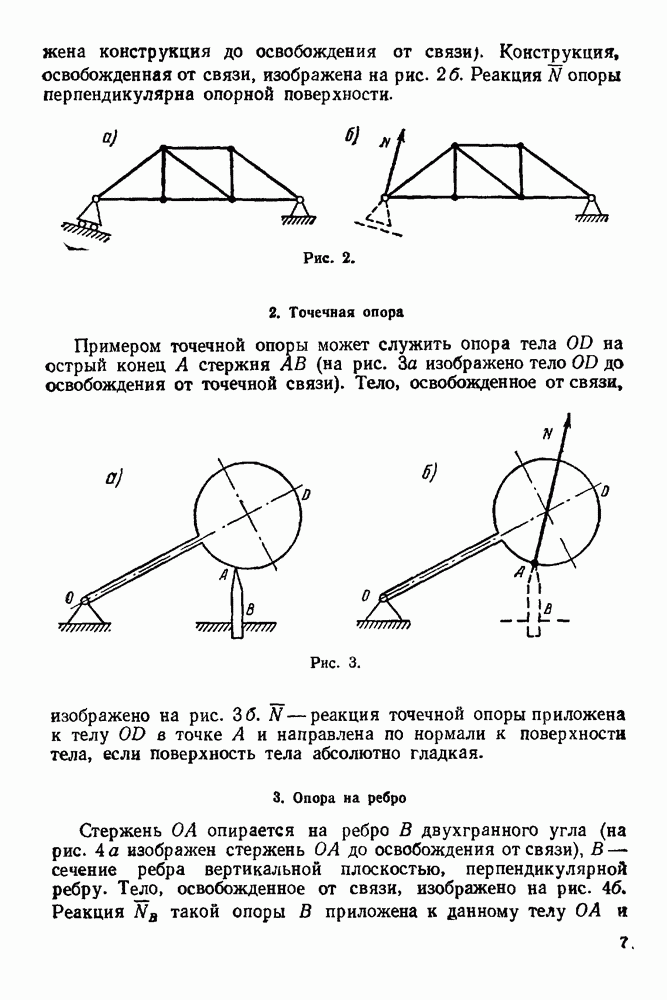
- 2. Точечная опора
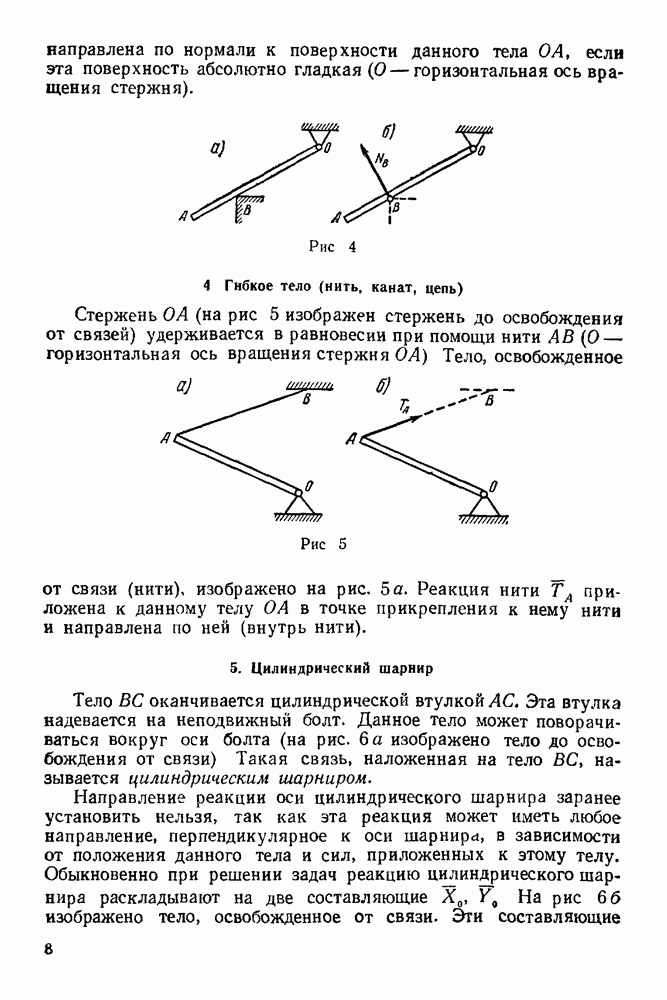
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
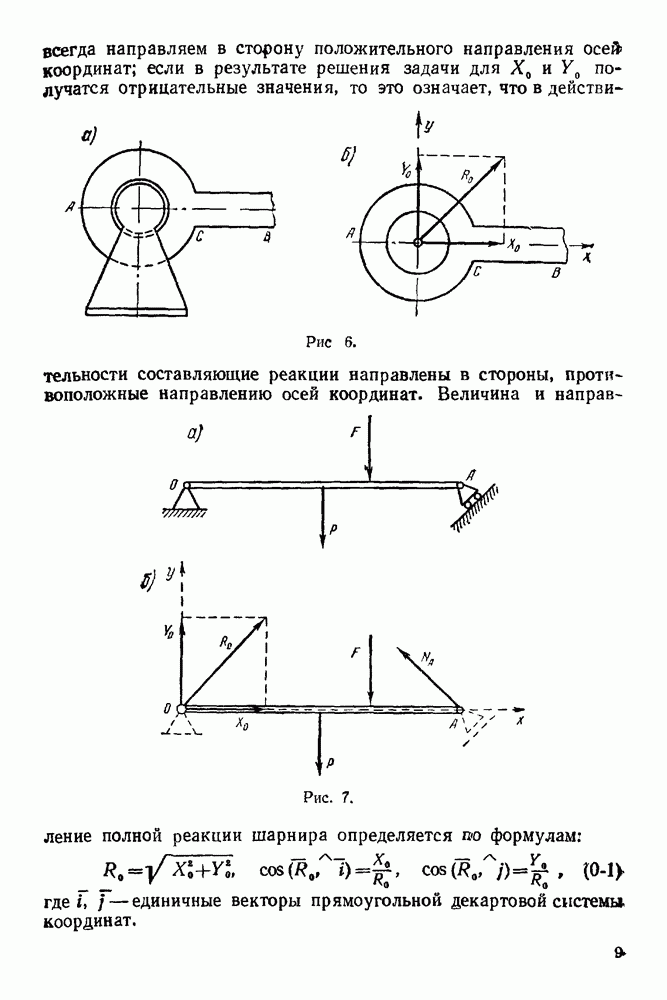
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
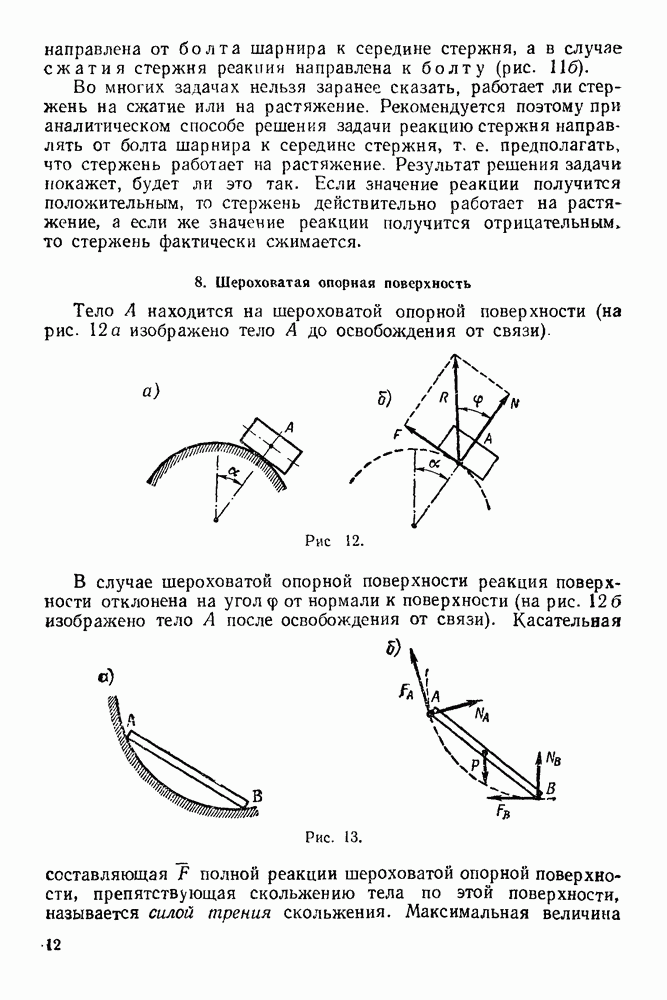
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
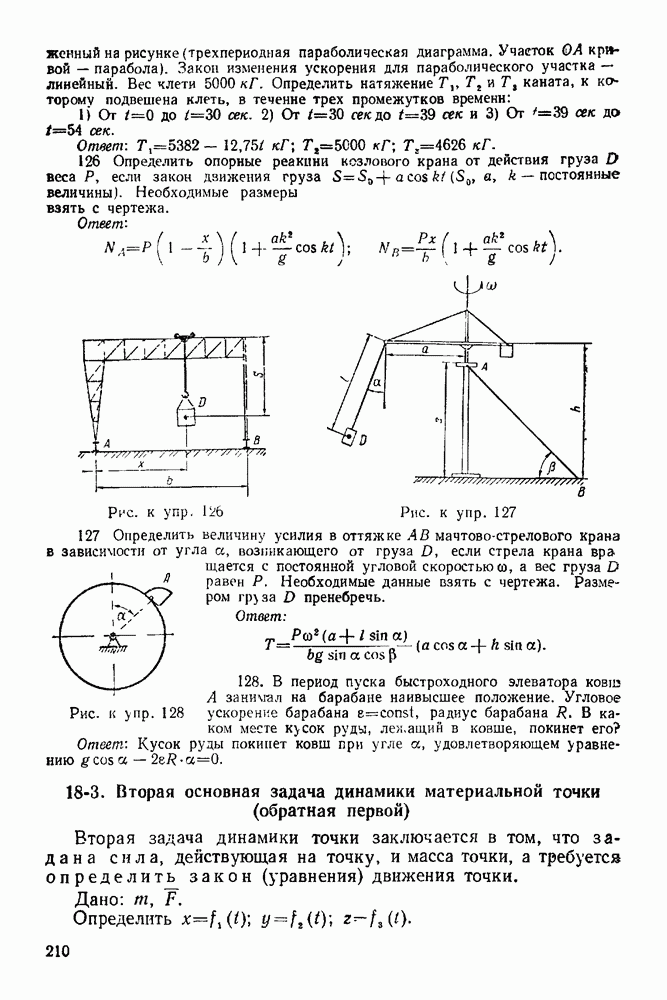
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
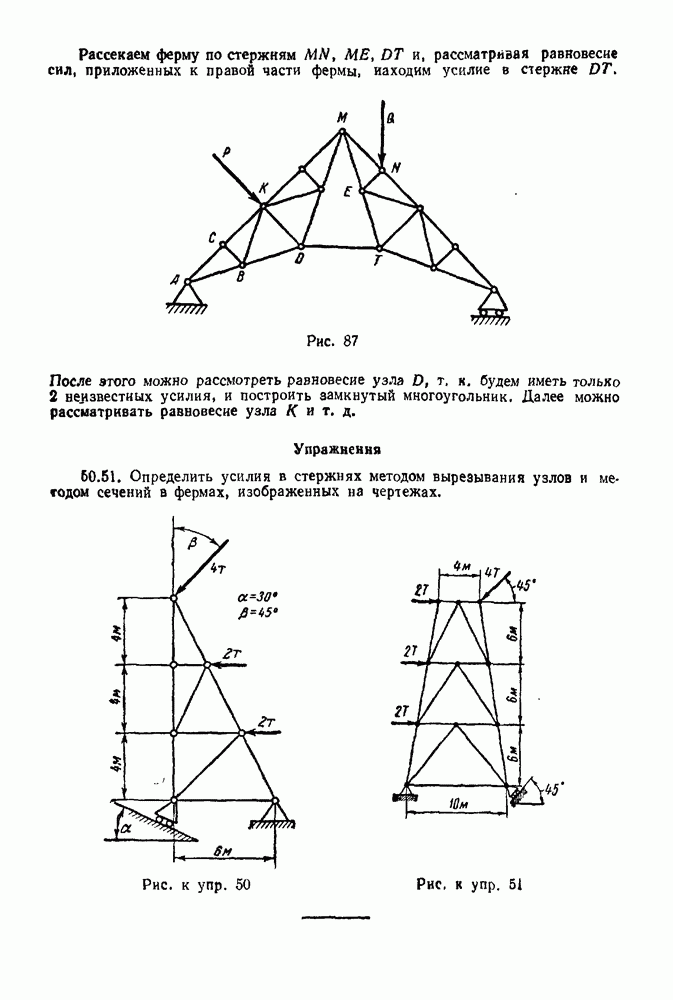
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
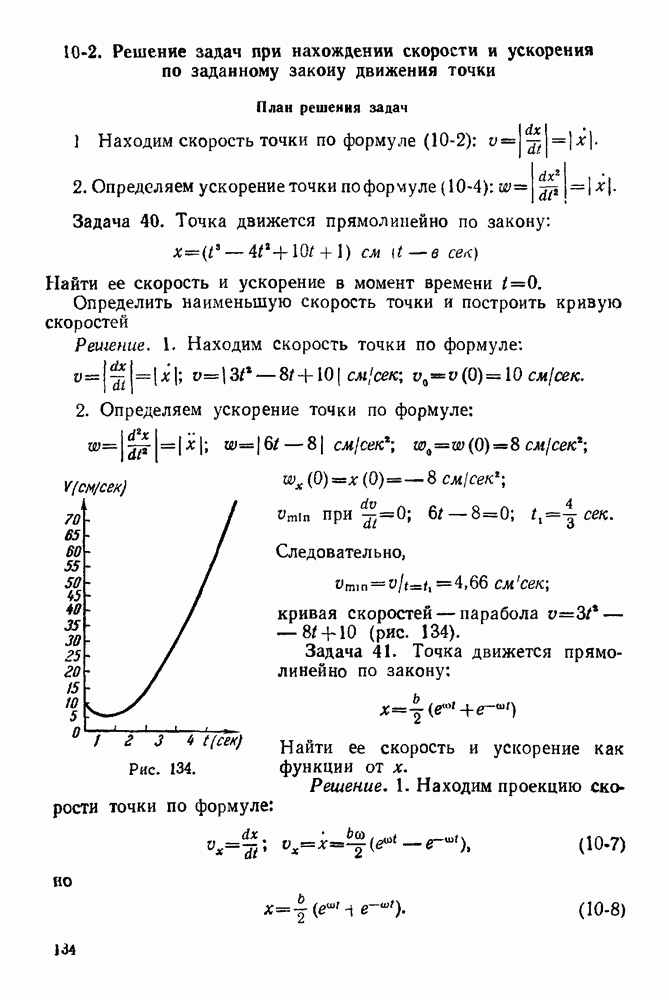
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
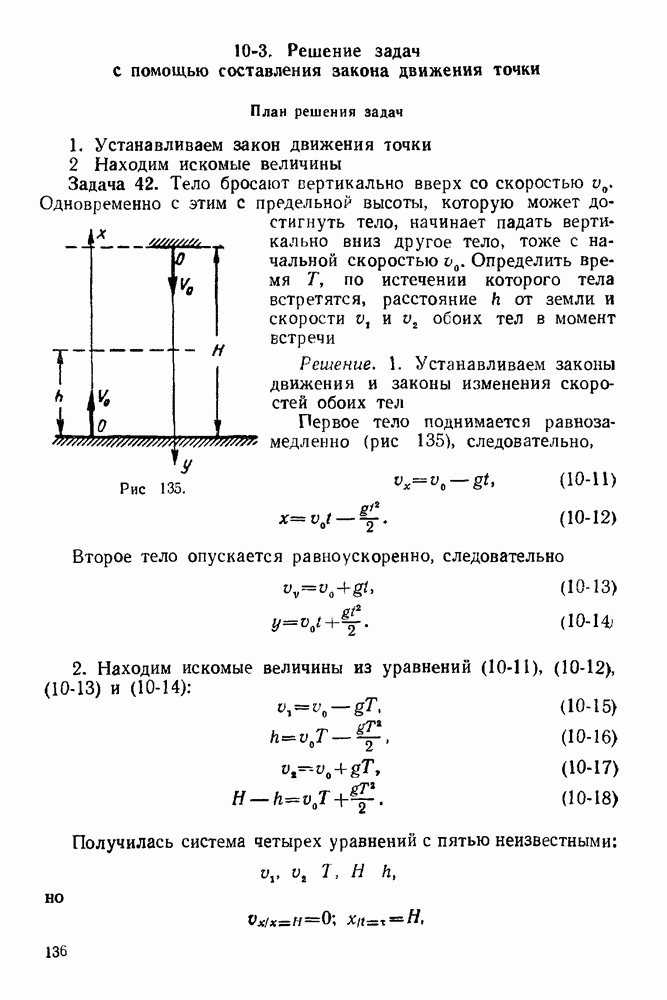
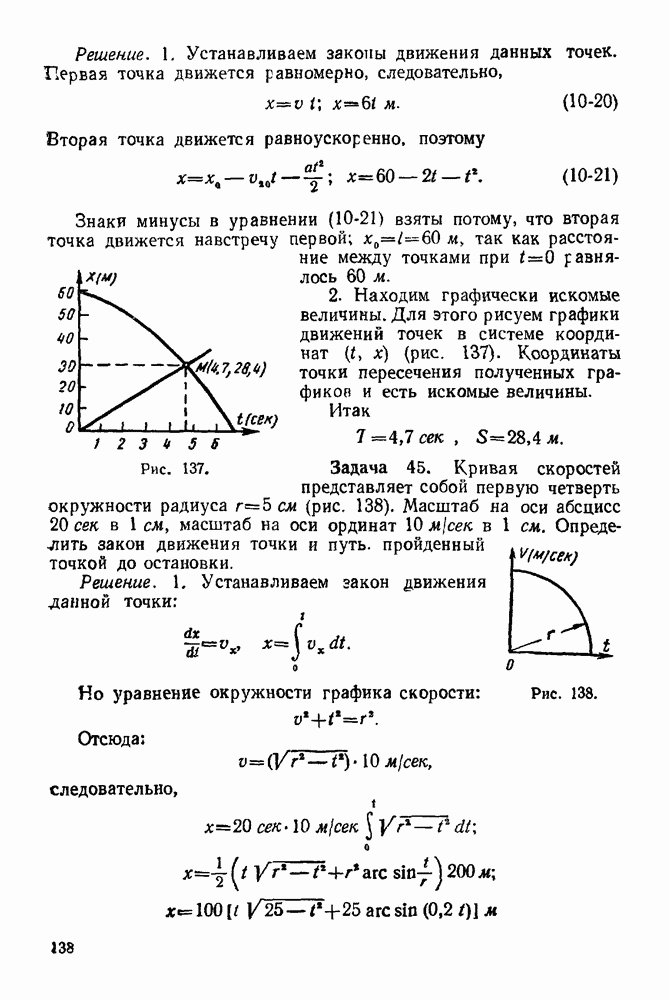
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
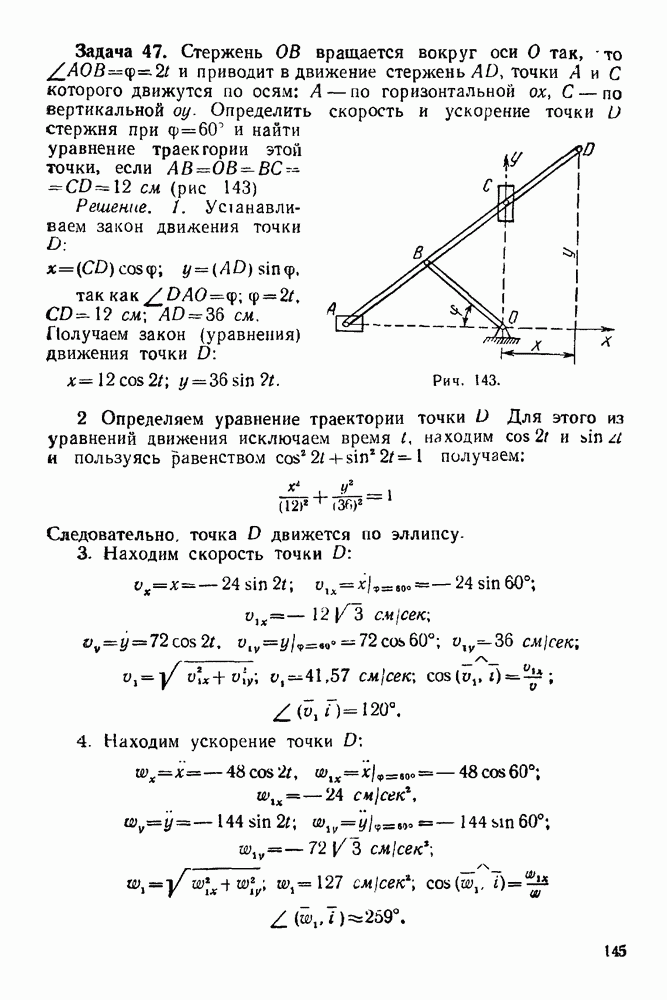
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
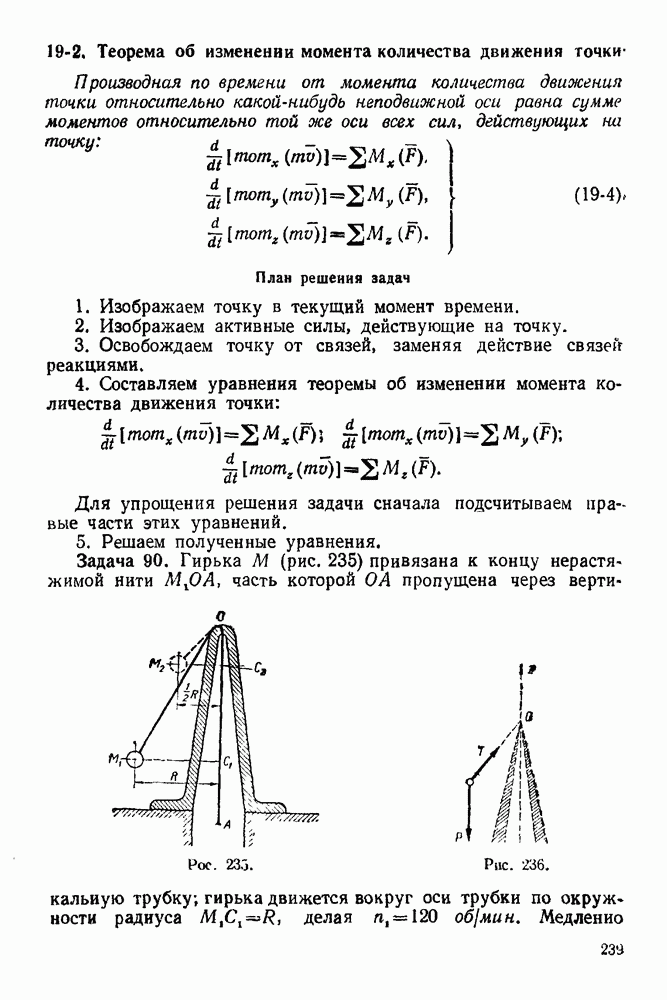
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР