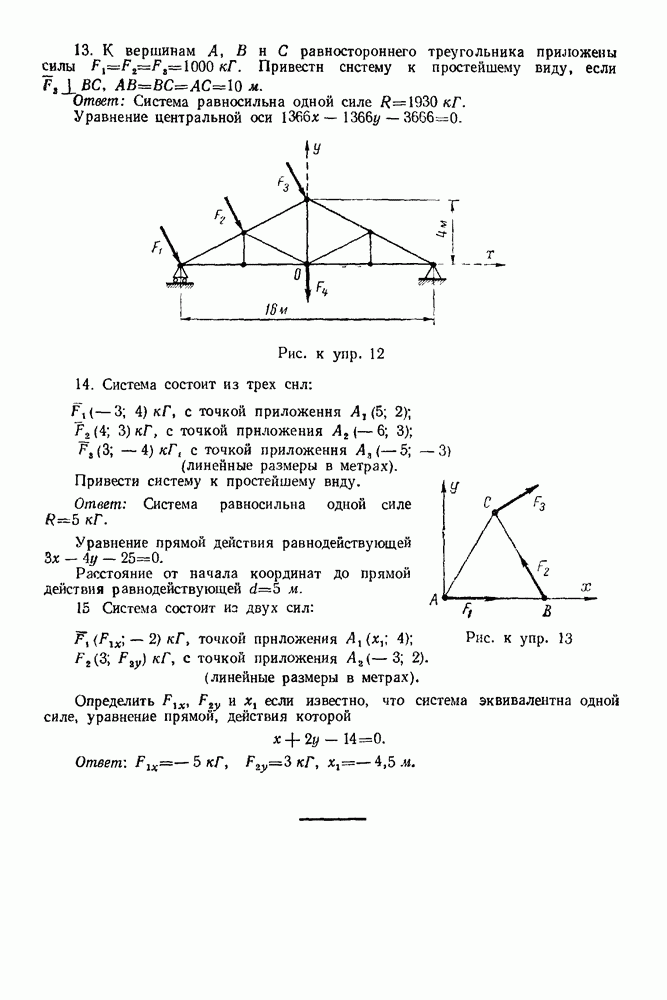
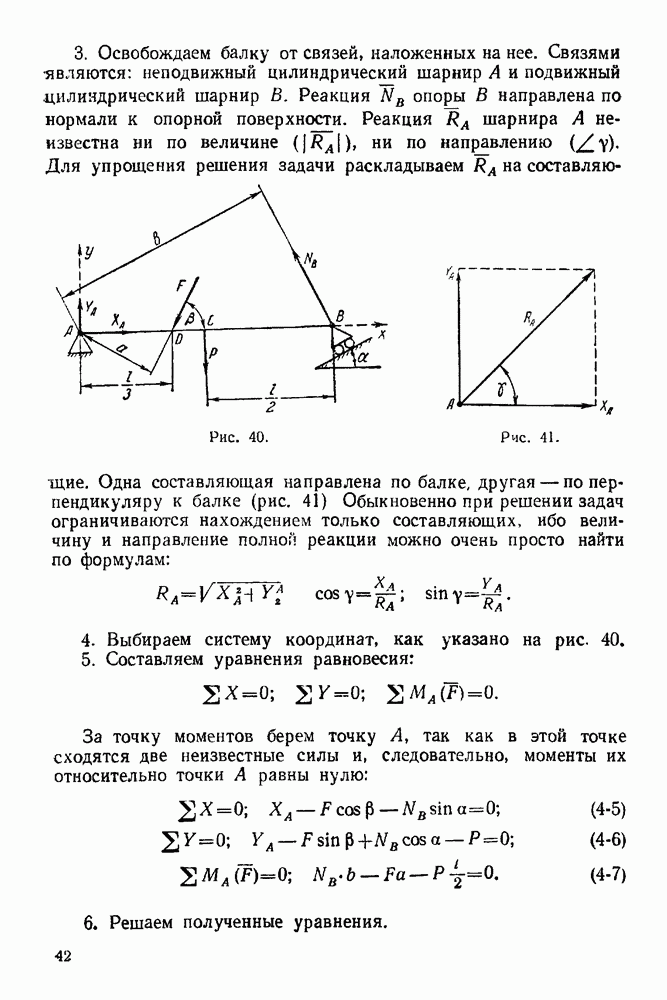
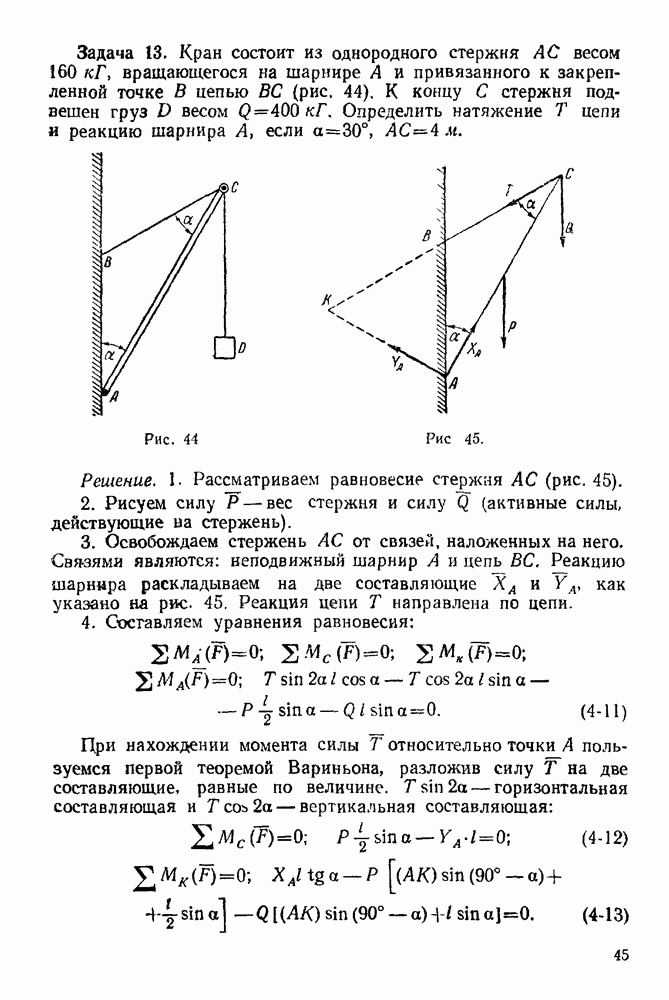
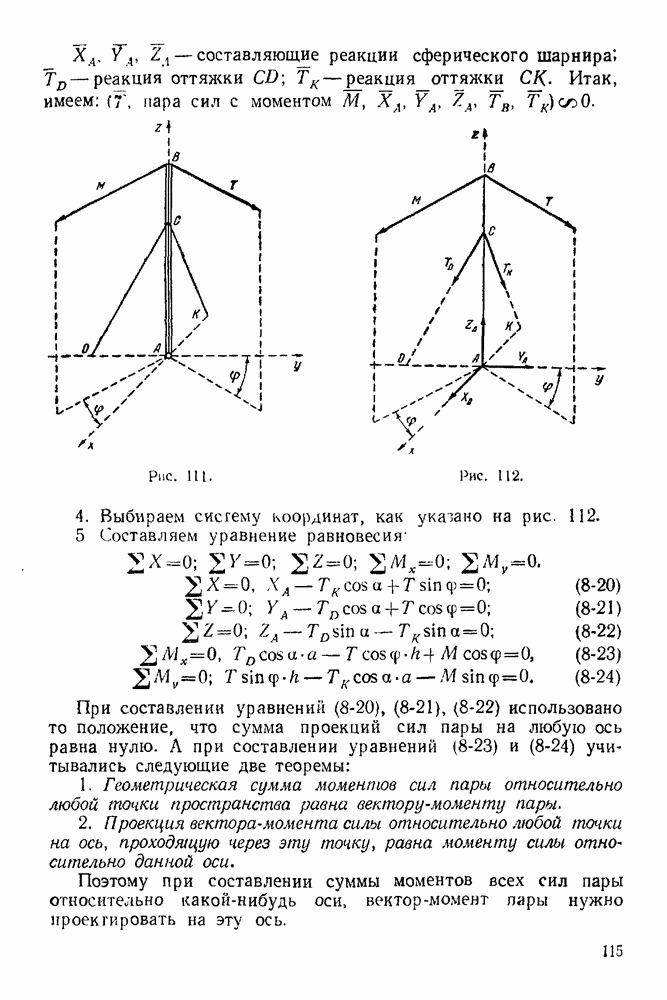
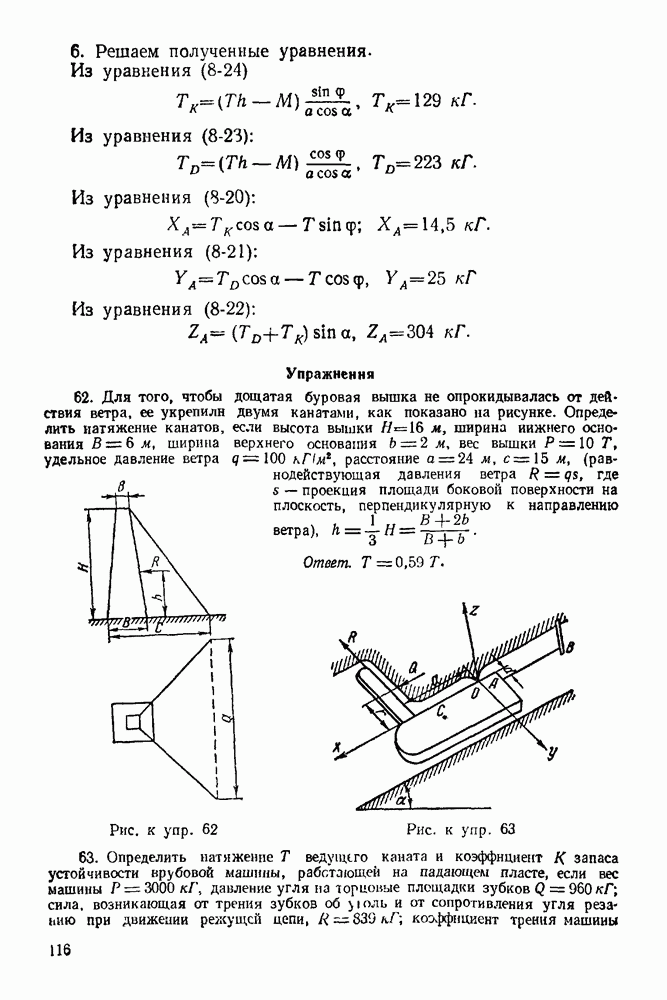
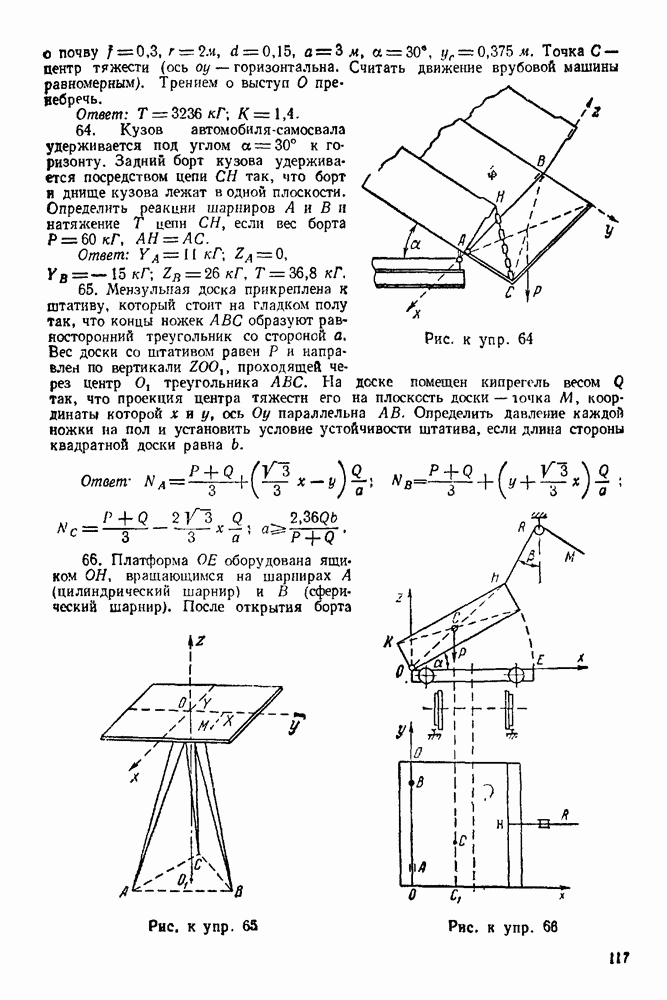
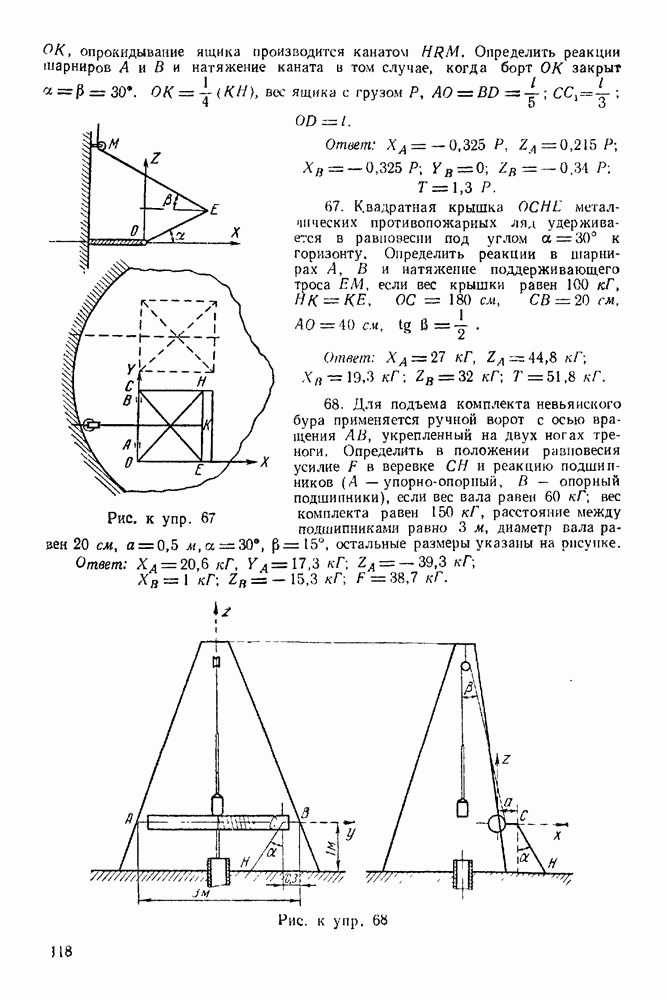
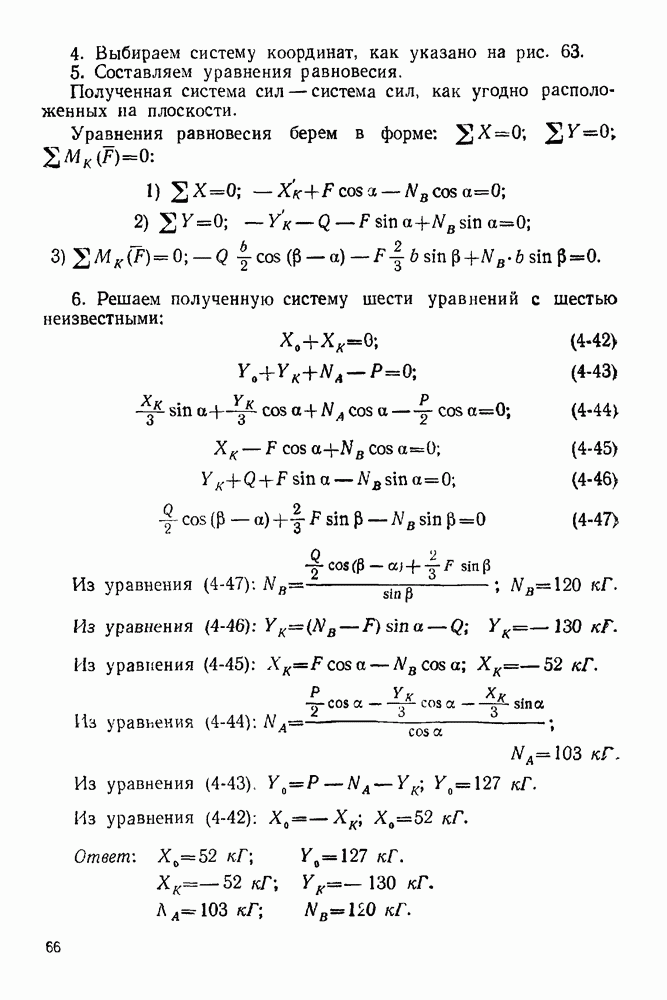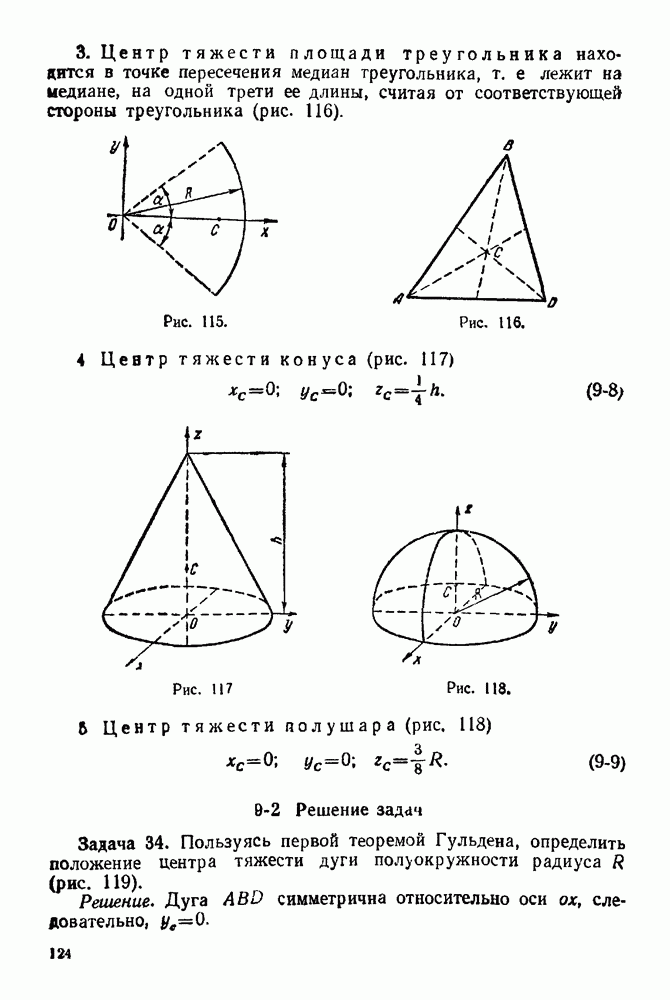| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5-3. Определение усилий в стержнях фермы
Основные положения
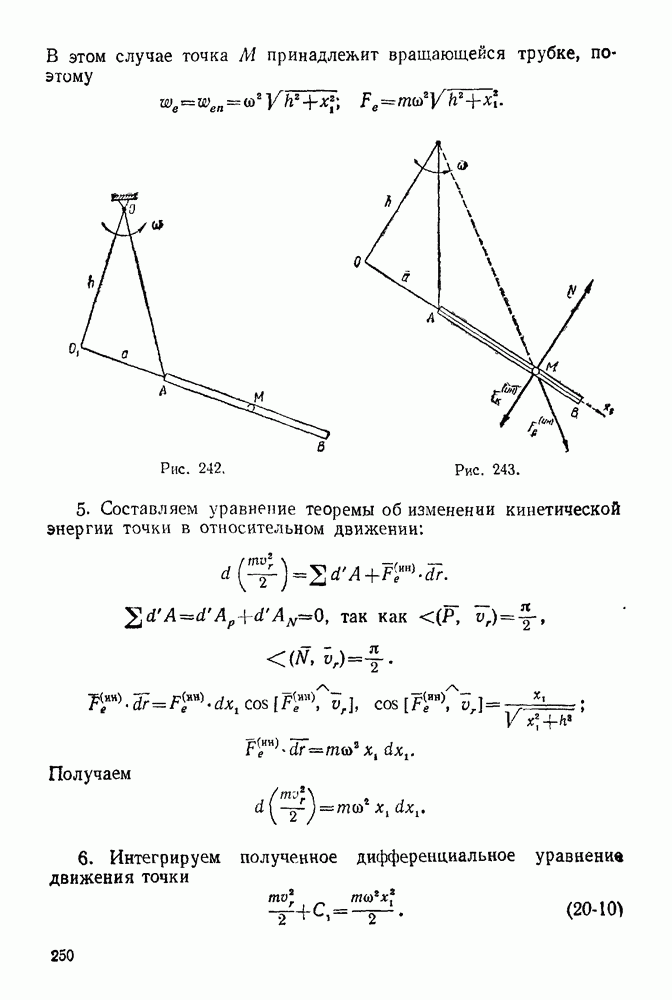
Фермой называется конструкция из стержней, соединенных между собою по концам шарнирно и образующих геометрически неизмеряемую систему (рис. 71).  -стержни фермы
-стержни фермы  узлы (шарниры) фермы.
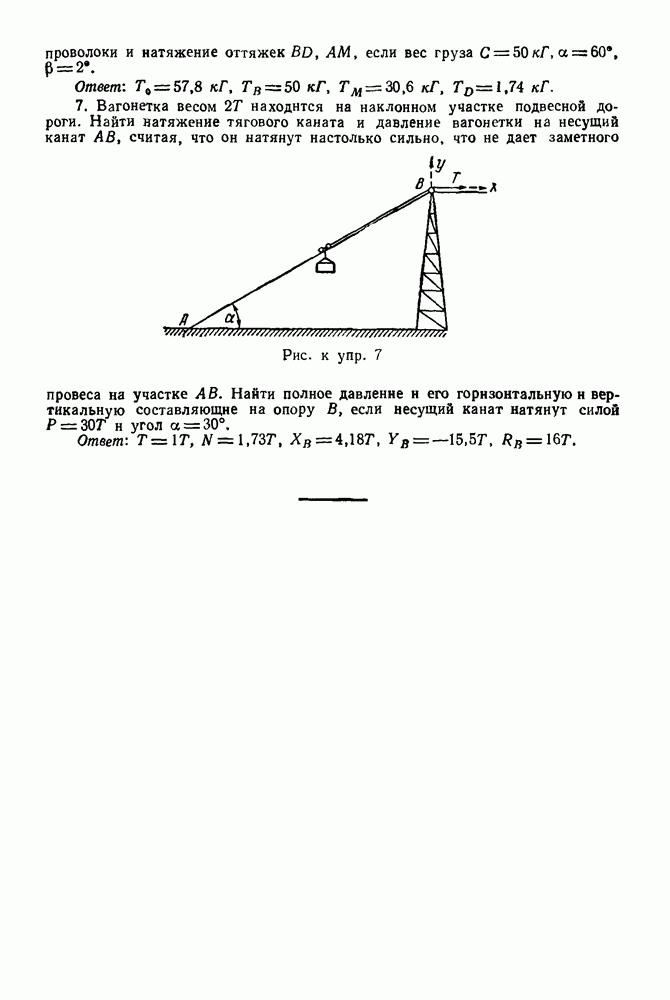
узлы (шарниры) фермы.

Рис. 71
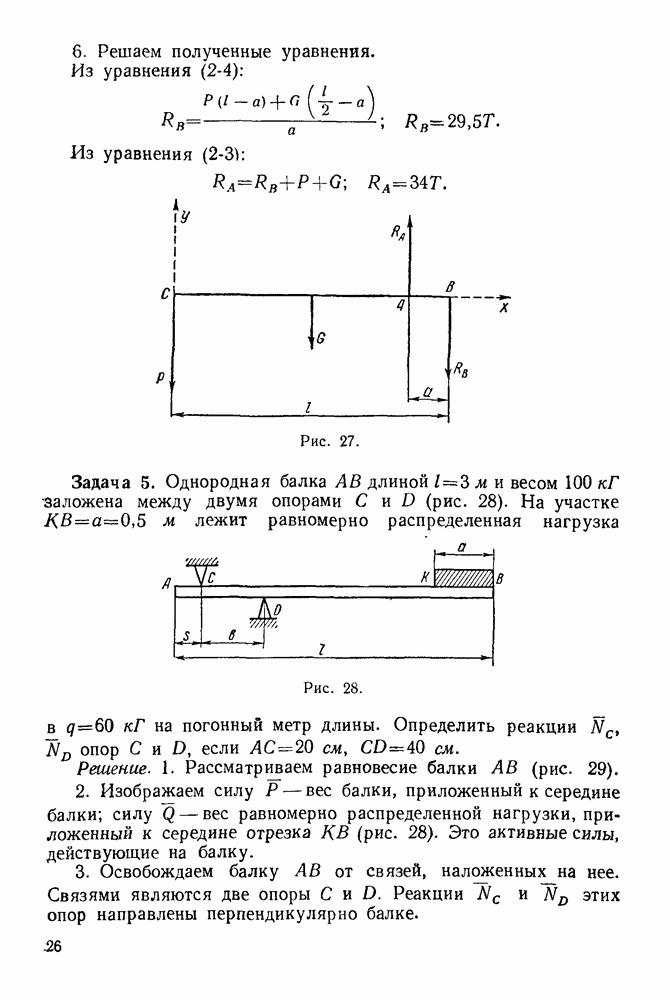
Фермой без лишних стержней называется такая ферма, в которой при удалении любого стержня нарушается ее геометрическая неизменяемость. Каждый стержень фермы испытывает только сжатие или растяжение, если выполняются следующие условия:
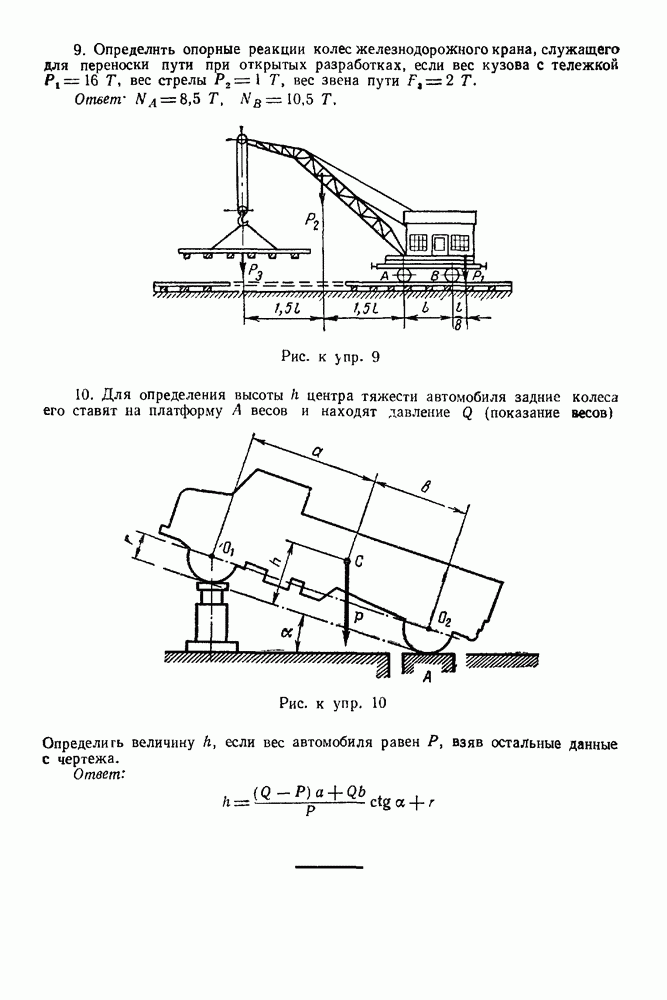
1. Все стержни прямолинейные.
2. Трение в шарнирах отсутствует.
3. Заданные (активные) силы лежат в плоскости фермы рассматриваем плоские фермы) и приложены только к узлам фермы.
4. Весом каждого стержня можно пренебречь по сравнению с силами, приложенными к узлам фермы.
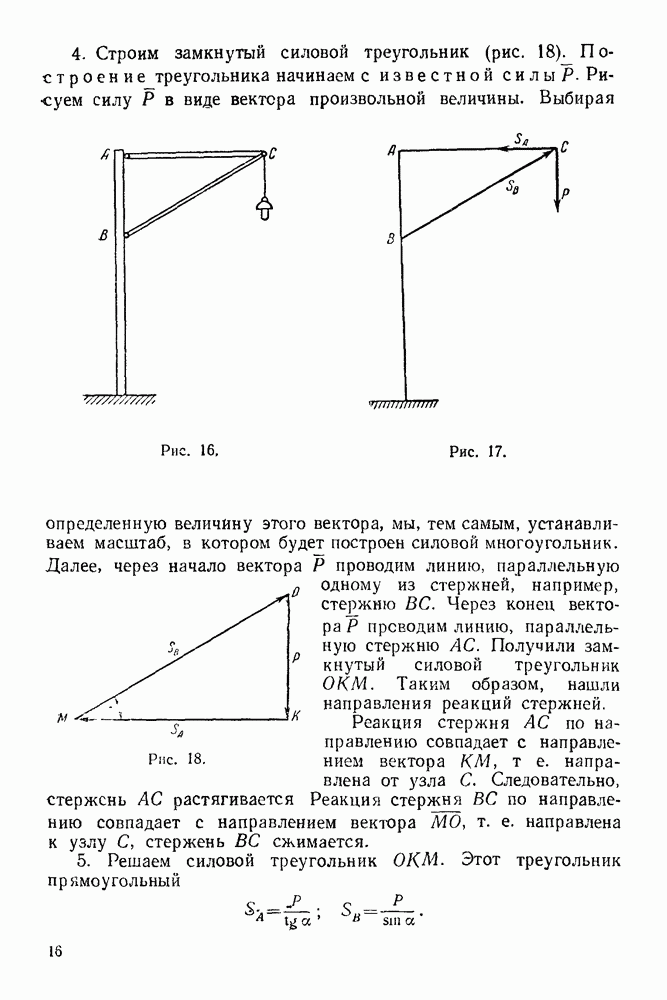
Основная задача, которую мы будем решать графически, заключается в том, что известны силы, приложенные к узлам фермы, а требуется определить реакции опор и усилия в стержнях фермы.
Ферма без лишних стержней является фермой статически определимой Это условие выражается формулой:

где  число стержней фермы
число стержней фермы  число узлов фермы.
число узлов фермы.
План решения задач
1 Проверяем статическую определимость данной фермы по формуле: 
2. Определяем графически опорные реакции фермы (см. § 5—2).
3. Находим усилия в стержнях фермы с помощью построения диаграммы Максвелла — Кремоны:
а) Изображаем ферму и все силы, действующие на нее, в выбранном масштабе. Рекомендуется векторы сил, действующих на узлы фермы, изображать так, чтобы они не пересекали области, ограниченные стержнями фермы (рис. 72 и рис. 73).
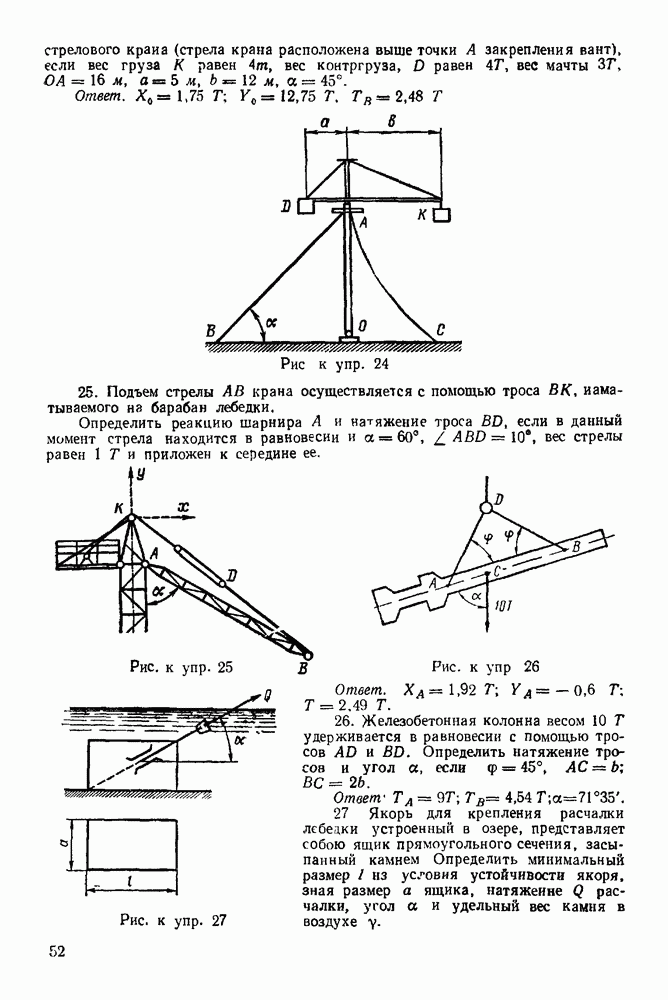
б) Обозначаем области между прямыми действия всех сил (активных, опорных реакций и усилий в стержнях фермы) цифрами 
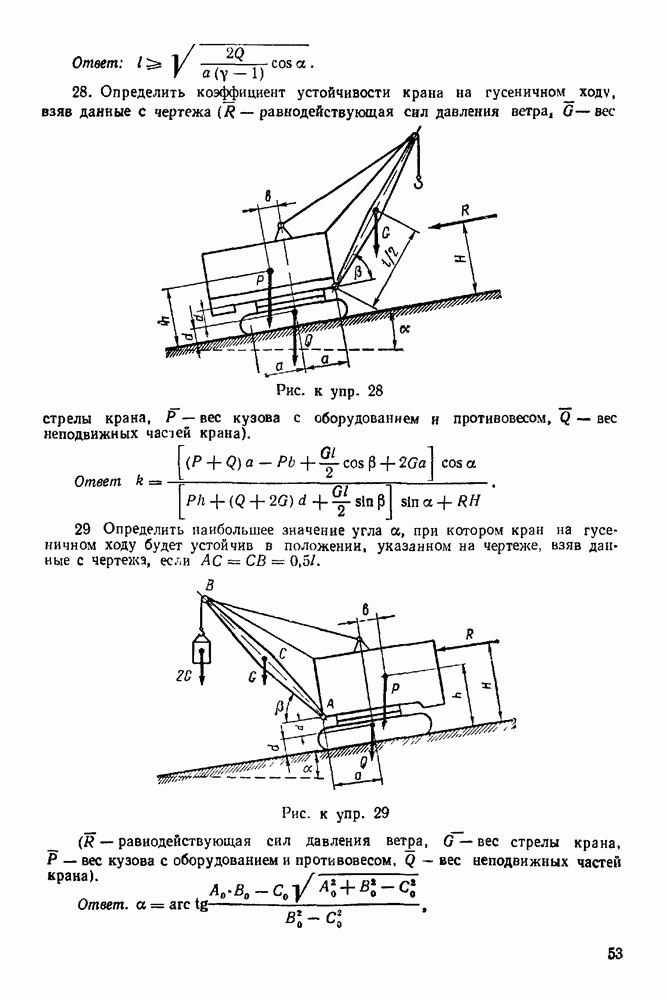
с) Строим в выбранном масштабе замкнутый многоугольник внешних сил (внешние силы — активные силы и реакции связей).
Для этого контур фермы обходим в определенном порядке, например, по направлению вращения часовой стрелки и к концу предыдущей силы, встречаемой при этом обходе, пристраиваем начало последующей.

Рис. 72

Рис. 73
Если сила, действующая на ферму, разграничивает области  и II, то в начале вектора силы в силовом многоугольнике должны поставить цифру
и II, то в начале вектора силы в силовом многоугольнике должны поставить цифру  а в конце — цифру 2, так как, обходя контур фермы по направлению вращения часовой стрелки, при переходе через прямую действия данной силы мы идем из области I в область
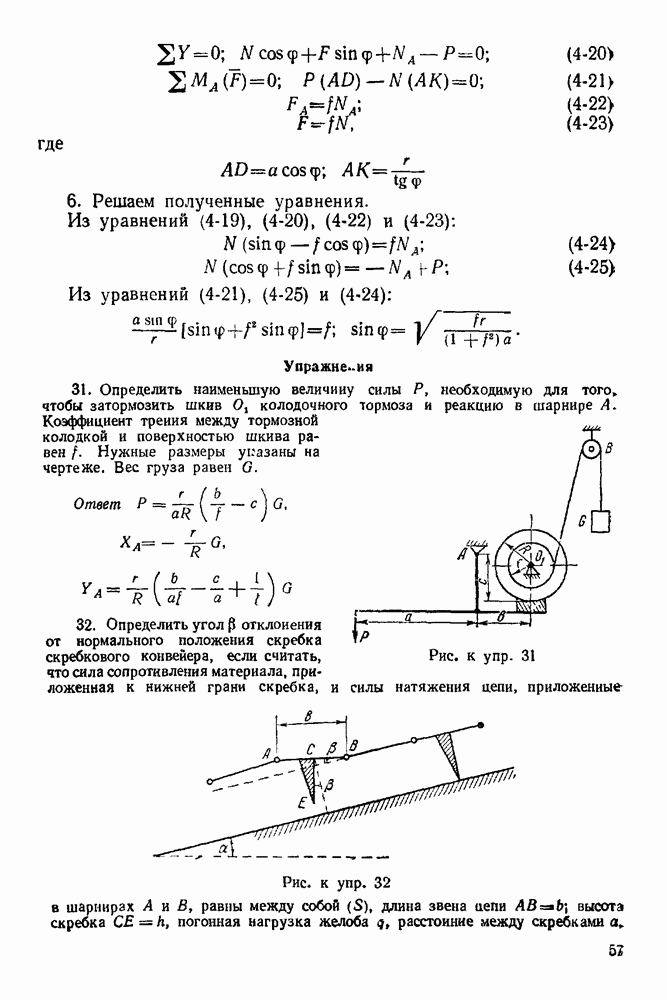
а в конце — цифру 2, так как, обходя контур фермы по направлению вращения часовой стрелки, при переходе через прямую действия данной силы мы идем из области I в область  К полученному многоугольнику внешних сил пристраиваем многоугольники внутренних сил — усилий в стержнях фермы, действующих на болт каждого шарнира (узла). При этом обходим узел также по направлению вращения часовой стрелки и начинаем рассмотрение равновесия того узла, где сходятся не больше, чем две неизвестные силы. Затем пристраиваем силовой многоугольник усилий, действующих
К полученному многоугольнику внешних сил пристраиваем многоугольники внутренних сил — усилий в стержнях фермы, действующих на болт каждого шарнира (узла). При этом обходим узел также по направлению вращения часовой стрелки и начинаем рассмотрение равновесия того узла, где сходятся не больше, чем две неизвестные силы. Затем пристраиваем силовой многоугольник усилий, действующих  тот узел, где сходятся также не более двух неизвестных сил,
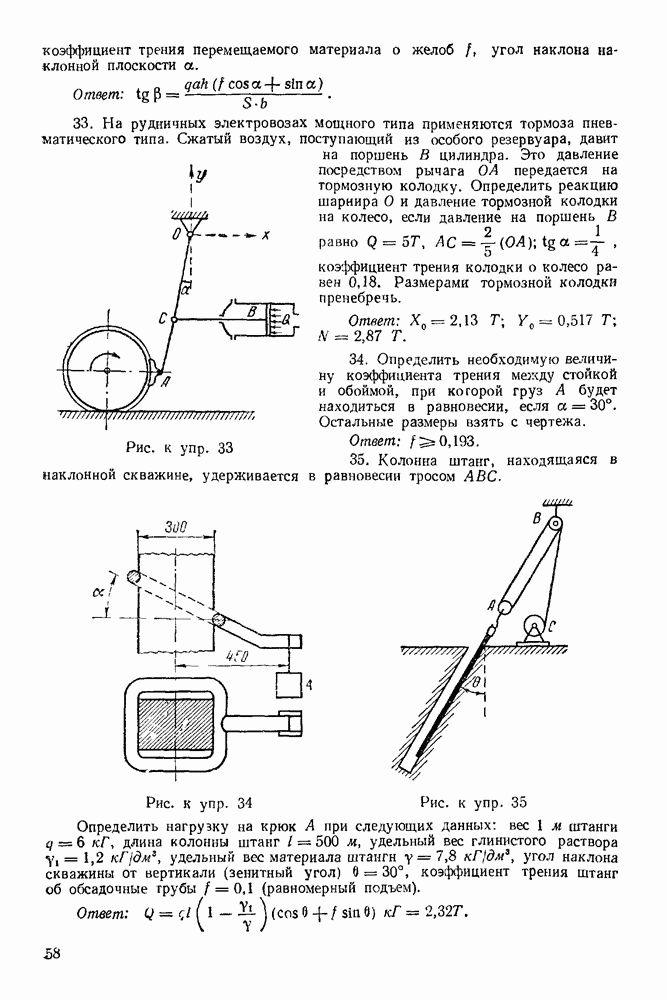
тот узел, где сходятся также не более двух неизвестных сил,  Таким образом, получим диаграмму Максвелла — Кремоны.
Таким образом, получим диаграмму Максвелла — Кремоны.

Рис. 74
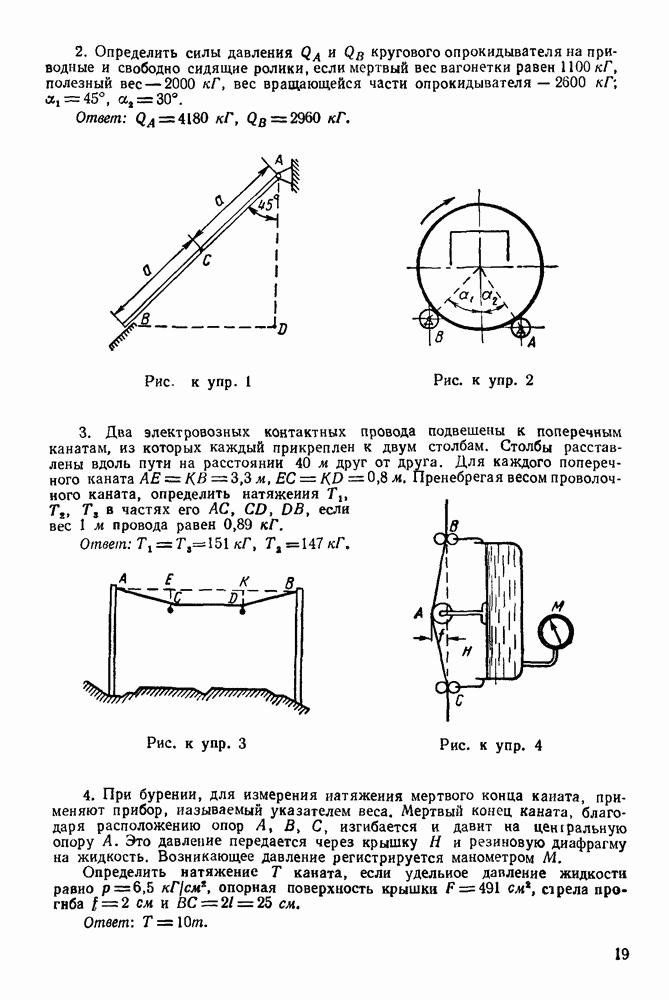
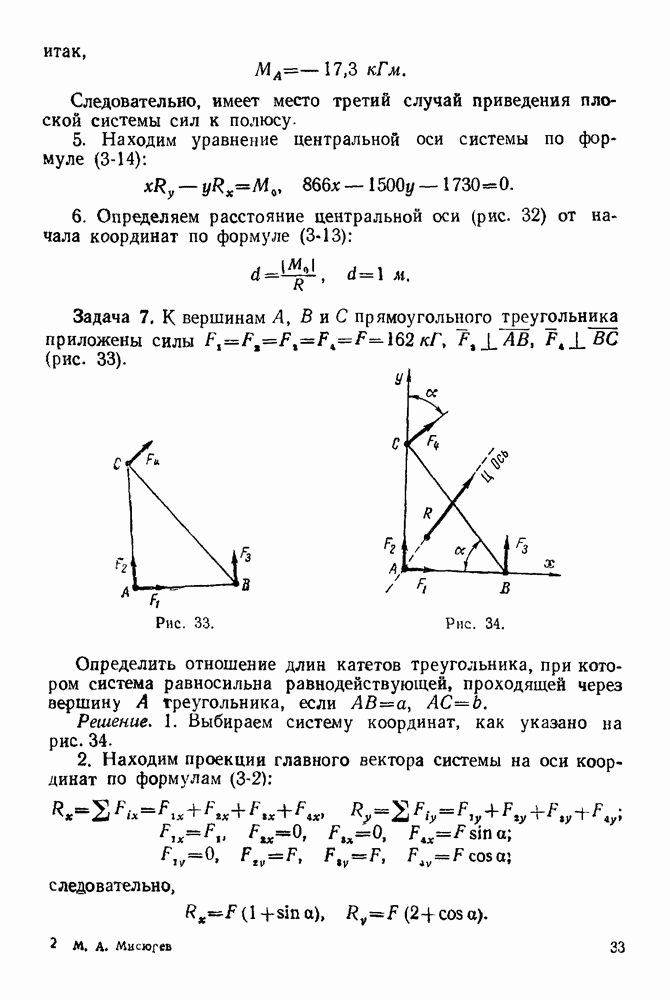
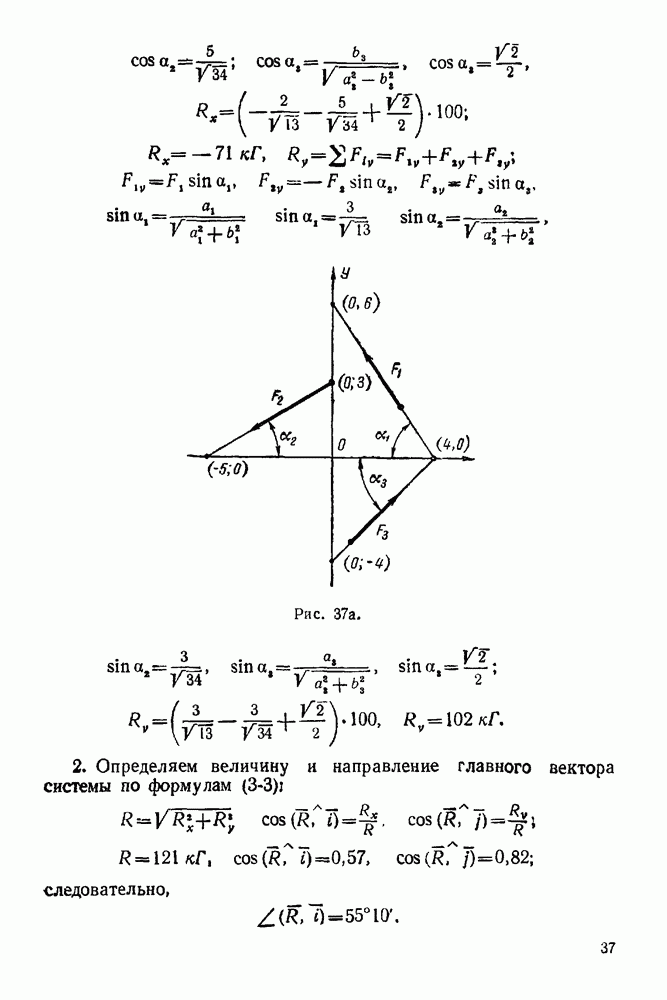
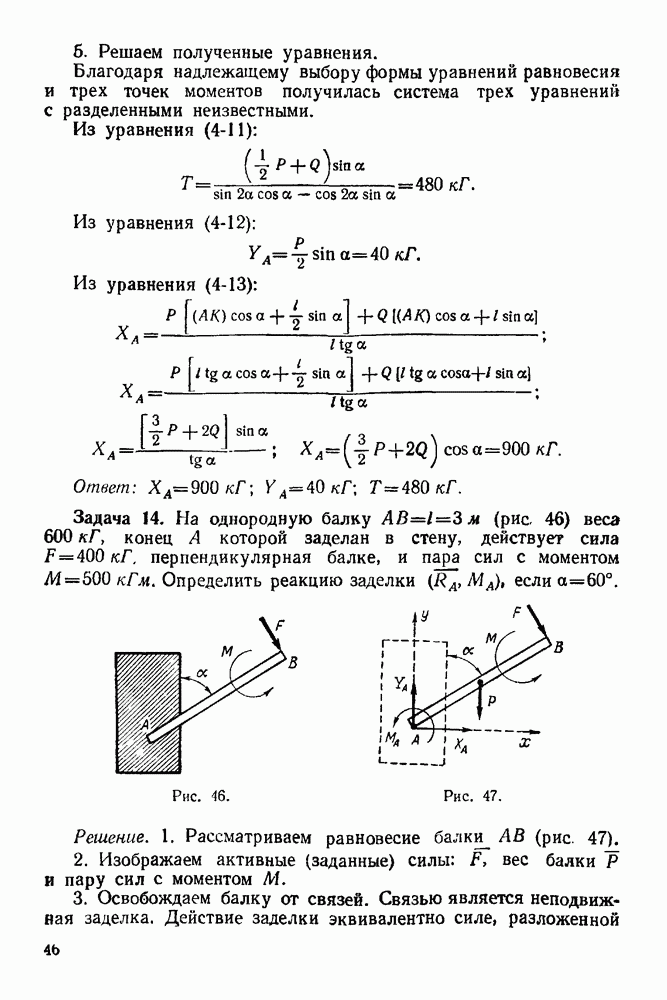
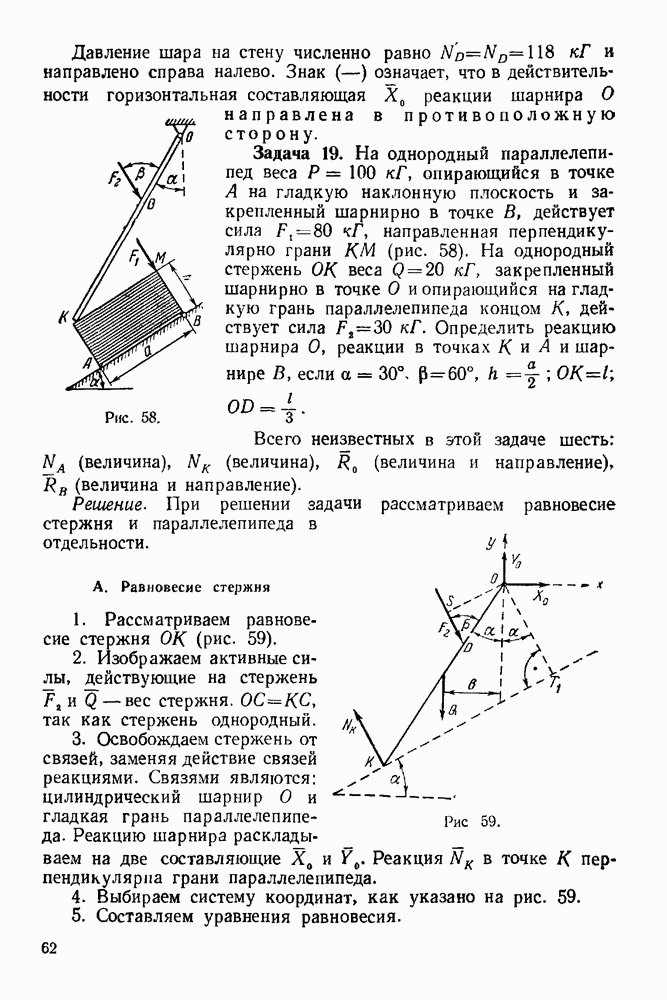
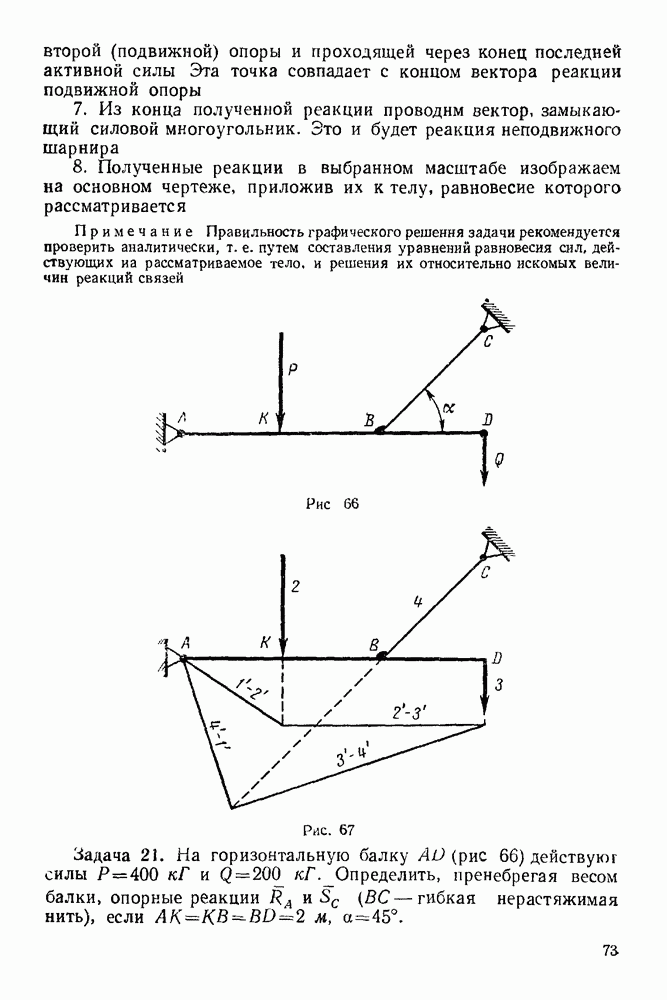
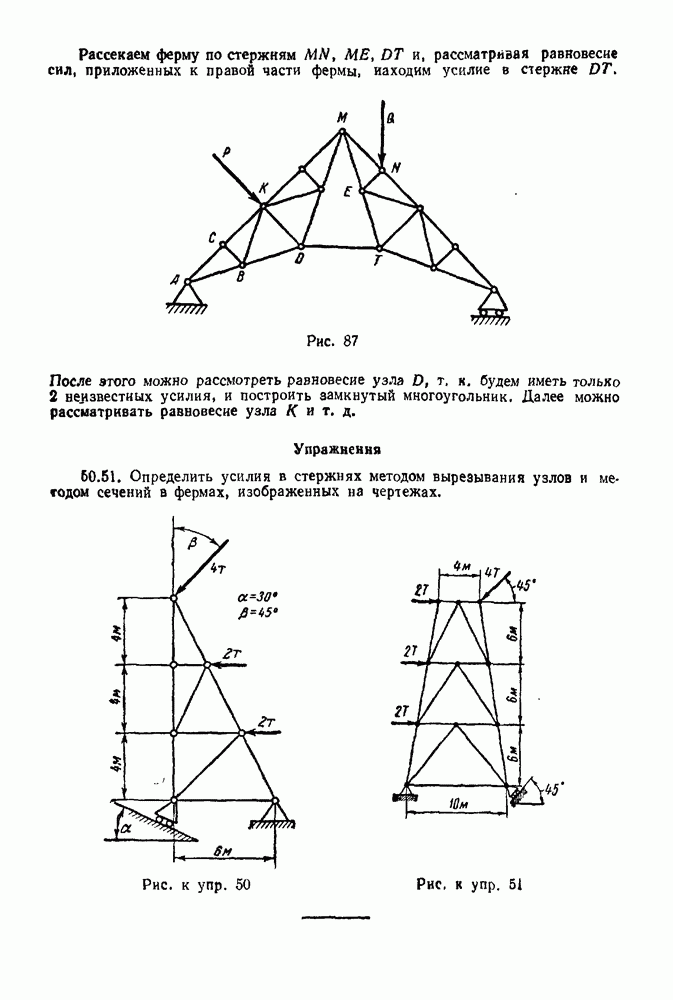
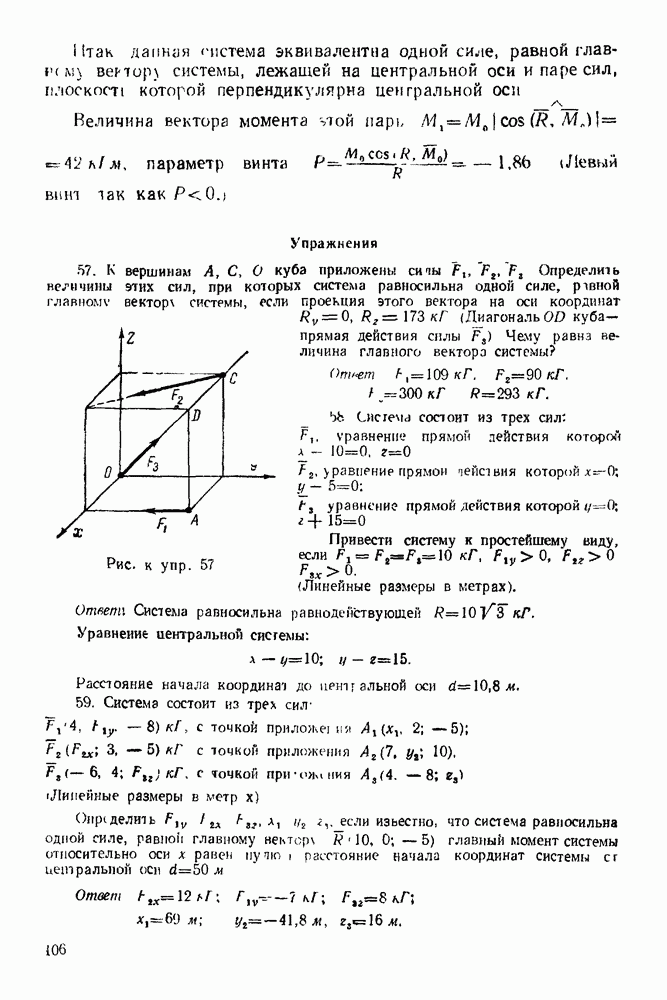
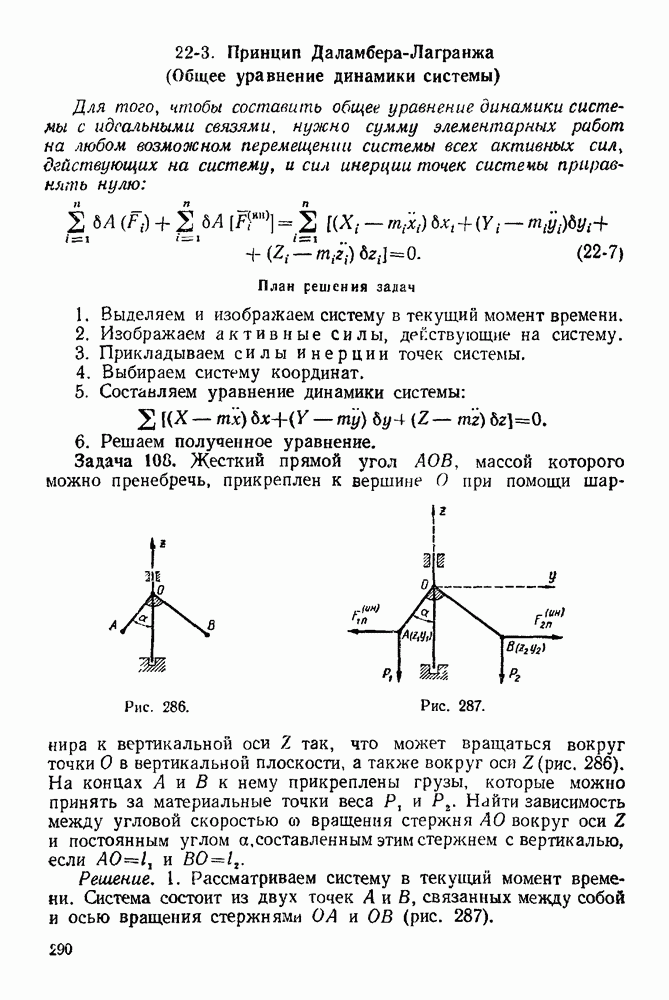
Задача 22. На узлы  фермы (рис. 74) действуют силы
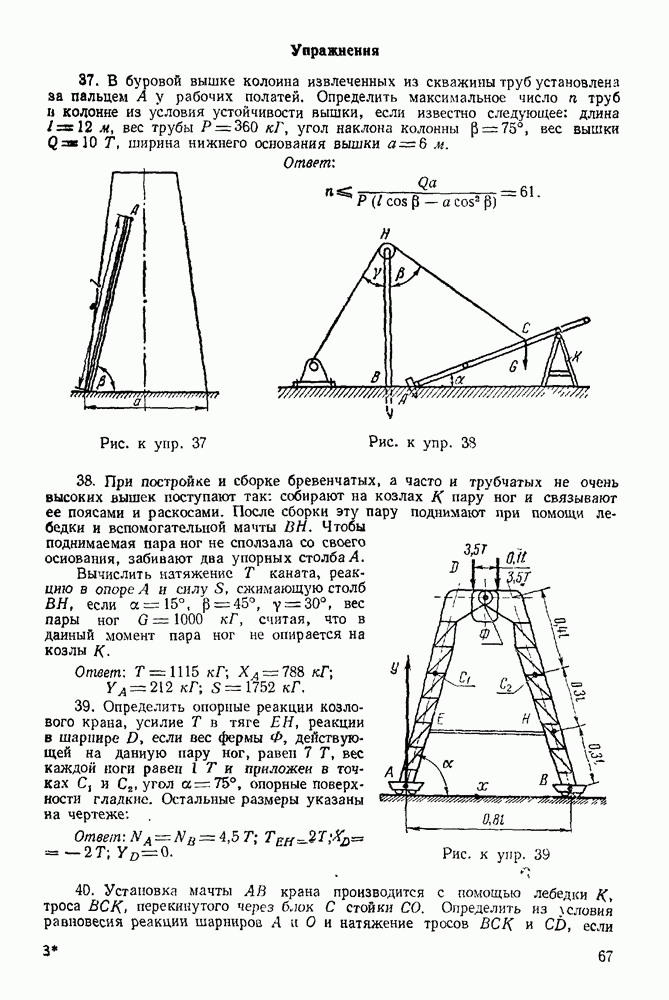
фермы (рис. 74) действуют силы  Определить графически опорные реакции и усилия в стержнях фермы, если
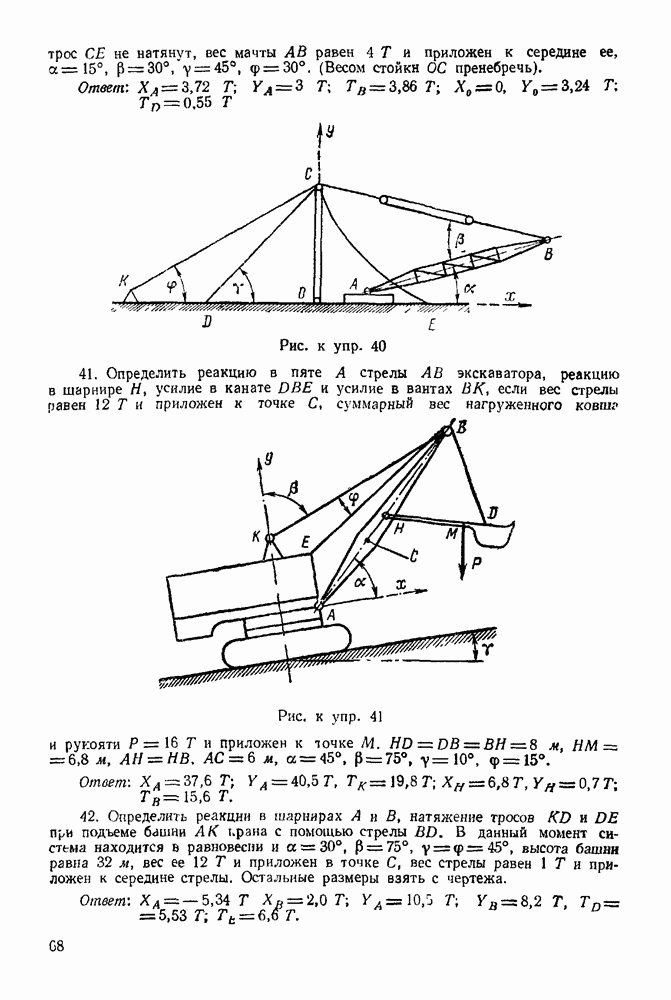
Определить графически опорные реакции и усилия в стержнях фермы, если 
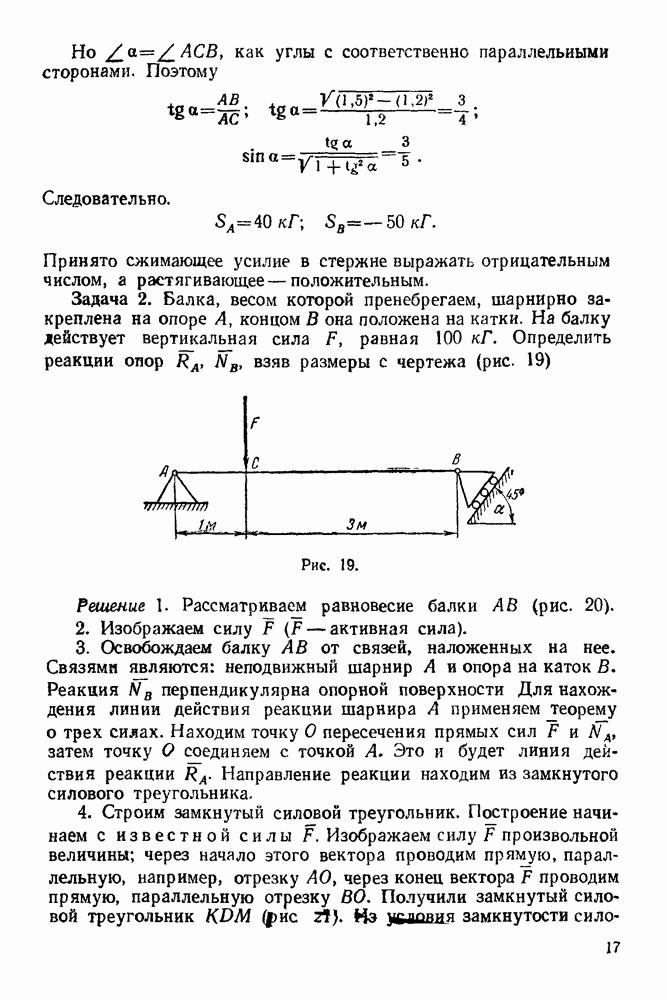
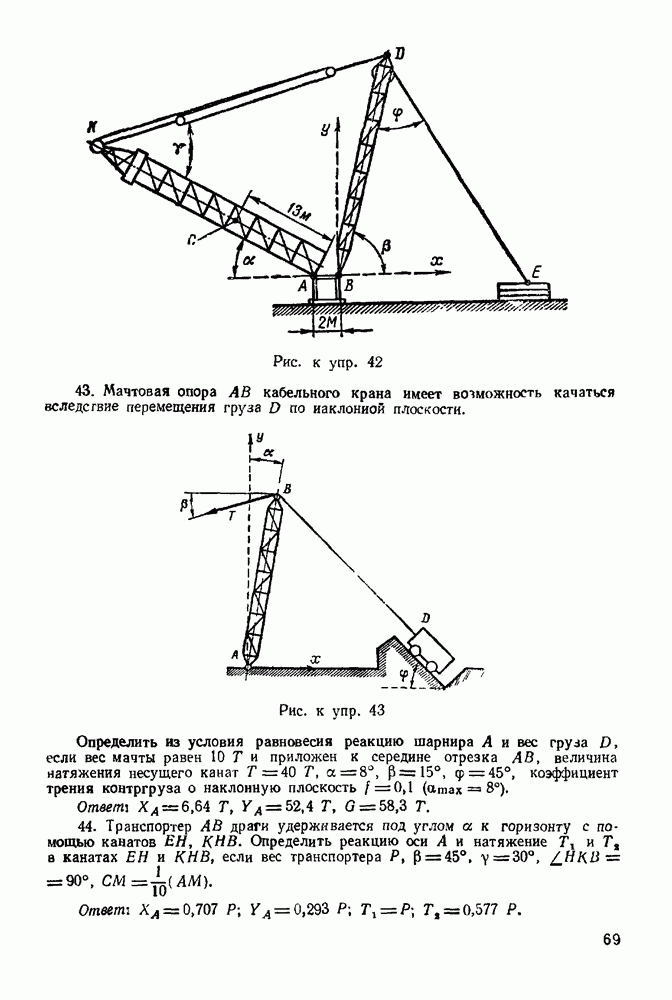
Решение При решении задачи следует придерживаться вышеизложенного порядка
1 Проверяем статическую определимость данной фермы по формуле 
Число стержней в этой ферме  число узлов
число узлов 
следовательно, по этой формуле получаем тождество  ферма статически определимая.
ферма статически определимая.
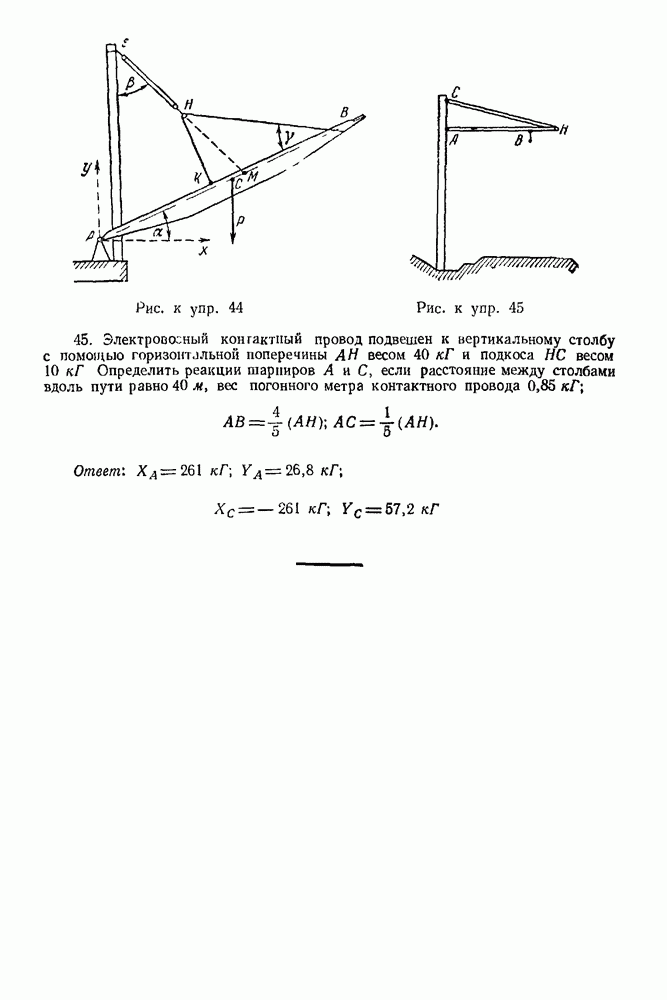
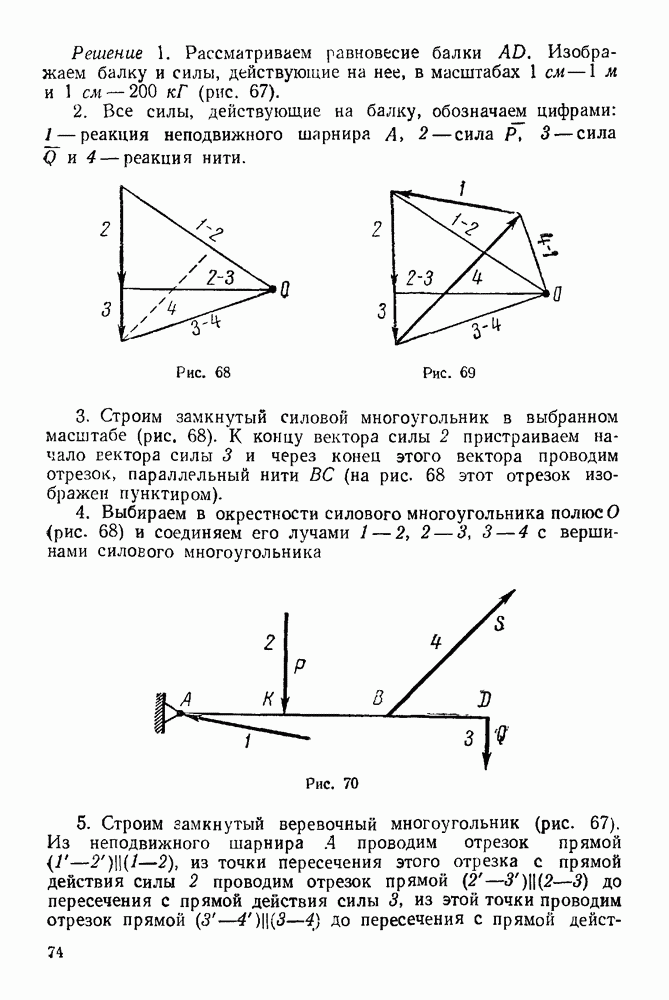
2. Определяем графически опорные реакции по правилу, сформулированному в § 5—2 (рис. 75. рис. 76). Масштаб длин взят  в 1 см. Масштаб сил —
в 1 см. Масштаб сил —  в 1 см.
в 1 см.

Рис. 75

Рис. 76
Таким образом, нашли, что величина реакции подвижного шарнира В равна  неподвижного шарнира
неподвижного шарнира  абсолютная величина горизонтальной составляющей, а
абсолютная величина горизонтальной составляющей, а  абсолютная величина вертикальной составляющей).
абсолютная величина вертикальной составляющей).
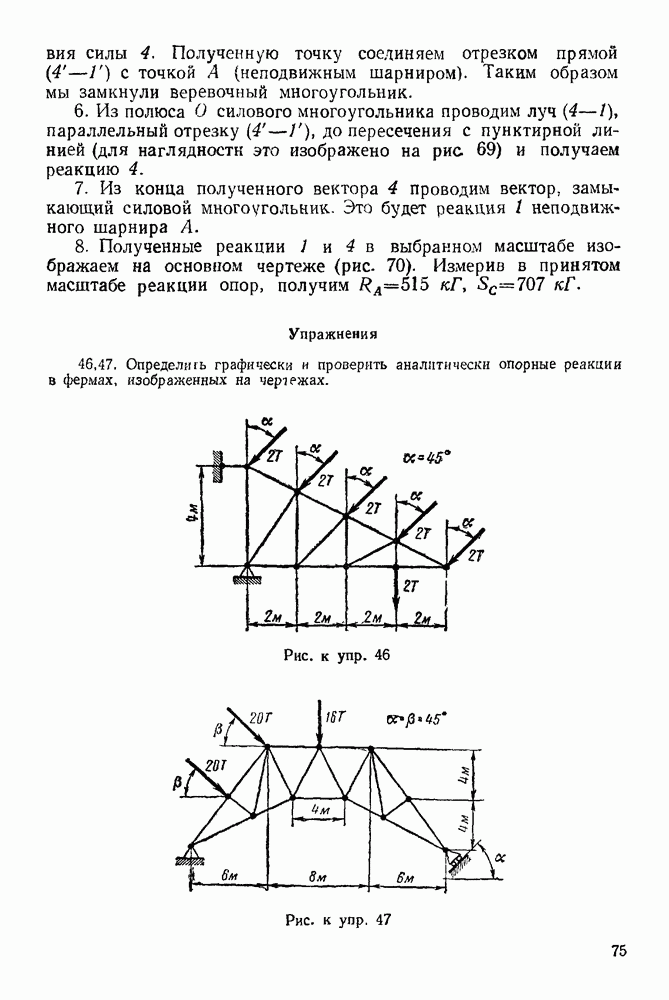
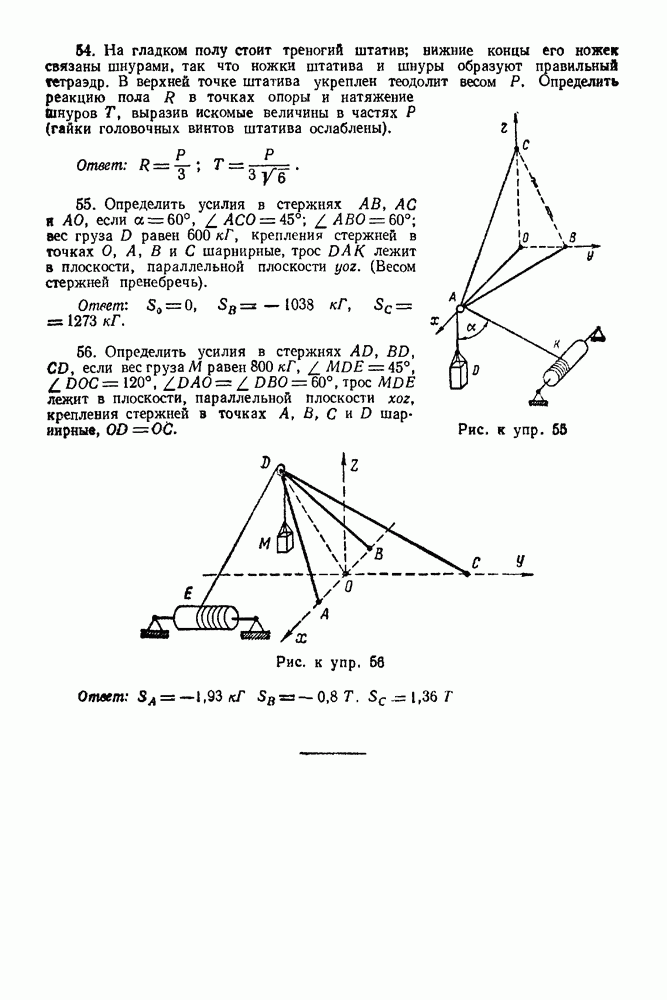
3. Находим усилия в стержнях фермы с помощью построения диаграммы Максвелла — Кремоны:
а) Изображаем ферму в масштабе  в 1 см и все силы действующие на ферму, в масштабе
в 1 см и все силы действующие на ферму, в масштабе  см (рис. 77).
см (рис. 77).

Рис. 77

Рис. 78
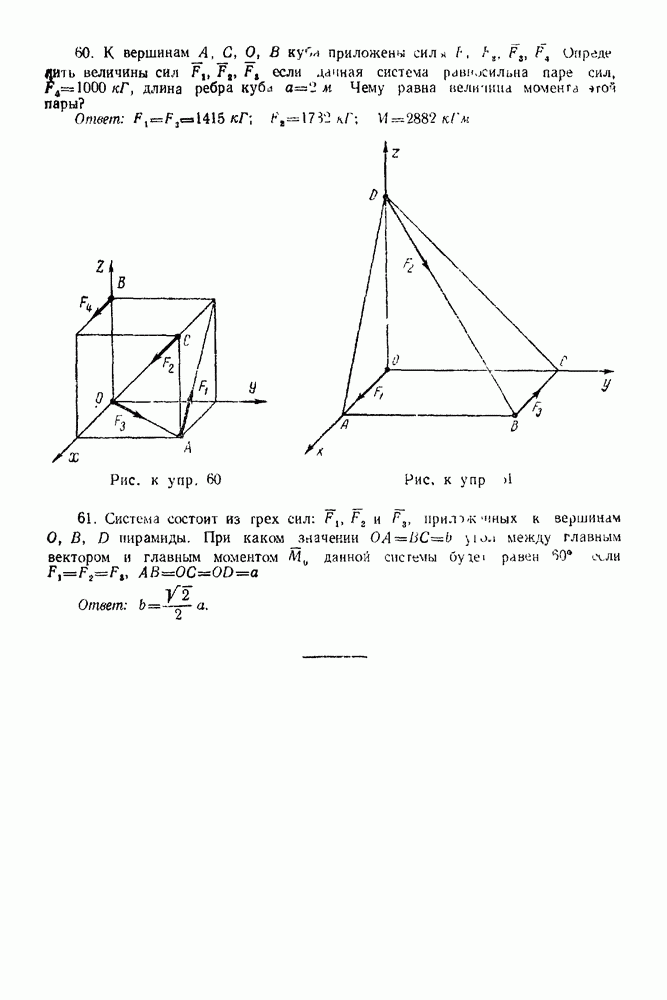
в) Обозначаем поля между прямыми действия всех сил цифрами 1, II и  Так например, область I ограничена прямыми действия усилия в стержне
Так например, область I ограничена прямыми действия усилия в стержне  силой, приложенной к узлу
силой, приложенной к узлу  и реакцией неподвижного шарнира А, область V ограничена прямыми действия усилий в стержнях
и реакцией неподвижного шарнира А, область V ограничена прямыми действия усилий в стержнях  и
и  фермы.
фермы.
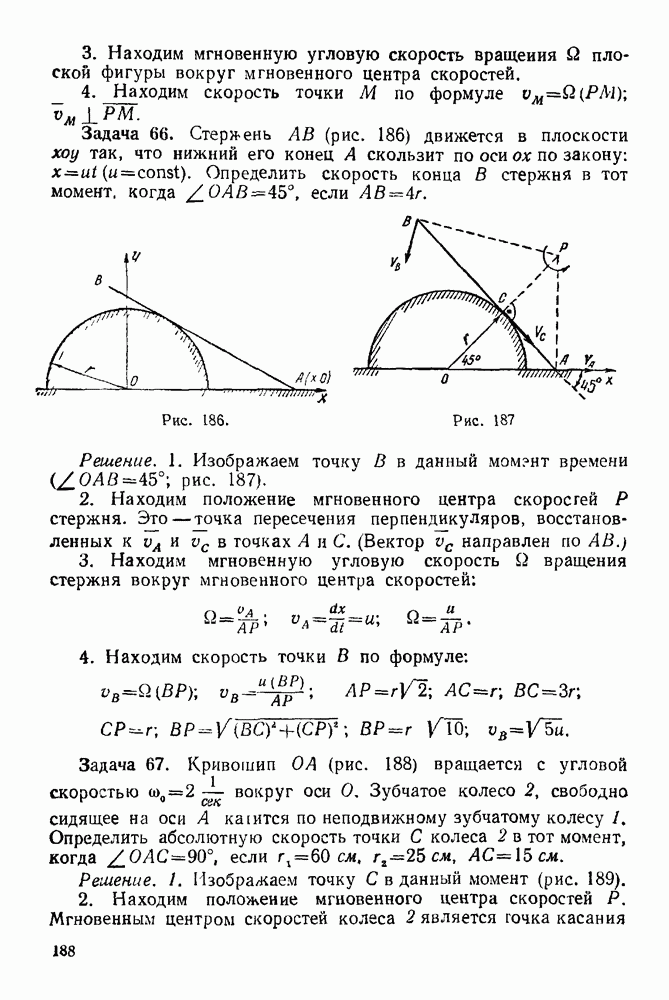
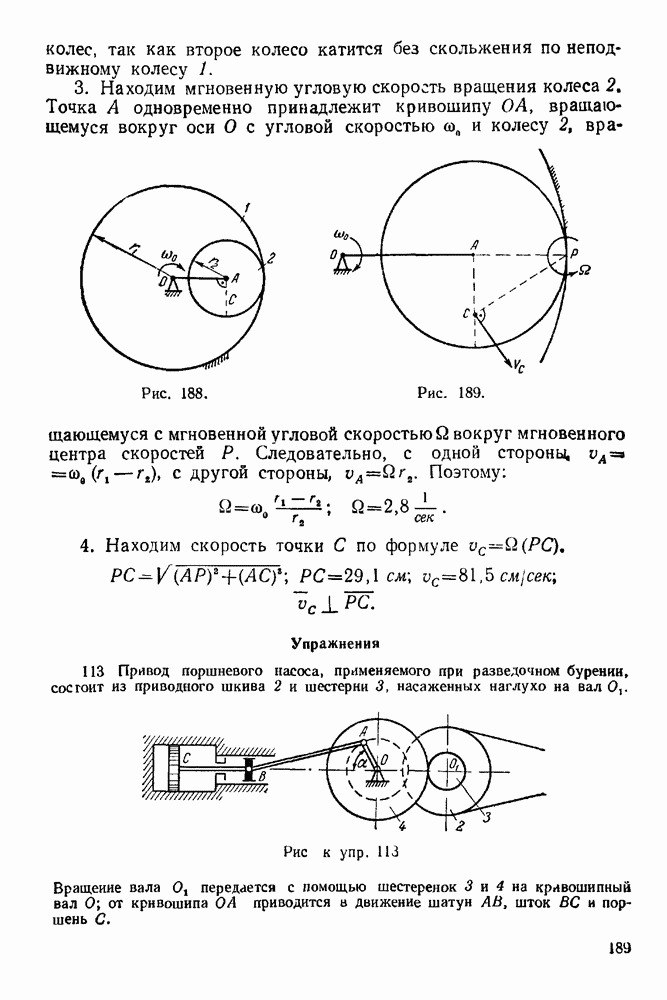
c) Строим в выбранном масштабе многоугольник внешних сил. (Внешние силы — активные силы, действующие на ферму и опорные реакции; рис. 78).
Контур фермы обходим по направлению вращения часовой стрелки, а к концу предыдущей силы, встречаемой при этом обходе, пристраиваем начало последующей. Реакция неподвижного шарнира А должна быть обозначена так: в начале вектора силы нужно поставить цифру 1, а в конце 2, так как, обходя контур фермы по направлению вращения часовой стрелки, при переходе через прямую действия этой реакции мы идем из области I в область II.
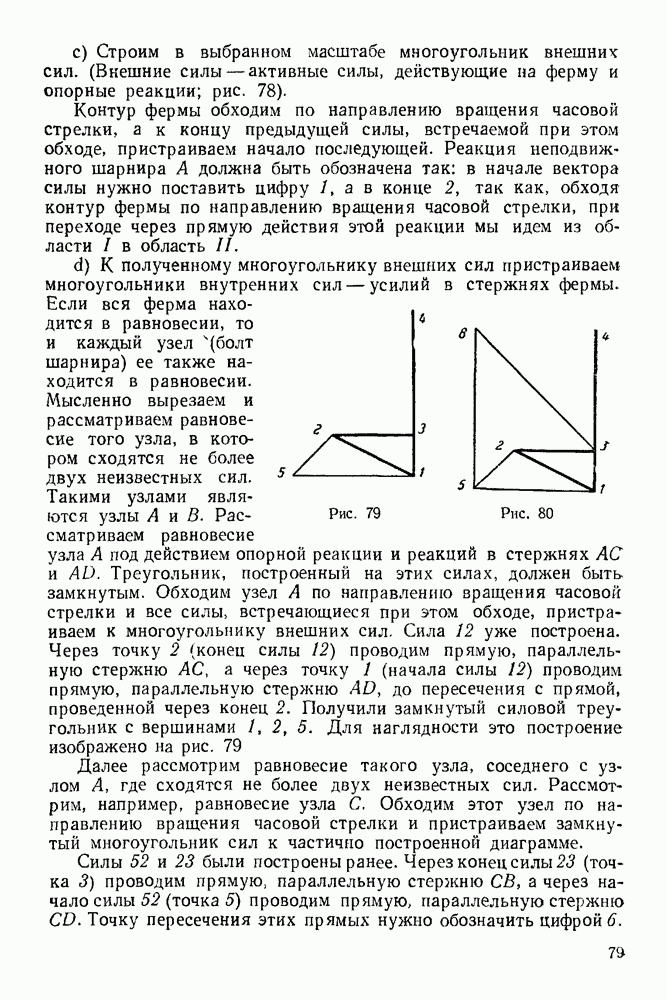
d) К полученному многоугольнику внешних сил пристраиваем многоугольники внутренних сил — усилий в стержнях фермы. Если вся ферма находится в равновесии, то и каждый узел 4 (болт шарнира) ее также находится в равновесии.

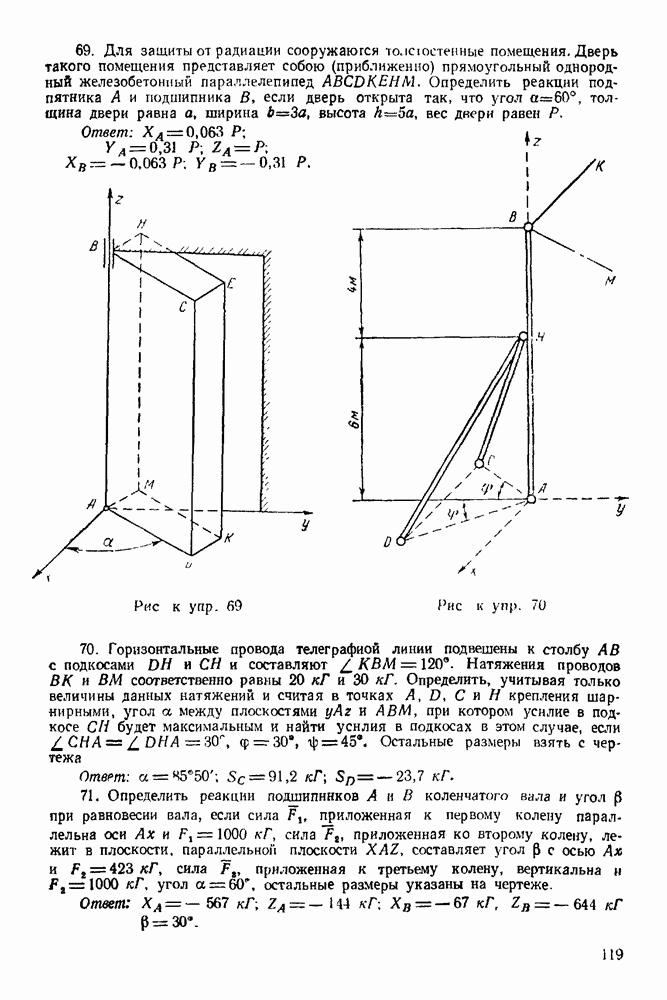
Рис. 79

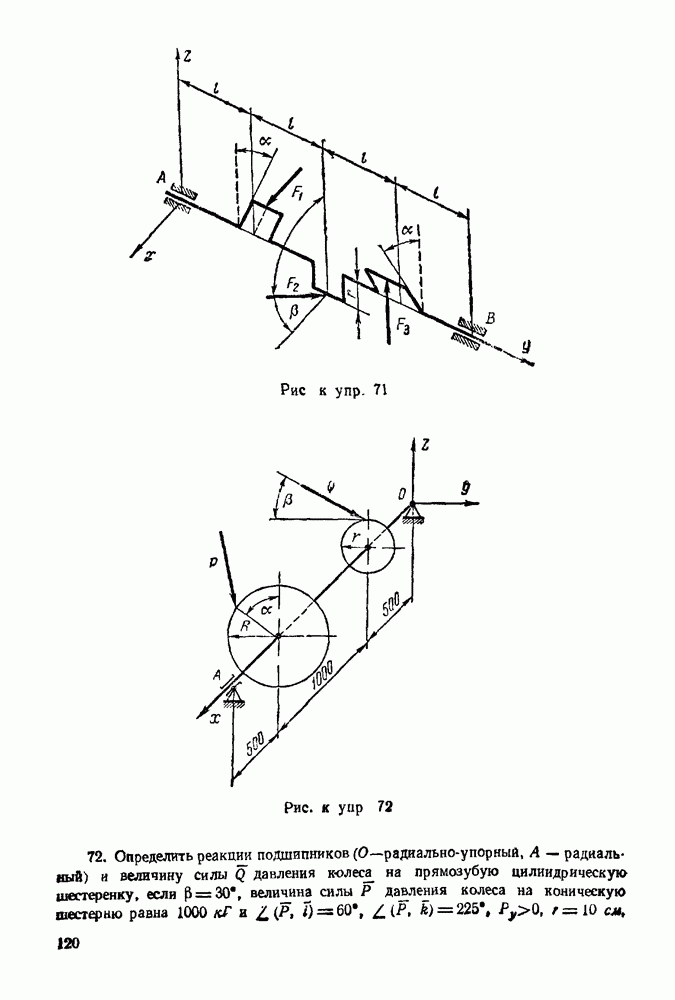
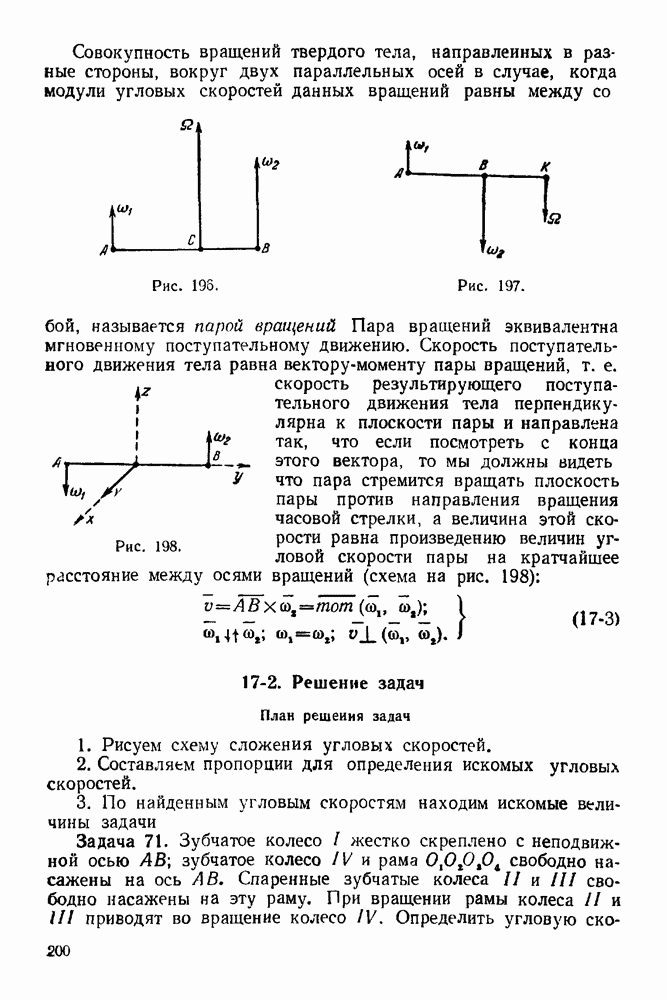
Рис. 80 Мысленно вырезаем и рассматриваем равновесие того узла, в котором сходятся не более двух неизвестных сил. Такими узлами являются узлы  Рассматриваем равновесие узла А под действием опорной реакции и реакций в стержнях
Рассматриваем равновесие узла А под действием опорной реакции и реакций в стержнях  и
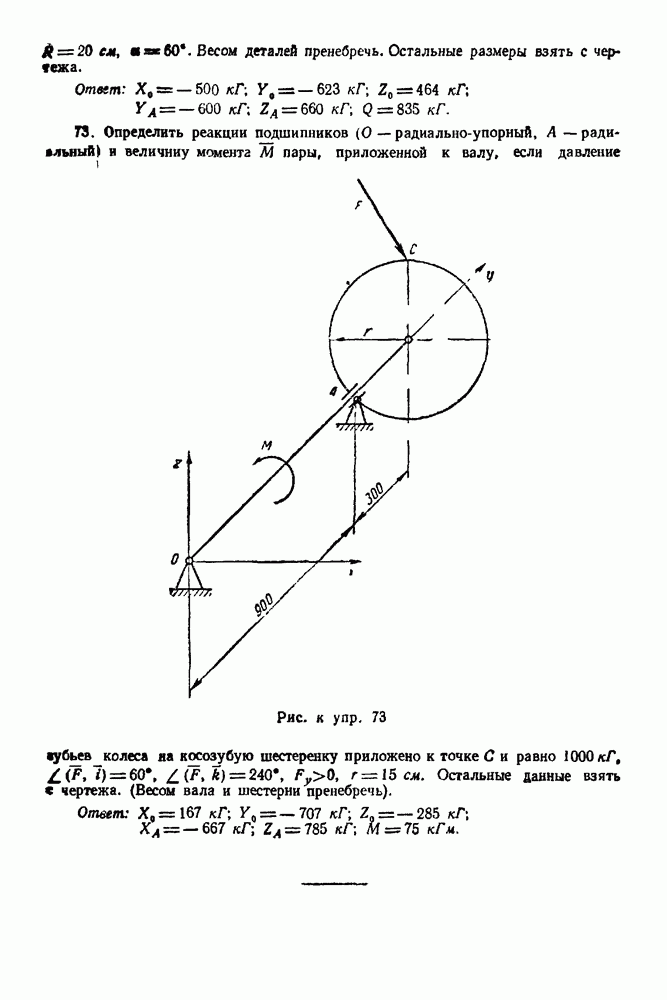
и  Треугольник, построенный на этих силах, должен быть замкнутым. Обходим узел А по направлению вращения часовой стрелки и все силы, встречающиеся при этом обходе, пристраиваем к многоугольнику внешних сил. Сила 12 уже построена. Через точку 2 (конец силы 12) проводим прямую, параллельную стержню
Треугольник, построенный на этих силах, должен быть замкнутым. Обходим узел А по направлению вращения часовой стрелки и все силы, встречающиеся при этом обходе, пристраиваем к многоугольнику внешних сил. Сила 12 уже построена. Через точку 2 (конец силы 12) проводим прямую, параллельную стержню  а через точку 1 (начала силы 12) проводим прямую, параллельную стержню
а через точку 1 (начала силы 12) проводим прямую, параллельную стержню  до пересечения с прямой, проведенной через конец 2. Получили замкнутый силовой треугольник с вершинами 1, 2, 5. Для наглядности это построение изображено на рис. 79
до пересечения с прямой, проведенной через конец 2. Получили замкнутый силовой треугольник с вершинами 1, 2, 5. Для наглядности это построение изображено на рис. 79
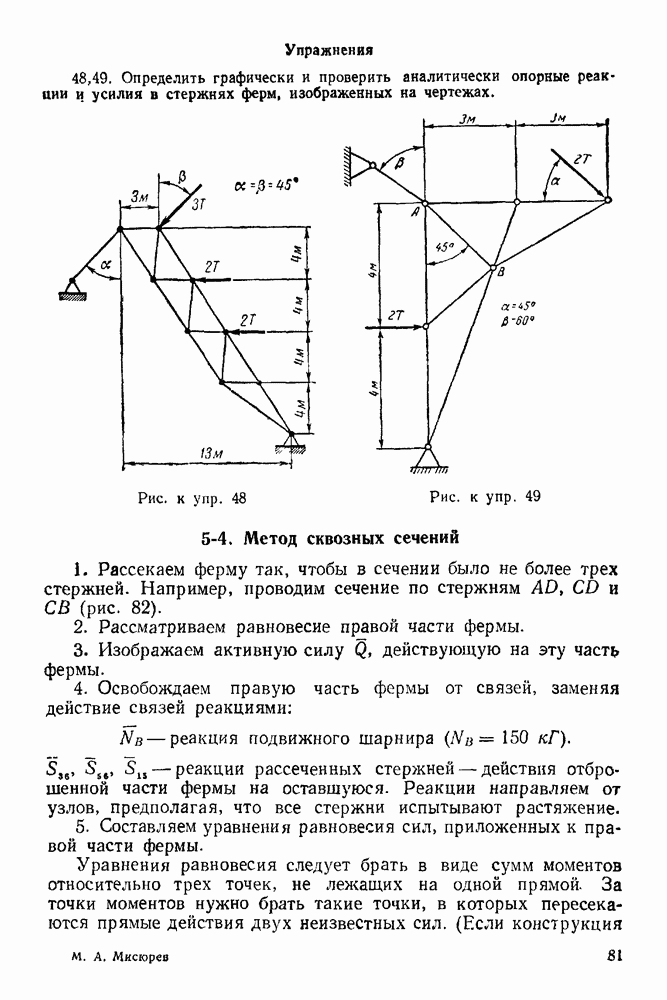
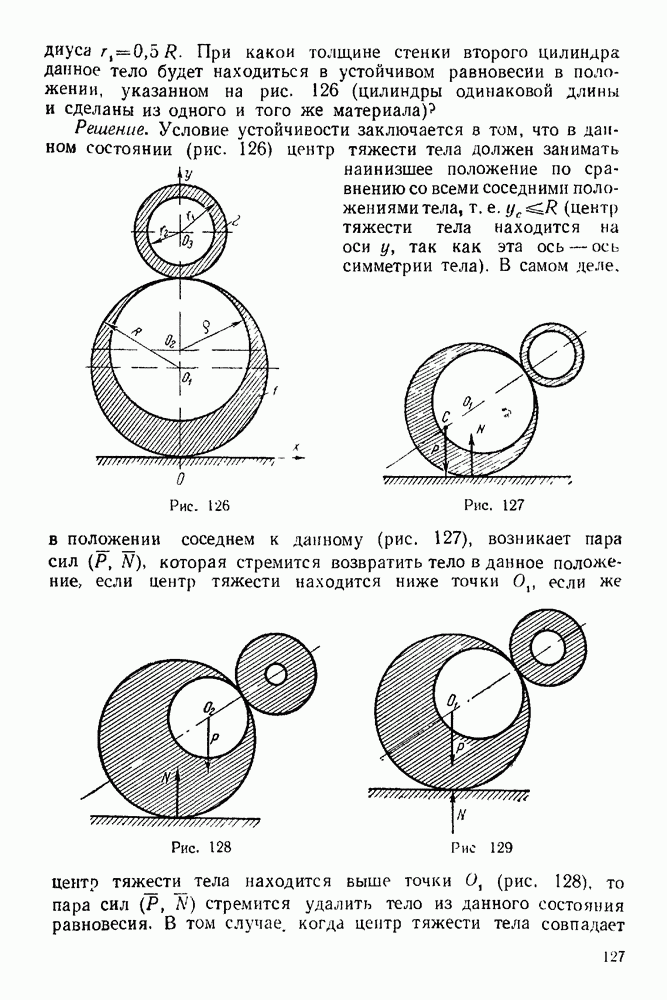
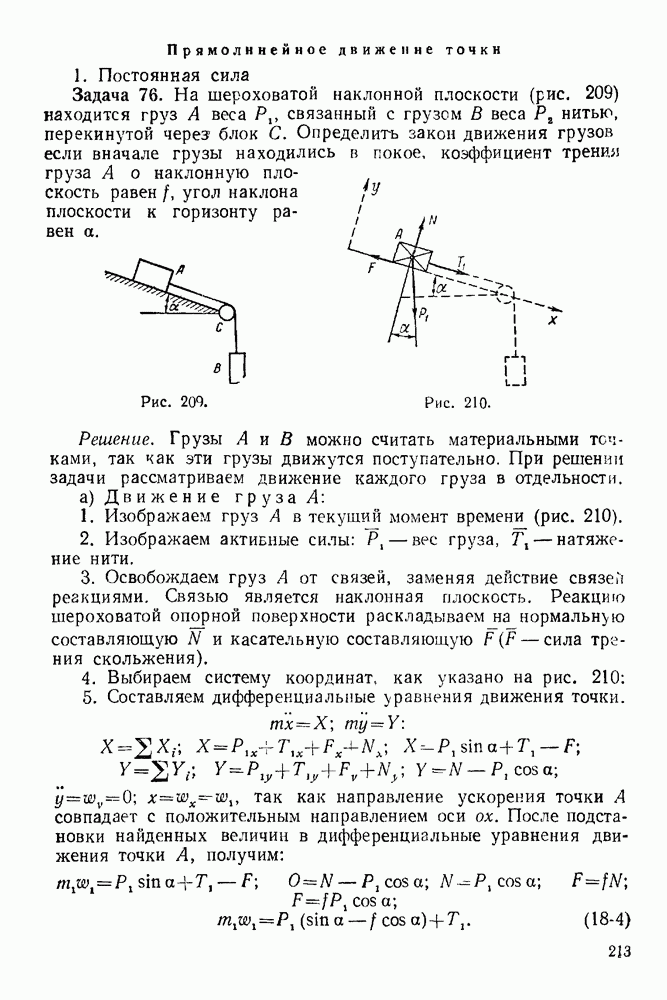
Далее рассмотрим равновесие такого узла, соседнего с узлом А, где сходятся не более двух неизвестных сил. Рассмотрим, например, равновесие узла С. Обходим этот узел по направлению вращения часовой стрелки и пристраиваем замкнутый многоугольник сил к частично построенной диаграмме.
Силы 52 и 23 были построены ранее. Через конец силы 23 (точка 3) проводим прямую, параллельную стержню  а через начало силы 52 (точка 5) проводим прямую, параллельную стержню
а через начало силы 52 (точка 5) проводим прямую, параллельную стержню  Точку пересечения этих прямых нужно обозначить цифрой 6.
Точку пересечения этих прямых нужно обозначить цифрой 6.
Замкнутый силовой многоугольник, соответствующий узлу  будет иметь вершины 5, 2, 3 и 6 (рис. 80). И, наконец, рассматриваем равновесие узла
будет иметь вершины 5, 2, 3 и 6 (рис. 80). И, наконец, рассматриваем равновесие узла  обходя его по направлению вращения часовой стрелки. Силы 41, 15, 56 уже построены ранее.
обходя его по направлению вращения часовой стрелки. Силы 41, 15, 56 уже построены ранее.
Так как точки  также построены, то их нужно соединить и получим замкнутый многоугольник (рис. 81). Таким образом, полностью построили диаграмму Максвелла — Кремоны для данной фермы.
также построены, то их нужно соединить и получим замкнутый многоугольник (рис. 81). Таким образом, полностью построили диаграмму Максвелла — Кремоны для данной фермы.
Для последнего узла В замкнутый многоугольник уже построен — это треугольник с вершинами 3, 4 и 6. Следовательно, рассмотрение равновесия последнего узла фермы служит для контроля правильности построения диаграммы Максвелла — Кремоны.
Измерив в принятом масштабе усилия в стержнях фермы по диаграмме Максвелла — Кремоны, нужно их значение внести в таблицу.

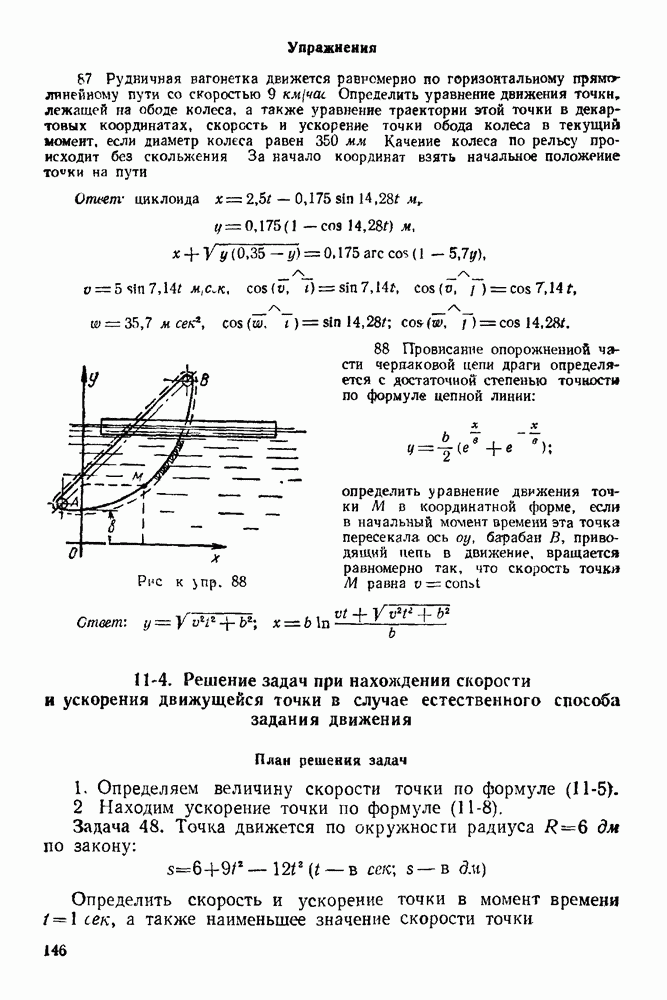
Рис. 81
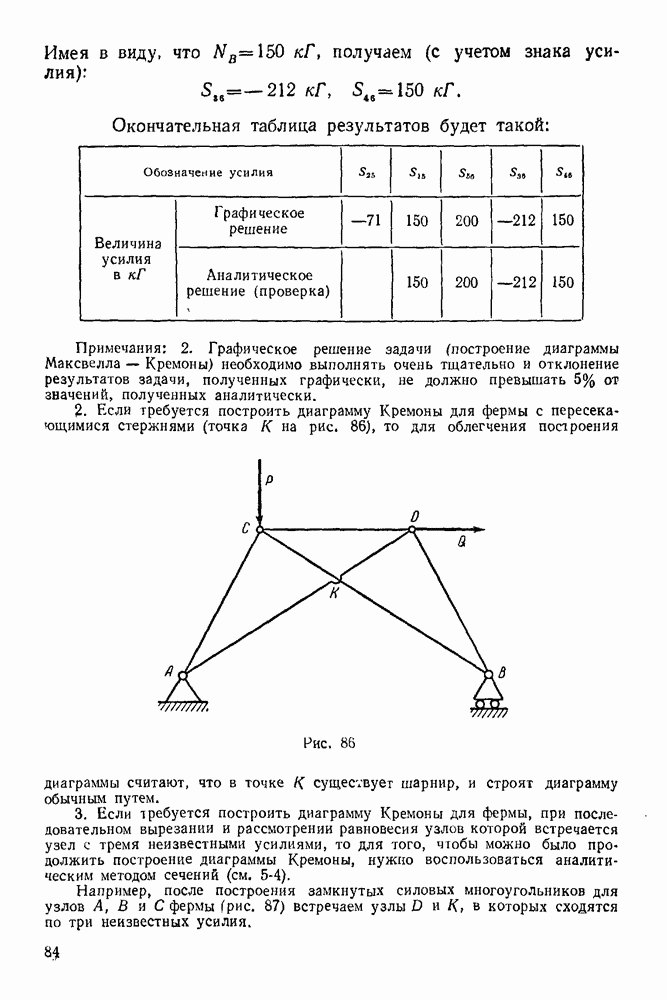
Как установлено ранее (см. стр. 11,7-й тип связи), если реакция стержня направлена от узла, то стержень испытывает растяжение  в противном случае — сжатие
в противном случае — сжатие 
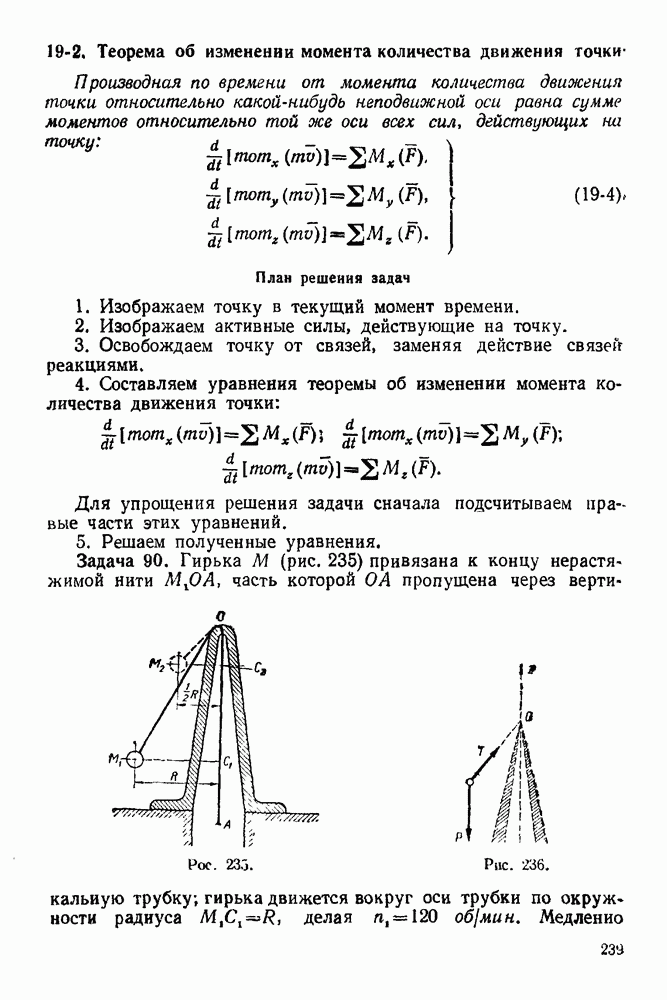
Для того, чтобы определить, испытывает ли какой-нибудь стержень фермы (например, стержень  растяжение или сжатие, нужно обойти один из двух узлов, которые соединяет этот стержень.
растяжение или сжатие, нужно обойти один из двух узлов, которые соединяет этот стержень.
Для определенности обходим узел С, пересекая стержень  Реакция этого стержня, приложенная к узлу С, изображается на диаграмме вектором 52 (так как при обходе узла С по направлению вращения часовой стрелки идем из области У в область II), если мысленно вектор 52 перенести на стержень
Реакция этого стержня, приложенная к узлу С, изображается на диаграмме вектором 52 (так как при обходе узла С по направлению вращения часовой стрелки идем из области У в область II), если мысленно вектор 52 перенести на стержень  то увидим, что этот вектор направлен к узлу, т. е. стержень
то увидим, что этот вектор направлен к узлу, т. е. стержень  испытывает сжатие.
испытывает сжатие.
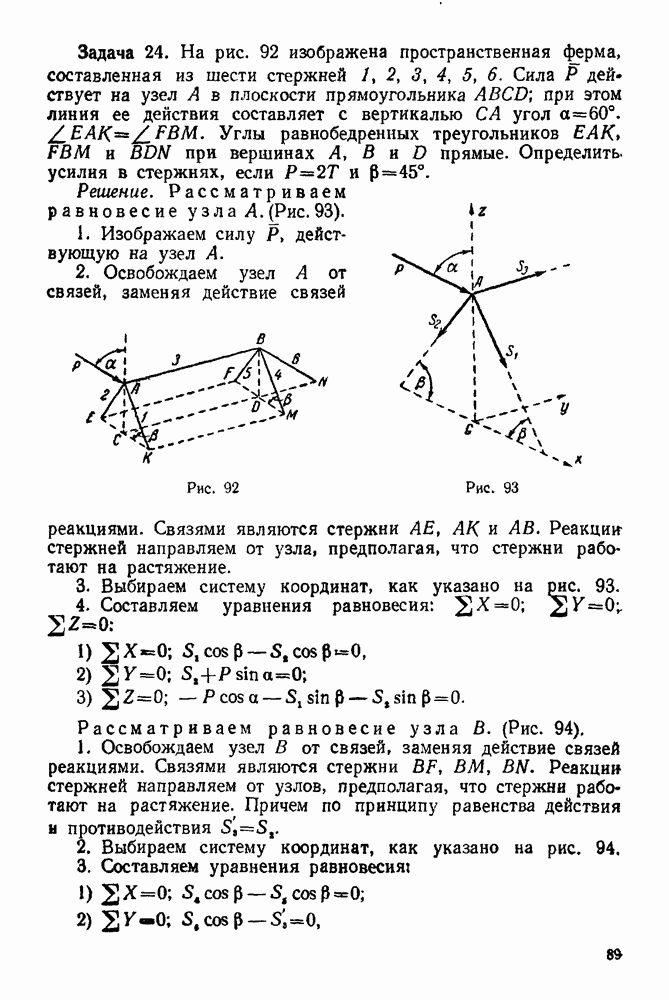
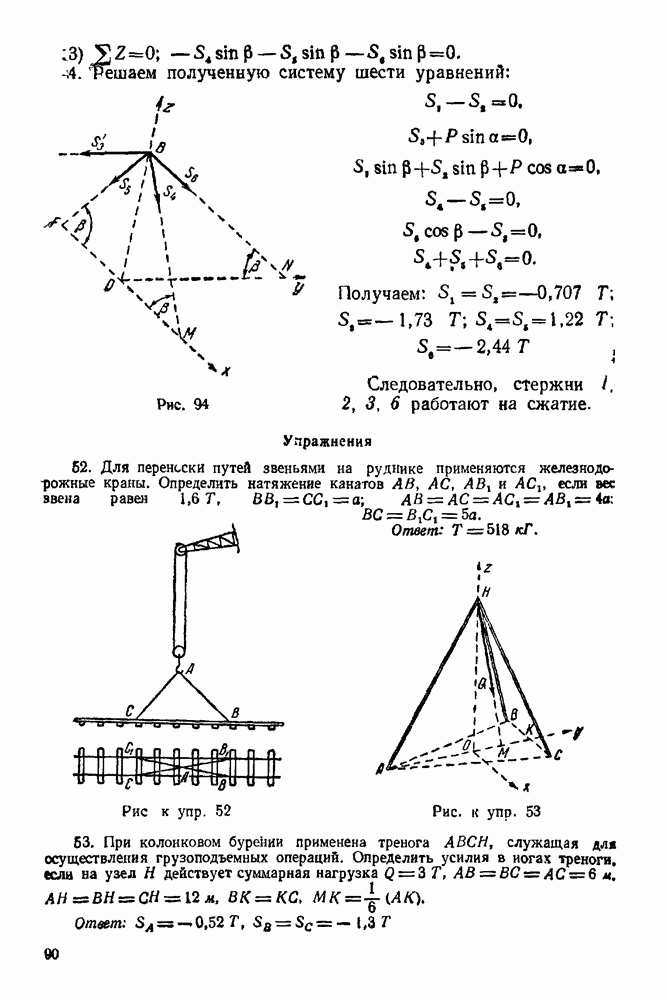
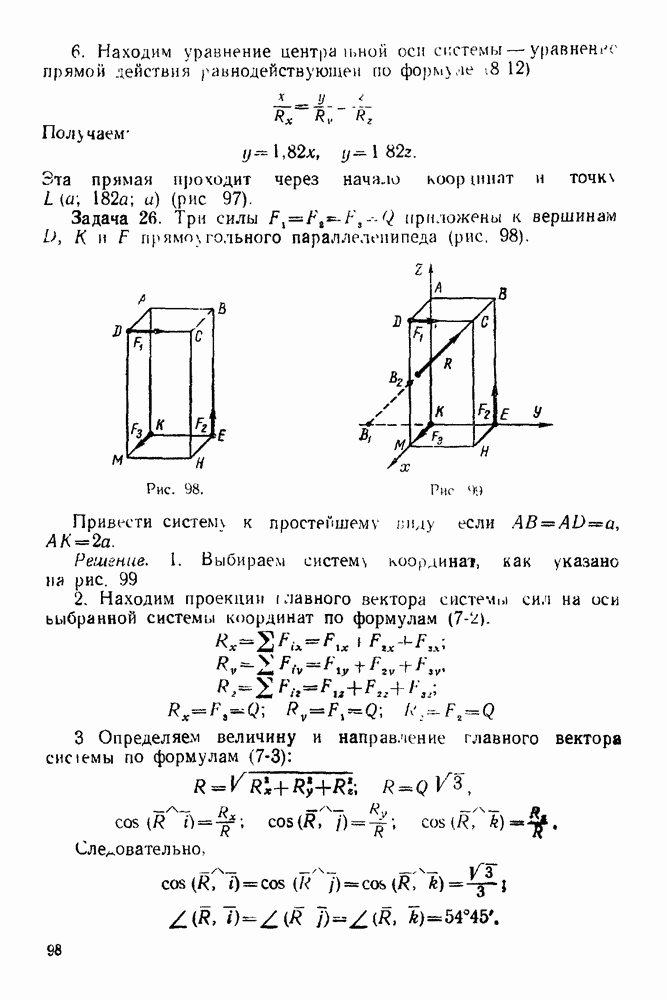
(см. скан)
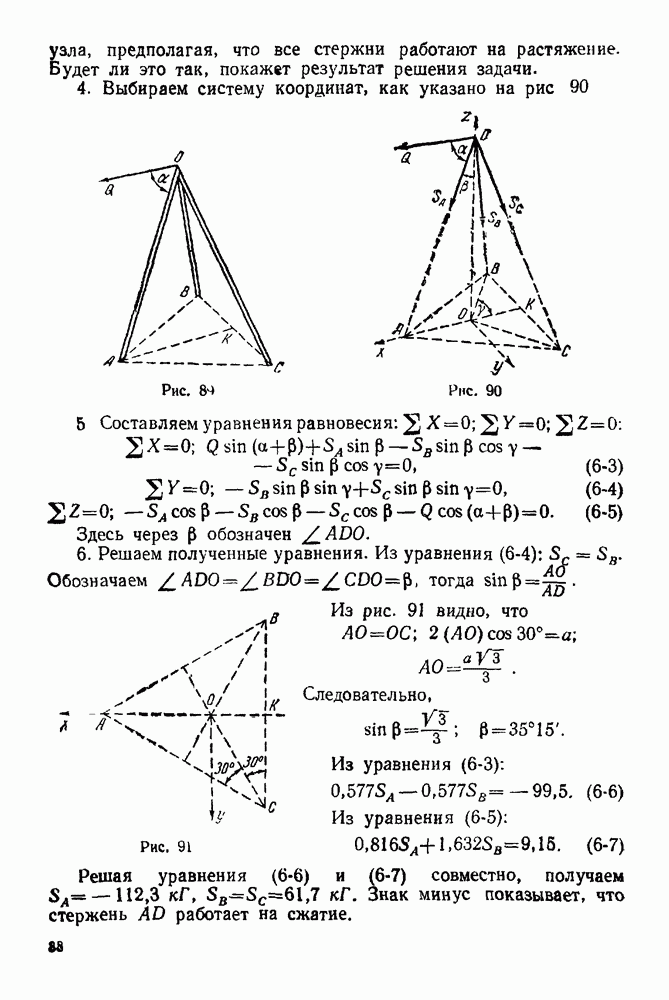
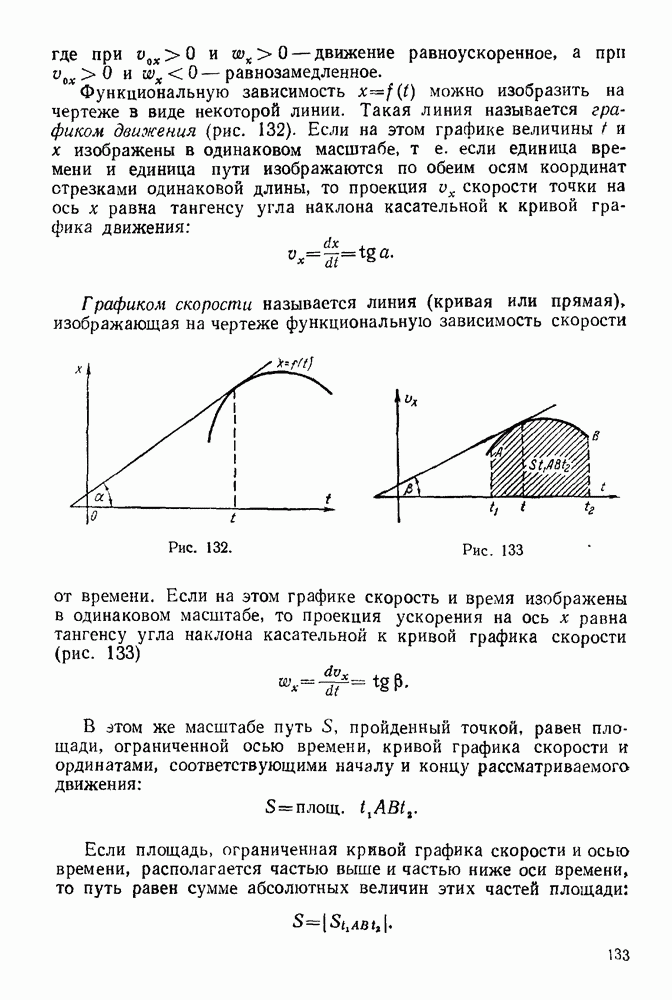
После построения диаграммы Кремоны и нахождения усилий в стержнях фермы рекомендуется для контроля в некоторых стержнях найти усилия аналитически, применяя либо метод сечений, либо метод вырезывания узлов.
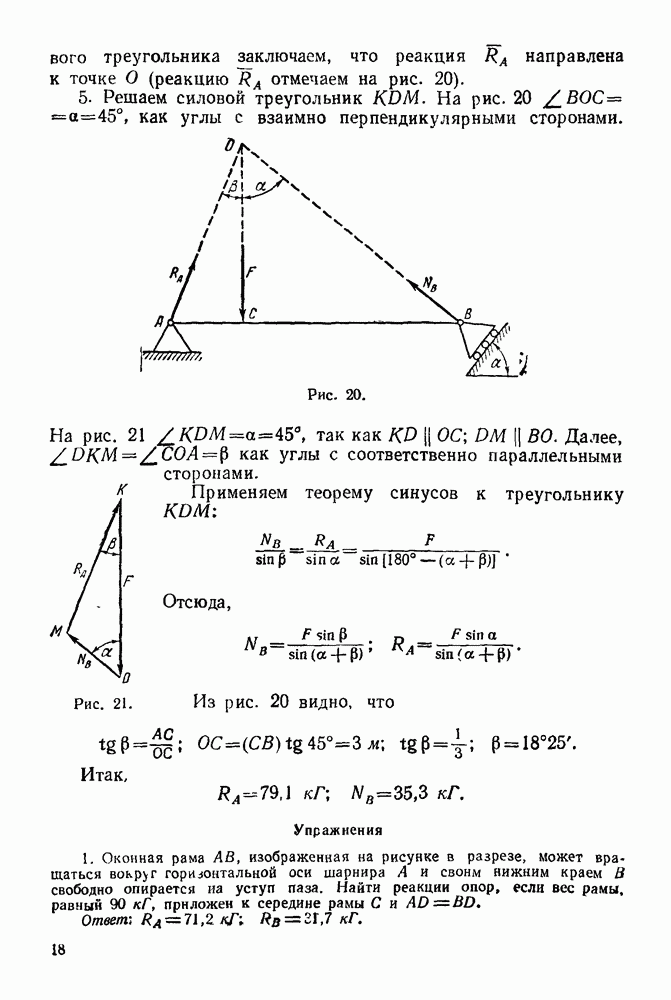
Упражнения
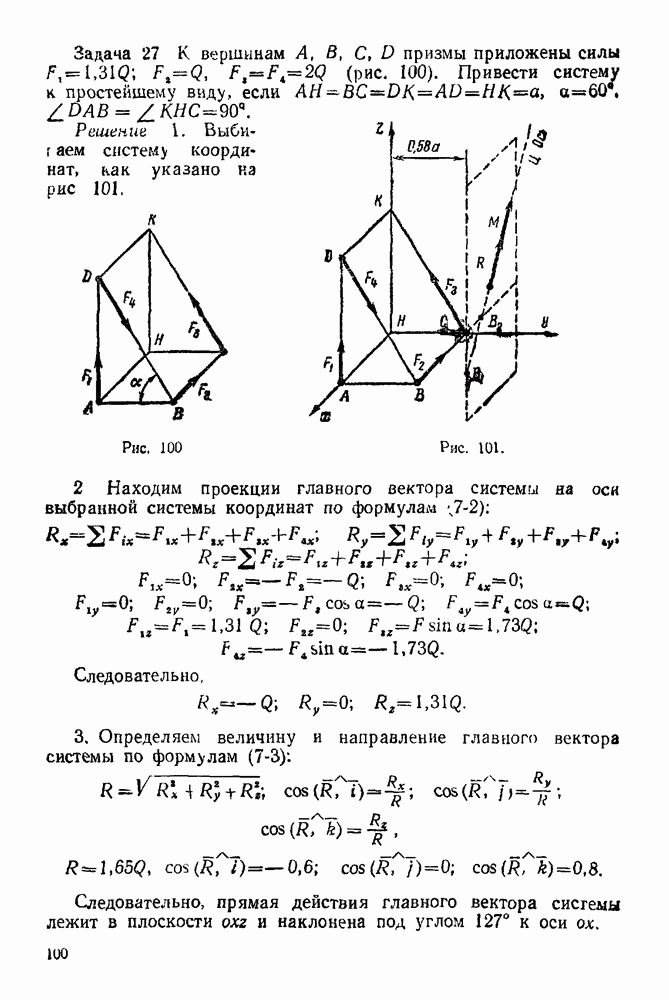
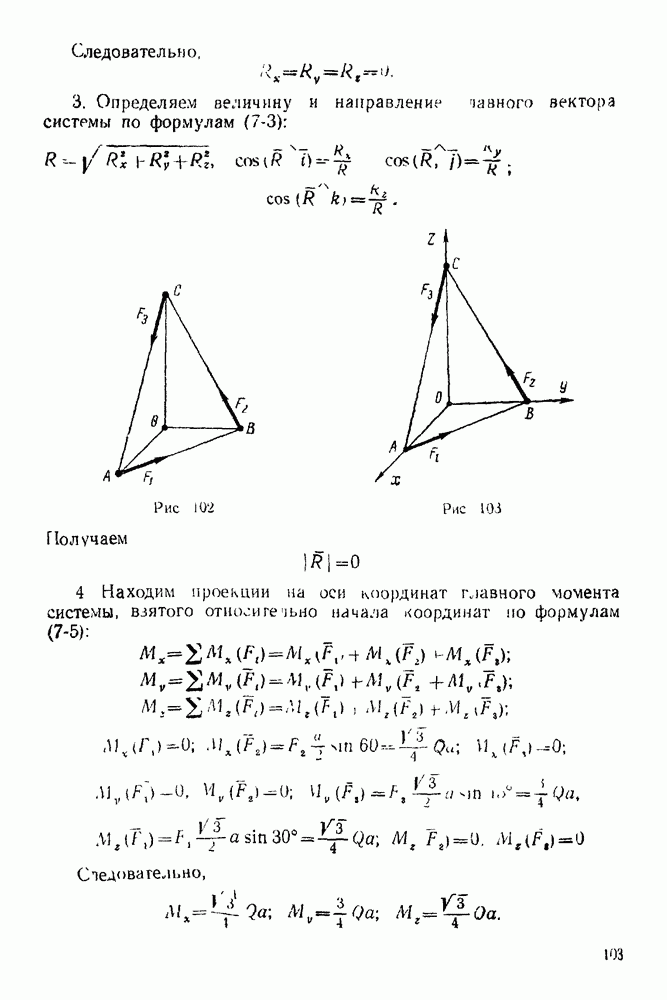
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
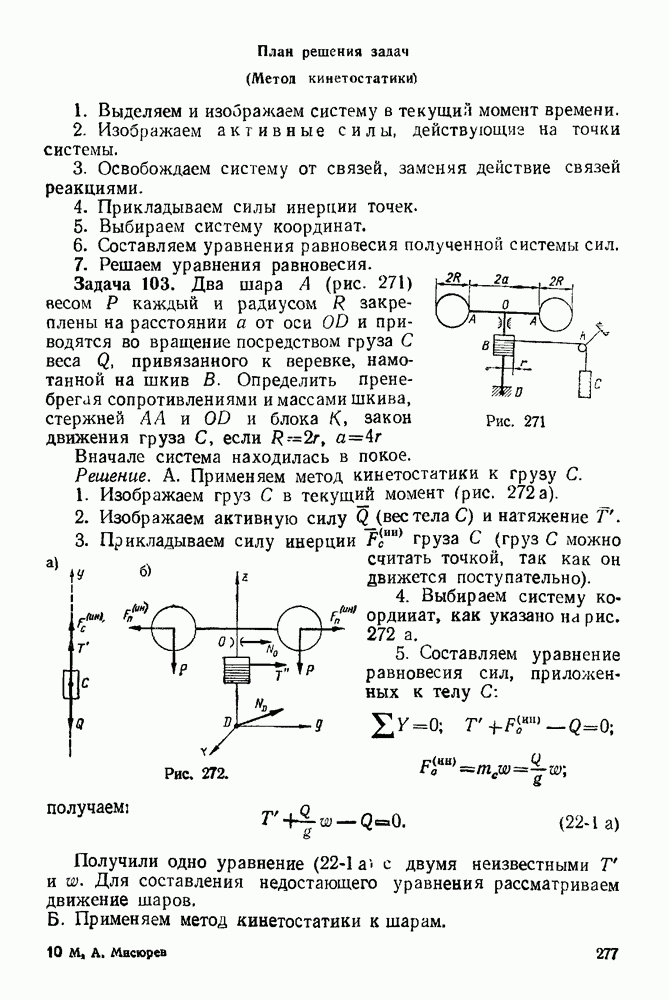
- Предмет статики. Связи и реакции связей
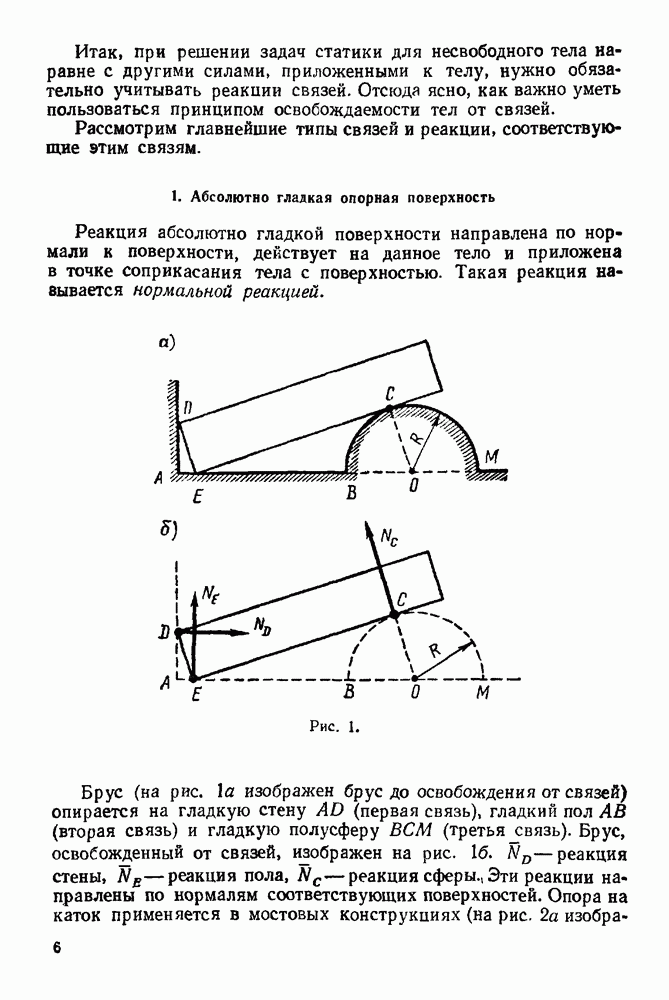
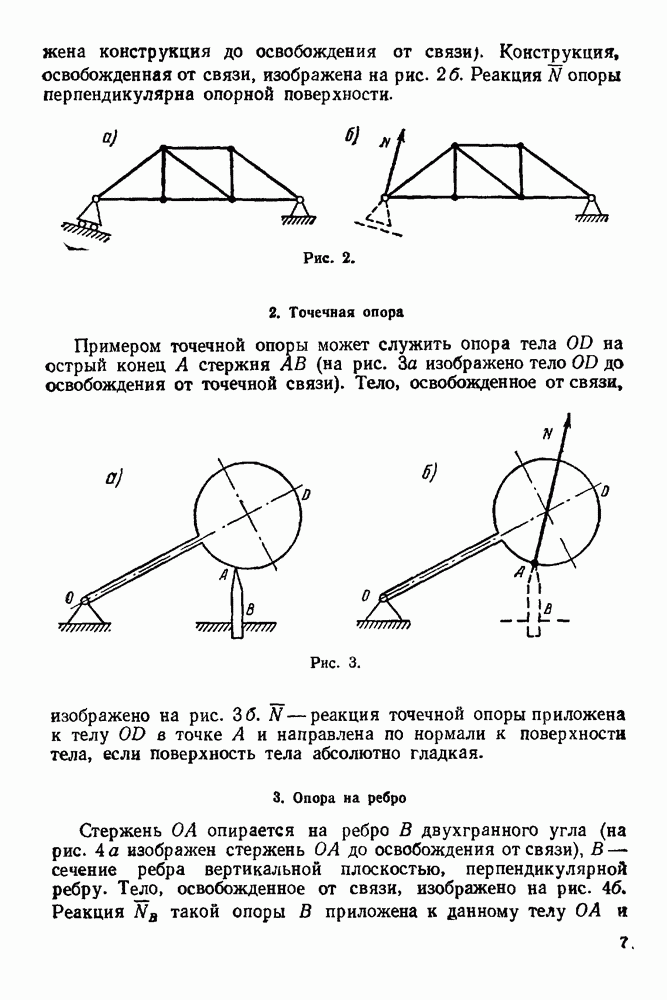
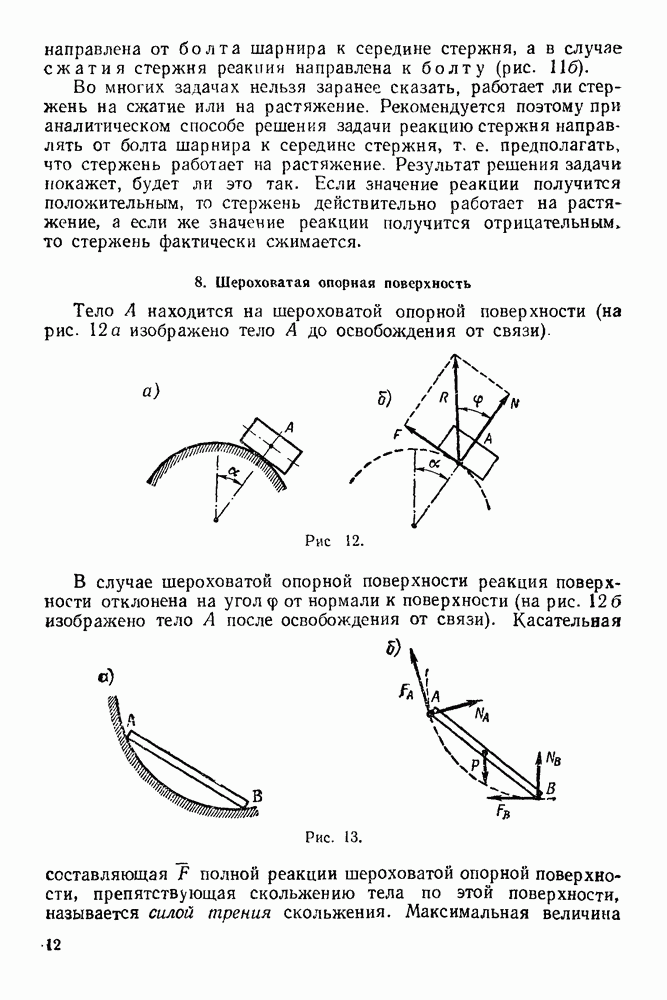
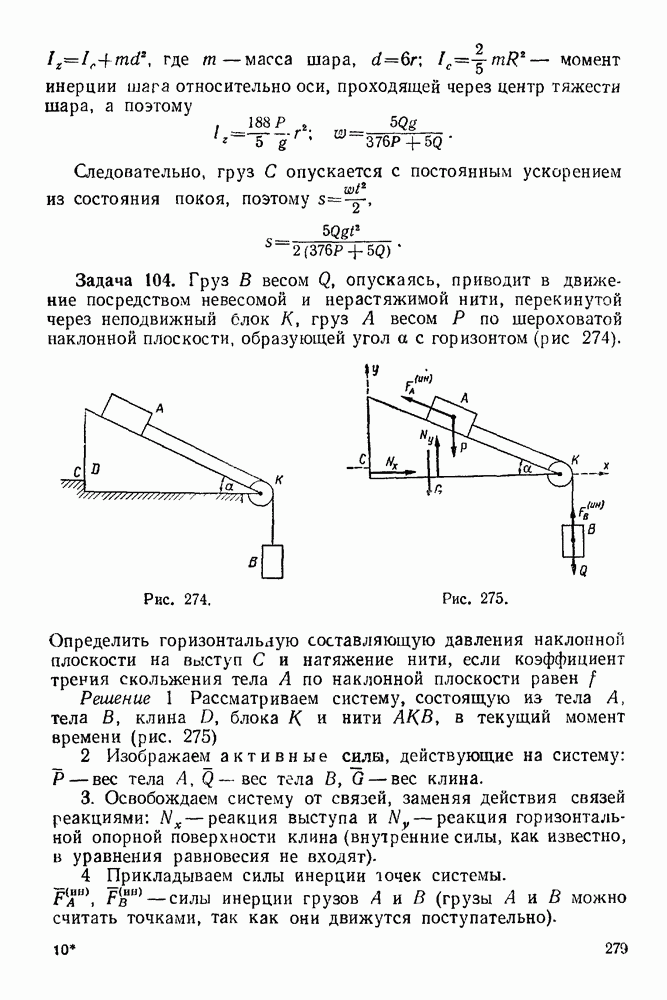
- 1. Абсолютно гладкая опорная поверхность
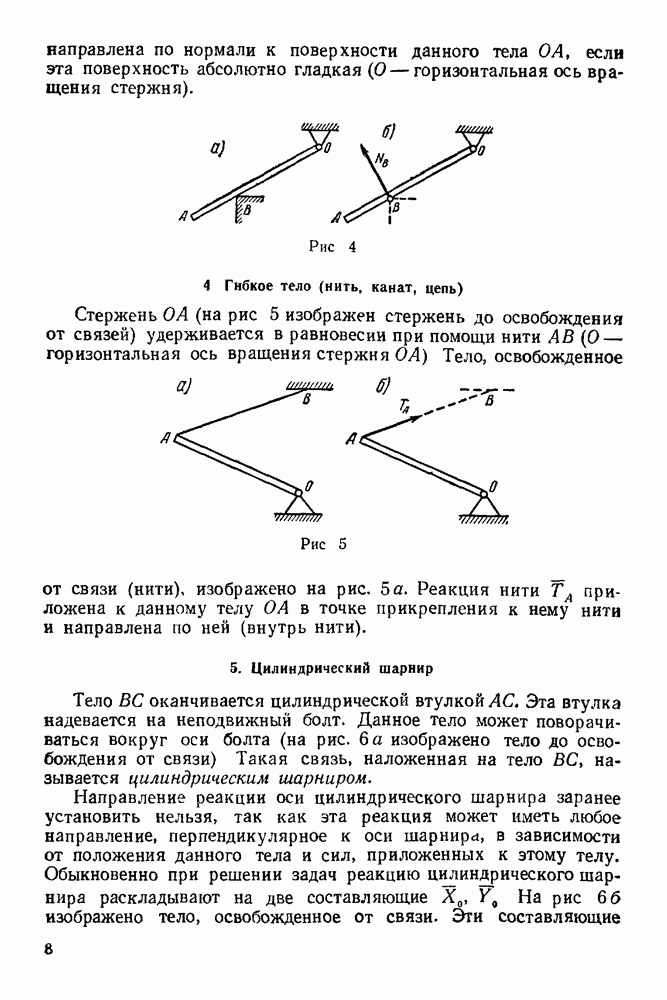
- 2. Точечная опора
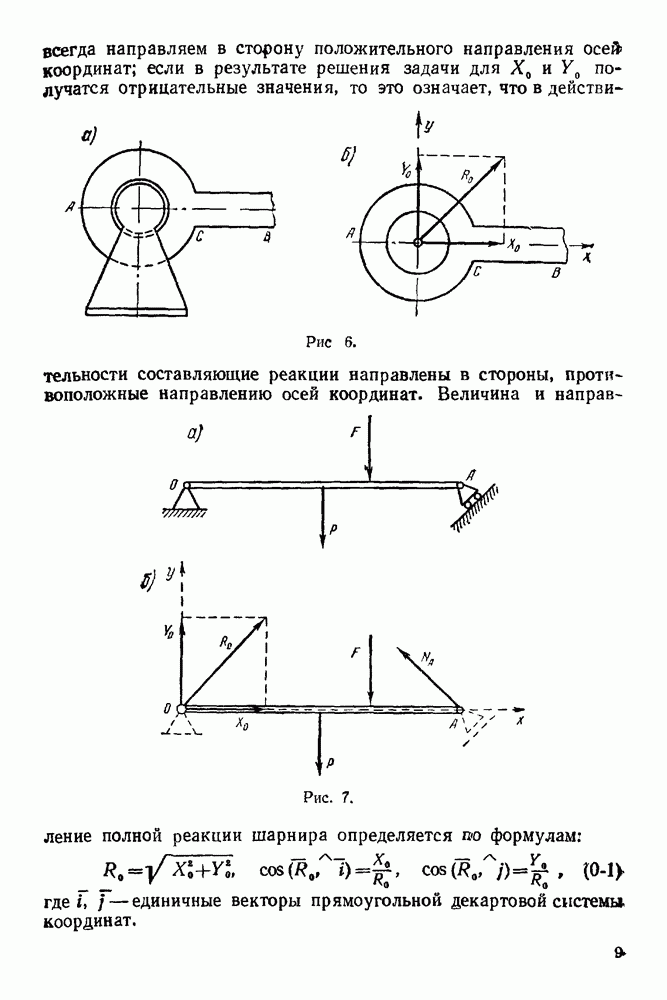
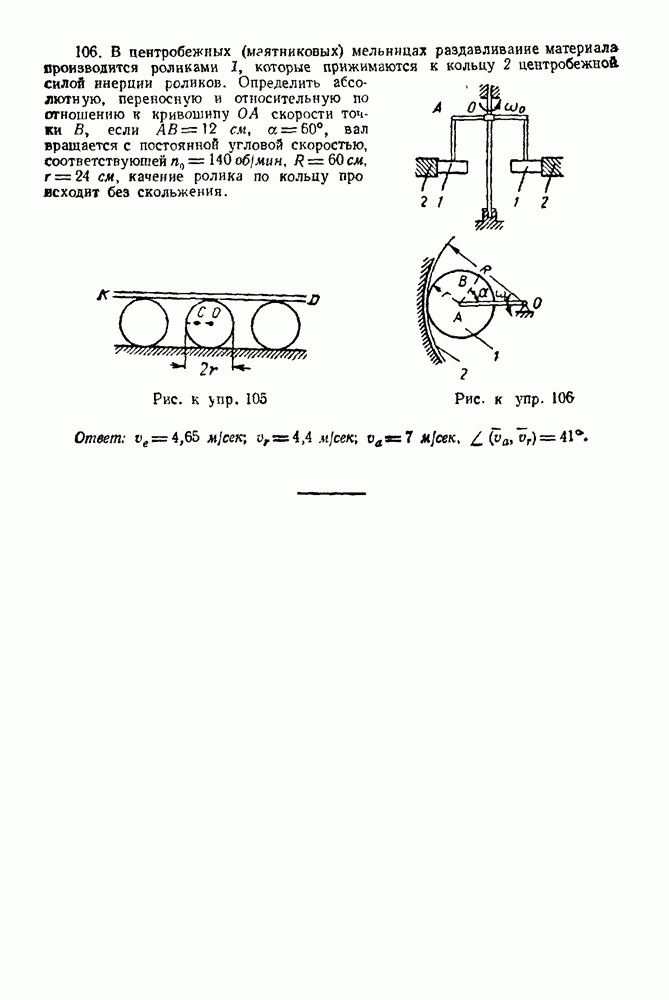
- 3. Опора на ребро
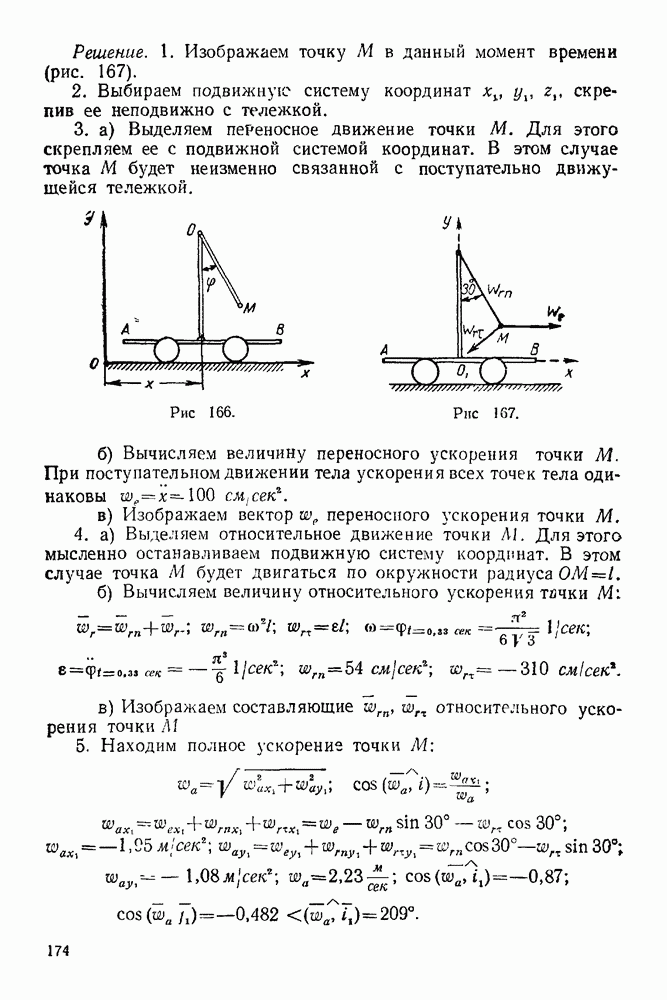
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
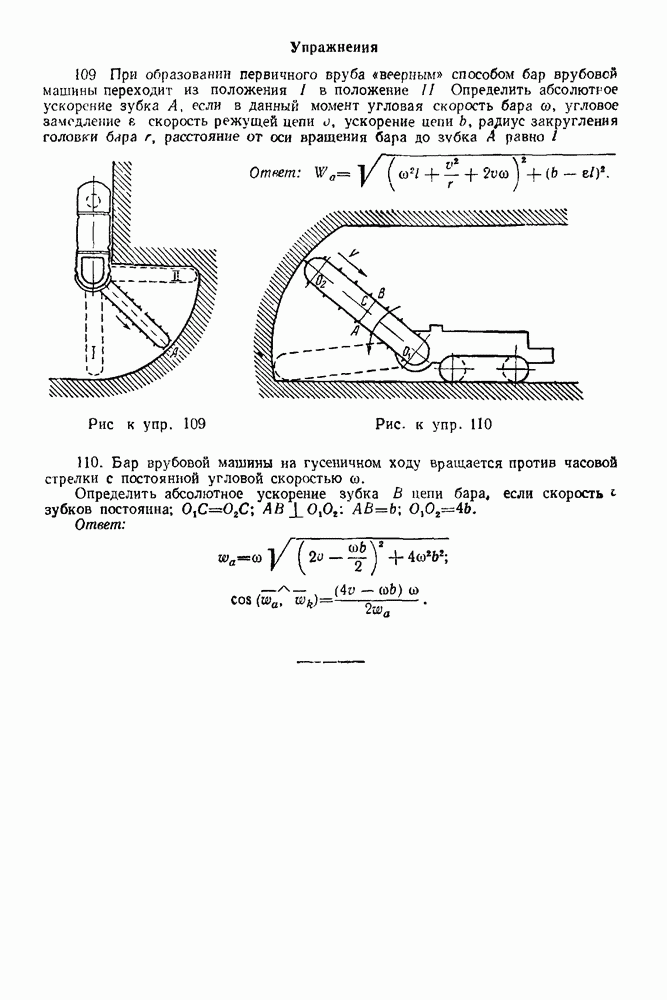
- 6. Сферический шарнир
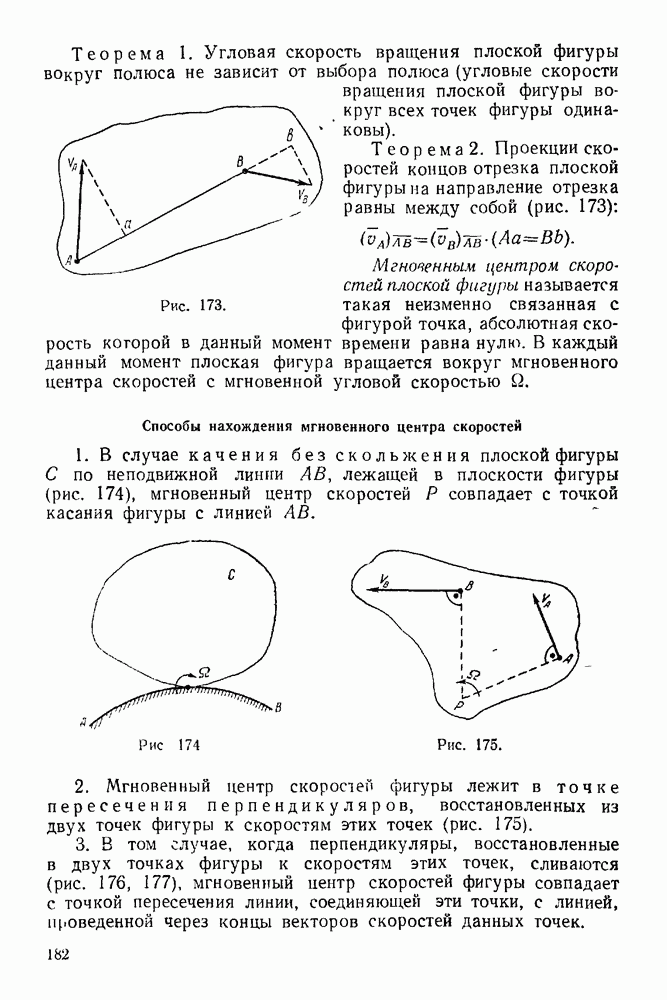
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
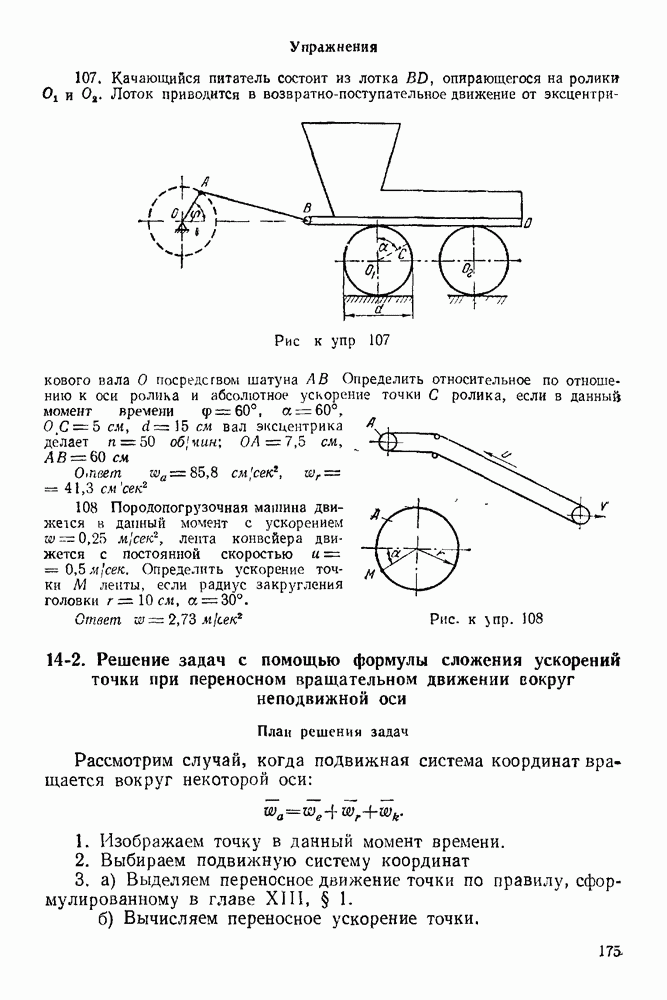
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
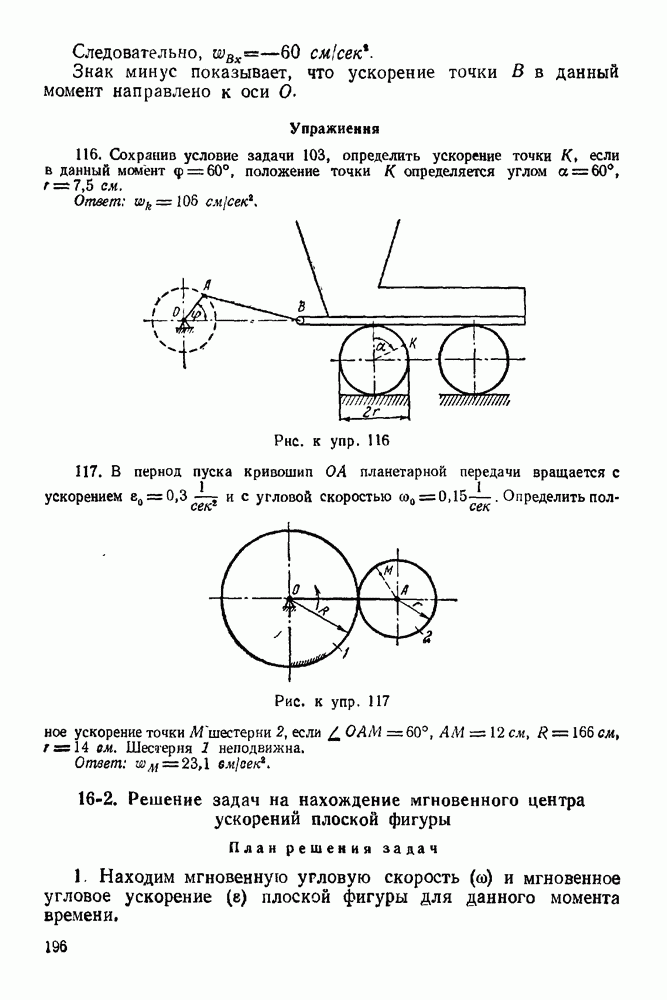
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
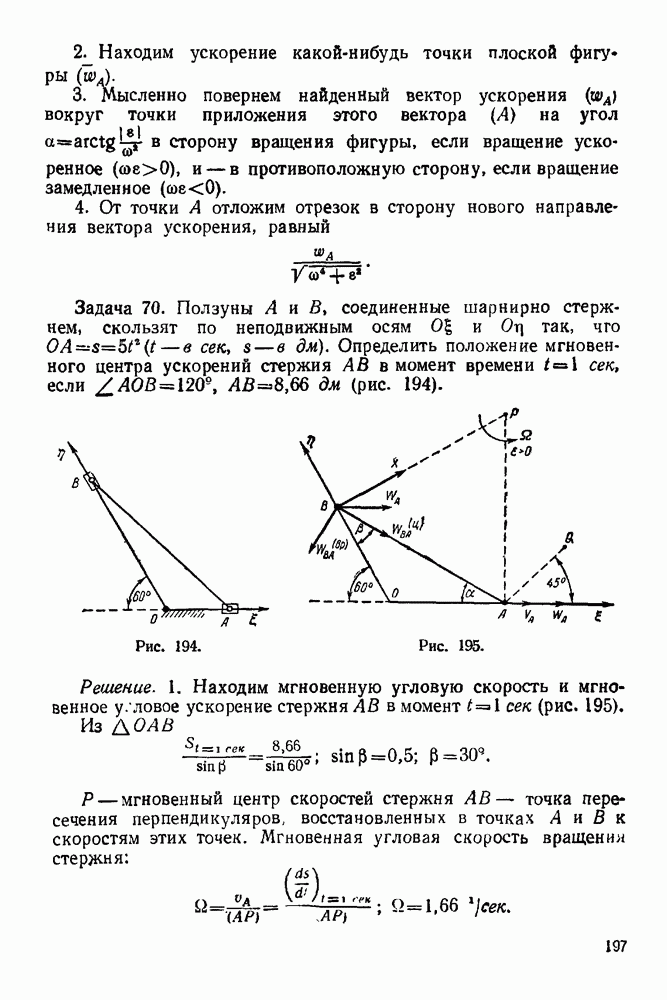
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
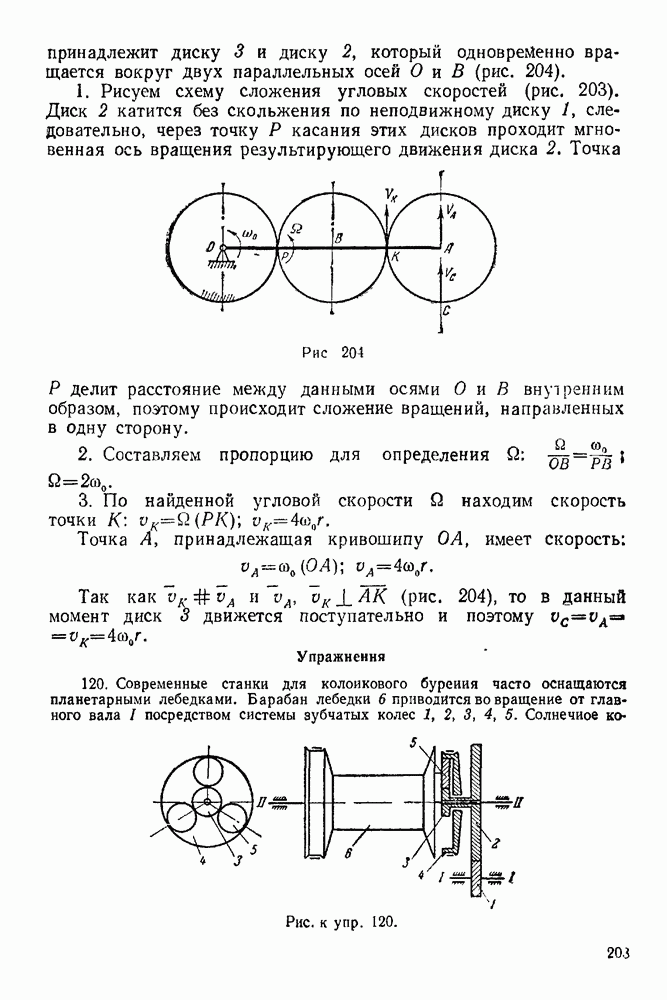
- 4-3. Решение задач на опрокидывание
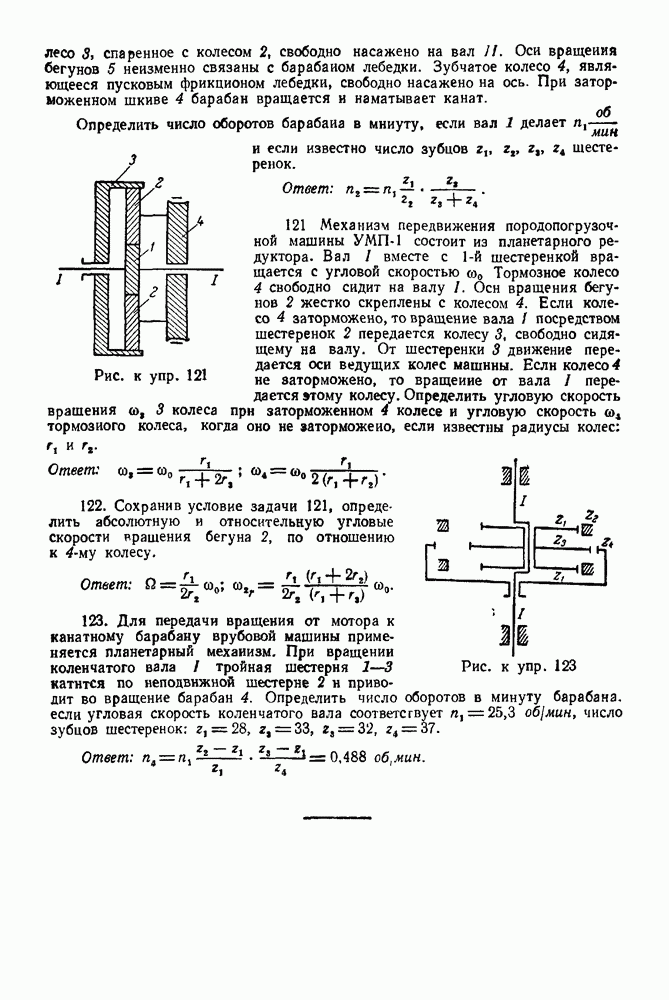
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
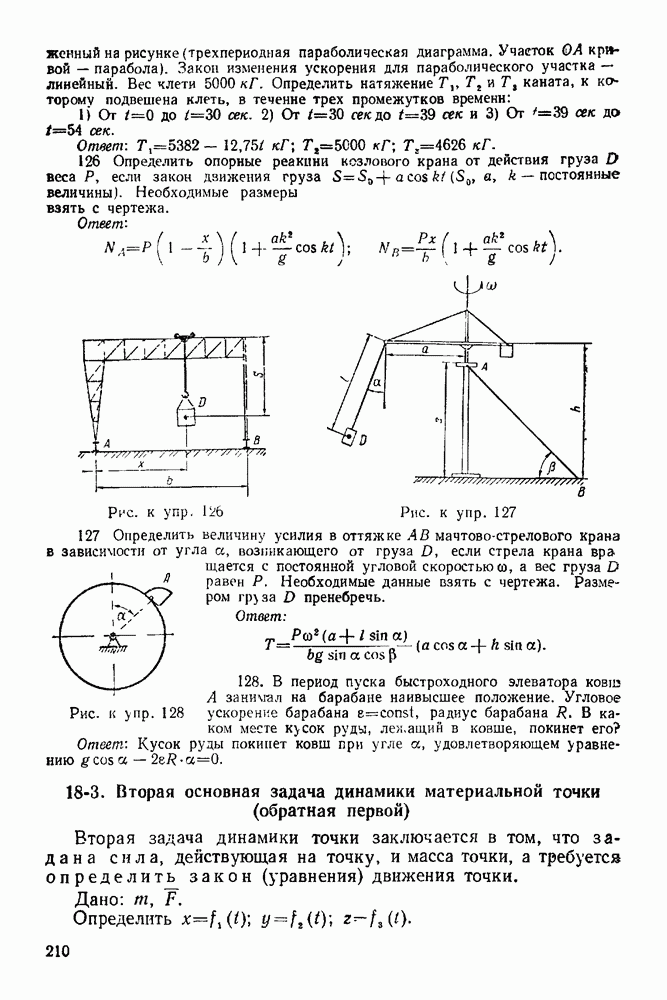
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
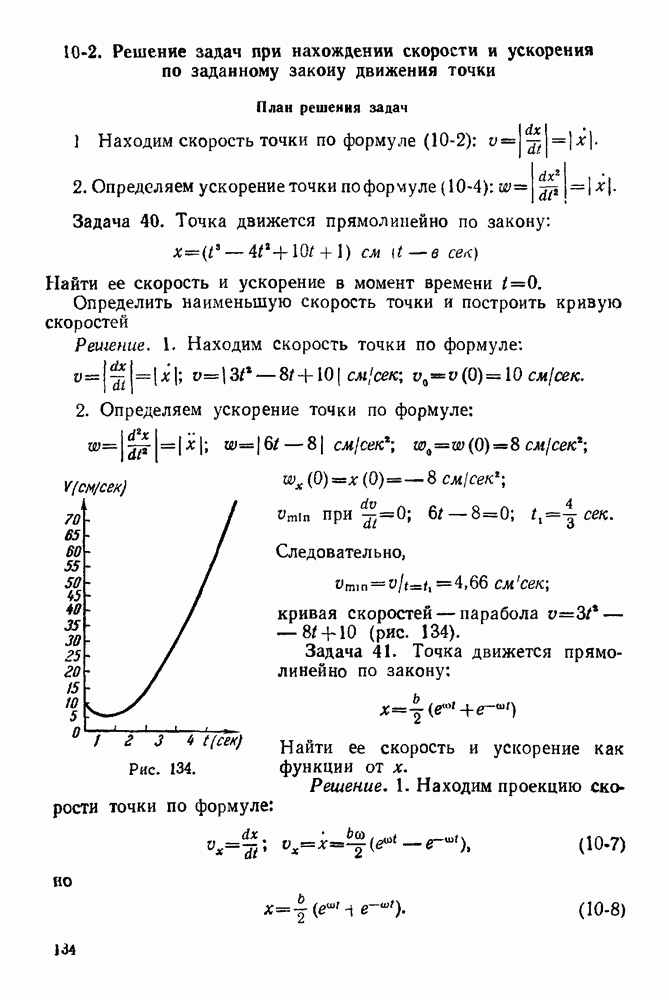
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
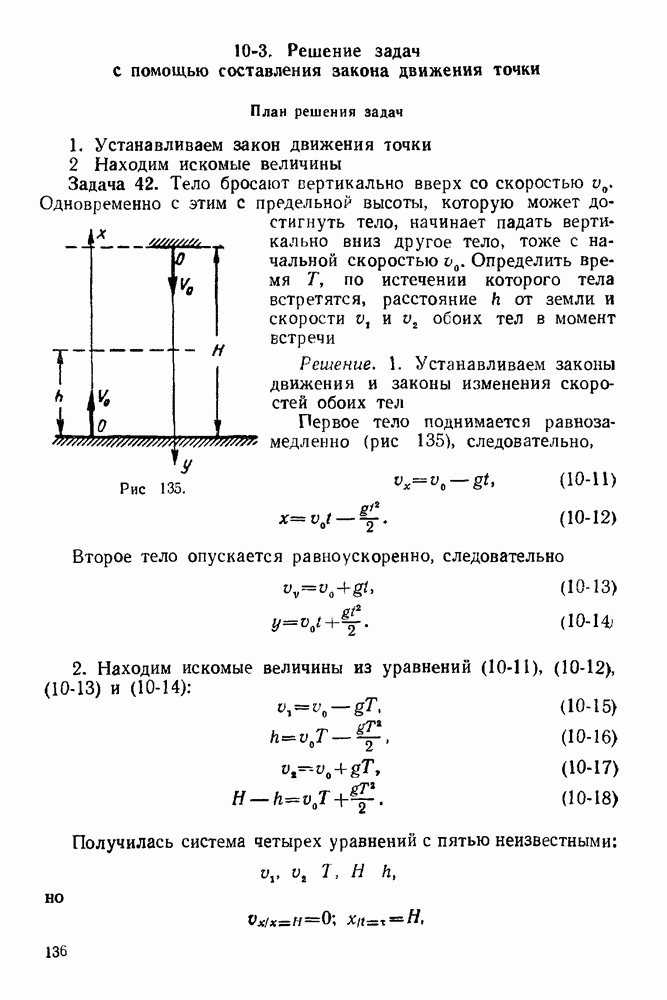
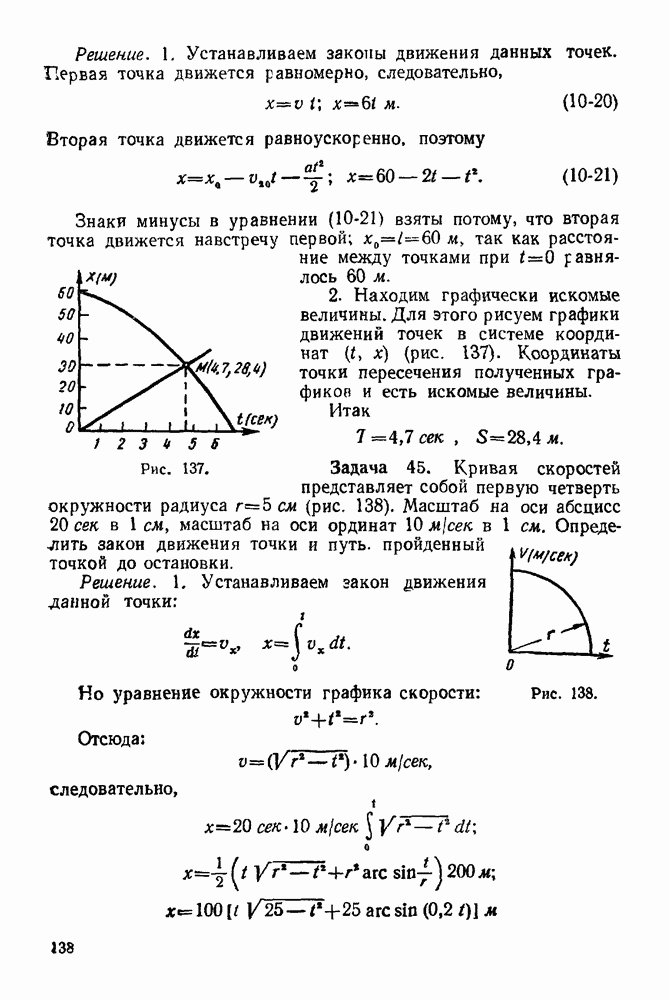
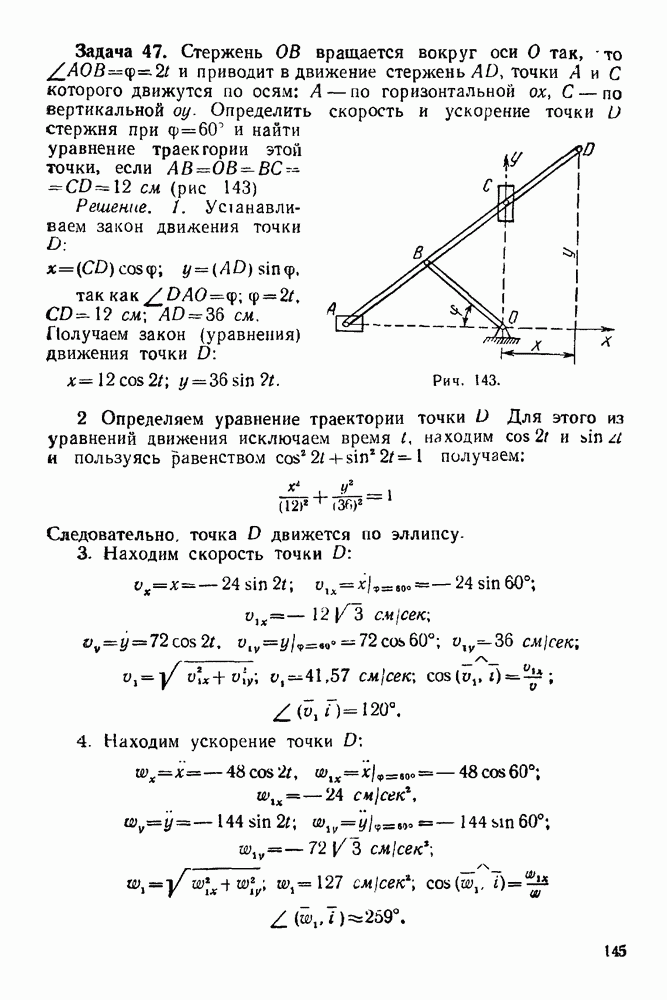
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
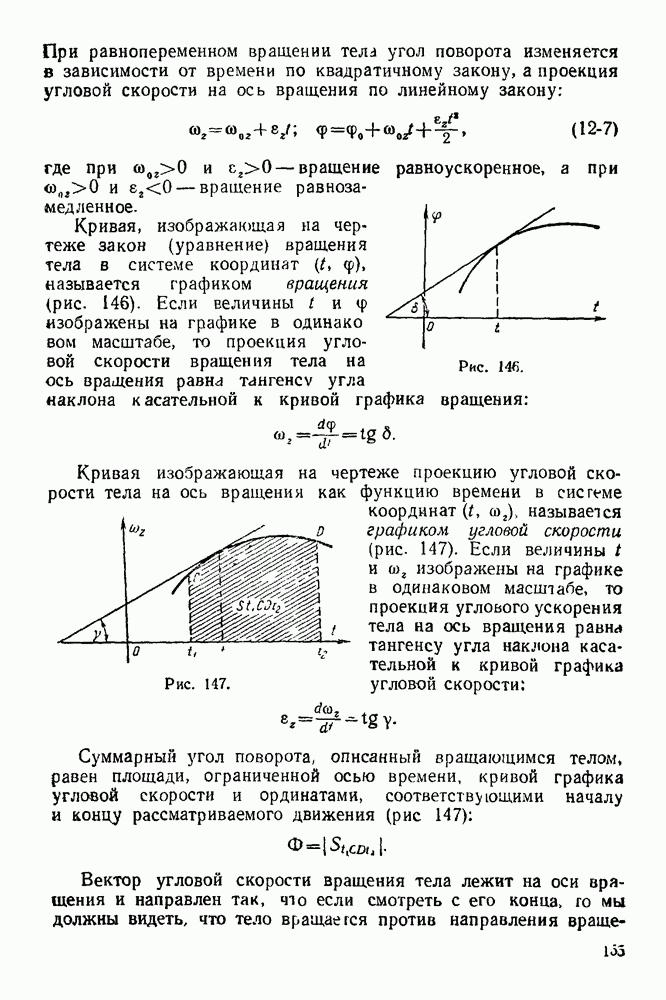
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
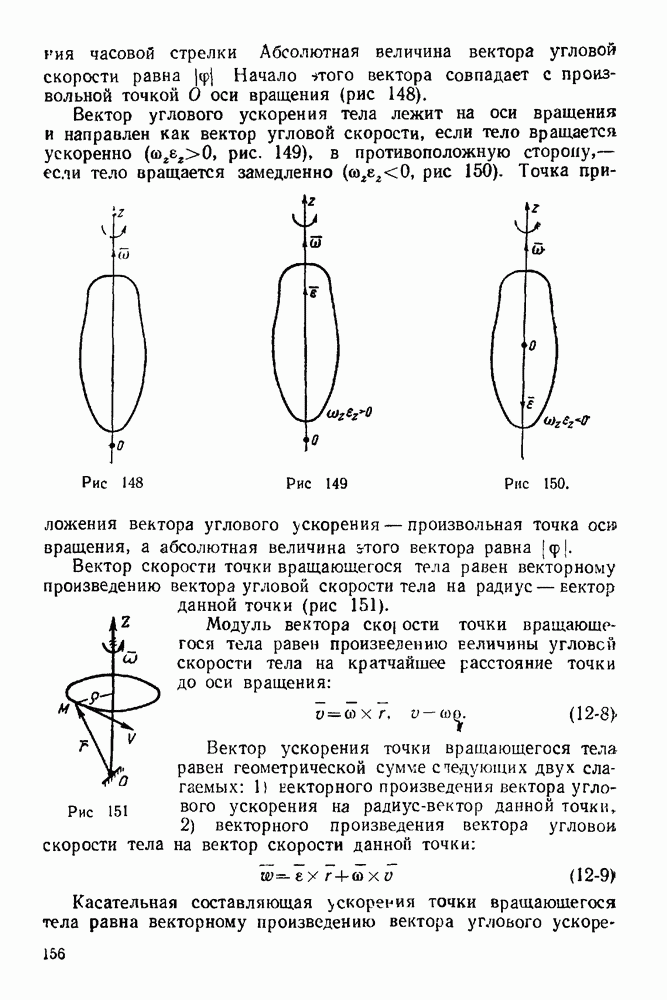
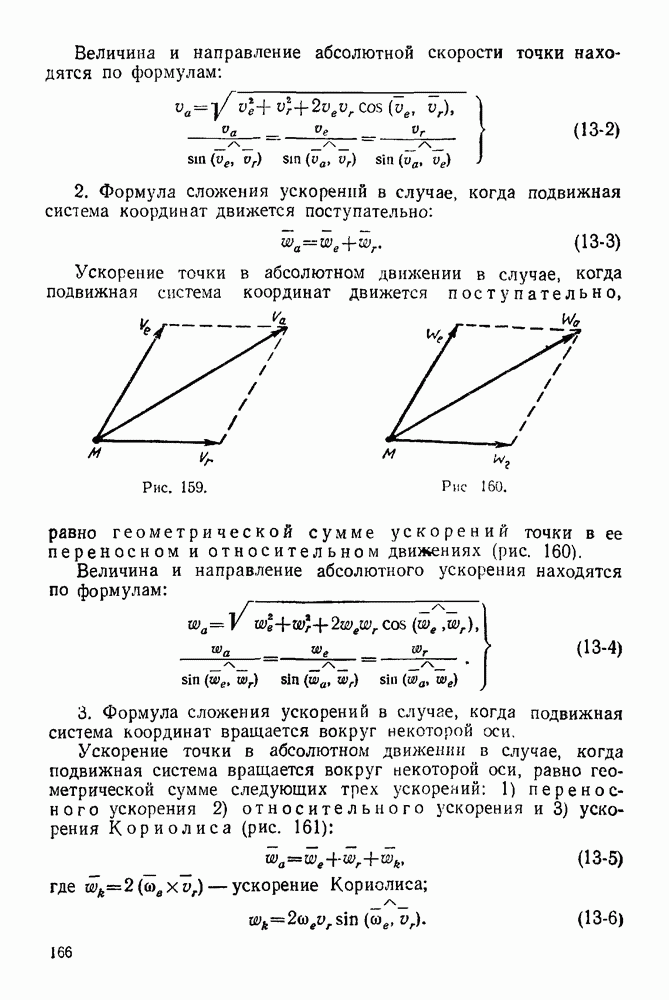
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
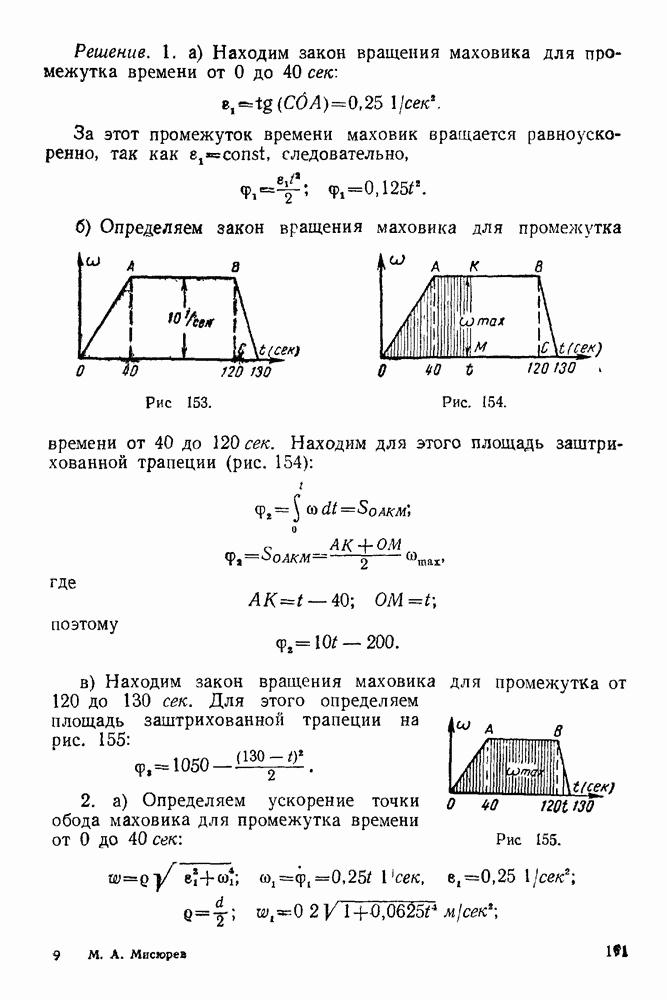
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
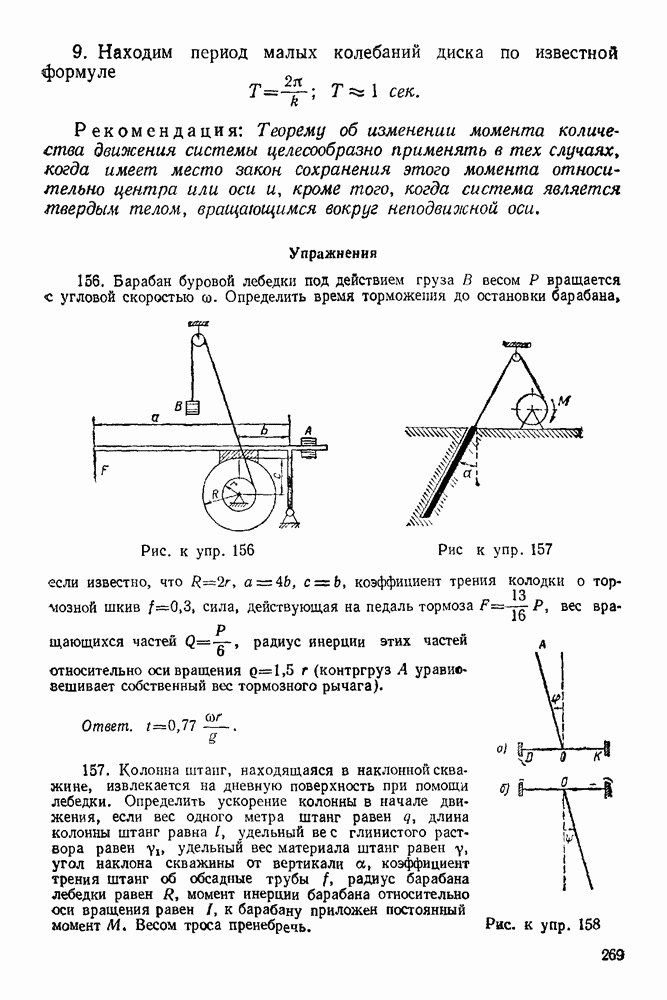
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
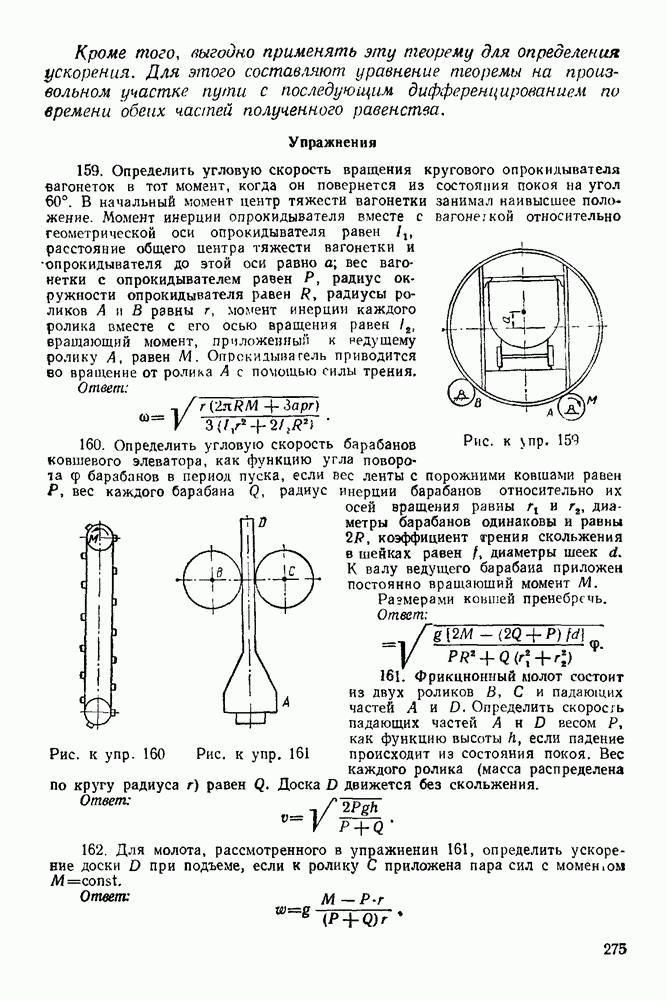
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
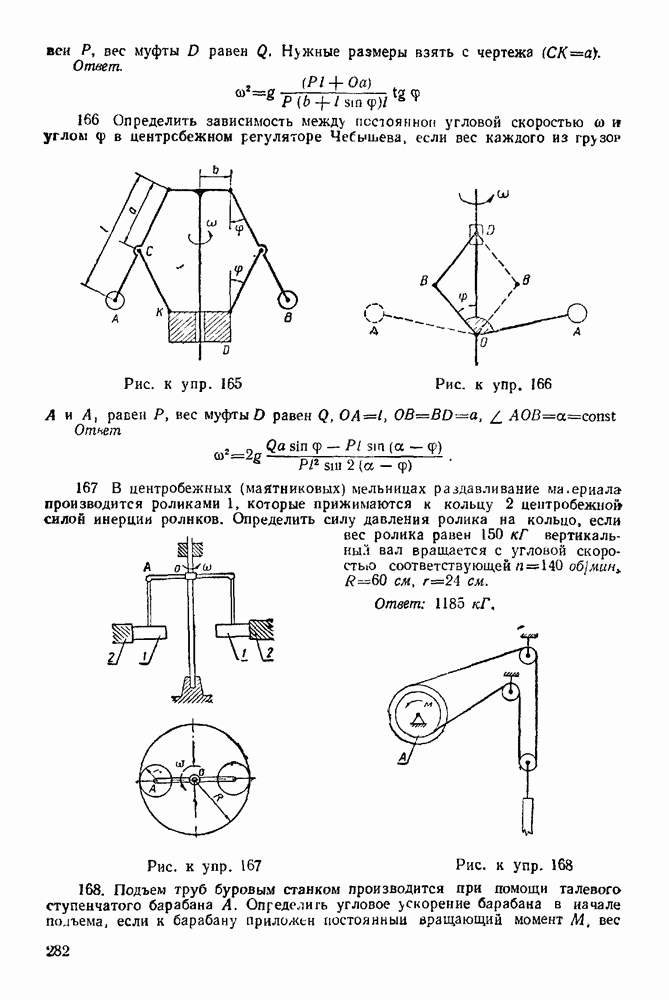
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
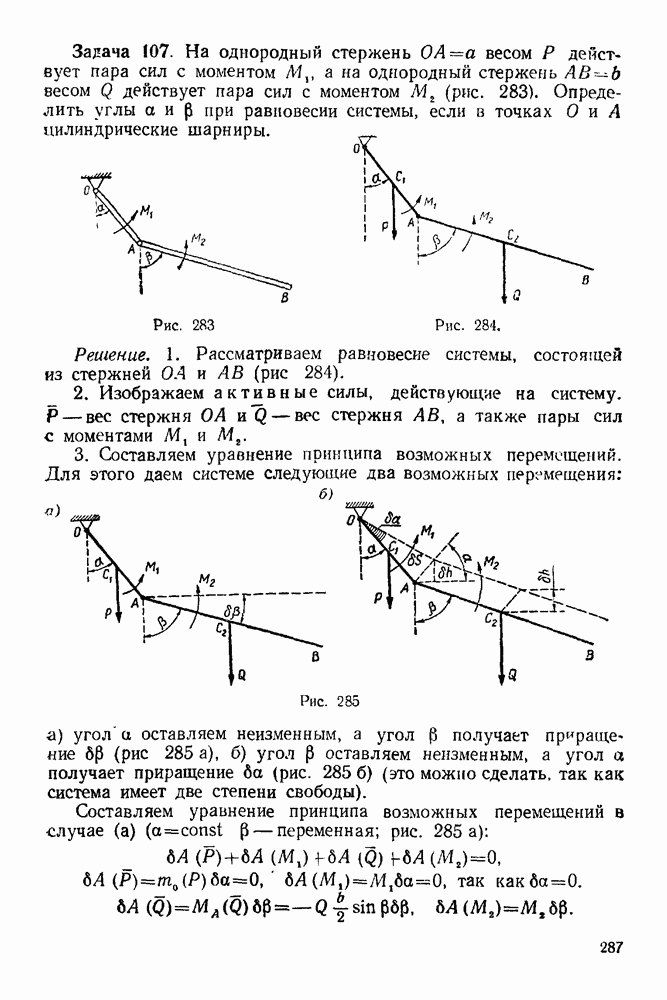
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
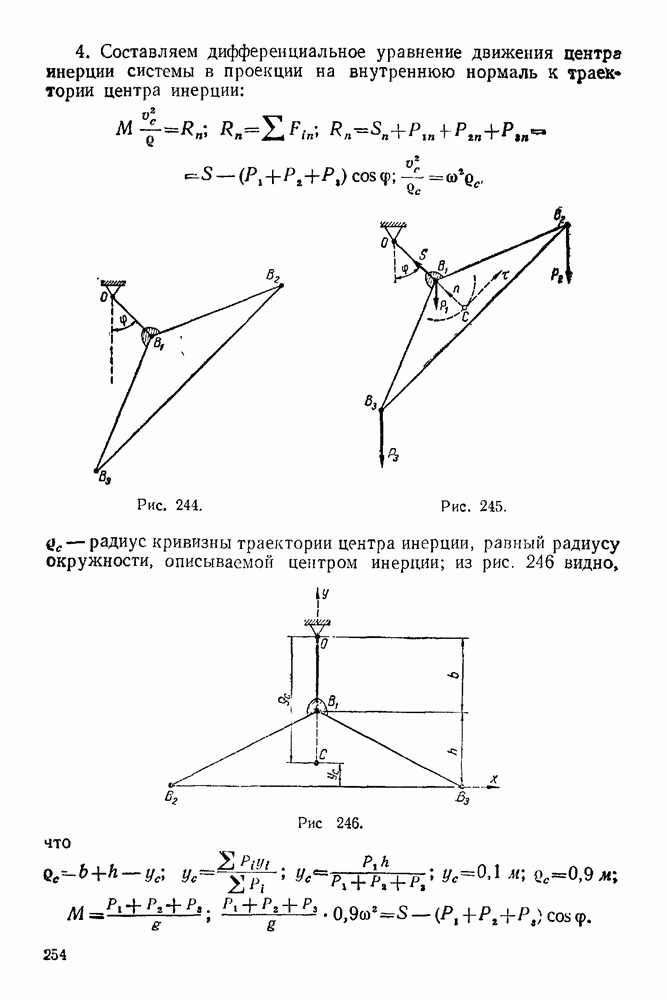
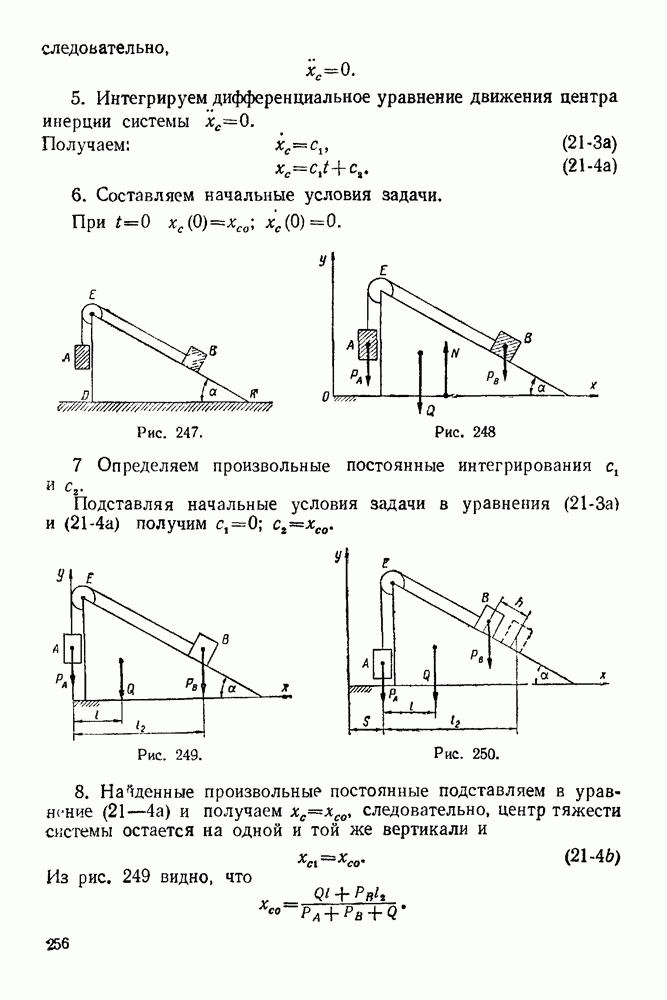
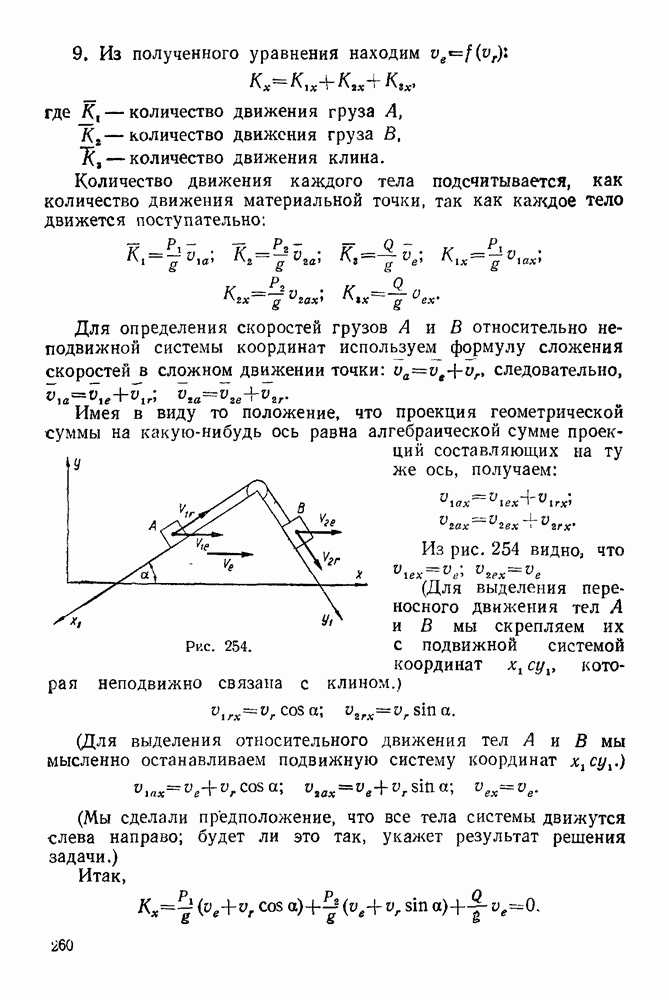
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
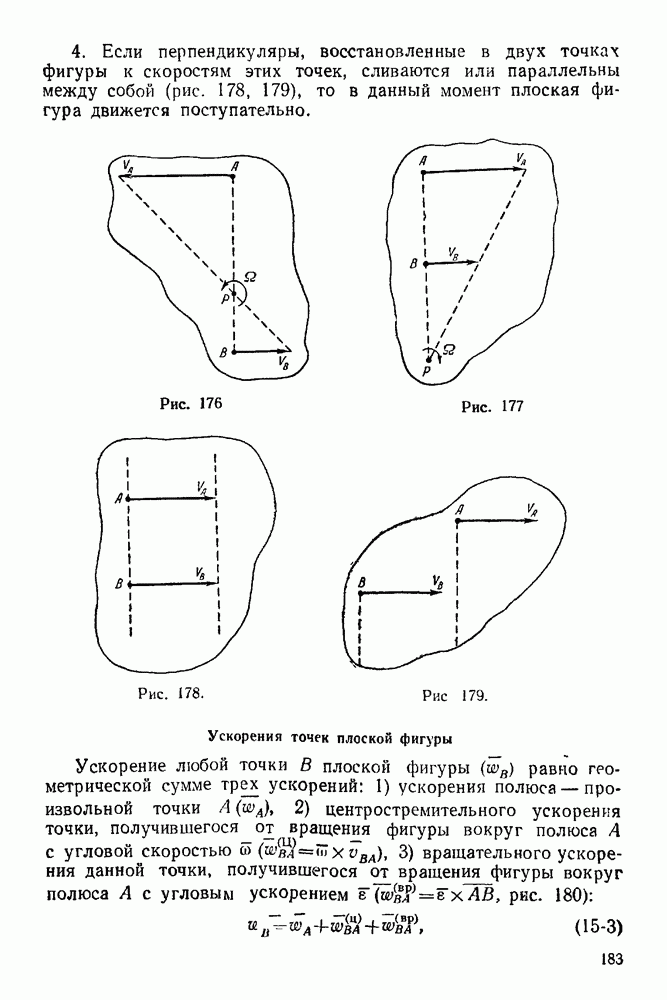
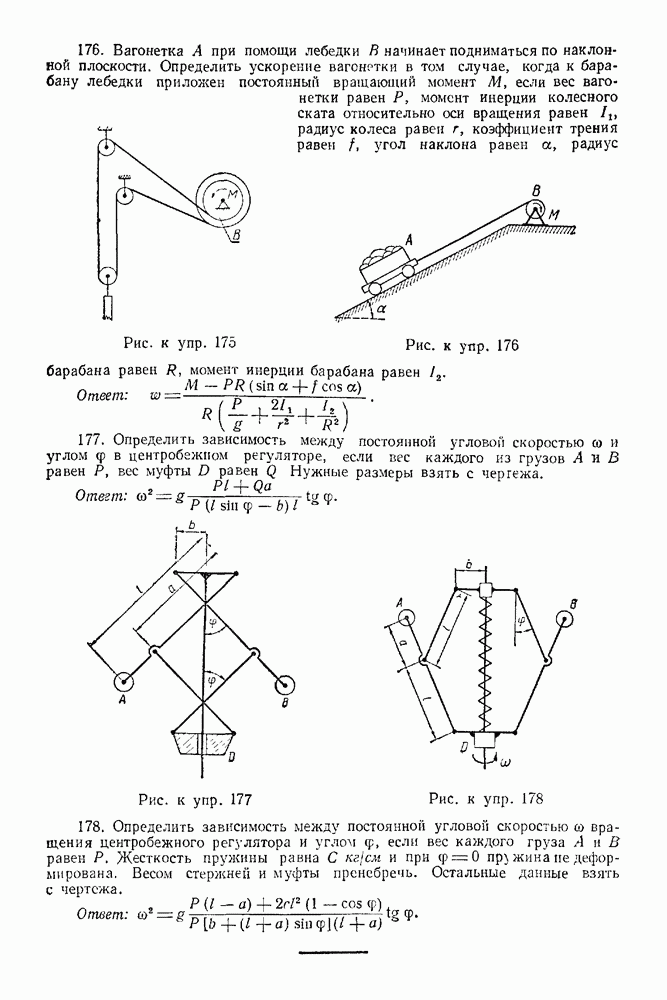
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
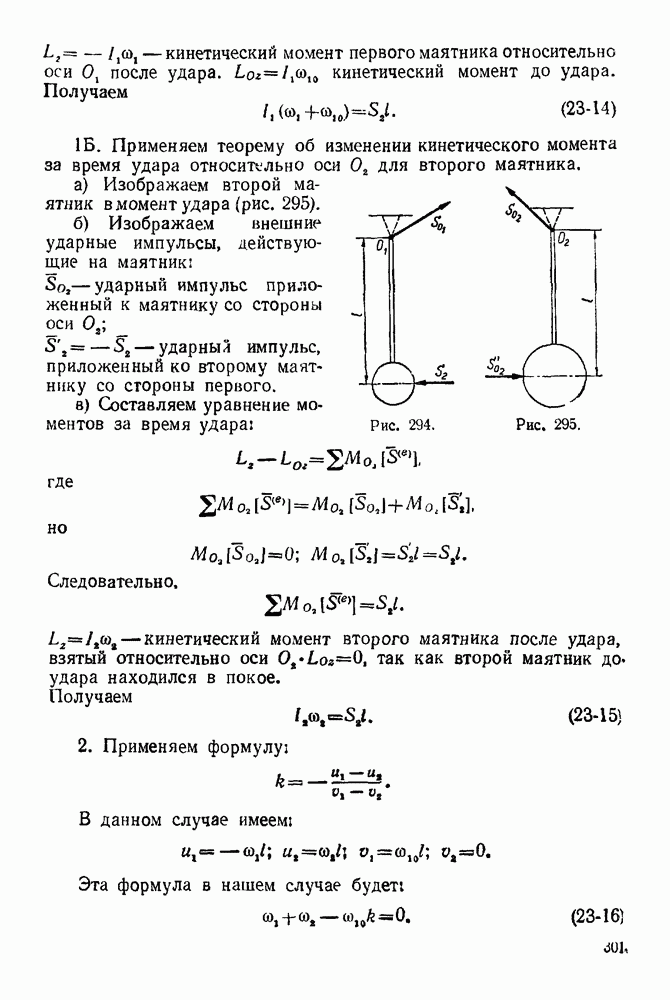
- ГЛАВА XXIII. УДАР