| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
22-2. Принцип возможных перемещений
Для того, чтобы система с идеальными связями оставалась в равновесии в данном положении, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на систему, на любом возможном перемещении системы равнялась нулю (связи удерживающие):

Возможным перемещением системы называется всякое бесконечно малое перемещение точек системы которое допускается а данный момент связями, наложенными на систему.
 возможное перемещение точки номера
возможное перемещение точки номера  системы
системы
Связи наложенные на систему, называются идеальными (совершенными), если сумма элементарных работ всех реакций связей на любом возможном перемещении системы равна нулю:

К числу идеальных связей относятся связи, осуществленные в виде гладких поверхностей, линий, гибких нерастяжимых нитей, шарниров без трения и  - вариации декартовых координат точки номера
- вариации декартовых координат точки номера  системы — бесконечно малые изменения координат получившиеся от возможного перемещения системы. Для того чтобы вычислить вариацию декартовой координаты какой-нибудь точки системы, нужно взять полный дифференциал от функции связывающей декартову координату с обобщенными координатами системы
системы — бесконечно малые изменения координат получившиеся от возможного перемещения системы. Для того чтобы вычислить вариацию декартовой координаты какой-нибудь точки системы, нужно взять полный дифференциал от функции связывающей декартову координату с обобщенными координатами системы  и всюду значок
и всюду значок  заменить значком
заменить значком  .
.

План решения задач
1. Выделяем систему равновесие которой следует рассмотреть.
2. Изображаем активные силы, действующие на систему.
3. Выбираем систему координат (если задачу решаем при помощи аналитического выражения элементарной работы).
4. Составляем уравнение принципа возможных перемещений системы:

Для этого сначала нужно найти проекции  активных сил, действующих на систему, а также координаты точек приложения этих сил как функции обобщенных координат, затем по известному правилу найти вариации
активных сил, действующих на систему, а также координаты точек приложения этих сил как функции обобщенных координат, затем по известному правилу найти вариации  декартовых координат точек системы.
декартовых координат точек системы.
5. Решаем получен ное уравнение принципа возможных перемещений.
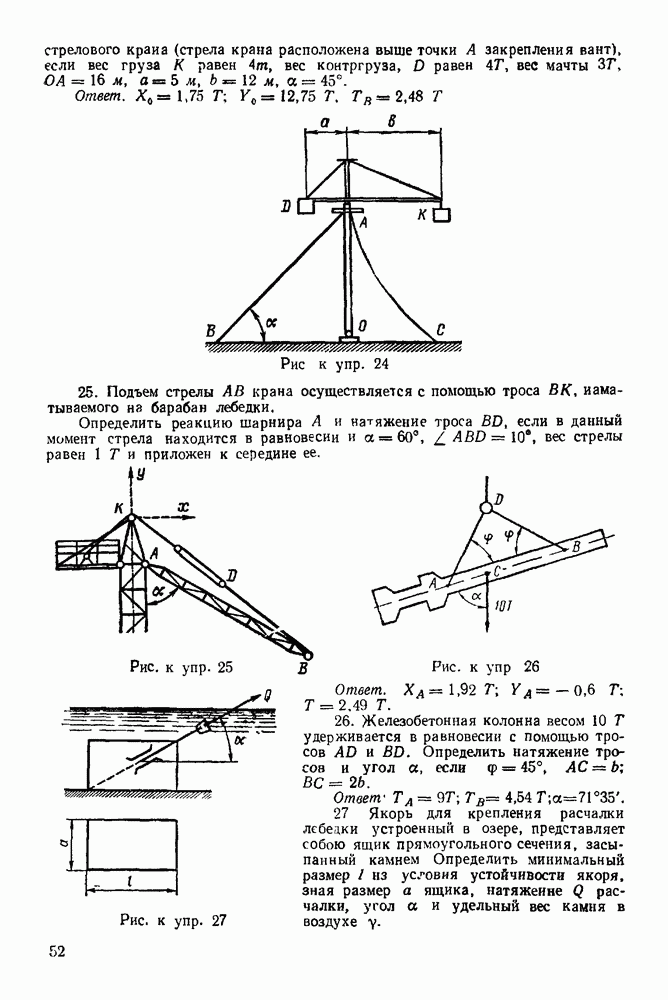
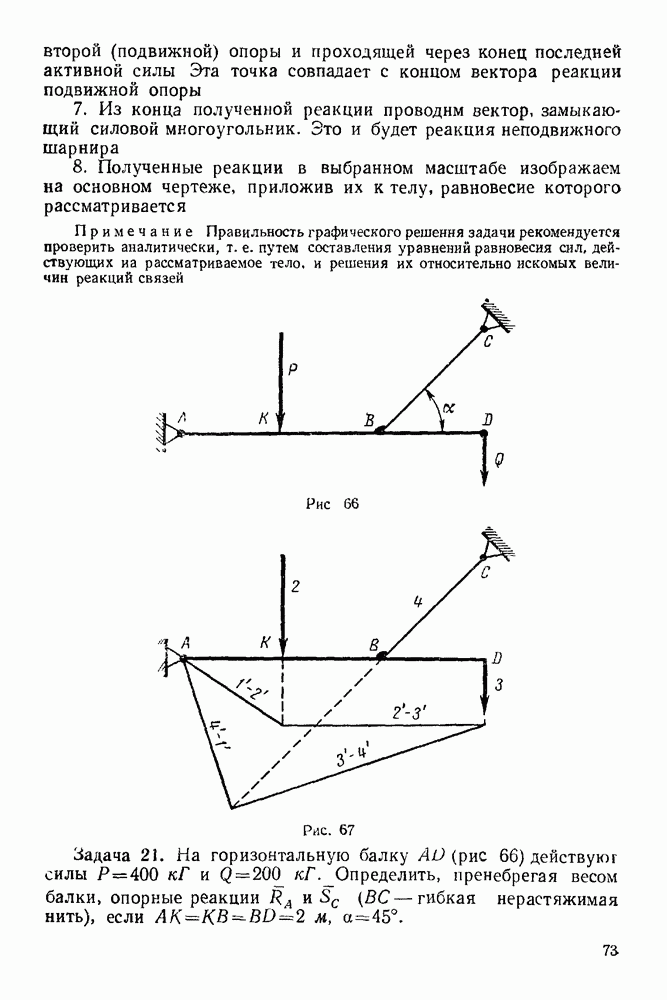
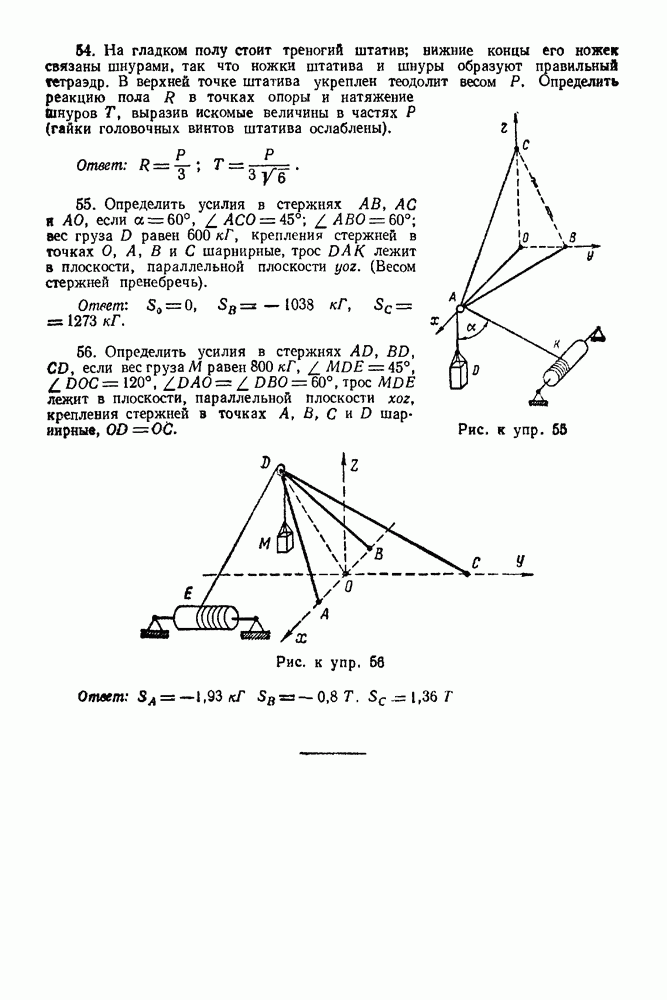
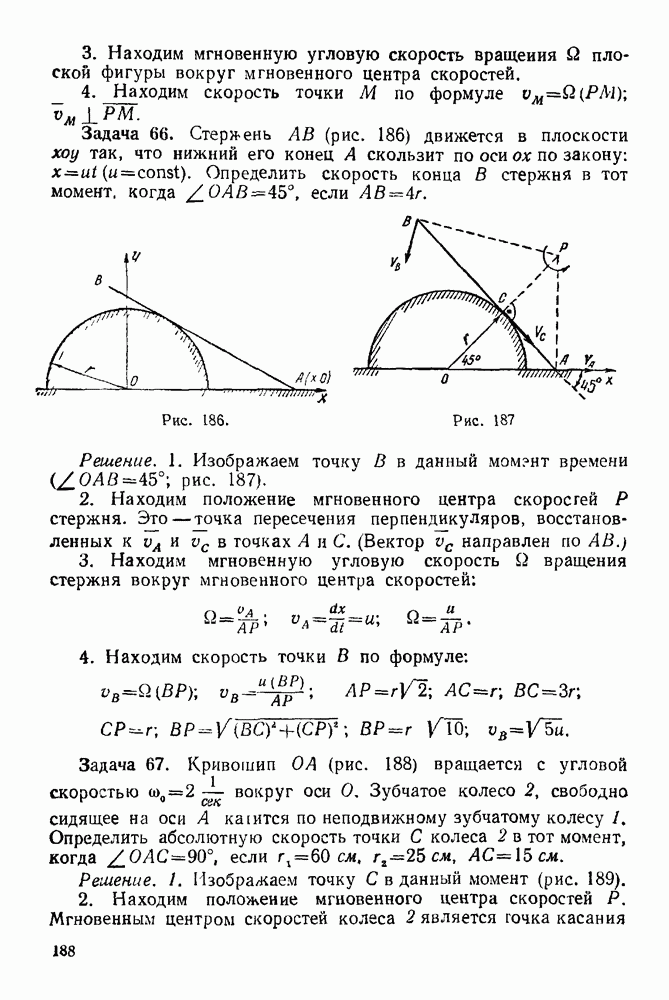
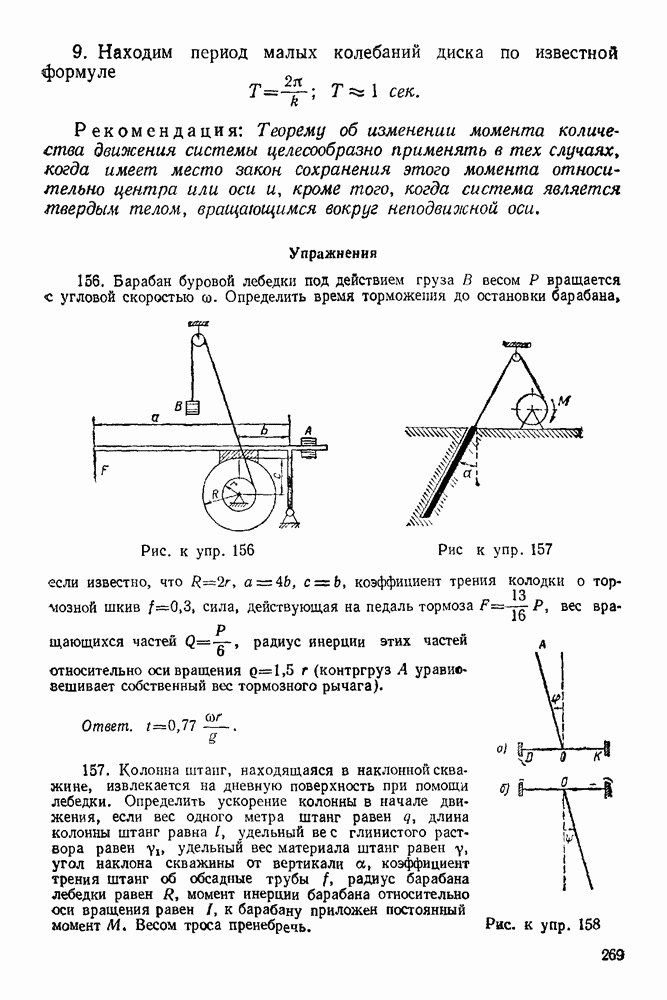
Задача 105. Шарнирный четы рехзвенник  (рис. 278) удерживается в равновесии грузом
(рис. 278) удерживается в равновесии грузом  весом
весом  с помощью веревки
с помощью веревки  перекинутой через блок
перекинутой через блок 

Рис. 278.

Рис. 279.
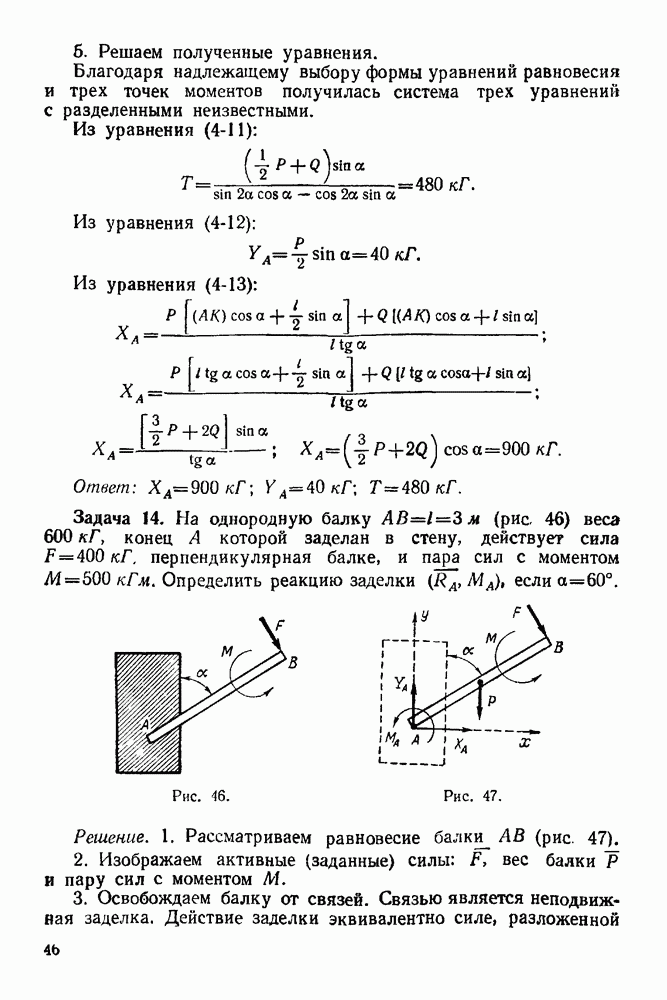
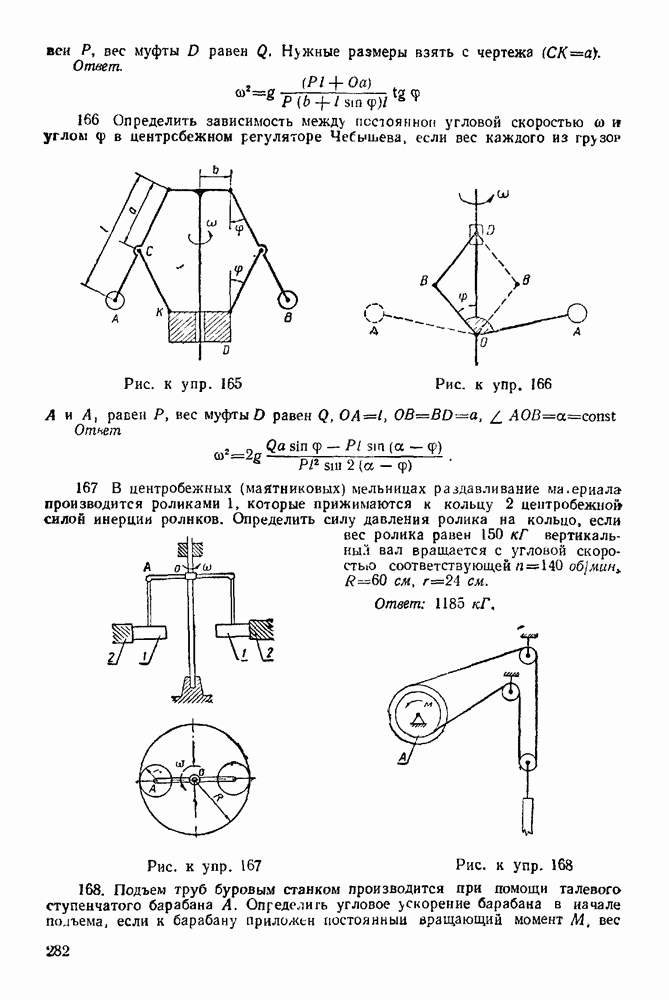
Определить угол а из условия равновесия системы если стержни однородные,  и вес каждого стержня равен
и вес каждого стержня равен 
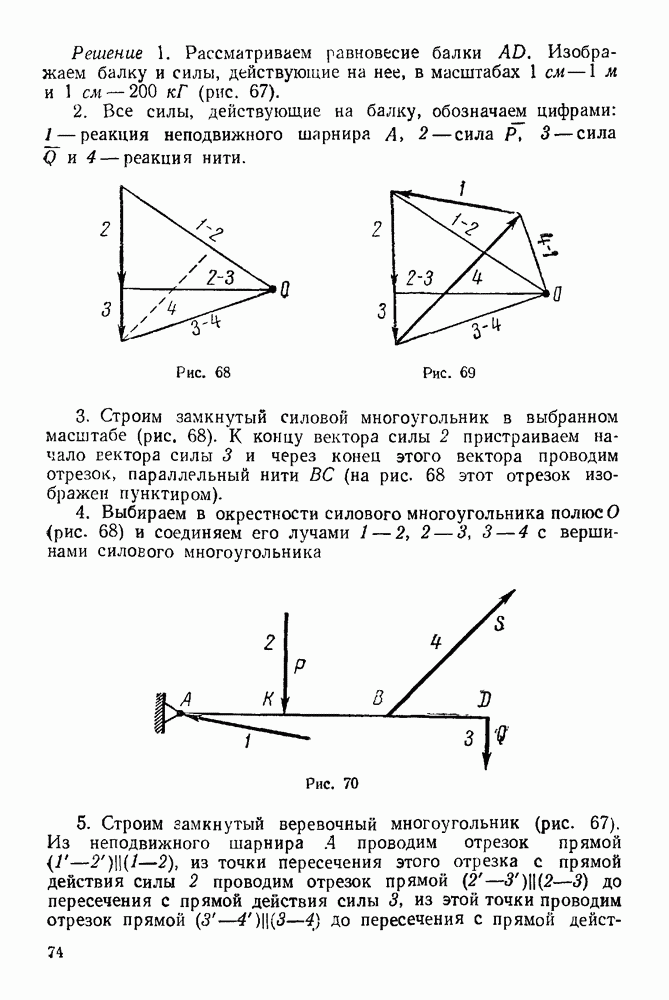
Решение. 1. Рассматриваем равновесие системы стержней  и
и  (рис. 279)
(рис. 279)
2. Изображаем активные силы, действующие на систему!  веса стержней и
веса стержней и  вес груза
вес груза 
3. Выбираем систему координат, как указано на рис 279.
4. Составляем уравнение принципа возможных перемещений:

где а — обобщенная координата системы.


Уравнение принципа  будет иметь вид:
будет иметь вид: 
5. Решаем полученное уравнение.
Так как  то
то

Следовательно,

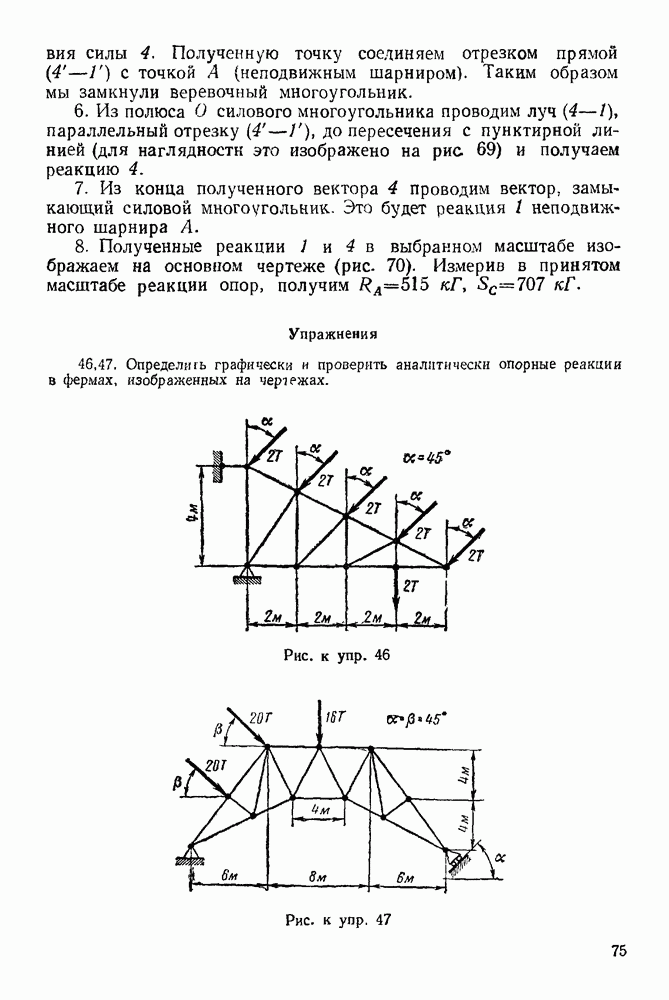
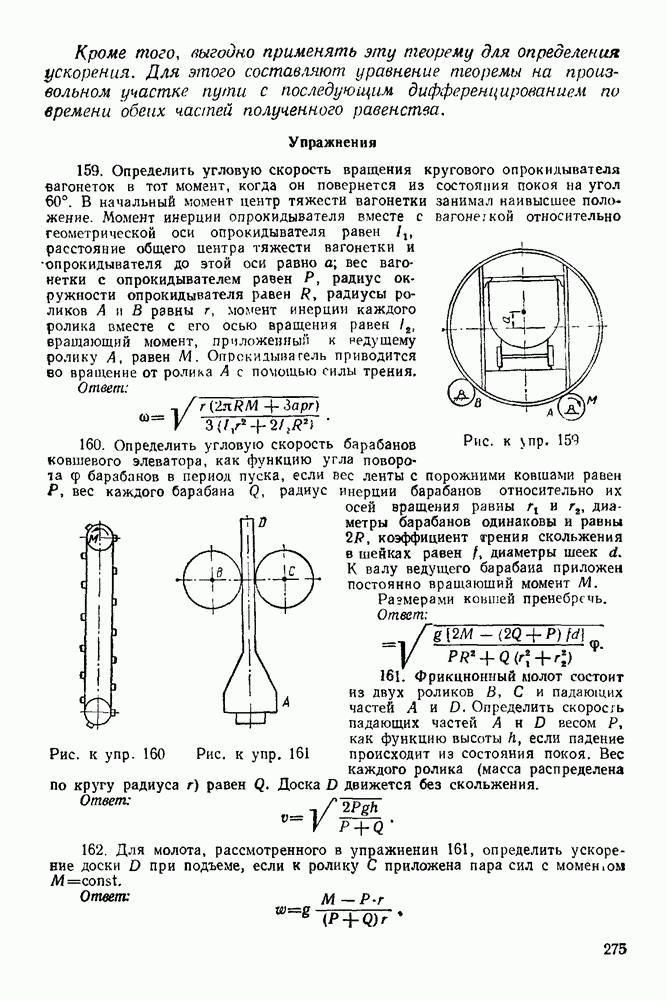
Задача 106. Четыре стержня равной длины и равного веса соединены друг с другом шарнирами 

Рис. 280.

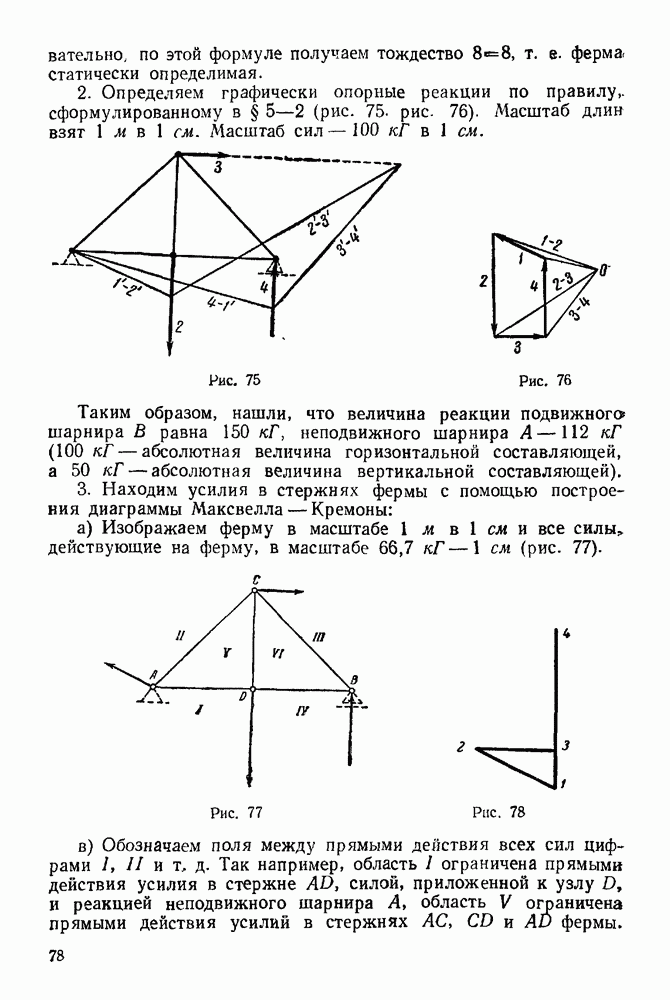
Рис. 281.
Два крайних стержня вращаются в вертикальной плоскости на шарнирах около неподвижных точек  лежащих на одной горизонтали. Определить зависимость между углами
лежащих на одной горизонтали. Определить зависимость между углами  в положении равновесия (рис. 280), если
в положении равновесия (рис. 280), если 
Решение. 1. Рассматриваем равновесие системы, состоящей из стержней  (рис. 281).
(рис. 281).
2. Рисуем активные силы, действующие на систему:  — веса стержней.
— веса стержней.
3. Выбираем систему координат, как указано на рис. 281
4. Составляем уравнение принципа возможных перемещений:

Уравнение принципа  будет иметь вид:
будет иметь вид:

5. Решаем полученное уравнение.
Для этого прежде всего установим зависимость между  и 60. Из рис. 282 видно, что
и 60. Из рис. 282 видно, что 

Получаем:


Рис. 282.
После варьирования обеих частей этого равенства будем иметь:

Найденную вариацию  подставляем в уравнение принципа, тогда это уравнение примет следующй вид:
подставляем в уравнение принципа, тогда это уравнение примет следующй вид:

Так как  следовательно,
следовательно,

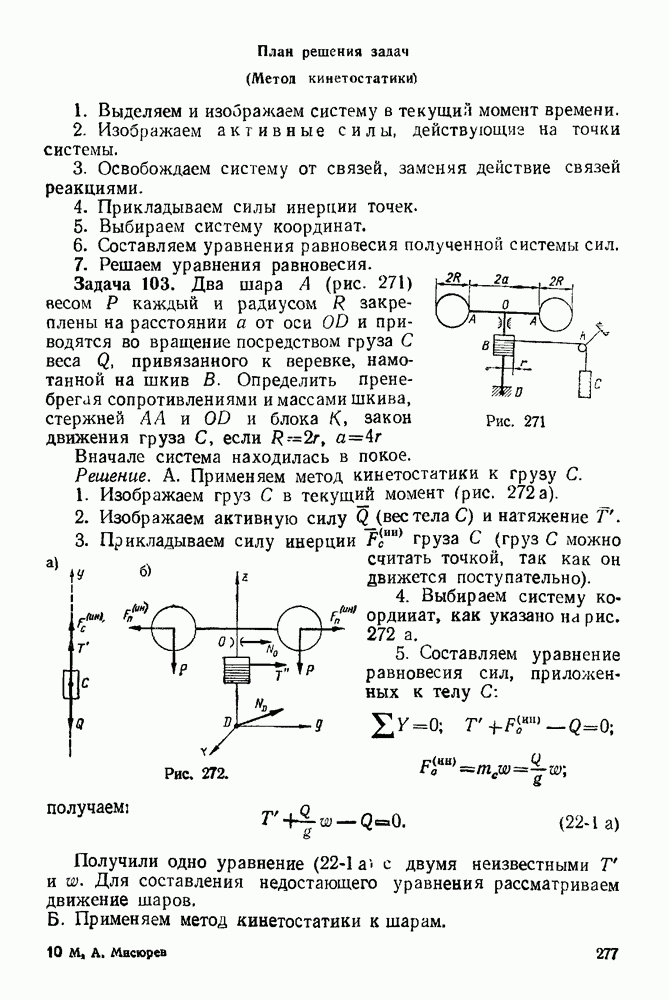
Задача  На однородный стержень
На однородный стержень  весом
весом  действует пара сил с моментом
действует пара сил с моментом  а на однородный стержень
а на однородный стержень  весом
весом  действует пара сил с моментом
действует пара сил с моментом  Определить углы
Определить углы  при равновесии системы, если в точках
при равновесии системы, если в точках  цилиндрические шарниры.
цилиндрические шарниры.

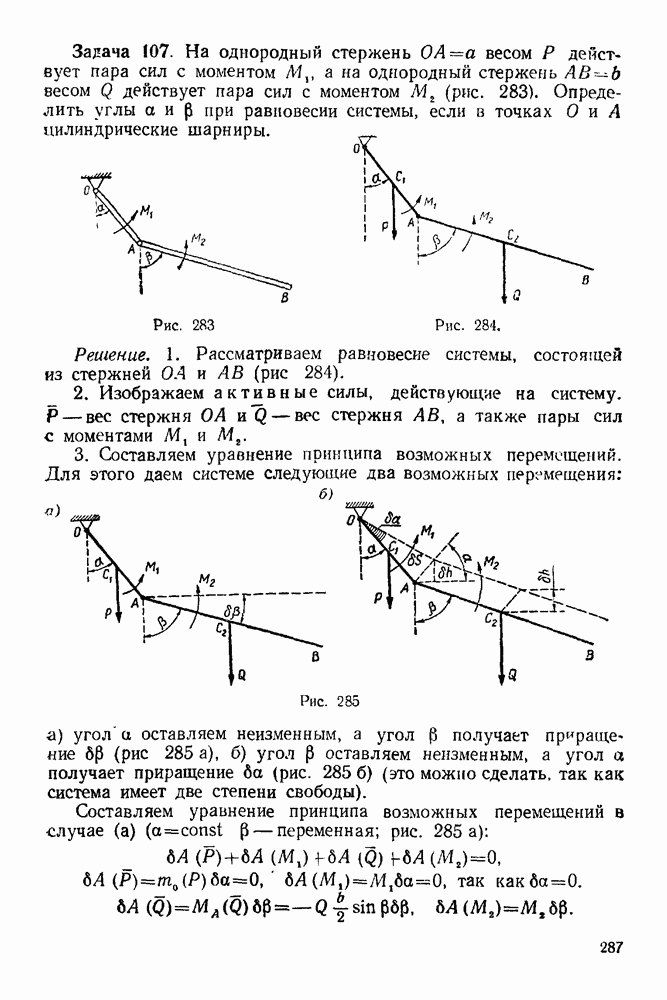
Рис. 283

Рис. 284.
Решение. 1. Рассматриваем равновесие системы, состоящей из стержней  (рис 284).
(рис 284).
2. Изображаем активные силы, действующие на систему.  вес стержня
вес стержня  и
и  вес стержня
вес стержня  а также пары сил с моментами
а также пары сил с моментами  и
и 
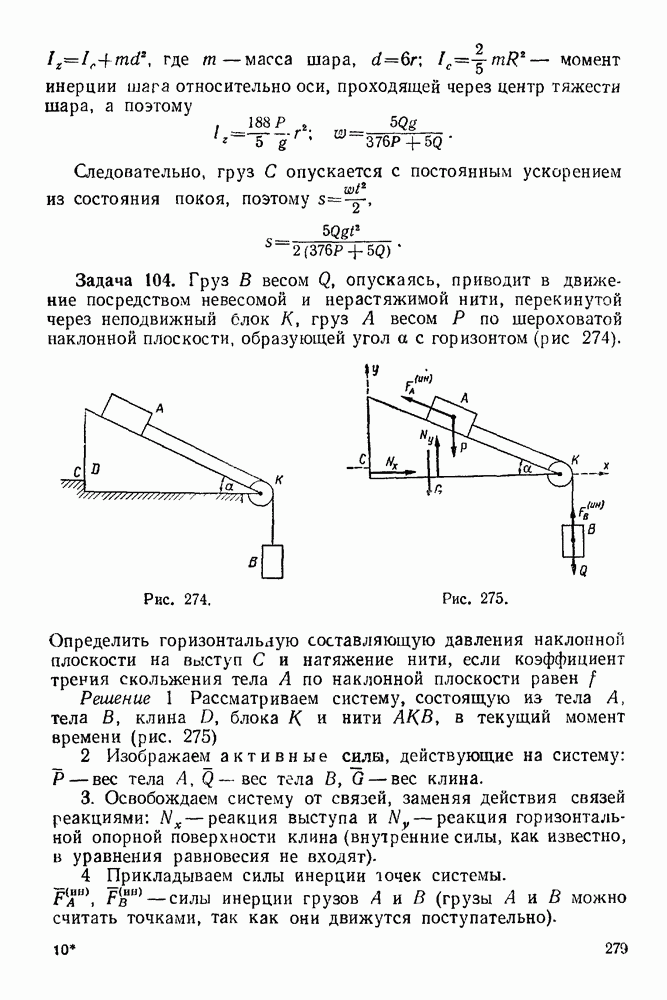
3. Составляем уравнение принципа возможных перемещений. Для этого даем системе следующие два возможных перемещения:

Рис. 285
а) угол а оставляем неизменным, а угол (3 получает приращение  (рис 285 а), б) угол
(рис 285 а), б) угол  оставляем неизменным, а угол а получает приращение 6а (рис. 285 б) (это можно сделать, так как система имеет две степени свободы).
оставляем неизменным, а угол а получает приращение 6а (рис. 285 б) (это можно сделать, так как система имеет две степени свободы).
Составляем уравнение принципа возможных перемещений в случае  переменная; рис. 285 а):
переменная; рис. 285 а):

Получаем:

Составляем уравнение принципа возможных перемещений в случае  [а — переменная, Р=const; рис. 285-6].
[а — переменная, Р=const; рис. 285-6].

Получаем:

4. Решаем полученные уравнения (22-5) и (22-6). Так как  и
и  то получим следующие два уравнения:
то получим следующие два уравнения:

Следовательно,

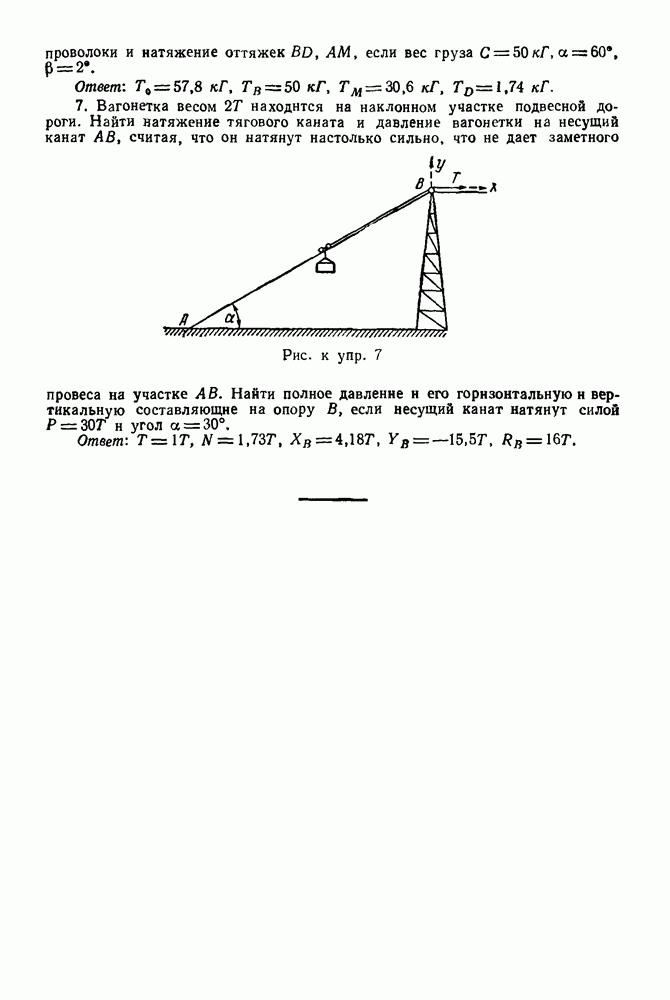
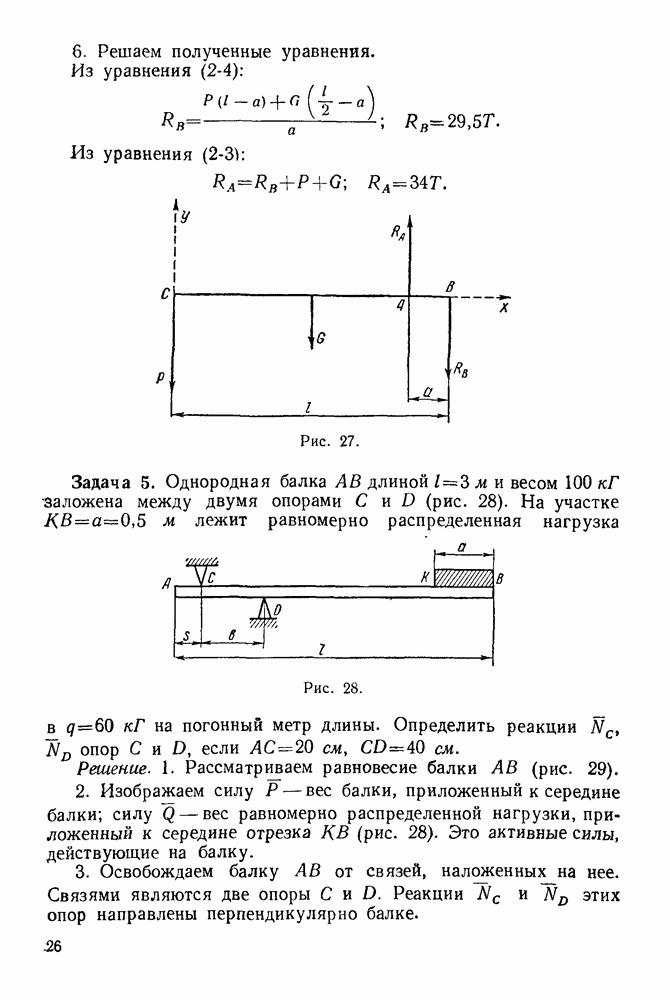
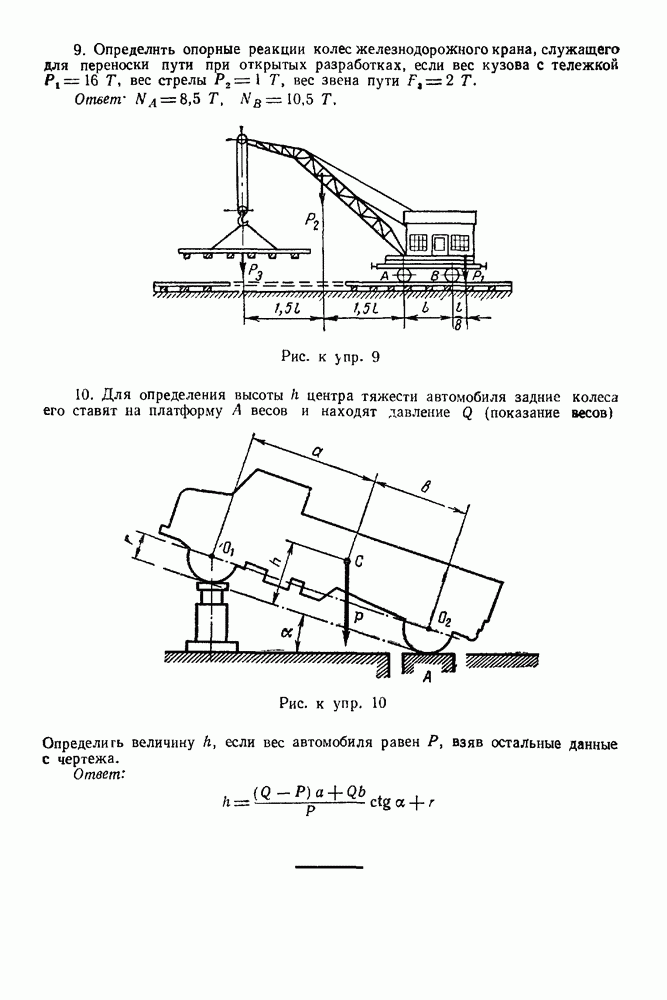
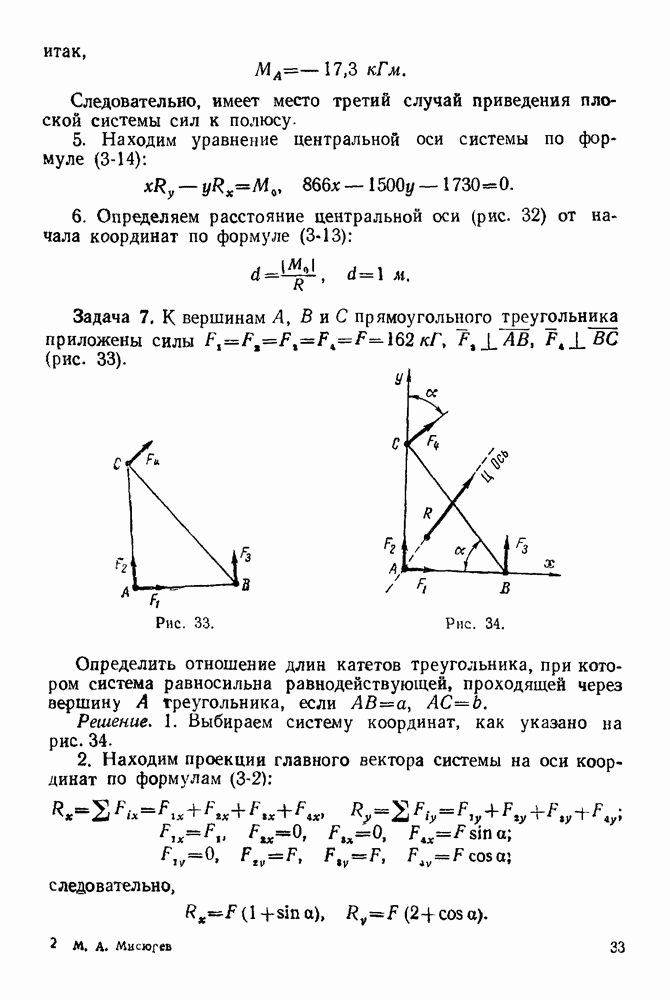
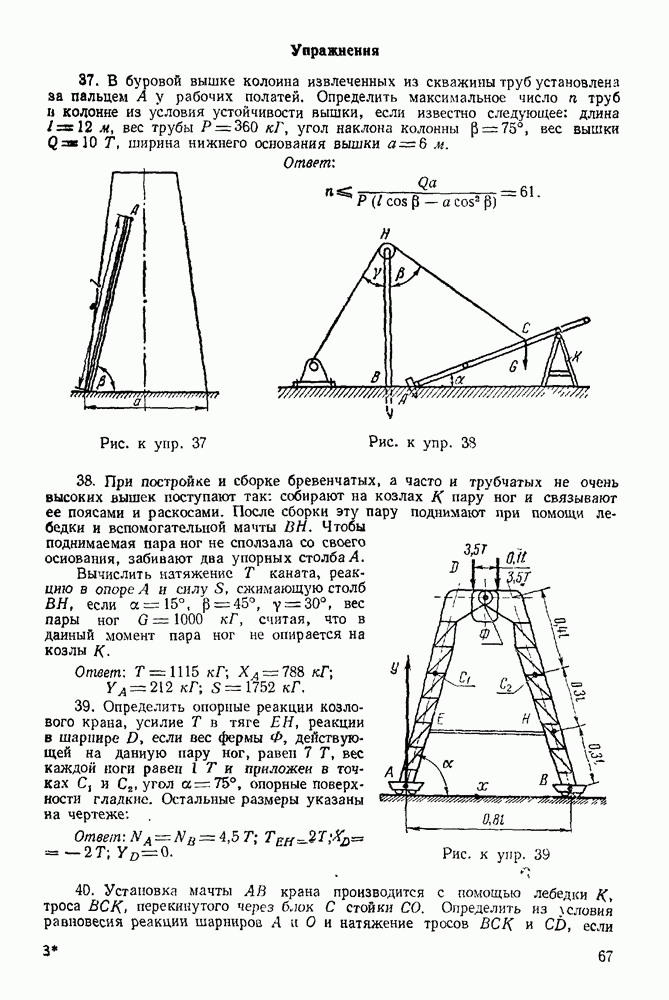
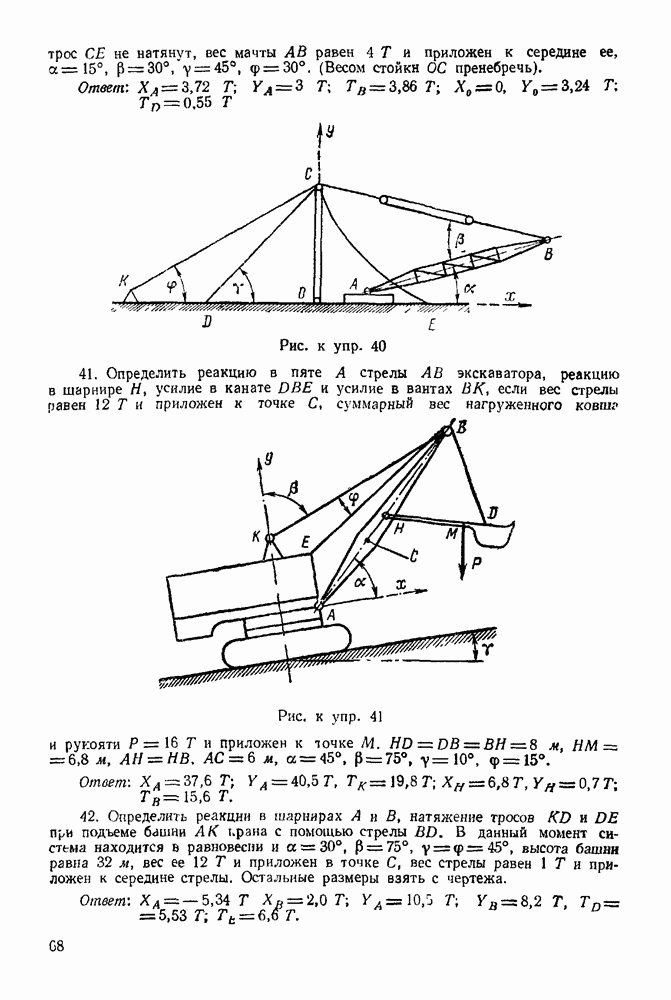
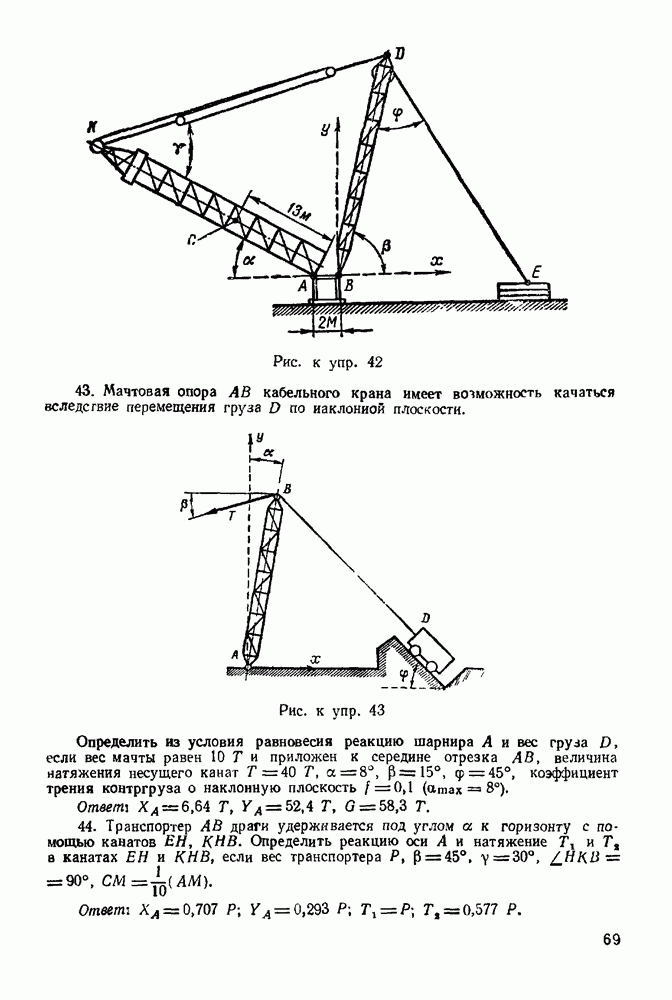
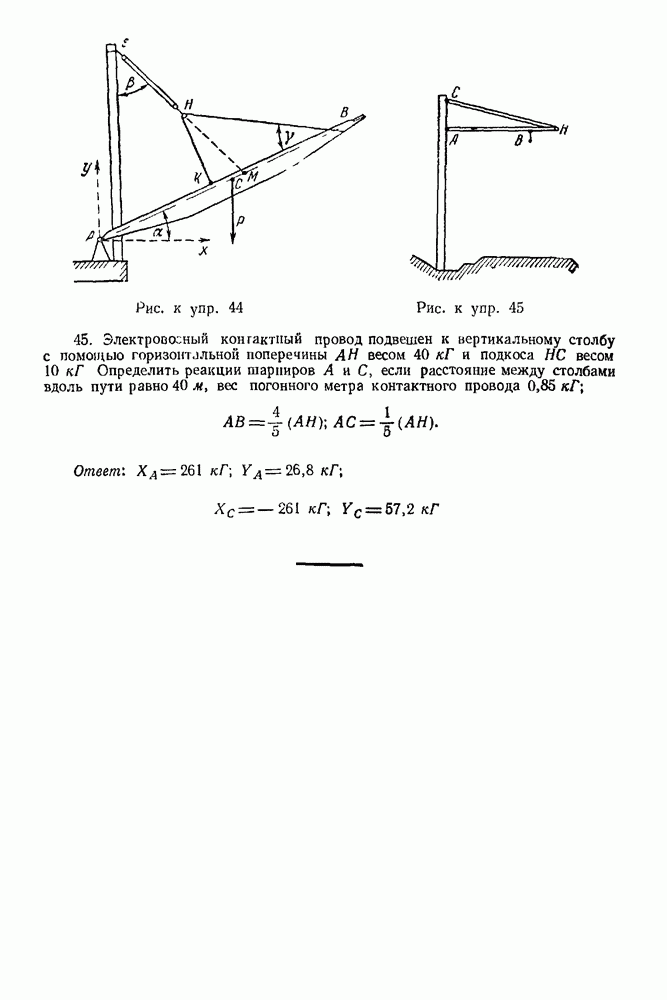
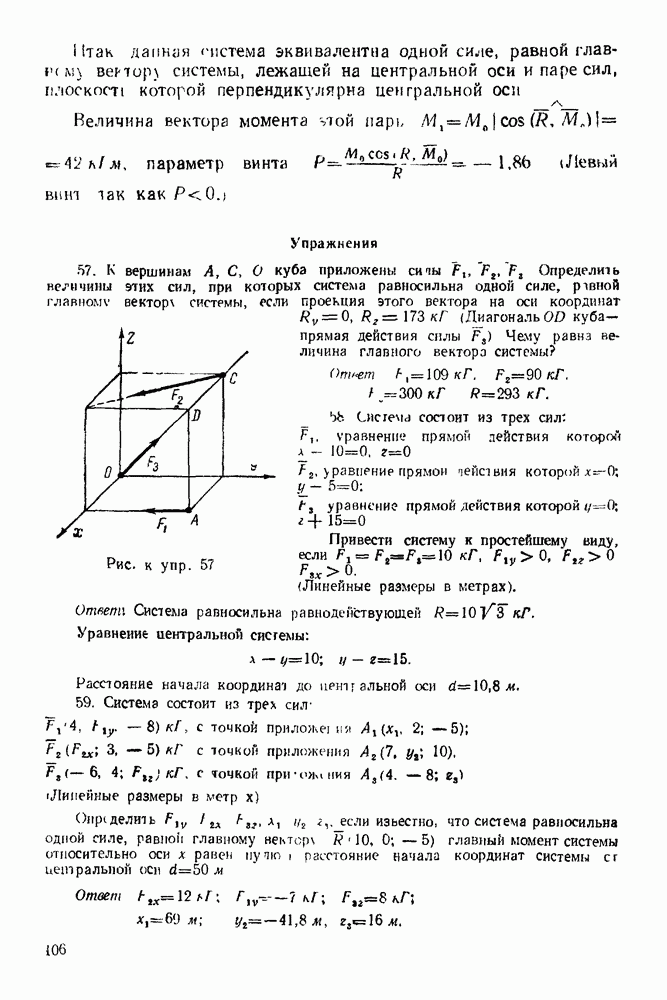
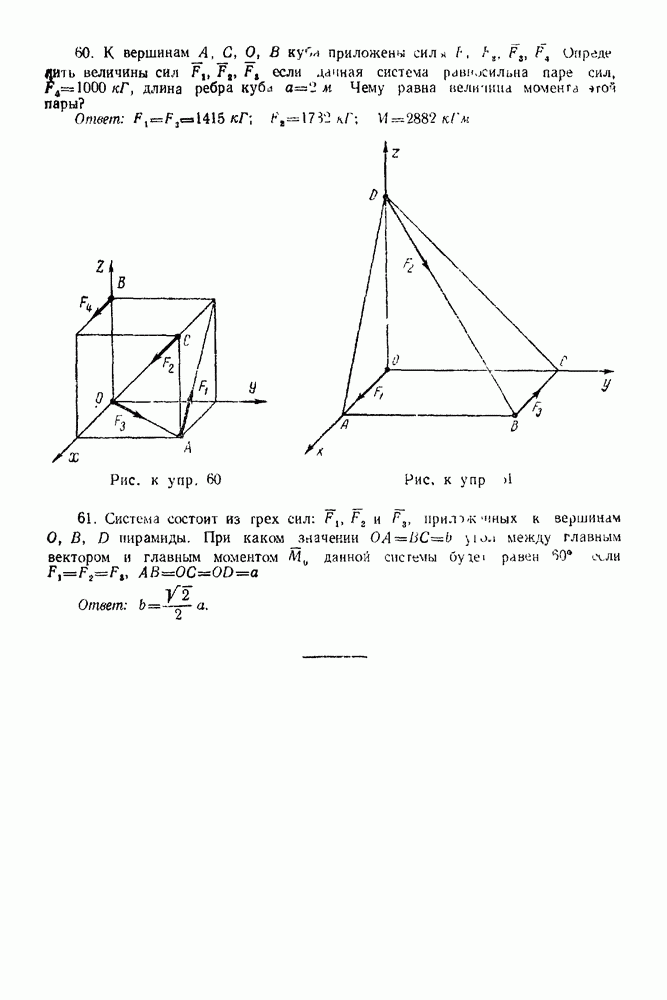
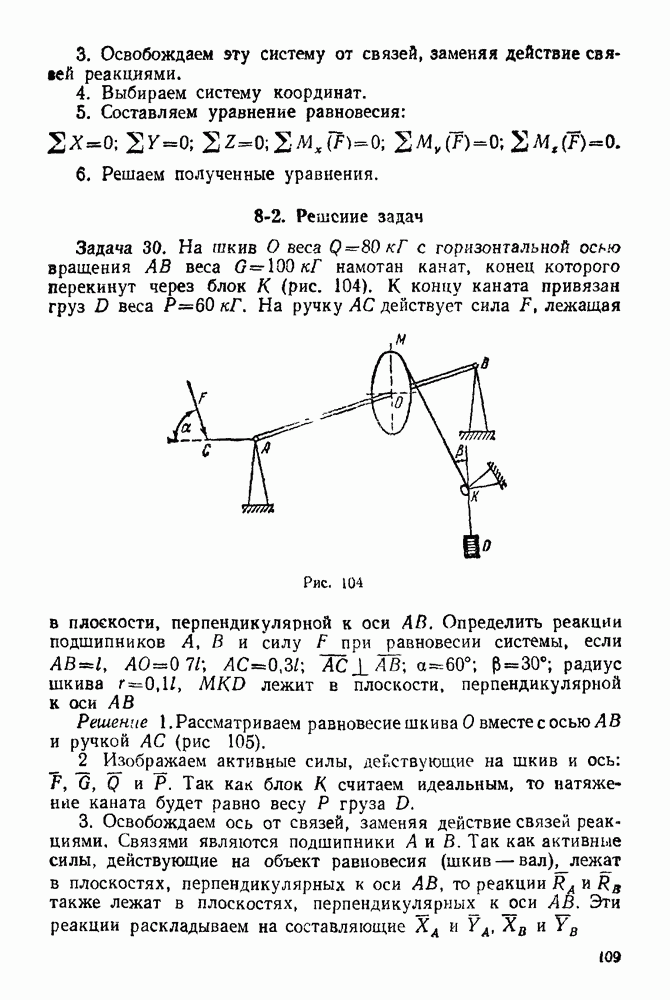
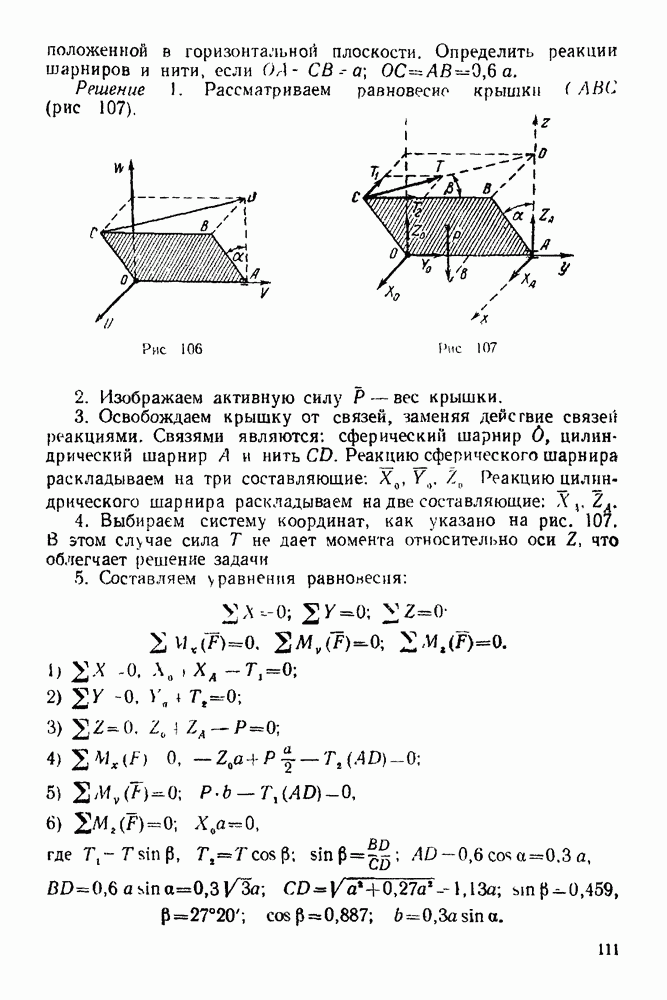
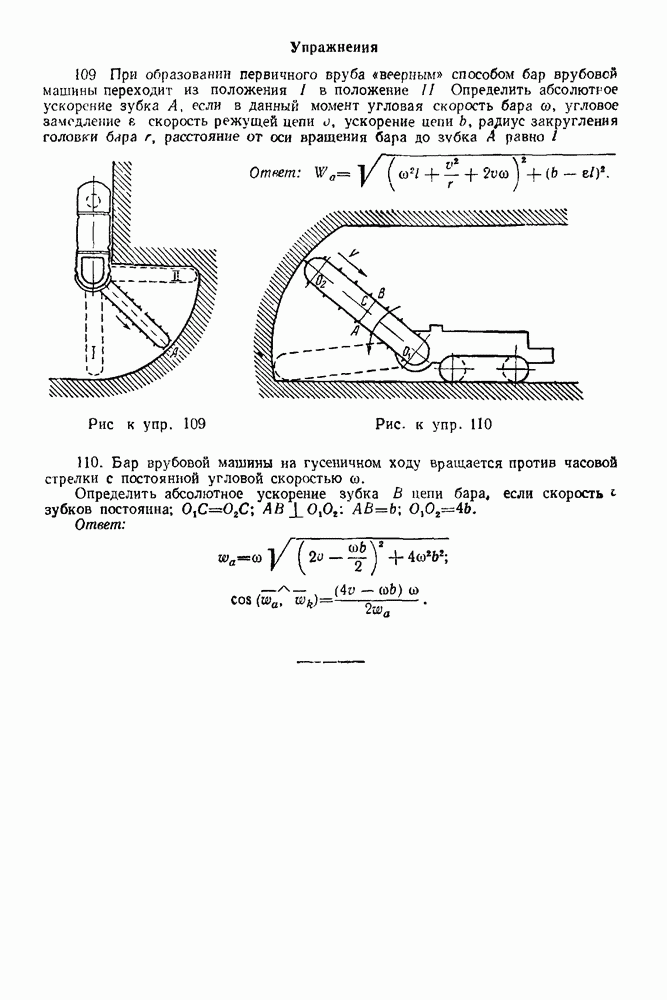
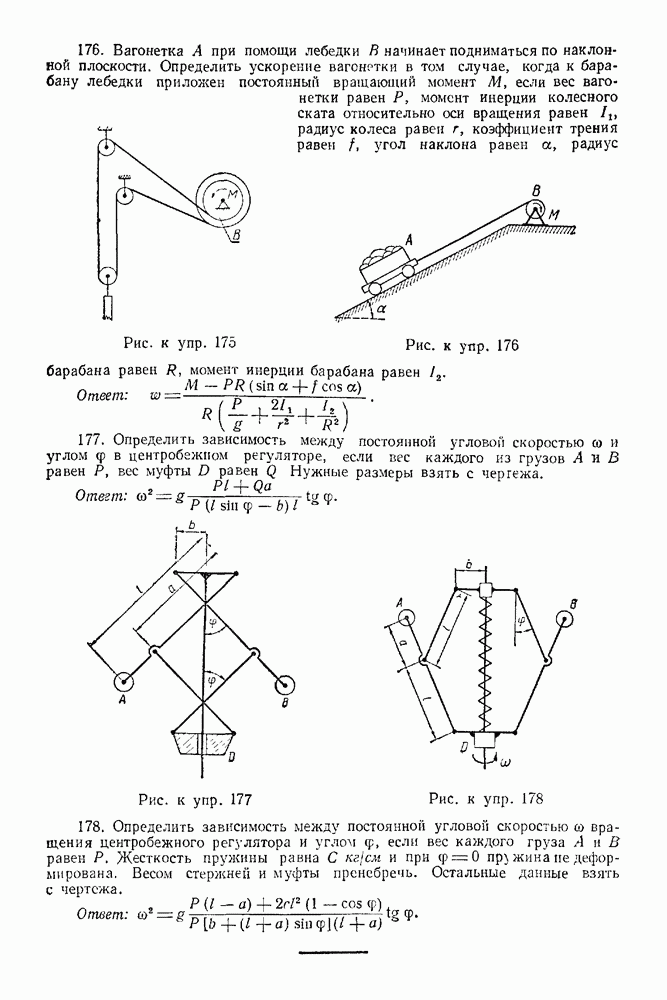
Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
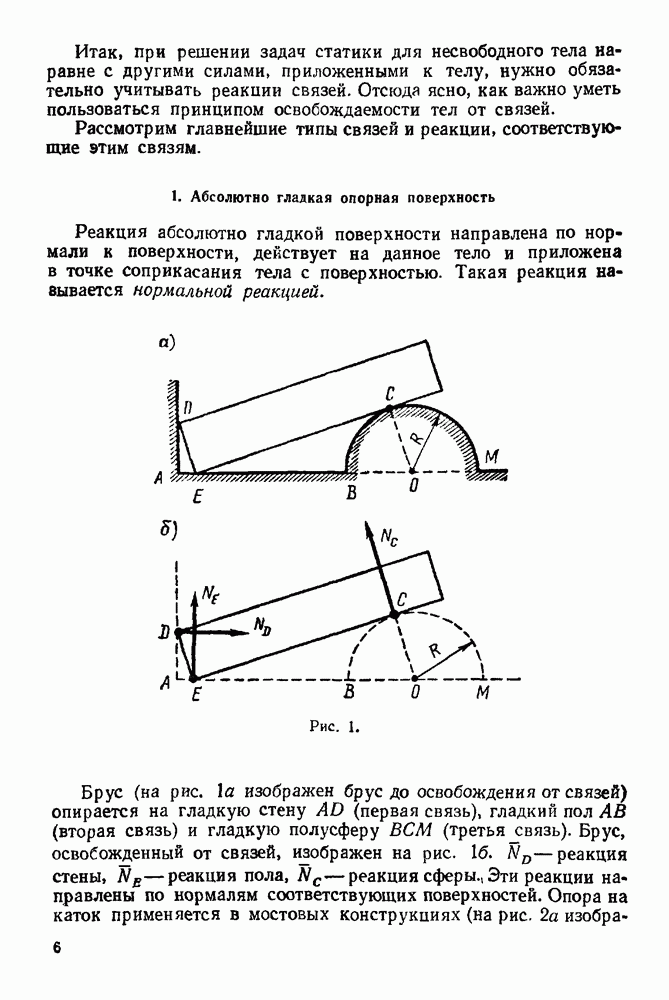
- 1. Абсолютно гладкая опорная поверхность
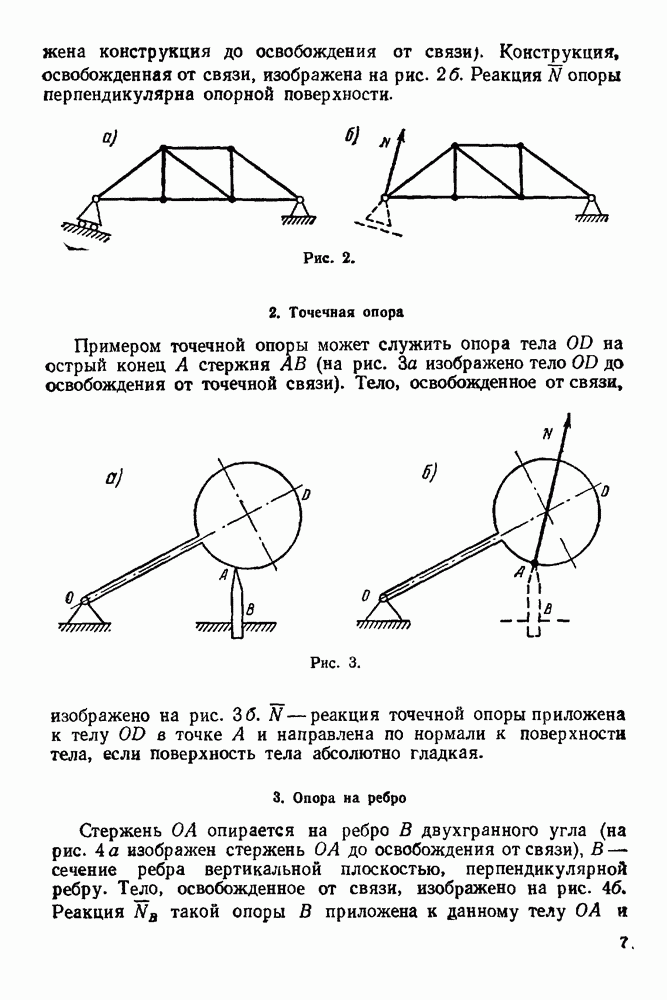
- 2. Точечная опора
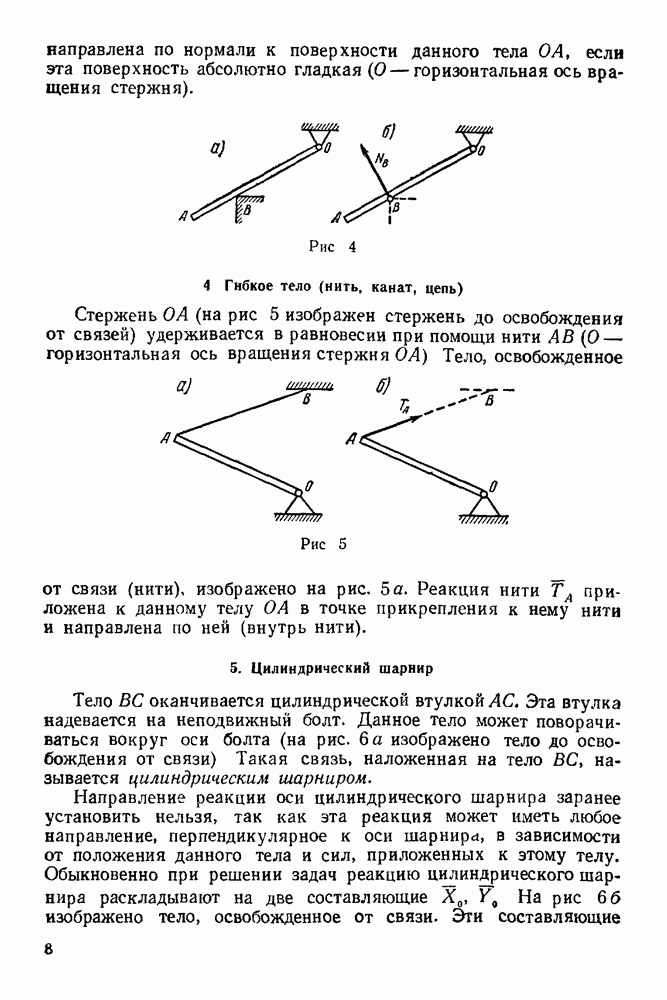
- 3. Опора на ребро
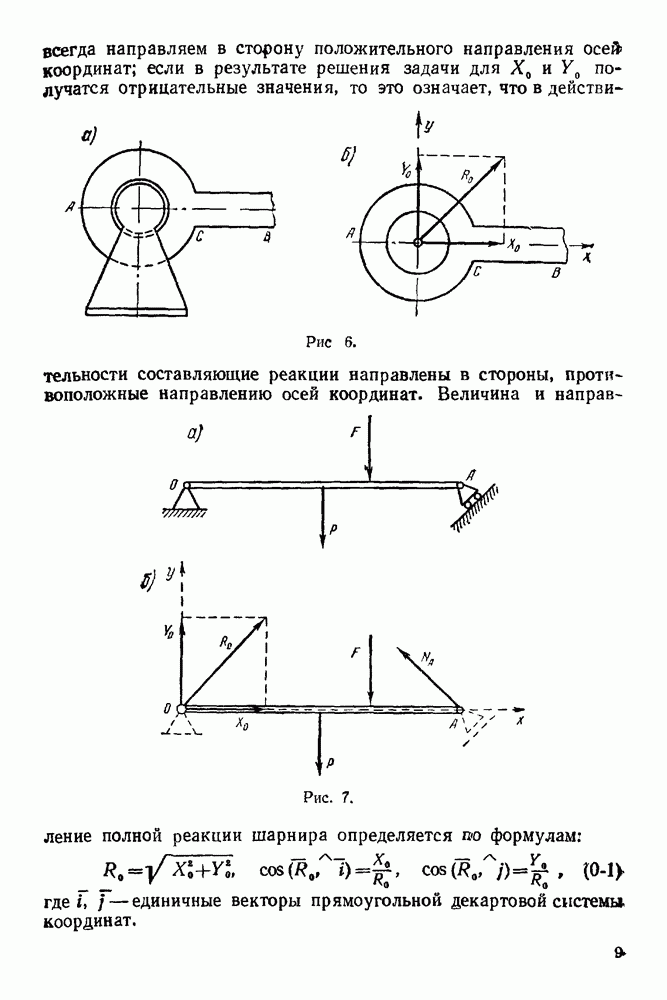
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
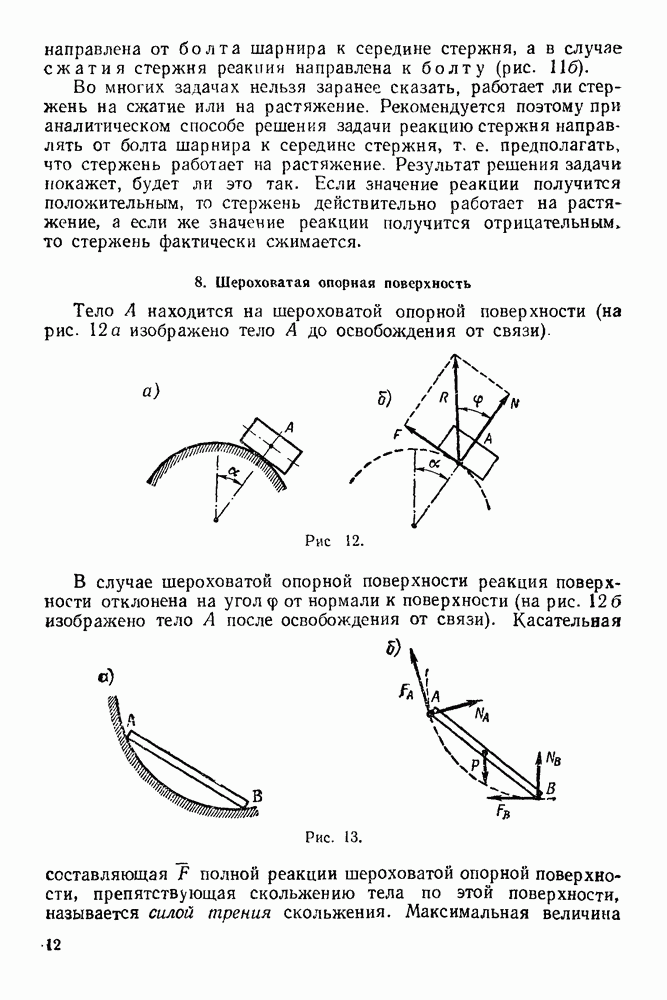
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
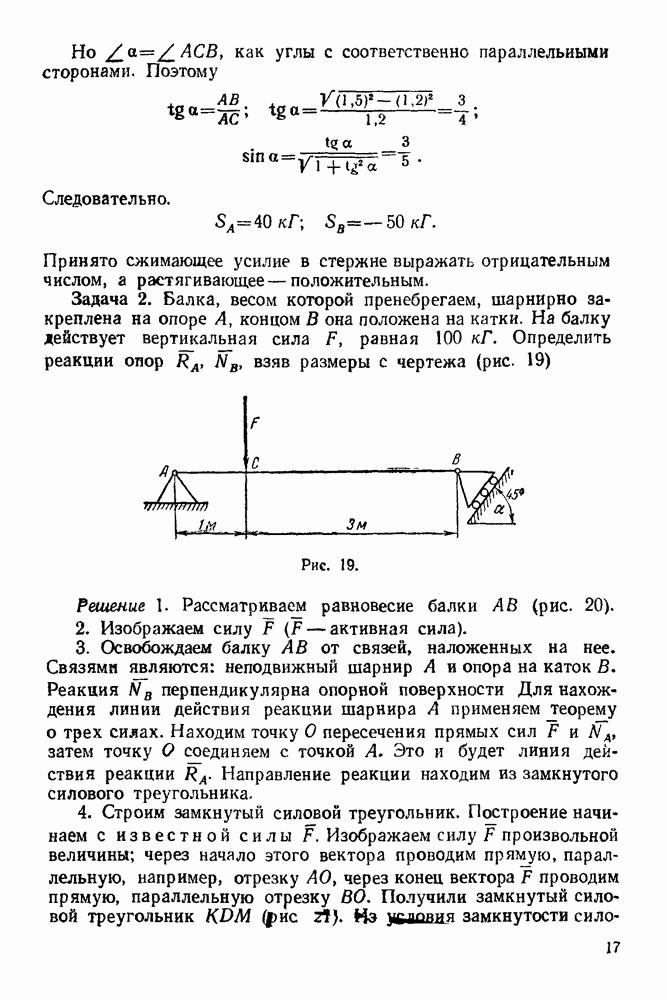
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
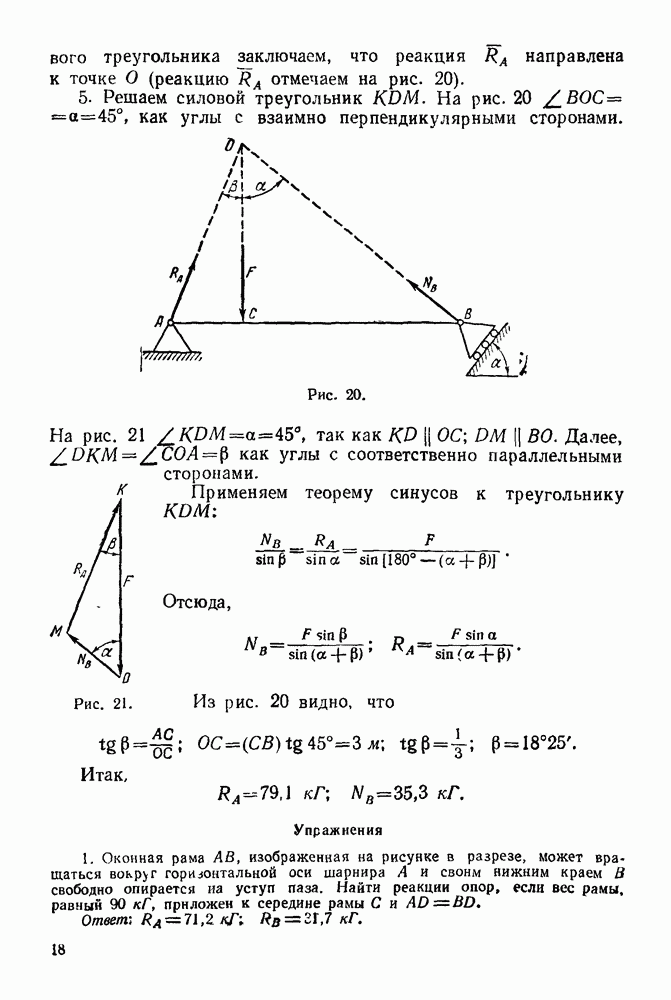
- 4-5. Решение задач на равновесие системы сочлененных тел
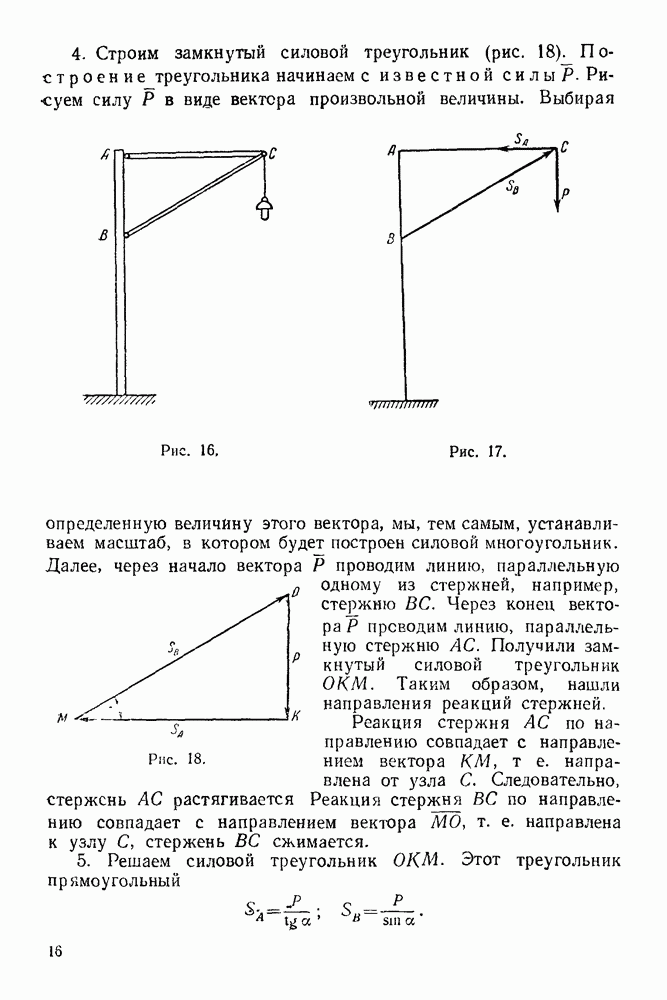
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
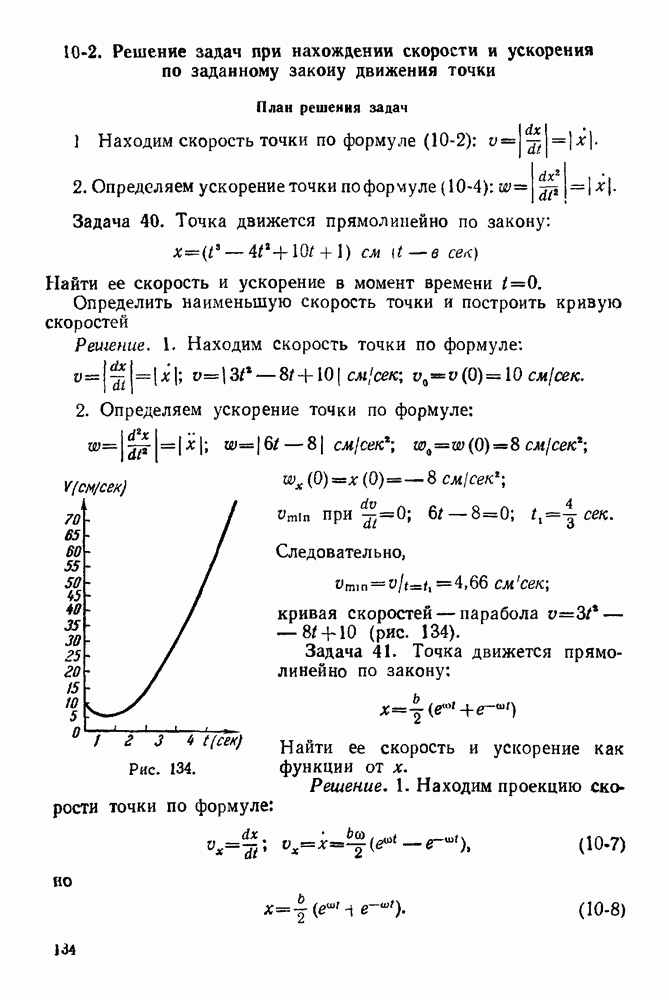
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
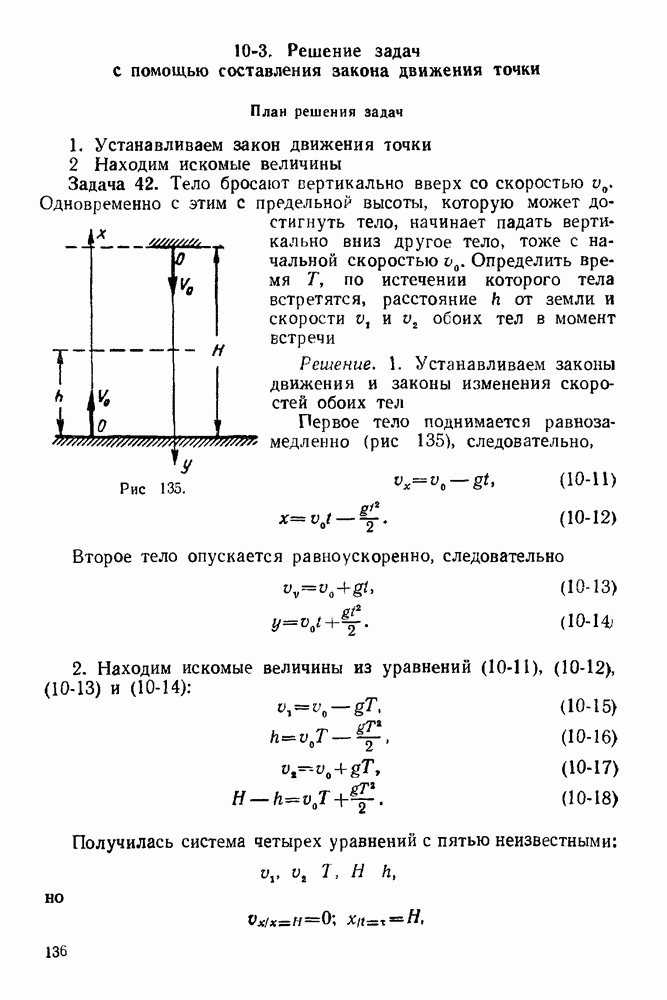
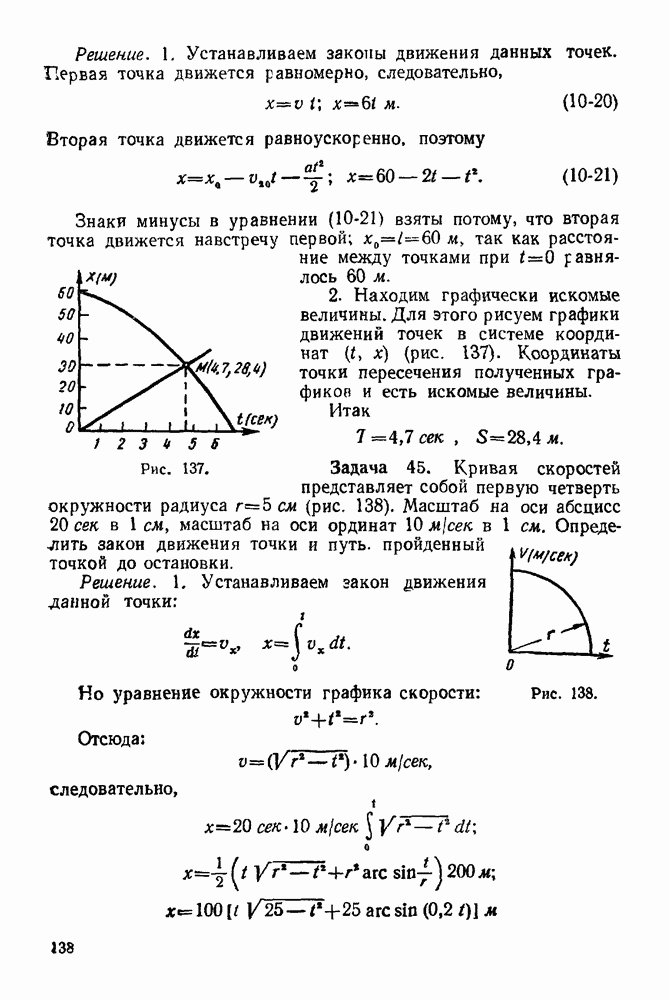
- 10-3. Решение задач с помощью составления закона движения точки
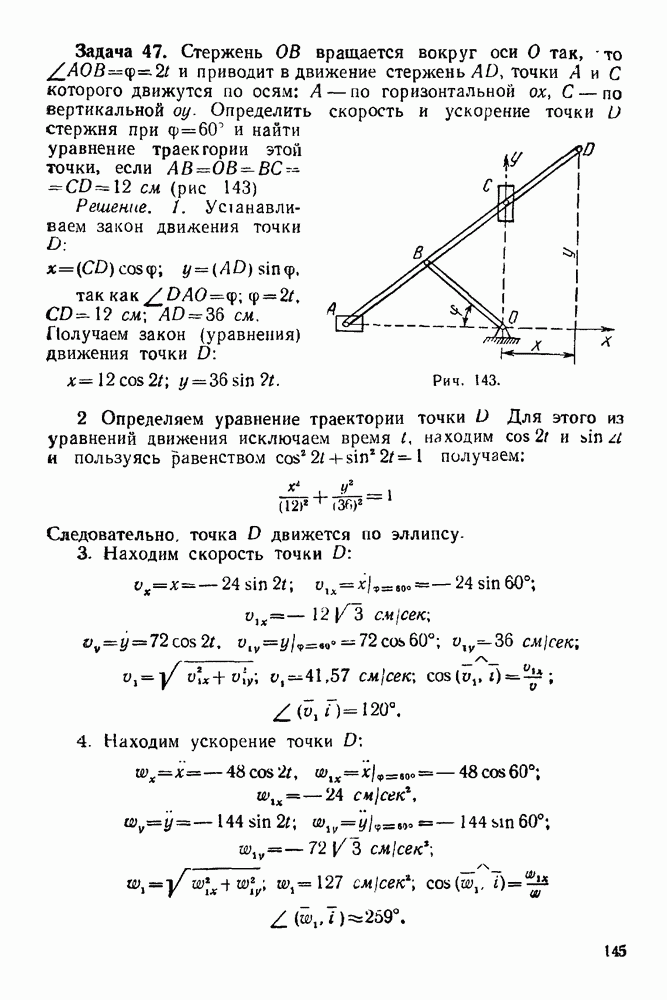
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
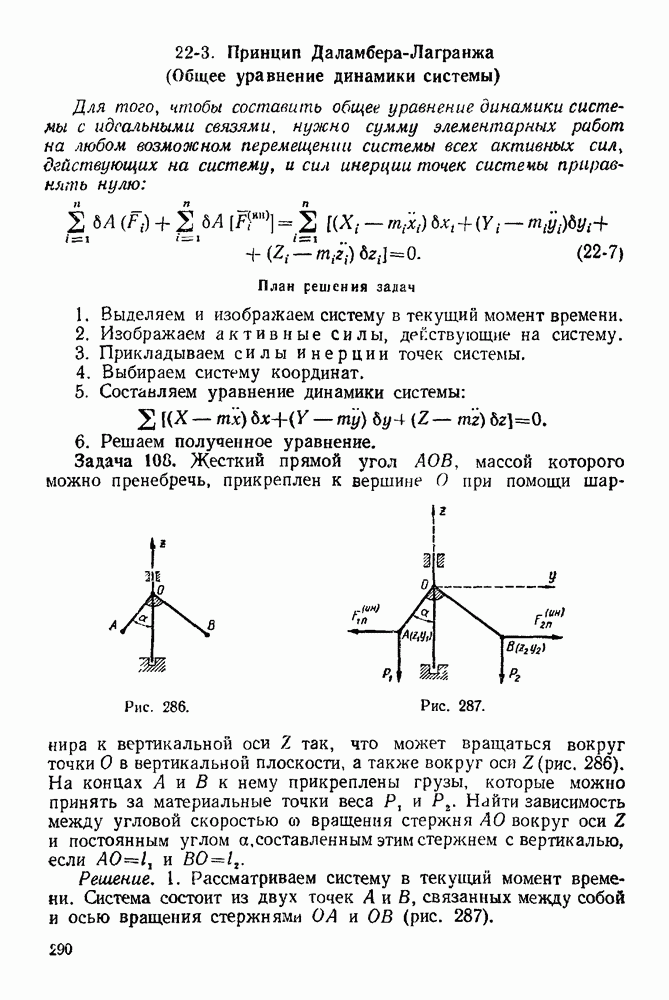
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР