| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18-3. Вторая основная задача динамики материальной точки (обратная первой)
Вторая задача динамики точки заключается в том, что задана сила, действующая на точку, и масса точки, а требуется определить закон (уравнения) движения точки.
Дано: 
Определить 
Эта задача решается интегрированием дифференциальных уравнений движения точки:  После интегрирования уравнений возникают произвольные постоянные. Эти произвольные постоянные определяются по начальным условиям движения. Начальные условия берутся из текста задачи. С точки зрения математики начальные условия движения заключаются в том, что при заданном значении аргумента задаются значения функций
После интегрирования уравнений возникают произвольные постоянные. Эти произвольные постоянные определяются по начальным условиям движения. Начальные условия берутся из текста задачи. С точки зрения математики начальные условия движения заключаются в том, что при заданном значении аргумента задаются значения функций  и их первых производных
и их первых производных  . С точки зрения кинематики начальные условия движения заключаются в том, что при заданном значении времени
. С точки зрения кинематики начальные условия движения заключаются в том, что при заданном значении времени  задается положение точки
задается положение точки  и скорость точки через ее проекции на оси координат:
и скорость точки через ее проекции на оси координат:

В самом общем случае правые части дифференциальных уравнений зависят от времени  положения точки
положения точки  и скорости точки
и скорости точки  . Такие дифференциальные уравнения интегрируются до конца только в частных случаях, когда, например, правая часть является постоянной величиной, либо простейшей функцией только времени, либо только расстояния, проходимого точкой, либо только скорости точки и др.
. Такие дифференциальные уравнения интегрируются до конца только в частных случаях, когда, например, правая часть является постоянной величиной, либо простейшей функцией только времени, либо только расстояния, проходимого точкой, либо только скорости точки и др.
План решения задач
1. Изображаем материальную точку в текущий момент времени.
2. Изображаем активные силы, действующие на точку.
3. Освобождаем точку от связей, заменяя действие связей реакциями.
4. Выбираем систему координат. Начало координат системы следует помещать в начальном положении точки и оси координат направлять так, чтобы координата точки в текущий момент и проекции скорости ее на эти оси были положительными 
Если точка движется по окружности, то рекомендуется выбрать оси естественной системы координат, совместив начало координат с текущим положением точки, и направить касательную к траектории точки так, чтобы для текущего положения точки естественная координата и проекция скорости точки на касательную были положительными  Главную нормаль нужно направить в сторону вогнутости траектории.
Главную нормаль нужно направить в сторону вогнутости траектории.
5. Составляем дифференциальные уравнения движения точки в выбранной системе координат. При этом следует помнить, что а полученных дифференциальных уравнениях проекции всех сил
необходимо выразить через те переменные  от которых эти силы зависят.
от которых эти силы зависят.
6. Проинтегрируем полученные дифференциальные уравнения движения точки. Способ интегрирования уравьений зависит от их вида.
Если на точку действуют, кроме постоянных сил, силы, зависящие только от одной переменной, то чаще всего такие уравнения решаются путем разделения переменных (см. решение задач 77, 78, 79, 81). Иногда систему трех дифференциальных уравнений второго порядка:

выгодно заменить эквивалентной системой, состоящей из шести уравнений, но первого порядка:

(см. решение 77, 78, 81).
В том случае, когда по условию задачи нужно найти скорость точки как функцию текущих координат ее и сила зависит только от этих координат или скорости точки, то из дифференциальных уравнений переменную  исключаем с помощью подстановок:
исключаем с помощью подстановок:

В простейших случаях дифференциальные уравнения движения точки будут иметь вид:

(см. решение задач 78, 79).
7. Составляем начальные условия движения по тексту задачи.
8. По начальным условиям определяем произвольные постоянные интегрирования.
9. Найденные произвольные постоянные подставляем в результат интегрирования дифференциальных уравнений движения точки. Это и будут уравнения движения точки (закон движения).
Прямолинейное движение точки
1. Постоянная сила
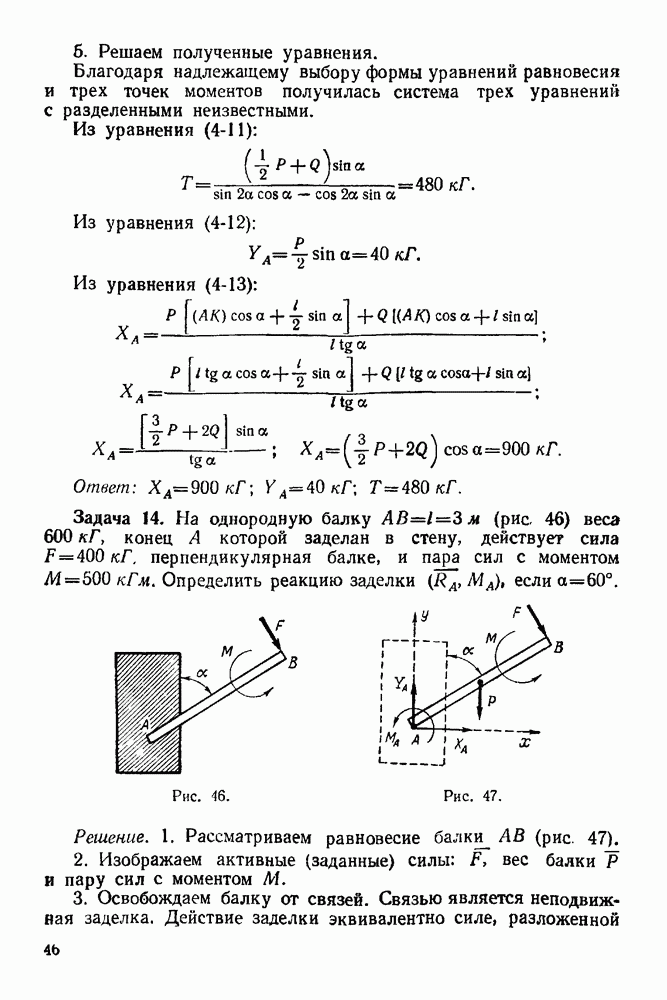
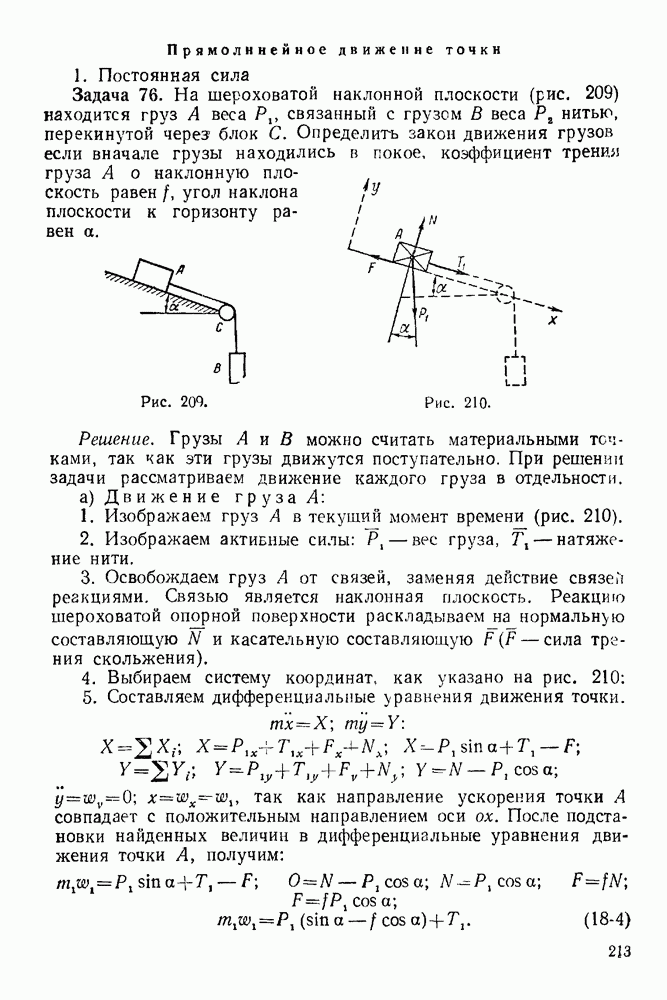
Задача 76. На шероховатой наклонной плоскости (рис. 209) находится груз  веса
веса  связанный с грузом В веса
связанный с грузом В веса  нитью, перекинутой через блок С. Определить закон движения грузов если вначале грузы находились в покое, коэффициент трения груза А о наклонную плоскость равен
нитью, перекинутой через блок С. Определить закон движения грузов если вначале грузы находились в покое, коэффициент трения груза А о наклонную плоскость равен  угол наклона плоскости к горизонту равен а.
угол наклона плоскости к горизонту равен а.

Рис. 209.

Рис. 210.
Решение. Грузы  можно считать материальными точками, так как эти грузы движутся поступательно. При решении задачи рассматриваем движение каждого груза в отдельности.
можно считать материальными точками, так как эти грузы движутся поступательно. При решении задачи рассматриваем движение каждого груза в отдельности.
а) Движение груза Л:
1. Изображаем груз А в текущий момент времени (рис. 210).
2. Изображаем активные силы:  вес груза,
вес груза,  натяжение нити.
натяжение нити.
3. Освобождаем груз А от связей, заменяя действие связей реакциями. Связью является наклонная плоскость. Реакцию шероховатой опорной поверхности раскладываем на нормальную составляющую  и касательную составляющую
и касательную составляющую  сила трения скольжения).
сила трения скольжения).
4. Выбираем систему координат, как указано на рис. 210:
5. Составляем дифференциальные уравнения движения точки.

 так как направление ускорения точки А совпадает с положительным направлением оси
так как направление ускорения точки А совпадает с положительным направлением оси  После подстановки найденных величин в дифференциальные уравнения движения точки
После подстановки найденных величин в дифференциальные уравнения движения точки  получим:
получим:

б) Движение груза В.
1. Изображаем груз В в текущий момент времени (рис. 211).
2. Изображаем активную силу  вес груза
вес груза  натяжение нити.
натяжение нити.
3. Выбираем систему координат, как указано на рис. 211. Достаточно выбрать одну ось  так как тело движется по вертикали.
так как тело движется по вертикали.
4. Составляем дифференциальное уравнение движения:

Из уравнений (18-4) и (18-5) находим ускорение грузов, имея в виду, что 


Рис. 211.
Следовательно, точки  движутся прямолинейно и равномерноускоренно:
движутся прямолинейно и равномерноускоренно:

но  так как грузы движутся из состояния покоя; начало координат выбираем так, что
так как грузы движутся из состояния покоя; начало координат выбираем так, что  Следовательно,
Следовательно,

Вывод. В том случае, когда на точку, участвующую в прямолинейном движении, действуют постоянные силы, то эта точка движется равнопеременно. Ускорение равнопеременного движения находится из дифференциальных уравнений движения. Для нахождения закона движения точки нужно найденное ускорение подставить в кинематическую формулу пути равнопеременного прямолинейного движения.
2. Сила—функция времени.
Задача 77. Тело  начинает скользить по гладкой наклонной плоскости без начальной скорости в среде с сопротивлением, равным
начинает скользить по гладкой наклонной плоскости без начальной скорости в среде с сопротивлением, равным  некоторое положительное число,
некоторое положительное число,  вес тела
вес тела  Определить уравнение движения тела, если угол наклона плоскости к горизонту
Определить уравнение движения тела, если угол наклона плоскости к горизонту  (рис. 212).
(рис. 212).
Решение. 1. Изображаем тело  в текущий момент времени (рис. 213); тело можно считать за точку, так как тело движется поступательно.
в текущий момент времени (рис. 213); тело можно считать за точку, так как тело движется поступательно. 
2. Изображаем активную силу  вес тела и силу
вес тела и силу  сопротивление среды.
сопротивление среды.
3. Освобождаем тело  от связи, заменяя действие связи нормальной реакцией N (наклонная плоскость гладкая).
от связи, заменяя действие связи нормальной реакцией N (наклонная плоскость гладкая).
4. Выбираем систему координат, как указано на рис. 213.

Рис. 212.

Рис. 213.
5. Составляем дифференциальное уравнение движения:

6. Интегрируем полученное дифференциальное уравнение движения точки  Это уравнение с разделяющимися переменными:
Это уравнение с разделяющимися переменными: 
После интегрирования получим:

Откуда:

7. Составляем начальные условия движения (по тексту задачи) для определения произвольных постоянных интегрирования С, и 
При 
Так как начало координат помещено в начальном положении тела  то
то 
8 Начальные условия движения подставляем в уравнения  и (18-7):
и (18-7):

9. Найденные  подставляем в результат интегрирования дифференциального уравнения движения точки (уравнениз 18—7):
подставляем в результат интегрирования дифференциального уравнения движения точки (уравнениз 18—7):

3. Сила — функция скорости точки.
Задача 78. Тело А весом  получившее начальную скорость
получившее начальную скорость  скользит вверх по шероховатой наклонной плоскости, испытывая сопротивление среды, пропорциональное квадрату скорости тела причем коэффициент пропорциональности равен
скользит вверх по шероховатой наклонной плоскости, испытывая сопротивление среды, пропорциональное квадрату скорости тела причем коэффициент пропорциональности равен  масса тела). Определить расстояние, проходимое телом, как функцию скорости его если коэффициент трения скольжения равен
масса тела). Определить расстояние, проходимое телом, как функцию скорости его если коэффициент трения скольжения равен  угол наклона плоскости к горизонту равен а (рис. 214).
угол наклона плоскости к горизонту равен а (рис. 214).

Рис. 214.

Рис. 215.
Решение. 1. Изображаем тело А в текущий момент времени (рис. 215). Тело А можно считать материальной точкой, так как оно движется поступательно. 
2. Изображаем активную силу  вес тела и
вес тела и  силу сопротивления среды.
силу сопротивления среды.
3. Освобождаем тело А от связи, заменяя действие связи реакцией. Связью является наклонная плоскость. Реакцию плоскости раскладываем на нормальную составляющую  и на касательную составляющую
и на касательную составляющую  сила трения скольжения).
сила трения скольжения).
4. Выбираем оси координат, как указано на рис.  упрощения решения задачи рекомендуется одну из осей направить в сторону движения тела А
упрощения решения задачи рекомендуется одну из осей направить в сторону движения тела А
5 Составляем дифференциальные уравнения движения:

следовательно,

Так как скорость точки — сложная функция времени  то
то  следовательно,
следовательно, 
Поэтому дифференциальное уравнение движения тела А получится таким:

6. Интегрируем дифференциальное уравнение движения тела Это уравнение с разделяющимися переменными:

7. Составляем начальные условия для определения произвольной постоянной с.
При 
 так как начало координат помещено в том месте, откуда началось движение тела А).
так как начало координат помещено в том месте, откуда началось движение тела А).
8. Определяем произвольную постоянную с. Для этого начальные условия задачи подставляем в уравнение (18-8), получим:

9. Подставляем найденное с в уравнение (18-8):

4. Сила — функция координаты движущейся точки.
Задача 79. Тело А находится на гладкой горизонтальной плоскости и притягивается к неподвижному центру О силой, пропорциональной массе тела и обратно пропорциональной кубу расстояния тела от этого центра, причем коэффициент пропорциональности равен к. В начальный момент расстояние тела от О равно а, а скорость его равна нулю. Найти закон движения тела
Решение. 1. Изображаем тело А в текущий момент времени Крис. 216). Тело можно считать за материальную точку, так как это тело движется поступательно. 
2. Изображаем активные силы, действующие на тело:  вес тела,
вес тела,  сила притяжения тела к центру О.
сила притяжения тела к центру О.
3. Освобождаем тело от связи, заменяя действие связи реакцией. Связью является горизонтальная гладкая плоскость;  нормальная реакция этой плоскости.
нормальная реакция этой плоскости.
4. Выбираем систему координат, как указано на рис. 216.
5. Составляем дифференциальное уравнение движения тела А:


Рис. 216.
6. Интегрируем дифференциальное уравнение движения точки:

Скорость тела  -сложная функция времени
-сложная функция времени  следовательно,
следовательно,

После интегрирования будем иметь:

7. Составляем начальные условия для определения произвольных постоянных с, и 
При
8. Определяем по начальным условиям задачи произвольные постоянные  и
и 
Подставляя начальные условия в уравнения (18-9) и (18-10), получим: 
9. Найденные  подставляем в уравнение (18—10) и получаем закон движения тела А:
подставляем в уравнение (18—10) и получаем закон движения тела А:

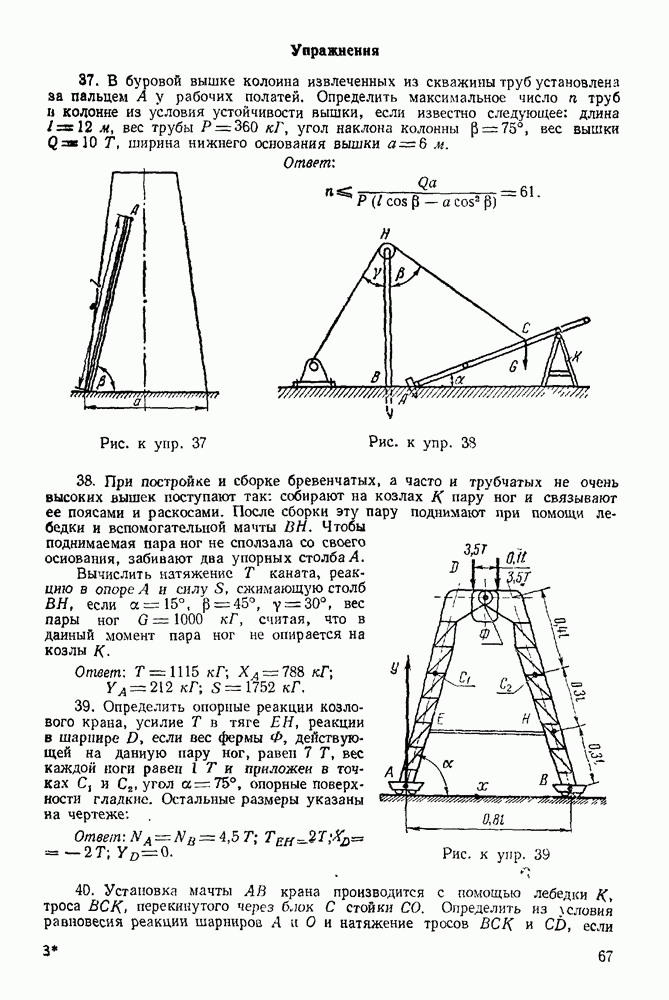
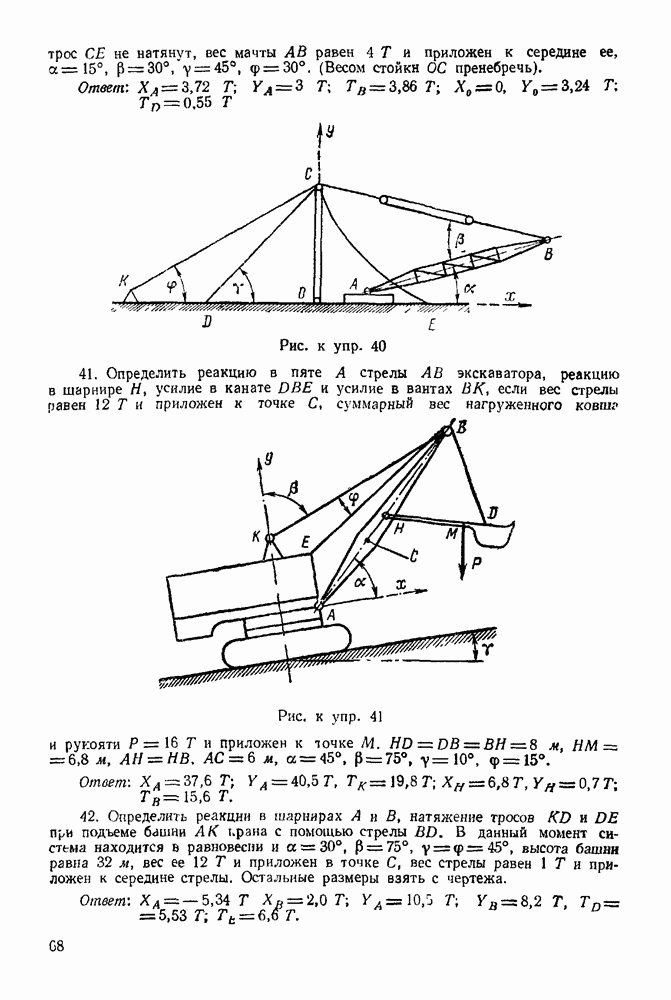
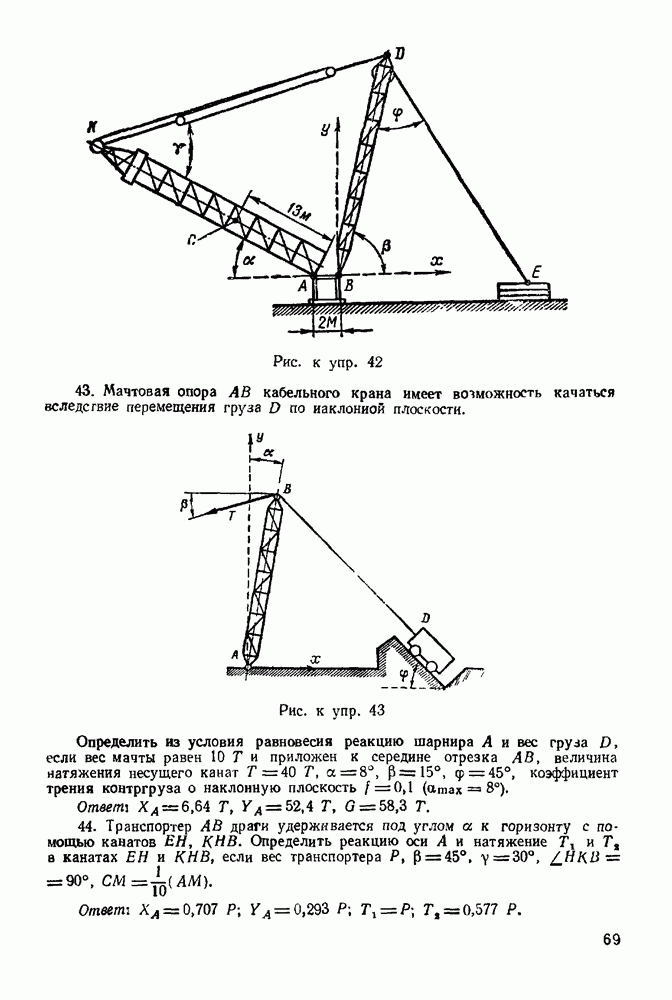
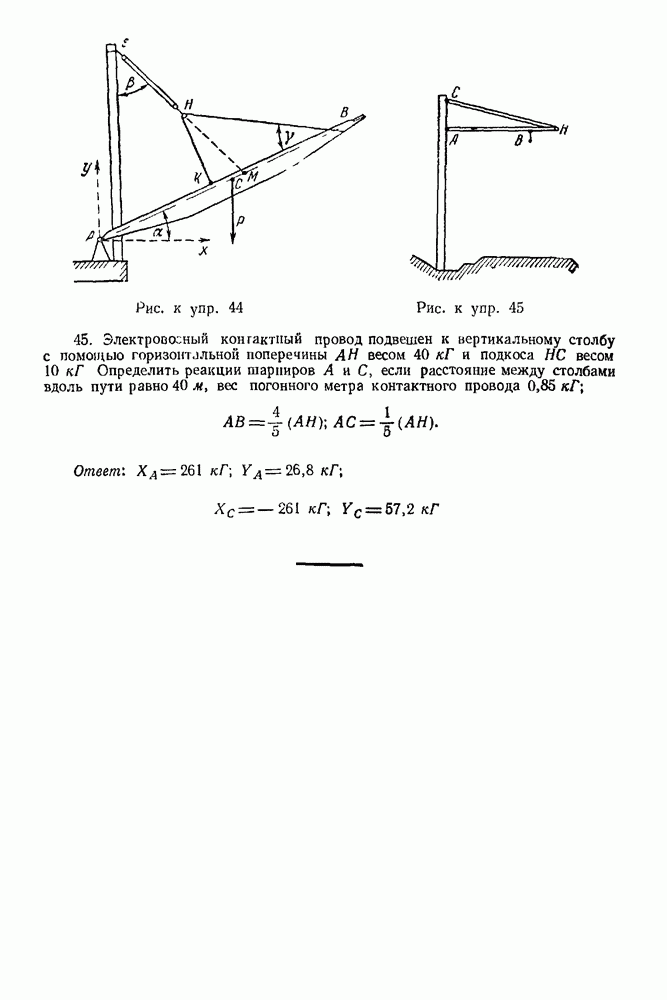
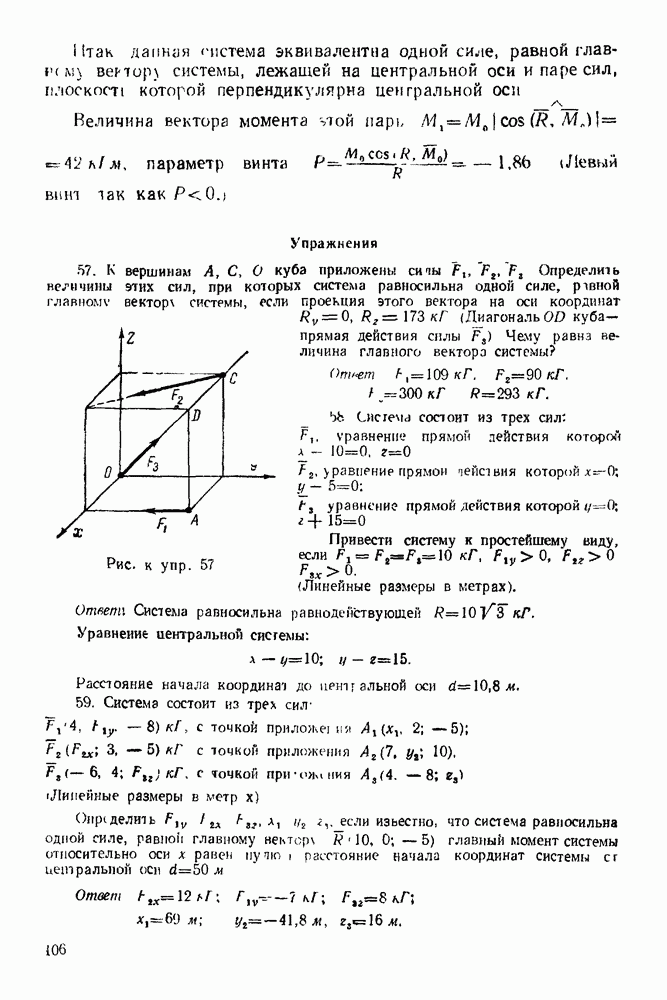
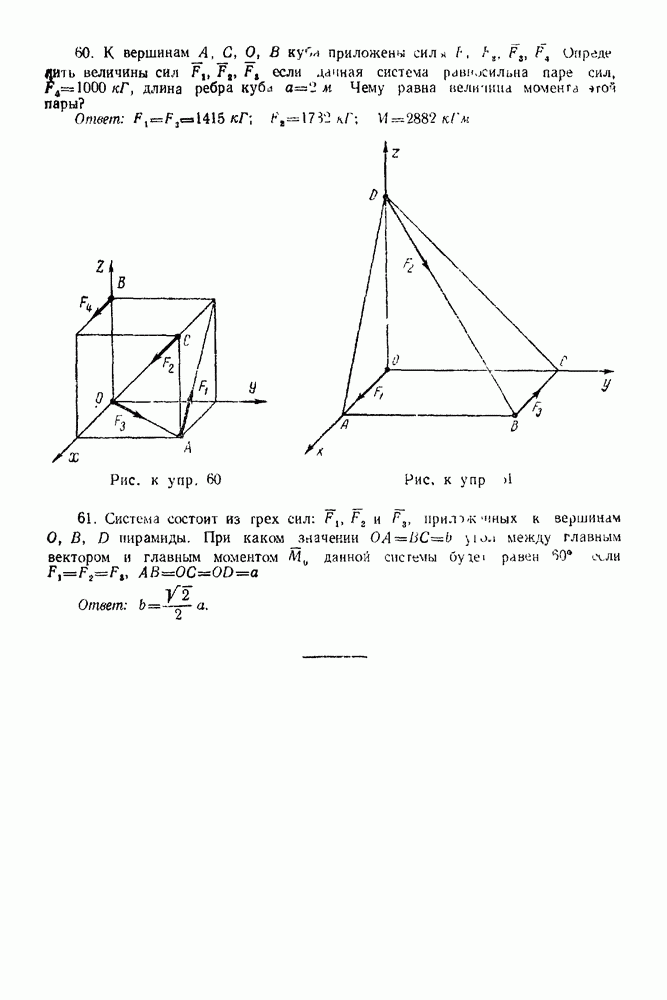
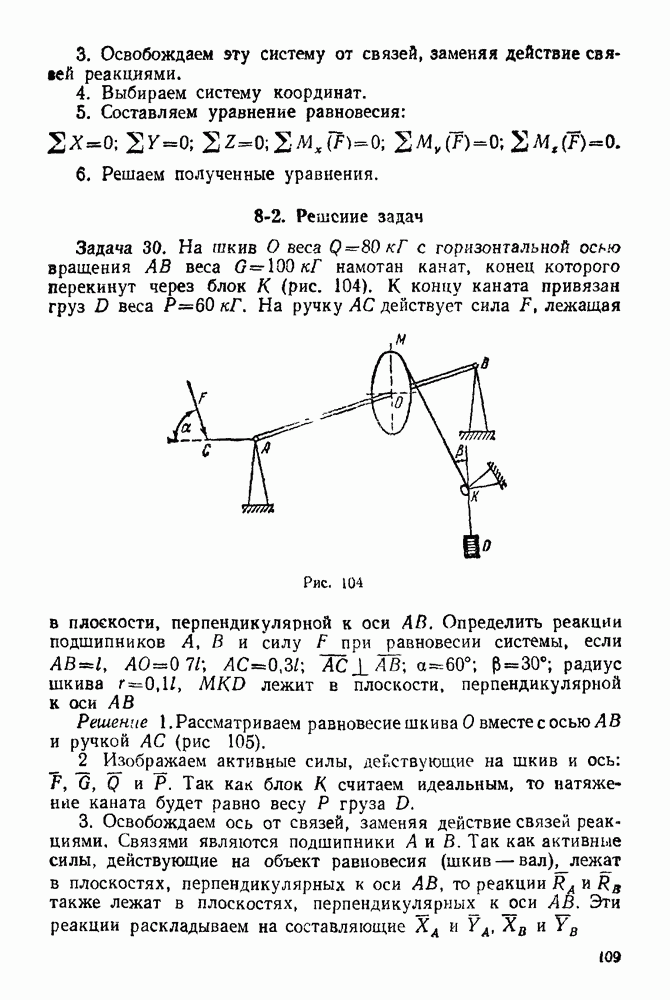
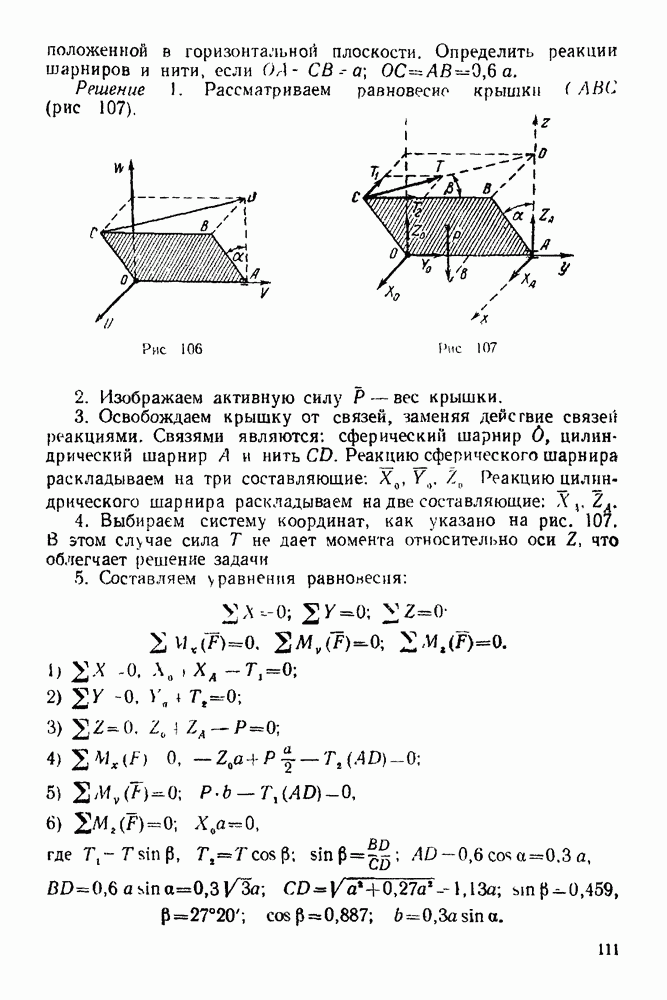
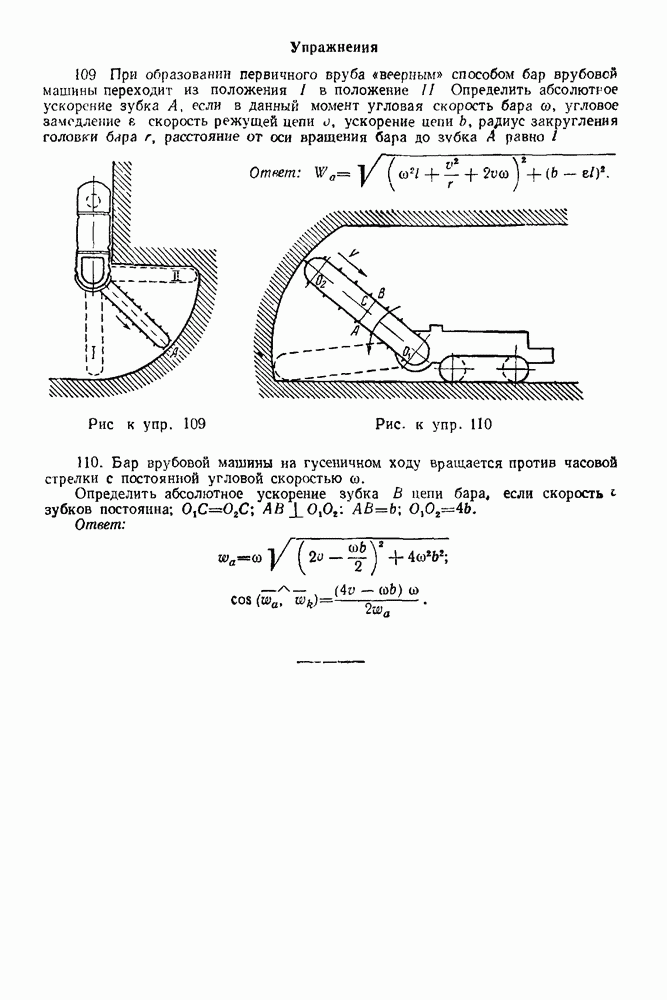
Упражнения
(см. скан)
Криволинейное движение свободной точки
1. Постоянная сила
Задача 80. Материальная точка весом  брошена со скоростью
брошена со скоростью  под углом а к горизонту. Определить, пренебрегая сопротивлением воздуха, закон движения точки.
под углом а к горизонту. Определить, пренебрегая сопротивлением воздуха, закон движения точки.
Решение. 1. Изображаем точку  в текущий момент времени (рис. 217).
в текущий момент времени (рис. 217).
2. Изображаем силы, действующие «а точку. В данном случае действует единственная сила  вес точки.
вес точки.
3. Выбираем систему координат, жак указано на рис. 217 (начало координат помещаем в месте выброса точки; вектор  лежит в плоскости
лежит в плоскости 
4. Составляем дифференциальные уравнения движения точки:  получаем следующие три дифференциальные уравнения
получаем следующие три дифференциальные уравнения


Рис. 217.
5 Интегрируем дифференциальные уравнения движения точки.

6. Составляем начальные условия задачи: при 

7. Определяем по начальным условиям произвольные постоянные интегрирования 
Из уравнений (18-11), (18-12) после подстановки в них начальных условий получим:

8. Найденные произвольные постоянные подставляем в результат интегрирования дифференциальных уравнений (18-12); получим закон движения точки или уравнение траектории точки в параметрической форме (роль параметра играет время 


Рис. 218.
После исключения параметра  из уравнений движения уравнение траектории будет иметь вид:
из уравнений движения уравнение траектории будет иметь вид:

Следовательно, материальная точка  движется по параболе» расположенной в вертикальной плоскости (рис. 218).
движется по параболе» расположенной в вертикальной плоскости (рис. 218).
2. Сила — функция скорости точки.
Задача 81. Материальная точка массы  брошена с начальной скоростью
брошена с начальной скоростью  под углом а к горизонту. Сила сопротивления воздуха
под углом а к горизонту. Сила сопротивления воздуха  где
где  постоянный коэффициент и
постоянный коэффициент и  скорость точки. Найти уравнения движения и наибольшую высоту подъема точки.
скорость точки. Найти уравнения движения и наибольшую высоту подъема точки.
Решение. 1. Изображаем точку  в текущий момент времени (рис. 219).
в текущий момент времени (рис. 219).
2. Изображаем силы, действующие на точку:  вес точки,
вес точки,  силу сопротивления воздуха, направленную в сторону, противоположную направлению скорости гочки.
силу сопротивления воздуха, направленную в сторону, противоположную направлению скорости гочки.
3. Выбираем систему координат, как указано на рис. 219. Начало координат помещаем в месте выброса точки; вектор ил лежит в плоскости 

Рис. 219.
4. Составляем дифференциальные уравнения движения точки;

Получаем следующие дифференциальные уравнения движения:

5. Интегрируем полученные дифференциальные уравнения движения точки.
После интегрирования первого уравнения имеем:

Интегрируем второе уравнение:

Интегрируем третье уравнение:


6. Составляем начальные условия для определения произвольных постоянных интегрирования 

7. Определяем произвольные постоянные по составленным начальным условиям.
После подстановки в уравнения (18-13), (18-14) и (18-15); (18-16); (18-17); (18-18) начальных условий получим:

8. Подставляем найденные произвольные постоянные в уравнения (18-14), (18-16), (18-18) и находим закон движения точки;

Для нахождения  используем то положение, что в наивысшей точке траектории вектор скорости материальной точки горизонтален (рис. 220) и, следовательно
используем то положение, что в наивысшей точке траектории вектор скорости материальной точки горизонтален (рис. 220) и, следовательно


Рис. 220.
3. Сила — функция координат движущейся точки.
Задача 82. Точка  массы
массы  притягивается неподвижным центром О с силой
притягивается неподвижным центром О с силой  где
где  постоянный коэффициент и
постоянный коэффициент и  расстояние точки
расстояние точки  от О. В начальный момент расстояние
от О. В начальный момент расстояние  а скорость направлена перпендикулярно
а скорость направлена перпендикулярно  Найти уравнение движения точки
Найти уравнение движения точки  и ее траекторию, принимая прямую
и ее траекторию, принимая прямую  за ось
за ось  и пренебрегая весом точки.
и пренебрегая весом точки.
Решение. 1. Изображаем точку  в текущий момент времени (рис. 221).
в текущий момент времени (рис. 221).

Рис. 221.
2. Изображаем силу  действующую на точку.
действующую на точку.
3. Выбираем систему координат, как указано на рис. 221.
4. Составляем дифференциальные уравнения движения точки:

но

Следовательно,

5. Интегрируем дифференциальные уравнения движения  Эти уравнения однородные линейные второго порядка с постоянными коэффициентами. Для решения такого уравнения нужно составить характеристическое уравнение и найти его корнн:
Эти уравнения однородные линейные второго порядка с постоянными коэффициентами. Для решения такого уравнения нужно составить характеристическое уравнение и найти его корнн:  где
где 
Общее решение первого уравнения будет:  где с, и с, — произвольные постоянные. Далее используем формулы Эйлера:
где с, и с, — произвольные постоянные. Далее используем формулы Эйлера:

Получаем:  где
где  новые произвольные постоянные. Если ввести произвольные постоянные
новые произвольные постоянные. Если ввести произвольные постоянные  связав их
связав их  получчм общие решения данных дифференциальных уравнений:
получчм общие решения данных дифференциальных уравнений: 
6 Составляем начальные условия движения для определения произвольных постоянных 
При
7. По начальным условиям движения определяем произвольные постоянные. Подставляя начальные условия задачи  общие
общие
решения дифференциальных уравнений движения точки, а также в выражения, которые получаются после дифференцирования этих решений, получим:

Из уравнения (18—20):  так как
так как 
Из уравнения (18—19):  из уравнений (18—21) и (18—22):
из уравнений (18—21) и (18—22):

Из уравнения (18—22) 
8. Подставляем найденные произвольные постоянные в общие решения дифференциальных уравнений и получаем закон движения материальной точки:

Для нахождения траектории точки исключаем время  из уравнений движения. С этой целью находим
из уравнений движения. С этой целью находим  затем, возводим в квадрат и складываем:
затем, возводим в квадрат и складываем:

Следовательно, точка движется по эллипсу (рис. 222).

Рис. 222.
Криволинейное движение не свободной точки
Задача 83 Колечко скользит под действием собственного веса по проволочной окружности радиуса  расположенной в вертикальной плоскости, выходя без начальной скорости из конца горизонтального диаметра Зная коэффициент трения
расположенной в вертикальной плоскости, выходя без начальной скорости из конца горизонтального диаметра Зная коэффициент трения  колечка об окружность, определить скорость прохождения колечка через нижнюю точку окружности.
колечка об окружность, определить скорость прохождения колечка через нижнюю точку окружности.
Решение 1. Изображаем точку  в текущий момент времени (рис. 223).
в текущий момент времени (рис. 223).
2. Изображаем активную силу  вес точки.
вес точки.
3. Освобождаем точку  от связей, заменяя действие связи реакцией. Связью является шероховатая окружность. Реакцию окружности раскладываем на две составляющие:
от связей, заменяя действие связи реакцией. Связью является шероховатая окружность. Реакцию окружности раскладываем на две составляющие:  нормальная
нормальная
составляющая и  касательная составляющая (сила трения скольжения).
касательная составляющая (сила трения скольжения).
4. Выбираем систему координат, как указано на рис. 223 (оси естественного трехгранника).
5. Составляем дифференциальные уравнения движения точки в естественной форме:


Рис. 223.
Из уравнений (1) и (2) получаем:

но  следовательно, Так как
следовательно, Так как  то дифференциальное уравнение движения точки принимает вид:
то дифференциальное уравнение движения точки принимает вид:

6. Интегрируем дифференциальное уравнение движения точки. Это уравнение можно представить в следующем виде:

Общее решение этого уравнения  где
где  общее решение однородного дифференциального уравнения;
общее решение однородного дифференциального уравнения;  частное решение данного дифференциального уравнения:
частное решение данного дифференциального уравнения:

Частное решение ищем в следующем виде:

Это решение должно обращать дифференциальное уравнение (18-23) в тождество. Отсюда находим коэффициенты  и В:
и В:

Итак, общее решение дифференциального уравнения (18-23) имеет следующий вид;

где  имеют вышенайденные значения.
имеют вышенайденные значения.
7. Составляем начальные условия для определения произвольной постоянной С.
При 
8. Определяем произвольную постоянную интегрирования. После подстановки начальных условий движения в уравнение (18-24) получим 
9. Подставляем найденную произвольную постоянную в уравнение (18-24):

Когда материальная точка проходит нижнюю точку кольца, то 

Упражнения
(см. скан)
(см. скан)
Прямолинейные колебания материальной точки
1. Гармонические колебания
Задача 84. Пружина закреплена в точке А, ко второму концу пружины прикреплен груз  веса
веса  Статическое удлинение
Статическое удлинение  пружины, вызываемое этим грузом, равно 6 см. Пренебрегая сопротивлениями, определить закон движения груза, если вначале пружина была недеформирована и груз был предоставлен самому себе (рис. 224):
пружины, вызываемое этим грузом, равно 6 см. Пренебрегая сопротивлениями, определить закон движения груза, если вначале пружина была недеформирована и груз был предоставлен самому себе (рис. 224): 
Решение. 1. Изображаем груз  в текущий момент времени (рис. 225).
в текущий момент времени (рис. 225).
2. Изображаем силы, действующие на груз М:  вес груза
вес груза  силу упругости пружины.
силу упругости пружины.

Рис. 224.

Рис. 225.

Рис. 226.
3. Выбираем систему координат, как указано на рис. 225. Для упрощения решения задачи начало координат рекомендуется помещать в положении статического равновесия груза. На рис. 225 имеем следующее:  длина недеформированной пружины;
длина недеформированной пружины;  статическое удлинение пружины под действием данного груза
статическое удлинение пружины под действием данного груза  положение статического равновесия груза.
положение статического равновесия груза.
4. Составляем дифференциальное уравнение движения груза (груз можно считать материальной точкой, так как он движется поступательно):

Сила упругости пропорциональна удлинению пружины (рассматриваем малые удлинения):

Для упрощения правой части рассматриваем равновесие груза в положении статического равновесия  (рис. 226):
(рис. 226):

Следовательно,

получаем:

5. Решаем дифференциальное уравнение движения груза:

Общее решение этого дифференциального уравнения имеет следующий вид:

6. Составляем начальные условия движения для определения произвольных постоянных  .
.
При 
7. Определяем произвольные постоянные интегрирования по начальным условиям движения. Для этого подставляем начальные условия в выражения:

получаем:

Из уравнений (18-28) и (18-29):

8. Найденные произвольные постоянные подставляем в общее решение  дифференциального уравнения движения точки и получаем:
дифференциального уравнения движения точки и получаем:

где  определяем из уравнения равновесия (18-25):
определяем из уравнения равновесия (18-25):

Груз  совершает прямолинейные гармонические колебания. Период колебания
совершает прямолинейные гармонические колебания. Период колебания

2. Затухающие колебания
Задача 85. Тело  весом
весом  подвешено на пружине, статическое удлинение
подвешено на пружине, статическое удлинение  которой под действием этого веса равно 1 см (рис. 227). Второй конец пружины закреплен в неподвижной точке А. Сила сопротивления воздуха при движении тела пропорциональна скорости и при скорости в
которой под действием этого веса равно 1 см (рис. 227). Второй конец пружины закреплен в неподвижной точке А. Сила сопротивления воздуха при движении тела пропорциональна скорости и при скорости в  равна
равна
 Определить закон движения грза. если вначале пружина была растянута на
Определить закон движения грза. если вначале пружина была растянута на  и груз был предоставлен самому себе.
и груз был предоставлен самому себе. 
Решение. 1. Изображаем точку  в текущий момент времени (рис. 228). Тело можно считать материальной точкой, так как оно движется поступательно.
в текущий момент времени (рис. 228). Тело можно считать материальной точкой, так как оно движется поступательно.
2. Изображаем силы, действующие на точку:  вес точки,
вес точки,  силу сопротивления воздуха и
силу сопротивления воздуха и  силу упругости пружины.
силу упругости пружины.
3 Выбираем систему координат, как указано на рис. 228. Как и в задаче 84, начало координат помещаем в положении  статического равновесия груза, причем АВ — длина недеформированной пружины,
статического равновесия груза, причем АВ — длина недеформированной пружины,  статическое удлинение пружины.
статическое удлинение пружины.

Рис. 227.

Рис. 228.

Рис. 229.
4. Составляем дифференциальное уравнение движения точки 
(см. скан)
Для упрощения правой части полученного уравнения рассматриваем равновесие груза (рис. 229):

следовательно,

Дифференциальное уравнение движения груза будет иметь вид.

где

5. Интегрируем дифференциальное уравнение (18-31) движения груза. Это уравнение — линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Находим корни характеристического уравнения:

Поэтому

Общее решение дифференциального уравнения будет:

После преобразования по формулам Эйлера будем иметь:

6. Составляем начальные условия движения для определения произвольных постоянных 
При 
7. Определяем произвольные постоянные интегрирования по начальным условиям задачи. Для этого составленные начальные условия подставляем в уравнение (18-32) и в уравнение, полученное из уравнения (18-32) путем дифференцирования его по времени, получим

8. Найденные произвольные постоянные подставляем в уравнение (18-32) и получаем закон движения груза:

3. Вынужденные колебания.
Задача 86. (Сопротивление среды отсутствует; нерезонансный случай.)

Рис. 230.
Материальная точка массы  совершает прямолинейные" колебания по оси х под действием восстанавливающей силы, пропорциональной расстоянию точки от начала координат, причем коэффициент пропорциональности равен 8, и возмущающей силы
совершает прямолинейные" колебания по оси х под действием восстанавливающей силы, пропорциональной расстоянию точки от начала координат, причем коэффициент пропорциональности равен 8, и возмущающей силы  Найти закон движения точки, если в начальный момент
Найти закон движения точки, если в начальный момент 
Решение. 1. Изображаем точку  в текущий момент времени (рис. 230).
в текущий момент времени (рис. 230).
2. Изображаем силы, действующие на точку:  восстанавливающая сила, 5 — возмущающая сила (весом точки пренебрегаем).
восстанавливающая сила, 5 — возмущающая сила (весом точки пренебрегаем).
8. Выбираем систему координат, как указано на рис. 230
4. Составляем дифференциальное уравнение движения точки

5. Интегрируем дифференциальное уравнение движения точки  Это уравнение — неоднородное линейное с постоянными коэффициентами, дифференциальное уравнение второго порядка. Его решение
Это уравнение — неоднородное линейное с постоянными коэффициентами, дифференциальное уравнение второго порядка. Его решение  где
где  общее решение однородного дифференциального уравнения
общее решение однородного дифференциального уравнения  следовательно,
следовательно,  частное решение дифференциального уравнения
частное решение дифференциального уравнения  Берем
Берем  причем коэффициент
причем коэффициент  находим из того условия, что
находим из того условия, что  обращает данное дифференциальное уравнение в тождество. Следовательно,
обращает данное дифференциальное уравнение в тождество. Следовательно,  .
.
Таким образом, общее решение дифференциального уравнения будет:

6. Составляем начальные условия задачи для определения произвольных постоянных  .
.
При 
7. Определяем произвольные постоянные по начальным условиям. Для этого начальные условия подставляем в выражение (18-33) и в выражение  полученное из (18-33) путем его дифференцирования. Тогда
полученное из (18-33) путем его дифференцирования. Тогда 
8. Подставляем найденные произвольные постоянные в общее решение дифференциального уравнения движения точки и получим закон движения точки:

Задача 87. (Случай резонанса). Тело веса  прикреплено к пружине, второй конец которой прикреплен к неподвижной точке А. Определить закон движения груза, если для растяжения пружины на 1 см требуется сила в
прикреплено к пружине, второй конец которой прикреплен к неподвижной точке А. Определить закон движения груза, если для растяжения пружины на 1 см требуется сила в  на тело действует возмущающая сила
на тело действует возмущающая сила  см; вначале пружина была растянута на
см; вначале пружина была растянута на  см, и тело находилось в покое. Сопротивлением воздуха пренебречь.
см, и тело находилось в покое. Сопротивлением воздуха пренебречь.

Решение. 1. Изображаем тело  в текущий момент времени (рис. 231).
в текущий момент времени (рис. 231).
2. Изображаем силы, действующие на тело:  вес тела,
вес тела,  сила упругости пружины,
сила упругости пружины,  возмущающая сила.
возмущающая сила.
3. Выбираем систему координат, как указано на рис. 231. АВ - недеформированная длина пружины,  положение статического равновесия груза,
положение статического равновесия груза,  статическое удлинение пружины.
статическое удлинение пружины.
4. Составляем дифференциальное уравнение движения груза (груз можно считать за точку, так как он движется поступательно).

Но из условия равновесия груза в положении  статического равновесия заключаем, что
статического равновесия заключаем, что  дифференциальное уравнение движения груза будет иметь вид:
дифференциальное уравнение движения груза будет иметь вид:

где


Рис. 231.
5. Решаем дифференциальное уравнение движения груза:

В данном случае  следовательно, имеет место явление, называемое резонансом. Общее решение дифференциального уравнения ищем в виде
следовательно, имеет место явление, называемое резонансом. Общее решение дифференциального уравнения ищем в виде  где
где  решение однородного уравнениях
решение однородного уравнениях  следовательно,
следовательно,  частное решение данного дифференциального уравнения ищем в виде:
частное решение данного дифференциального уравнения ищем в виде:

Коэффициенты  находим из того условия, что
находим из того условия, что  обращает неоднородное дифференциальное уравнение в тождество. Получим:
обращает неоднородное дифференциальное уравнение в тождество. Получим:

6. Составляем начальные условия.

7. Определяем произвольные постоянные а и а по начальным условиям.
Для этого подставляем начальные условия движения в выражение (18-34) и в выражение

полученное из выражения (18-34) путем дифференцирования: 
8. Подставляя найденные произвольные постоянные в общее решение (18-34) дифференциального уравнения движения точки, получаем закон движения точки:

Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
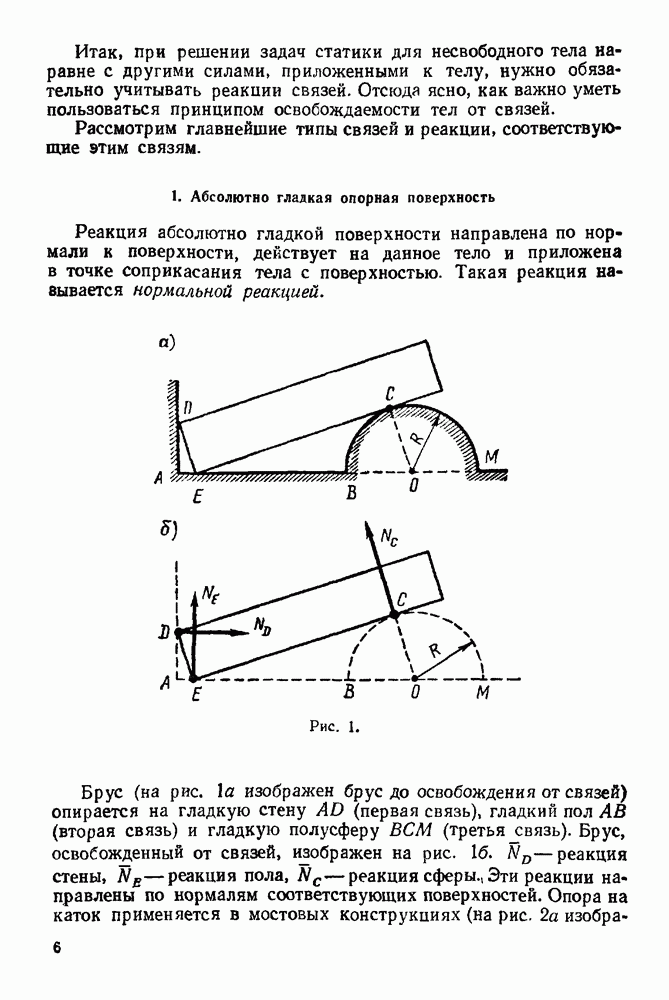
- 1. Абсолютно гладкая опорная поверхность
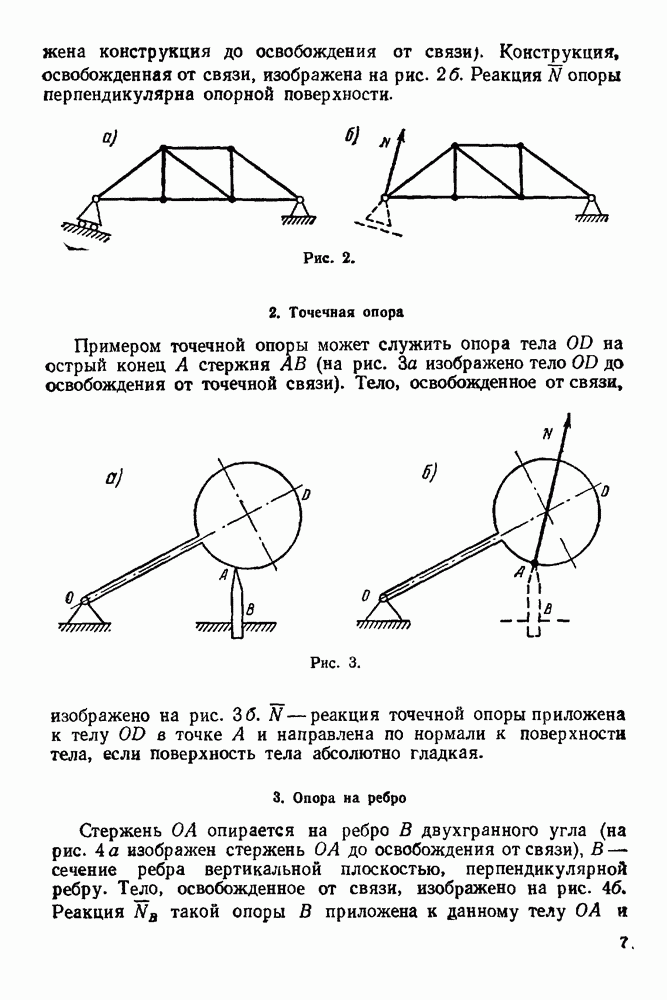
- 2. Точечная опора
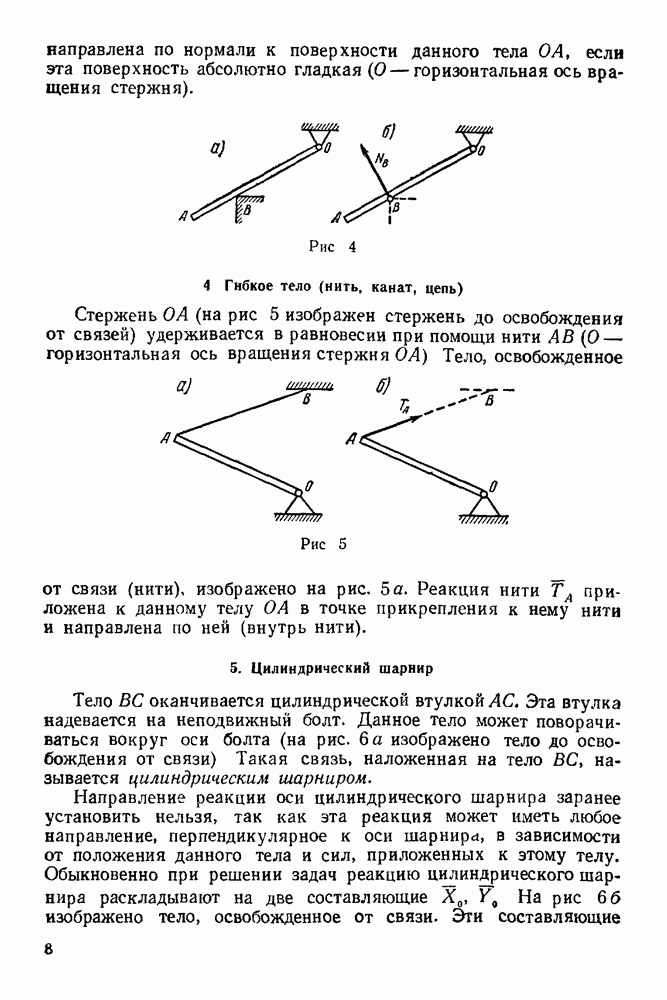
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
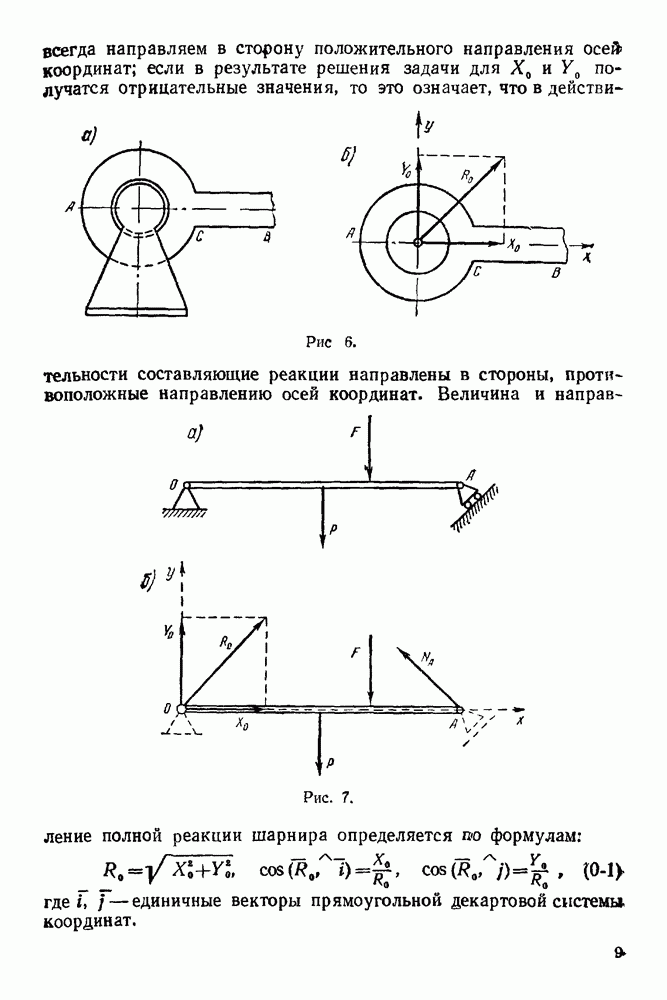
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
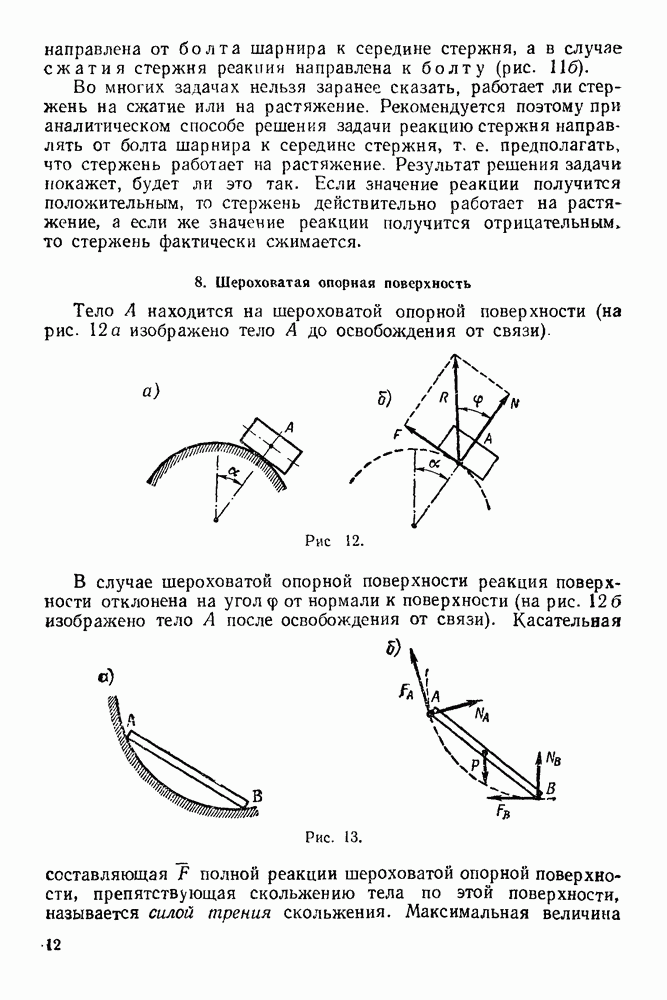
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
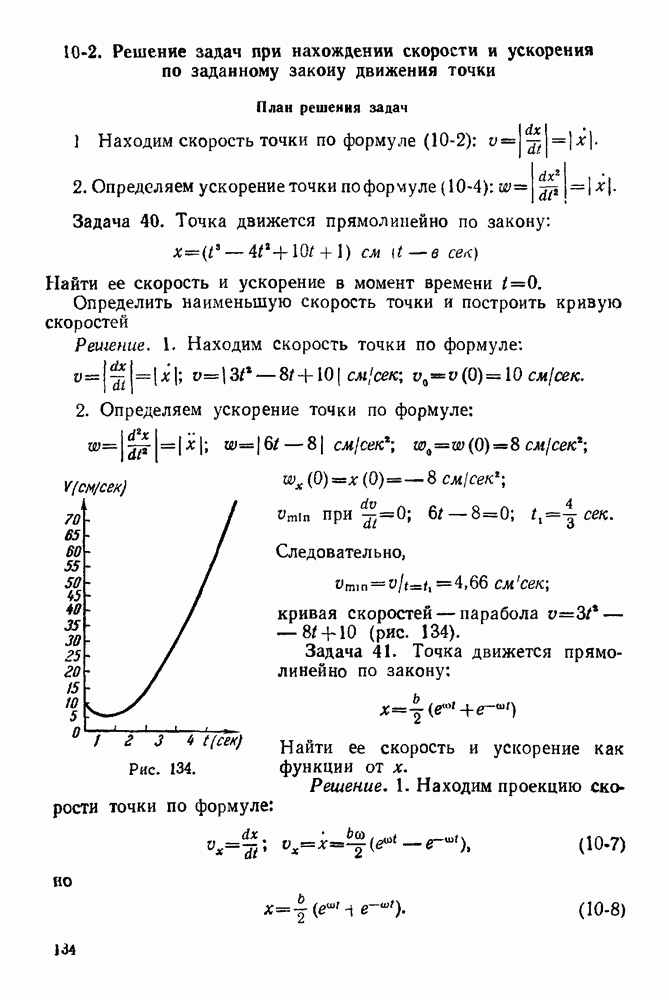
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
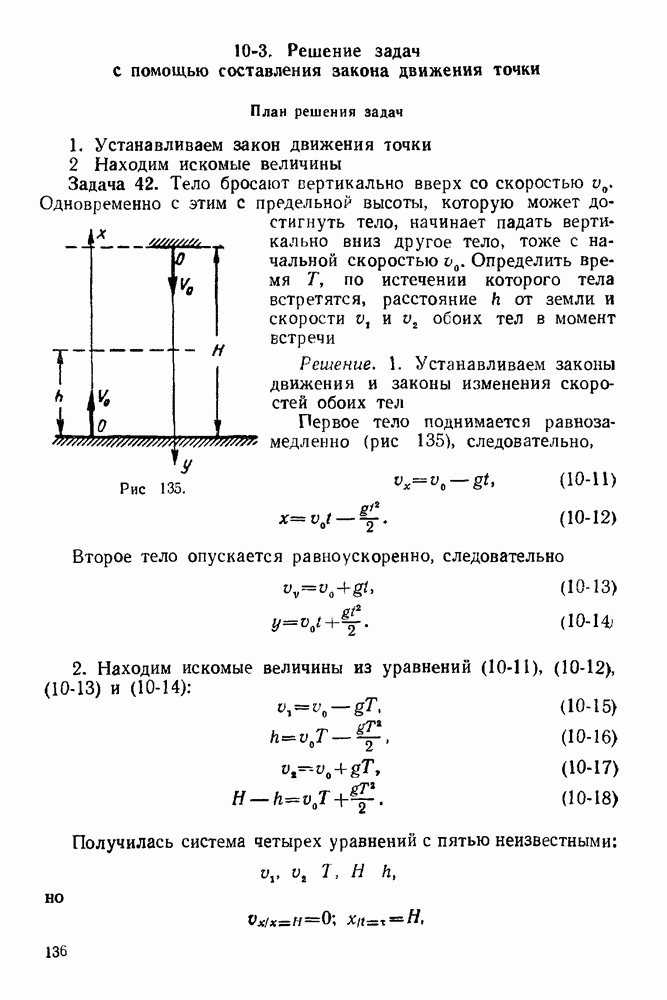
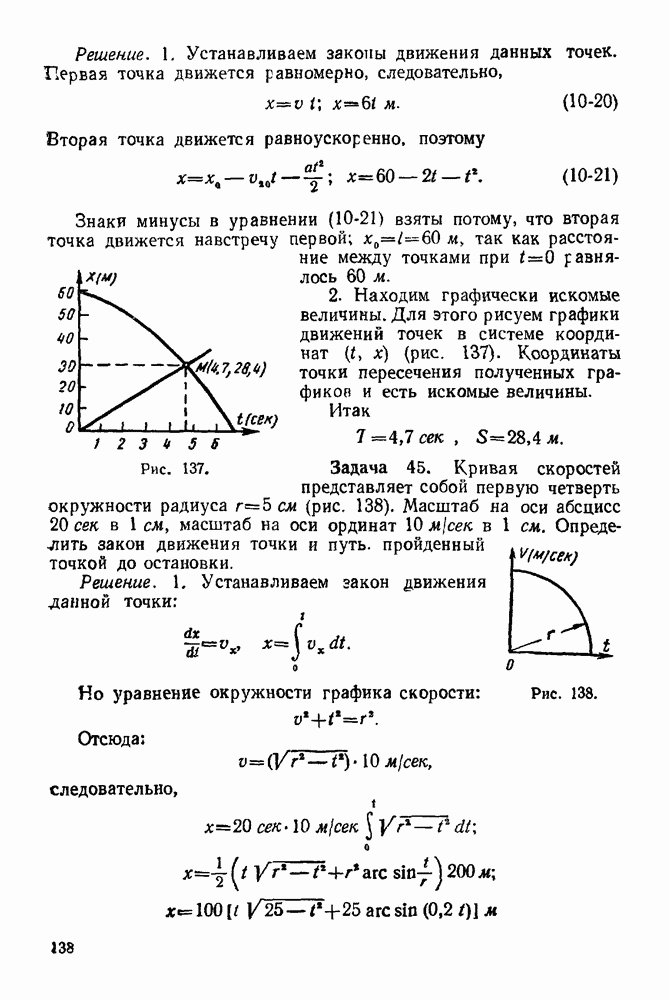
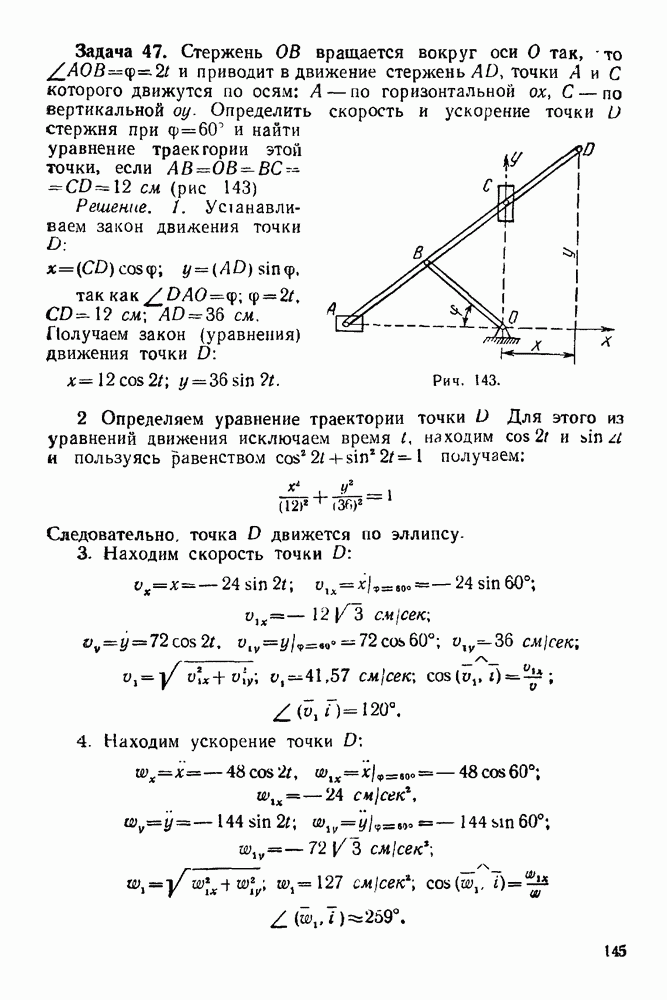
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР