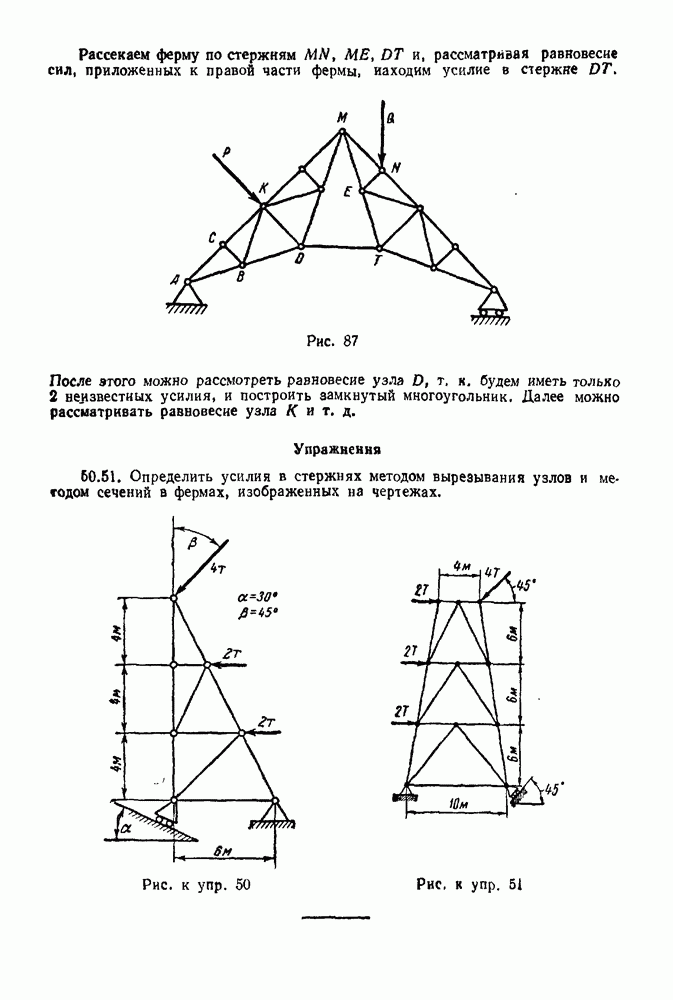
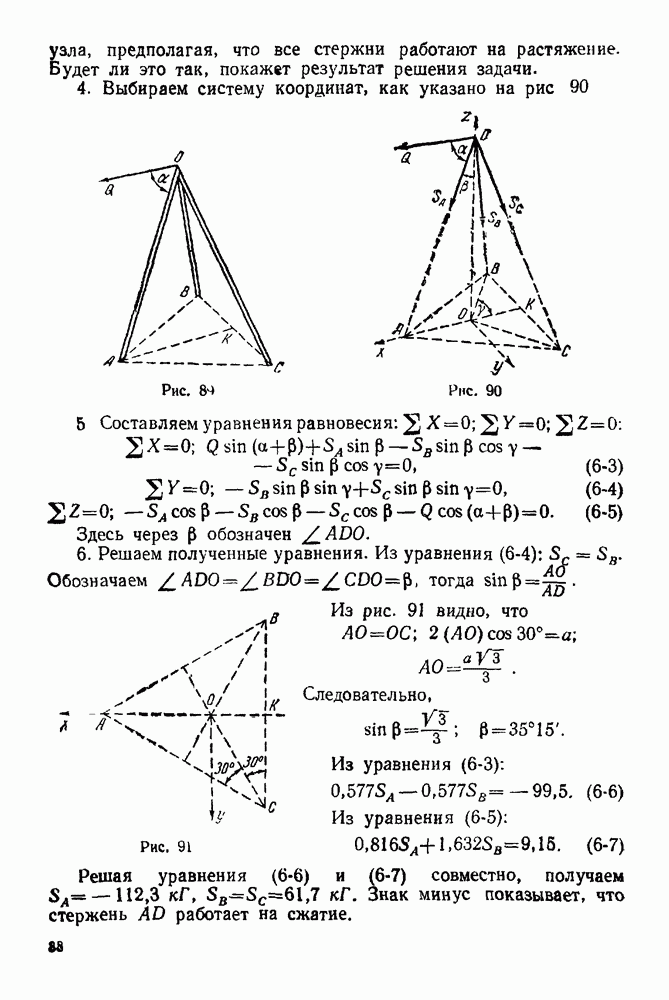
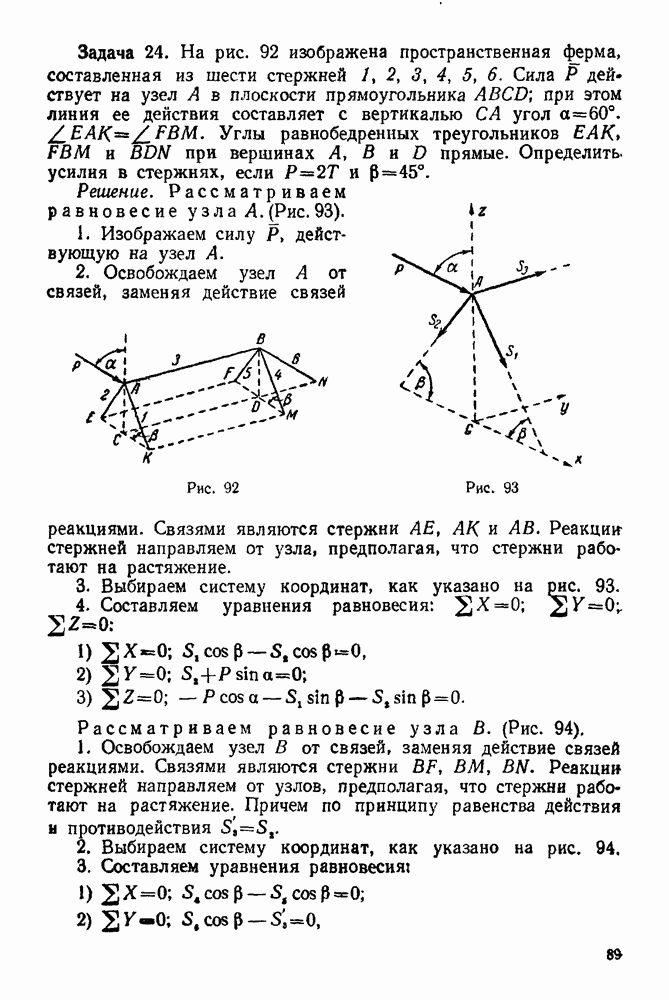
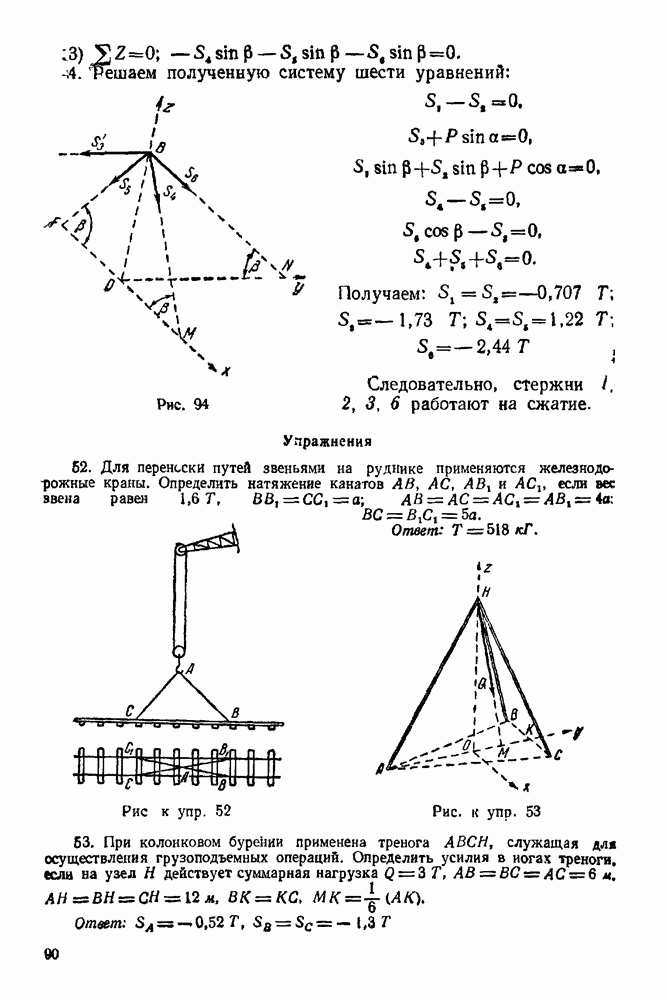
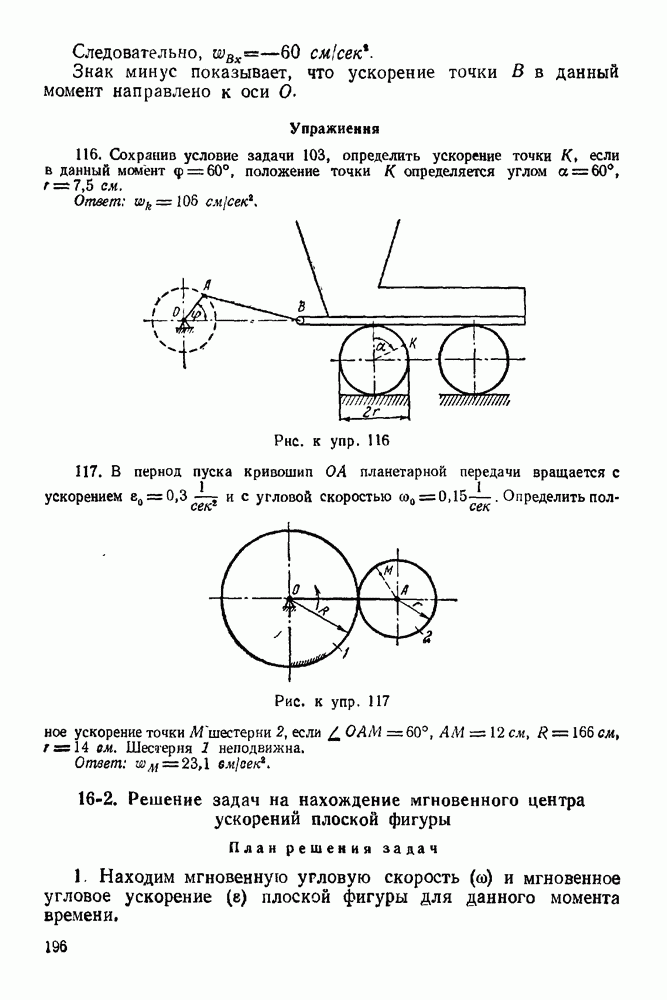
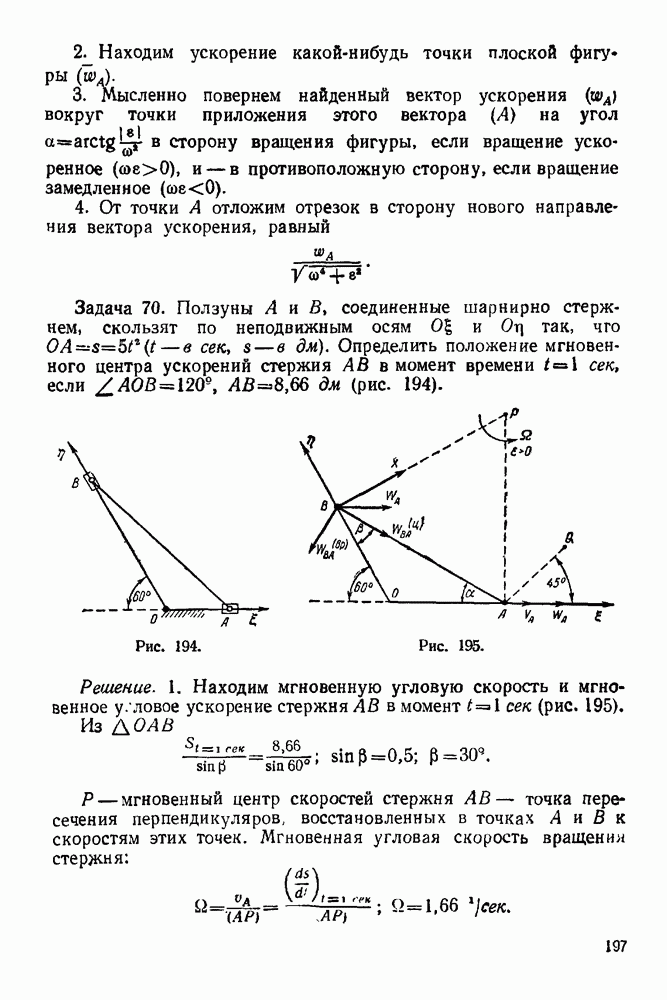
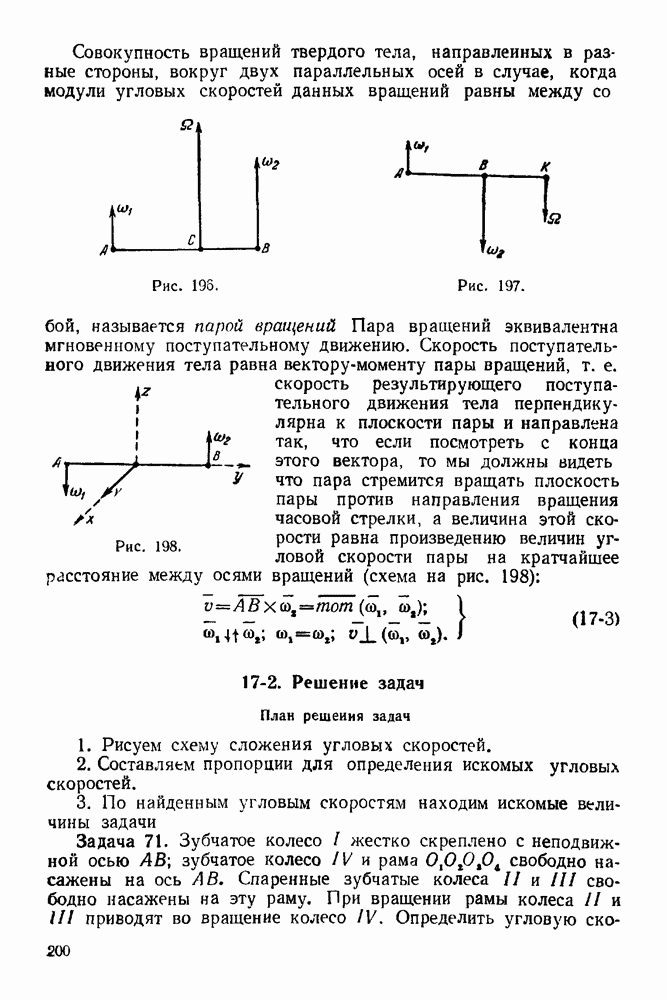
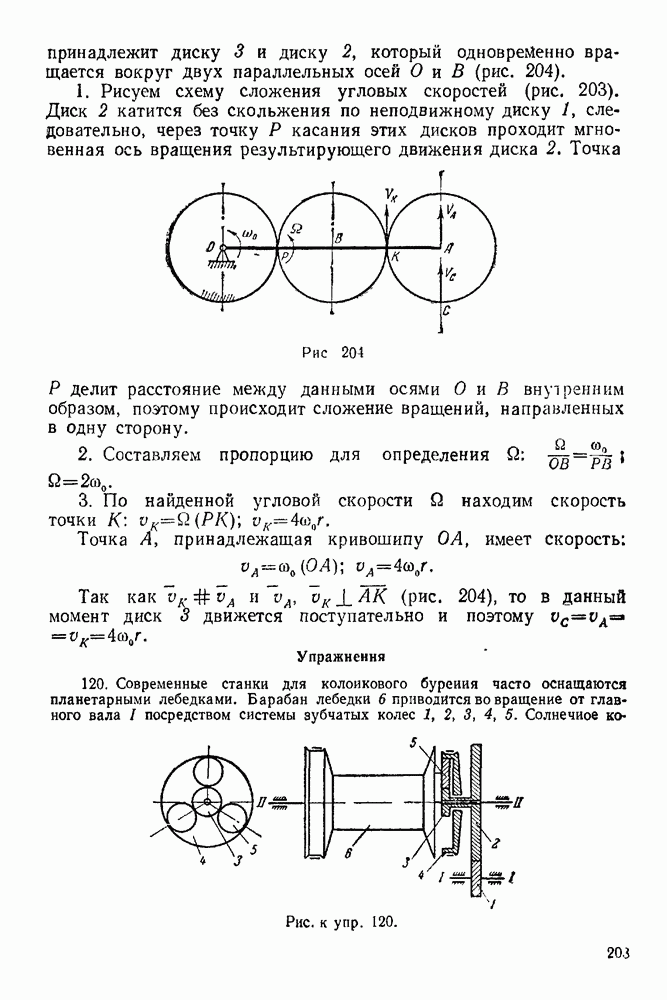
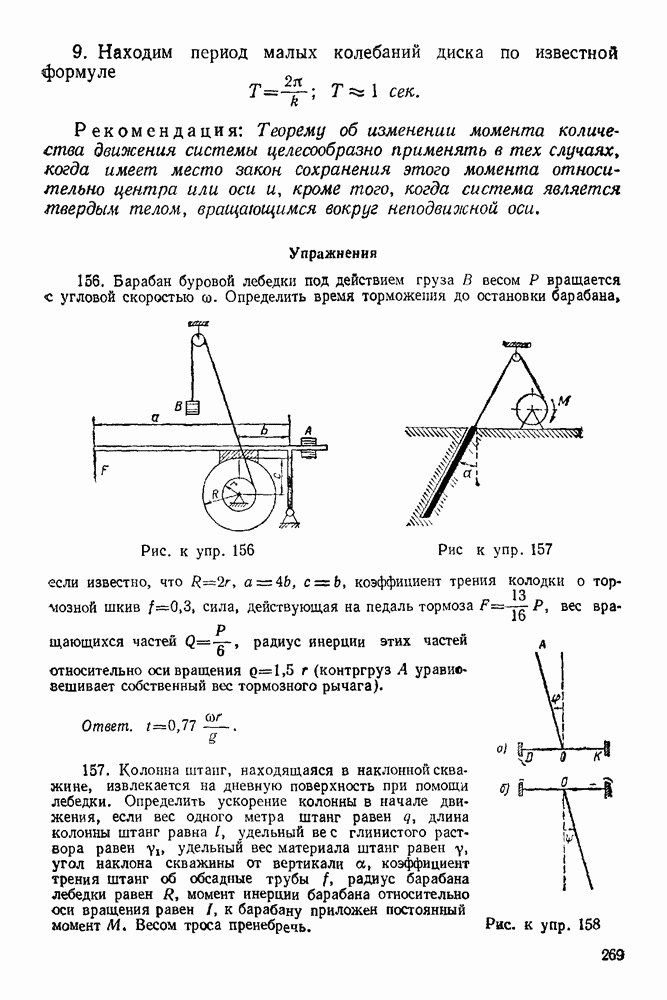
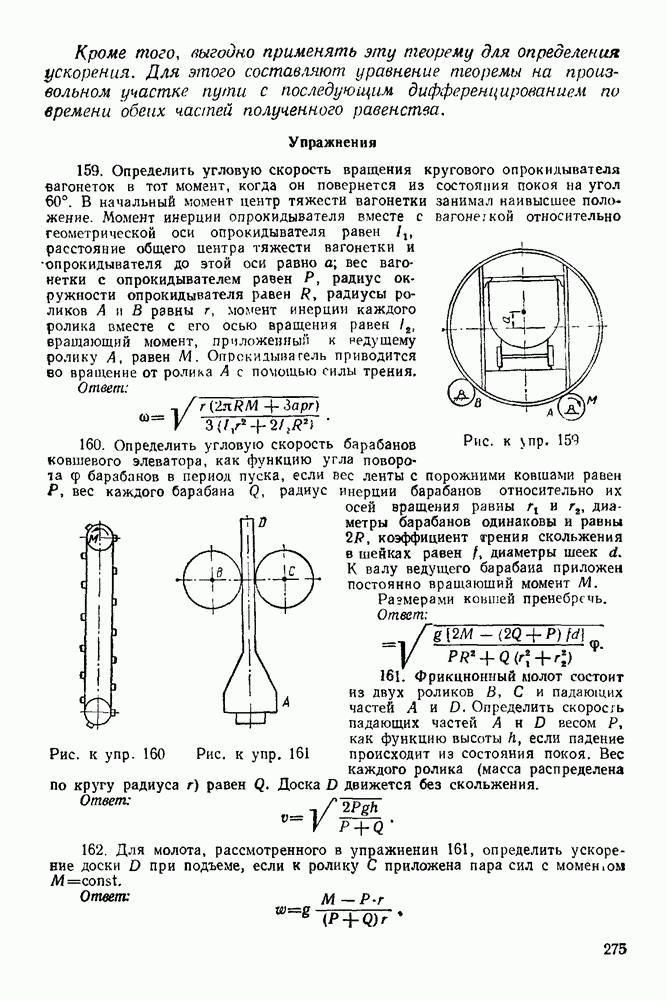
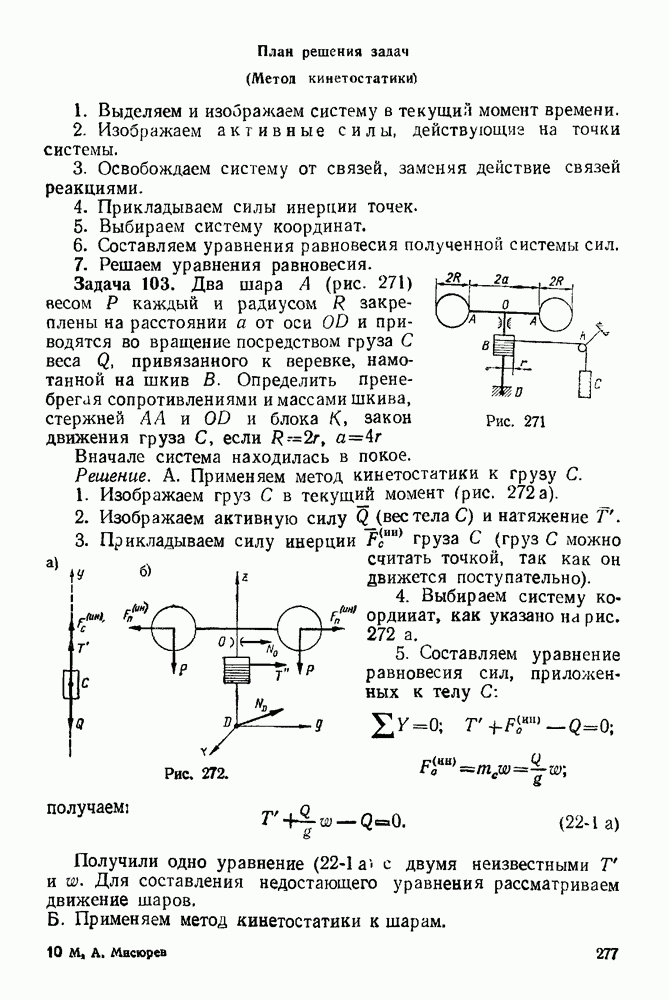
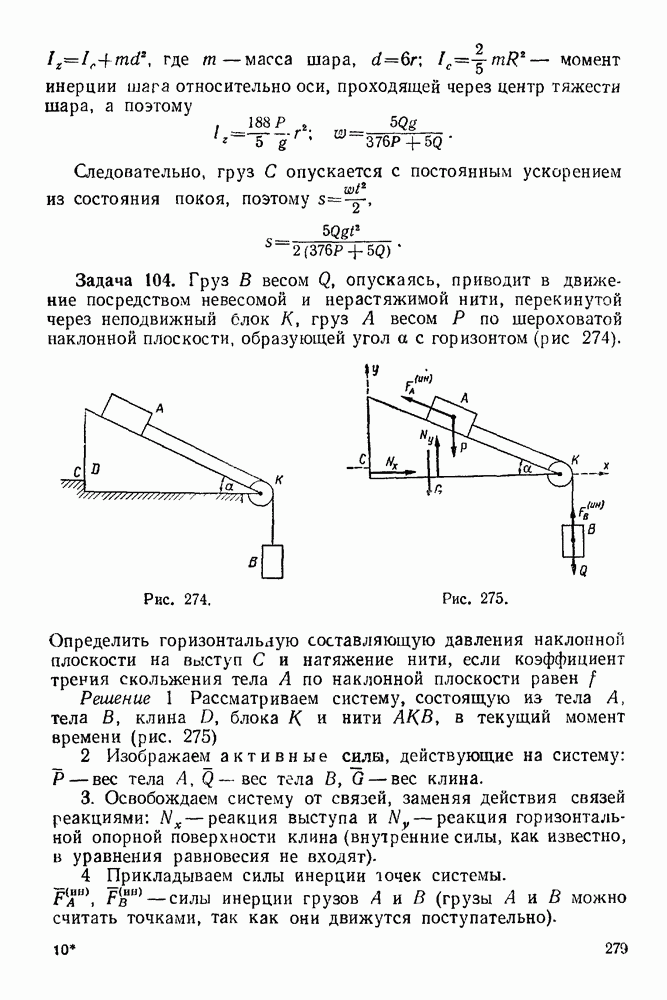
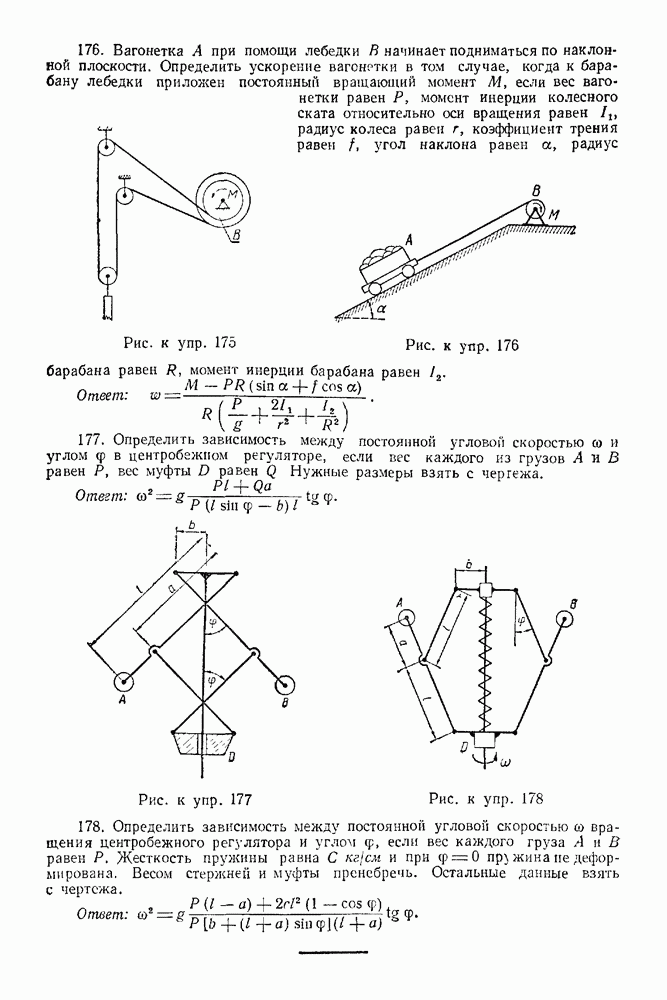
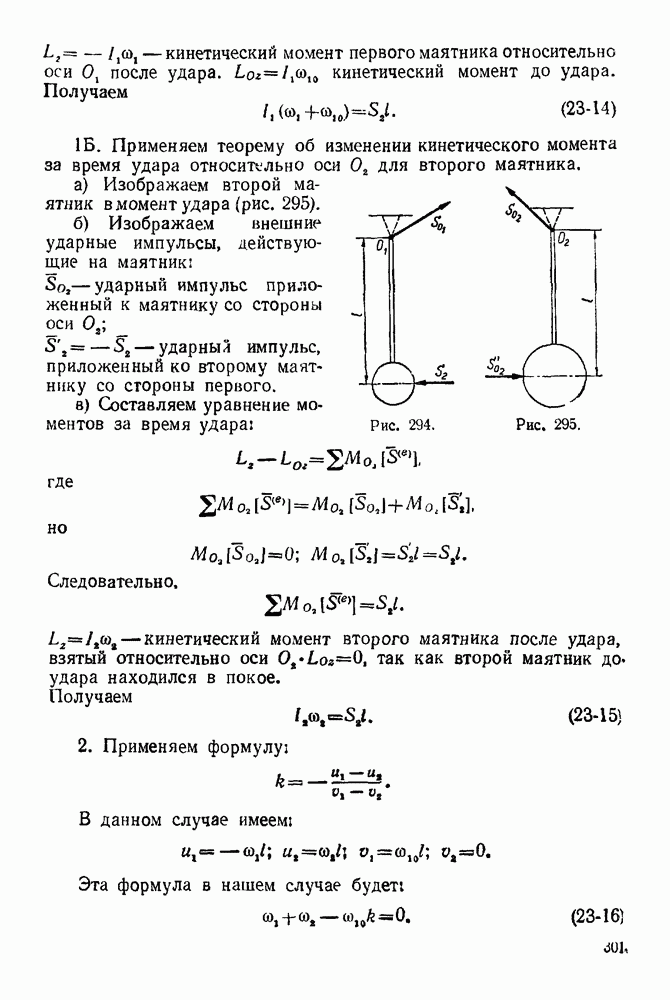
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
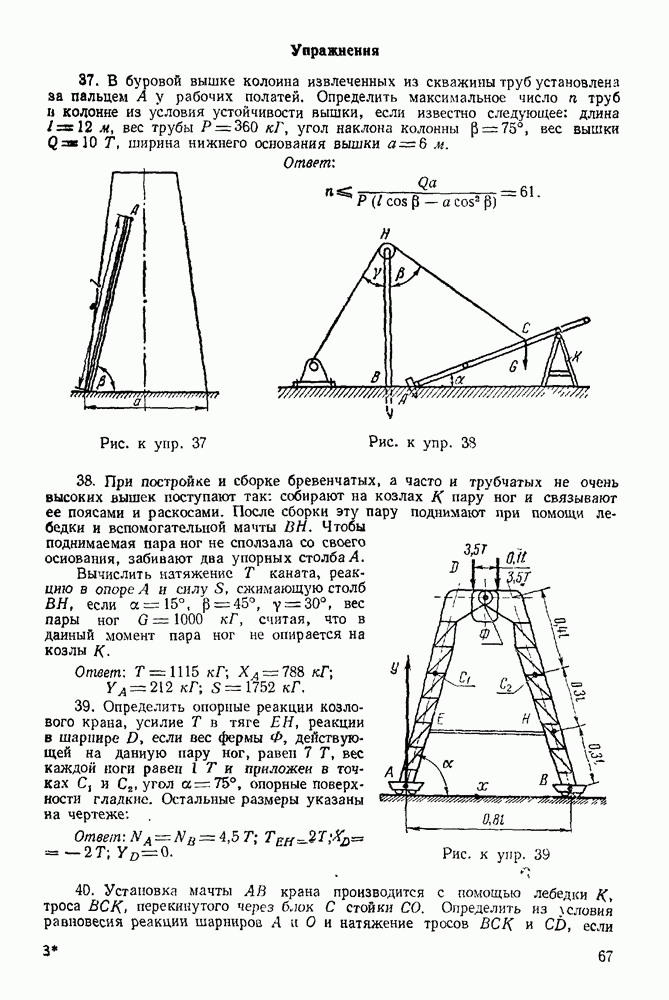
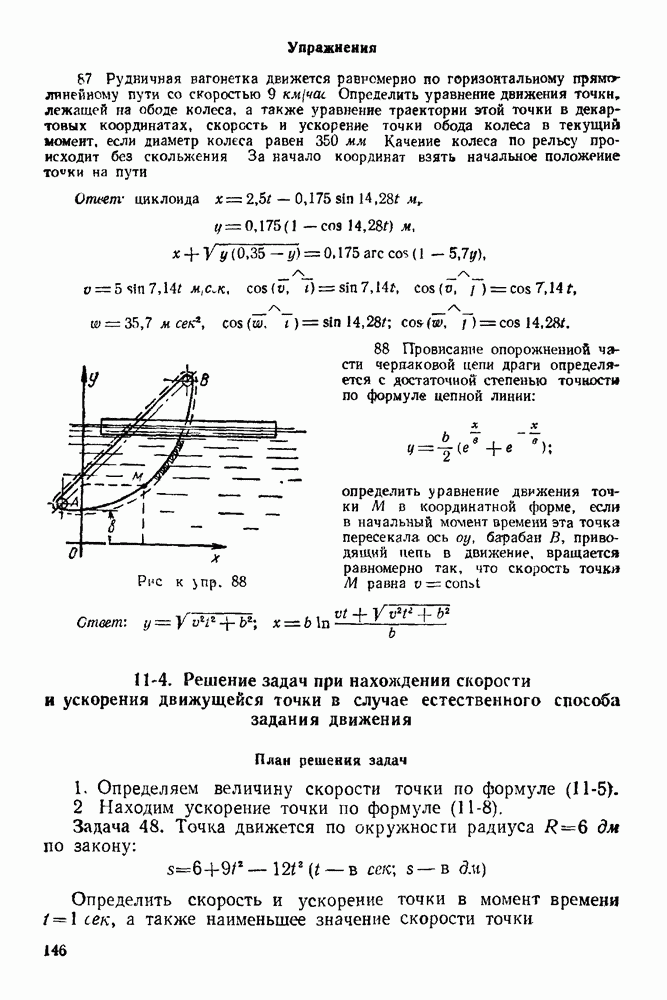
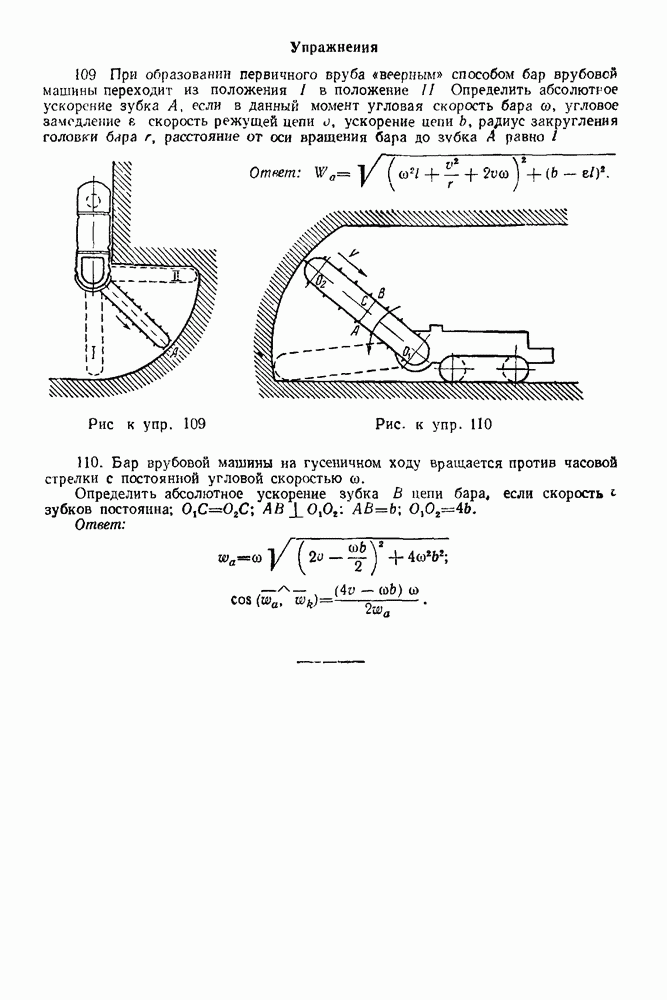
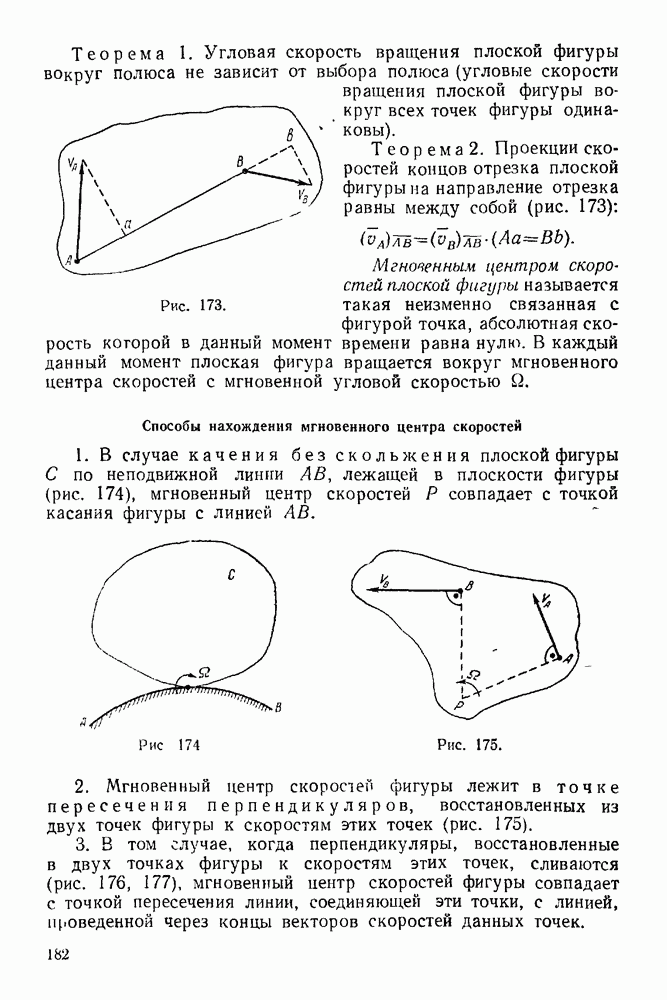
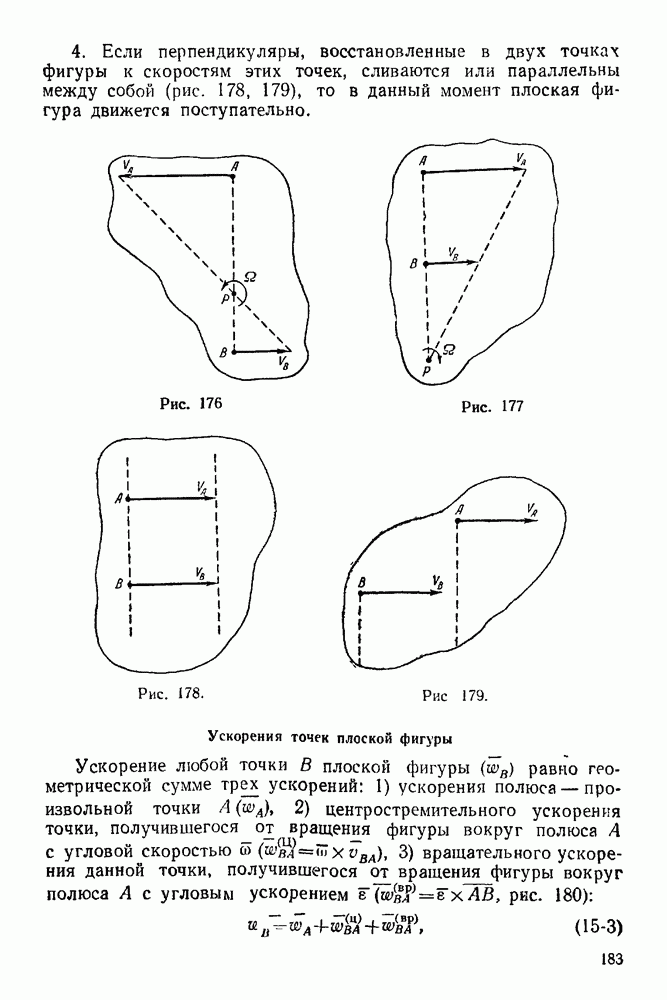
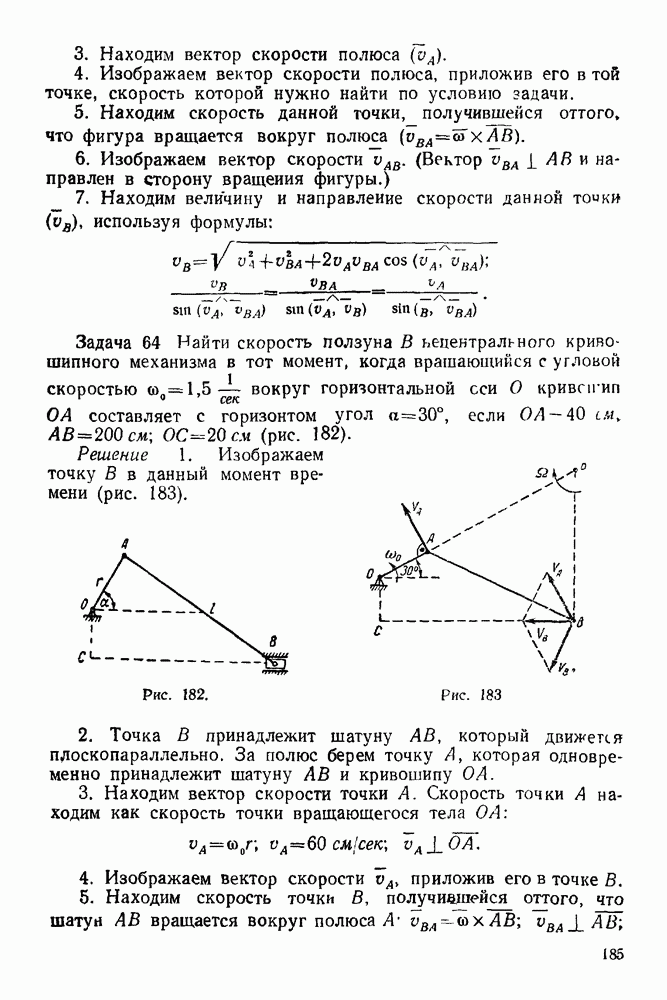
Часть третья. ДИНАМИКА
VII. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ГЛАВА XVIII. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
18-1. Основные положения. Дифференциальные уравнения движения материальной точки
В разделе «Динамика» изучается механическое движение материальных тел в связи с приложенными к ним силами. В целях большей систематичности изложения материала, динамика делится на динамику материальной точки и системы материальных точек. Материальной точкой называется тело таких малых размеров, что можно пренебречь скоростями и ускорениями в его вращательном движении по сравнению с кинематическими элементами поступательного движения.
Масса материальной точки равна ее весу, разделенному на ускорение силы тяжести, в данном месте земной поверхности:

Физические величины в механике измеряются или в технической системе единиц или в системе CGS. В основе технической системы лежат: единица длины — метр  единица времени секунда (сек) и единица силы — килограмм
единица времени секунда (сек) и единица силы — килограмм  Единица массы — производная от этих трех единиц. Единицей массы в технической системе является такая масса, которой сила, равная
Единица массы — производная от этих трех единиц. Единицей массы в технической системе является такая масса, которой сила, равная  сообщает ускорение, равное
сообщает ускорение, равное 
В основе системы CGS лежат: единица длины — сантиметр (см), единица времени — секунда (сек) и единица массы — грамм-масса  т. е. масса 1 кубического сантиметра чистой воды при нормальном барометрическом давлении (
т. е. масса 1 кубического сантиметра чистой воды при нормальном барометрическом давлении (
и при температуре  Единица силы — дина
Единица силы — дина  есть производная от этих единиц. Дина — такая сила, которая массе, равной
есть производная от этих единиц. Дина — такая сила, которая массе, равной  сообщает ускорение, равное
сообщает ускорение, равное 

Дифференциальные уравнения движения материальной точки в декартовых координатах:

где  координаты движущейся точки,
координаты движущейся точки,  — проекции на оси неподвижной декартовой прямоугольной системы координат равнодействующей всех сил, действующих на материальную точку.
— проекции на оси неподвижной декартовой прямоугольной системы координат равнодействующей всех сил, действующих на материальную точку.
Дифференциальные уравнения движения материальной точки в естественной форме:

где  радиус кривизны траектории точки;
радиус кривизны траектории точки;  проекции соответственно на касательную, главную нормаль и бинормаль к траектории точки равнодействующей всех сил, действующих на материальную точку.
проекции соответственно на касательную, главную нормаль и бинормаль к траектории точки равнодействующей всех сил, действующих на материальную точку.
В частном случае прямолинейного движения точки, для упрощения решения задачи, при составлении дифференциальных уравнений (18-2) движения рекомендуется одну из осей координат направлять по траектории точки в сторону движения. В случае плоского движения точки систему координат  нужно брать в плоскости движения, причем так, чтобы координаты текущего положения точки были положительными. При составлении дифференциальных уравнений (18-3) касательную к траектории точки следует направлять в сторону положительного направления отсчета дуг, а главную нормаль — в сторону вогнутости траектории.
нужно брать в плоскости движения, причем так, чтобы координаты текущего положения точки были положительными. При составлении дифференциальных уравнений (18-3) касательную к траектории точки следует направлять в сторону положительного направления отсчета дуг, а главную нормаль — в сторону вогнутости траектории.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
- 1. Абсолютно гладкая опорная поверхность
- 2. Точечная опора
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
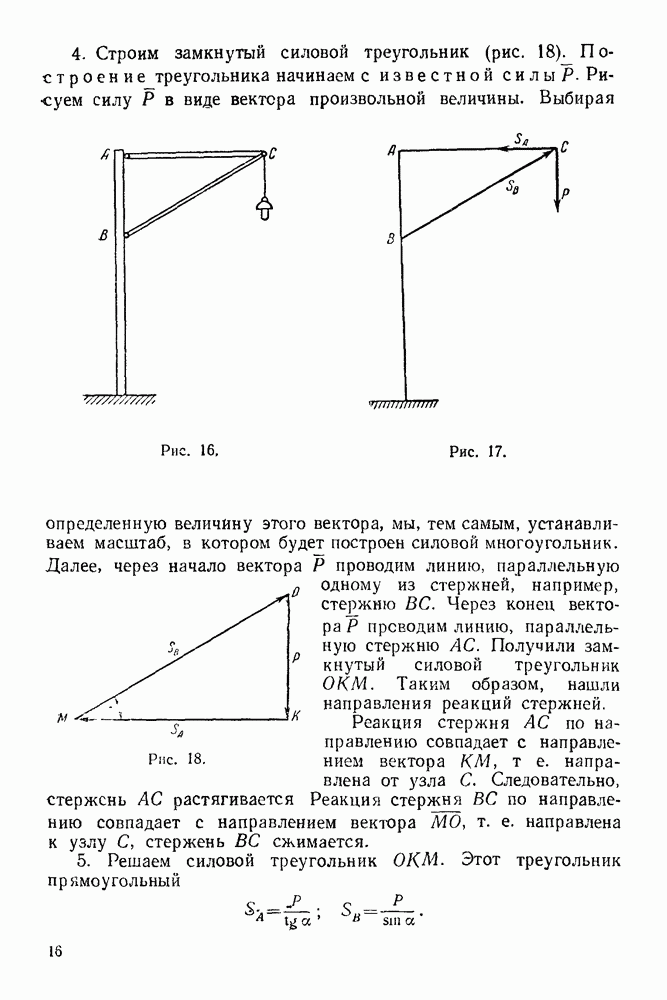
- 7. Стержневая опора
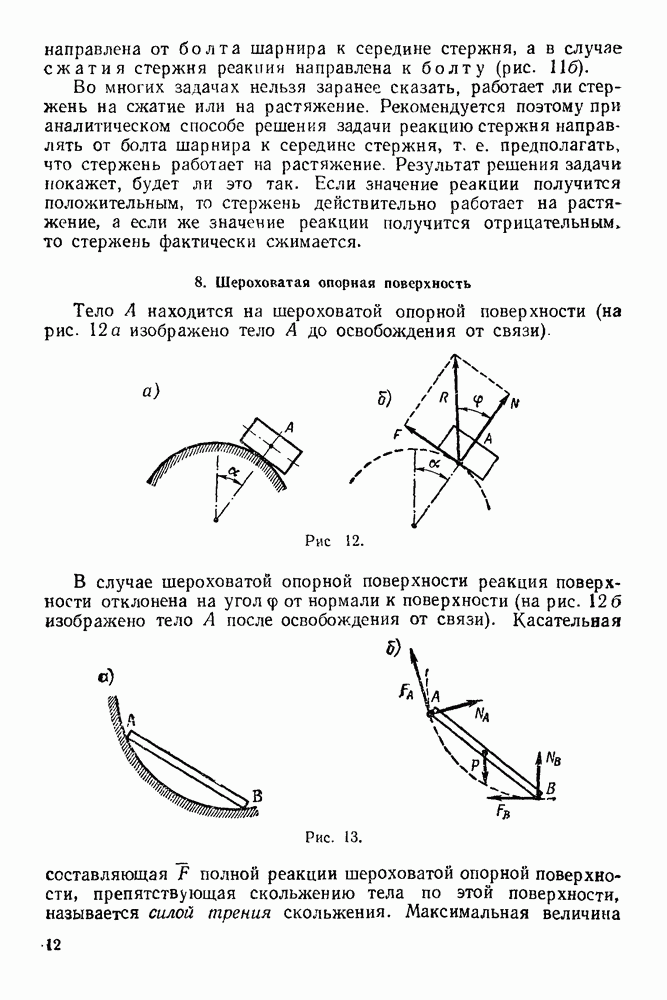
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
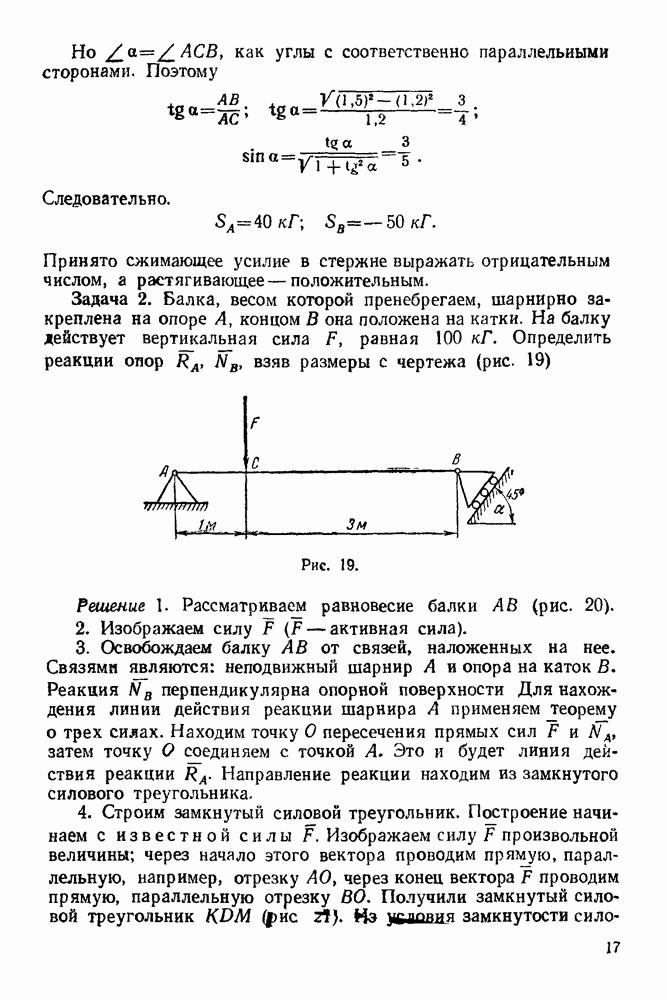
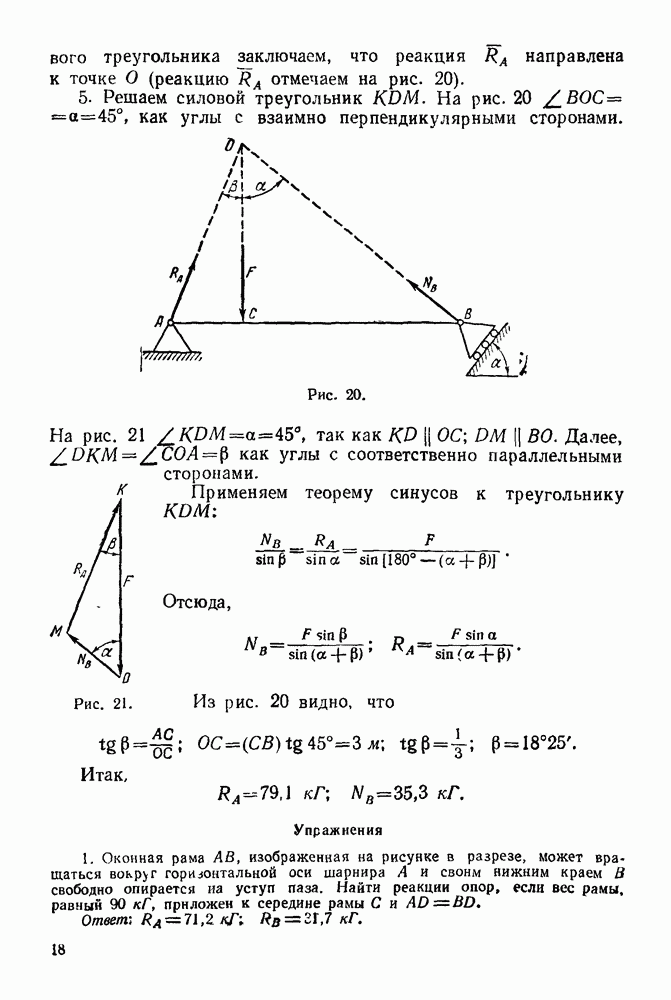
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
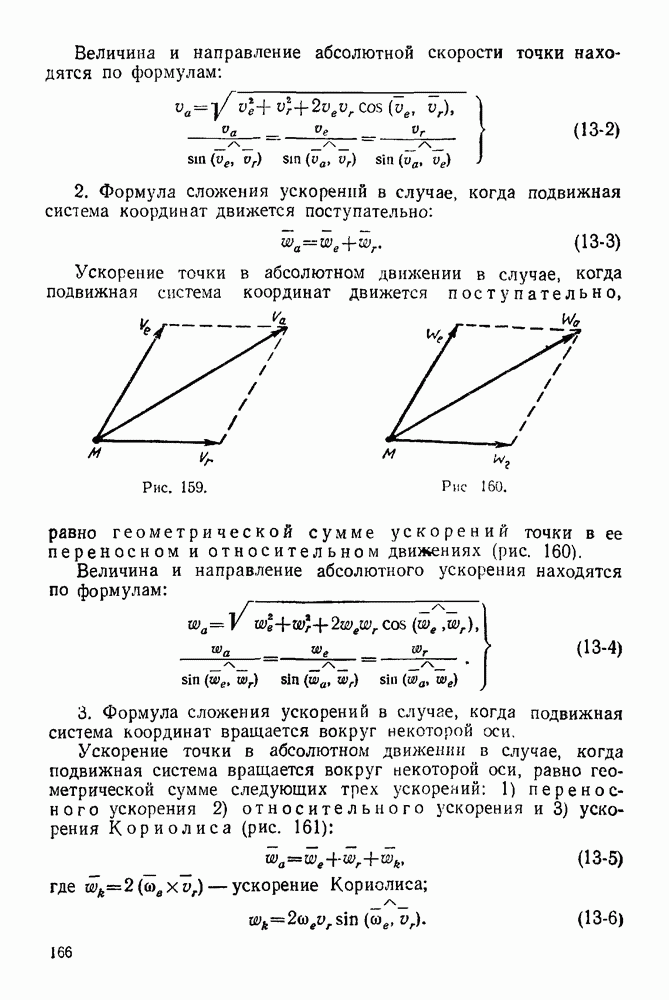
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
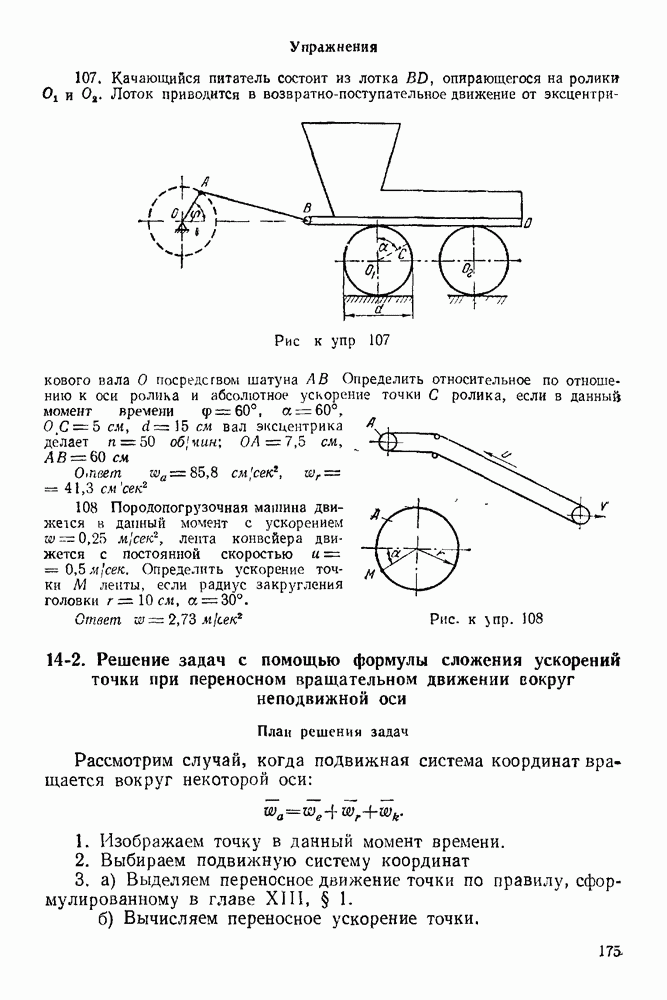
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР