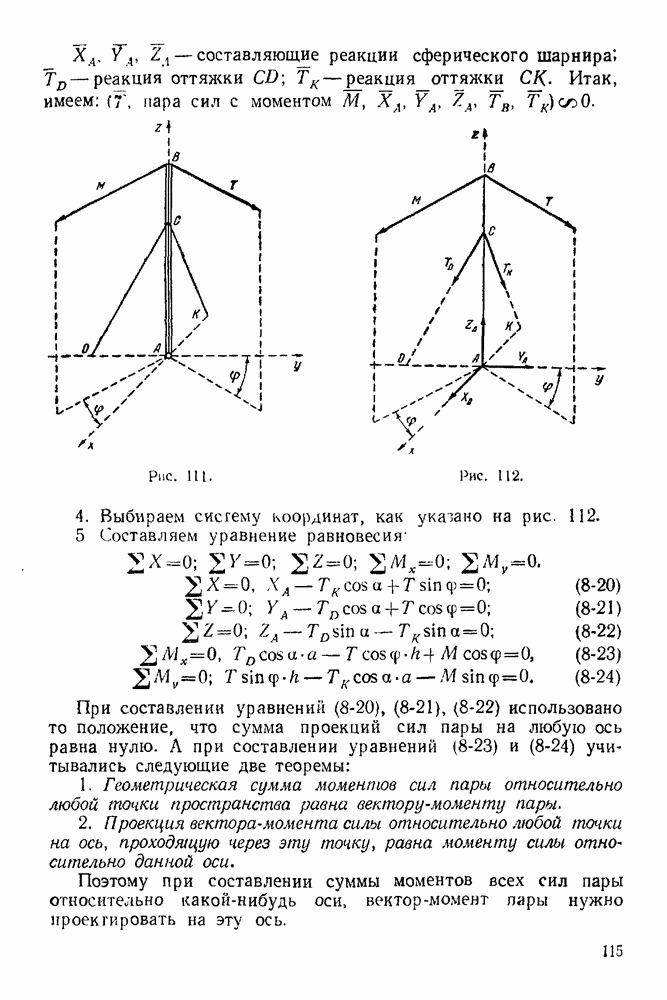
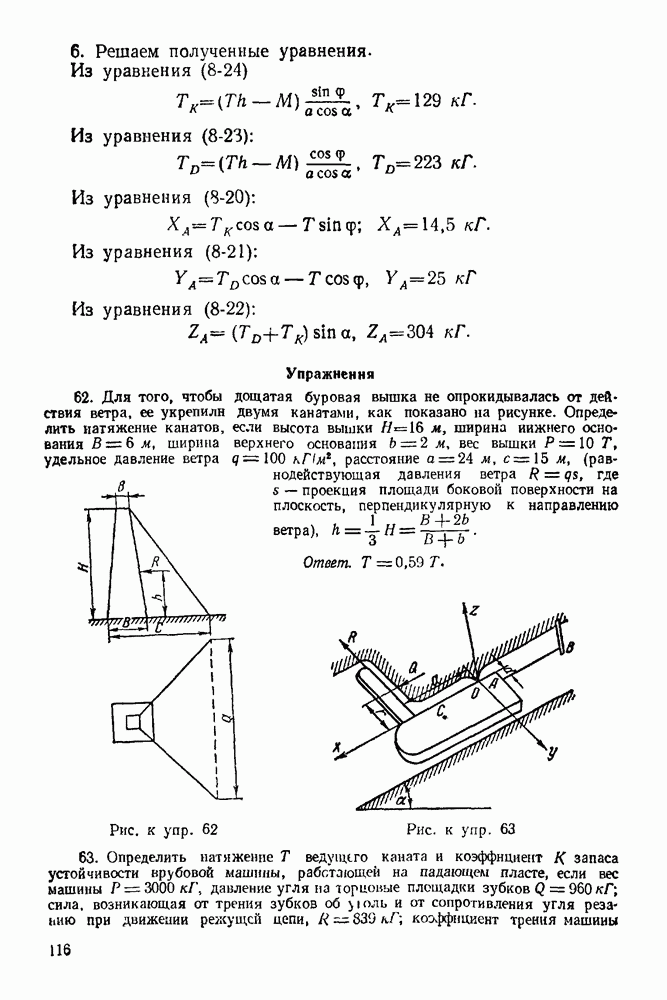
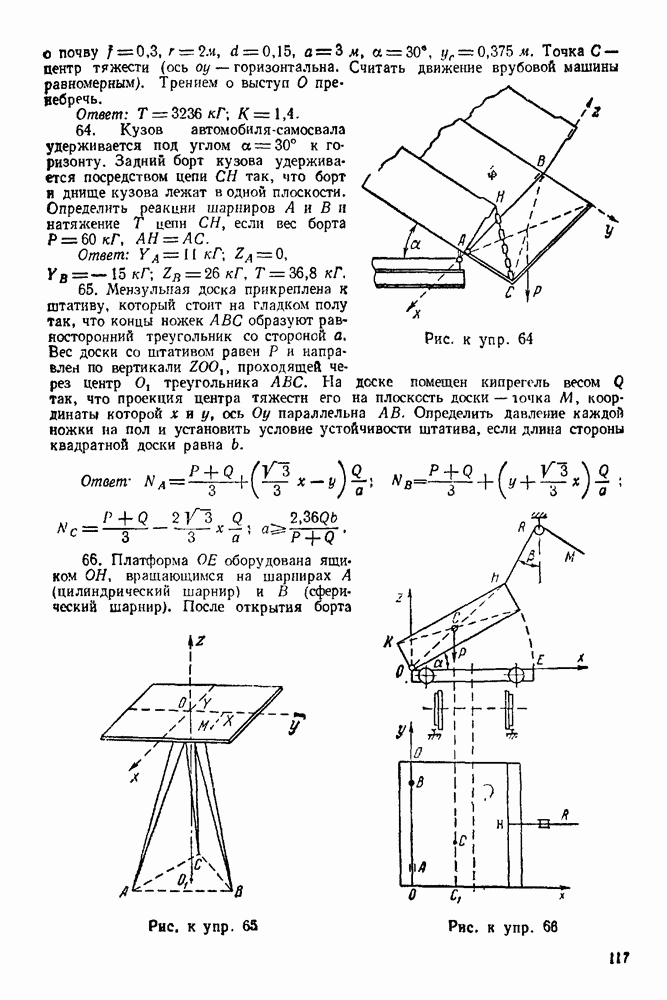
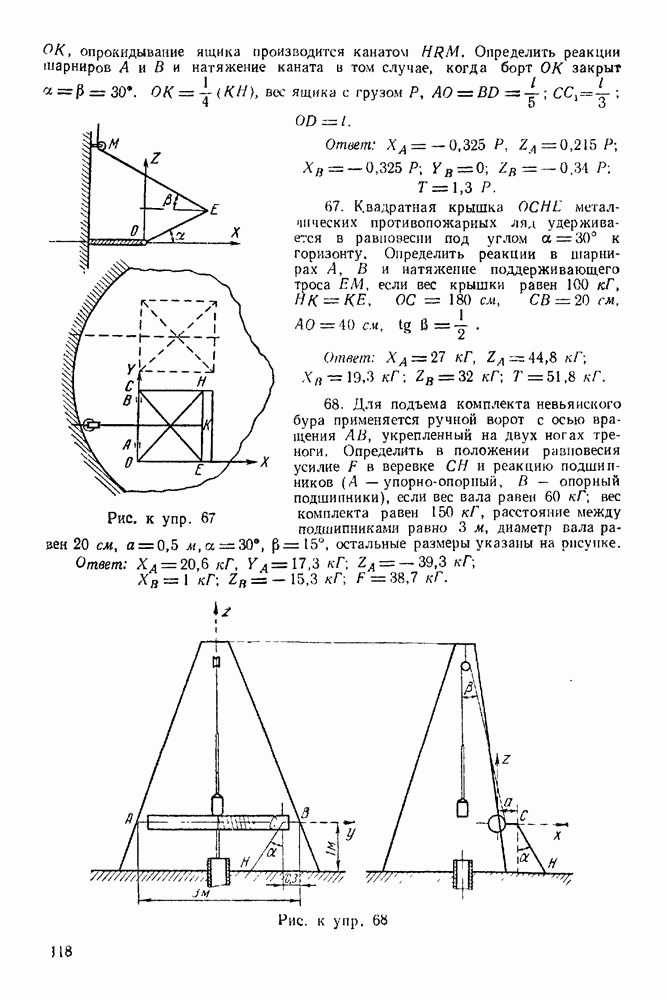
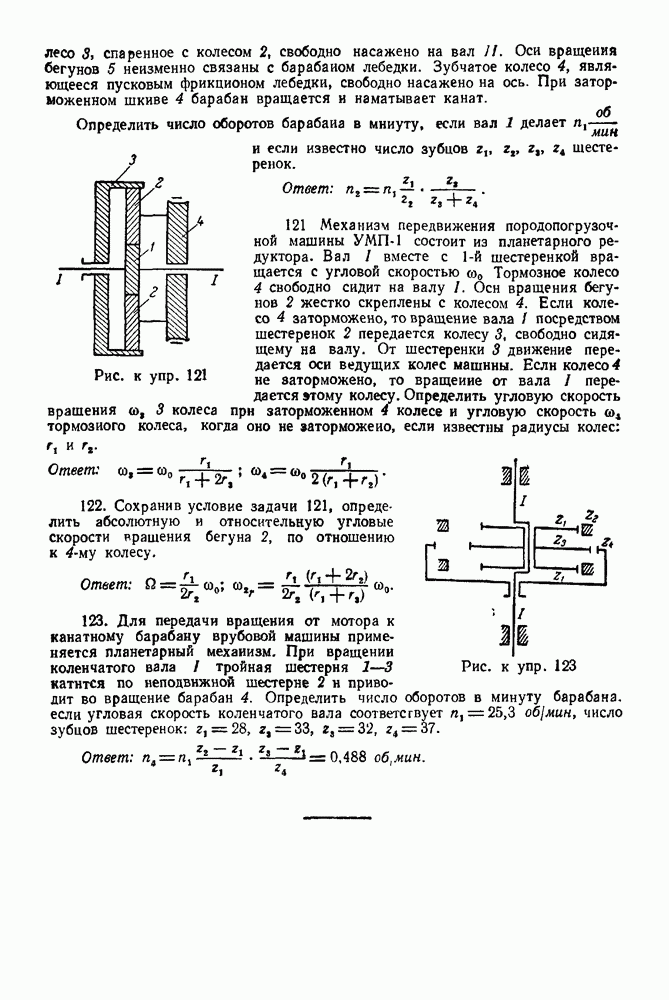
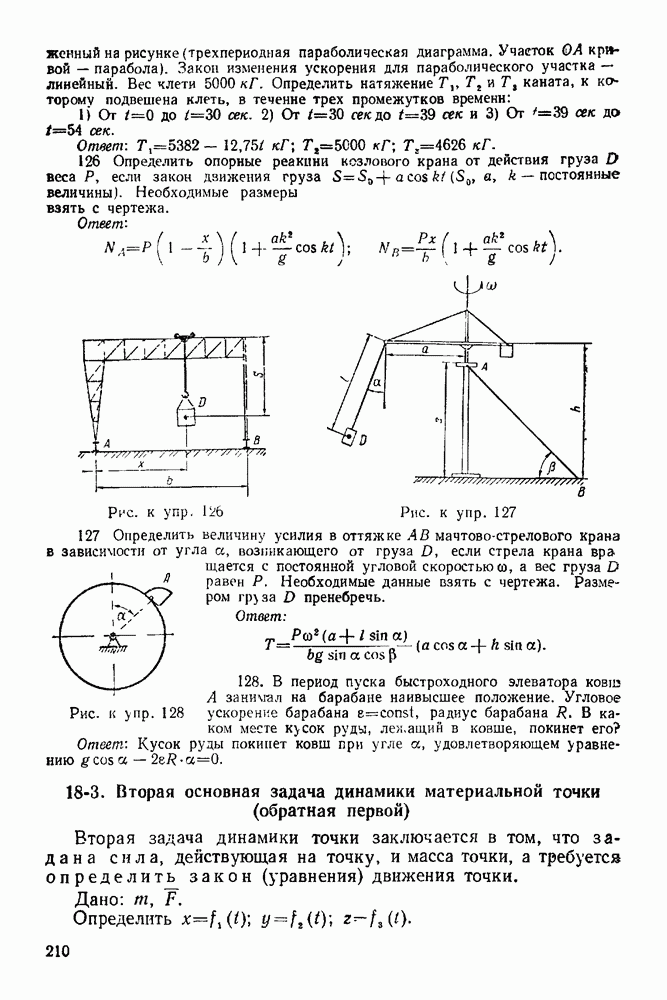
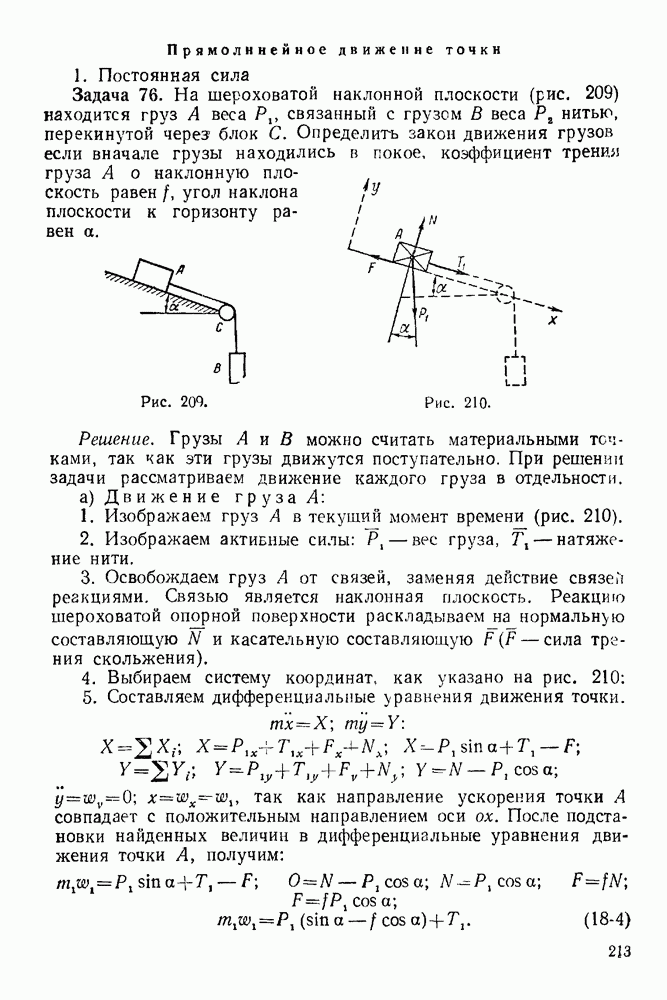
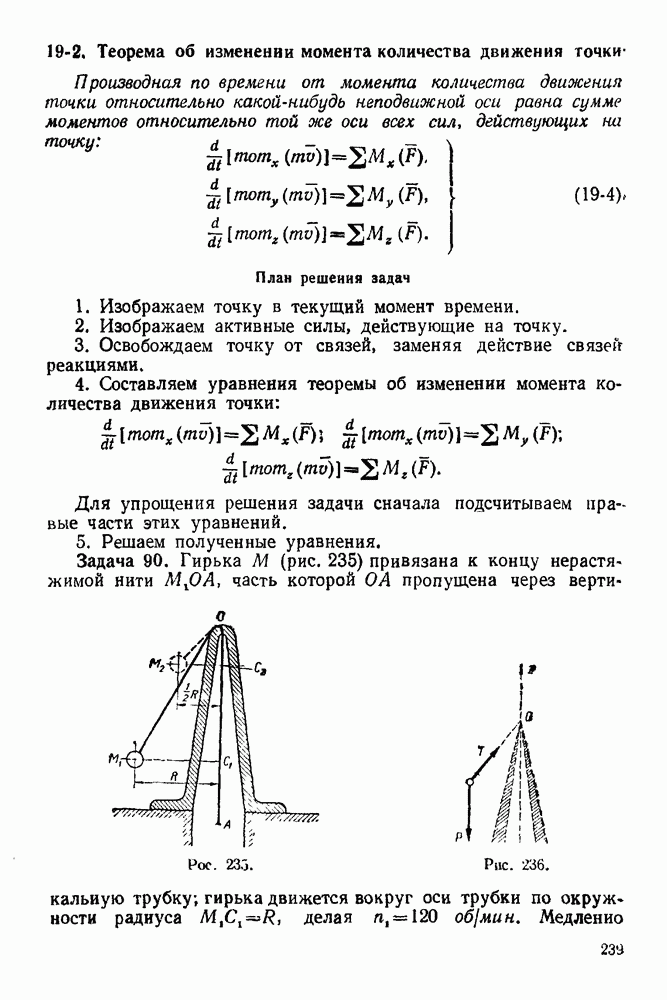
| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА XXIII. УДАР
23-1. Основные положения
Ударом называется такое явление, при котором за весьма малый промежуток времени (время удара  ) скорость точек движущегося объекта изменяется на конечную величину. За время удара действуют ударные (импульсивные) силы. Ударной силой называется такая сила, которая действует на тело (на материальную точку) в течение весьма короткого промежутка времени, но достигает при этом весьма большого значения, так что ее импульс является величиной конечной.
) скорость точек движущегося объекта изменяется на конечную величину. За время удара действуют ударные (импульсивные) силы. Ударной силой называется такая сила, которая действует на тело (на материальную точку) в течение весьма короткого промежутка времени, но достигает при этом весьма большого значения, так что ее импульс является величиной конечной.
Изменение за время удара проекции количества движения материальной точки на какую нибудь неподвижную ось равно проекции на ту же ось ударного импульса, приложенного к этой точке:

За время удара перемещением материальной точки и действием на точку неударных сил можно пренебречь.
Изменение за время удара момента относительно какой-нибудь неподвижной оси количества движения материальной точки раьно моменту относительно той же оси ударного импульса, приложенного к этой точке:

Удар двух поступательно движущихся тел называется прямым и центральным, если общая нормаль к поверхностям соударяющихся тел в точке их соприкосновения в начале удара проходит через их центры тяжести и скорости обоих тел в начале удара направлены по этой нормали. Коэффициент восстановления  зависит от материалов соударяющихся тел и при прямом центральном ударе двух поступательно движущихся тел равен отношению, взятому со знаком минус относительной скорости движения первого тела по отношению ко второму после удара к относительной скорости до удара:
зависит от материалов соударяющихся тел и при прямом центральном ударе двух поступательно движущихся тел равен отношению, взятому со знаком минус относительной скорости движения первого тела по отношению ко второму после удара к относительной скорости до удара:

где если  то удар называется неупругим; если
то удар называется неупругим; если  то удар называется вполне упругим и если
то удар называется вполне упругим и если  то удар называется не вполне упругим; у и
то удар называется не вполне упругим; у и  проекции скоростей тел до удара на линию удара,
проекции скоростей тел до удара на линию удара,  проекции скоростей тел после удара на то же направление.
проекции скоростей тел после удара на то же направление.
Скорости после прямого центрального удара двух тел находятся по формулам:

Кинетическая энергия теряемая материальной системой при  ударе, равна
ударе, равна  доле кинетической энергии, соответствующей потерянным скоростям:
доле кинетической энергии, соответствующей потерянным скоростям:

Эту потерю кинетической энергии при прямом центральном ударе двух тел можно найти по формуле:

Изменение за время удара проекции на какую-нибудь неподвижную ось количества движения системы равно проекции на ту же ось главного вектора всех внешних ударных импульсов, приложенных к системе:

Изменение за время удара проекции на какую-нибудь неподвижную ось количества движения центра масс системы, считая, что в этом центре сосредоточена масса всей системы, равно
проекции на ту же ось главного вектора всех внешних ударных импульсов, приложенных к этой системе:

Изменение за время удара кинетического момента системы, взятого относительно какой-нибудь неподвижной оси, равно главному моменту относительно той же оси всех внешних ударных импульсов, приложенных к этой системе:

23-2. Решение задач
Задача 110. В диск радиуса  и веса
и веса  ударяется горизонтально летящее тело В веса
ударяется горизонтально летящее тело В веса  (рис. 290). Найти такую скорость
(рис. 290). Найти такую скорость  этого тела до удара, при которой диск, вращаясь вокруг горизонтальной оси О, совершит полный оборот, если Удар считать неупругим, сопротивлениями пренебречь,
этого тела до удара, при которой диск, вращаясь вокруг горизонтальной оси О, совершит полный оборот, если Удар считать неупругим, сопротивлениями пренебречь, 

Рис. 290
План решения задачи
А. Применяем теорему об изучении за время удара относительно оси вращения кинетического момента системы, состоящей из диска и тела В:

Из этого уравнения найдем угловую скорость диска после удара.
Б. Применяем теорему об изменении кинетической энергии этой системы  на перемещении центра тяжести диска из наинизшего положения в наивысшее, считая, что в наивысшем положении центр тяжести будет обладать скоростью
на перемещении центра тяжести диска из наинизшего положения в наивысшее, считая, что в наивысшем положении центр тяжести будет обладать скоростью  При этом условии диск может совершить один оборот (центр тяжести системы «диск — тело В» можно считать совпадающим с центром тяжести диска так как
При этом условии диск может совершить один оборот (центр тяжести системы «диск — тело В» можно считать совпадающим с центром тяжести диска так как 
Решение. А Применяем теорему об изменении за время удара относительно оси вращения кинетического момента системы, состоящей из тела В и диска.
Для этого: 1. Изображаем систему «диск — тело В» во время удара (рис. 291).
2. Изображаем внешние ударные импульсы, действующие на систему. На данную систему действует только один внешний ударный импульс — ударный импульс, приложенный к диску со стороны оси подшипника О.

Рис. 291.
3. Составляем уравнение моментов за время удара:

Очевидно,

 кинетический момент относительно оси вращения диска системы «диск — тело
кинетический момент относительно оси вращения диска системы «диск — тело  до удара. Так как до удара двигалось только тело В, то
до удара. Так как до удара двигалось только тело В, то

 -кинетический момент относительно той же оси данной системы после удара.
-кинетический момент относительно той же оси данной системы после удара.
После удара диск будет обладать угловой скоростью  а тело В будет двигаться вместе с диском, так как удар неупругий
а тело В будет двигаться вместе с диском, так как удар неупругий  Следовательно
Следовательно

где  кинетический момент диска;
кинетический момент диска;  кинетический момент тела (точки) В. По геореме о связи моментов инерции тела относительно параллельных осей имеем:
кинетический момент тела (точки) В. По геореме о связи моментов инерции тела относительно параллельных осей имеем:

Момент инерции точки В относительно оси  будет;
будет;

Таким образом, получили

После подстановки найденных величин в уравнение (23 10) получим:

Б. Применяем теорему об изменении кинетической энергии этой системы после удара на перемещении центра тяжести диска из наинизшего положения в наивысшее.
1. Изображаем систему «диск — тело В» в текущий момент времени 
2. Изображаем внешние силы, действующие на эту систему. Такими силами являются  реакция оси вращения).
реакция оси вращения).

Рис. 292.
3. Составляем уравнение теоремы об изменении кинетической энергии системы:

 так как точка приложения О силы
так как точка приложения О силы  не перемещается
не перемещается

Получаем:

 кинетическая энергия данной системы после удара:
кинетическая энергия данной системы после удара:

 кинетическая энергия системы в конце движения, когда центр тяжести диска будет находиться в наивысшем положении и скорость его равняется нулю. Следовательно,
кинетическая энергия системы в конце движения, когда центр тяжести диска будет находиться в наивысшем положении и скорость его равняется нулю. Следовательно, 
Подставляя найденные величины в уравнение (23-121, получим:

Из выражений (23-11) и (23-13) находим искомую скорость и тела В до удара;

Так как  то
то

Задача 111. Два маятника могут вращаться вокруг горизон тальных осей  и
и  (рис. 293). Моменты инерции маятникор относительно этих осей равны
(рис. 293). Моменты инерции маятникор относительно этих осей равны  Левый маятник отклоняют от вертикали на некоторый угол и затем отпускают. В момент удара его угловая скорость равна
Левый маятник отклоняют от вертикали на некоторый угол и затем отпускают. В момент удара его угловая скорость равна  Определить угловые скорости обоих маятников после удара, если коэффициент восстановления равен
Определить угловые скорости обоих маятников после удара, если коэффициент восстановления равен  а расстояния точек
а расстояния точек  от линии удара равны между собой.
от линии удара равны между собой.

Рис. 293.
План решения задачи
1. Применяем теорему об изменении кинетического момента системы за время удара относительно оси О, для первого маятника и относительно оси  для второго маятника.
для второго маятника.
2. Используем формулу (23.3):

 Из полученных уравнений находим искомые величины. Решение.
Из полученных уравнений находим искомые величины. Решение.  Применяем теорему об изменении кинетического момента за время удара относительно оси О, для первого маятника.
Применяем теорему об изменении кинетического момента за время удара относительно оси О, для первого маятника.
а) Изображаем первый маятник в положении удара (рис. 294).
б) Изображаем внешние ударные импульсы, действующие на первый маятник:
 ударный импульс приложенный к маятнику со стороны оси
ударный импульс приложенный к маятнику со стороны оси 
— ударный импульс, приложенный к первому маятнику со стороны второго маятника.
в) Составляем уравнение моментов за время удара:

где

Но

Следовательно,

 кинетический момент первого маятника относительно оси 0, после удара.
кинетический момент первого маятника относительно оси 0, после удара.  кинетический момент до удара. Получаем
кинетический момент до удара. Получаем

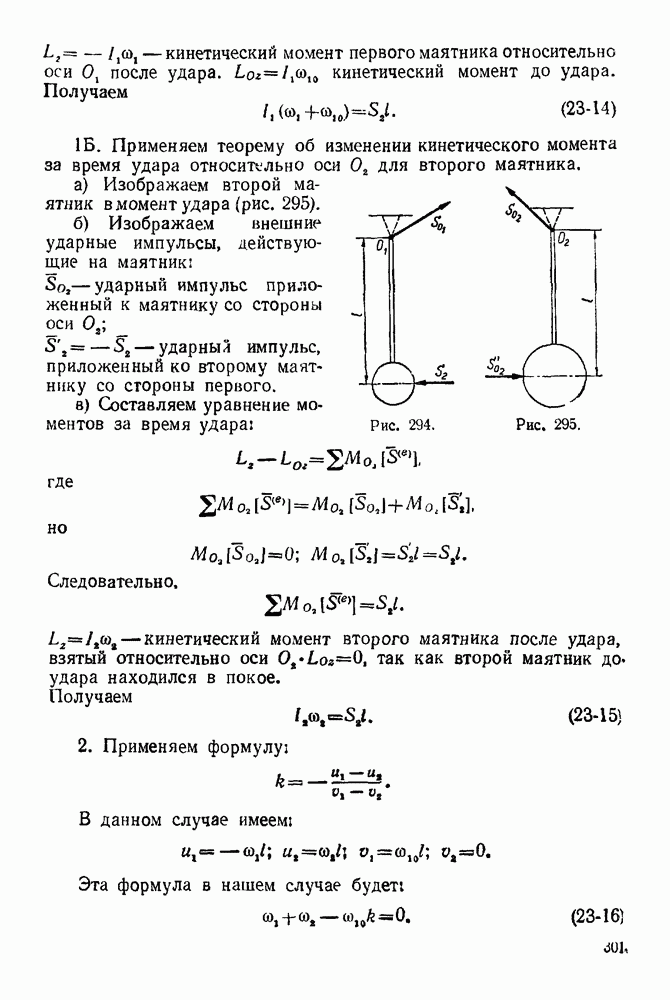
 Применяем теорему об изменении кинетического момента за время удара относительно оси
Применяем теорему об изменении кинетического момента за время удара относительно оси  для второго маятника.
для второго маятника.
а) Изображаем второй маятник в момент удара (рис. 295)

Рис. 294.

Рис. 295.
б) Изображаем внешние ударные импульсы, действующие на маятник;  ударный импульс приложенный к маятнику со стороны оси
ударный импульс приложенный к маятнику со стороны оси 
— ударный импульс, приложенный ко второму маятнику со стороны первого.
в) Составляем уравнение моментов за время удара:

где

но

Следовательно

 кинетический момент второго маятника после удара, взятый относительно оси
кинетический момент второго маятника после удара, взятый относительно оси  так как второй маятник до. удара находился в покое. Получаем
так как второй маятник до. удара находился в покое. Получаем

2. Применяем формулу:

В данном случае имеем:

Эта формула в нашем случае будет!

3. Из полученных уравнений (23-14), (23-15), (23-16) находим искомые абсолютные значения величин со, и 

Задача 112. Два шкива вращаются в одной плоскости вокруг своих осей с угловыми скоростями  Определить, как изменяются угловые скорости после того, как на шкивы будет накинут ремень. Радиусы шкивов равны соответственно
Определить, как изменяются угловые скорости после того, как на шкивы будет накинут ремень. Радиусы шкивов равны соответственно  Удар считать неупругим
Удар считать неупругим  скольжением и массой ремня пренебречь.
скольжением и массой ремня пренебречь.
Решение. Решаем задачу с помощью формулы (23—12). В нашем случае  следовательно, получаем:
следовательно, получаем:

но  кинетическая энергия потерянных скоростей. В случае вращающихся тел эта энергия находится по формуле:
кинетическая энергия потерянных скоростей. В случае вращающихся тел эта энергия находится по формуле:

Итак, решаем задачу с помощью формулы:

 — кинетическая энергия до удара системы, состоящей из двух шкивов.
— кинетическая энергия до удара системы, состоящей из двух шкивов.
 кинетическая энергия той же системы после удара.
кинетическая энергия той же системы после удара.

Рис. 296.
Угловые скорости шкивов после удара связаны друг с другом. Если пренебречь скольжением ремня,  (рис. 296)
(рис. 296)

Получаем уравнение для определения 

следовательно,

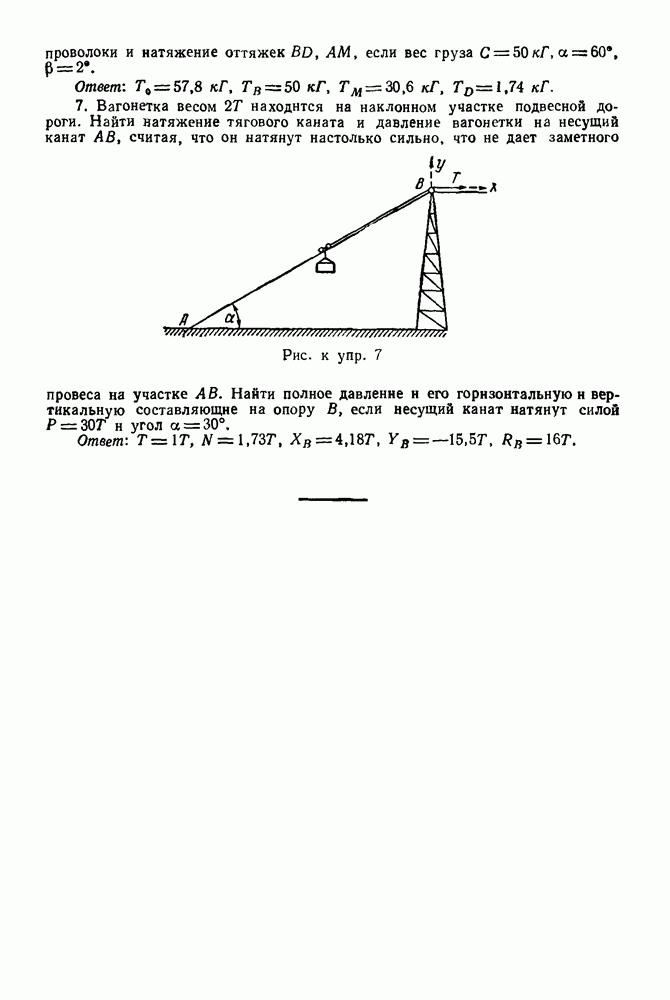
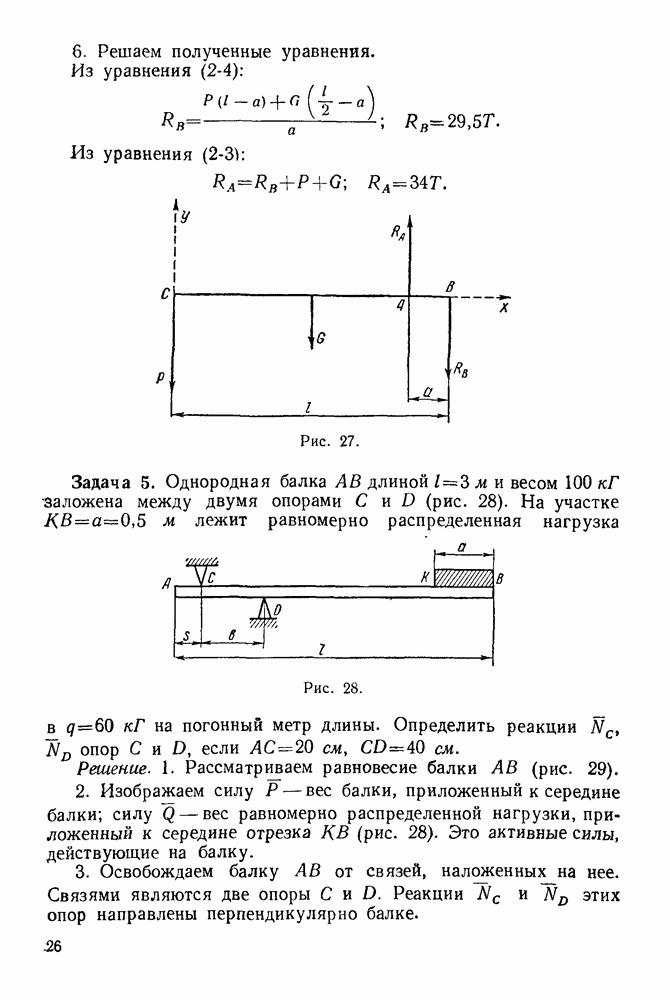
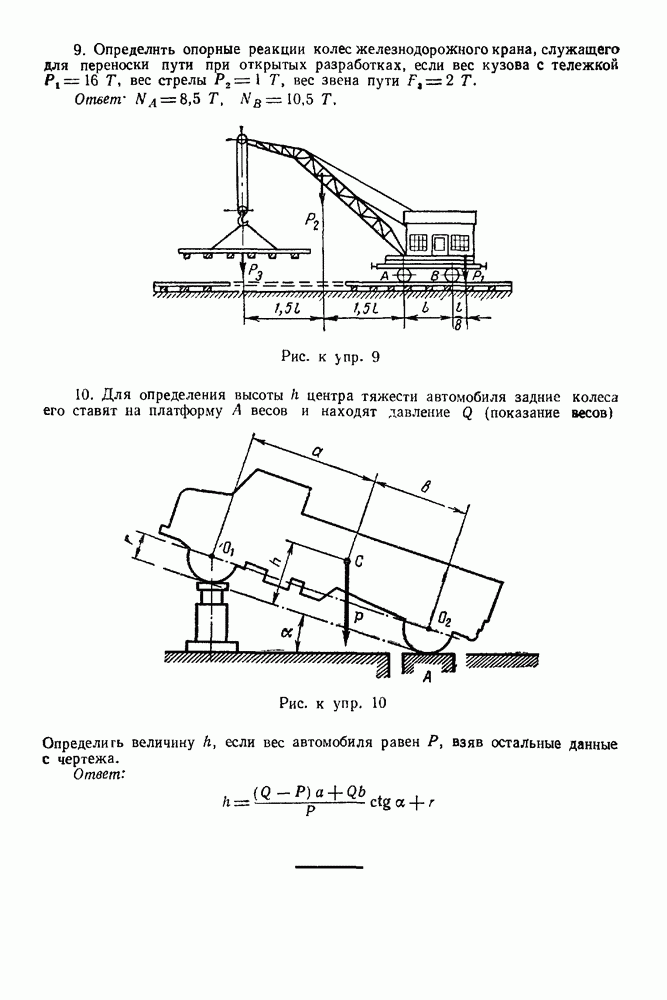
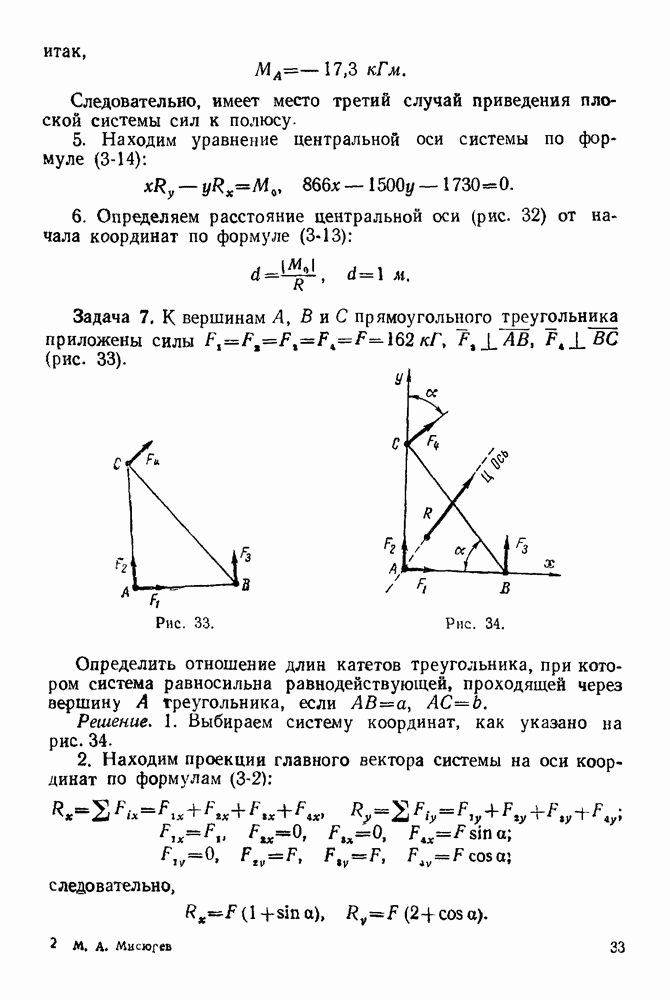
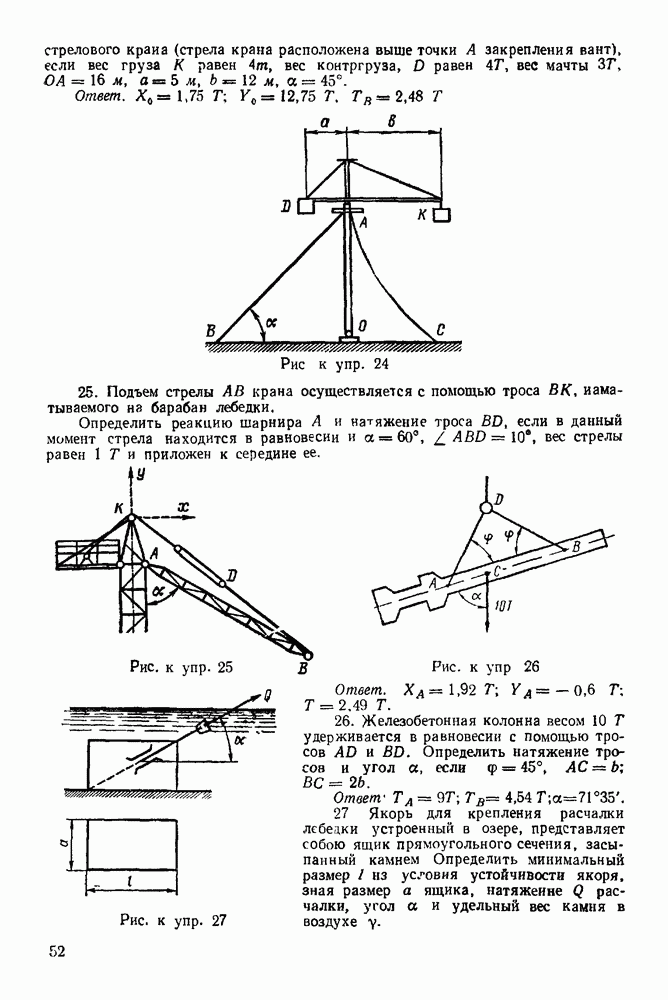
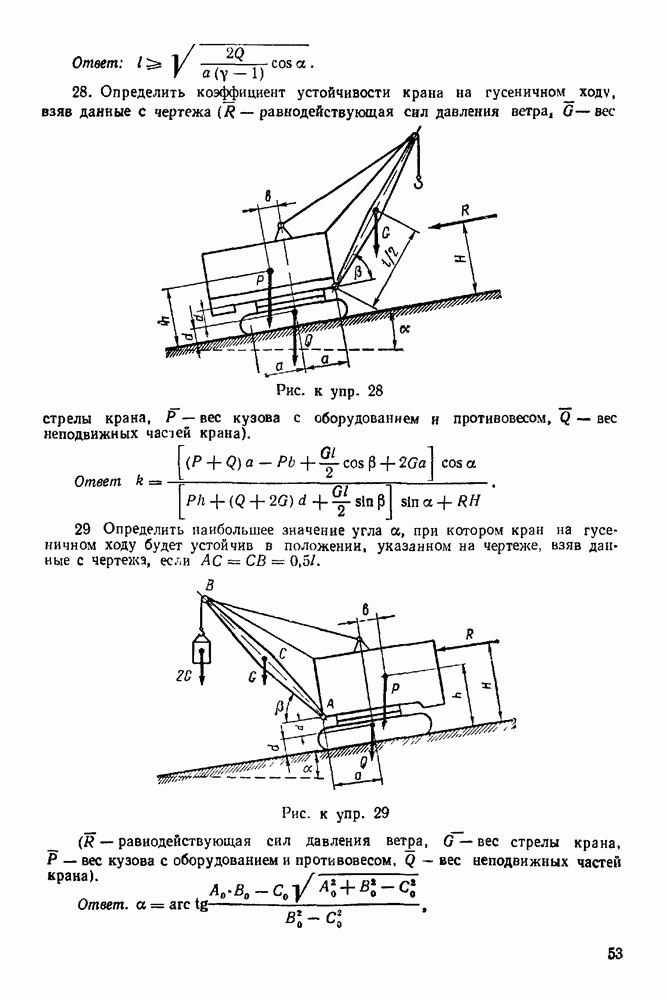
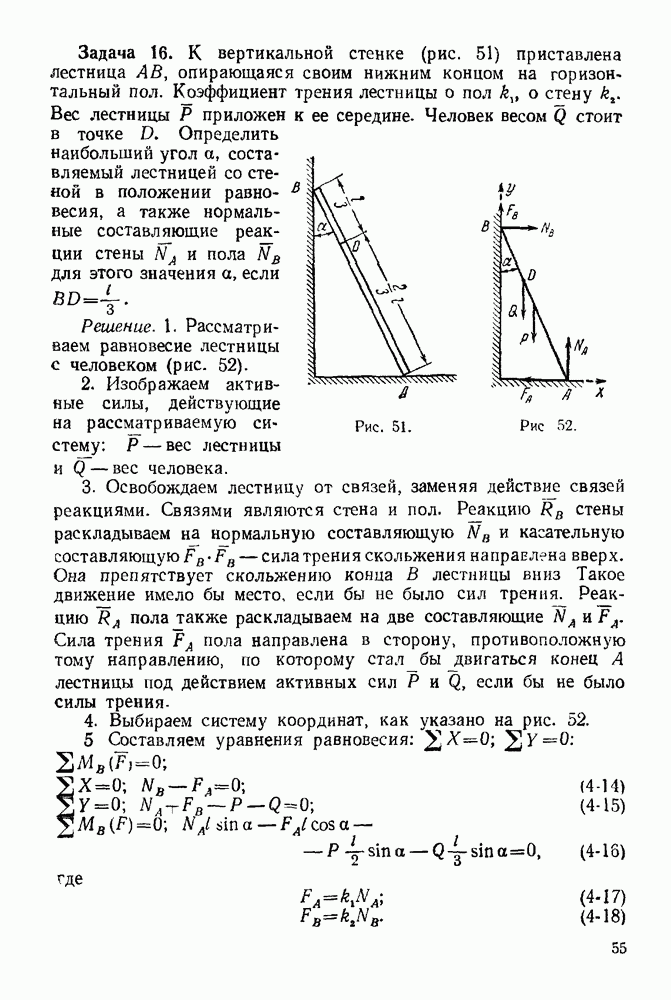
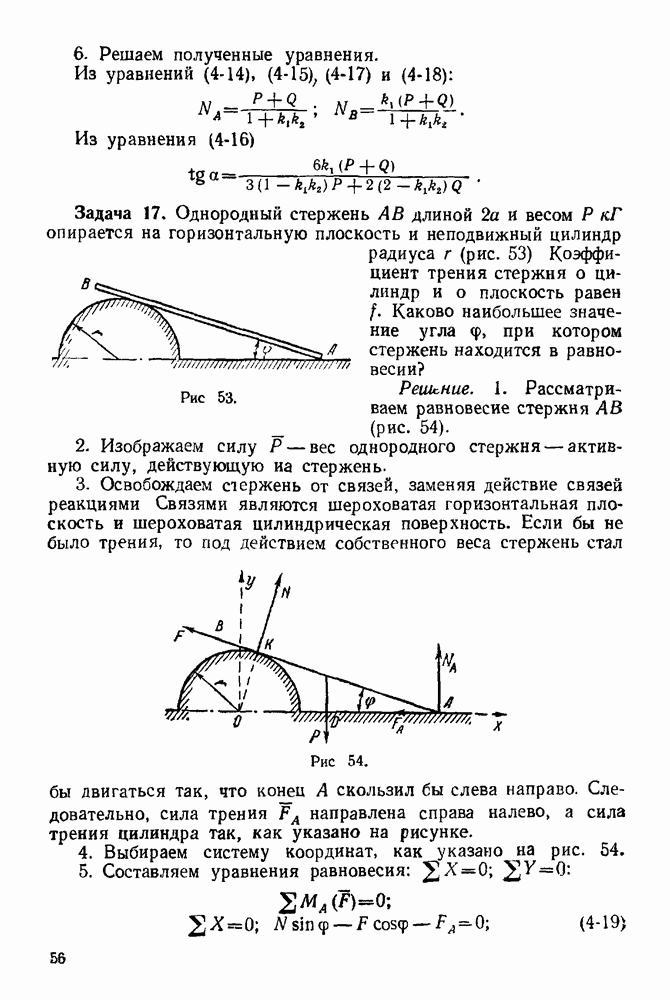
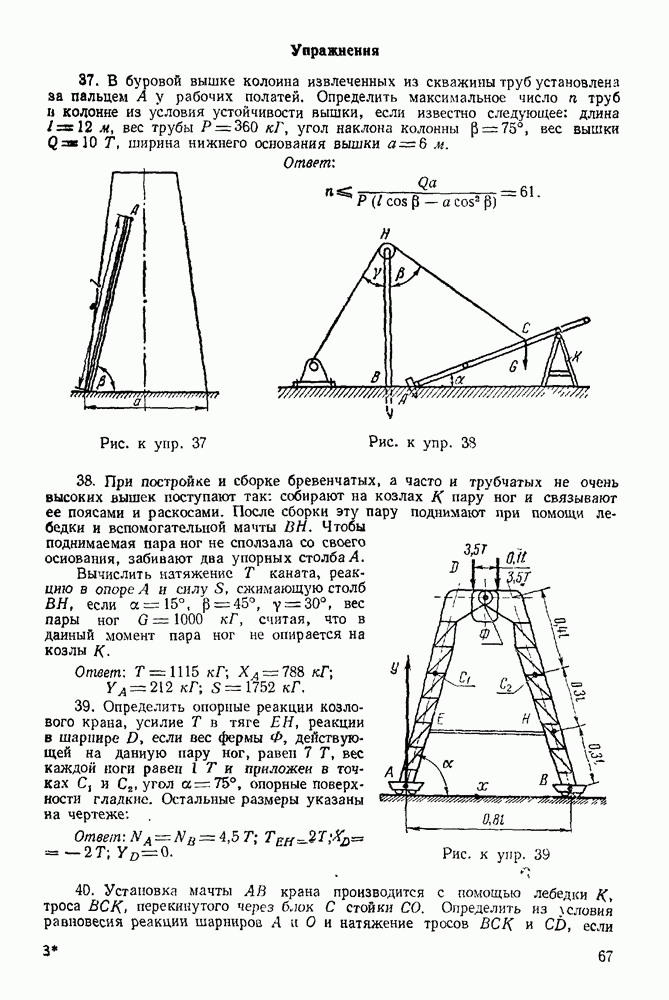
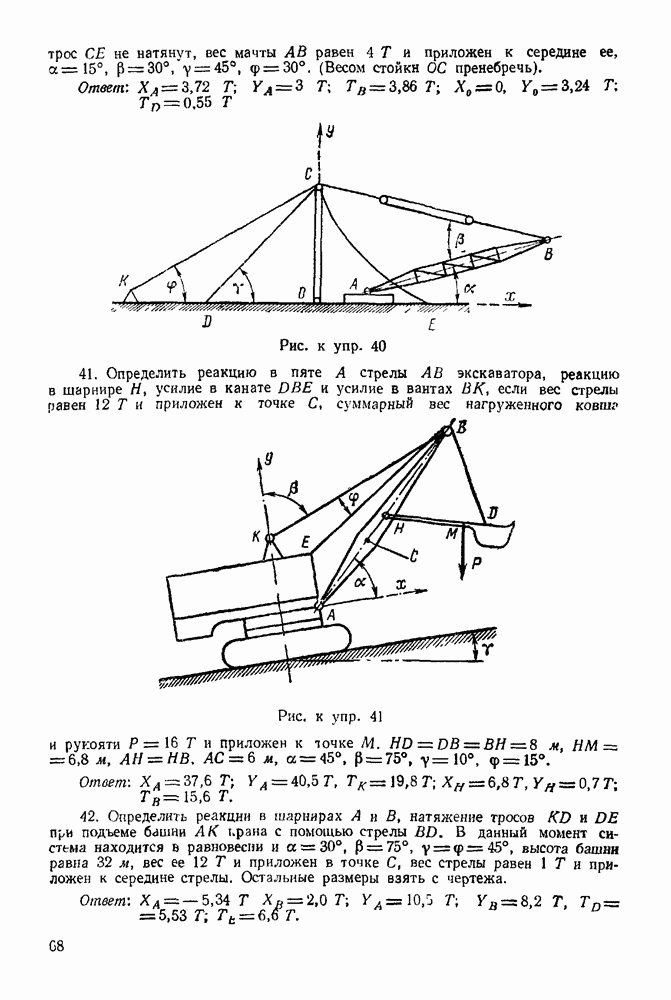
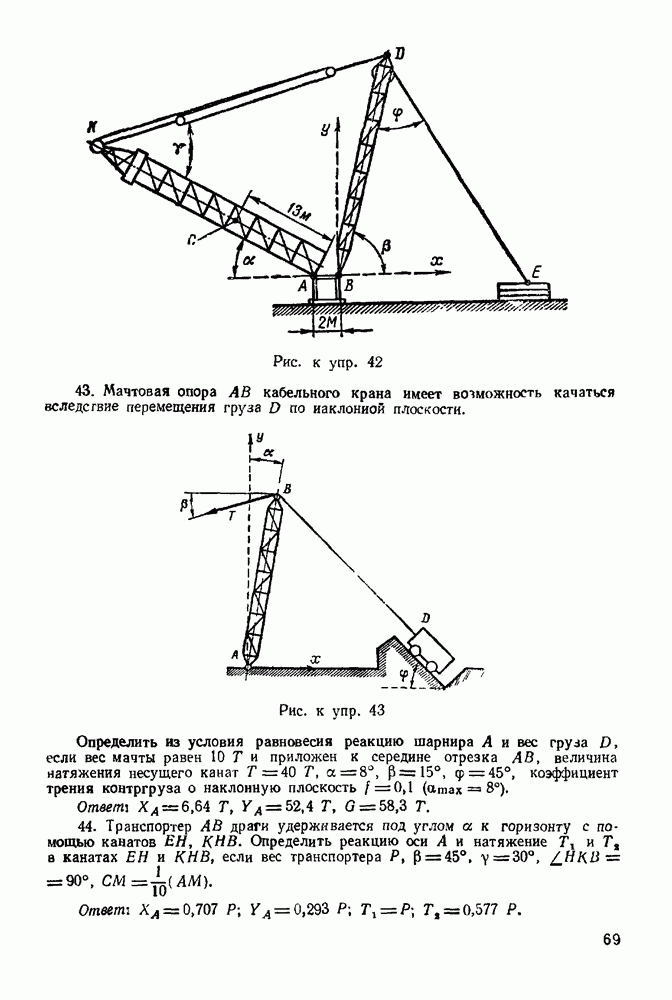
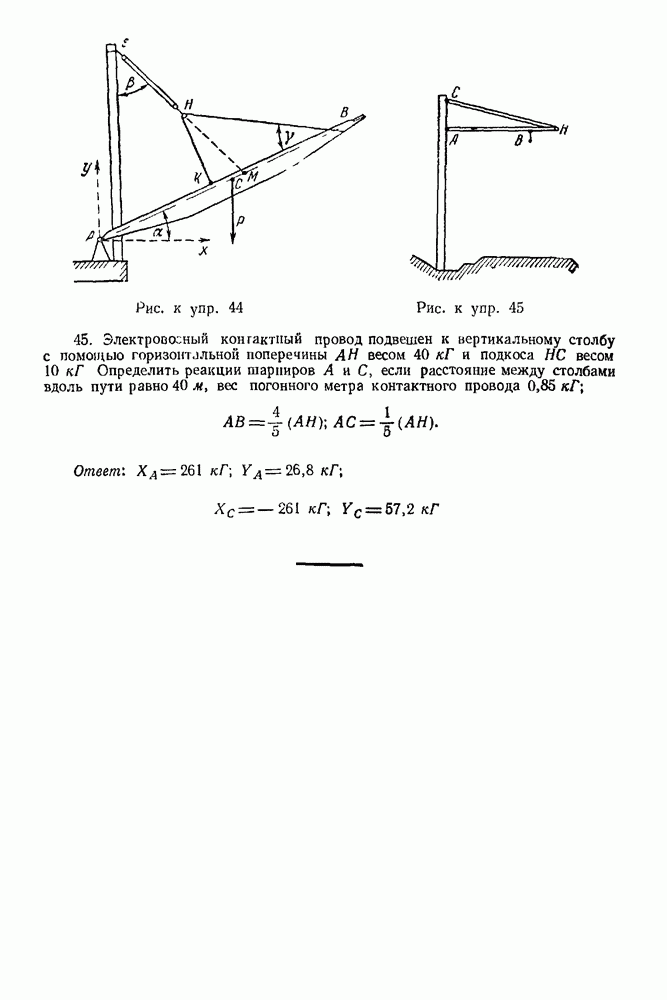
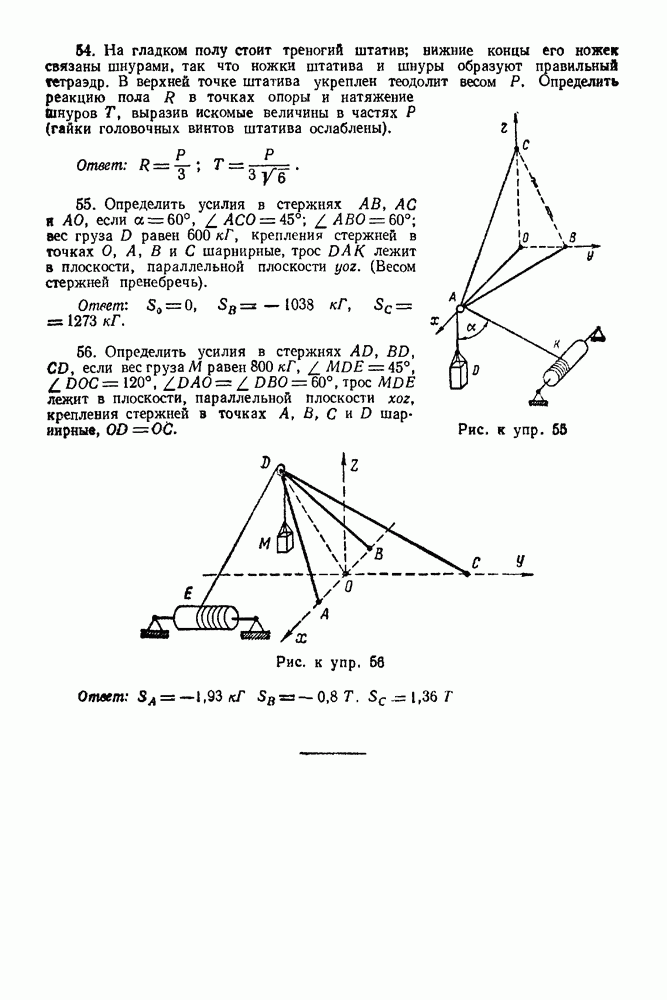
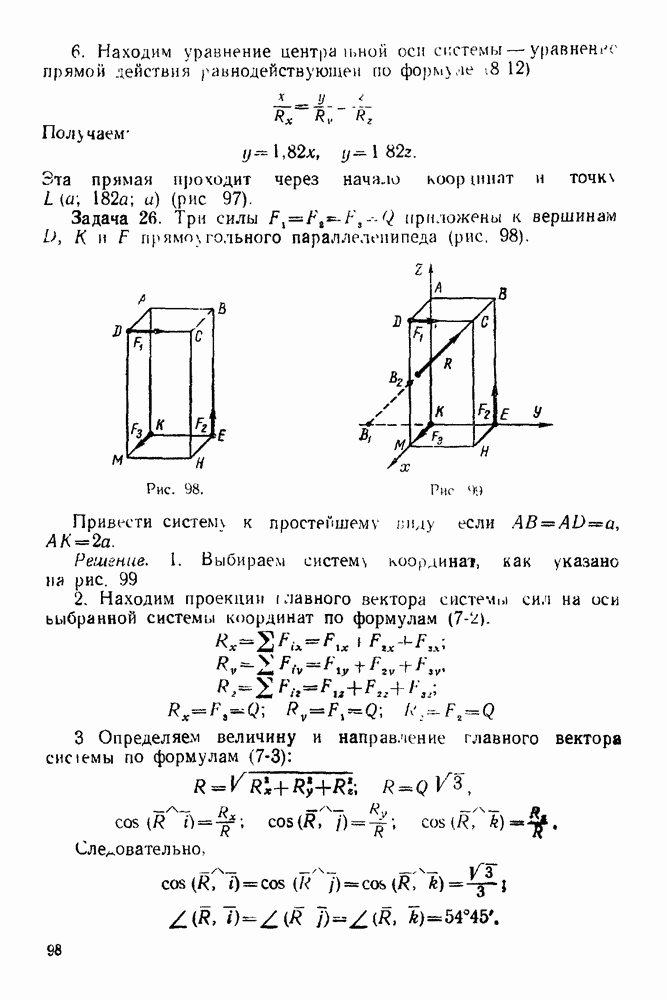
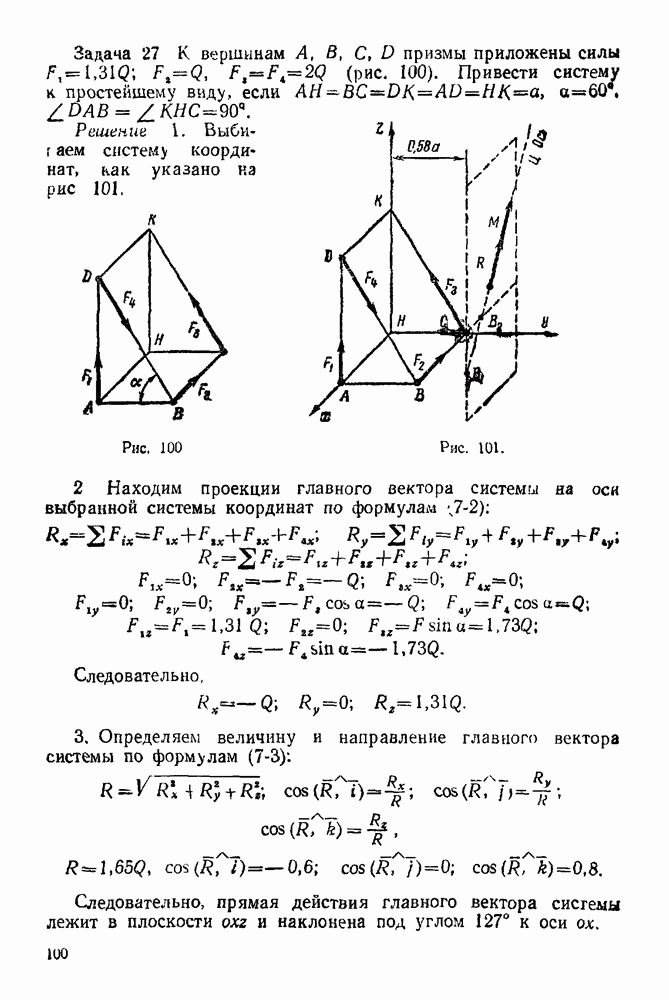
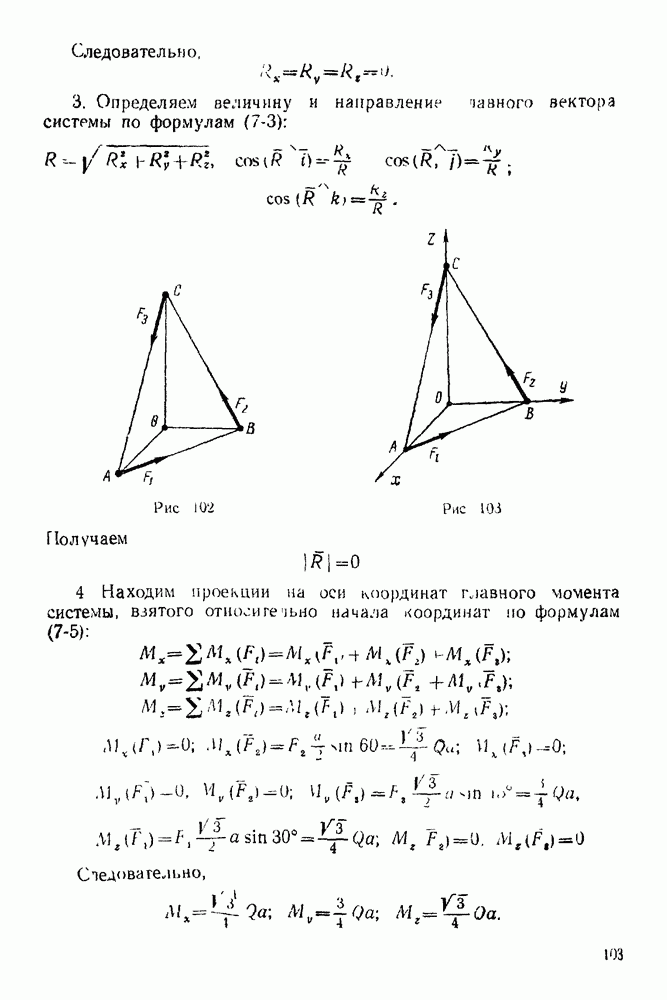
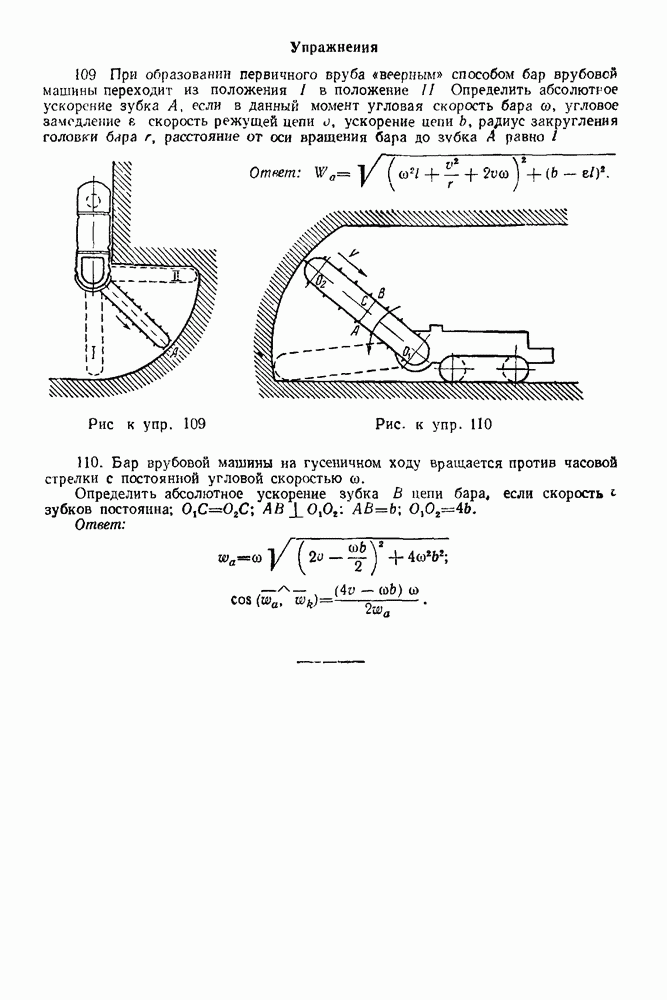
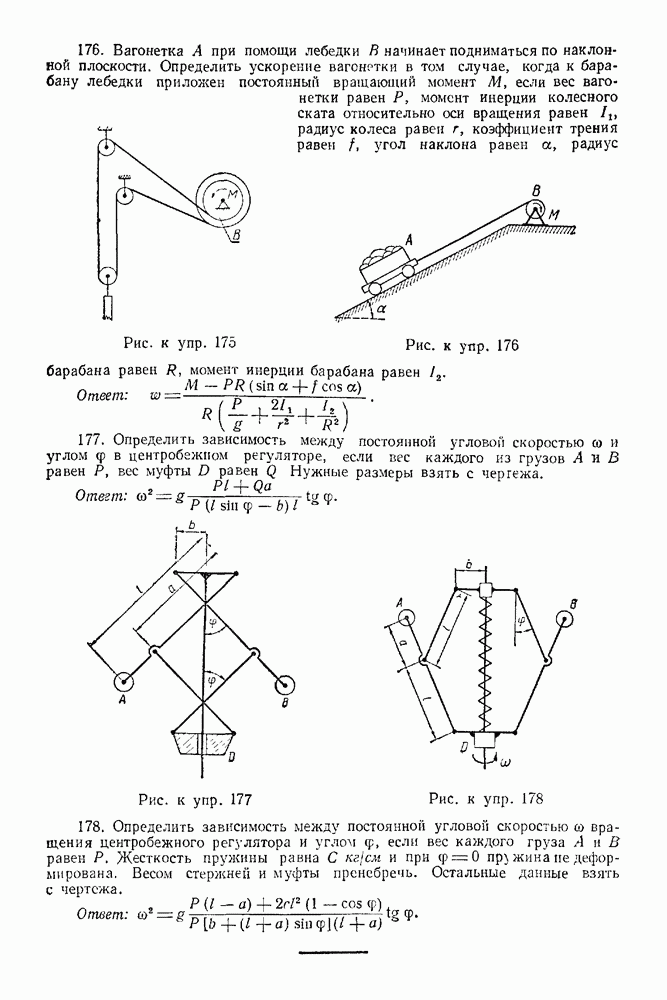
Упражнения
(см. скан)
Литература
(см. скан)
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
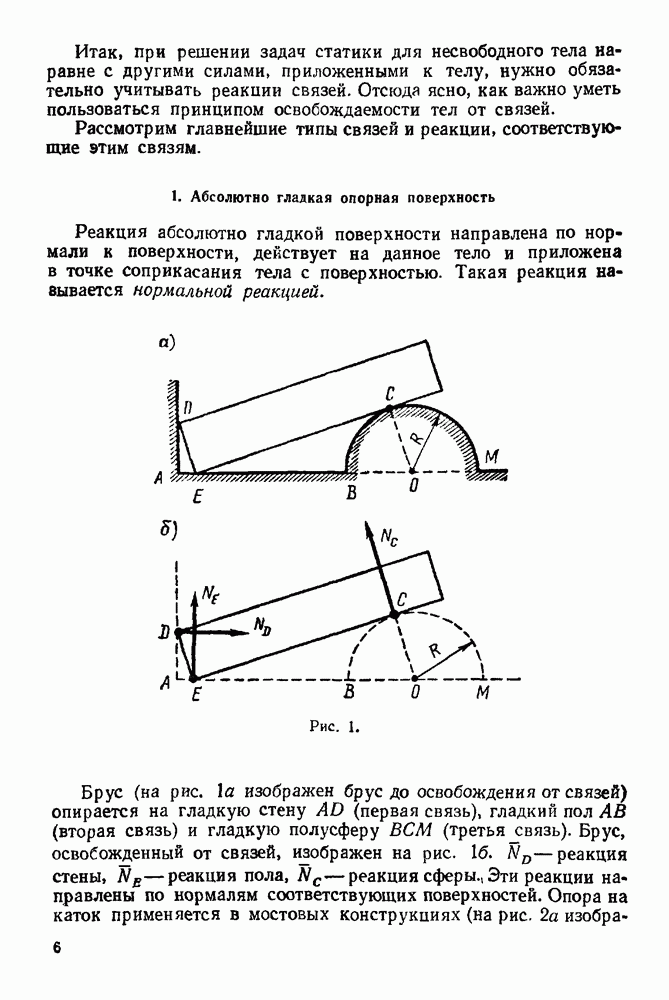
- 1. Абсолютно гладкая опорная поверхность
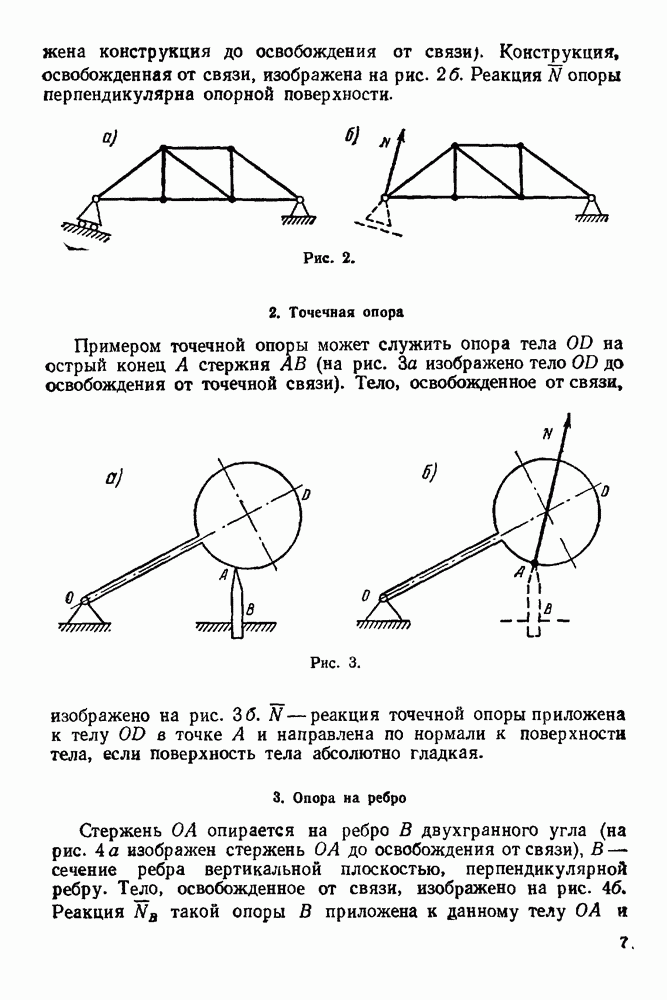
- 2. Точечная опора
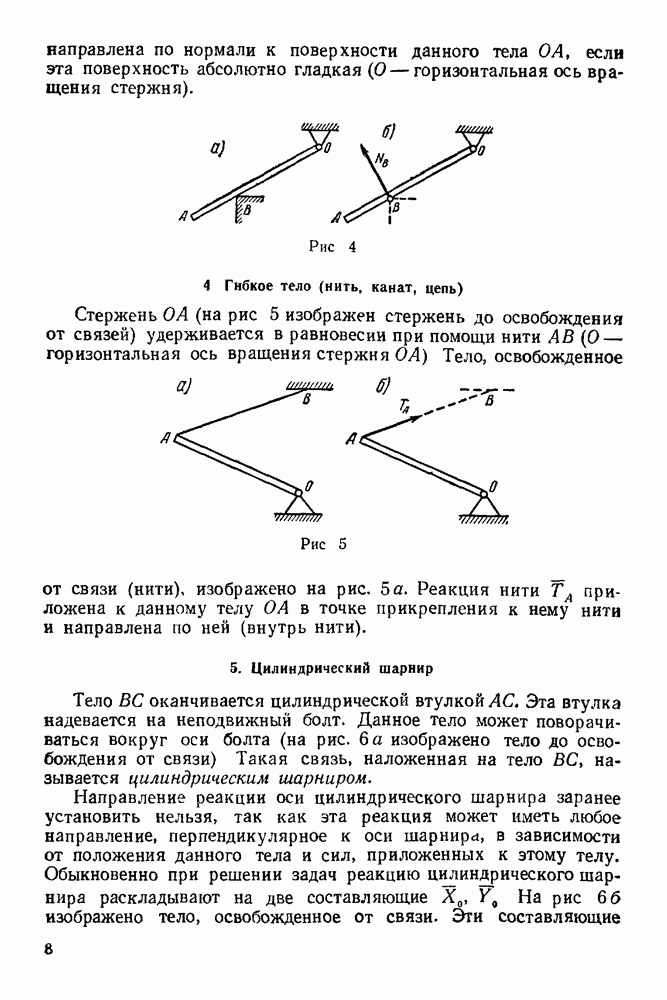
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
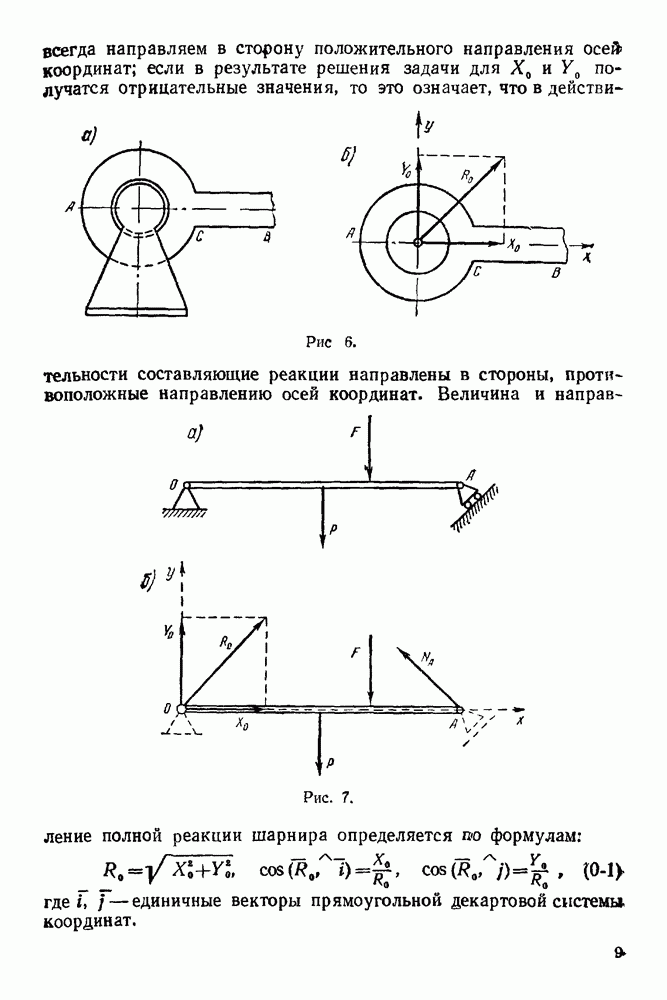
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
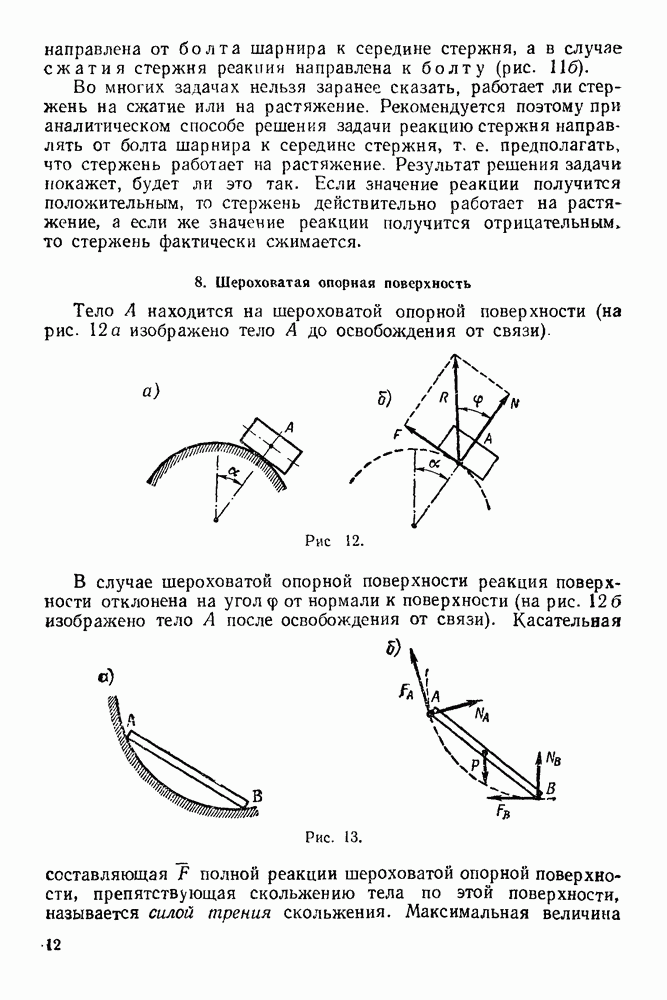
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
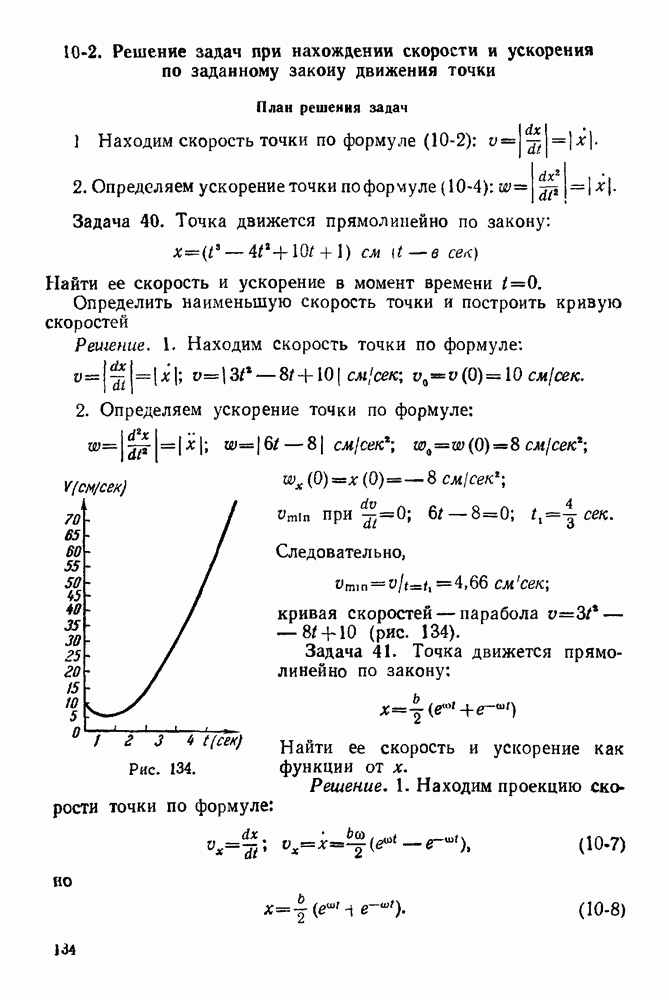
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
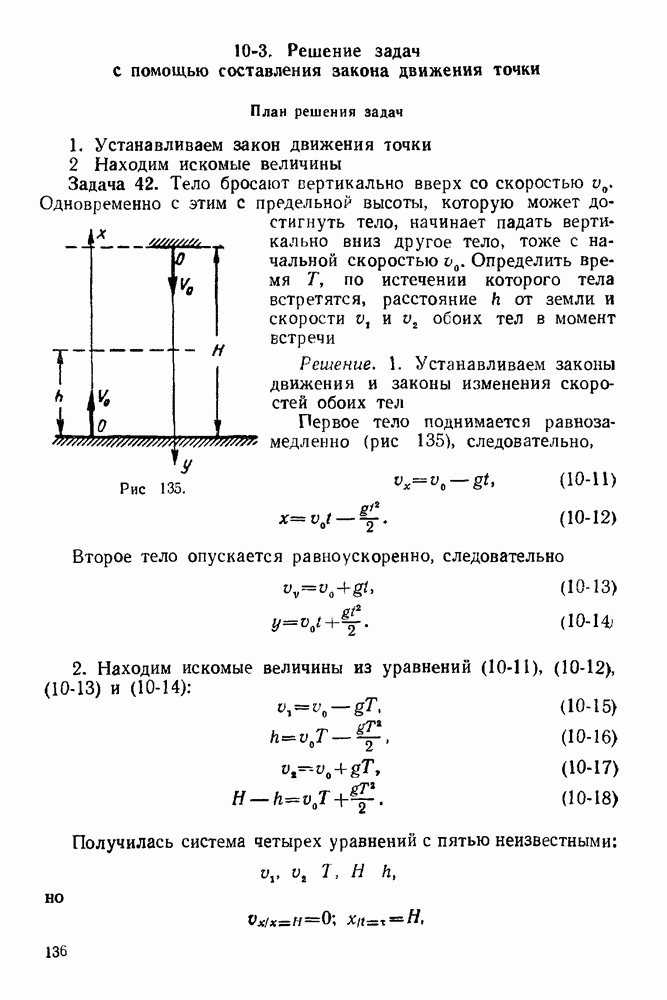
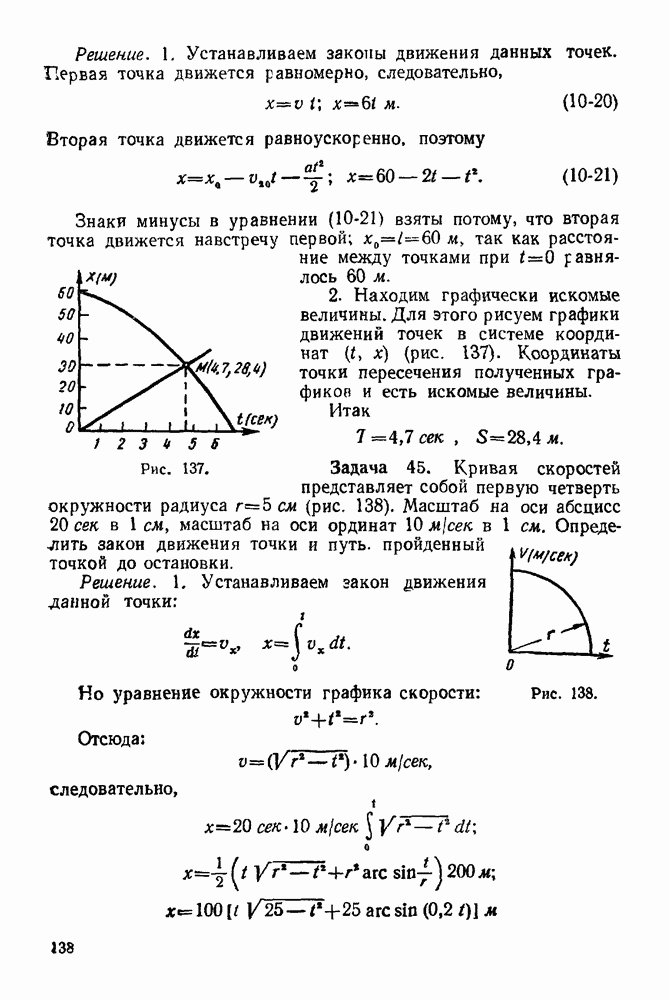
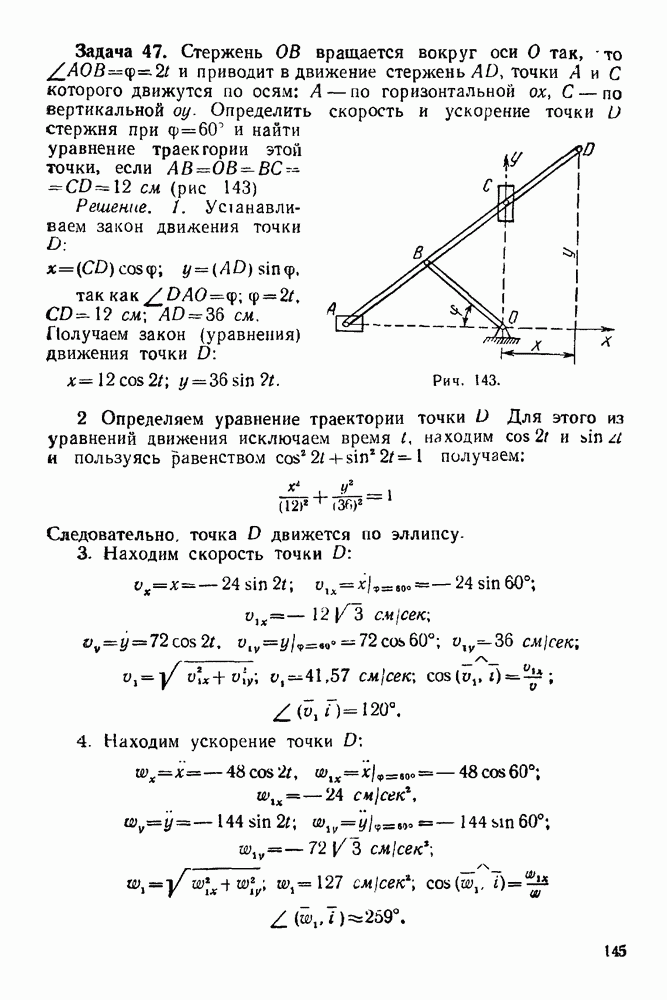
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР