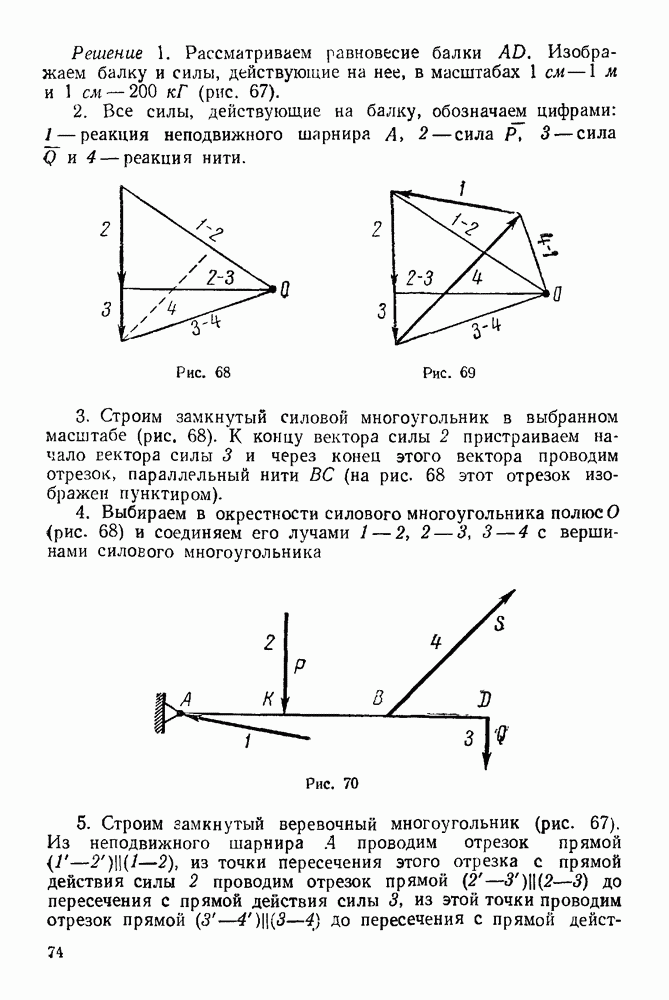
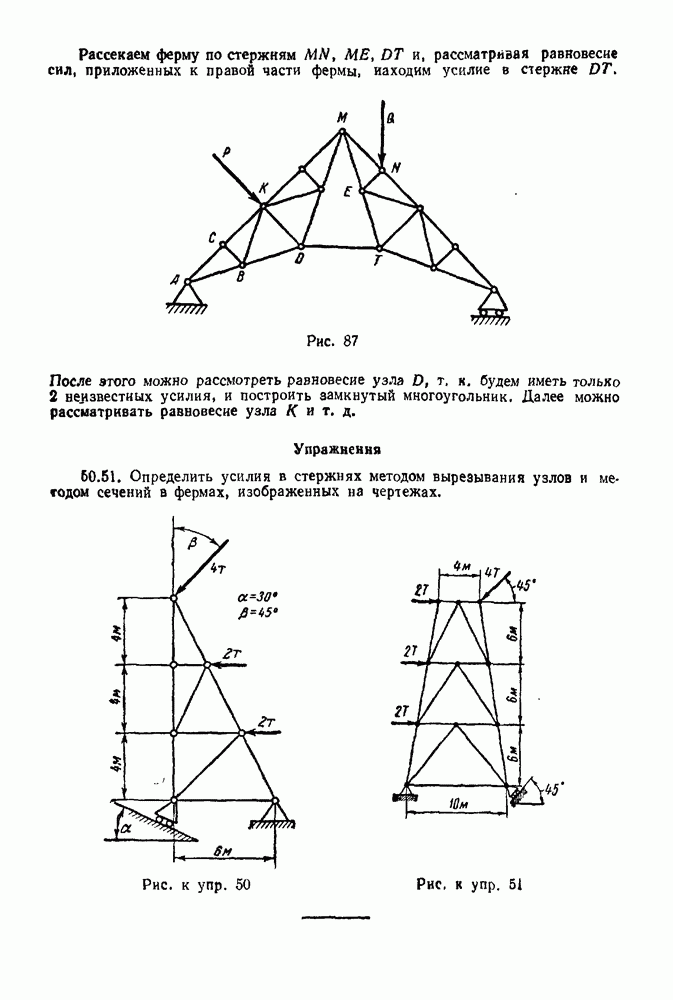
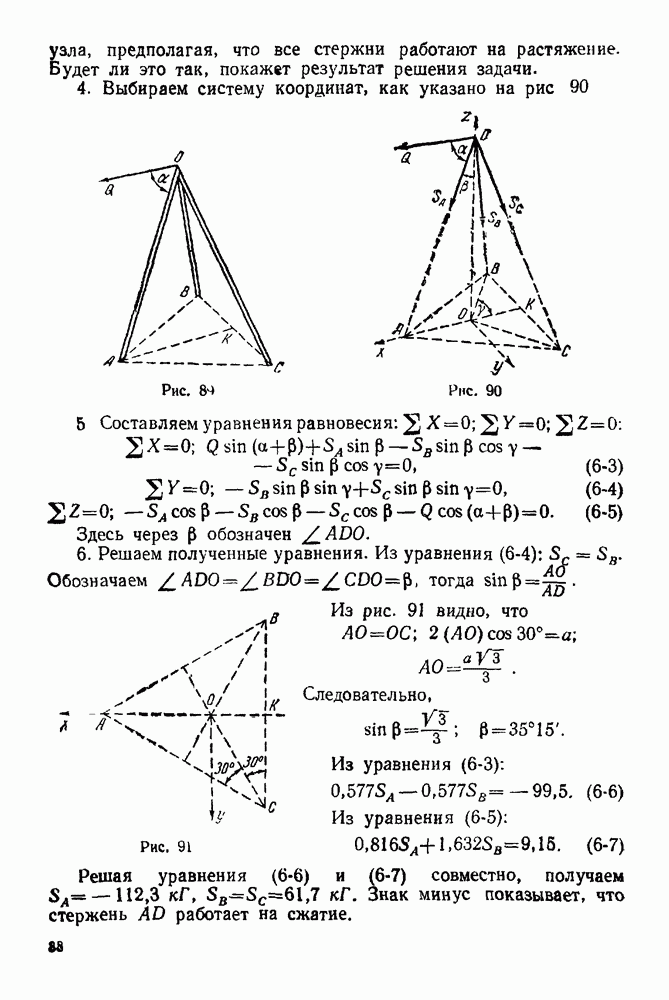
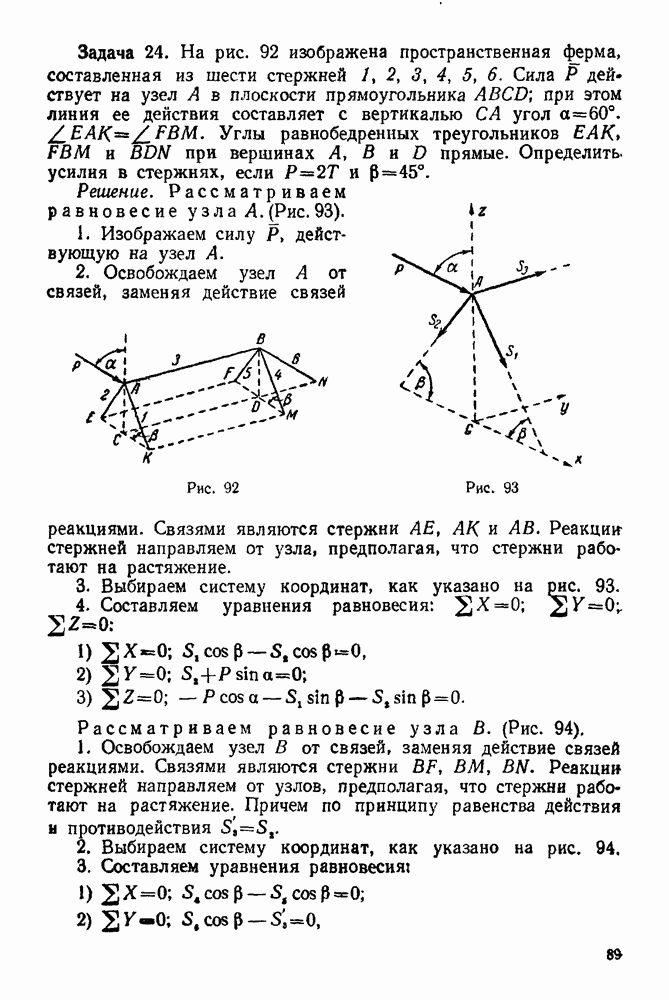
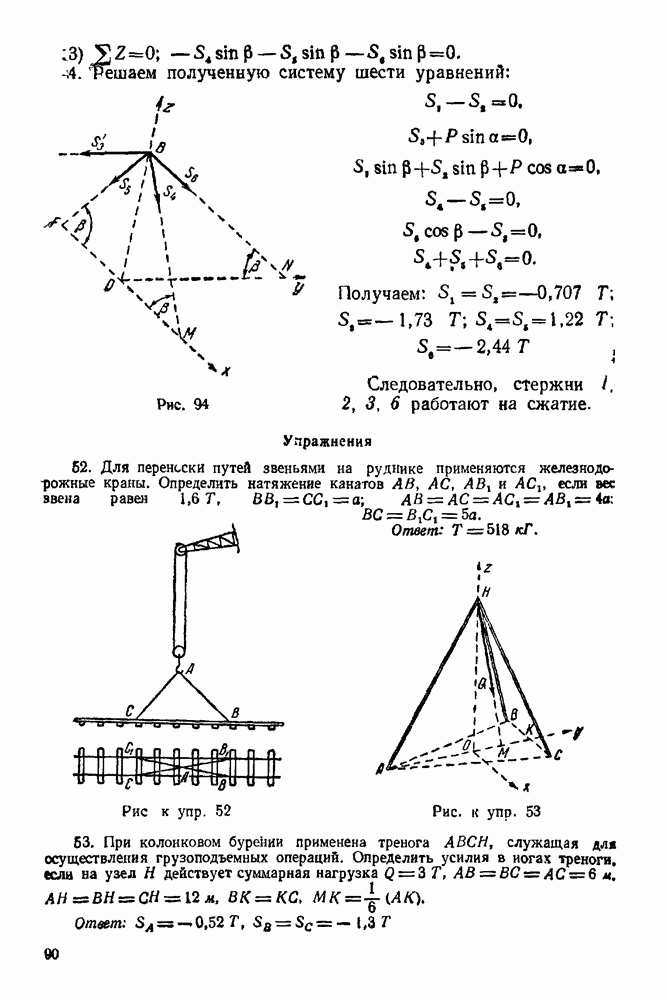
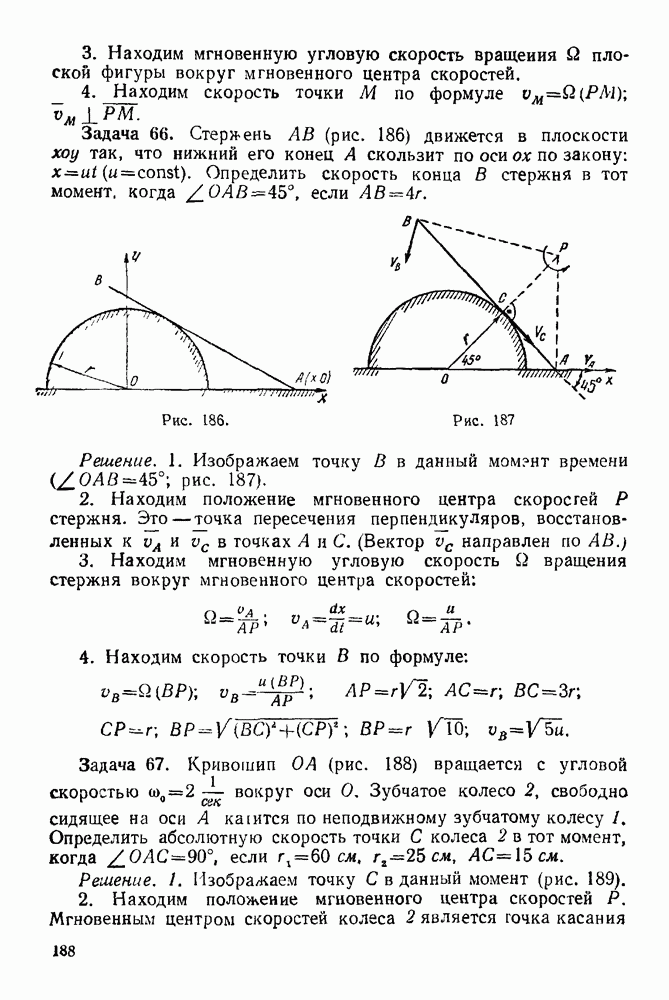
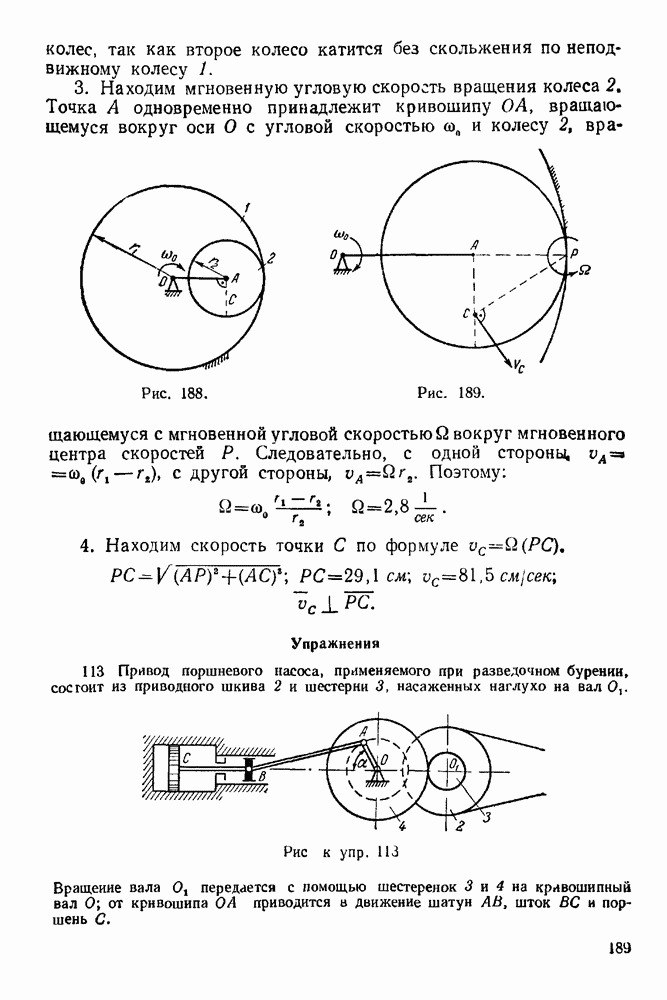
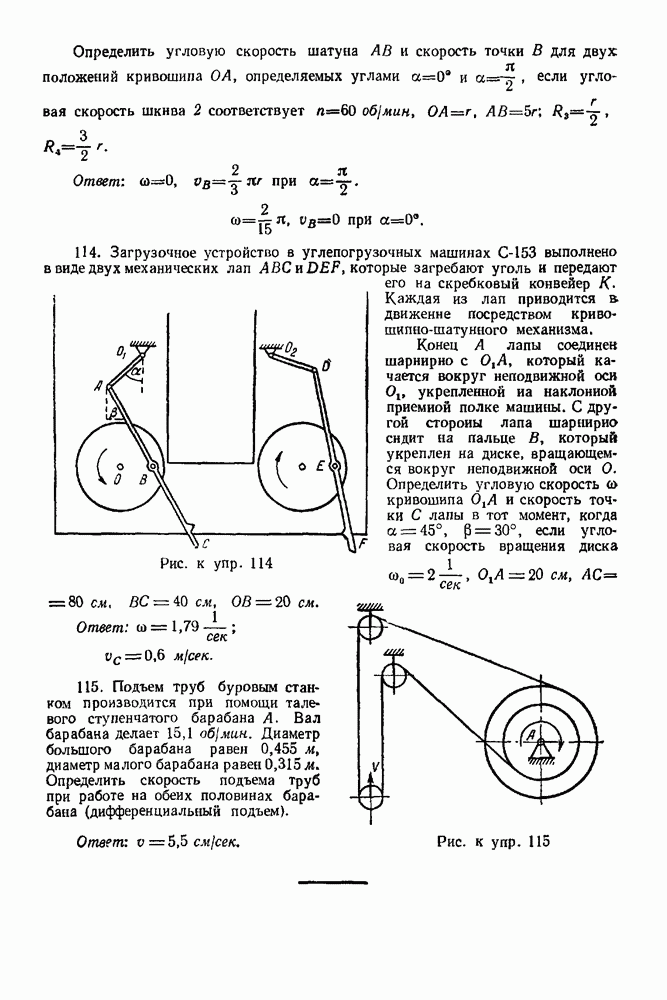
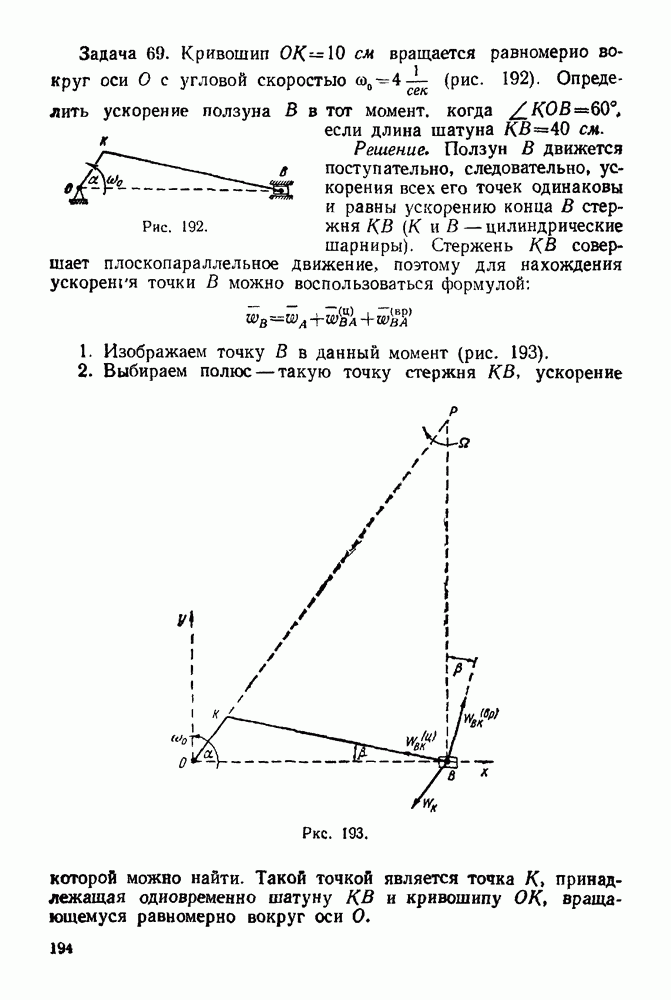
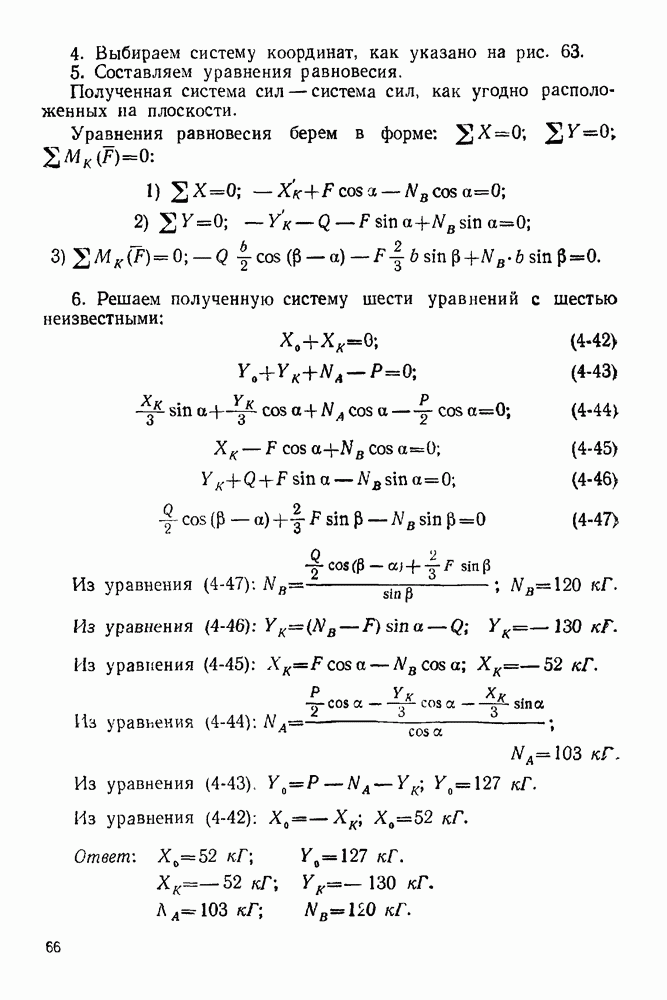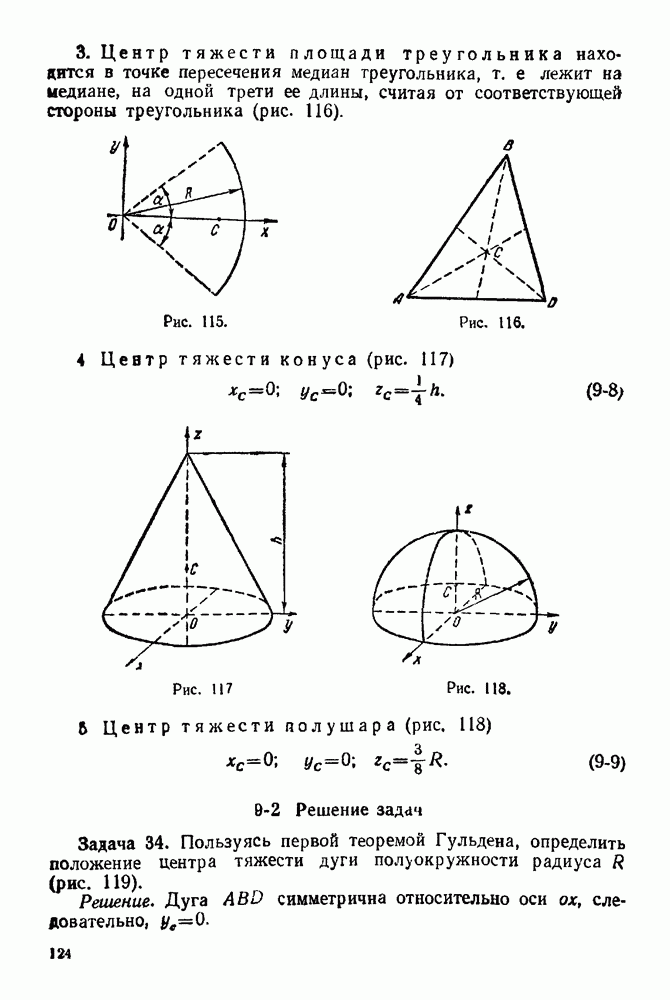| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4-5. Решение задач на равновесие системы сочлененных тел
Системой сочлененных твердых тел называется несколько твердых тел, касающихся друг друга или соединенных между собой посредством шарниров, стержней, нитей. Во многих задачах на равновесие системы сочлененных тел требуется найти силу, с которой одно сочлененное тело действует на другое. Такие задачи чаще всего решаются путем рассмотрения равновесия каждого тела в отдельности (если вся система тел находится в равновесии, то и каждое тело системы находится в равновесии). При рассмотрении равновесия каждого тела системы остальные тела системы будут являться связями, наложенными на это тело, а при освобождении данного тела от связей, действия связей заменяем силами — реакциями связей. При этом следует помнить, что силы взаимодействия двух тел равны между собой по абсолютной величине, лежат на одной прямой и направлены в разные стороны (по принципу равенства действия и противодействия). Иногда бывает выгодно рассматривать равновесие системы всех тел, вместе взятых, а затем уже рассматривать равновесие отдельного тела. Имея в виду принцип затвердевания (при затвердевании всякого нетвердого тела равновесие его не нарушается), всю совокупность тел нужно рассматривать как одно твердое тело. В этом случае в уравнения равновесия сил не войдут силы, с которыми отдельные тела действуют друг на друга.
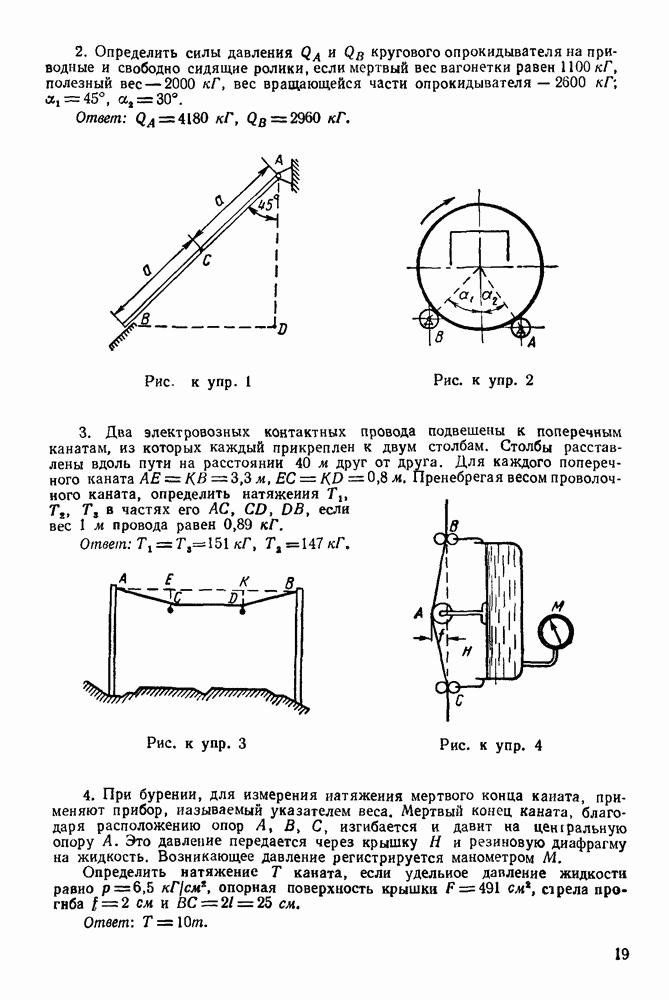
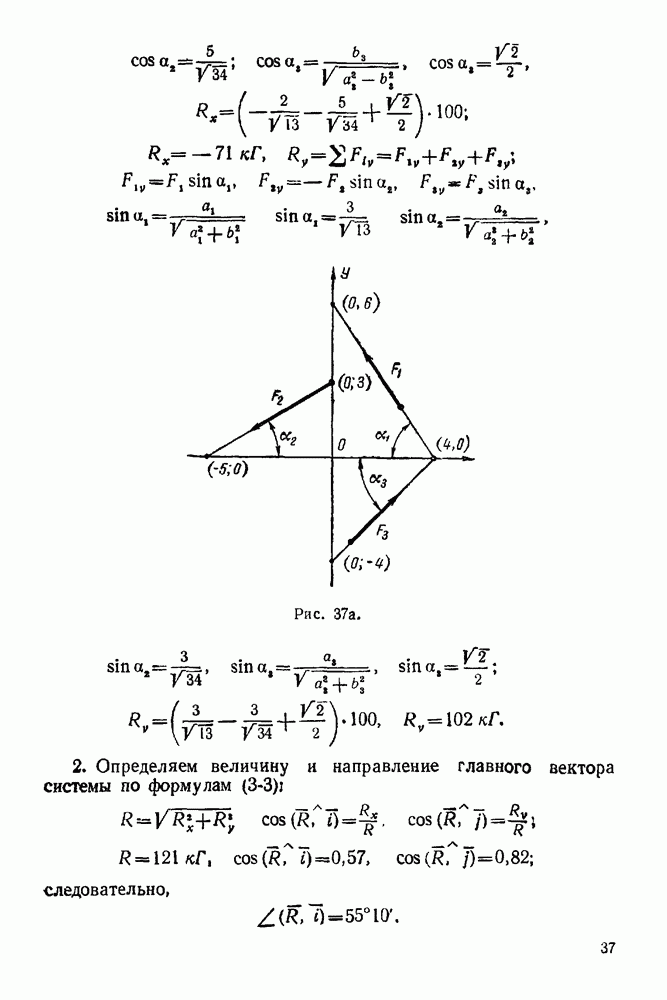
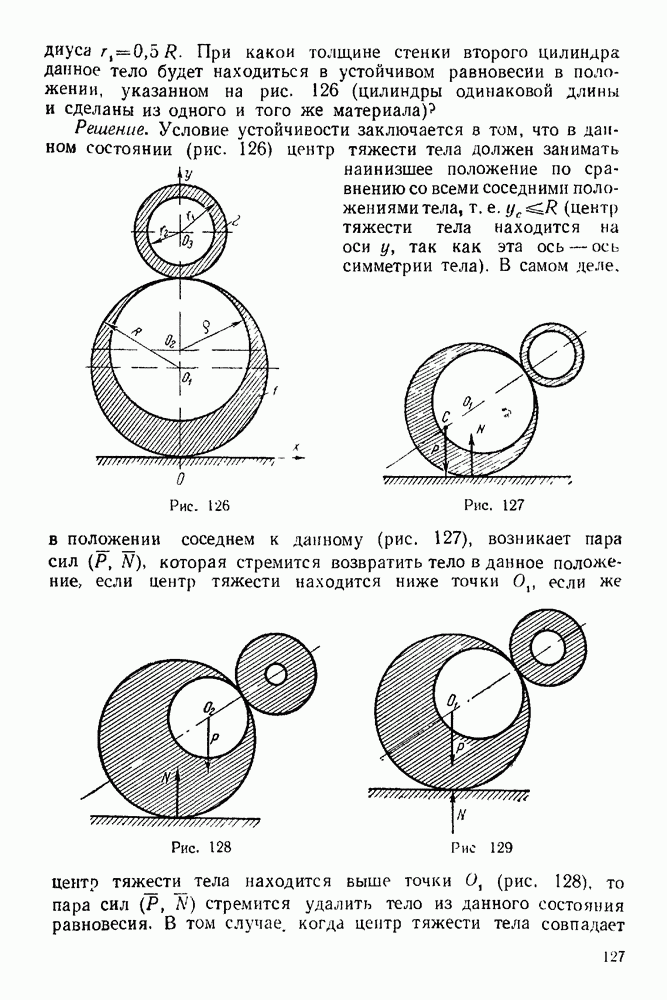
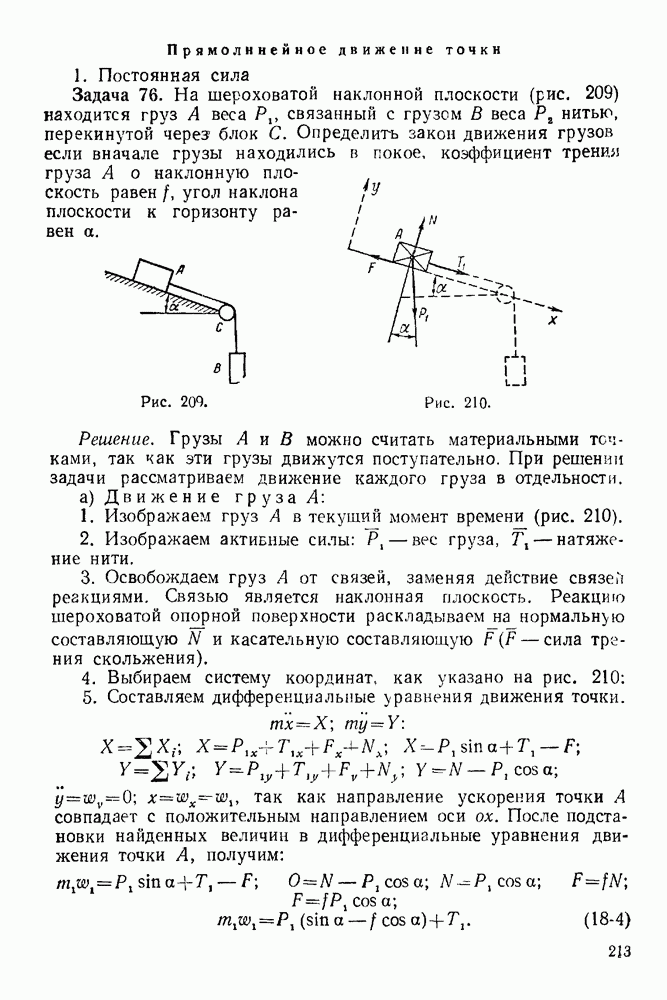
Задача 18. На шар веса  опирающийся на вертикальную стенку и наклонную балку
опирающийся на вертикальную стенку и наклонную балку  действует сила
действует сила  (рис. 55) Однородная балка
(рис. 55) Однородная балка  веса
веса  закреплена в точке О шарнирно и удерживается в наклонном положении при помощи вертикального троса
закреплена в точке О шарнирно и удерживается в наклонном положении при помощи вертикального троса  Определить, пренебрегая трением, давление шара на балку и стену, реакцию шарнира и натяжение троса, если
Определить, пренебрегая трением, давление шара на балку и стену, реакцию шарнира и натяжение троса, если 

Рис. 55.
Всего в данной задаче пять неизвестных:  величина и направление реакции
величина и направление реакции 
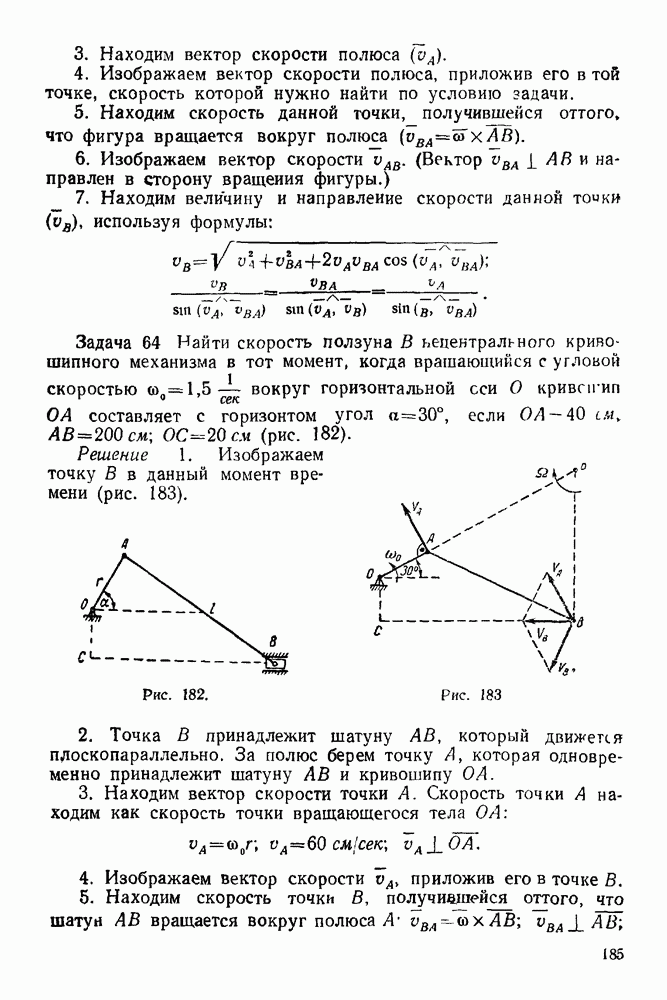
Решение Рассматриваем равновесие балки и шара, вместе взятых, а затем равновесие только шара, придерживаясь плана решения задачи, изложенного ранее
А. Равновесие балки и шара
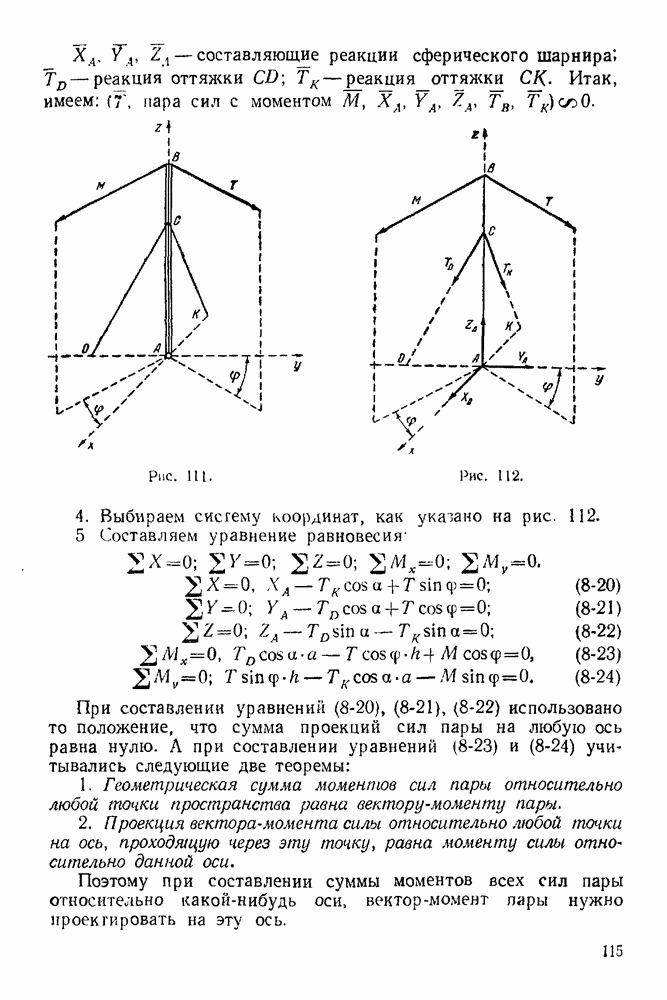
1 Рассматриваем равновесие балки и шара (рис. 56).
2. Изображаем активные  действующие на балку и шар:
действующие на балку и шар:  вес шара, сила
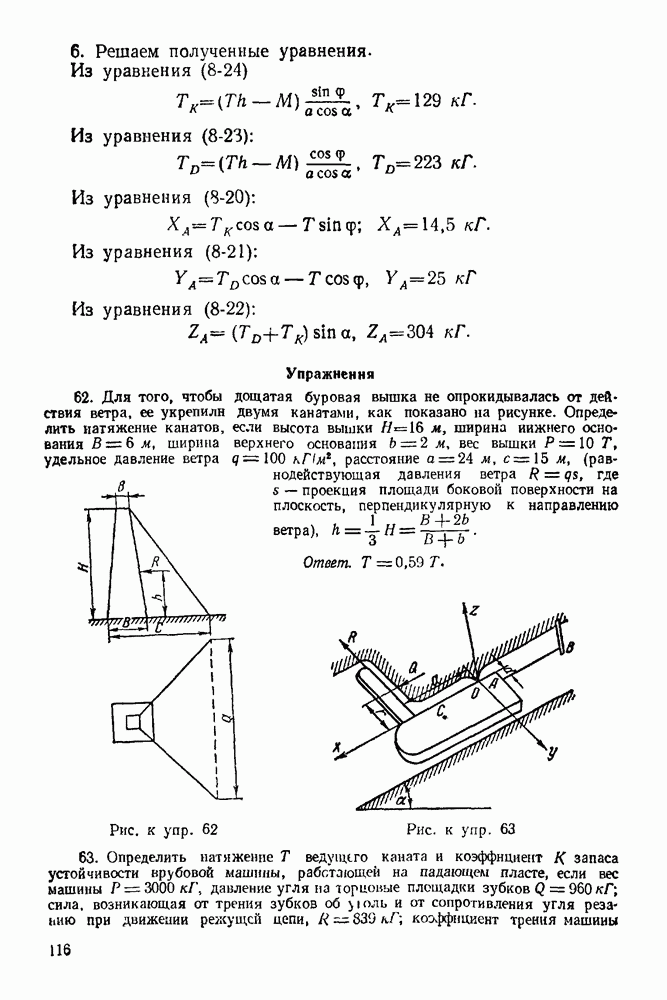
вес шара, сила  вес однородной Салки
вес однородной Салки
3 Освобождаем балку и шар от связей, заменяя действие связей реакциями. Связями являются вертикальная стена, цилиндрический шарнир О и трос  Реакция
Реакция  стены направлена перпендикулярно стене (по радиусу шара). Реакция
стены направлена перпендикулярно стене (по радиусу шара). Реакция  троса направлена по тросу. Реакцию шарнира О раскладываем на две составляющие
троса направлена по тросу. Реакцию шарнира О раскладываем на две составляющие 

Рис. 56.
4 Выбираем систему координат, как указано на рис. 56.
5. Составляем уравнения равновесия системы сил, действующих на балку и шар. Эта система — система сил, как угодно расположенных на плоскости. Берем уравнения равновесия в следующей форме: 

Б. Равновесие шара
1. Рассматриваем равновесие шара (рис. 57).
2. Изображаем активные силы:  вес шара и силу
вес шара и силу 
3. Освобождаем шар от связей, заменяя действие связей реакциями. Связями являются: балка  и вертикальная стена. Реакция
и вертикальная стена. Реакция  стены направлена перпендикулярно стене, реакция
стены направлена перпендикулярно стене, реакция  балки направлена перпендикулярно балке
балки направлена перпендикулярно балке

Рис. 57.
4. Выбираем систему координат, как указано на рис. 57.
5 Составляем уравнения равновесия системы сил, действующих на шар. Эта система — система сходящихся сил на плоскости. Следовательно, уравнения равновесия будут:

6. Решаем полученную систему пяти уравнений с пятью неизвестными:

так как 
Из уравнения (4-35): 
Из уравнения (4-34). 
Из уравнения (4-31): 
Из уравнения (4-33) 
Из уравнения (4-32): 
Ответ. 
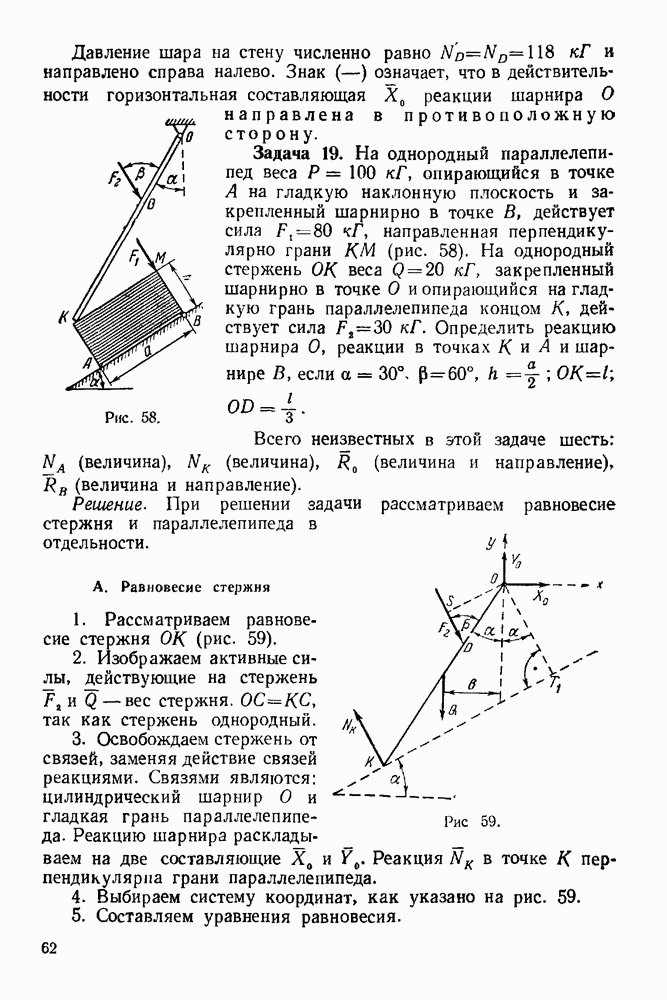
Давление шара на стену численно равно  и направлено справа налево. Знак
и направлено справа налево. Знак  означает, что в действительности горизонтальная составляющая
означает, что в действительности горизонтальная составляющая  реакции шарнира О направлена в противоположную сторону.
реакции шарнира О направлена в противоположную сторону.
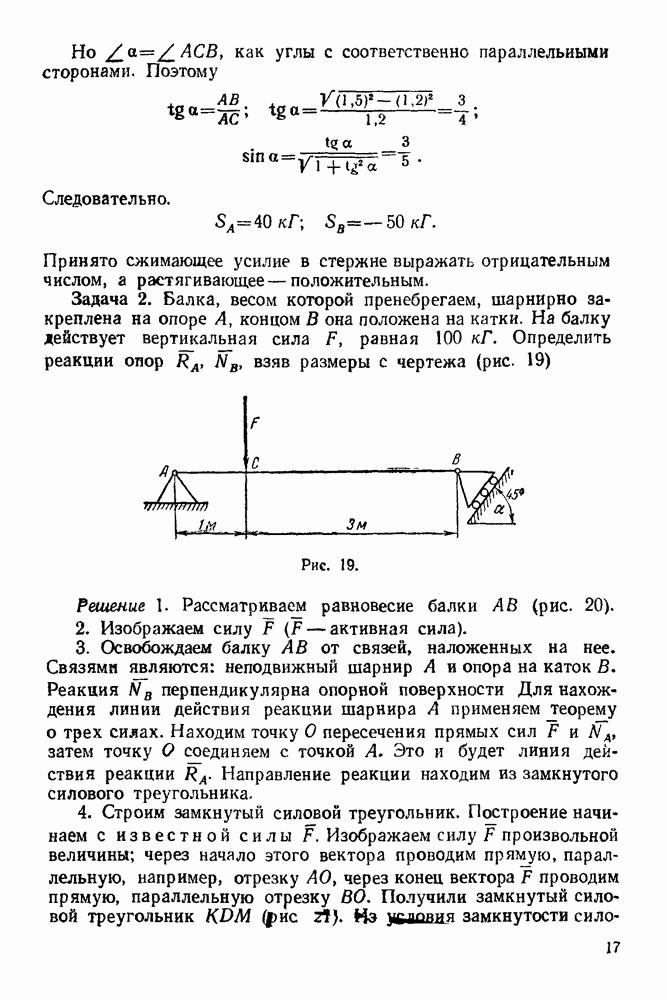
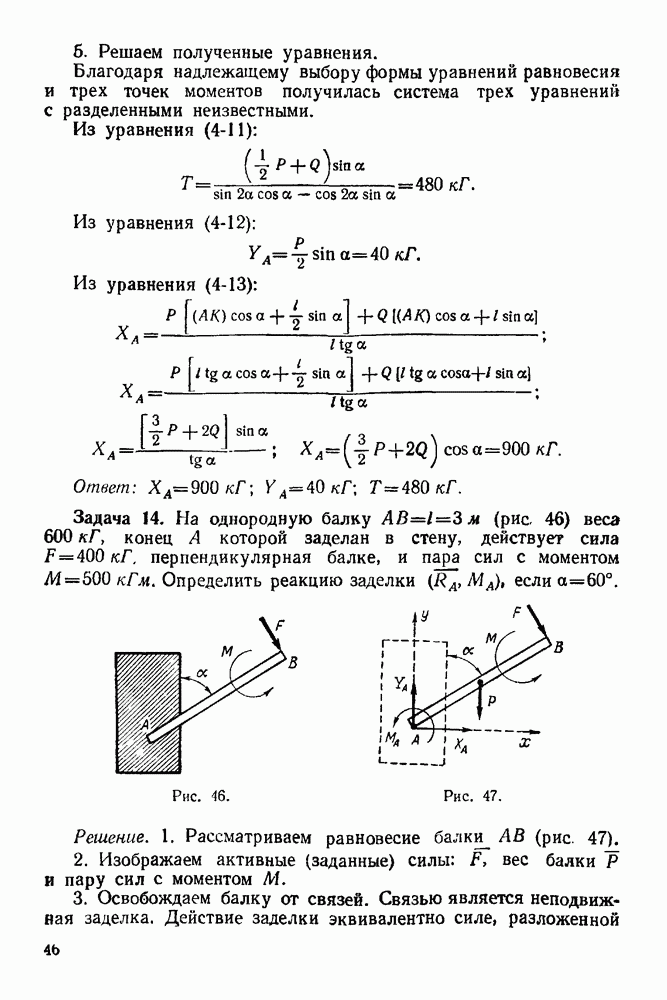
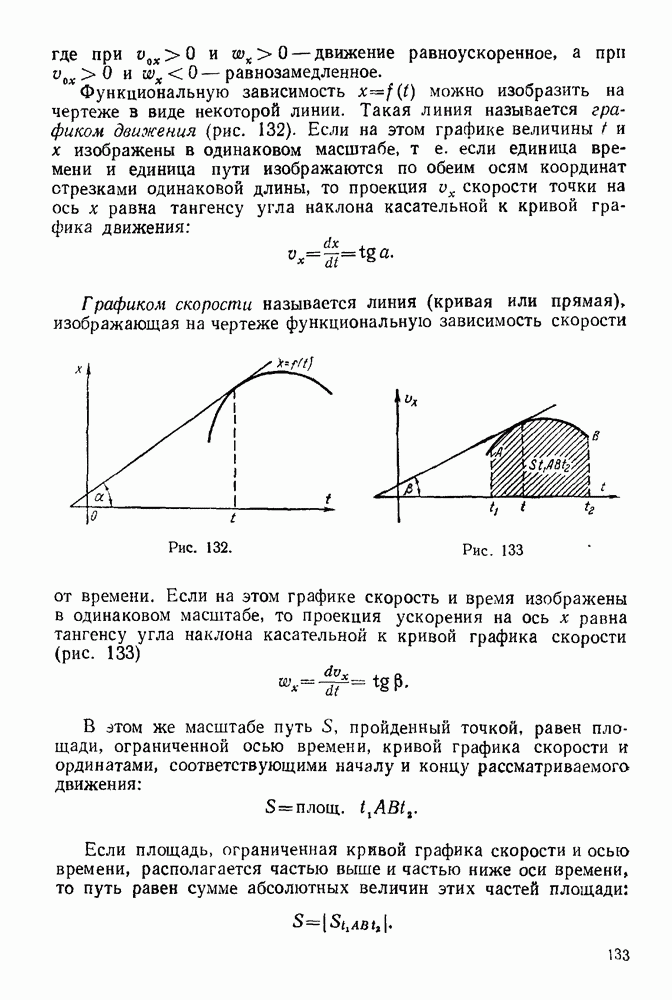
Задача 19. На однородный параллелепипед веса  опирающийся в точке А на гладкую наклонную плоскость и закрепленный шарнирно в точке В, действует сила
опирающийся в точке А на гладкую наклонную плоскость и закрепленный шарнирно в точке В, действует сила  направленная перпендикулярно грани
направленная перпендикулярно грани  (рис. 58). На однородный стержень
(рис. 58). На однородный стержень  веса
веса  закрепленный шарнирно в точке О и опирающийся на гладкую грань параллелепипеда концом К, действует сила
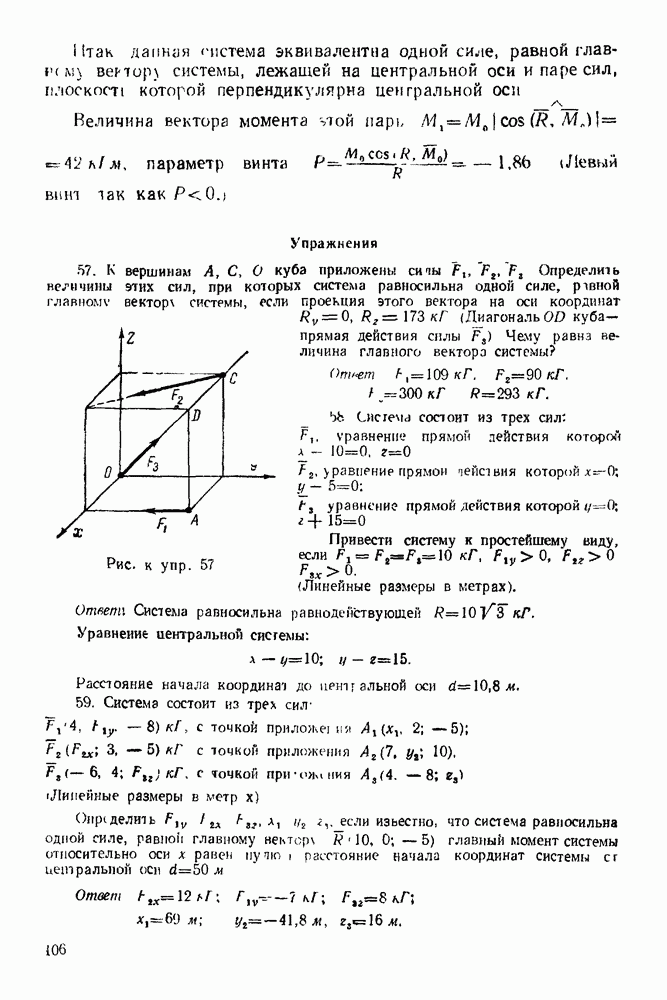
закрепленный шарнирно в точке О и опирающийся на гладкую грань параллелепипеда концом К, действует сила  Определить реакцию шарнира О, реакции в точках
Определить реакцию шарнира О, реакции в точках  и шарнире В, если
и шарнире В, если 

Рис. 58.

Рис. 59.
Всего неизвестных в этой задаче шесть:  (величина),
(величина),  (величина),
(величина),  (величина и направление),
(величина и направление),  (величина и направление).
(величина и направление).
Решение. При решении задачи рассматриваем равновесие стержня и параллелепипеда в отдельности.
А. Равновесие стержня
1. Рассматриваем равновесие стержня  (рис. 59).
(рис. 59).
2. Изображаем активные силы, действующие на стержень  вес стержня.
вес стержня.  так как стержень однородный.
так как стержень однородный.
3. Освобождаем стержень от связей, заменяя действие связей реакциями. Связями являются: цилиндрический шарнир О и гладкая грань параллелепипеда. Реакцию шарнира раскладываем на две составляющие  Реакция
Реакция  в точке К перпендикулярна грани параллелепипеда.
в точке К перпендикулярна грани параллелепипеда.
4. Выбираем систему координат, как указано на рис. 59.
5. Составляем уравнения равновесия.
Полученная система — система сил, как угодно расположенных на плоскости.
Уравнения равновесия берем в следующей форме:

где 
Б. Равновесие параллелепипеда
1. Рассматриваем равновесие параллелепипеда (рис. 60).
2. Изображаем активные силы, действующие на параллелепипед:  вес однородного параллелепипеда и
вес однородного параллелепипеда и  давление стержня
давление стержня  По принципу равенства действия и противодействия
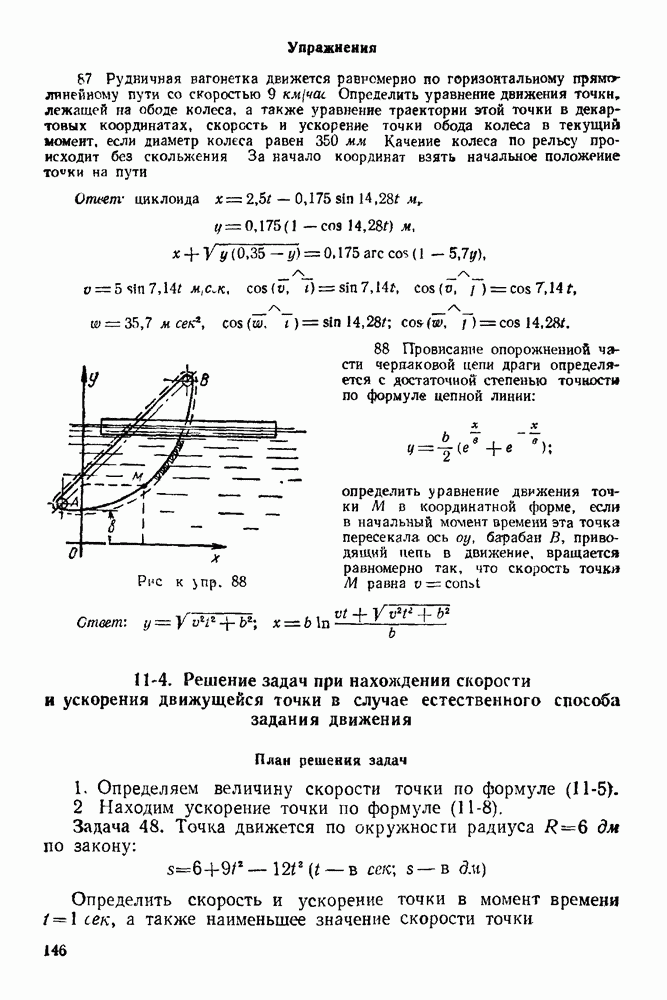
По принципу равенства действия и противодействия  и направлена противоположно направлению
и направлена противоположно направлению 

Рис. 60.
3. Освобождаем параллелепипед от связей, заменяя действие связей реакциями. Связями, наложенными на параллелепипед, являются: а) цилиндрический шарнир В и б) гладкая опора в точке  Реакцию шарнира В раскладываем на две составляющие:
Реакцию шарнира В раскладываем на две составляющие:  Реакция в точке
Реакция в точке  перпендикулярна наклонной плоскости.
перпендикулярна наклонной плоскости.
4. Выбираем оси, как указано на рис. 60.
5. Составляем уравнения равновесия.
Полученная система — система сил, как угодно расположенных на плоскости.
Уравнения равновесия берем в следующей форме:

Для того чтобы облегчить нахождение момента силы  относительно точки В, мы воспользовались теоремой Вариньона, разложив силу
относительно точки В, мы воспользовались теоремой Вариньона, разложив силу  на составляющие по осям
на составляющие по осям  величина составляющей по оси
величина составляющей по оси  величина составляющей по оси х).
величина составляющей по оси х).
6. Решаем полученную систему шести уравнений с шестью неизвестными:

Из уравнения (4-38): 
Из уравнения (4-37): 
Из уравнения (4-36): 
Из уравнения (4-39): 
Из уравнения (4-41). 
Из уравнения (4-40): 
Ответ. 
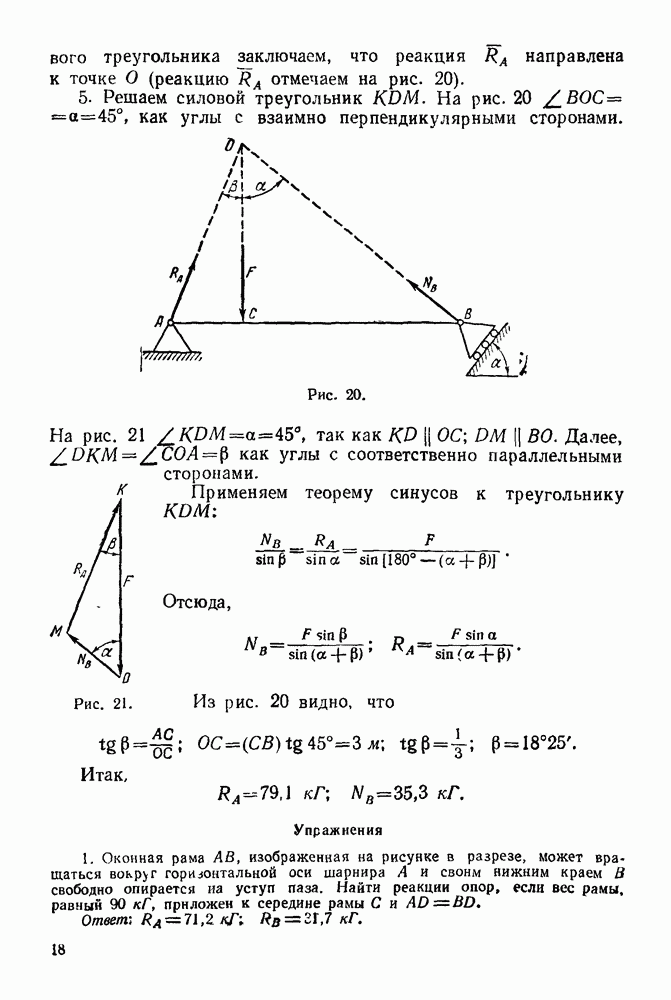
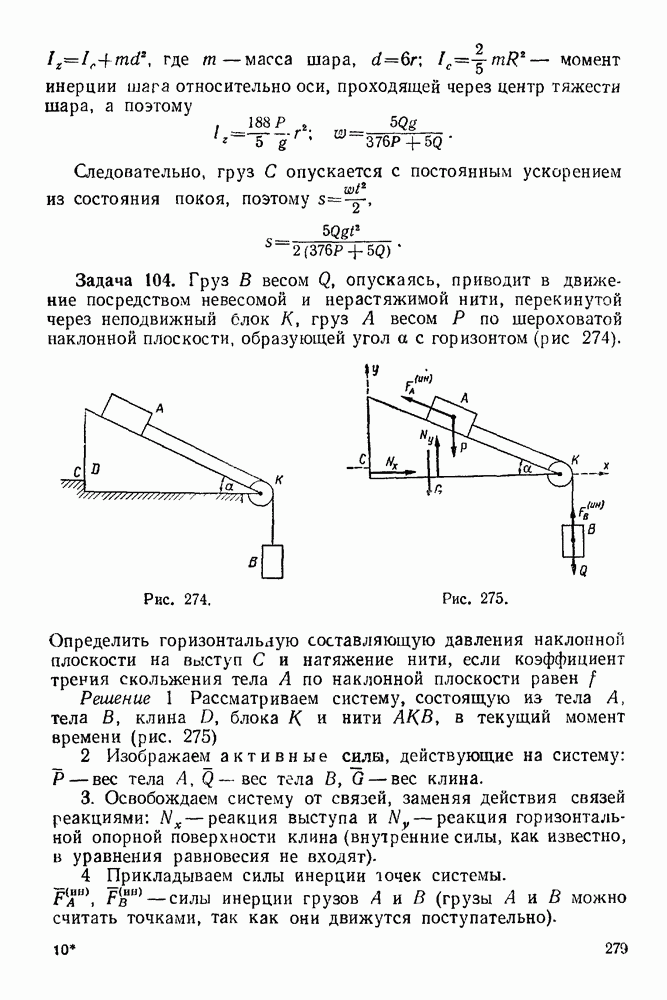
Задача 20. Однородный стержень  веса
веса  (рис. Ы) концом О шарнирно прикреплен к стене, а концом А опирается на гладкий пол. Однородный стержень
(рис. Ы) концом О шарнирно прикреплен к стене, а концом А опирается на гладкий пол. Однородный стержень  веса
веса  прикреплен в точке К шарнирно к стержню
прикреплен в точке К шарнирно к стержню  Конец В стержня опирается на гладкую наклонную плоскость. В точке
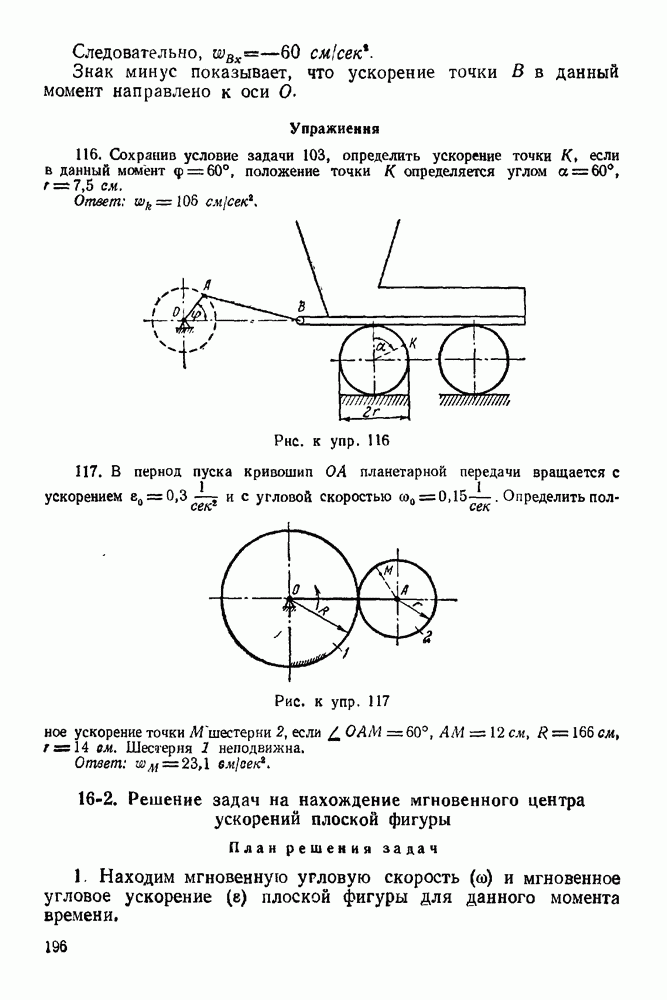
Конец В стержня опирается на гладкую наклонную плоскость. В точке  стержня приложена сила
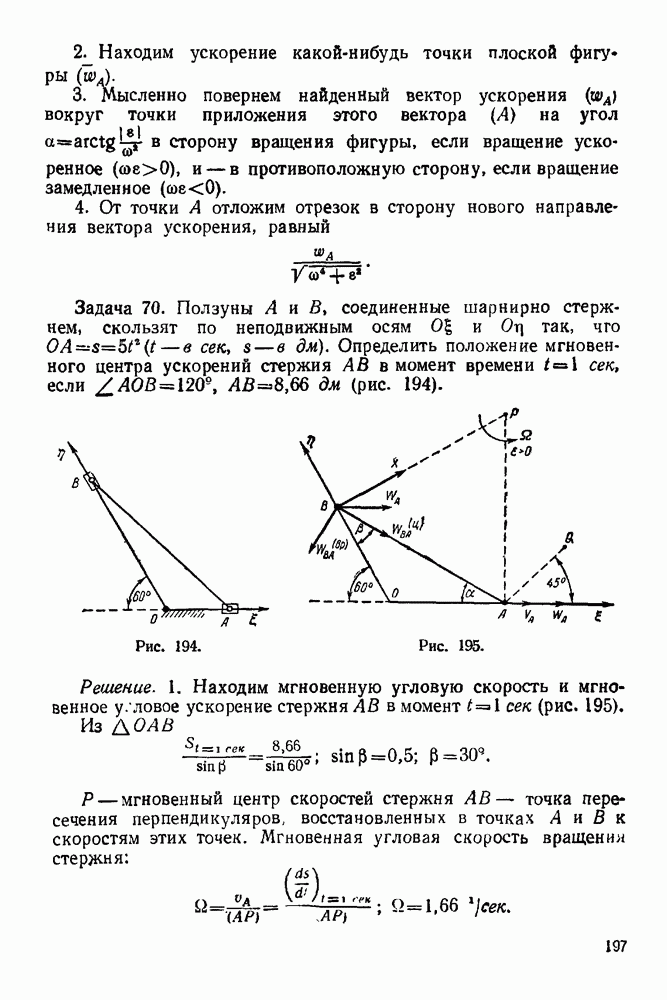
стержня приложена сила  Определить реакцию шарниров
Определить реакцию шарниров  а также реакции опорных поверхностей в точках
а также реакции опорных поверхностей в точках  если
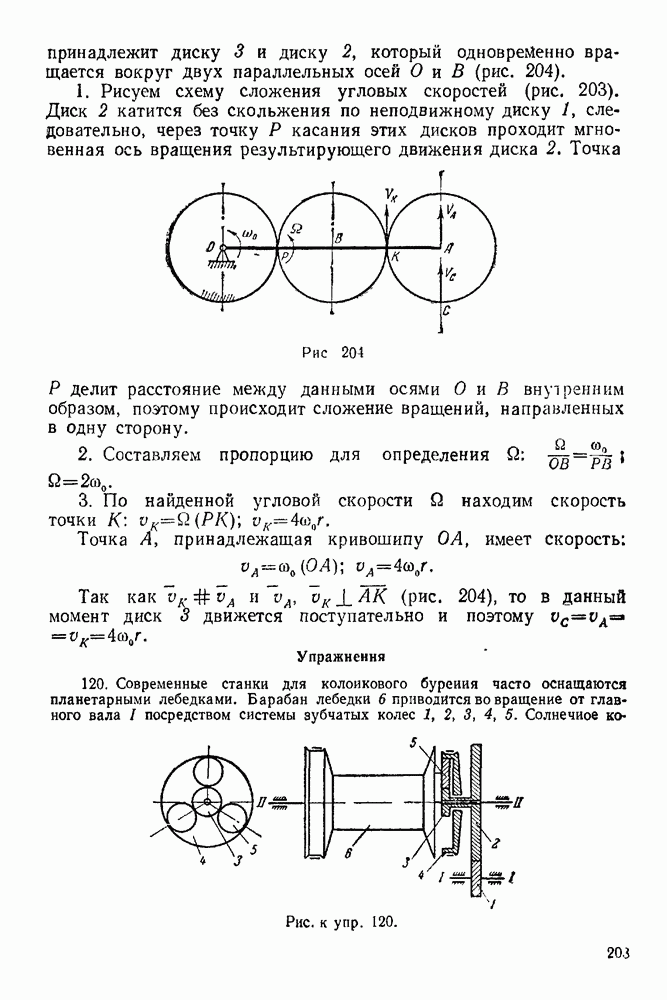
если 

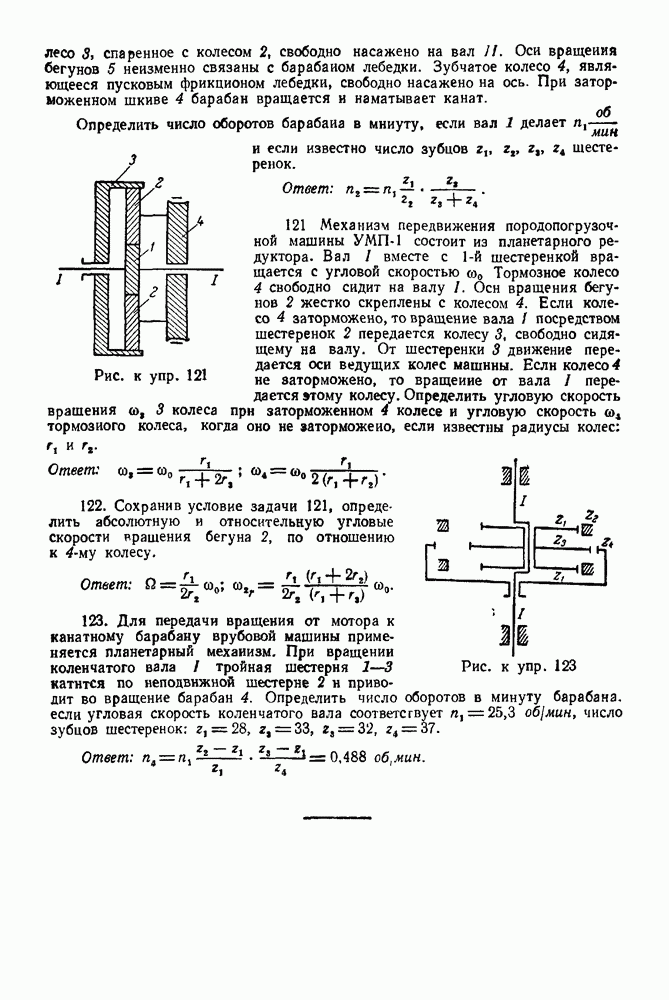
Рис. 61
В этой задаче шесть неизвестных:  (величина),
(величина),  (величина),
(величина),  (величина и направление),
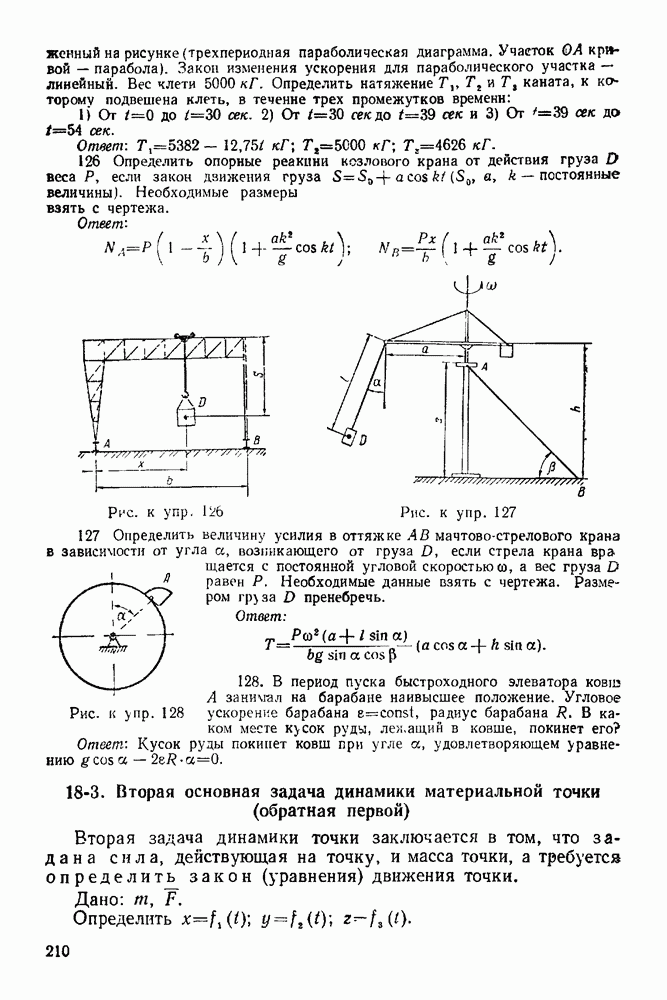
(величина и направление),  (величина и направление). При решении задачи рассматриваем равновесие обоих стержней в отдельности.
(величина и направление). При решении задачи рассматриваем равновесие обоих стержней в отдельности.
А. Равновесие стержня OA
1. Рассматриваем равновесие стержня  (рис. 62).
(рис. 62).
2 Изображаем активную силу  вес стержня.
вес стержня.
3. Освобождаем стержень от связей, заменяя действие связей реакциями. Связями явтяются: а) цилиндрический шарнир О, б) гладкая опора в точке  стержень
стержень  прикрепленный к стержню
прикрепленный к стержню  при помощи цилиндрического шарнира
при помощи цилиндрического шарнира  Реакцию шарнира О раскладываем на две составляющие:
Реакцию шарнира О раскладываем на две составляющие:  Реакцию шарнира К также раскладываем на две составляющие:
Реакцию шарнира К также раскладываем на две составляющие:  Реакция
Реакция  направлена перпендикулярно опорной поверхности.
направлена перпендикулярно опорной поверхности.

Рис. 62
4. Выбираем систему координат, как указано на рис. 62.
5. Составляем уравнения равновесия.
Полученная система сил — система сил, как угодно расположенных на плоскости.
Уравнения равновесия берем в форме:

Б. Равновесие стержня BK
1. Рассматриваем равновесие стержня  (рис. 63).
(рис. 63).
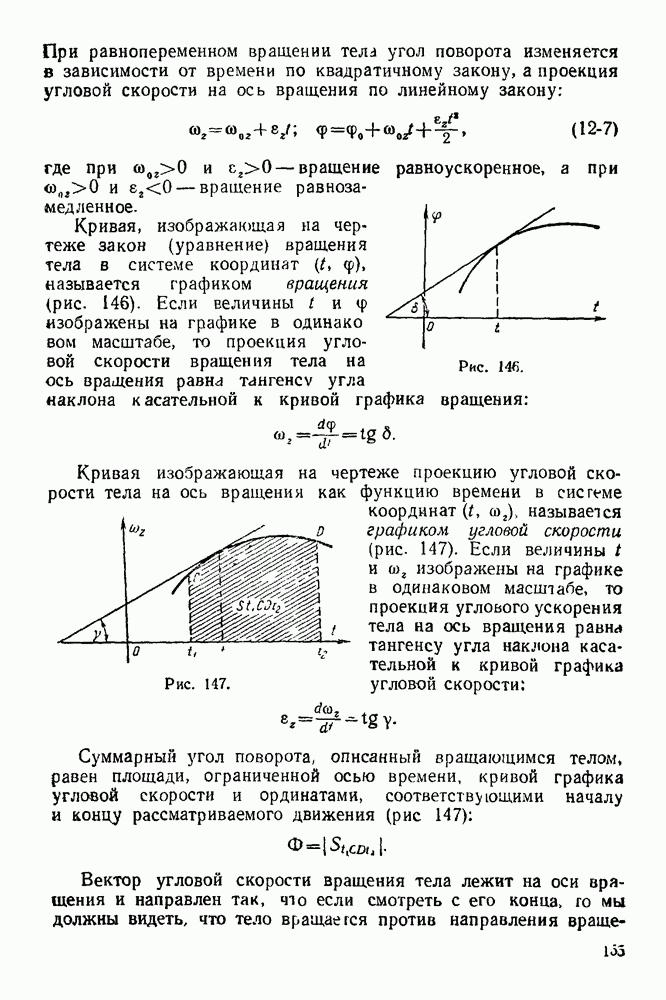
2. Изображаем активные силы, действующие на стержень: 
— вес однородного стержня.

Рис. 63
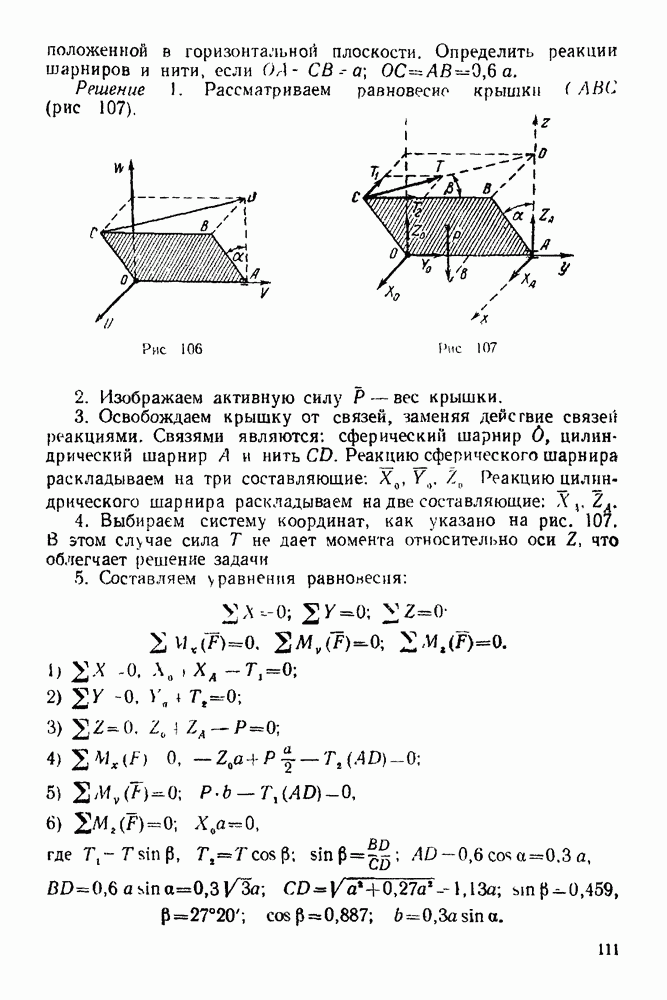
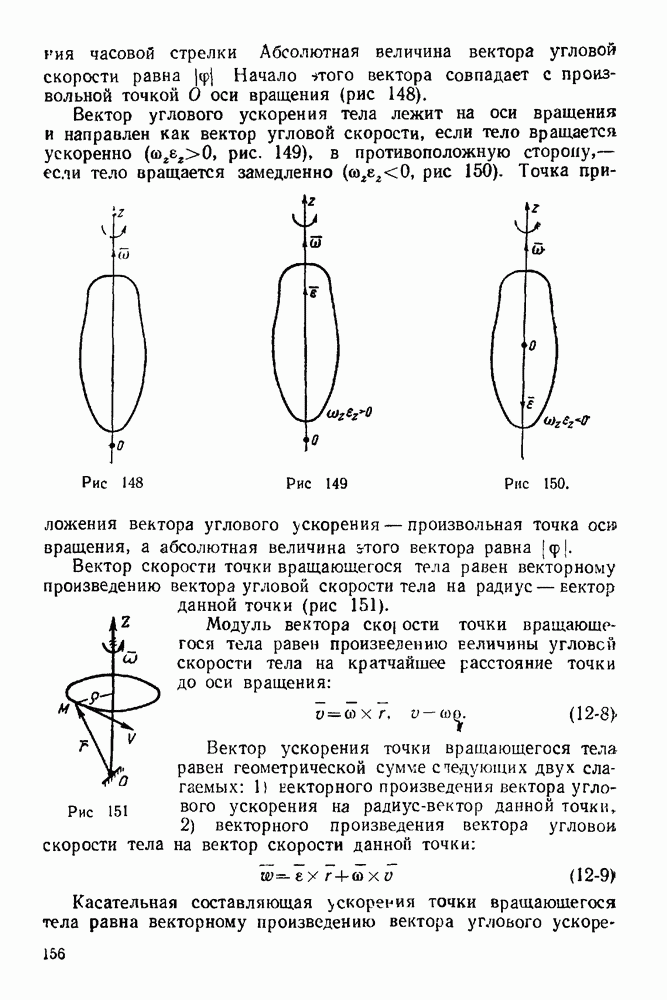
3. Освобождаем стержень В К от связей, заменяя действие связей реакциями. Связями являются: а) гладкая наклонная стенка и б) стержень  прикрепленный к стержню
прикрепленный к стержню  при помощи шарнира
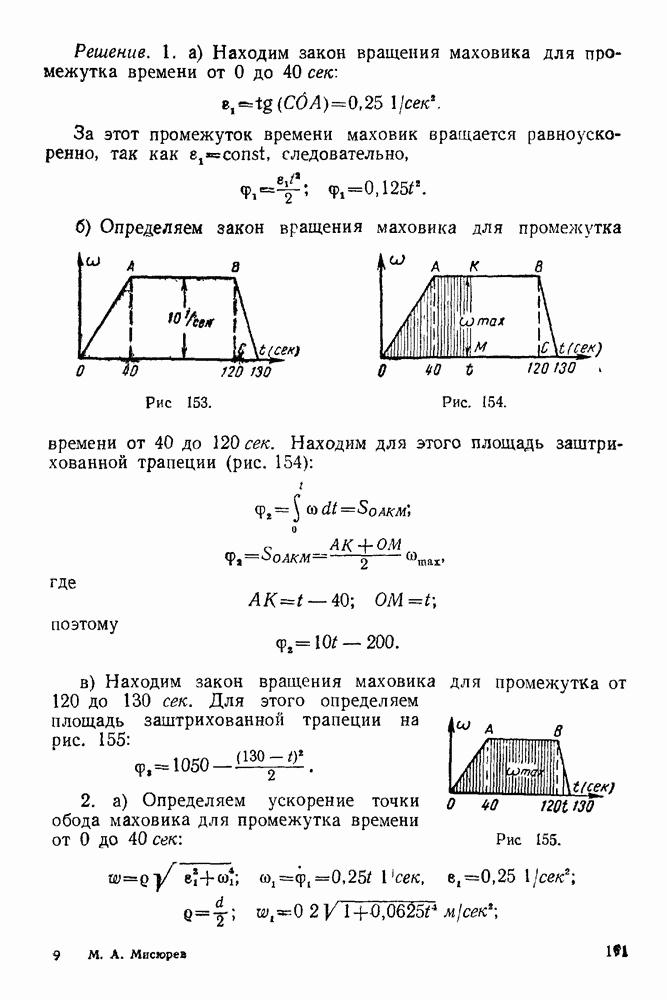
при помощи шарнира  Реакция
Реакция  стенки перпендикулярна стенке.
стенки перпендикулярна стенке.  Реакцию шарнира К раскладываем на две составляющие:
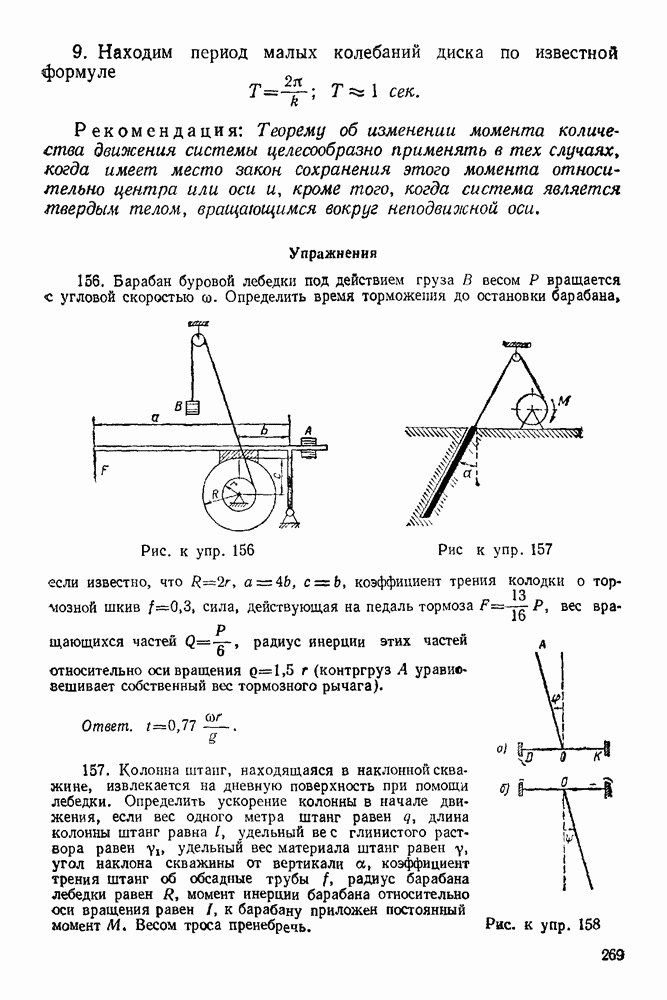
Реакцию шарнира К раскладываем на две составляющие:  и
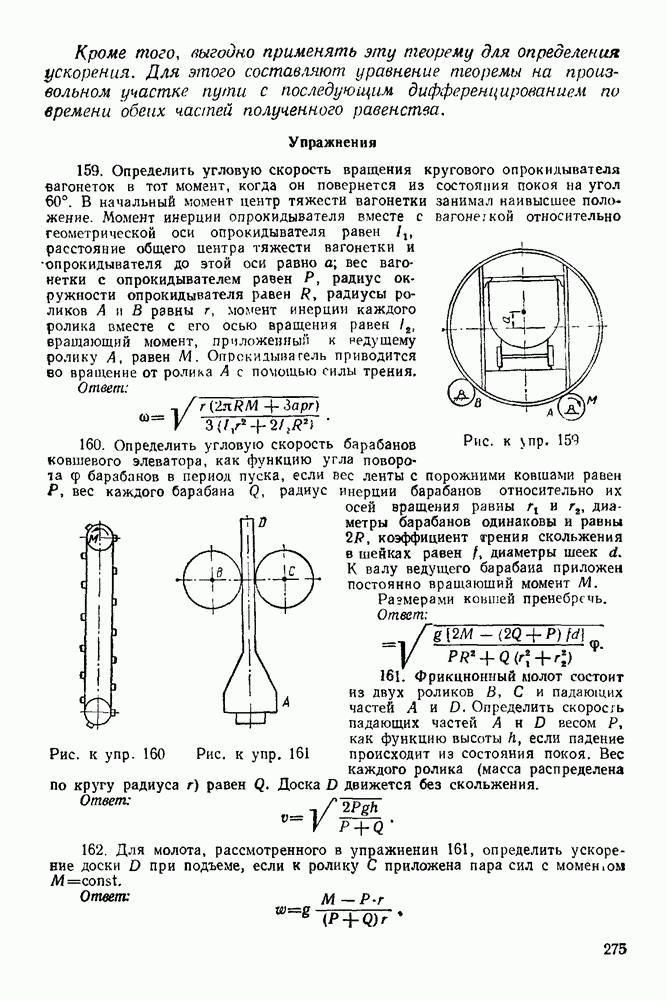
и  причем в силу принципа равенства действия и противодействия
причем в силу принципа равенства действия и противодействия  составляющая
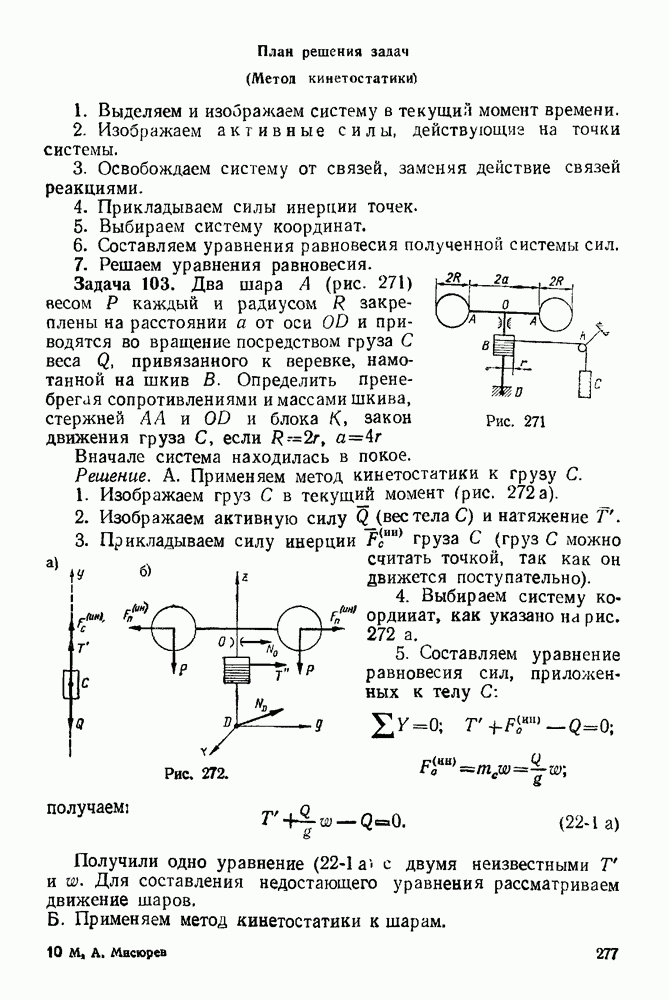
составляющая  направлена противоположно направлению составляющей
направлена противоположно направлению составляющей  а составляющая
а составляющая  направлена противоположно направлению составляющей
направлена противоположно направлению составляющей 
4. Выбираем систему координат, как указано на рис. 63.
5. Составляем уравнения равновесия.
Полученная система сил — система сил, как угодно расположенных на плоскости.
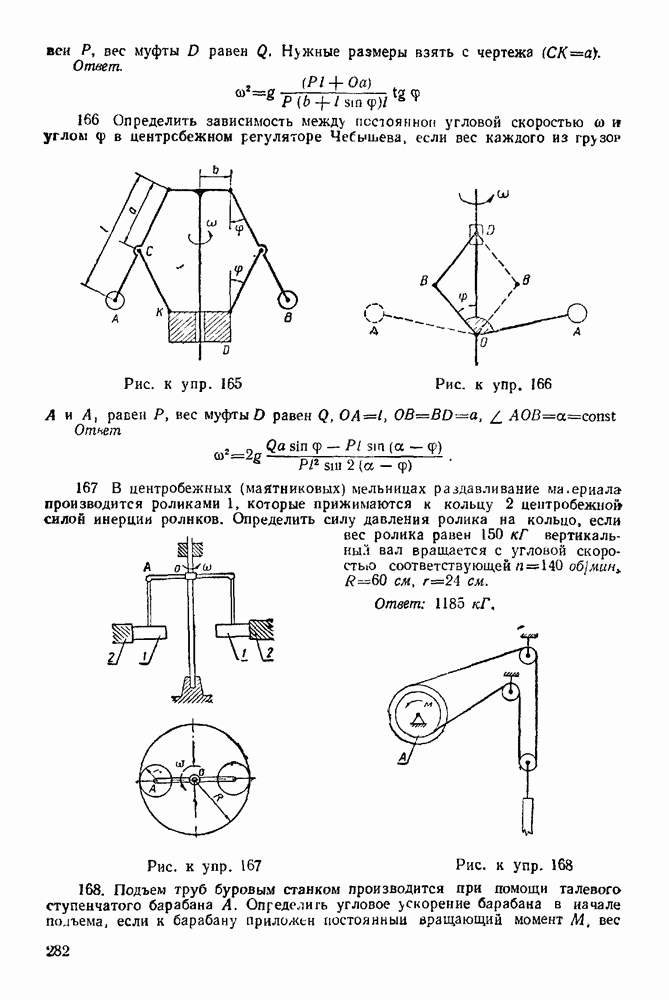
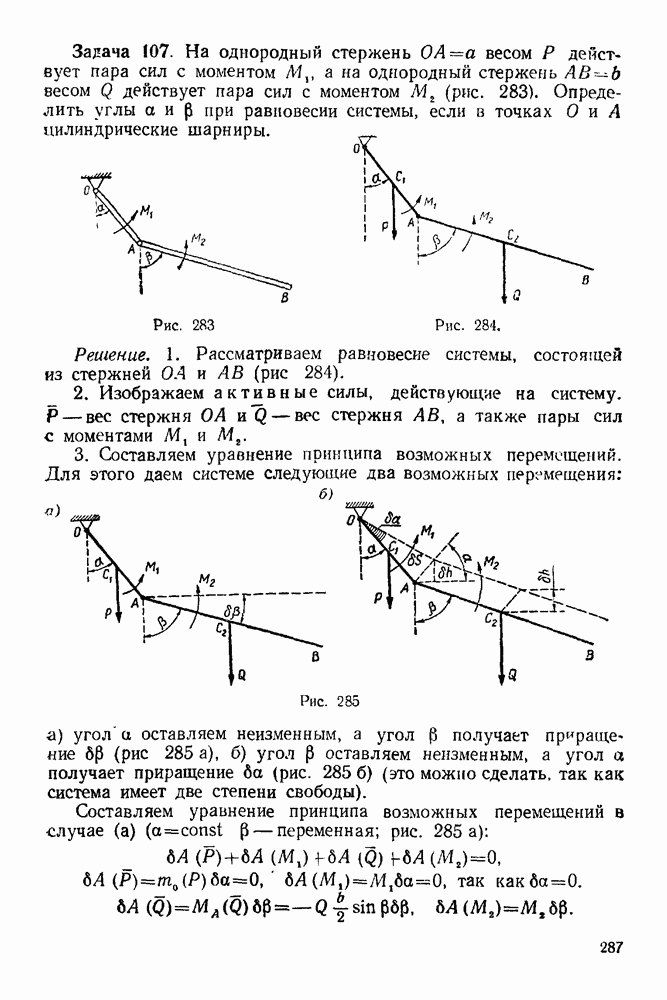
Уравнения равновесия берем в форме: 0:

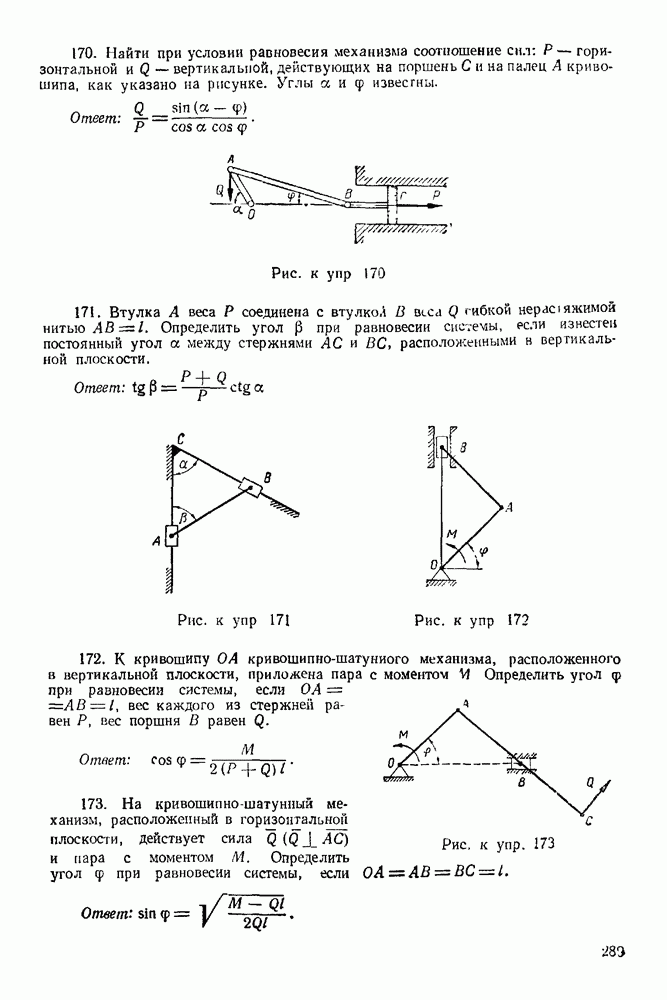
6. Решаем полученную систему шести уравнений с шестью неизвестными:

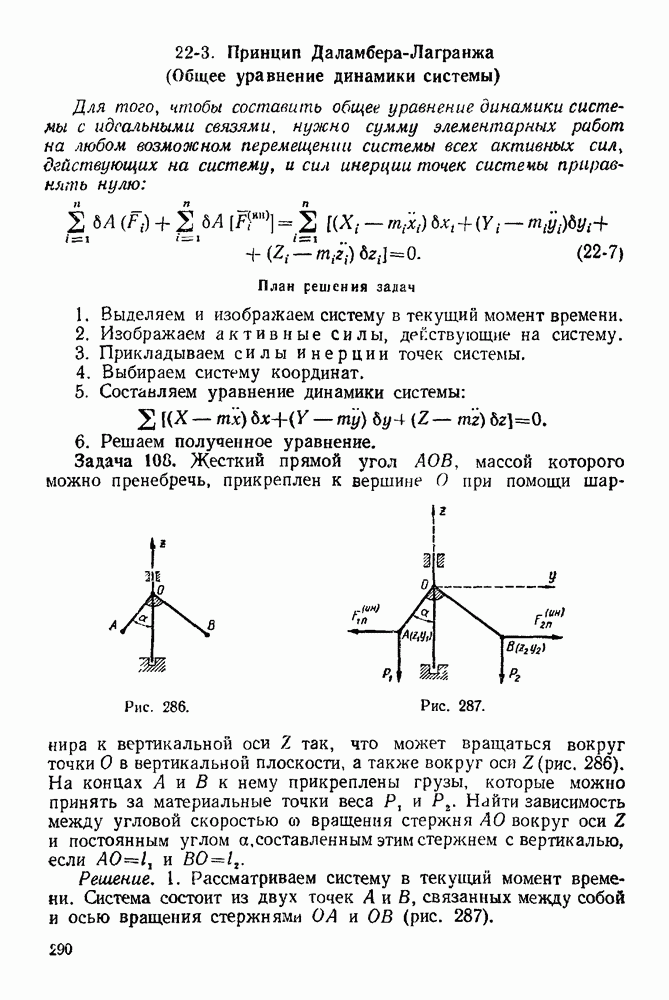
Из уравнения (4-47): 
Из уравнения (4-46): 
Из уравнения (4-45): 
Из уравнения (4-44): 
Из уравнения (4-43).  Из уравнения (4-42):
Из уравнения (4-42): 
Ответ: 
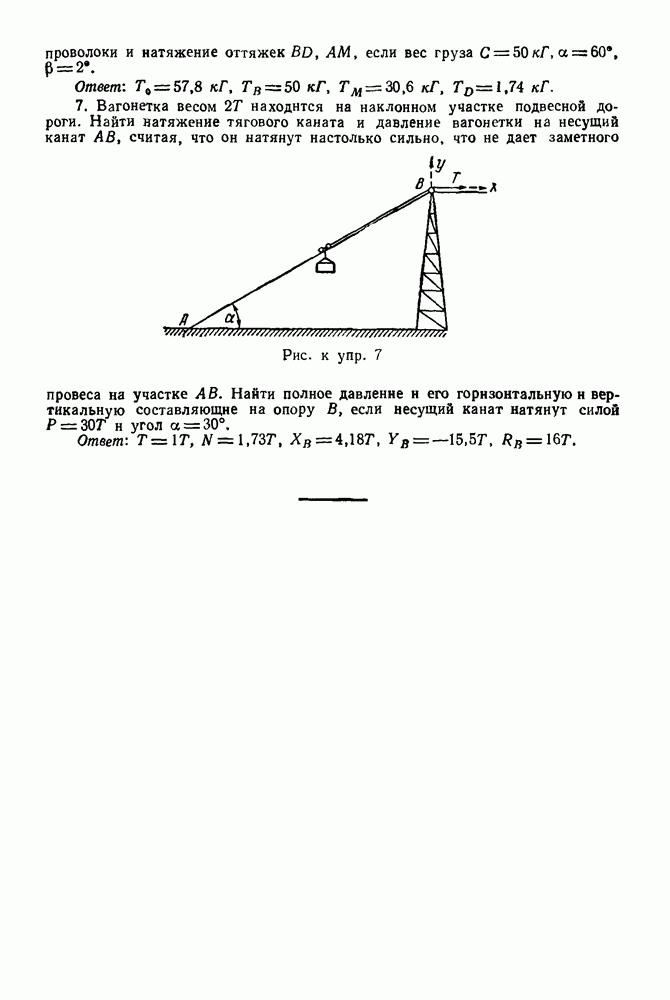
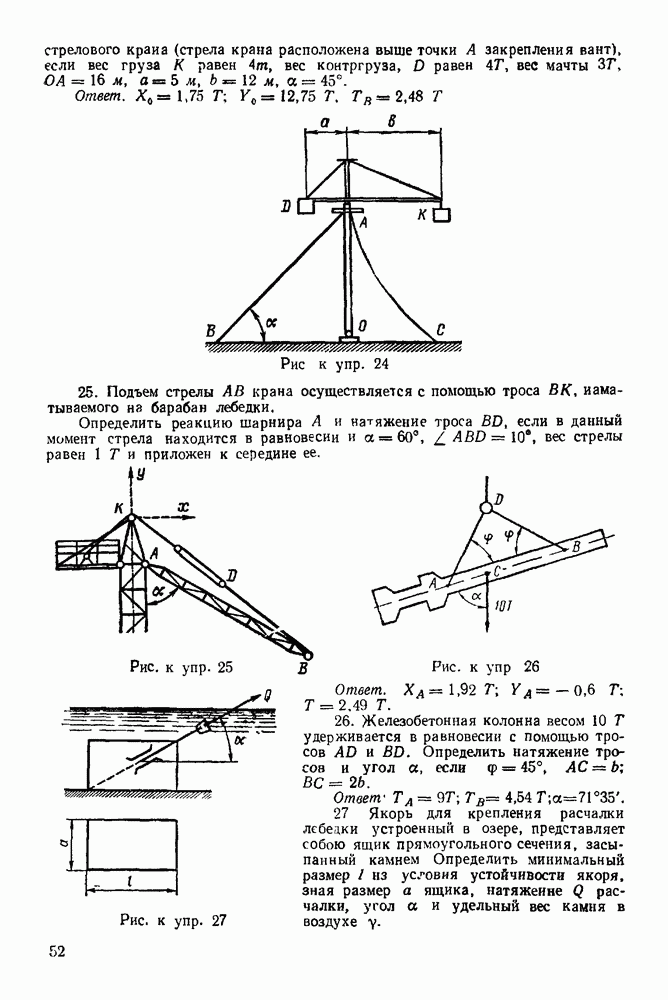
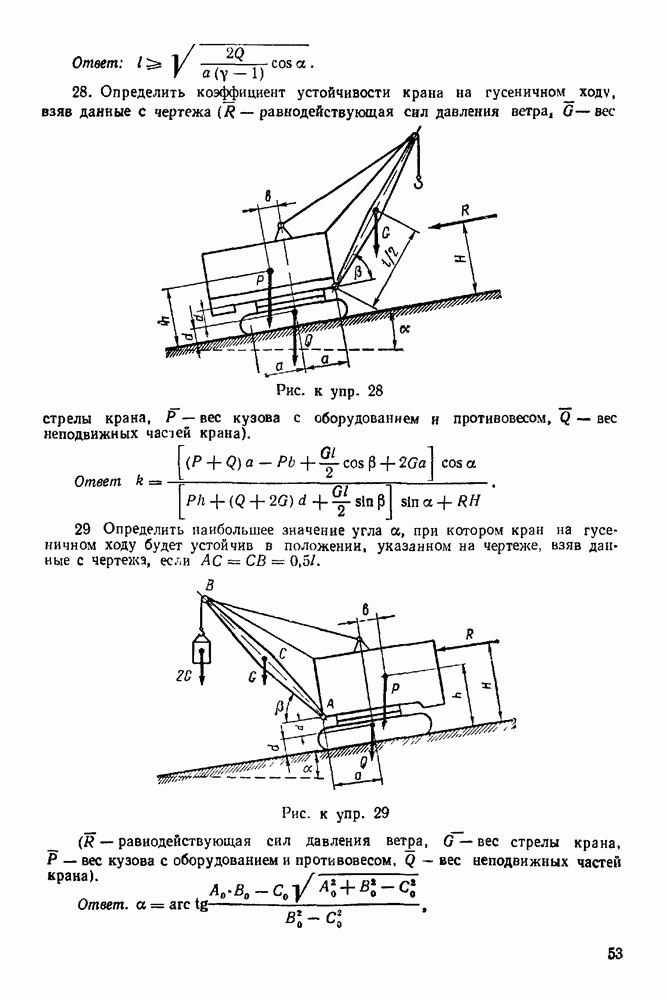
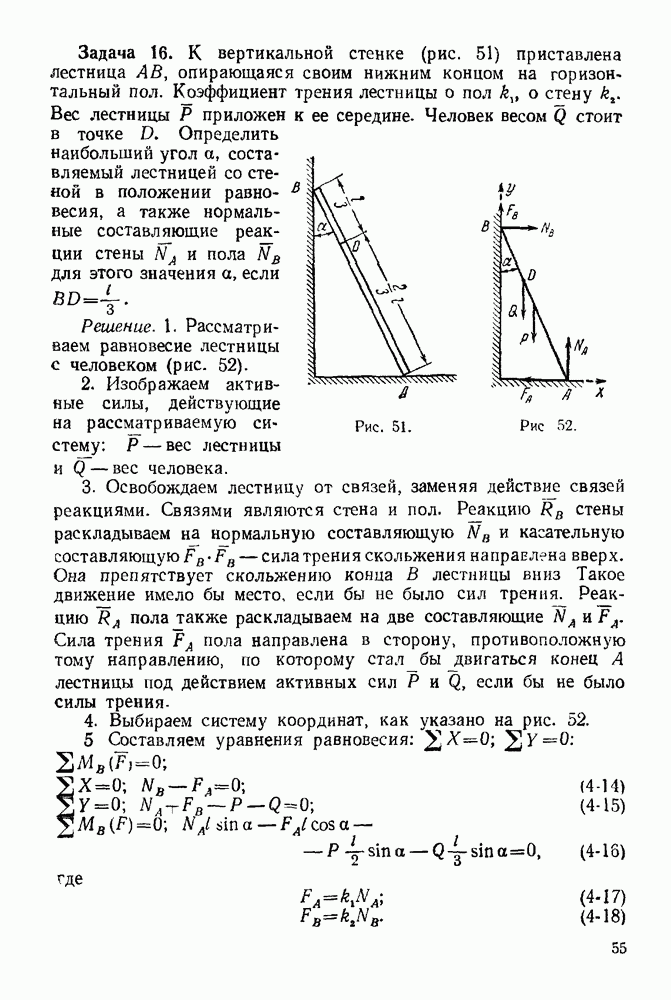
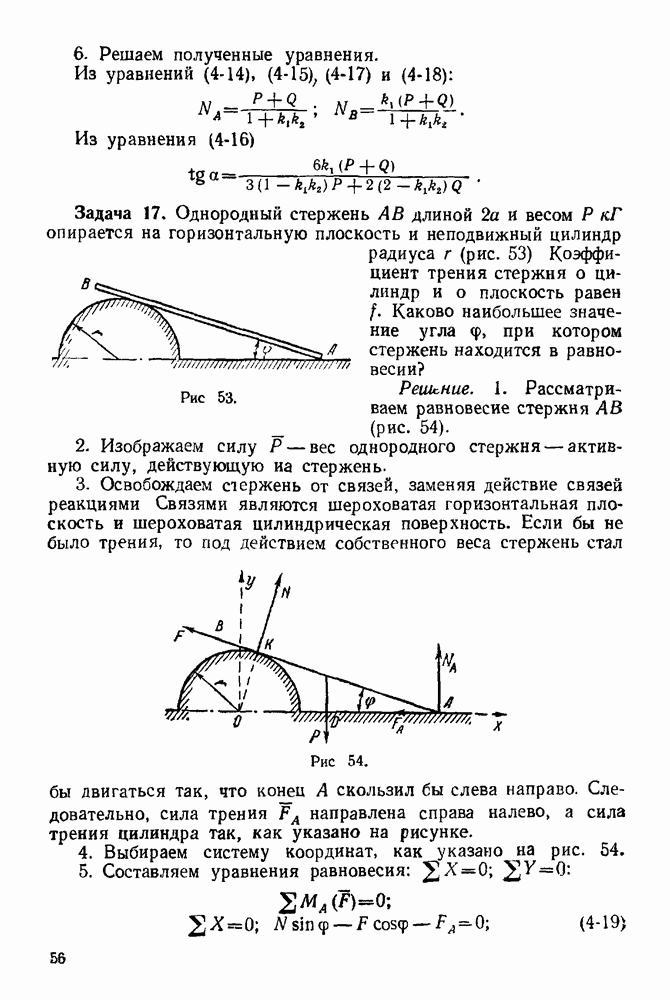
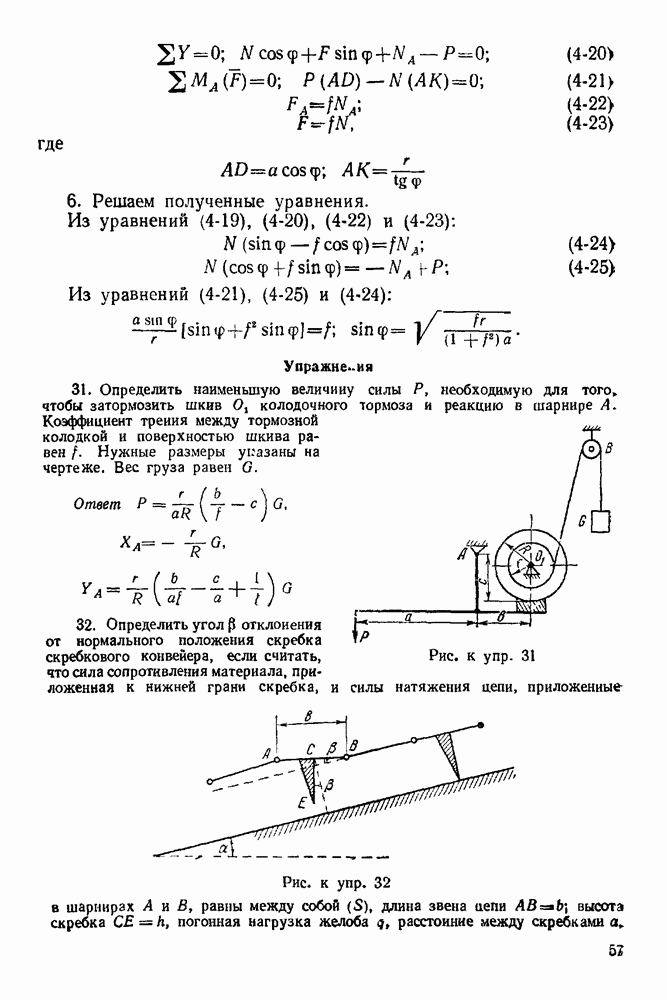
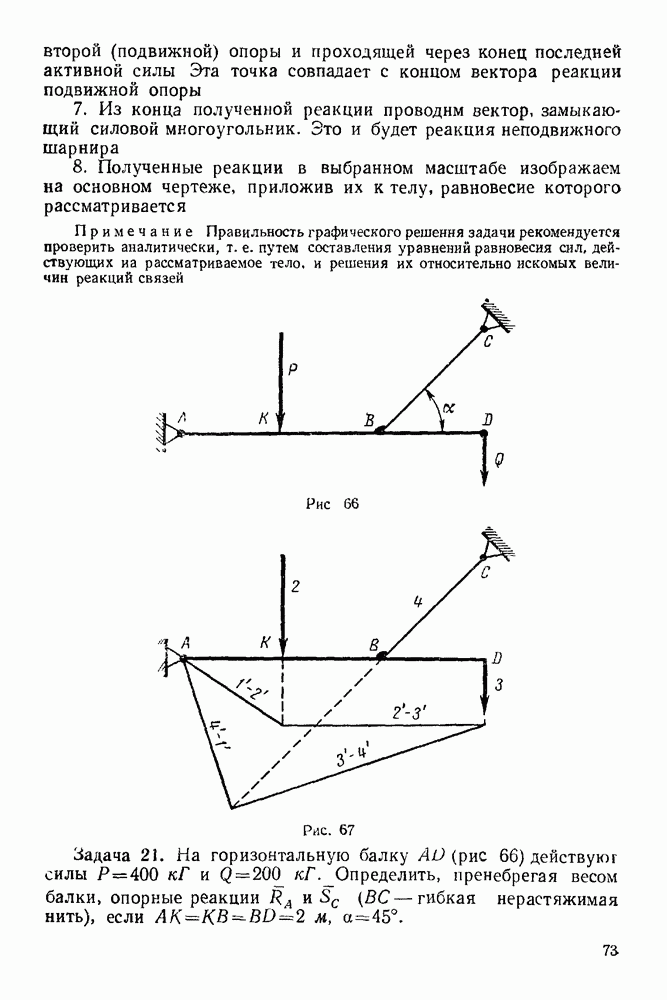
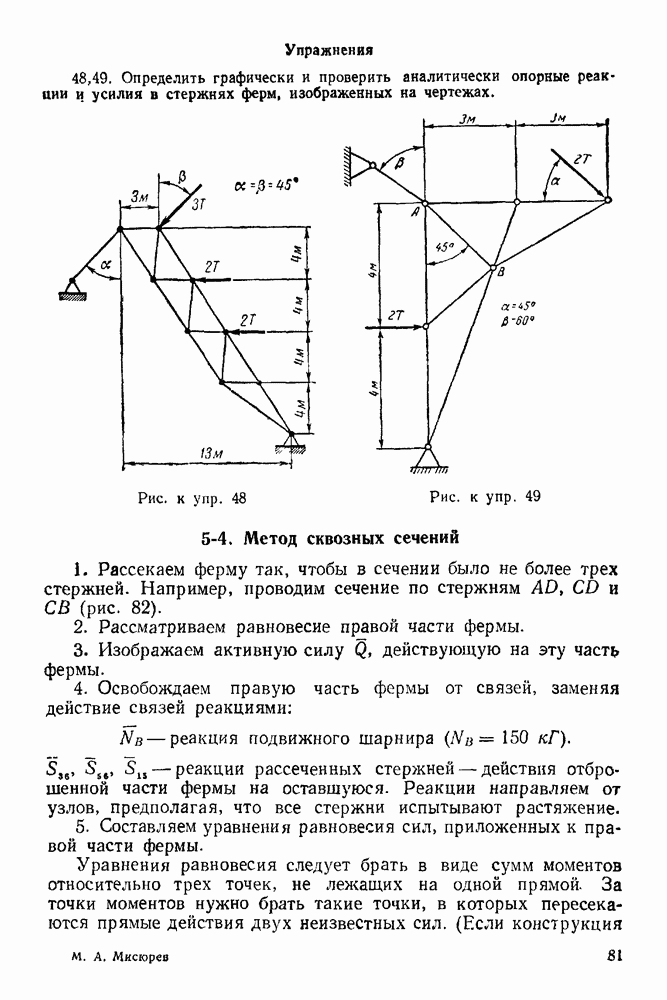
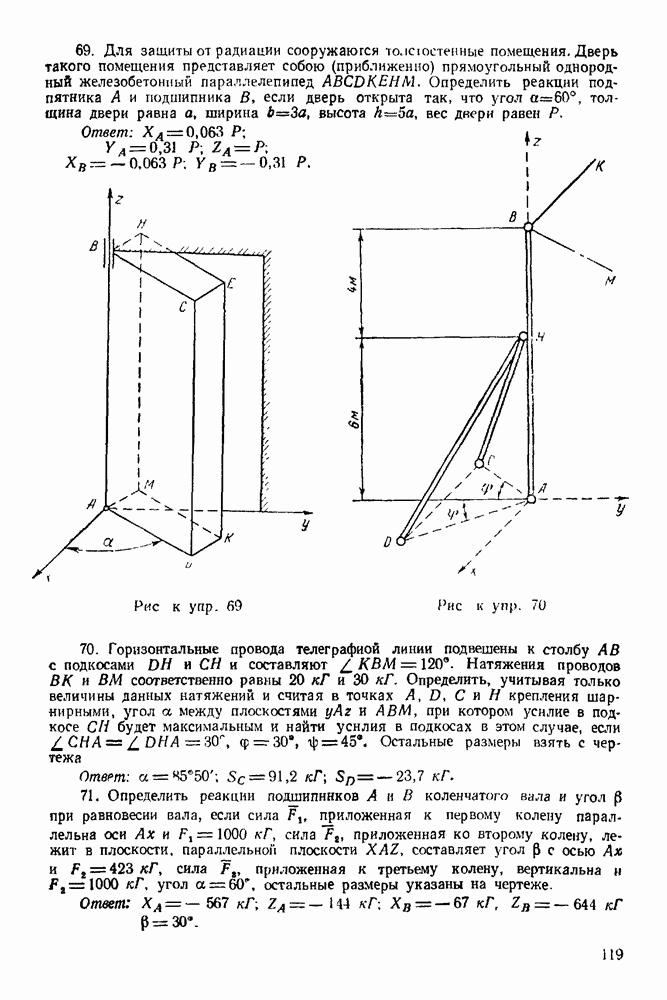
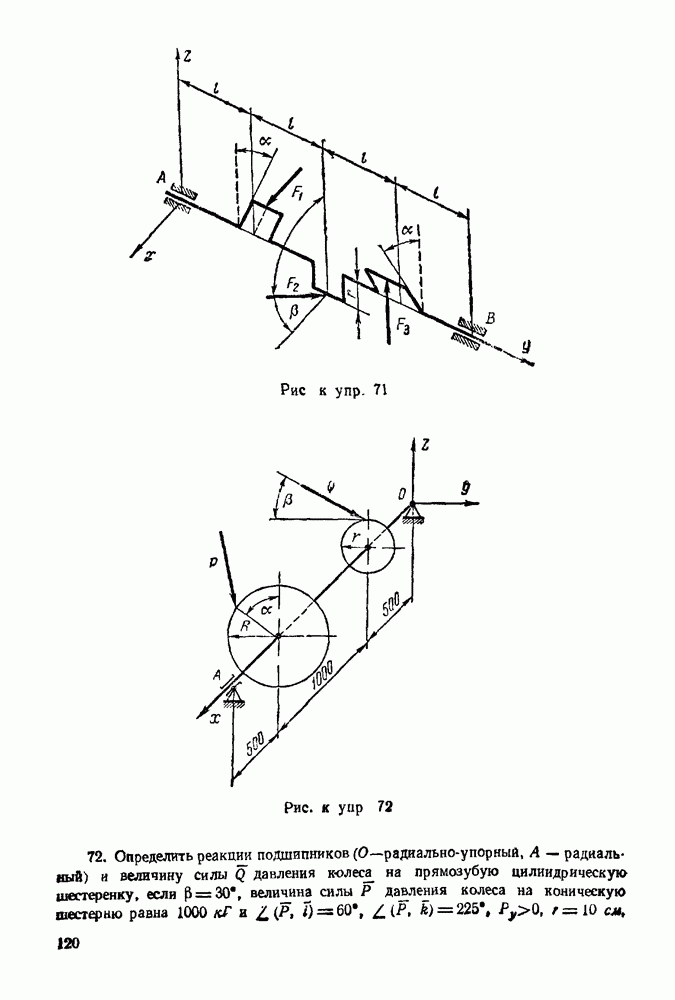
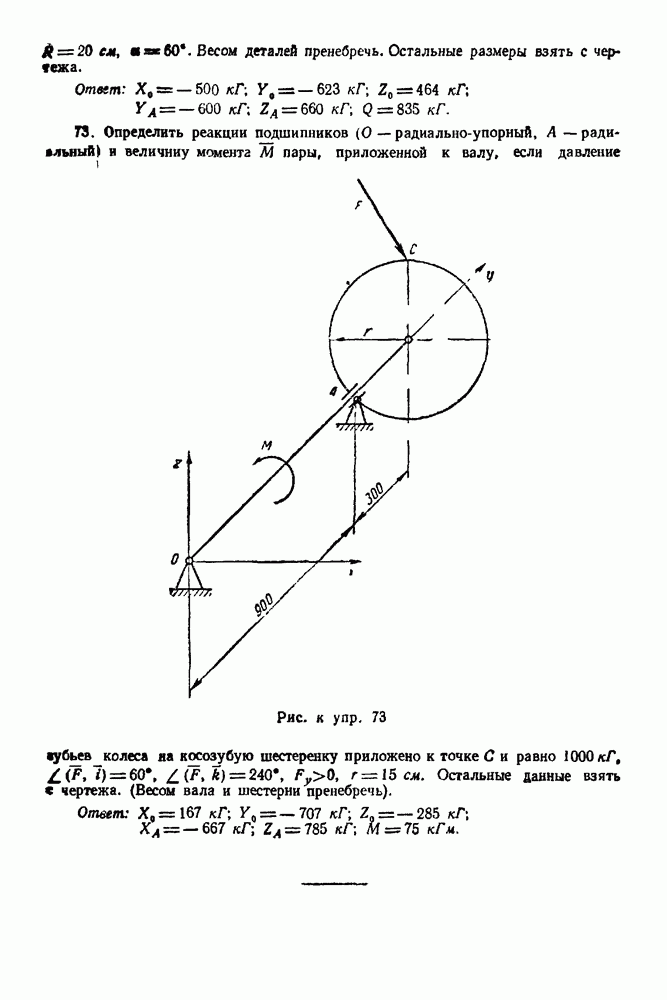
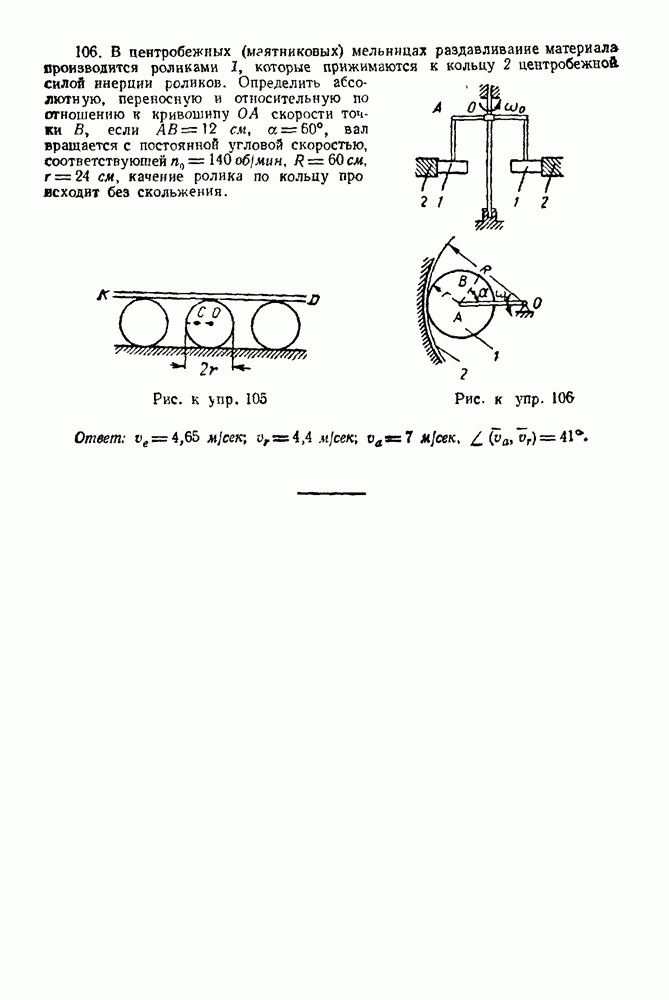
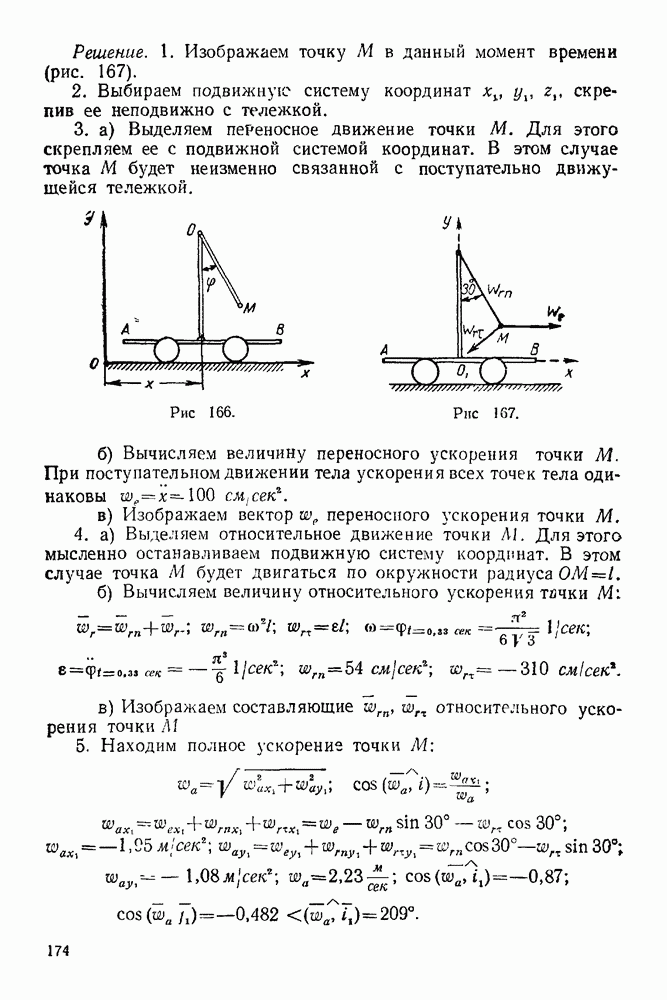
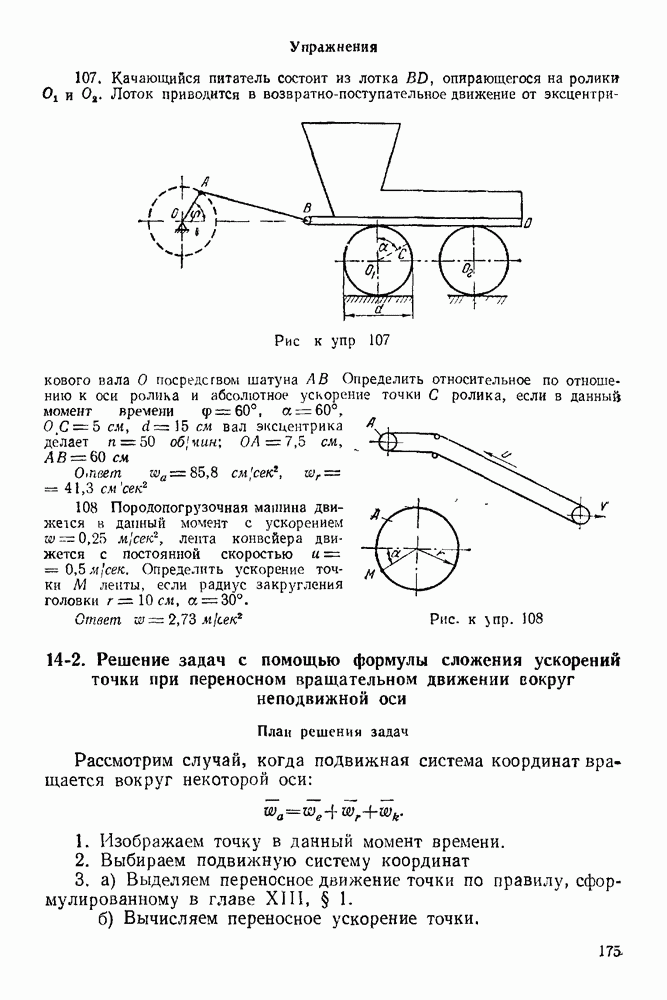
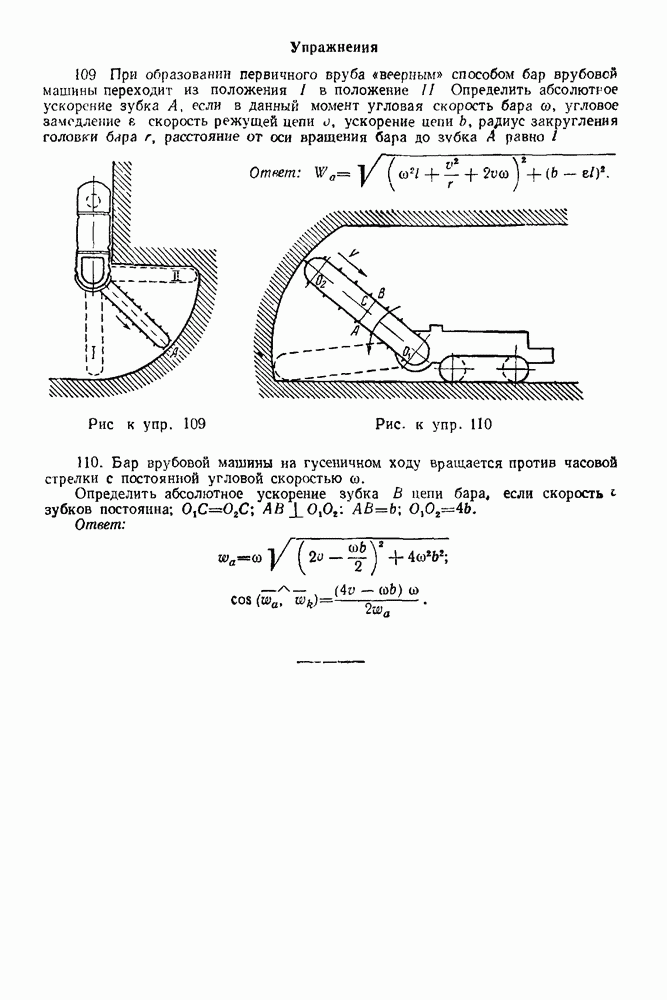
Упражнения
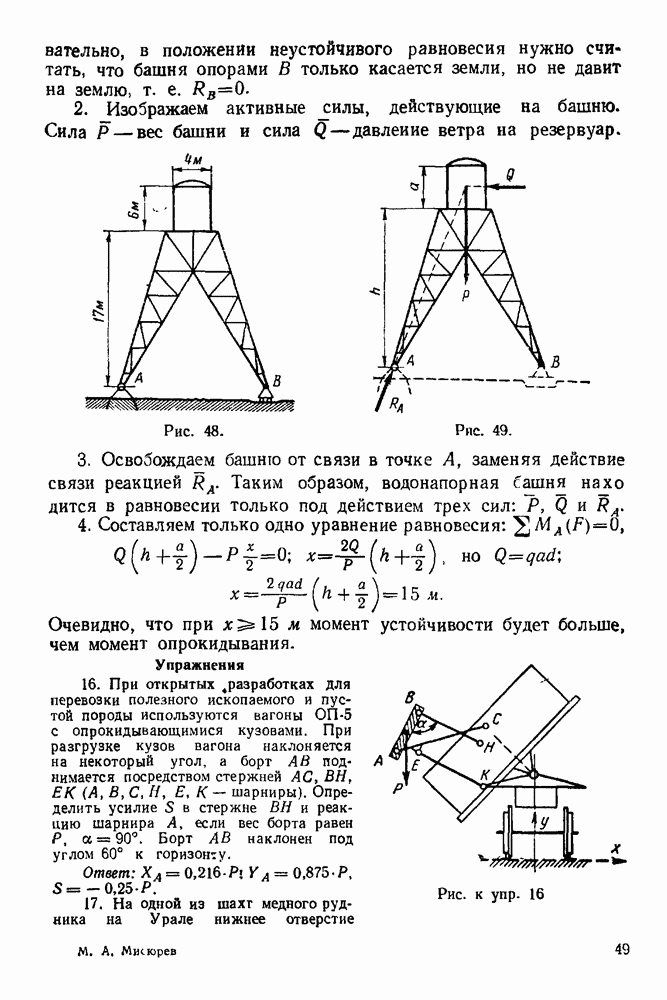
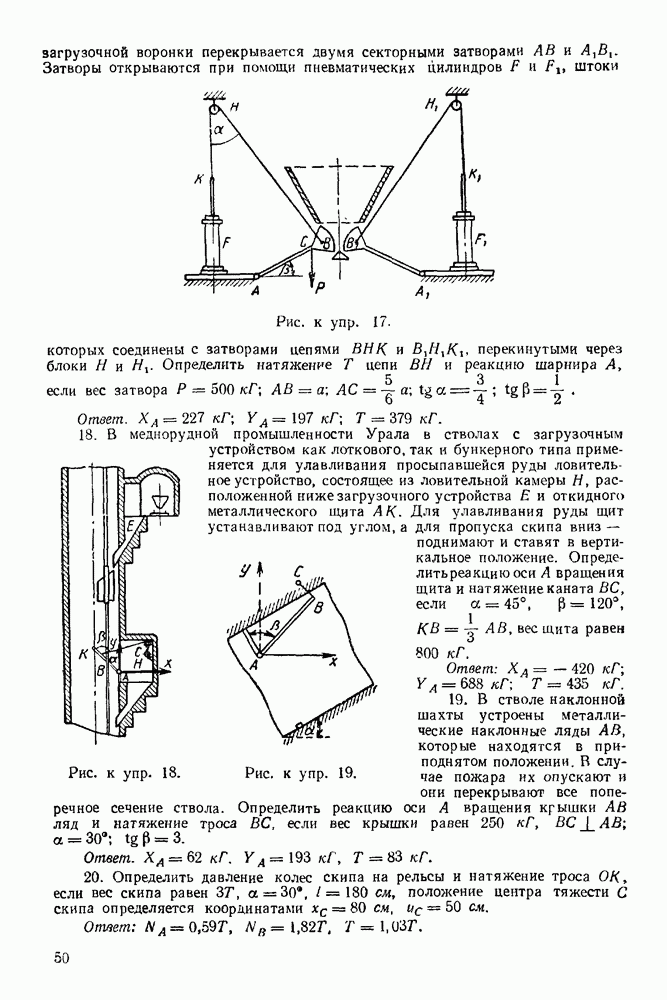
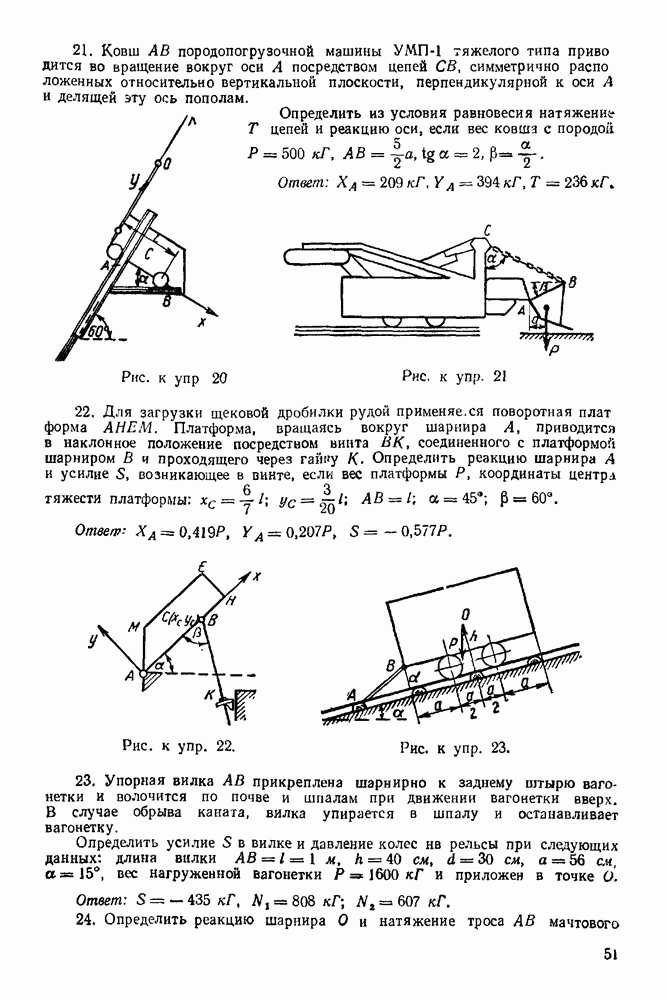
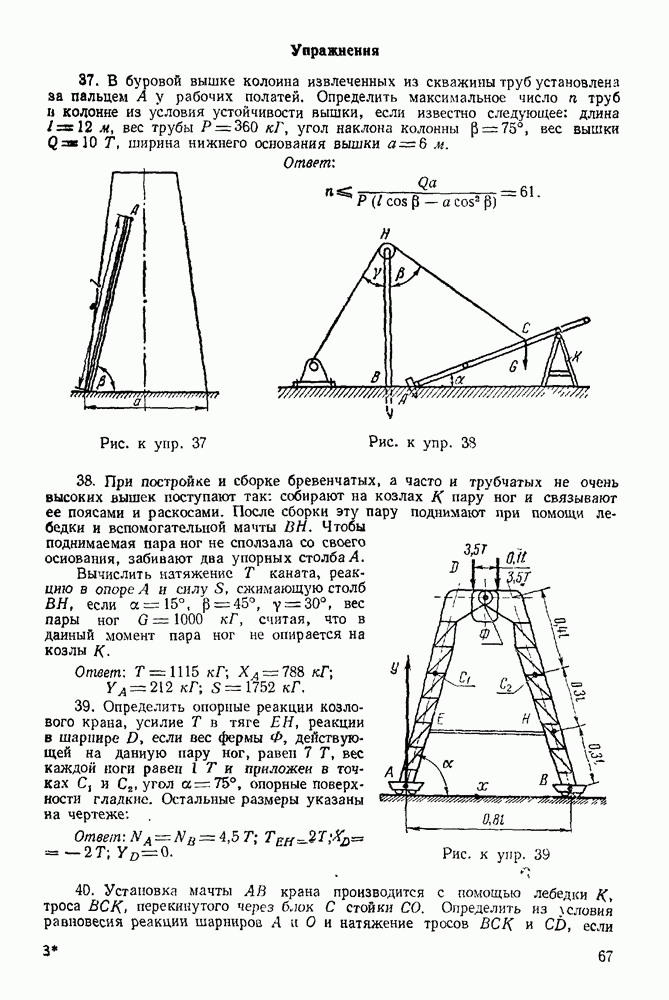
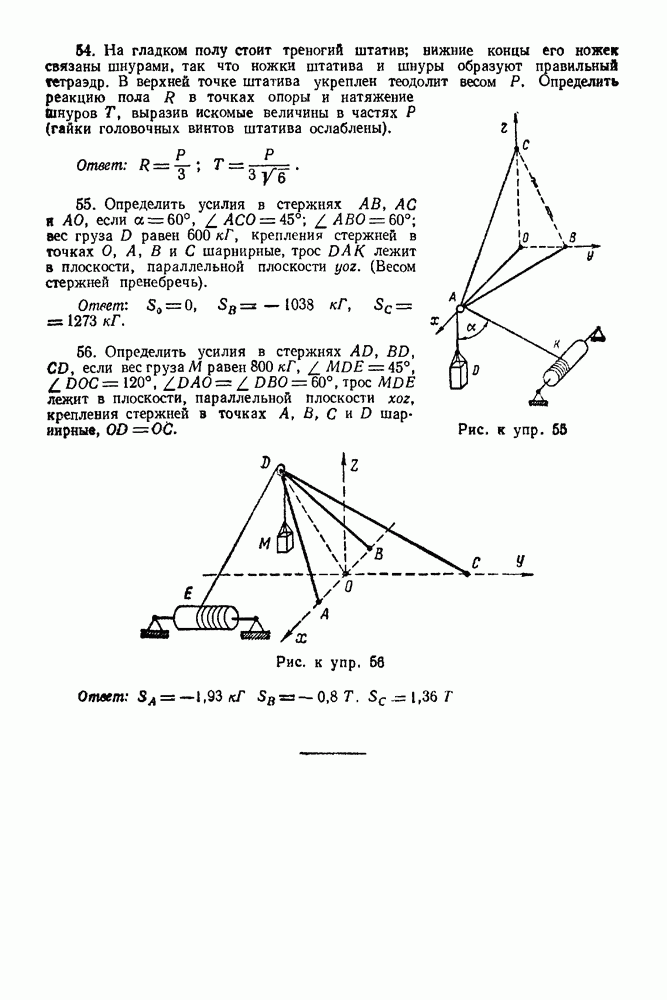
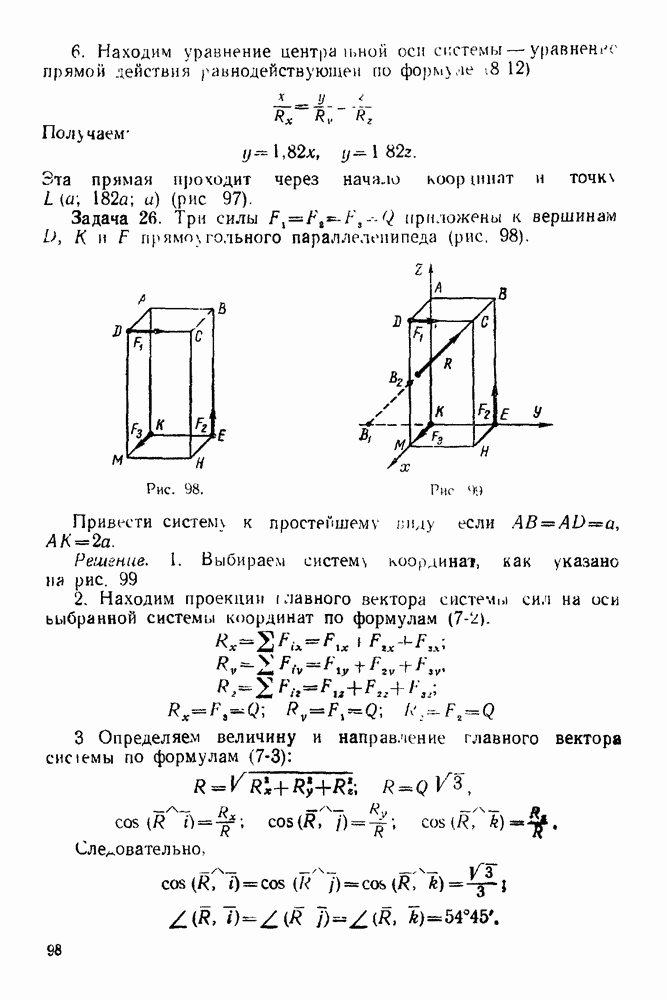
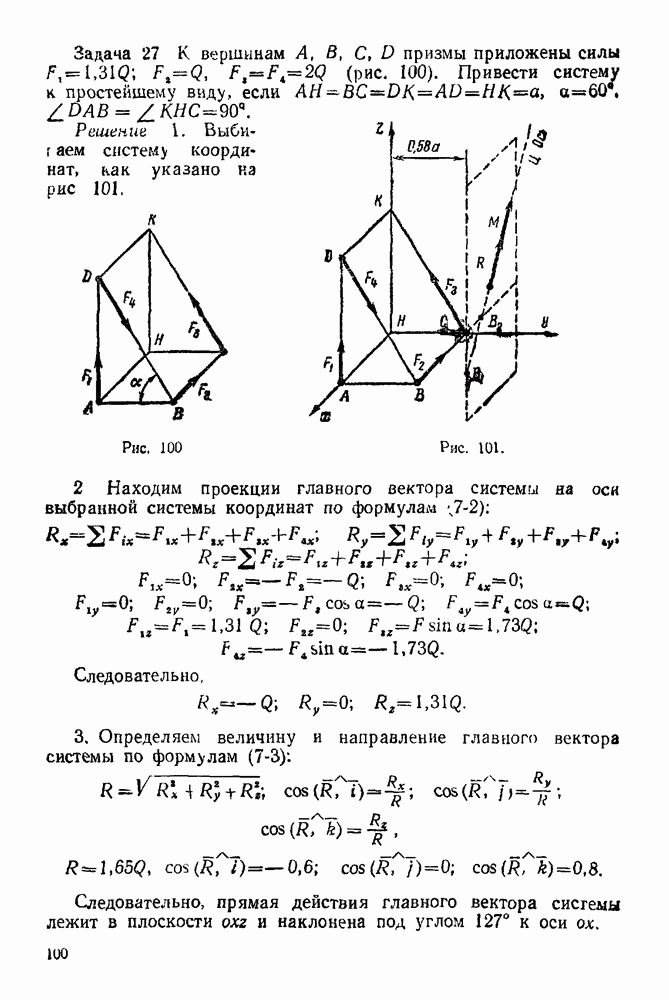
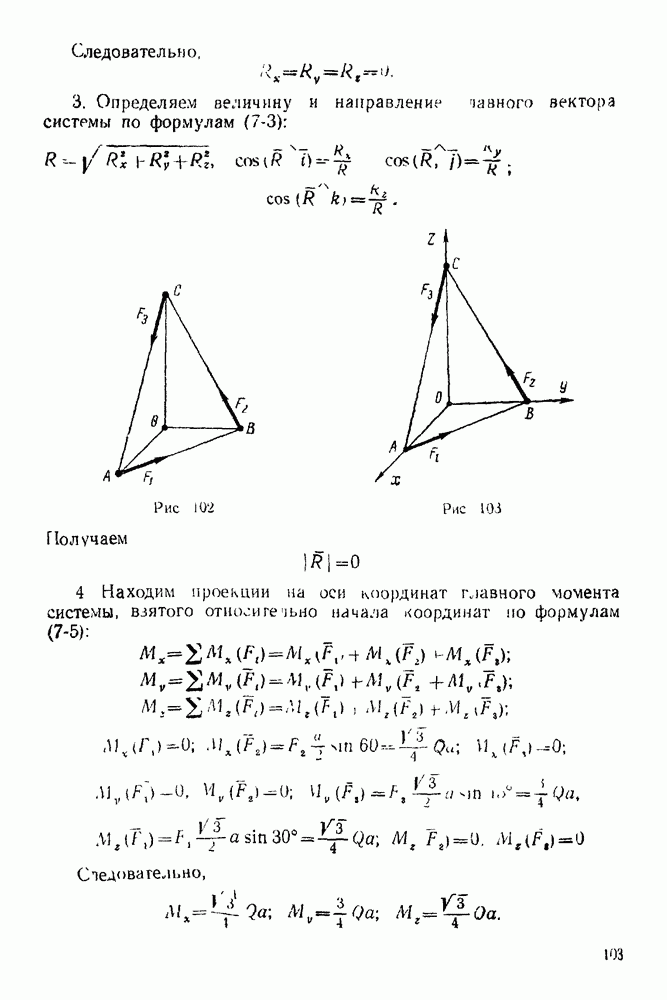
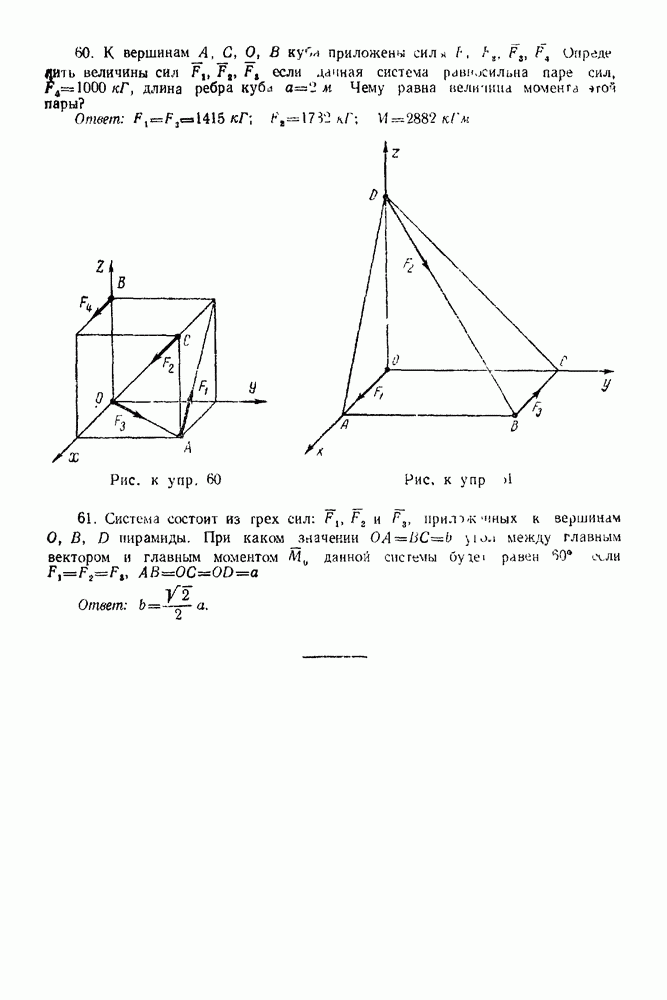
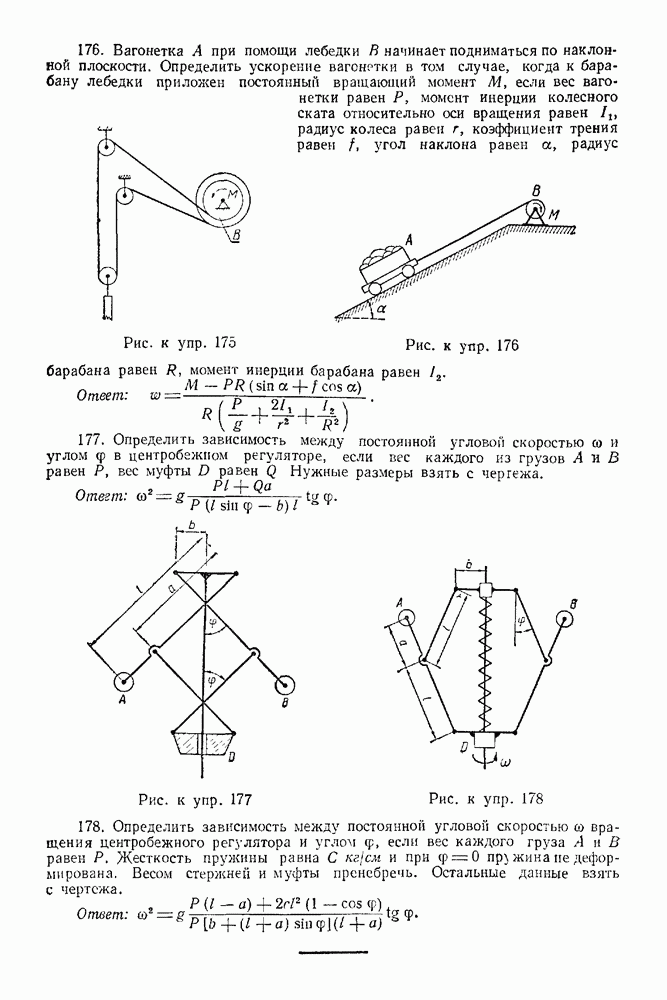
(см. скан)
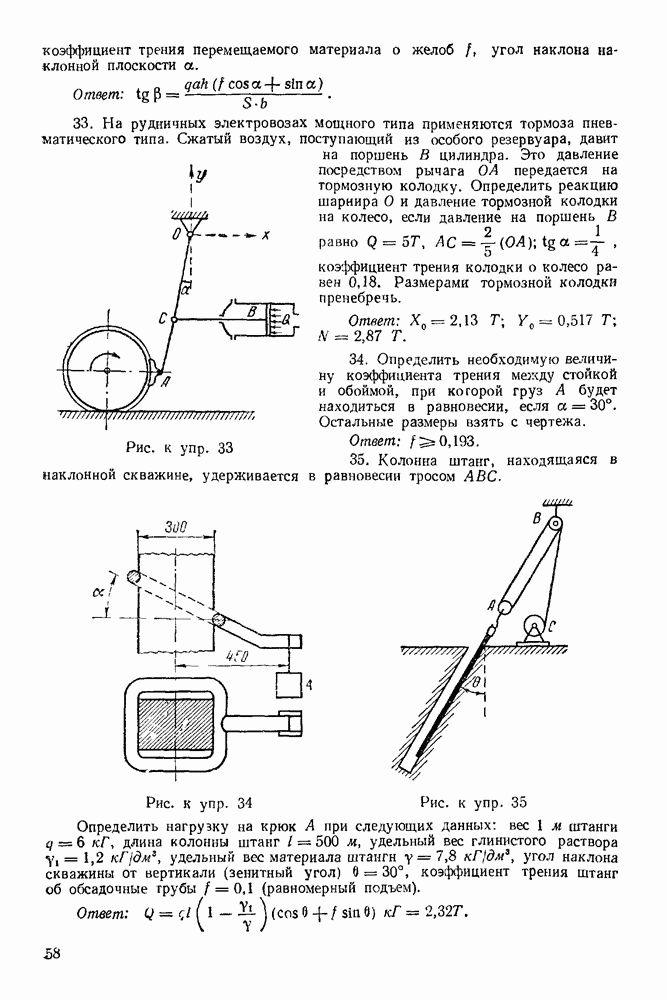
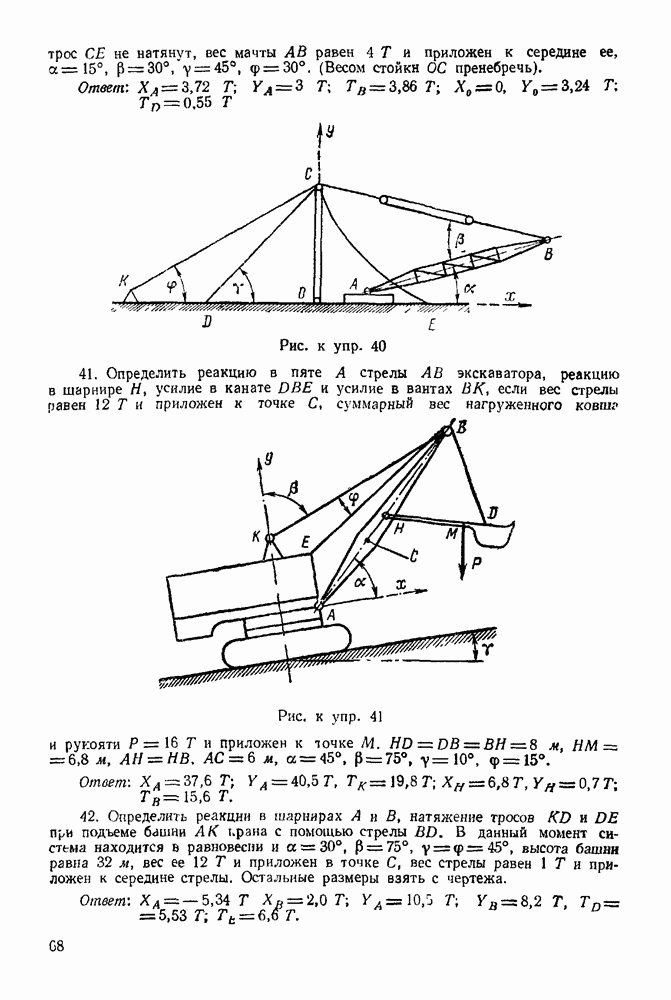
(см. скан)
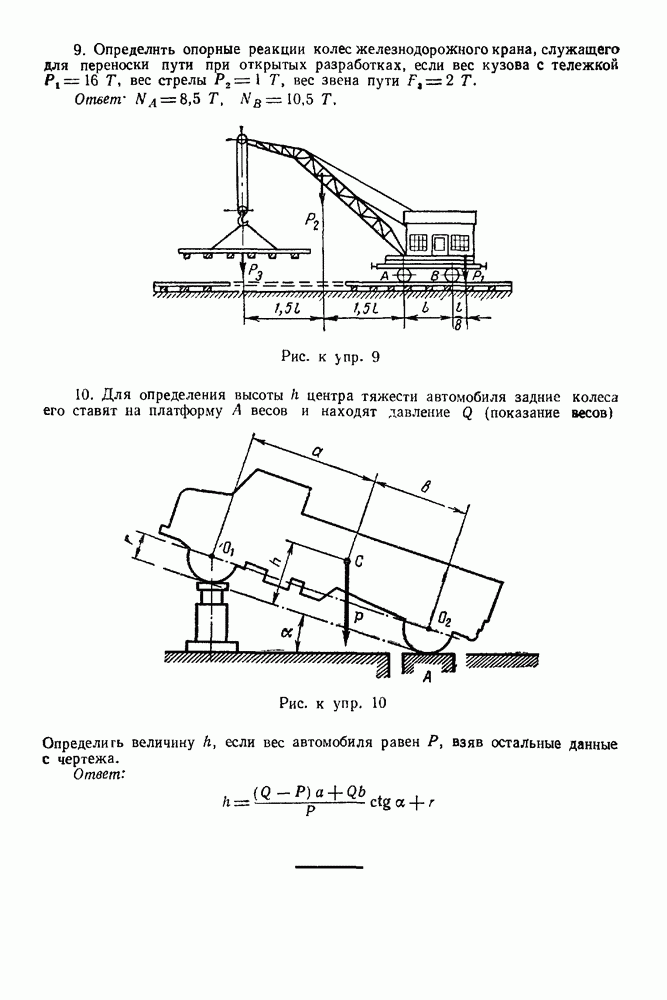
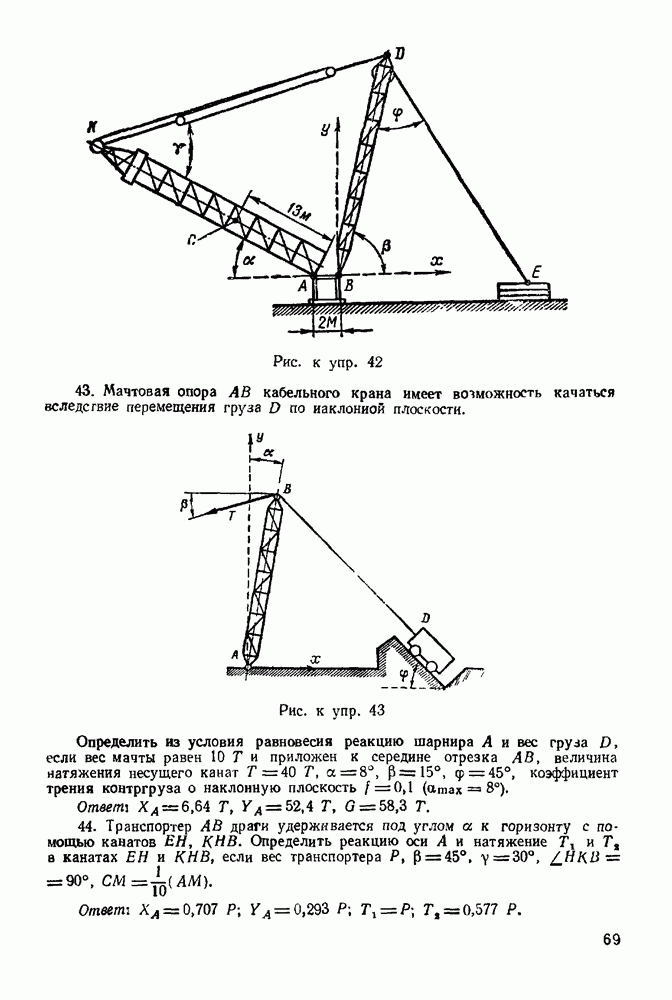
(см. скан)
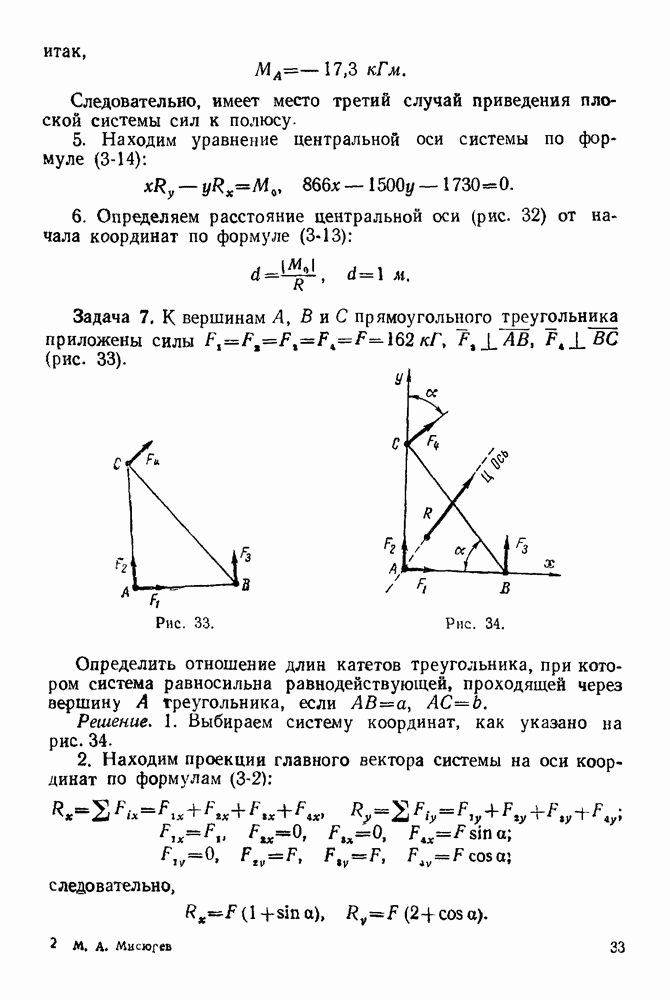
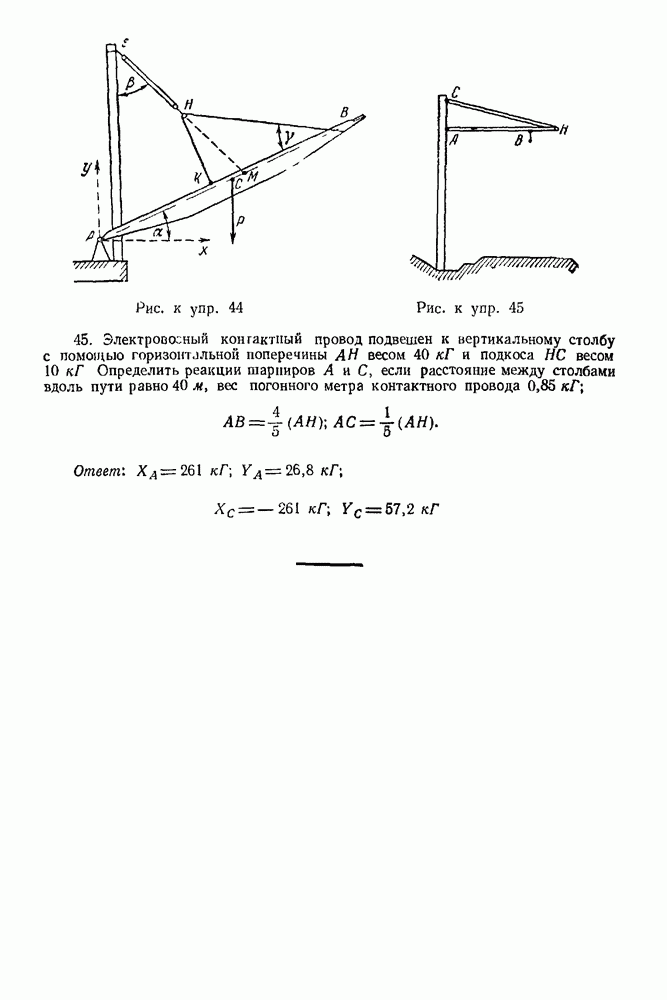
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
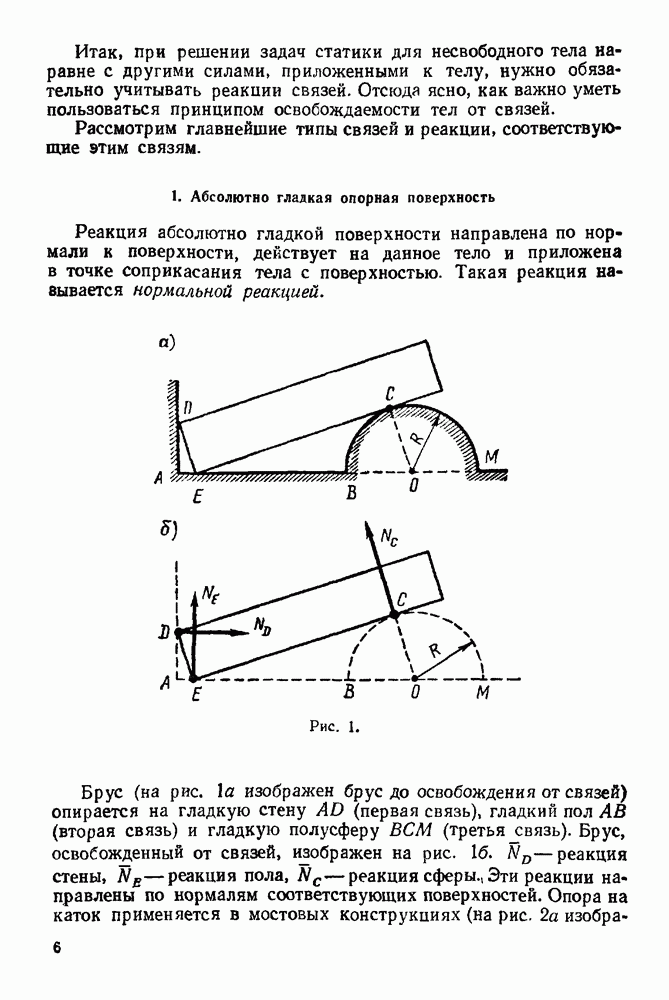
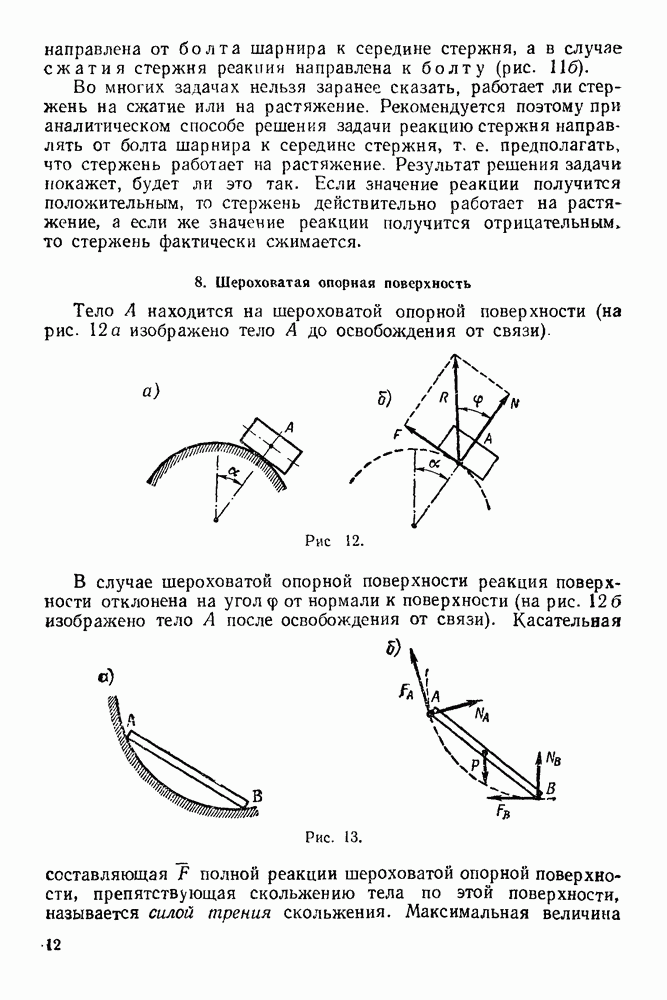
- 1. Абсолютно гладкая опорная поверхность
- 2. Точечная опора
- 3. Опора на ребро
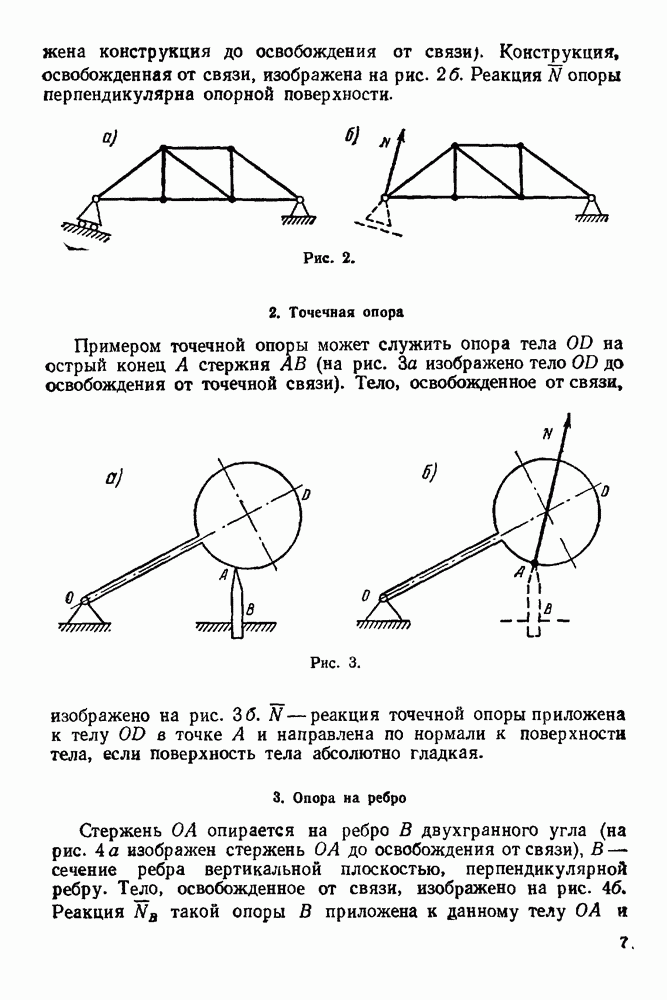
- 4. Гибкое тело (нить, канат, цепь)
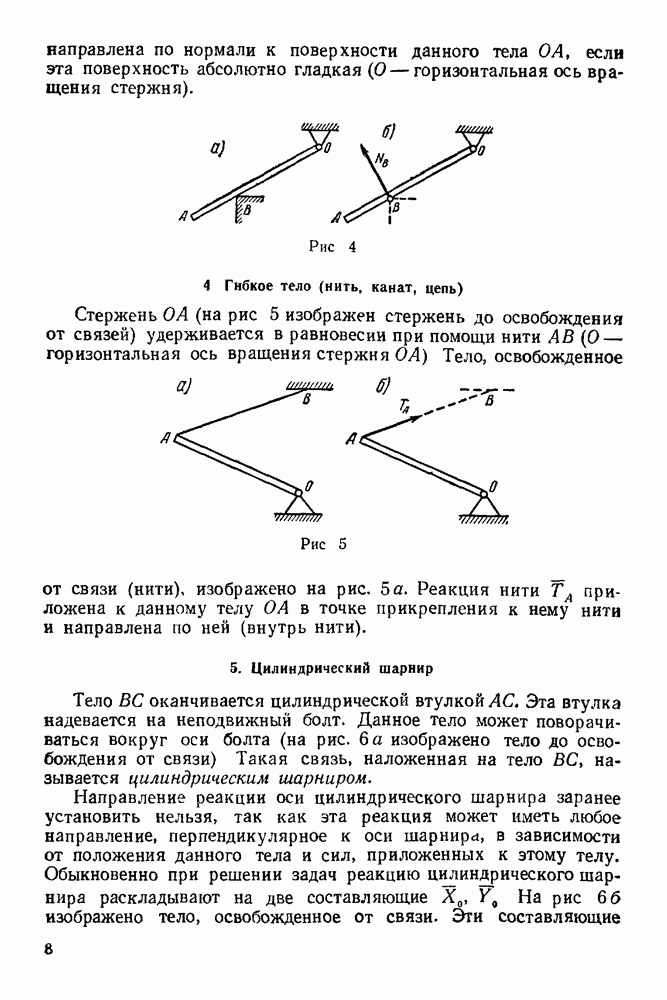
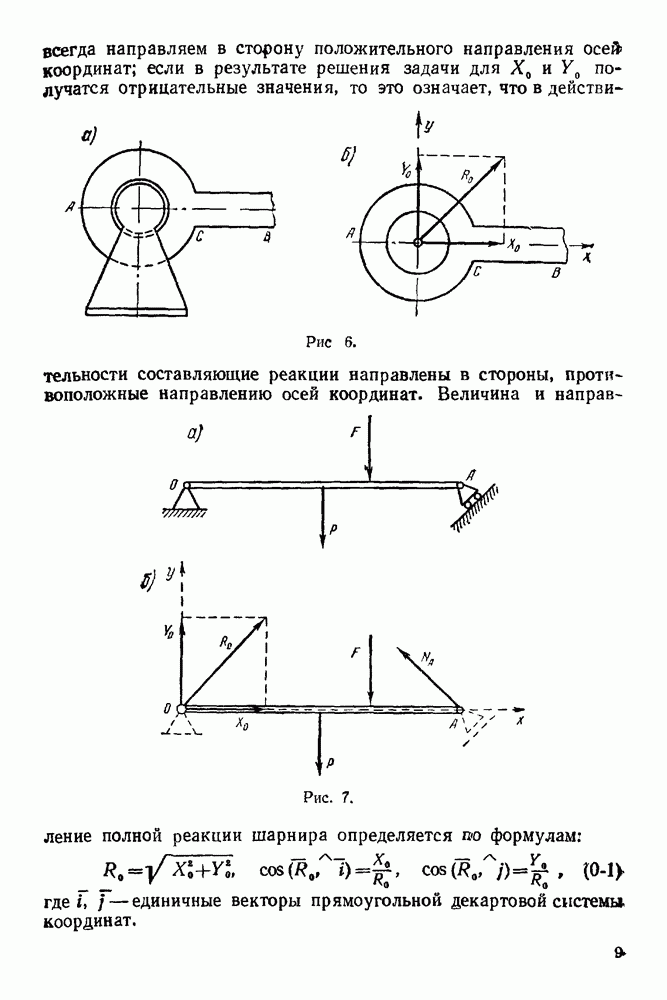
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
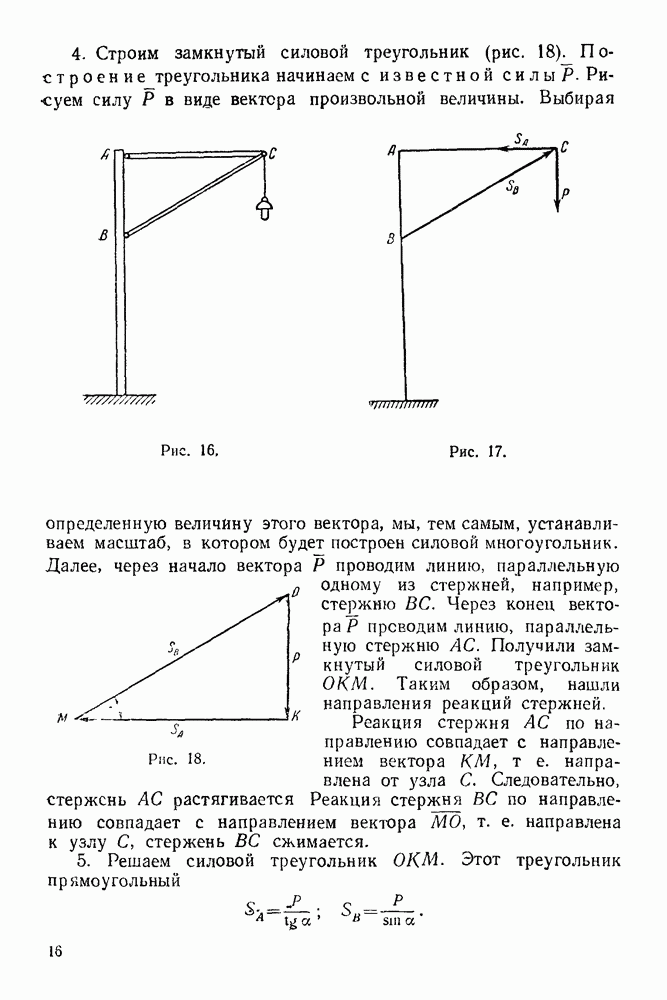
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
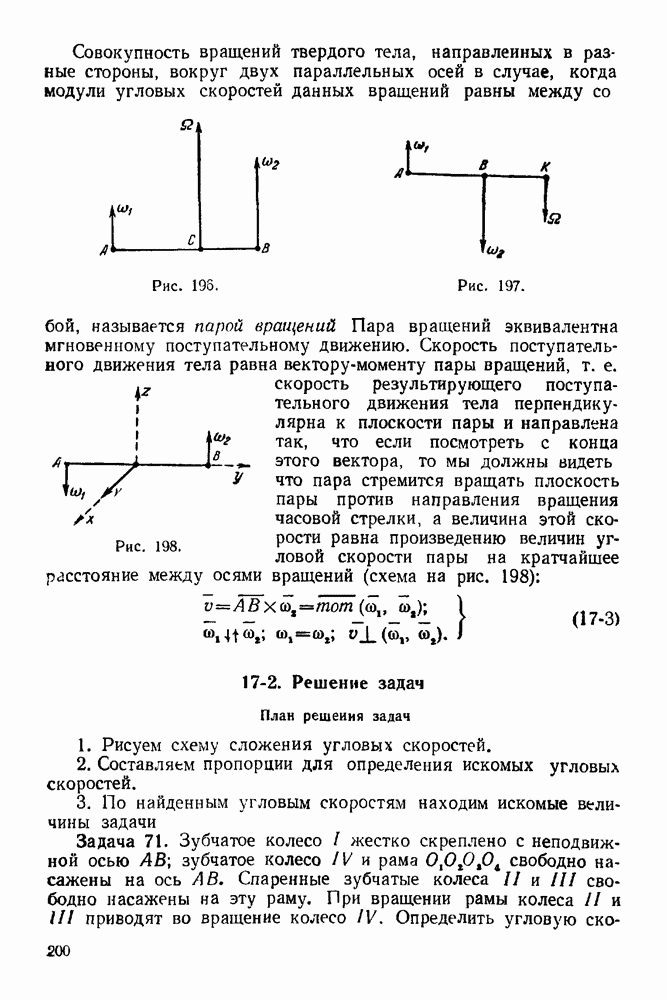
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
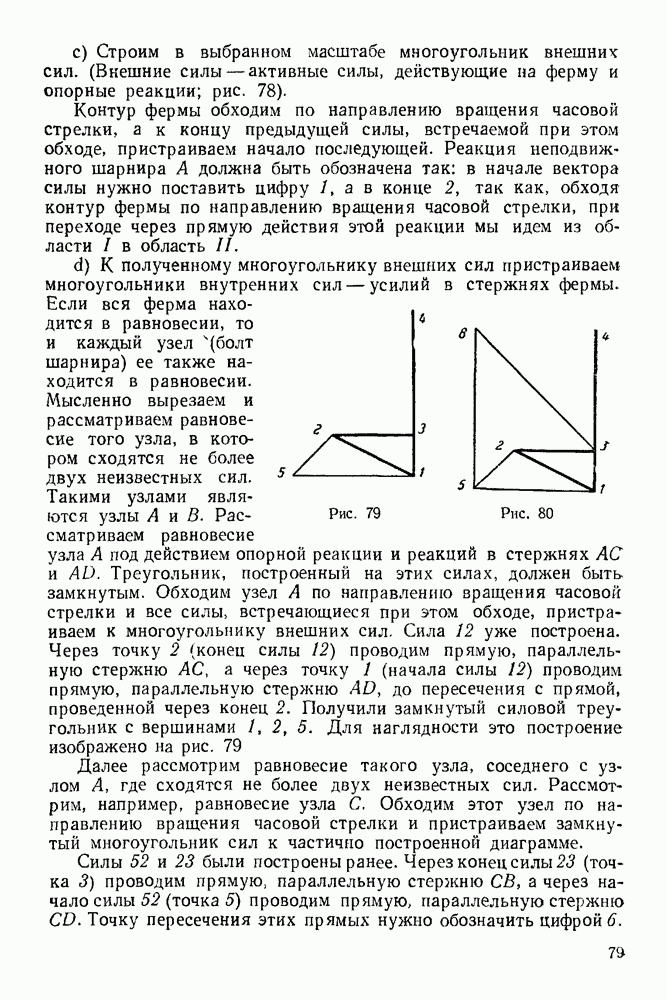
- 5-3. Определение усилий в стержнях фермы
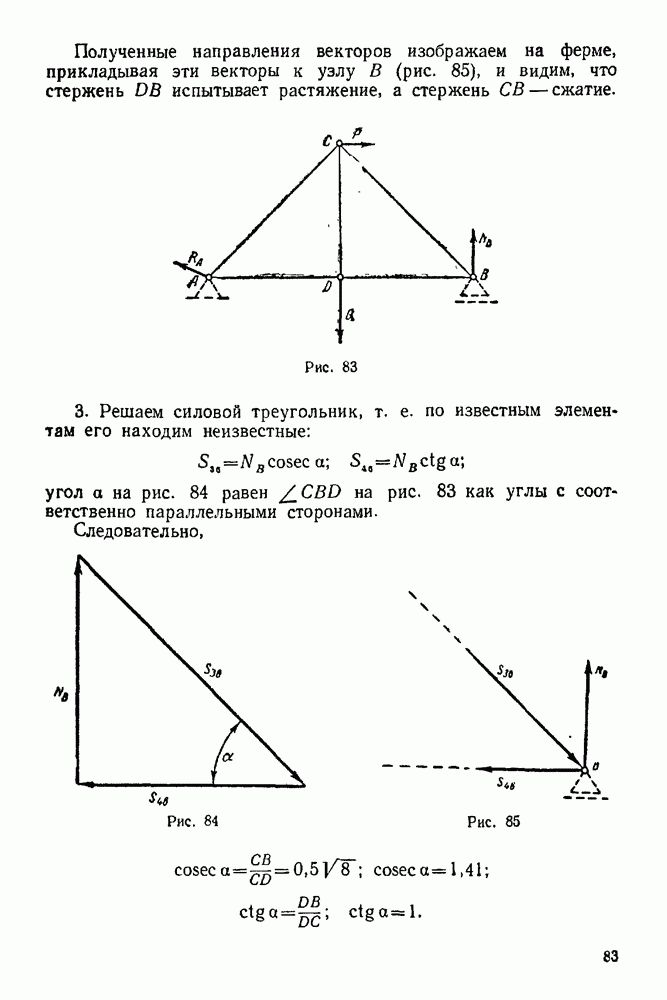
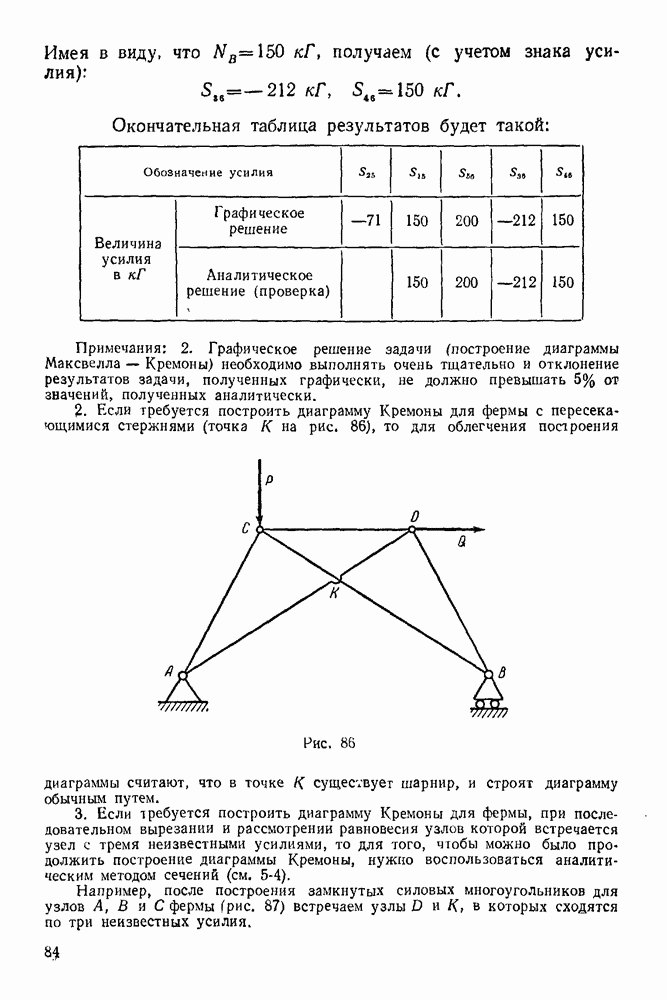
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
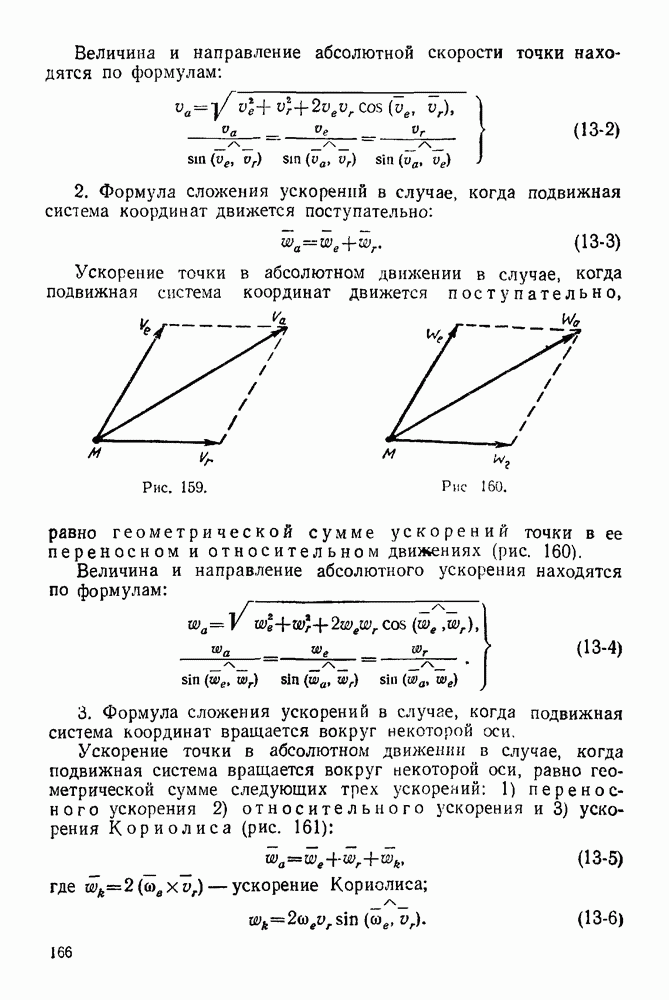
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
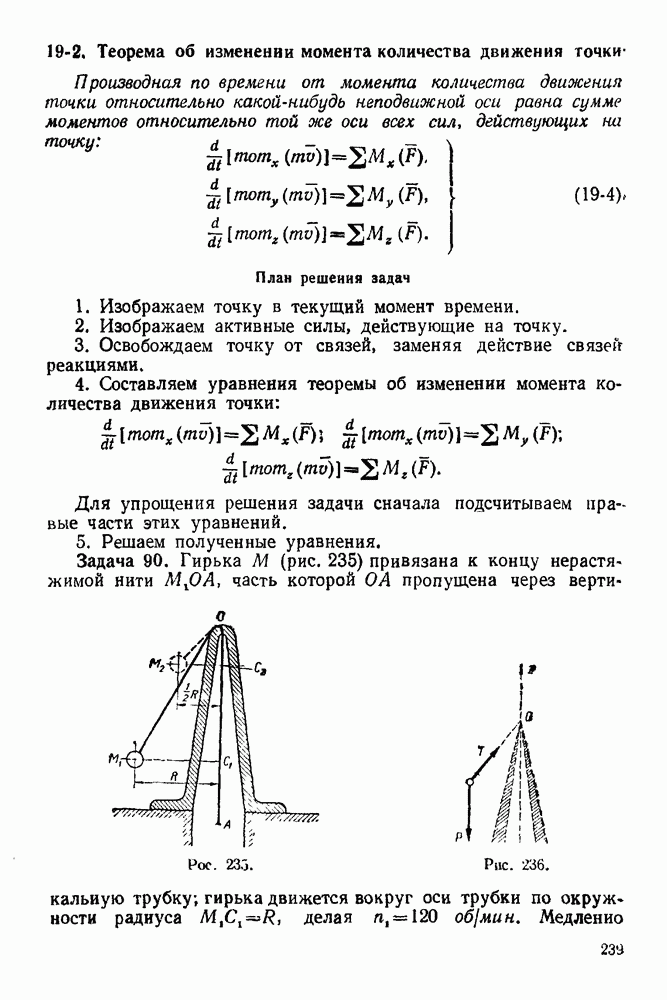
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
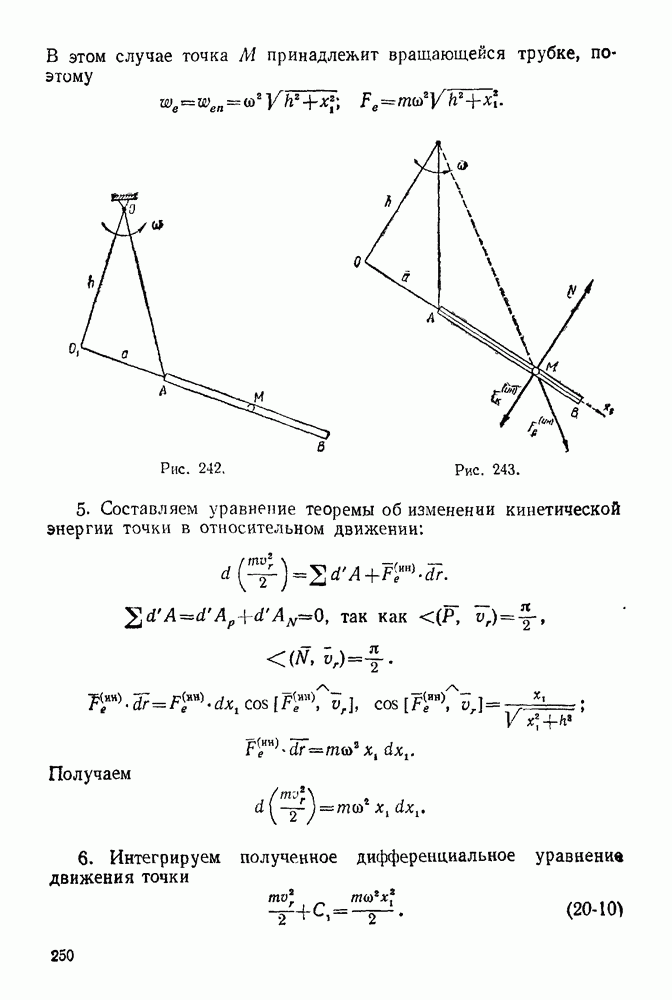
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
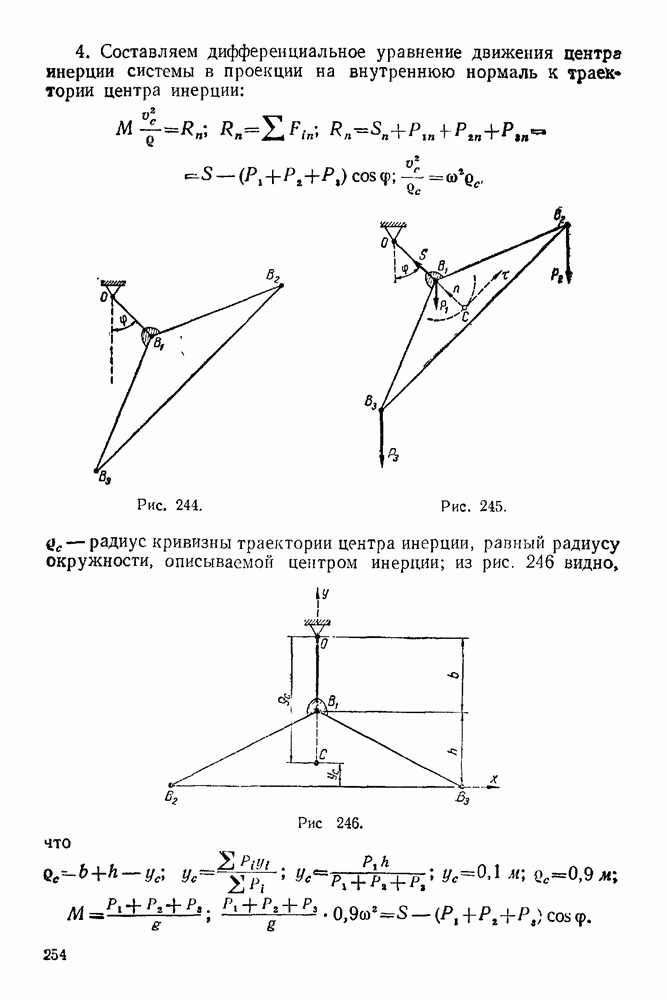
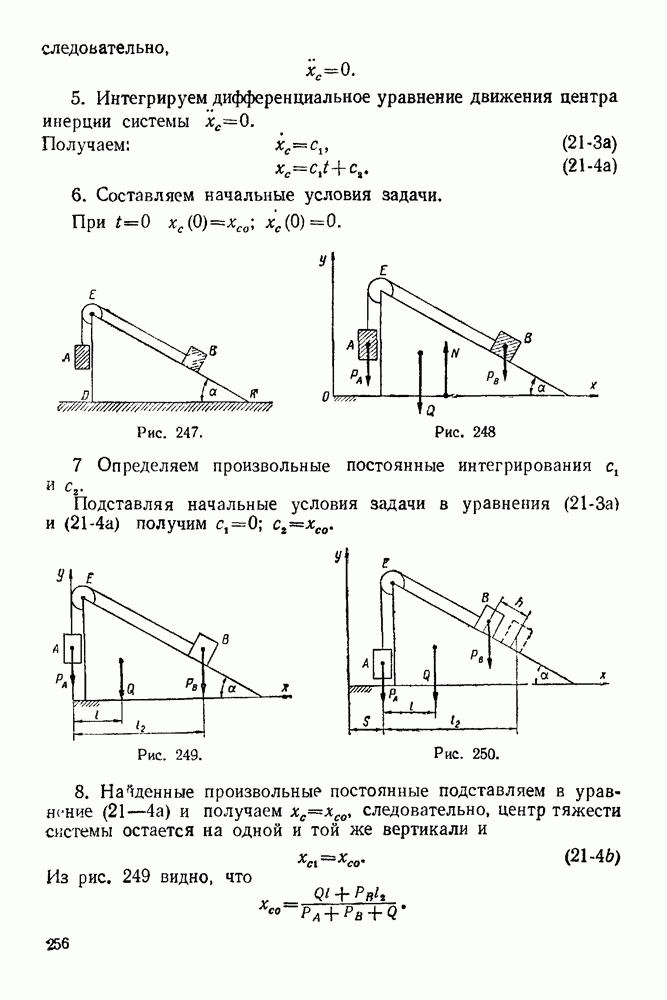
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
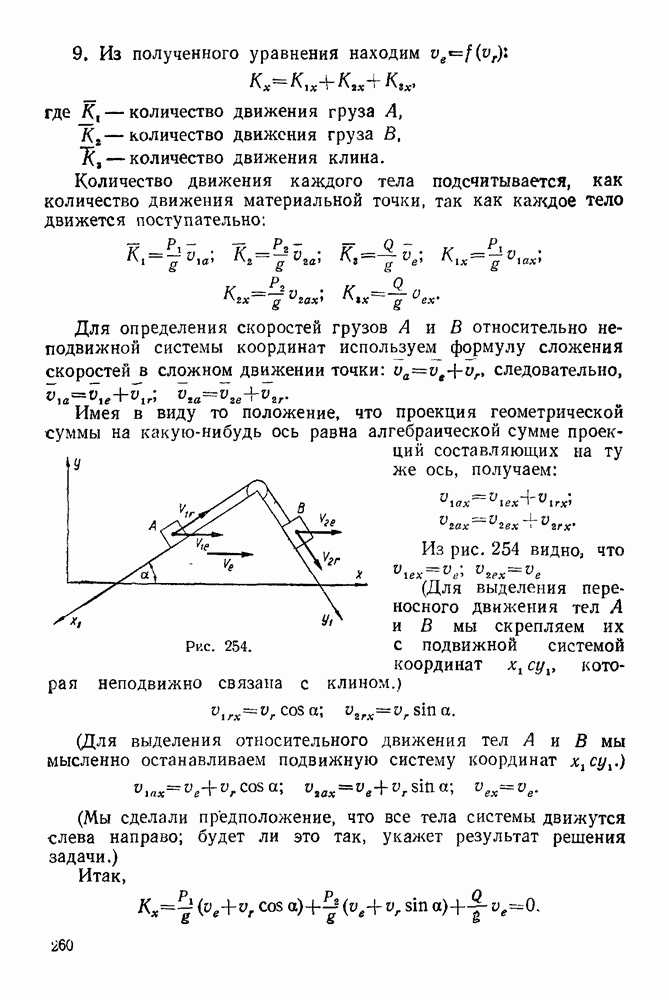
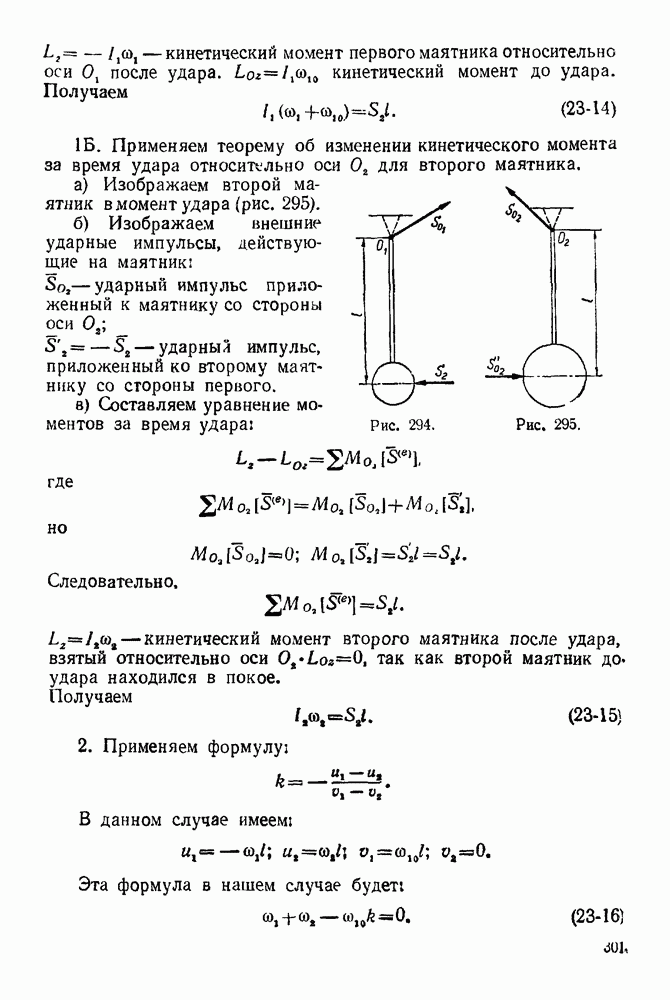
- ГЛАВА XXIII. УДАР