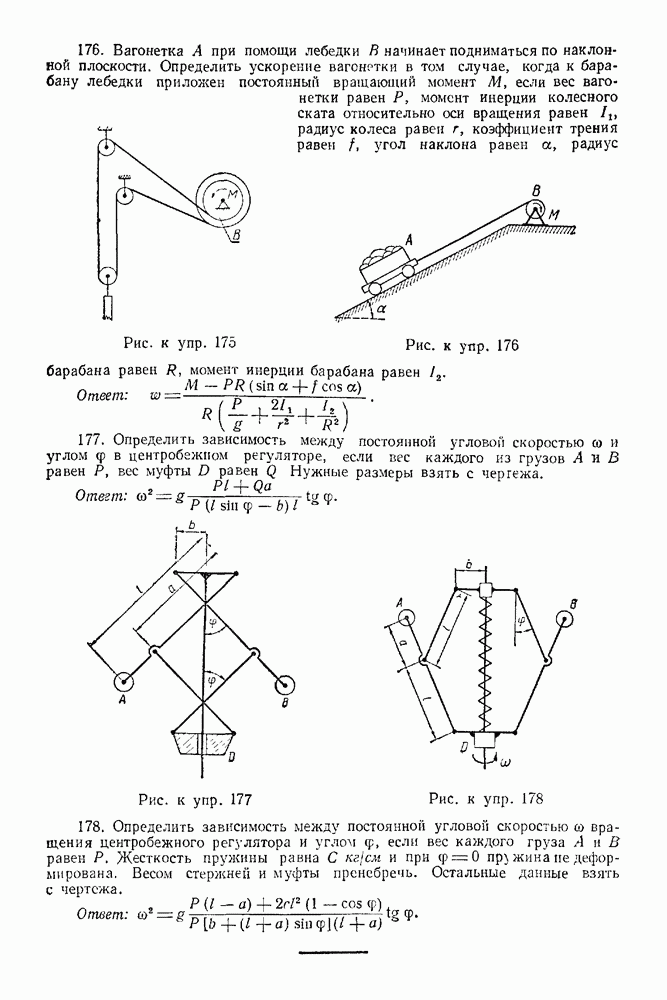
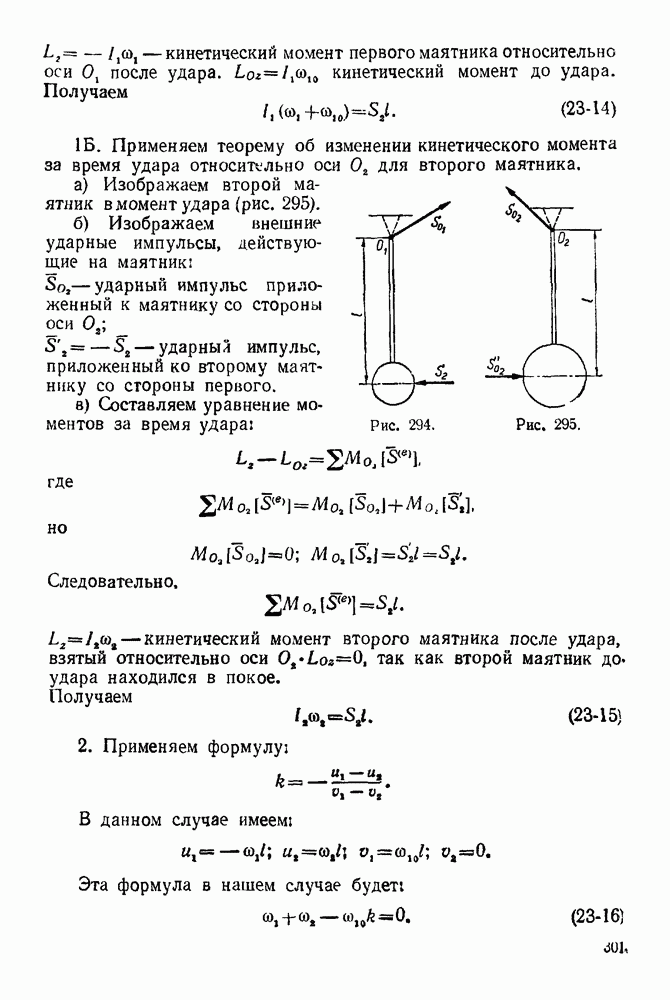
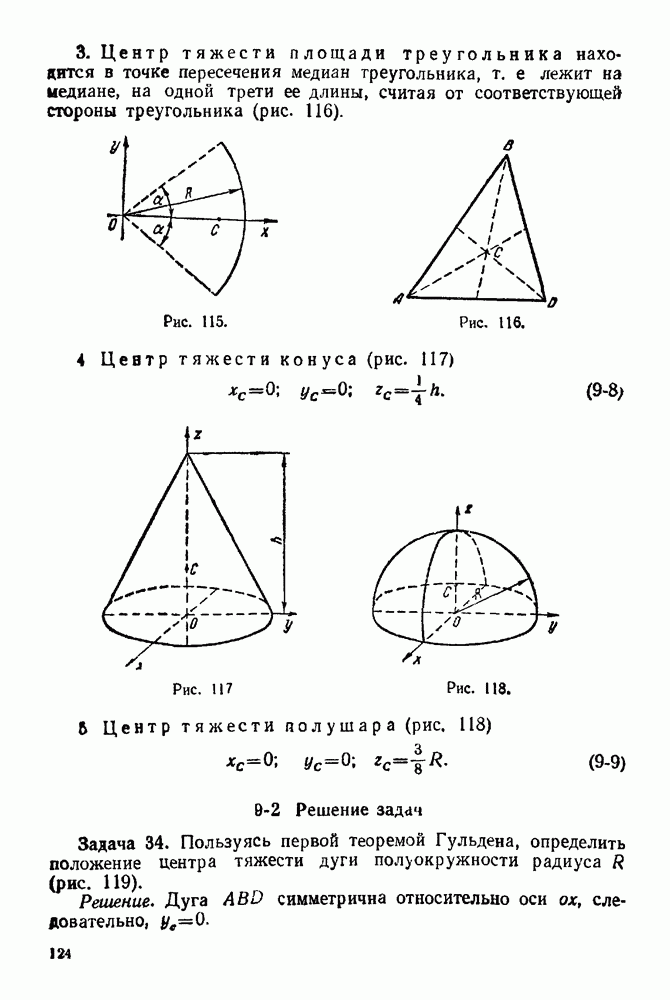| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
9-1. Основные положения
Центр тяжести твердого тела есть центр параллельных сил, лредставляющих веса материальных частиц твердого тела. Координаты центра тяжести однородного тела трех измерений (центр тяжести объема V) определяются по следующим формулам:

Координаты центра тяжести однородной плоской фигуры (центр тяжести площади s):

Координаты центра тяжести однородной линии длиною 

Практические способы нахождения координат центра тяжести
1. Способ симметрии Если тело имеет плоскость симметрии или линию симметрии или центр симметрии, то центр тяжести находится соответственно в плоскости симметрии, на линии симметрии или в центре симметрии.
2. Спосоо разбиения. Если твердое тело можно разбить на такие части, положения центров тяжести которых известны, то центр тяжести тела находится как центр тяжести совокупности материальных точек, которые мы получим, если массу каждой части тела сосредоточим в ее центре тяжести
8. Способ отрицательных масс Если тело имеет вырез (отверстие), то для нахождения центра тяжести этого тела нужно применить способ разбиения, считая, что тело состоит из двух частей: одна часть — объем всего тела, включая и объем выреза, заполненный равномерно массой тела; вторая часть — вырез, заполненный массой, которую нужно брать со знаком минус.
4 Способ Гульдена. Первая теорема Гульдена. Площадь поверхности, полученной сращением отрезка плоской кривой (ломаной) около оси, лежащей в плоскости отрезка, но его не пересекающей, равна длине отрезка, умноженной на длину окружности, описанной центром тяжести отрезка (рис. 113):

где  центр тяжести отрезка,
центр тяжести отрезка,  длина отрезка
длина отрезка  ось вращения. Следовательно,
ось вращения. Следовательно,


Рис. 113

Рис. 114
Вторая теорема Гульдена. Объем тела, полученного вращением плоской фигуры около оси, лежащей в плоскости фигуры, но ее не пересекающей, равен площади фигуры, умноженной на длину окружности, описанной центром тяжести фигуры (рис 114):

где с — центр тяжести плоской фигуры,  площадь фигуры,
площадь фигуры,  ось вращения фигуры. Следовательно,
ось вращения фигуры. Следовательно,

Центры тяжести некоторых однородных линий, плоских фигур и тел
1. Центр тяжести дуги окружности (рис 115)

2. Центр тяжести кругового сектора

3. Центр тяжести площади треугольника находится в точке пересечения медиан треугольника, т. е. лежит на медиане, на одной трети ее длины, считая от соответствующей стороны треугольника (рис. 116).

Рис. 115.

Рис. 116.
4 Центр тяжести конуса (рис. 117)


Рис. 117

Рис. 118.
5. Центр тяжести полушара (рис. 118)

9-2 Решение задач
Задача 34. Пользуясь первой теоремой Гульдена, определить положение центра тяжести дуги полуокружности радиуса  (рис. 119).
(рис. 119).
Решение. Дуга  симметрична относительно оси
симметрична относительно оси  следовательно,
следовательно, 
Для нахождения  применяем первую теорему Гульдена. При вращении дуги
применяем первую теорему Гульдена. При вращении дуги  вокруг оси
вокруг оси  (рис. 120) получается сферическая поверхность радиуса
(рис. 120) получается сферическая поверхность радиуса  с площадью длина дуги полуокружности
с площадью длина дуги полуокружности 


Рис. 119.

Рис. 120.
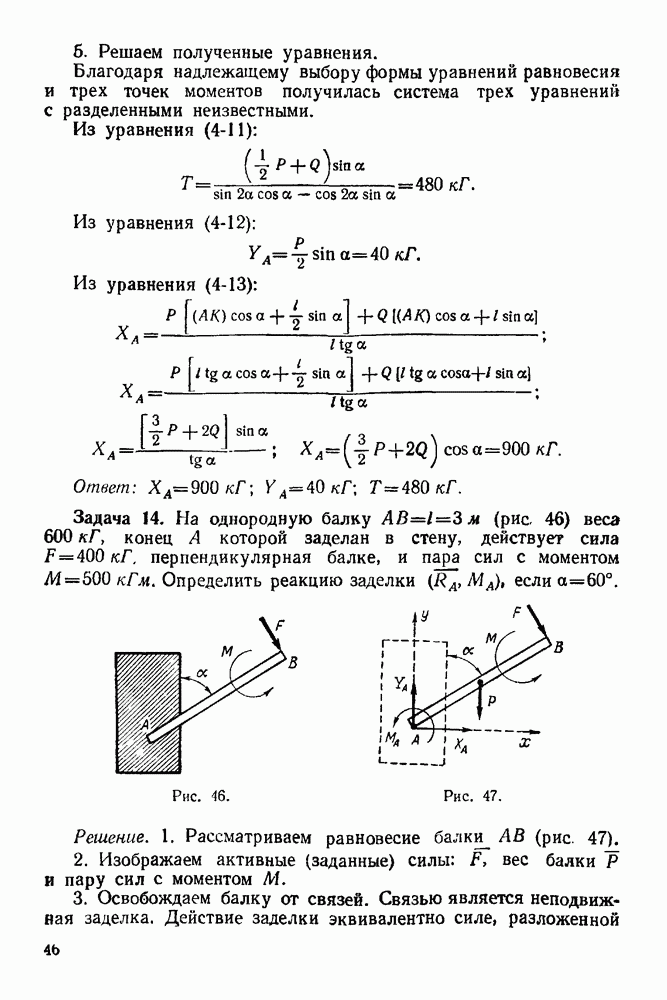
Ответ: 
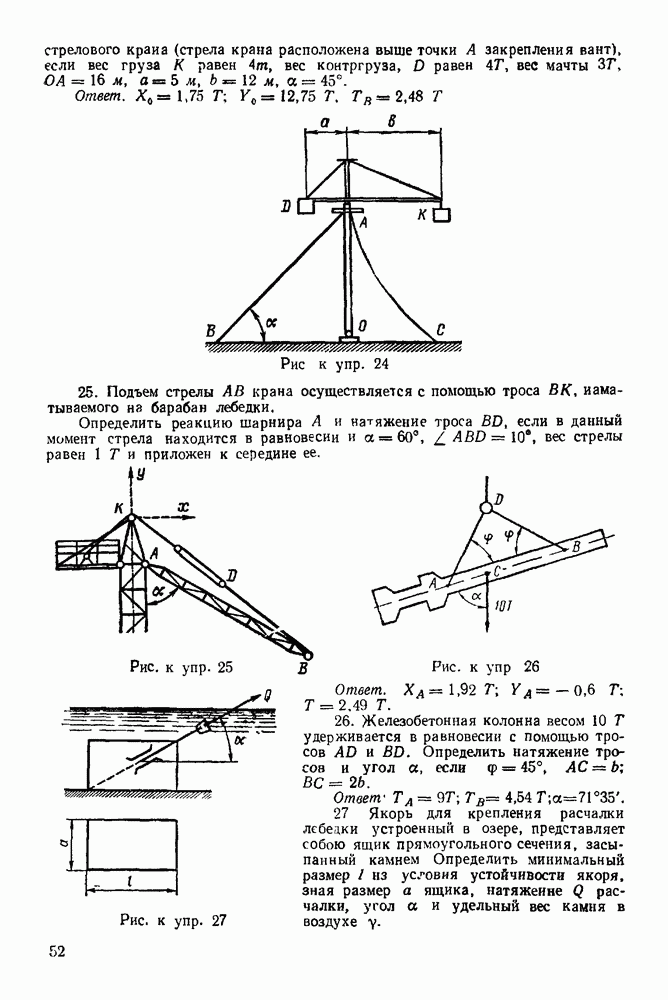
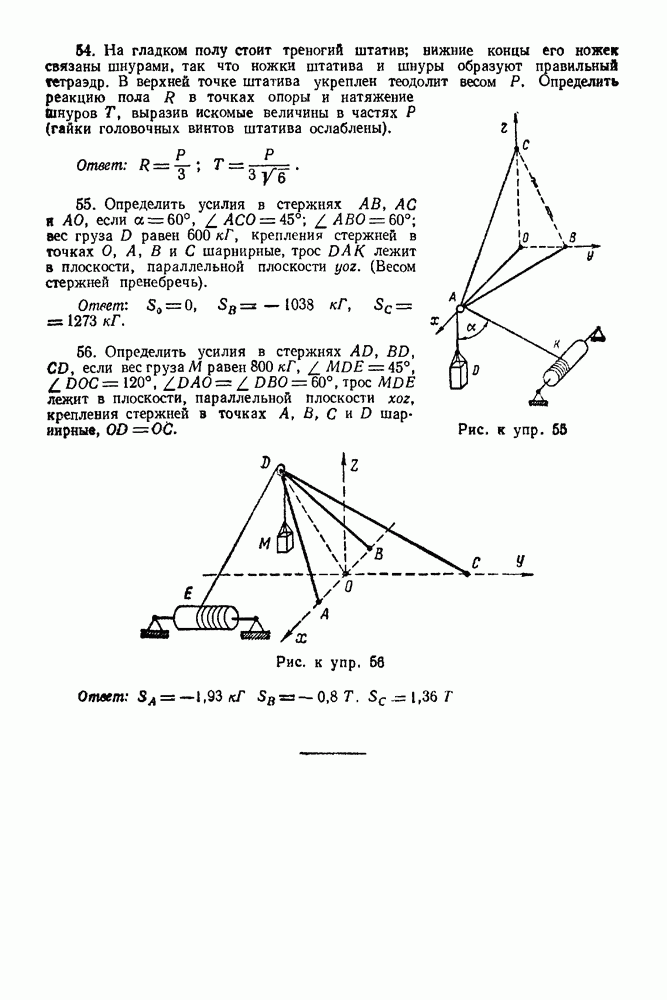
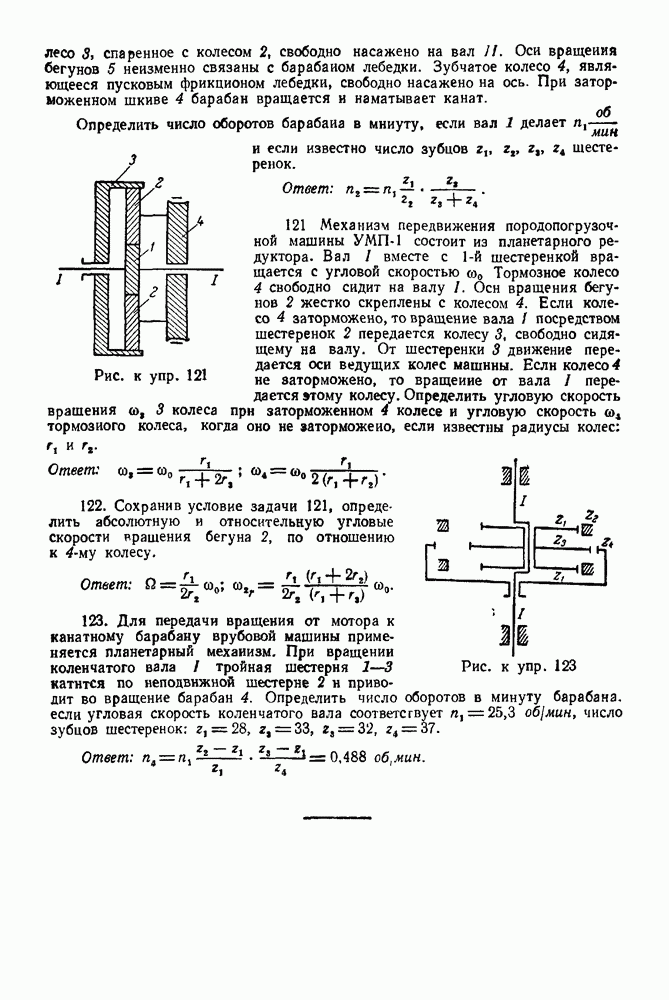
Задача 35. Определить положение центра тяжести фигуры, представленной на рис. 121, состоящей из стержней:  а и дуги
а и дуги  полуокружности радиуса а, если сечения стержней одинаковы, стержни однородны и сделаны из одного и того же материала.
полуокружности радиуса а, если сечения стержней одинаковы, стержни однородны и сделаны из одного и того же материала.

Рис. 121.

Рис. 122.
Решение. Используем метод разбиения (рис 122) Разбиваем фигуру на стержни  В этом случае координаты центра тяжести тела определяются по следующим формулам:
В этом случае координаты центра тяжести тела определяются по следующим формулам:

где

 координаты центров тяжестей стержней, 1, 2, 3 — соответственно. После подсчета получаем.
координаты центров тяжестей стержней, 1, 2, 3 — соответственно. После подсчета получаем.  а.
а.
Задача 36. Пользуясь второй теоремой Гульдена, определить положение центра тяжести площади полукруга (рис. 123).
Решение. Ось  является осью симметрии пластинки, следовательно,
является осью симметрии пластинки, следовательно,  Для нахождения
Для нахождения  применяем вторую теорему Гульдена:
применяем вторую теорему Гульдена:

где V — объем сферы, получившийся от вращения вокруг оси  (рис. 124),
(рис. 124),  площадь полукруга;
площадь полукруга;


Рис. 123.

Рис. 124.
Получаем:

Ответ: 
Задача 37. В полукруге  радиуса
радиуса  (рис. 125) требуется найти такую точку С, которая будет центром тяжести площади, полученной из полукруга путем выреза равнобедренного треугольника
(рис. 125) требуется найти такую точку С, которая будет центром тяжести площади, полученной из полукруга путем выреза равнобедренного треугольника 
Решение. Для решения задачи используем способ разбиения и способ отрицательных площадей:

где  высота треугольника
высота треугольника  площадь полукруга
площадь полукруга 
— абсцисса центра тяжести полукруга,  площадь треугольника
площадь треугольника  абсцисса центра тяжести треугольника
абсцисса центра тяжести треугольника 

Получаем: 
Ответ. 
Задача 38. В однородном цилиндре  радиуса
радиуса  сделай соприкасающийся с ним цилиндрический вырез радиуса
сделай соприкасающийся с ним цилиндрический вырез радиуса  К этому цилиндру прикреплен пустотелый цилиндр (2)
К этому цилиндру прикреплен пустотелый цилиндр (2)

Рис. 125
радиуса  При какой толщине стенки второго цилиндра данное тело будет находиться в устойчивом равновесии в положении, указанном на рис. 126 (цилиндры одинаковой длины и сделаны из одного и того же материала)?
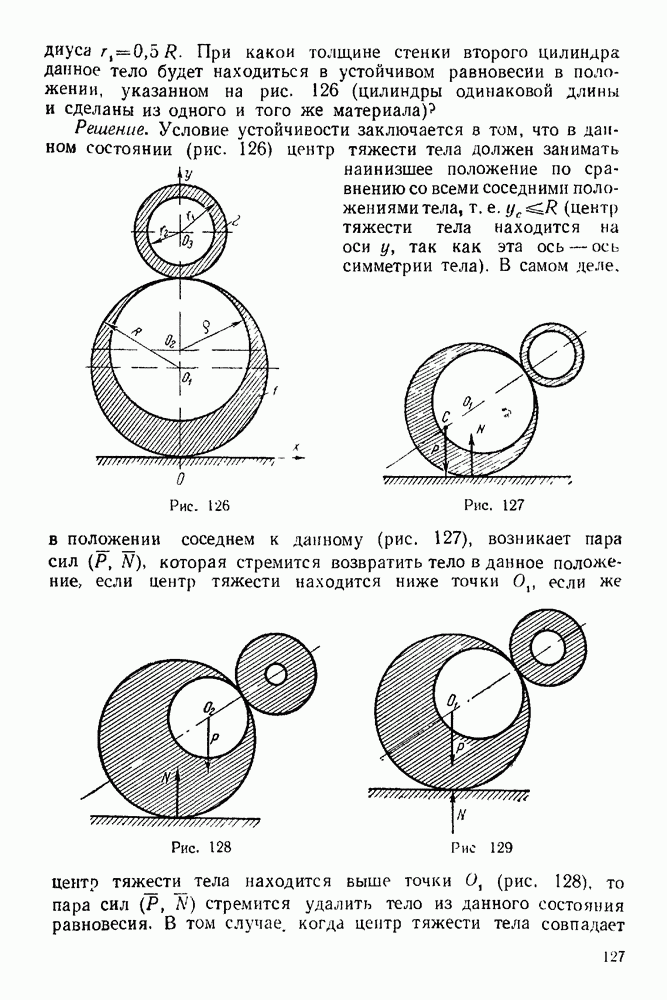
При какой толщине стенки второго цилиндра данное тело будет находиться в устойчивом равновесии в положении, указанном на рис. 126 (цилиндры одинаковой длины и сделаны из одного и того же материала)?
Решение. Условие устойчивости заключается а том, что в данном состоянии (рис. 126) центр тяжести тела должен занимать наинизшее положение по сравнению со всеми соседними положениями тела, т. е.  (центр тяжести тела находится на оси у, так как эта ось — ось симметрии тела).
(центр тяжести тела находится на оси у, так как эта ось — ось симметрии тела).

Рис. 126

Рис. 127
В самом деле. в положении соседнем к данному (рис. 127), возникает пара сил  которая стремится возвратить тело в данное положение, если центр тяжести находится ниже точки
которая стремится возвратить тело в данное положение, если центр тяжести находится ниже точки  если же центр тяжести тела находится выше точки О, (рис. 128), то пара сил
если же центр тяжести тела находится выше точки О, (рис. 128), то пара сил  стремится удалить тело из данного состояния равновесия.
стремится удалить тело из данного состояния равновесия.

Рис. 128

Рис. 129
В том случае, когда центр тяжести тела совпадает
с точкой О, пары, стремящейся повернуть тело, не существует. В этом случае тело находится в состоянии безразличного равновесия (рис. 129).
При решении задачи используем способ разбиения тела на части и способ отрицательных площадей:

где  площадь круга радиуса
площадь круга радиуса  — координата центра тяжести этого круга;
— координата центра тяжести этого круга;  площадь кругового зыреза радиуса
площадь кругового зыреза радиуса  координата центра тяжести этого выреза;
координата центра тяжести этого выреза;  площадь круга радиуса
площадь круга радиуса  координата центра тяжести этого круга;
координата центра тяжести этого круга;  площадь кругового выреза радиуса
площадь кругового выреза радиуса  координата центра тяжести этого выреза;
координата центра тяжести этого выреза;

Получаем 
Очевидно, что
Ответ. 
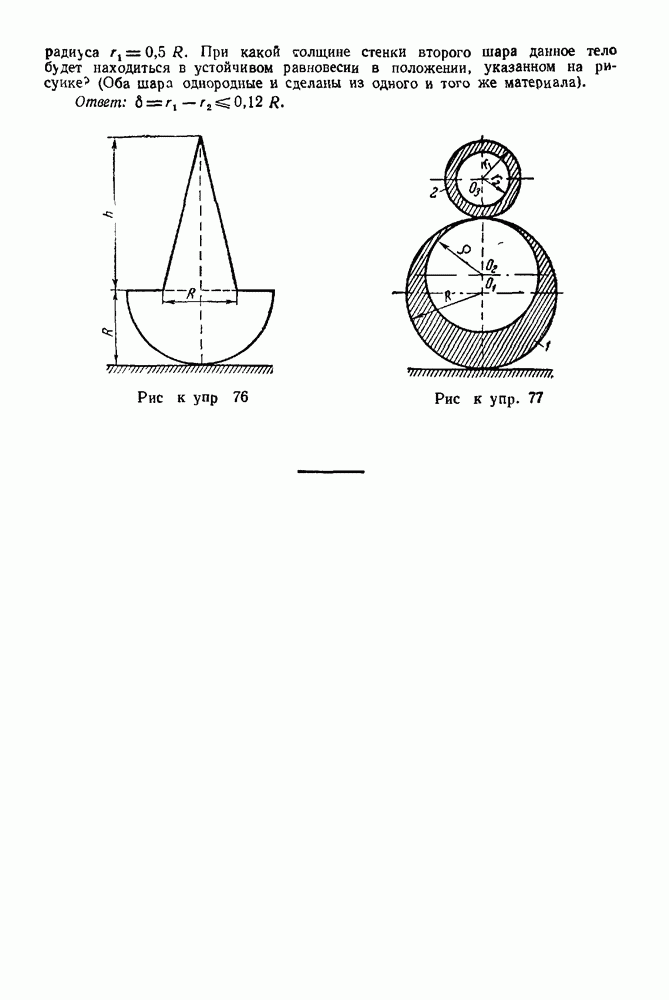
Задача 39. Тело состоит из однородного полушара радиуса  и однородного цилиндра того же радиуса, скрепленных друг с другом, как указано на рис. 130. Какоза должна быть высота
и однородного цилиндра того же радиуса, скрепленных друг с другом, как указано на рис. 130. Какоза должна быть высота  конусоидального выреза, чтобы тело находилось в данном состоянии в положении устойчивого равновесия (шар и цилиндр сделаны из одного и того же материала)?
конусоидального выреза, чтобы тело находилось в данном состоянии в положении устойчивого равновесия (шар и цилиндр сделаны из одного и того же материала)? 

Рис. 130.
Решение. Для того, чтобы тело находилось в данном состоянии в положении устойчивого равновесия, необходимо и достаточно, чтобы  где
где  координата центра тяжести тела (см решение задачи 38). Для нахождения
координата центра тяжести тела (см решение задачи 38). Для нахождения  воспользуемся способом разбиения тела на части и способом отрицательных объемов Разбиваем тело на полушар, цилиндр и пустотелый конус (отрицательный объем). Тогда будем иметь:
воспользуемся способом разбиения тела на части и способом отрицательных объемов Разбиваем тело на полушар, цилиндр и пустотелый конус (отрицательный объем). Тогда будем иметь:

где  объем полушара;
объем полушара;  координата центра тяжести этого полушара,
координата центра тяжести этого полушара,  объем цилиндра,
объем цилиндра,  координата центра тяжести этого цилиндра; V, — объем конуса; у, — координата центра тяжести конуса.
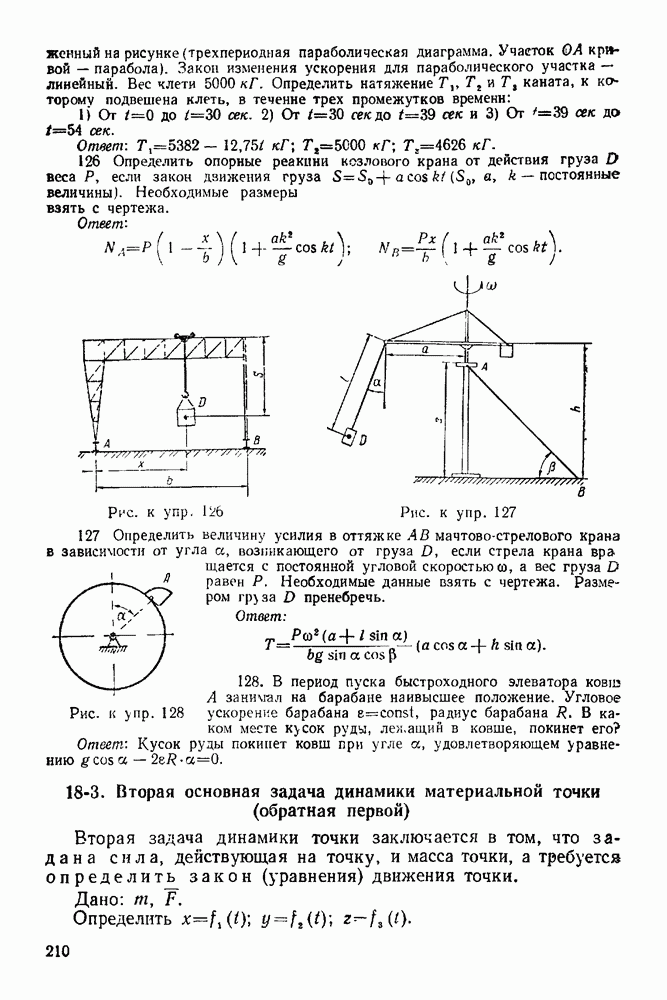
координата центра тяжести этого цилиндра; V, — объем конуса; у, — координата центра тяжести конуса.

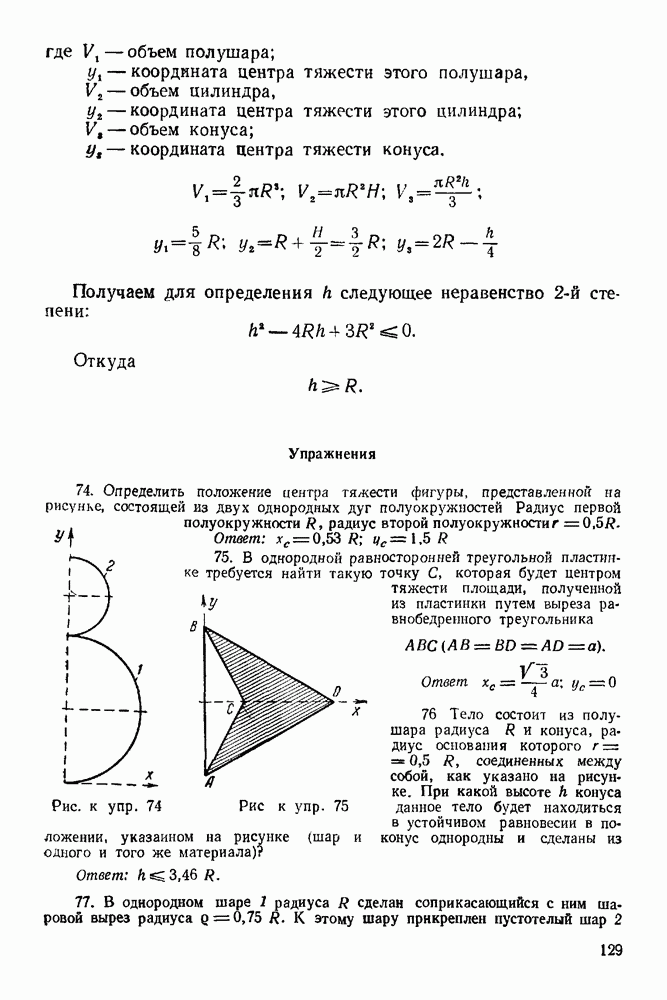
Получаем для определения  следующее неравенство 2-й степени:
следующее неравенство 2-й степени:

Откуда

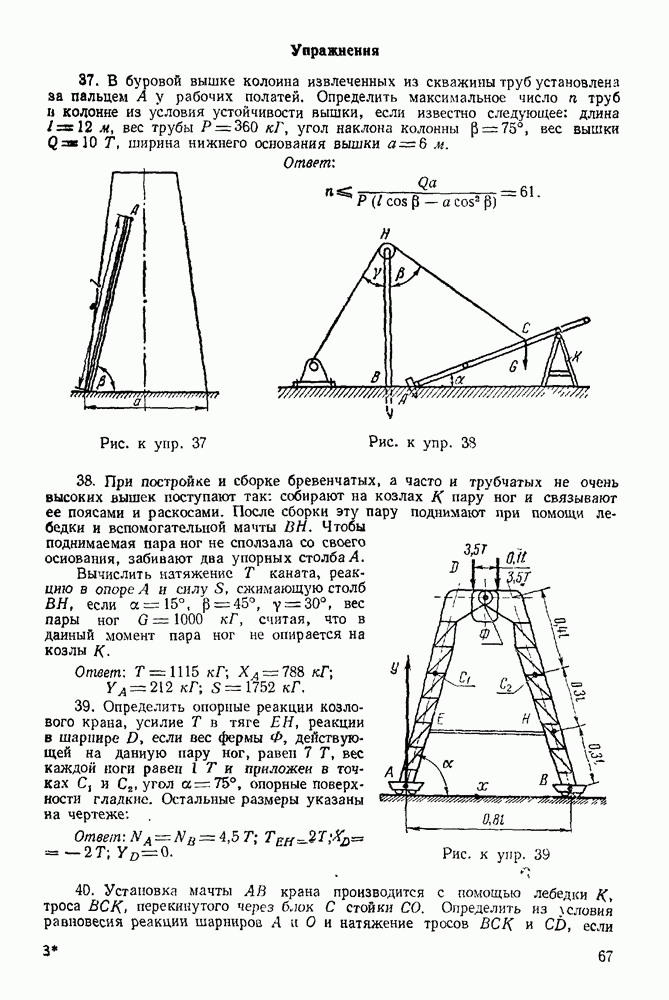
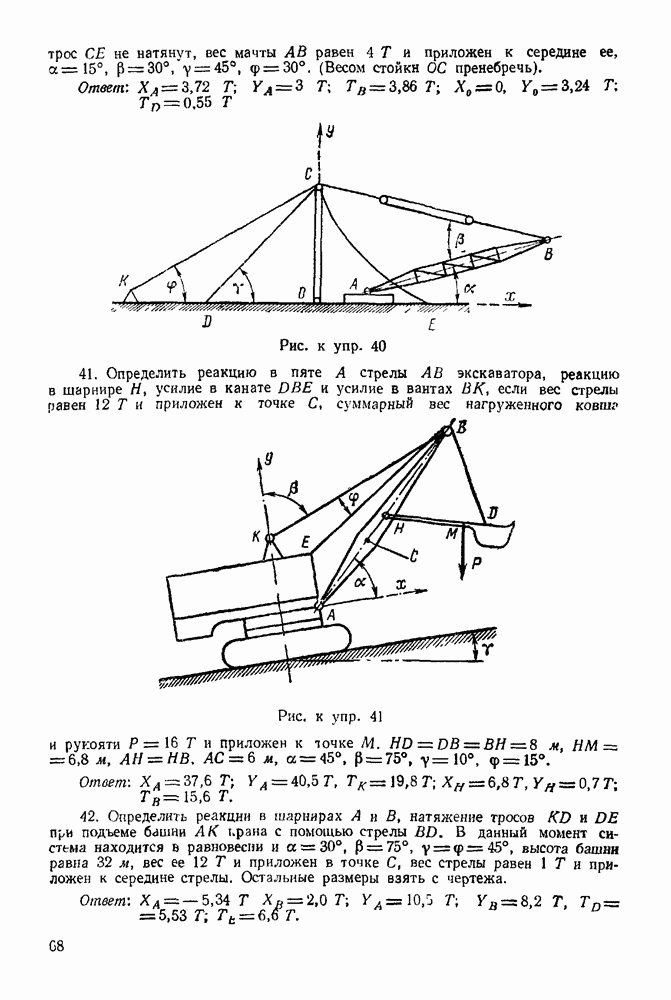
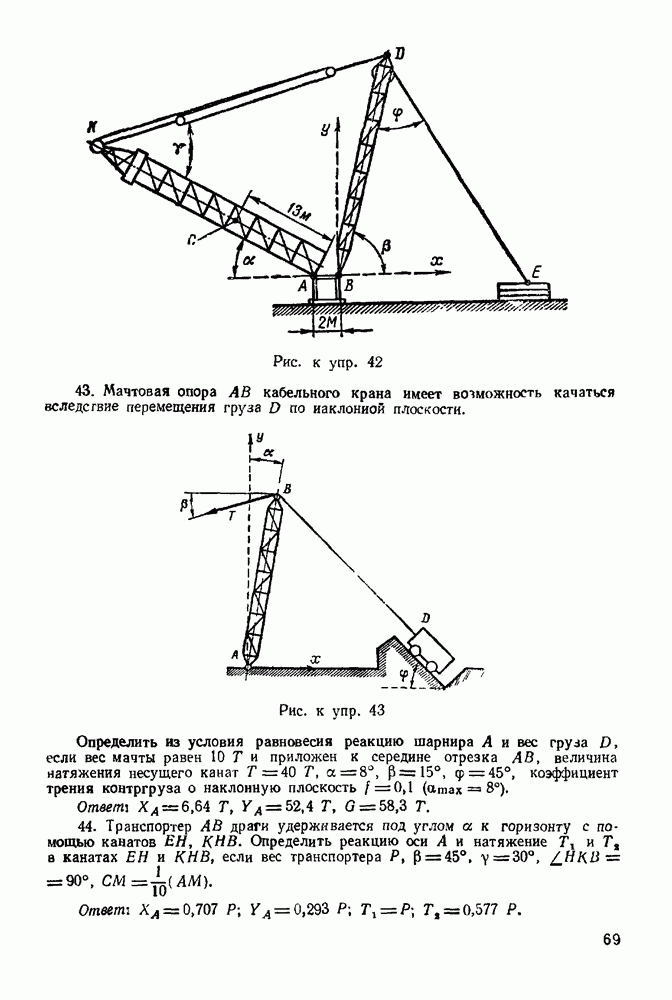
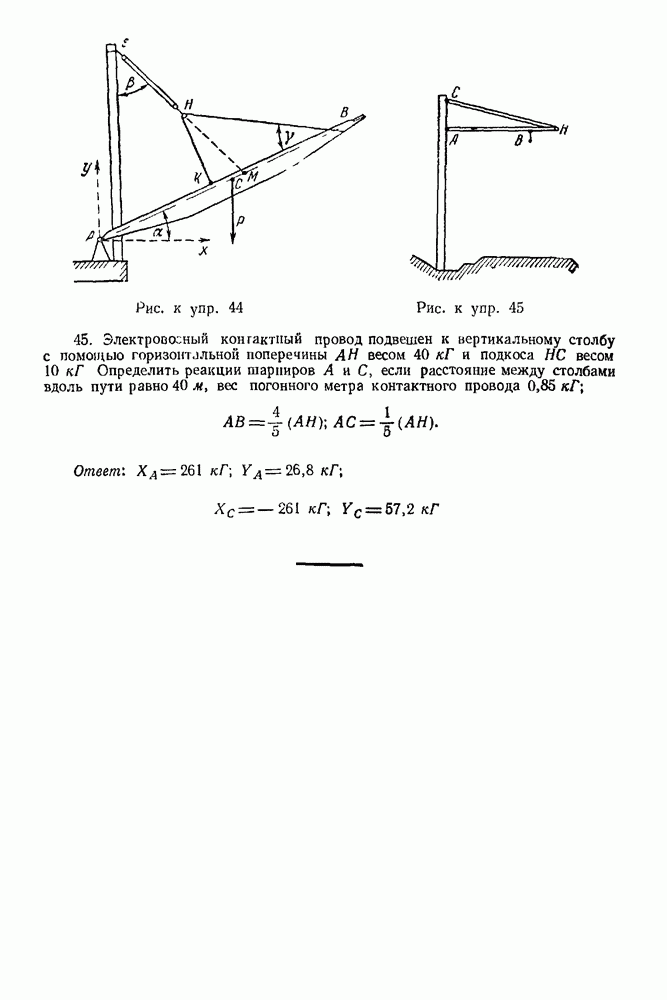
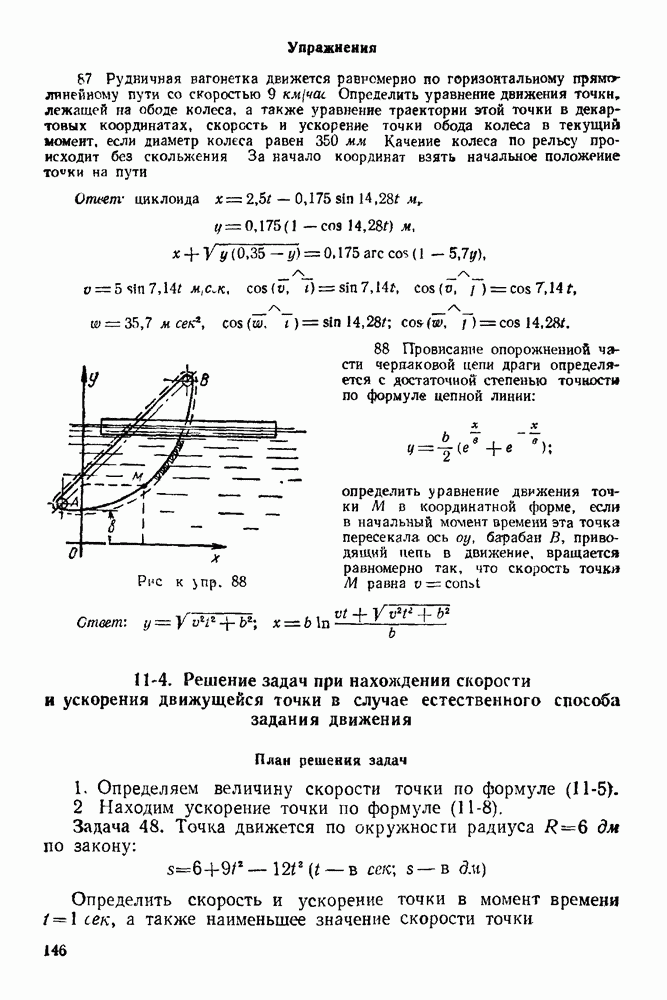
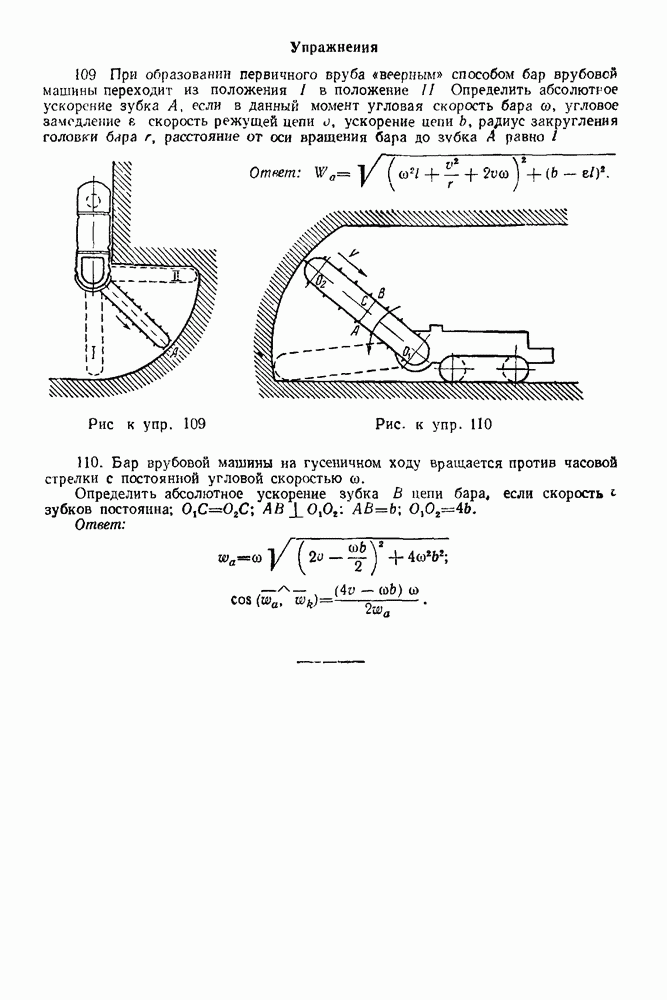
Упражнения
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
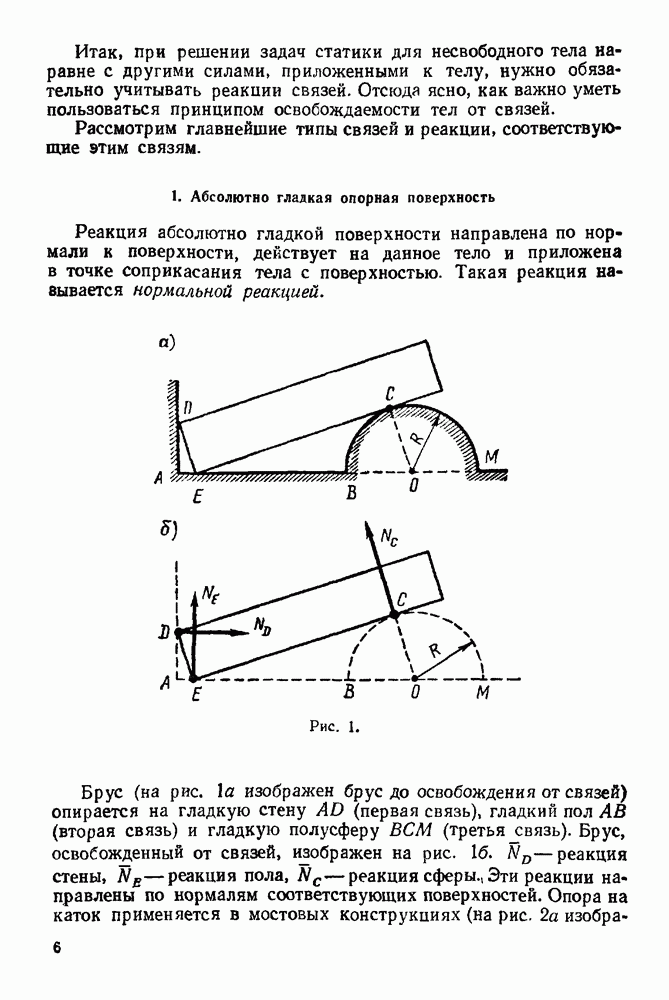
- 1. Абсолютно гладкая опорная поверхность
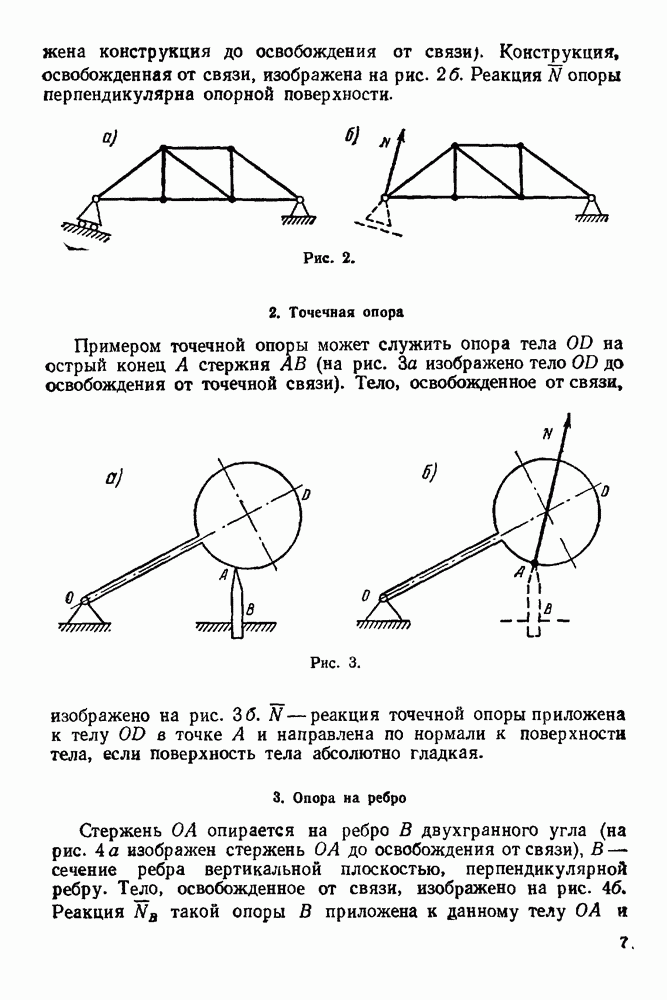
- 2. Точечная опора
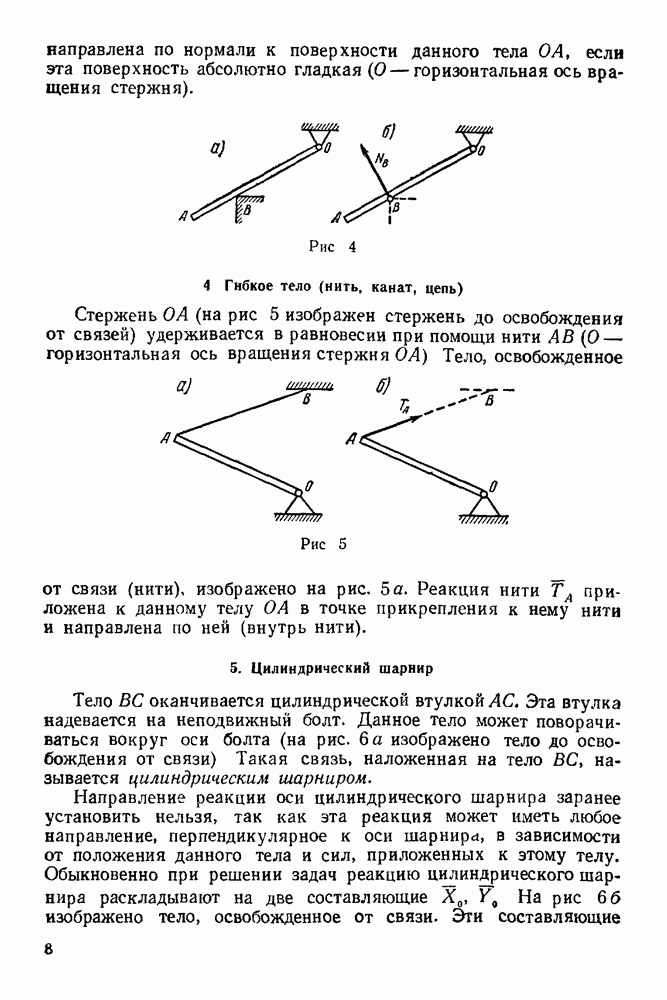
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
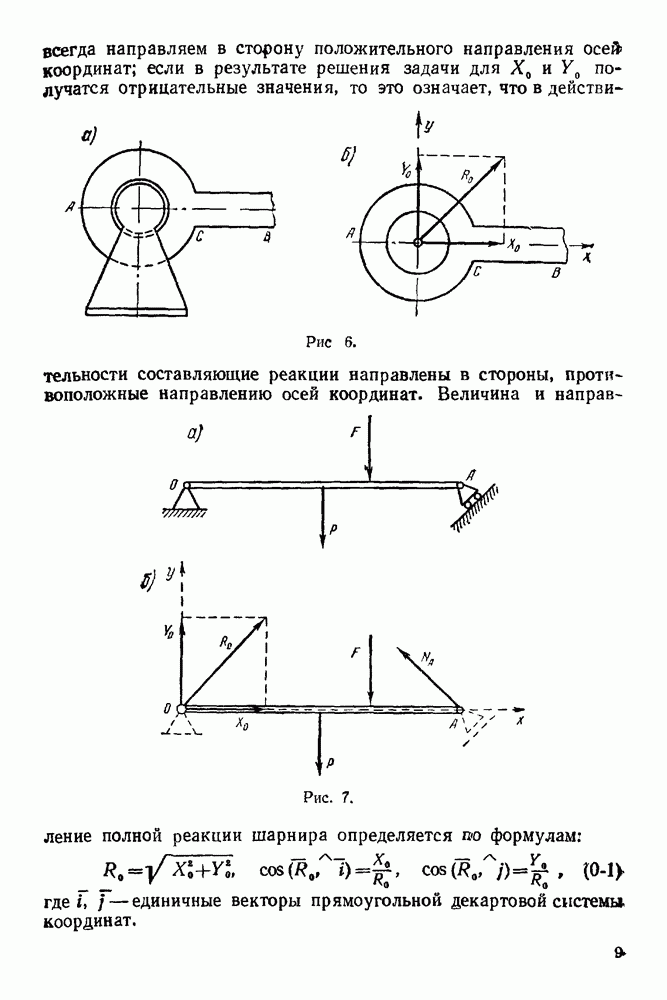
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
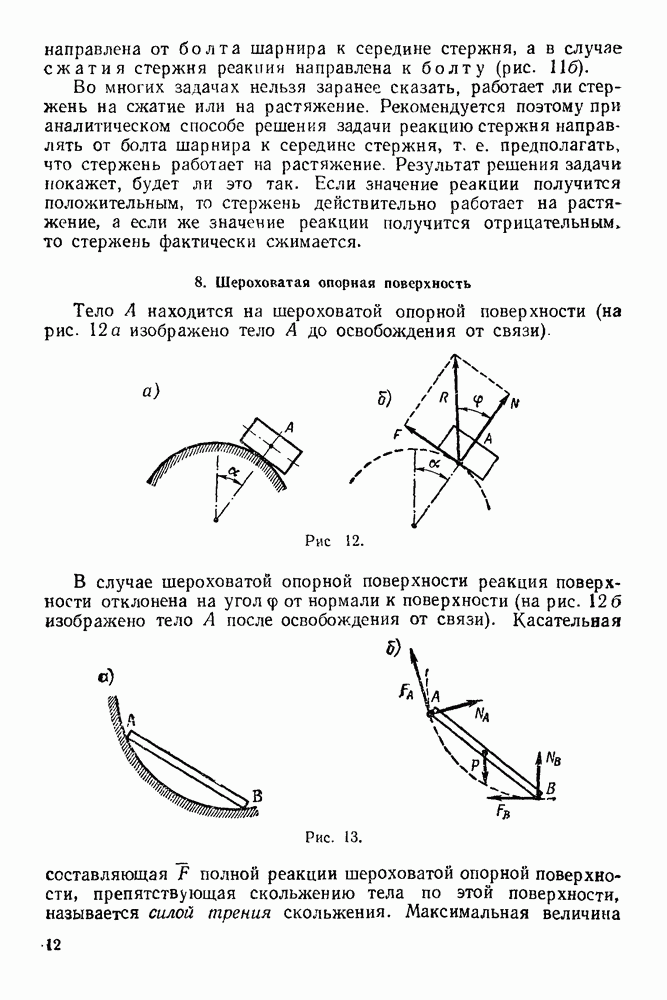
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
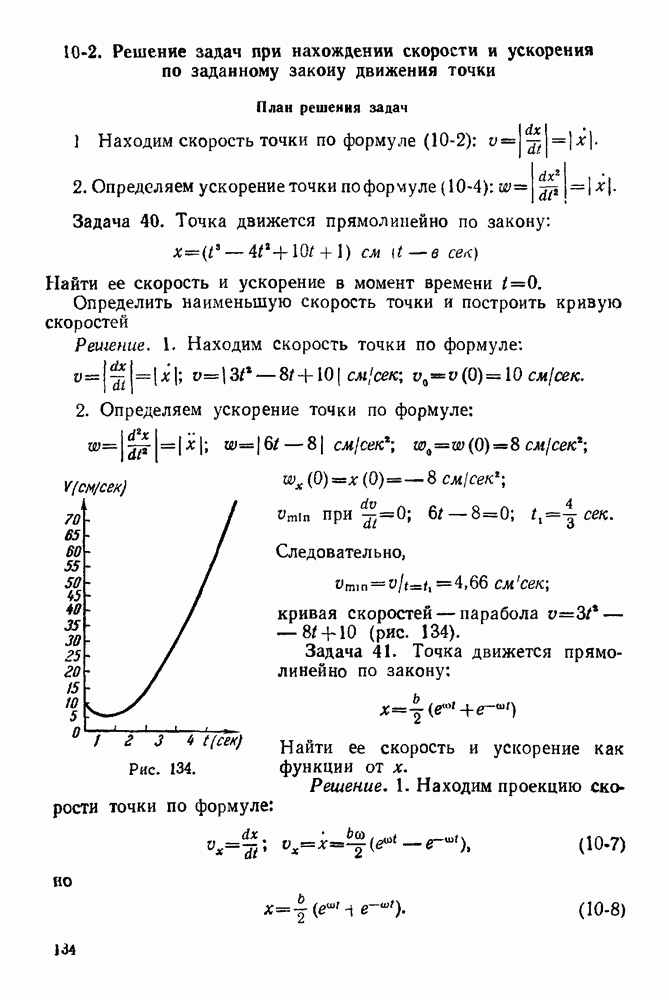
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
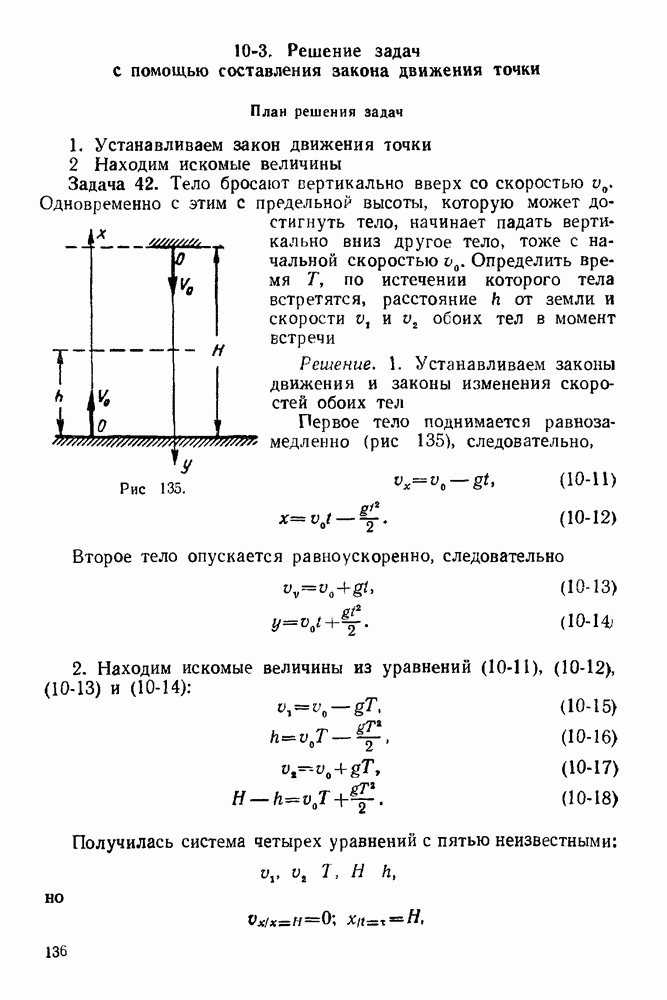
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
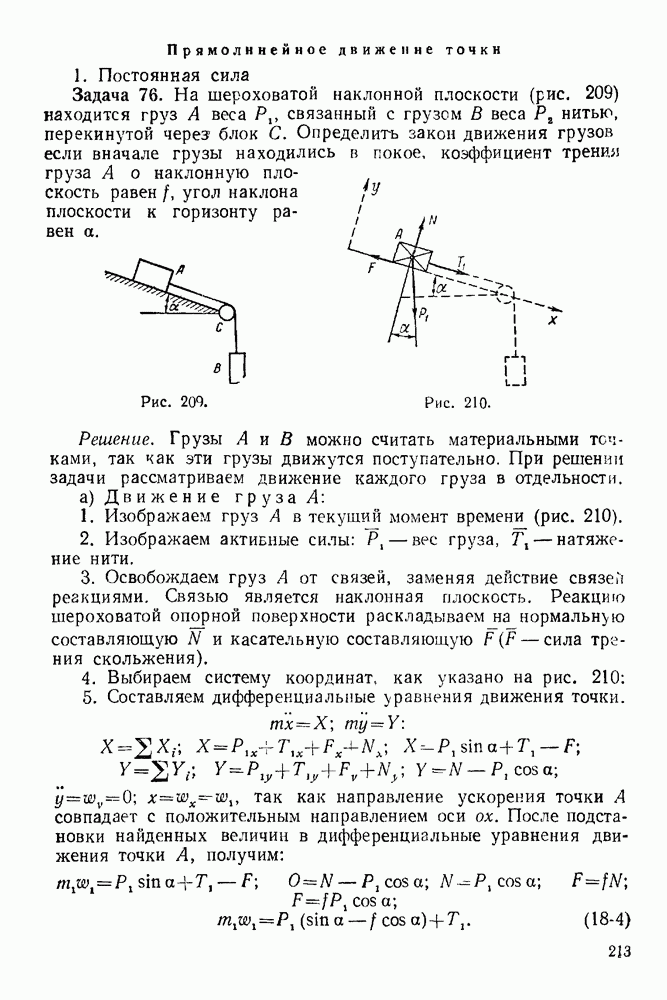
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
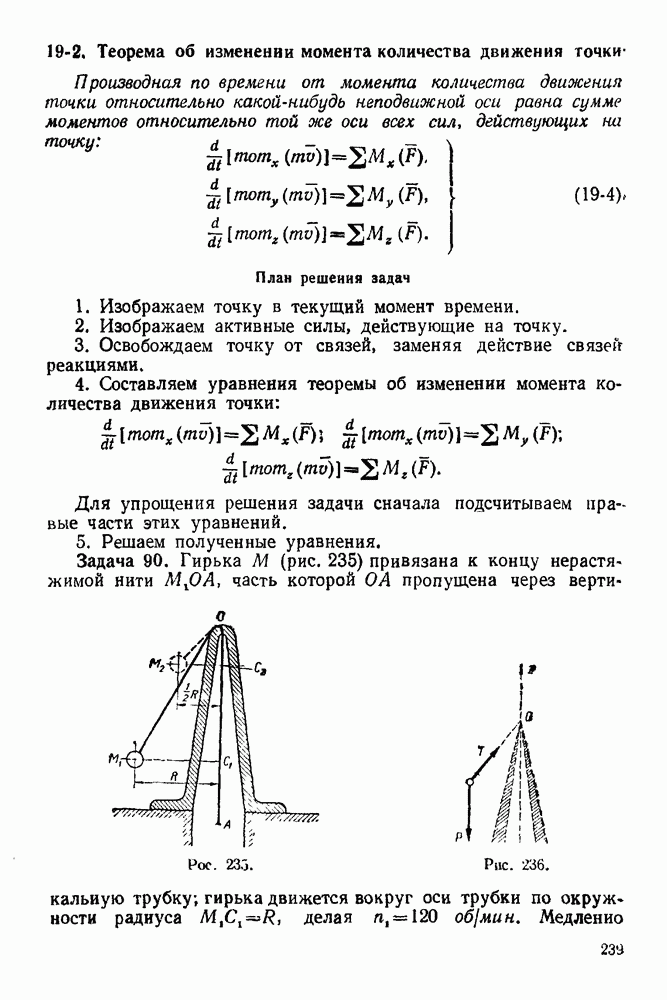
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
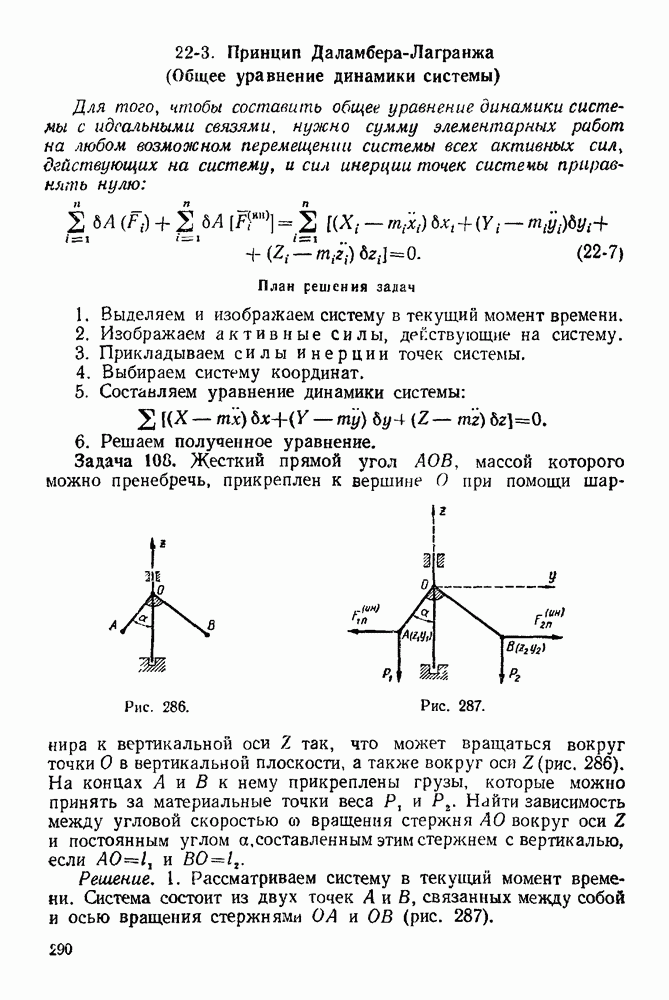
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР