| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
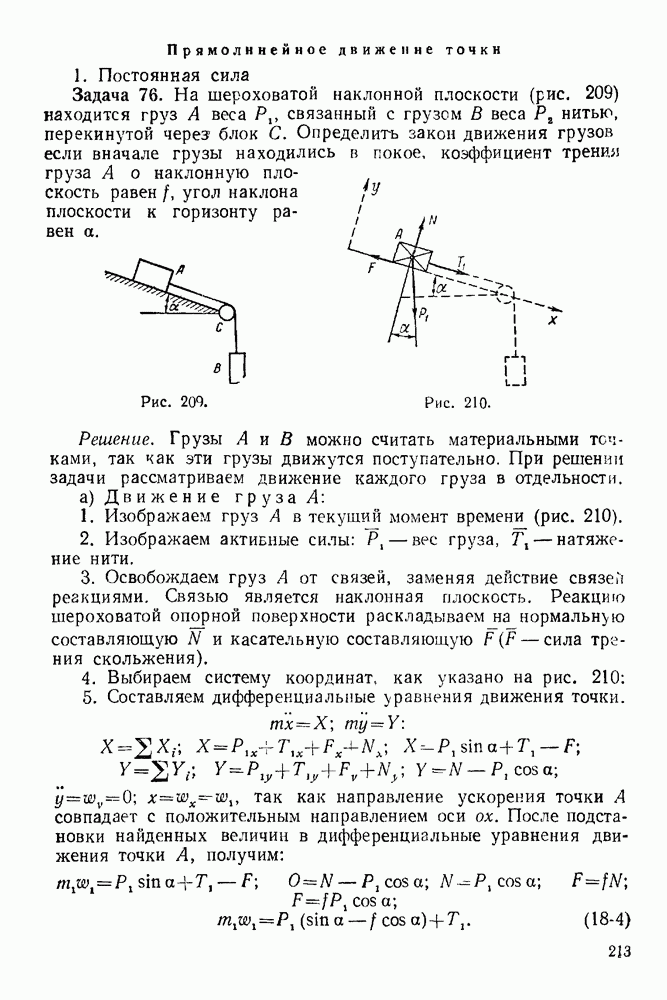
21-4. Теорема об изменении кинетической энергии системы
Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:

Изменение кинетической энергии системы за некоторый промежуток времени равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующем перемещении системы:

Кинетическая энергия системы равна сумме кинетических энергий точек системы:

Если система неизменяемая, т. е. расстояния между точками системы остаются неизменными (частным случаем такой системы является абсолютно твердое тело), то сумма работ всех внутренних сил системы равна нулю:

Кинетическая энергия системы равна кинетической энергии центра масс системы, считая, что в нем сосредоточена масса всей системы, плюс кинетическая энергия системы в ее относительном движении но отношению к поступательно движущейся системе координат, с началом в центре масс:

Кинетическая энергия поступательно движущегося твердого тела равна кинетической энергии любой точки этого тела, считая, что в этой точке сосредоточена масса всего тела:

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости вращения тела:

Кинетическая энергия тела, участвующего в плоскопараллельном движении, равна кинетической энергии центра тяжести тела, считая, что в нем сосредоточена масса всего тела, плюс кинетическая энергия тела в относительном (вращательном) движении тела по отношению к поступательно движущейся системе координат с началом в центре тяжести (ось  перпендикулярна к направляющей плоскости):
перпендикулярна к направляющей плоскости):

Элементарная работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на элементарный угол поворота тела:

Сумма элементарных работ сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна главному моменту сил, действующих на тело, относительно оси вращения, умноженному на элементарный угол поворота тела:

План решения задач
1. Выделяем и изображаем систему в текущий момент времени.
2. Изображаем внешние и внутренние силы, действующие на систему.
3. Составляем уравнение теоремы об изменении кинетическол энергии системы:

(Если силы, действующие на систему, переменные, а траектории точек приложения сил криволинейные, то следует брать теорему об изменении кинетической энергии системы в дифференциальной форме с последующим переходом к конечной форме путем интегрирования.)
4. Из полученного уравнения находим неизвестные величины.
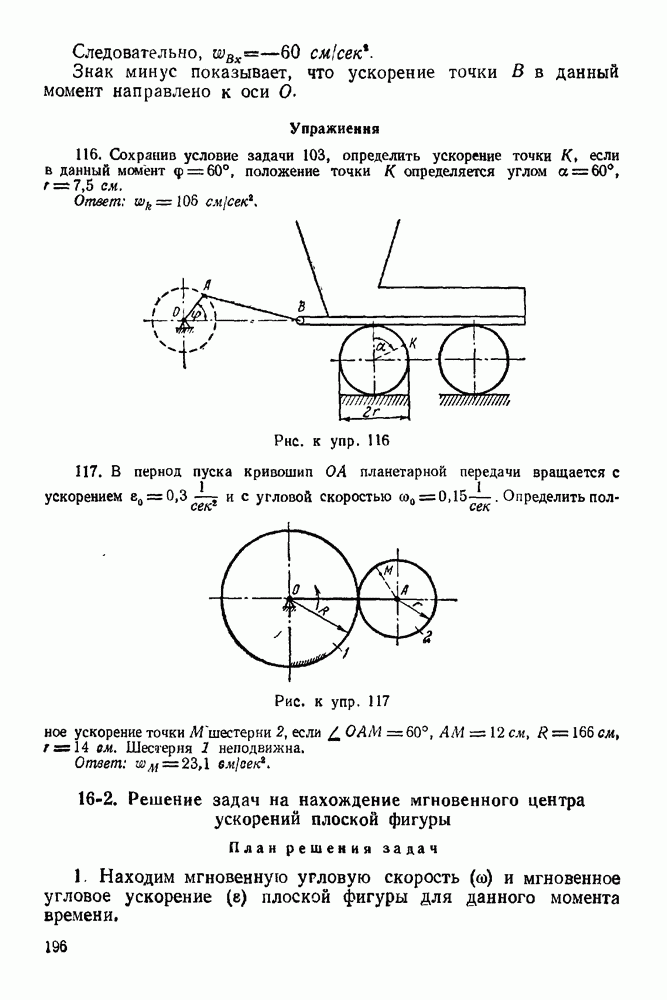
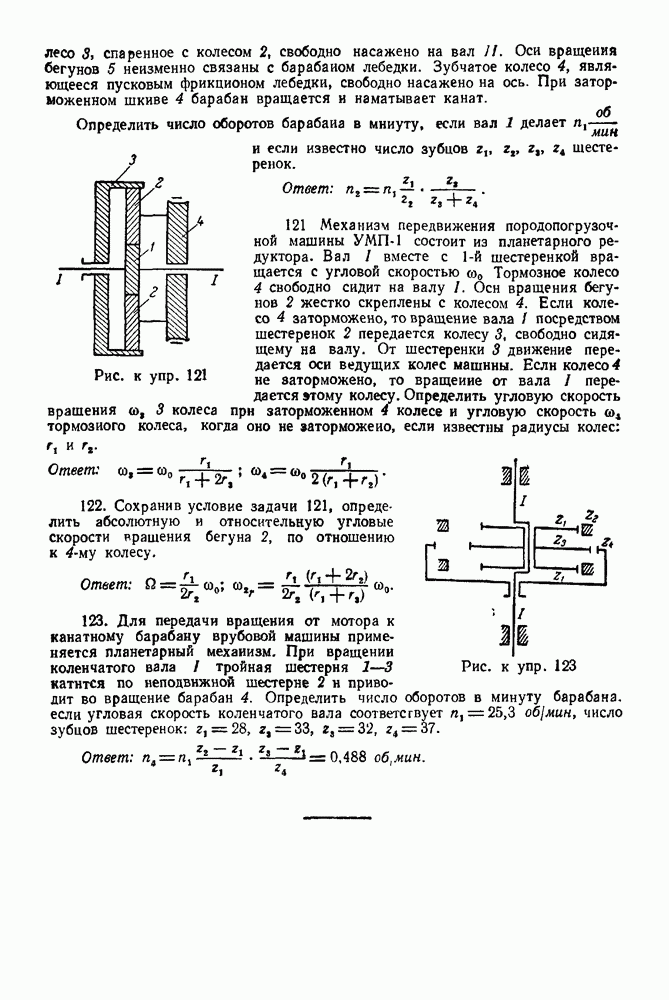
Задача 101. В однородном тяжелом диске радиуса  сделан круговой вырез радиуса
сделан круговой вырез радиуса  Какую скорость нужно сообщить точке А диска, чтобы диаметр
Какую скорость нужно сообщить точке А диска, чтобы диаметр  сделал у оборота (О — горизонтальная ось вращения диска, сопротивлениями пренебречь,
сделал у оборота (О — горизонтальная ось вращения диска, сопротивлениями пренебречь, 

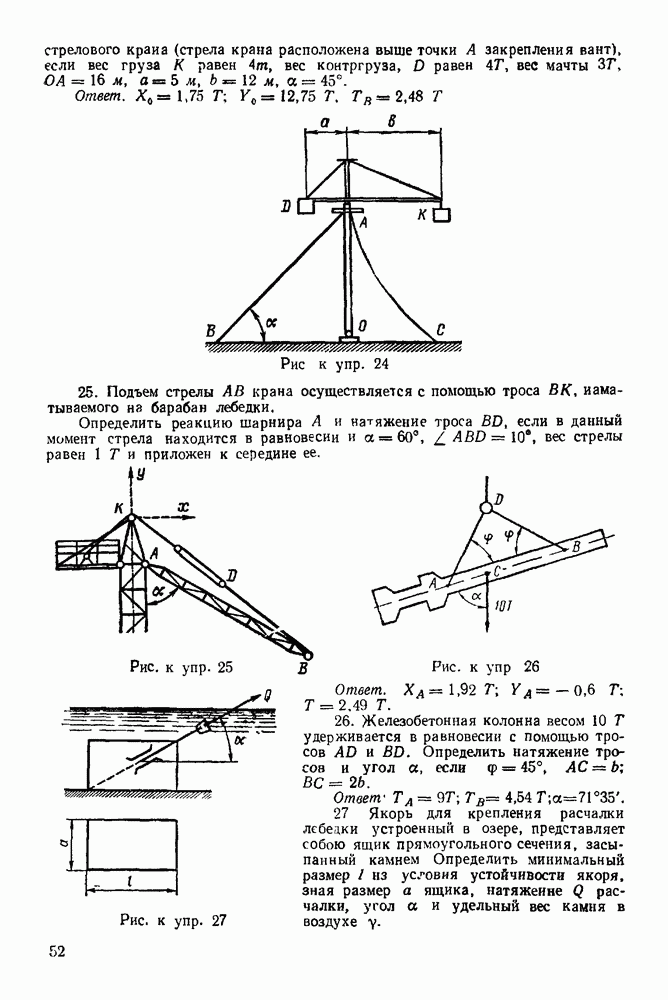
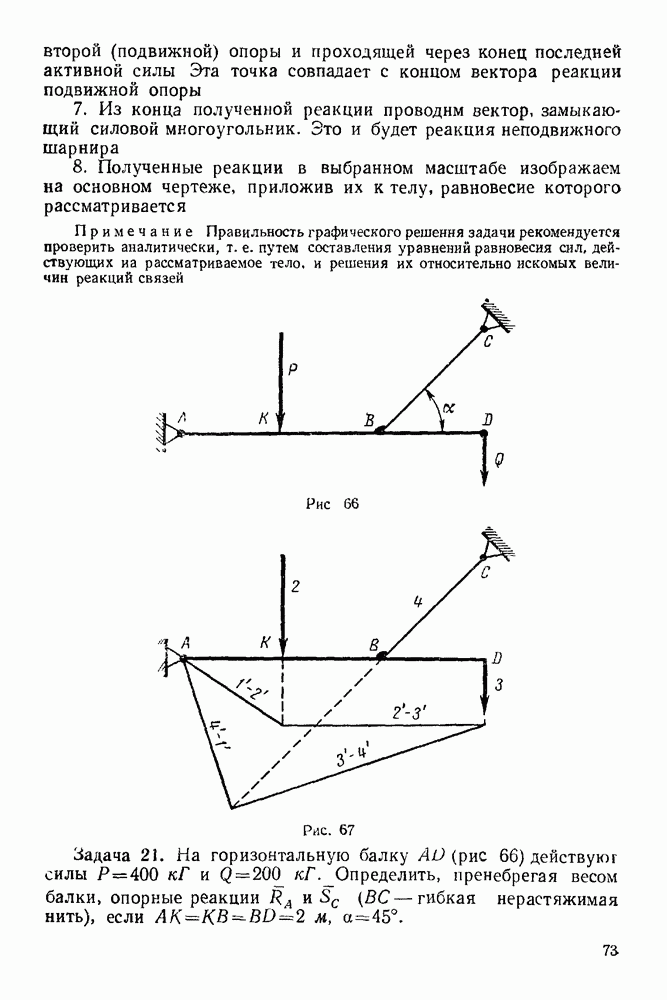
Рис. 266.

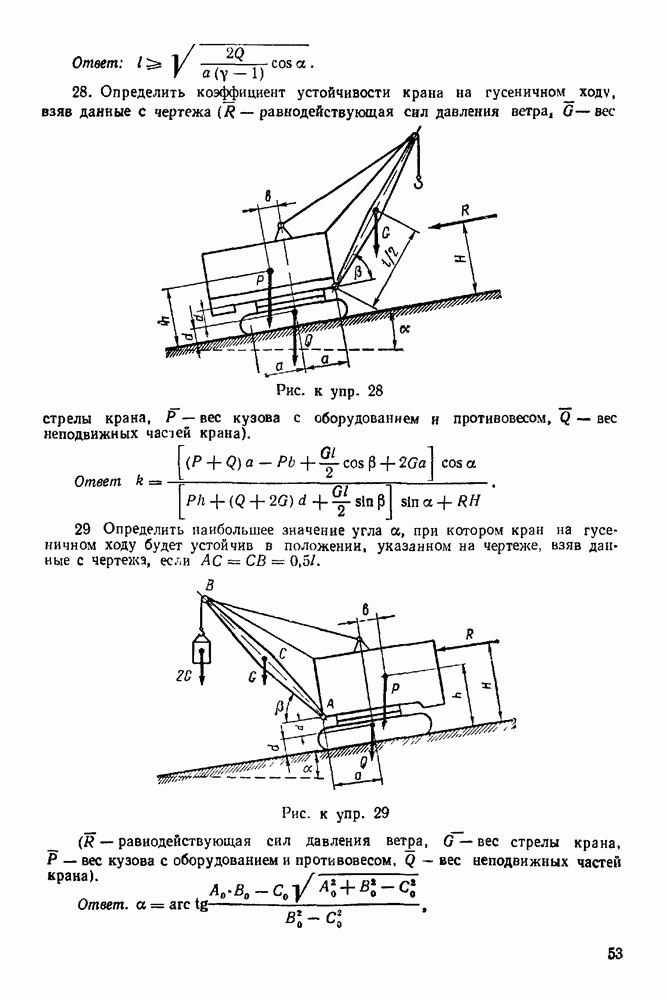
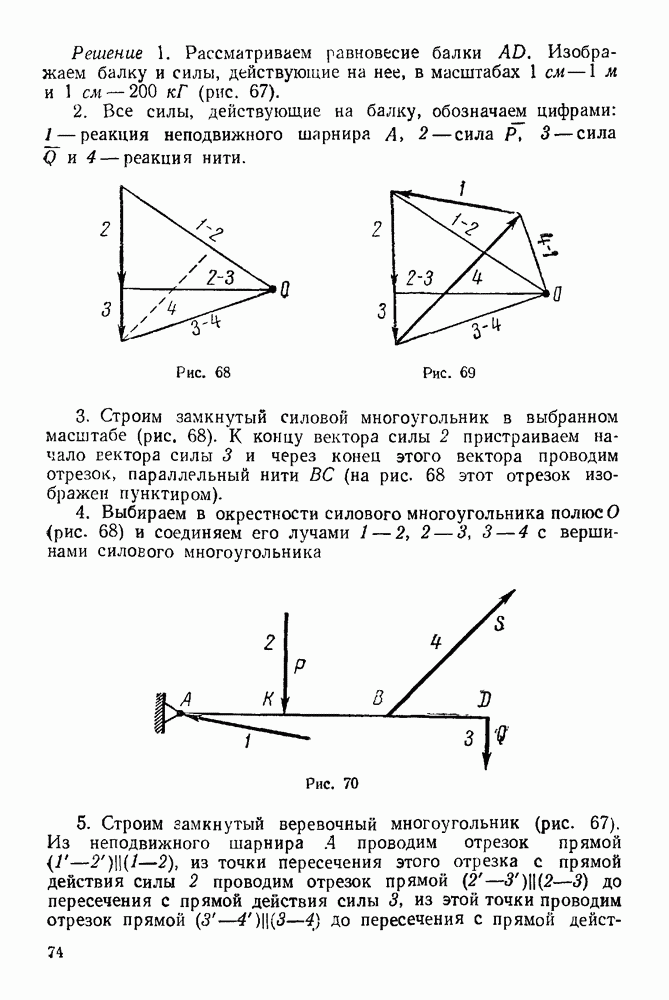
Рис. 267.
Решение. 1 Изображаем диск (диск — материальная система, состоящая из бесчисленного множества точек) в текущий момент времени (рис. 267).
2. Изображаем внешние силы, действующие на диск;  вес диска и
вес диска и  реакция оси вращения диска.
реакция оси вращения диска.
3 Составляем уравнение теоремы об изменении кинетической энергии системы в конечной форме:  повороте диска на 120°.
повороте диска на 120°.
 так как диск — неизменяемая система.
так как диск — неизменяемая система.
 так как точка приложения реакции
так как точка приложения реакции  неподвижна:
неподвижна:

 кинетическая энергия диска в конце движения.
кинетическая энергия диска в конце движения.

Найденные величины подставляем в уравнение теоремы и получим:

4. Решаем полученное уравнение 

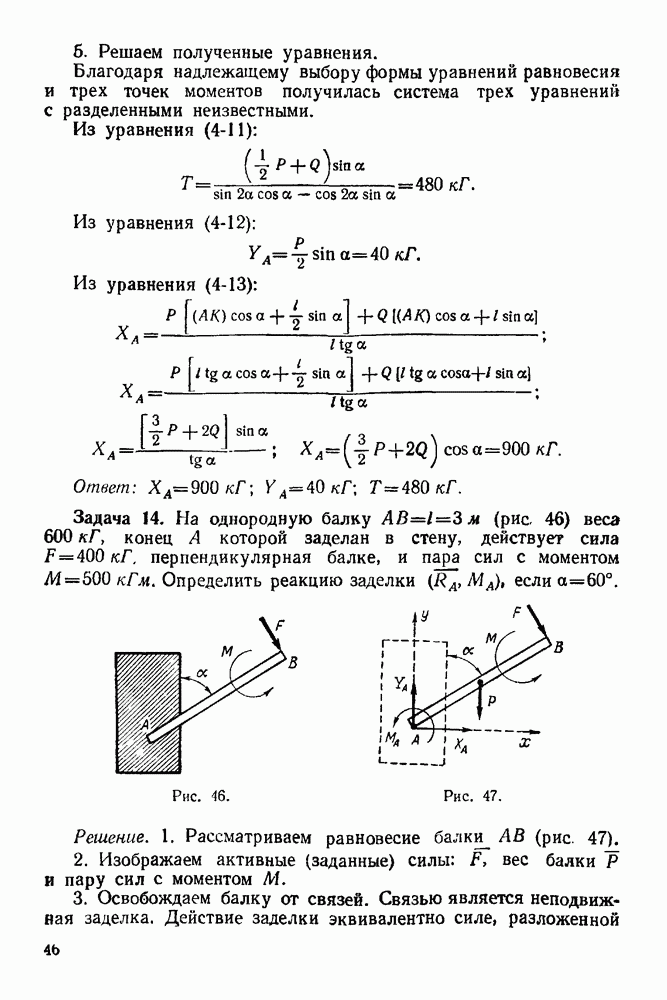
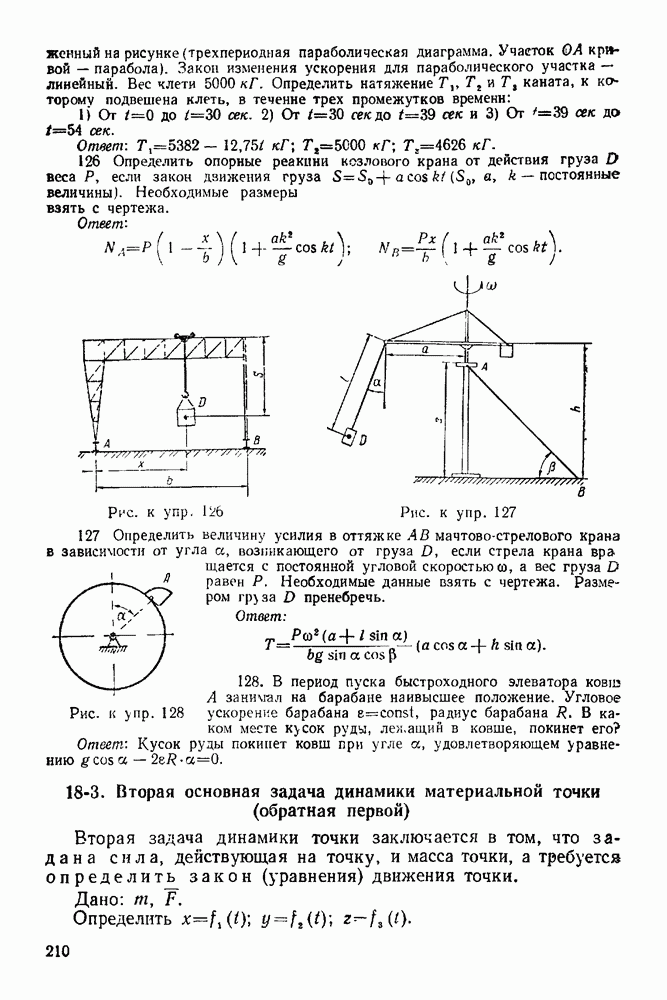
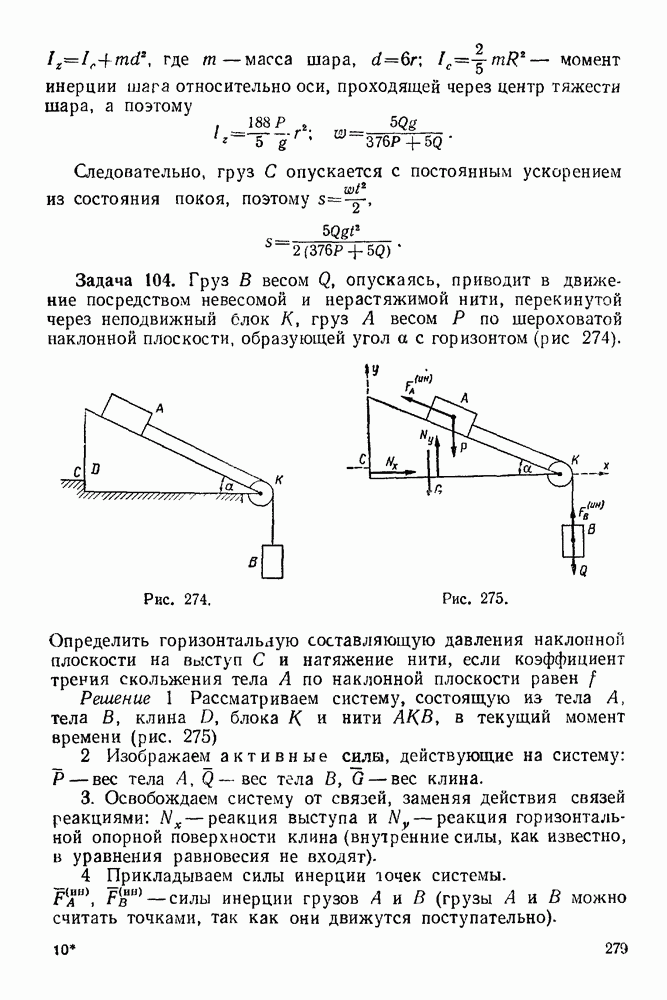
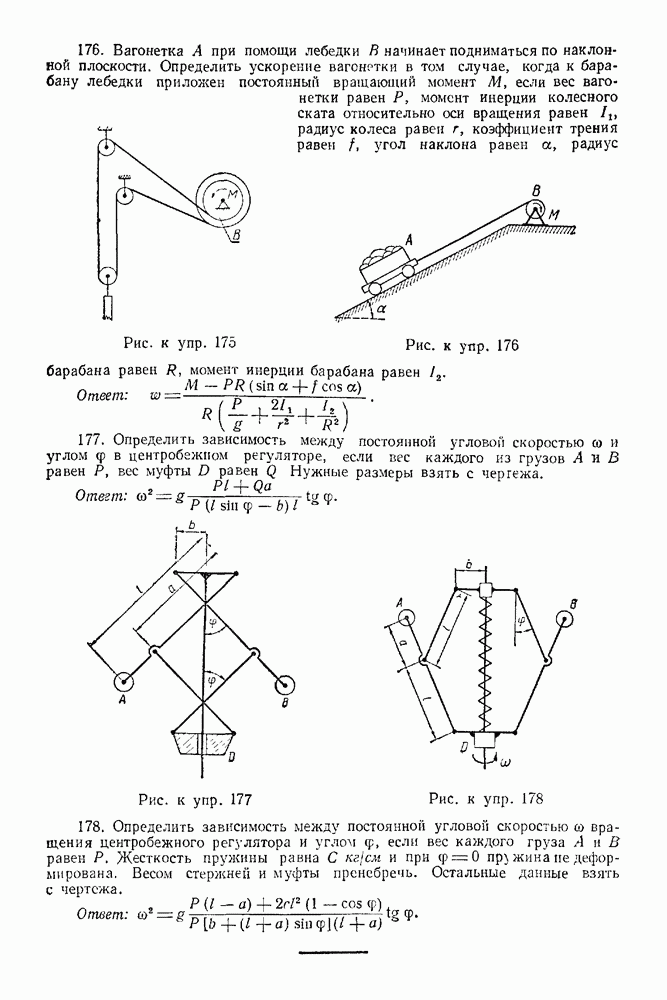
Задача 102. Груз А веса  поднимается по шероховатой наклонной плоскости с помощью барабана В веса
поднимается по шероховатой наклонной плоскости с помощью барабана В веса  и верезки. наматываемой на барабан (рис 268) Барабан приводится во ирацение вокруг горизонтальной оси О парой сил с моментом
и верезки. наматываемой на барабан (рис 268) Барабан приводится во ирацение вокруг горизонтальной оси О парой сил с моментом  Определить скорость тела
Определить скорость тела  как функцию расстояния
как функцию расстояния  проходимого этим грузом, а также ускорение груза
проходимого этим грузом, а также ускорение груза  если коэффициент трения скольжения груза по наклонной плоскости равен
если коэффициент трения скольжения груза по наклонной плоскости равен  угол наклона плоскости к горизонту равен а, радиус барабана рачен
угол наклона плоскости к горизонту равен а, радиус барабана рачен  радиус инерции барабана относительно оси вращения равен
радиус инерции барабана относительно оси вращения равен  Вначале система находилась в покое; массой веревки пренебречь.
Вначале система находилась в покое; массой веревки пренебречь.

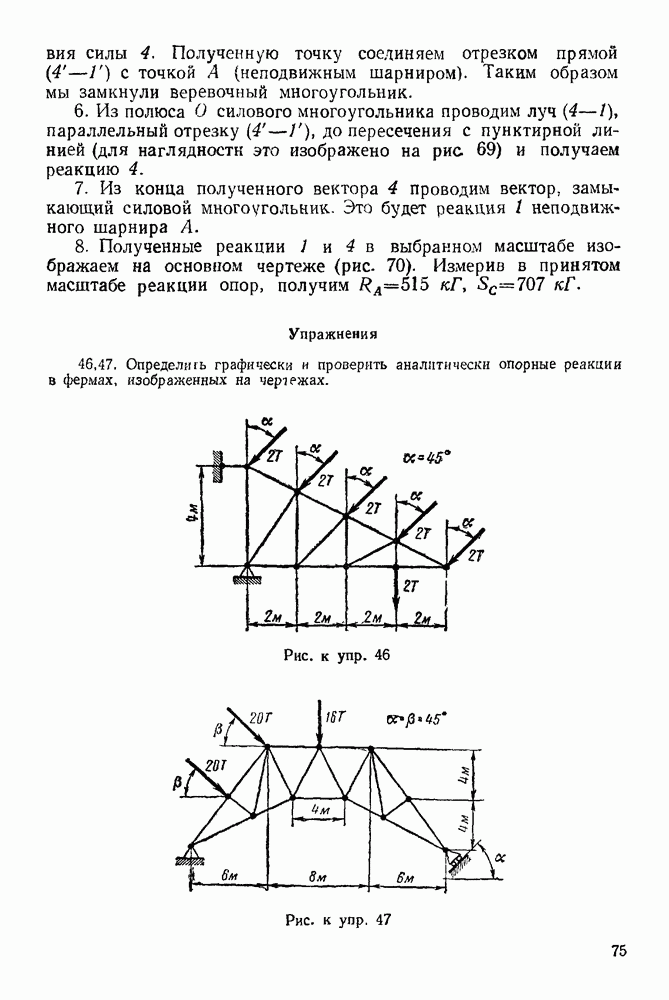
Рис. 268
Решение. 1 Изображаем систему состоящую из груза  барабана В и веревки (рис. 269) в текущий момент
барабана В и веревки (рис. 269) в текущий момент
2. Изображаем внешние силы действующие на систему:  вес барабана,
вес барабана,  вес тела
вес тела  реакция оси барабана,
реакция оси барабана,  нормальная составляющая шероховатой опорной плоскости и
нормальная составляющая шероховатой опорной плоскости и  -сила трения скольжения (весом веревки пренебрегаем) и пар
-сила трения скольжения (весом веревки пренебрегаем) и пар  с моментом
с моментом 

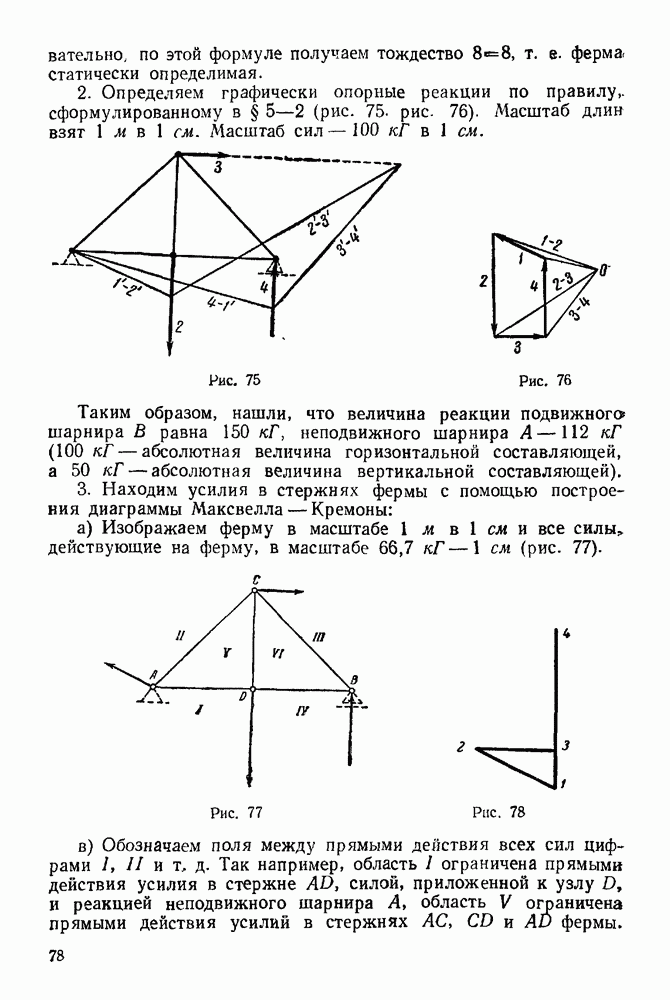
Рис. 269.
3. Составляем уравнение теоремы об изменении кинетической энергии системы в конечной форме  так как система состоит из трердых тел и гибкой нерастяжимой нити (связь, осуществленная в виде гибкой перастяжимой нити, является совершенной сьязью, т. е. 0):
так как система состоит из трердых тел и гибкой нерастяжимой нити (связь, осуществленная в виде гибкой перастяжимой нити, является совершенной сьязью, т. е. 0):

так как точки приложения этих сил не перемещаются:

где  угол поворота барабана при перемещении тела А на расстояние
угол поворота барабана при перемещении тела А на расстояние  Очевидно,
Очевидно, 

Для определения реакции  составляем дифференциальное уравнение движения поступательно движущегося груза А в проекции на ось у (рис. 270):
составляем дифференциальное уравнение движения поступательно движущегося груза А в проекции на ось у (рис. 270):

Следовательно,

 так как вначале система находилась в покое. Получаем:
так как вначале система находилась в покое. Получаем:


Рис. 270.
Найденные величины подставляем в уравнение теоремы:

4. Решаем полученное уравнение (21-25)

Для определения ускорения груз) А нужно продифференцировать уравнение (21-25) по времени, имея в виду, что

Теорему об изменении кинетической энергии системы целесообразно применять в тех случаях, когда из совокупности следующих величин: силы системы, совершающие работу, начальные и конечные скорости точек системы и их пути, неизвестна какая-нибудь одна величина и ее нужно определить.
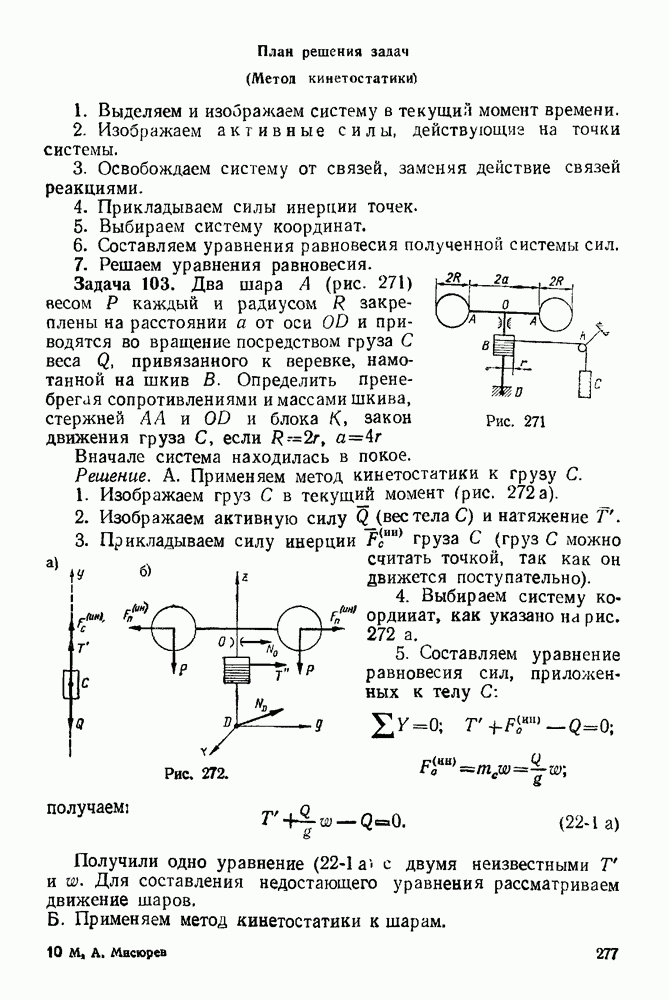
Кроме того, выгодно применять эту теорему для определения ускорения. Для этого составляют уравнение теоремы на произвольном участке пути с последующим дифференцированием по времени обеих частей полученного равенства.
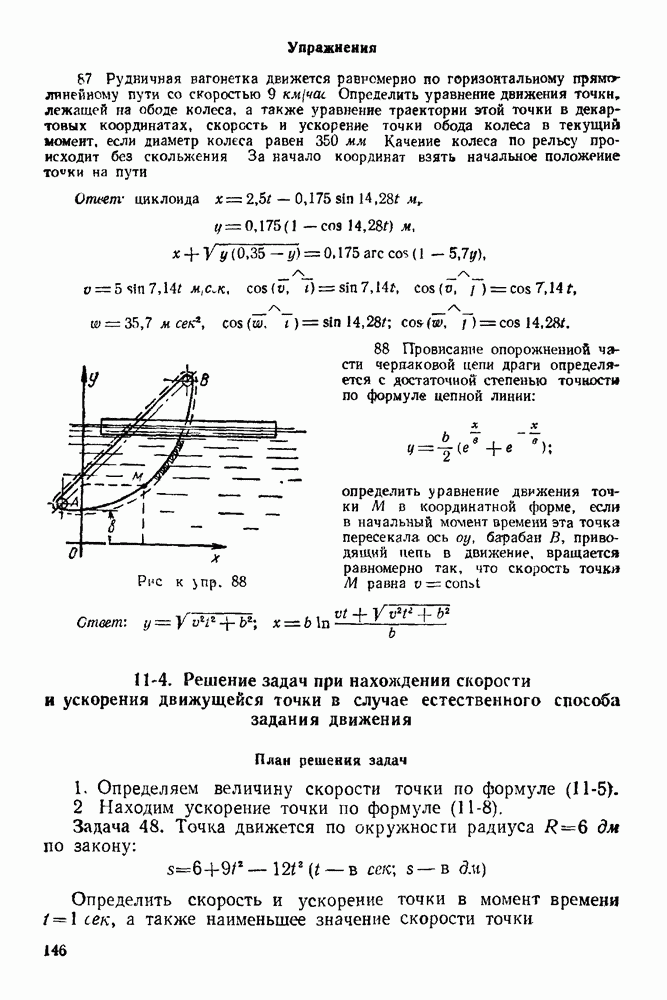
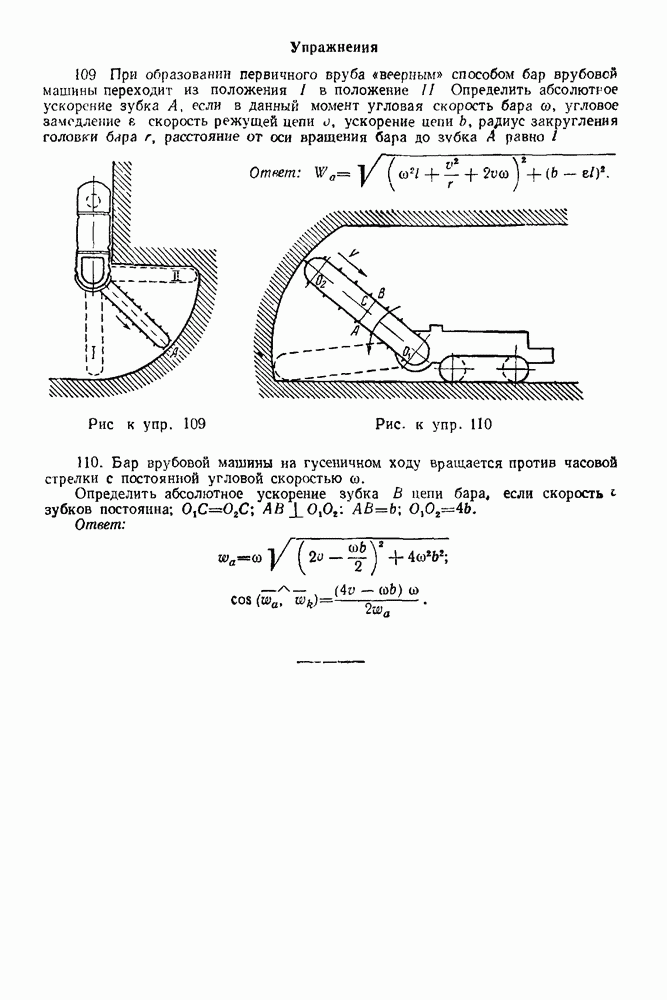
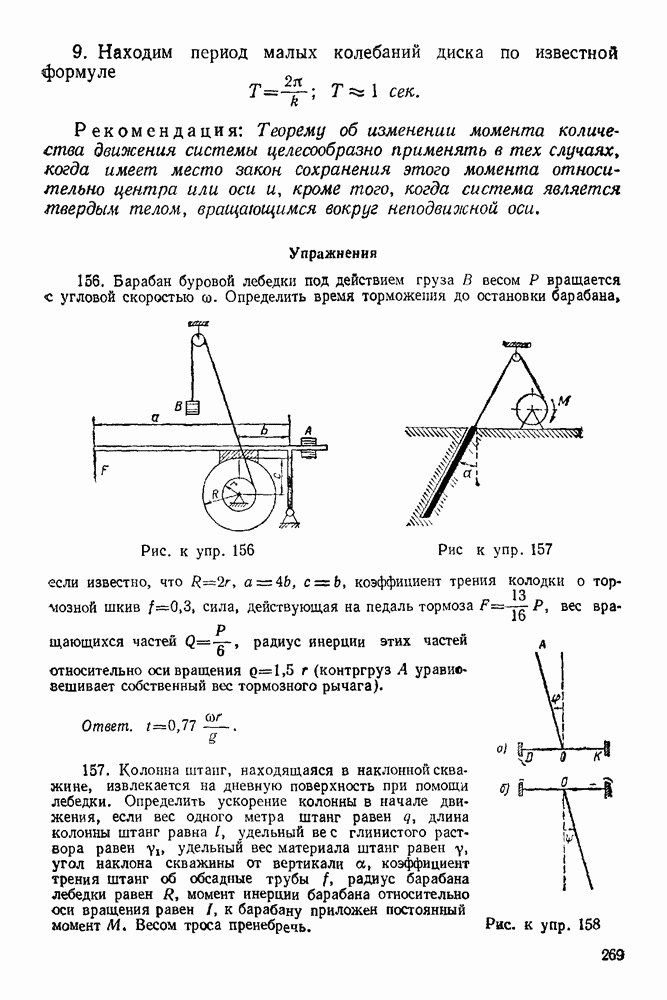
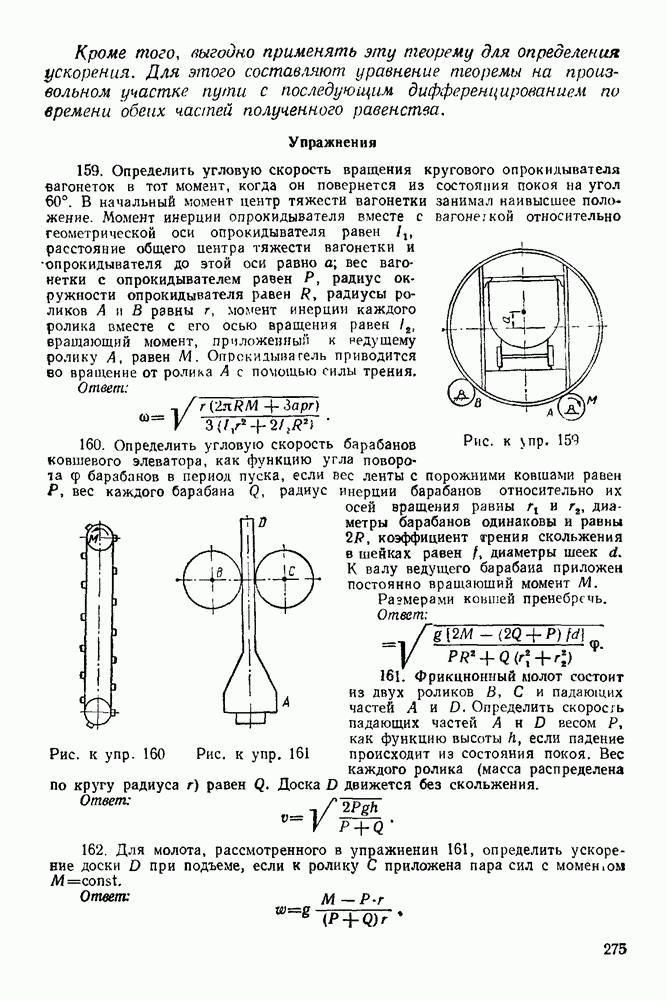
Упражнения
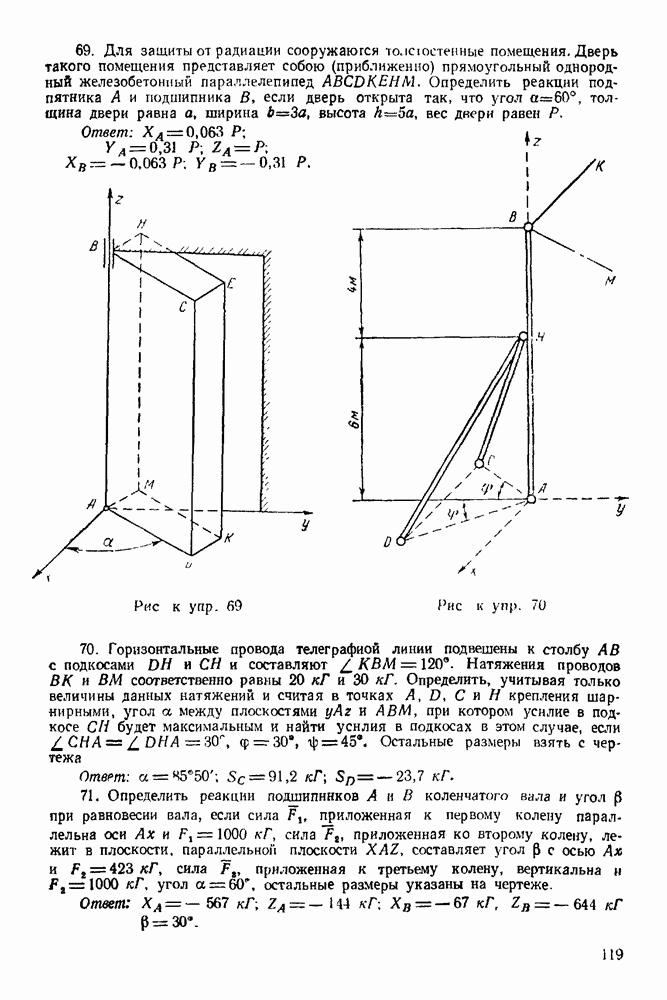
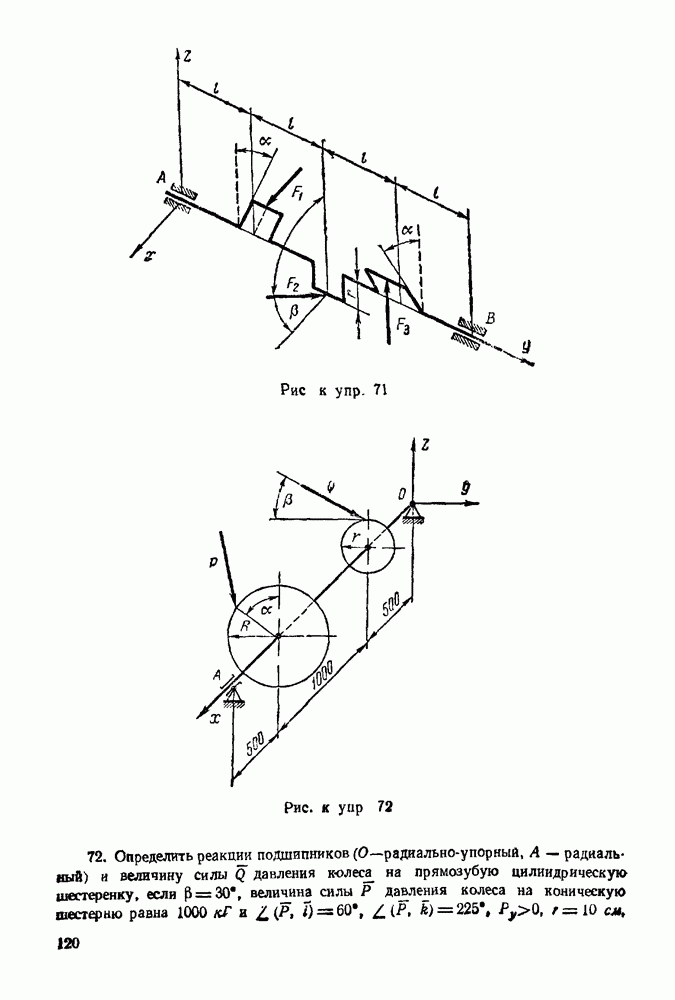
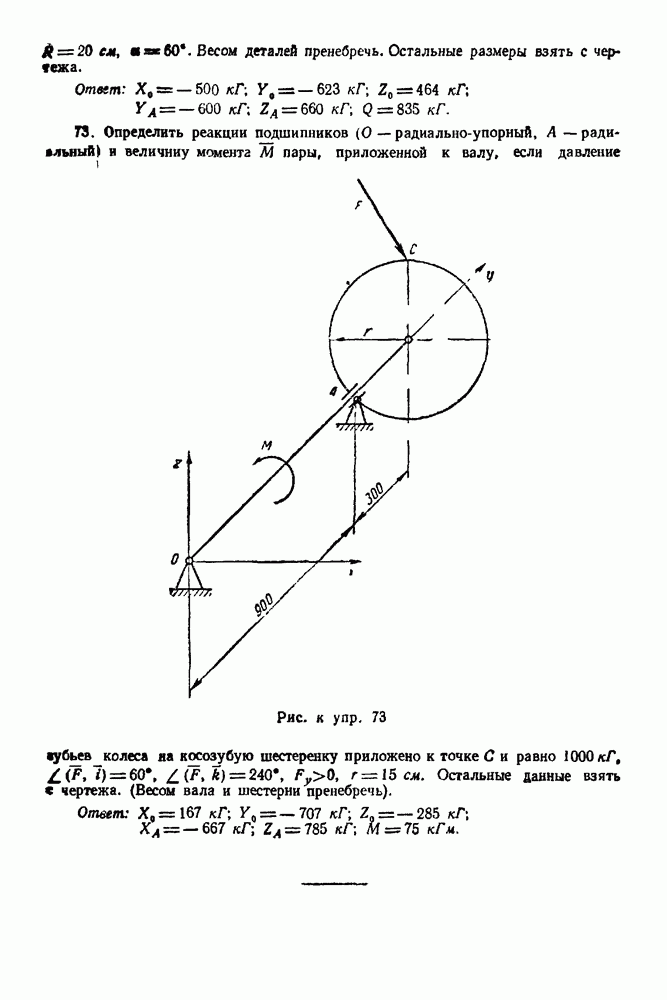
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
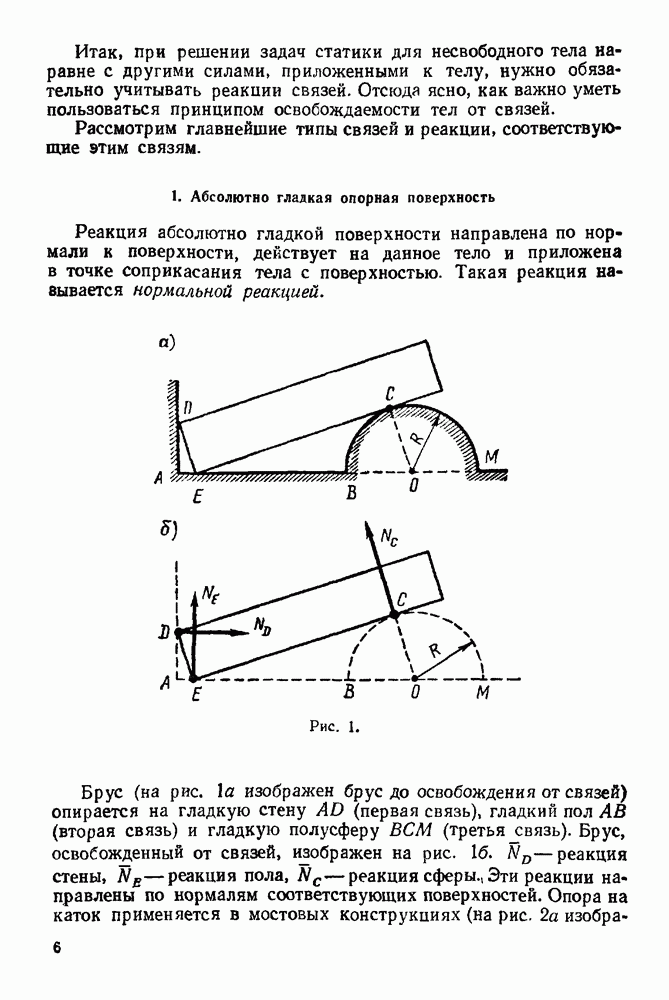
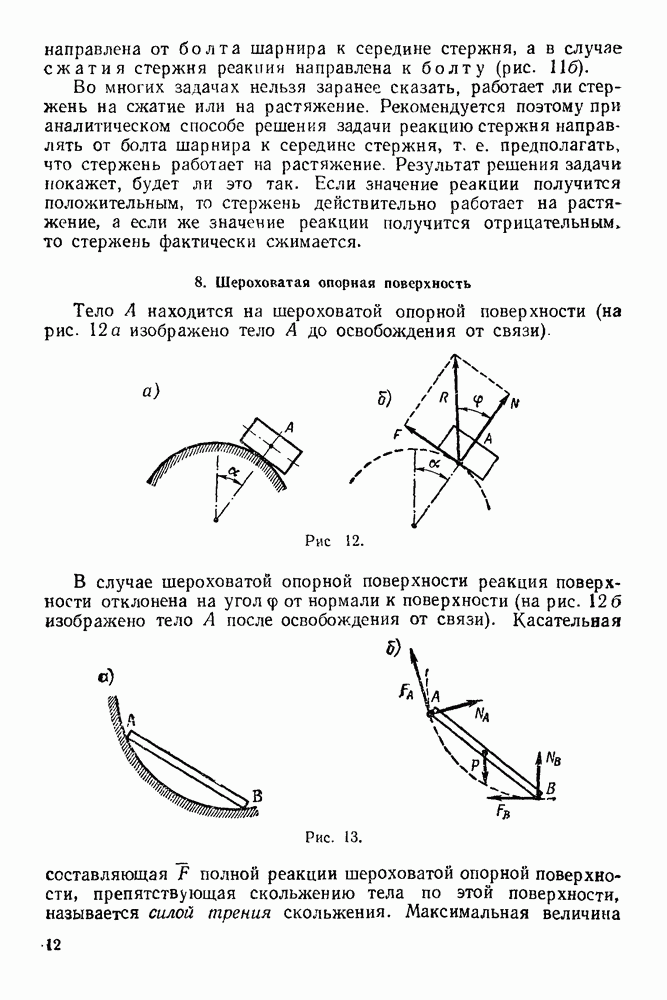
- 1. Абсолютно гладкая опорная поверхность
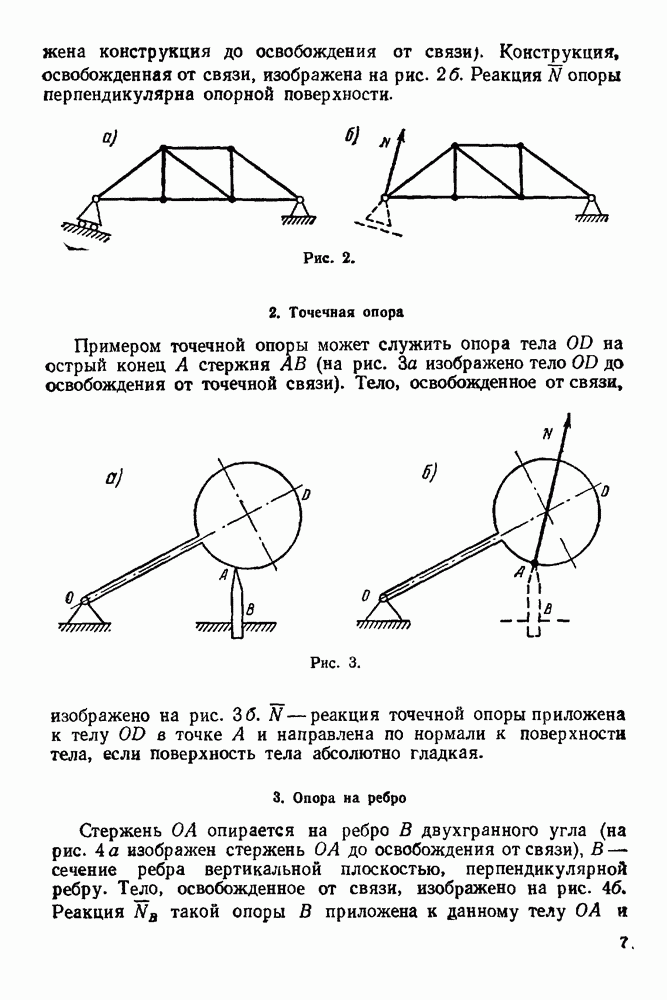
- 2. Точечная опора
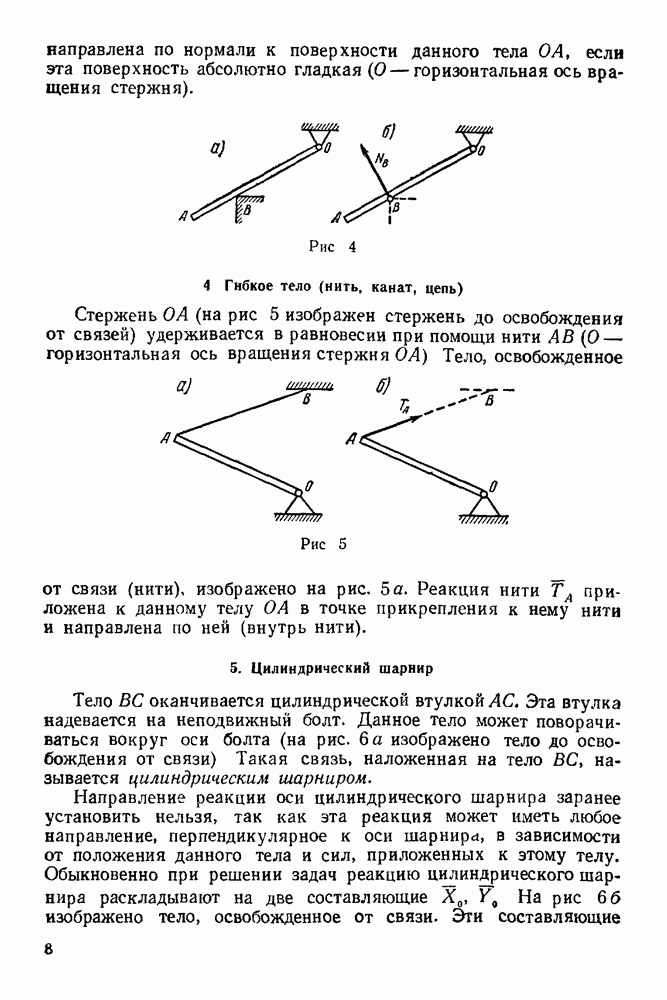
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
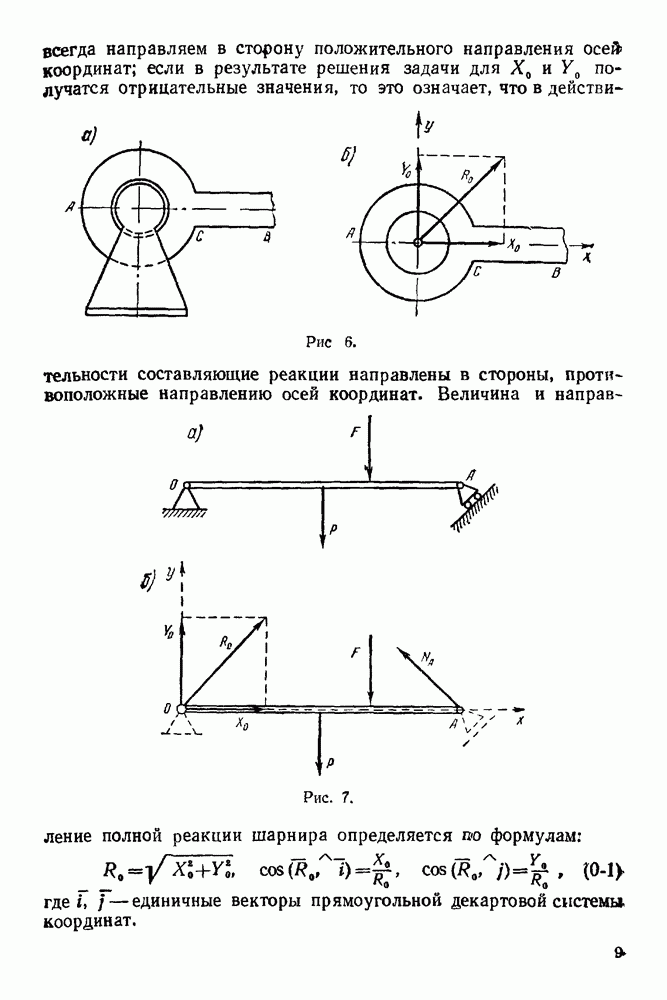
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
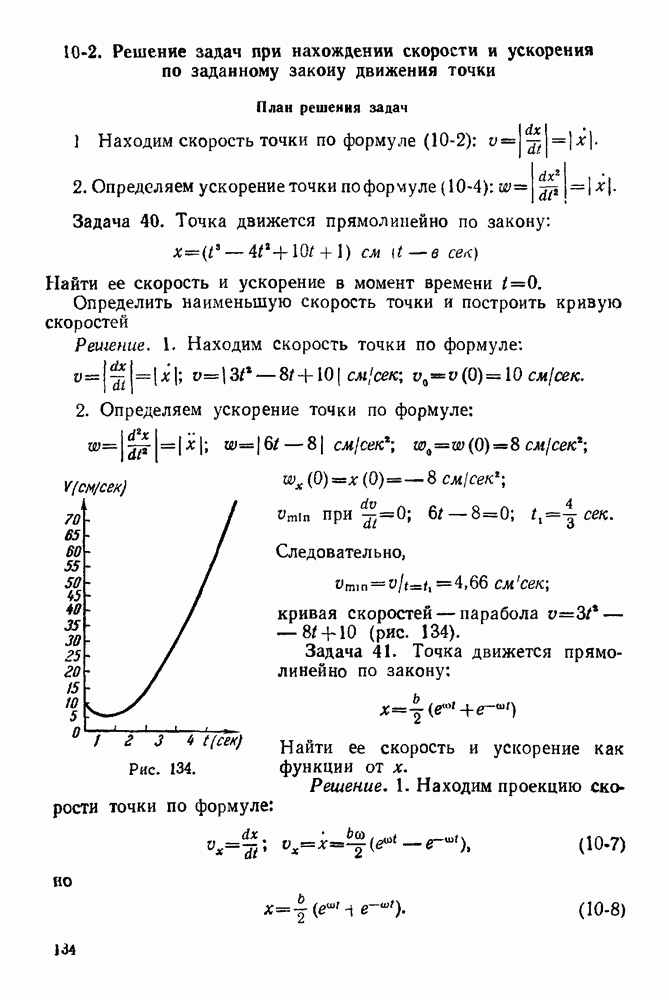
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
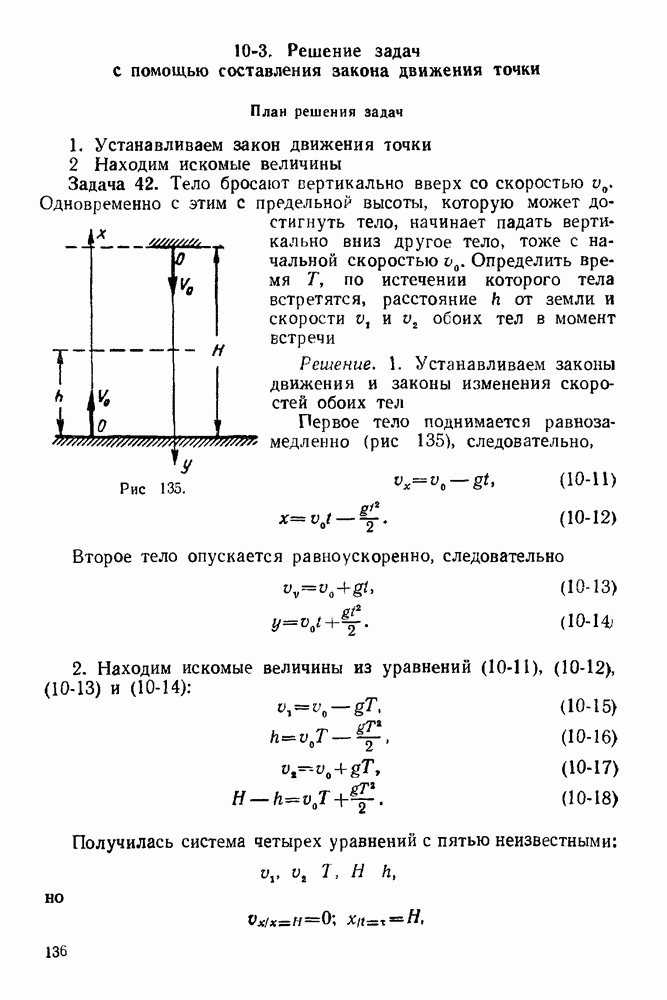
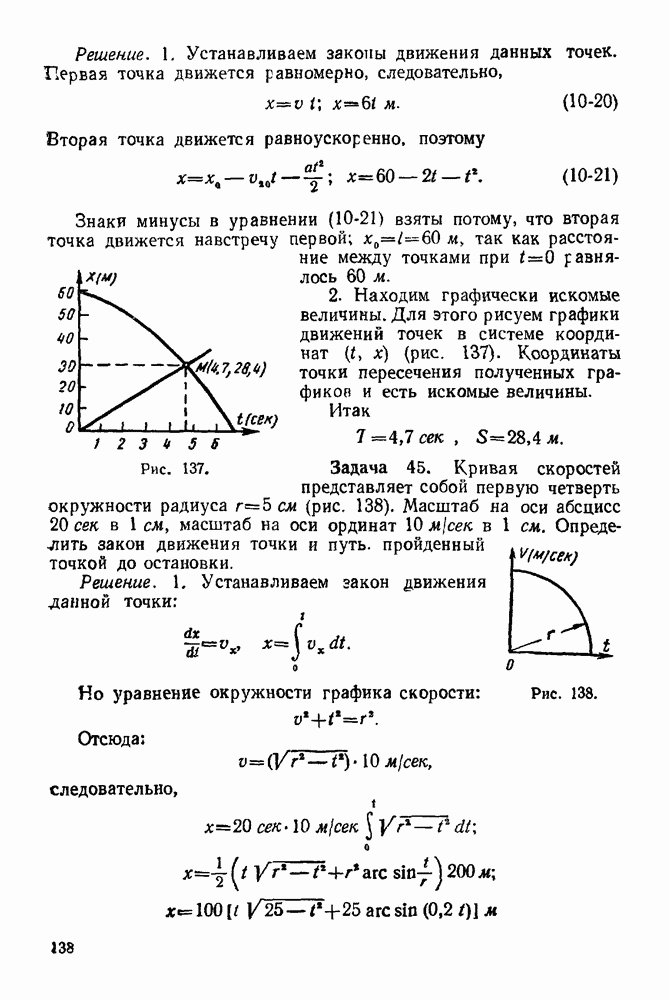
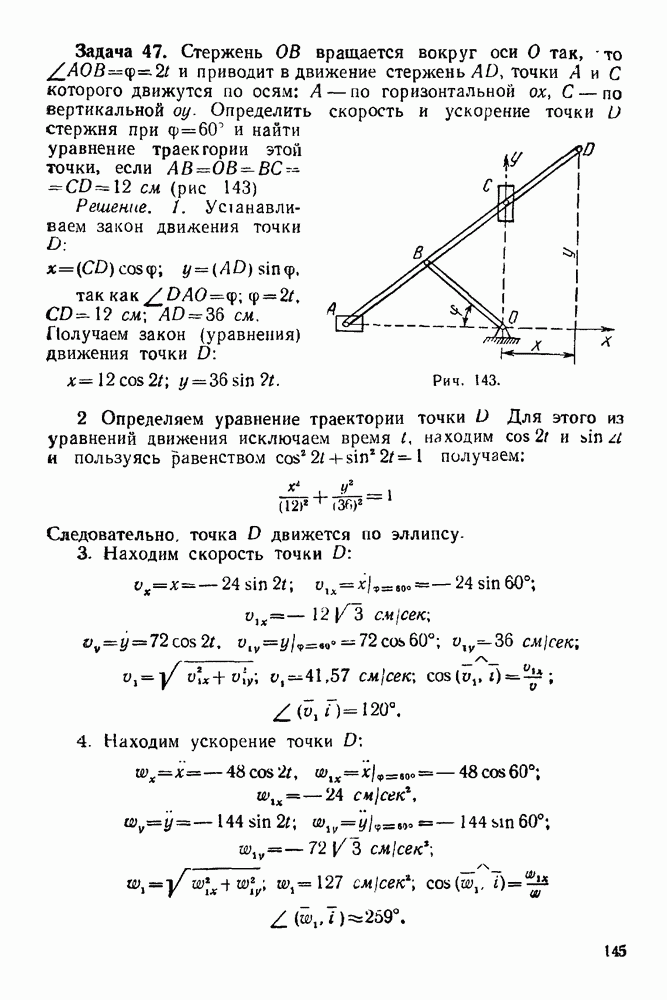
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
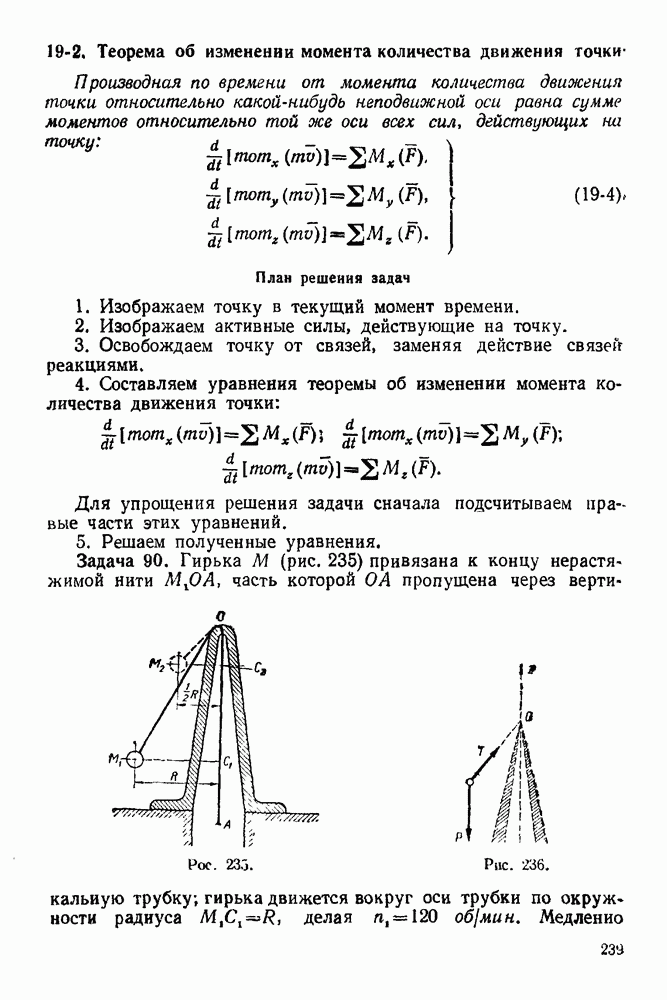
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР