| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
21-1. Принцип Даламбера
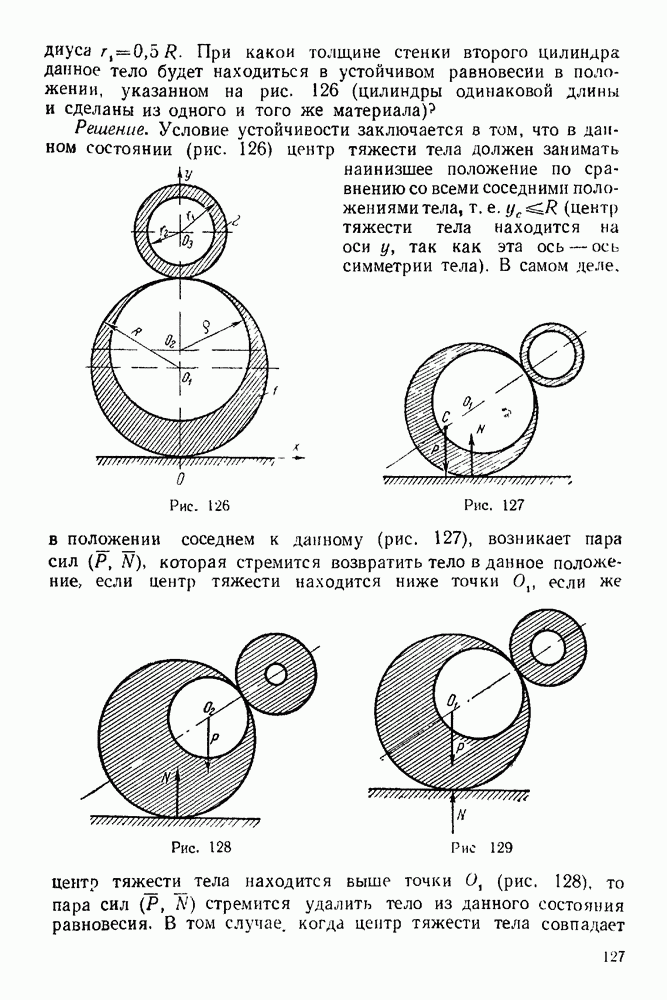
Если точки движущейся материальной системы мгновенно остановить и, кроме действующих на точки активных сил и реакций связей, приложить к ним силы инерции этих точек, имевшие место к моменту остановки, то и в дальнейшем эта система будет оставаться в покое.
Силой инерции точки называется сила, равная по величине произведению массы точки на величину ускорения этой точки и направленная противоположно ускорению:

Совокупность сил инерции частиц твердого тела, движущегося поступательно с ускорением  эквивалентна равнодействующей
эквивалентна равнодействующей  масса тела,
масса тела,  ускорение центра тяжести тела), линия действия которой проходит через центр тяжести тела.
ускорение центра тяжести тела), линия действия которой проходит через центр тяжести тела.
Совокупность сил инерции частиц твердого тела, имеющего плоскость симметрии, перпендикулярную оси вращения, проходящей через центр тяжести, эквивалентна паре, плоскость которой перпендикулярна оси вращения и момент которой равен  момент инерции тела относительно оси вращения).
момент инерции тела относительно оси вращения).
Совокупность сил инерции частиц твердого тела, движущегося плоскопараллельно, в том случае, когда плоскость симметрии тела параллельна направляющей плоскости, а центр тяжести лежит на общей нормали к подвижной и неподвижной центроидам, проходящей через мгновенный центр скоростей, эквивалентна силе  проходящей через мгновенный центр скоростей, и паре с моментом
проходящей через мгновенный центр скоростей, и паре с моментом  момент инерции тела относительно мгновенной оси вращения тела).
момент инерции тела относительно мгновенной оси вращения тела).
План решения задач (Метод кинетостатики)
1. Выделяем и изображаем систему в текущий момент времени.
2. Изображаем активные силы, действующие на точки системы.
3. Освобождаем систему от связей, заменяя действие связей реакциями.
4. Прикладываем силы инерции точек.
5. Выбираем систему координат.
6. Составляем уравнения равновесия полученной системы сил.
7. Решаем уравнения равновесия.

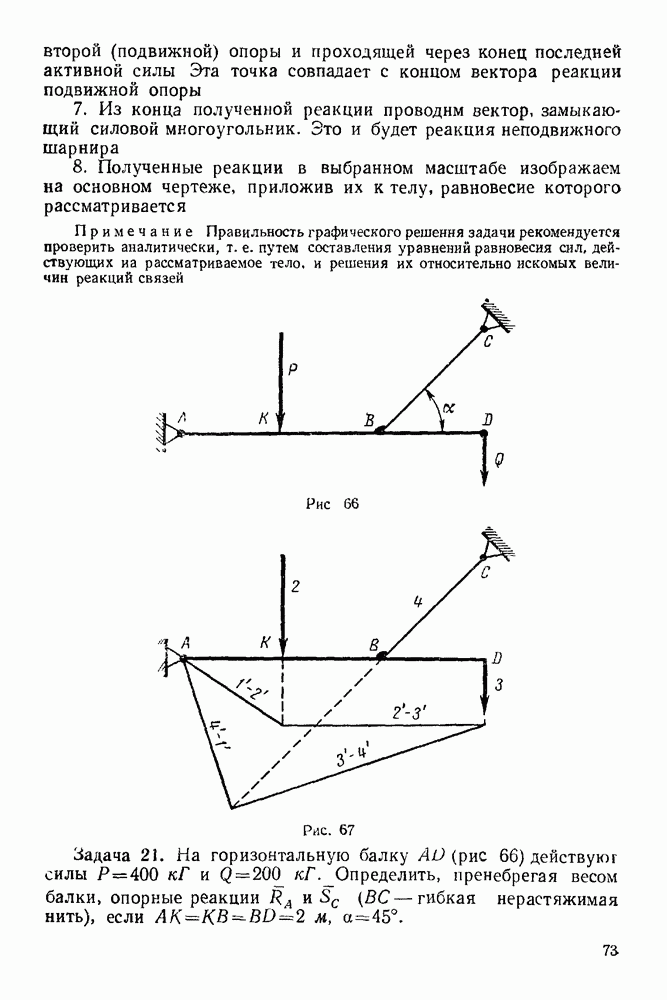
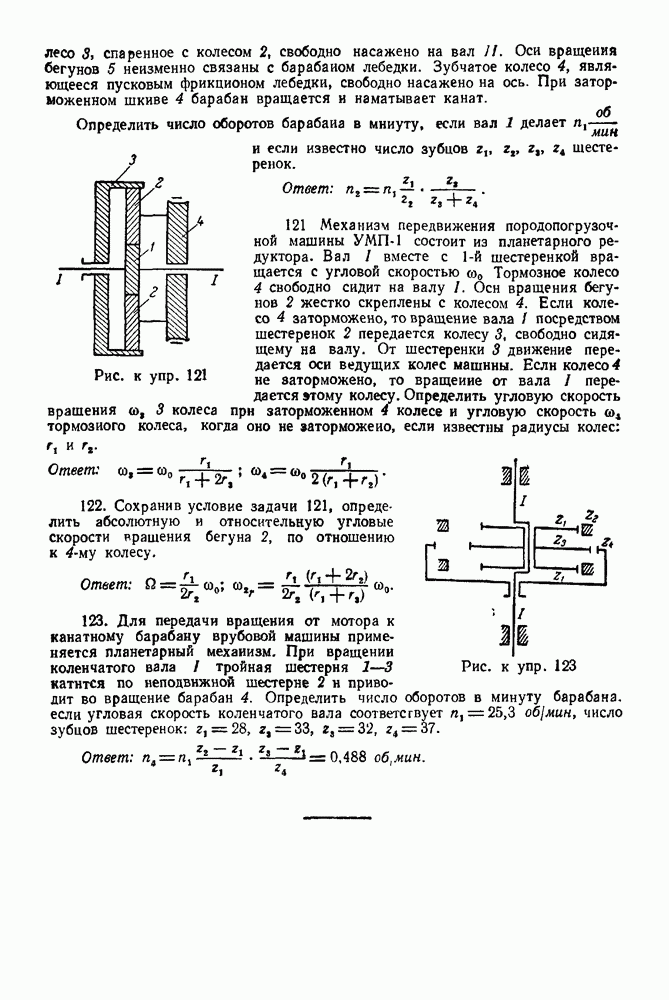
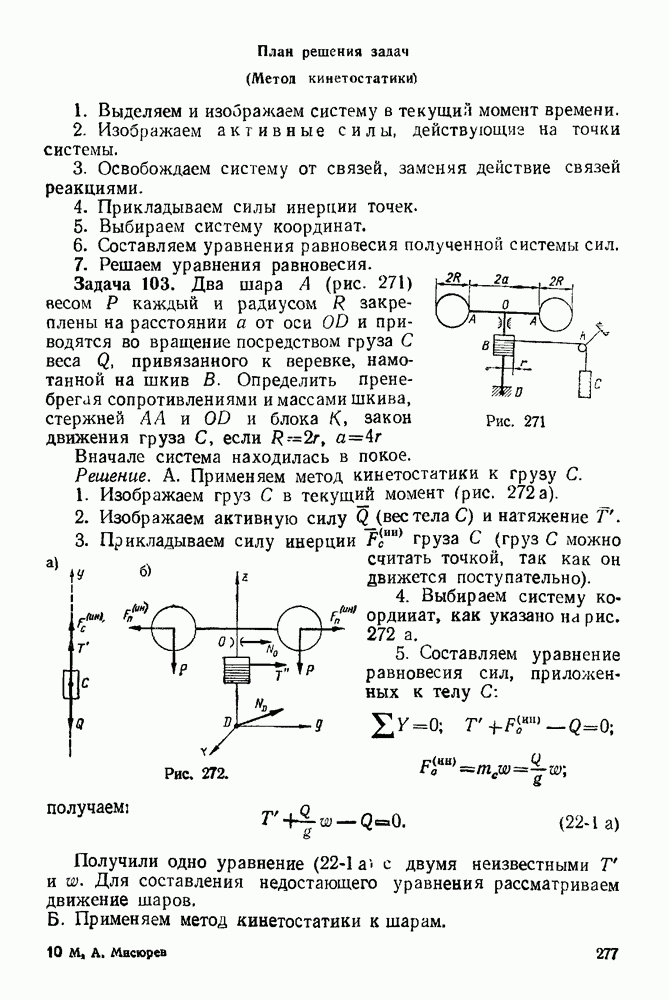
Рис. 271
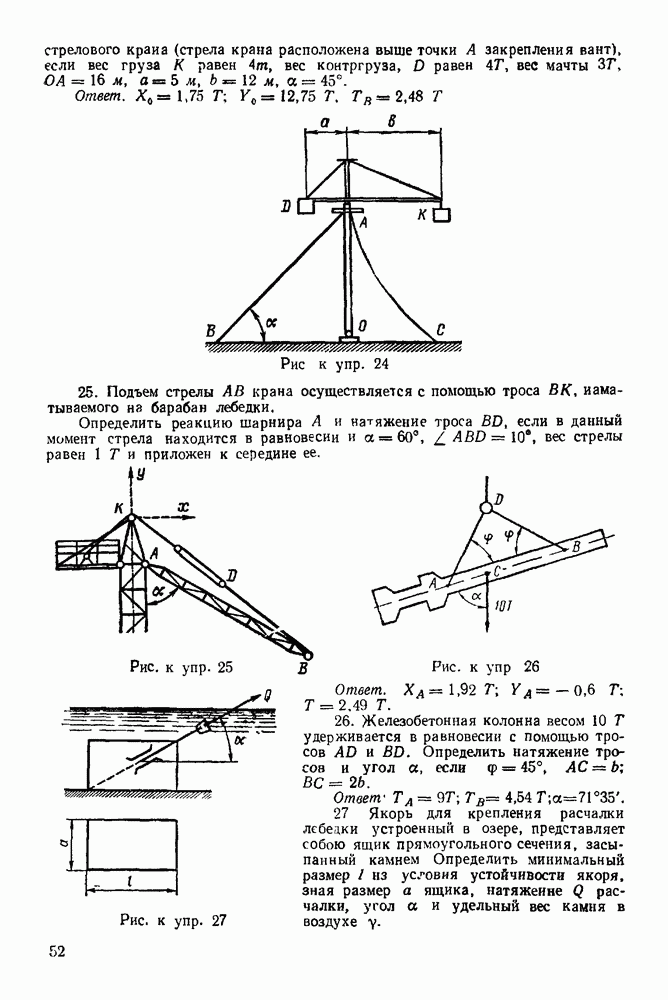
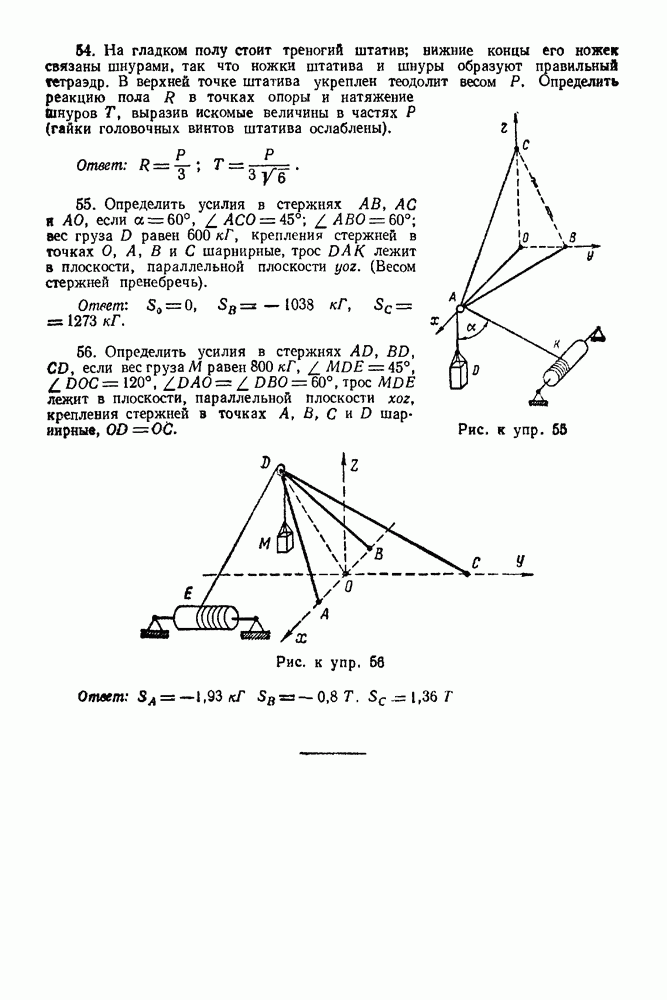
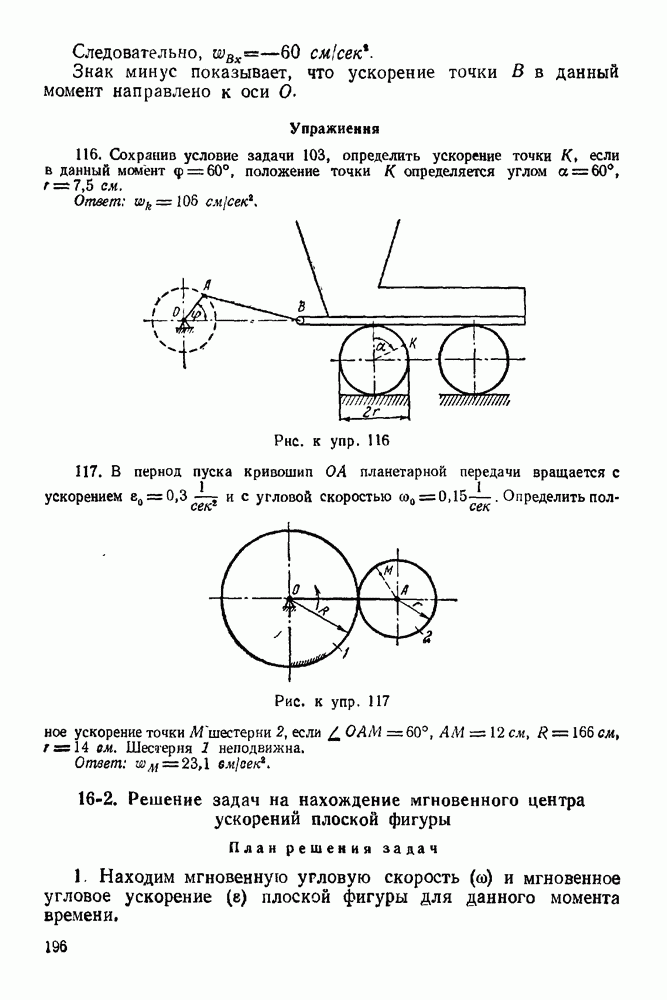
Задача 103. Два шара  (рис. 271) весом
(рис. 271) весом  каждый и радиусом
каждый и радиусом  закреплены на расстоянии а от оси
закреплены на расстоянии а от оси  и приводятся во вращение посредством груза С веса
и приводятся во вращение посредством груза С веса  привязанного к веревке, намотанной на шкив В. Определить пренебрегая сопротивлениями и массами шкива, стержней
привязанного к веревке, намотанной на шкив В. Определить пренебрегая сопротивлениями и массами шкива, стержней  и блока К, закон движения груза С, если
и блока К, закон движения груза С, если  Вначале система находилась в покое. Решение. А. Применяем метод кинетостатики к грузу С.
Вначале система находилась в покое. Решение. А. Применяем метод кинетостатики к грузу С.
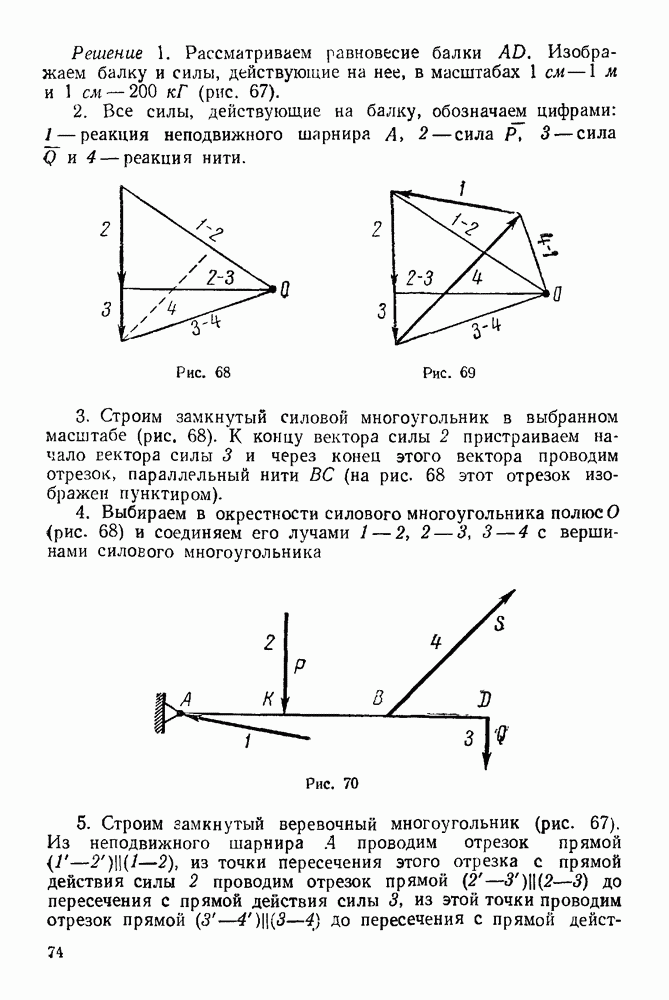
1. Изображаем груз С в текущий момент (рис. 272 а).
2. Изображаем активную силу  (вес тела С) и натяжение
(вес тела С) и натяжение 
3. Прикладываем силу инерции  груза С (груз С можно считать точкой, так как он движется поступательно).
груза С (груз С можно считать точкой, так как он движется поступательно).
4. Выбираем систему координат, как указано на рис. 272 а.

Рис. 272.
5. Составляем уравнение равновесия сил, приложенных к телу С:

получаем:

Получили одно уравнение  с двумя неизвестными Т и w. Для составления недостающего уравнения рассматриваем движение шаров.
с двумя неизвестными Т и w. Для составления недостающего уравнения рассматриваем движение шаров.
Б. Применяем метод кинетостатики к шарам.
1 Рассматриваем систему в текущий момент времени (рис. 272 6). Система состоит из двух шаров А и шкива В, связанных между собой стержнями  и
и 
2 Рисуем активные силы, действующие на систему:  вес шара,
вес шара,  натяжение веревки.
натяжение веревки.
3 Освобождаем систему от связей, заменяя действия связей реакциями:  реакция подпятника и
реакция подпятника и  реакция подшипника.
реакция подшипника.

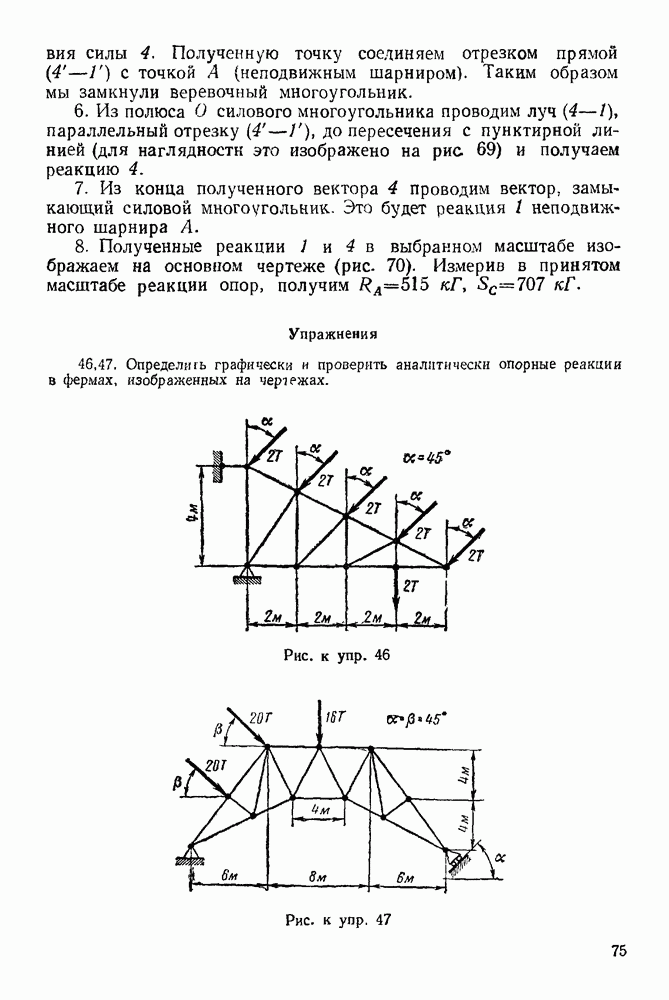
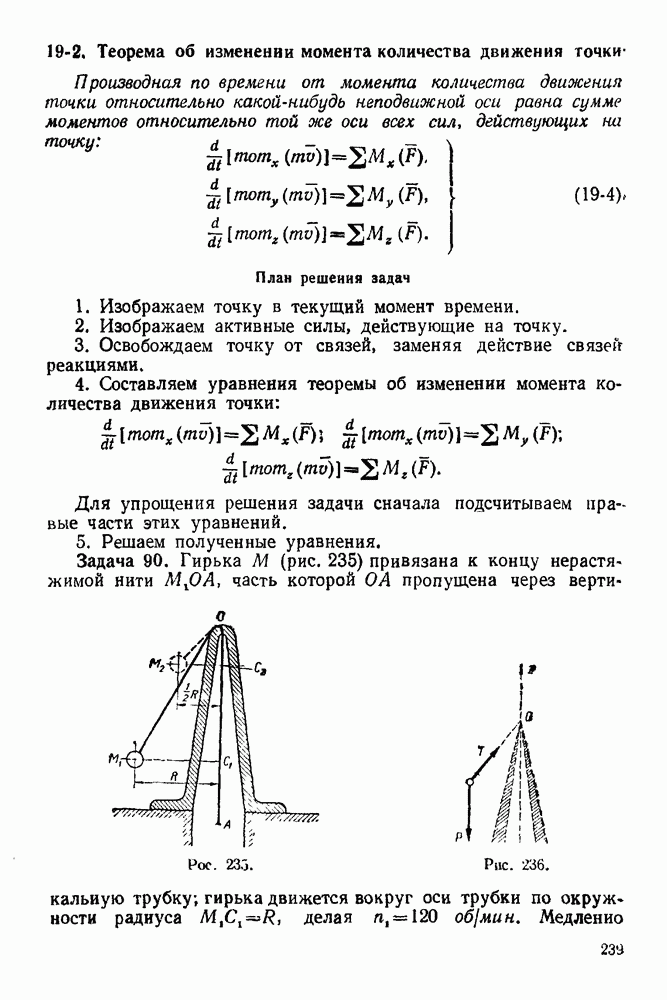
Рис. 273.
4. Прикладываем силы инерции точек системы В шарах А берем точки одинаковых масс  отстоящие на одинаковых расстояниях
отстоящие на одинаковых расстояниях  от оси вращения (рис. 273). Силы инерции этих точек раскла дываем на касательные и нормальные составляющие (эти составля ющие, очевидно, будут попарно равными по величине).
от оси вращения (рис. 273). Силы инерции этих точек раскла дываем на касательные и нормальные составляющие (эти составля ющие, очевидно, будут попарно равными по величине).
5. Выбираем систему координат, как указано на рис. 272 6.
6. Составляем уравнение равновесия сил, приложенных к системе:

 так как линия действия силы
так как линия действия силы  параллельна оси
параллельна оси  так как линия действия силы
так как линия действия силы  пересекает ось;
пересекает ось;

Следовательно,

Уравнение моментов принимает следующий вид:

7. Решаем полученные уравнения (22-1 а) и ( Так
Так

то получаем:

 масса шара,
масса шара,  момент инерции шага относительно оси, проходящей через центр тяжести шара, а поэтому
момент инерции шага относительно оси, проходящей через центр тяжести шара, а поэтому

Следовательно, груз С опускается с постоянным ускорением из состояния покоя, поэтому 

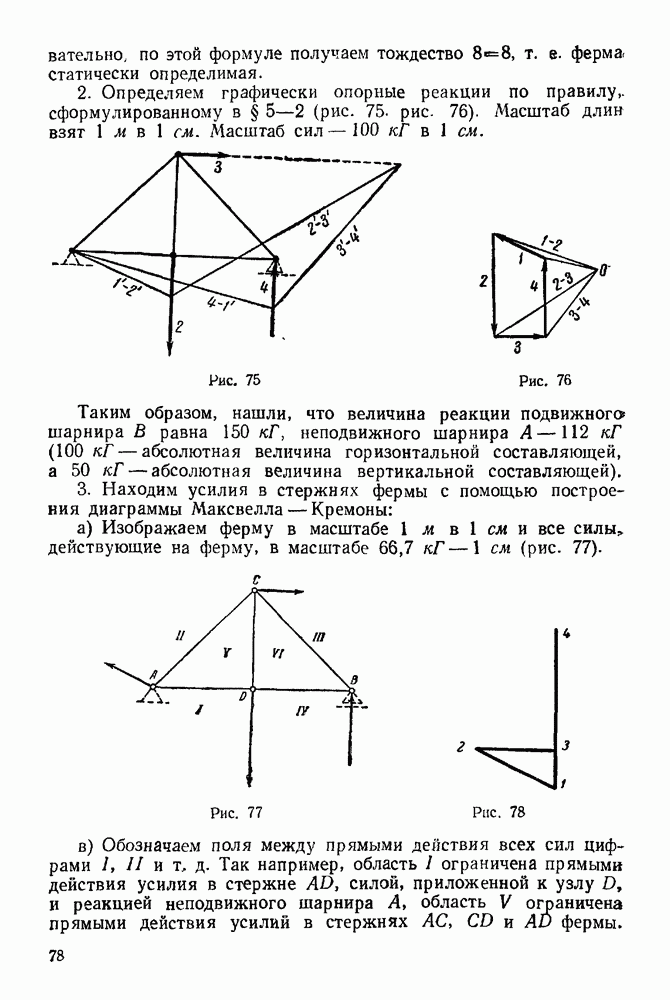
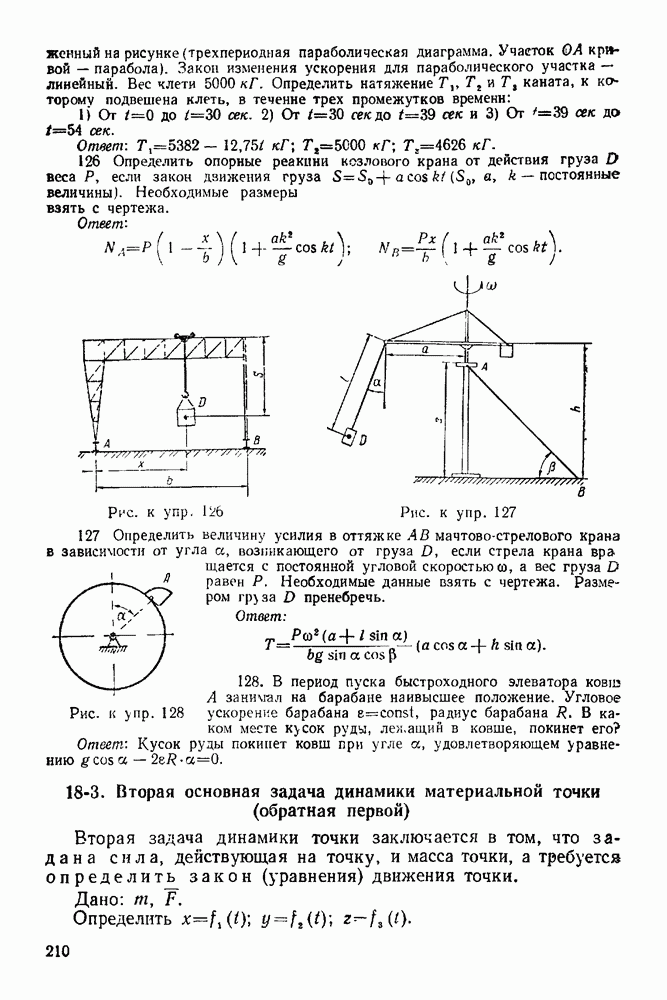
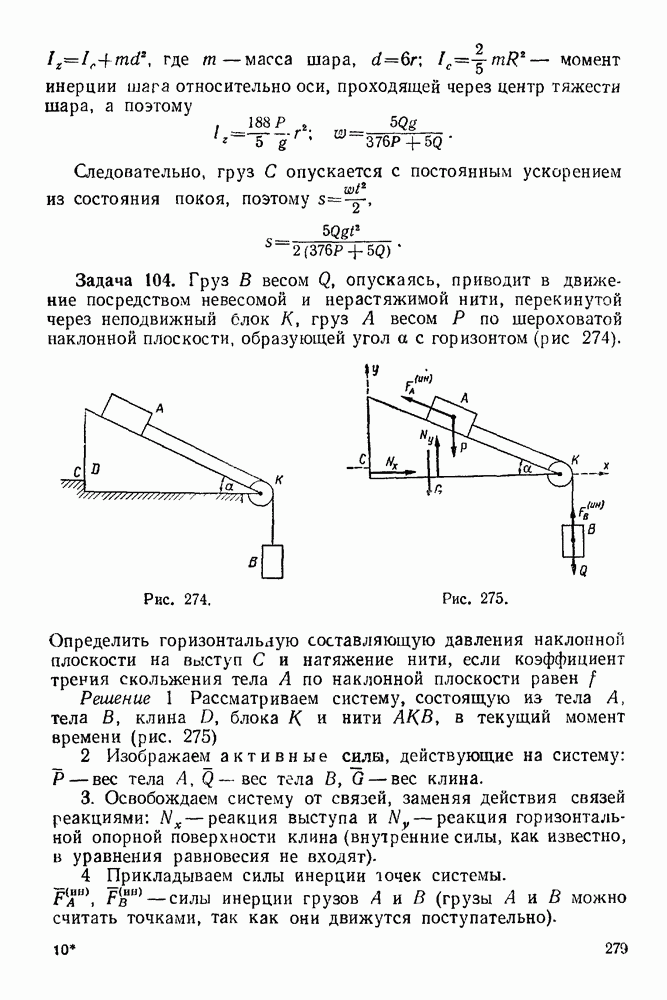
Задача 104. Груз В весом  опускаясь, приводит в движение посредством невесомой и нерастяжимой нити, перекинутой через неподвижный блок К, груз А весом
опускаясь, приводит в движение посредством невесомой и нерастяжимой нити, перекинутой через неподвижный блок К, груз А весом  по шероховатой наклонной плоскости, образующей угол а с горизонтом (рис 274).
по шероховатой наклонной плоскости, образующей угол а с горизонтом (рис 274).

Рис. 274,

Рис. 275.
Определить горизонтальную составляющую давления наклонной плоскости на выступ С и натяжение нити, если коэффициент трения скольжения тела А по наклонной плоскости равен 
Решение 1 Рассматриваем систему, состоящую из тела А, тела В, клина  блока К и нити
блока К и нити  в текущий момент времени (рис. 275)
в текущий момент времени (рис. 275)
2 Изображаем активные силы, действующие на систему:  вес тела
вес тела  вес тела
вес тела  вес клина.
вес клина.
3. Освобождаем систему от связей, заменяя действия связей реакциями:  реакция выступа и
реакция выступа и  реакция горизонтальной опорной поверхности клина (внутренние силы, как известно, в уравнения равновесия не входят).
реакция горизонтальной опорной поверхности клина (внутренние силы, как известно, в уравнения равновесия не входят).
4 Прикладываем силы инерции точек системы.  — силы инерции грузов
— силы инерции грузов  (грузы
(грузы  можно считать точками, так как они движутся поступательно).
можно считать точками, так как они движутся поступательно).
5. Выбираем систему координат, как указано на рис. 275
6. Составляем уравнение равновесия системы:

Получили одно уравнение (22-1 с) с двумя неизвестными  Для составления недостающих уравнений рассматриваем движение грузов
Для составления недостающих уравнений рассматриваем движение грузов  в отдельности, применяя принцип Даламбера.
в отдельности, применяя принцип Даламбера.
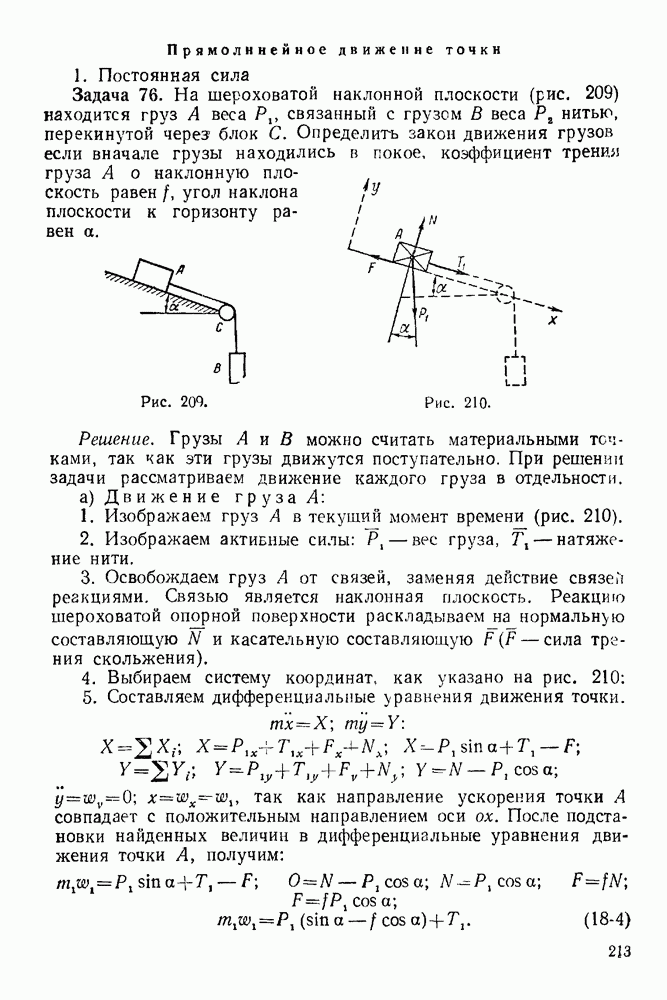
А. 1. Рассмотрим систему, состоящую из тела А, в текущий момент (рис. 276).
2 Изображаем активную силу  действующую на тело, и натяжение
действующую на тело, и натяжение  нити
нити

Рис. 276.

Рис. 277.
3. Освобождаем тело А от связей, заменяя действие связей реакциями:  (нормальная составляющая полной реакции шероховатой опорной плоскости),
(нормальная составляющая полной реакции шероховатой опорной плоскости),  (касательная составляющая полной реакции шероховатой опорной плоскости — сила трения скольжения).
(касательная составляющая полной реакции шероховатой опорной плоскости — сила трения скольжения).
4. Прикладываем силу инерции  груза А.
груза А.
5. Выбираем систему координат, как указано на рис. 276
6. Составляем уравнения равновесия сил:

Из этих уравнений получаем:

Б. 1. Рассматриваем систему, состоящую из тела В, в текущий момент времени (рис. 277).
2. Изображаем активную силу Q (вес тела В), действующую на тело  и натяжение нити
и натяжение нити 
3. Прикладываем силу инерции  груза В.
груза В.
4 Выбираем систему координат, как указано на рис. 277. 5. Составляем уравнения равновесия сил, приложенных к телу В:

Получаем:

Из уравнений (22-1 с), (22-1 d) и (22-1 е) находим неизвестные величины, имея в Еиду, что 

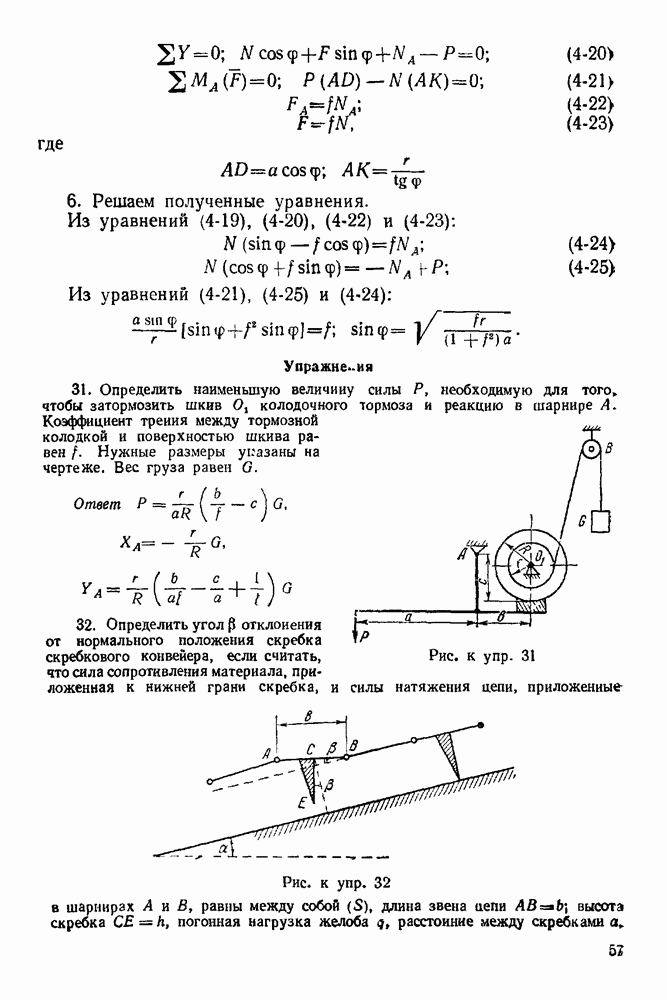
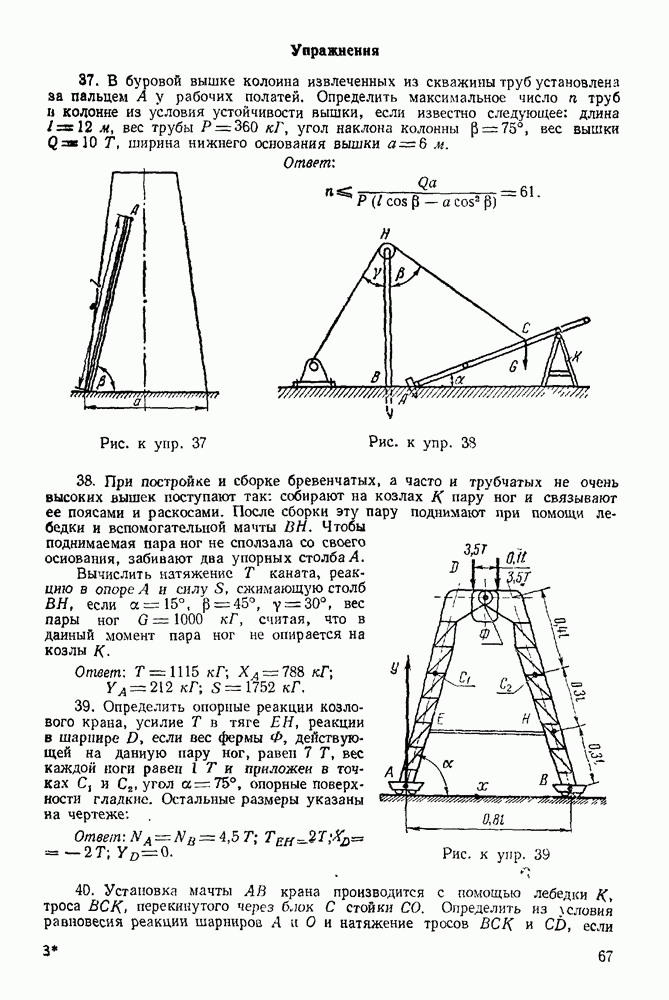
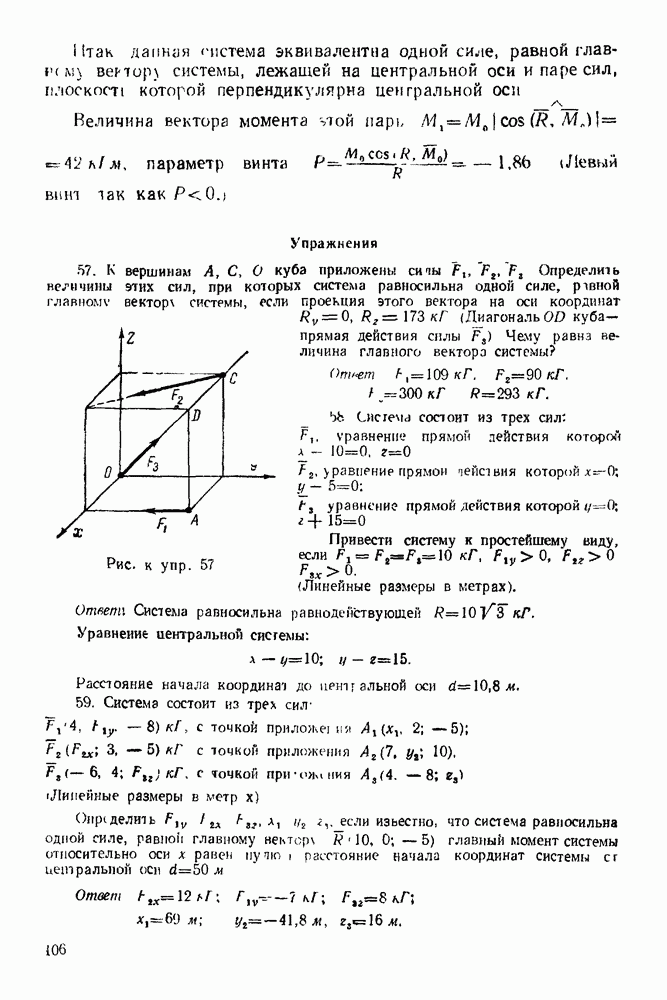
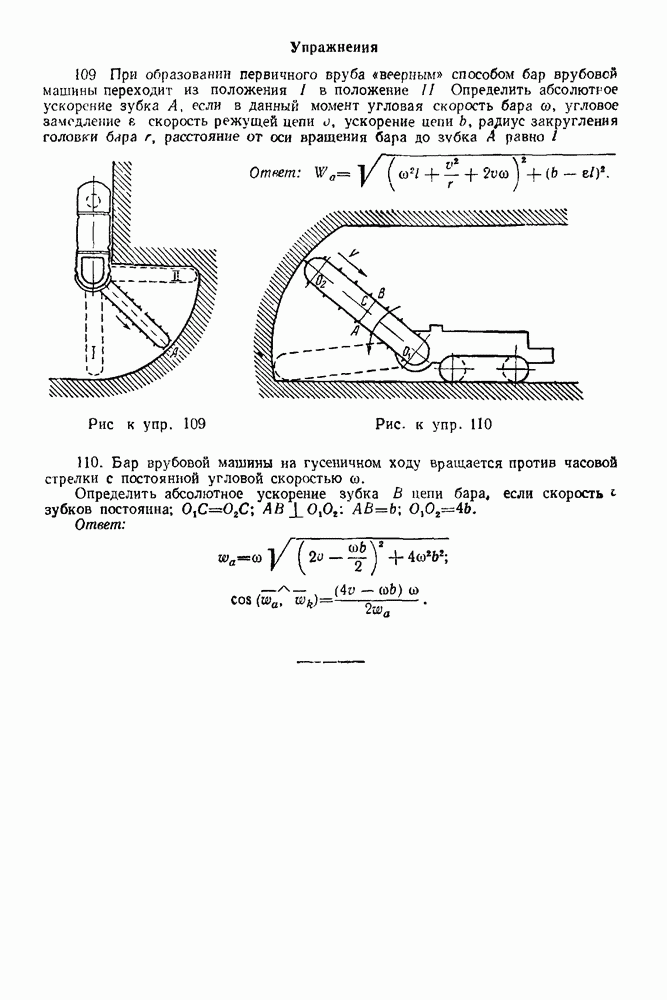
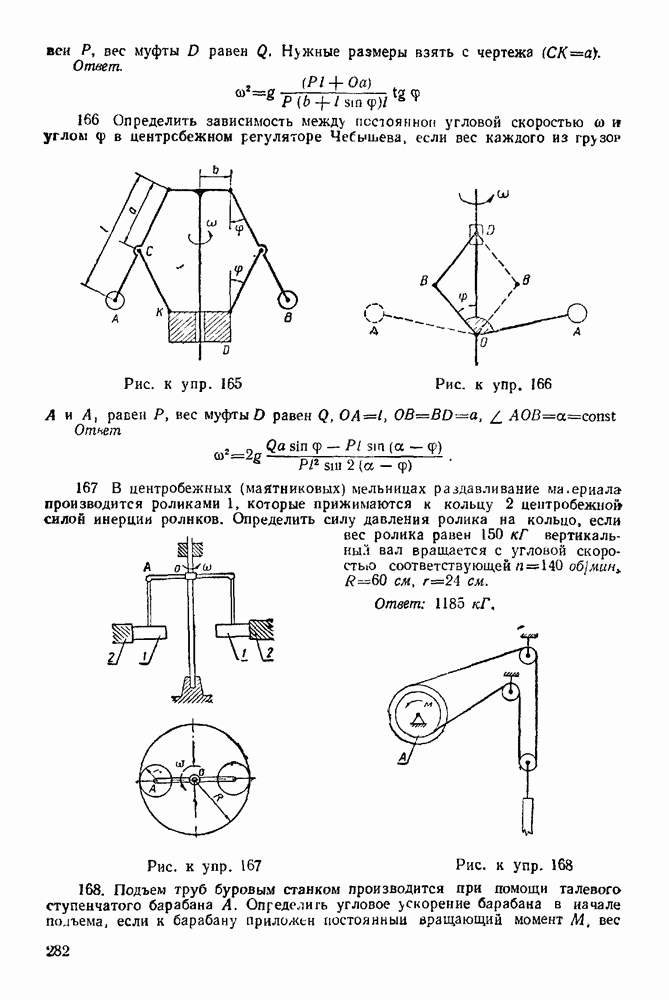
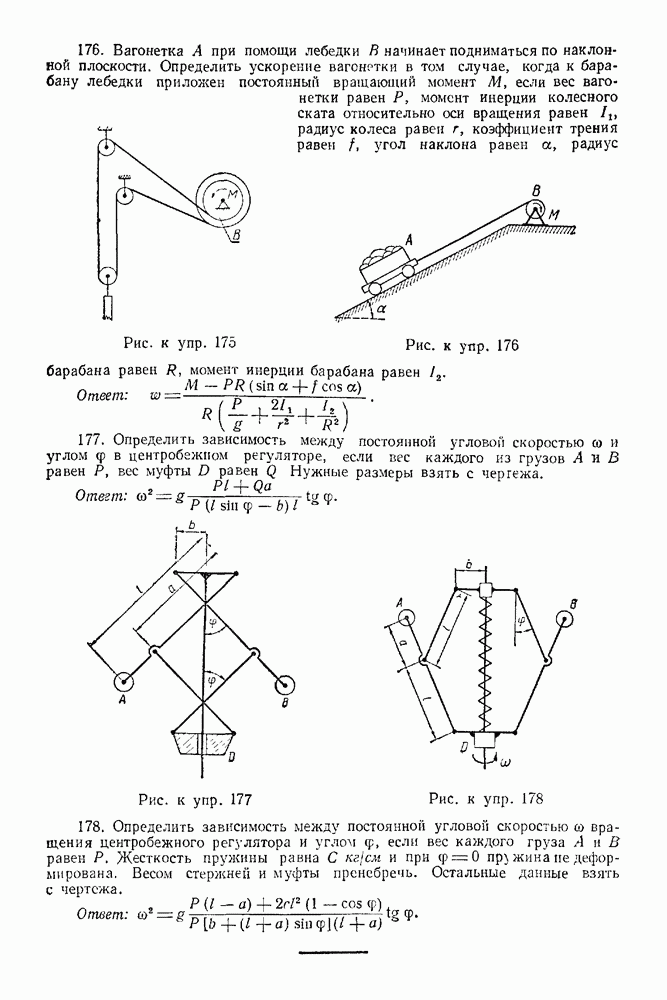
Упражнения
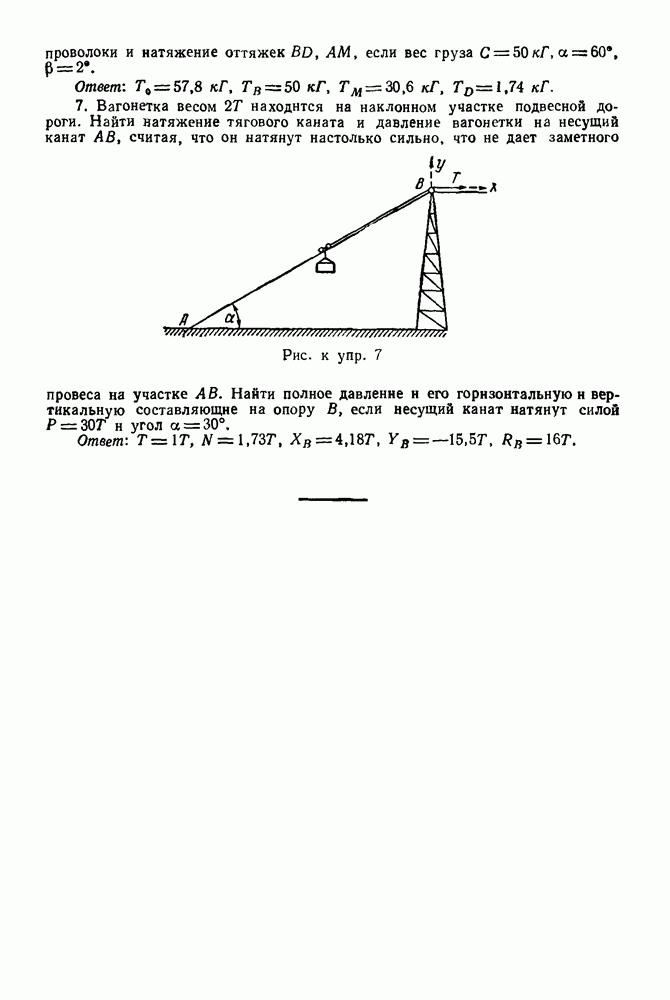
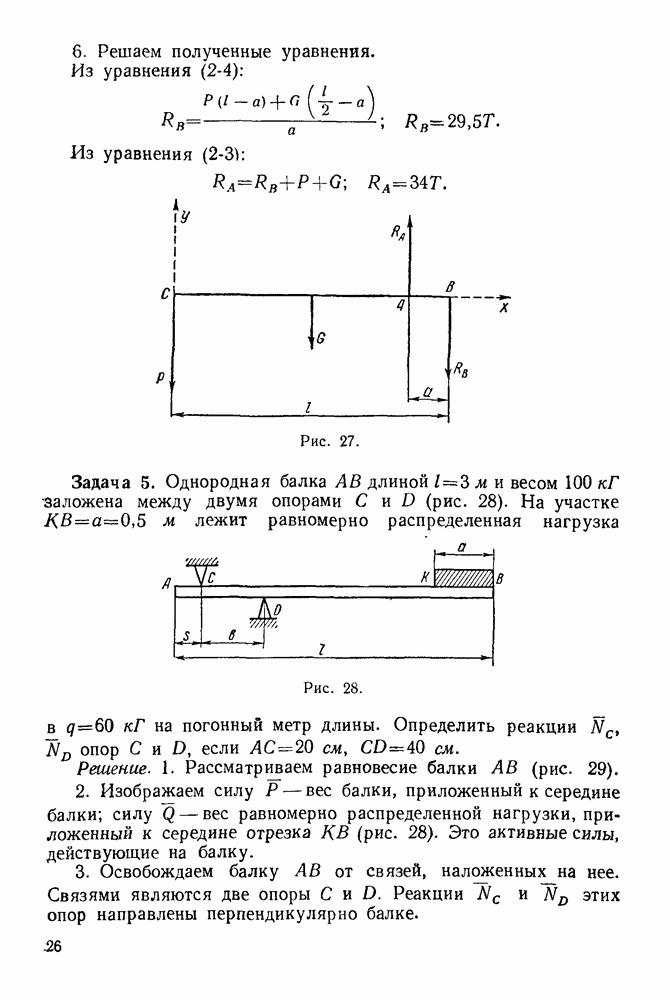
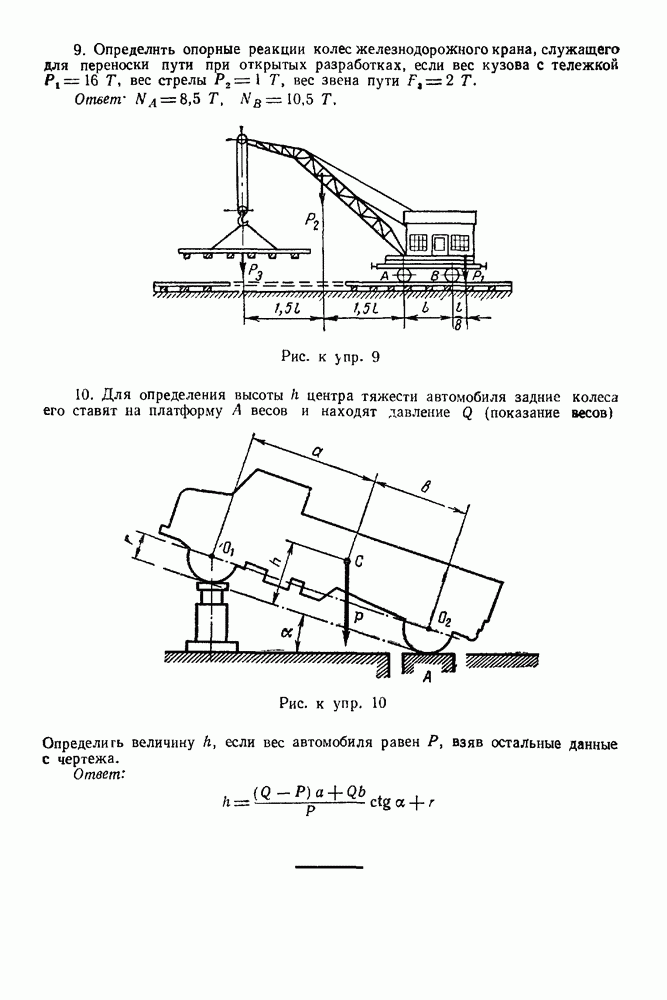
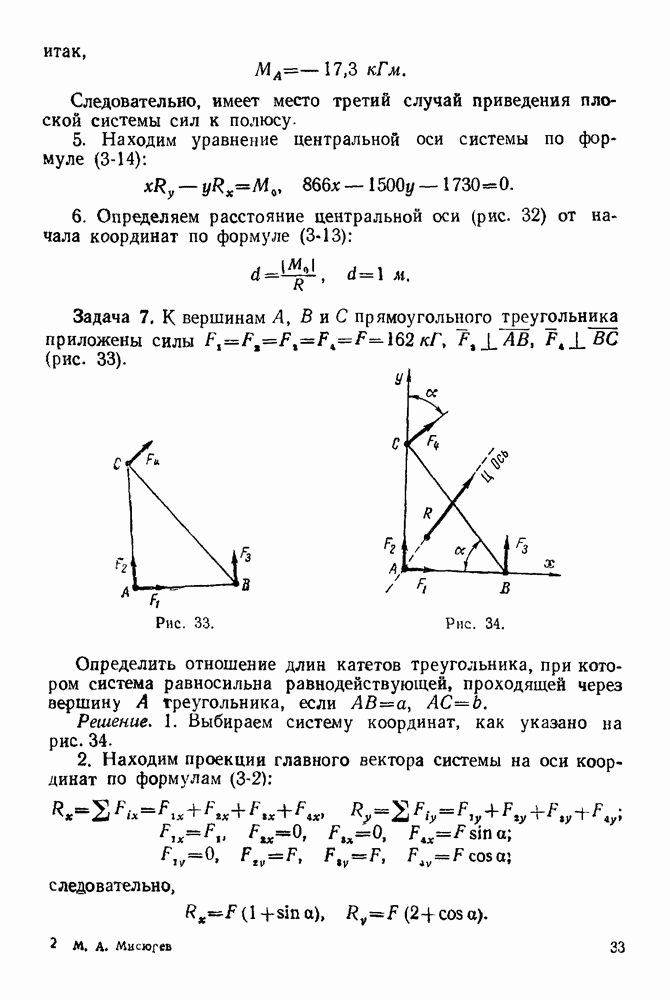
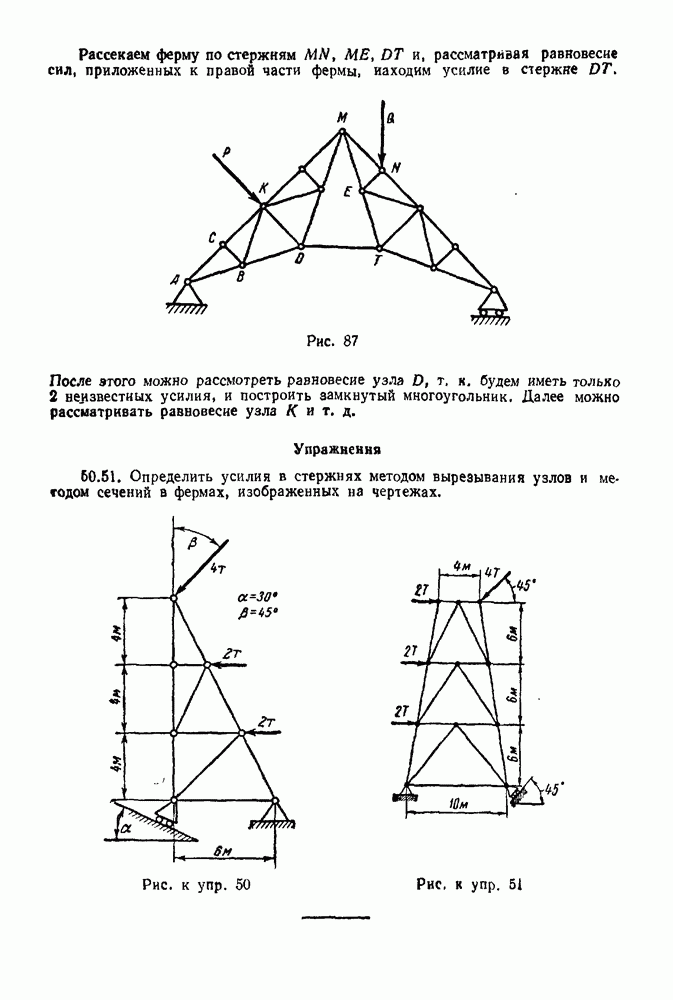
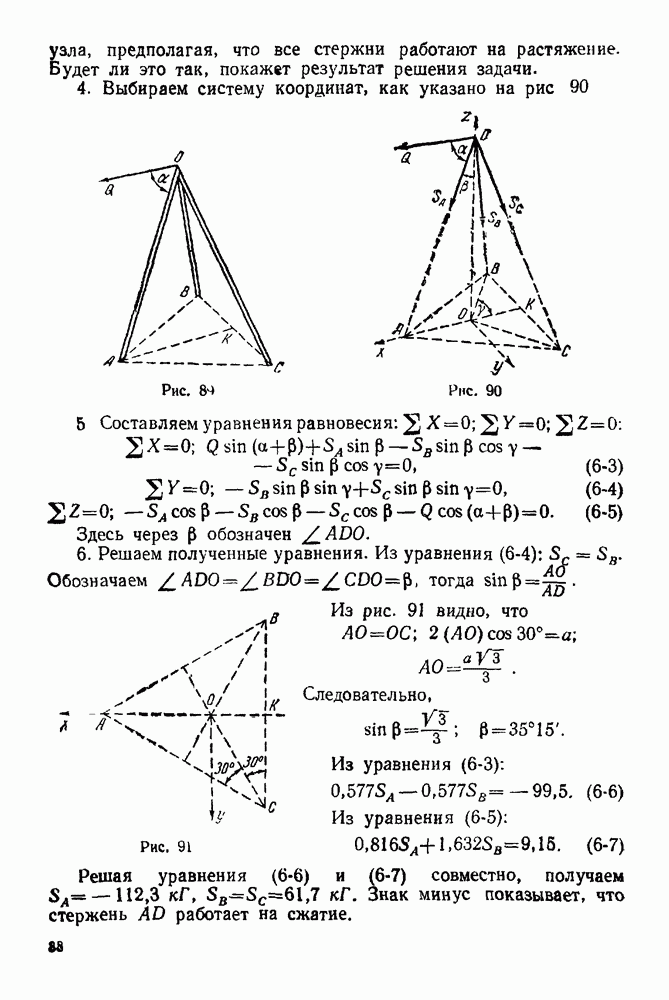
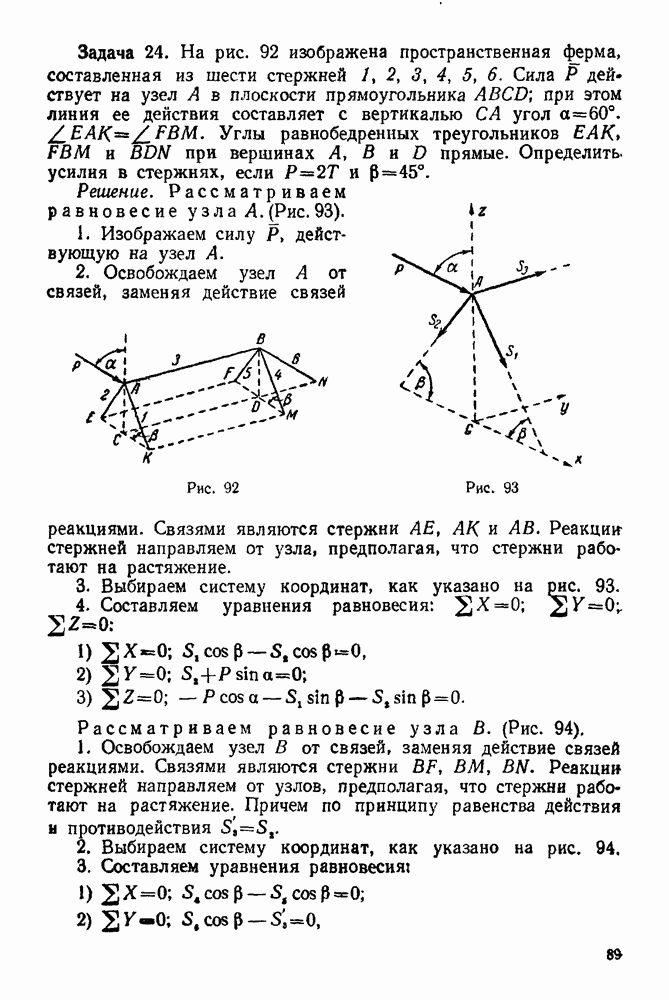
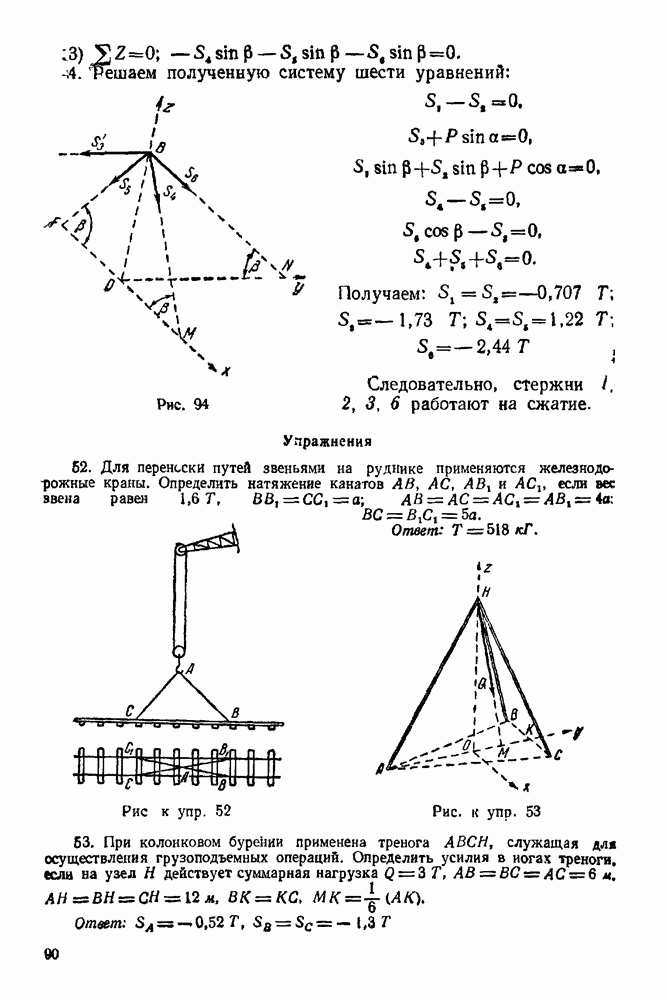
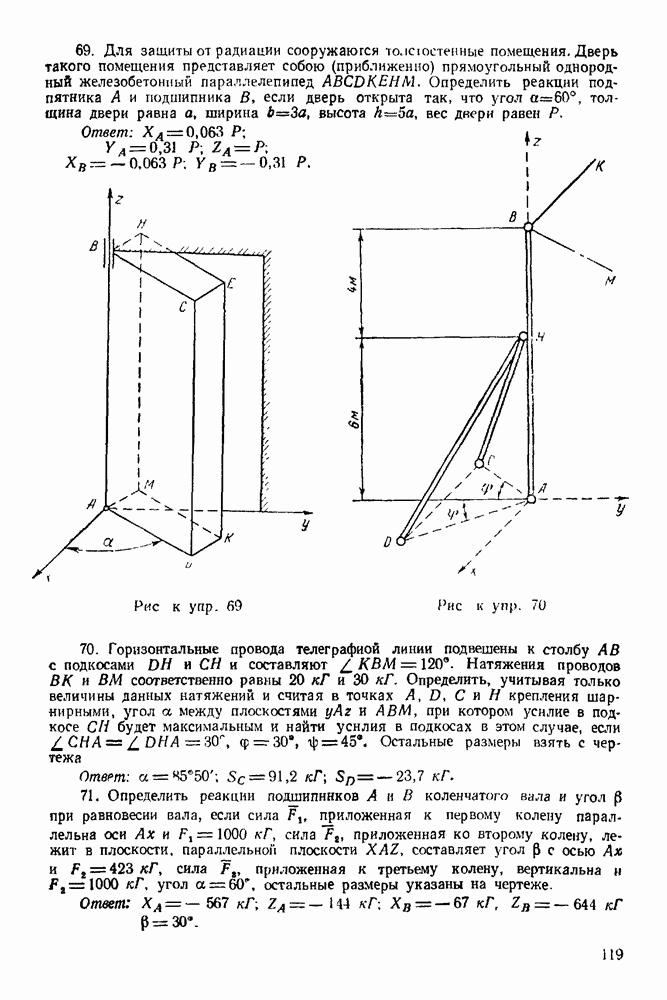
(см. скан)
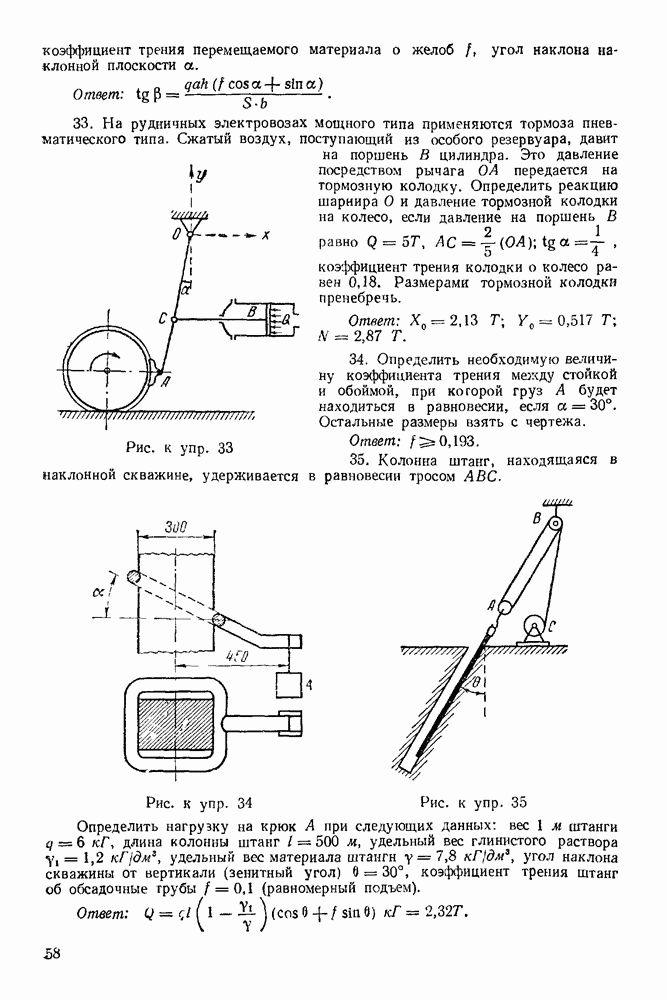
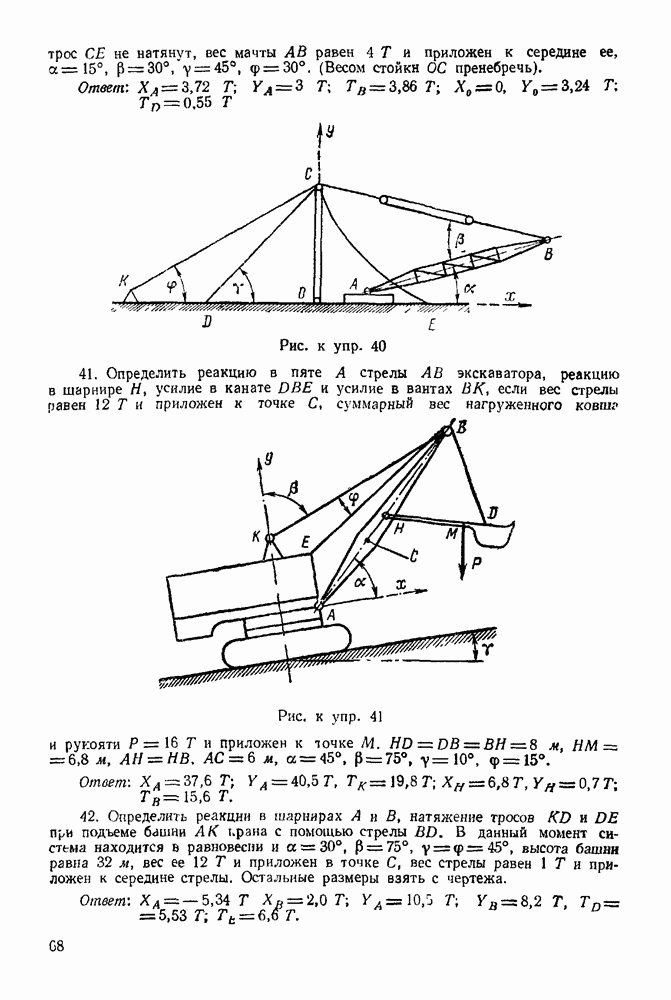
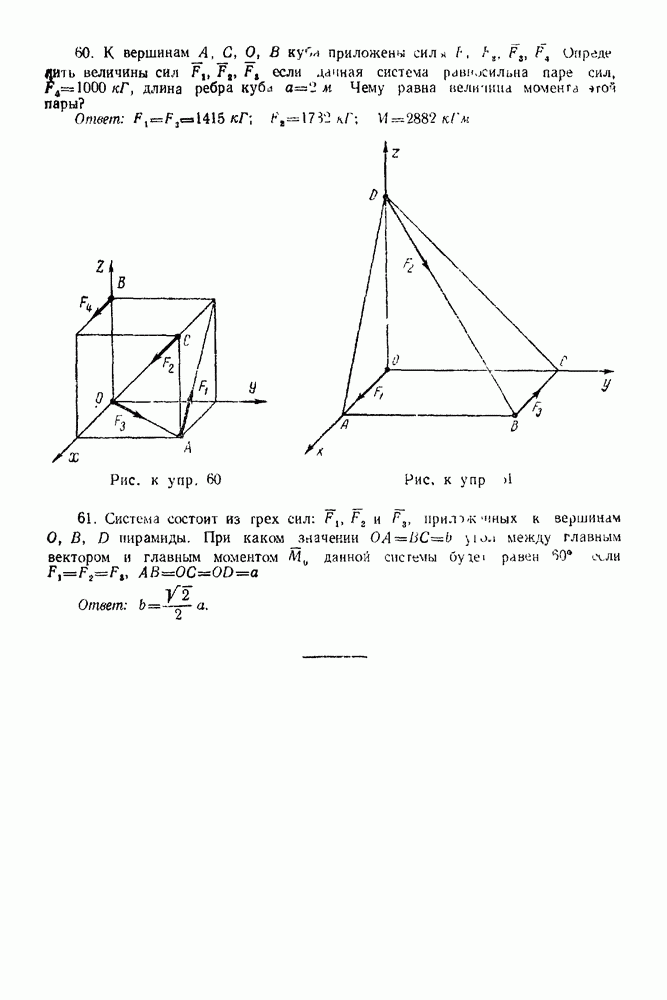
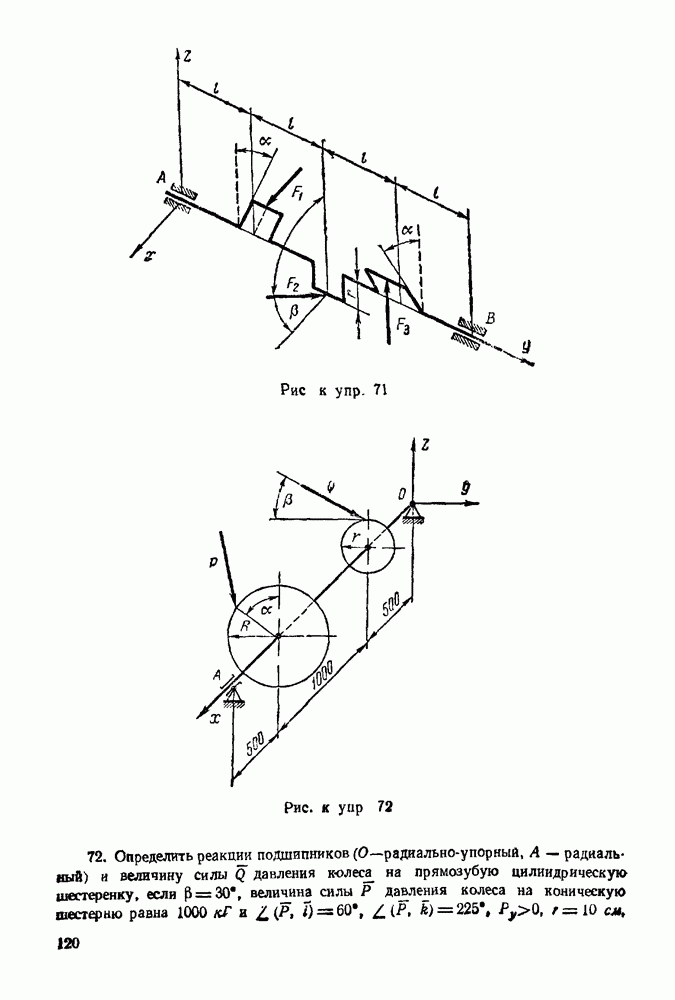
(см. скан)
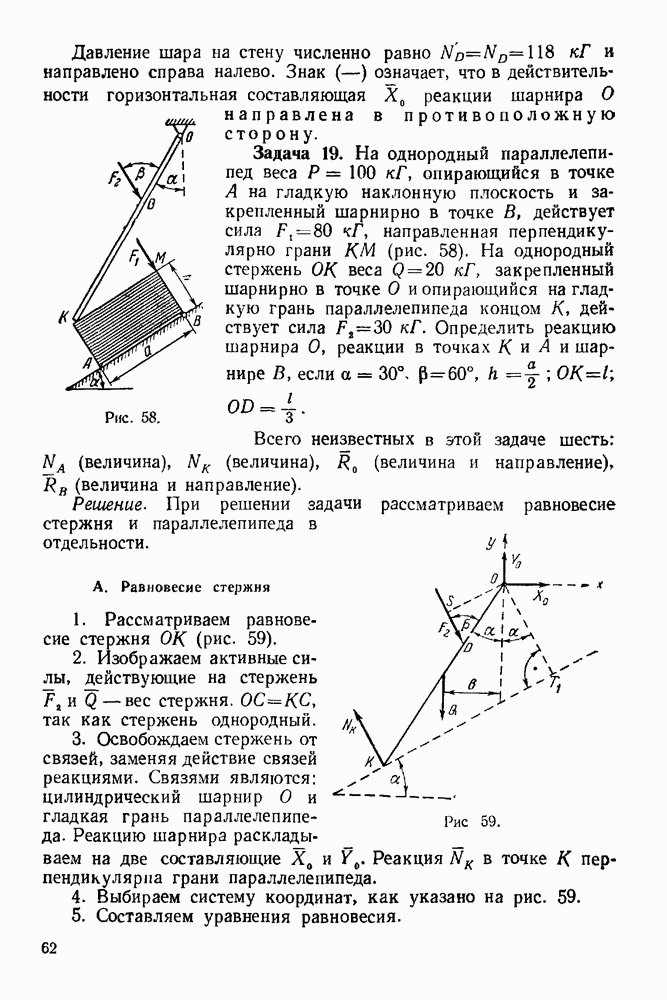
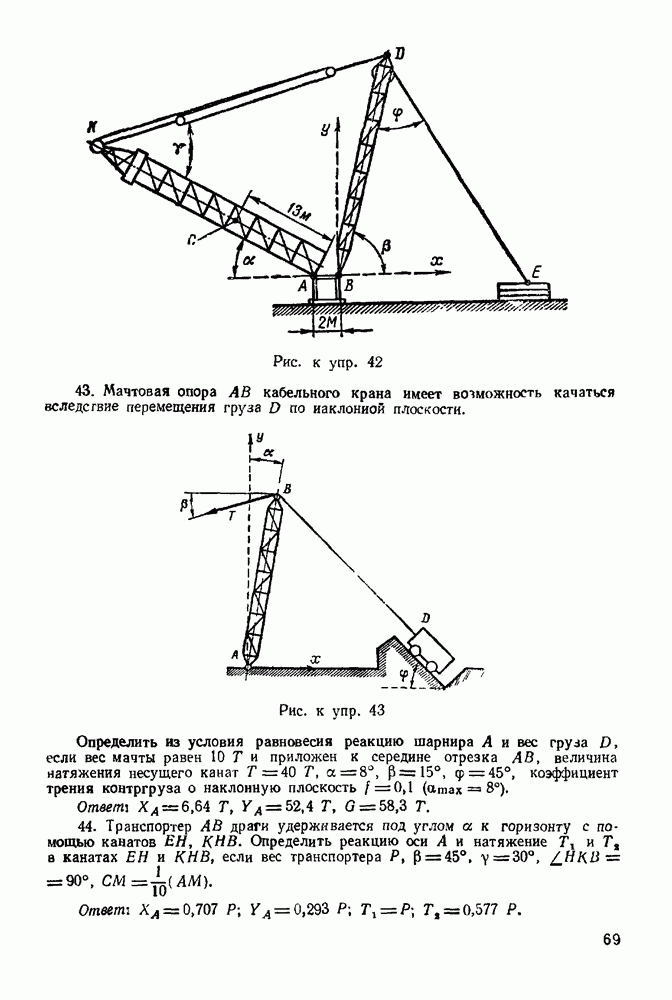
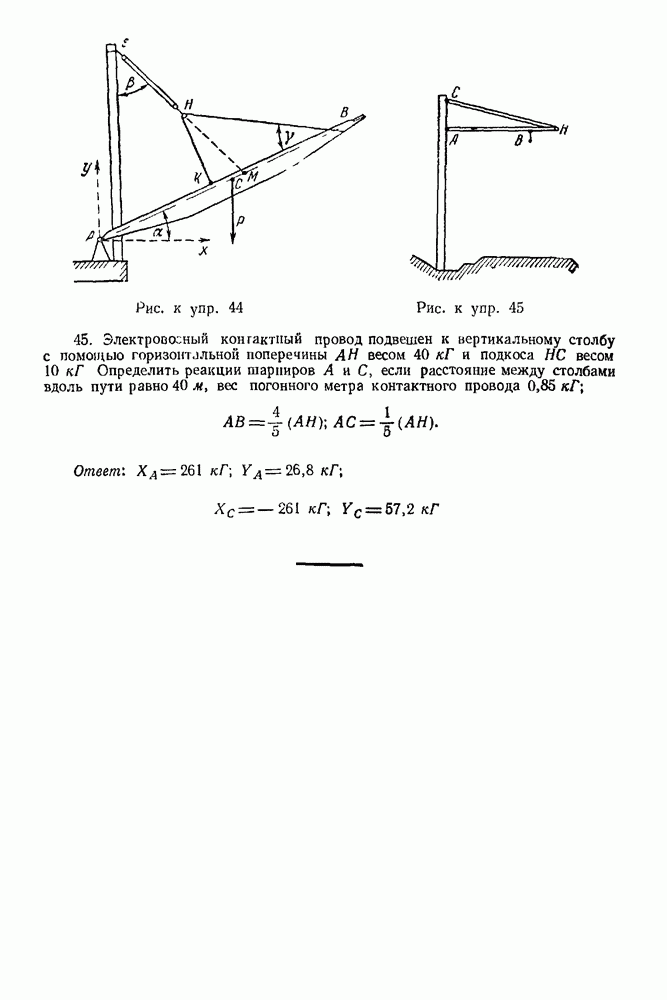
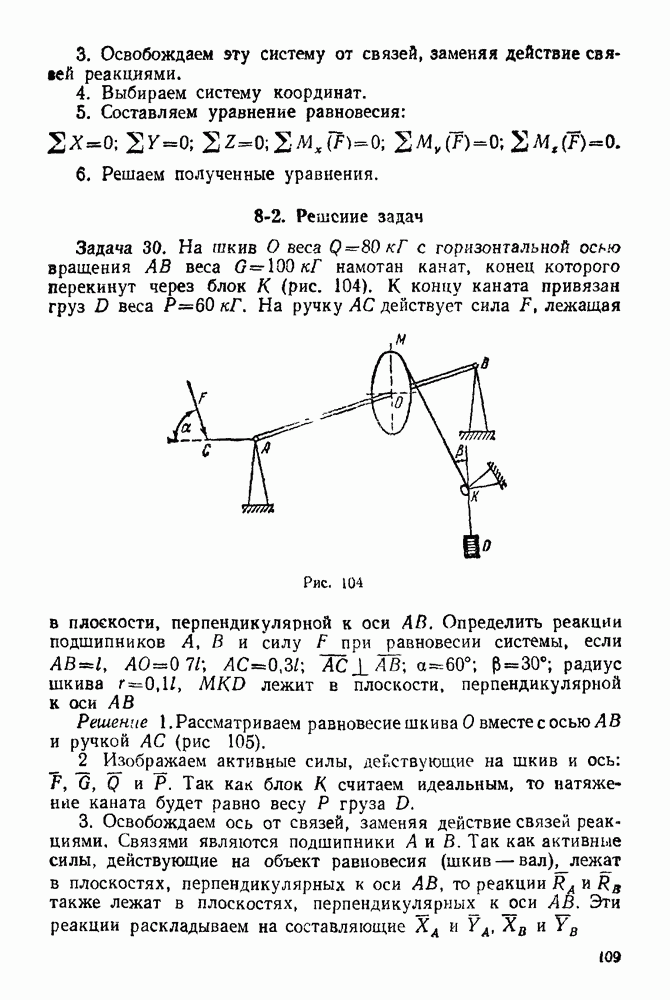
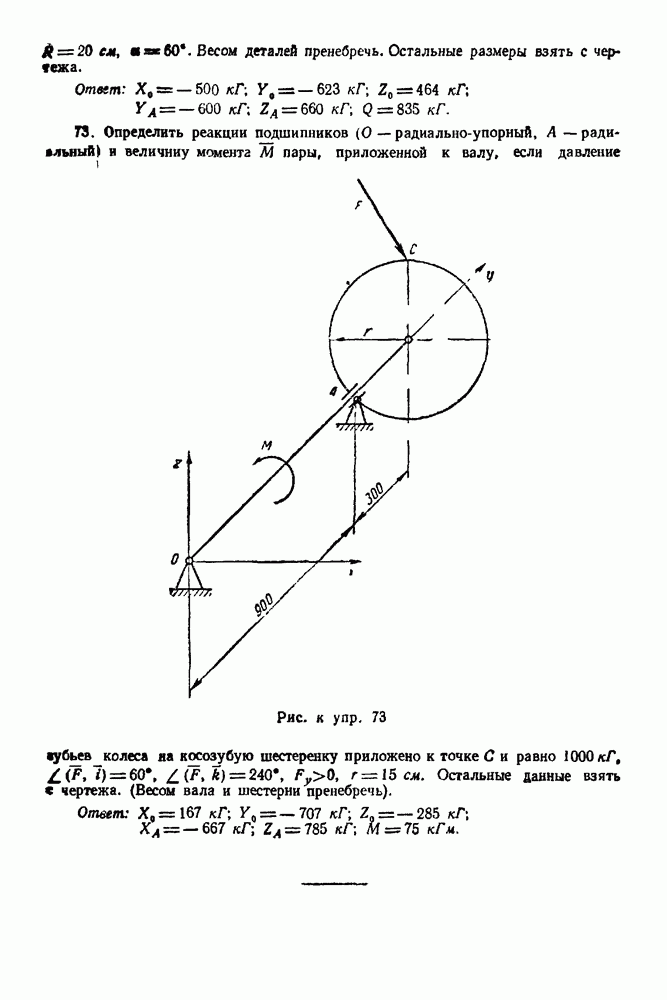
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
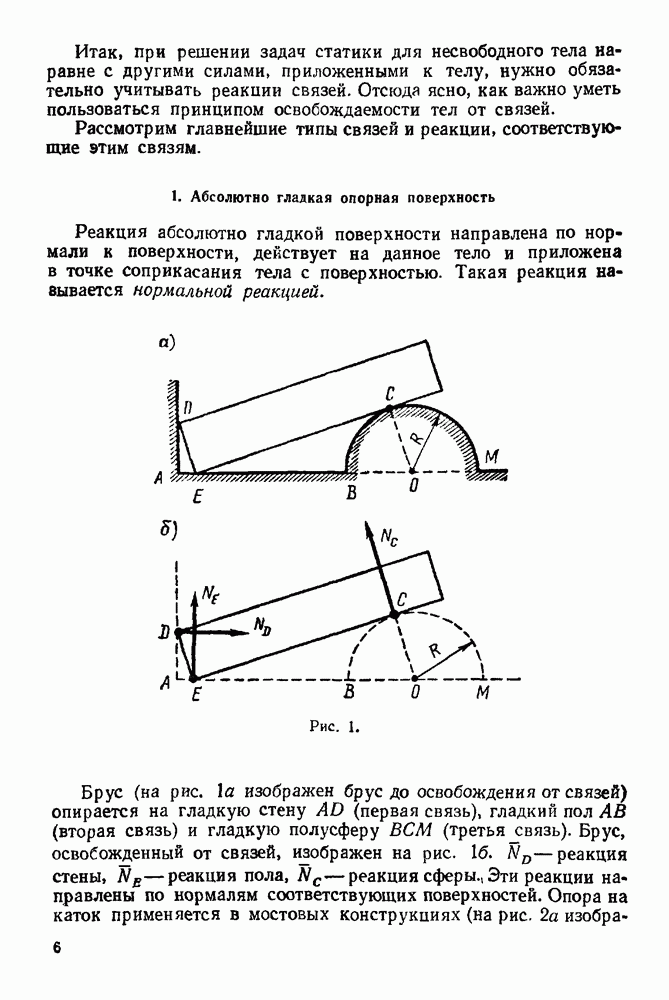
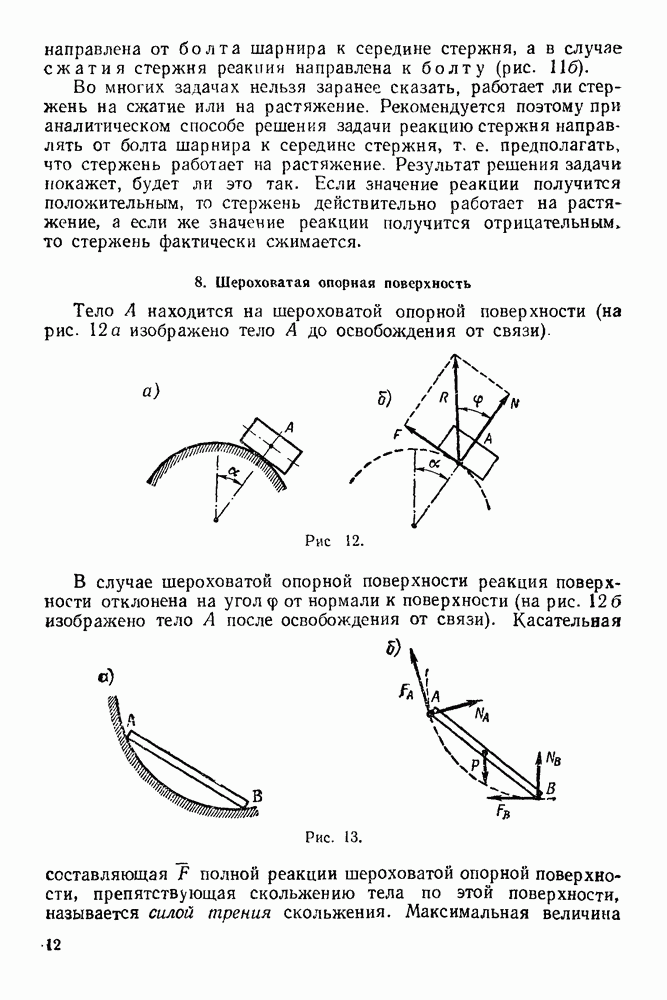
- 1. Абсолютно гладкая опорная поверхность
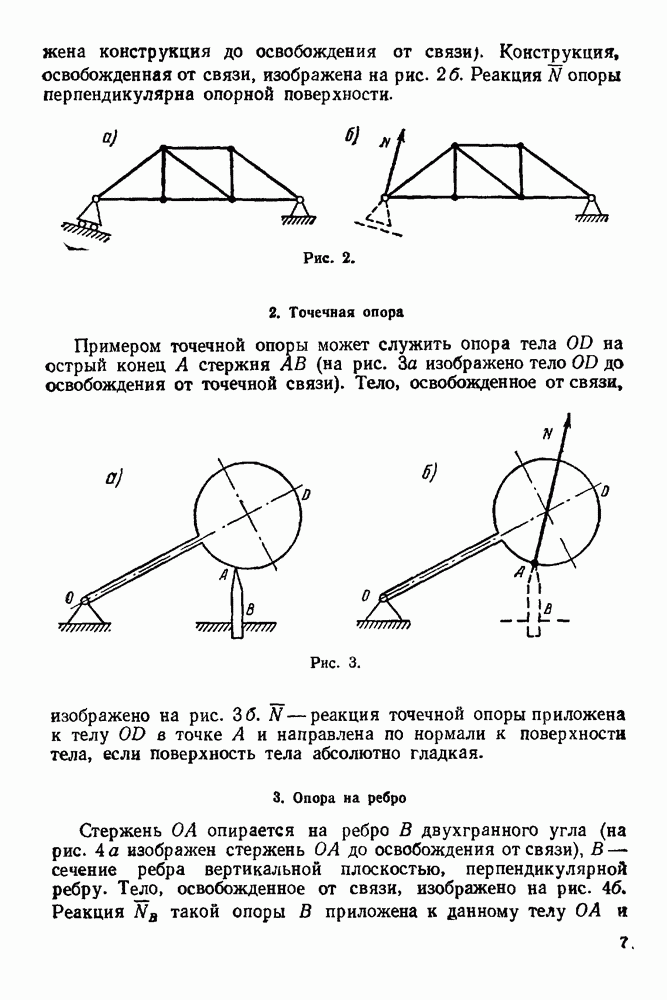
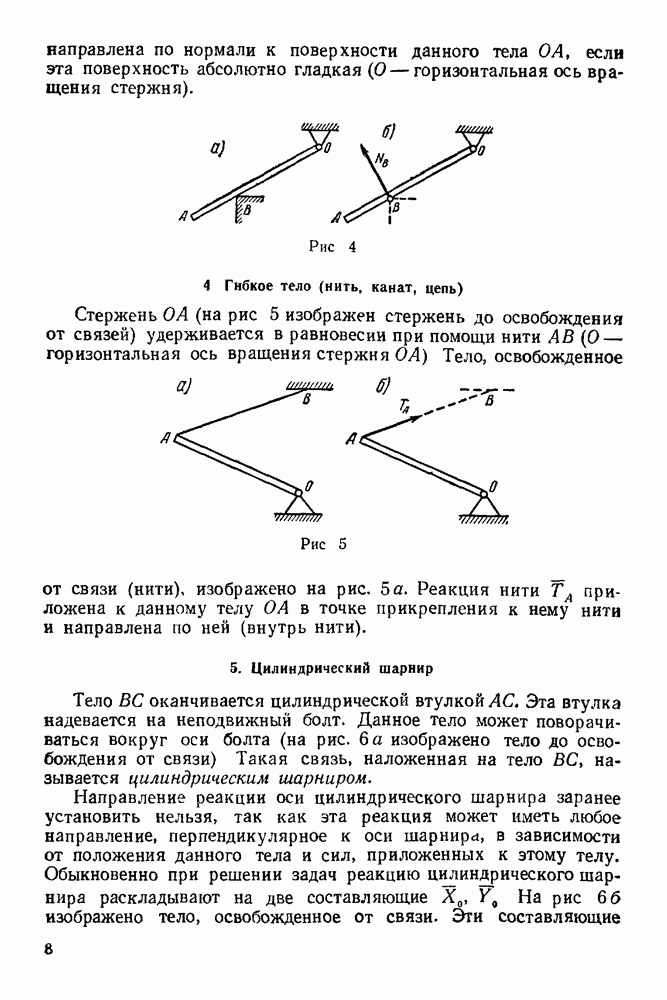
- 2. Точечная опора
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
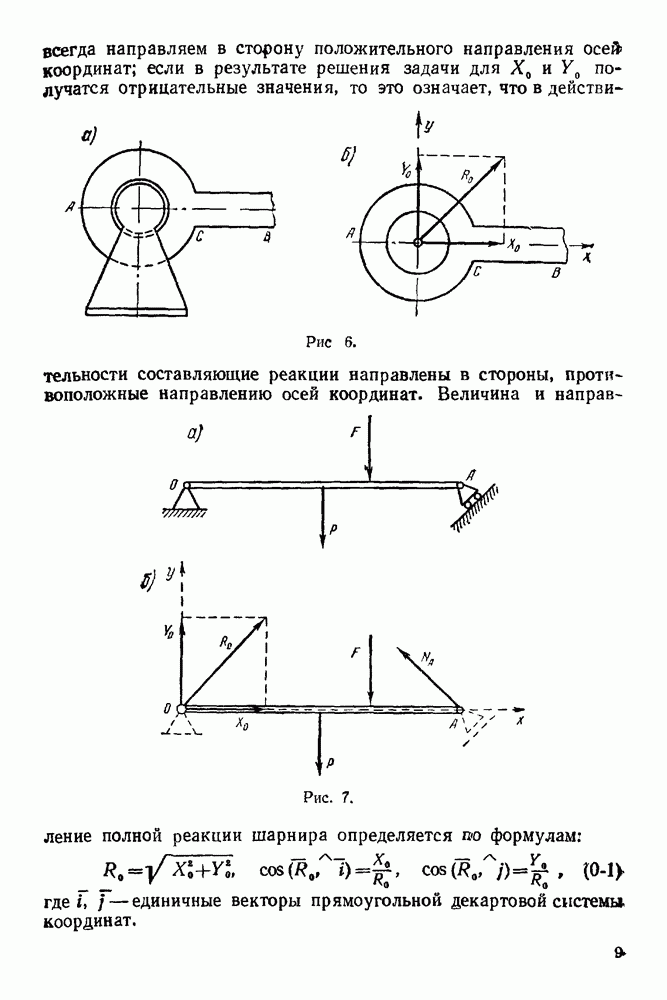
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
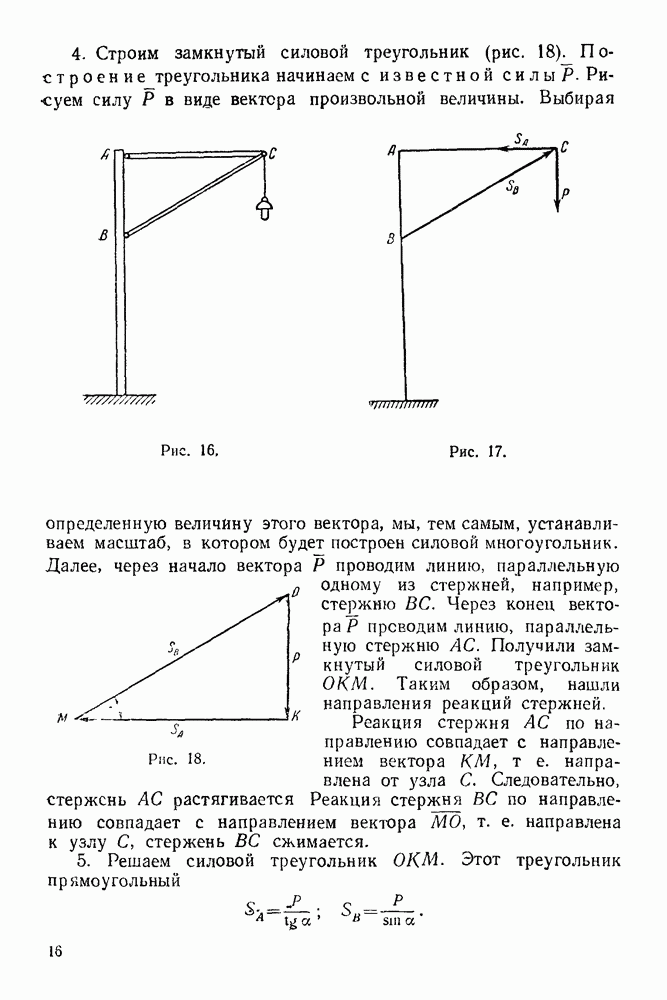
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
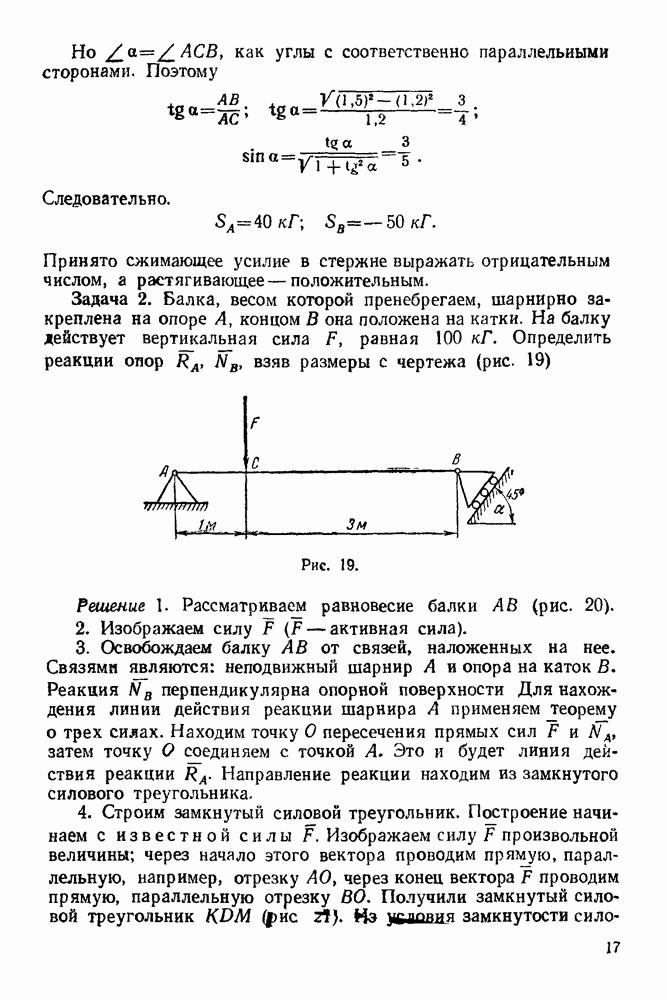
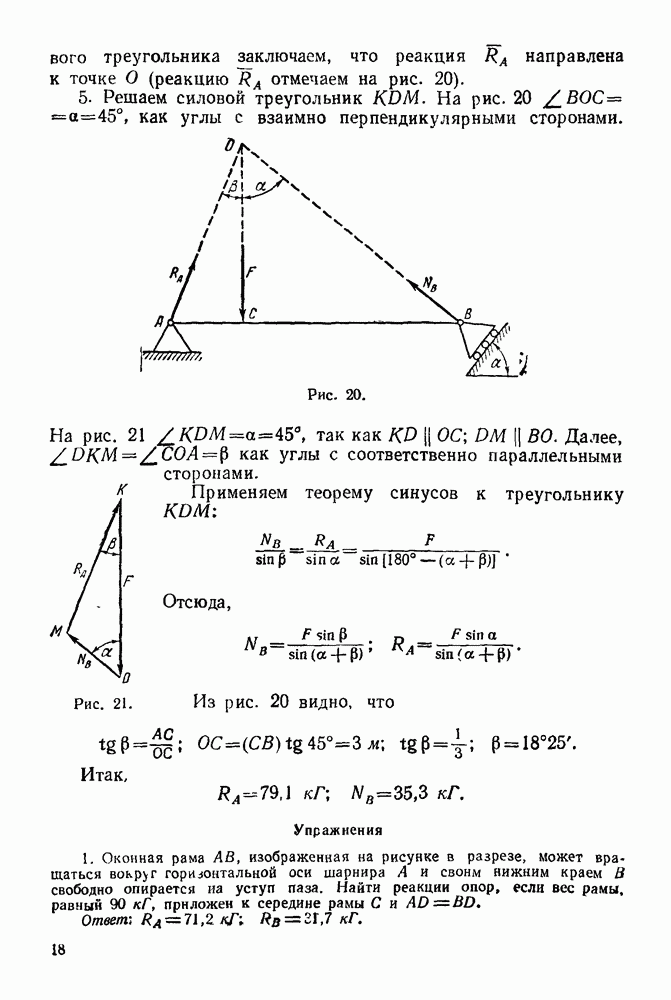
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
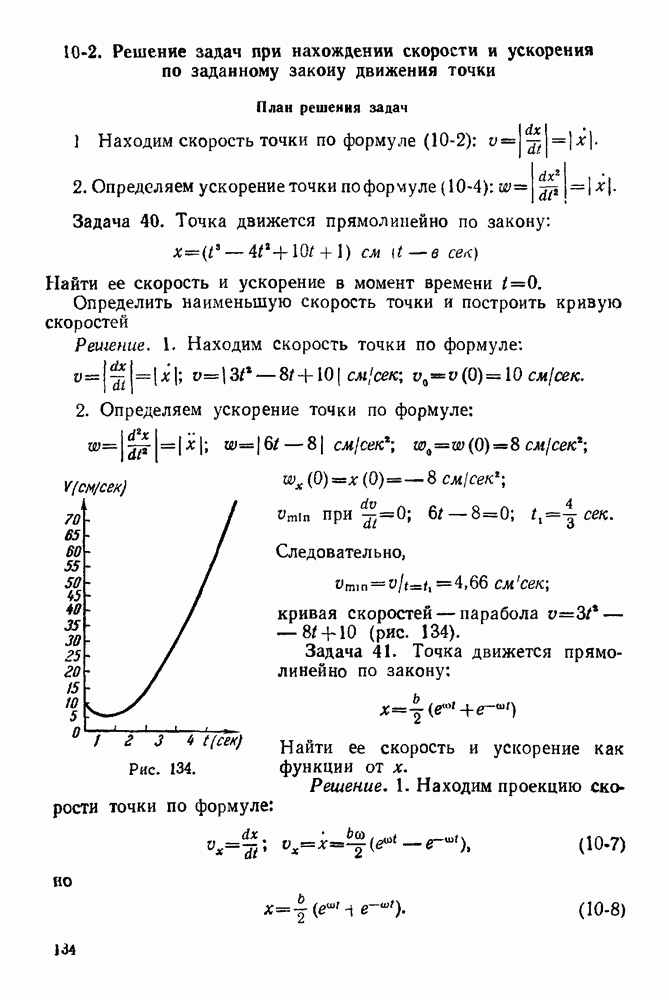
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
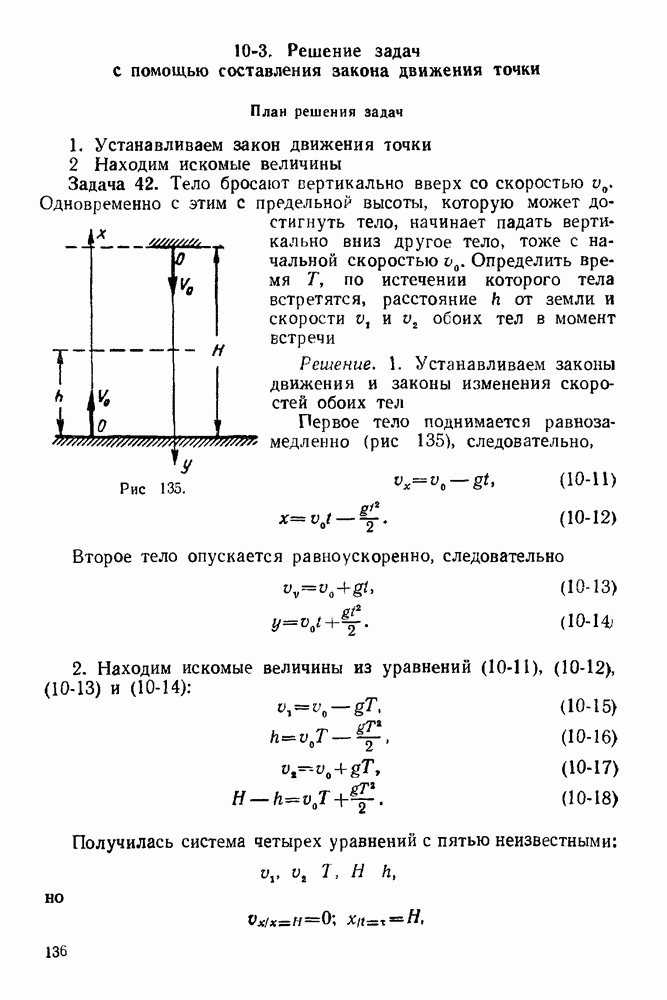
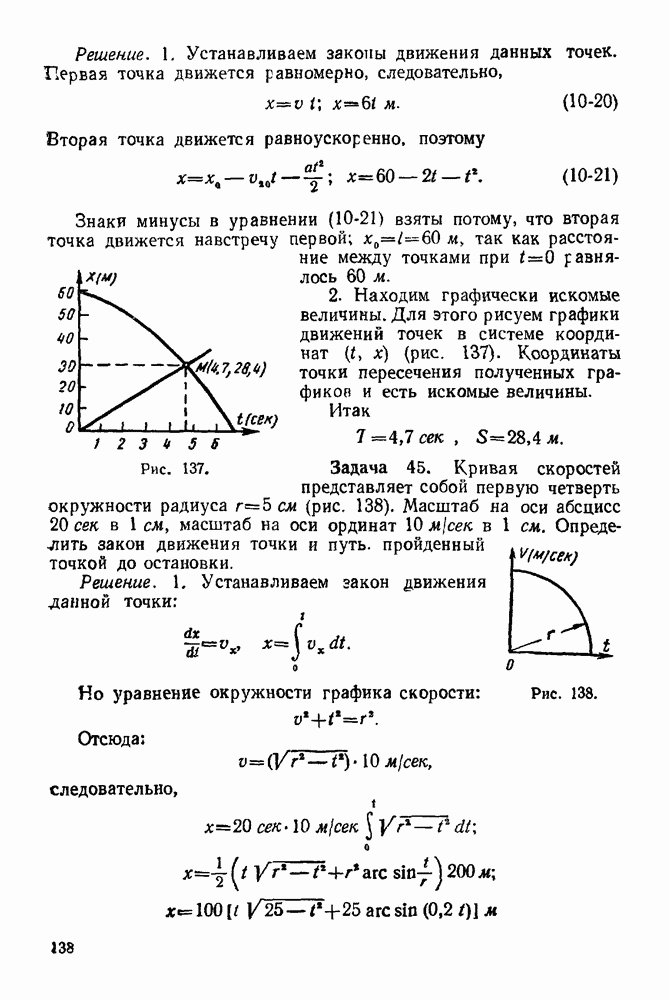
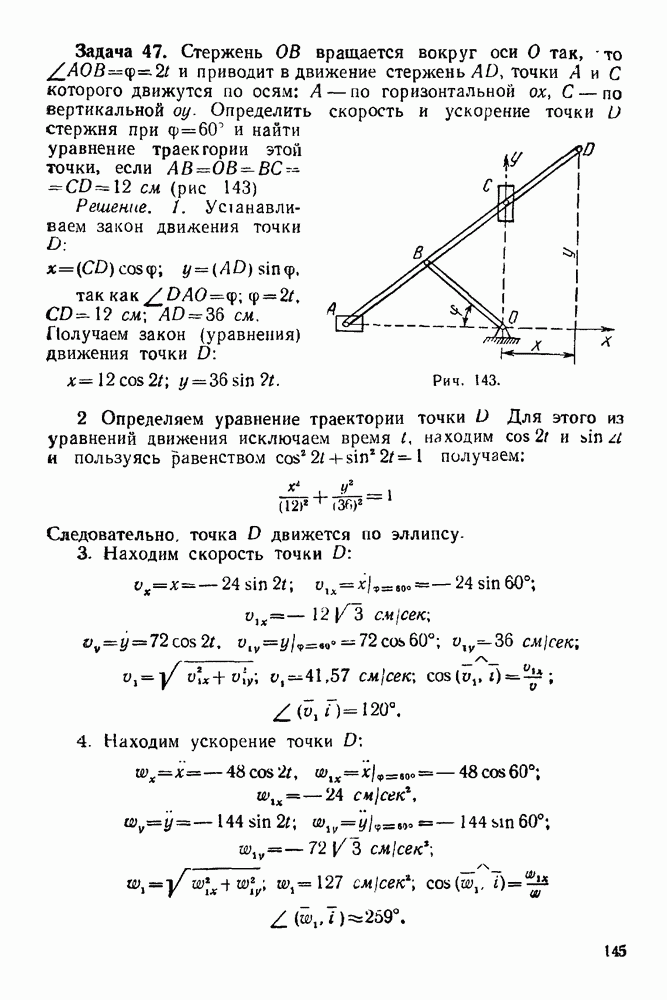
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР