| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
21-2. Теорема об изменении количества движения системы
Производная по времени от количества движения системы равна главному вектору всех внешних сил, действующих на систему:

где  количество движения системы;
количество движения системы;  главный вектор внешних сил, действующих на систему.
главный вектор внешних сил, действующих на систему.
Производная по времени от проекции количества движения системы на какую-нибудь неподвижную ось равна проекции на ту же ось главного вектора всех внешних сил, действующих на систему:

Количество движения системы равно количеству движения центра инерции системы, считая, что в этом центре сосредоточена масса всей системы:

где  масса всей системы,
масса всей системы,  скорость центра инерции системы.
скорость центра инерции системы.
Теорема об изменении количества движения системы в преобразованном  Эйлером виде часто применяется к изучению движения сплошных сред (жидкостей и газов при скоростях, далеких от скорости звука).
Эйлером виде часто применяется к изучению движения сплошных сред (жидкостей и газов при скоростях, далеких от скорости звука).
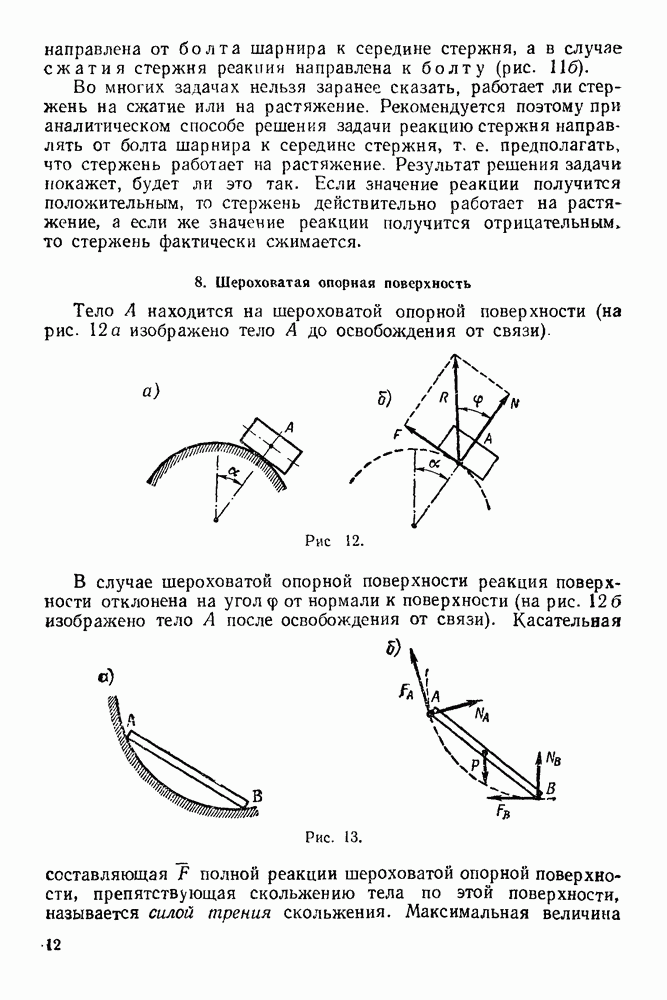
Главные векторы объемных и поверхностных сил и векторы количества движения масс жидкости, входящих и выходящих сквозь сечения трубы в единицу времени, направленные внутрь выделенного объема, образуют замкнутый многоугольник (геометрическая сумма этих векторов равна нулю — рис. 251а и 251б):


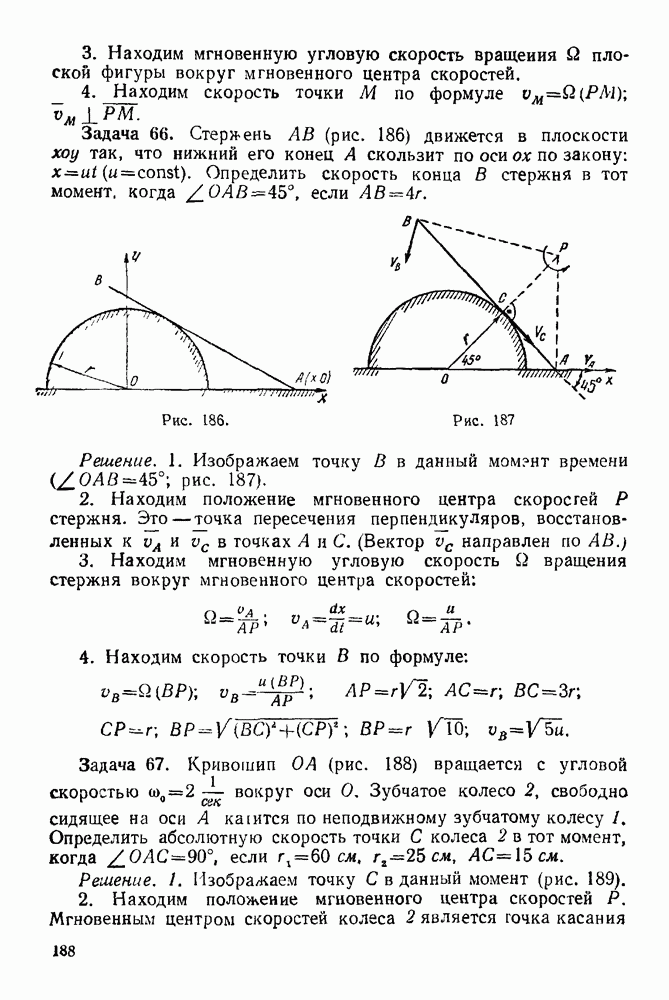
Рис. 251.
План решения задач (Система дискретных точек и тел)
1. Выделяем и изображаем систему в текущий момент.
2. Изображаем внешние силы, действующие на систему.
3. Выбираем неподвижную систему координат.
4. Составляем уравнения теоремы об изменении количества движения системы в проекциях на оси выбранной системы координат.
5. Интегрируем полученные дифференциальные уравнения.
6. Составляем начальные условия задачи.
7. Определяем произвольные постоянные интегрирования по начальным условиям.
8 Найденные произвольные постоянные подстазляем в результат интегрирования дифференциальных уравнений.
9. Из полученных уравнений находим неизвестные величины.
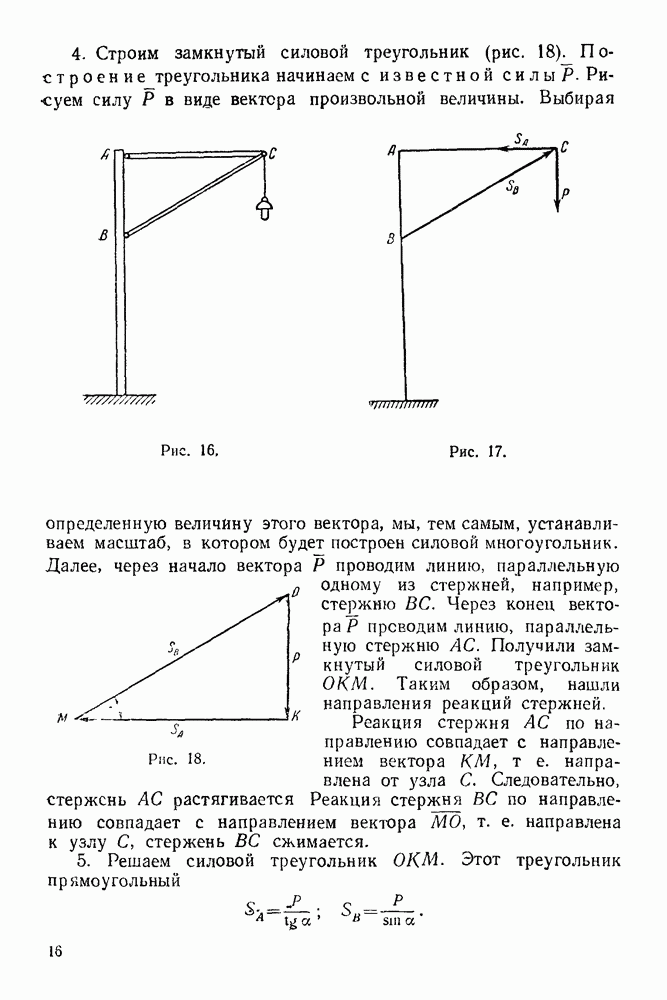
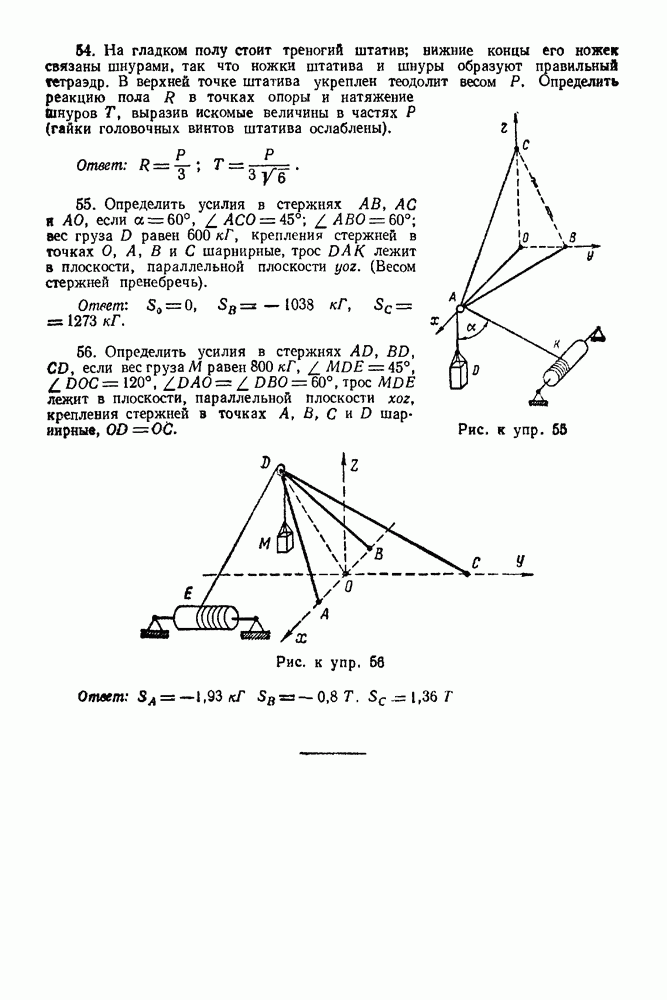
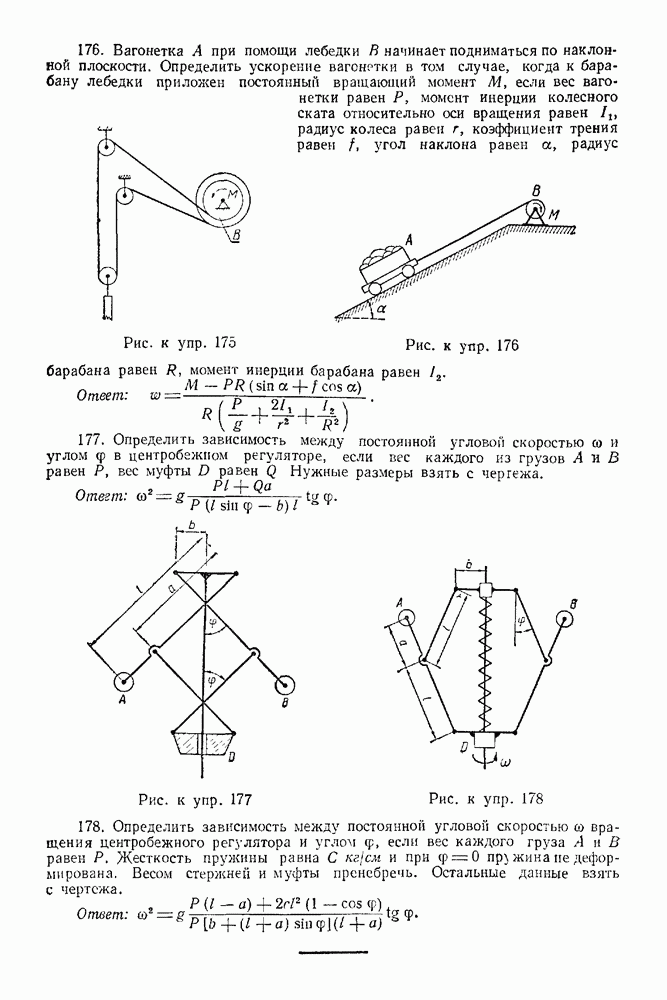
Задача 97. Прямоугольный клин с углом а весом  поставлен на горизонтальную плоскость (рис. 252). На него положено тело
поставлен на горизонтальную плоскость (рис. 252). На него положено тело  весом
весом  и тело В весом
и тело В весом  связанные между собо
связанные между собо  гибкой нерастяжимой нитью
гибкой нерастяжимой нитью  перекинутой через блок С. Определить зависимость между скоростью клина и относительной по отношению к клину скоростью грузов
перекинутой через блок С. Определить зависимость между скоростью клина и относительной по отношению к клину скоростью грузов  если опорные поверхности гладкие и в начале движения система находилась в покое. Массами блока и нити пренебречь.
если опорные поверхности гладкие и в начале движения система находилась в покое. Массами блока и нити пренебречь.
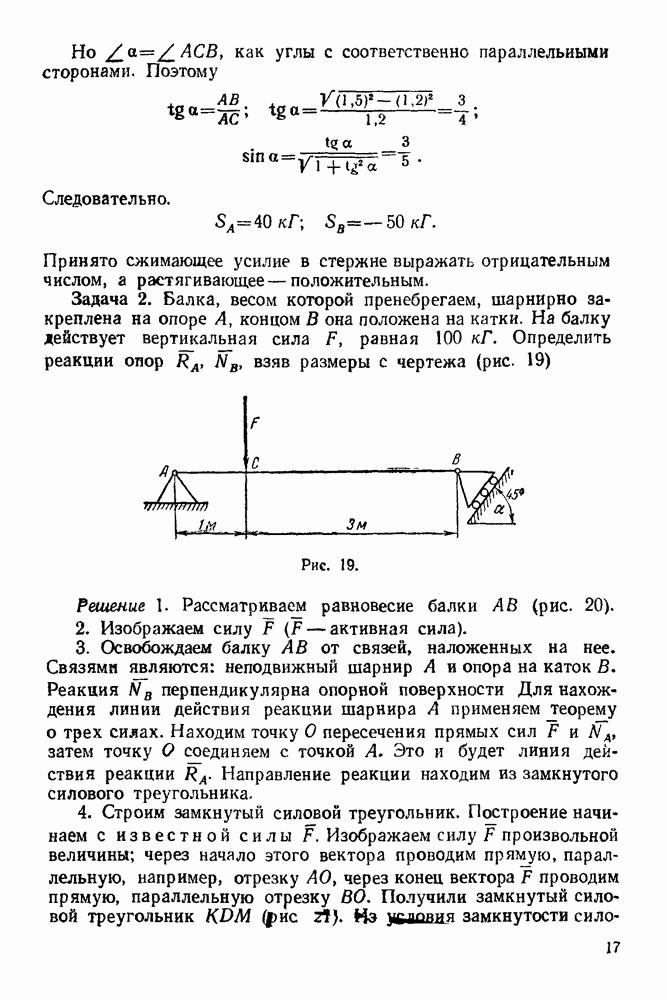
Решение. 1. Изображаем систему, состоящую из грузов  клина, нити и блока С а текущий момент времени (рис. 253).
клина, нити и блока С а текущий момент времени (рис. 253).
2. Изображаем внешние силы  действующие на систему
действующие на систему  нормальная реакция гладкой горизонтальной опорной плоскости).
нормальная реакция гладкой горизонтальной опорной плоскости).

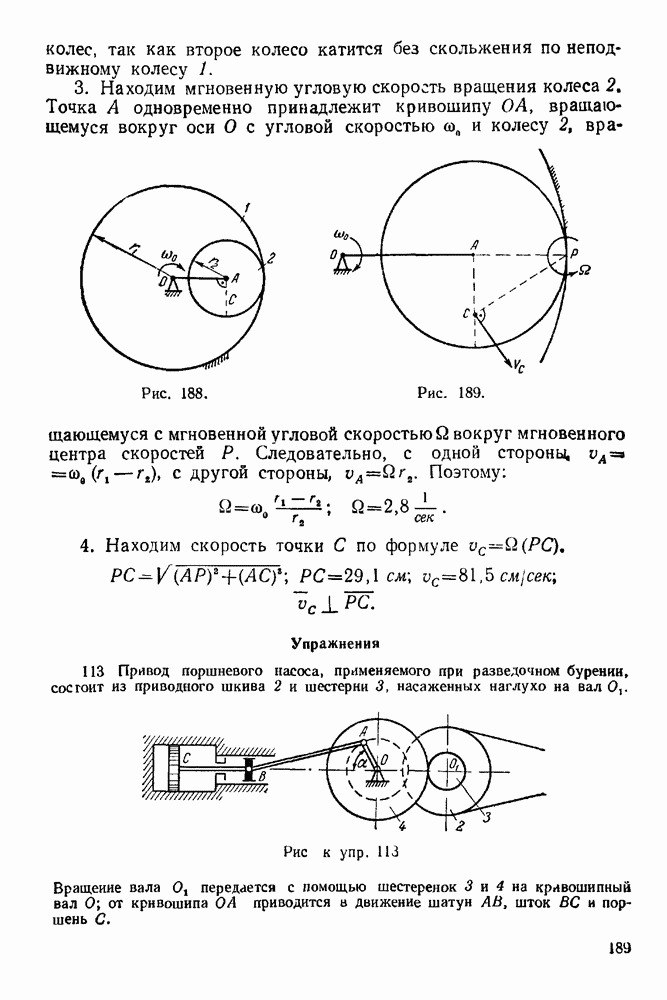
Рис. 252.
3. Выбираем систему координат, как указано на рис. 253.
4. Составляем уравнение теоремы об изменении количества движения системы в проекции на ось 

Следовательно 
5. Интегрируем полученное дифференциальное уравнение 

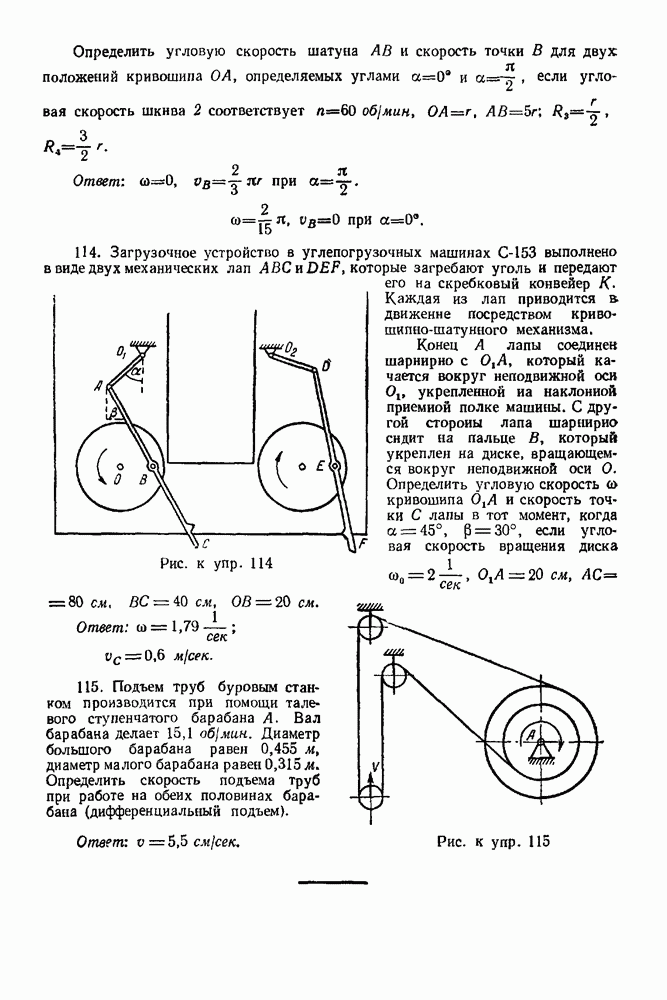
Рис. 253.
Получаем:

где  произвольная постоянная интегрирования.
произвольная постоянная интегрирования.
6. Составляем начальные условия: при 
7. Определяем произвольную постоянную с, по начальному условию движения, получаем 
8. Найденную произвольную постоянную подставляем в уравнение (21-8а), будем иметь: 
9. Из полученного уравнения находим 

где  количество движения груза
количество движения груза  - количество движения груза
- количество движения груза  количество движения клина.
количество движения клина.
Количество движения каждого тела подсчитывается, как количество движения материальной точки, так как каждое тело движется поступательно:
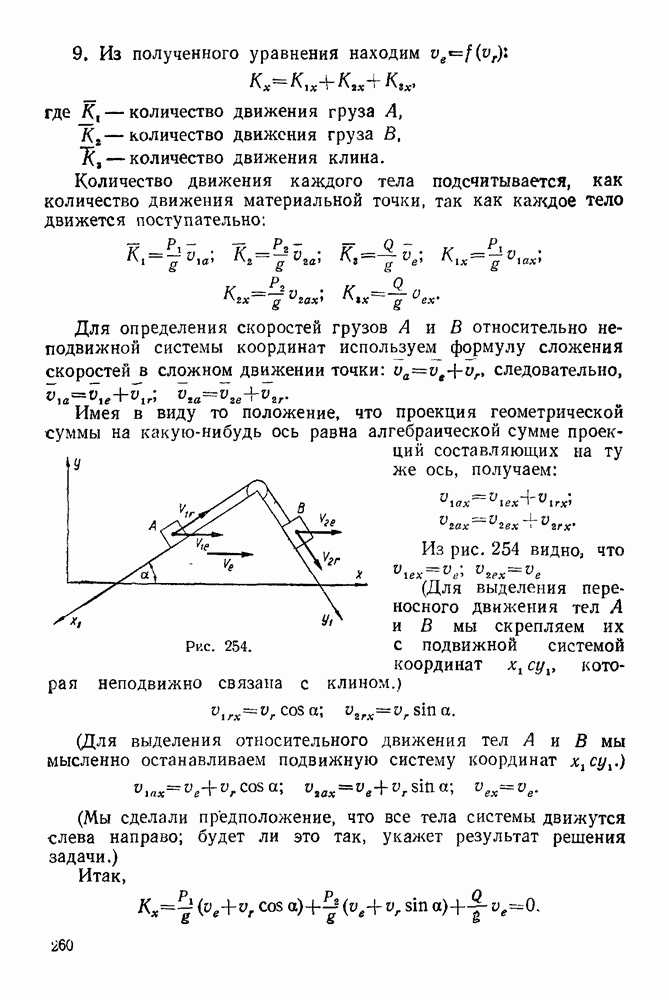
Для определения скоростей грузов  относительно неподвижной системы координат используем формулу сложения скоростей в сложном движении точки:
относительно неподвижной системы координат используем формулу сложения скоростей в сложном движении точки:  следовательно,
следовательно,
Имея в виду то положение, что проекция геометрической суммы на какую-нибудь ось равна алгебраической сумме проекций составляющих на ту же ось, получаем:

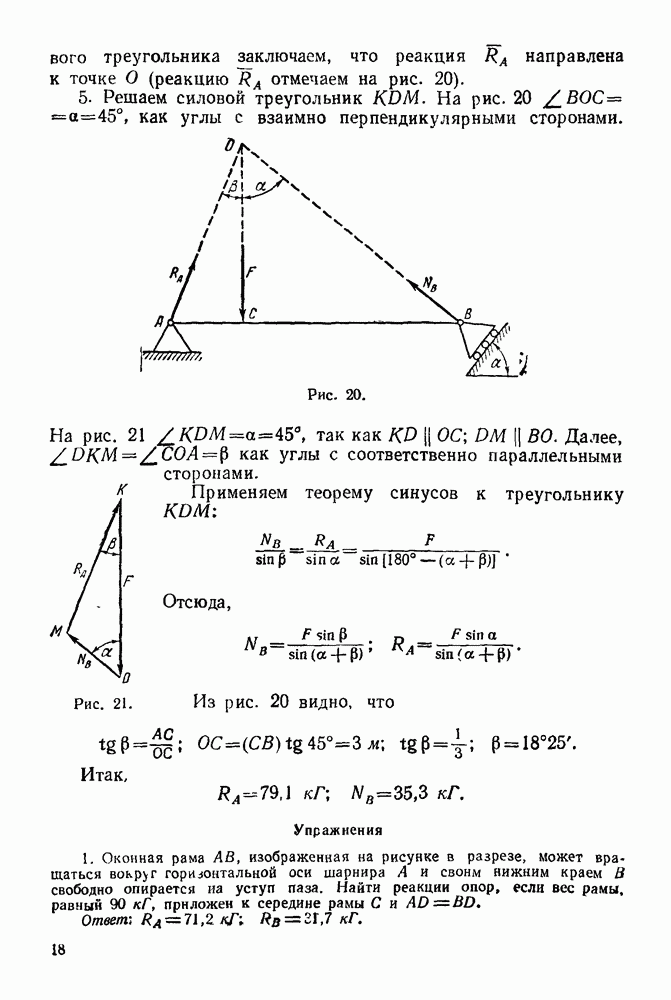
Из рис. 254 видно, что


Рис. 254.
(Для выделения переносного движения тел  мы скрепляем их с подвижной системой координат
мы скрепляем их с подвижной системой координат  которая неподвижно связана с клином.)
которая неподвижно связана с клином.)

(Для выделения относительного движения тел  мы мысленно останавливаем подвижную систему координат
мы мысленно останавливаем подвижную систему координат 

(Мы сделали предположение, что все тела системы движутся слева направо; будет ли это так, укажет результат решения задачи.)
Итак,

Отсюда:

Знак  показывает, что клин движется справа налево.
показывает, что клин движется справа налево.
План решения задач (Движение жидкости)
1. Выделяем объем жидкости в трубе.
2. Изображаем объемные силы  поверхностные силы
поверхностные силы  действующие на выделенный объем, а также векторы количеств движения масс жидкости, входящих и выходящих сквозь сечения трубы в единицу времени, направляя эти векторы внутрь выделенного объема.
действующие на выделенный объем, а также векторы количеств движения масс жидкости, входящих и выходящих сквозь сечения трубы в единицу времени, направляя эти векторы внутрь выделенного объема.
3. Выбираем систему координат.
4. Составляем уравнения равновесия сил, приложенных к выделенному объему:

5. Из уравнений равновесия находим неизвестные величины.
Задача 98. Определить добавочное давление на опору А колена трубы, если ось трубы расположена в горизонтальной плоскости, скорость воды при входе  диаметр сечения равен 30 см, скорость течения воды при выходе
диаметр сечения равен 30 см, скорость течения воды при выходе  (рис. 255).
(рис. 255).

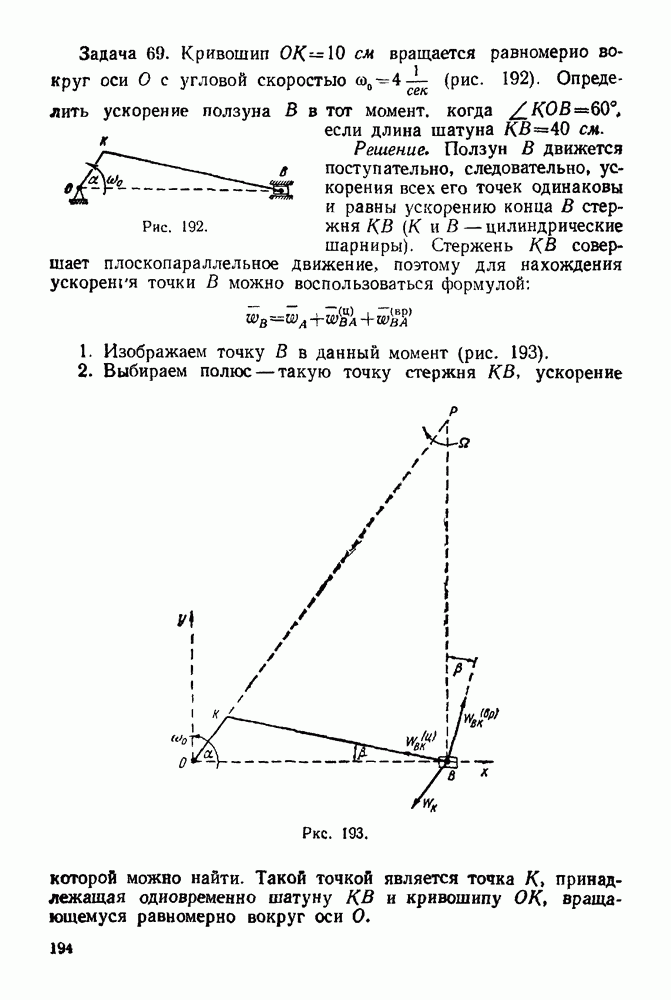
Рис. 255.

Рис. 256.
Решение. 1. Выделяем объем трубы  (рис. 256).
(рис. 256).
2. Изображаем реакцию RA опоры А (поверхностная сила), векторы  (вес колена трубы и весжидкости, заключенной в этом колене, не оказывают влияния на величину до» бавочного давления).
(вес колена трубы и весжидкости, заключенной в этом колене, не оказывают влияния на величину до» бавочного давления).
3. Выбираем систему координат, как указано на рис. 256.
4. Составляем уравнения равновесия сил, действующих на колено и лежащих в горизонтальной плоскости:

5. Из полученных уравнений равновесия находим неизвестные величины: 

где 

Рекомендация: Теорему об изменении количества движения системы целесообразно применять в тех случаях, когда имеет место закон сохранения количества движения системы и, кроме того, когда система представляет собою сплошную среду (жидкость или газ, при скоростях, далеких от скорости звука), движущуюся в сосуде; нужно найти давление среды на стенки сосуда.
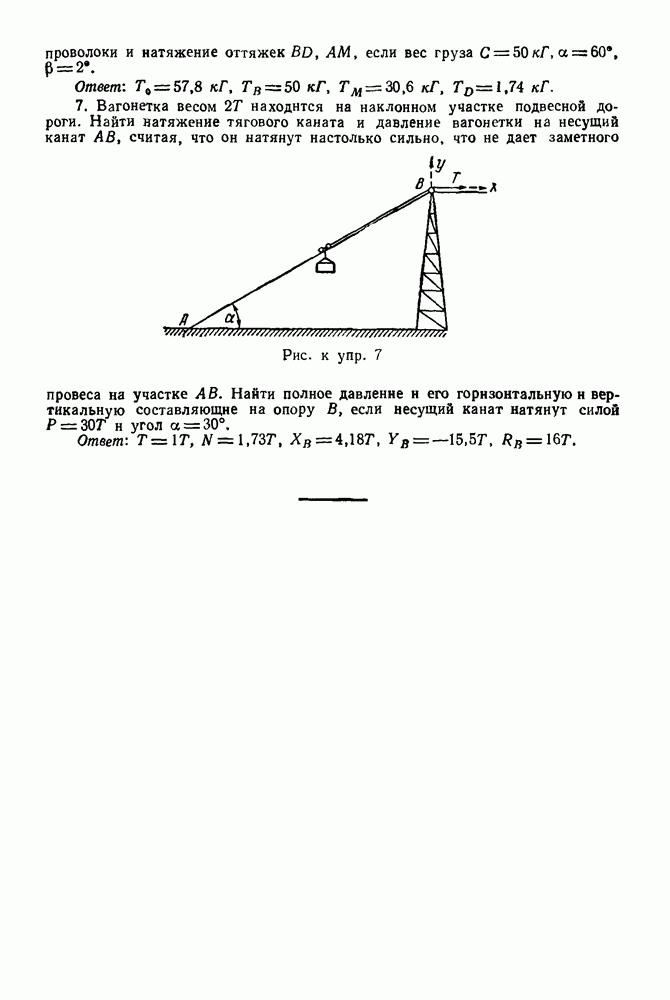
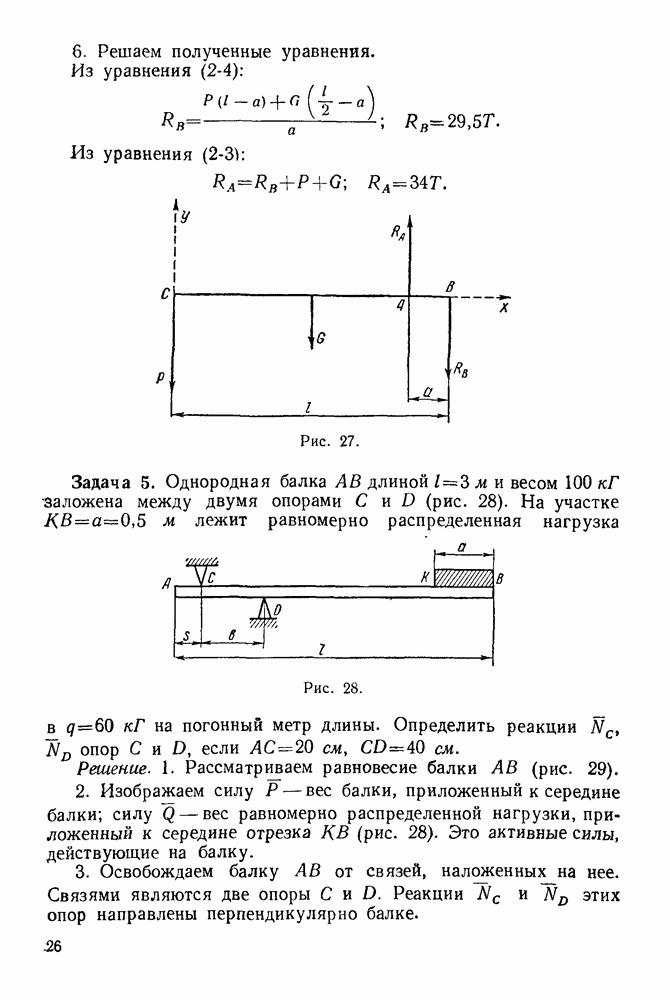
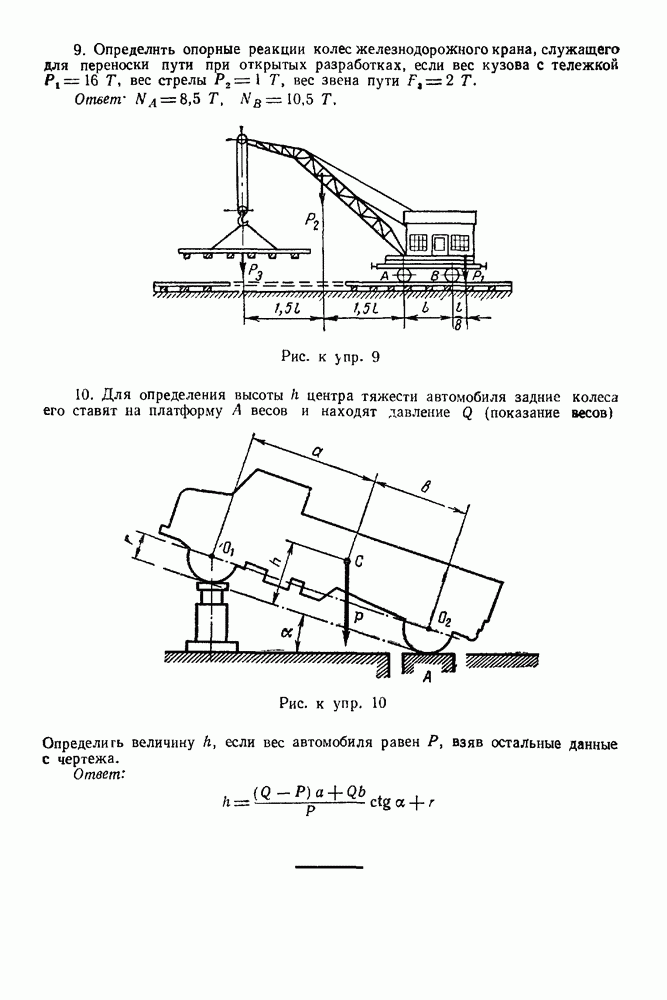
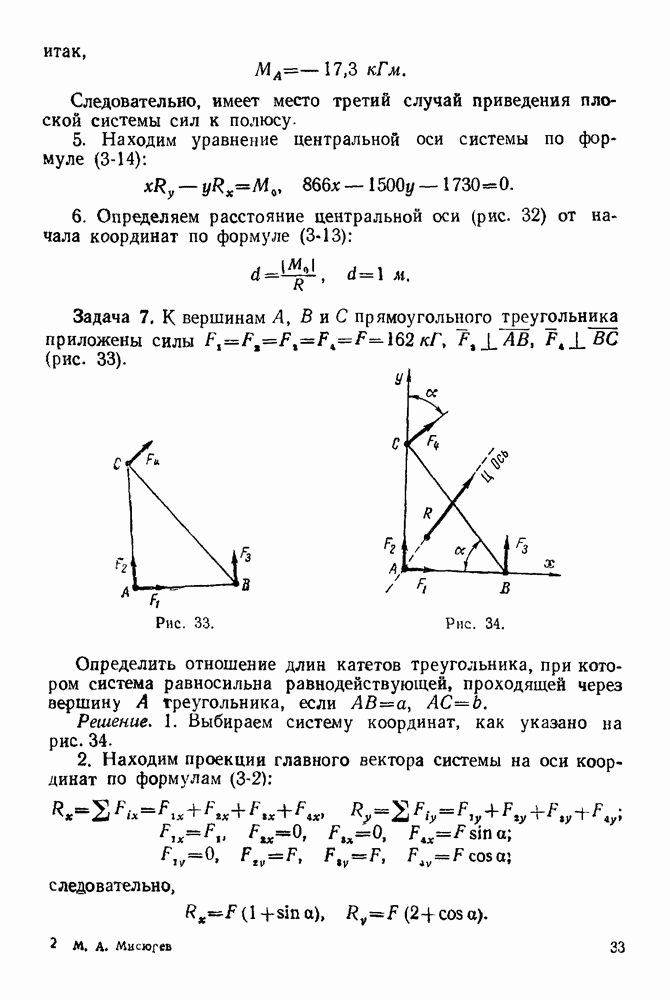
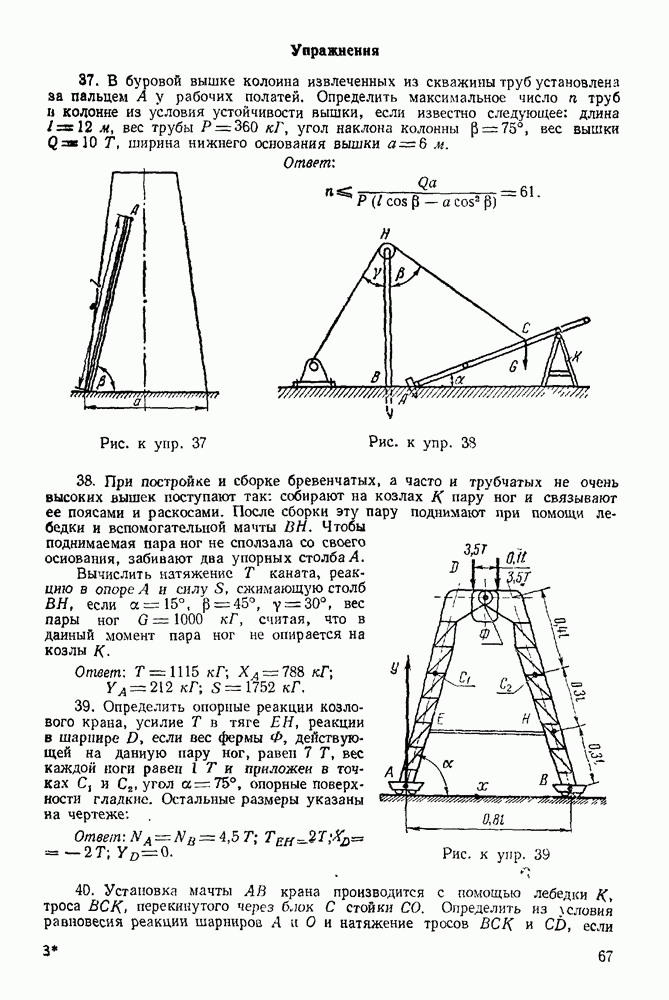
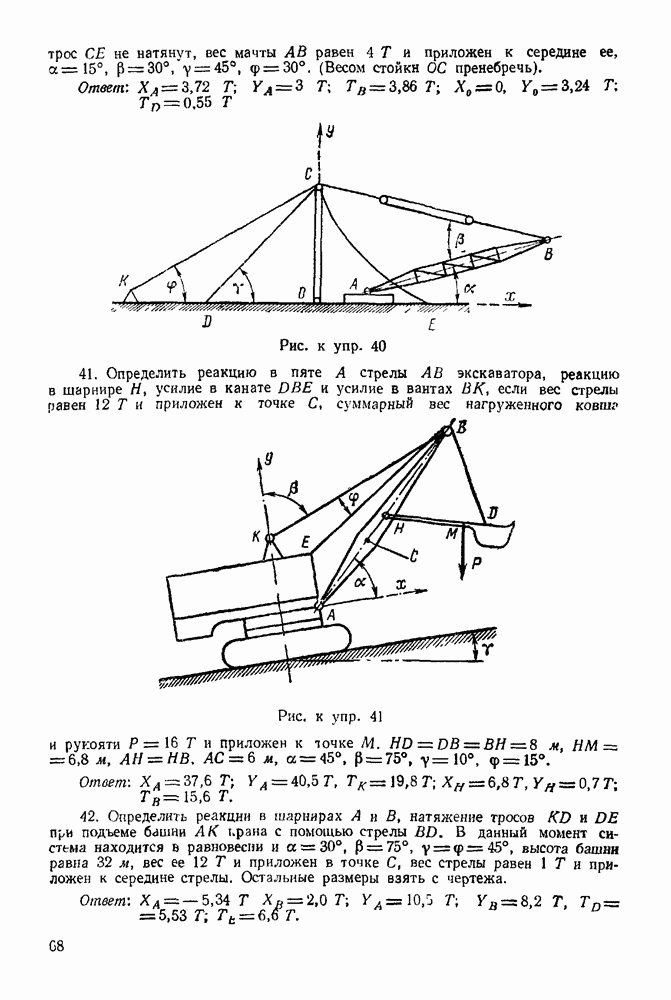
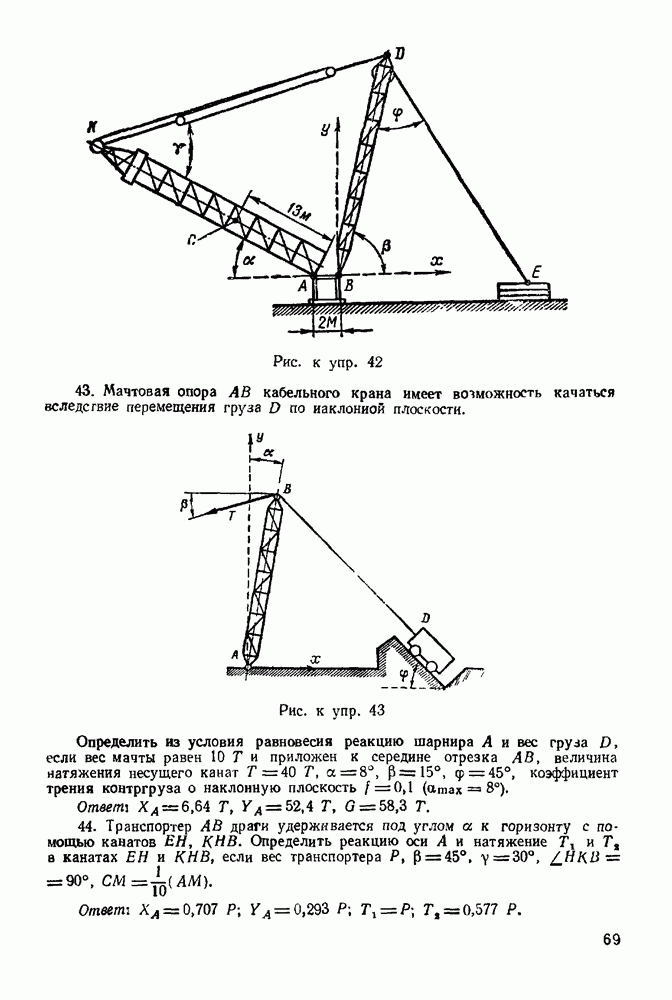
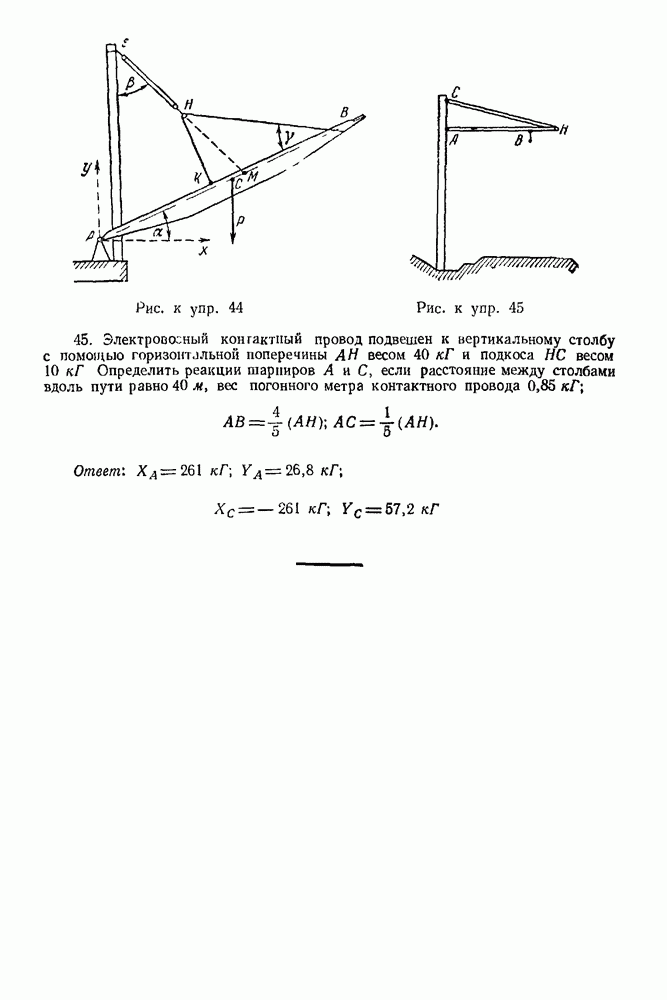
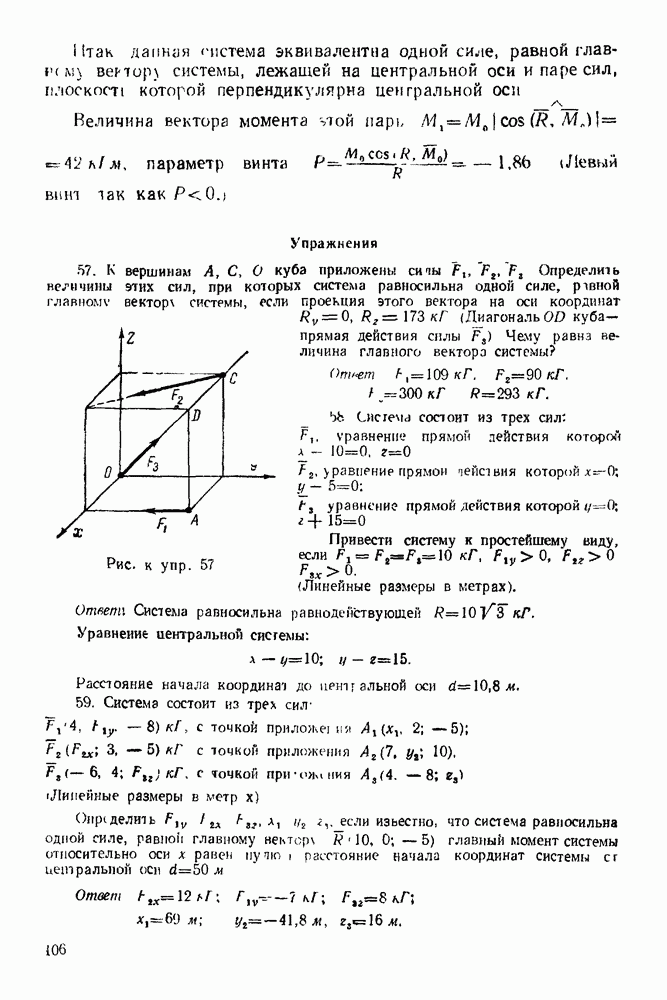
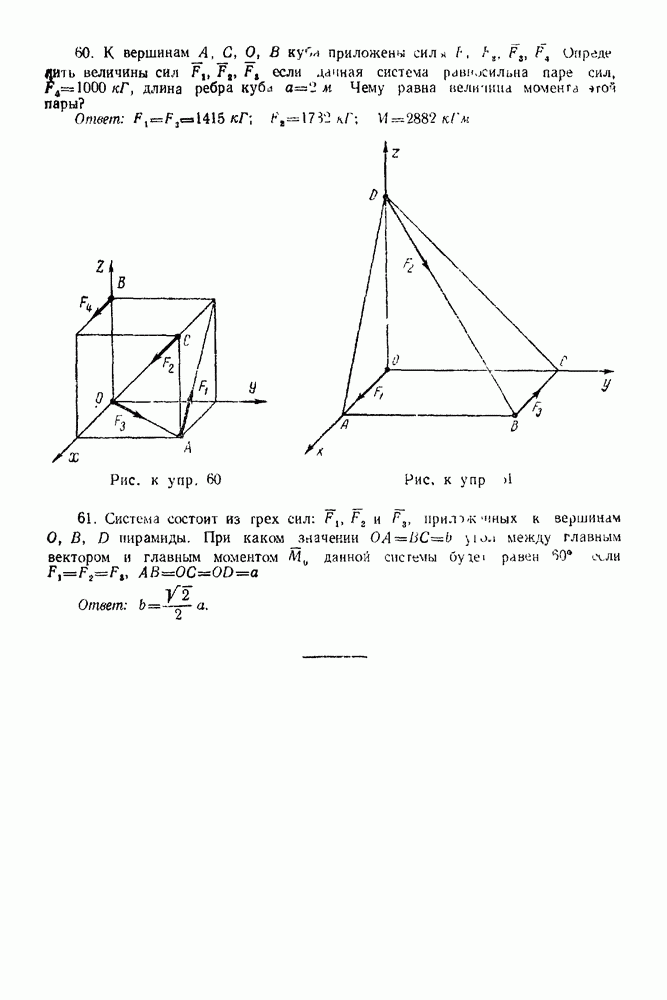
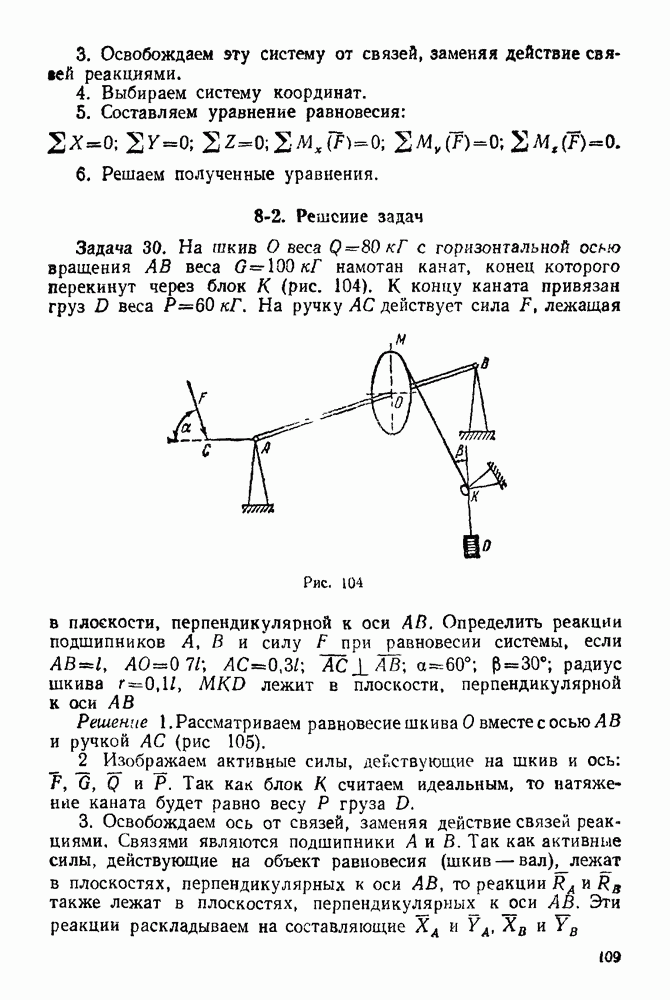
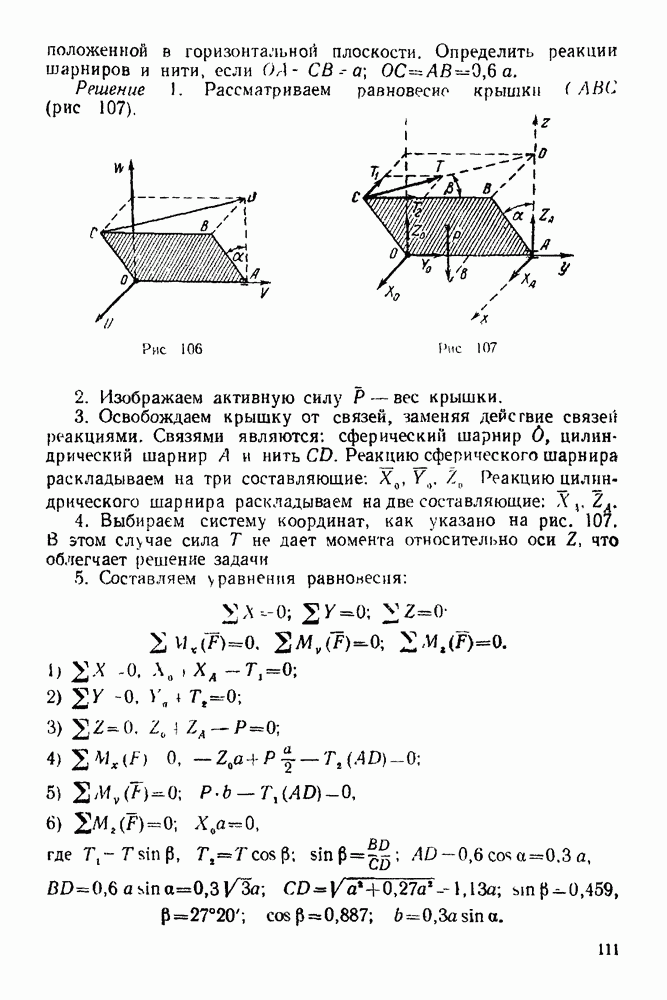
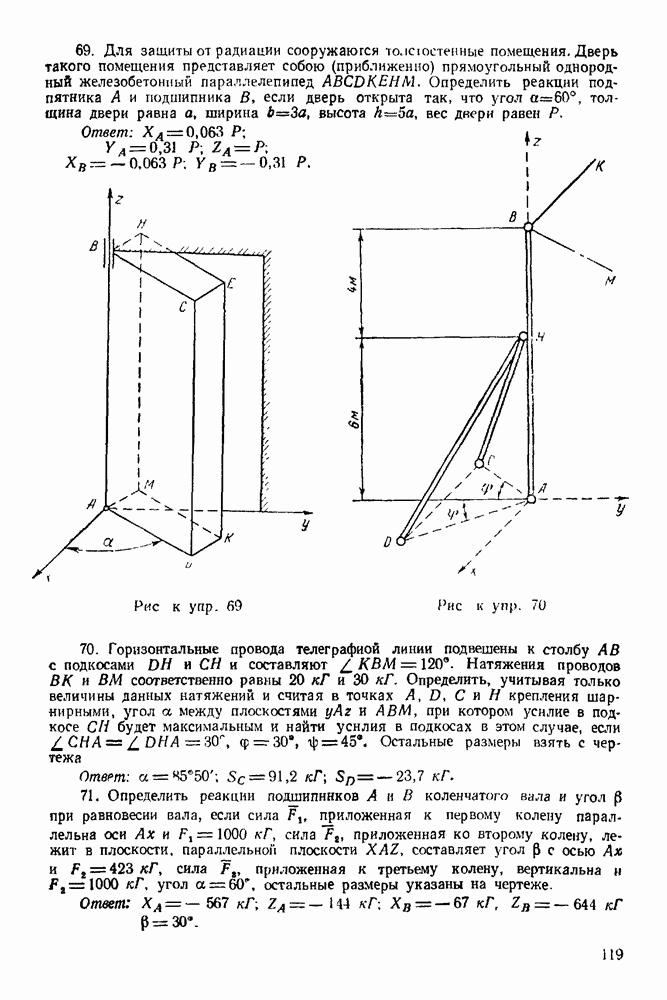
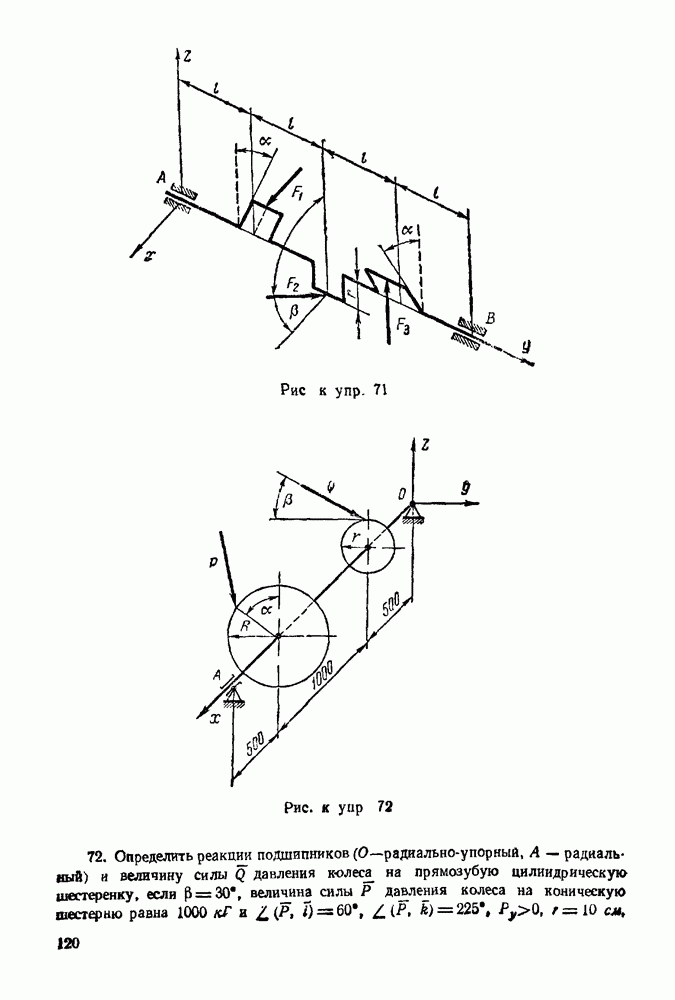
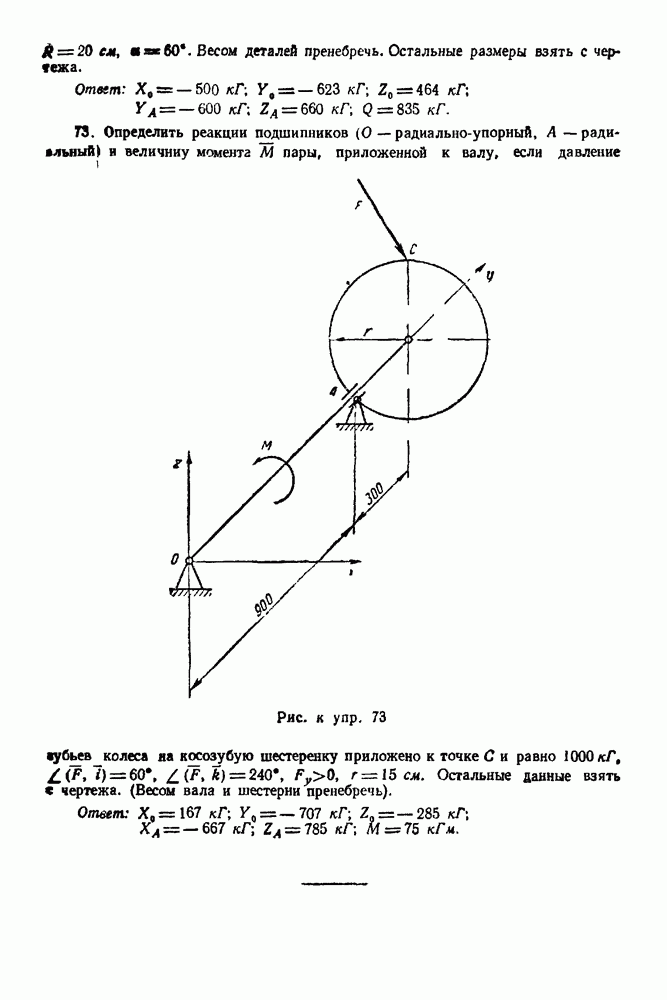
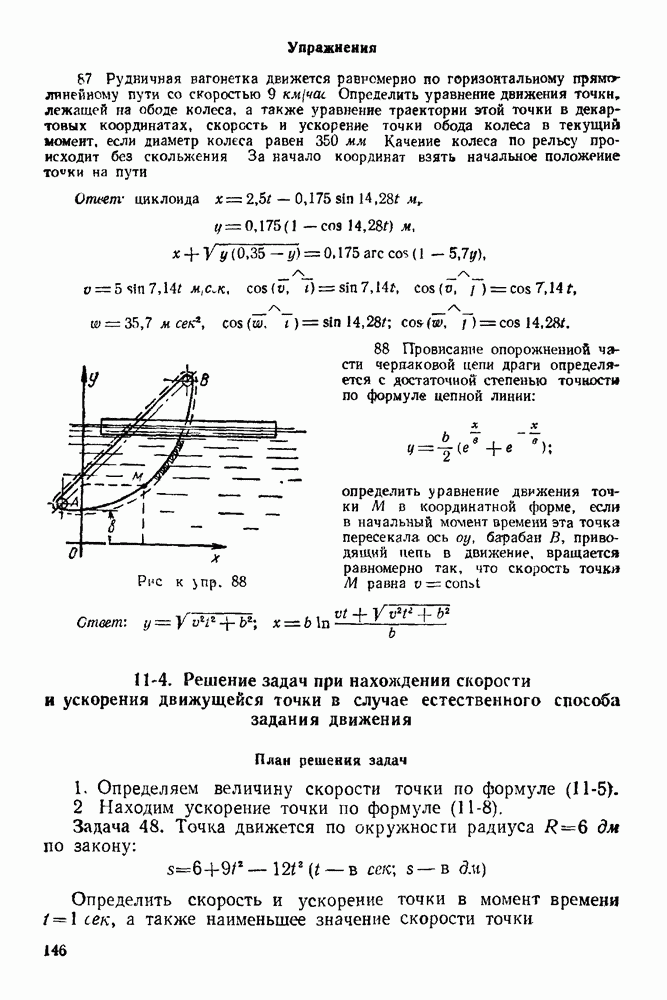
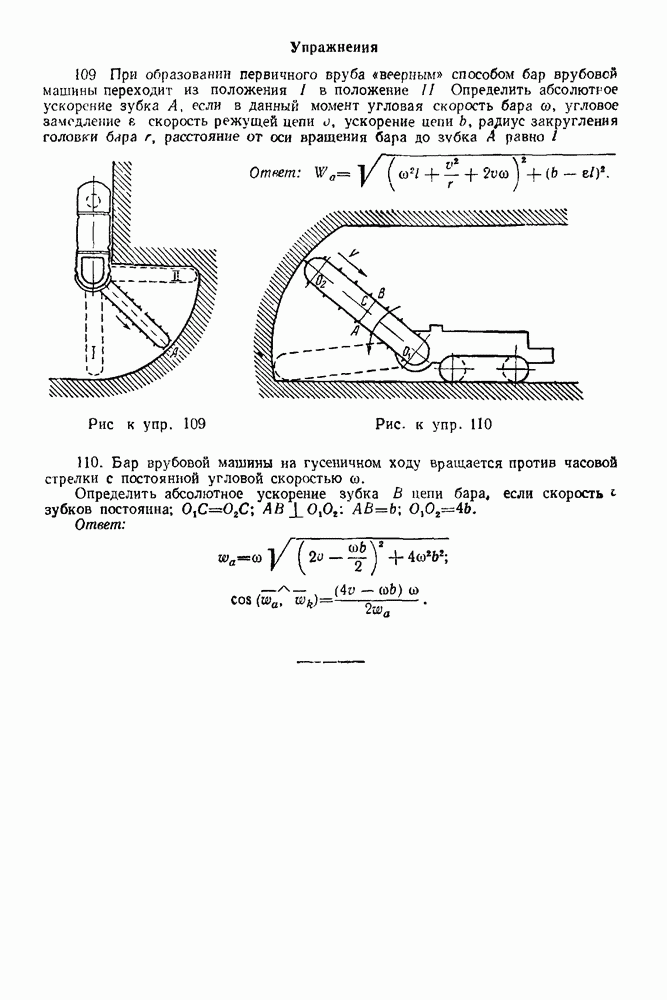
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
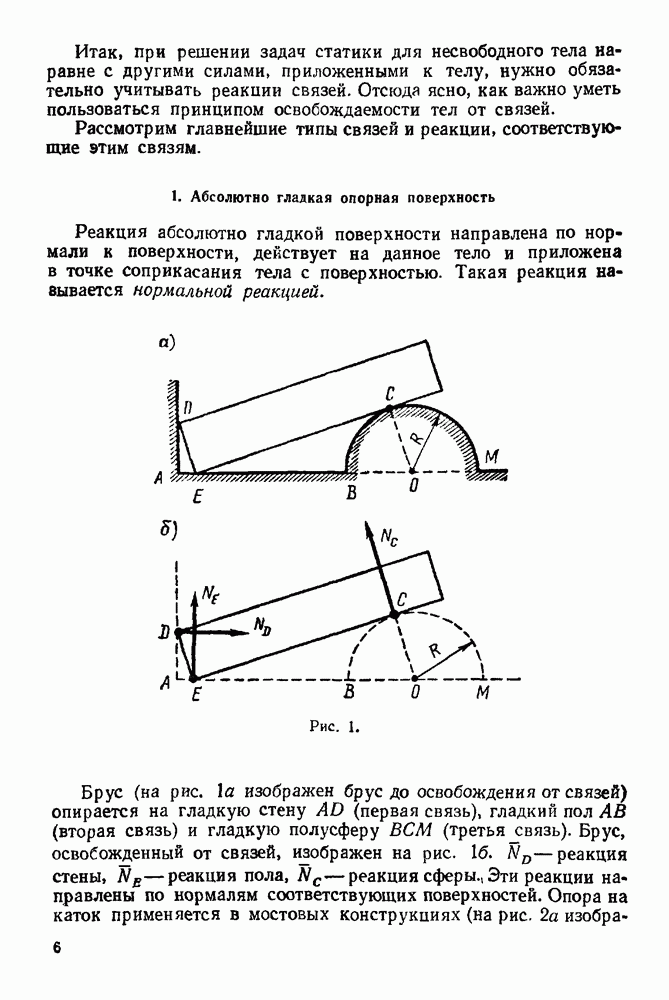
- 1. Абсолютно гладкая опорная поверхность
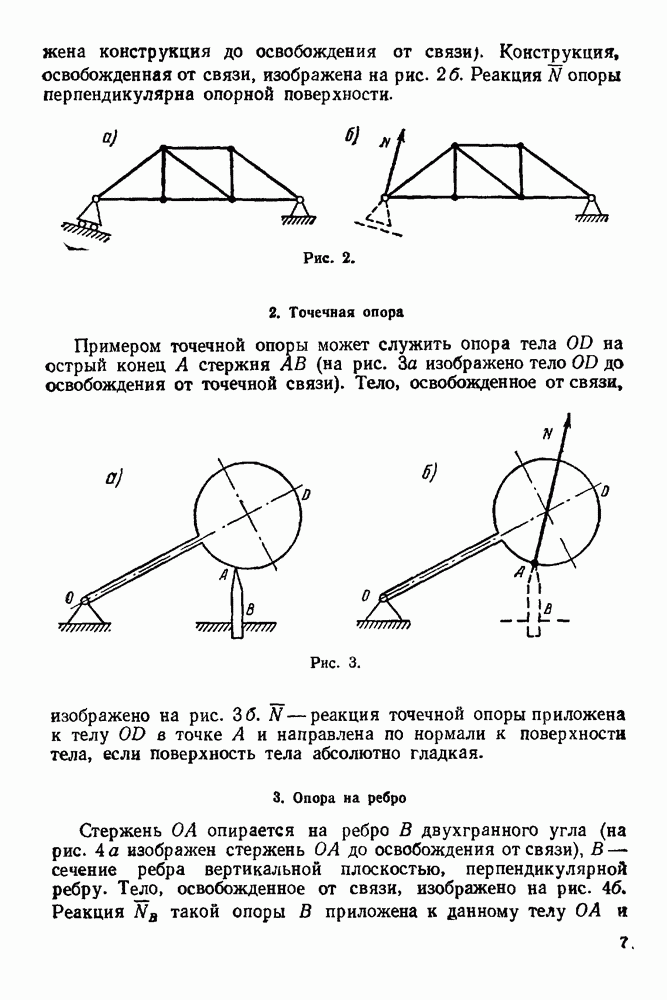
- 2. Точечная опора
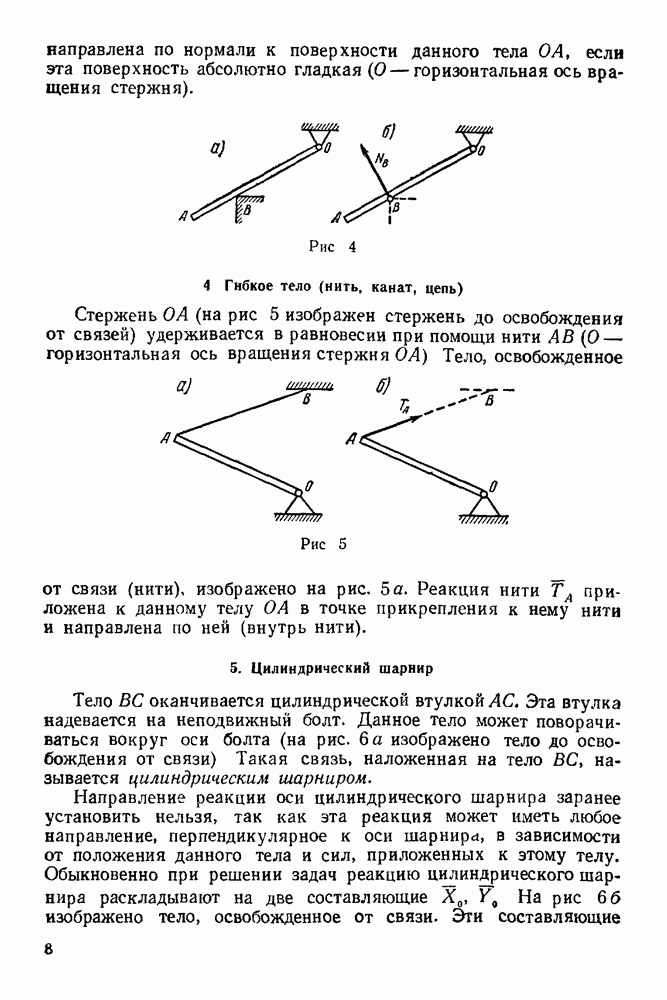
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
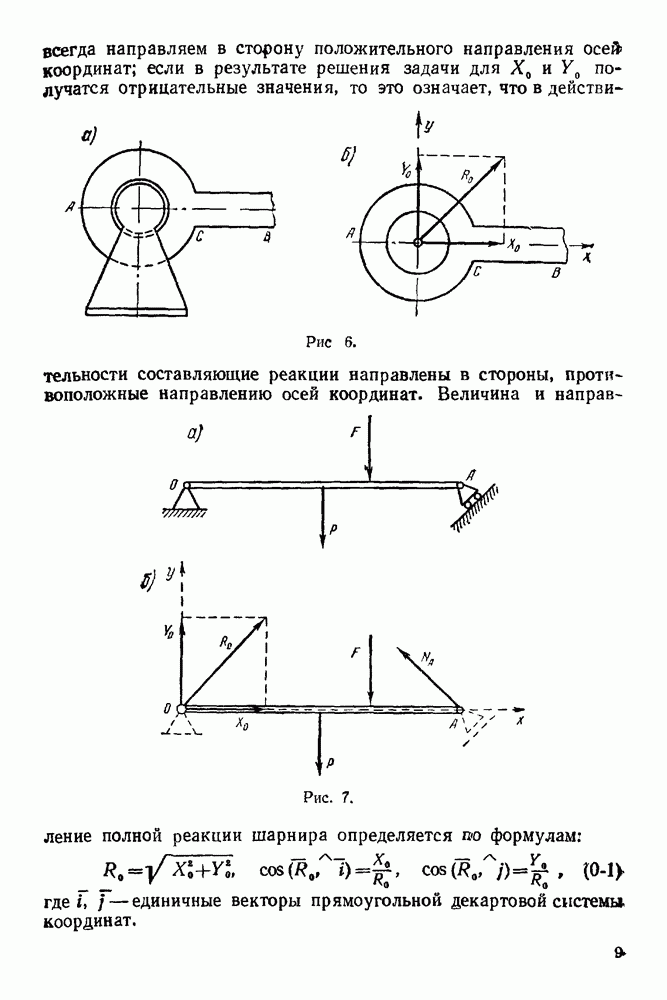
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
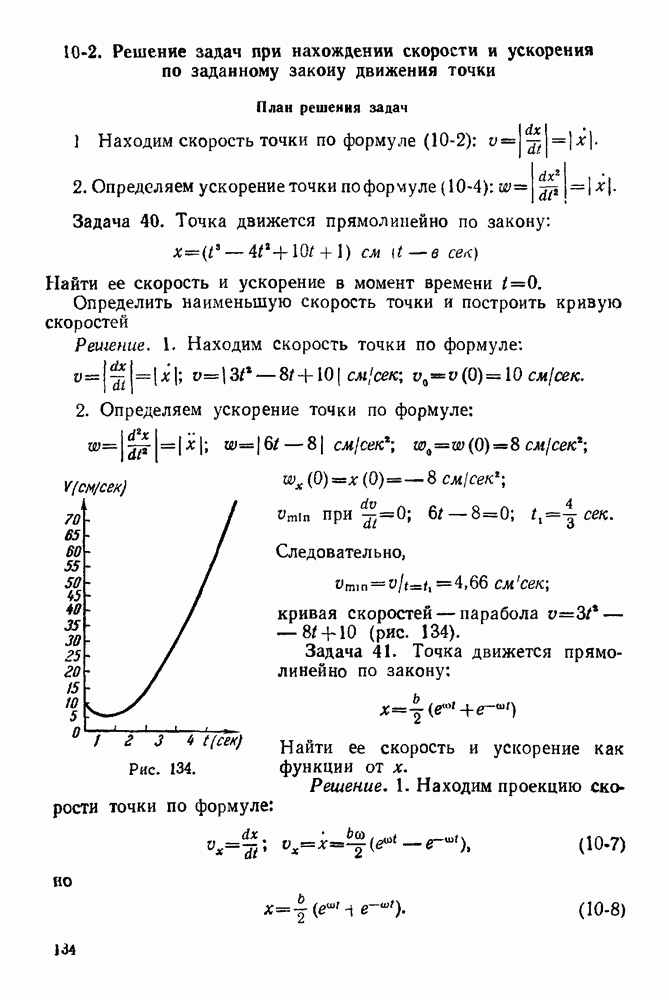
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
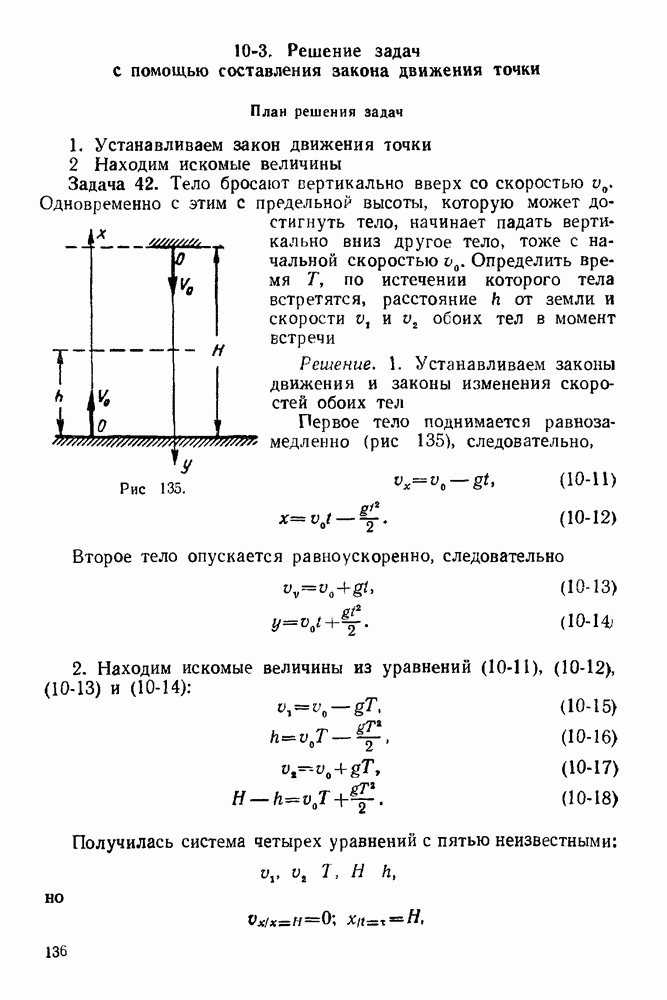
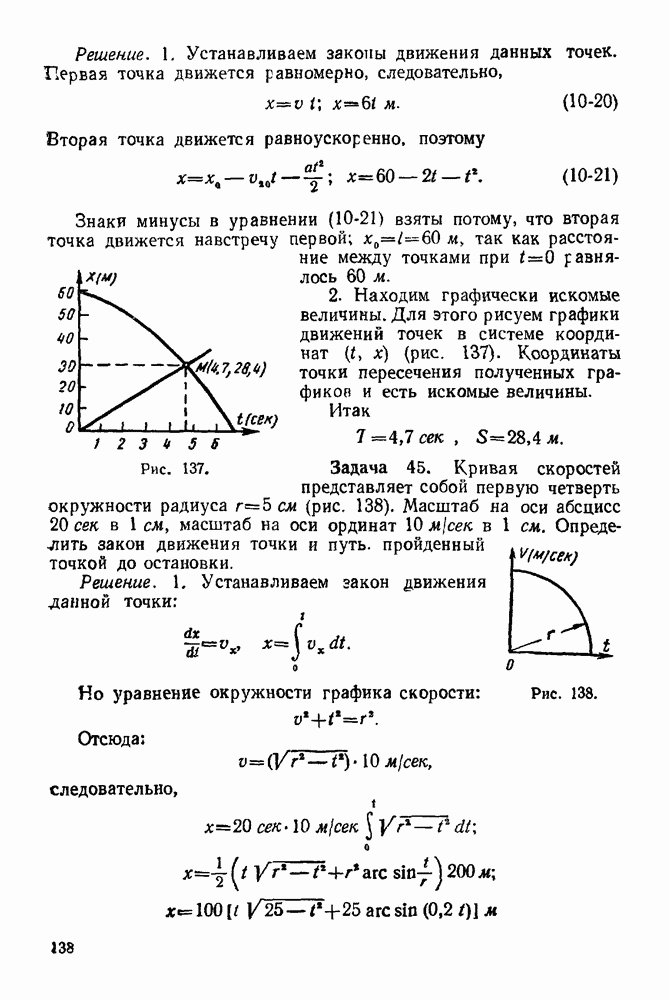
- 10-3. Решение задач с помощью составления закона движения точки
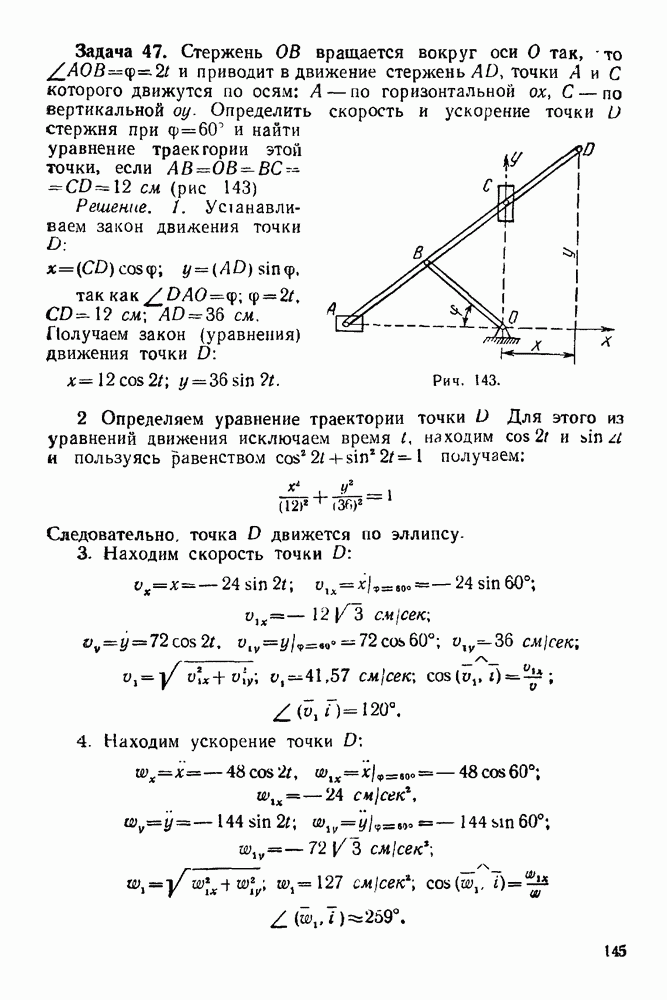
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
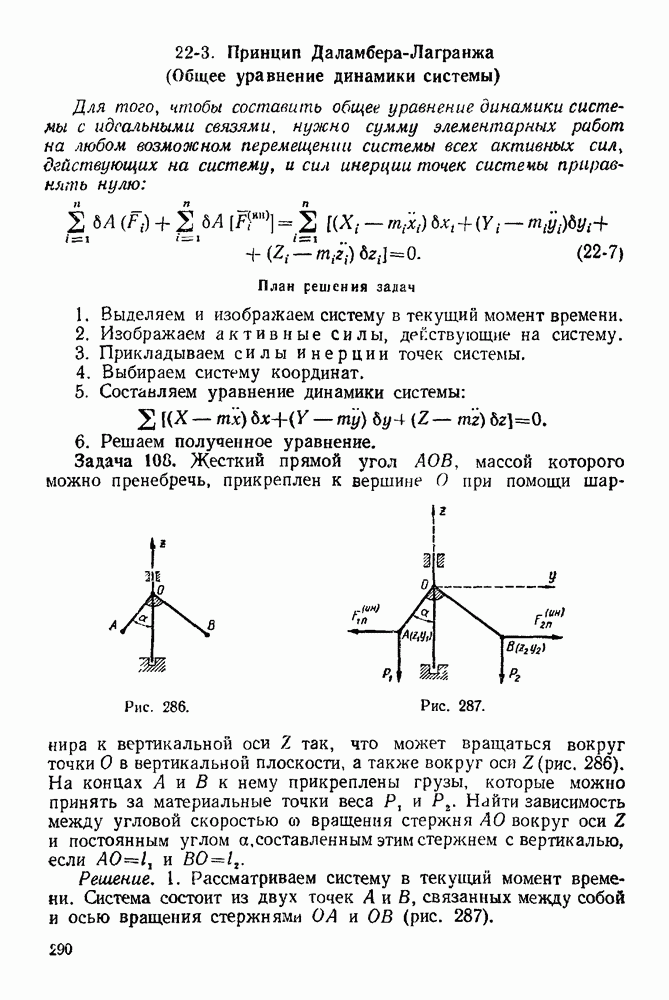
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР