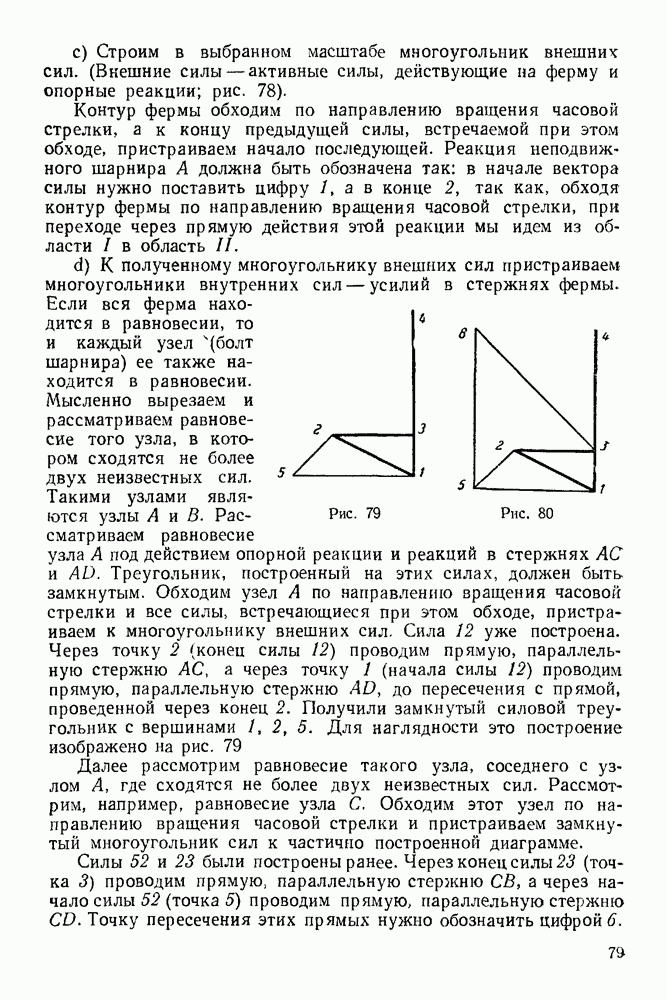
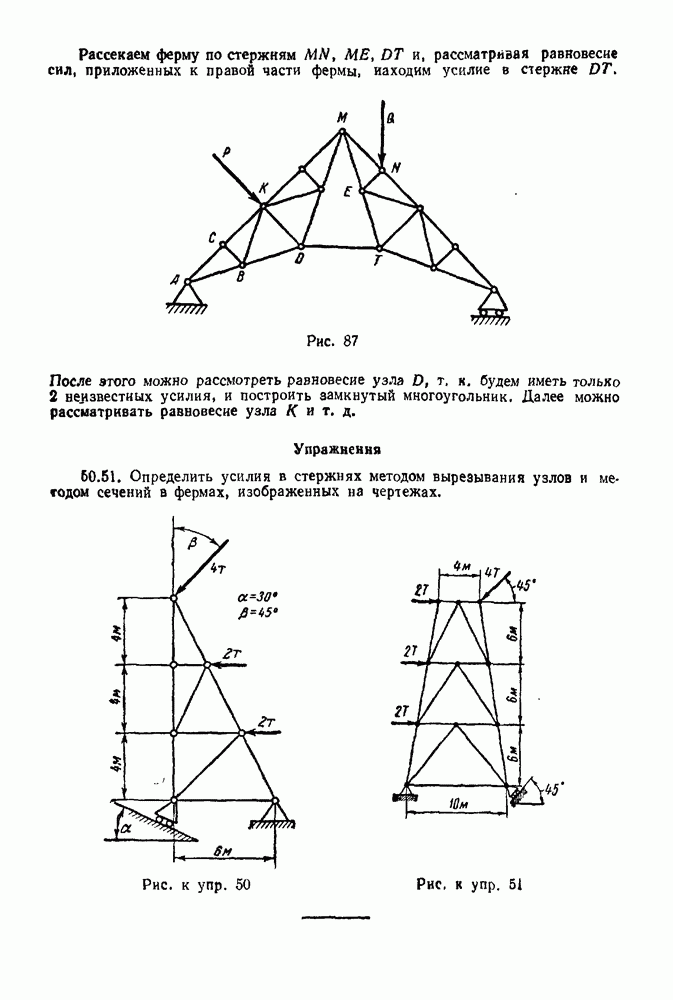
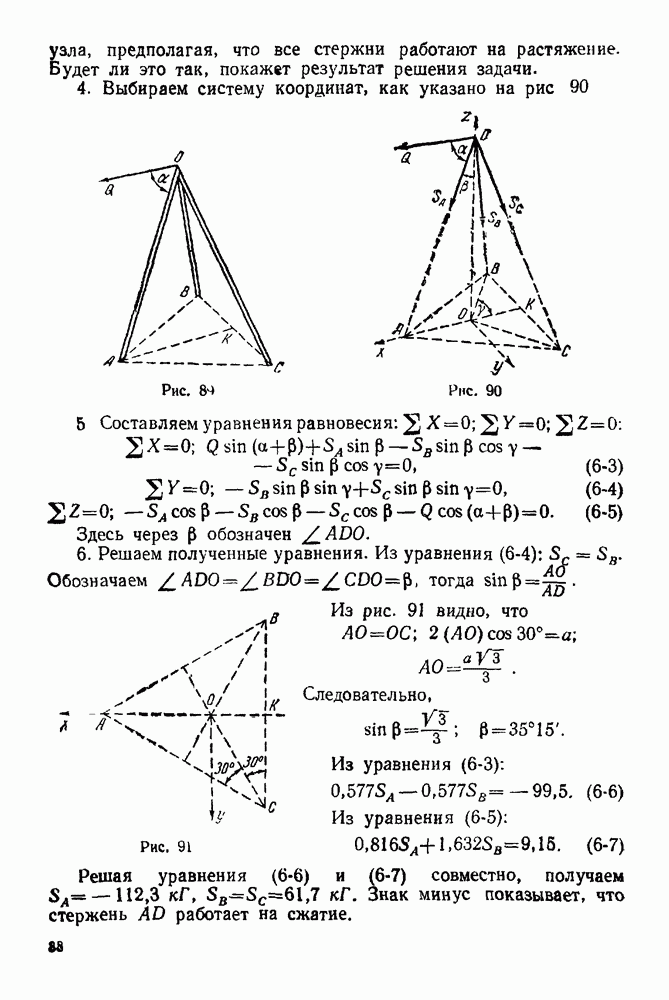
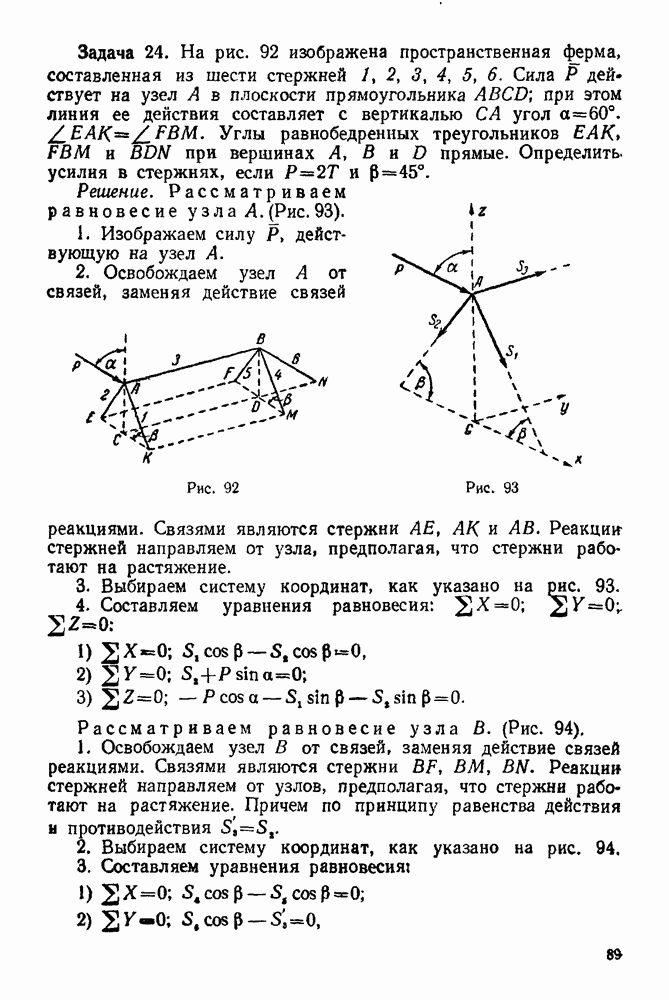
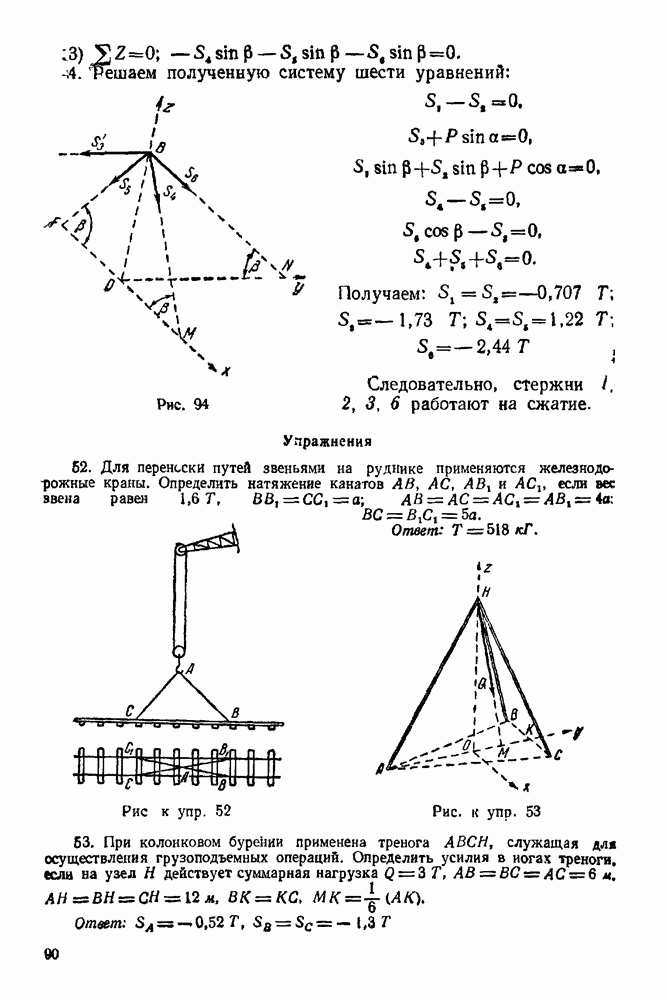
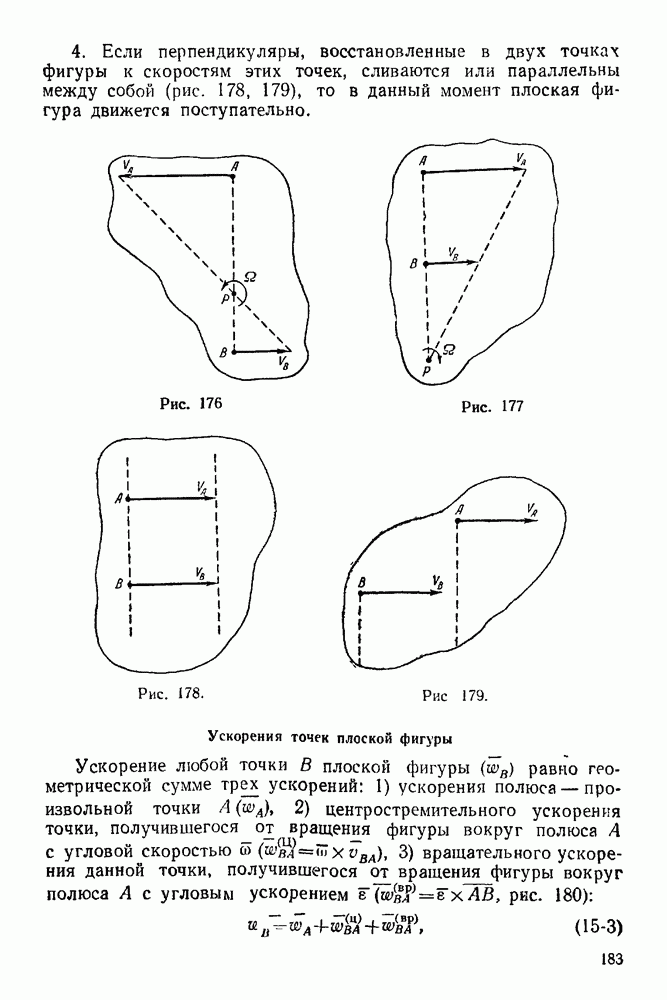
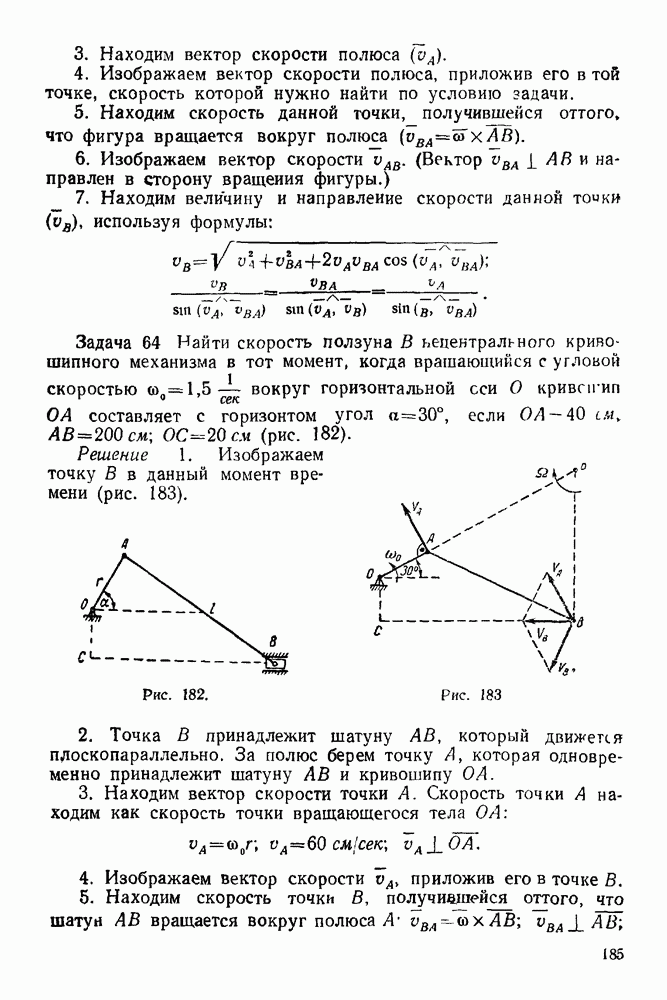
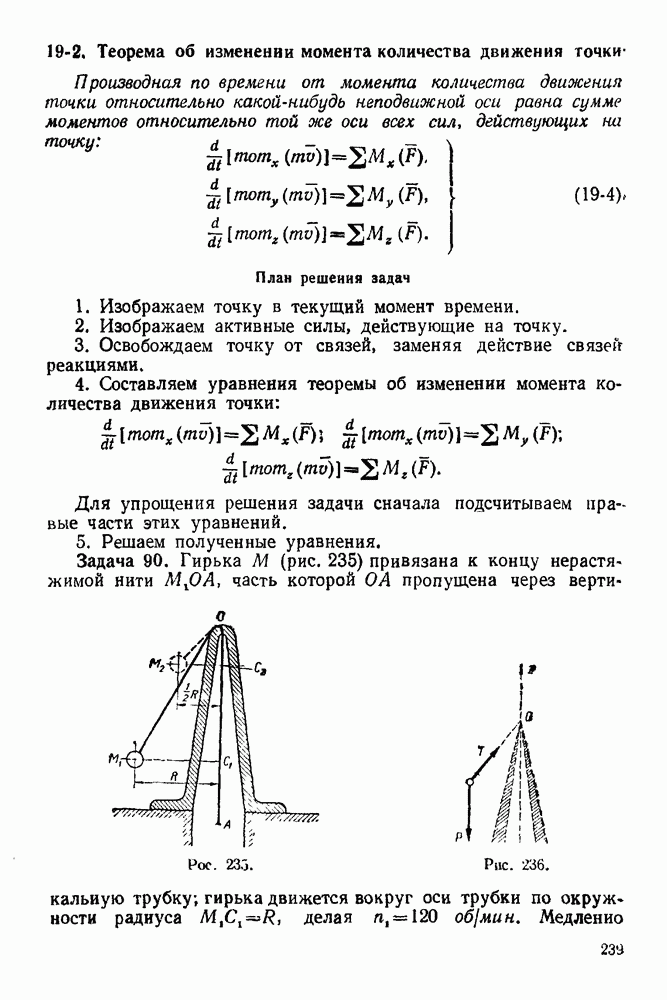
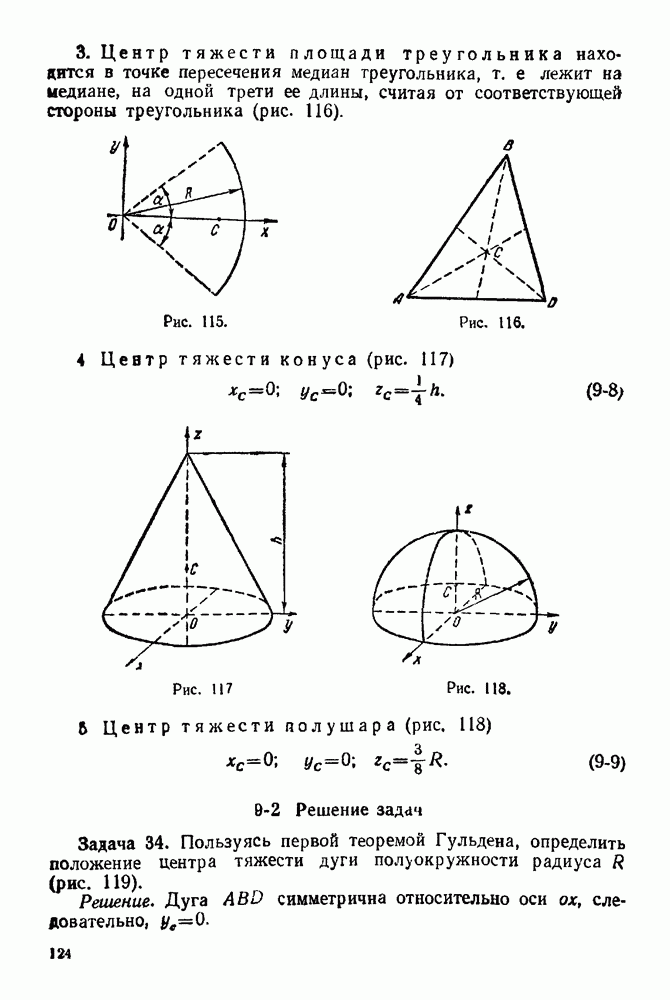| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
I. ПЛОСКАЯ СИСТЕМА СИЛ
ГЛАВА I. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
1-1. Равновесие трех сил
Рассмотрим равновесие тела под действием только трех сил, а затем перейдем к рассмотрению равновесия тела под действием какого угодно количества сил линии действия которых пересекаются в одной точке.
При решении задач на равновесие трех сил удобно пользоваться геометрическим способом, как наиболее наглядным.

Рис. 15
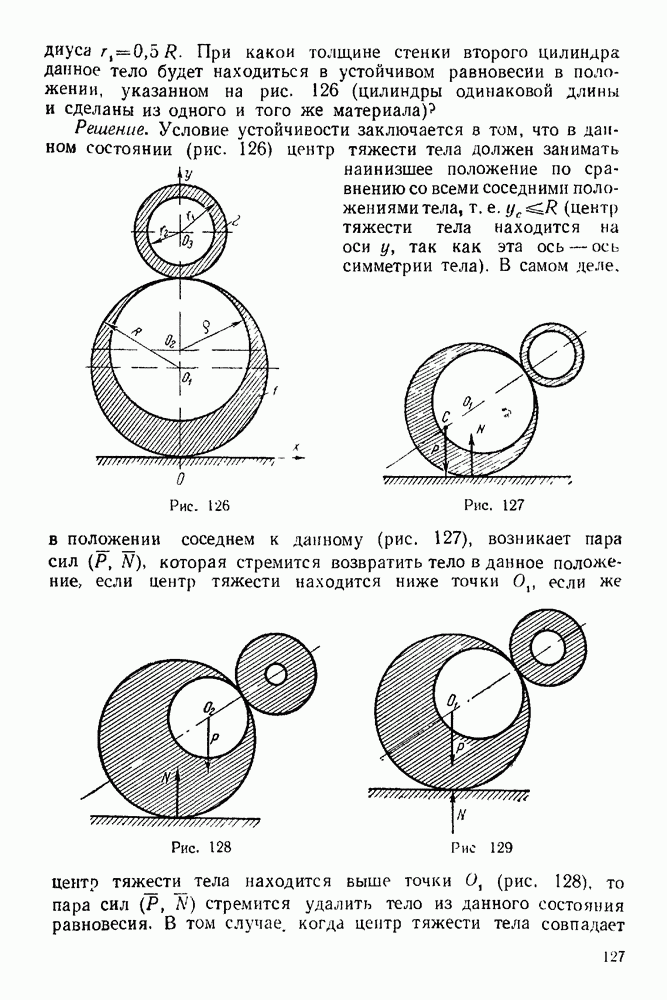
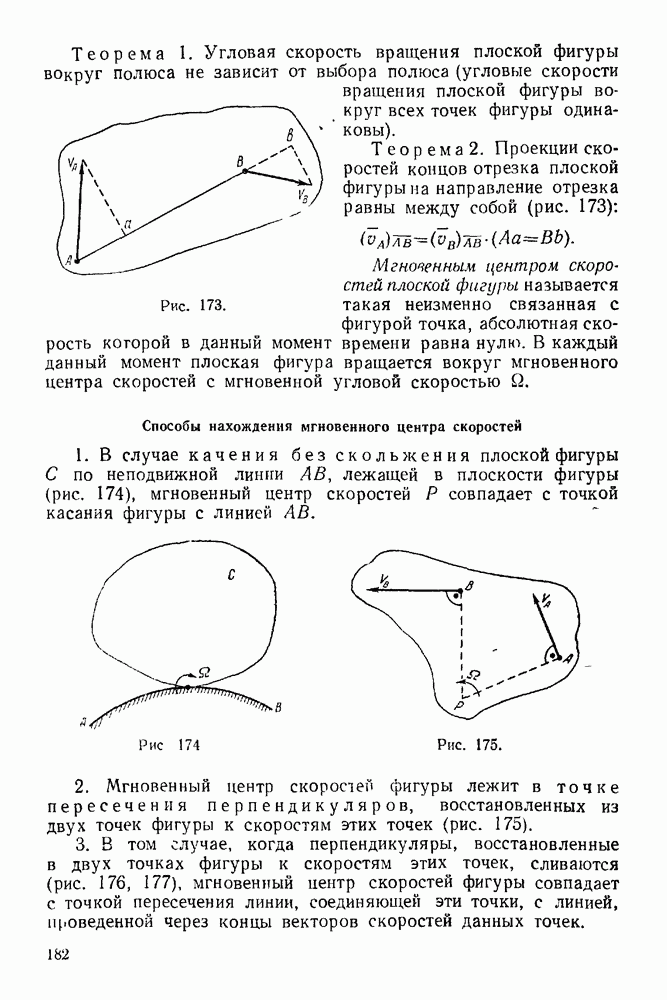
Для того, чтобы три силы, приложенные в одной точке твердого тела, находились в равновесии, необходимо и достаточно, чтобы силовой треугольник, построенный на этих силах, был замкнутым. Следует обратить внимание: что в замкнутом силовом треугольнике конец каждого предыдущего вектора совпадает с началом следующего (рис. 15), и на теорему о трех силах.
Если три непараллельные силы, лежащие в одной плоскости, уравновешиваются, то их линии действия пересекаются в одной точке.
План решения задач
При решении задач необходимо придерживаться следующего плана:
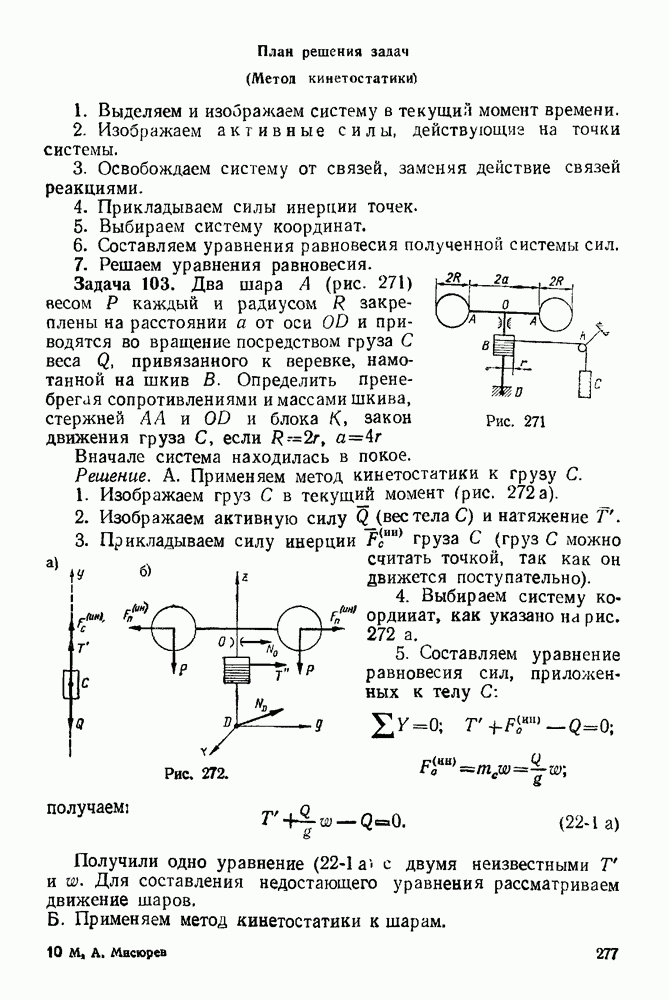
1 Выделяем материальную систему (тело или материальную частицу), равновесие которой следует рассмотреть. Такой
системой является то тело, к которому приложены заданные силы и искомые реакции.
2. Изображаем активную силу, действующую на материальную систему, равновесие которой рассматриваем.
3. Освобождаем эту систему от связен, заменяя действие связей реакциями.
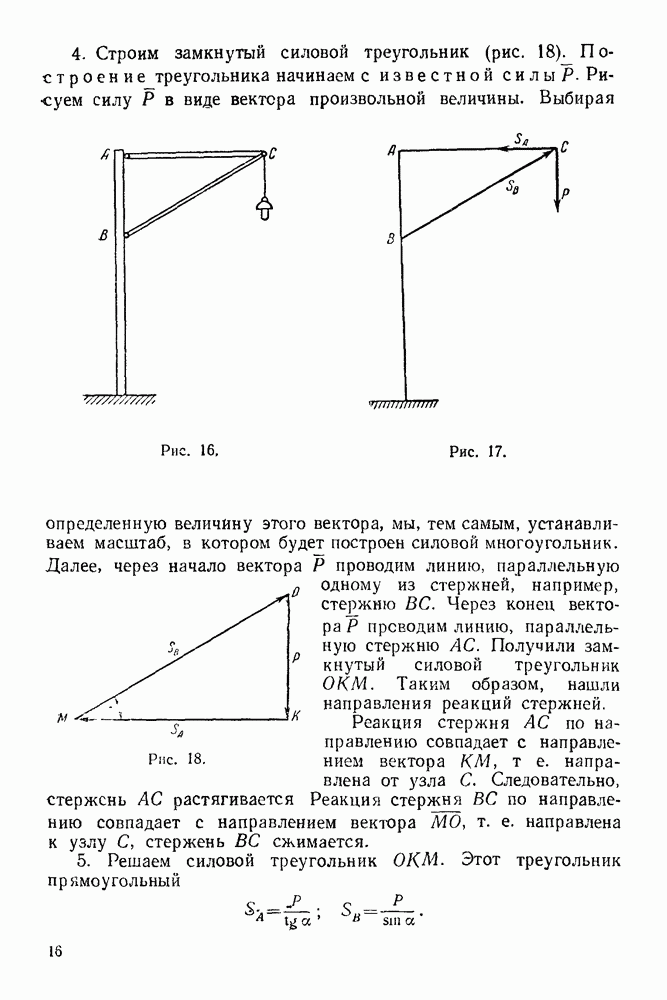
4. Строим замкнутый силовой треугольник. Построение замкнутого силового треугольника всегда начинаем с известной силы.
В том случае, когда возникают затруднения в выборе правильного направления реакции в ту или иную сторону (например, выбор направления реакции тонкого невесомого стержия), рекомендуется это направление установить из условия замкнутости силового треугольника и затем изобразить реакции на основном чертеже, с целью выяснения характера работы данного элемента конструкции (так, например, можно узнать, работает ли стержень на сжатие или растяжение).
5- Решаем силовой треугольник. По известным элементам треугольника находим его неизвестные элементы.
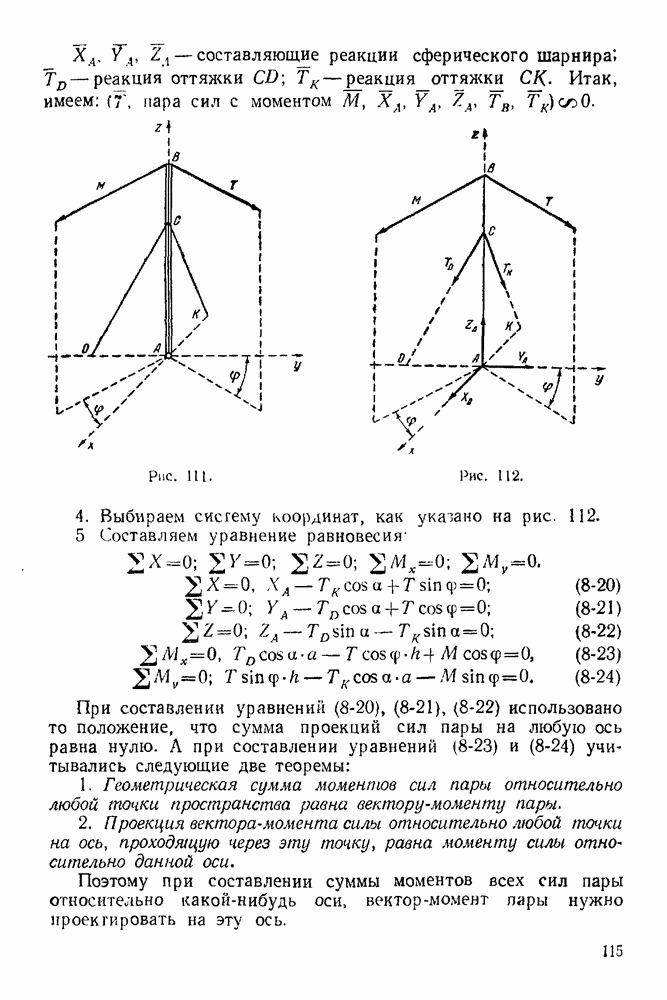
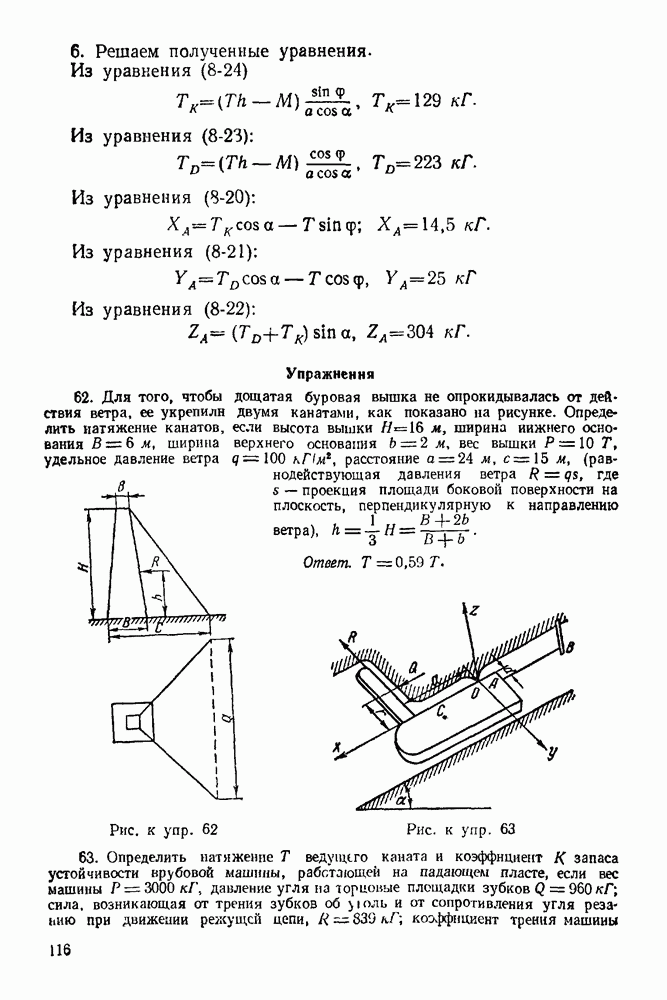
Если силовой треугольник косоугольный, то при решении используется теорема синусов. Иногда выгодно использовать условие пропорциональности сторон двух подобных треугольников (силового и треугольника на основном чертеже).
Для удобства рекомендуется получить решение задачи, если это не усложняет решение, в алгебраическом (общем) виде, проверить правильность полученных формул по размерностям всех слагаемых (размерности всех слагаемых должны быть одинаковыми). Затем необходимо выбрать систему единиц, в которой нужно получить ответ, и все данные, перед подстановкой их в полученные формулы, перевести в эту систему. Большинство задач надо решать с точностью до трехзначных цифр (точность логарифмической линейки). У полученного численного результата нужно писать наименование.
1-2. Решение задач
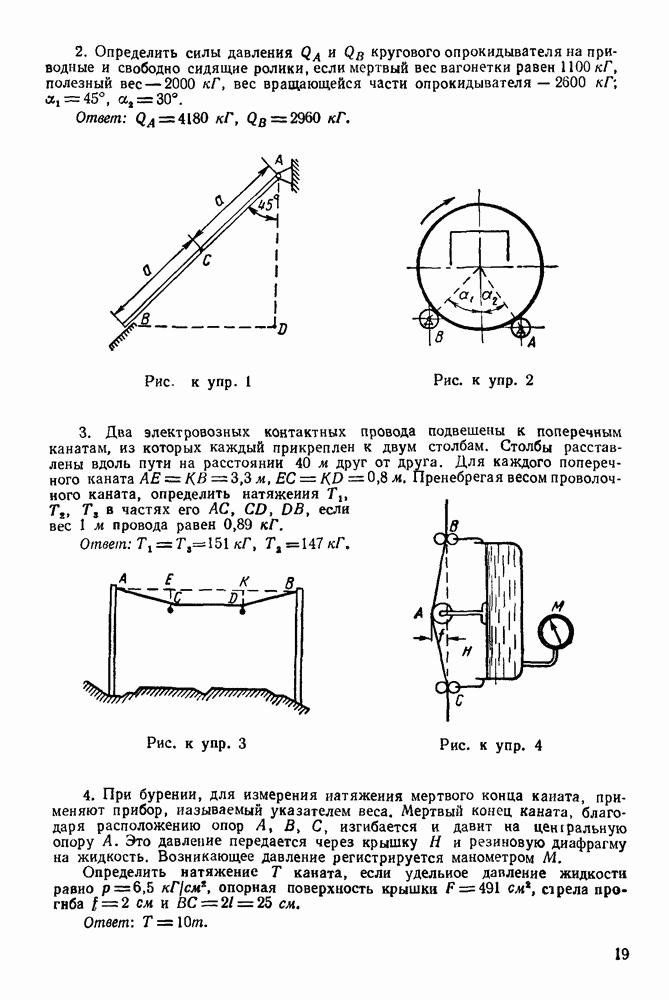
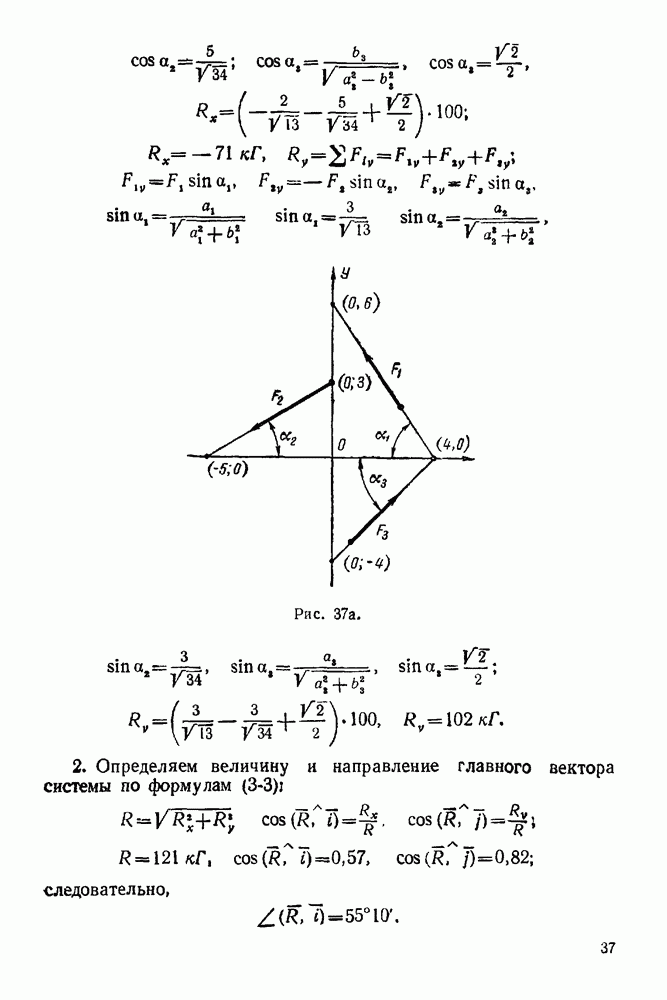
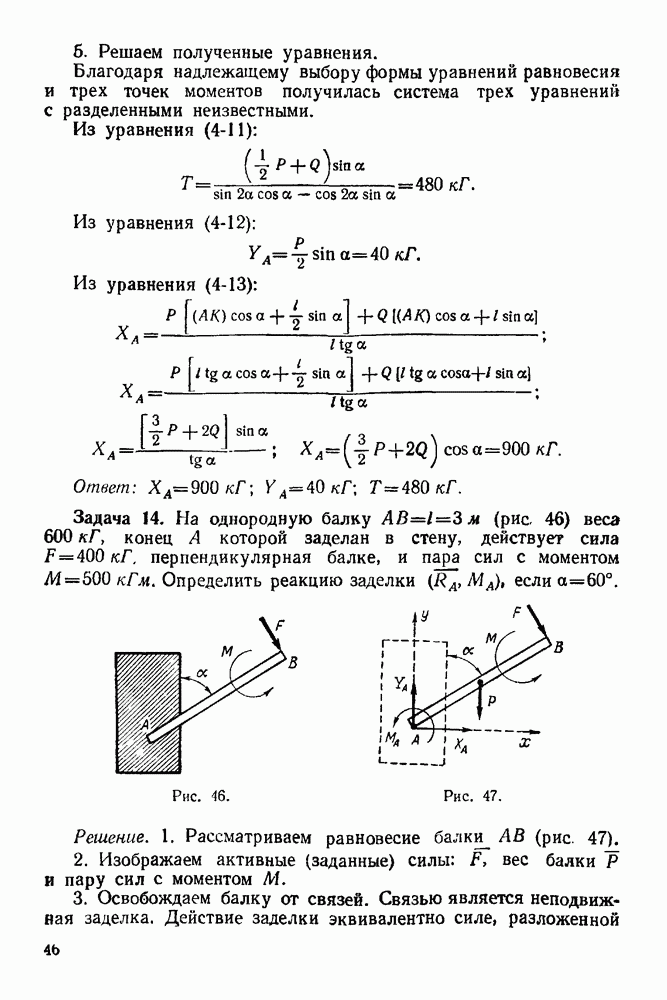
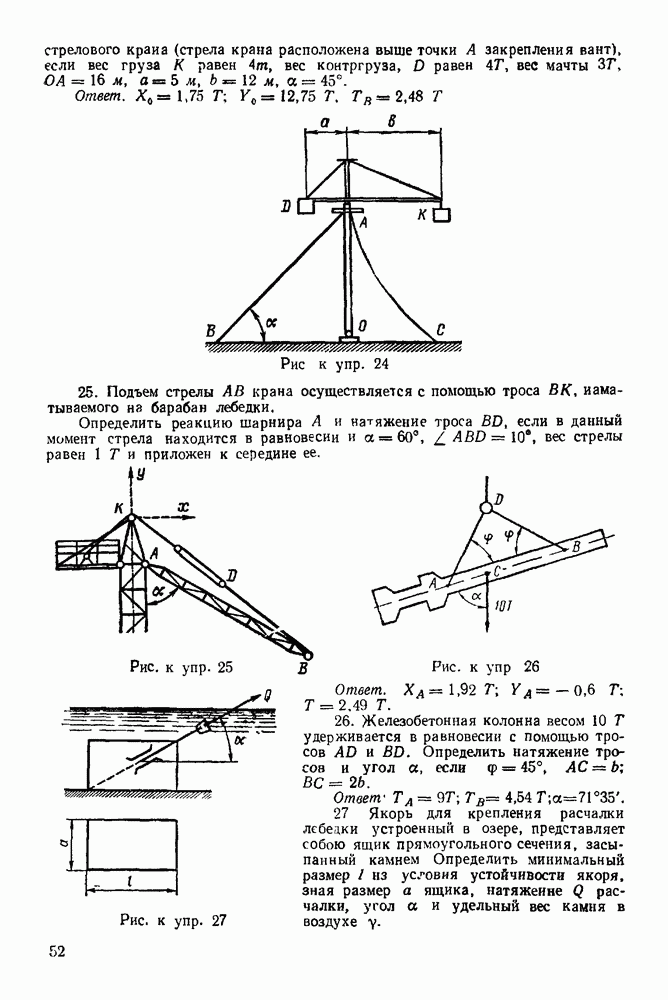
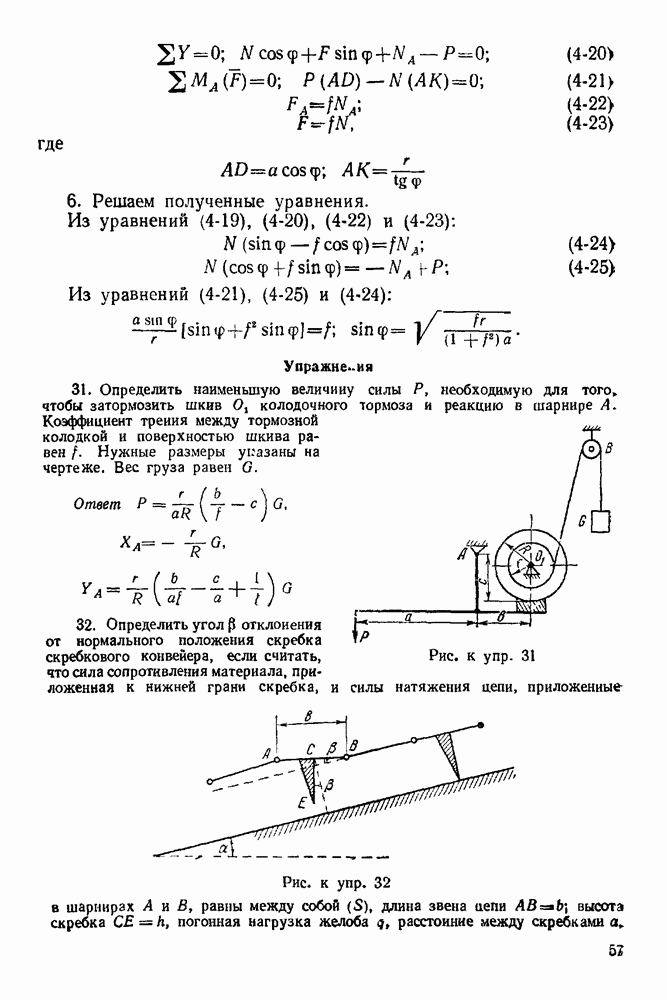
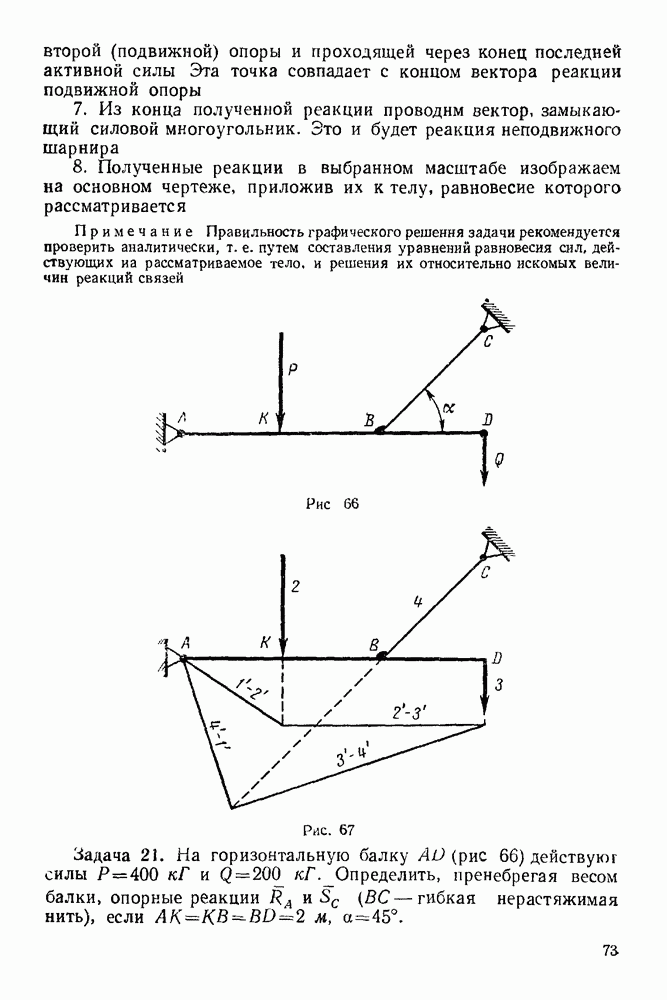
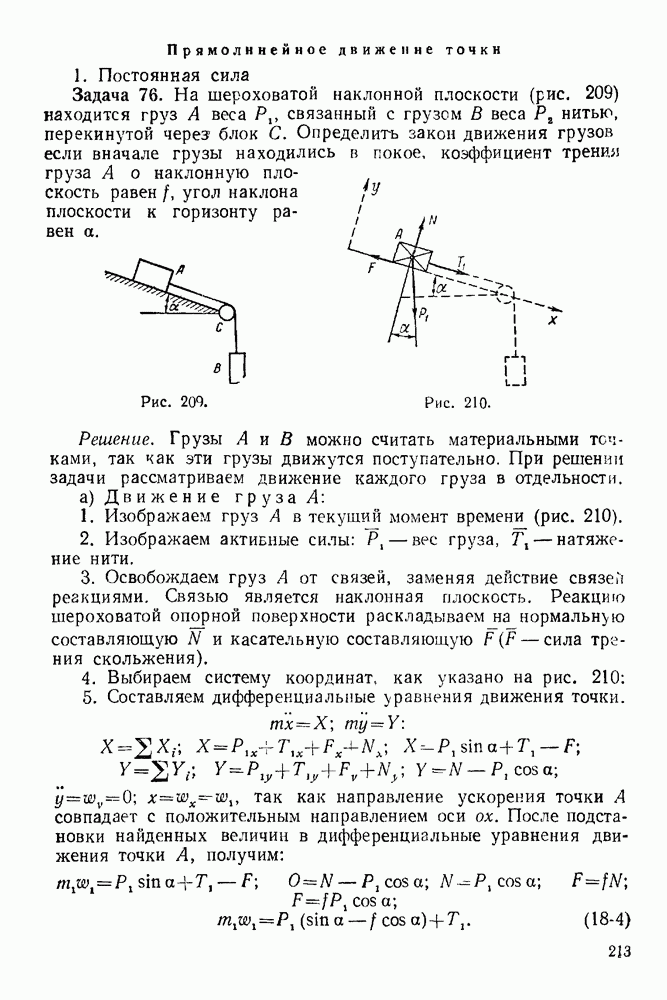
Задача 1. Уличный фонарь (рис. 16) весом  подвешен к столбу с горизонтальной поперечиной
подвешен к столбу с горизонтальной поперечиной  и подкосом
и подкосом  Найти усилия и
Найти усилия и  в стержнях
в стержнях  и
и  считая крепления в точках
считая крепления в точках  шарнирными.
шарнирными.
Решение 1. Рассматриваем равновесие узла С (болт шарнира С).
2. Изображаем активную силу  действующую на узел С.
действующую на узел С.
3. Освобождаем узел С от связей, наложенных на него Связями являются стержни  и
и  Реакции стержней лежат на осях стержней (рис. 17). Направление реакций найдем из. силового треугольника.
Реакции стержней лежат на осях стержней (рис. 17). Направление реакций найдем из. силового треугольника.
4. Строим замкнутый силовой треугольник (рис. Построение треугольника начинаем с известной силы  Рисуем силу
Рисуем силу  в виде вектора произвольной величины.
в виде вектора произвольной величины.

Рис. 16.

Рис. 17.
Выбирая определенную величину этого вектора, мы, тем самым, устанавливаем масштаб, в котором будет построен силовой многоугольник. Далее, через начало вектора  проводим линию, параллельную одному из стержней, например, стержню
проводим линию, параллельную одному из стержней, например, стержню  Через конец вектора
Через конец вектора  проводим линию, параллельную стержню
проводим линию, параллельную стержню  Получили замкнутый силовой треугольник
Получили замкнутый силовой треугольник  Таким образом, нашли направления реакций стержней.
Таким образом, нашли направления реакций стержней.

Рис. 18.
Реакция стержня  по направлению совпадает с направлением вектора
по направлению совпадает с направлением вектора  направлена от узла С. Следовательно, стержень
направлена от узла С. Следовательно, стержень  растягивается Реакция стержня
растягивается Реакция стержня  по направлению совпадает с направлением вектора
по направлению совпадает с направлением вектора  т. е. направлена к узлу С, стержень
т. е. направлена к узлу С, стержень  сжимается.
сжимается.
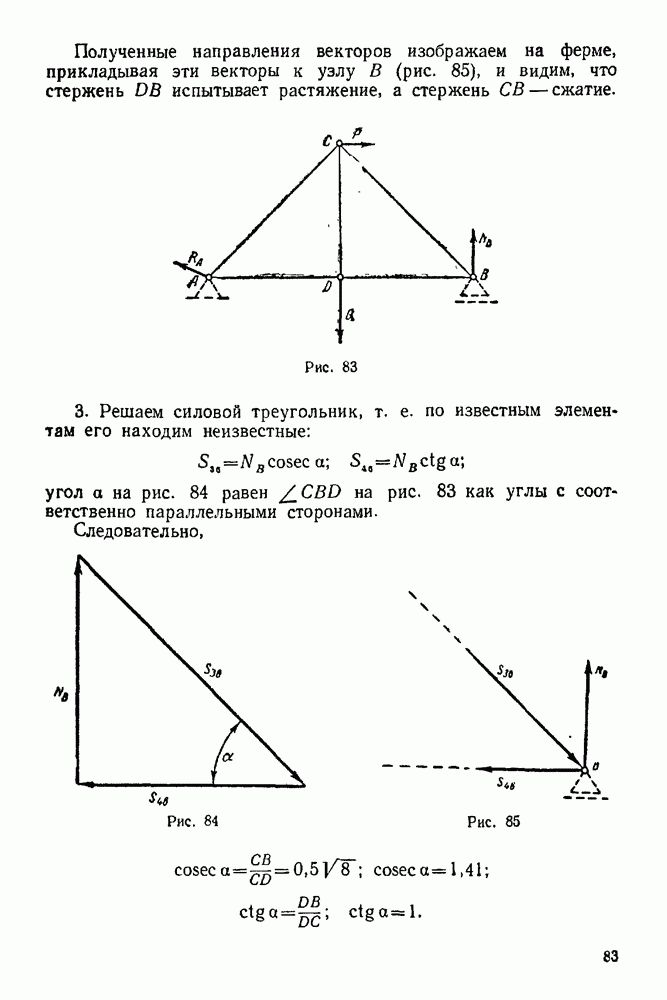
5. Решаем силовой треугольник  Этот треугольник прямоугольный
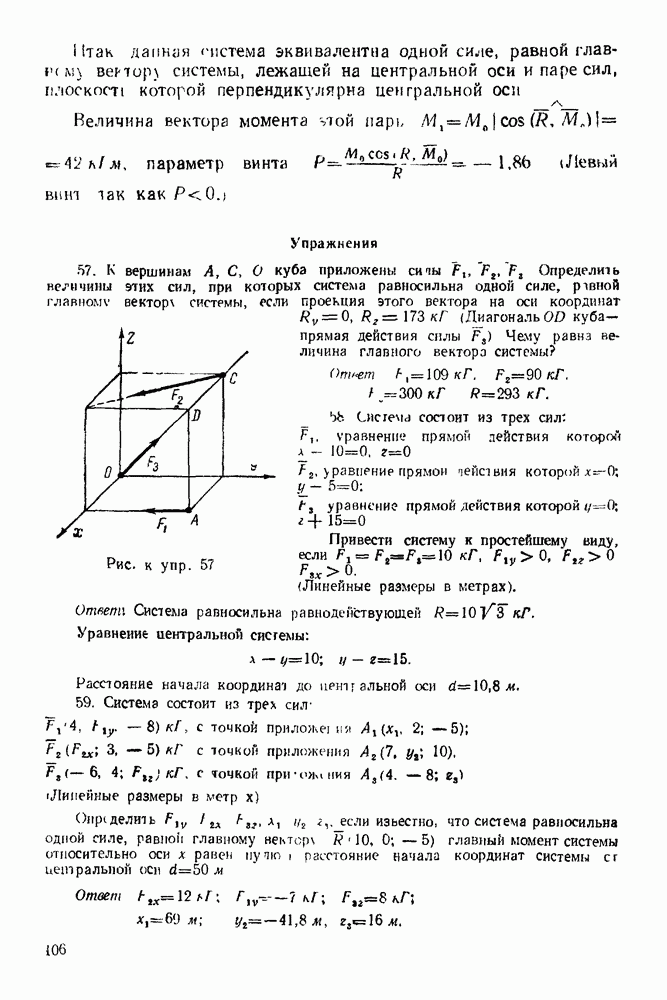
Этот треугольник прямоугольный

Но  как углы с соответственно параллельными сторонами. Поэтому
как углы с соответственно параллельными сторонами. Поэтому

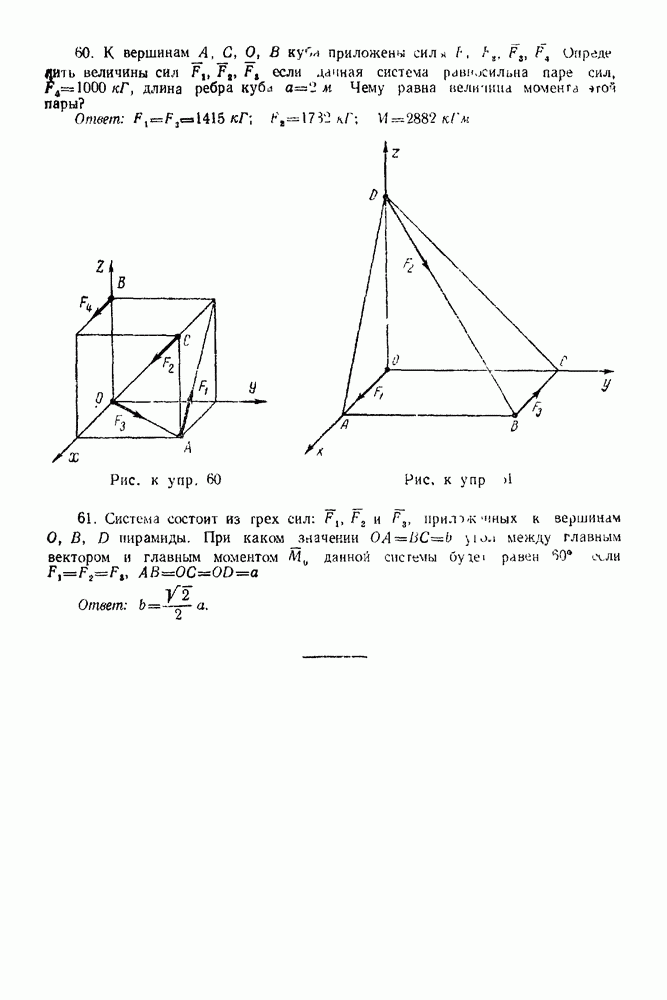
Следовательно.

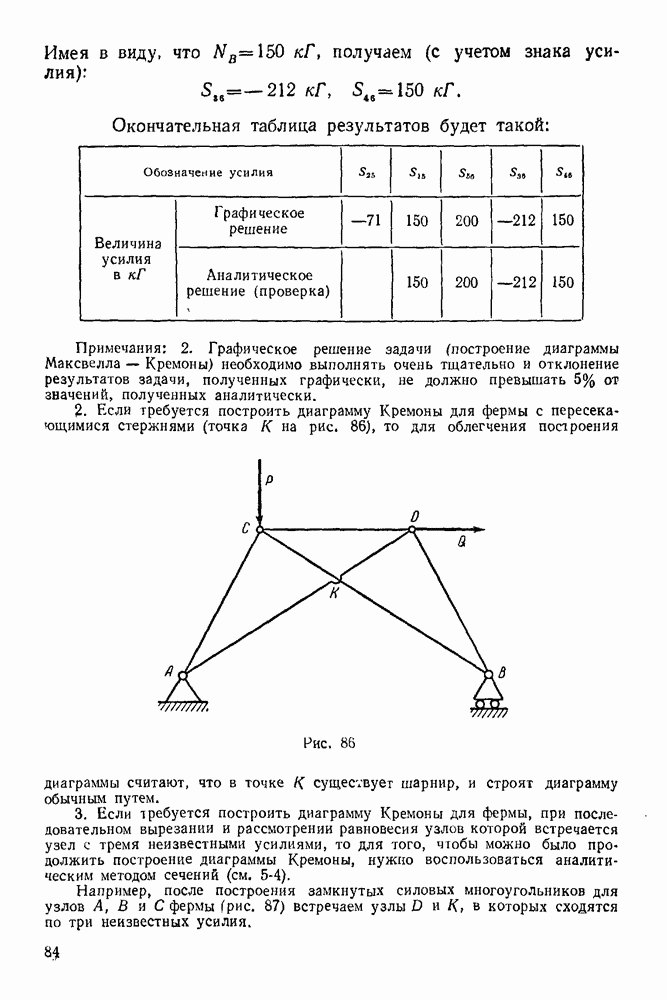
Принято сжимающее усилие в стержне выражать отрицательным числом, а растягивающее — положительным.
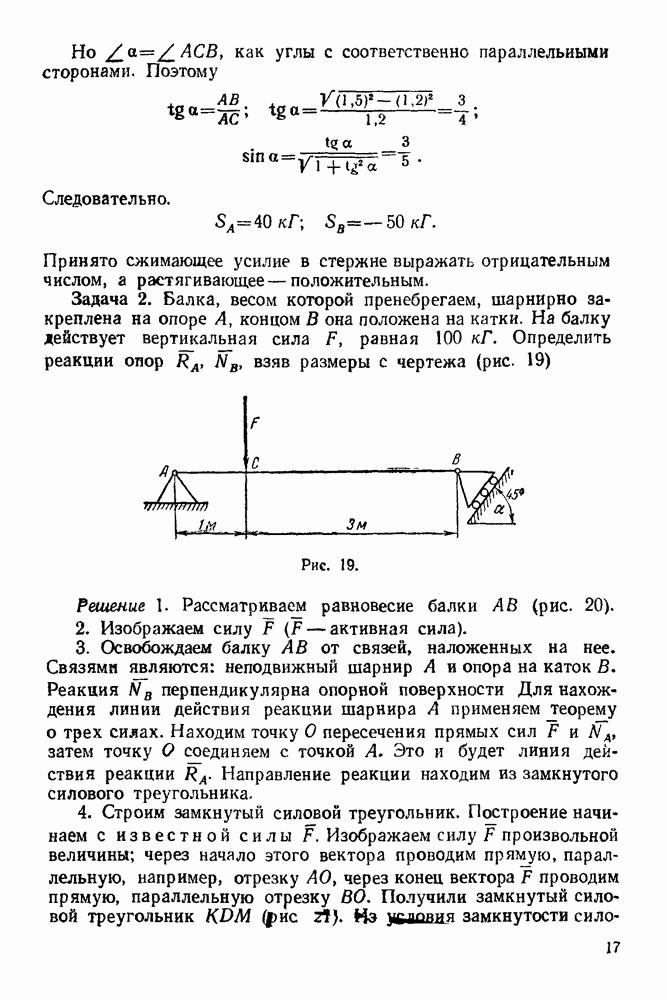
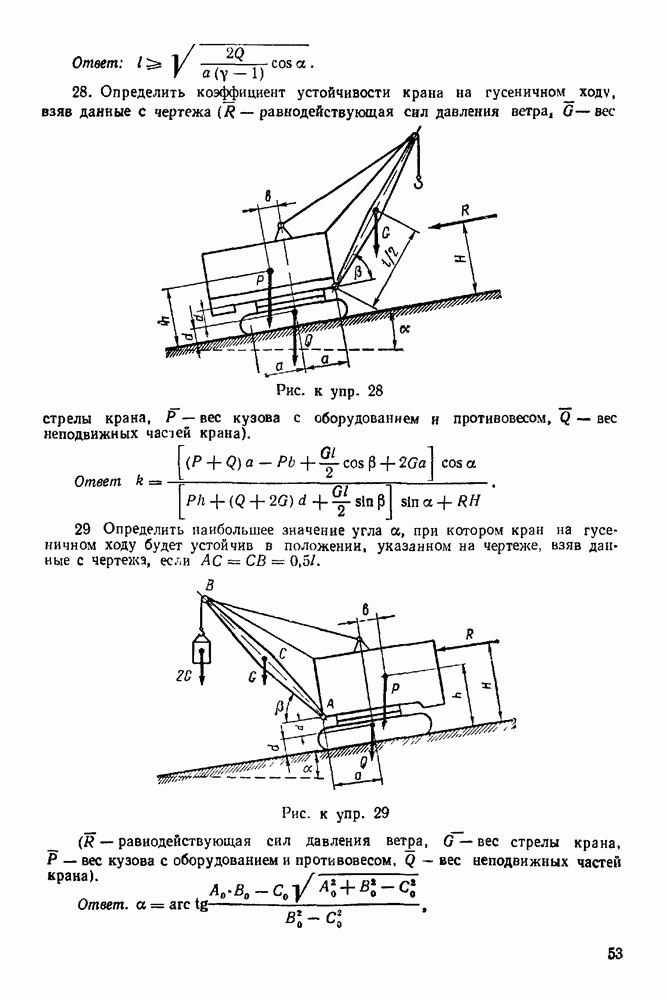
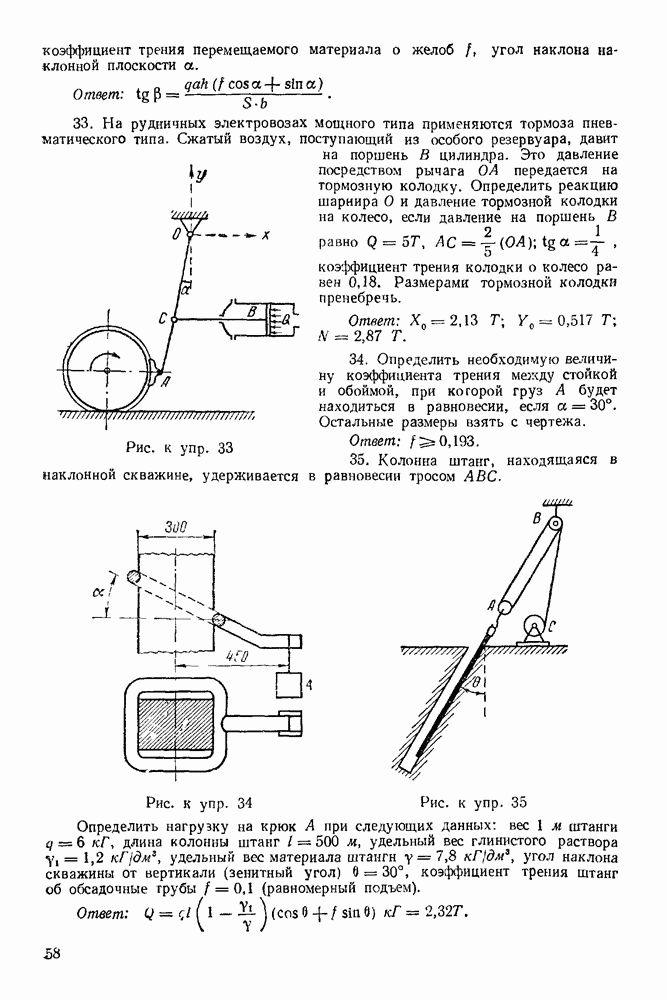
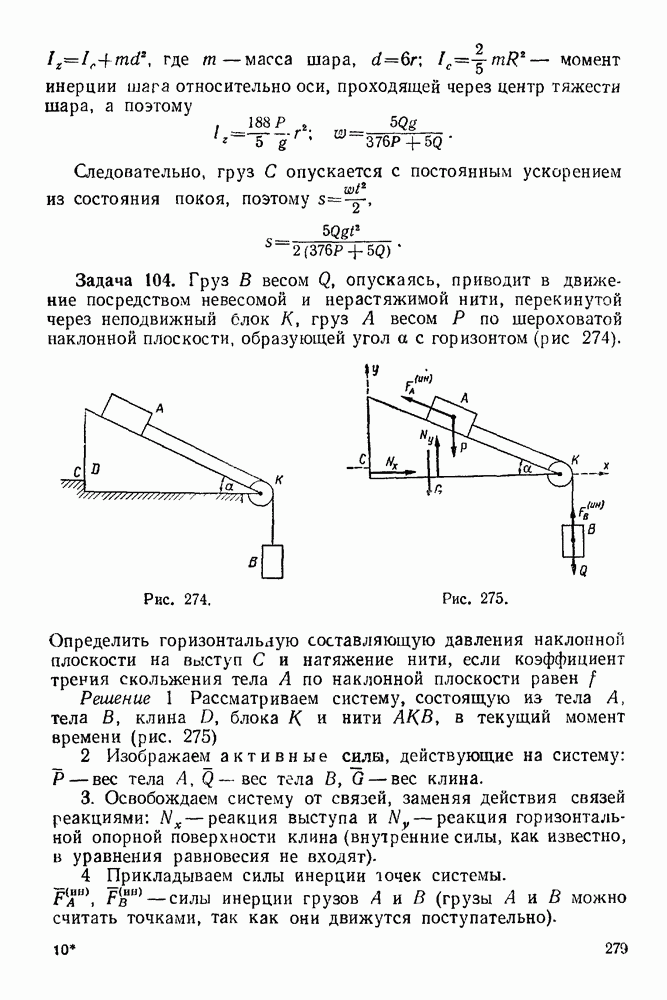
Задача 2. Балка, весом которой пренебрегаем, шарнирно закреплена на опоре А, концом В она положена на катки. На балку действует вертикальная сила  равная
равная  Определить реакции опор
Определить реакции опор  взяв размеры с чертежа (рис. 19)
взяв размеры с чертежа (рис. 19)

Рис. 19.
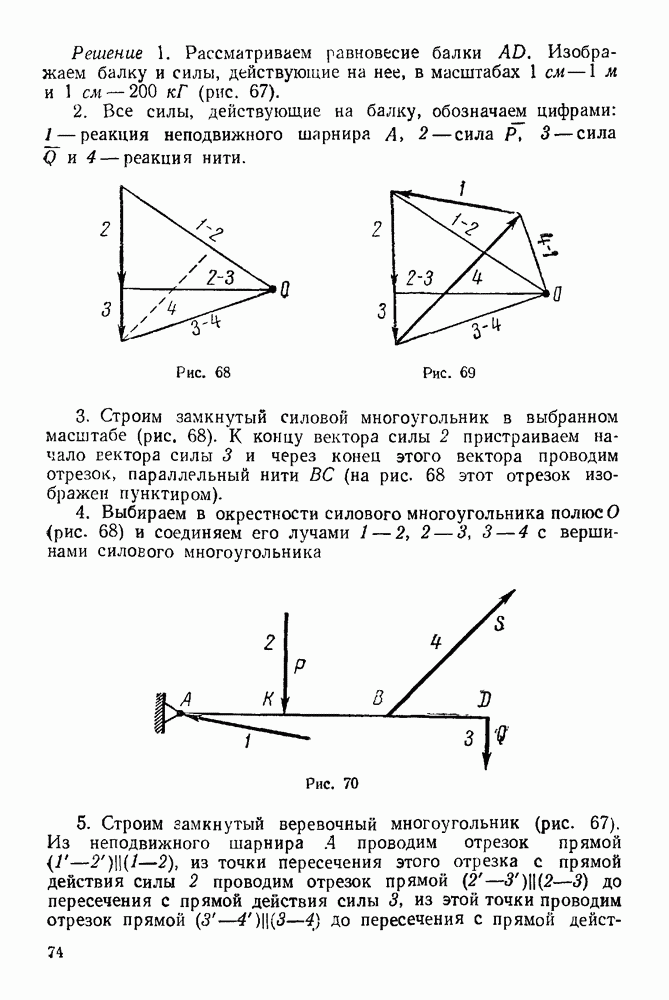
Решение 1. Рассматриваем равновесие балки  (рис. 20).
(рис. 20).
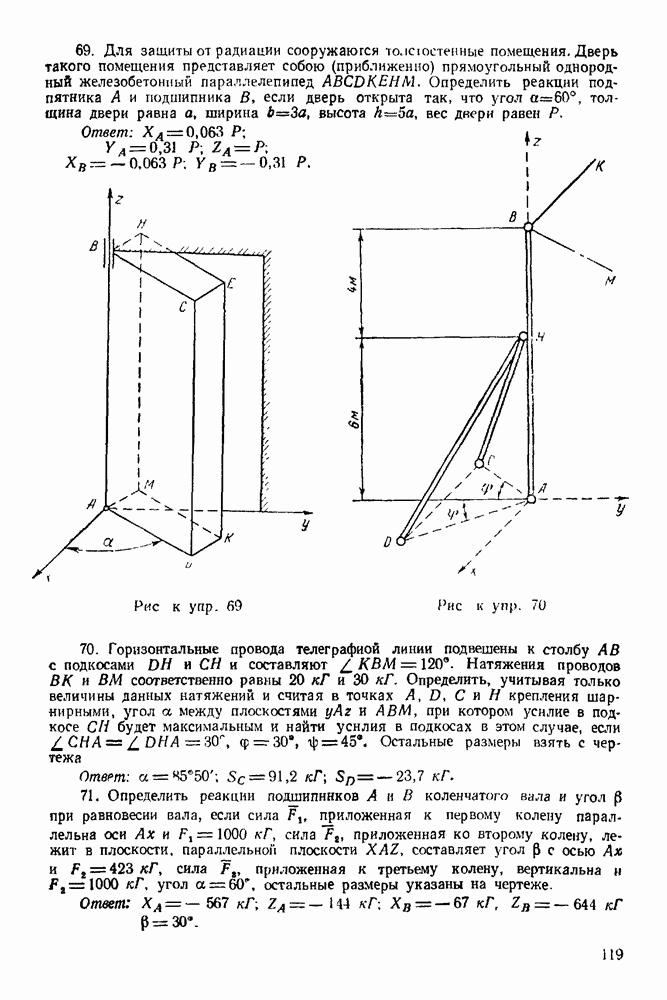
2. Изображаем силу  активная сила).
активная сила).
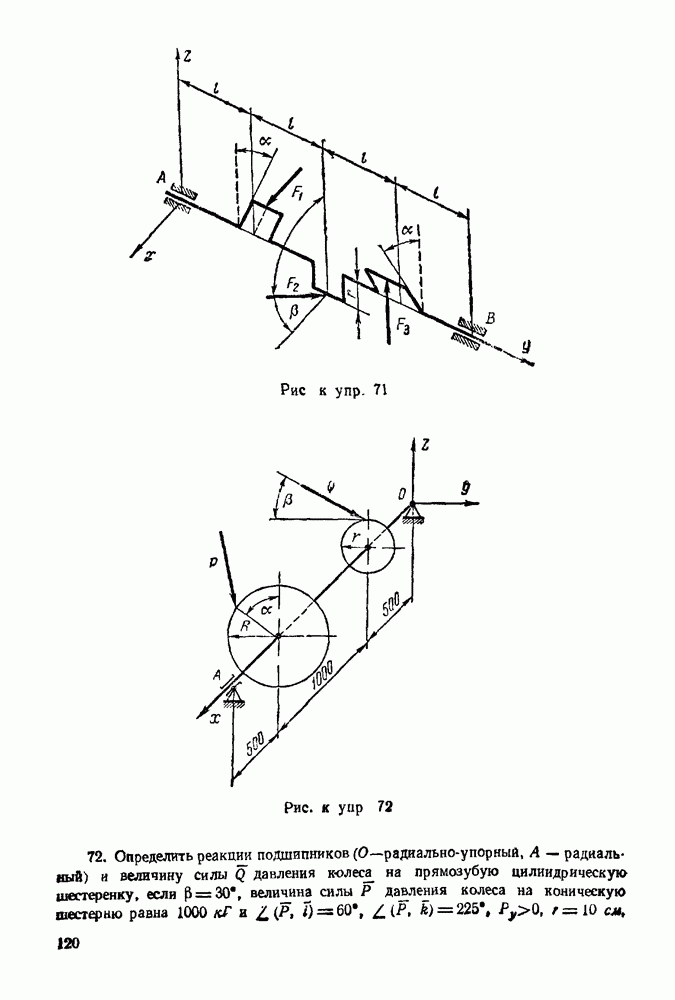
3. Освобождаем балку  от связей, наложенных на нее. Связями являются: неподвижный шарнир А и опора на каток В. Реакция
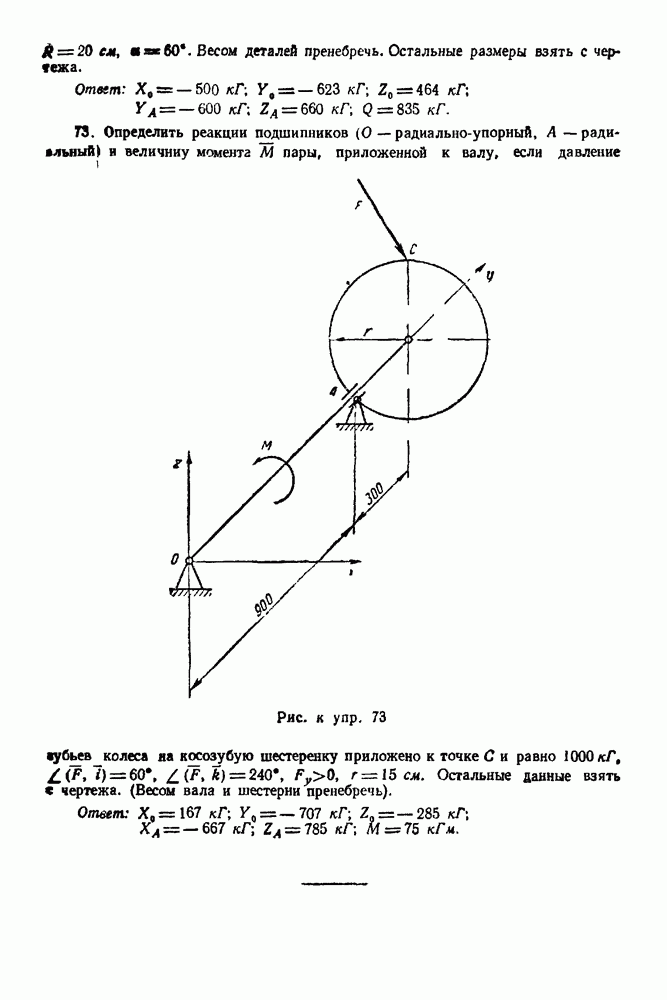
от связей, наложенных на нее. Связями являются: неподвижный шарнир А и опора на каток В. Реакция  перпендикулярна опорной поверхности Для нахождения линии действия реакции шарнира А применяем теорему о трех силах. Находим точку О пересечения прямых сил
перпендикулярна опорной поверхности Для нахождения линии действия реакции шарнира А применяем теорему о трех силах. Находим точку О пересечения прямых сил  , затем точку О соединяем с точкой А. Это и будет линия действия реакции
, затем точку О соединяем с точкой А. Это и будет линия действия реакции  Направление реакции находим из замкнутого силового треугольника.
Направление реакции находим из замкнутого силового треугольника.
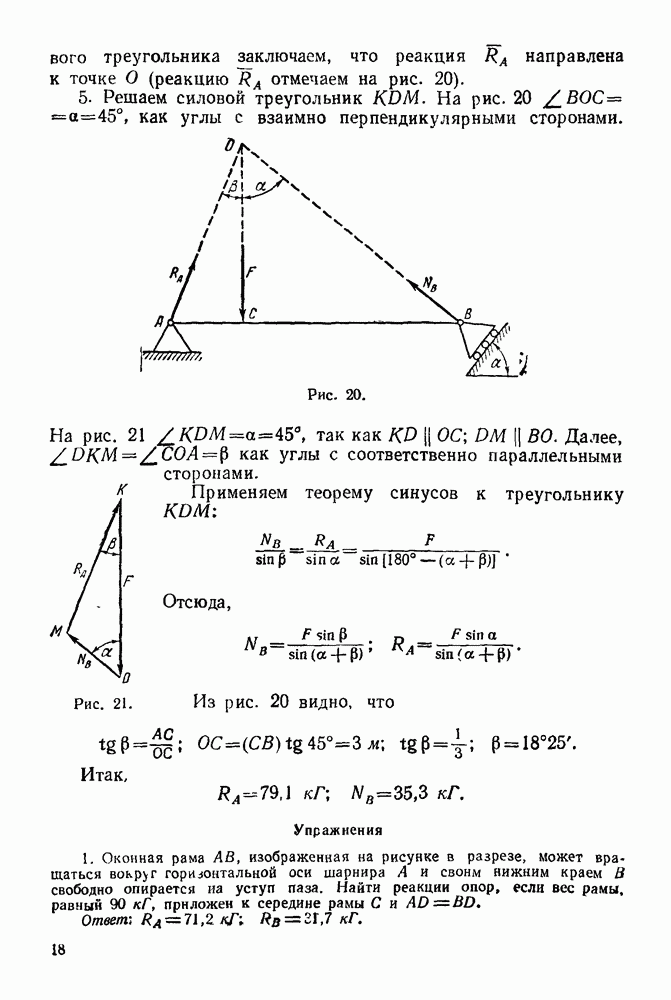
4. Строим замкнутый силовой треугольник. Построение начинаем с известной силы  Изображаем силу
Изображаем силу  произвольной величины; через начало этого вектора проводим прямую, параллельную, например, отрезку
произвольной величины; через начало этого вектора проводим прямую, параллельную, например, отрезку  через конец вектора
через конец вектора  проводим прямую, параллельную отрезку
проводим прямую, параллельную отрезку  Получили замкнутый силовой треугольник
Получили замкнутый силовой треугольник  (рис. 21). Из условия замкнутости
(рис. 21). Из условия замкнутости
вого треугольника заключаем, что реакция  направлена к точке О (реакцию
направлена к точке О (реакцию  отмечаем на рис. 20).
отмечаем на рис. 20).
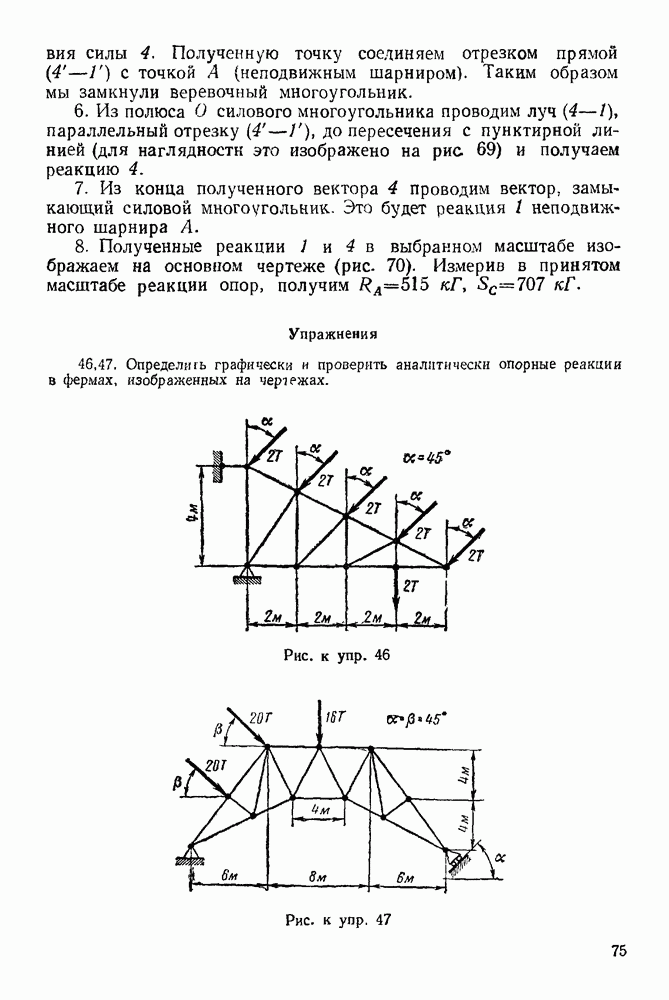
5. Решаем силовой треугольник  На рис.
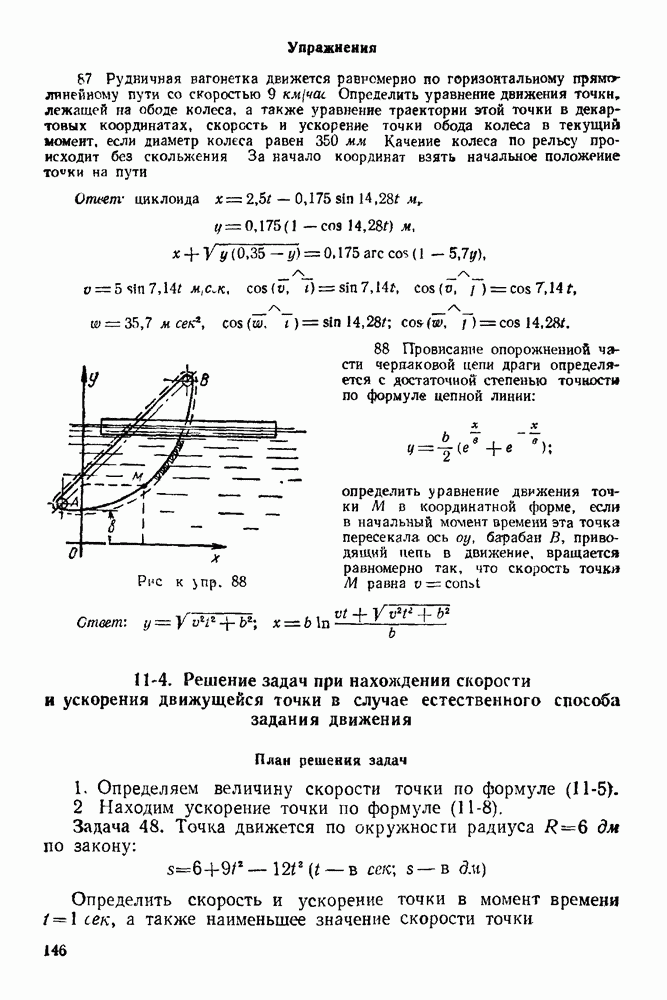
На рис.  как углы с взаимно перпендикулярными сторонами.
как углы с взаимно перпендикулярными сторонами.

Рис. 20.

Рис. 21.
На рис. 21  , так как
, так как  Далее, как углы с соответственно параллельными сторонами.
Далее, как углы с соответственно параллельными сторонами.
Применяем теорему синусов к треугольнику 

Отсюда,

Из рис. 20 видно, что

Итак,

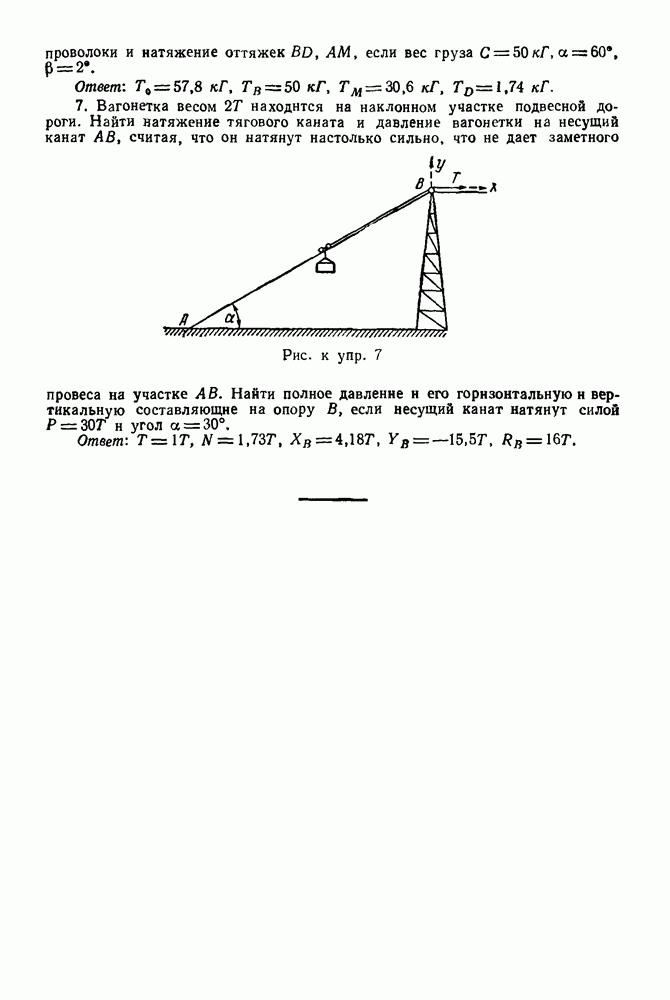
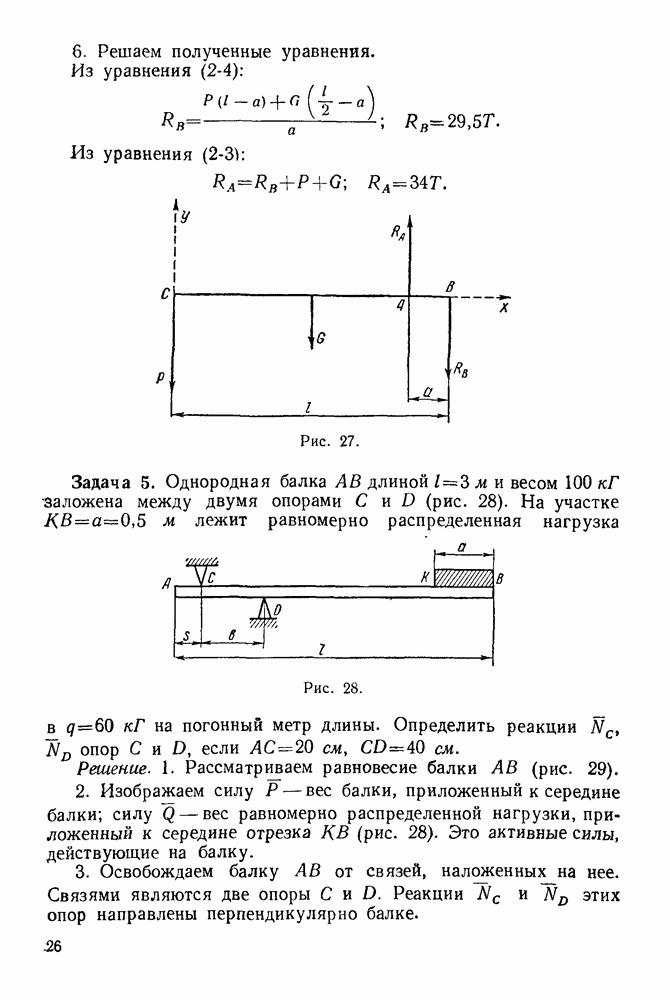
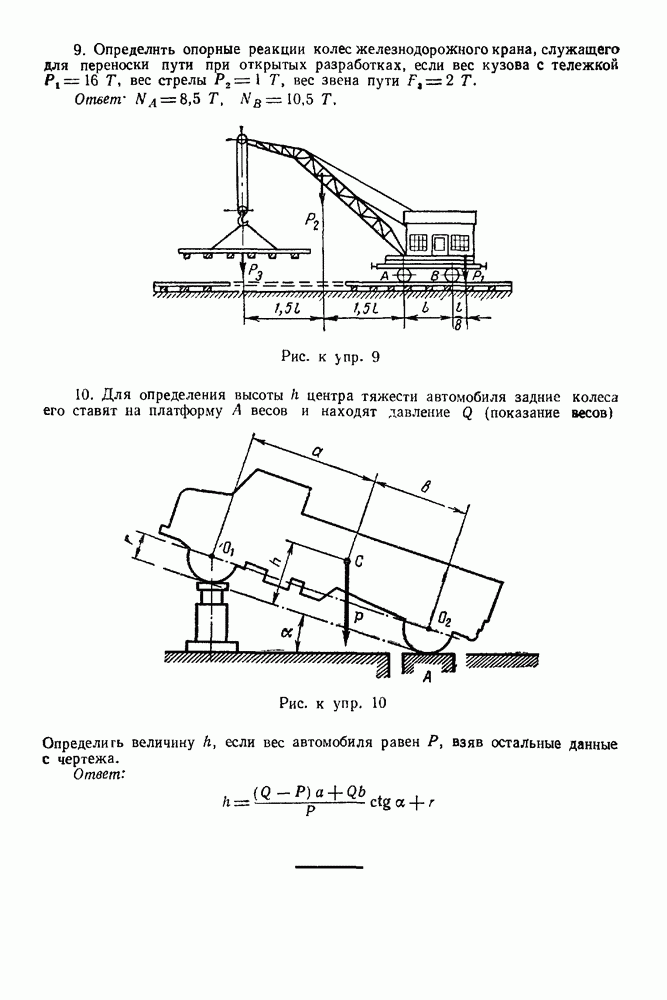
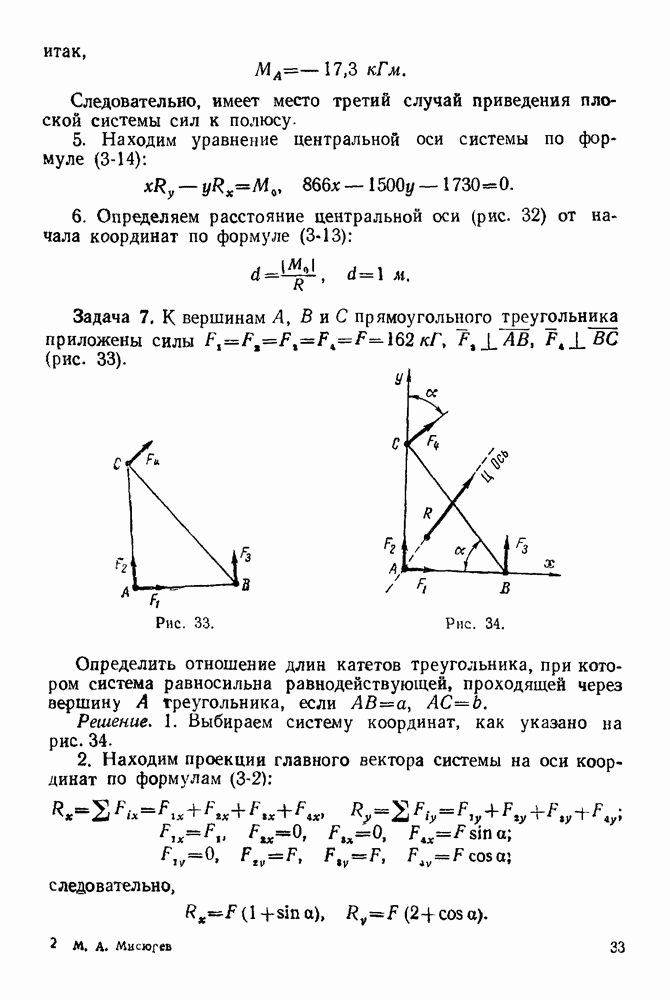
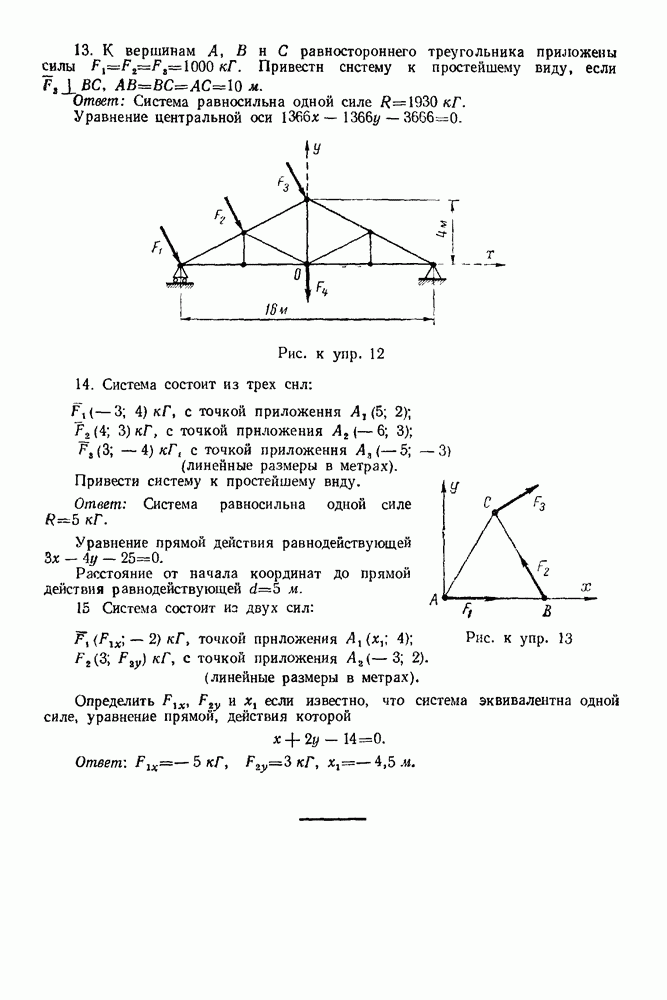
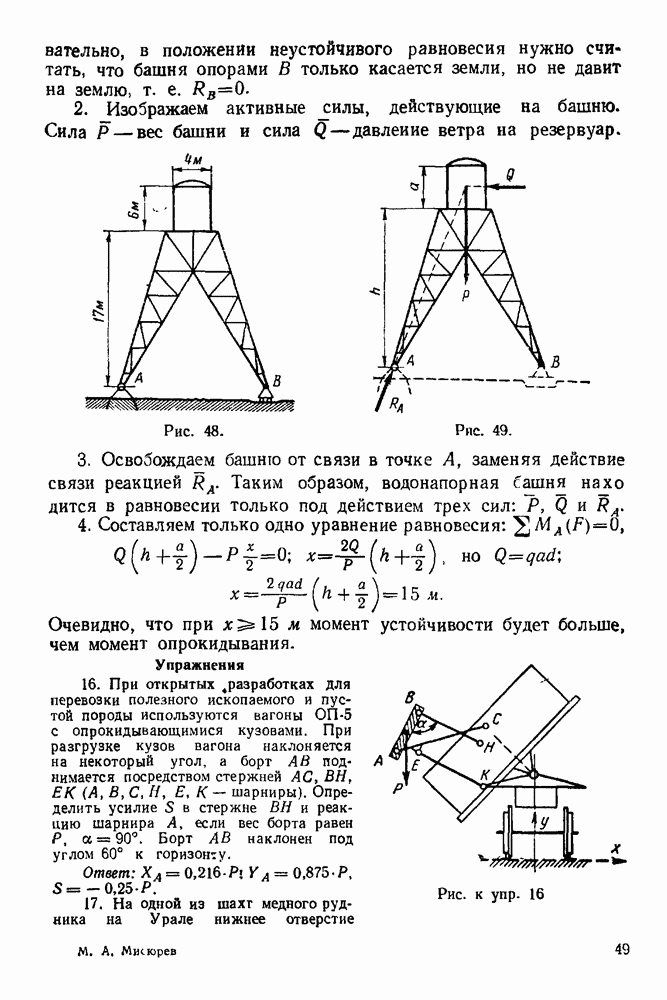
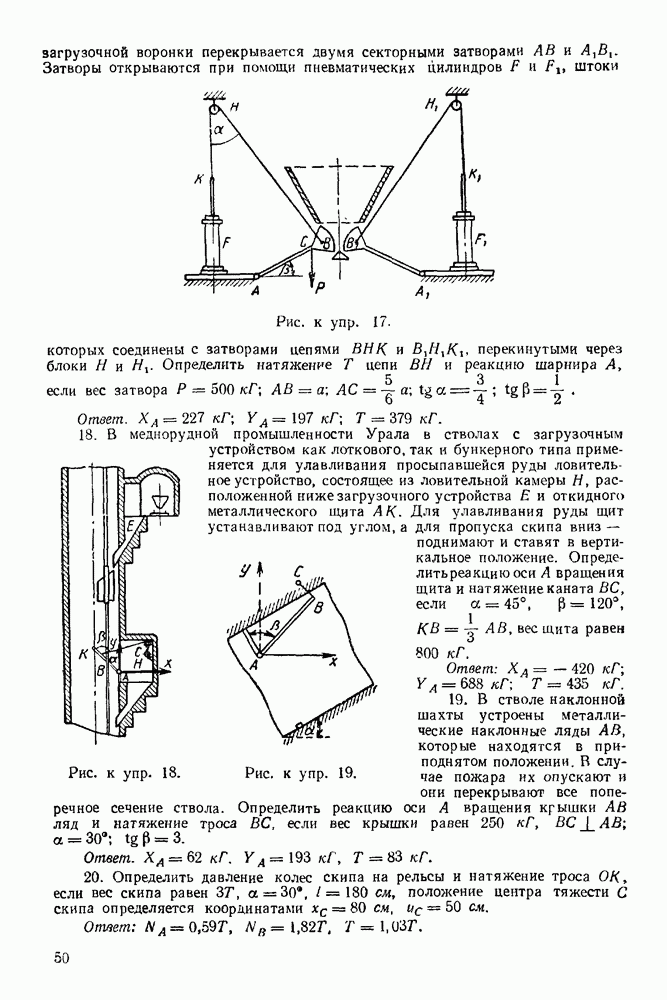
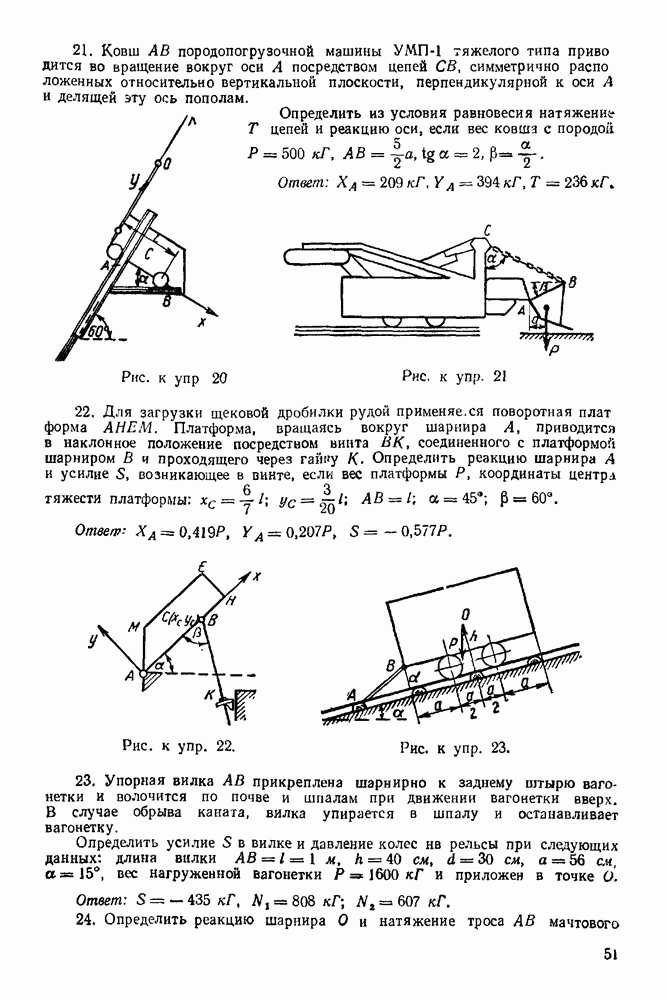
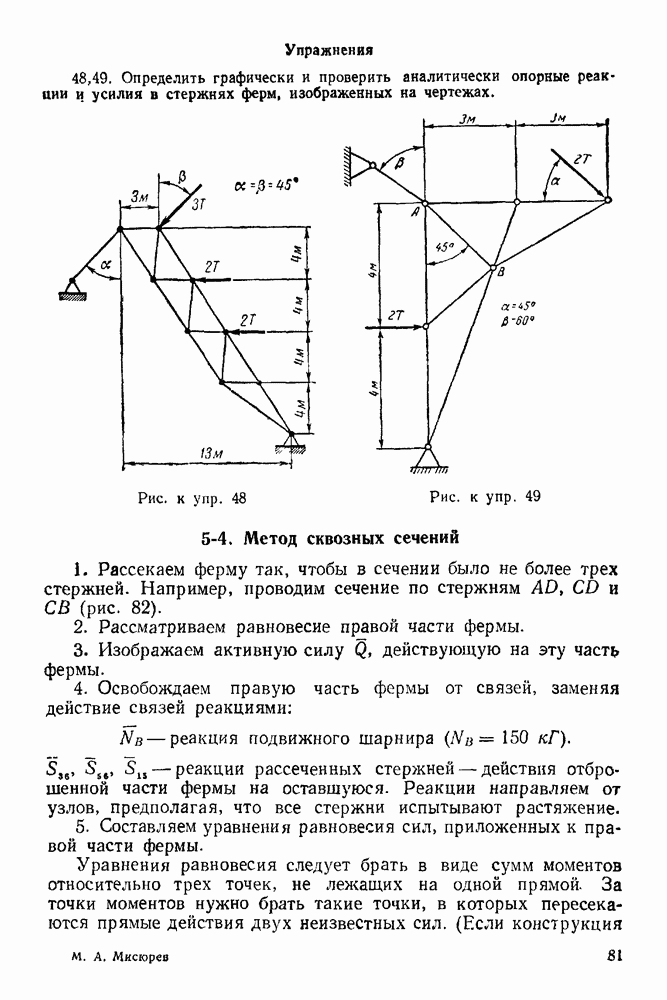
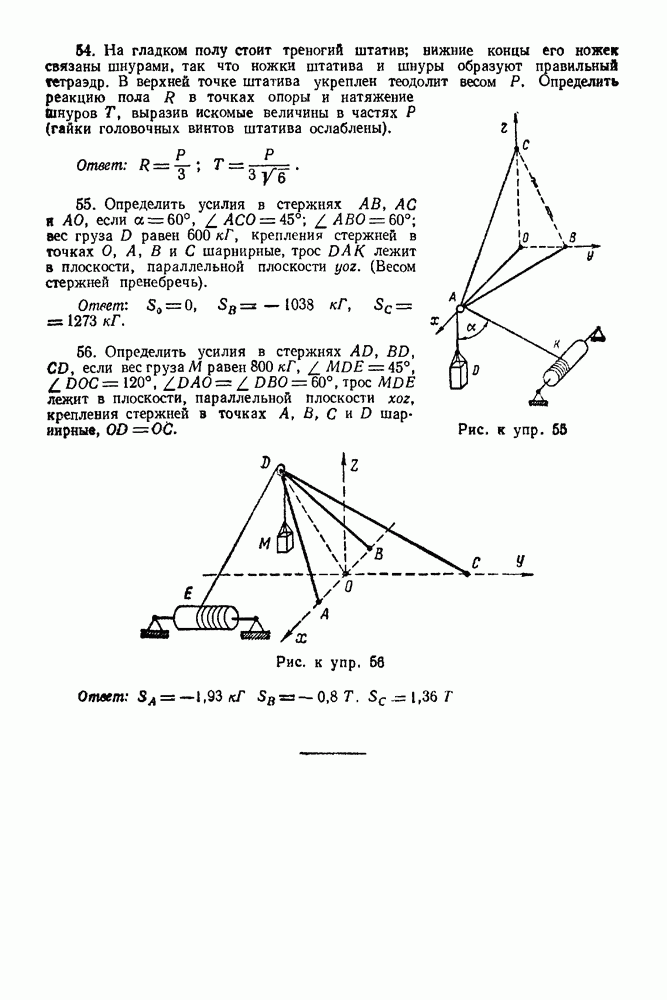
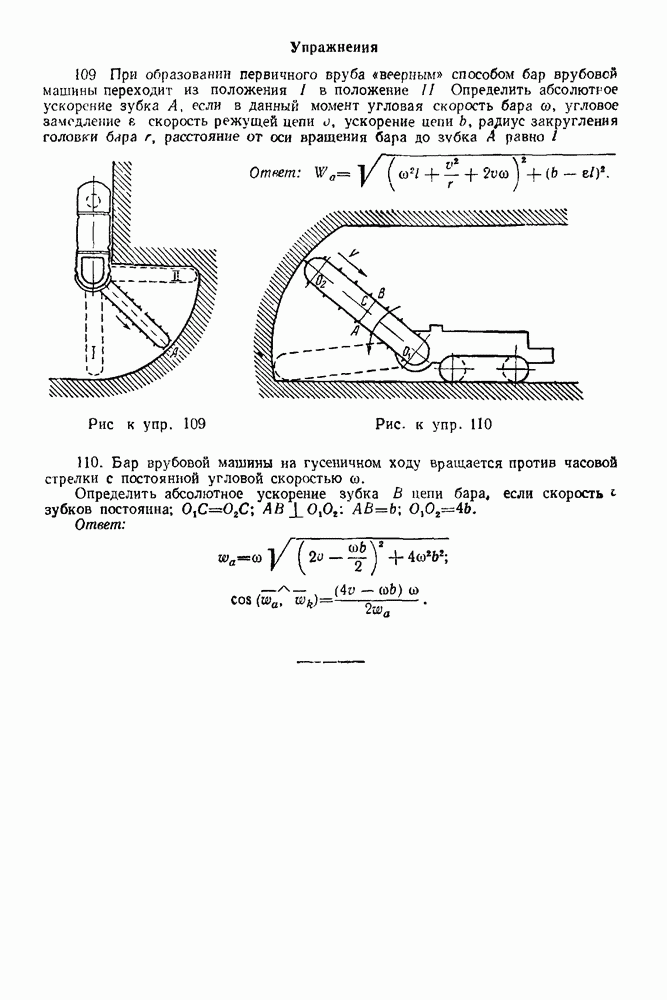
Упражнения
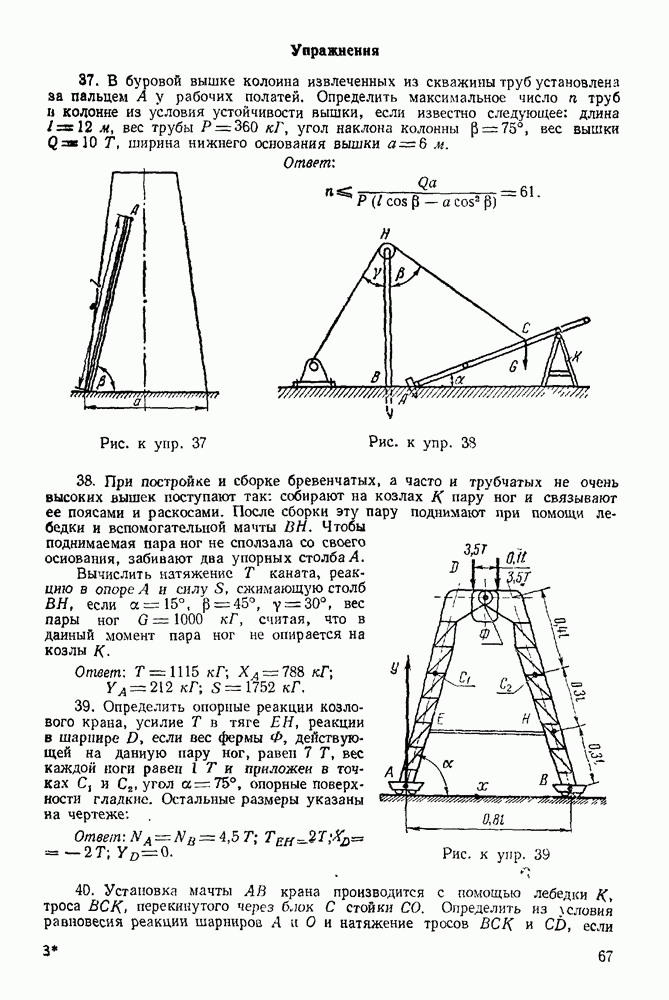
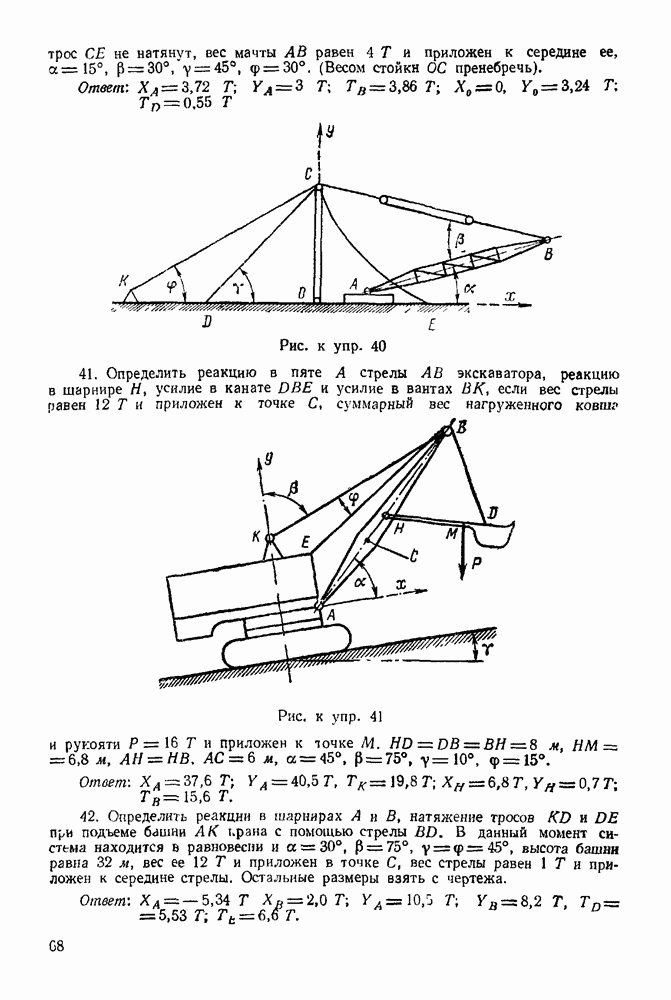
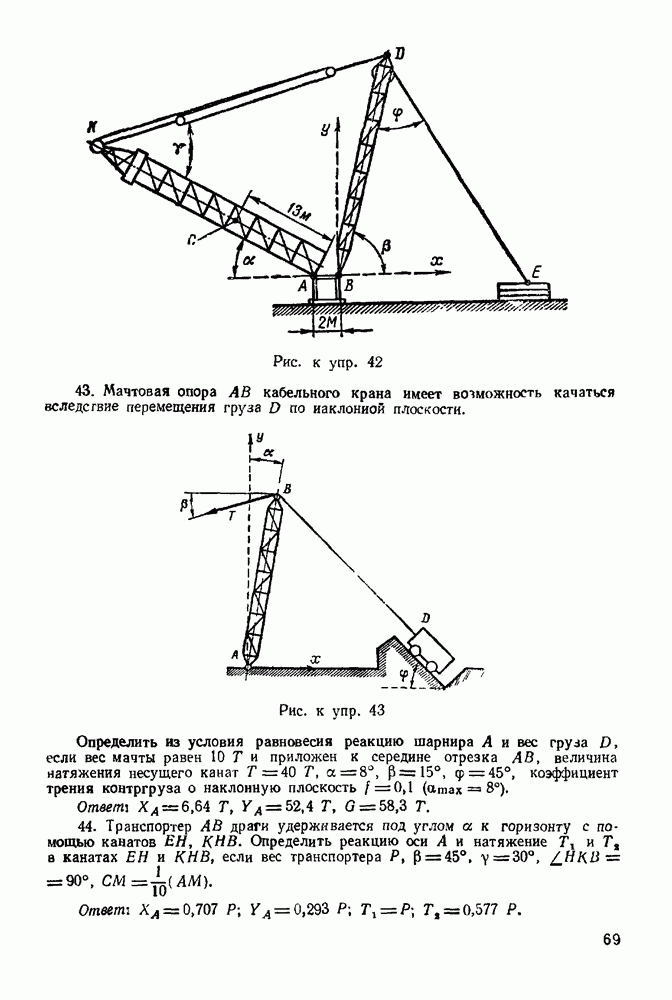
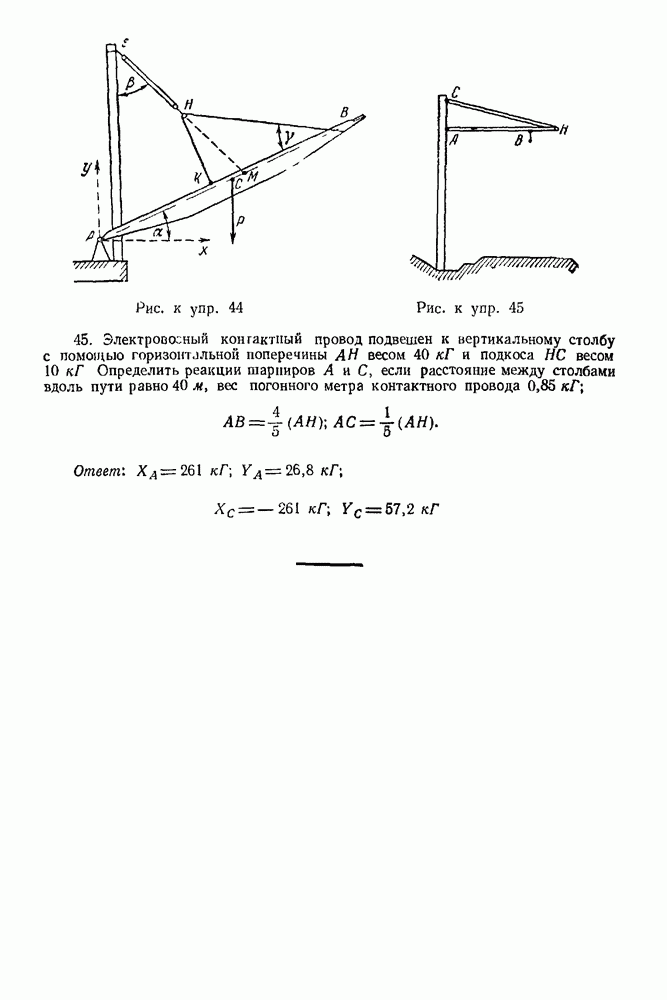
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
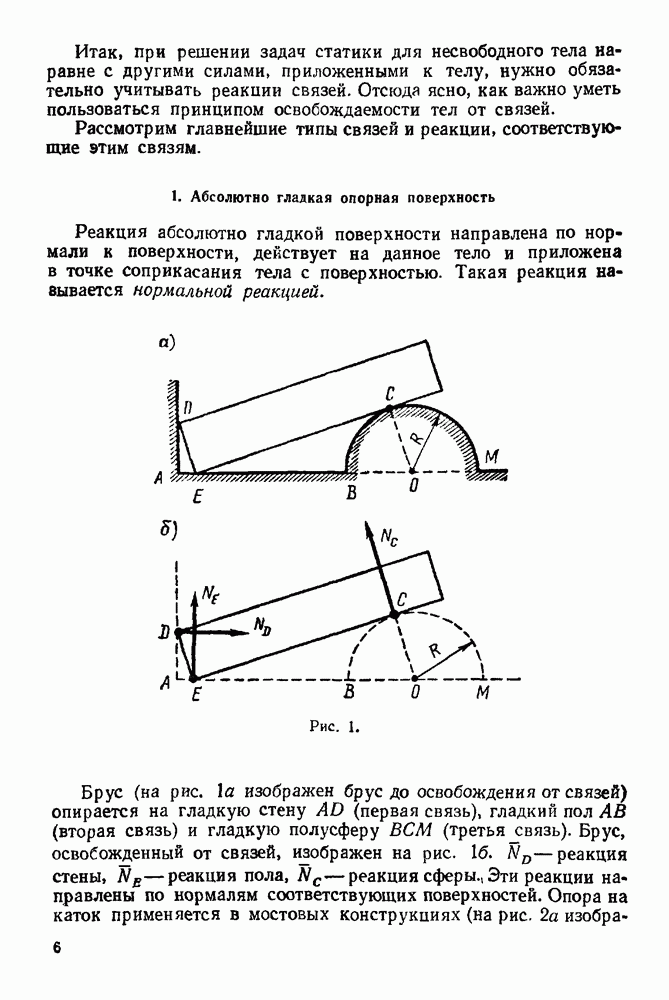
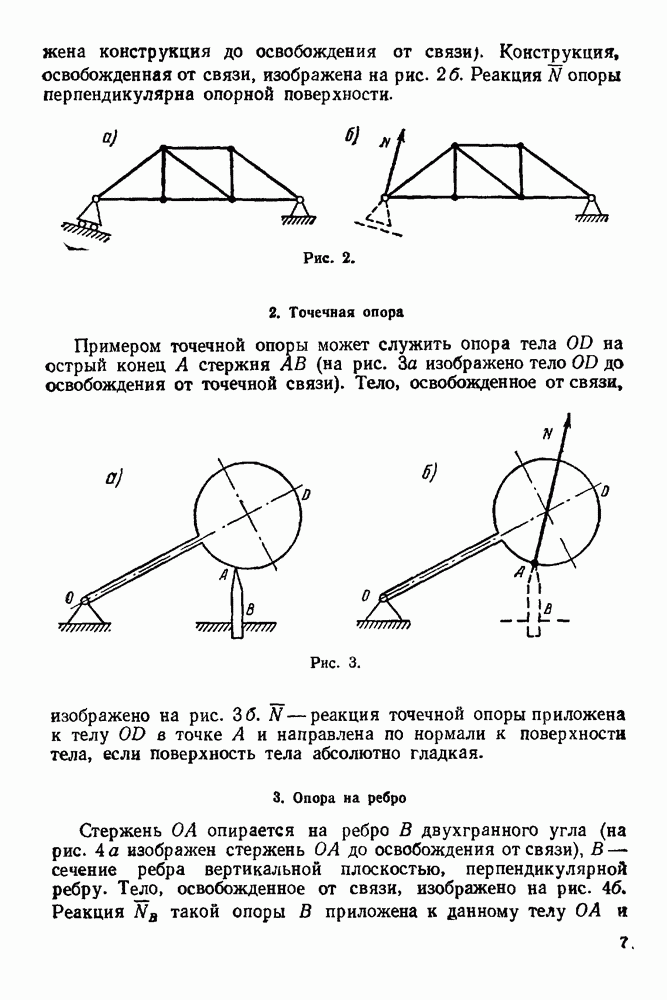
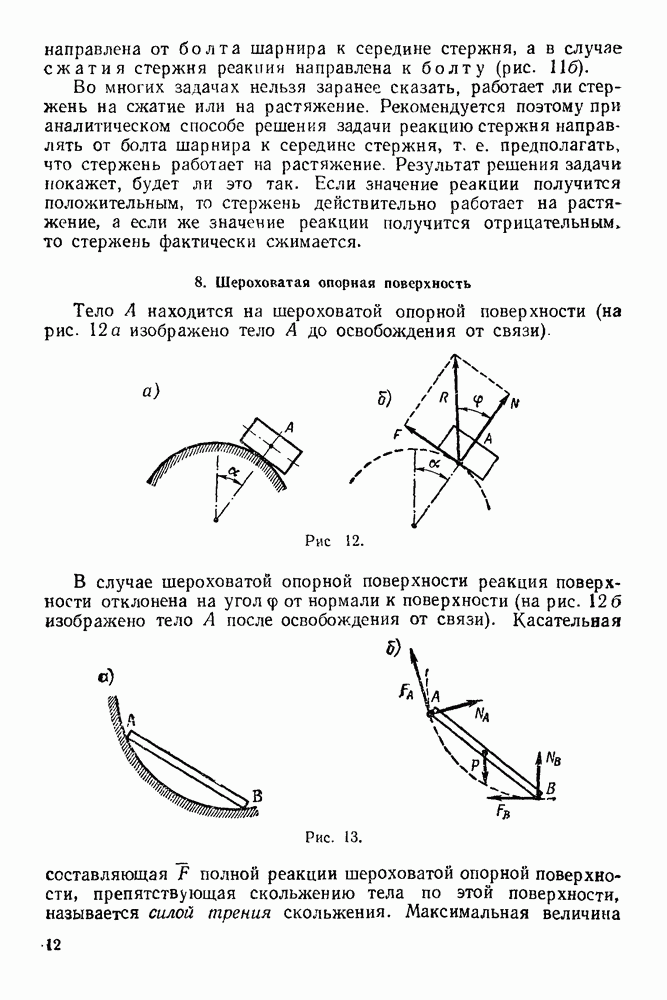
- 1. Абсолютно гладкая опорная поверхность
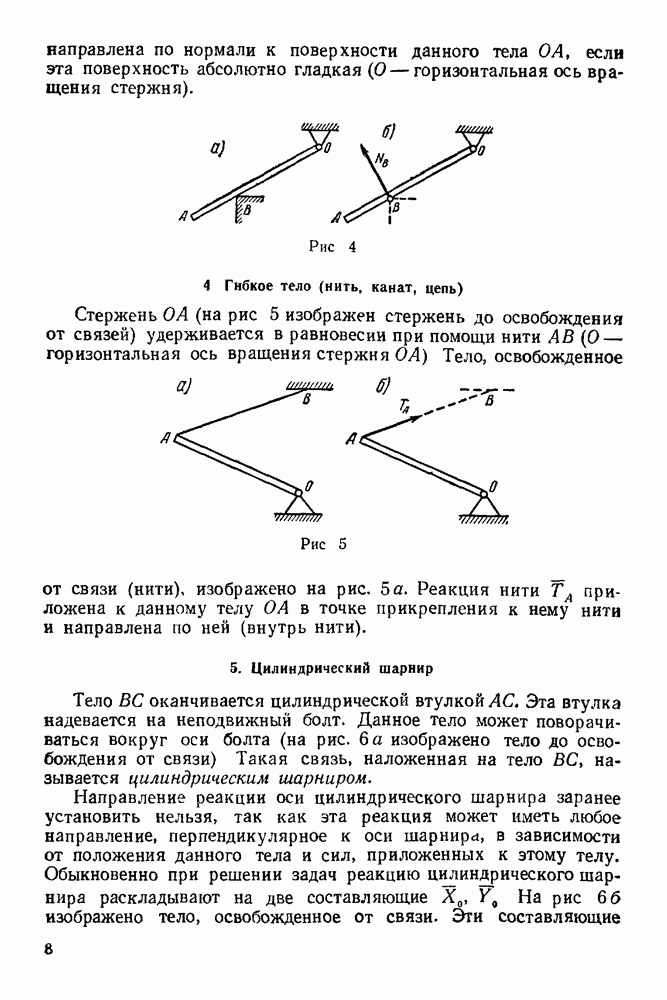
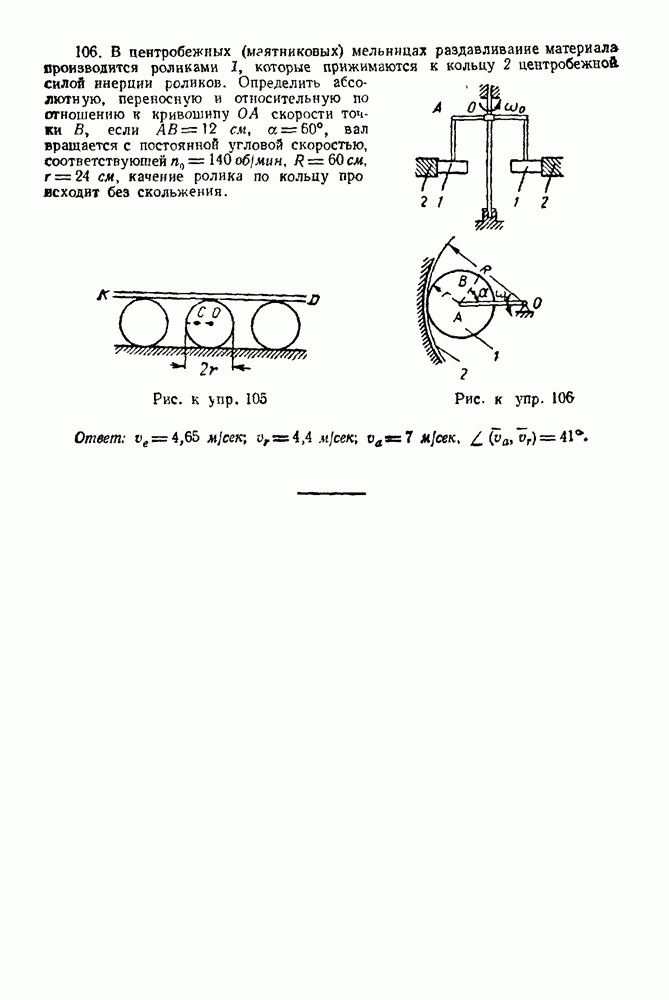
- 2. Точечная опора
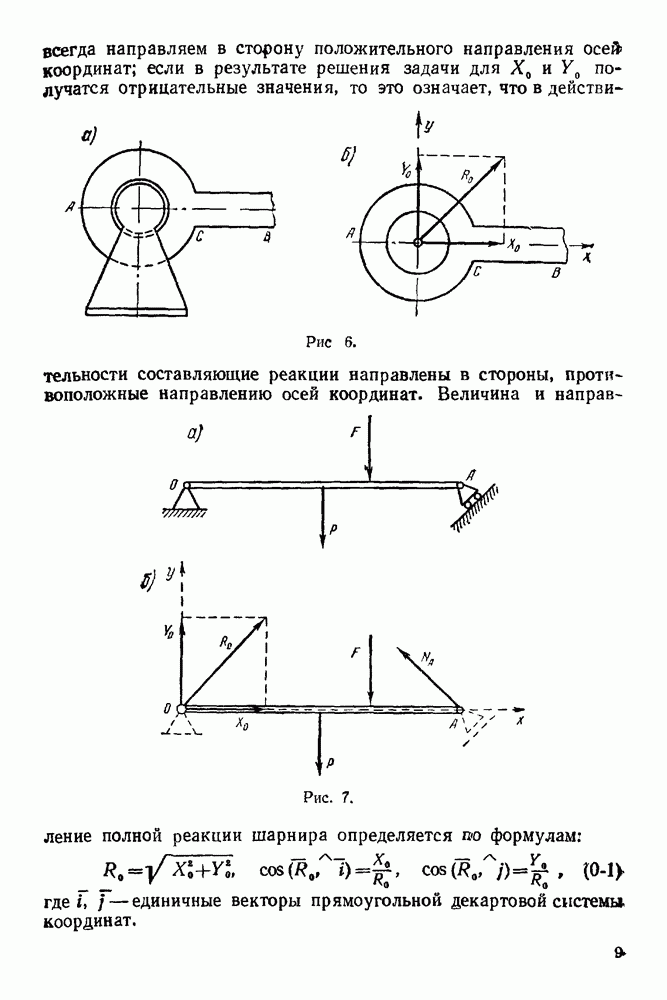
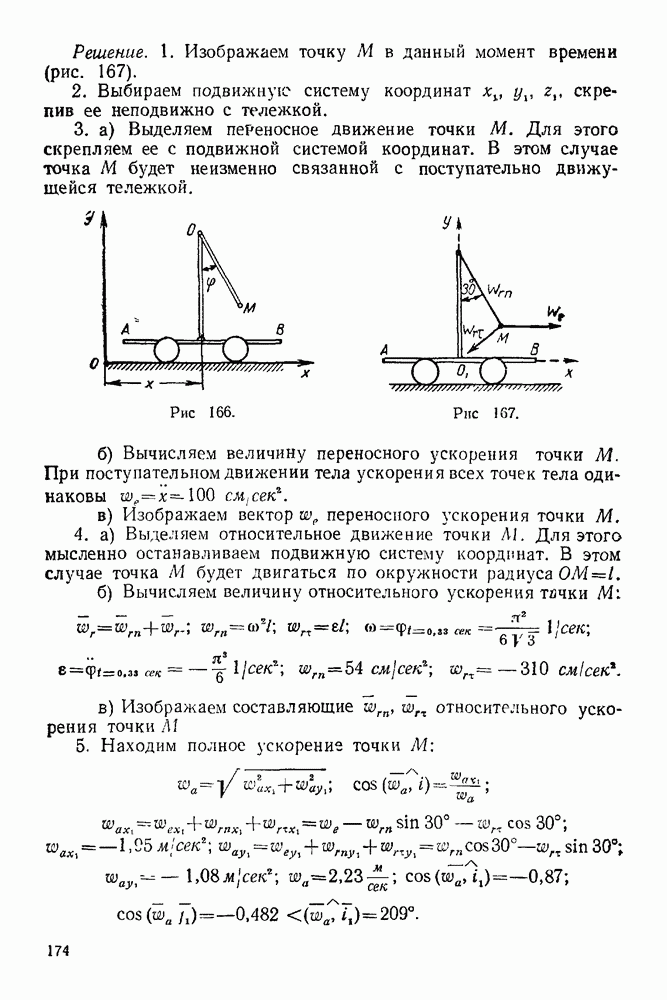
- 3. Опора на ребро
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
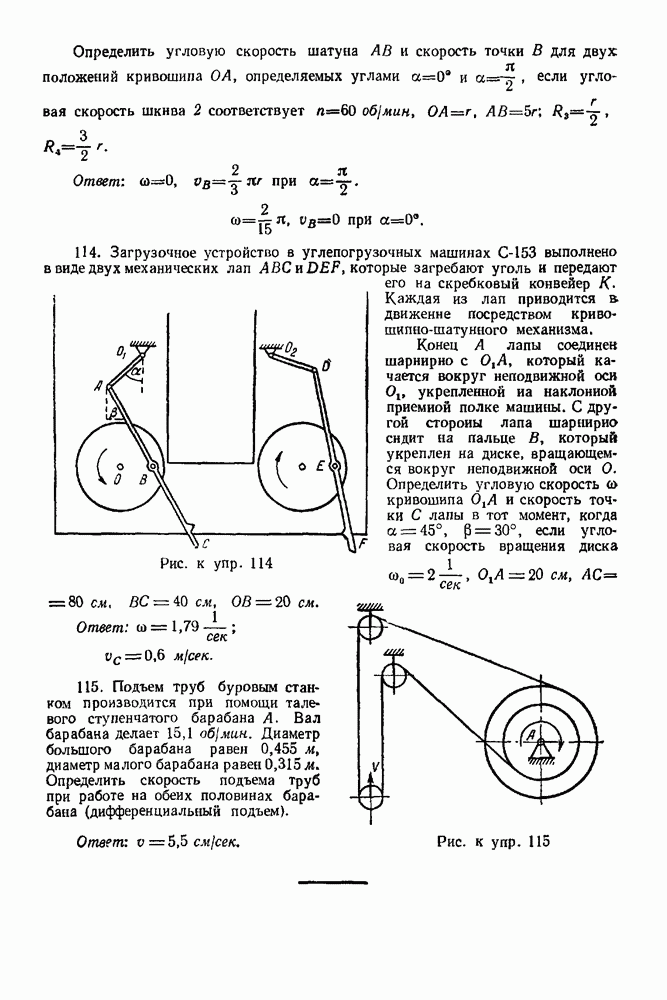
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
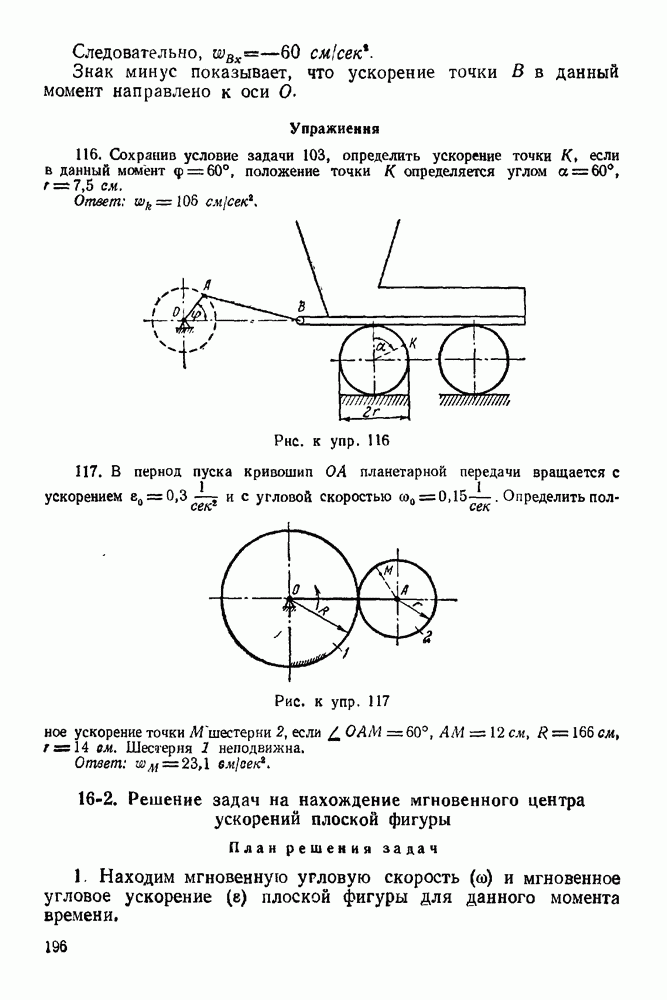
- 1-3. Равновесие какого угодно числа сил
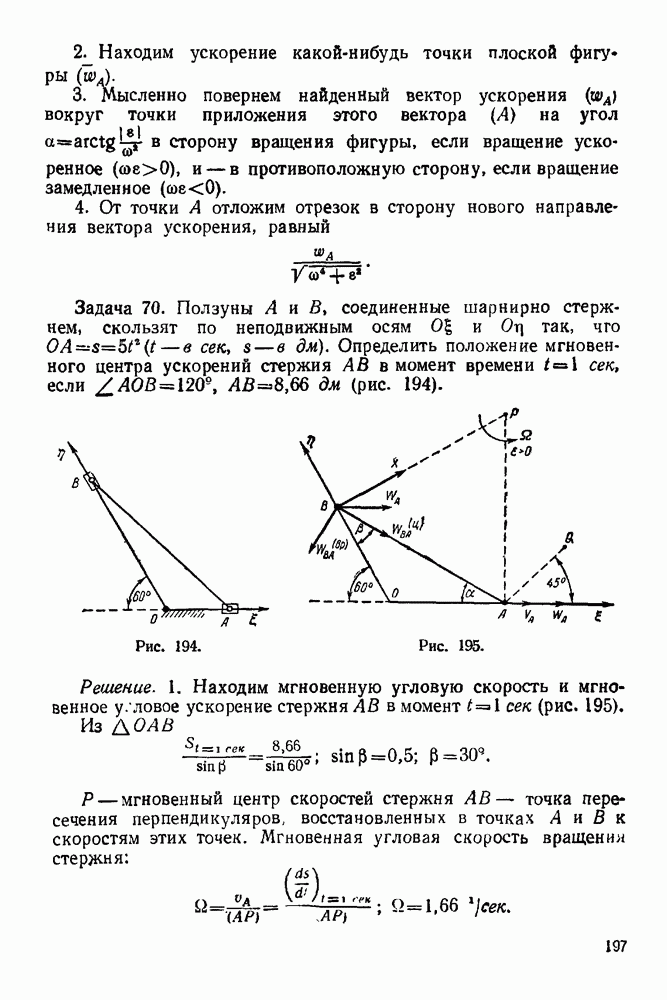
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
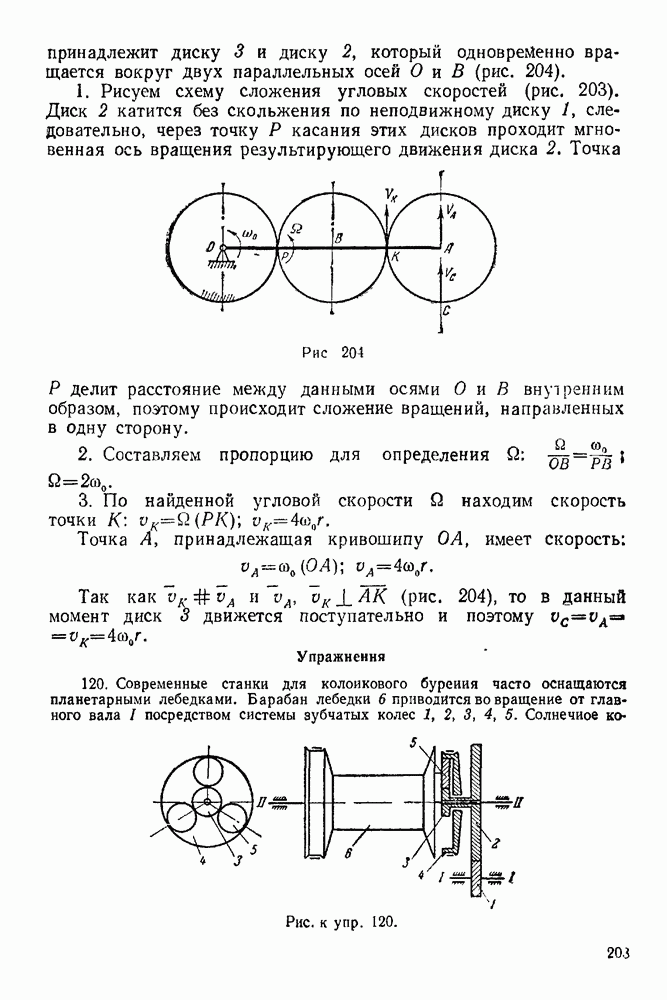
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
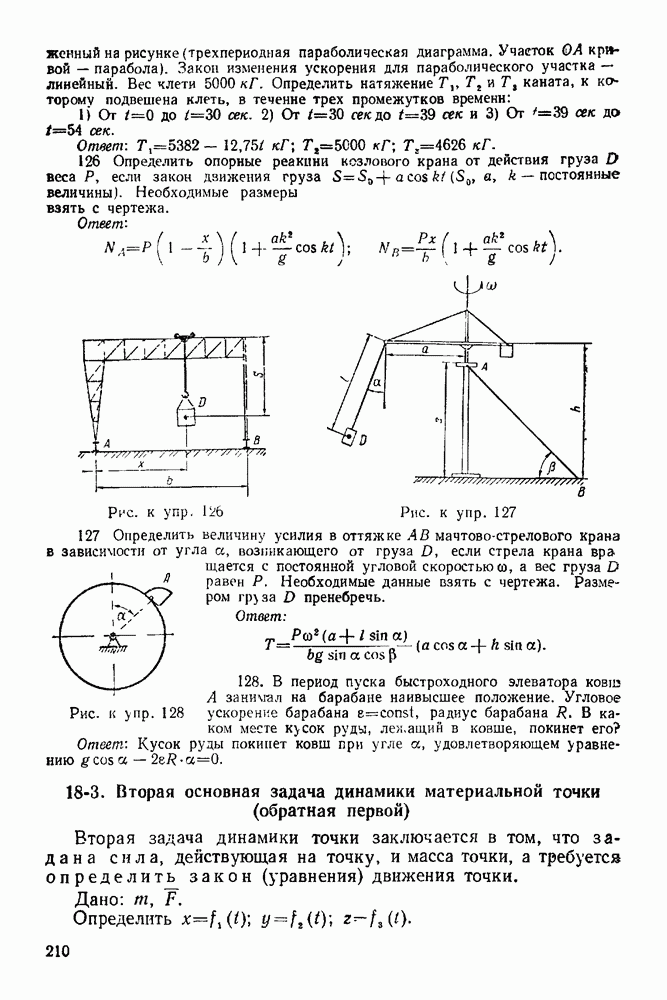
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
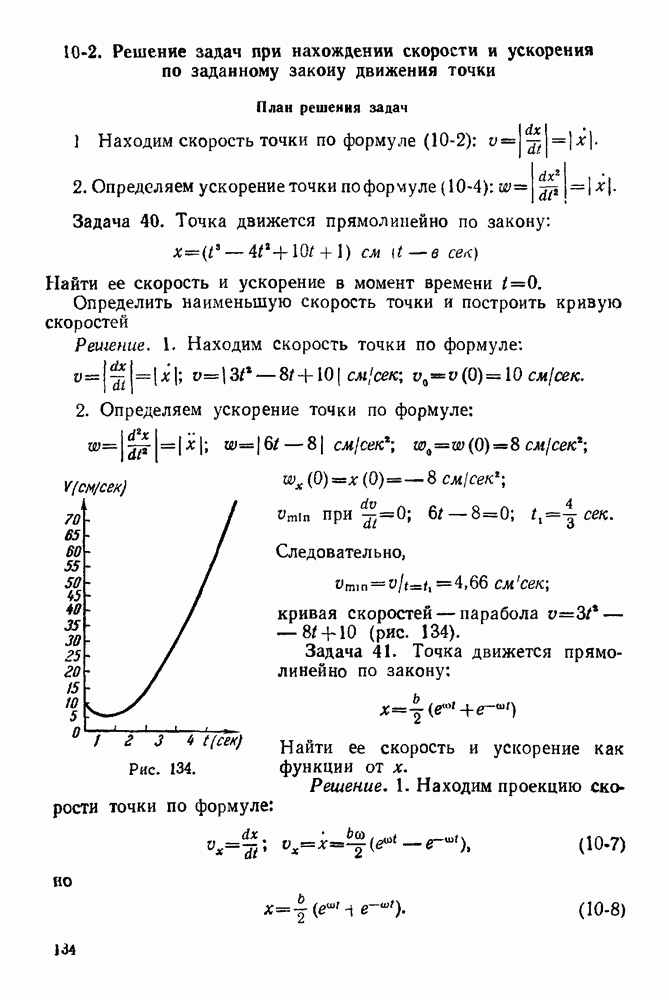
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
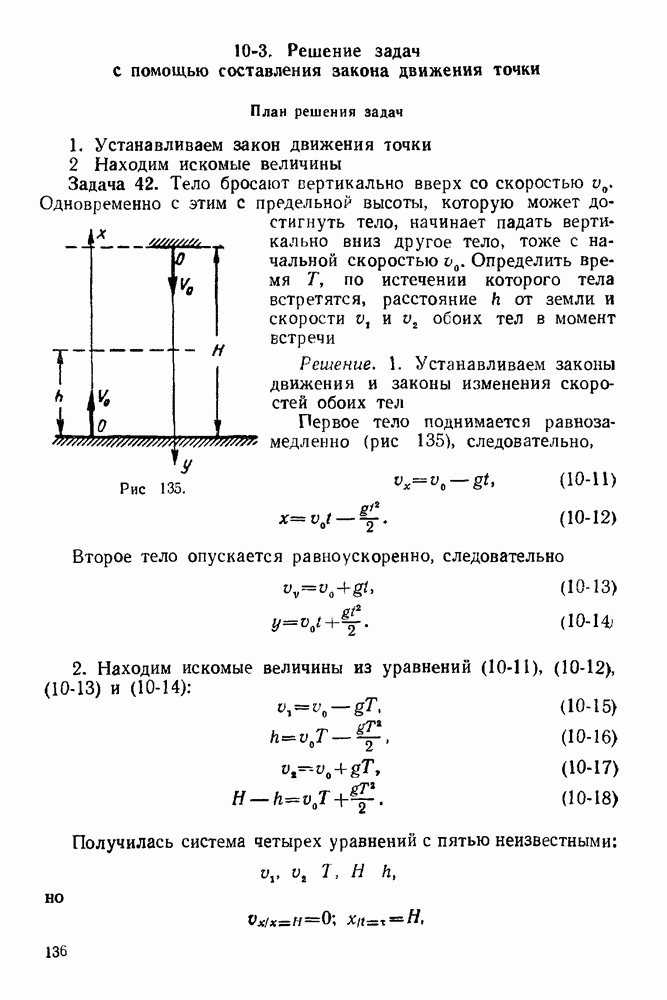
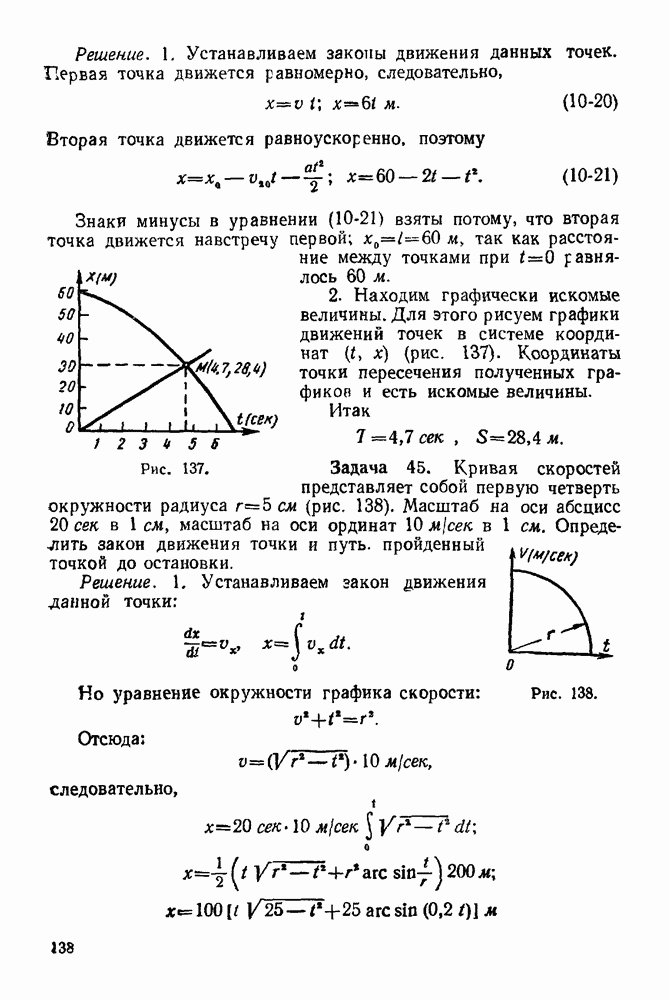
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
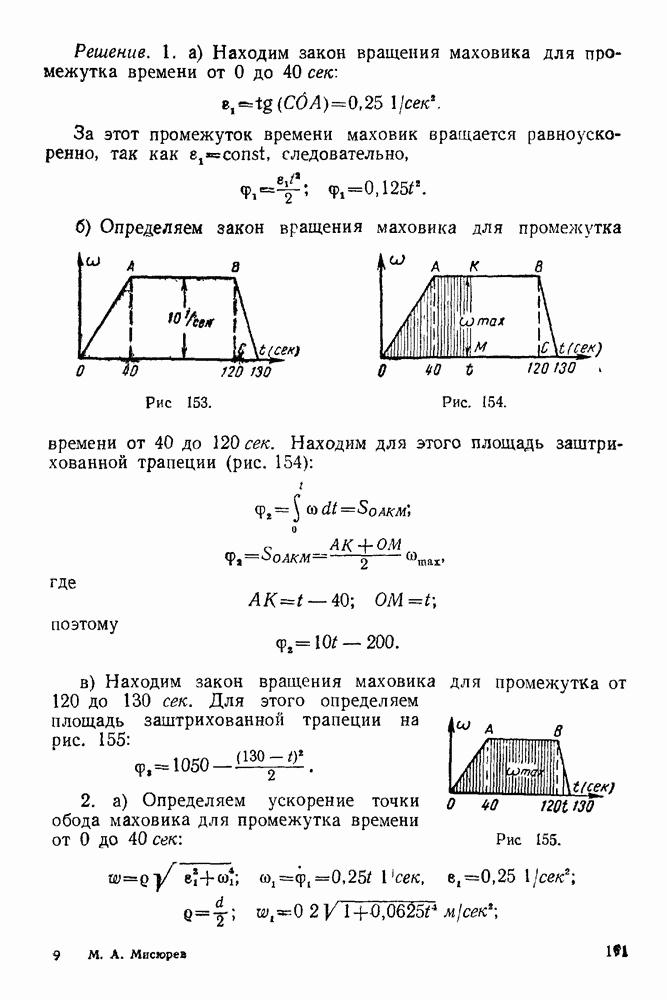
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
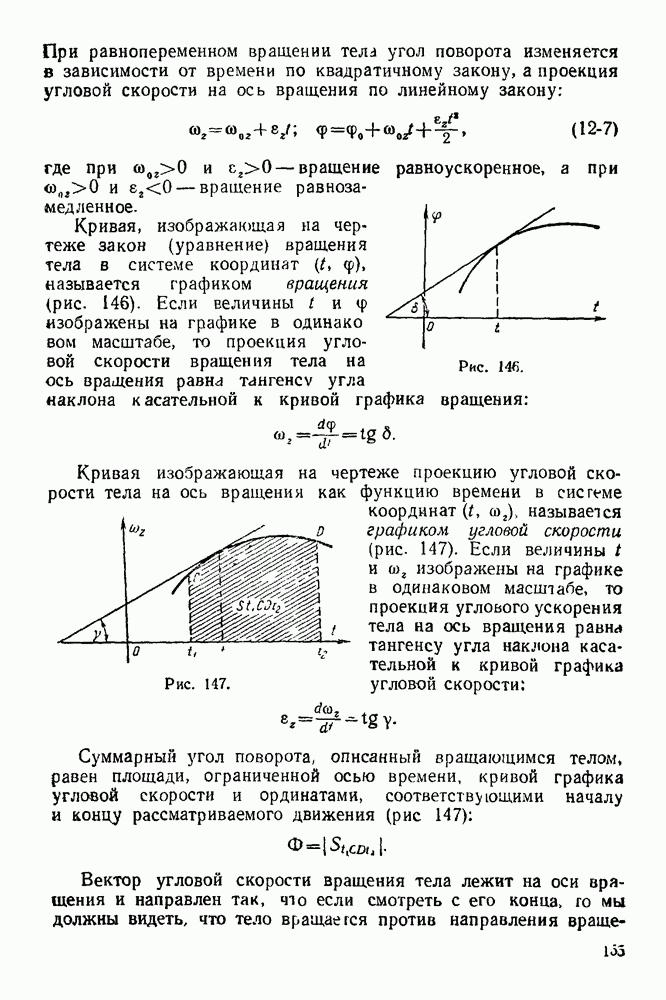
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
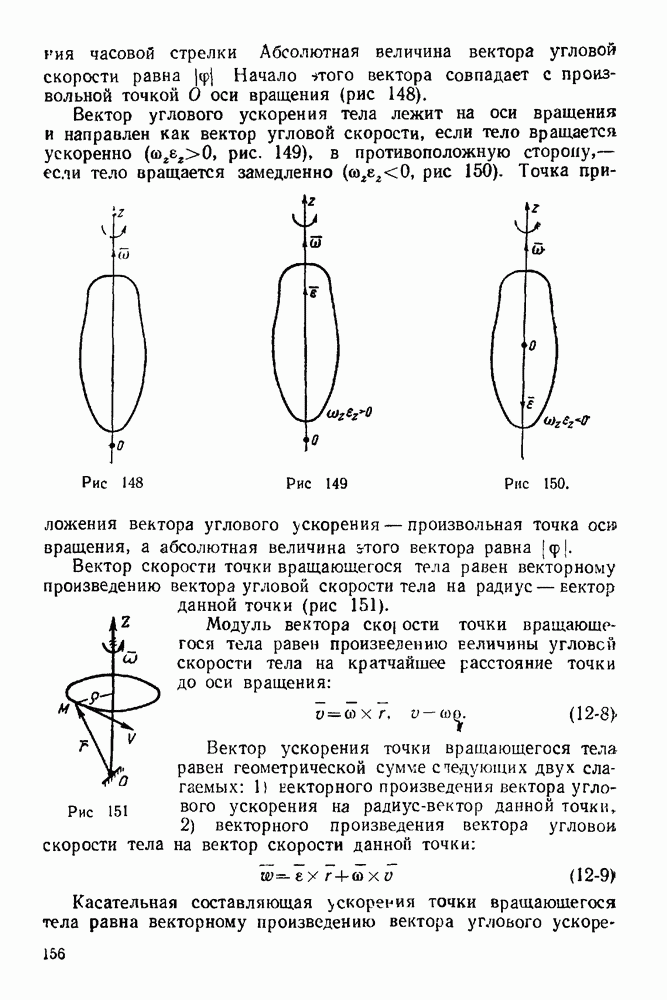
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
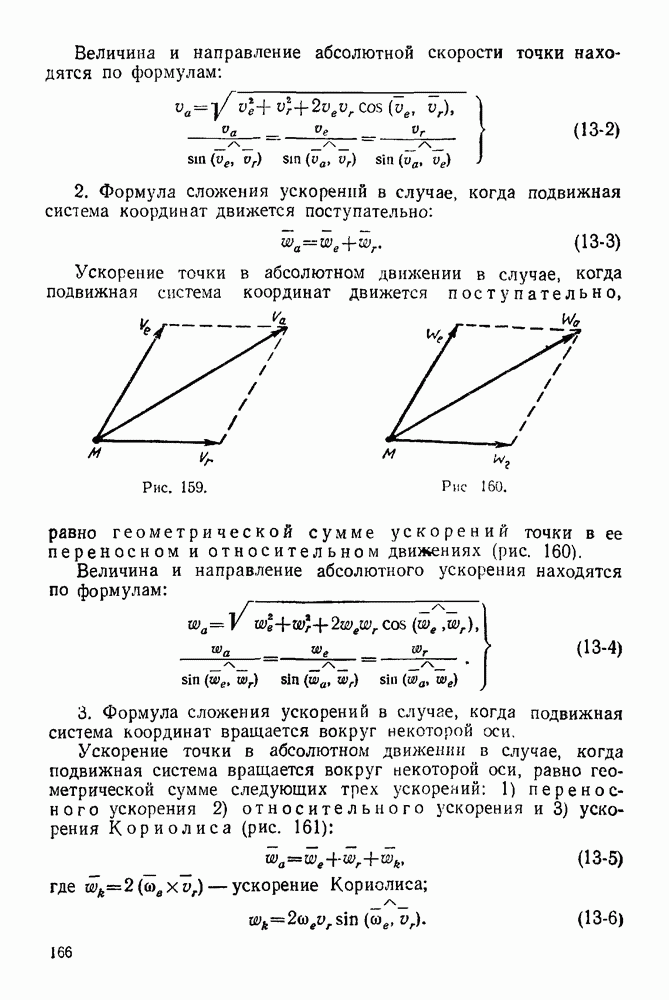
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
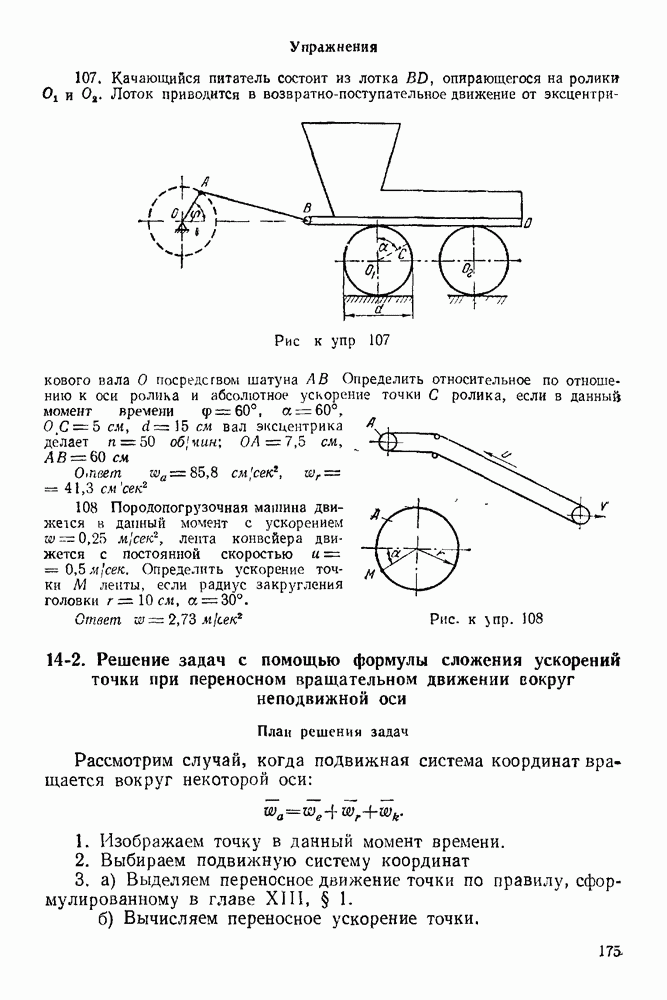
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
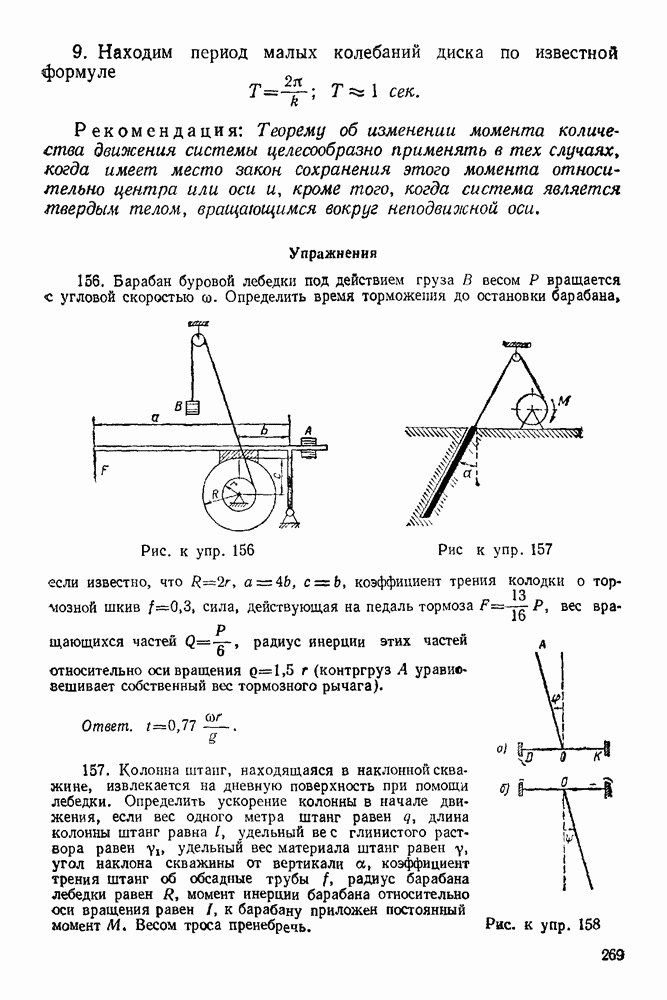
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
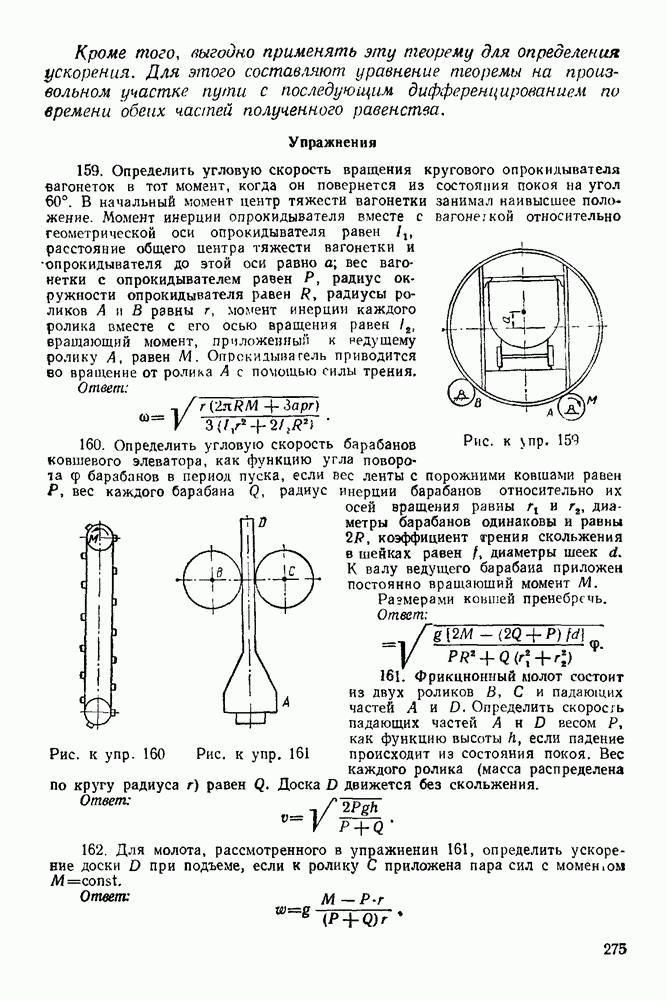
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
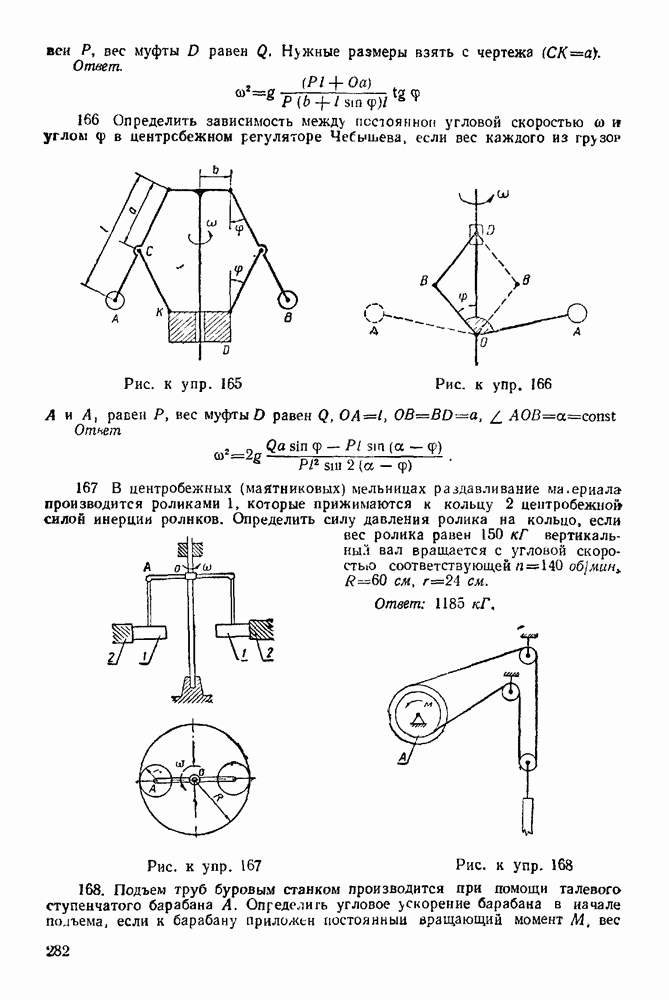
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
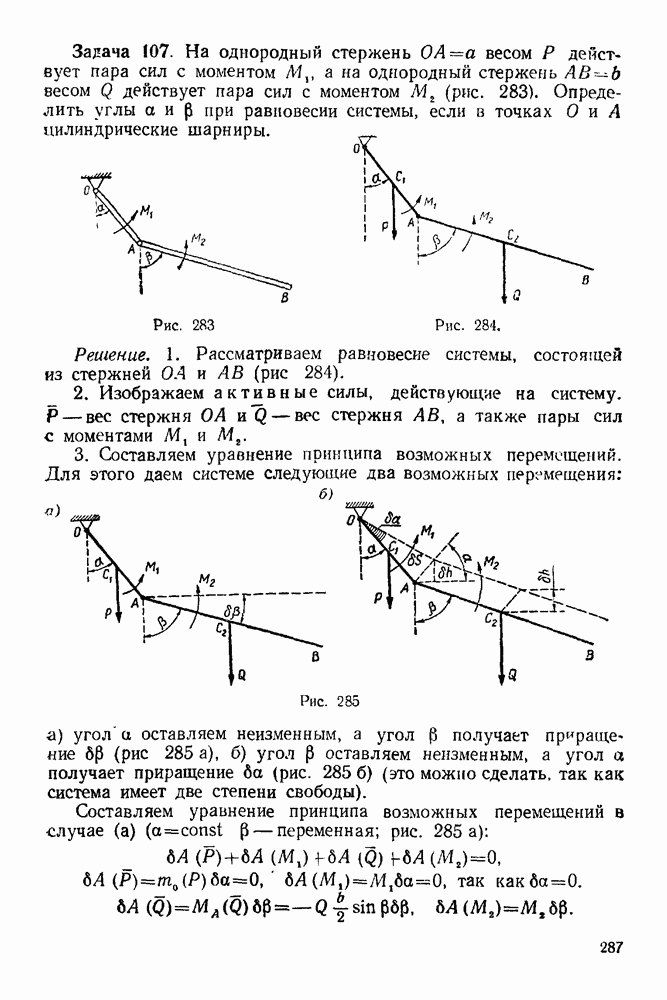
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
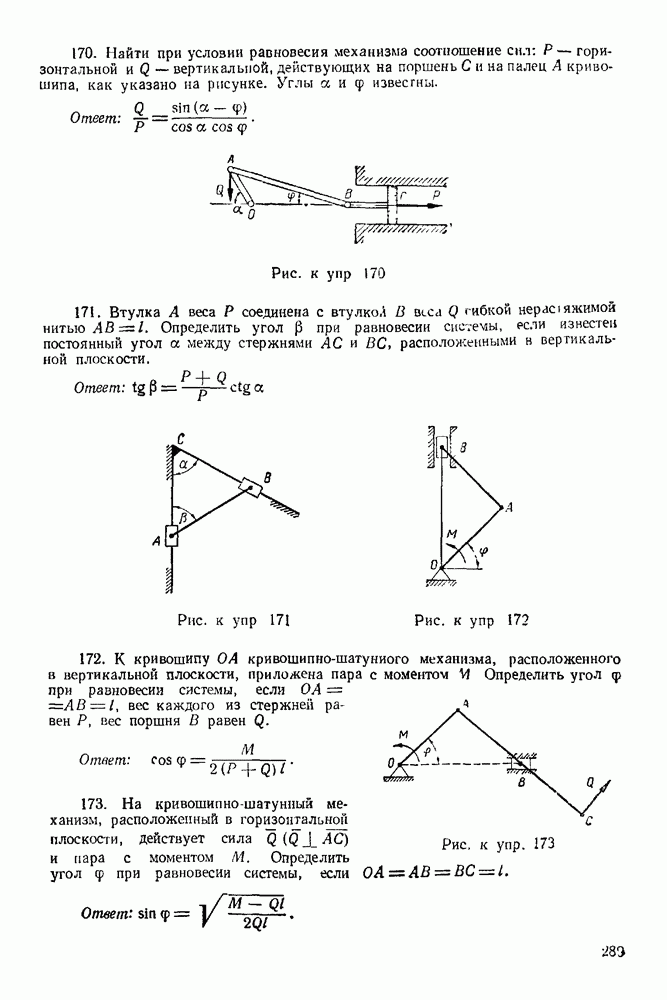
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
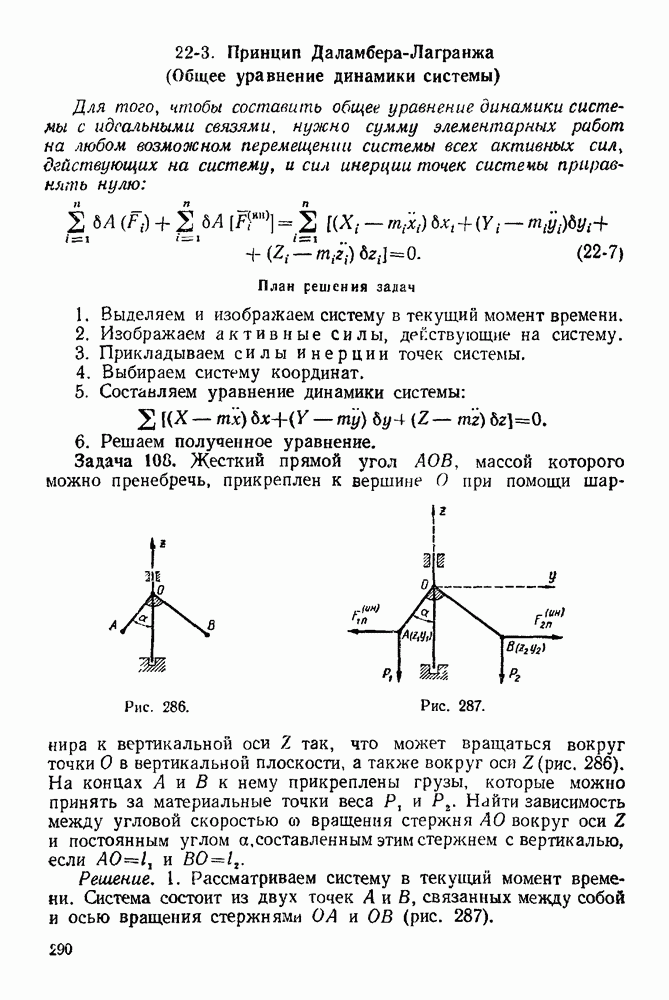
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
- ГЛАВА XXIII. УДАР