| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
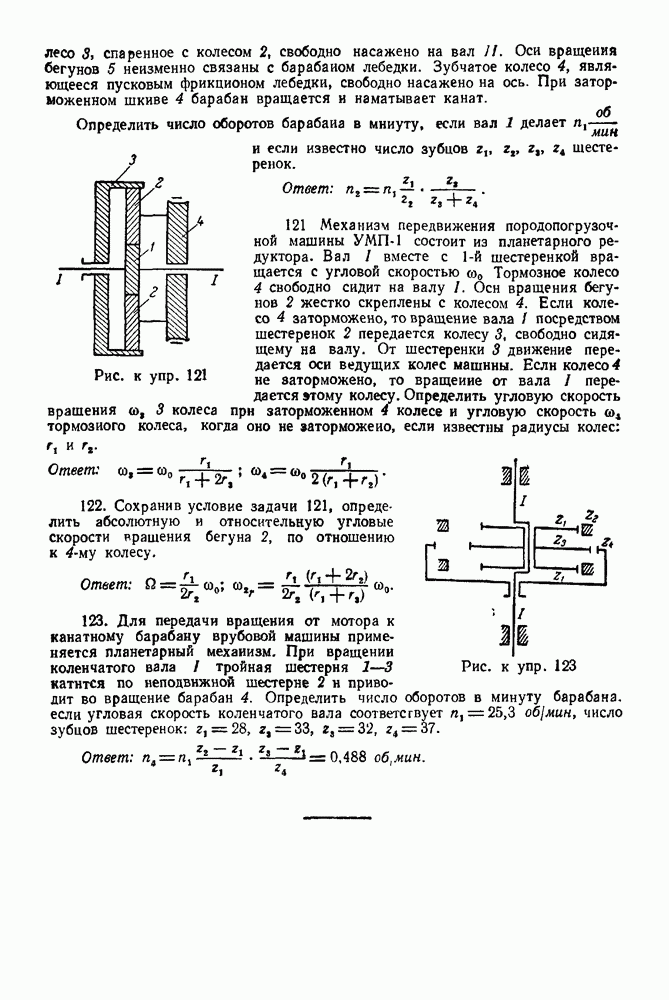
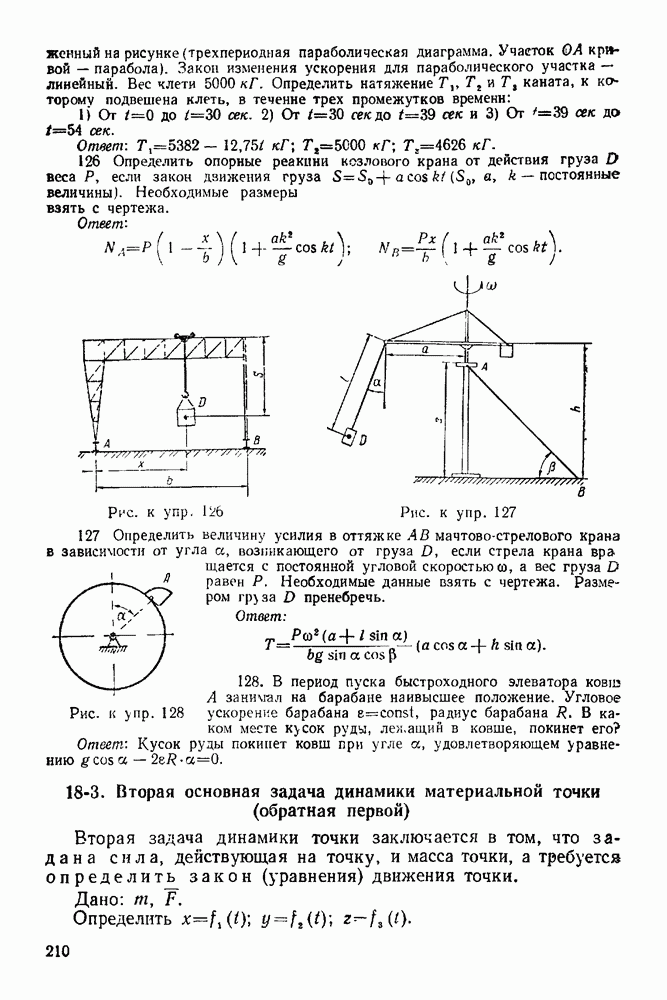
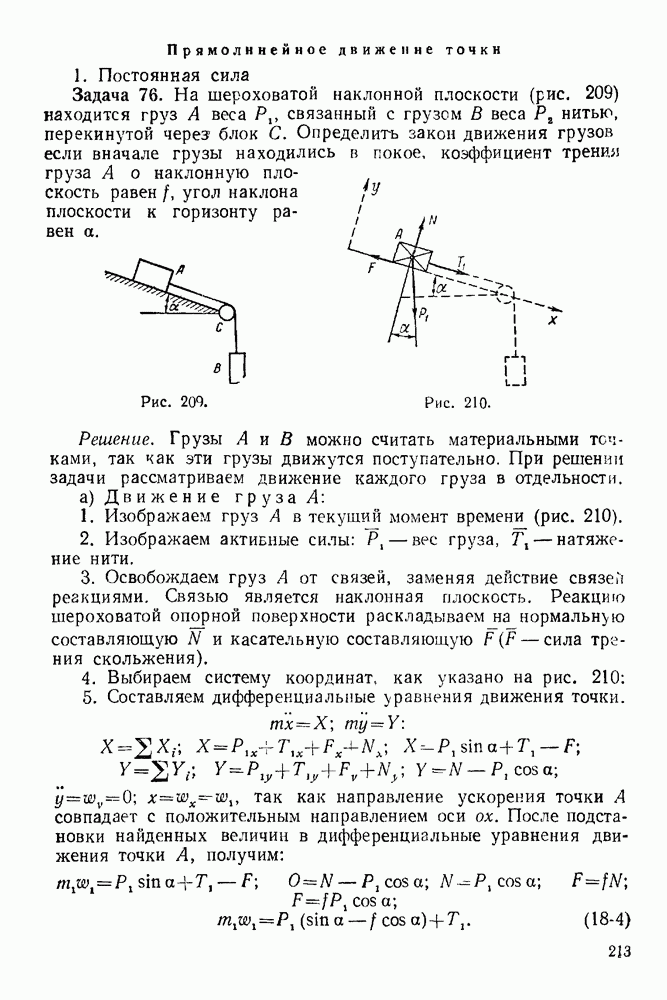
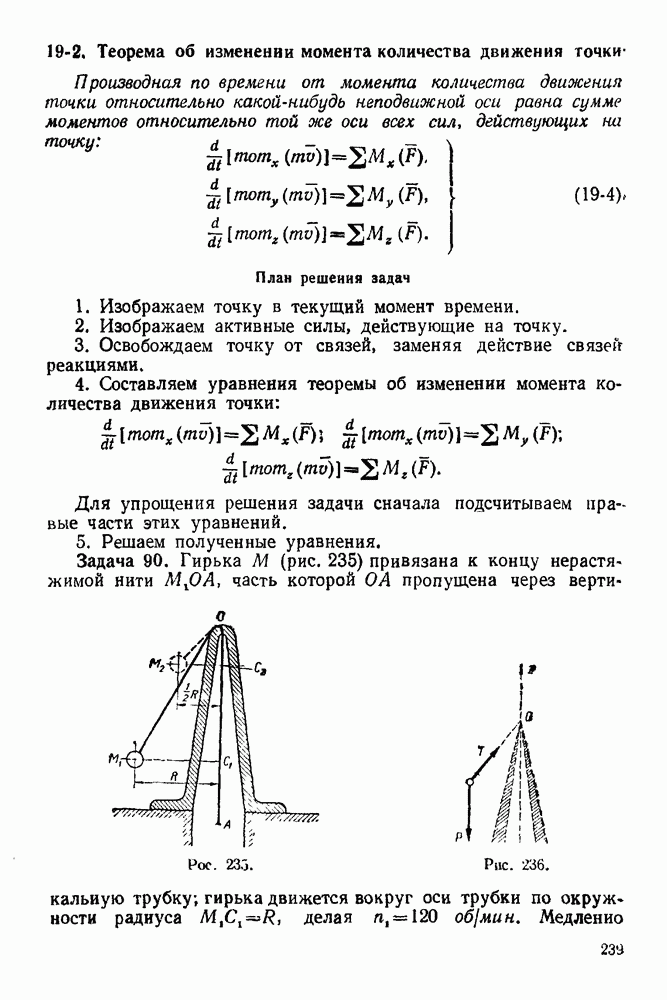
21-3. Теорема об изменении момента количества движения системы
Производная по времени от момента количества движения системы, взятого относительно какого-нибудь неподвижного центра, равна главному моменту относительно того же центра всех внешних сил, действующих на систему:

Производная по времени от момента количества движения системы, взятого относительно какой-нибудь неподвижной оси, равна главному моменту относительно той же оси всех внешних сил, действующих на систему:

где 

Кинетический момент твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции тела относительно оси вращения на угловую скорость вращения тела;

Моменты инерции некоторых однородных тел
1. Момент инерции тонкого стержня (рис. 257):

где  длина стержня,
длина стержня,  масса стержня.
масса стержня.
2. Момент инерции толстостенного цилиндра (рис. 258):

где  масса цилиндра,
масса цилиндра,  внешний радиус цилиндра,
внешний радиус цилиндра,  внутренний радиус цилиндра.
внутренний радиус цилиндра.

Рис. 257.

Рис. 258.
3. Момент инерции диска (цилиндра) (рис. 259):

где  масса цилиндра,
масса цилиндра,  радиус основания диска (цилиндра).
радиус основания диска (цилиндра).

Рис. 259.

Рис. 260.
4. Момент инерции тонкостенного цилиндра (кольца, обруча) (рис. 260):

где  масса тонкостенного цилиндра;
масса тонкостенного цилиндра;  радиус цилиндра. Момент инерции твердого тела относительно любой оси равен моменту инерции тела относительно оси, параллельной данной и проходящей через центр тяжести тела, плюс масса тела, умноженная на квадрат расстояния между осями (рис. 261):
радиус цилиндра. Момент инерции твердого тела относительно любой оси равен моменту инерции тела относительно оси, параллельной данной и проходящей через центр тяжести тела, плюс масса тела, умноженная на квадрат расстояния между осями (рис. 261):


Рис. 261.
Радиусом инерции тела относительно какой-нибудь оси называется такое расстояние от оси, в конце которого нужно в одной точке сосредоточить массу тела так, чтобы момент инерции точки относительно данной оси равнялся моменту инерции тела относительно той же оси: 

План решения задач
1. Выделяем и изображаем систему в текущий момент времени.
2. Изображаем внешние силы, действующие на систему.
3. Выбираем систему координат.
4. Составляем уравнения теоремы об изменении момента Количества движения системы в скалярной форме:

Для упрощения решения задач рекомендуется сначала вычислять правые части уравнений.
5. Проинтегрируем полученные дифференциальные уравнения.
6. Составляем начальные условия задачи для определения произвольных постоянных интегрирования.
7. Определяем произвольные постоянные интегрирования по начальным условиям задачи.
8. Найденные произвольные постоянные подставляем в результат интегрирования уравнений.
9. Из полученных уравнений находим неизвестные величины задачи.
Задача 99. По хорде  горизонтальной платформы веса
горизонтальной платформы веса  вращающейся вокруг вертикальной оси, проходящей через ее центр, идет человек веса
вращающейся вокруг вертикальной оси, проходящей через ее центр, идет человек веса 

Рис. 262.

Рис. 263.
Найти угловую скорость вращения платформы, если масса платформы равномерно распределена по всему кругу; человек движется по закону  В начальный момент платформа находилась в покое; радиус платформы
В начальный момент платформа находилась в покое; радиус платформы  (рис. 262).
(рис. 262).
Решение. 1. Изображаем систему в текущий момент времени. Система состоит из платформы, человека и оси  Массой оси пренебрегаем (рис. 263).
Массой оси пренебрегаем (рис. 263).
2 Изображаем внешние силы, действующие на систему:  вес человека,
вес человека,  вес платформы,
вес платформы,  реакция подшипника
реакция подшипника  реакция подпятника В,
реакция подпятника В,
3. Выбираем систему координат, как указано на рис. 263.
4. Составляем уравнение  теоремы об изменении момента количества движения системы:
теоремы об изменении момента количества движения системы:

так как линии действия этих сил параллельны оси моментов, либо пересекают ось. Следовательно,

5. Интегрируем полученное уравнение получаем

6. Составляем начальные условия движения. При 
7. Определяем произвольную постоянную интегрирования с. Так как

получаем 
8. Найденную произвольную постоянную с, подставляем, в уравнение (21-16а) — результат интегрирования дифференциального уравнения. Будем иметь 
9. Из полученного уравнения находим неизвестную угловую скорость  . Для этого подсчитываем
. Для этого подсчитываем  для нашей системы:
для нашей системы:

где  момент количества движения платформы относительно оси
момент количества движения платформы относительно оси  — момент количества движения человека (точки) относительно с
— момент количества движения человека (точки) относительно с 

Мы сделали предположение, что платформа вращается против направления вращения часовой стрелки. Будет ли это так, покажет результат решения задачи.
Для нахождения  воспользуемся теоремой Вариньона:
воспользуемся теоремой Вариньона:

так как
(см. скан)
Следовательно,


Рис. 264.
Знак  показывает, что платформа вращается по направлению вращения часовой стрелки.
показывает, что платформа вращается по направлению вращения часовой стрелки.
Задача 100. Однородный диск радиуса  см совершает колебания вокруг горизонтальной оси, перпендикулярной к плоскости диска и проходящей через точку А, причем
см совершает колебания вокруг горизонтальной оси, перпендикулярной к плоскости диска и проходящей через точку А, причем  Найти закон движения и период малых колебаний диска, если в начальный момент диаметр диска, проходящий через ось подвеса, был отклонен на угол
Найти закон движения и период малых колебаний диска, если в начальный момент диаметр диска, проходящий через ось подвеса, был отклонен на угол  и диск был предоставлен самому себе.
и диск был предоставлен самому себе.

Рис. 265.
Решение. 1. Изображаем систему в текущий момент времени. Материальной системой является диск (рис. 265).
2. Изображаем внешние силы, действующие на систему:  вес диска;
вес диска;  составляющие реакции горизонтальной оси подвеса диска.
составляющие реакции горизонтальной оси подвеса диска.
3. Выбираем систему координат, как указано на рис, 265 (правая система координат).
4. Составляем уравнение теоремы об изменении момента количества движения системы относительно оси подвеса
диска:

 так как линии действия этих сил пересекают ось моментов.
так как линии действия этих сил пересекают ось моментов.

получаем

Рассматриваем малые колебания, т. е.  следовательно,
следовательно,

Дифференциальное уравнение малых колебаний диска будет иметь следующий вид:

где 
5. Интегрируем полученное дифференциальное уравнение движения диска 
Общее решение этого дифференциального уравнения:

(см. решение задачи 82).
6. Составляем начальные условия движения для определения произвольных постоянных.
При 
7. Определяем произвольные постоянные интегрирования а и а по начальным условиям задачи. Для этого подставляем начальные условия в уравнения:

Получаем:

следовательно,

8. Найденные произвольные постоянные подставляем в общее решение дифференциального уравнения движения диска и получаем закон движения диска:

9. Находим период малых колебаний диска по известной формуле

Рекомендация: Теорему об изменении момента количества движения системы целесообразно применять в тех случаях, когда имеет место закон сохранения этого момента относительно центра или оси и, кроме того, когда система является твердым телом, вращающимся вокруг неподвижной оси.
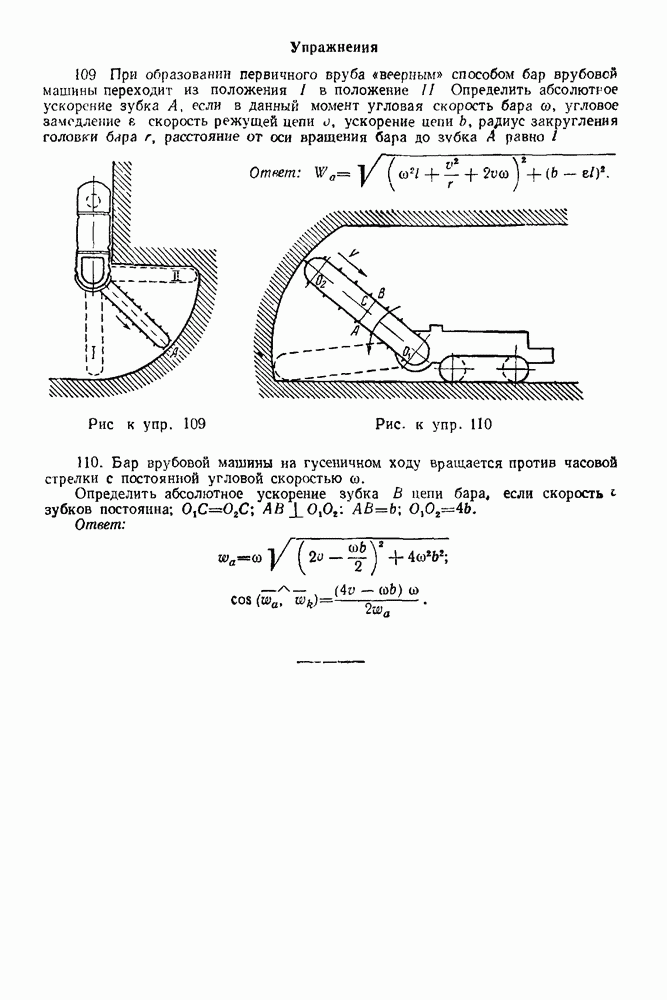
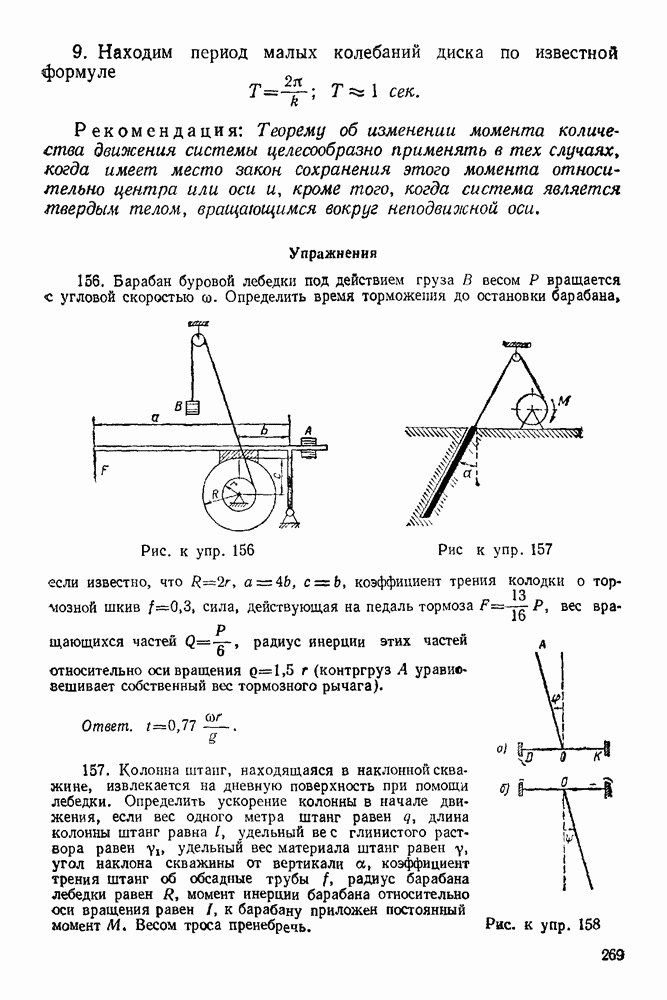
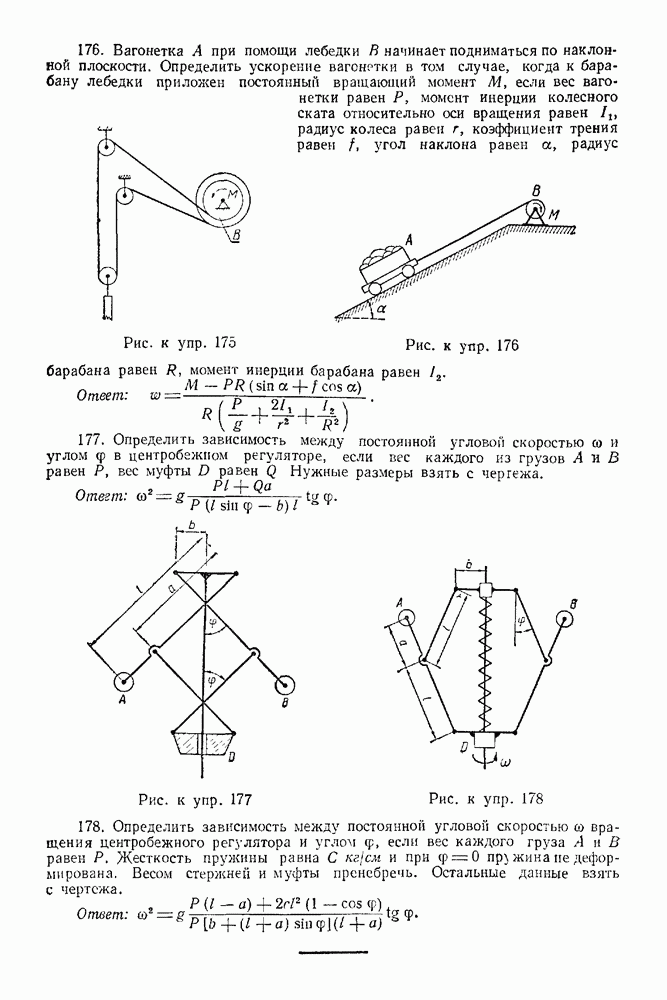
Упражнения
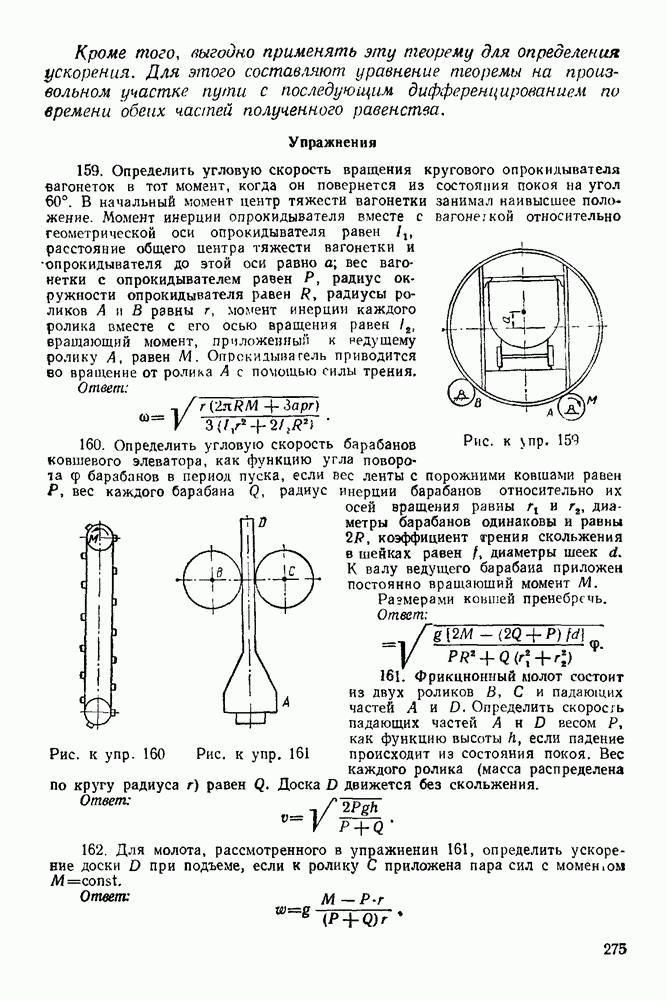
(см. скан)
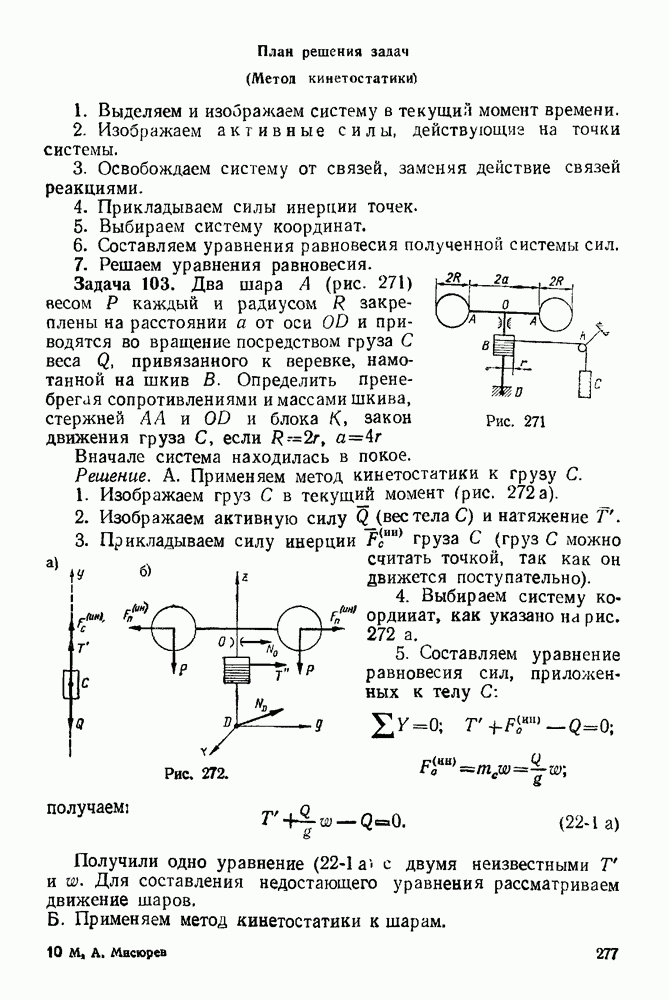
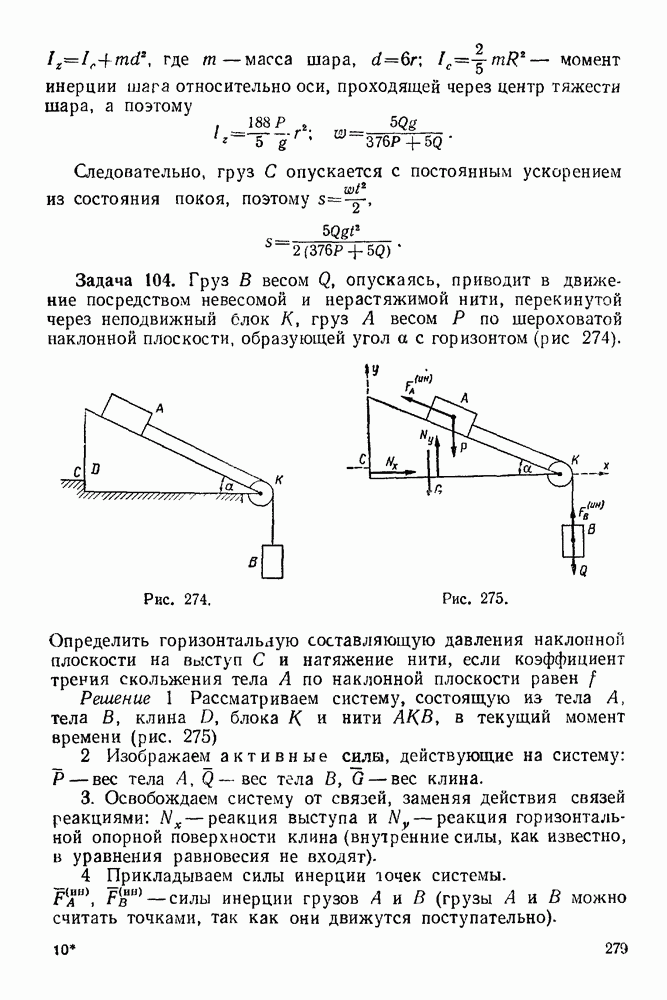
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть первая. СТАТИКА
- Предмет статики. Связи и реакции связей
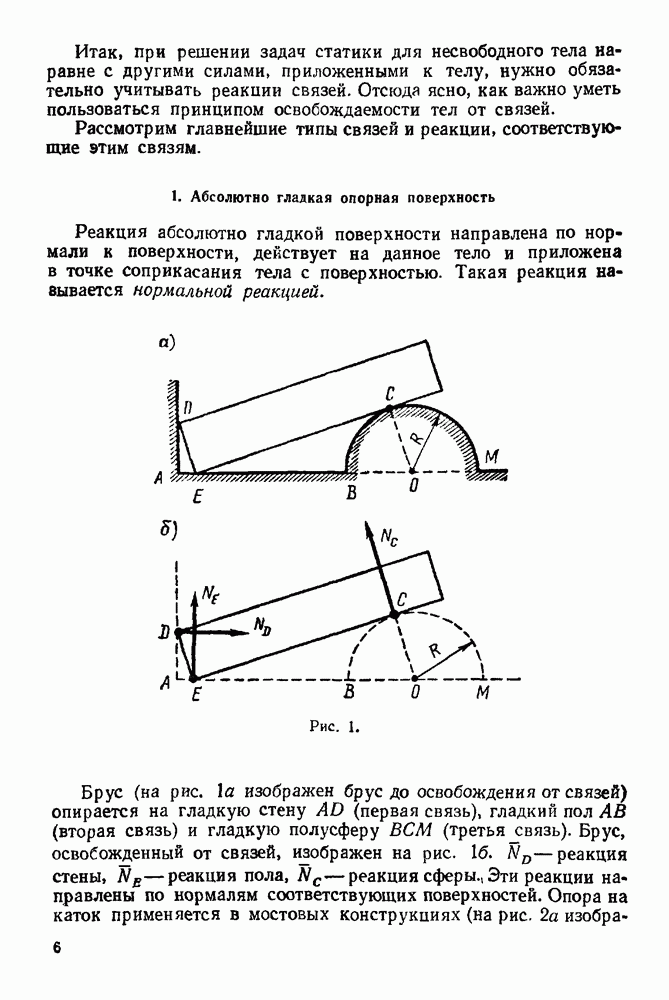
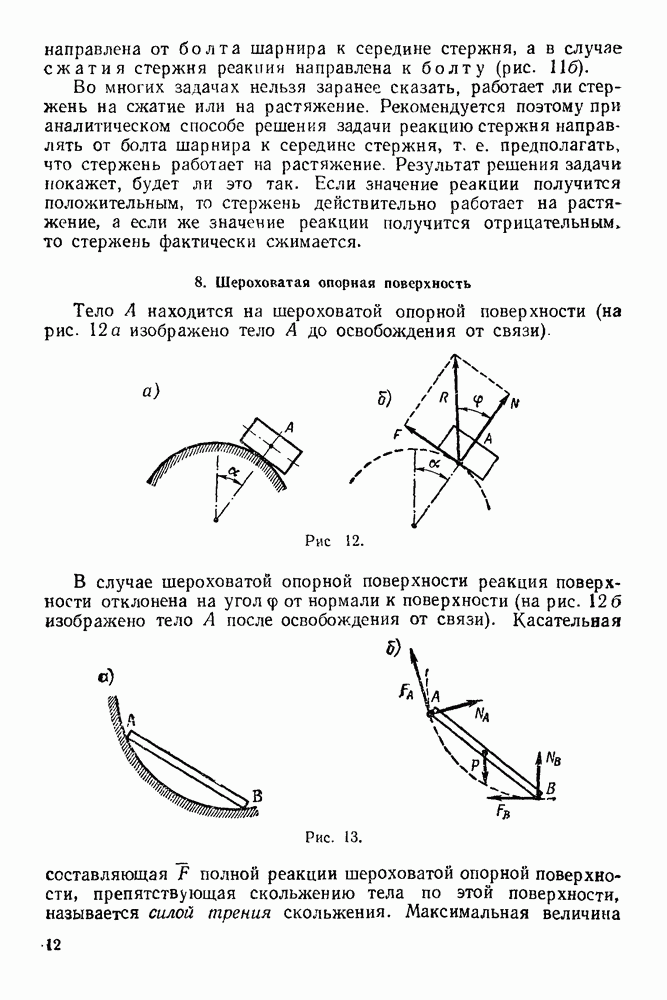
- 1. Абсолютно гладкая опорная поверхность
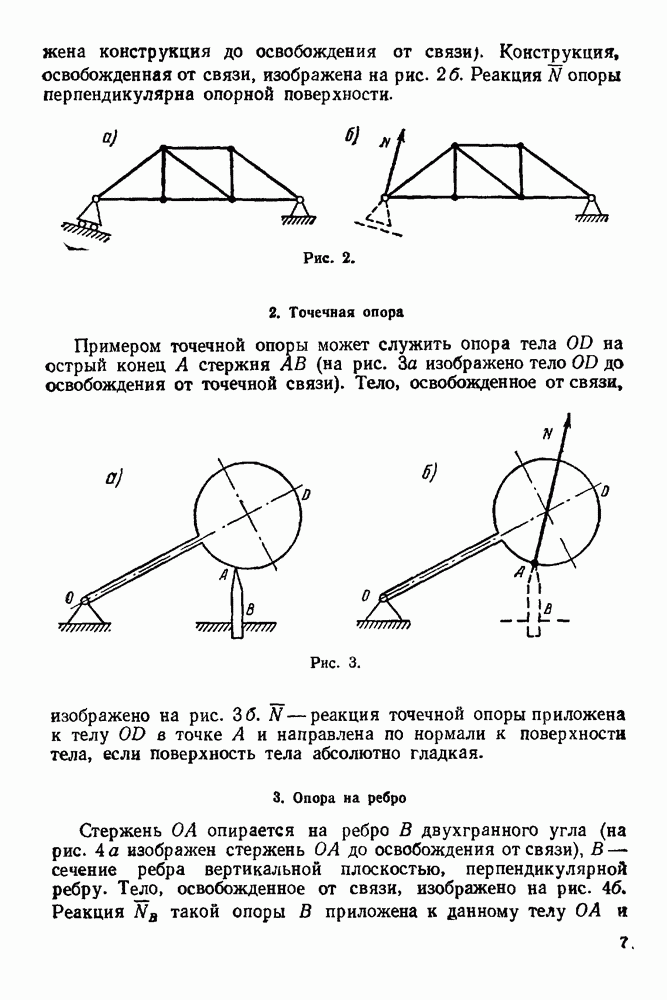
- 2. Точечная опора
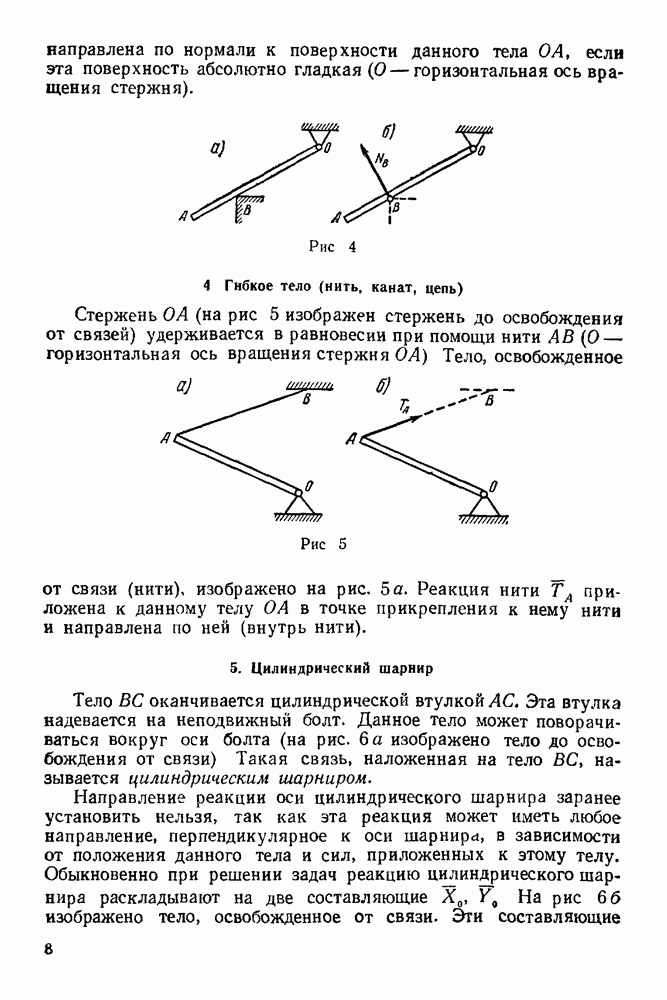
- 3. Опора на ребро
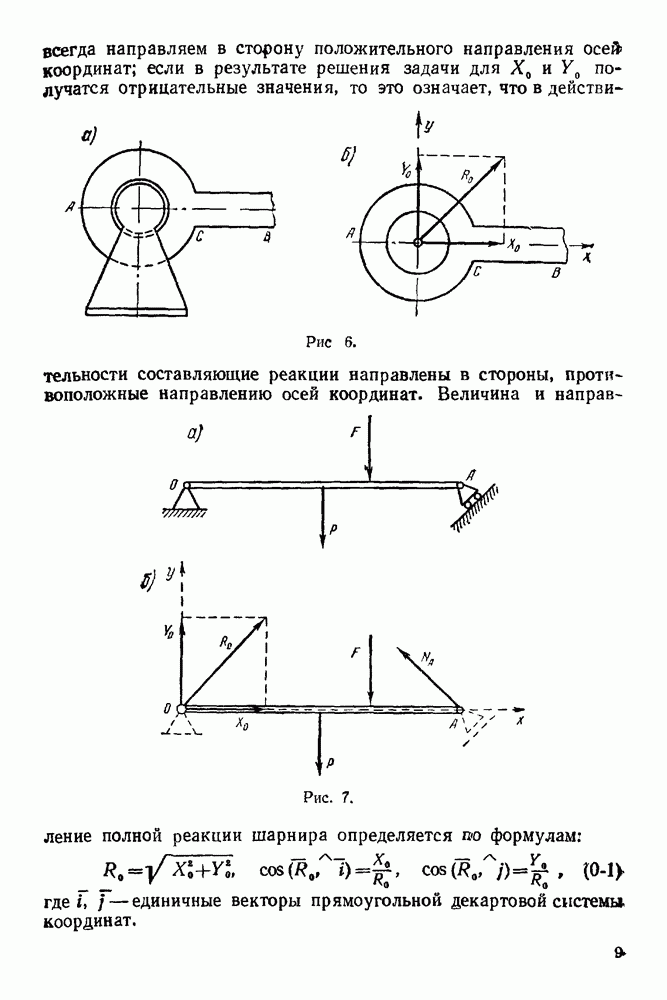
- 4. Гибкое тело (нить, канат, цепь)
- 5. Цилиндрический шарнир
- 6. Сферический шарнир
- 7. Стержневая опора
- 8. Шероховатая опорная поверхность
- 9. Неподвижная жесткая заделка
- I. ПЛОСКАЯ СИСТЕМА СИЛ
- 1-1. Равновесие трех сил
- 1-3. Равновесие какого угодно числа сил
- ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ
- ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
- 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует)
- 4-3. Решение задач на опрокидывание
- 4-4. Решение задач на равновесие тел при наличии трения
- 4-5. Решение задач на равновесие системы сочлененных тел
- ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА
- 5-3. Определение усилий в стержнях фермы
- 5-4. Метод сквозных сечений
- 5-5. Метод вырезывания узлов
- II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
- ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ
- Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ
- ГЛАВА VIII. РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
- ГЛАВА IX. ЦЕНТР ТЯЖЕСТИ
- Часть вторая. КИНЕМАТИКА
- 10-1. Предмет кинематики. Основные положения
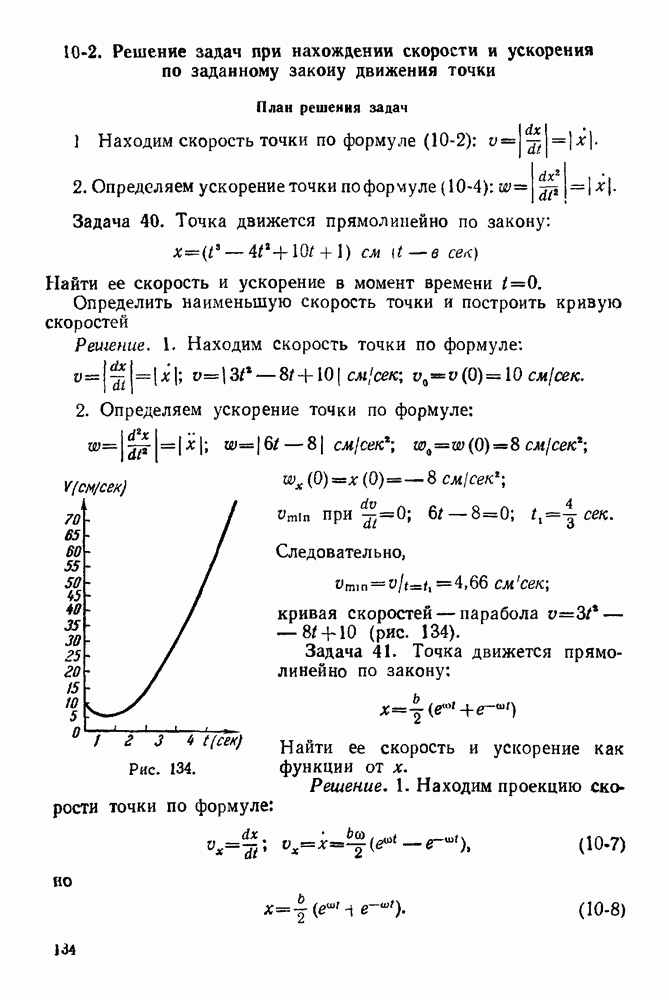
- 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки
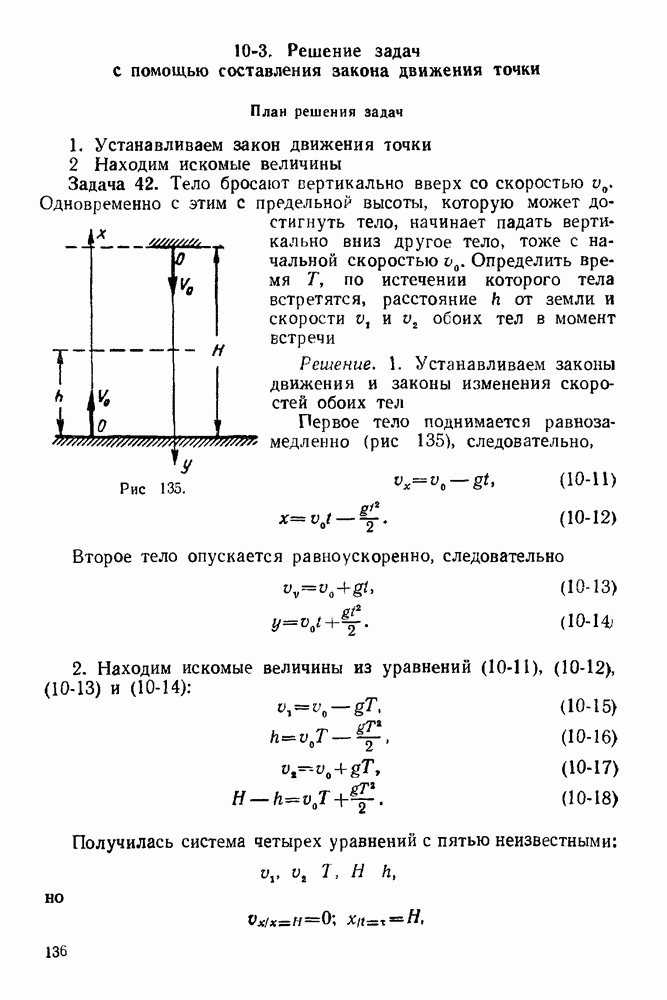
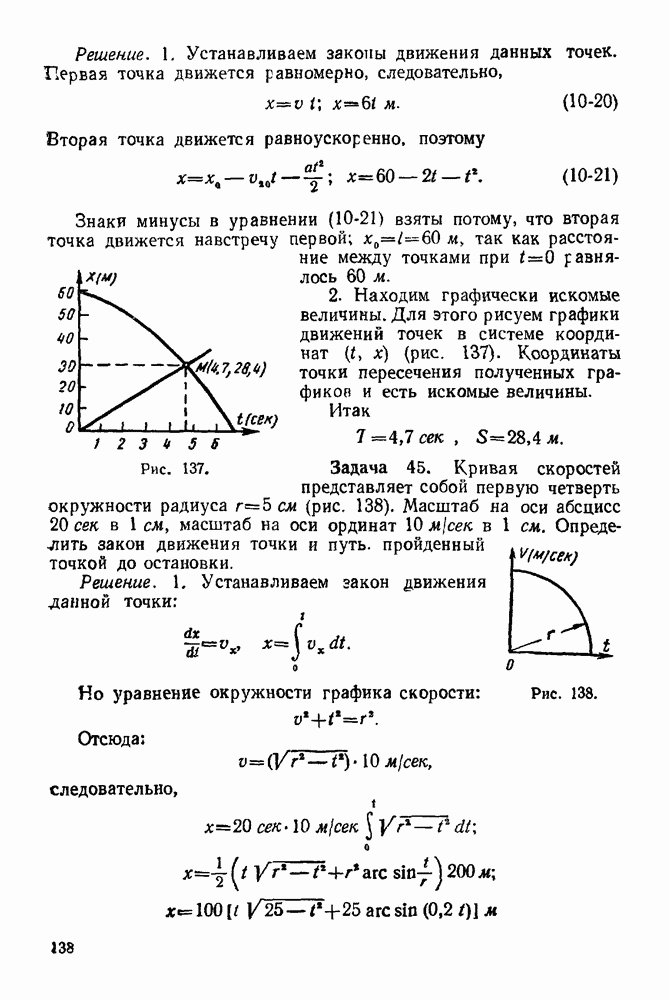
- 10-3. Решение задач с помощью составления закона движения точки
- ГЛАВА XI. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
- 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме
- 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи
- 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения
- 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи
- 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме
- IV. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- ГЛАВА XII. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА
- 12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела
- 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи
- 12-4. Решение задач в случае преобразования простейших движений твердого тела
- V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ
- 13-1. Основные положения теории сложного движения точки
- 13-2. Решение задач с помощью формулы сложения скоростей точки
- ГЛАВА XIV. СЛОЖЕНИЕ УСКОРЕНИЙ ТОЧКИ
- 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении
- 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси
- VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- 15-1. Основные положения теории плоскопараллельного движения твердого тела
- 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей
- 15-3. Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей
- ГЛАВА XVI. УСКОРЕНИЕ ТОЧЕК ТЕЛА В ПЛОСКОМ ДВИЖЕНИИ
- 16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений
- 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры
- ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ)
- Часть третья. ДИНАМИКА
- 18-1. Основные положения. Дифференциальные уравнения движения материальной точки
- 18-2. Первая основная задача динамики материальной точки
- 18-3. Вторая основная задача динамики материальной точки (обратная первой)
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
- 19-1. Теорема об изменении количества движения точки
- 19-2. Теорема об изменении момента количества движения точки
- 19-3. Теорема об изменении кинетической энергии точки
- ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
- XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- 21-1. Теорема о движении центра инерции системы
- 21-2. Теорема об изменении количества движения системы
- 21-3. Теорема об изменении момента количества движения системы
- 21-4. Теорема об изменении кинетической энергии системы
- ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ
- 21-1. Принцип Даламбера
- 22-2. Принцип возможных перемещений
- 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы)
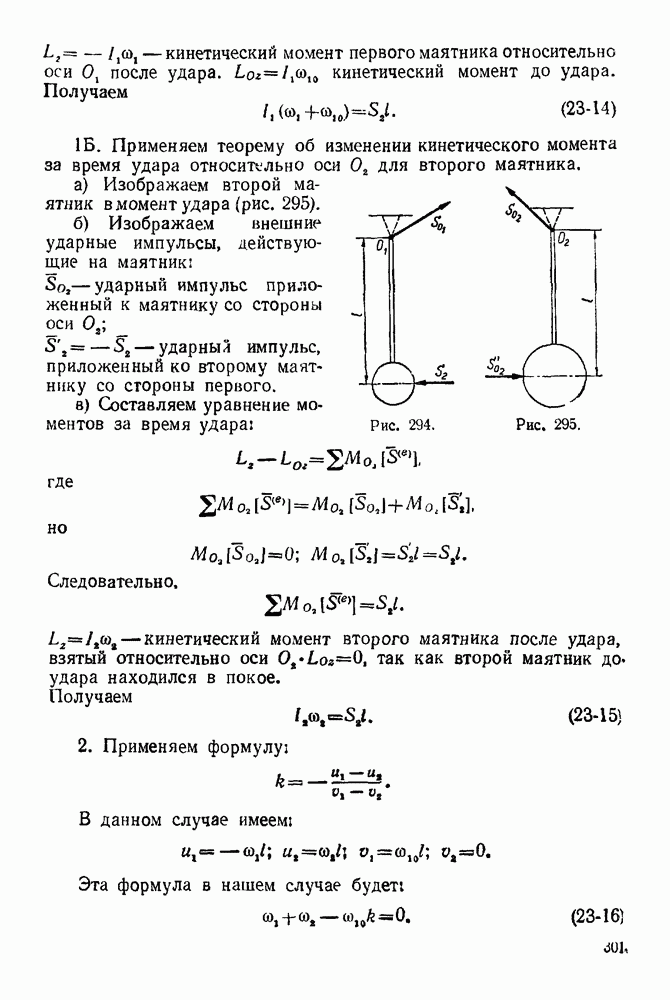
- ГЛАВА XXIII. УДАР