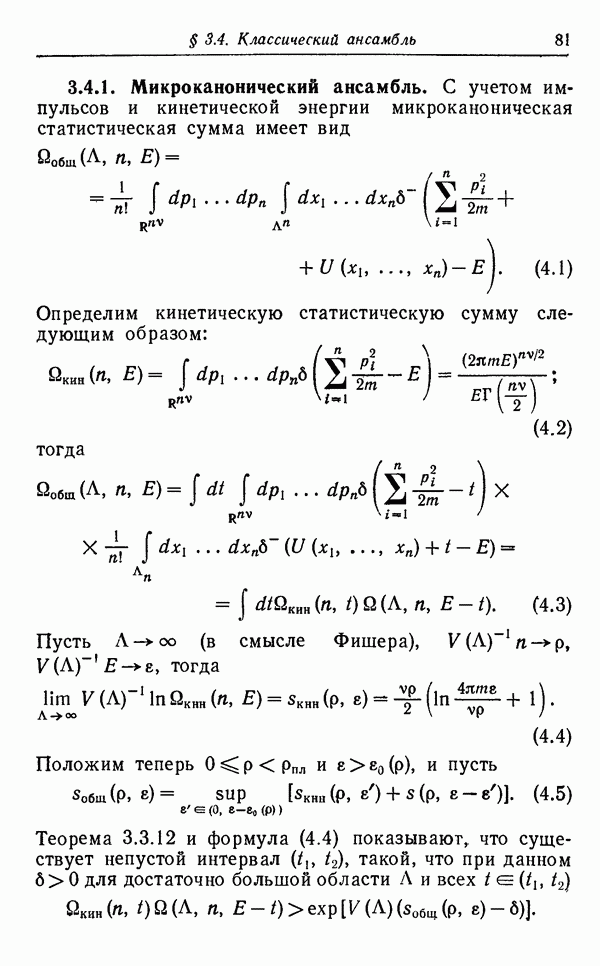| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.2. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
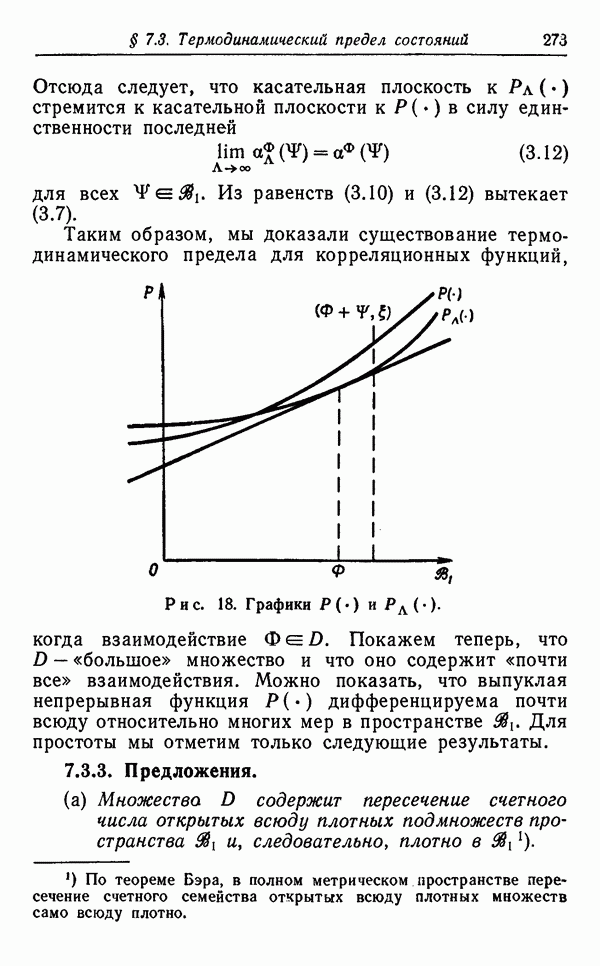
Корреляционные функции удовлетворяют различным системам линейных интегральных уравнений (в частности, уравнениям Кирквуда—Зальцбурга и Майера — Монтролла). Эти интегральные уравнения являются мощным средством изучения корреляционных функций при малых значениях активности.
4.2.1. Уравнения Кирквуда—Зальцбурга. Обозначим через  характеристическую функцию ограниченного, измеримого по Лебегу множества Л с
характеристическую функцию ограниченного, измеримого по Лебегу множества Л с  Положим
Положим

Предположим, что потенциал парного взаимодействия Ф устойчив и регулярен. Положим

и

где  Формулы (1.2) и (1.3) можно теперь переписать в виде
Формулы (1.2) и (1.3) можно теперь переписать в виде

Введем следующие обозначения:

Тогда

Положим  и введем ядро
и введем ядро

Подставляя (2.8) в (2.5), получим

где

Перемену порядка суммирования и интегрирования можно обосновать, используя условие устойчивости.
Если в формуле (2.11) воспользоваться определением (2.5) корреляционной функции  то получится, что
то получится, что

и

Уравнения (2.12) и (2.13) называются уравнениями Кирквуда — Зальцбурга  Они образуют неоднородную систему линейных уравнений относительно корреляционных функций
Они образуют неоднородную систему линейных уравнений относительно корреляционных функций  при
при 
4.2.2. Банаховы пространства  Пусть
Пусть  Обозначим через
Обозначим через  пространство последовательностей
пространство последовательностей  измеримых по Лебегу комплекснозначных функций
измеримых по Лебегу комплекснозначных функций  заданных на пространстве
заданных на пространстве  и таких, что
и таких, что

Из условия устойчивости (2.5) следует, что

так что  Перепишем теперь уравнения Кирквуда—Зальцбурга как уравнения относительно
Перепишем теперь уравнения Кирквуда—Зальцбурга как уравнения относительно  в пространстве Е.
в пространстве Е.
Введем линейный оператор  в Е полагая
в Е полагая

Оператор  идемпотентен, и его норма равна 1. Определим оператор К равенствами
идемпотентен, и его норма равна 1. Определим оператор К равенствами

Из условия устойчивости следует, что потенциал Ф ограничен снизу числом —  Отсюда, используя условие регулярности 4.1.2, получим оценку
Отсюда, используя условие регулярности 4.1.2, получим оценку

Итак, оператор К отображает пространство  в
в  Пользуясь введенными обозначениями и сформулированным результатом, мы можем переписать равенства (2.12) и (2.13) как уравнения в пространстве
Пользуясь введенными обозначениями и сформулированным результатом, мы можем переписать равенства (2.12) и (2.13) как уравнения в пространстве

в котором  при
при 
Мы покажем, что уравнение (2.20) можно рассматривать в одном из пространств  (а не только в
(а не только в  Для этого мы должны избавиться от множителя
Для этого мы должны избавиться от множителя  который возникает в оценке (2.19) из-за множителя
который возникает в оценке (2.19) из-за множителя  участвующего в определении (2.18). Переменная
участвующего в определении (2.18). Переменная  играет в равенстве (2.18) особую роль, но мы можем переставить переменные и
играет в равенстве (2.18) особую роль, но мы можем переставить переменные и
рассмотреть равенства, в которых роль  играет любая из переменных
играет любая из переменных  заменяется соответственно на
заменяется соответственно на  . Заметим теперь, что
. Заметим теперь, что

Отсюда следует, что для каждого набора  можно выбрать значение
можно выбрать значение  так, чтобы
так, чтобы

Условие (2.22) позволяет построить оператор  в пространстве
в пространстве  который для каждого набора
который для каждого набора  переводит функцию
переводит функцию  , а подстановка
, а подстановка  выбрана так, что
выбрана так, что  Поскольку корреляционные функции
Поскольку корреляционные функции  симметричны по всем своим т. аргументам, то уравнение (2.20) можно заменить на следующее;
симметричны по всем своим т. аргументам, то уравнение (2.20) можно заменить на следующее;

При этом оценка (2.19) заменится на

Поэтому оператор  отображает пространство
отображает пространство  в себя и его норма удовлетворяет оценке
в себя и его норма удовлетворяет оценке

Кроме уравнения (2.23), рассмотрим также уравнение

В уравнениях (2.23) и (2.26) параметр  может принимать и комплексные значения. Ввиду оценки (2.24) норма линейных операторов, стоящих в правых частях этих уравнений, не превосходит числа
может принимать и комплексные значения. Ввиду оценки (2.24) норма линейных операторов, стоящих в правых частях этих уравнений, не превосходит числа

Поэтому каждое из уравнений (2.23) и (2.26) имеет единственное решение в пространстве 

и

если только выражение (2.27) не превосходит 1, т. е. если

Последнее неравенство может быть удовлетворено, если (возьмем 

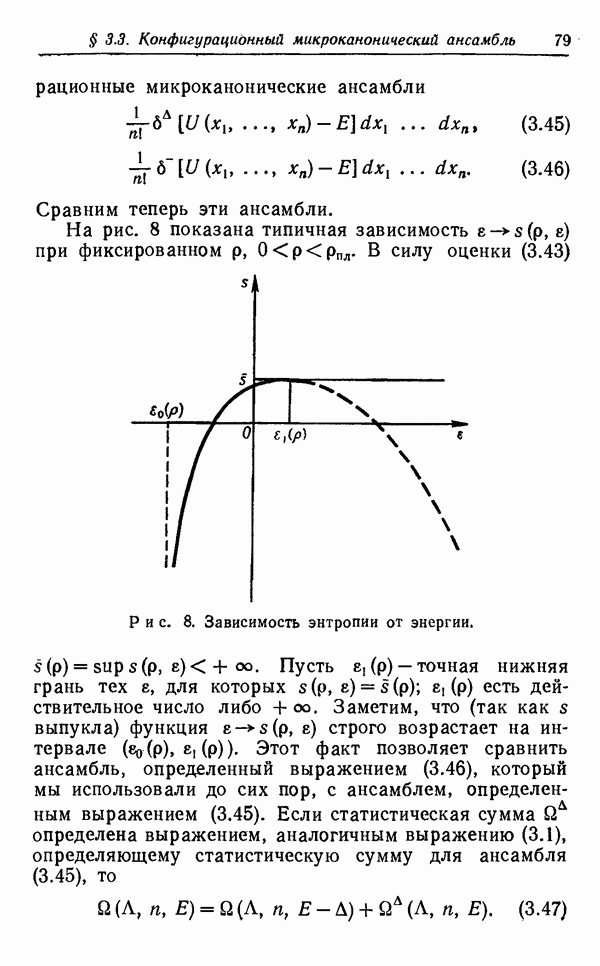
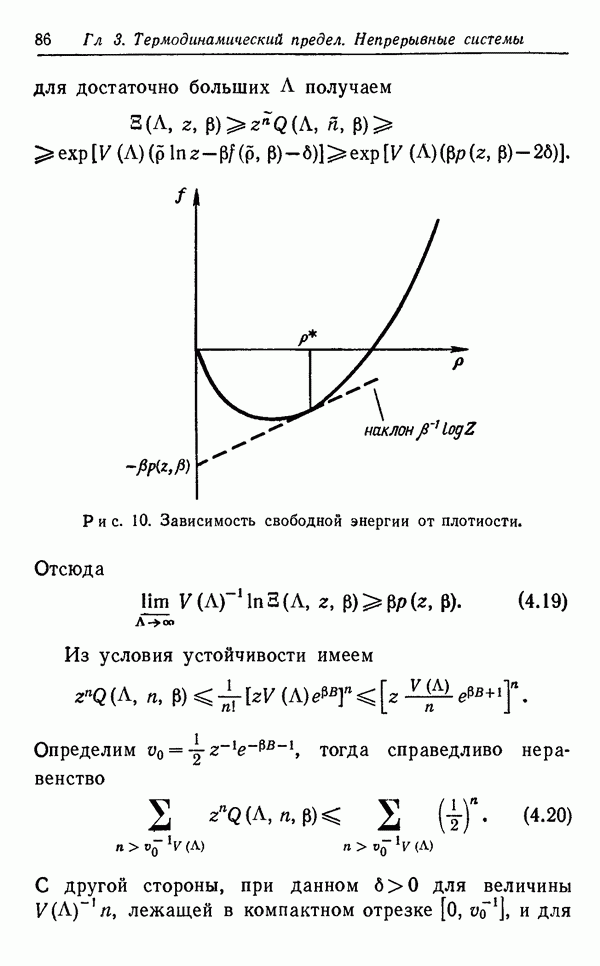
Описанная ситуация изображена на рис. 11.

Рис. 11. Неравенство  выполняется в заштрихованной области.
выполняется в заштрихованной области.
Из оценок (2.15) и единственности решения уравнения (2.28) следует, что это решение служит аналитическим продолжением корреляционных функций на множество комплексных значений активности  , удовлетворяющих условию (2.31).
, удовлетворяющих условию (2.31).
Для вещественных положительных значений активности из определений (2.4) и (2.5) следует, что

Из выражения (2.28) следует, что функция, стоящая в левой части (2.32), продолжается до аналитической функции параметра  внутри круга (2.31). Это показывает, что внутри этого круга большая статистическая сумма
внутри круга (2.31). Это показывает, что внутри этого круга большая статистическая сумма  которая является аналитической функцией от
которая является аналитической функцией от  не обращается в нуль. Таким образом, определение (2.5) корреляционных функций имеет смысл для всех комплексных
не обращается в нуль. Таким образом, определение (2.5) корреляционных функций имеет смысл для всех комплексных  лежащих в круге (2.31), и при аналитическом продолжении оно приводит к той же функции, что и уравнение (2.28).
лежащих в круге (2.31), и при аналитическом продолжении оно приводит к той же функции, что и уравнение (2.28).
4.2.3. Теорема. Пусть Ф — устойчивый регулярный потенциал парного взаимодействия, и пусть комплексное число  удовлетворяет условию
удовлетворяет условию

Тогда большая статистическая сумма  не обращается в нуль в круге (2.33). Если определить корреляционные функции
не обращается в нуль в круге (2.33). Если определить корреляционные функции  равенством (2.5) для всех
равенством (2.5) для всех  из круга (2.33), то существуют предельные корреляционные функции
из круга (2.33), то существуют предельные корреляционные функции  и такая положительная убывающая функция
и такая положительная убывающая функция  что
что

и

если параметры  удовлетворяют условию (2.30), а к обозначает наименьшее расстояние от точек
удовлетворяют условию (2.30), а к обозначает наименьшее расстояние от точек  до границы сосуда
до границы сосуда  .
.
Последовательность  функций
функций  и последовательность
и последовательность  функций
функций  являются единственными решениями уравнений (2.23) и (2.26) соответственно в пространстве
являются единственными решениями уравнений (2.23) и (2.26) соответственно в пространстве  если только
если только  удовлетворяет условию (2.30) (в частности, если
удовлетворяет условию (2.30) (в частности, если  последовательности
последовательности  аналитически зависят от
аналитически зависят от 
Нам осталось доказать только оценку (2.35). Как мы сейчас убедимся, она получается почленным сравнением степенных рядов для 
Пусть  тогда
тогда

Пусть  — множество точек области
— множество точек области  , отстоящих от ее границы больше чем на
, отстоящих от ее границы больше чем на  .
.
Из определений (1.4) и (2.9) и неравенств (2.36) следует, что

где мы обозначили

Поэтому из определений оператора К (формулы (2.17) и (2.18)) и оператора  следует
следует

или, переходя к операторной норме,

где

Обозначим через  множество точек сосуда
множество точек сосуда  стоящих от его границы больше, чем на
стоящих от его границы больше, чем на  ; из оценки (2.39) вытекают неравенства
; из оценки (2.39) вытекают неравенства

и

из которых следует, что

Поэтому

Заменяя в последней оценке 6 на  мы получим неравенство
мы получим неравенство

справедливое при  . С другой стороны,
. С другой стороны,

Из оценок (2.42), (2.43) и (2.44) получаем

Правая часть неравенства (2.45) стремится к нулю, когда  стремятся к бесконечности. Полагая
стремятся к бесконечности. Полагая  найдем, что существует положительная убывающая и не зависящая от области
найдем, что существует положительная убывающая и не зависящая от области  функция
функция  такая, что
такая, что

и

Используя уравнения (2.28) и (2.29), окончательно получим, что

4.2.4. Дополнения к теореме 4.2.3.
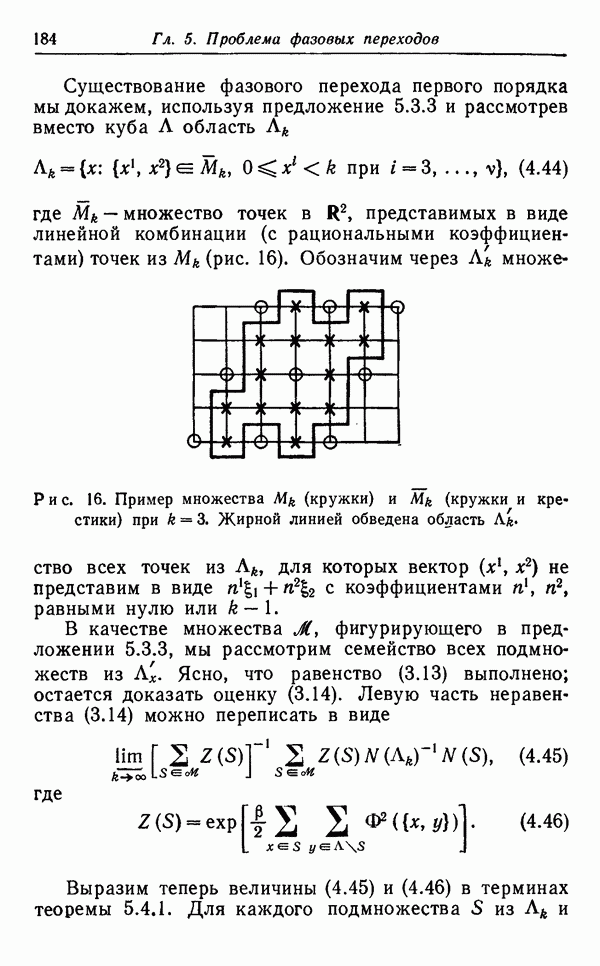
(а) Если К — компактное подмножество области, выделяемое неравенством (2.33) и  то функцию
то функцию  связанную с
связанную с  равенством
равенством  можно выбрать так, чтобы она не зависела от
можно выбрать так, чтобы она не зависела от  при
при  Это очевидно следует из оценки (2.45).
Это очевидно следует из оценки (2.45).
(б) Если функция  непрерывна в
непрерывна в  (а это обычный случай), то можно рассматривать банахово пространство ограниченных непрерывных функций вместо ограниченных измеримых; в частности, функции
(а это обычный случай), то можно рассматривать банахово пространство ограниченных непрерывных функций вместо ограниченных измеримых; в частности, функции  в этом случае непрерывны.
в этом случае непрерывны.
4.2.5. Уравнения Майера — Монтролла. Положим

Можно показать, что

Эти интегральные уравнения называются уравнениями Майера — Монтролла; они образуют неоднородную систему линейных уравнений относительно корреляционных функций  при
при  Вместо уравнений Кирквуда—Зальцбурга для изучения предела корреляционных функций при неограниченном возрастании объема можно воспользоваться уравнениями Майера — Монтролла. Но они оказываются полезными только при изучении положительных потенциалов, или потенциалов с твердой сердцевиной.
Вместо уравнений Кирквуда—Зальцбурга для изучения предела корреляционных функций при неограниченном возрастании объема можно воспользоваться уравнениями Майера — Монтролла. Но они оказываются полезными только при изучении положительных потенциалов, или потенциалов с твердой сердцевиной.
4.2.6. Решетчатые системы. Рассмотрим классическую решетчатую систему (в смысле 2.4). Предположим, что  и пусть
и пусть  если только число элементов X не равно 1 или 2. Положим
если только число элементов X не равно 1 или 2. Положим

Тот факт, что  эквивалентен следующему свойству функции
эквивалентен следующему свойству функции 

Теперь, считая  потенциалом парного взаимодействия, мы можем построить «дискретную» теорию, совершенно аналогичную соответствующей теории для непрерывных систем. При этом все интегралы по
потенциалом парного взаимодействия, мы можем построить «дискретную» теорию, совершенно аналогичную соответствующей теории для непрерывных систем. При этом все интегралы по  очевидно, заменятся суммами по
очевидно, заменятся суммами по  Заметим, что из условия (2.54) вытекают условия устойчивости (ввиду соотношения (4.8)
Заметим, что из условия (2.54) вытекают условия устойчивости (ввиду соотношения (4.8)
гл. 2) и регулярности парного потенциала. Для доказательства последнего утверждения заметим, что

Здесь мы воспользовались сверхаддитивностью функции  на полуоси
на полуоси  Мы предлагаем читателю самостоятельно переформулировать теорему
Мы предлагаем читателю самостоятельно переформулировать теорему
4.2.3 для данного случая.
Укажем другой способ изучения решетчатых систем, применимый не только к системам с парным взаимодействием. Этот подход аналогичен подходу, основанному на уравнениях Кирквуда — Зальцбурга, но существенно использует тот факт, что две различные частицы не могут занимать одну ячейку.
Потенциал взаимодействия Ф является функцией от конечных подмножеств решетки  Предположим, что
Предположим, что  если
если  (т. е. если подмножество X содержит только одну точку решетки
(т. е. если подмножество X содержит только одну точку решетки  химический потенциал войдет в активность
химический потенциал войдет в активность  Предположим также, что
Предположим также, что

Это условие более обременительно, чем условие  использованное в п. 2.4, но ему удовлетворяют все парные потенциалы, для которых выполнено (2.54). Введем обозначения
использованное в п. 2.4, но ему удовлетворяют все парные потенциалы, для которых выполнено (2.54). Введем обозначения

Пусть X — конечное подмножество решетки  Обозначим через X множество, получаемое удалением одной
Обозначим через X множество, получаемое удалением одной
точки из X, например, первой в смысле лексикографического порядка  Введем обозначения:
Введем обозначения:

В определении (2.62) сумма  распространяется на все наборы
распространяется на все наборы  непустых подмножеств множества
непустых подмножеств множества  покрывающие
покрывающие  |т. е.
|т. е.  Отметим тождества
Отметим тождества

и

Из предположения (2.56) следует неравенство

Отсюда, учитывая сверхаддитивность функции  при
при  получаем, что
получаем, что

и поэтому

Пусть  если
если  в противном случае. Используя соотношения (2.63) и (2.64), мы получим
в противном случае. Используя соотношения (2.63) и (2.64), мы получим

и поэтому

4.2.7. Теорема. Пусть Е — банахово пространство ограниченных комплекснозначных функций, заданных на непустых подмножествах решетки  наделенное равномерной нормой. Пусть X — конечное подмножество в
наделенное равномерной нормой. Пусть X — конечное подмножество в  Обозначим через X подмножество, получающееся удалением из X первого элемента (в смысле лексикографического порядка в
Обозначим через X подмножество, получающееся удалением из X первого элемента (в смысле лексикографического порядка в  Определим оператор К, действующий в Е, равенством да
Определим оператор К, действующий в Е, равенством да

где  и К (X, Т) определяются равенствами (2.59) и (2.62) соответственно, а первое слагаемое в квадратных скобках
и К (X, Т) определяются равенствами (2.59) и (2.62) соответственно, а первое слагаемое в квадратных скобках  отсутствует при
отсутствует при  Полагая
Полагая

мы получим, что

при условии, что

В круге на плоскости  в котором выполняется условие (2.72), большая статистическая сумма В, определенная равенством (2.57), не обращается в нуль и вектор
в котором выполняется условие (2.72), большая статистическая сумма В, определенная равенством (2.57), не обращается в нуль и вектор  задаваемый выражением (2.58), является единственным решением в пространстве Е следующего уравнения-.
задаваемый выражением (2.58), является единственным решением в пространстве Е следующего уравнения-.

где  если
если  в противном случае. Для каждого
в противном случае. Для каждого  можно указать такое конечное множество А с:
можно указать такое конечное множество А с:  что
что

если  является единственным решением уравнения
является единственным решением уравнения

принадлежащим пространству Е. Вектор  аналитически зависит от
аналитически зависит от  если
если  лежит в области (2.72).
лежит в области (2.72).
Докажем сначала неравенство (2.71). Заметим, что если а — вещественное число, то кривая

представляет собой окружность, симметричную относительно вещественной оси. Поэтому, учитывая оценку (2.67), достаточно доказать, что

для положительных вещественных значений  . А для них это следует из неравенства
. А для них это следует из неравенства  и того факта, что правая часть в (2.76) меньше единицы (ввиду условия (2.72)).
и того факта, что правая часть в (2.76) меньше единицы (ввиду условия (2.72)).
Уравнение (2.73) в точности совпадает с (2.68). Остальные утверждения доказываются точно так же, как при доказательстве теоремы 4.2.3.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- Глава 1. ТЕРМОДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ. АНСАМБЛИ
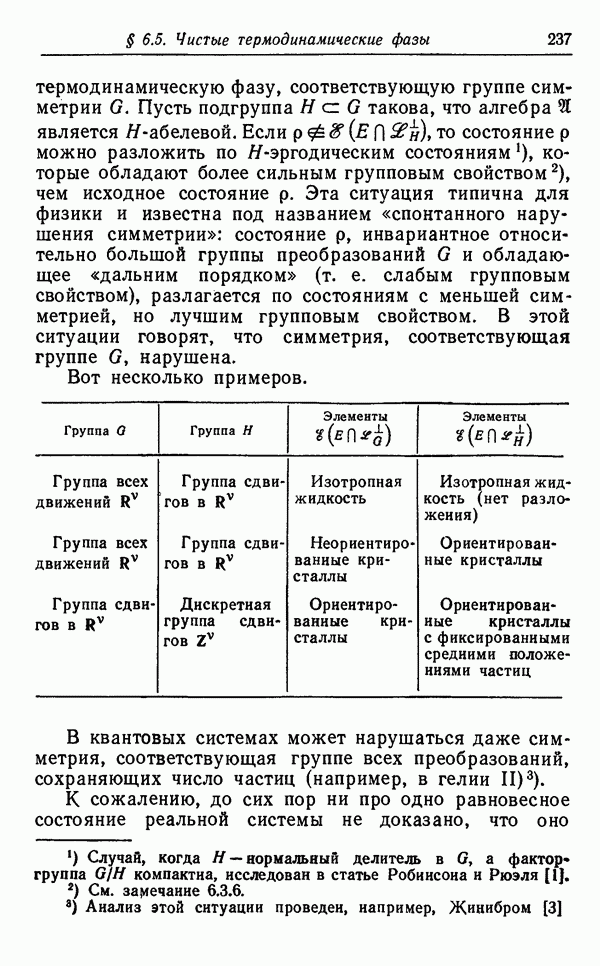
- § 1.2. КЛАССИЧЕСКИЕ СИСТЕМЫ И АНСАМБЛИ
- 1.2.2. Классические непрерывные системы частиц с твердыми сердцевинами.
- 1.2.3. Классические решетчатые системы.
- § 1.3. КВАНТОВЫЕ СИСТЕМЫ И АНСАМБЛИ
- 1.3.2. Квантовые непрерывные системы с твердыми сердцевинами.
- 1.3.3. Квантовые решетчатые системы.
- § 1.4. РАВНОВЕСНЫЕ СОСТОЯНИЯ И ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- Глава 2. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ: РЕШЕТЧАТЫЕ СИСТЕМЫ
- § 2.2. ВЗАИМОДЕЙСТВИЯ В КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМАХ
- § 2.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМ
- § 2.4. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КЛАССИЧЕСКИХ РЕШЕТЧАТЫХ СИСТЕМ
- § 2.5. НЕКОТОРЫЕ НЕРАВЕНСТВА ДЛЯ КВАНТОВЫХ СИСТЕМ
- Глава 3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ: НЕПРЕРЫВНЫЕ СИСТЕМЫ
- § 3.1. ВЗАИМОДЕЙСТВИЯ В КЛАССИЧЕСКИХ НЕПРЕРЫВНЫХ СИСТЕМАХ
- § 3.2. УСТОЙЧИВЫЕ ВЗАИМОДЕЙСТВИЯ
- § 3.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КОНФИГУРАЦИОННОГО МИКРОКАНОНИЧЕСКОГО АНСАМБЛЯ
- § 3.4. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КЛАССИЧЕСКИХ АНСАМБЛЕЙ
- § 3.5. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КВАНТОВЫХ АНСАМБЛЕЙ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 4. СТЕПЕННЫЕ РАЗЛОЖЕНИЯ ПРИ МАЛЫХ ПЛОТНОСТЯХ И КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- § 4.2. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
- § 4.3. РЯДЫ МАЙЕРА И ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ
- § 4.4. АЛГЕБРАИЧЕСКИЙ МЕТОД
- § 4.5. ПОЛОЖИТЕЛЬНЫЕ ПОТЕНЦИАЛЫ
- § 4.6. КВАНТОВЫЕ СИСТЕМЫ
- § 4.7. ПОСТРОЕНИЕ ГИЛЬБЕРТОВА ПРОСТРАНСТВА
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 5. ПРОБЛЕМА ФАЗОВЫХ ПЕРЕХОДОВ
- § 5.2. ОТСУТСТВИЕ ФАЗОВЫХ ПЕРЕХОДОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 5.3. СУЩЕСТВОВАНИЕ ФАЗОВОГО ПЕРЕХОДА ПЕРВОГО РОДА ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- § 5.4. НЕРАВЕНСТВА ГРИФФИТСА
- § 5.5. ТЕОРЕМА МЕРМИНА И ВАГНЕРА
- § 5.6. ОДНОМЕРНЫЕ СИСТЕМЫ
- § 5.7. ЗАМЕЧАНИЯ О ФАЗОВЫХ ПЕРЕХОДАХ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 6. ГРУППОВАЯ ИНВАРИАНТНОСТЬ ФИЗИЧЕСКИХ СОСТОЯНИЙ
- § 6.2. ИНВАРИАНТНЫЕ СОСТОЯНИЯ
- § 6.3. ЭРГОДИЧЕСКИЕ СОСТОЯНИЯ
- § 6.4. РАЗЛОЖЕНИЕ ИНВАРИАНТНЫХ СОСТОЯНИЙ ПО ЭРГОДИЧЕСКИМ
- § 6.5. ЧИСТЫЕ ТЕРМОДИНАМИЧЕСКИЕ ФАЗЫ КАК ЭРГОДИЧЕСКИЕ СОСТОЯНИЯ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 7. СОСТОЯНИЯ В СТАТИСТИЧЕСКОЙ МЕХАНИКЕ
- § 7.2. ЭНТРОПИЯ
- § 7.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ СОСТОЯНИЙ
- § 7.4. ВАРИАЦИОННЫЙ ПРИНЦИП
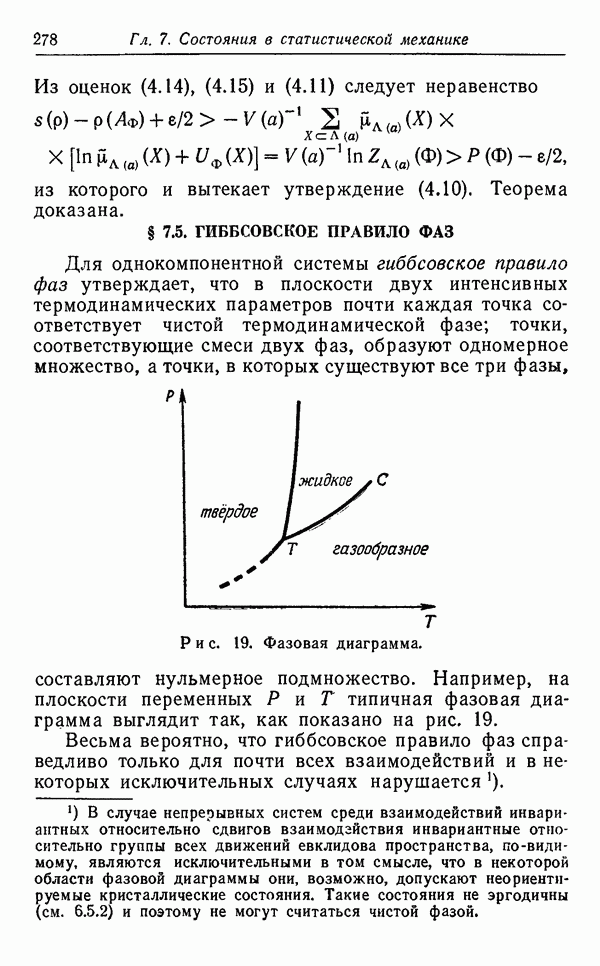
- § 7.5. ГИББСОВСКОЕ ПРАВИЛО ФАЗ
- § 7.6. ЭВОЛЮЦИЯ ВО ВРЕМЕНИ КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМ И ГРАНИЧНЫЕ УСЛОВИЯ КУБО — МАРТИНА — ШВИНГЕРА
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- ДОБАВЛЕНИЕ. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
- Д.1. НЕКОТОРЫЕ ТЕРМИНЫ
- Д.2. ОБЩИЕ СВЕДЕНИЯ О В-АЛГЕБРАХ
- Д.3. СОСТОЯНИЯ НА В-АЛГЕБРАХ
- Д.4. АЛГЕБРЫ ФОН НЕЙМАНА
- Д.5. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ НА КОМПАКТНЫХ ВЫПУКЛЫХ МНОЖЕСТВАХ
- Д.6. ГРУППЫ С ИНВАРИАНТНЫМ СРЕДНИМ
- ЛИТЕРАТУРА
- ПРИЛОЖЕНИЕ. ОБЗОР РЯДА НЕДАВНИХ РЕЗУЛЬТАТОВ
- § 1. ГИББСОВСКИЕ СОСТОЯНИЯ ДЛЯ БЕСКОНЕЧНЫХ СИСТЕМ
- § 2. ЭКВИВАЛЕНТНОСТЬ АНСАМБЛЕЙ И ЦЕНТРАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ЧИСЛА ЧАСТИЦ И ЭНЕРГИИ
- § 3. ЯВЛЕНИЕ РАЗДЕЛЕНИЯ ФАЗ ПРИ ФАЗОВОМ ПЕРЕХОДЕ ПЕРВОГО РОДА В РЕШЕТЧАТЫХ МОДЕЛЯХ ГАЗА
- § 4. НЕКОТОРЫЕ НОВЫЕ РЕЗУЛЬТАТЫ ОБ ОДНОМЕРНЫХ МОДЕЛЯХ
- § 5. СУЩЕСТВОВАНИЕ ФАЗОВОГО ПЕРЕХОДА В СПИНОВЫХ МОДЕЛЯХ
- § 6. КИНЕТИКА БЕСКОНЕЧНЫХ СИСТЕМ
- § 7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- ЛИТЕРАТУРА К ПРИЛОЖЕНИЮ