| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7.6. ЭВОЛЮЦИЯ ВО ВРЕМЕНИ КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМ И ГРАНИЧНЫЕ УСЛОВИЯ КУБО — МАРТИНА — ШВИНГЕРА
В этом параграфе мы кратко опишем результаты, связанные с временной эволюцией квантовых решетчатых систем. Эти результаты по существу относятся к равновесной статистической механике, и техника, используемая для их доказательства, близка по духу к технике предыдущих параграфов.
Введем норму  в пространстве
в пространстве 

и определим банахово пространство  как пополнение
как пополнение  по этой норме.
по этой норме.
Для системы с взаимодействием Ф, занимающей конечную область  развитие во времени определяется однопараметрической группой автоморфизмов алгебры
развитие во времени определяется однопараметрической группой автоморфизмов алгебры  которые переводят «наблюдаемую» А при
которые переводят «наблюдаемую» А при  в «наблюдаемую» в момент времени
в «наблюдаемую» в момент времени  по формуле
по формуле

где

7.6.1. Лемма. Пусть  тогда
тогда

В формуле

положим

и заметим, что можно ограничиться суммированием по множествам  удовлетворяющим условиям
удовлетворяющим условиям  Здесь
Здесь  при
при  Заметим, что множество
Заметим, что множество  состоит не более чем из
состоит не более чем из  элементов; поэтому
элементов; поэтому

Воспользуемся теперь тем, что

Используя эту оценку в (6.6), мы и получим неравенство (6.4).
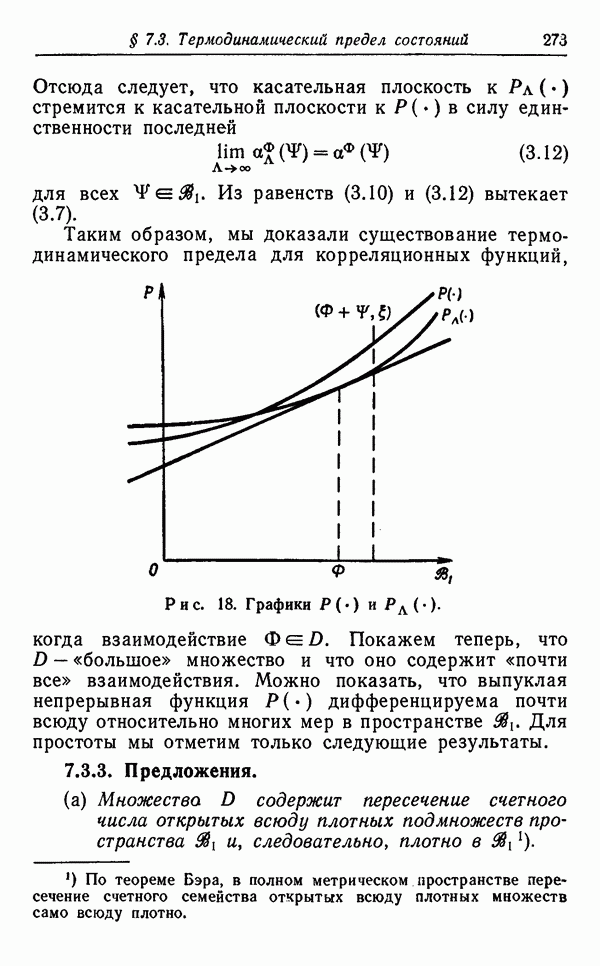
7.6.2. Теорема. Пусть взаимодействие Фе. Существует непрерывная в сильной топологии однопараметрическая группа автоморфизмов  определяемая следующим образом. Пусть
определяемая следующим образом. Пусть  при некотором конечном
при некотором конечном  и пусть область А стремится к бесконечности в том смысле, что каждое конечное подмножество решетки
и пусть область А стремится к бесконечности в том смысле, что каждое конечное подмножество решетки  в конце концов попадает в область А. Тогда
в конце концов попадает в область А. Тогда

Доказательство состоит из четырех пунктов.
а) Легко убедиться в почленном равенстве

Если  то из соотношений (6.4) и (6.2) следует, что равенство
то из соотношений (6.4) и (6.2) следует, что равенство

определяет 
б) Отображение  по непрерывности продолжается до автоморфизма алгебры
по непрерывности продолжается до автоморфизма алгебры  .
.
(в) Если числа  лежат в интервале
лежат в интервале  то
то

Мы можем определить  для всех вещественных значений
для всех вещественных значений  так, чтобы равенство (6.10) выполнялось при всех
так, чтобы равенство (6.10) выполнялось при всех  Тогда для всех
Тогда для всех  будет выполняться и равенство (6.9).
будет выполняться и равенство (6.9).
(г) Из соотношений (6.8) и (6.4) следует, что  при малых
при малых  является суммой сходящегося степенного ряда. Поэтому
является суммой сходящегося степенного ряда. Поэтому

для всех элементов Лей. На этом доказательство теоремы заканчивается.
7.6.3. Теорема. Пусть  определяется, как в теореме 7.5.1. Тогда справедливы следующие утверждения:
определяется, как в теореме 7.5.1. Тогда справедливы следующие утверждения:
а) инвариантность  для всех
для всех 
б) граничные условия Кубо—Мартина—Швингера (КМШ): Для любых двух элементов  существует ограниченная непрерывная функция
существует ограниченная непрерывная функция  определенная в полосе
определенная в полосе  аналитическая в области
аналитическая в области  и такая, что для всех вещественных
и такая, что для всех вещественных 

Очевидно, что инвариантность достаточно доказать только для операторов  при конечном
при конечном  Из
Из
7.3.4 следует

где  в смысле Ван Хова. Полезно заметить, что равенство (6.13) остается справедливым, если область
в смысле Ван Хова. Полезно заметить, что равенство (6.13) остается справедливым, если область  , заменить на произвольное непустое конечное подмножество решетки
, заменить на произвольное непустое конечное подмножество решетки  — на произвольный элемент алгебры 91 при условии, что
— на произвольный элемент алгебры 91 при условии, что  в правой части равенства (6.13) подходящим образом аппроксимировано элементами из
в правой части равенства (6.13) подходящим образом аппроксимировано элементами из  В силу теоремы 7.6.2 по заданному
В силу теоремы 7.6.2 по заданному  можно найти конечное подмножество
можно найти конечное подмножество  такое, что
такое, что

и, значит,

где мы воспользовались коммутативностью  Если в равенстве (6.13) заменить
Если в равенстве (6.13) заменить  , на
, на  на
на  и воспользоваться свойством (6.14), то получим
и воспользоваться свойством (6.14), то получим

и, следовательно, 

что и доказывает утверждение 
Для того чтобы установить граничные условия КМШ, рассмотрим целую функцию  определяемую равенством
определяемую равенством

Здесь  Используя свойство (6.14), получим, что при всех вещественных
Используя свойство (6.14), получим, что при всех вещественных 

Каждая из функций  так же как и ее производная
так же как и ее производная  ограничена в полосе
ограничена в полосе  Кроме того, при
Кроме того, при  справедливы следующие оценки, равномерные по
справедливы следующие оценки, равномерные по  :
:

и

Поэтому функции  ограничены в полосе
ограничены в полосе  равномерно по А и мы можем так выбрать последовательность областей
равномерно по А и мы можем так выбрать последовательность областей  чтобы функции
чтобы функции  сходились равномерно на каждом компактном подмножестве этой полосы. Предел
сходились равномерно на каждом компактном подмножестве этой полосы. Предел  этой последовательности функций
этой последовательности функций  очевидно, удовлетворяет граничным условиям КМШ.
очевидно, удовлетворяет граничным условиям КМШ.
Теперь мы должны избавиться от условия  Пусть последовательность
Пусть последовательность  принадлежащая объединению
принадлежащая объединению  , а сходится по норме к некоторому элементу
, а сходится по норме к некоторому элементу  При этом функции
При этом функции  стремятся к своим пределам равномерно.
стремятся к своим пределам равномерно.
Поэтому то же самое верно и для функций  (Поскольку функции
(Поскольку функции  ограничены, то для них справедлив принцип максимума модуля.) Отметим некоторые следствия из граничных условий КМШ.
ограничены, то для них справедлив принцип максимума модуля.) Отметим некоторые следствия из граничных условий КМШ.
7.6.4. Предложение. Пусть  Центр алгебры
Центр алгебры  содержится в коммутанте
содержится в коммутанте 

Пусть С лежит в центре алгебры  выберем последовательность
выберем последовательность  так, чтобы элементы
так, чтобы элементы  сильно сходились к С и чтобы
сильно сходились к С и чтобы  при всех
при всех  Это можно сделать ввиду теоремы Капланского о плотности (см.
Это можно сделать ввиду теоремы Капланского о плотности (см.  так как алгебра
так как алгебра  проста.
проста.
Пусть  функции, аналитические в полосе
функции, аналитические в полосе  с граничными значениями
с граничными значениями  при
при  при
при  Из оценок (6.15) и (6.16) вытекает равномерная ограниченность производных функций
Из оценок (6.15) и (6.16) вытекает равномерная ограниченность производных функций  в полосе
в полосе  Поэтому
Поэтому  и функция
и функция  аналитична в полосе
аналитична в полосе  а на границе принимает значения
а на границе принимает значения  при
при  при
при  Отсюда следует, что функцию
Отсюда следует, что функцию  можно продолжить до периодической аналитической функции (так, что
можно продолжить до периодической аналитической функции (так, что  для всех комплексных
для всех комплексных  А так как функция
А так как функция  ограничена, то она является константой, которую мы обозначим через К
ограничена, то она является константой, которую мы обозначим через К

Полагая  мы получим
мы получим

Отсюда видно, что  не зависит от
не зависит от  Предложение доказано.
Предложение доказано.
7.6.5. Следствие. Если состояние  эргодично относительно сдвигов во времени, то
эргодично относительно сдвигов во времени, то  представляет собой факторсостояние (см. упражнение 6.Д).
представляет собой факторсостояние (см. упражнение 6.Д).
Это следствие вытекает из утверждений 6.3.3 (б) и 7.6.3.
Наконец, мы отметим следующий, результат, связывающий алгебры 
7.6.6. Теорема. Пусть  Существует такой антиунитарный оператор
Существует такой антиунитарный оператор  в что
в что  и
и

Доказательство использует теорию квазигильбертовых алгебр.
В том случае, когда алгебра  является фактором, возможные типы этого фактора рассматриваются в работах Гугенгольца [1] и Штёрмера [2].
является фактором, возможные типы этого фактора рассматриваются в работах Гугенгольца [1] и Штёрмера [2].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- Глава 1. ТЕРМОДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ. АНСАМБЛИ
- § 1.2. КЛАССИЧЕСКИЕ СИСТЕМЫ И АНСАМБЛИ
- 1.2.2. Классические непрерывные системы частиц с твердыми сердцевинами.
- 1.2.3. Классические решетчатые системы.
- § 1.3. КВАНТОВЫЕ СИСТЕМЫ И АНСАМБЛИ
- 1.3.2. Квантовые непрерывные системы с твердыми сердцевинами.
- 1.3.3. Квантовые решетчатые системы.
- § 1.4. РАВНОВЕСНЫЕ СОСТОЯНИЯ И ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- Глава 2. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ: РЕШЕТЧАТЫЕ СИСТЕМЫ
- § 2.2. ВЗАИМОДЕЙСТВИЯ В КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМАХ
- § 2.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМ
- § 2.4. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КЛАССИЧЕСКИХ РЕШЕТЧАТЫХ СИСТЕМ
- § 2.5. НЕКОТОРЫЕ НЕРАВЕНСТВА ДЛЯ КВАНТОВЫХ СИСТЕМ
- Глава 3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ: НЕПРЕРЫВНЫЕ СИСТЕМЫ
- § 3.1. ВЗАИМОДЕЙСТВИЯ В КЛАССИЧЕСКИХ НЕПРЕРЫВНЫХ СИСТЕМАХ
- § 3.2. УСТОЙЧИВЫЕ ВЗАИМОДЕЙСТВИЯ
- § 3.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КОНФИГУРАЦИОННОГО МИКРОКАНОНИЧЕСКОГО АНСАМБЛЯ
- § 3.4. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КЛАССИЧЕСКИХ АНСАМБЛЕЙ
- § 3.5. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ ДЛЯ КВАНТОВЫХ АНСАМБЛЕЙ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 4. СТЕПЕННЫЕ РАЗЛОЖЕНИЯ ПРИ МАЛЫХ ПЛОТНОСТЯХ И КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- § 4.2. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
- § 4.3. РЯДЫ МАЙЕРА И ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ
- § 4.4. АЛГЕБРАИЧЕСКИЙ МЕТОД
- § 4.5. ПОЛОЖИТЕЛЬНЫЕ ПОТЕНЦИАЛЫ
- § 4.6. КВАНТОВЫЕ СИСТЕМЫ
- § 4.7. ПОСТРОЕНИЕ ГИЛЬБЕРТОВА ПРОСТРАНСТВА
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 5. ПРОБЛЕМА ФАЗОВЫХ ПЕРЕХОДОВ
- § 5.2. ОТСУТСТВИЕ ФАЗОВЫХ ПЕРЕХОДОВ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
- § 5.3. СУЩЕСТВОВАНИЕ ФАЗОВОГО ПЕРЕХОДА ПЕРВОГО РОДА ПРИ НИЗКИХ ТЕМПЕРАТУРАХ
- § 5.4. НЕРАВЕНСТВА ГРИФФИТСА
- § 5.5. ТЕОРЕМА МЕРМИНА И ВАГНЕРА
- § 5.6. ОДНОМЕРНЫЕ СИСТЕМЫ
- § 5.7. ЗАМЕЧАНИЯ О ФАЗОВЫХ ПЕРЕХОДАХ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 6. ГРУППОВАЯ ИНВАРИАНТНОСТЬ ФИЗИЧЕСКИХ СОСТОЯНИЙ
- § 6.2. ИНВАРИАНТНЫЕ СОСТОЯНИЯ
- § 6.3. ЭРГОДИЧЕСКИЕ СОСТОЯНИЯ
- § 6.4. РАЗЛОЖЕНИЕ ИНВАРИАНТНЫХ СОСТОЯНИЙ ПО ЭРГОДИЧЕСКИМ
- § 6.5. ЧИСТЫЕ ТЕРМОДИНАМИЧЕСКИЕ ФАЗЫ КАК ЭРГОДИЧЕСКИЕ СОСТОЯНИЯ
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- Глава 7. СОСТОЯНИЯ В СТАТИСТИЧЕСКОЙ МЕХАНИКЕ
- § 7.2. ЭНТРОПИЯ
- § 7.3. ТЕРМОДИНАМИЧЕСКИЙ ПРЕДЕЛ СОСТОЯНИЙ
- § 7.4. ВАРИАЦИОННЫЙ ПРИНЦИП
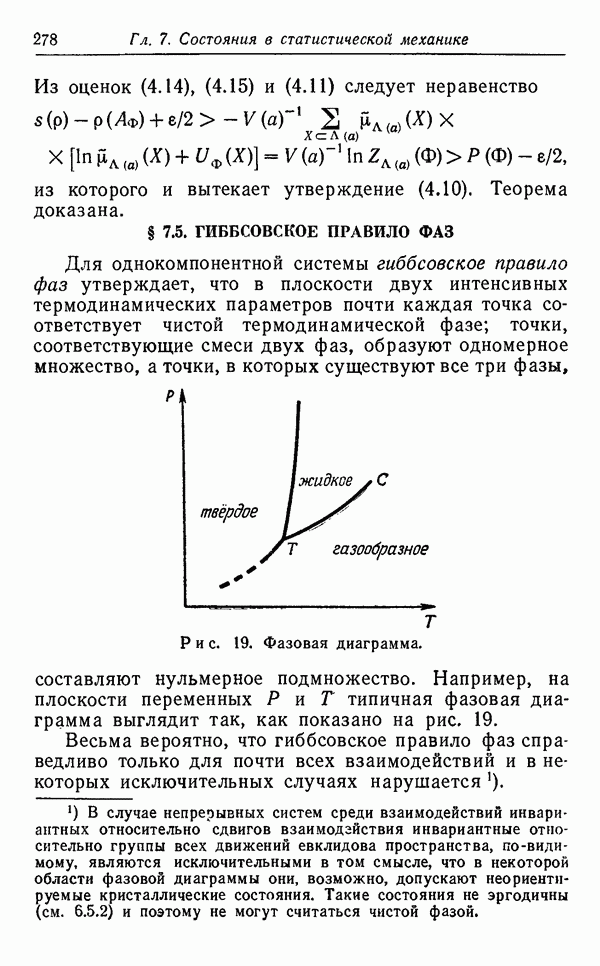
- § 7.5. ГИББСОВСКОЕ ПРАВИЛО ФАЗ
- § 7.6. ЭВОЛЮЦИЯ ВО ВРЕМЕНИ КВАНТОВЫХ РЕШЕТЧАТЫХ СИСТЕМ И ГРАНИЧНЫЕ УСЛОВИЯ КУБО — МАРТИНА — ШВИНГЕРА
- БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- ДОБАВЛЕНИЕ. НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ СРЕДСТВА
- Д.1. НЕКОТОРЫЕ ТЕРМИНЫ
- Д.2. ОБЩИЕ СВЕДЕНИЯ О В-АЛГЕБРАХ
- Д.3. СОСТОЯНИЯ НА В-АЛГЕБРАХ
- Д.4. АЛГЕБРЫ ФОН НЕЙМАНА
- Д.5. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ НА КОМПАКТНЫХ ВЫПУКЛЫХ МНОЖЕСТВАХ
- Д.6. ГРУППЫ С ИНВАРИАНТНЫМ СРЕДНИМ
- ЛИТЕРАТУРА
- ПРИЛОЖЕНИЕ. ОБЗОР РЯДА НЕДАВНИХ РЕЗУЛЬТАТОВ
- § 1. ГИББСОВСКИЕ СОСТОЯНИЯ ДЛЯ БЕСКОНЕЧНЫХ СИСТЕМ
- § 2. ЭКВИВАЛЕНТНОСТЬ АНСАМБЛЕЙ И ЦЕНТРАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ЧИСЛА ЧАСТИЦ И ЭНЕРГИИ
- § 3. ЯВЛЕНИЕ РАЗДЕЛЕНИЯ ФАЗ ПРИ ФАЗОВОМ ПЕРЕХОДЕ ПЕРВОГО РОДА В РЕШЕТЧАТЫХ МОДЕЛЯХ ГАЗА
- § 4. НЕКОТОРЫЕ НОВЫЕ РЕЗУЛЬТАТЫ ОБ ОДНОМЕРНЫХ МОДЕЛЯХ
- § 5. СУЩЕСТВОВАНИЕ ФАЗОВОГО ПЕРЕХОДА В СПИНОВЫХ МОДЕЛЯХ
- § 6. КИНЕТИКА БЕСКОНЕЧНЫХ СИСТЕМ
- § 7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ
- ЛИТЕРАТУРА К ПРИЛОЖЕНИЮ