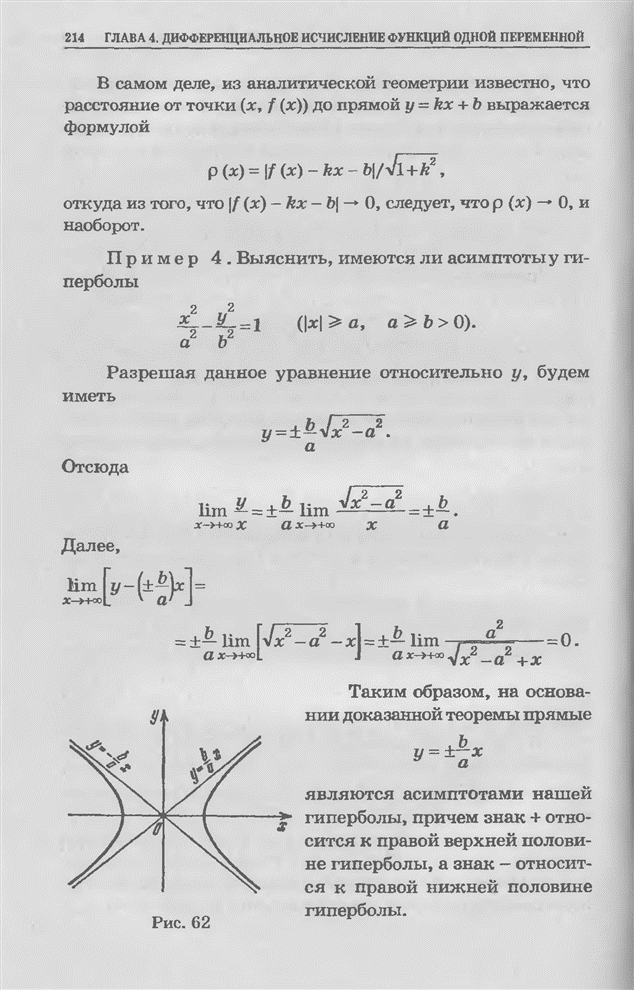
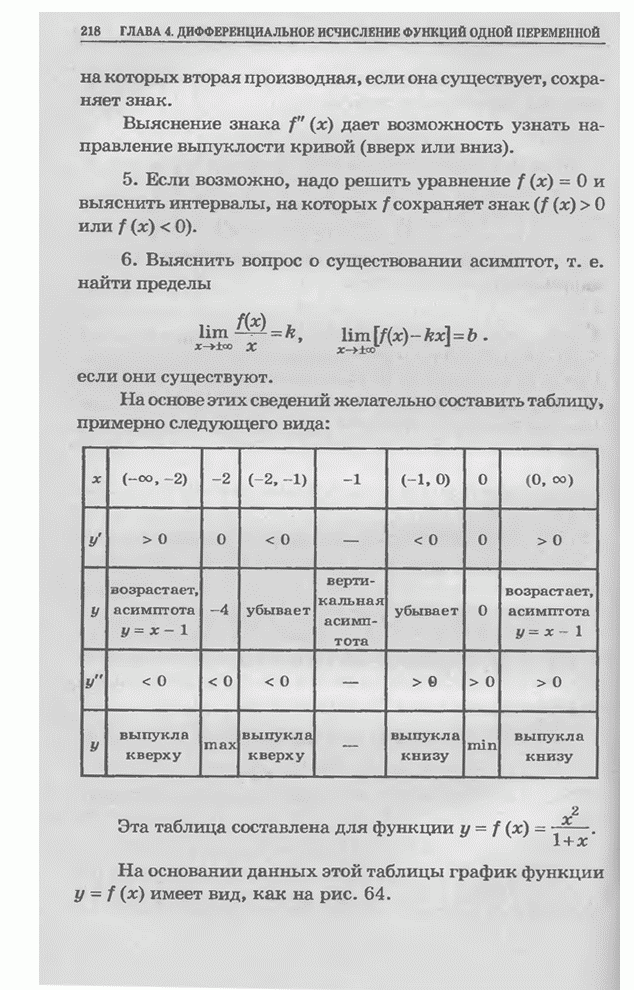
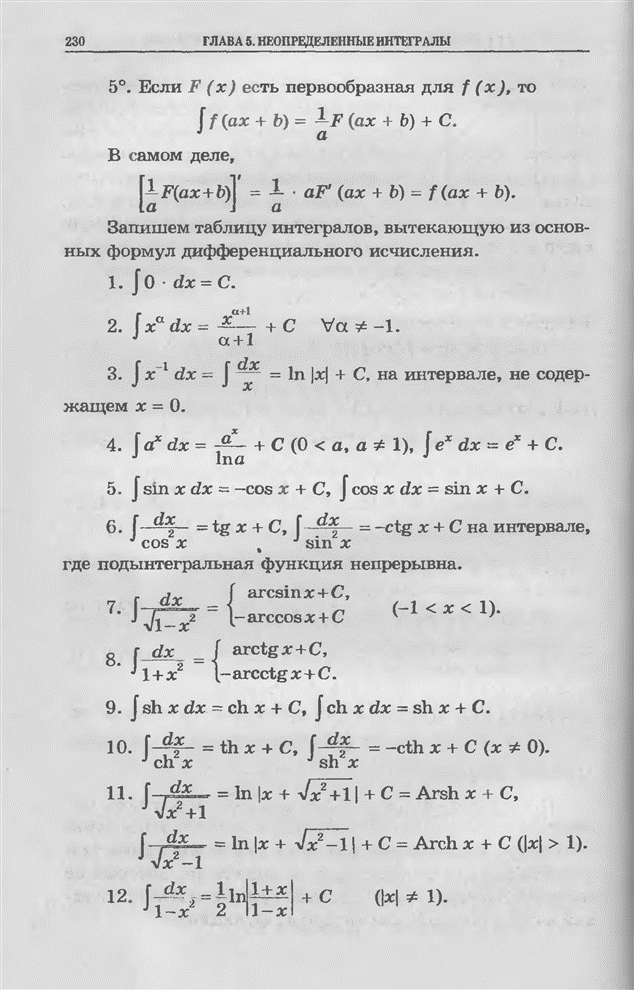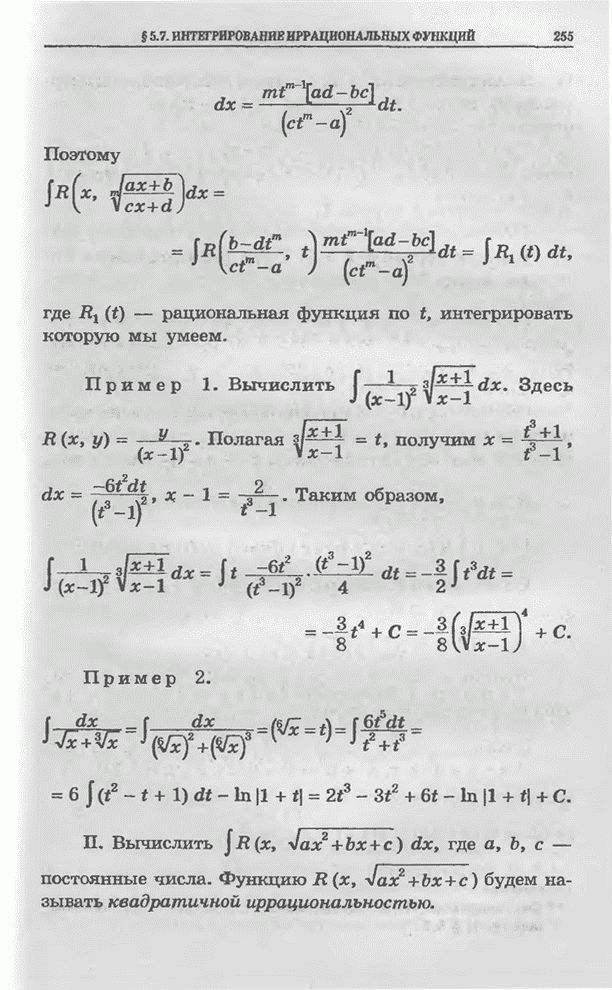| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.8. Аксиоматический подход к понятию действительного числа
Мы назвали
бесконечные десятичные дроби действительными числами, ввели для них понятия ![]() и арифметические
операции, и сформулировали их основные свойства I – V, которые могут быть доказаны.
и арифметические
операции, и сформулировали их основные свойства I – V, которые могут быть доказаны.
Нужно сказать, что свойства I – V подобраны экономно и полно, настолько, что из них можно получить логически все остальные свойства чисел.
Существует
аксиоматический подход к определению действительного числа, заключающийся в
том, что действительными числами называются некоторые объекты (вещи) ![]() , удовлетворяющие
свойствам I – V. При таком
подходе свойства I – V
называются аксиомами числа.
, удовлетворяющие
свойствам I – V. При таком
подходе свойства I – V
называются аксиомами числа.
При аксиоматическом
подходе формулировки свойств (теперь аксиом) должны быть несколько
видоизменены. Аксиомы II теперь уже формулируются так:
каждой паре чисел, в силу некоторого закона, соответствует число ![]() , называемое их
суммой, при этом выполняются аксиомы
, называемое их
суммой, при этом выполняются аксиомы ![]() -
-![]() . Аксиома
. Аксиома ![]() должна
быть сформулирована в виде: существует число 0 (нуль) такое, что
должна
быть сформулирована в виде: существует число 0 (нуль) такое, что ![]() для всех
для всех ![]() . Аксиома
. Аксиома ![]() формулируется
так: для любого числа
формулируется
так: для любого числа ![]() существует число, обозначаемое через
существует число, обозначаемое через ![]() такое, что
такое, что ![]() . Наконец, аксиома
. Наконец, аксиома ![]() принимает
вид: существует число 1 (единица), отличное от 0, такое, что
принимает
вид: существует число 1 (единица), отличное от 0, такое, что ![]() для всех
для всех ![]() .
.
Обозначим через
![]() множество
всех действительных чисел, т. е. всех вещей, подчиняющихся аксиомам I – V . Тогда
в
множество
всех действительных чисел, т. е. всех вещей, подчиняющихся аксиомам I – V . Тогда
в ![]() имеется
нуль 0 и единица 1. С помощью аксиом можно доказать, что
имеется
нуль 0 и единица 1. С помощью аксиом можно доказать, что ![]() и имеют смысл числа
и имеют смысл числа ![]() и числа
и числа ![]() . В результате
получим множество всех целых чисел (различных между собой!)
. В результате
получим множество всех целых чисел (различных между собой!)
![]() .
.
На основании
аксиом эти числа можно делить друг на друга, исключая деление на 0. Поэтому в ![]() есть
рациональные числа
есть
рациональные числа ![]() . Но тогда в
. Но тогда в ![]() имеются также и конечные
десятичные дроби. Из последних можно построить ограниченные сверху неубывающие
последовательности. На основании аксиомы V в
имеются также и конечные
десятичные дроби. Из последних можно построить ограниченные сверху неубывающие
последовательности. На основании аксиомы V в ![]() должны
существовать пределы таких последовательностей. Некоторые из этих пределов не
являются конечными десятичными дробями - это числа, отличные от конечных
десятичных дробей. Их удобно записывать в виде бесконечных десятичных дробей. В
результате, от аксиом с помощью логических рассуждений можно прийти к
бесконечным десятичным дробям. Конечно, мы здесь привели только схему
рассуждений, которая не претендует на доказательство.
должны
существовать пределы таких последовательностей. Некоторые из этих пределов не
являются конечными десятичными дробями - это числа, отличные от конечных
десятичных дробей. Их удобно записывать в виде бесконечных десятичных дробей. В
результате, от аксиом с помощью логических рассуждений можно прийти к
бесконечным десятичным дробям. Конечно, мы здесь привели только схему
рассуждений, которая не претендует на доказательство.
Из сказанного следует, что с формальной точки зрения все равно, исходим ли мы при определении действительных чисел из бесконечных десятичных дробей или из аксиоматического подхода.
Конечно, с философской точки зрения второй подход более приемлем: числа суть абстракции, выражающие количественные отношения реального мира, а десятичные дроби – формальные символы, их представляющие.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
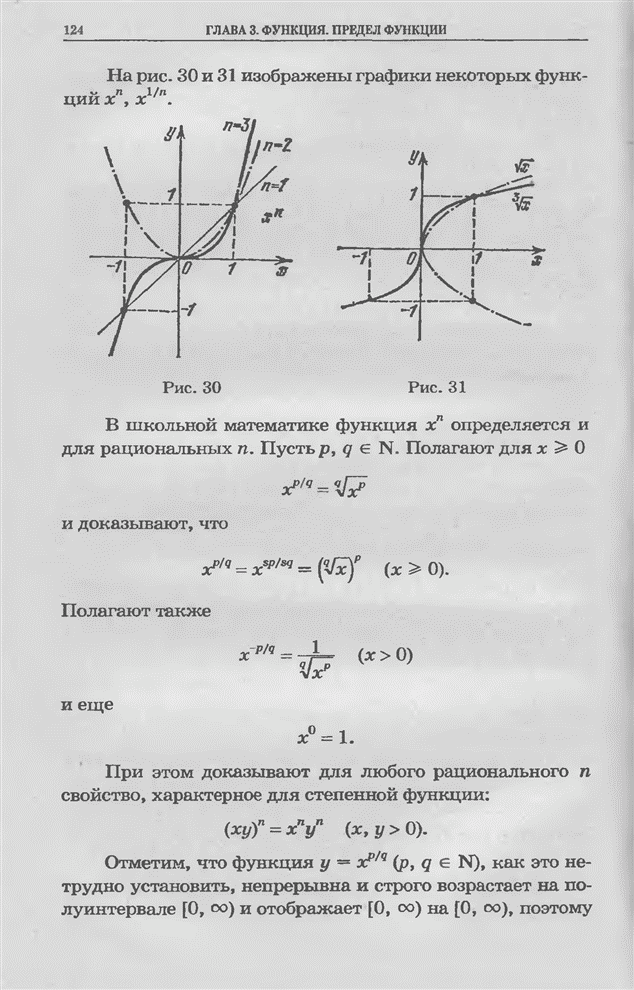
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
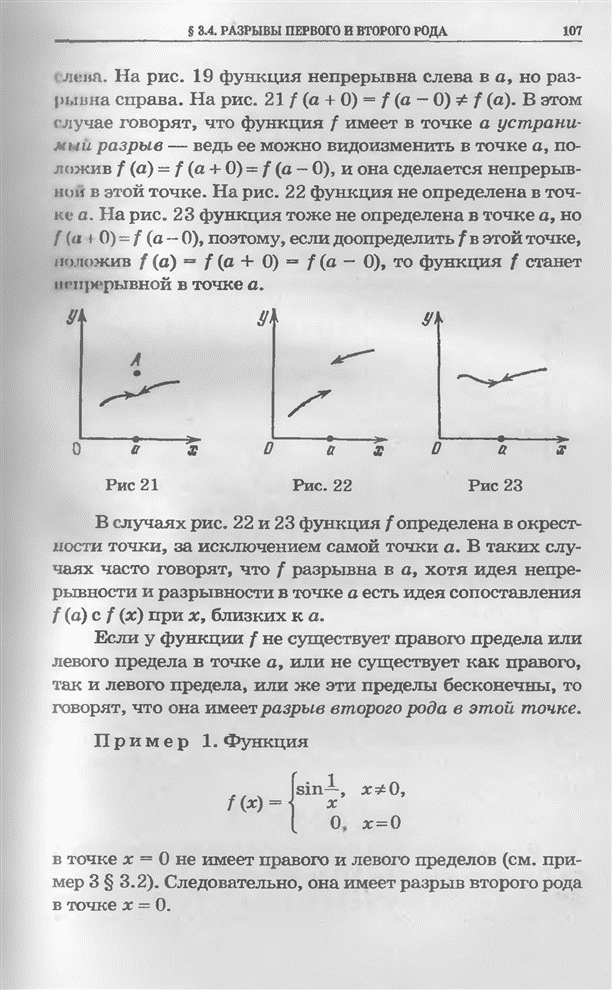
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
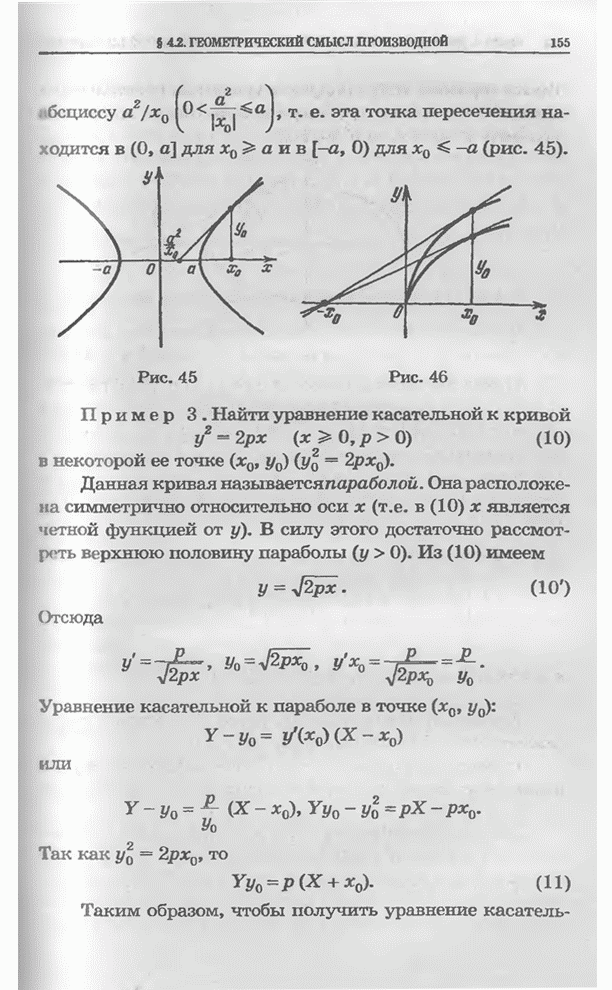
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
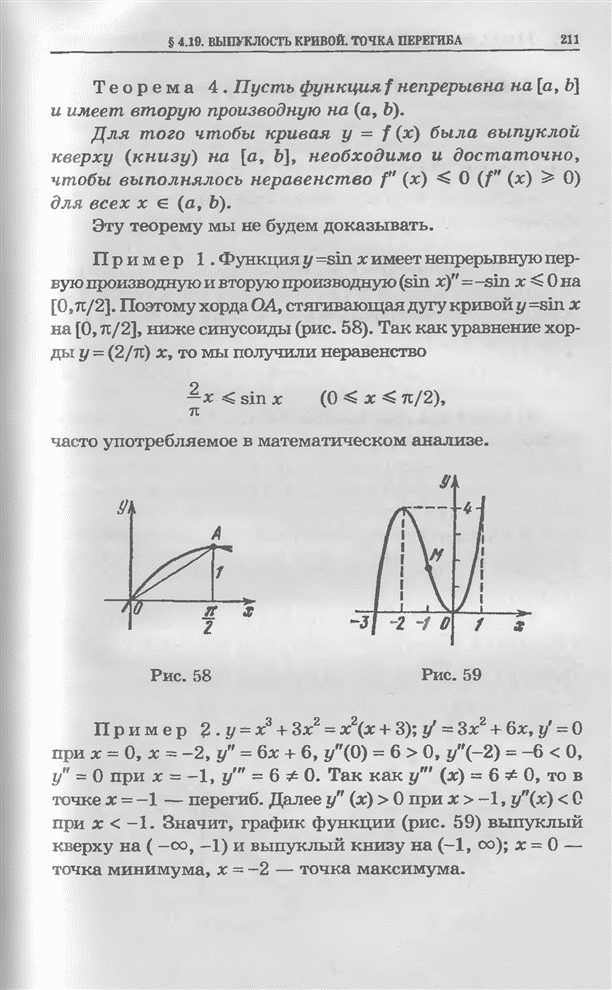
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
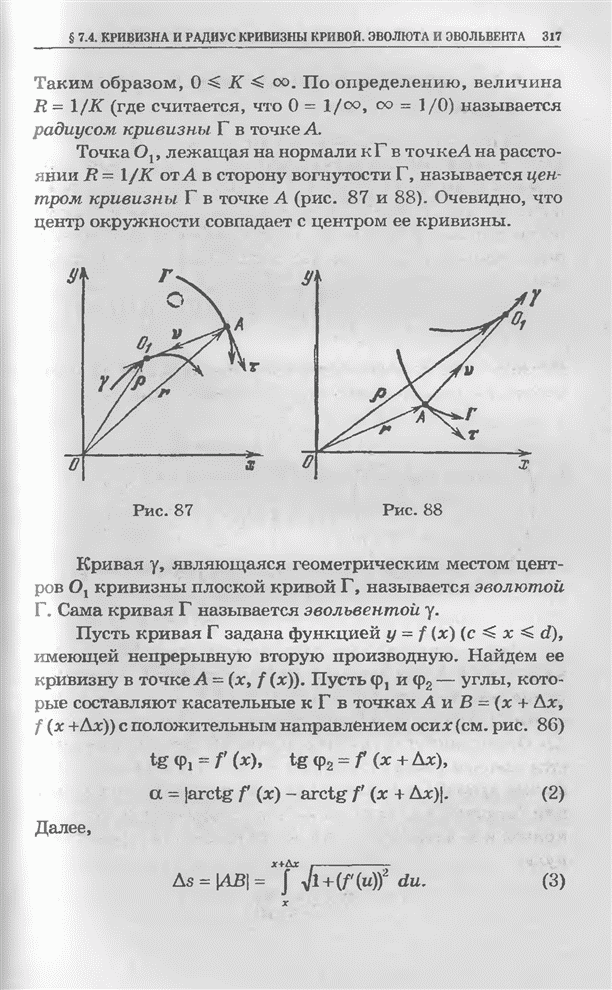
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
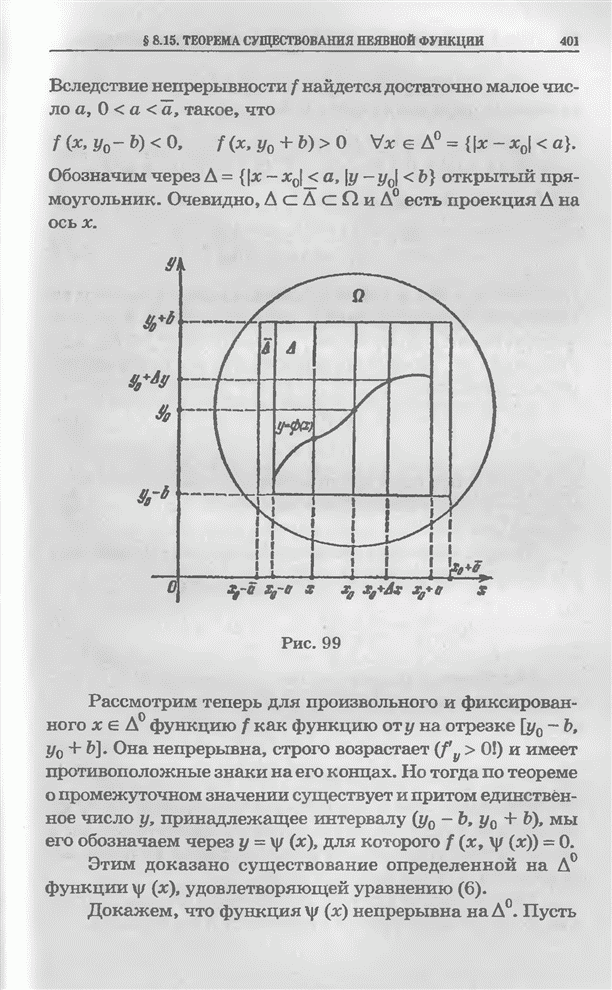
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
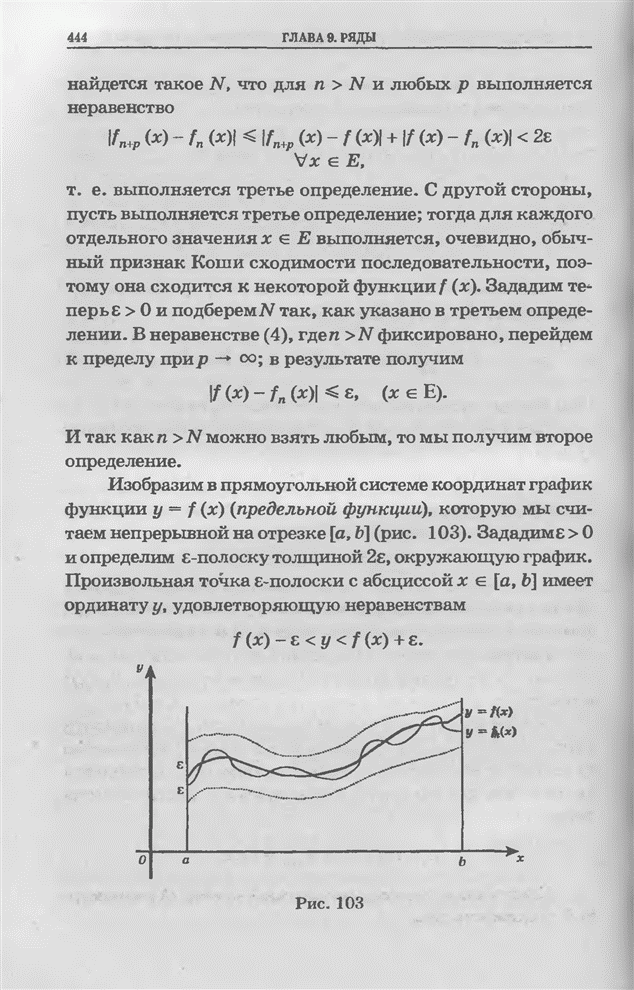
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей