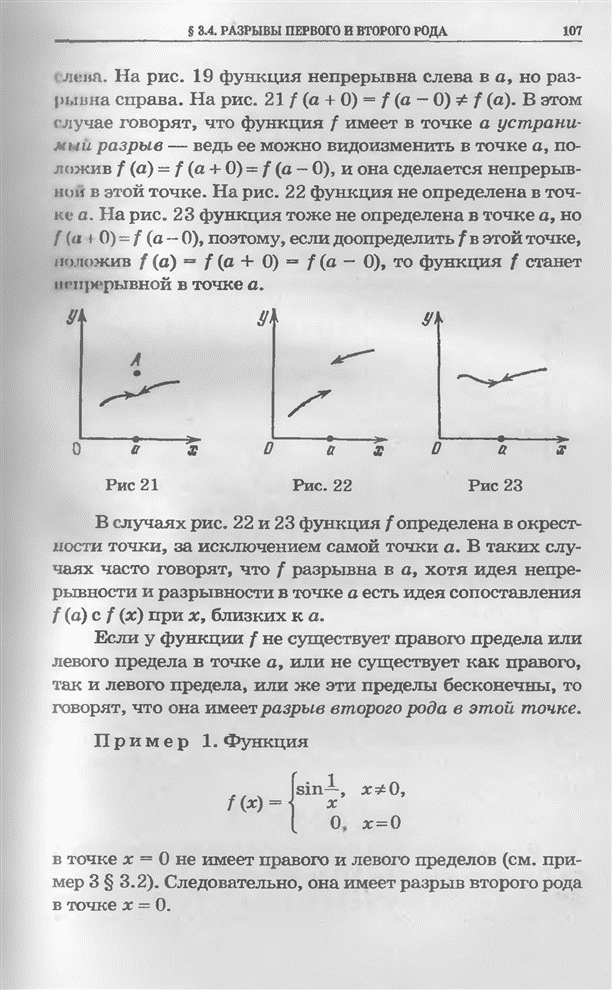
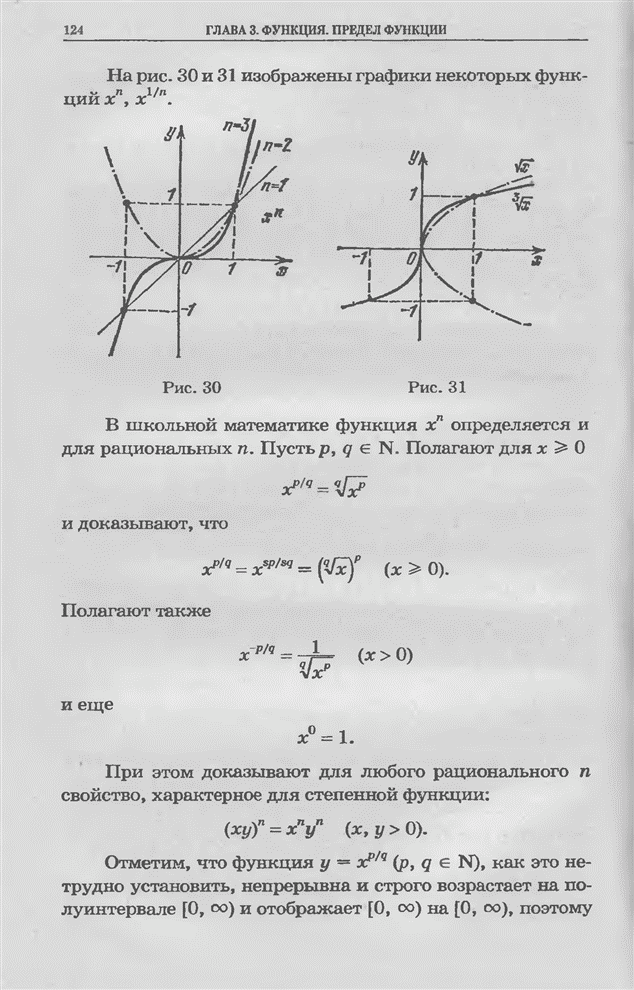
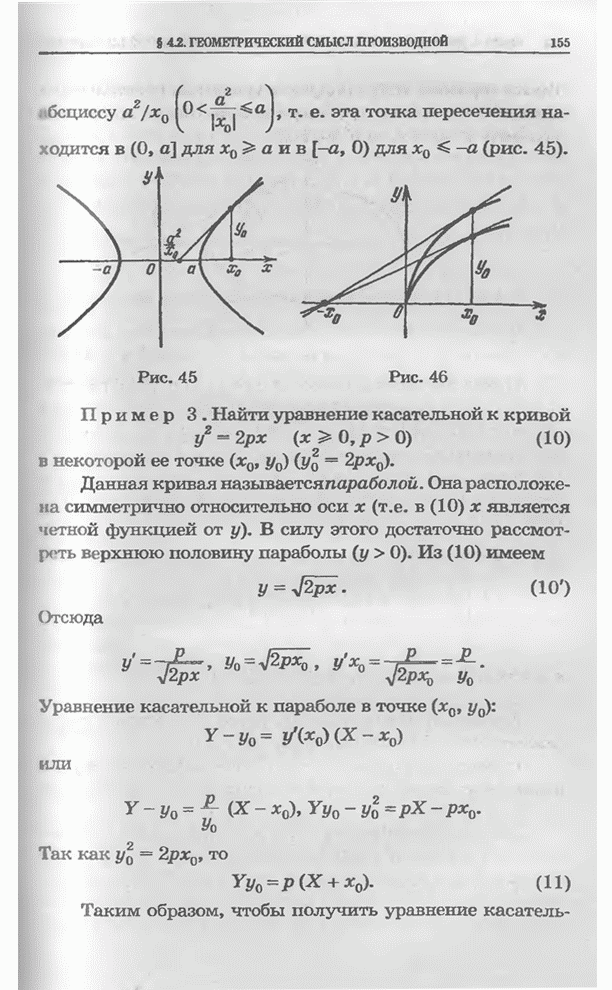
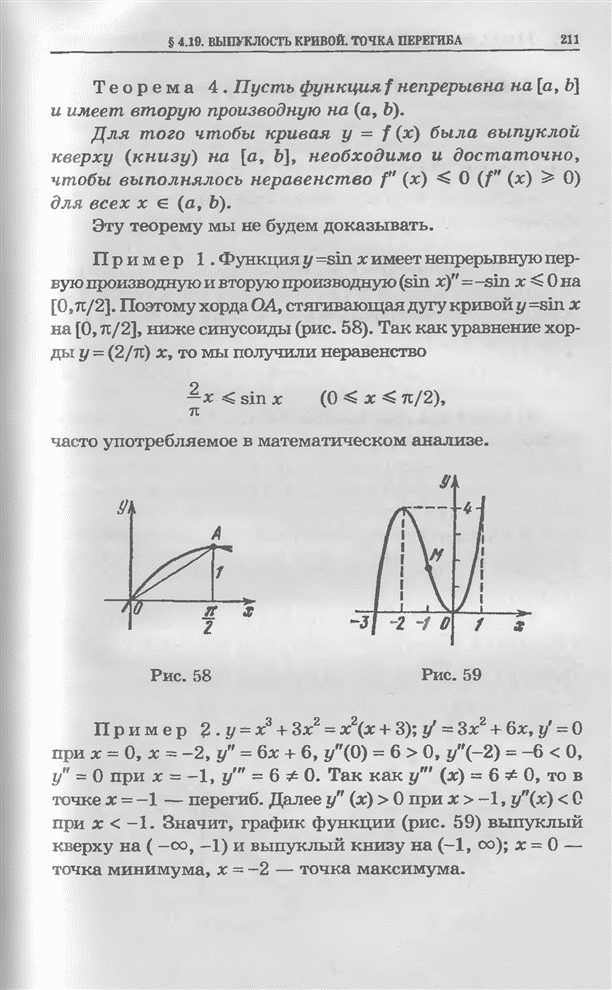
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 7. Приложения интегралов. Приближенные методы
§ 7.1. Площадь в полярных координатах
Площадь ![]() фигуры,
ограниченной двумя выходящими из полярного полюса лучами,
фигуры,
ограниченной двумя выходящими из полярного полюса лучами, ![]() , и кривой
, и кривой ![]() , заданной в
полярных координатах непрерывной функцией
, заданной в
полярных координатах непрерывной функцией ![]() , может быть определена следующим
образом (рис. 80). Производим разбиение отрезка
, может быть определена следующим
образом (рис. 80). Производим разбиение отрезка ![]() :
:
![]() .
.
Элемент площади фигуры,
ограниченной кривой ![]() и лучами
и лучами ![]() , приближенно выражаем
площадью кругового сектора, ограниченного теми же лучами и окружностью радиуса
, приближенно выражаем
площадью кругового сектора, ограниченного теми же лучами и окружностью радиуса ![]() , равной
, равной
![]() .
.
Естественно считать, по определению,
 . (1)
. (1)
Мы получили формулу площади
фигуры в полярных координатах. Для непрерывной функции ![]() интеграл (1), как мы знаем,
существует и, следовательно, предел любой интегральной суммы равен этому
интегралу.
интеграл (1), как мы знаем,
существует и, следовательно, предел любой интегральной суммы равен этому
интегралу.

Рис. 80 Рис. 81
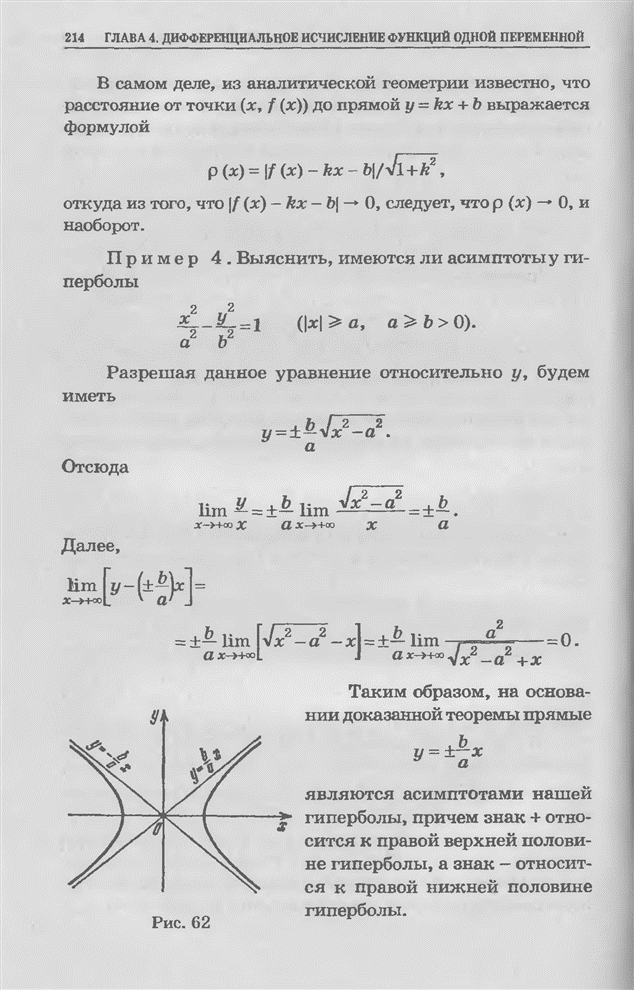
П р и м е р. Изображенная на рис. 81 окружность в полярных
координатах определяется уравнением ![]() . В силу (1) площадь круга
. В силу (1) площадь круга
 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей