§ 3.4. Разрывы первого и второго рода

По определению функция  непрерывна в точке   справа (слева), если

 (соответственно )

(см. конец §3.2).

Непрерывность  в точке  можно определить также следующим образом: функция  непрерывна в точке ,  если она определена в некоторой окрестности этой точки, в том числе и в самой точке , и существуют пределы и такие, что

                               (1)

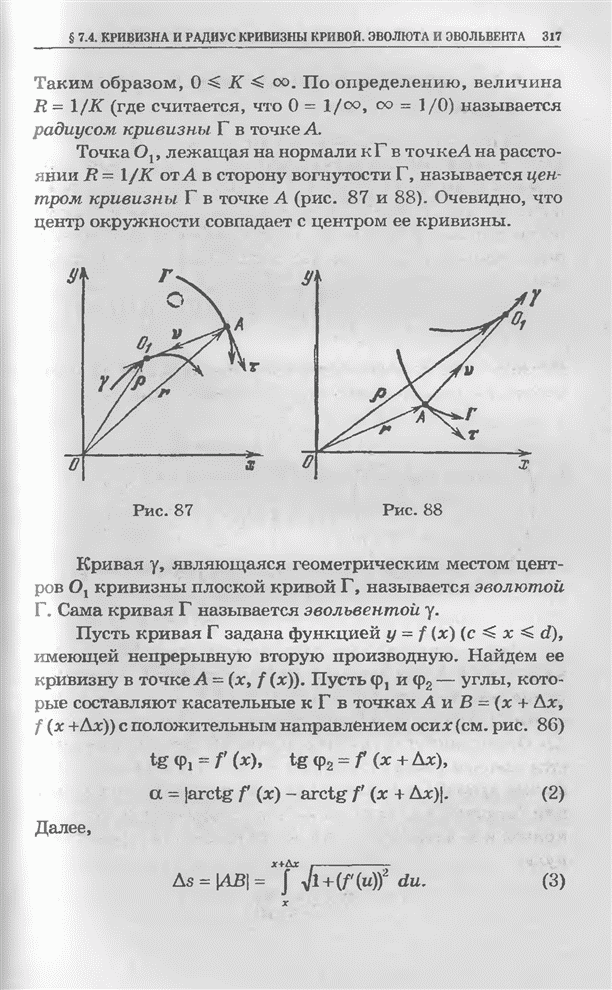
Рис. 18                               Рис. 19                                   Рис. 20

Если функция  такова, что для нее существуют пределы , , однако равенства (1)  не выполняются, то очевидно, она разрывна (не непрерывна) в точке . В этом случае говорят, что функция   в точке  имеет разрыв первого рода.

На рис. 18 – 23 приведены шесть графиков функций, имеющих разрыв первого рода в точке . Буква  обозначает точку   графика функций. Стрелка на конце куска кривой обозначает, что концевая точка, где находится стрелка, выброшена.

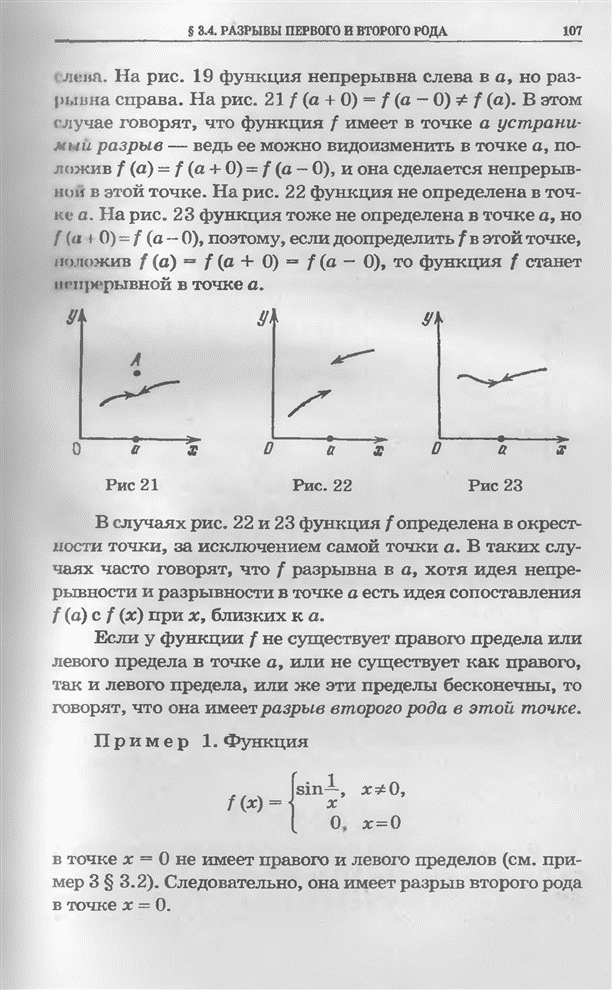
На рис 18 – 21 даны графики функций, для которых все три числа , ,  имеют смысл. На рис. 18 три числа  , ,  попарно различны – функция не только разрывна в , но разрывна также справа и слева. На рис. 19 функция непрерывна слева в , но разрывна справа. На рис. 21 . В этом случае говорят, что функция   имеет в точке  устранимый разрыв – ведь ее можно видоизменить в точке , положив , и она сделается непрерывной в этой точке. На рис. 22 функция не определена в точке . На рис. 23 функция тоже не определена в точке , но , поэтому, если доопределить  в этой точке, положив , то функция  станет непрерывной в точке .

Рис. 21                                     Рис. 22                                 Рис. 23

В случаях рис. 22 и 23 функция  определена в окрестности точки, за исключением самой точки . В таких случаях часто говорят, что  разрывна в , хотя идея непрерывности и разрывности в точке  есть идея сопоставления  с  при , близких к .

Если у функции  не существует правого предела или левого предела в точке , или не существует как правого, так и левого предела, или же эти пределы бесконечны, то говорят, что она имеет разрыв второго рода в этой точке.

П р и м е р  1. Функция

в точке  не имеет правого и левого пределов (см. пример 3 §3.2). Следовательно, она имеет разрыв второго рода в точке .

П р и м е р  2. Функция

очевидно, непрерывна для , а в точке  имеет разрыв первого рода. При этом  , .

П р и м е р  3. Функция  - целая часть  - для  имеет график, изображенный на рис. 24. Она непрерывна для нецелых , а если  целое, то  и , и, следовательно, имеет место разрыв первого рода.

Рис. 24

П р и м е р  4. Функция

непрерывна для . Правый и левый пределы в точке  равны бесконечности, поэтому функция имеет разрыв второго рода в этой точке.  В этом случае также говорят, что функция имеет бесконечный разрыв в этой точке.

Т е о р е м а  1. Если функция  не убывает на отрезке, то существуют пределы и .

Д о к а з а т е л ь с т в о. Из условия следует, что

,

т. е.  ограничена сверху числом  на полуинтервале . Но тогда существует точная верхняя грань  на этом полуинтервале:

.

В силу свойства точной верхней грани для всякого  найдется  такое, что

,                                     (2)

а в силу того, что  не убывает, имеет место

.                              (3)

Из (2) и (3) следует, что

,

и мы доказали, что существует левый предел  в точке :

.

Аналогично, рассматривая неравенство  для , докажем существование

.

С л е д с т в и е. Если функция  не убывает на отрезке , то в любой точке  существует правый предел  и в любой точке  существует левый предел .

В самом деле, для точек  это утверждение доказано в теореме 1. Пусть . На отрезках  и  функция  не убывает, поэтому по теореме 1 существуют  ,  и .

В данном случае, очевидно, что для того чтобы функция  была непрерывной в точке , необходимо и достаточно, чтобы .

Если , то функция  имеет в точке  разрыв первого ряда.

Т е о р е м а  2. Множество точек разрыва функции , неубывающей на отрезке , не более чем счетно.

Д о к а з а т е л ь с т в о. Пусть функция  имеет больше чем одну точку разрыва, и пусть  и  - два какие-либо из них. Так как

,

то

и интервалы ,  оси   не пересекаются.

Каждой точке  разрыва функции  соответствует интервал . Внутри его выберем одну рациональную точку . После сказанного ясно, что разным точкам разрыва  соответствуют разные точки . Но множество всех рациональных чисел счетно. Поэтому множество всех точек , также как и множество всех точек  (разрыва ), не более чем счетно. Теорема доказана.