| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3.3. Непрерывность функции
На рис. 15, а
изображен график функции ![]() . Его естественно назвать непрерывным
графиком, потому что он может быть нарисован одним движением карандаша без
отрыва от бумаги. Зададим произвольную точку (число)
. Его естественно назвать непрерывным
графиком, потому что он может быть нарисован одним движением карандаша без
отрыва от бумаги. Зададим произвольную точку (число) ![]() . Близкая к ней другая точка
. Близкая к ней другая точка ![]() может быть записана
в виде
может быть записана
в виде ![]() ,
где
,
где ![]() есть
число положительное или отрицательное, называемое приращением
есть
число положительное или отрицательное, называемое приращением ![]() . Разность
. Разность
![]()
называется приращением функции
![]() в
точке
в
точке ![]() ,
соответствующим приращению
,
соответствующим приращению ![]() . Здесь имеется в виду
. Здесь имеется в виду ![]() такое, что
такое, что ![]() . На рис. 15, а
. На рис. 15, а ![]() равно длине отрезка
равно длине отрезка
![]() .
.

Рис. 15
Будем стремить ![]() к нулю; тогда для
рассматриваемой функции, очевидно, и
к нулю; тогда для
рассматриваемой функции, очевидно, и ![]() будет стремиться к нулю:
будет стремиться к нулю:
![]() .
(1)
.
(1)
Рассмотрим
теперь график на рис 15, б. Он состоит из двух непрерывных кусков ![]() и
и ![]() . Однако эти куски
не соединены непрерывно, и потому график естественно назвать разрывным. Чтобы
график изображал однозначную функцию
. Однако эти куски
не соединены непрерывно, и потому график естественно назвать разрывным. Чтобы
график изображал однозначную функцию ![]() в точке
в точке ![]() , условимся, что
, условимся, что ![]() равно длине отрезка,
соединяющего
равно длине отрезка,
соединяющего ![]() и
и
![]() ; в знак
этого точка
; в знак
этого точка ![]() изображена
на графике кружком, в то время как у точки
изображена
на графике кружком, в то время как у точки ![]() нарисована стрелка, указывающая, что
нарисована стрелка, указывающая, что ![]() не принадлежит
графику. Если бы точка
не принадлежит
графику. Если бы точка ![]() принадлежала графику, то функция
принадлежала графику, то функция ![]() была бы двузначной
в точке
была бы двузначной
в точке ![]() .
.
Придадим теперь
![]() приращение
приращение
![]() и
определим соответствующее приращение функции:
и
определим соответствующее приращение функции:
![]() .
.
Если мы будем ![]() стремить к нулю, то теперь уже
нельзя сказать, что
стремить к нулю, то теперь уже
нельзя сказать, что ![]() будет стремиться к нулю. Для
отрицательных
будет стремиться к нулю. Для
отрицательных ![]() ,
стремящихся к нулю, это так, но для положительных вовсе не так: из рисунка
видно, что если
,
стремящихся к нулю, это так, но для положительных вовсе не так: из рисунка
видно, что если ![]() ,
оставаясь положительным, стремится к нулю, то соответствующее приращение
,
оставаясь положительным, стремится к нулю, то соответствующее приращение ![]() при этом стремится
к положительному числу, равному длине отрезка
при этом стремится
к положительному числу, равному длине отрезка ![]() .
.
После этих
рассмотрений естественно функцию ![]() , заданную на отрезке
, заданную на отрезке ![]() , называть
непрерывной в точке
, называть
непрерывной в точке ![]() этого отрезка, если приращение ее в
этой точке, соответствующее приращению
этого отрезка, если приращение ее в
этой точке, соответствующее приращению ![]() , стремится к нулю при любом способе
стремления
, стремится к нулю при любом способе
стремления ![]() к
нулю. Это (свойство непрерывности
к
нулю. Это (свойство непрерывности ![]() в
в ![]() ) записывается в виде соотношения (1)
или еще так:
) записывается в виде соотношения (1)
или еще так:
![]() .
(2)
.
(2)
Запись (2) читается так: предел ![]() равен нулю, когда
равен нулю, когда ![]() стремится к нулю по
любому закону. Впрочем, выражение «по любому закону» обычно опускают,
подразумевая его.
стремится к нулю по
любому закону. Впрочем, выражение «по любому закону» обычно опускают,
подразумевая его.
Если
определенная на ![]() функция
функция
![]() не
является непрерывной в точке
не
является непрерывной в точке ![]() , т. е. если для нее не выполняется
свойство (2) хотя бы при одном способе стремления
, т. е. если для нее не выполняется
свойство (2) хотя бы при одном способе стремления ![]() к нулю, то она называется разрывной
в точке
к нулю, то она называется разрывной
в точке ![]() .
.
Функция,
изображенная на рис. 15, а, непрерывна в любой точке ![]() , функция же, изображенная на
рис. 15, б, очевидно, непрерывна в любой точке
, функция же, изображенная на
рис. 15, б, очевидно, непрерывна в любой точке ![]() , за исключением точки
, за исключением точки ![]() , потому что для
последней соотношение (2) не выполняется, когда
, потому что для
последней соотношение (2) не выполняется, когда ![]() , оставаясь положительным.
, оставаясь положительным.
Функция, непрерывная в любой точке отрезка (интервала), называется непрерывной на этом отрезке (интервале).
Непрерывная
функция математически выражает свойство, с которым нам приходится часто
встречаться на практике, заключающееся в том, что малому приращению независимой
переменной соответствует малое же приращение зависимой от нее переменной
(функции). Прекрасными примерами непрерывной функции могут служить различные
законы движения тел ![]() , выражающие зависимости пути
, выражающие зависимости пути ![]() , пройденного телом,
от времени
, пройденного телом,
от времени ![]() .
Время и пространство непрерывны. Тот или иной закон движения
.
Время и пространство непрерывны. Тот или иной закон движения ![]() устанавливает между
ними определенную непрерывную связь, характеризующуюся тем, что малому
приращению времени соответствует малое приращение пути.
устанавливает между
ними определенную непрерывную связь, характеризующуюся тем, что малому
приращению времени соответствует малое приращение пути.
К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые, сплошные среды – твердые, жидкие или газообразные, например металлы, воду, воздух. На самом деле, всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды непрерывно распределенной без всяких просветов в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности, естественно, играет в этих дисциплинах, как и во многих других, большую роль.
Непрерывные функции образуют основной класс функций, с которыми оперирует математический анализ.
Примерами
непрерывных функций могут служить элементарные функции (см. ниже §
3.8). Они непрерывны на интервалах изменения ![]() , где они определены.
, где они определены.
Разрывные
функции в математике отражают скачкообразные процессы, встречающиеся в природе.
При ударе, например, величина скорости тела меняется скачкообразно. Многие
качественные переходы сопровождаются скачками. Например, зависимость ![]() между температурой
одного грамма воды (льда) и количеством
между температурой
одного грамма воды (льда) и количеством ![]() калорий находящегося в ней тепла,
когда
калорий находящегося в ней тепла,
когда ![]() изменяется
между
изменяется
между ![]() и
и ![]() , если принять
условно, что при
, если принять
условно, что при ![]() величина
величина
![]() ,
выражается следующими формулами:
,
выражается следующими формулами:
![]()
Мы считаем, что теплоемкость льда
равна 0,5. При ![]() эта
функция оказывается неопределенной – многозначной; можно для удобства
условиться, что при
эта
функция оказывается неопределенной – многозначной; можно для удобства
условиться, что при ![]() она принимает вполне определенное
значение, например
она принимает вполне определенное
значение, например ![]() . Функция
. Функция ![]() , очевидно, разрывная при
, очевидно, разрывная при ![]() , изображена на рис.
16.
, изображена на рис.
16.

Рис. 16
Дадим определение непрерывности
функции ![]() в
точке.
в
точке.
Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() , если она определена в некоторой
окрестности этой точки, в том числе в самой точке
, если она определена в некоторой
окрестности этой точки, в том числе в самой точке ![]() , и если ее приращение в этой точке,
соответствующее приращению аргумента
, и если ее приращение в этой точке,
соответствующее приращению аргумента ![]() , стремится к нулю при
, стремится к нулю при ![]() :
:
![]() . (3)
. (3)
Если положить ![]() , то получим
следующее эквивалентное определение непрерывности
, то получим
следующее эквивалентное определение непрерывности ![]() в
в ![]() : функция
: функция ![]() непрерывна в точке
непрерывна в точке
![]() , если
она определена в некоторой окрестности этой точки, в том числе в самой точке
, если
она определена в некоторой окрестности этой точки, в том числе в самой точке ![]() , и если
, и если
![]() ;
(4)
;
(4)
или еще на языке ![]() ,
, ![]() : если для всякого
: если для всякого ![]() найдется
найдется ![]() такое, что
такое, что
![]() .
.
Равенство (4) можно еще записать следующим образом:
 .
(4’)
.
(4’)
Оно показывает, что под знаком непрерывной функции можно переходить к пределу.
П р и м е р 1.
Постоянная ![]() есть
функция, непрерывная в любой точке
есть
функция, непрерывная в любой точке ![]() . В самом деле, точке
. В самом деле, точке ![]() соответствует
значение функции
соответствует
значение функции ![]() ,
точке
,
точке ![]() соответствует
то же значение
соответствует
то же значение ![]() .
Поэтому
.
Поэтому ![]() и
и
![]() .
.
П р и м е р 2.
Функция ![]() непрерывна
для любого значения
непрерывна
для любого значения ![]() , потому что
, потому что ![]() и, следовательно,
и, следовательно, ![]() при
при ![]() .
.
П р и м е р 3.
Функция ![]() непрерывна
для любого
непрерывна
для любого ![]() .
В самом деле,
.
В самом деле,
 . (5)
. (5)
Но для любого ![]() имеет место неравенство
имеет место неравенство
![]() (6)
(6)
Если ![]() , то это следует из
рис. 17, где изображена окружность радиуса 1 (дуга длины
, то это следует из
рис. 17, где изображена окружность радиуса 1 (дуга длины ![]() больше стягиваемой ею хорды,
имеющей длину
больше стягиваемой ею хорды,
имеющей длину ![]() ).
При
).
При ![]() неравенство
(6) обращается в равенство. Если же
неравенство
(6) обращается в равенство. Если же ![]() , то
, то ![]() . Наконец, если
. Наконец, если ![]() , то
, то ![]() . Из (5) на основании (6)
следует
. Из (5) на основании (6)
следует
![]() ,
,
т. е.
![]() .
.
Но тогда, очевидно,
![]() .
.
Можно еще
сказать, что для всякого ![]() можно найти
можно найти ![]() , именно
, именно ![]() такое, что
такое, что
![]() .
.

Рис. 17.
Отметим важную теорему.
Т е о р е м а
1. Если функции ![]() и
и ![]() непрерывны в точке
непрерывны в точке ![]() , то непрерывны также в этой
точке их сумма, разность, произведение и частное (при
, то непрерывны также в этой
точке их сумма, разность, произведение и частное (при ![]() ).
).
Эта теорема непосредственно вытекает из теоремы 6 §3.2, если учесть, что в данном случае
![]() .
.
Справедлива также важная теорема о непрерывности функции от функции (сложной функции).
Т е о р е м а
2. Пусть задана функция ![]() , непрерывная в точке
, непрерывная в точке ![]() , и еще другая
функция
, и еще другая
функция ![]() ,
непрерывная в точке
,
непрерывная в точке ![]() , и пусть
, и пусть ![]() . Тогда сложная функция
. Тогда сложная функция ![]() непрерывна в точке
непрерывна в точке
![]() .
.
Д о к а з а т е
л ь с т в о. Заметим, что по определению непрерывности функции ![]() в точке
в точке ![]() следует, что она
определена в некоторой окрестности этой точки. Поэтому
следует, что она
определена в некоторой окрестности этой точки. Поэтому
![]() .
.
Здесь введена
подстановка ![]() и
учтена непрерывность
и
учтена непрерывность ![]() в точке
в точке ![]() .
.
П р и м е р 4. Функция
![]() ,
,
где ![]() - постоянные коэффициенты, называется многочленом
степени
- постоянные коэффициенты, называется многочленом
степени ![]() .
Она непрерывна для любого
.
Она непрерывна для любого ![]() . Ведь чтобы получить
. Ведь чтобы получить ![]() , надо, исходя из
постоянных чисел
, надо, исходя из
постоянных чисел ![]() и
функции
и
функции ![]() ,
произвести конечное число арифметических действий - сложения, вычитания и
умножения. Но постоянная есть непрерывная функция (см. пример 1), а функция
,
произвести конечное число арифметических действий - сложения, вычитания и
умножения. Но постоянная есть непрерывная функция (см. пример 1), а функция ![]() тоже непрерывна
(см. пример 2), поэтому непрерывность
тоже непрерывна
(см. пример 2), поэтому непрерывность ![]() следует из теоремы 1.
следует из теоремы 1.
П р и м е р
5. Функция ![]() непрерывна.
Она является композицией двух непрерывных функций:
непрерывна.
Она является композицией двух непрерывных функций: ![]() ,
, ![]() .
.
П р и м е р 6. Функция
![]() ,
,
непрерывна для указанных ![]() , потому что (см.
теорему 1) она равна частному от деления непрерывных функций и при этом
делитель не равен нулю (при указанных
, потому что (см.
теорему 1) она равна частному от деления непрерывных функций и при этом
делитель не равен нулю (при указанных ![]() ).
).
П р и м е р 7. Функция
![]()
непрерывна для любого ![]() , потому что она
является композицией непрерывных функций:
, потому что она
является композицией непрерывных функций: ![]() ,
, ![]() ,
, ![]() (см. теорему. 2).
(см. теорему. 2).
П р и м е р 8. Функция ![]() непрерывна
непрерывна ![]() , потому что
, потому что
![]() при
при ![]() .
.
П р и м е р 9.
Если функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
то непрерывна также в этой точке и функция
,
то непрерывна также в этой точке и функция ![]() .
.
Это следует из
теоремы 2 и примера 8, потому что функция ![]() есть композиция двух непрерывных
функций
есть композиция двух непрерывных
функций ![]() ,
,
![]() .
.
Отметим еще две теоремы, которые непосредственно следуют из соответствующих теорем 1 и 2 §3.2 для предела функции.
Т е о р е м а
3. Если функция ![]() непрерывна в точке
непрерывна в точке ![]() , то существует окрестность
, то существует окрестность ![]() этой точки, на
которой
этой точки, на
которой ![]() ограничена.
ограничена.
Т е о р е м а
4. Если функция ![]() непрерывна в точке
непрерывна в точке ![]() и
и ![]() , то существует окрестность
, то существует окрестность ![]() точки
точки ![]() , на которой
, на которой
![]() .
.
Больше того, если ![]() , то
, то
![]() ,
,
а если ![]() , то
, то
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
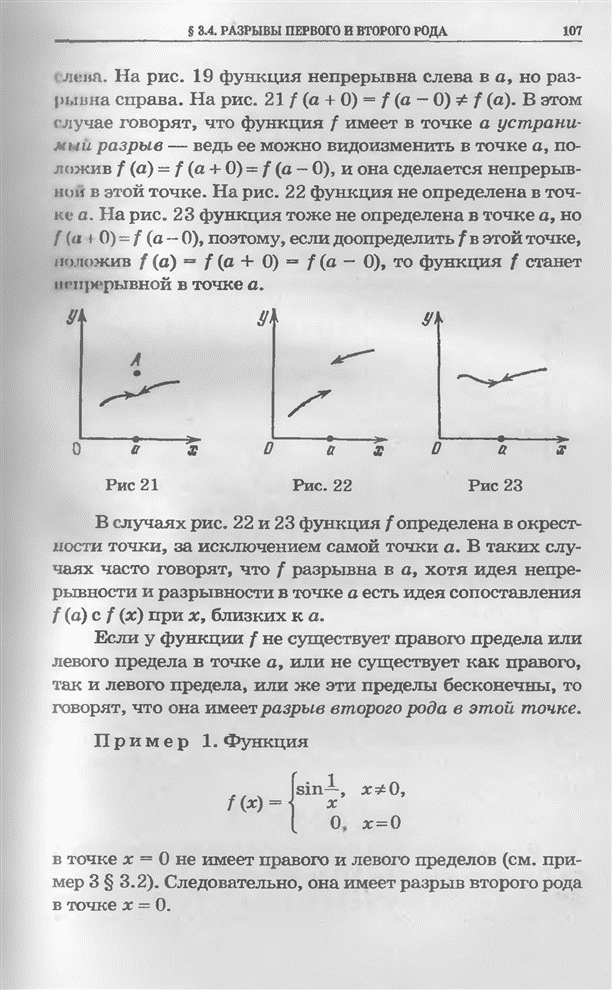
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
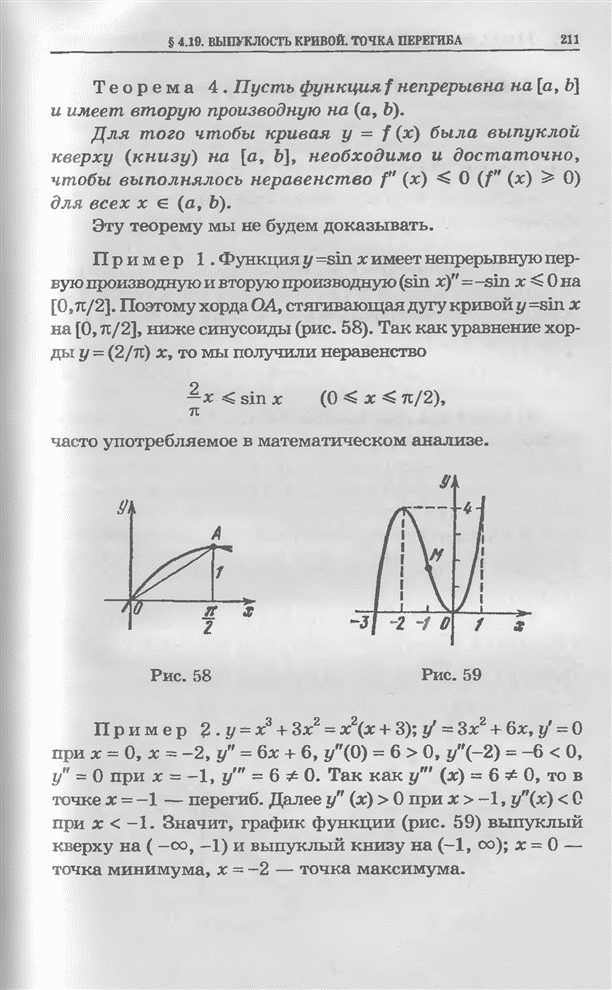
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей