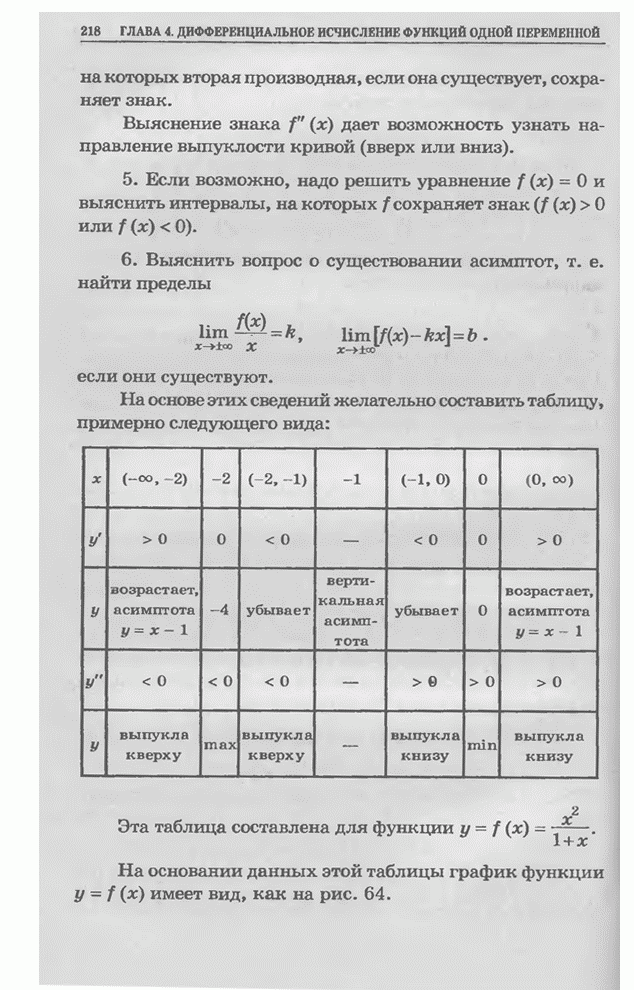
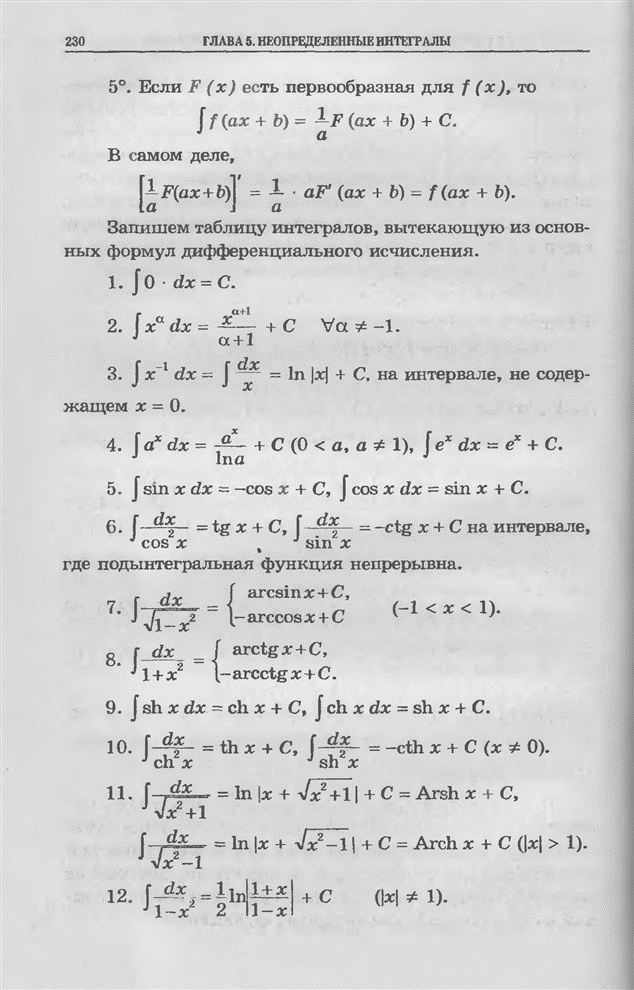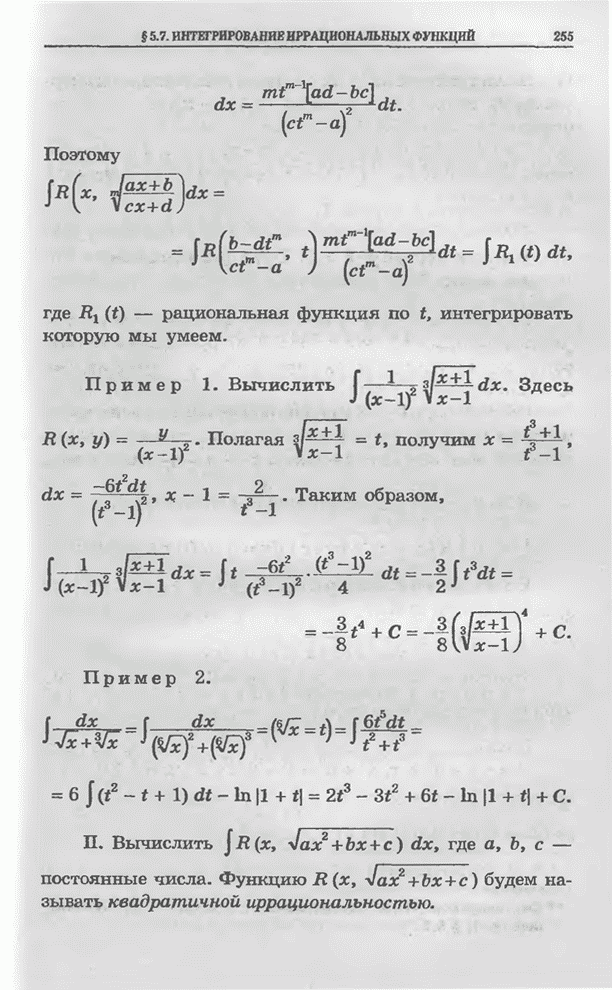| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4.16. Формулы и ряды Тейлора элементарных функций
1. ![]() . Эта функция бесконечно
дифференцируема (имеет производные любого порядка) на
. Эта функция бесконечно
дифференцируема (имеет производные любого порядка) на ![]() ). При этом
). При этом
![]() .
.
Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
 , (1)
, (1)
где ![]() может быть положительным и
отрицательным. На отрезке
может быть положительным и
отрицательным. На отрезке ![]() ,
, ![]() ,
,
 . (2)
. (2)
Это показывает (см. теорему 1 §
4.15), что функция ![]() разлагается на
разлагается на ![]() в сходящийся ряд Тейлора по
степеням
в сходящийся ряд Тейлора по
степеням ![]() (ряд
Маклорена):
(ряд
Маклорена):
 . (3)
. (3)
Но ![]() - произвольное число, поэтому это
равенство имеет место на всей действительной оси
- произвольное число, поэтому это
равенство имеет место на всей действительной оси ![]() . В данном случае
. В данном случае  на отрезке
на отрезке ![]() , и чтобы получить
равенство (3), можно было бы воспользоваться теоремой 2 § 4.15.
, и чтобы получить
равенство (3), можно было бы воспользоваться теоремой 2 § 4.15.
Вычислим число ![]() с точностью до 0,001. Имеем
(см. (1))
с точностью до 0,001. Имеем
(см. (1))
 (4)
(4)
где
 .
(5)
.
(5)
Надо подобрать ![]() настолько большим,
чтобы
настолько большим,
чтобы
 .
.
Так как ![]() , то для этого достаточно
решить неравенство
, то для этого достаточно
решить неравенство ![]() . Оно выполняется при
. Оно выполняется при ![]() . Следовательно,
. Следовательно,
![]()
с точностью до 0,001.
П р и м е ч а н и е . Так как ![]() при
при ![]() , то при
, то при ![]() , где
, где ![]() . Поэтому равенство
(4) можно записать в следующем виде:
. Поэтому равенство
(4) можно записать в следующем виде:
 .
.
Эта формула была использована (в
§ 2.6, формула (3)) для доказательства иррациональности числа ![]() .
.
2. ![]() . Данная функция имеет производную
любого порядка и
. Данная функция имеет производную
любого порядка и
![]() .
.
Поэтому по теореме 2 § 4.15
функция ![]() разлагается
в сходящийся к ней на
разлагается
в сходящийся к ней на ![]() ряд Тейлора по степеням
ряд Тейлора по степеням ![]() :
:
 .
.
Надо учесть, что

Формула Тейлора функции ![]() по степеням
по степеням ![]() имеет вид
имеет вид
 , (6)
, (6)
где
 .
.
Отсюда следует, что

и
 .
.
3. ![]() . Совершенно аналогично можно получить,
что
. Совершенно аналогично можно получить,
что
 .
.
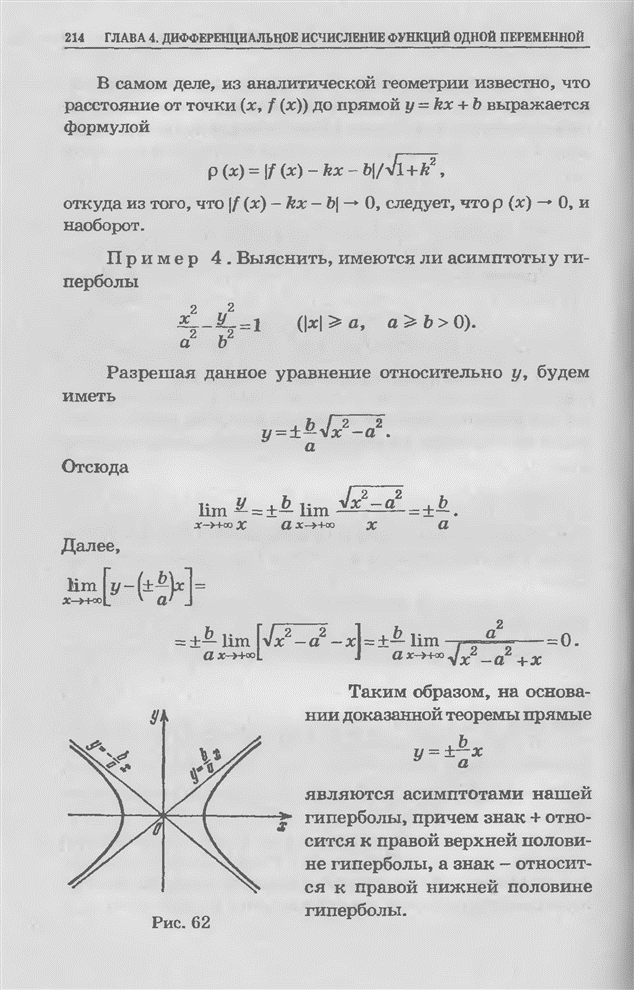
П р и м е р 1. Найти ![]() .
.
Имеем
![]() ,
(7)
,
(7)
поэтому
 ,
,
т. е.
![]() .
.
На самом деле в (7) остаток имеет
вид  . Но
для наших целей достаточно
. Но
для наших целей достаточно  . Надо иметь в виду, что если некоторая
функция от
. Надо иметь в виду, что если некоторая
функция от ![]() есть
есть
 , то она
есть также
, то она
есть также  (но
вообще не наоборот!).
(но
вообще не наоборот!).
4. Функция ![]() определена и сколько угодно
раз дифференцируема для
определена и сколько угодно
раз дифференцируема для ![]() . Поэтому для нее формулу Тейлора можно
написать для любого
. Поэтому для нее формулу Тейлора можно
написать для любого ![]() при
при ![]() . Так как
. Так как
 ,
,
то формула Тейлора имеет вид
![]() .
.
Используя формы Лагранжа и Коши остаточного члена, можно показать, что
![]() .
.
В самом деле, используя форму
Лагранжа остаточного члена, имеем для ![]() :
:
 ;
;
используя форму Коши остаточного
члена (см. § 4.14, (10)), имеем для ![]() :
:

 .
.
Поэтому функция ![]() разлагается в
указанном промежутке в ряд Тейлора по степеням
разлагается в
указанном промежутке в ряд Тейлора по степеням ![]() :
:
 .
.
5. Функция ![]() . Для этой функции
. Для этой функции
![]() ,
,
![]() .
.
Формула Тейлора по степеням ![]() имеет вид
имеет вид
![]() .
.
Можно доказать, что при любом ![]()
![]() .
.
Поэтому для любого
действительного ![]() имеет
место разложение функции
имеет
место разложение функции ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]()
 . (8)
. (8)
Если ![]() натуральное, то функция
натуральное, то функция ![]() есть многочлен. В
этом случае
есть многочлен. В
этом случае ![]() для
для
![]() , и ряд
справа в (8) представляет собой конечную сумму – многочлен Тейлора
(см. § 4.14).
, и ряд
справа в (8) представляет собой конечную сумму – многочлен Тейлора
(см. § 4.14).
При ![]() исследование
поведения остаточного члена (в форме Коши или Лагранжа) требует больших усилий.
Отметим лишь, что при
исследование
поведения остаточного члена (в форме Коши или Лагранжа) требует больших усилий.
Отметим лишь, что при ![]() ряд Тейлора (8) сходится при
ряд Тейлора (8) сходится при ![]() , а при
, а при ![]() для
для ![]() .
.
Приведем частные случаи ряда (8)
при ![]() ;
; ![]() :
:
![]()
- обыкновенная геометрическая
прогрессия, расходящаяся при ![]() ;
;
![]()
![]() :
:
здесь ряд справа сходится при ![]() .
.
П р и м е р 2. Вычислить предел ![]()


П р и м е р 3.

 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
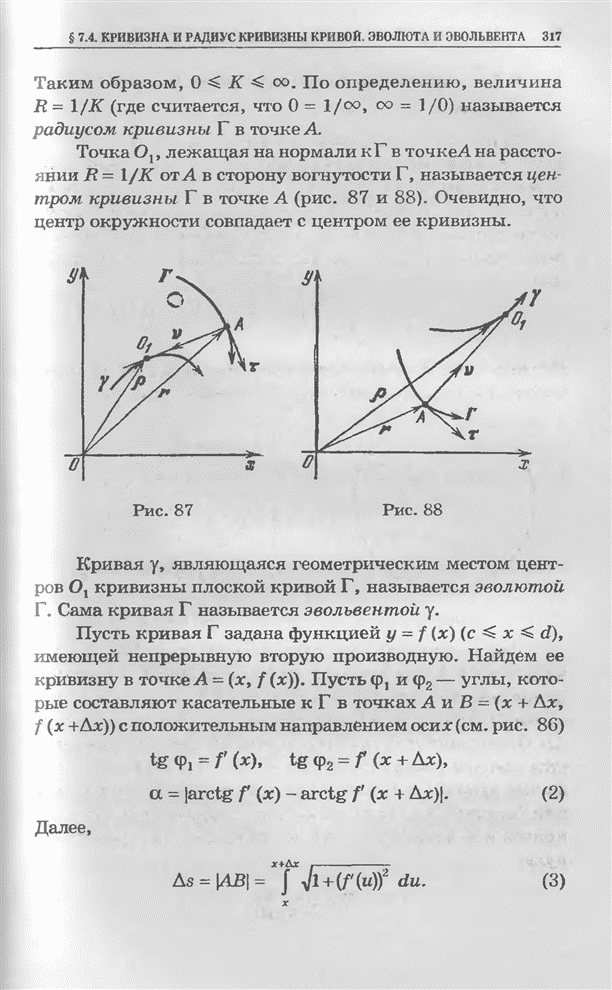
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
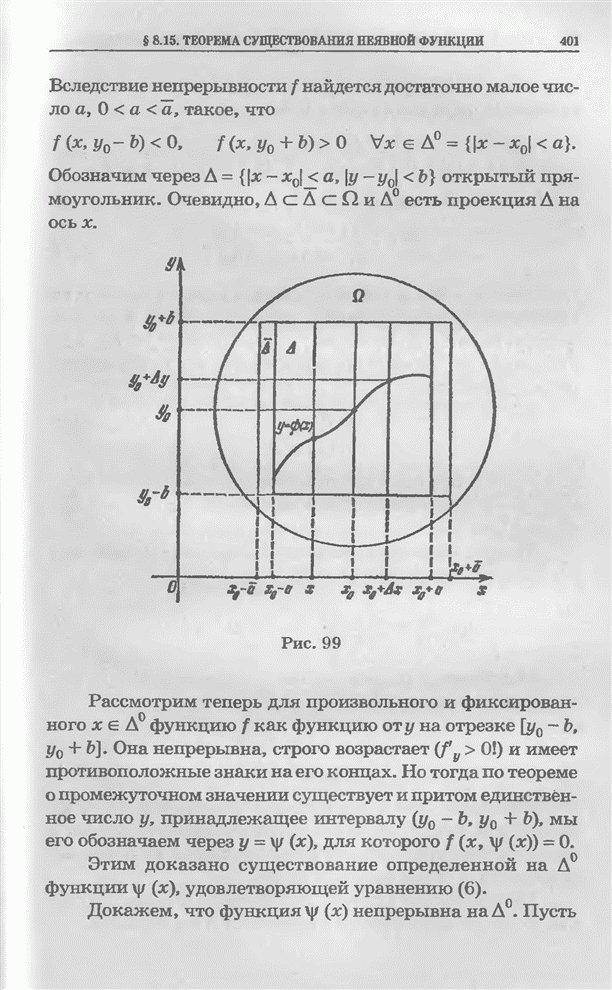
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
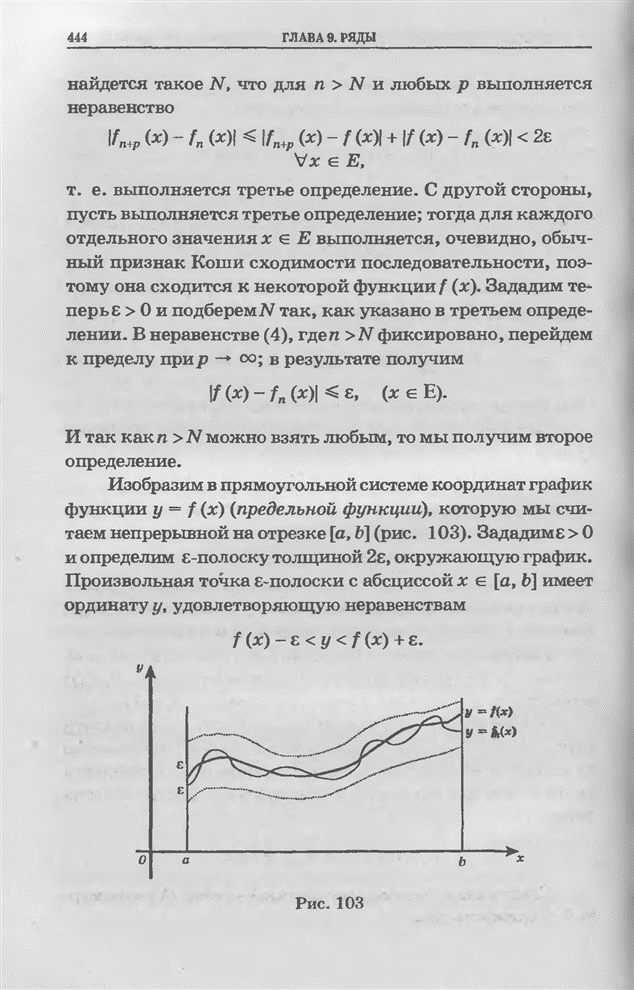
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей