| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4.2. Геометрический смысл производной
Пусть на
интервале ![]() задана
непрерывная функция
задана
непрерывная функция ![]() . Ее график называется непрерывной
кривой. Обозначим его через
. Ее график называется непрерывной
кривой. Обозначим его через ![]() . Зададим на
. Зададим на ![]() точку
точку ![]() (рис. 37 и 38) и поставим
целью определить касательную к
(рис. 37 и 38) и поставим
целью определить касательную к ![]() в этой точке. Для этого введем на
в этой точке. Для этого введем на ![]() другую точку
другую точку ![]() , где
, где ![]() (на рис. 37
изображен случай
(на рис. 37
изображен случай ![]() ,
а на рис. 38 – случай
,
а на рис. 38 – случай ![]() ). Прямую, проходящую через точки
). Прямую, проходящую через точки ![]() и
и ![]() , направленную в
сторону возрастания
, направленную в
сторону возрастания ![]() (отмеченную стрелкой), назовем секущей
и обозначим через
(отмеченную стрелкой), назовем секущей
и обозначим через ![]() .
.

Рис. 37 Рис. 38
Угол, который ![]() образует с
положительным направлением оси
образует с
положительным направлением оси ![]() , обозначим через
, обозначим через ![]() . Мы считаем, что
. Мы считаем, что ![]() . При
. При ![]() угол отсчитывается
от оси
угол отсчитывается
от оси ![]() против
часовой стрелки, а при
против
часовой стрелки, а при ![]() - по часовой стрелке. На данных
рисунках
- по часовой стрелке. На данных
рисунках ![]() .
На рис. 37
.
На рис. 37 ![]() ,
,
![]() , а на
рис. 38
, а на
рис. 38 ![]() ,
, ![]() . В обоих случаях
. В обоих случаях ![]() .
.
Если ![]() , то
, то ![]() и точка
и точка ![]() , двигаясь по
, двигаясь по ![]() , стремится к
, стремится к ![]() . Если при этом угол
. Если при этом угол
![]() стремится
к некоторому значению
стремится
к некоторому значению ![]() , отличному от
, отличному от ![]() и
и ![]() , то существует предел
, то существует предел
![]() ,
(1)
,
(1)
равный производной (конечной) от ![]() в точке
в точке ![]() :
:
![]() .
(2)
.
(2)
Обратно, если существует
(конечная) производная ![]() , то
, то ![]() .
.
При стремлении ![]() к
к ![]() секущая
секущая ![]() стремится занять
положение направленной прямой
стремится занять
положение направленной прямой ![]() , проходящей через точку
, проходящей через точку ![]() и образующей угол
и образующей угол ![]() с положительным
направлением оси
с положительным
направлением оси ![]() .
.
Направленная
прямая ![]() называется
касательной к кривой
называется
касательной к кривой ![]() в ее точке
в ее точке ![]() .
.
О п р е д е л е
н и е. Касательной к кривой ![]()
![]() в ее точке
в ее точке ![]() называется направленная
прямая
называется направленная
прямая ![]() , к
которой стремится секущая
, к
которой стремится секущая ![]() (направленная в сторону
возрастания
(направленная в сторону
возрастания ![]() прямая),
проходящая через
прямая),
проходящая через ![]() и точку
и точку ![]() , когда
, когда ![]() .
.
Мы доказали,
что если непрерывная функция ![]() имеет конечную производную
имеет конечную производную ![]() в точке
в точке ![]() , то ее график
, то ее график ![]() в соответствующей
точке имеет касательную с угловым коэффициентом
в соответствующей
точке имеет касательную с угловым коэффициентом ![]()
![]() . Обратно, существование предела
. Обратно, существование предела
![]()
влечет за собой существование
конечной производной ![]() и справедливость равенств (1),
(2).
и справедливость равенств (1),
(2).

Рис. 39
Может
случиться, что ![]() имеет
в точке
имеет
в точке ![]() правую
и левую производные, отличные между собой:
правую
и левую производные, отличные между собой:
![]() .
.
Тогда ![]() есть угловая точка
есть угловая точка ![]() . В этом случае
касательная
. В этом случае
касательная ![]() в
в
![]() не
существует, но можно говорить, что существует правая и левая касательные с
разными угловыми коэффициентами:
не
существует, но можно говорить, что существует правая и левая касательные с
разными угловыми коэффициентами:
 .
.
На рис. 39 приведен пример такого случая.
Пусть теперь
производная от ![]() в
точке
в
точке ![]() бесконечна:
бесконечна:
![]() .
.
Отметим четыре важных случая:
1) ![]() (рис. 40).
(рис. 40).
2) ![]() (рис. 41).
(рис. 41).

Рис. 40 Рис. 41
3)  ,
,  .
.
Левая
касательная перпендикулярна оси ![]() и направлена вниз. Правая касательная
перпендикулярна оси
и направлена вниз. Правая касательная
перпендикулярна оси ![]() и направлена вверх (рис. 42).
и направлена вверх (рис. 42).
4)  ,
,  .
.
Левая и правая
касательные перпендикулярны параллельно оси ![]() , первая вверх, вторая вниз (рис.
43).
, первая вверх, вторая вниз (рис.
43).

Рис. 42 Рис. 43
П р и м е ч а н
и е. Обычное определение касательной к кривой ![]() следующее: касательная
следующее: касательная ![]() к кривой
к кривой ![]() в ее точке
в ее точке ![]() есть прямая, к
которой стремится секущая
есть прямая, к
которой стремится секущая ![]() , проходящая через точку
, проходящая через точку ![]() и другую точку
и другую точку ![]() , когда последняя,
двигаясь по
, когда последняя,
двигаясь по ![]() ,
стремится к
,
стремится к ![]() .
.
В этом
определении не предполагается, что ![]() и
и ![]() - направленные прямые. Это определение
вполне корректно в случае касательной на параллельной оси
- направленные прямые. Это определение
вполне корректно в случае касательной на параллельной оси ![]() . Однако, если применить его,
например, к случаю 4) (см. рис. 43, где
. Однако, если применить его,
например, к случаю 4) (см. рис. 43, где ![]() - угловая точка), то получим, что
данная кривая имеет в точке
- угловая точка), то получим, что
данная кривая имеет в точке ![]() единственную касательную. Это не
вяжется с нашим представлением о гладкости кривой, имеющей касательную.
единственную касательную. Это не
вяжется с нашим представлением о гладкости кривой, имеющей касательную.
Приведенное
нами определение дает в точке ![]() две касательные (сливающиеся), имеющие
противоположные направления. Угол между ними равен
две касательные (сливающиеся), имеющие
противоположные направления. Угол между ними равен ![]() .
.
Из
аналитической геометрии известно, что уравнение прямой (в плоскости),
проходящей через точку ![]() под углом
под углом ![]() к положительному направлению
оси
к положительному направлению
оси ![]()
![]() , имеет вид
, имеет вид ![]() . Отсюда уравнение касательной к
кривой
. Отсюда уравнение касательной к
кривой ![]() в
точке
в
точке ![]() имеет
вид
имеет
вид
![]() (3)
(3)
где ![]() ,
, ![]() .
.
Прямая,
проходящая через точку ![]() перпендикулярна к касательной к
перпендикулярна к касательной к ![]() в этой точке,
называется нормалью к
в этой точке,
называется нормалью к ![]() в точке
в точке ![]() . Ее уравнение, очевидно,
имеет вид
. Ее уравнение, очевидно,
имеет вид
![]() (4)
(4)
П р и м е р 1.
Найти уравнение касательной к кривой
 (5)
(5)
в некоторой ее точке ![]() , т. е.
, т. е.  .
.
Кривая (5)
называется эллипсом. Очевидно, что эллипс расположен симметрично
относительно осей координат, так как его уравнение не меняется при замене ![]() на
на ![]() и
и ![]() на
на ![]() . При выводе
уравнения касательной будем считать, что
. При выводе
уравнения касательной будем считать, что ![]() ,
, ![]() . Из (5) имеем
. Из (5) имеем
![]() . (5’)
. (5’)
Отсюда  .
.
Вычислим функцию ![]() и производную
и производную ![]() в точке
в точке ![]() :
:
 ,
,
 . (6)
. (6)
Уравнение касательной к эллипсу в точке ![]() :
:
![]() .
(7)
.
(7)
Умножая (7) на ![]() , в силу (6) будем иметь
, в силу (6) будем иметь
 .
.
Так как у нас  , то уравнение касательной
запишется:
, то уравнение касательной
запишется:
![]() .
(8)
.
(8)
Таким образом, чтобы получить
уравнение касательной к эллипсу в его точке ![]() , нужно в уравнении эллипса (5)
заменить
, нужно в уравнении эллипса (5)
заменить ![]() на
на
![]() , и
, и ![]() на
на ![]() .
.

Рис. 44
При
отрицательных значениях ![]()
![]() рассуждения те же самые и (8) будет
уравнением касательной в любой точке эллипса
рассуждения те же самые и (8) будет
уравнением касательной в любой точке эллипса ![]() . Из уравнения (8) видно, что
касательная к эллипсу в его точке
. Из уравнения (8) видно, что
касательная к эллипсу в его точке ![]() пересекает ось
пересекает ось ![]() в точке с абсциссой
в точке с абсциссой ![]() , т. е. при
, т. е. при ![]() эта точка
пересечения находится правее эллипса, а при
эта точка
пересечения находится правее эллипса, а при ![]() - левее (рис. 44).
- левее (рис. 44).
П р и м е р 2. Найти уравнение касательной к кривой
 (9)
(9)
в некоторой ее точке ![]()
 .
.
Кривая (9) называется гиперболой. Эта кривая также симметрична относительно осей координат.
Проводя рассуждения, как в примере 1, получим уравнение касательной к гиперболе в виде
![]() .
.
Точка пересечения этой
касательной с осью ![]() имеет абсциссу
имеет абсциссу ![]()
 , т. е. эта точка пересечения
находится в
, т. е. эта точка пересечения
находится в ![]() для
для
![]() и в
и в ![]() для
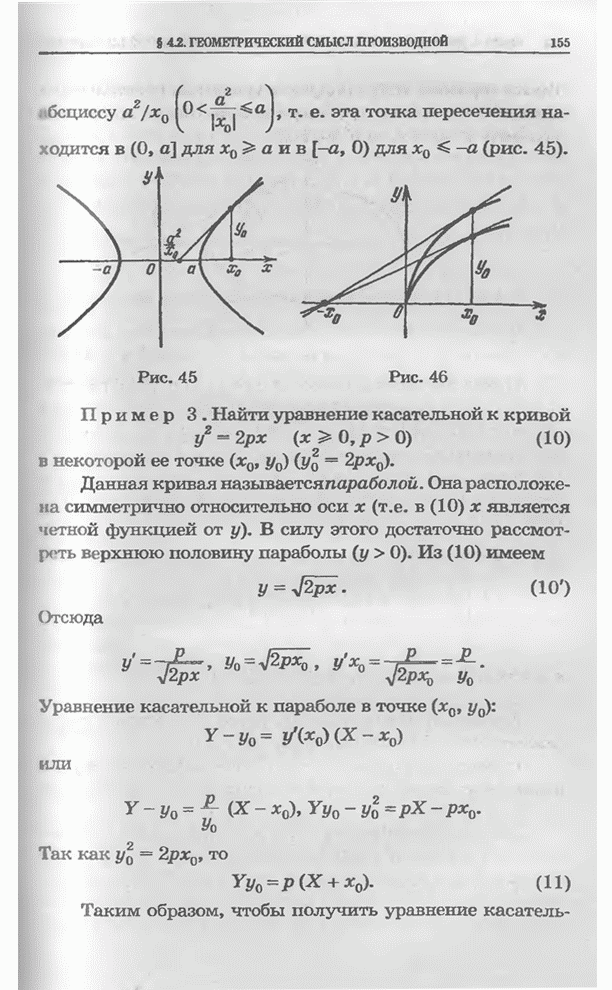
для ![]() (рис. 45).
(рис. 45).

Рис. 45 Рис. 46
П р и м е р 3. Найти уравнение касательной к кривой
![]() (10)
(10)
в некоторой ее точке ![]()
![]() .
.
Данная кривая
называется параболой. Она расположена симметрично относительно оси ![]() (т. е. в (10)
(т. е. в (10) ![]() является четной
функцией от
является четной
функцией от ![]() ).
В силу этого достаточно рассмотреть верхнюю половину параболы
).
В силу этого достаточно рассмотреть верхнюю половину параболы ![]() . Из (10) имеем
. Из (10) имеем
![]() (10’)
(10’)
Отсюда
![]() .
.
Уравнение касательной к параболе в точке ![]() :
:
![]()
или
![]() .
.
Так как ![]() , то
, то
![]() .
(11)
.
(11)
Таким образом, чтобы получить
уравнение касательной к параболе в ее точке ![]() , нужно в уравнении параболы (10)
заменить
, нужно в уравнении параболы (10)
заменить ![]() на
на
![]() , а
, а ![]() на
на ![]() .
.
Касательная (11) к параболе (10’)
в ее точке ![]() пересекает
ось
пересекает
ось ![]() в
точке с абсциссой
в
точке с абсциссой ![]() (рис.
46) независимо от величины
(рис.
46) независимо от величины ![]() , т. е. касательные к любым параболам
, т. е. касательные к любым параболам ![]() в точке
в точке ![]() пересекают ось
пересекают ось ![]() в одной и той же
точке
в одной и той же
точке ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
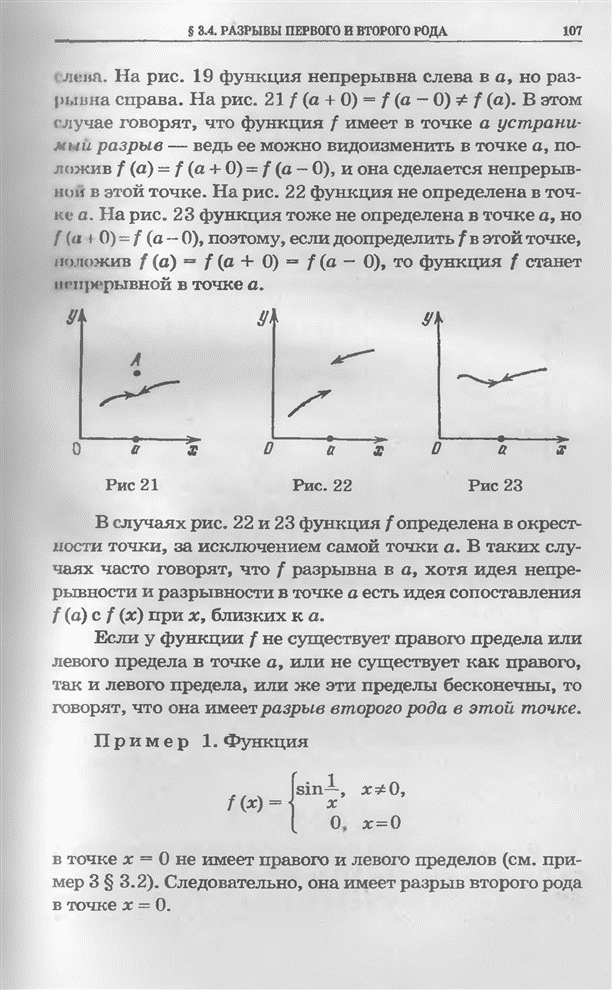
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
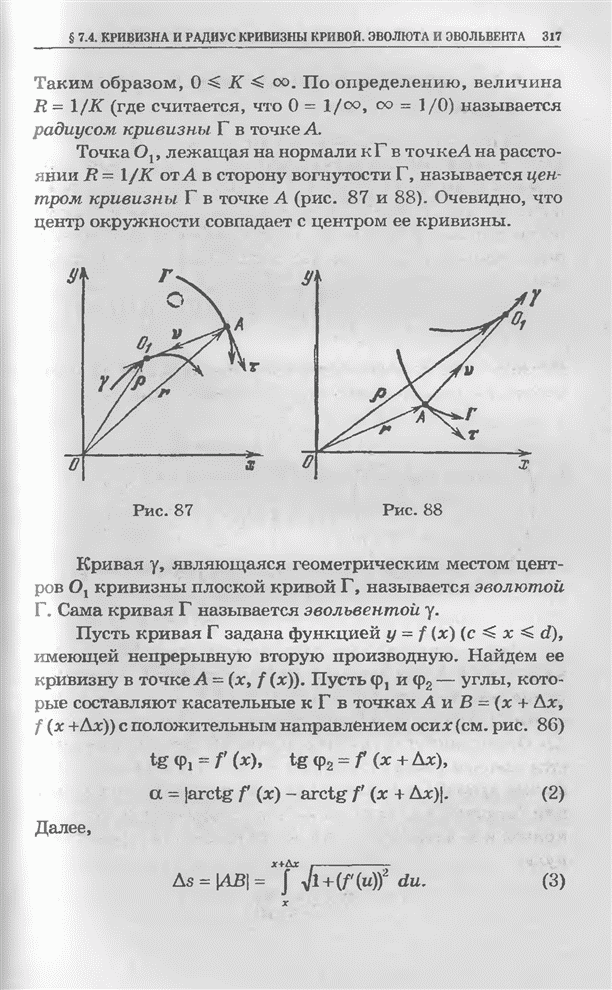
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
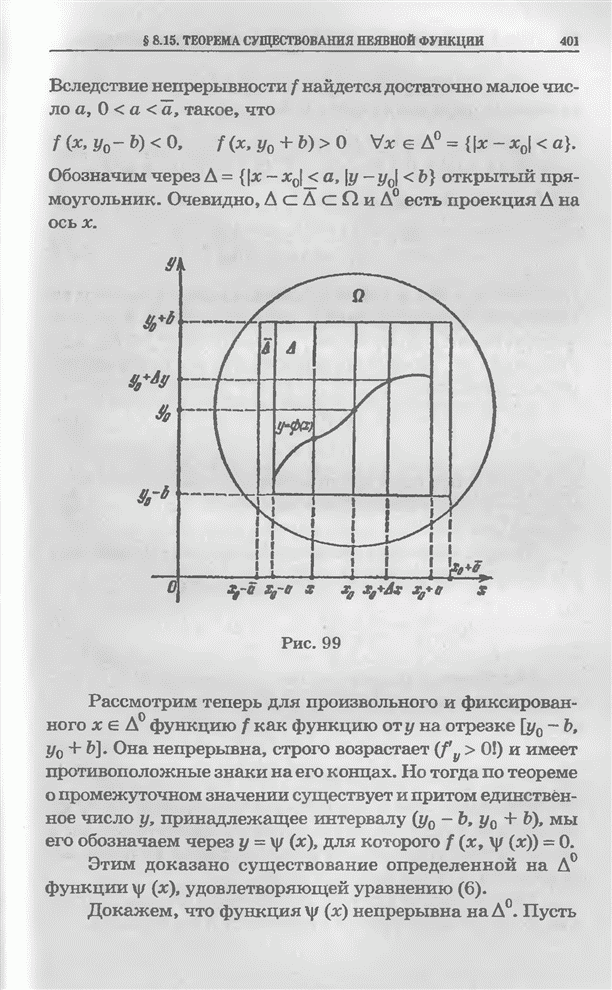
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
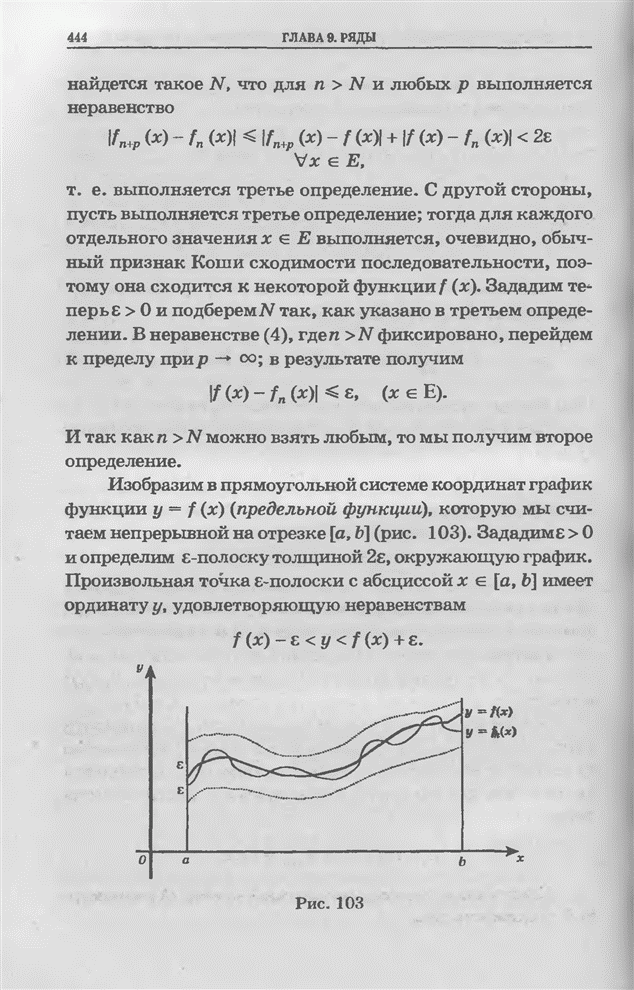
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей