| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8.17. Системы функций, заданных неявно
Выше мы рассмотрели вопрос о существовании непрерывной и дифференцируемой неявной функции, определяемой одним уравнением.
Здесь мы рассмотрим аналогичный
вопрос для совокупности неявных функций ![]() , определяемых системой уравнений
, определяемых системой уравнений
 (1)
(1)
Таким образом, мы ищем функции ![]() от
от ![]() , как решения
системы (1):
, как решения
системы (1): ![]() .
.
Выясним те условия, которые
обеспечивают существование решения системы (1) и дифференцируемость функций ![]() .
.
Т е о р е м а 1. Пусть задана система уравнений (1), удовлетворяющая следующим свойствам.
Функции ![]() определены на некоторой (
определены на некоторой (![]() -мерной) окрестности
-мерной) окрестности
![]() точки
точки ![]() пространства
пространства ![]() точек
точек ![]() и непрерывны там
вместе со своими частными производными первого порядка с якобианом
(определителем Якоби)
и непрерывны там
вместе со своими частными производными первого порядка с якобианом
(определителем Якоби)
 . (2)
. (2)
Кроме того, точка ![]() удовлетворяет системе (1).
удовлетворяет системе (1).
Пусть ![]() есть множество всех точек
есть множество всех точек ![]() , удовлетворяющих
системе (1) (в частности
, удовлетворяющих
системе (1) (в частности ![]() ).
).
Тогда, каково бы ни было ![]() , найдется
прямоугольник
, найдется
прямоугольник
![]() , (3)
, (3)
принадлежащий ![]() , такой, что
множество
, такой, что
множество ![]() описывается
непрерывно дифференцируемыми функциями
описывается
непрерывно дифференцируемыми функциями
![]() ,
(4)
,
(4)
![]() .
(5)
.
(5)
Другими словами, прямоугольник ![]() обладает тем
свойством, что на его проекции
обладает тем
свойством, что на его проекции ![]() на координатное подпространство
на координатное подпространство ![]() можно определить
непрерывно дифференцируемые функции (4), удовлетворяющие уравнениям (1):
можно определить
непрерывно дифференцируемые функции (4), удовлетворяющие уравнениям (1):
![]()
и неравенствам ![]() . Эти функции
единственны в том смысле, что любая точка
. Эти функции
единственны в том смысле, что любая точка ![]() имеет координаты, связанные
уравнениями (4).
имеет координаты, связанные
уравнениями (4).
В частности ![]() , потому что
, потому что ![]() .
.
З а м е ч а н и е 1. В теореме
можно считать, что прямоугольник ![]() и его проекция
и его проекция ![]() определяются неравенствами
определяются неравенствами
![]() , (3*)
, (3*)
![]() (5*)
(5*)
с различными, вообще говоря,
числами ![]() .
Ведь если теорема верна для прямоугольника (3*) при некоторых
.
Ведь если теорема верна для прямоугольника (3*) при некоторых ![]() , то, положив
, то, положив ![]() , можно вследствие
непрерывности функций
, можно вследствие
непрерывности функций ![]() указать такое число
указать такое число ![]() , что точки
, что точки
![]()
окажутся в прямоугольнике (3).
Заметим, однако, что вообще
невозможно добиться, чтобы ![]() и
и ![]() в (3) были равными, в чем легко
убедиться на примере одного уравнения
в (3) были равными, в чем легко
убедиться на примере одного уравнения ![]() .
.
Приведем доказательство теоремы 1 только для частного случая двух уравнений
 (1’)
(1’)
Нам надо доказать, что если
функции ![]() и
и
![]() непрерывно
дифференцируемы в некоторой окрестности точки
непрерывно
дифференцируемы в некоторой окрестности точки ![]() , удовлетворяющей уравнениям (1’), и
якобиан
, удовлетворяющей уравнениям (1’), и
якобиан
 (2’)
(2’)
в ![]() , то для любого
, то для любого ![]() найдется прямоугольник
найдется прямоугольник
![]() , (3’)
, (3’)
принадлежащий указанной окрестности, и существуют непрерывно дифференцируемые функции
 , (4’)
, (4’)
определенные на его проекции
![]() (5’)
(5’)
такие, что они удовлетворяют уравнениям (1’) и обладают свойствами
![]() .
.
При этом для ![]()
![]() . (6)
. (6)
Указанные функции ![]() - единственные,
описывающие все решения уравнений (1’) в прямоугольнике
- единственные,
описывающие все решения уравнений (1’) в прямоугольнике ![]() ; иначе говоря, если
какая-либо точка
; иначе говоря, если
какая-либо точка ![]() удовлетворяет уравнениям (1’), то ее
координаты связаны соотношениями (4’).
удовлетворяет уравнениям (1’), то ее
координаты связаны соотношениями (4’).
Из того, что якобиан (2’) не
равен нулю в ![]() ,
следует, что один из его элементов не равен нулю в
,
следует, что один из его элементов не равен нулю в ![]() . Не нарушая общности,
считаем, что
. Не нарушая общности,
считаем, что
 . (7)
. (7)
К этому неравенству всегда можно
прийти, соответственно перенумеровав в случае необходимости ![]() и
и ![]() .
.
Так как частные производные от ![]() и
и ![]() по условию
непрерывны, то существует достаточно малая окрестность точки
по условию
непрерывны, то существует достаточно малая окрестность точки ![]() , на которой не
только якобиан (2’), но и производная
, на которой не
только якобиан (2’), но и производная ![]() не равны нулю. Но тогда для первого
уравнения (1’), если его рассматривать относительно неизвестной функции
не равны нулю. Но тогда для первого
уравнения (1’), если его рассматривать относительно неизвестной функции ![]() от
от ![]() , выполняются
условия теоремы 1’ § 8.15. Поэтому для любого
, выполняются
условия теоремы 1’ § 8.15. Поэтому для любого ![]() существует прямоугольник
существует прямоугольник ![]()
![]() (8)
(8)
и непрерывно дифференцируемая функция
![]() ,
(9)
,
(9)
![]() ,
,
удовлетворяющая первому уравнению (1’):
![]() , (10)
, (10)
где
![]() . (11)
. (11)
При этом функция ![]() единственна в том
смысле, что любая точка
единственна в том
смысле, что любая точка ![]() , принадлежащая к
, принадлежащая к ![]() и удовлетворяющая первому
уравнению (1’), имеет координаты, связанные равенством (9); в частности,
и удовлетворяющая первому
уравнению (1’), имеет координаты, связанные равенством (9); в частности,
![]() .
(12)
.
(12)
З а м е ч а н и е 2. Отметим,
что в (8) мы могли бы на первом этапе рассуждений считать ![]() . Но в дальнейшем придется
числа
. Но в дальнейшем придется
числа ![]() несколько
уменьшить, вообще говоря, непропорционально. Уменьшенные
несколько
уменьшить, вообще говоря, непропорционально. Уменьшенные ![]() и
и ![]() пригодны и для
рассматриваемого первого этапа рассуждений.
пригодны и для
рассматриваемого первого этапа рассуждений.
Итак, мы получили тождество (10),
верное, каковы бы ни были независимые ![]() . Но это тождество остается верным и
если считать, что
. Но это тождество остается верным и
если считать, что ![]() есть любая непрерывно
дифференцируемая функция
есть любая непрерывно
дифференцируемая функция ![]() , такая, однако, чтобы
, такая, однако, чтобы
![]() . (13)
. (13)
Но таких функций ![]() бесконечное
множество. Цель наша выбрать среди них такую, чтобы функции
бесконечное
множество. Цель наша выбрать среди них такую, чтобы функции
 (14)
(14)
тождественно удовлетворяли
второму уравнению (1’). Первому уравнению (1’) они уже удовлетворяют. Итак,
подставим найденную функцию ![]() во второе из уравнений (1’):
во второе из уравнений (1’):
![]() (15)
(15)
и будем искать функцию ![]() от
от ![]() , ему удовлетворяющую. Положим
, ему удовлетворяющую. Положим
![]() .
.
Функция ![]() непрерывно дифференцируема
для любых
непрерывно дифференцируема
для любых ![]() (см.
(11)). Она удовлетворяет равенствам
(см.
(11)). Она удовлетворяет равенствам
![]()
(см. условие теоремы и (12)). Кроме того,
![]() .
.
В самом деле, для точек ![]() (пояснения ниже)
(пояснения ниже)

 . (16)
. (16)
В первом равенстве (16) применено правило о производной сложной функции, во втором надо учесть, что, согласно (10),
 .
.
Конечно, там где мы пишем частные
производные от ![]() и
и
![]() ,
считается, что они вычисляются в точках
,
считается, что они вычисляются в точках ![]() . В последнем соотношении (16) надо
учесть (2’) и (7).
. В последнем соотношении (16) надо
учесть (2’) и (7).
Мы видим, что левая часть
уравнения (15) удовлетворяет всем условиям теоремы 1’ § 8.15. Поэтому в
прямоугольнике ![]() (см.
(9)) найдется новый, вообще говоря, меньший прямоугольник, который мы снова
обозначим через
(см.
(9)) найдется новый, вообще говоря, меньший прямоугольник, который мы снова
обозначим через ![]() (см.
выше замечание 2), и найдется непрерывно дифференцируемая функция
(см.
выше замечание 2), и найдется непрерывно дифференцируемая функция
![]()
![]() ,
,
удовлетворяющая уравнению (15):
![]()
![]() ,
,
![]() .
.
При этом любая точка ![]() , удовлетворяющая
уравнению (15), имеет координаты, связанные равенством
, удовлетворяющая
уравнению (15), имеет координаты, связанные равенством ![]() . Но тогда выполняется такое
соотношение (см. (11)):
. Но тогда выполняется такое
соотношение (см. (11)):
![]() .
.
Итак, доказано существование непрерывно дифференцируемых функций
 ,
,
удовлетворяющих обоим уравнениям (1’) и притом так, что
![]() .
.
При этом
![]() (17)
(17)
и любая точка ![]() , удовлетворяющая уравнениям (1’),
имеет вид, как в (17).
, удовлетворяющая уравнениям (1’),
имеет вид, как в (17).
Переход от ![]() к
к ![]() можно осуществить с помощью замечания
1.
можно осуществить с помощью замечания
1.
З а м е ч а н и е 3. Укажем способ нахождения частных
производных ![]() .
.
Пусть все условия теоремы 1
выполнены. Тогда, подставляя функции ![]() в (1), получим систему тождеств:
в (1), получим систему тождеств:
 (18)
(18)
Дифференцируя по ![]() каждое тождество
системы (18) как сложную функцию, получим:
каждое тождество
системы (18) как сложную функцию, получим:
 (19)
(19)
Система (19) является линейной
относительно неизвестных производных  . Определителем ее является якобиан
. Определителем ее является якобиан
 .
.
Поэтому система (19) имеет единственное решение:


| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
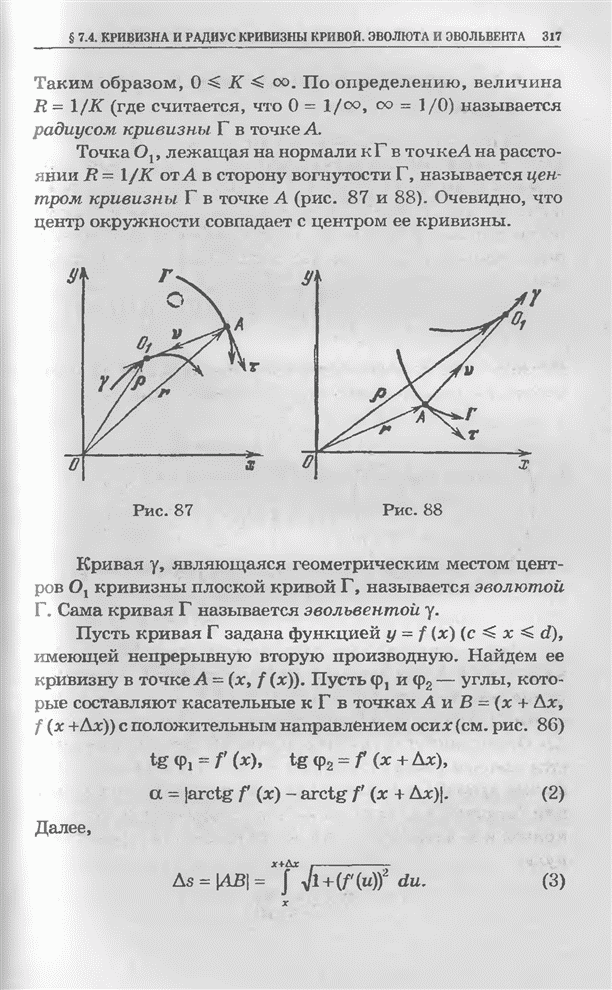
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
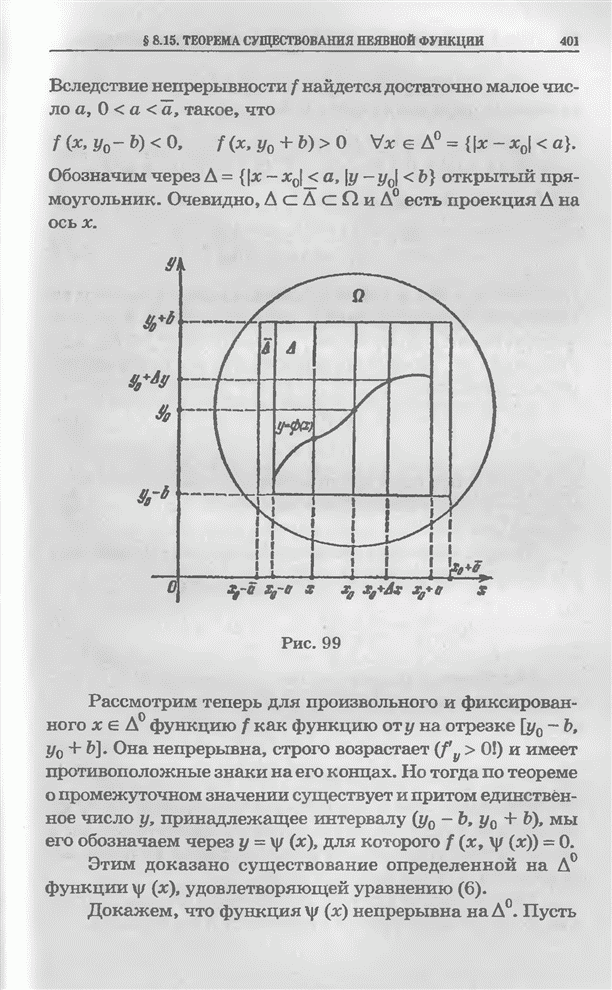
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
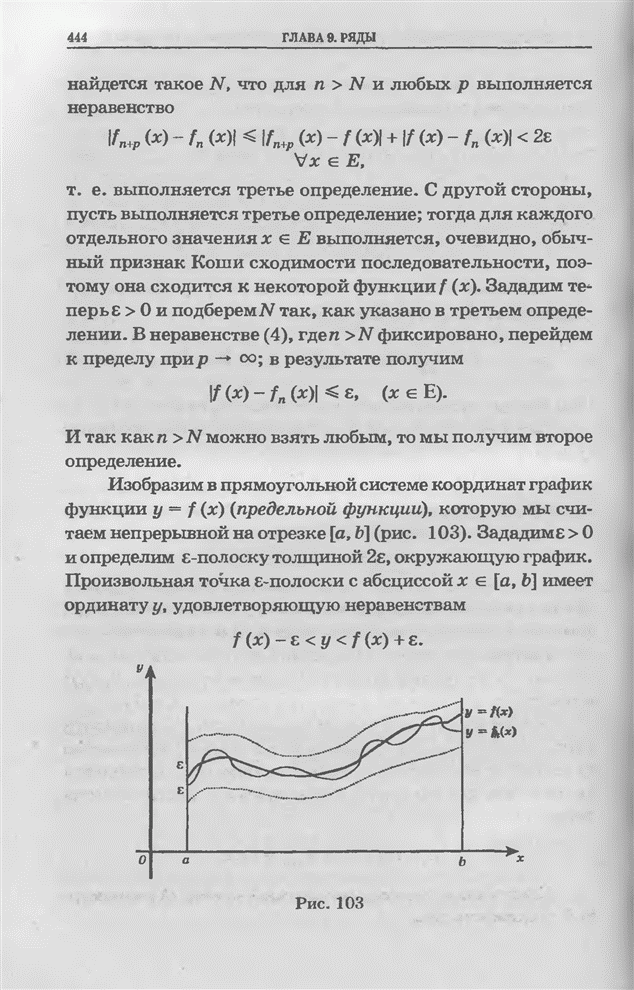
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей