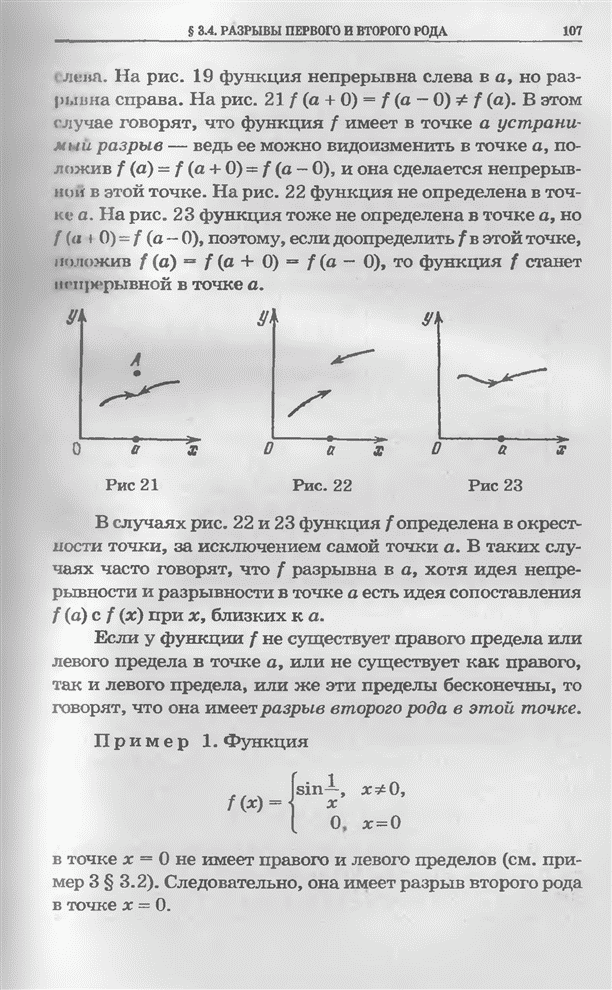
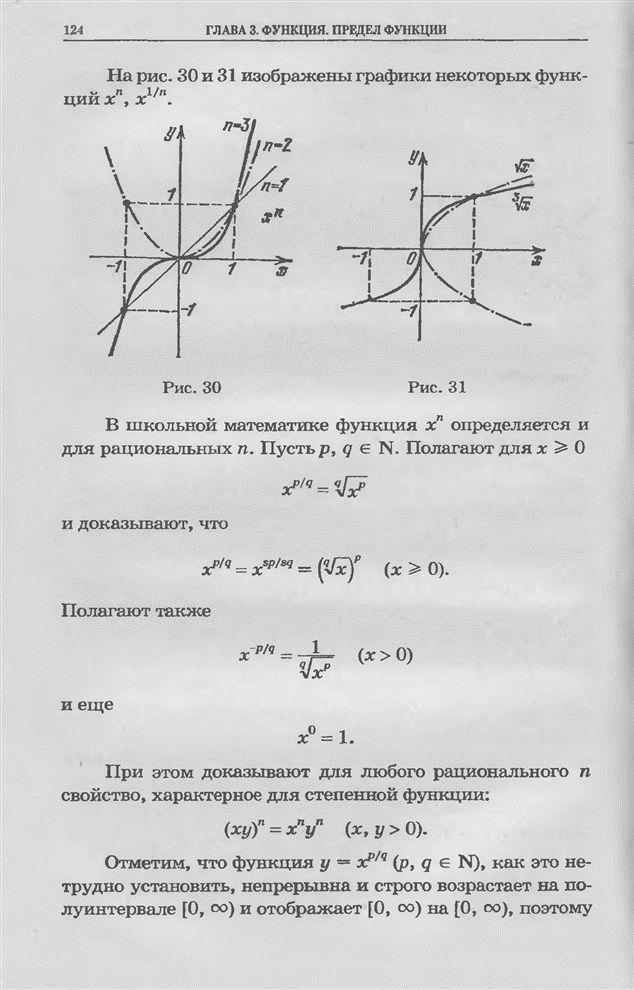
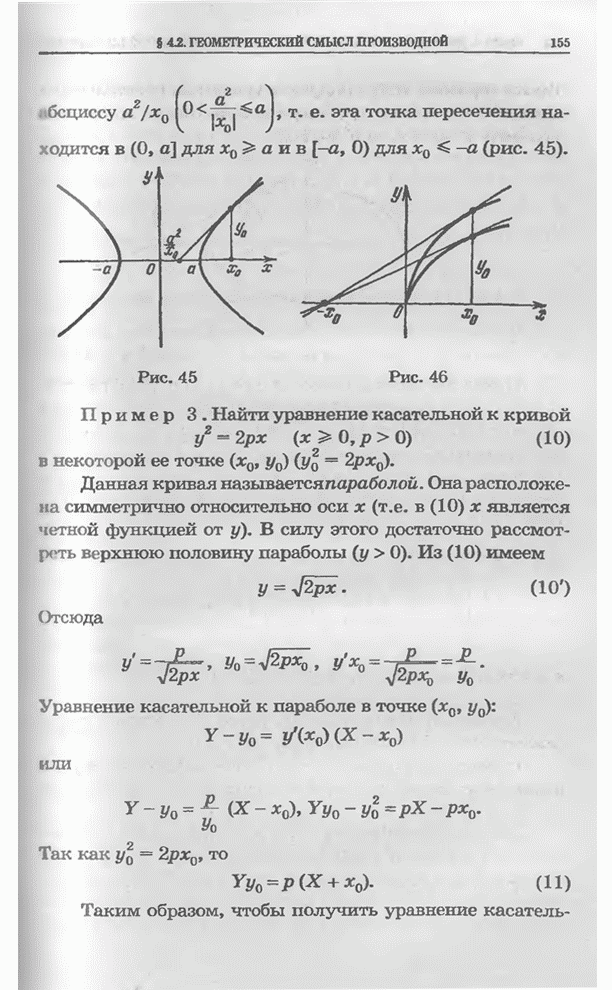
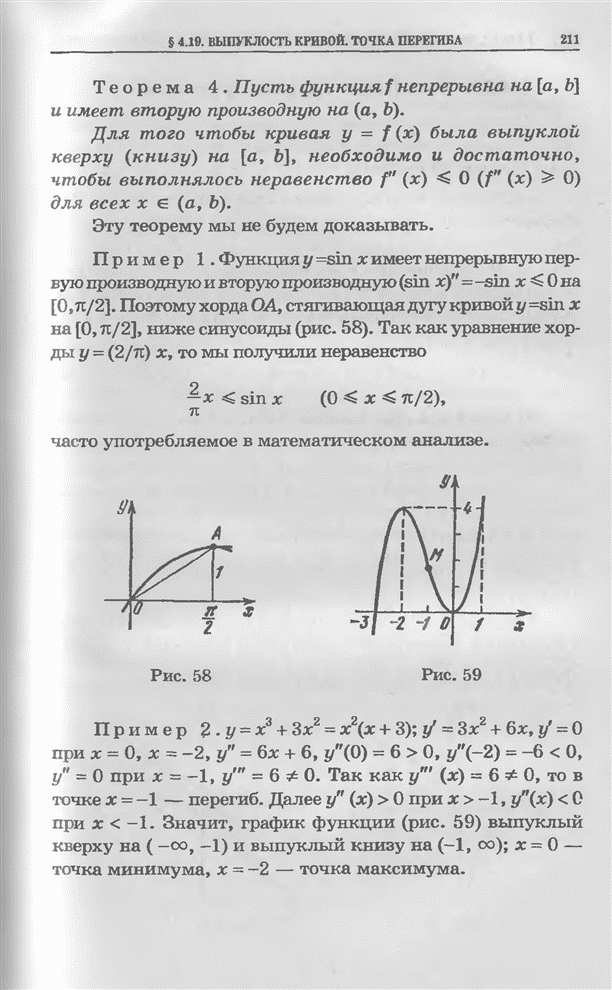
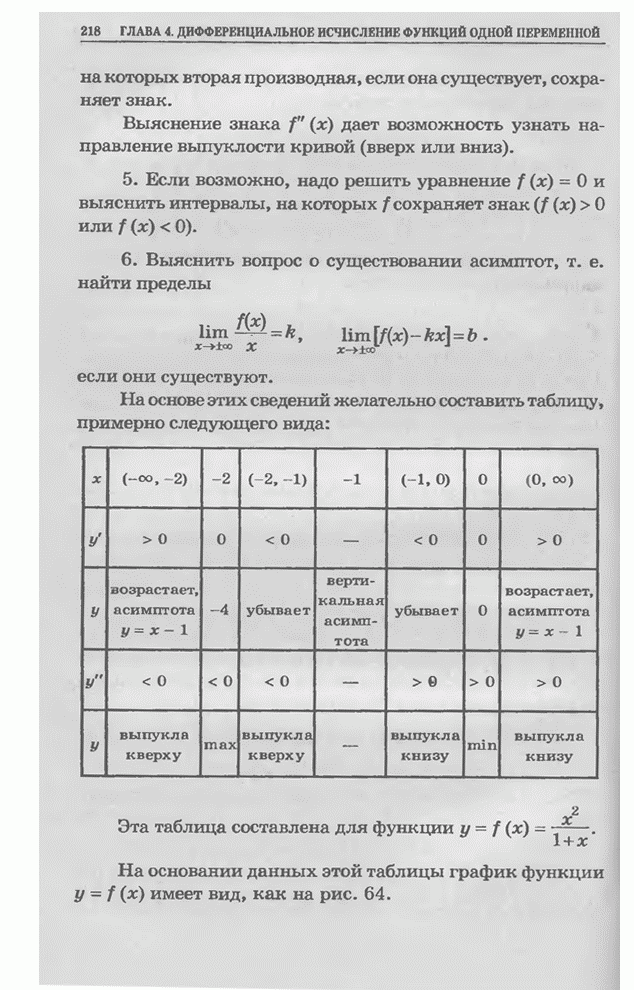
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5.3. Комплексные числа
Комплексными числами называются выражения
![]() ,
,
где ![]() - действительные числа, а
- действительные числа, а ![]() - специальный
символ; при этом для комплексных чисел
- специальный
символ; при этом для комплексных чисел ![]() введены понятии равенства и
арифметические операции по следующим правилам:
введены понятии равенства и
арифметические операции по следующим правилам:
1) ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() ;
; ![]() .
.
2) ![]() .
.
3) ![]() .
.
4)  .
.
Из ![]() и
и ![]() следует, что
следует, что
![]() .
.
Таким образом, введенные операции
сложения и умножения обладают свойствами коммутативности ![]() , ассоциативности
, ассоциативности ![]()
![]() ,
, ![]() , дистрибутивности
, дистрибутивности  .
.
Можно еще сказать, что с
комплексными числами можно оперировать в точности так же, как мы привыкли оперировать
с буквенными выражениями в алгебре, но при этом операции упрощаются тем, что ![]() .
.
Из свойства ![]() следует, что множество
комплексных чисел содержит в себе как часть множество всех действительных чисел.
При этом легко видеть, что применение арифметических действий
следует, что множество
комплексных чисел содержит в себе как часть множество всех действительных чисел.
При этом легко видеть, что применение арифметических действий ![]() к выражениям
к выражениям ![]() приводит
соответственно к
приводит
соответственно к ![]() .
.
Число ![]() называется сопряженным к
комплексному числу
называется сопряженным к
комплексному числу ![]() . Действительное число
. Действительное число ![]() называется модулем
комплексного числа
называется модулем
комплексного числа ![]() . Очевидно, что
. Очевидно, что ![]() .
.
Если комплексное число ![]() трактовать как
точку (вектор)
трактовать как
точку (вектор) ![]() плоскости
плоскости
![]() , то
, то ![]() равен расстоянию
точки
равен расстоянию
точки ![]() от
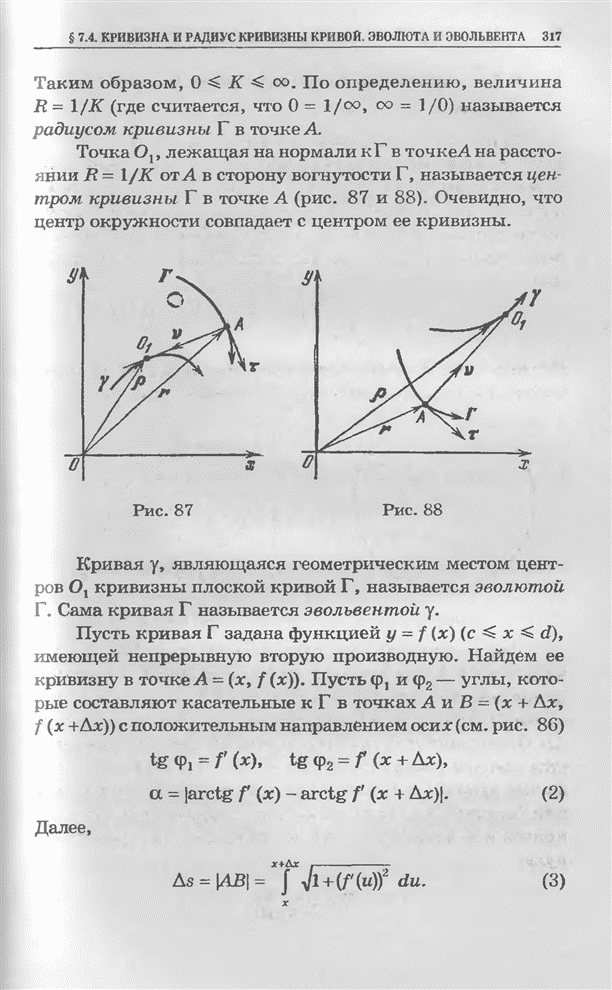
начала координат (рис. 74).
от
начала координат (рис. 74).

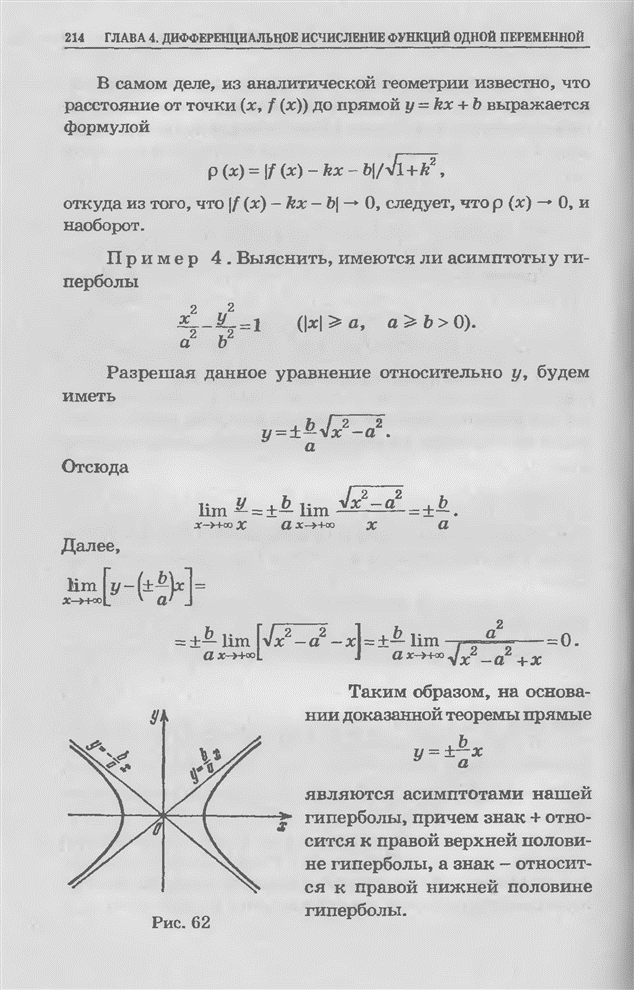
Рис. 74
Если на плоскости ввести полярные координаты ![]() , то
, то

 . (1)
. (1)
В силу этого, комплексное число ![]() можно записать в
форме
можно записать в
форме
![]() , (2)
, (2)
где ![]() - модуль числа
- модуль числа ![]() ,
, ![]() - угол (в радианах), который
составляет вектор
- угол (в радианах), который
составляет вектор ![]() с
положительным направлением оси
с
положительным направлением оси ![]() . Этот угол называют еще аргументом
комплексного числа
. Этот угол называют еще аргументом
комплексного числа ![]() и обозначают символом
и обозначают символом ![]() .
.
Очевидно, ![]() есть однозначная функция от
есть однозначная функция от ![]() . Вводят еще и многозначную
функцию (аргумент
. Вводят еще и многозначную
функцию (аргумент ![]() с большой буквы)
с большой буквы)
![]()
![]() ,
,
которая дает все значения ![]() , для которых для
данного
, для которых для
данного ![]() удовлетворяются
два равенства (1).
удовлетворяются
два равенства (1).
Число ![]() единственное, для которого
не имеет смысла его аргумент, но зато его можно определить как число, модуль
которого равен нулю
единственное, для которого
не имеет смысла его аргумент, но зато его можно определить как число, модуль
которого равен нулю ![]() .
.
![]() (с малой буквы) называют еще аргументом
в приведенной форме. Иногда бывает удобно считать аргументом в приведенной
форме угол, принадлежащий к другому полуинтервалу
(с малой буквы) называют еще аргументом
в приведенной форме. Иногда бывает удобно считать аргументом в приведенной
форме угол, принадлежащий к другому полуинтервалу ![]() длины
длины ![]() , например
, например ![]() .
.
Числа ![]() и
и ![]() называют действительной и
мнимой частями
называют действительной и
мнимой частями ![]() и обозначают символами
и обозначают символами ![]() . Таким образом,
. Таким образом,
![]() .
.
Если ![]() , то множество точек
, то множество точек ![]() плоскости
плоскости ![]() , удовлетворяющих
равенству
, удовлетворяющих
равенству ![]() ,
есть окружность радиуса
,
есть окружность радиуса ![]() с центром в начале координат.
с центром в начале координат.
По определению
![]() . (3)
. (3)
Очевидно, что ![]() есть комплексная функция
(принимающая комплексные значения) от действительного аргумента
есть комплексная функция
(принимающая комплексные значения) от действительного аргумента ![]() . Ясно, что
. Ясно, что ![]() - периодическая
функция периода
- периодическая
функция периода ![]() :
:
![]() .
.
Так как ![]() , то при непрерывном
изменении
, то при непрерывном
изменении ![]() на
полуинтервале
на
полуинтервале ![]() ,
точка
,
точка ![]() непрерывно
описывает окружность радиуса 1 с центром в точке
непрерывно
описывает окружность радиуса 1 с центром в точке ![]() .
.
Справедливы равенства
![]() .
(4)
.
(4)
В самом деле,
![]()
![]() ,
,
![]() .
.
Для произвольной комплексной
переменной ![]() функция
функция
![]() определяется
при помощи равенства
определяется
при помощи равенства
![]() .
.
Отсюда в силу (3)
![]() .
(5)
.
(5)
На основании (2), (3) всякое
комплексное число ![]() можно
представить в форме
можно
представить в форме
![]() ,
(6)
,
(6)
где неотрицательное число ![]() для данного
для данного ![]() единственно, а при
единственно, а при ![]() угол
угол
![]()
определен с точностью до ![]()
![]() .
.
Выражения (2) и (6) называются
соответственно тригонометрической и показательной формами комплексного числа
![]() .
.
Приведем примеры комплексных
чисел, записанных в показательной форме (считая ![]() ):
):
![]() ,
,
![]() .
.
Из равенств (3), (4) легко получаем формулу Муавра
![]() . (7)
. (7)
Справедливо также равенство
![]() ,
,
т. е. при перемножении комплексных чисел их модули перемножаются, а аргументы складываются независимо от того, в какой форме они взяты – в приведенной или нет.
Операция построения сопряженного комплексного числа обладает следующими простыми свойствами:
 . (8)
. (8)
В самом деле,
![]()
![]() ;
;
далее, так как
![]() ,
,
то
![]()
![]() .
.
Подобное доказательство имеет место и в случае частного.
Рассмотрим задачу о вычислении
корня ![]() -й
степени из числа
-й
степени из числа ![]() .
Требуется, таким образом, найти все числа
.
Требуется, таким образом, найти все числа ![]() такие, что
такие, что ![]() . Но тогда
. Но тогда ![]() и, вследствие
единственности представления комплексного числа в показательной форме,
и, вследствие
единственности представления комплексного числа в показательной форме, ![]() . Из первого
равенства следует
. Из первого
равенства следует ![]() (
(![]() - арифметическое
значение корня
- арифметическое
значение корня ![]() -й
степени из положительного числа
-й
степени из положительного числа ![]() ). Из второго же, что
). Из второго же, что ![]()
![]() .
.
Так как функция ![]() периодическая с
периодом
периодическая с
периодом ![]() ,
то значения
,
то значения ![]() ,
дающие существенно различные корни
,
дающие существенно различные корни ![]() -й степени из
-й степени из ![]() , соответствуют только
, соответствуют только ![]() значениям
значениям ![]() :
:
![]() . (9)
. (9)
Остальным целым ![]() соответствуют
значения
соответствуют
значения ![]() ,
отличающиеся от одного из значений (9) на величину, кратную
,
отличающиеся от одного из значений (9) на величину, кратную ![]() .
.
Мы доказали, что у комплексного
числа ![]() существует
существует
![]() (и только
(и только
![]() ) корней
степени
) корней
степени ![]() ,
записываемых по формуле
,
записываемых по формуле
![]() ,
,
где ![]() определяются равенствами (9).
определяются равенствами (9).
П р и м е р ы:
![]() .
.  .
.
![]() .
.  .
.
![]() .
.  .
.
![]()
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей