| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 6. Определенный Интеграл
§ 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
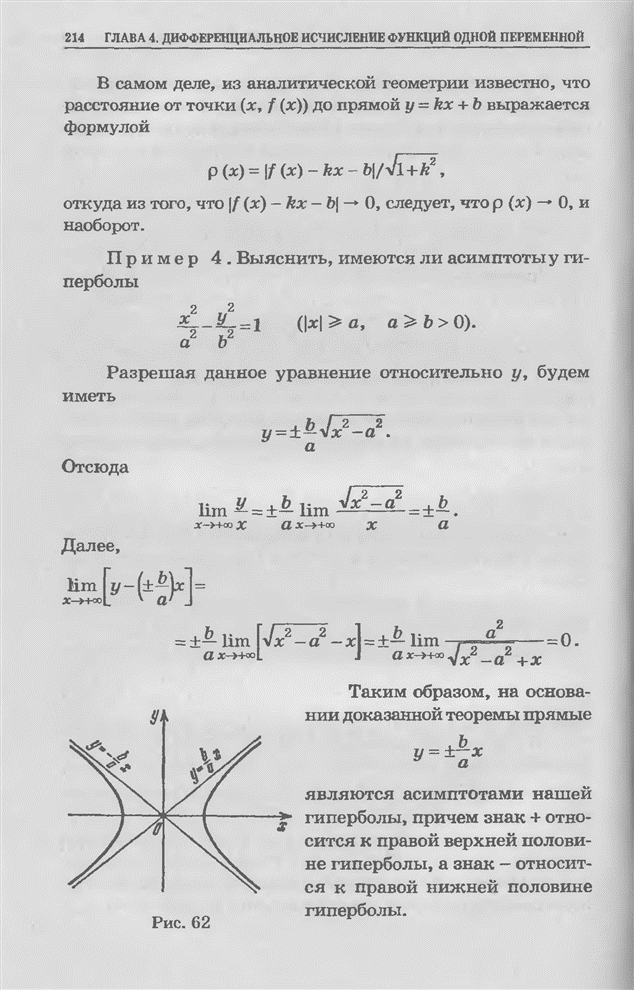
а) Зададим на отрезке ![]() (
(![]() и
и ![]() - конечные числа)
неотрицательную непрерывную функцию
- конечные числа)
неотрицательную непрерывную функцию ![]() . График ее изображен на рис. 75.
Поставим задачу: требуется определить понятие площади фигуры, ограниченной
кривой
. График ее изображен на рис. 75.
Поставим задачу: требуется определить понятие площади фигуры, ограниченной
кривой ![]() ,
осью
,
осью ![]() ,
прямыми
,
прямыми ![]() и
и
![]() , и
вычислить эту площадь. Поставленную задачу естественно решить так.
, и
вычислить эту площадь. Поставленную задачу естественно решить так.
Произведем разбиение отрезка ![]() на
на ![]() частей точками
частей точками
![]() , (1)
, (1)

Рис. 75
выберем на каждом из полученных частичных отрезков
![]() (2)
(2)
по произвольной точке ![]() , определим
значения функции
, определим
значения функции ![]() в
этих точках и составим сумму
в
этих точках и составим сумму
 (3)
(3)
которую называют интегральной суммой и которая, очевидно, равна сумме площадей заштрихованных прямоугольников (см. рис. 75).
Будем теперь стремить все ![]() к нулю и притом
так, чтобы максимальный (самый большой) частичный отрезок разбиения стремился к
нулю. Если при этом величина
к нулю и притом
так, чтобы максимальный (самый большой) частичный отрезок разбиения стремился к
нулю. Если при этом величина ![]() стремится к определенному пределу
стремится к определенному пределу ![]() , не зависящему от
способов разбиения (1) и выбора точек
, не зависящему от
способов разбиения (1) и выбора точек ![]() на частичных отрезках, то естественно
величину
на частичных отрезках, то естественно
величину ![]() называть
площадью нашей криволинейной фигуры. Таким образом,
называть
площадью нашей криволинейной фигуры. Таким образом,
 (4)
(4)
Итак, мы дали определение площади
нашей криволинейной фигуры (трапеции). Возникает вопрос, имеет ли каждая такая
фигура площадь, иначе говоря, стремится ли на самом деле к конечному пределу ее
интегральная сумма ![]() , когда
, когда ![]() ? В дальнейшем будет доказано, что этот
вопрос решается положительно: каждая определенная выше криволинейная фигура,
соответствующая некоторой непрерывной функции
? В дальнейшем будет доказано, что этот
вопрос решается положительно: каждая определенная выше криволинейная фигура,
соответствующая некоторой непрерывной функции ![]() , действительно имеет площадь в смысле
сделанного определения, таким образом, зависящим от этой фигуры числом
, действительно имеет площадь в смысле
сделанного определения, таким образом, зависящим от этой фигуры числом ![]() .
.
Другой возникающий здесь вопрос, насколько естественно данное определение площади, как всегда в таких случаях, решается практикой. Мы скажем только, что практика полностью оправдала это определение. У нас будет много случаев убедиться в правильности сделанного определения.
б) Дан линейный неоднородный
стержень, лежащий на оси ![]() в пределах отрезка
в пределах отрезка ![]() . Требуется определить массу
этого стержня. Пусть плотность распределения массы вдоль стержня есть некоторая
непрерывная функция от
. Требуется определить массу
этого стержня. Пусть плотность распределения массы вдоль стержня есть некоторая
непрерывная функция от ![]() :
: ![]() .
.
Для определения
массы стержня разобьем его на ![]() произвольных частей точками
произвольных частей точками ![]() . В пределах каждой
части
. В пределах каждой
части ![]() выберем
по произвольной точке
выберем
по произвольной точке ![]() .
.
Так как в
пределах ![]() функция
функция
![]() изменяется
мало, то массу части стержня, соответствующей отрезку
изменяется
мало, то массу части стержня, соответствующей отрезку ![]() , можно считать приближенно
равной
, можно считать приближенно
равной ![]() ,
где
,
где ![]() .
.
Масса же ![]() всего стержня приближенно
равна
всего стержня приближенно
равна
 .
.
Точное значение массы, очевидно, получим в пределе, когда наибольший частичный отрезок стремится к нулю, т. е.
 (4’)
(4’)
Обе рассмотренные задачи привели
нас к одной и той же математической операции над функциями различного
происхождения, заданными на отрезке ![]() . Нам встретится много других
конкретных задач, решение которых сводится к подобной операции над функцией,
заданной на отрезке. Эта операция называется операцией интегрирования функции
на отрезке, а ее результат – число – называется определенным интегралом
от функции на отрезке.
. Нам встретится много других
конкретных задач, решение которых сводится к подобной операции над функцией,
заданной на отрезке. Эта операция называется операцией интегрирования функции
на отрезке, а ее результат – число – называется определенным интегралом
от функции на отрезке.
О п р е д е л е
н и е 1. Пусть на отрезке ![]() задана функция
задана функция ![]() . Разделим
. Разделим ![]() на части
произвольными точками:
на части
произвольными точками:
![]() ,
,
и будем говорить, что этим
произведено разбиение ![]() отрезка
отрезка ![]() . На каждом частичном отрезке
. На каждом частичном отрезке ![]() разбиения выберем
точку
разбиения выберем
точку ![]() и
составим сумму
и
составим сумму
 ,
,
называемую интегральной суммой функции ![]() , соответствующей
разбиению
, соответствующей
разбиению ![]() .
.
Обозначим через
![]()
максимальную длину частичных
отрезков ![]() разбиения
разбиения
![]() .
.
Предел (если он существует), к
которому стремится интегральная сумма ![]() , когда
, когда ![]() , называется определенным интегралом от
функции
, называется определенным интегралом от
функции ![]() на
отрезке
на
отрезке ![]() и
обозначается следующим образом:
и
обозначается следующим образом:
 . (5)
. (5)
Число ![]() называется нижним
пределом определенного интеграла, а число
называется нижним
пределом определенного интеграла, а число ![]() - верхним его пределом.
- верхним его пределом.
Определение 1 эквивалентно следующему.
О п р е д е л е
н и е 1’. Определенным интегралом от функции ![]() на отрезке
на отрезке ![]() называется число
называется число ![]() , удовлетворяющее
следующему свойству: для всякого
, удовлетворяющее
следующему свойству: для всякого ![]() можно найти число
можно найти число ![]() такое, что для любого
разбиения
такое, что для любого
разбиения ![]() отрезка
отрезка
![]() , у
которого
, у
которого ![]() ,
выполняется неравенство
,
выполняется неравенство

при произвольном выборе точек ![]() .
.
Понятие определенного интеграла так, как мы его определили, было введено для непрерывных функций французским математиком Коши и в общем случае Риманом - для функций не обязательно непрерывных (интегрируемых по Риману). Обычно предел (5) называют интегралом Римана и функцию, для которой этот предел существует, называют интегрируемой в смысле Римана.
Если функция ![]() непрерывна на
непрерывна на ![]() , то для нее всегда,
как мы узнаем, предел (5) существует.
, то для нее всегда,
как мы узнаем, предел (5) существует.
Говорят также,
что непрерывная на отрезке ![]() функция интегрируема на нем в
смысле Коши.
функция интегрируема на нем в
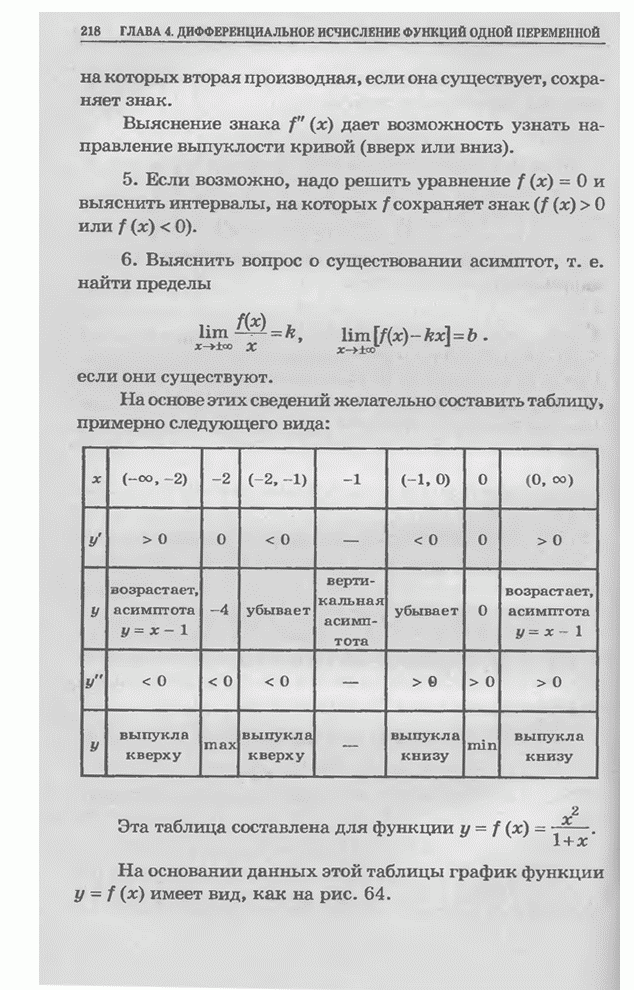
смысле Коши.
В п. ![]() мы определили (см.
рис. 75) площадь плоской фигуры, ограниченную сверху графиком непрерывной
функции
мы определили (см.
рис. 75) площадь плоской фигуры, ограниченную сверху графиком непрерывной
функции ![]() ,
снизу осью
,
снизу осью ![]() и
с боков прямыми
и
с боков прямыми ![]() и
и
![]() . Мы можем
теперь сказать, что площадь этой фигуры равна определенному интегралу от
. Мы можем
теперь сказать, что площадь этой фигуры равна определенному интегралу от ![]() на отрезке
на отрезке ![]() :
:
 .
.
Мы можем еще сказать, что масса
стержня, о котором шла речь в п. ![]() , равна определенному интегралу от его
линейной плотности
, равна определенному интегралу от его
линейной плотности ![]() в пределах
в пределах ![]() :
:
 .
.
Итак, по
определению определенным интегралом от функции ![]() на отрезке
на отрезке ![]() называется предел
интегральной суммы (5), когда максимальный частичный отрезок разбиения
называется предел
интегральной суммы (5), когда максимальный частичный отрезок разбиения ![]() стремится к нулю.
стремится к нулю.
В этом
определении, которое теперь уже не связано с задачей о нахождении площади,
функция ![]() не
обязательно непрерывна и неотрицательна на
не
обязательно непрерывна и неотрицательна на ![]() . Надо отметить, что это определение не
утверждает существование определенного интеграла для всякой функции
. Надо отметить, что это определение не
утверждает существование определенного интеграла для всякой функции ![]() , заданной на
, заданной на ![]() , т. е.
существование предела (5). Оно только говорит, что если этот предел существует
для заданной на
, т. е.
существование предела (5). Оно только говорит, что если этот предел существует
для заданной на ![]() функции
функции
![]() , то он
называется определенным интегралом от
, то он
называется определенным интегралом от ![]() на
на ![]() .
.
Следует иметь в
виду также, что когда говорят, что указанный предел ![]() существует, то
подразумевают, что он не зависит от способов разбиения отрезка
существует, то
подразумевают, что он не зависит от способов разбиения отрезка ![]() на части и выбора
на полученных частичных отрезках точек
на части и выбора
на полученных частичных отрезках точек ![]() .
.
Непосредственное вычисление определенного интеграла по формуле (5) связано с трудностями – интегральные суммы сколько-нибудь сложных функций имеют громоздкий вид и зачастую нелегко преобразовать их к виду, удобному для вычисления пределов.
Во всяком случае, на этом пути не удалось создать общих методов. Интересно отметить, что впервые задачу этого рода решил Архимед. При помощи рассуждений, которые отдаленно напоминают современный метод пределов, он вычислил площадь сегмента параболы. В дальнейшем на протяжении веков многие математики решали задачи на вычисление площади фигур и объемов тел. Все же еще в XVII веке постановка таких задач и методы их решения носили сугубо частный характер. Существенный сдвиг в этом вопросе внесли Ньютон и Лейбниц, указавшие общий метод решения таких задач. Они показали, что вычисление определенного интеграла от функции может быть сведено к отысканию ее первообразной.
Как было
отмечено выше, непрерывная на ![]() функция интегрируема на
функция интегрируема на ![]() . Это будет доказано
в § 6.7 .
. Это будет доказано
в § 6.7 .
Будет также
доказано, что монотонная на отрезке ![]() функция интегрируема на нем. Надо
учесть, что монотонная функция может иметь разрывы в конечном или даже счетном
числе (см. теорему 2 § 3.4).
функция интегрируема на нем. Надо
учесть, что монотонная функция может иметь разрывы в конечном или даже счетном
числе (см. теорему 2 § 3.4).

Рис. 76
На рис. 76
изображен график функции ![]() , заданной на отрезке
, заданной на отрезке ![]() . Эта функция
непрерывна на
. Эта функция
непрерывна на ![]() ,
убывает на
,
убывает на ![]() и
возрастает на
и
возрастает на ![]() .
Следовательно, она интегрируема на каждом из этих отрезков. Но тогда, на
основании аддитивных свойств интеграла, о которых речь будет впереди, наша
функция интегрируема на всем отрезке
.
Следовательно, она интегрируема на каждом из этих отрезков. Но тогда, на
основании аддитивных свойств интеграла, о которых речь будет впереди, наша
функция интегрируема на всем отрезке ![]() (см. § 6.2, теорема 3).
(см. § 6.2, теорема 3).
Таким образом,
если отрезок ![]() ,
на котором задана функция
,
на котором задана функция ![]() , можно разрезать на конечное число
частичных отрезков, на каждом из которых она непрерывна или монотонна, то
такая функция интегрируема на
, можно разрезать на конечное число
частичных отрезков, на каждом из которых она непрерывна или монотонна, то
такая функция интегрируема на ![]() .
.
Ньютон и Лейбниц доказали теорему, связывающую два важных понятия математического анализа – интеграла и производной. Эта теорема выражается соотношением (формулой Ньютона – Лейбница)
 . (6)
. (6)
Здесь ![]() есть произвольная
непрерывная на
есть произвольная
непрерывная на ![]() функция,
а
функция,
а ![]() -
какая-либо ее первообразная на
-
какая-либо ее первообразная на ![]()
![]() .
.
Таким образом, для
того чтобы вычислить определенный интеграл от непрерывной функции ![]() на отрезке
на отрезке ![]() , надо узнать ее
первообразную функцию
, надо узнать ее
первообразную функцию ![]() и взять разность
и взять разность ![]() значений этой первообразной
на концах отрезка
значений этой первообразной
на концах отрезка ![]() .
.
Если уже
считать известным, что непрерывная на отрезке ![]() функция
функция ![]() интегрируема на нем и что для этой
функции существует первообразная
интегрируема на нем и что для этой
функции существует первообразная ![]() , то формулу (6) можно вывести без
труда.
, то формулу (6) можно вывести без
труда.
Пусть ![]() есть произвольное
разбиение
есть произвольное
разбиение
![]()
отрезка ![]() на части. Тогда (пояснения
ниже)
на части. Тогда (пояснения
ниже)
![]()

 , (7)
, (7)
откуда и следует формула (6).
В четвертом равенстве (7) мы применили теорему Лагранжа о среднем
![]() ,
,
в силу которой ![]() есть некоторая
точка интервала
есть некоторая
точка интервала ![]() .
Последнее соотношение следует из того факта, что функция
.
Последнее соотношение следует из того факта, что функция ![]() непрерывна на
непрерывна на ![]() , следовательно,
интегрируема на
, следовательно,
интегрируема на ![]() ,
и потому ее любая интегральная сумма и, в частности, полученная нами
применением теоремы Лагранжа, стремится при
,
и потому ее любая интегральная сумма и, в частности, полученная нами
применением теоремы Лагранжа, стремится при ![]() к определенному интегралу от
к определенному интегралу от ![]() на
на ![]() .
.
Справедлива теорема.
Т е о р е м а
1. Неограниченная на отрезке ![]() функция не интегрируема на этом
отрезке.
функция не интегрируема на этом
отрезке.
Таким образом, для
того чтобы функция ![]() была интегрируемой на отрезке
была интегрируемой на отрезке ![]() , необходимо, чтобы
она была ограниченной на этом отрезке.
, необходимо, чтобы
она была ограниченной на этом отрезке.
Однако это условие не является достаточным.
П р и м е р. Функция
![]()
ограничена: ![]() , но не интегрируема на любом
отрезке
, но не интегрируема на любом
отрезке ![]()
![]() .
.
В самом деле, если в ее интегральной сумме за точки ![]() выбрать
рациональные числа, то
выбрать
рациональные числа, то
 .
.
Если же выбрать ![]() иррациональным, то
иррациональным, то
 .
.
Это показывает, что ![]() не может иметь один
и тот же предел при любом выборе
не может иметь один
и тот же предел при любом выборе ![]() , и, следовательно, функция
, и, следовательно, функция ![]() не интегрируема на
не интегрируема на ![]() .
.
Д о к а з а т е л ь с т в о т е о р е м ы 1. Пусть

есть интегральная сумма функции ![]() , соответствующая
некоторому разбиению
, соответствующая
некоторому разбиению ![]() :
: ![]() . Если допустить, что функция
. Если допустить, что функция ![]() не ограничена на
не ограничена на ![]() , то она необходимо
не ограничена на одном из частичных отрезков, пусть на
, то она необходимо
не ограничена на одном из частичных отрезков, пусть на ![]() . Зафиксируем
. Зафиксируем ![]() для всех
для всех ![]() , а
, а ![]() будем пока считать
переменной. Слагаемое
будем пока считать
переменной. Слагаемое ![]() не ограничено на
не ограничено на ![]() , а сумма остальных слагаемых
есть определенное число. Но тогда
, а сумма остальных слагаемых
есть определенное число. Но тогда ![]() можно сделать как угодно большим при
соответствующем подборе точки
можно сделать как угодно большим при
соответствующем подборе точки ![]() и функция
и функция ![]() не может быть интегрируемой
на
не может быть интегрируемой
на ![]() . Ведь
из интегрируемой функции
. Ведь
из интегрируемой функции ![]() на
на ![]() следует, что ее интегральные суммы
ограничены при любом выборе
следует, что ее интегральные суммы
ограничены при любом выборе ![]() .
.
Впрочем, в дальнейшем будет введено понятие несобственного интеграла. Некоторые неограниченные на отрезке функции интегрируемы в несобственном смысле. Но об этом будет речь позднее.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
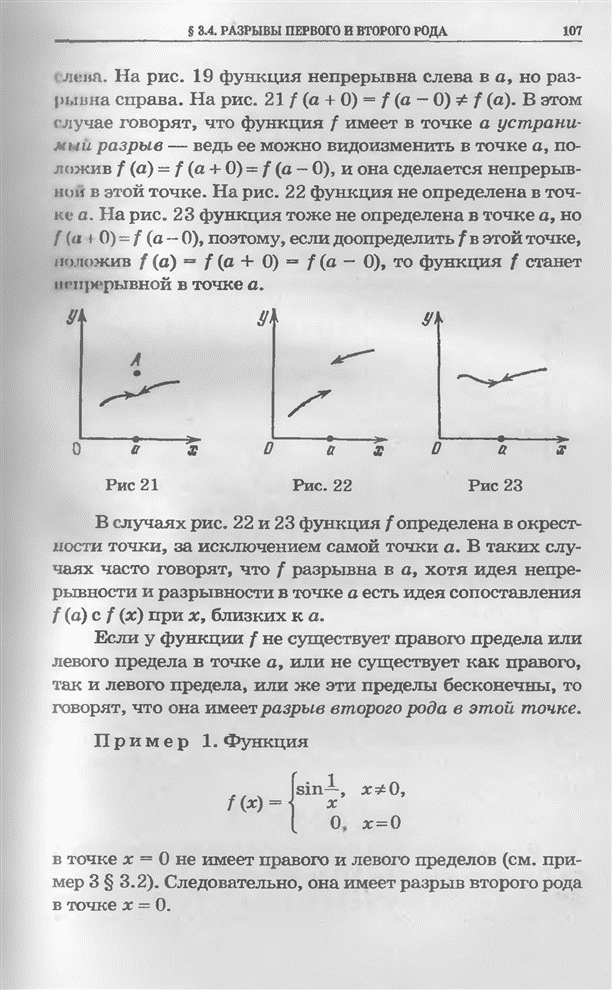
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
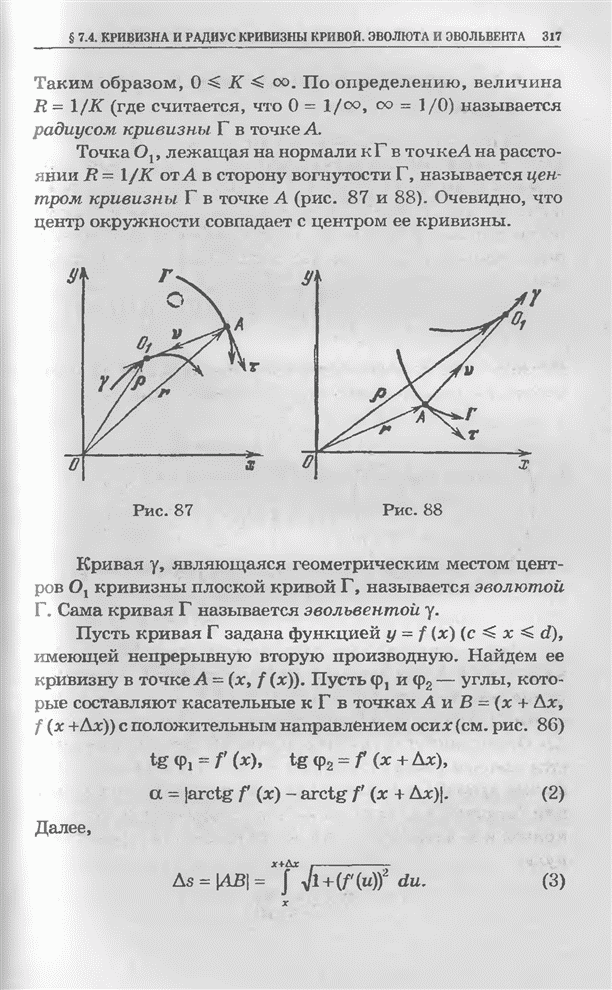
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
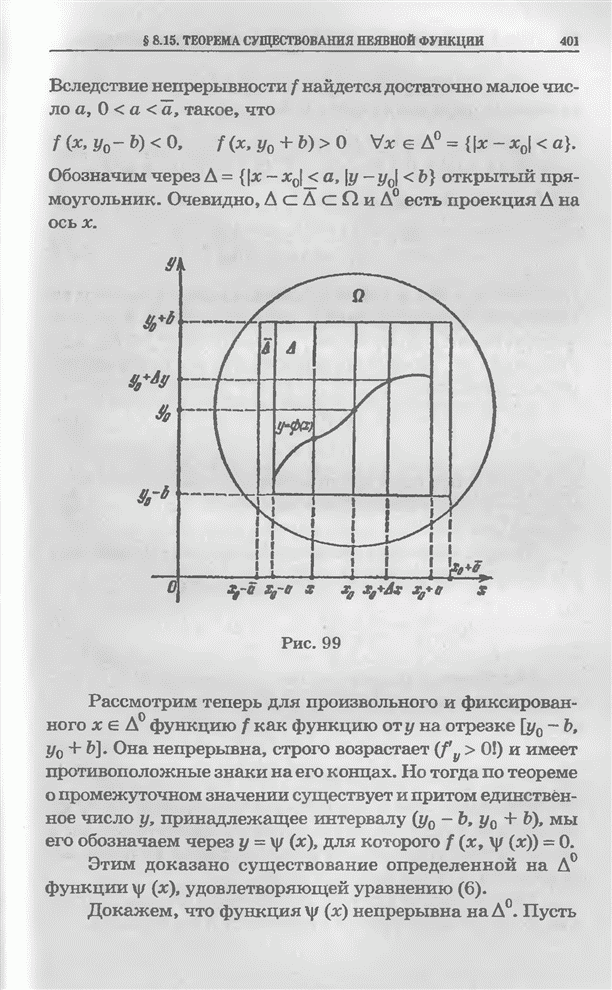
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
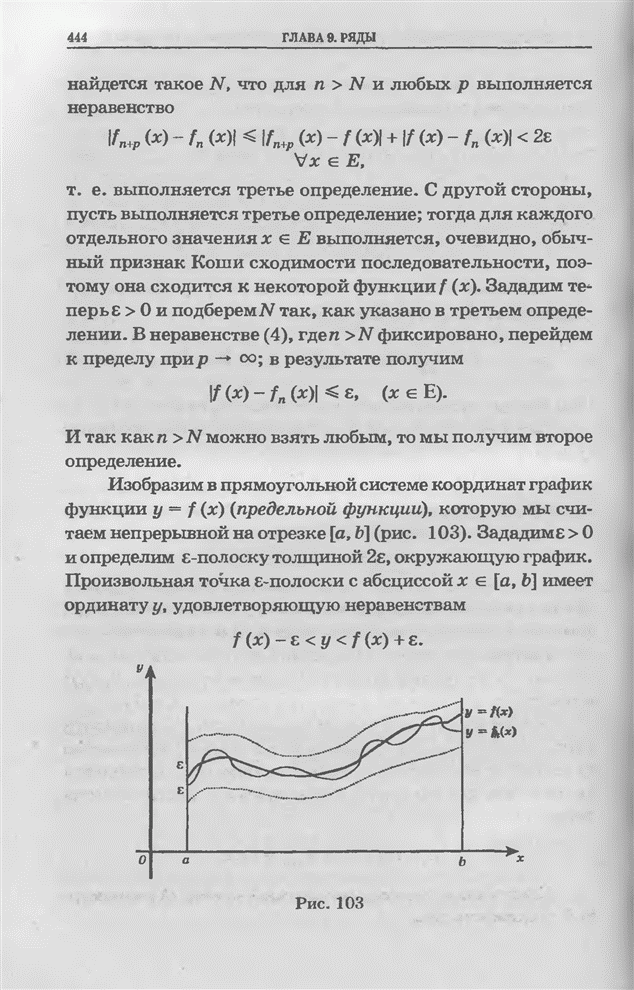
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей