§ 6. Разностная аппроксимация эллиптических уравнений

По сравнению с краевыми задачами для обыкновенных дифференциальных уравнений при построении разностных схем в многомерном случае возникают дополнительные трудности, связанные в основном с аппроксимацией граничных условий.

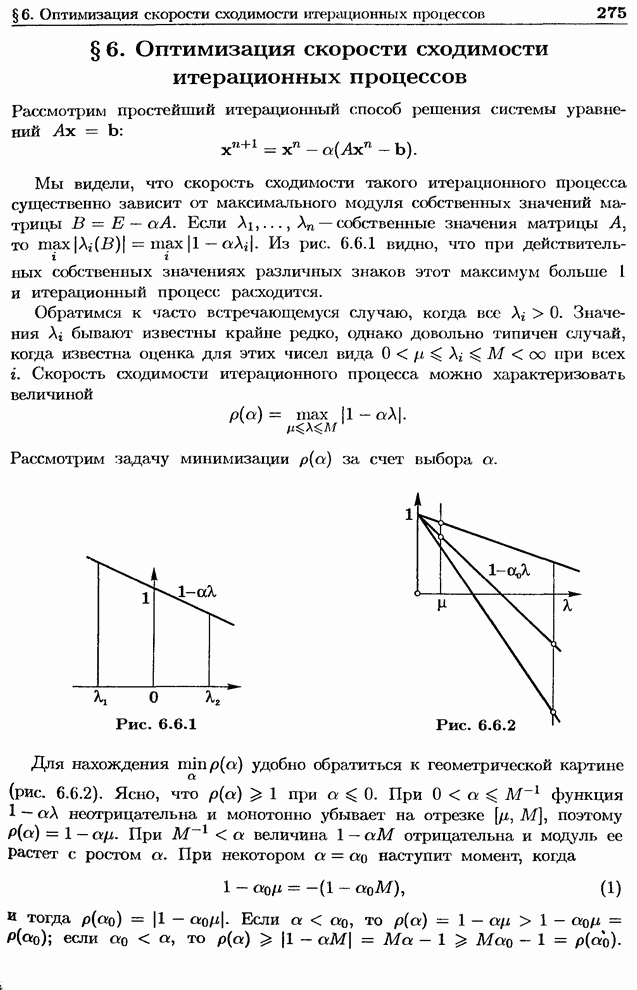
Рассмотрим простейшую краевую задачу — задачу Дирихле для уравнения Пуассона. Пусть область О представляет единичный квадрат: — граница . Требуется найти функцию и, дважды непрерывно дифференцируемую внутри и непрерывную в замкнутой области , которая внутри области удовлетворяет уравнению

и принимает на границе заданное значение

В дальнейшем независимые переменные будем обозначать как буквами так и .

Опишем построение сетки. Разобьем плоскость прямоугольной сеткой с шагами . Для определенности будем считать, что . Точки вида будем называть узлами сетки и обозначать их Узлы, лежащие внутри , будем называть внутренними узлами и множество таких узлов будем обозначать ;

узлы, которые лежат на , будем называть граничными узлами и множество таких узлов будем обозначать (см. рис. 10.6.1).

Рис. 10.6.1

Рис. 10.6.2

Пусть - значение решения в узле . Сеточную функцию, принимающую в узлах значения , будем обозначать .

Заменяя в (1) производные разностными отношениями, получим систему уравнений

здесь , где операторы и определены соотношениями

Граничные условия заменим на следующие:

Соотношения (3), (4) будем называть разностной схемой, аппроксимирующей задачу (1), (2). Функция решение (3), (4) — определена на сетке .

Совокупность узлов , соответствующих значениям , входящим в уравнение (3), образует шаблон разностной схемы. Уравнение Пуассона (1), таким образом, аппроксимируется на пятиточечном шаблоне «крест». Если — внутренний узел, то окрестностью этого узла будем называть остальные точки шаблона (рис. 10.6.2). Если в окрестности узла есть точки границы, то этот узел будем называть приграничным. Заметим, что значения и на границе известны и поэтому могут быть исключены из системы уравнений (3), (4). А именно, подставляя в (3) значения из (4) и перенося известные члены в правую часть, получим систему линейных алгебраических уравнений

Нетрудно видеть, что уравнения (5) отличаются от (3) лишь в приграничных узлах. Так, например, в узлах вида уравнения (5) будут выглядеть следующим образом:

Число уравнений в системе (5) совпадает с числом неизвестных. Поэтому матрицу системы уравнений (5) можно трактовать как некоторый линейный оператор, отображающий пространство сеточных функций, определенных на , в себя.

Опишем подробно структуру матрицы системы уравнений (5) в случае . Упорядочим компоненты вектора неизвестных «естественным» образом:

и умножим обе части (5) на . Тогда матрица системы линейных уравнений будет иметь блочно-трехдиагональную форму.

где матрицы размера имеют вид

Оценим погрешность аппроксимации схемы (3), (4). При и имеют место соотношения

поэтому

При подстановке точного решения и в (4) обнаруживаем, что краевые условия (2) выполняются точно; является погрешностью аппроксимации разностной схемы. Из проведенных рассмотрений следует, что разностная схема (3), (4) имеет второй порядок аппроксимации. Исследуем разрешимость системы уравнений (3), (4).

Лемма 1 (Сеточный принцип максимума). Пусть функция определена на и в узлах выполняется условие . Тогда хотя бы в одной точке границы функция достигает наибольшего значения.

Доказательство. Допустим противное, т.е. что максимальное значение достигается во внутреннем узле (вообще говоря, таких узлов может быть несколько). Среди всех таких узлов выберем тот, у которого наибольшая абсцисса, т.е. узел в котором . Тогда, рассматривая в точке , получаем

что противоречит условию леммы; дело заключается в том, что , а остальные выражения, стоящие в круглых скобках, неотрицательны, поскольку — точка максимума. Таким образом, исходная предпосылка является неверной. Утверждение леммы доказано.

Доказанный принцип максимума справедлив и в случае областей более общего вида.

Аналогично доказывается

Лемма 2. Пусть определена на и в узлах выполнено условие . Тогда наименьшее значение достигается функцией хотя бы в одной точке границы .

Из лемм 1 и 2 непосредственно следует

Теорема 1. Пусть определена на и в узлах удовлетворяет уравнению

Тогда достигает своего наибольшего по модулю значения на границе .

Теорема 1 является разностным аналогом принципа максимума для гармонических функций. Из нее следует, что система уравнений (3), (4) с имеет только нулевое решение, поскольку наибольшее по модулю значение равно нулю. Следовательно, определитель системы линейных уравнений (3), (4) (число уравнений равно числу неизвестных) отличен от нуля и при любых система (3), (4) имеет единственное решение. Заметим также, что отсюда следует однозначная разрешимость системы уравнений (5) при любой правой части .

Конкретизируем общие построения § 1 этой главы. Пусть — некоторые пространства функций, определенных на и . Введем в них нормы, согласованные с нормами соответствующих пространств в непрерывном случае. Согласно определению (см. § 1) разностная задача (3), (4) будет устойчивой, если существует постоянная , не зависящая от , такая, что для решения системы уравнений (3), (4) справедлива оценка

Исследуем устойчивость схемы (3), (4) и оценим близость к . Пусть нормы в заданы следующим образом:

Вследствие (6) для любого многочлена второй степени выполняется равенство

так как четвертые производные, входящие в (6), обращаются в нуль. Возьмем и построим вспомогательную функцию

которую будем рассматривать в узлах сетки . Из вышесказанного следует, что в любом внутреннем узле

Тогда разность в узлах удовлетворяет неравенству

По лемме 1 функция принимает наибольшее значение на границе . Но на справедливо отношение

Таким образом, , т.е. . Аналогично, рассматривая функцию , устанавливаем, что

Тогда из леммы 2 следует оценка или же . Таким образом, всюду в установлено неравенство и поэтому

(8)

Заменяя это неравенство более сильным

получаем оценку (7). Таким образом, разностная схема (3), (4) устойчива в сеточном аналоге нормы пространства С.

Оценим сходимость разностной схемы (3), (4). Для этого запишем уравнение для погрешности :

здесь — погрешность аппроксимации. В силу того, что граничные условия выполняются точно, имеем

Так как радиус R области равен , то используя оценку (8), получаем

Таким образом, решение сеточной задачи (3), (4) сходится к точному решению дифференциальной задачи в сеточной норме пространства С. Напомним, что все рассуждения проводились в предположении, что решение задачи (1), (2) обладает достаточной гладкостью, а именно что имеет непрерывные четвертые производные в .

Из доказательства сходимости видно, что основным моментом являлось получение оценки (8), характеризующей устойчивость разностной схемы. Сходимость же схемы является следствием аппроксимации и устойчивости, причем порядок скорости сходимости совпадает с порядком аппроксимации. Проведенное выше доказательство сходимости схемы является частным случаем теоремы Филиппова.

Описанный метод дает приближенное решение, сходящееся к точному со скоростью . По аналогии с одномерным случаем можно построить разностные схемы, обладающие более высоким порядком сходимости. Наметим пути получения более точных схем. Предположим, что решение и непрерывно дифференцируемо шесть раз в замкнутой области . Тогда вместо (6) можно написать равенство

Дифференцируя (1) два раза по , получаем

Таким образом,

Заменяя производные в правой части разностными отношениями, имеем

Аналогично устанавливаем, что

Складывая полученные равенства, получаем

Искомая разностная схема четвертого порядка аппроксимации будет иметь вид

Нетрудно видеть, что шаблон схемы (9) состоит из девяти точек (рис. 10.6.3).

Рис. 10.6.3

Схемы более высокого порядка, в отличие от одномерного случая, будут содержать тем большее, количество узлов, чем выше порядок аппроксимации разностной схемы. В случае, если область является объединением прямоугольников со сторонами, параллельными осям координат, и , при гладком решении рассмотренная схема будет иметь четвертый порядок сходимости. Более точно, если решение и исходной задачи имеет шестые ограниченные производные в замкнутой области П, то справедлива оценка

где — решение системы сеточных уравнений (9), (4).

Пусть является объединением конечного числа прямоугольников со сторонами, параллельными осям координат, причем стороны, параллельные оси , лежат на прямых , - целое, а параллельные оси прямых , — целое. Тогда построение и исследование разностной схемы проводится аналогично.

Расмотрим наиболее простые методы аппроксимации граничных условий в случае области с криволинейной границей. Ограничимся рассмотрением равномерного шага, т. е. . Рассмотрим множество прямых . Точки их пересечения между собой, а также точки их пересечения с будем называть узлами. Через обозначим узлы, лежащие на , а через — узлы с целыми координатами лежащие в , расстояние от которых до границы , измеряемое вдоль направления какой-либо из осей координат, меньше h. Остальные узлы сетки, лежащие в , обозначим . Тогда в каждом узле (т. е. в точке с координатами ) сеточной области , можно записать уравнение

Простейший способ аппроксимации граничных условий заключается в сносе граничных условий в узлы , т.е. полагаем

где — ближайшая к узлу точка границы. В этом случае — внутренние узлы сеточной области, а — граничные. Нетрудно видеть, что при таком способе задания граничных условий порядок аппроксимации будет . Исследование устойчивости и сходимости разностной схемы (10), (11) проводится точно так же, как для схемы (3), (4), однако в данном случае получается порядок сходимости . Это является следствием довольно грубой аппроксимации граничных условий.

Рассмотрим еще один способ аппроксимации граничных условий. Назовем узлы приграничными, а узлы , — границей сеточной области. В узлах уравнение (1) заменим уравнением (10); в положим , т. е. в этом случае граничные условия выполняются точно. Пусть - узел . Для определенности будем считать, что узлы не лежат на (отрезки, соединяющие их с узлом , принадлежат ), а узел лежит на . (В этом случае узел соответствует точке (см. рис. )) Тогда аппроксимация (1) в приграничном узле берется в виде

Здесь — расстояние между узлами и . Аналогично осуществляется аппроксимация уравнения (1) в других узлах .

Рис. 10.6.4

Итак, в узлах уравнение (1) аппроксимируется обычным образом, а аппроксимация на неравномерной сетке используется только в узлах . Поэтому узлы называют регулярными, а узлы нерегулярными. Аппроксимация уравнения (1) в нерегулярных узлах в данном случае имеет порядок .

Для рассмотренной схемы имеет место

Теорема 2 (без доказательства). Если решение задачи (1) и , то разностная схема (10) с аппроксимацией (12) в нерегулярных узлах имеет второй порядок сходимости в сеточной норме пространства С, т. е.

Замечание. Довольно распространенным является другой способ аппроксимации уравнения (1) в нерегулярных узлах. А именно, полагают (см. рис. 10.6.4)

В этом случае погрешность аппроксимации в таких узлах имеет порядок и теорема 2 будет справедлива. Однако если систему линейных уравнений путем исключения граничных значений привести к виду (5), то получится система уравнений с несимметричной матрицей. Таким образом, в данном случае сеточная задача теряет важное свойство, присущее исходной задаче — симметричность оператора.

При исследовании краевых задач с другими граничными условиями и эллиптическими дифференциальными операторами более общего вида, а также краевых задач для систем уравнений в частных производных принцип максимума, разностный аналог которого использовался при исследовании устойчивости и сходимости разностной схемы, вообще говоря, не имеет места. Кроме этого, часто бывает необходимо оценивать не только близость получаемого приближения к точному решению, но и близость их производных. Все это приводит к необходимости создания методов исследования разностных схем, не использующих принцип максимума. Как и ранее, проиллюстрируем методику исследования на модельной задаче Дирихле для уравнения Пуассона в прямоугольнике (1), (2) и на соответствующей разностной схеме (3), (4).

Пусть . Исключая граничные условия (4) из (3), получаем систему уравнений (5). Обозначим через Н линейное пространство сеточных функций, определенных на . Таким образом, элементы Н можно рассматривать как векторы размерности ; компоненты этих векторов являются значениями функций в узлах . Матрица системы уравнений (5) порождает линейный невырожденный оператор в Н. Тогда если , то система уравнений (5) может быть записана в операторной форме:

Здесь — оператор, соответствующий матрице системы уравнений (5). Введем в Н скалярное произведение

Скалярное произведение (15) согласовано со скалярным произведением функкций в , т.е.

для непрерывных функций из .

Пусть . Справедлива

Лемма 3. Оператор , является симметричным и положительно определенным на Н, и для него выполнена оценка

где не зависят от .

Доказательство. Заметим прежде всего, что симметричность оператора , следует из симметричности соответствующей ему матрицы. Проведем, однако, доказательство этого факта другим методом. Пусть ; обозначим через сеточную функцию, совпадающую с на , и равную нулю на . Тогда из определения , можно записать

Представим , в виде , где

т.е. являются одномерными сеточными операторами, соответствующими дифференциальным операторам и . Покажем, что симметричен и положительно определен. Пусть для определенности . Используя формулу суммирования по частям (9.8.14), получим

Функции и входят в правую часть равенства симметричным образом, поэтому

т. е. оператор симметричен. С другой стороны, из разностного аналога теоремы вложения (§ 9.8) получаем

Используя аналогичную оценку для оператора , получаем

т.е. левая часть (16) доказана.

В другую сторону оценка получается намного проще. Поскольку , то

откуда

Лемма доказана.

Задача 1. В случае прямоугольника со сторонами и показать, что минимальным и максимальным собственными значениями оператора являются соответственно

Таким образом, (16) выполняется при , что по порядку при совпадает с оценками, полученными выше.

Из проведенных выше рассуждений вытекает возможность введения в пространстве Н нормы

которую называют энергетической. Название связано с тем, что в непрерывном случае при , имеющем физический смысл отклонения мембраны и , выражение пропорционально потенциальной энергии мембраны.

Будем исследовать устойчивость разностной схемы (14) в Н. Умножим обе части (14) скалярно в Н на ; применяя (16). получим

Поэтому справедлива оценка

что означает устойчивость разностной схемы. Отсюда, в частности, следует, что система уравнений (14) при имеет лишь тривиальное решение , т. е. мы еще раз доказали, что (14) разрешима при любой правой части единственным образом.

Оценим скорость сходимости разностной схемы (3), (4) в энергетической норме. Как и ранее, будем предполагать, что решение и дифференциальной краевой задачи (1), (2) имеет непрерывные четвертые производные в замкнутой области. Тогда погрешность будет удовлетворять уравнению

где — погрешность аппроксимации. Применяя оценку (17), имеем

Таким образом, рассматриваемая разностная схема имеет второй порядок сходимости по h в энергетической норме.

При исследовании скорости сходимости в энергетической норме мы предполагали, что решение имеет непрерывные четвертые производные. Оказывается, что это требование является завышенным и тот же результат можно получить в предположении, что решение обладает только третьими непрерывными производными в . Это связано с тем, что погрешность аппроксимации имеет дивергентный (дипольный) характер. Используя формулу Тейлора, получаем

здесь . Аналогичная формула получается и для разности по второй переменной. Следовательно погрешность будет удовлетворять уравнению (18) с правой частью, равной

Умножим обе части (18) скалярно в Н на . Используя формулы суммирования по частям, правую часть преобразуем к виду

Таким образом,

поэтбму , откуда следует .

При построении разностной схемы, аппроксимирующей уравнение (1) с краевыми условиями второго или третьего рода, можно воспользоваться методами, которые применялись в одномерном случае. Пусть для определенности рассматривается задача для уравнения (1) с краевым условием третьего рода

Напомним, что в качестве области мы рассматриваем единичный квадрат. Для определенности рассмотрим аппроксимацию условия (19) на участке границы . Тогда, заменяя производную в (19) разностным соотношением, получим

Найдем погрешность аппроксимации

Таким образом, погрешность аппроксимации граничных условий (20) имеет первый порядок по h. Выражая из уравнения (1), получаем . Тогда

Поэтому если рассмотреть аппроксимацию граничного условия (19) вида

то в силу проведенных выше построений получаем, что соотношение (21) аппроксимирует краевое условие (19) с порядком . Приводя подобные члены, преобразуем (21) к виду

Отсюда ясно, как будет записываться аппроксимация граничного условия в других узлах . В частности, с помощью подобных рассуждений получаем аппроксимацию в угловом узле :

Заметим, что в данном случае граница сеточной области включает угловые точки.

Другой способ аппроксимации граничного условия (19) опирается на то, что берется другая сетка. Рассмотрим множество узлов

и пусть — множество узлов сетки, лежащих в . Тогда, как и ранее, уравнение (1) можно аппроксимировать в узлах обычной пятиточечной схемой. Краевые условия (19) на такой сетке будем аппроксимировать следующим образом:

Предположим, что решение дифференциальной задачи может быть продолжено за пределы области с сохранением свойств гладкости. Тогда выражение (24) аппроксимирует краевое условие (19) на участке границы порядком . Это можно непосредственно проверить, подставляя решение и в (24) и воспользовавшись формулой Тейлора в точке .

Метод конечных элементов.

До сих пор рассматривалась разностная задача Дирихле для уравнения Пуассона, которая строилась непосредственно путем замены производных в дифференциальном уравнении разностными отношениями. Аналогично случаю краевых задач для обыкновенных дифференциальных уравнений рассмотрим способы построения дискретных аппроксимаций, основанные на вариационных и проекционных принципах. Будем рассматривать краевую задачу (1), (2) с однородными граничными условиями.

На множестве непрерывно дифференцируемых функций, обращающихся в нуль на границе еЮ, введем норму

Замыкание множества таких функций в этой норме является гильбертовым пространством; обозначим его через (ранее мы его обозначали .

Рассмотрим задачу о нахождении минимума функционала

на пространстве функций . Если классическое решение и задачи (1), (2) при существует и принадлежит , то оно дает минимум функционалу (26). Обратное, вообще говоря, неверно; функция, доставляющая минимум функционалу (26) на , не обязательно должна обладать вторыми производными.

Таким образом, задачу нахождения решения (1), (2) можно заменить задачей о нахождении минимума квадратичного функционала (26) на . Решение, получаемое в результате минимизации функционала (26) на , является обобщенным решением краевой задачи (1), (2).

Для построения вариационно-разностной схемы воспользуемся методом Ритца. Аппроксимируем некоторым конечномерным подпространством ; в методе Ритца за приближенное решение задачи (26) принимают функцию минимизирующую функционал (26) на подпространстве .

Подпространство построим следующим способом. Пусть

Разобьем на квадратные ячейки со стороной h и вершинами в узлах . Каждую ячейку разобьем диагональю, проходящей через вершины . Таким образом, вся область будет разбита на прямоугольные треугольники с катетами, равными h. Эти треугольники будем называть элементарными, а разбиение области на треугольники — триангуляцией области .

В качестве подпространства пространства возьмем пространство непрерывных в функций, линейных на каждом элементарном треугольнике и обращающихся в нуль на . Каждая функция из однозначно определяется своими значениями в узлах и, обратно, каждая сеточная функция, которая принимает в узлах сетки заданные значения, однозначно определяет функцию из . При этом функция из называется кусочно-линейным восполнением сеточной функции. Таким образом, существует взаимно однозначное соответствие между Н и , где Н — пространство сеточных функций, определенных на и принимающих нулевые значения на . Функции :

образуют базис в Н. Соответствующие им кусочно-линейные функции из , принимающие значения, равные единице в узле и нулю в других узлах, будут образовывать базис в .

В качестве приближенного решения задачи (26) возьмем функцию , которая минимизирует функционал (26) на подпространстве , т.е.

Предположим, что существует; представим ее в виде

где - неизвестные коэффициенты разложения. Отметим, что , в силу выбора функций является значением в точке . Таким образом, отыскание приближенного решения состоит в определении коэффициентов . Выпишем уравнения для определения этих коэффициентов. В точке минимума функции должны выполняться равенства

Вычислим левую часть этого соотношения:

Следовательно, система уравнений относительно будет иметь вид

Количество уравнений в (28) совпадает с количеством неизвестных.

Рис. 10.6.5.

Функция отлична от нуля лишь в тех элементарных треугольниках, которые имеют узел своей вершиной. Поэтому в каждом из уравнений (28) интегрирование ведется не по всей области , а лишь по пересечению таких треугольников с . Множество точек, где образует шестиугольник (см. рис. 10.6.5). Обозначим этот шестиугольник через , а входящие в него треугольники — через . Положим

поскольку , то

Отсюда видно, что лишь при . Проводя соответствующие вычисления, получаем

Аналогично, для получаем

в остальных случаях .

Таким образом, уравнение, соответствующее узлу записывается в виде

где . Разделив обе части на , получим систему сеточных уравнений

структура которой полностью совпадает с (5). Единственное отличие заключается в другом способе вычисления правой части. Однако если вычислять приближенно, полагая

то получится разностная схема, полностью идентичная (5).

Так как левая часть системы (29) совпадает с левой частью системы (5), то система уравнений (29) имеет единственное решение при любой . Справедливы неравенства

Таким образом, в случае описываемого метода требования к гладкости решения существенно меньше, чем в случае применения метода конечных разностей.

Построение разностных схем таким способом особенно целесообразно в случае уравнений и систем с естественными граничными условиями, когда непосредственная аппроксимация граничных условий вызывает затруднения.

В последнее время получили широкое распространение проекционно-разностные методы решения краевых задач (метод конечных элементов). Описанный выше метод построения разностных схем с помощью метода Ритца является одной из разновидностей метода конечных элементов.

Опишем в общих чертах суть проекционно-разностного подхода на другой модельной задаче (ср. с § 9.11). За основу метода обычно берется интегральное тождество для определения обобщенного решения. Итак, предположим, что в квадрате требуется найти решение краевой задачи

где Г — участок границы, лежащий на прямой . Предположим, что классическое решение этой задачи существует. Умножим обе части уравнения (30) на функцию , частные производные которой являются кусочно-непрерывными и .

Интегрируя по частям и используя краевые условия, получим

Соотношение (31) называется интегральным тождеством; оно имеет место для любой функции , где — пространство, являющееся замыканием множества гладких функций, равных нулю на в норме (25). Если и является классическим решением задачи (30) и имеет суммируемые в квадрате производные, то оно удовлетворяет (31) и . Обратное, вообще говоря, неверно. Можно указать функции и , для которых выполнено (31), однако классическое решение задачи (30) существовать не будет. Функцию и , удовлетворяющую интегральному тождеству (31), называют обобщенным решением задачи (30). Обобщенное решение, определяемое из интегрального тождества (31), совпадает с обобщенным решением, определяемым минимизацией функционала

Подобное обстоятельство всегда имеет место в случаях, когда исходный дифференциальный оператор является симметричным и положительно определенным. Если эти условия не выполнены, то задача определения обобщенного решения не может быть сформулирована в терминах минимизации некоторого квадратичного функционала, но может быть сформулирована при помощи интегрального тождества типа (31).

Поступим аналогично предыдущему случаю. Триангулируем область и введем пространство функций, кусочно-линейных на элементарных треугольниках и обращающихся в нуль на . Приближенным решением задачи (31) назовем функцию такую, что для любой выполняется равенство

Таким образом, интегральное тождество (32) совпадает с (31) с той лишь разницей, что в (32) решение и пробные функции берутся из подпространства .

Функция полностью определяется своими значениями в узлах сетки. Для того чтобы удовлетворяла (32), необходимо и достаточно, чтобы (32) было справедливо для любой функции , входящей в базис . В качестве базисных функций возьмем функции из , которые равны единице в одном из узлов и нулю во всех остальных узлах. Это дает нам систему сеточных уравнений. Обратим внимание на тот факт, что теперь в базис входят функции, которые, вообще говоря, отличны от нуля на Г.

Представим в виде , где неизвестные коэффициенты. Подставляя это выражение в (32), получаем

Совокупность соотношений (33) образует систему линейных алгебраических уравнений относительно неизвестных коэффициентов и порождает некоторую проекционно-разностную схему (эта схема могла бы быть получена и как вариационно-разностная). Так как любая функция может быть разложена по функциям , то из выполнения (33) будет следовать справедливость (32). Таким образом, выражения (32) и (33) эквивалентны.

Для доказательства устойчивости (33) положим в . Тогда

где

Таким образом, . Это означает устойчивость проекционно-разностной схемы, т.е. малым изменениям в норме соответствуют малые изменения в норме .

Рассмотрим структуру матрицы системы уравнений (33). Если то , поэтому интеграл по Г в (33) равен нулю. В этом случае выражение (33) совпадает с (28), и, следовательно, уравнение, соответствующее функции , имеет вид

где

D точках Г, т. е. в узлах вида , имеем

Здесь . В случае, когда b не вычисляются в явном виде, их можно вычислять приближенно, используя квадратурные формулы. Например,

В заключение кратко опишем построение проекционно-разностной схемы в случае криволинейной границы и возможные обобщения этого метода. Пусть для простоты рассматривается задача Дирихле для уравнения Пуассона и — плоская односвязная область с кусочно-гладкой границей состоит из конечного числа гладких , пересекающихся между собой под ненулевыми углами. Зададимся параметром — шагом сетки. Построим ломаную обладающую следующими свойствами:

а) область ограниченная содержится в ;

б) между точками можно установить взаимно однозначное соответствие, т. е. существует взаимно однозначное отображение , которое имеет кусочно-непрерывную производную , где С не зависит от ;

в) расстояние от точек до не превосходит величины , где — некоторая постоянная, не зависящая от ;

г) длина звеньев ломаной ограничена снизу величиной . При принятых допущениях относительно области такое построение всегда возможно. Разобьем область на треугольники (которые будем называть элементарными) так, что:

а) длины сторон треугольников находятся в пределах — постоянные, не зависящие от ;

б) площади треугольников находятся в пределах ;

в) любые два треугольника либо не пересекаются, либо имеют только одну общую сторону, либо обшую вершину.

Описанное выше построение называется квазиравномерной триангуляцией области ; вершины треугольников называются узлами сетки. Можно доказать, что такая триангуляция осуществима. Пусть Н — пространство непрерывных функций, кусочно-линейных над элементарными треугольниками и обращающихся в нуль на . Задаче (1) с однородным граничным условием (2) поставим в соответствие проекционно-разностную задачу — найти функцию , удовлетворяющую при любой соотношению

Функция полностью определяется своими значениями в узлах сетки. Поэтому если в качестве брать базисные функции пространства Н (равные единице в одном узле и нулю в остальных узлах и кусочно-линейные над треугольниками , то (34) является системой линейных алгебраических уравнений относительно значений в узлах.

Доказательство устойчивости проводится точно так же, как и выше. При исследовании же сходимости следует дополнительно оценить норму решения в в приграничной полосе . С учетом этих оценок можно получить следующее соотношение:

где постоянная с зависит от нормы решения в .

При построении проекционно-разностной схемы можно использовать более сложные конечные элементы, за счет чего может быть достигнута большая точность. Например, кроме узлов сетки, можно также в качестве узлов рассматривать середины сторон треугольников.

Пусть Н — подпространство непрерывных в функций, равных нулю на и являющихся полиномом второй степени в каждом элементарном треугольнике . Пусть . В качестве базисных функций в Н можно рассмотреть функции, которые равны единице в одном узле, а в других узлах равны нулю и принадлежат Н (под узлами здесь понимаются как вершины, так и середины сторон треугольников). Тогда можно получить оценку

Аналогично могут быть построены проекционно-разностные схемы с более высоким порядком скорости сходимости. При этом используются способы интерполяции, рассмотренные в § 5.5. Заметим, что структура матрицы системы линейных алгебраических уравнений ухудшается; а именно, возрастает количество ненулевых элементов в строке матрицы и ширина ленты.

Заметим, что в случае бигармонического уравнения и области с криволинейной границей такой подход нуждается в уточнении, так как получаемые приближения могут, вообще говоря, не сходиться к точному решению задачи при .

Кратко осветим историю вопроса. Вариационные и проекционные методы при небольшом числе базисных функций применялись издавна, еще до появления ЭВМ. Применение ЭВМ позволило увеличить число базисных функций; при этом часто возрастало суммарное влияние вычислительной погрешности и погрешности, возникающей при аппроксимации интегралов квадратурными суммами.

Это обстоятельство ставило ограничение на точность, с которой могли быть получены решения с помощью вариационных методов. Были проведены теоретические исследования, показавшие, что для устойчивости вариационных методов существенно выполнение некоторого условия на систему базисных функций, называемого условием сильной минимальности. Построение системы базисных функций, удовлетворяющей этому условию, в случае областей сложной формы иногда бывает непросто.

Параллельно шло интенсивное развитие теории и практики применения конечно-разностных методов.

Если при использовании классических вариационных методов для решения линейных задач возникают линейные системы уравнений с полностью заполненной матрицей, то при использовании конечно-разностных уравнений возникают системы уравнений с матрицей, содержащей относительно малое число ненулевых элементов. Это обстоятельство позволяет решать с теми же затратами процессорного времени системы уравнений с существенно большим числом неизвестных. Однако в случае областей сложной формы применение конечно-разностных методов представляет определенные неудобства вследствие неоднородности построения разностных уравнений в приграничных точках.

Получивший в последнее время интенсивное развитие метод конечных элементов свободен от ряда недостатков описанных методов: он не требует специальных усилий по построению системы базисных функций, являющейся сильно минимальной, при его использовании упрощается написание уравнений вблизи границы. Матрица линейной системы уравнений содержит относительно малое число ненулевых элементов. Большая «технологичность» метода позволила создать на его основе ряд промышленных систем стандартных программ решения краевых задач, в частности задач теории упругости. При использовании таких систем не требуется знание теории численных методов и тонкостей программирования. Исследователь должен лишь задать триангуляцию области, а часто система и сама осуществляет такую триангуляцию. Эти методы сходятся при меньших требованиях гладкости, чем конечно-разностные методы. В случае квазиравномерных триангуляций базисные функции метода автоматически удовлетворяют условию сильной минимальности.

В то же время увеличивается объем работы при вычислении матрицы системы уравнений. Поэтому при решении крупных задач зачастую все-таки применяют конечно-разностные методы или приходят к составлению систем уравнений с помощью аппроксимации минимизирующего функционала (или интегрального тождества) (см. § 9.12).

Традиционно для решения эллиптических задач применялись методы теории потенциала. С появлением ЭВМ они были практически вытеснены конечно-разностными методами. Однако в последнее время в вычислительную практику стал интенсивно проникать метод граничных элементов, имеющий некоторые общие черты с методом потенциала.