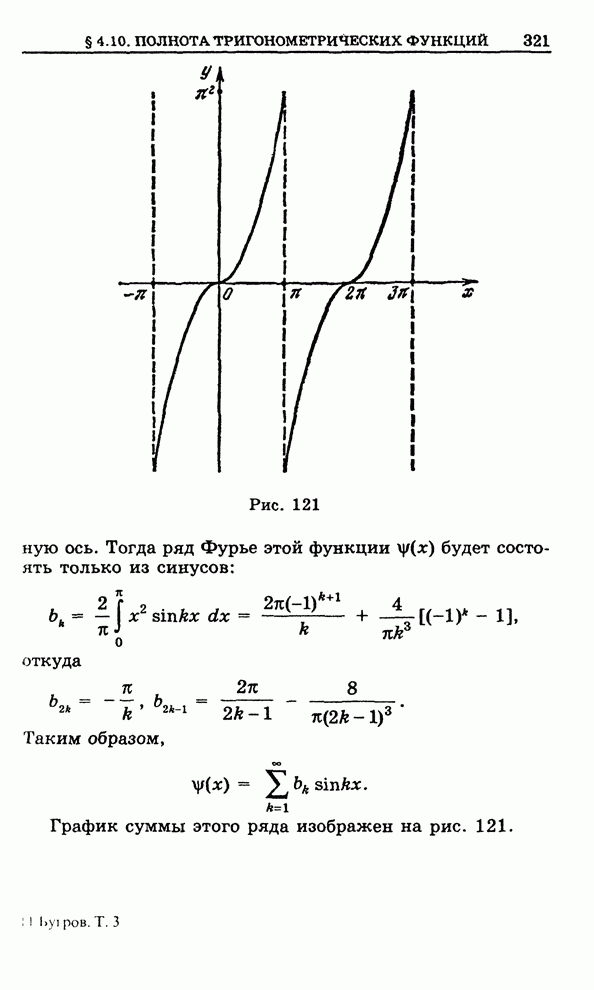| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3.13. Дивергенция. Теорема Гаусса—Остроградского
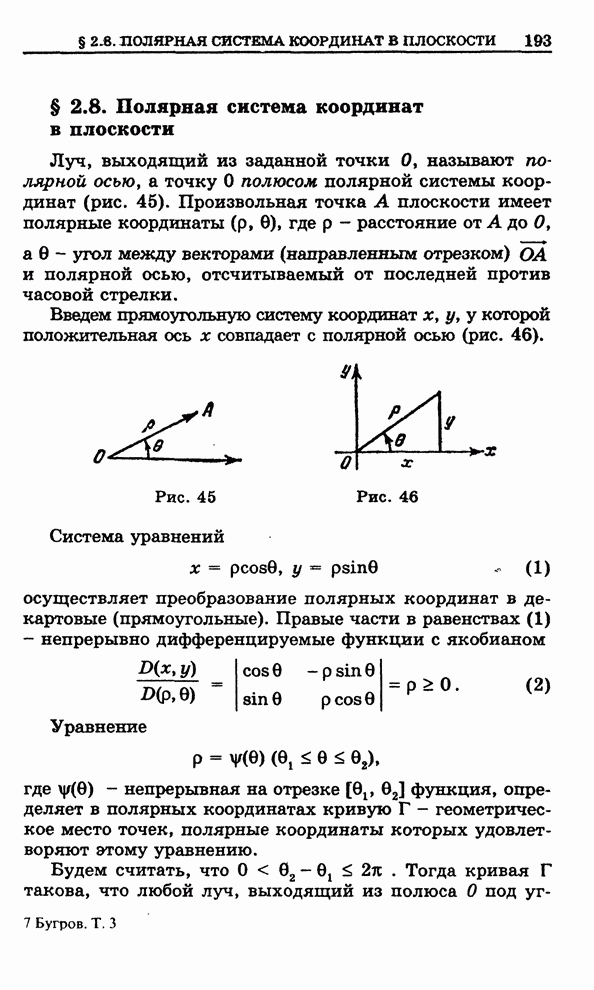
Пусть
![]() есть
трехмерное пространство, где задана прямоугольная система координат
есть
трехмерное пространство, где задана прямоугольная система координат ![]() и
и ![]() - область с
кусочно-гладкой границей
- область с
кусочно-гладкой границей ![]() , на которой определено поле вектора
, на которой определено поле вектора
![]() . (1)
. (1)
Будем
предполагать, что ![]() непрерывны на
непрерывны на ![]() , откуда следует, что для
вектора
, откуда следует, что для
вектора ![]() имеет
смысл непрерывная функция
имеет
смысл непрерывная функция
![]() , (2)
, (2)
называемая дивергенцией вектора ![]() .
.
Легко видеть, что
 ,
,
т. е. дивергенция
равна скалярному произведению символического вектора ![]() (оператора Гамильтона) (см.
§ 3.4) и вектора
(оператора Гамильтона) (см.
§ 3.4) и вектора ![]() .
.
Будем
считать, что поверхность ![]() ориентирована при помощи единичной
нормали
ориентирована при помощи единичной
нормали ![]() , направленной
во внешность
, направленной
во внешность ![]() .
.
Целью нашей будет доказать равенство
![]() (3)
(3)
при некоторых
дополнительных условиях, налагаемых на ![]() . Это равенство называют формулой
Гаусса-Остроградского по имени математиков, ее доказавших.
. Это равенство называют формулой
Гаусса-Остроградского по имени математиков, ее доказавших.
Формула
Гаусса-Остроградского говорит, что объемный (тройной) интеграл от дивергенции
вектора по области ![]() равен потоку вектора через границу
этой области, ориентированную в направлении ее внешней нормали.
равен потоку вектора через границу
этой области, ориентированную в направлении ее внешней нормали.

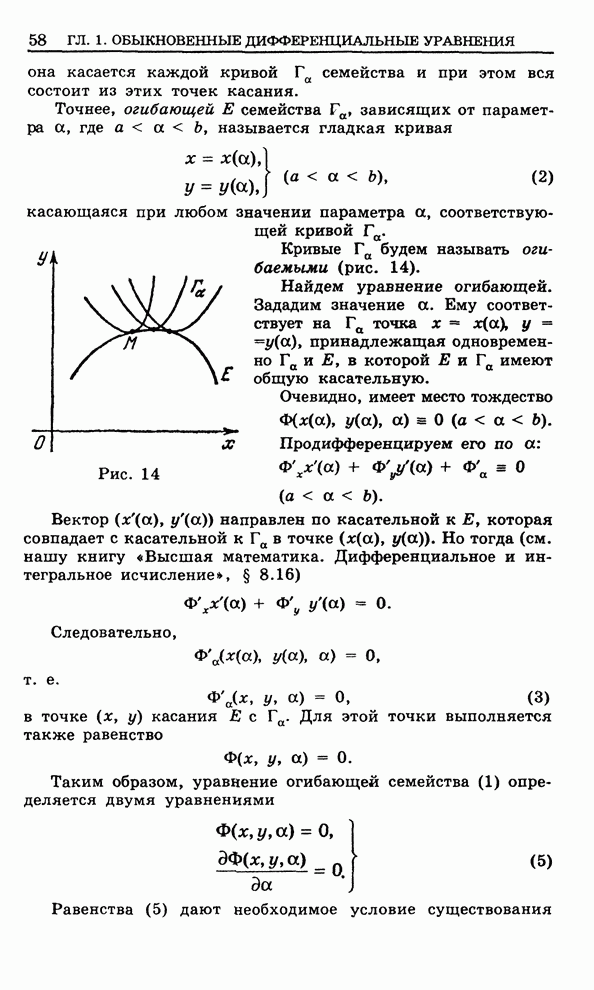
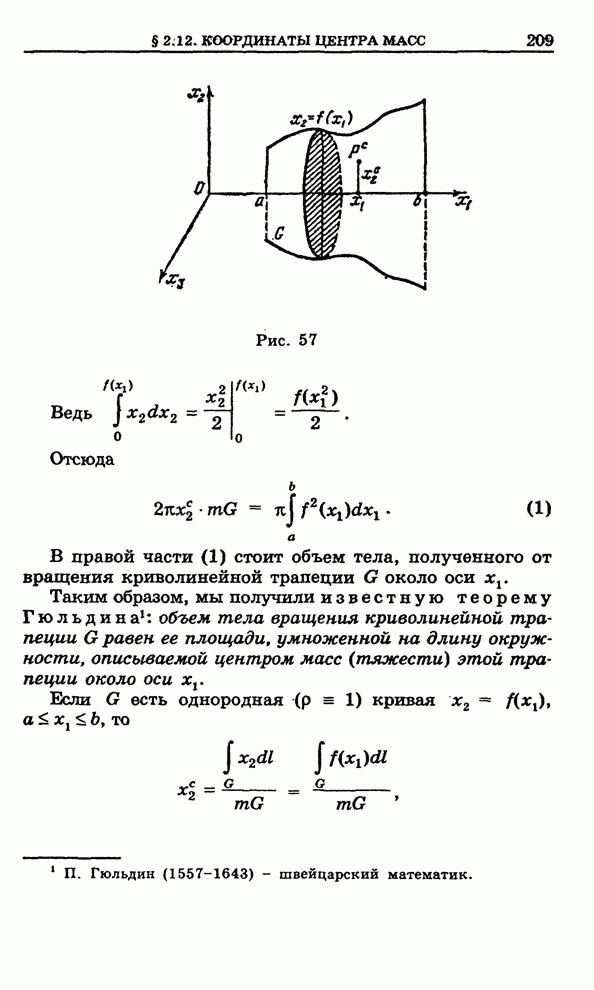
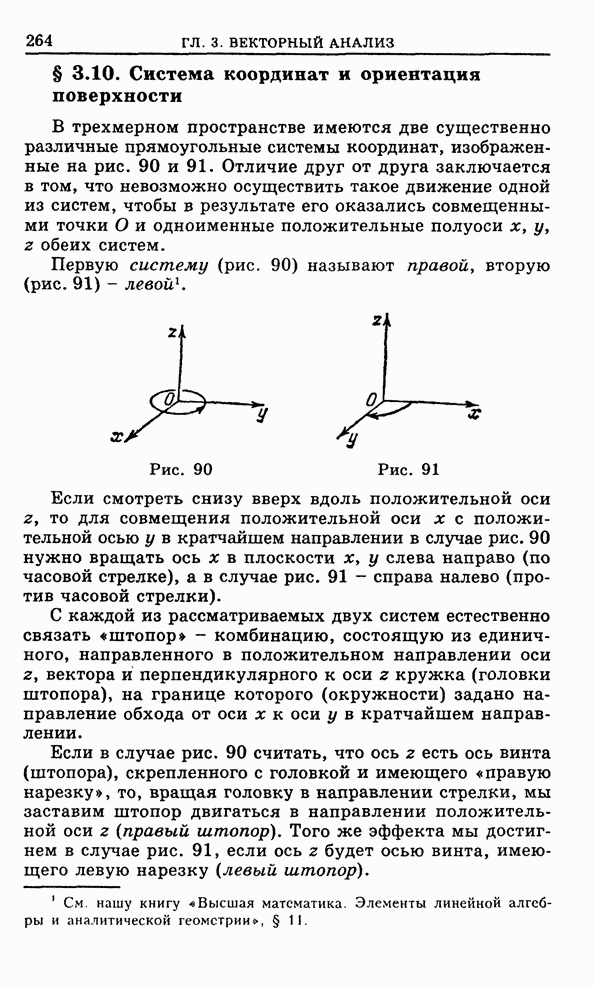
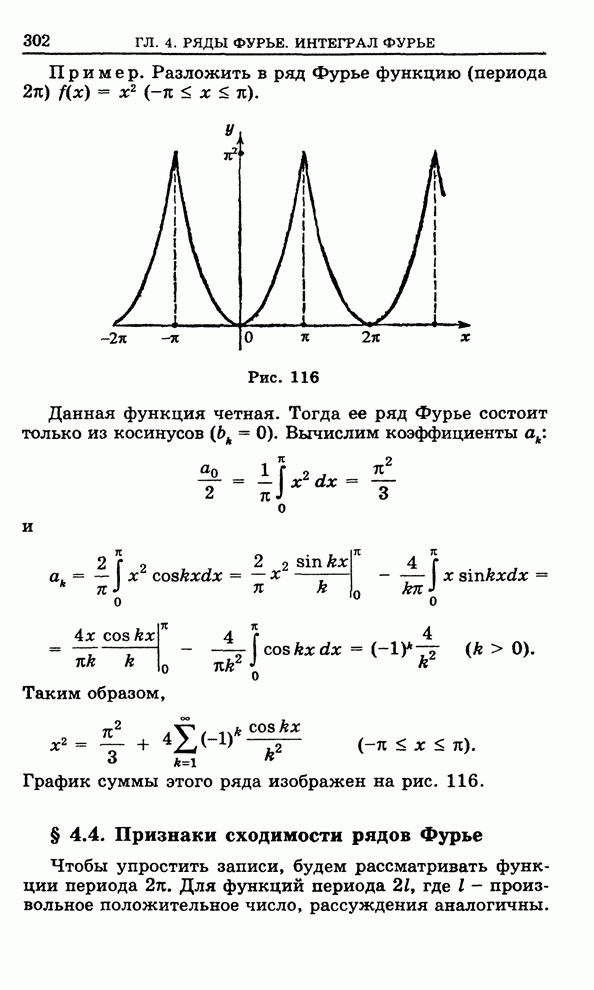
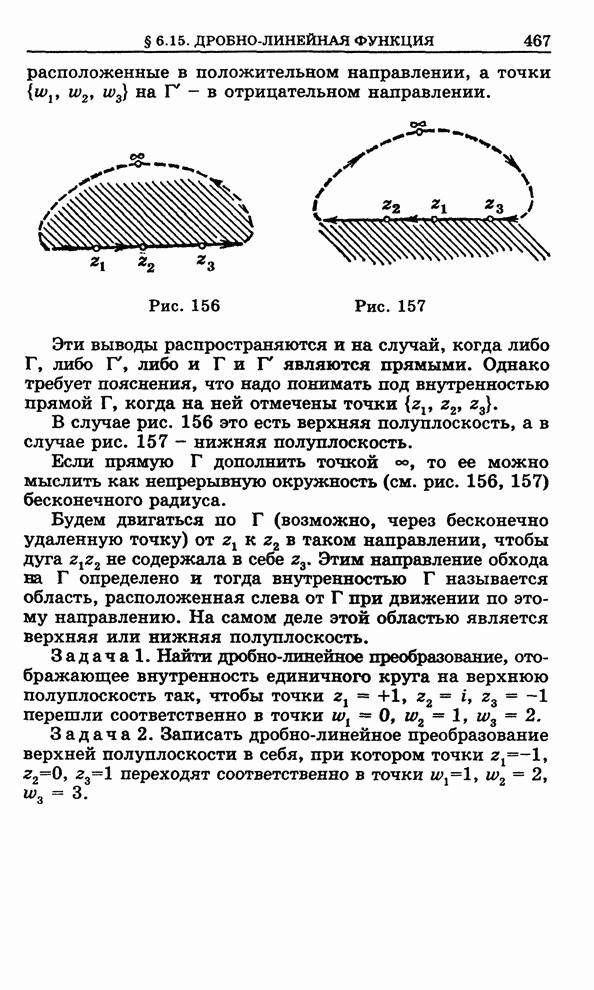
Рис. 103
Начнем
с того, что рассмотрим область ![]() , изображенную на рис. 103, которую мы
будем называть элементарной
, изображенную на рис. 103, которую мы
будем называть элементарной ![]() -областью. Снизу и сверху
-областью. Снизу и сверху ![]() ограничена
поверхностями
ограничена
поверхностями ![]() и
и
![]() с
кусочно-гладкими краями, определяемыми соответственно уравнениями
с
кусочно-гладкими краями, определяемыми соответственно уравнениями
![]() ,
,
где ![]() - плоская область с
кусочно-гладкой границей
- плоская область с
кусочно-гладкой границей ![]() , а
, а ![]() непрерывны на
непрерывны на ![]() и имеют непрерывные частные
производные на открытом множестве
и имеют непрерывные частные
производные на открытом множестве ![]() . С боков
. С боков ![]() ограничена цилиндрической поверхностью
ограничена цилиндрической поверхностью
![]() с направляющей
с направляющей
![]() и
образующей параллельной оси
и
образующей параллельной оси ![]() .
.
Пусть
![]() есть
граница
есть
граница ![]() ,
ориентированная при помощи внешней к
,
ориентированная при помощи внешней к ![]() нормали (пояснения ниже). Тем самым
нижний и верхний куски
нормали (пояснения ниже). Тем самым
нижний и верхний куски ![]() , так же как боковая поверхность
, так же как боковая поверхность ![]() области
области ![]() , соответственно
ориентированы. Для области
, соответственно
ориентированы. Для области ![]() имеют место равенства (пояснения ниже)
имеют место равенства (пояснения ниже)
 (4)
(4)
Нормаль
![]() к
к ![]() образует с осью
образует с осью ![]() соответственно
тупой и острый углы, поэтому проекции
соответственно
тупой и острый углы, поэтому проекции ![]() , кусков
, кусков ![]() на плоскость
на плоскость ![]() ориентированы первая
отрицательно, а вторая положительно. Это обосновывает переход от третьего члена
цепи (4) к четвертому. К сумме, составляющей четвертый член, можно формально
добавить интеграл
ориентированы первая
отрицательно, а вторая положительно. Это обосновывает переход от третьего члена
цепи (4) к четвертому. К сумме, составляющей четвертый член, можно формально
добавить интеграл
![]() ,
,
потому что ![]() вдоль
вдоль ![]() . Но тогда
полученная сумма трех интегралов равна интегралу, стоящему в качестве
последнего члена цепи (4) (потоку вектора
. Но тогда
полученная сумма трех интегралов равна интегралу, стоящему в качестве
последнего члена цепи (4) (потоку вектора ![]() через
через ![]() ).
).
Этим
мы доказали теорему Гаусса-Остроградского для элементарной ![]() -области и вектора
-области и вектора ![]() .
.
Назовем теперь
область ![]() -областью,
если ее замыкание
-областью,
если ее замыкание ![]() можно
разрезать на конечное число элементарных
можно
разрезать на конечное число элементарных ![]() -областей
-областей

так, что нижние
и верхние куски границы ![]() суть части ориентированной границы
суть части ориентированной границы ![]() области
области ![]() , и докажем, что для
, и докажем, что для
![]() и вектора
и вектора
![]() тоже
справедлива теорема Гаусса-Остроградского.
тоже
справедлива теорема Гаусса-Остроградского.
В
самом деле, обозначим соответственно через ![]() нижние и верхние куски границ
нижние и верхние куски границ ![]() , и через
, и через ![]() - боковые куски
- боковые куски ![]() . Тогда (пояснения
ниже)
. Тогда (пояснения
ниже)

потому что
интегралы по ![]() ,
очевидно, равны нулю, а куски
,
очевидно, равны нулю, а куски ![]() и
и ![]() , составляют в совокупности поверхность
, составляют в совокупности поверхность
![]() , либо
только часть
, либо
только часть ![]() ,
а остальная часть
,
а остальная часть ![]() с
с
![]() имеет
нормаль в любой ее точке перпендикулярную к оси
имеет
нормаль в любой ее точке перпендикулярную к оси ![]() . Но тогда интеграл по
. Но тогда интеграл по ![]() равен нулю.
равен нулю.
По
аналогии можно ввести понятия ![]() -области и
-области и ![]() -области. Например,
-области. Например, ![]() -область обладает
тем свойством, что ее замыкание можно разрезать на конечное число замыканий
элементарных
-область обладает
тем свойством, что ее замыкание можно разрезать на конечное число замыканий
элементарных ![]() -областей.
Элементарная же
-областей.
Элементарная же ![]() -область
определяется так же, как элементарная
-область
определяется так же, как элементарная ![]() -область, только роль
-область, только роль ![]() теперь играет
теперь играет ![]() . По аналогии
доказывается, что для
. По аналогии
доказывается, что для ![]() -области
-области ![]() имеет место равенство
имеет место равенство
 ,
,
т. е. формула
Гаусса—Остроградского для вектора ![]() , а для
, а для ![]() -области
-области ![]() - формула
- формула
 .
.
Если
теперь ![]() есть
одновременно
есть
одновременно ![]() и
и
![]() - область,
то для нее, очевидно, верна теорема Гаусса-Остроградского для произвольного
непрерывно дифференцируемого на
- область,
то для нее, очевидно, верна теорема Гаусса-Остроградского для произвольного
непрерывно дифференцируемого на ![]() вектора
вектора ![]() , т. е. верно равенство
, т. е. верно равенство
 , (5)
, (5)
где интеграл справа есть интеграл
по поверхности ![]() ,
ориентированной внешней нормалью к
,
ориентированной внешней нормалью к ![]() .
.
Если
в формуле Гаусса—Остроградского положить ![]() , то получим выражение для объема
области
, то получим выражение для объема
области ![]()

через интеграл
по ее ориентированной внешней нормалью границе ![]() .
.
Области,
с которыми приходится обычно иметь дело, являются одновременно ![]() - областями.
- областями.
Пример
1. Шар ![]() есть
есть
![]() -область,
даже элементарная
-область,
даже элементарная ![]() -область,
потому что вся его внутренность ограничена двумя лежащими друг над другом
гладкими на круге
-область,
потому что вся его внутренность ограничена двумя лежащими друг над другом
гладкими на круге ![]() поверхностями
поверхностями
![]() ,
,
непрерывными на
замкнутом круге ![]() ,
имеющем гладкую границу. Очевидно, шар есть также
,
имеющем гладкую границу. Очевидно, шар есть также ![]() и
и ![]() -область.
-область.
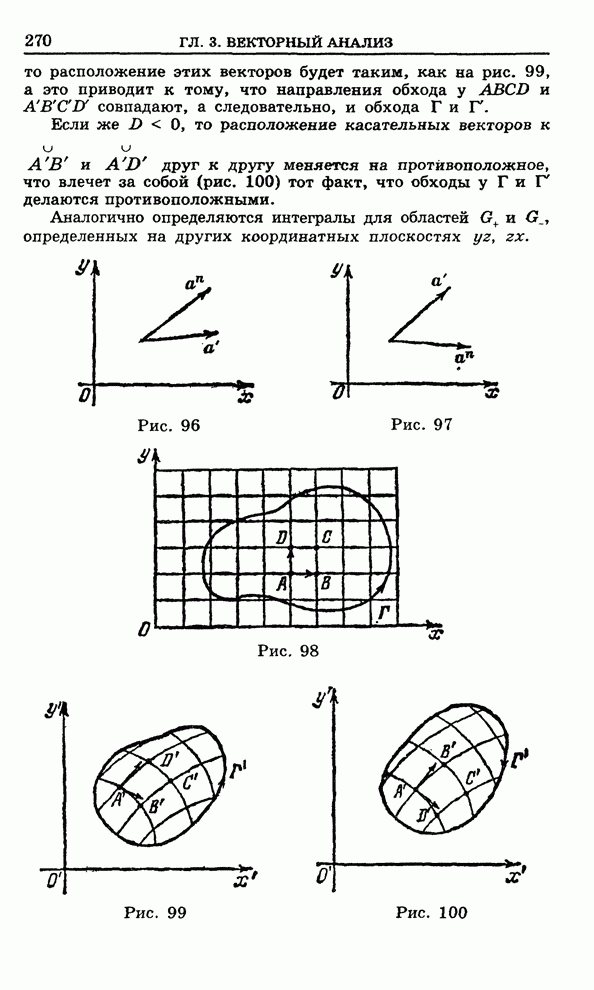
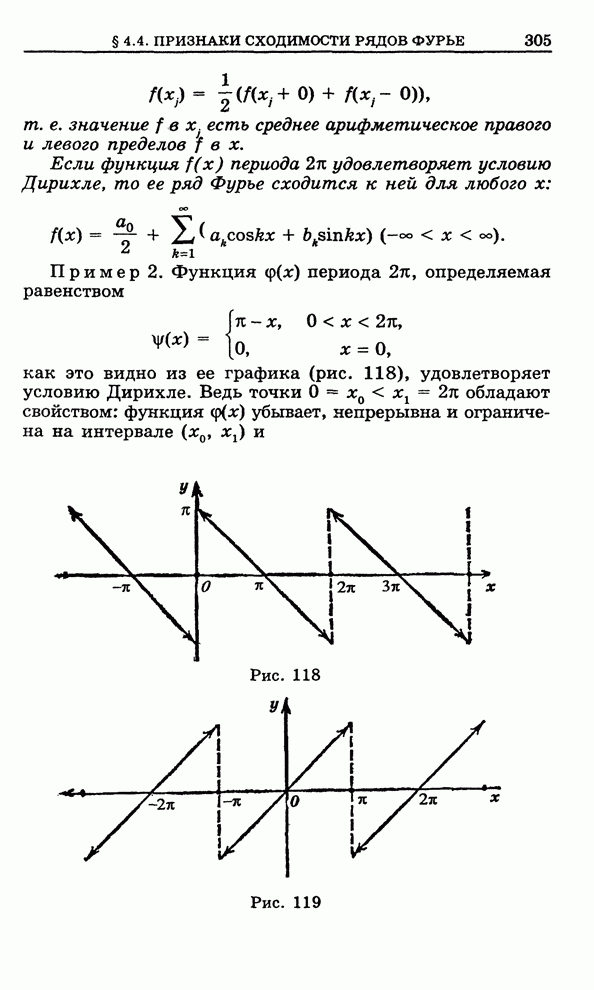
Пример
2. Тор. В плоскости ![]() зададим окружность радиуса
зададим окружность радиуса ![]() с центром в точке
с центром в точке ![]() . Ее уравнение
имеет вид
. Ее уравнение
имеет вид ![]() .
Вращение данной окружности как твердого тела в пространстве
.
Вращение данной окружности как твердого тела в пространстве ![]() вокруг оси
вокруг оси ![]() приводит к
поверхности
приводит к
поверхности ![]() ,
называемой тором (на рис. 104 показана половина тора). Уравнение тора в
декартовых координатах имеет вид
,
называемой тором (на рис. 104 показана половина тора). Уравнение тора в
декартовых координатах имеет вид
![]()

Рис. 104
Чтобы
убедиться в том, что ![]() есть
есть ![]() -область, достаточно поверхность
-область, достаточно поверхность ![]() разделить на две
части плоскостью
разделить на две
части плоскостью ![]() .
Далее, плоскости
.
Далее, плоскости ![]() рассекают
рассекают
![]() на четыре
элементарные
на четыре
элементарные ![]() -области,
а плоскости
-области,
а плоскости ![]() -
на четыре элементарные
-
на четыре элементарные ![]() -области.
-области.
Формула Гаусса—Остроградского преобразует объемный интеграл в интеграл по поверхности.
Чтобы
выяснить физический смысл понятия дивергенции, будем считать, что в ![]() имеет место
стационарное течение жидкости, скорость которой в произвольной точке
имеет место
стационарное течение жидкости, скорость которой в произвольной точке ![]() равна
равна ![]() . Зададим
произвольную, но фиксированную точку
. Зададим
произвольную, но фиксированную точку ![]() и окружим ее шаром
и окружим ее шаром ![]() радиуса
радиуса ![]() . Пусть
. Пусть ![]() есть его граница (шаровая
поверхность), ориентированная посредством внешней нормали. Тогда на основании
формулы Гаусса-Остроградекого
есть его граница (шаровая
поверхность), ориентированная посредством внешней нормали. Тогда на основании
формулы Гаусса-Остроградекого
![]() .
.
Левая часть этого
равенства выражает количество жидкости, вытекающее из ![]() (вовне
(вовне ![]() ) за единицу времени.
Применяя к правой его части теорему о среднем, получим
) за единицу времени.
Применяя к правой его части теорему о среднем, получим
![]() , (6)
, (6)
где ![]() есть объем
есть объем ![]() , а
, а ![]() - скорость жидкости
в некоторой точке из
- скорость жидкости
в некоторой точке из ![]() . Разделив обе части полученного
равенства на
. Разделив обе части полученного
равенства на ![]() и
перейдя к пределу при
и
перейдя к пределу при ![]() , получим в силу непрерывности
, получим в силу непрерывности ![]() , что существует
предел, равный дивергенции
, что существует
предел, равный дивергенции ![]() :
:
 (7)
(7)
в точке ![]() . Таким образом,
. Таким образом, ![]() представляет собой производительность
источников, непрерывно распределенных по
представляет собой производительность
источников, непрерывно распределенных по ![]() в точке
в точке ![]() . Если в точке
. Если в точке ![]() (или всюду на
(или всюду на ![]() )
) ![]() , то это значит, что
в
, то это значит, что
в ![]() (или
всюду на
(или
всюду на ![]() )
производительность источников равна нулю. Если
)
производительность источников равна нулю. Если ![]() , то это значит, что на самом деле в
соответствующей точке имеет место сток.
, то это значит, что на самом деле в
соответствующей точке имеет место сток.
Из
физических соображений ясно, что ![]() есть инвариант относительно любых
преобразований прямоугольных координат. Но это заключение можно сделать и на основании
математических соображений.
есть инвариант относительно любых
преобразований прямоугольных координат. Но это заключение можно сделать и на основании
математических соображений.
Как
мы знаем (см. нашу книгу «Высшая математика. Элементы линейной алгебры и
аналитической геометрии», § 18) скалярное произведение векторов есть ивариант
при преобразованиях координат, поэтому и дивергенция (равна скалярному
произведению символического вектора ![]() и вектора
и вектора ![]() ) есть инвариант относительно
преобразований прямоугольных координат. Конечно, мы считаем (по определителю),
что координаты символического вектора
) есть инвариант относительно
преобразований прямоугольных координат. Конечно, мы считаем (по определителю),
что координаты символического вектора ![]() преобразуются по тем же формулам, что
и координаты обычных векторов. Точнее, если формулы преобразования от координат
преобразуются по тем же формулам, что
и координаты обычных векторов. Точнее, если формулы преобразования от координат
![]() точки
(вектора) в первой системе координат к ее координатам
точки
(вектора) в первой системе координат к ее координатам ![]() во второй системе имеют вид
во второй системе имеют вид
 , (8)
, (8)
где ![]() - соответствующая ортогональная
матрица, то
- соответствующая ортогональная
матрица, то
 . (9)
. (9)
Оператор
Гамильтона применяется к дифференцируемой функции ![]() . В результате мы получаем вектор
. В результате мы получаем вектор
 ,
,
называемый, как
мы знаем, градиентом функции ![]() . Функция
. Функция ![]() в этом исчислении считается скаляром.
Таким образом,
в этом исчислении считается скаляром.
Таким образом, ![]() есть
произведение вектора
есть
произведение вектора ![]() на скаляр
на скаляр ![]() - результат есть вектор.
- результат есть вектор.
В системе
координат ![]()
 ,
,
где ![]() - орты системы
- орты системы ![]() . При этом в силу
(9)
. При этом в силу
(9)
 . (10)
. (10)
Формулы
(10) согласуются с правилами дифференцирования сложной функции ![]() , у которой
, у которой
 . (11)
. (11)
Формулы
(11) являются обратными к формулам (8) (![]() , т. е. координаты
, т. е. координаты ![]() выражаются через координаты
выражаются через координаты ![]() с помощью
с помощью ![]() -го столбца матрицы
-го столбца матрицы ![]() ).
).
Здесь мы получили формулы (10), пользуясь только символическим исчислением.
Теперь,
если одно и то же поле вектора определено в двух прямоугольных системах
координат ![]() и
и
![]() соответственно
функциями
соответственно
функциями

где координаты ![]() и
и ![]() связаны по формулам (8),
(11) (с заменой в них
связаны по формулам (8),
(11) (с заменой в них ![]() на
на ![]() ), то в одной и той же точке
), то в одной и той же точке
 .
.
Таким образом, мы еще раз доказали инвариантность дивергенции при преобразованиях прямоугольных координат пользуясь только символическим исчислением.
Формулу
Гаусса—Остроградского можно записать в плоском случае, когда ![]() есть область в
плоскости
есть область в
плоскости ![]() и
и
![]()
- определенное
на ней поле. Если ![]() есть
внешняя нормаль к кусочно-гладкому контуру
есть
внешняя нормаль к кусочно-гладкому контуру ![]() области
области ![]() , то имеет место равенство
, то имеет место равенство
 ,
,
где ![]() - дифференциал дуги
- дифференциал дуги ![]() .
.

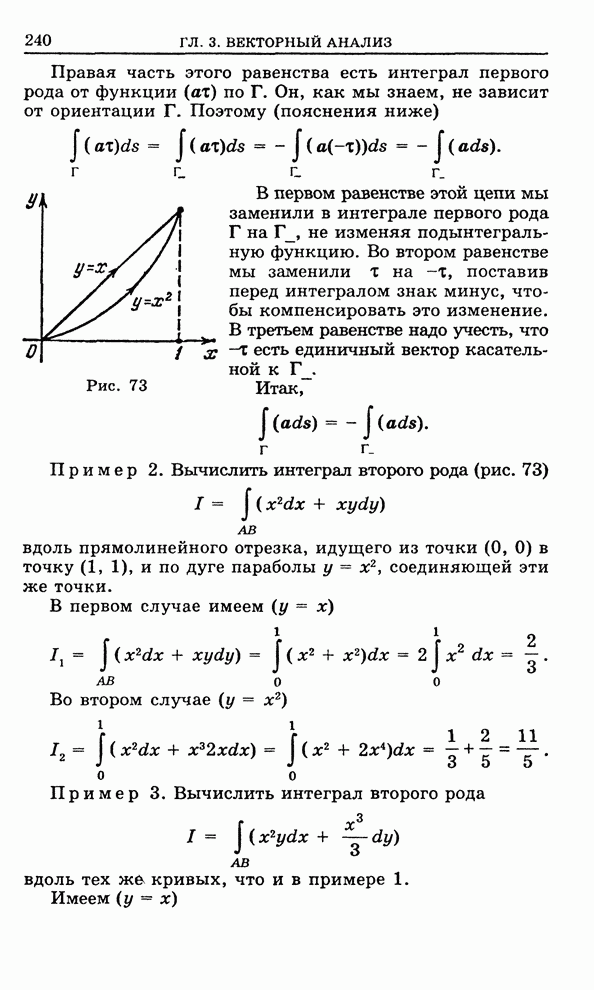
Рис. 105
Если
считать, что направление касательной в точке ![]() совпадает с положительным направлением
обхода по
совпадает с положительным направлением
обхода по ![]() ,
вдоль которого исчисляется также длина дуги контура
,
вдоль которого исчисляется также длина дуги контура ![]() , то (рис. 105)
, то (рис. 105)

Поэтому

Если
в этой формуле заменить соответственно ![]() на
на ![]() , то мы придем к формуле Грина, которая
была получена в § 3.7.
, то мы придем к формуле Грина, которая
была получена в § 3.7.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
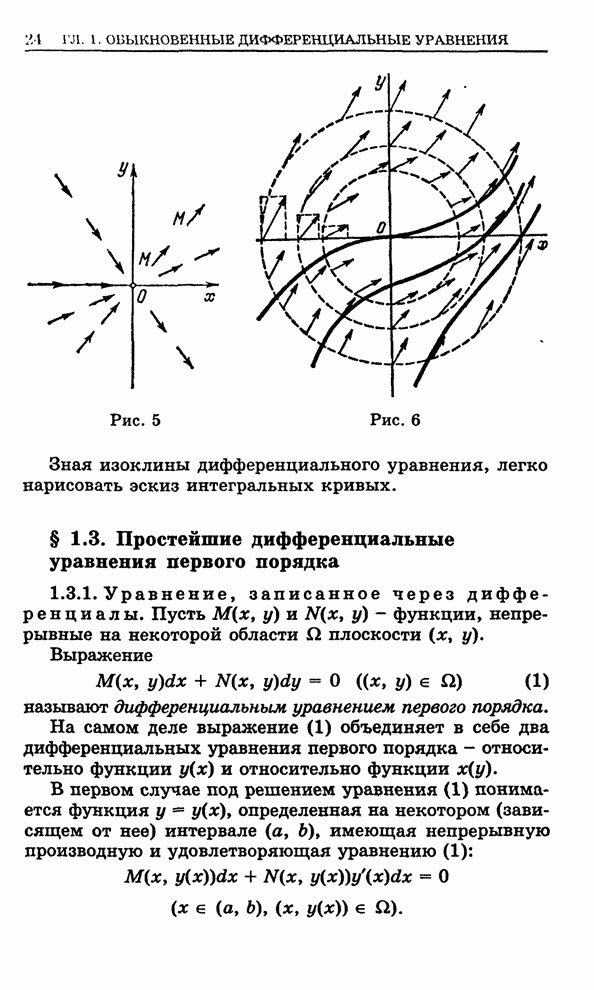
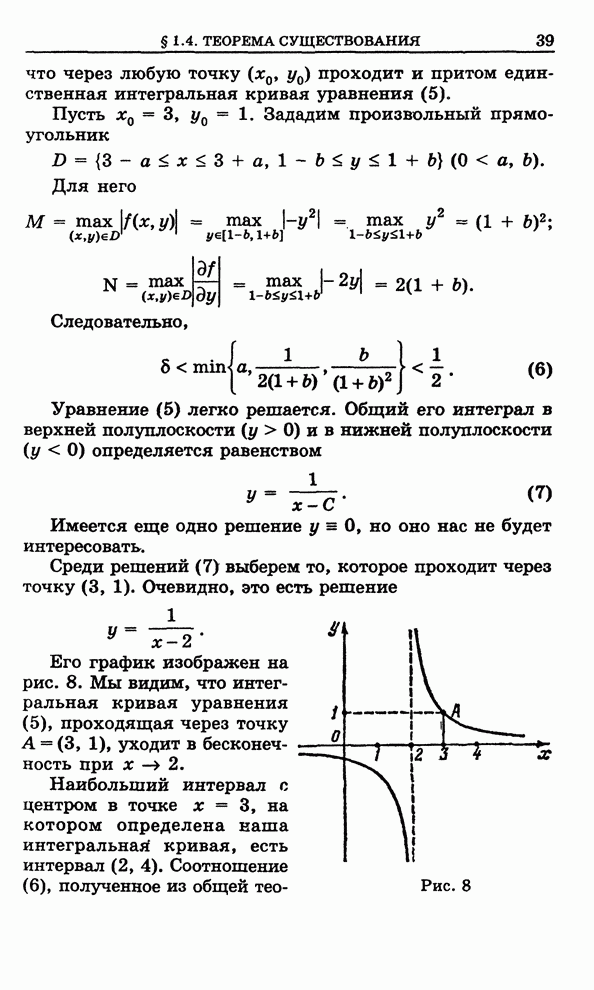
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
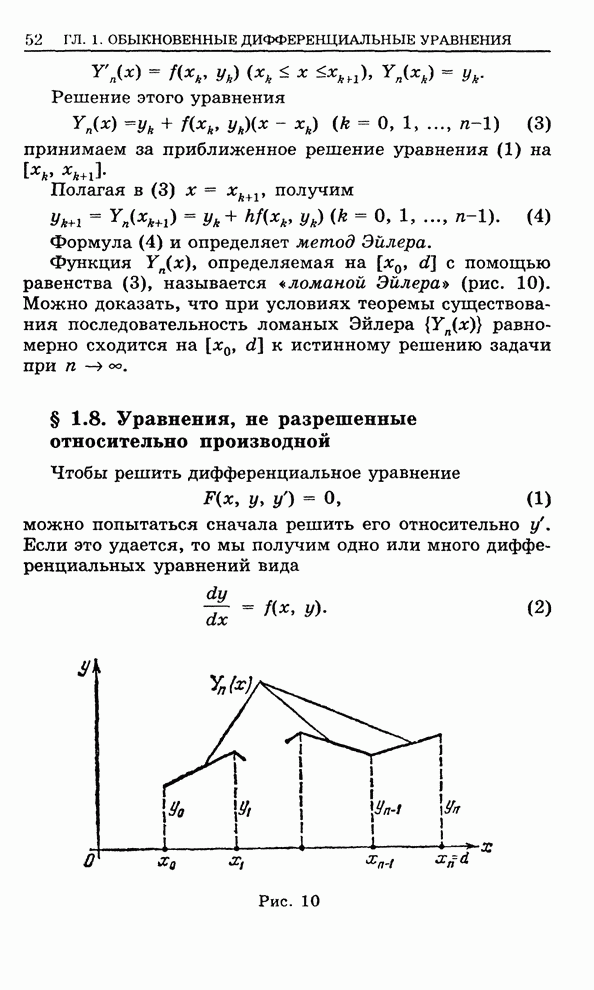
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
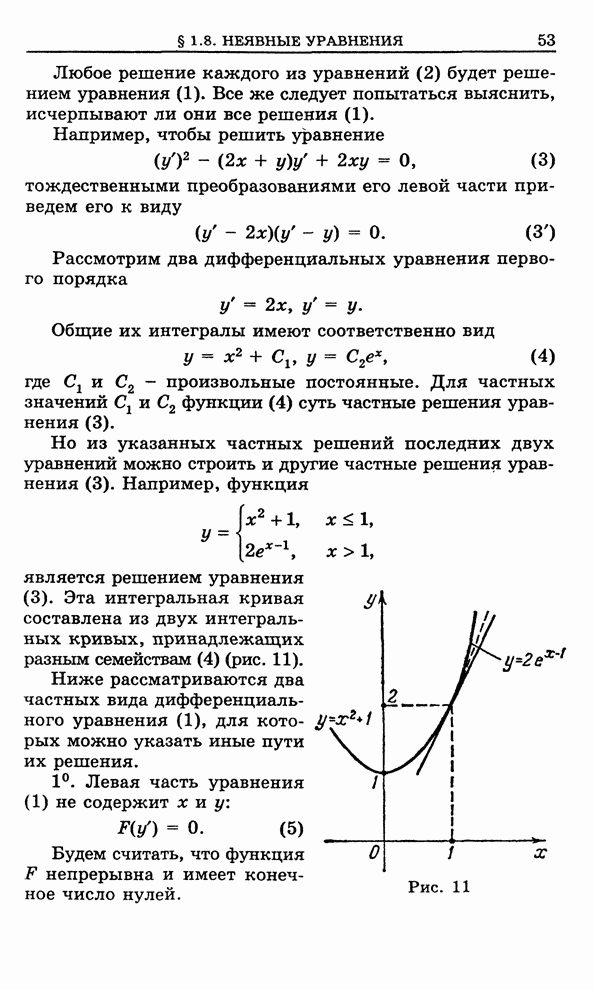
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций