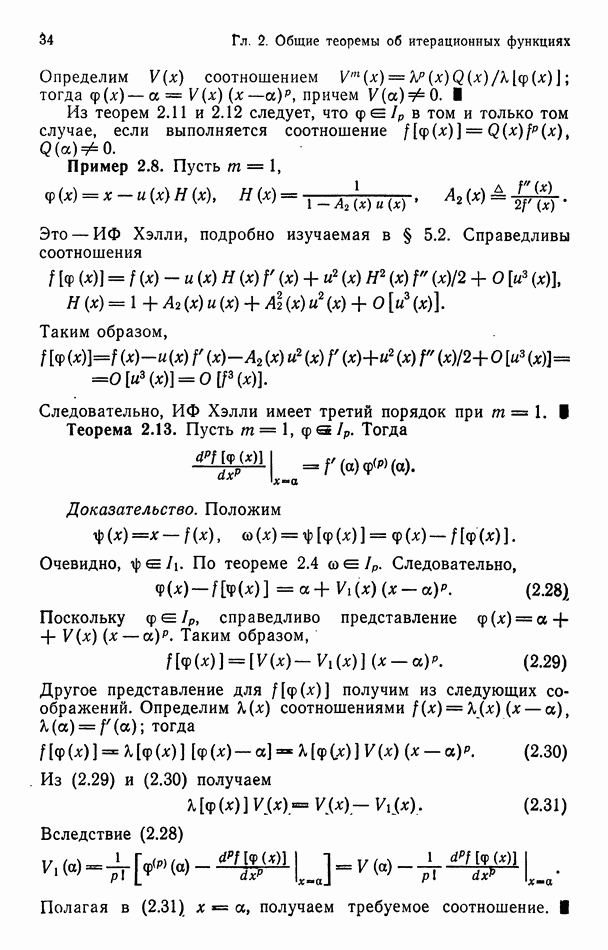| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. ИТЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Этот параграф посвящен разработке исчисления для итерационных функций. Содержащиеся в нем результаты играют ключевую роль в значительной части дальнейших исследований. Отметим, что они неприменимы к ИФ с памятью. В проводимых ниже рассуждениях мы будем предполагать, что порядок является целым; относительно же структуры ИФ никаких предположений не делается. Теоремы 8.1 и 8.2, также относящиеся к итерационному исчислению, помещены по месту их применения в гл. 8. Некоторые из приводимых результатов для случая простых корней имеются в работах Zajta [2.3-1], Ehrmann [2.3-2].
2.3.1. Подготовка.
В этом параграфе мы рассматриваем нули произвольной кратности. Кратность нуля обозначим буквой 
а принадлежность  классу ИФ, имеющих порядок
классу ИФ, имеющих порядок  будем записывать в виде
будем записывать в виде  Мы исходим из предположения, что
Мы исходим из предположения, что  имеет порядок
имеет порядок  для всех функций
для всех функций  с нулями одинаковой кратности. При этом допускается, что
с нулями одинаковой кратности. При этом допускается, что  имеет разные порядки для простых и кратных нулей. В последнем случае будет оговариваться, что
имеет разные порядки для простых и кратных нулей. В последнем случае будет оговариваться, что  для некоторых значений
для некоторых значений 
Пример 2.3. Пусть  Тогда
Тогда  для простых нулей и
для простых нулей и  для кратных нулей. В то же время
для кратных нулей. В то же время  для нулей кратности
для нулей кратности  для нулей произвольной кратности (подробности приведены в гл. 7).
для нулей произвольной кратности (подробности приведены в гл. 7).
Предположим, что производная  непрерывна в окрестности точки а. Если
непрерывна в окрестности точки а. Если  то по теореме 2.2
то по теореме 2.2

Разложив  в ряд Тейлора с центром в точке а, получаем
в ряд Тейлора с центром в точке а, получаем

где  заключено в промежутке между
заключено в промежутке между  Хотя зависимость
Хотя зависимость  от х не является непрерывной,
от х не является непрерывной,  можно представить как непрерывную функцию аргумента х следующим образом. Положим
можно представить как непрерывную функцию аргумента х следующим образом. Положим

Применив  раз правило Лопиталя, получаем
раз правило Лопиталя, получаем  Следовательно,
Следовательно,

причем  непрерывная функция аргумента
непрерывная функция аргумента  Таким образом, ИФ порядка
Таким образом, ИФ порядка  всегда имеет нуль а кратности
всегда имеет нуль а кратности 
Сравнивая (2.17) и (1.14), получаем, что  где С — константа асимптотики погрешности.
где С — константа асимптотики погрешности.
Представим уравнение (2.17) в форме, более удобной для дальнейших применений. Предположим, что производная  непрерывна в окрестности точки а и
непрерывна в окрестности точки а и  простой корень. Тогда
простой корень. Тогда  а). Положим
а). Положим

Тогда

причем  непрерывная функция аргумента
непрерывная функция аргумента  Из (2.17) и (2.18) получаем
Из (2.17) и (2.18) получаем

где  Следовательно, функция
Следовательно, функция  непрерывна, если
непрерывна, если  непрерывны, то
непрерывны, то  не обращается в нуль. Кроме того,
не обращается в нуль. Кроме того,

Если кратность  больше единицы, то функция
больше единицы, то функция  не пропорциональна
не пропорциональна  а, поэтому получить выражение вида (2.19), содержащее
а, поэтому получить выражение вида (2.19), содержащее  невозможно. Однако функция
невозможно. Однако функция  имеет только простые корни, что позволяет легко обобщить (2.19). В самом деле, пусть производная
имеет только простые корни, что позволяет легко обобщить (2.19). В самом деле, пусть производная  непрерывна и а имеет кратность
непрерывна и а имеет кратность  С помощью рассуждений, аналогичных проведенным выше, доказывается существование непрерывных функций
С помощью рассуждений, аналогичных проведенным выше, доказывается существование непрерывных функций  таких, что
таких, что

где

Следовательно,

где  Из (2.17) и (2.20) получаем
Из (2.17) и (2.20) получаем

где функция  непрерывна,
непрерывна,

Соотношения (2.17), (2.19) и (2.21) играют в дальнейшем исключительно важную роль. В частности, мы будем использовать (2.21) в форме

2.3.2. Теоремы итерационного исчисления.
В доказываемых ниже теоремах мы не будем формулировать условия непрерывности производных функций  характер этих условий будет ясен из доказательств. Используемые ниже обозначения были введены в
характер этих условий будет ясен из доказательств. Используемые ниже обозначения были введены в 
Теорема 2.4. Предположим, что  для некоторой совокупности значений
для некоторой совокупности значений  Тогда для этих значений
Тогда для этих значений  имеем
имеем 
Доказательство. Из (2.17) следует, что

Тогда

Положим  Нетрудно видеть, что
Нетрудно видеть, что

Замечание. Соотношение (2.23) выражает связь между константой асимптотики погрешности составной ИФ и константами асимптотики погрешности составляющих ее ИФ.
Следствие. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Положим
Положим 
— перестановка чисел 
Тогда  для этих значений
для этих значений  В частности, если
В частности, если  для
для  то
то 
Пример 2.4. Положим  (ИФ Ньютона). Очевидно,
(ИФ Ньютона). Очевидно,  Поэтому
Поэтому

Теорема 2.5. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Тогда для этих
Тогда для этих  существует функция
существует функция  такая, что
такая, что 
Доказательство. Поскольку  найдется функция
найдется функция  для которой
для которой  Ввиду
Ввиду  имеем
имеем  Следовательно, а является простым нулем функции
Следовательно, а является простым нулем функции  поэтому найдется такая функция
поэтому найдется такая функция  что
что  причем
причем 
Теорему 2.5 можно переформулировать следующим образом. Если а —нуль  порядка функции
порядка функции  а при
а при  то а является простым нулем функции
то а является простым нулем функции  Пример функций
Пример функций  имеющих первый порядок, показывает, что при
имеющих первый порядок, показывает, что при  теорема неверна.
теорема неверна.
Пример 2.5. Если порядок  больше единицы, то ИФ
больше единицы, то ИФ  имеет только простые нули. Поэтому любая ИФ, имеющая порядок
имеет только простые нули. Поэтому любая ИФ, имеющая порядок  для функций
для функций  с простыми нулями, сохранит порядок
с простыми нулями, сохранит порядок  если в ней
если в ней  заменить на
заменить на  Так, если
Так, если  заменить на
заменить на  в ИФ Ньютона, получим
в ИФ Ньютона, получим

причем  Пусть
Пусть  есть ИФ Ньютона, тогда
есть ИФ Ньютона, тогда  Эта ИФ, обобщающая ИФ Ньютона и имеющая второй порядок для корней любой кратности, вновь появится в гл. 7.
Эта ИФ, обобщающая ИФ Ньютона и имеющая второй порядок для корней любой кратности, вновь появится в гл. 7.
Теорема 2.6. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Тогда для этих значений
Тогда для этих значений  существует ограниченная в окрестности точки а функция
существует ограниченная в окрестности точки а функция  такая, что
такая, что

где

Доказательство. 1. Пусть  Предположим для определенности, что
Предположим для определенности, что  Ввиду (2.21)
Ввиду (2.21)

Положим  Соотношения
Соотношения  завершают рассмотрение первого случая.
завершают рассмотрение первого случая.
2. Пусть  Тогда
Тогда

Положим  Соотношения
Соотношения

завершают рассмотрение второго случая.
3. Пусть  Поскольку
Поскольку  найдется такое целое
найдется такое целое  что
что  и дальнейшие рассуждения совпадают с предыдущим случаем. I
и дальнейшие рассуждения совпадают с предыдущим случаем. I
С точки зрения дальнейших приложений наибольший интерес представляет случай  Докажем теорему, обратную к теореме 2.6.
Докажем теорему, обратную к теореме 2.6.
Теорема 2.7. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Тогда для этих значений
Тогда для этих значений  где
где

Доказательство. 1. Пусть  Предположим для определенности, что
Предположим для определенности, что  Тогда
Тогда

Положим  Соотношение
Соотношение  завершает рассмотрение первого случая.
завершает рассмотрение первого случая.
2. Пусть  Тогда
Тогда

Положим  Соотношения
Соотношения

завершают рассмотрение этого случая.
3. Случай  рассматривается аналогично предыдущему.
рассматривается аналогично предыдущему.
Только что доказанная «теорема сравнения» позволяет установить порядок ИФ, отличающийся от ИФ известного порядка членами порядка  Следующая теорема позволяет вычислить константу асимптотики погрешности для ИФ порядка
Следующая теорема позволяет вычислить константу асимптотики погрешности для ИФ порядка  если известна константа асимптотики погрешности какой-либо другой ИФ этого же порядка. Напомним, что константа асимптотики погрешности С определяется соотношением
если известна константа асимптотики погрешности какой-либо другой ИФ этого же порядка. Напомним, что константа асимптотики погрешности С определяется соотношением

Теорема 2.8. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Положим
Положим

Пусть  константы асимптотики погрешности для
константы асимптотики погрешности для  Тогда для этих значений
Тогда для этих значений  справедливо
справедливо

Доказательство. Применив правило Лопиталя  раз, получим
раз, получим

Пример 2.6. Пусть

Тогда  для нулей кратности
для нулей кратности  . В п. 7.4.1 будет показано, что
. В п. 7.4.1 будет показано, что

где  При помощи этого соотношения нетрудно установить равенства
При помощи этого соотношения нетрудно установить равенства

что согласуется с теоремой 2.8. Положим

Поскольку  равны по абсолютной величине и противоположны по знаку,
равны по абсолютной величине и противоположны по знаку,  для всех
для всех 
Более полезный по сравнению с теоремой 2.8 результат содержит
Теорема 2.9. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Положим
Положим

Пусть  константы асимптотики погрешности функций
константы асимптотики погрешности функций  Тогда для этих значений
Тогда для этих значений 

Доказательство. Нетрудно показать, что

Из предыдущей теоремы следует, что

откуда получаем требуемое утверждение. I
Пример 2.7. Пусть  Тогда ИФ, задаваемые соотношениями
Тогда ИФ, задаваемые соотношениями

 имеют третий порядок, причем
имеют третий порядок, причем

Поскольку

имеем 
Следующая теорема тесно связана с теоремой 2.6. Ее утверждение формулируется в виде, удобном для использования в гл. 5, 6.
Теорема 2.10. Пусть  Тогда любая ИФ порядка
Тогда любая ИФ порядка  представима в виде
представима в виде

где  функция, ограниченная в окрестности точки а.
функция, ограниченная в окрестности точки а.
Доказательство. Из (2.19) получаем

Поэтому

Полагая в  получаем утверждение теоремы.
получаем утверждение теоремы. 
Отметим, что теорема 2.10 несправедлива при  Например,
Например,

имеет порядок  при
при 
Следующие две теоремы раскрывают другие свойства ИФ порядка 
Теорема 2.11. Пусть  для некоторой совокупности значений
для некоторой совокупности значений  Тогда для этих значений
Тогда для этих значений  найдется функция
найдется функция  такая, что
такая, что  причем
причем 
Доказательство. Предположим, что  нуль кратности
нуль кратности  . В п. 2.2.1 было показано, что в этом случае существует непрерывная функция
. В п. 2.2.1 было показано, что в этом случае существует непрерывная функция  для которой
для которой  Поэтому
Поэтому

Поскольку  функция
функция  , не обращается в нуль в некоторой окрестности точки а. Следовательно,
, не обращается в нуль в некоторой окрестности точки а. Следовательно,

Положим  Соотношение
Соотношение

завершает доказательство.
Справедлива и обратная теорема.
Теорема 2.12. Пусть для некоторой совокупности значений  выполняется
выполняется  причем
причем  Тогда
Тогда  для этих значений
для этих значений 
Доказательство. Очевидно,  где
где  то же, что и в предыдущей теореме. По предположению теоремы имеем
то же, что и в предыдущей теореме. По предположению теоремы имеем

Определим  соотношением
соотношением  тогда
тогда  причем
причем 
Из теорем 2.11 и 2.12 следует, что  в том и только том случае, если выполняется соотношение
в том и только том случае, если выполняется соотношение 
Пример 2.8. Пусть 

Это — ИФ Хэлли, подробно изучаемая в § 5.2. Справедливы соотношения

Таким образом,

Следовательно, ИФ Хэлли имеет третий порядок при  Теорема 2.13. Пусть
Теорема 2.13. Пусть  Тогда
Тогда

Доказательство. Положим

Очевидно,  По теореме
По теореме  Следовательно,
Следовательно,

Поскольку  справедливо представление
справедливо представление  Таким образом,
Таким образом,

Другое представление для  получим из следующих соображений. Определим
получим из следующих соображений. Определим  соотношениями
соотношениями  тогда
тогда

Из (2.29) и (2.30) получаем

Вследствие (2.28)

Полагая в  получаем требуемое соотношение.
получаем требуемое соотношение.
Предыдущую теорему обобщает
Теорема 2.14. Пусть  Тогда
Тогда

Доказательство. Положим  Из теоремы 2.11 следует, что
Из теоремы 2.11 следует, что  для
для  Поскольку
Поскольку  при
при  справедливость теоремы для этих значений
справедливость теоремы для этих значений  установлена.
установлена.
Пусть теперь  Заметим, что
Заметим, что

Налагая соответствующие ограничения на  мы можем добиться того, что у
мы можем добиться того, что у  и V будет требуемое количество непрерывных в окрестности точки а производных. Тогда
и V будет требуемое количество непрерывных в окрестности точки а производных. Тогда

где через  обозначены биномиальные коэффициенты. Следовательно,
обозначены биномиальные коэффициенты. Следовательно,

Нетрудно показать, что

откуда и следует утверждение теоремы.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- 1.2.2. Классификация итерационных функций.
- 1.2.3. Порядок.
- 1.2.4. Понятия, относящиеся к порядку.
- ГЛАВА 2. ОБЩИЕ ТЕОРЕМЫ ОБ ИТЕРАЦИОННЫХ ФУНКЦИЯХ
- 2.1. РЕШЕНИЕ ЗАДАЧИ О НЕПОДВИЖНОЙ ТОЧКЕ
- 2.2. ЛИНЕЙНАЯ И СВЕРХЛИНЕЙНАЯ СХОДИМОСТЬ
- 2.3. ИТЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
- ГЛАВА 3. МАТЕМАТИКА РАЗНОСТНЫХ ОТНОШЕНИЙ
- 3.1. О СХОДИМОСТИ РЕШЕНИЙ РАЗНОСТНЫХ НЕРАВЕНСТВ
- 3.2. ТЕОРЕМА О РЕШЕНИЯХ НЕКОТОРЫХ НЕОДНОРОДНЫХ РАЗНОСТНЫХ УРАВНЕНИЙ
- 3.3. О КОРНЯХ НЕКОТОРЫХ ХАРАКТЕРИСТИЧЕСКИХ УРАВНЕНИЙ
- 3.4. АСИМПТОТИЧЕСКИЕ СВОЙСТВА РЕШЕНИЙ НЕКОТОРЫХ РАЗНОСТНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ИНТЕРПОЛЯЦИОННЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 4.1. ИНТЕРПОЛЯЦИЯ И РЕШЕНИЕ УРАВНЕНИЙ
- 4.2. ПОРЯДОК ИНТЕРПОЛЯЦИОННЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 4.3. ПРИМЕРЫ
- ГЛАВА 5. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 5.2. РАЦИОНАЛЬНЫЕ АППРОКСИМАЦИИ Es
- 5.3. БАЗОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ИТЕРАЦИОННЫХ ФУНКЦИЙ, ПОРОЖДАЕМЫХ ПРЯМОЙ ИНТЕРПОЛЯЦИЕЙ
- 5.4. ОСНОВНАЯ ТЕОРЕМА ОБ ОДНОТОЧЕЧНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЯХ
- 5.5. КОЭФФИЦИЕНТЫ РЯДОВ ДЛЯ ПОГРЕШНОСТЕЙ ИТЕРАЦИОННЫХ ФУНКЦИЙ Es
- ГЛАВА 6. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 6.2. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ, ПОРОЖДАЕМЫЕ АППРОКСИМАЦИЕИ ПРОИЗВОДНОЙ
- 6.3. ОБСУЖДЕНИЕ ОДНОТОЧЕЧНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ С ПАМЯТЬЮ
- ГЛАВА 7. КРАТНЫЕ КОРНИ
- 7.2. ПОРЯДОК ИТЕРАЦИОННЫХ ФУНКЦИЙ Es
- 7.3. БАЗОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- 7.4. КОЭФФИЦИЕНТЫ РЯДОВ ДЛЯ ПОГРЕШНОСТЕЙ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 7.5. ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ ПРЯМОЙ ИНТЕРПОЛЯЦИЕЙ
- 7.6. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 7.7. НЕКОТОРЫЕ ОБЩИЕ РЕЗУЛЬТАТЫ
- 7.8. ИТЕРАЦИОННАЯ ФУНКЦИЯ НЕИЗМЕРИМОГО ПОРЯДКА
- ГЛАВА 8. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 8.2. ОДНА ЗАДАЧА ИНТЕРПОЛЯЦИИ
- 8.3. РЕКУРРЕНТНО ГЕНЕРИРУЕМЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 8.4. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ АППРОКСИМАЦИЕЙ ПРОИЗВОДНОЙ
- 8.5. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ СУПЕРПОЗИЦИЕЙ
- 8.6. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- ГЛАВА 9. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ. ПРОДОЛЖЕНИЕ
- 9.2. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ ПЕРВОГО ТИПА
- 9.3. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ ВТОРОГО ТИПА
- 9.4. ОБСУЖДЕНИЕ КРИТЕРИЕВ ВЫБОРА ИТЕРАЦИОННОЙ ФУНКЦИИ
- ГЛАВА 10. ИТЕРАЦИОННЫЕ ФУНКЦИИ, НЕ ИСПОЛЬЗУЮЩИЕ ЗНАЧЕНИЙ ПРОИЗВОДНЫХ
- 10.2. ИНТЕРПОЛЯЦИОННЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 10.3. НЕКОТОРЫЕ ДРУГИЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- ГЛАВА 11. СИСТЕМЫ УРАВНЕНИЙ
- 11.2. ПОСТРОЕНИЕ ВЕКТОРНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ ПРИ ПОМОЩИ ОБРАТНОЙ ИНТЕРПОЛЯЦИИ
- 11.3. ОЦЕНКИ ПОГРЕШНОСТЕЙ НЕКОТОРЫХ ВЕКТОРНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 11.4. ВЕКТОРНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, НЕ ИСПОЛЬЗУЮЩИЕ ЗНАЧЕНИЙ ПРОИЗВОДНЫХ
- ГЛАВА 12. ПЕРЕЧЕНЬ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 12.2. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 12.3. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 12.4. КРАТНЫЕ КОРНИ
- 12.5. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 12.6. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 12.7. СИСТЕМЫ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ А. ИНТЕРПОЛЯЦИЯ
- А.2. ЗАДАЧА ИНТЕРПОЛЯЦИИ И ЕЕ РЕШЕНИЕ
- А.3. СЛУЧАЙ СТАНДАРТНОЙ ИНФОРМАЦИИ
- А.4. АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ
- А.5. ПОГРЕШНОСТЬ АППРОКСИМАЦИИ ПРОИЗВОДНЫХ
- ПРИЛОЖЕНИЕ В. О J-Й ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ С. ВЕРНЫЕ ЦИФРЫ И ВЫЧИСЛИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ
- ПРИЛОЖЕНИЕ D. УСКОРЕНИЕ СХОДИМОСТИ
- D.2. «дельта2»-ПРЕОБРАЗОВАНИЕ ЭЙТКЕНА
- D.3. ИТЕРАЦИОННАЯ ФУНКЦИЯ СТЕФФЕНСОНА — ХАУСХОЛДЕРА — ОСТРОВСКОГО
- ПРИЛОЖЕНИЕ Е. ЧИСЛЕННЫЕ ПРИМЕРЫ
- ПРИЛОЖЕНИЕ F. НАПРАВЛЕНИЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ
- ЛИТЕРАТУРА