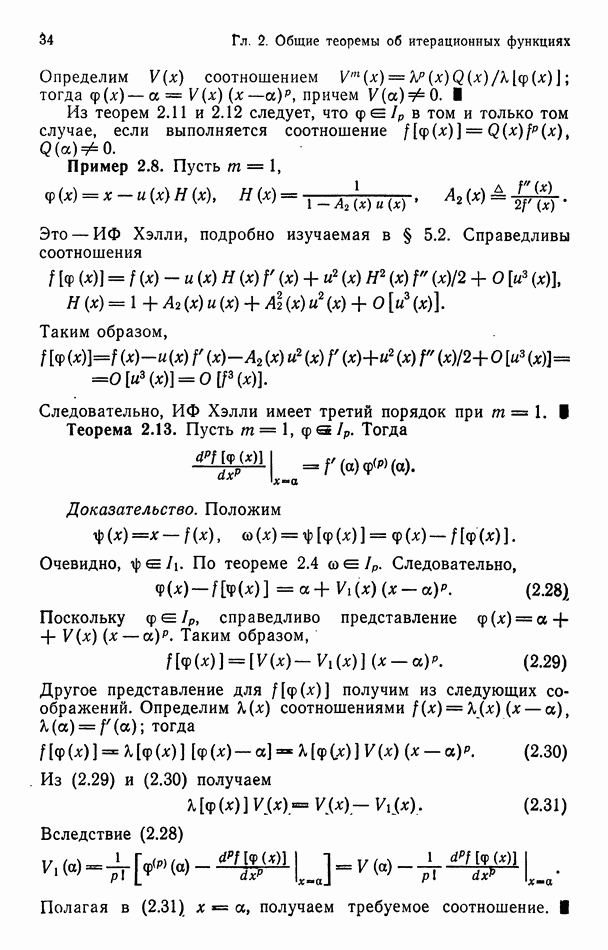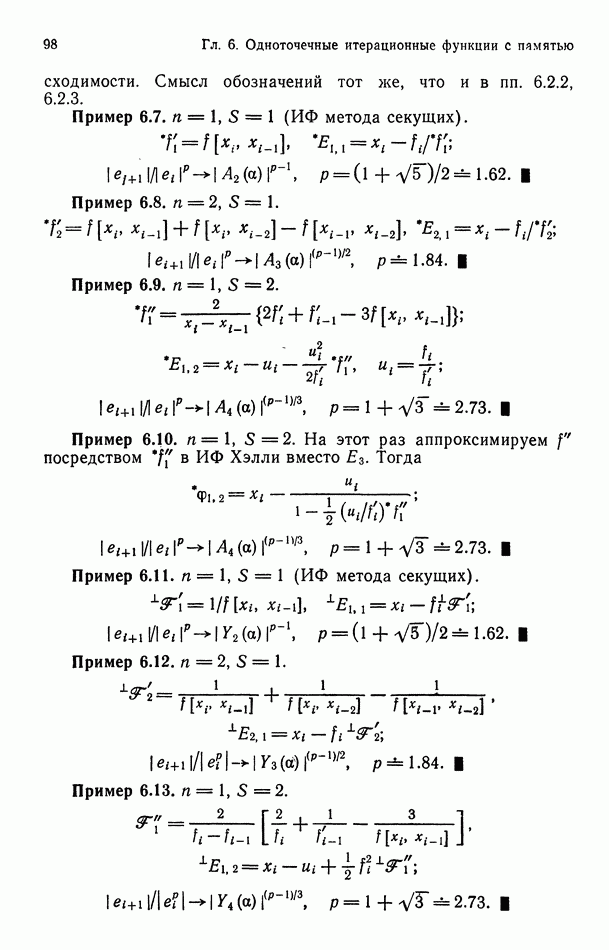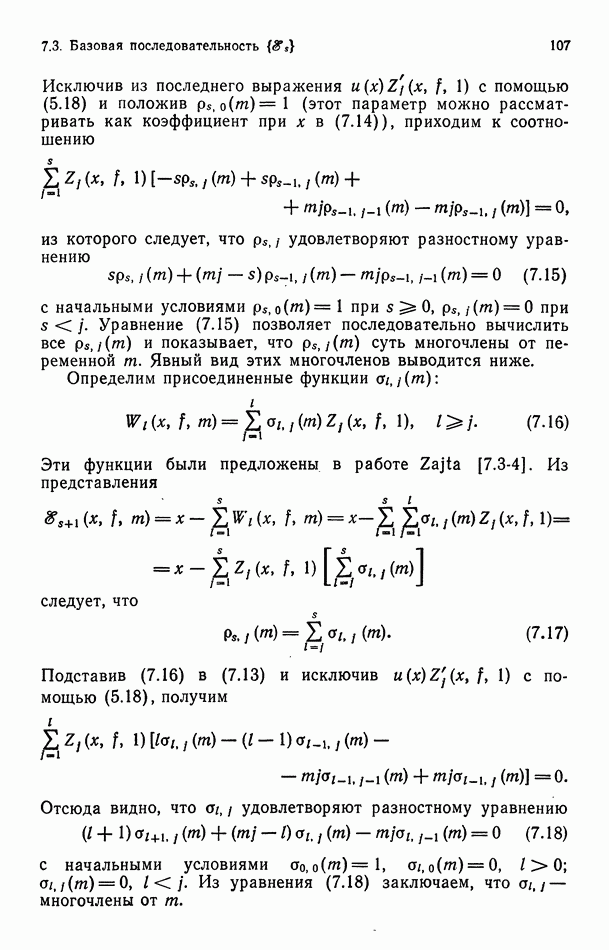| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 5. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
Эта глава посвящена теоретическим вопросам, относящимся к одноточечным ИФ. Все ИФ этого класса имеют целый порядок. В § 5.1 подробно рассматривается конкретная базовая последовательность  Использование
Использование  в качестве эталона позволяет выявить ряд характерных свойств всех одноточечных ИФ. Теорему 5.3 мы считаем основной теоремой об одноточечных ИФ.
в качестве эталона позволяет выявить ряд характерных свойств всех одноточечных ИФ. Теорему 5.3 мы считаем основной теоремой об одноточечных ИФ.
5.1. БАЗОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Напомним определение базовой последовательности. Базовой Последовательностью ИФ называется бесконечная последовательность ИФ,  член которой имеет порядок
член которой имеет порядок  Техника по строения базовых последовательностей рассматривается в работах Bodewig [5.1-1], Curry [5.1-2], Ehrmann [5.1-3], Е. Schroder [5.1-4], Schwerdtfeger [5.1-5], Whittaker [5.1-6], Durand [5.1-7], Householder [5.1-8, Chap. 3], Korganoff [5.1-9, Chap. 3], Ludwig [5.1-10], Ostrowski [5.Ы1, Appendix J], Zajta [5.1-12], а также в работах других авторов. Из теоремы 2.6 следует, что различные ИФ порядка
Техника по строения базовых последовательностей рассматривается в работах Bodewig [5.1-1], Curry [5.1-2], Ehrmann [5.1-3], Е. Schroder [5.1-4], Schwerdtfeger [5.1-5], Whittaker [5.1-6], Durand [5.1-7], Householder [5.1-8, Chap. 3], Korganoff [5.1-9, Chap. 3], Ludwig [5.1-10], Ostrowski [5.Ы1, Appendix J], Zajta [5.1-12], а также в работах других авторов. Из теоремы 2.6 следует, что различные ИФ порядка  отличаются друг от друга только членами порядка
отличаются друг от друга только членами порядка  Поэтому знание свойств какой-либо одной ИФ порядка
Поэтому знание свойств какой-либо одной ИФ порядка  позволяет вывести многие свойства произвольной ИФ этого порядка. Зная свойства базовой последовательности ИФ, можно вывести многие свойства ИФ произвольного порядка. В п. 5.1.1 мы изучим базовую последовательность ИФ относительно простой структуры, удобную для сравнений.
позволяет вывести многие свойства произвольной ИФ этого порядка. Зная свойства базовой последовательности ИФ, можно вывести многие свойства ИФ произвольного порядка. В п. 5.1.1 мы изучим базовую последовательность ИФ относительно простой структуры, удобную для сравнений.
5.1.1. Формула для E2.
ИФ  были введены и изучались в п. 4.2.2; в случае
были введены и изучались в п. 4.2.2; в случае  они не имеют «памяти». Ввиду особой важности ИФ
они не имеют «памяти». Ввиду особой важности ИФ  используем для них специальное обозначение
используем для них специальное обозначение  Условия сходимости порождаемой
Условия сходимости порождаемой  итерационной последовательности были сформулированы в п. 4.2.2; здесь мы предполагаем выполнение этих условий. В отличие от общего случая, потребовавшего сложных рассуждений, доказательство того, что
итерационной последовательности были сформулированы в п. 4.2.2; здесь мы предполагаем выполнение этих условий. В отличие от общего случая, потребовавшего сложных рассуждений, доказательство того, что  имеет порядок
имеет порядок  оказывается почти тривиальным.
оказывается почти тривиальным.
Для независимости относящегося к  материала нам придется снова привести здесь отдельные сведения. Пусть
материала нам придется снова привести здесь отдельные сведения. Пусть  не обращается в нуль в окрестности а, а производная
не обращается в нуль в окрестности а, а производная  непрерывна в этой окрестности. Тогда функция
непрерывна в этой окрестности. Тогда функция  обратима, причем
обратима, причем
производная  обратной функции непрерывна в окрестности нуля. Обозначим через
обратной функции непрерывна в окрестности нуля. Обозначим через  многочлен, первые
многочлен, первые  производных которого совпадают с соответствующими производными функции в точке
производных которого совпадают с соответствующими производными функции в точке  Тогда
Тогда

где  расположено между у и
расположено между у и  Положим
Положим  при этом
при этом

или

Кроме того,

где 
В (5.2) функция  записана в виде ряда по степеням
записана в виде ряда по степеням  В приложениях иногда бывает удобнее представление
В приложениях иногда бывает удобнее представление  в виде ряда по степеням и, где
в виде ряда по степеням и, где  Этот ряд имеет вид
Этот ряд имеет вид

Поскольку в практических задачах функция  неизвестна, следует выразить
неизвестна, следует выразить  через функцию
через функцию  и ее производные. Полагая
и ее производные. Полагая

получаем

Поэтому

Формально полагая в  получаем соотношение
получаем соотношение

Свойства  рассматриваются в п. 5.1.3.
рассматриваются в п. 5.1.3.
Предположим, что  не обращается в нуль в окрестности нуля. В силу равенства (5.5)
не обращается в нуль в окрестности нуля. В силу равенства (5.5)

Поскольку  имеем
имеем

Пусть  . Тогда (5.8) принимает вид
. Тогда (5.8) принимает вид 
Таким образом, порядок итерационной функции  равен
равен  а ее константа асимптотики погрешности равна
а ее константа асимптотики погрешности равна  Поскольку объем информационного запроса
Поскольку объем информационного запроса  также равен
также равен  то эффективность использования информации этой ИФ равна единице. Следовательно,
то эффективность использования информации этой ИФ равна единице. Следовательно,  образуют оптимальную базовую последовательность (определения этих терминов были даны в п. 1.2.4).
образуют оптимальную базовую последовательность (определения этих терминов были даны в п. 1.2.4).
Нетрудно видеть, что  где
где 
В работе Bodewig [5.1-13] открытие  приписывается Эйлеру (Euler [5.1-14]). Советские исследователи отдают первенство в этом вопросе Чебышеву, написавшему в студенческие годы работу «Calcul des racines d’une equation», удостоенную серебряной медали. С этой работой, выполненной в 1837 или 1838 г., нам не удалось ознакомиться
приписывается Эйлеру (Euler [5.1-14]). Советские исследователи отдают первенство в этом вопросе Чебышеву, написавшему в студенческие годы работу «Calcul des racines d’une equation», удостоенную серебряной медали. С этой работой, выполненной в 1837 или 1838 г., нам не удалось ознакомиться 
Покажем, что предложенная в работе Е. Schroder [5.1-15]j формула задает эквивалентную  ИФ. В самом деле,
ИФ. В самом деле,

Поэтому (5.2) можно представить в виде

что совпадает с формулой Шрёдера из указанной работы; ср. с формулой для ряда Бирмана, предложенной в книге Hildebrand [5.1-16, р. 25].
5.1.2. Один пример.
В некоторых случаях удается показать, что полученный из формальных соображений ряд (5.7) сходится к а. Метод решения квадратных уравнений с помощью рядов изучается в работе Е. Schroder [5.1-17].
Пример 5.1. Пусть  где
где  целое. Тогда при
целое. Тогда при  получаем формулу для корня
получаем формулу для корня  степени, а при
степени, а при  формулу для
формулу для  Обратная к
Обратная к  функция имеет вид
функция имеет вид  а производные
а производные  выражаются формулой
выражаются формулой

В этом случае (5.2) принимает вид

В частности, 
При  из последнего соотношения получается формула Ньютона — Херона для приближенного вычисления квадратных корней. Формула (5.9) была выведена в статье
из последнего соотношения получается формула Ньютона — Херона для приближенного вычисления квадратных корней. Формула (5.9) была выведена в статье  с использованием биномиального разложения. При
с использованием биномиального разложения. При  получаем соотношения
получаем соотношения

При  эта геометрическая прогрессия сходится к
эта геометрическая прогрессия сходится к  В статье
В статье  отмечается, что (5.10) можно использовать для деления чисел с многократной точностью.
отмечается, что (5.10) можно использовать для деления чисел с многократной точностью.
Построение аппроксимаций посредством итераций  рассматривается в работе
рассматривается в работе  ].
].
5.1.3. Свойства Es.
Выше мы определили  соотношениями
соотношениями

Нетрудно показать, что  удовлетворяют дифференциальноразностному уравнению
удовлетворяют дифференциальноразностному уравнению

Несколько первых  можно вычислить непосредственно из этого уравнения.
можно вычислить непосредственно из этого уравнения.
Явное представление для  выводится с помощью формулы для производной обратной функции
выводится с помощью формулы для производной обратной функции

где  , а суммирование ведется по всевозможным наборам неотрицательных целых
, а суммирование ведется по всевозможным наборам неотрицательных целых  для которых
для которых

(подробности см. в приложении В). Если  то полагаем
то полагаем  для всех
для всех  Из определения
Из определения  и (5.12) следует Теорема 5.1. Пусть
и (5.12) следует Теорема 5.1. Пусть

где  и суть взаимно обратные функции. Тогда
и суть взаимно обратные функции. Тогда

где  и суммирование ведется по всевозможным наборам неотрицательных целых
и суммирование ведется по всевозможным наборам неотрицательных целых  для которых
для которых 
Значения  для некоторых
для некоторых  приведены в табл. 5.1. Заметим, что
приведены в табл. 5.1. Заметим, что  зависят от производных функции
зависят от производных функции  и не зависят от самой
и не зависят от самой  Поэтому
Поэтому

Таблица 5.1. Выражения для 

где  а внутренняя сумма берется по всевозможным набором неотрицательных целых
а внутренняя сумма берется по всевозможным набором неотрицательных целых 
Заменяя верхний предел суммирования во внешней сумме на  получаем формальное представление для а в виде бесконечного ряда.
получаем формальное представление для а в виде бесконечного ряда.
Приведем формулы для  при малых
при малых 

Сформулируем несколько очевидных следствий теоремы 5.1.
Следствие а.  многочлен от переменных
многочлен от переменных 
Следствие Ь. Многочлен, выражающий  через
через  совпадает с многочленом, выражающим
совпадает с многочленом, выражающим  через
через 
Следствие с. Сумма коэффициентов этого многочлена равна единице.
Доказательство. Пусть  Очевидно, при
Очевидно, при  все
все  равны единице. Обратная для
равны единице. Обратная для  функция имеет вид
функция имеет вид  и если
и если  то
то  . Легко подсчитать, что при
. Легко подсчитать, что при  все
все  равны единице.
равны единице.
Следствие d. А присутствуют в формуле для  только в виде
только в виде 
Для удобства приложений введем обозначение

Тогда 

Следствие е. Справедливо представление

где суммирование ведется по целочисленным наборам  для которых
для которых  Таким образом,
Таким образом,  однородный многочлен нулевой степени.
однородный многочлен нулевой степени.
Нетрудно показать, что  удовлетворяют дифференциальноразностному уравнению
удовлетворяют дифференциальноразностному уравнению

С помощью оператора восходящей разности А это уравнение можно записать в виде

В леммах 5.1, 5.2 и теореме 5.2 мы воспользуемся тем обстоятельством, что  имеет порядок
имеет порядок  Следующая лемма устанавливает связь между константами асимптотики погрешности
Следующая лемма устанавливает связь между константами асимптотики погрешности  и произвольной ИФ порядка
и произвольной ИФ порядка 
Лемма 5.1. Пусть  —произвольная ИФ порядка
—произвольная ИФ порядка  с константой асимптотики погрешности С. Положим
с константой асимптотики погрешности С. Положим  Тогда
Тогда 
Доказательство. Положим  и воспользуемся теоремой 2.8, заметив, что константа асимптотики погрешности для
и воспользуемся теоремой 2.8, заметив, что константа асимптотики погрешности для  равна
равна 
Более полезный результат содержит
Лемма 5.2. Пусть  произвольная ИФ порядка
произвольная ИФ порядка  с константой асимптотики погрешности С,
с константой асимптотики погрешности С,

Тогда 
Доказательство. Из предыдущей леммы с учетом равенства  получаем
получаем

Пример 5.2. Рассмотрим ИФ Хэлли  которая будет получена в п. 5.2.1. Поскольку
которая будет получена в п. 5.2.1. Поскольку  нетрудно показать, что
нетрудно показать, что  Поэтому
Поэтому 
Для ИФ целого порядка порядок и константу асимптотики погрешности можно вычислять с помощью теоремы 2.2, которую, однако, удобно применять только для простейших ИФ. Следующая теорема позволяет находить порядок и константу асимптотики погрешности ИФ путем сравнения с  Эта теорема окажется особенно полезной в гл. 9.
Эта теорема окажется особенно полезной в гл. 9.
Теорема 5.2. Итерационная функция  имеет порядок
имеет порядок  в том и только том случае, если существует и не равен нулю предел
в том и только том случае, если существует и не равен нулю предел

Кроме того, этот предел равен константе асимптотики погрешности функции 
Доказательство. На основании (5.6) заключаем, что  Поэтому
Поэтому

Учитывая, что  получаем
получаем

Отметим, что в формулировке теоремы 5.2 участвуют ИФ, порядки которых различаются на единицу, в то время как в формулировках лемм 5.1 и 5.2 фигурируют ИФ одинакового порядка.
В п. 5.5.1 используется
Лемма 5.3. 
Доказательство. Ввиду (5.18)

откуда после очевидных упрощений получаем

Поскольку 

Равенство  завершает доказательство. Я
завершает доказательство. Я
Пример 5.3. Пусть  Тогда
Тогда

и вместе с тем

| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- 1.2.2. Классификация итерационных функций.
- 1.2.3. Порядок.
- 1.2.4. Понятия, относящиеся к порядку.
- ГЛАВА 2. ОБЩИЕ ТЕОРЕМЫ ОБ ИТЕРАЦИОННЫХ ФУНКЦИЯХ
- 2.1. РЕШЕНИЕ ЗАДАЧИ О НЕПОДВИЖНОЙ ТОЧКЕ
- 2.2. ЛИНЕЙНАЯ И СВЕРХЛИНЕЙНАЯ СХОДИМОСТЬ
- 2.3. ИТЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
- ГЛАВА 3. МАТЕМАТИКА РАЗНОСТНЫХ ОТНОШЕНИЙ
- 3.1. О СХОДИМОСТИ РЕШЕНИЙ РАЗНОСТНЫХ НЕРАВЕНСТВ
- 3.2. ТЕОРЕМА О РЕШЕНИЯХ НЕКОТОРЫХ НЕОДНОРОДНЫХ РАЗНОСТНЫХ УРАВНЕНИЙ
- 3.3. О КОРНЯХ НЕКОТОРЫХ ХАРАКТЕРИСТИЧЕСКИХ УРАВНЕНИЙ
- 3.4. АСИМПТОТИЧЕСКИЕ СВОЙСТВА РЕШЕНИЙ НЕКОТОРЫХ РАЗНОСТНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ИНТЕРПОЛЯЦИОННЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 4.1. ИНТЕРПОЛЯЦИЯ И РЕШЕНИЕ УРАВНЕНИЙ
- 4.2. ПОРЯДОК ИНТЕРПОЛЯЦИОННЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 4.3. ПРИМЕРЫ
- ГЛАВА 5. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 5.2. РАЦИОНАЛЬНЫЕ АППРОКСИМАЦИИ Es
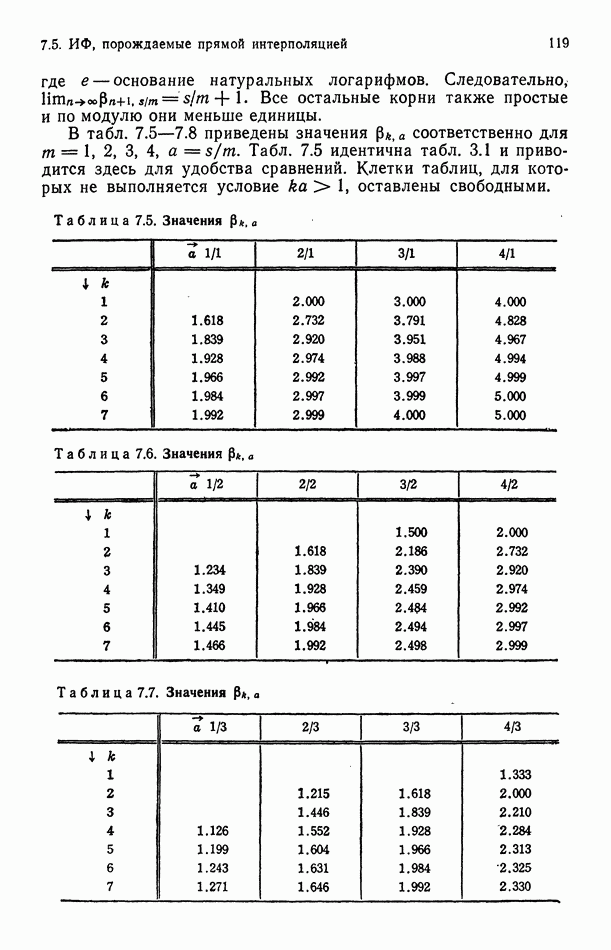
- 5.3. БАЗОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ИТЕРАЦИОННЫХ ФУНКЦИЙ, ПОРОЖДАЕМЫХ ПРЯМОЙ ИНТЕРПОЛЯЦИЕЙ
- 5.4. ОСНОВНАЯ ТЕОРЕМА ОБ ОДНОТОЧЕЧНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЯХ
- 5.5. КОЭФФИЦИЕНТЫ РЯДОВ ДЛЯ ПОГРЕШНОСТЕЙ ИТЕРАЦИОННЫХ ФУНКЦИЙ Es
- ГЛАВА 6. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 6.2. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ, ПОРОЖДАЕМЫЕ АППРОКСИМАЦИЕИ ПРОИЗВОДНОЙ
- 6.3. ОБСУЖДЕНИЕ ОДНОТОЧЕЧНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ С ПАМЯТЬЮ
- ГЛАВА 7. КРАТНЫЕ КОРНИ
- 7.2. ПОРЯДОК ИТЕРАЦИОННЫХ ФУНКЦИЙ Es
- 7.3. БАЗОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- 7.4. КОЭФФИЦИЕНТЫ РЯДОВ ДЛЯ ПОГРЕШНОСТЕЙ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 7.5. ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ ПРЯМОЙ ИНТЕРПОЛЯЦИЕЙ
- 7.6. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 7.7. НЕКОТОРЫЕ ОБЩИЕ РЕЗУЛЬТАТЫ
- 7.8. ИТЕРАЦИОННАЯ ФУНКЦИЯ НЕИЗМЕРИМОГО ПОРЯДКА
- ГЛАВА 8. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 8.2. ОДНА ЗАДАЧА ИНТЕРПОЛЯЦИИ
- 8.3. РЕКУРРЕНТНО ГЕНЕРИРУЕМЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 8.4. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ АППРОКСИМАЦИЕЙ ПРОИЗВОДНОЙ
- 8.5. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, ПОРОЖДАЕМЫЕ СУПЕРПОЗИЦИЕЙ
- 8.6. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- ГЛАВА 9. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ. ПРОДОЛЖЕНИЕ
- 9.2. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ ПЕРВОГО ТИПА
- 9.3. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ ВТОРОГО ТИПА
- 9.4. ОБСУЖДЕНИЕ КРИТЕРИЕВ ВЫБОРА ИТЕРАЦИОННОЙ ФУНКЦИИ
- ГЛАВА 10. ИТЕРАЦИОННЫЕ ФУНКЦИИ, НЕ ИСПОЛЬЗУЮЩИЕ ЗНАЧЕНИЙ ПРОИЗВОДНЫХ
- 10.2. ИНТЕРПОЛЯЦИОННЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 10.3. НЕКОТОРЫЕ ДРУГИЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- ГЛАВА 11. СИСТЕМЫ УРАВНЕНИЙ
- 11.2. ПОСТРОЕНИЕ ВЕКТОРНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ ПРИ ПОМОЩИ ОБРАТНОЙ ИНТЕРПОЛЯЦИИ
- 11.3. ОЦЕНКИ ПОГРЕШНОСТЕЙ НЕКОТОРЫХ ВЕКТОРНЫХ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 11.4. ВЕКТОРНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ, НЕ ИСПОЛЬЗУЮЩИЕ ЗНАЧЕНИЙ ПРОИЗВОДНЫХ
- ГЛАВА 12. ПЕРЕЧЕНЬ ИТЕРАЦИОННЫХ ФУНКЦИЙ
- 12.2. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 12.3. ОДНОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 12.4. КРАТНЫЕ КОРНИ
- 12.5. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ
- 12.6. МНОГОТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ ФУНКЦИИ С ПАМЯТЬЮ
- 12.7. СИСТЕМЫ УРАВНЕНИЙ
- ПРИЛОЖЕНИЕ А. ИНТЕРПОЛЯЦИЯ
- А.2. ЗАДАЧА ИНТЕРПОЛЯЦИИ И ЕЕ РЕШЕНИЕ
- А.3. СЛУЧАЙ СТАНДАРТНОЙ ИНФОРМАЦИИ
- А.4. АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ
- А.5. ПОГРЕШНОСТЬ АППРОКСИМАЦИИ ПРОИЗВОДНЫХ
- ПРИЛОЖЕНИЕ В. О J-Й ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
- ПРИЛОЖЕНИЕ С. ВЕРНЫЕ ЦИФРЫ И ВЫЧИСЛИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ
- ПРИЛОЖЕНИЕ D. УСКОРЕНИЕ СХОДИМОСТИ
- D.2. «дельта2»-ПРЕОБРАЗОВАНИЕ ЭЙТКЕНА
- D.3. ИТЕРАЦИОННАЯ ФУНКЦИЯ СТЕФФЕНСОНА — ХАУСХОЛДЕРА — ОСТРОВСКОГО
- ПРИЛОЖЕНИЕ Е. ЧИСЛЕННЫЕ ПРИМЕРЫ
- ПРИЛОЖЕНИЕ F. НАПРАВЛЕНИЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ
- ЛИТЕРАТУРА