| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
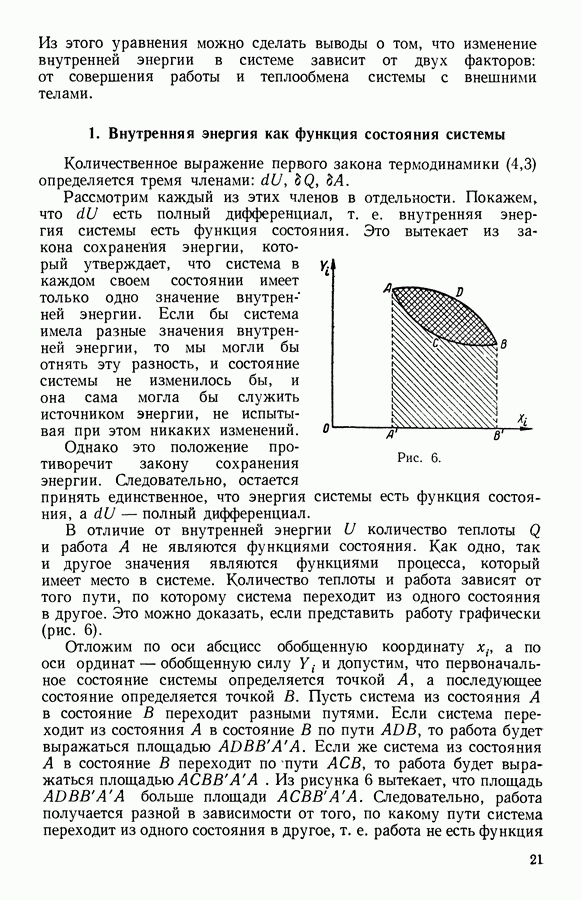
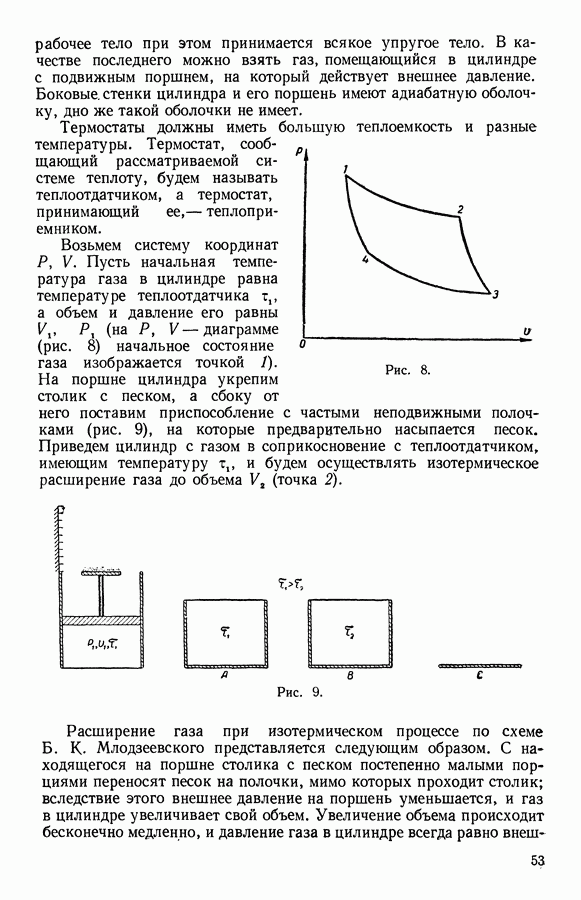
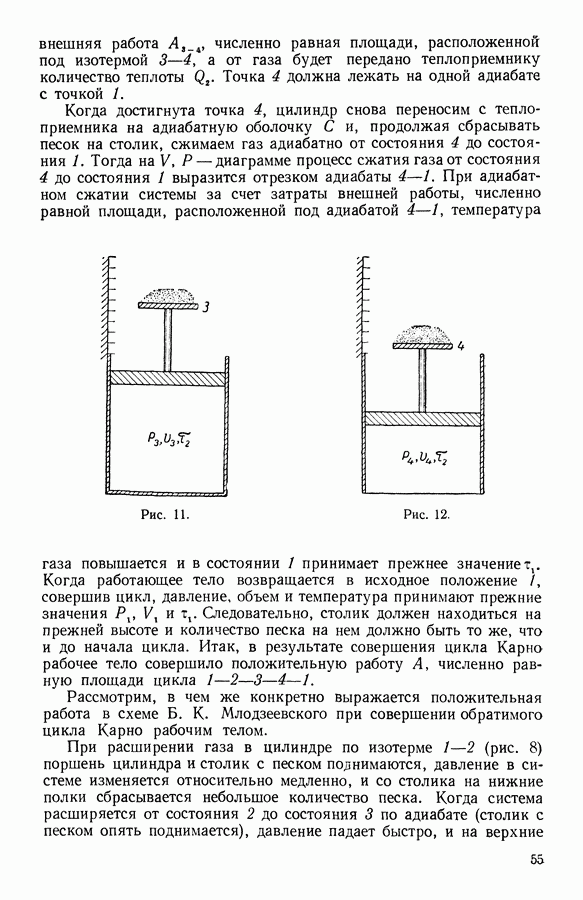
10. Работа
Понятие «работа», которую совершает система при изменении своего состояния, имеет важное значение в выводах термодинамики. Энгельс дал следующее определение работы: «Работа — это изменение формы движения, рассматриваемое с его количественной стороны» (Энгельс, Диалектика природы). Количественно она может быть определена лишь тогда, когда рассматриваемая система взаимодействует с внешними телами. Система совершает отличную от нуля работу только при перемещении внешних тел.
Опыт показывает, что различные тела (системы), взаимодействуя между собой, передают друг другу некоторое количество энергии. В процессе изменения состояния какой-либо системы она получает или, наоборот, отдает другим системам определенное количество энергии. Этот способ передачи энергии от одного тела (системы) к другому может состоять в совершении работы одного тела над другим. В этом случае увеличение энергии тела равно работе, произведенной над ним.
Количественное выражение работы в общем виде можно представить следующей формулой:

где  - бесконечно малая величина работы, причем знак
- бесконечно малая величина работы, причем знак  указывает, что
указывает, что  не есть полный дифференциал,
не есть полный дифференциал,  -обобщенная сила (давление
-обобщенная сила (давление  , напряженность магнитного поля
, напряженность магнитного поля  напряженность электрического поля
напряженность электрического поля  ),
),
 обобщенная координата (объем V, магнитный момент
обобщенная координата (объем V, магнитный момент  вектор поляризации диэлектрика
вектор поляризации диэлектрика  и т. д.).
и т. д.).
Исходя из общего определения работы, посмотрим на ряде примеров, как выражается работа в различных случаях. Начнем
рассмотрение с однородных систем, имеющих одинаковые физические свойства в любых произвольно выбранных частях, равных по объему.
1. Допустим, что имеется находящаяся под всесторонним одинаковым внешним давлением термодинамическая система, которая характеризуется тремя макроскопическими параметрами: температурой, объемом и давлением. Тогда уравнение состояния ее будет;

где  температура, или
температура, или

Простейшее уравнение состояния, уравнение Клапейрона — Менделеева, для одного моля имеет вид:

где  универсальная газовая постоянная.
универсальная газовая постоянная.
Газ, который в точности подчиняется уравнению Клапейрона — Менделеева, называется идеальным газом.
Состояние реального газа описывается уравнением Ван-дер-Ваальса:

где  постоянные, не зависящие от температуры. Член
постоянные, не зависящие от температуры. Член  характеризует силу взаимодействия между частицами газа; член
характеризует силу взаимодействия между частицами газа; член  объем самих газовых молекул системы. Оба эти уравнения вытекают из эксперимента. Из уравнения (1,1) видно, что независимыми параметрами могут быть любые два параметра:
объем самих газовых молекул системы. Оба эти уравнения вытекают из эксперимента. Из уравнения (1,1) видно, что независимыми параметрами могут быть любые два параметра:  , или
, или  и
и  или
или  третий же параметр будет функцией двух первых.
третий же параметр будет функцией двух первых.
Сила, действующая со стороны внешних тел на элемент поверхности  системы (рис. 1), смещает его на величину
системы (рис. 1), смещает его на величину  Элементарная работа при этом будет равна:
Элементарная работа при этом будет равна:

где  — внешняя сила, отнесенная к единице поверхности, а полная работа найдется по формуле:
— внешняя сила, отнесенная к единице поверхности, а полная работа найдется по формуле:

где  изменение объема системы.
изменение объема системы.
В случае равновесных процессов, т. е. термодинамических процессов, при которых система проходит непрерывный ряд равновесных состояний,

а работа расширения или сжатия равна:

Необходимо условиться относительно знака работы.
Работу будем считать положительной, если система совершает ее над внешними телами, и отрицательной, если, наоборот, внешние тела совершают работу над системой.
2. Рассмотрим стержень, один конец которого закреплен, а на другой действует растягивающая сила  величина которой ниже предела упругости стержня (рис. 2). Длина стержня I является функцией силы
величина которой ниже предела упругости стержня (рис. 2). Длина стержня I является функцией силы  и температуры.
и температуры.

Рис. 1.

Рис. 2.
Под действием силы  стержень изменяет свою длину
стержень изменяет свою длину  на величину
на величину  причем совершается работа:
причем совершается работа:

Знак минус в уравнении (1,4) объясняется тем, что работа совершается внешними телами.
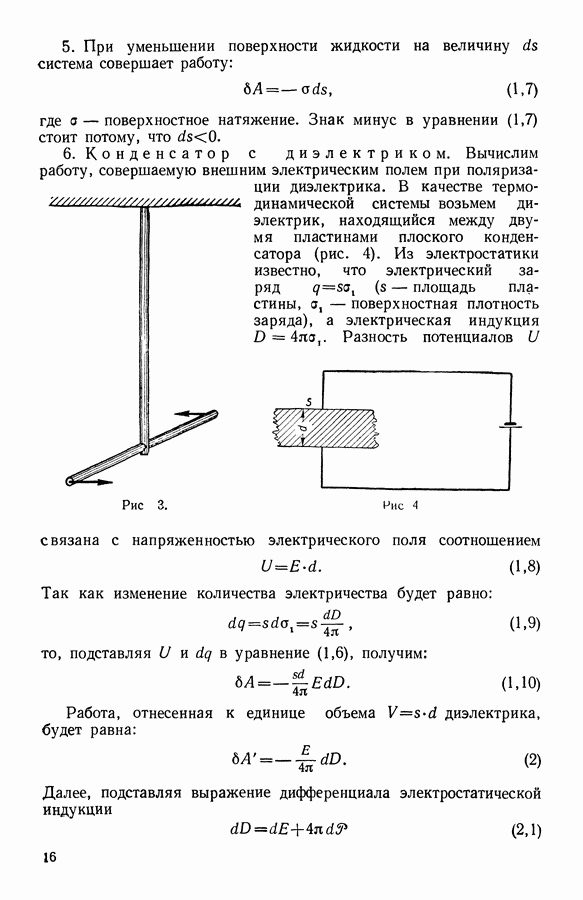
3. Под действием момента вращения  стержень закручивается на угол
стержень закручивается на угол  (рис. 3). Работа закручивания стержня на угол
(рис. 3). Работа закручивания стержня на угол  вычисляется, как и в предыдущем случае:
вычисляется, как и в предыдущем случае:

4. Работа, которую нужно совершить при переносе электрического заряда  между двумя точками с разностью потенциалов и, равна:
между двумя точками с разностью потенциалов и, равна:

5. При уменьшении поверхности жидкости на величину  система совершает работу:
система совершает работу:

где  поверхностное натяжение. Знак минус в уравнении (1,7) стоит потому, что
поверхностное натяжение. Знак минус в уравнении (1,7) стоит потому, что 
6. Конденсатор с диэлектриком. Вычислим работу, совершаемую внешним электрическим полем при поляризации диэлектрика. В качестве термодинамической системы возьмем диэлектрик, находящийся между двумя пластинами плоского конденсатора (рис. 4). Из электростатики известно, что электрический заряд  площадь пластины, а, — поверхностная плотность заряда), а электрическая индукция
площадь пластины, а, — поверхностная плотность заряда), а электрическая индукция 

Рис. 3.

Рис. 4.
Разность потенциалов  связана с напряженностью электрического поля соотношением
связана с напряженностью электрического поля соотношением

Так как изменение количества электричества будет равно:

то, подставляя  в уравнение (1,6), получим:
в уравнение (1,6), получим:

Работа, отнесенная к единице объема  диэлектрика, будет равна:
диэлектрика, будет равна:

Далее, подставляя выражение дифференциала электростатической индукции

в уравнение (2), получим:

где  — поляризация единицы объема диэлектрика. Второй член последнего выражения, как мы видим, зависит от поляризации вещества:
— поляризация единицы объема диэлектрика. Второй член последнего выражения, как мы видим, зависит от поляризации вещества:

Сравнение параметров в (2,3) и (1,3) показывает, что давлению  соответствует в данном случае напряженность поля а изменению объема
соответствует в данном случае напряженность поля а изменению объема  изменение поляризации
изменение поляризации
Далее, можно по аналогии с (1,1) записать и уравнение состояния:

Действительно, опыт показывает, что между этими параметрами существует следующая функциональная зависимость:

где  коэффициент поляризации,
коэффициент поляризации,  «статическая» диэлектрическая проницаемость тела, величина которой зависит от его температуры.
«статическая» диэлектрическая проницаемость тела, величина которой зависит от его температуры.
7. Совершенно таким же образом можно вычислить работу внешнего поля при намагничивании единицы объема магнетика:

где  напряженность магнитного поля,
напряженность магнитного поля,  магнитная индукция,
магнитная индукция,  магнитная проницаемость. Вектор магнитной индукции равен:
магнитная проницаемость. Вектор магнитной индукции равен:

где  величина намагниченности единицы объема магнетика. Отсюда
величина намагниченности единицы объема магнетика. Отсюда

Если мы подставим эту формулу в (2,6), то будем иметь

Это уравнение показывает, что второй член выражения (2,9) зависит от намагниченности вещества:

Сравнение параметров уравнений (3) и (1,3) показывает, что давлению  соответствует напряженность поля
соответствует напряженность поля  а изменению объема
а изменению объема  изменение вектора намагниченности
изменение вектора намагниченности  Это сравнение позволяет написать аналогичное (1,1) уравнение состояния для магнетика:
Это сравнение позволяет написать аналогичное (1,1) уравнение состояния для магнетика:

Исходя из закона Кюри, выведенного для идеального магнетика, можно записать:

или

где  постоянная величина.
постоянная величина.
Таким образом, и в данном случае опыт обнаруживает отмеченную выше функциональную зависимость между величинами  их.
их.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
- 11. Количественная формулировка второго закона
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
- 15. Температурная шкала идеального газа
- 16. Абсолютная газовая шкала температур
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
- 16. Возрастание энтропии при расширении газа в пустоту
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- 1. Фазовые превращения в однокомпонентных системах
- 2. Фазовые превращения первого рода
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
- 4. Фазовые превращения второго рода
- 5. Термодинамическая теория фазовых превращений второго рода
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
- 9. Сверхпроводящее состояние металлов
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
- 12. О взаимной растворимости жидкостей
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
- 17. Первый закон Д. П. Коновалова
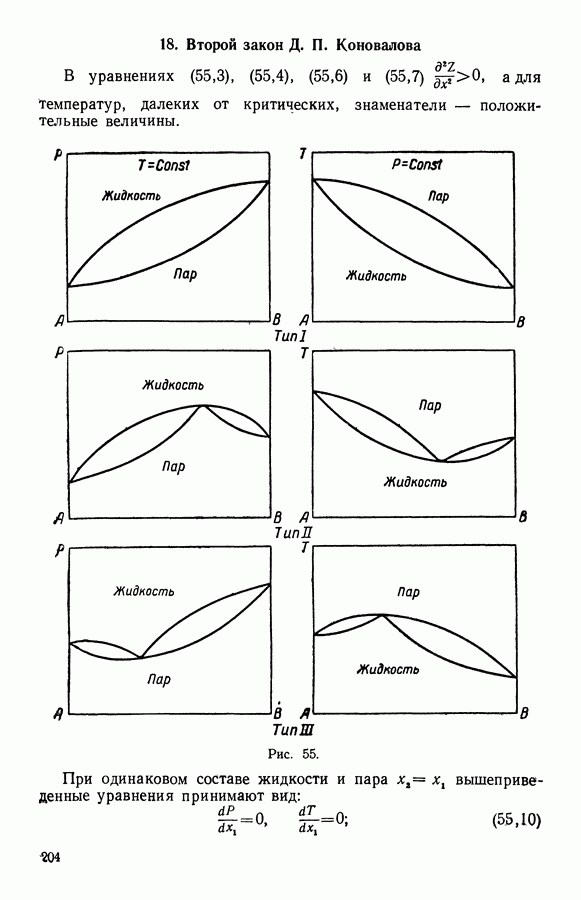
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
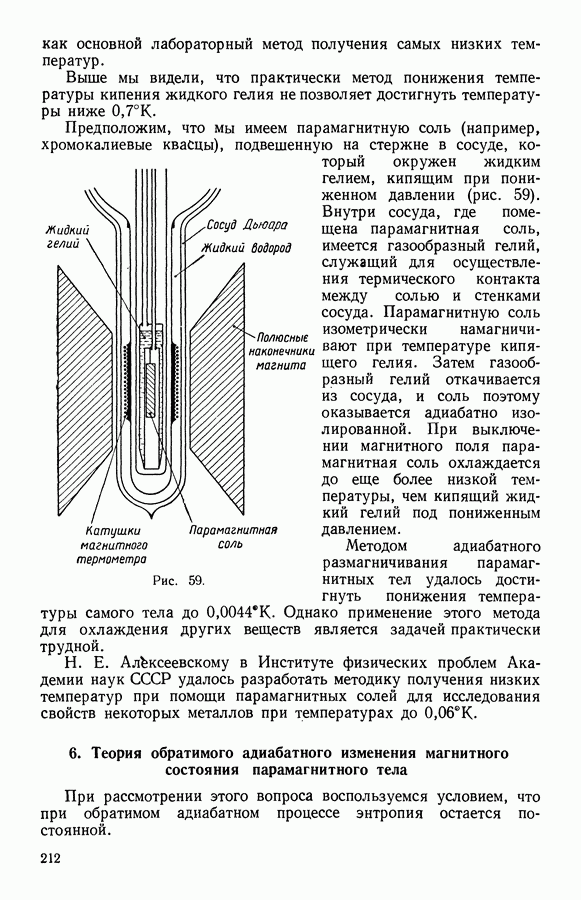
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
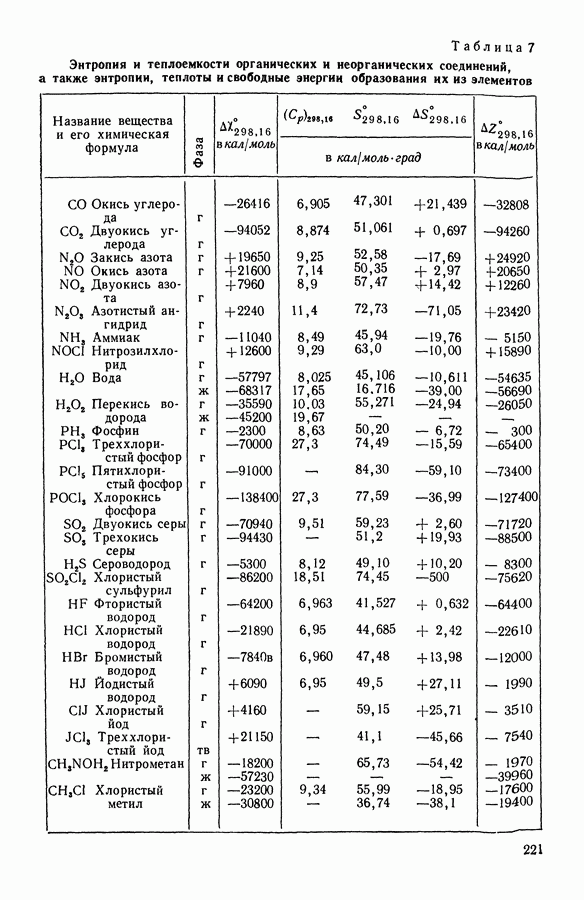
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса