| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Энтропия как функция T и Y
Полный дифференциал энтропии равен:

Найдем, далее, частные производные  принимая во внимание, что на основании уравнения (20,4) частная производная
принимая во внимание, что на основании уравнения (20,4) частная производная

Для определения частной производной (1 можно воспользоваться втором началом термодинамики, выведенным для обратимых процессов:

где  теплоемкость при постоянной обобщенной силе. Учитывая, что
теплоемкость при постоянной обобщенной силе. Учитывая, что

и подставляя частные производные  в уравнение (23), нетрудно получить:
в уравнение (23), нетрудно получить:

Используем теперь уравнение (15,9) для нахождения дифференциала энтальпии в переменных  :
:

Подставляя вместо  его значение, найдем:
его значение, найдем:

Сравнивая коэффициенты при дифференциалах  в выражении полного дифференциала энтальпии
в выражении полного дифференциала энтальпии

находим, что

Попытаемся применить полученные соотношения к конкретным системам.
1. Для системы, в которой обобщенная сила есть давление  а обобщенная координата является объемом
а обобщенная координата является объемом 
уравнения (23,3), (23,4), (23,6) и (23,7) запишутся в следующем виде;

2. При  найденные для общего случая уравнения получают следующие выражения:
найденные для общего случая уравнения получают следующие выражения:

3. Для системы, где обобщенная сила есть внешняя сила действующая на стержень, а обобщенная координата является длиной стержня  из уравнений, выведенных для общего случая, получаем новые выражения:
из уравнений, выведенных для общего случая, получаем новые выражения:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
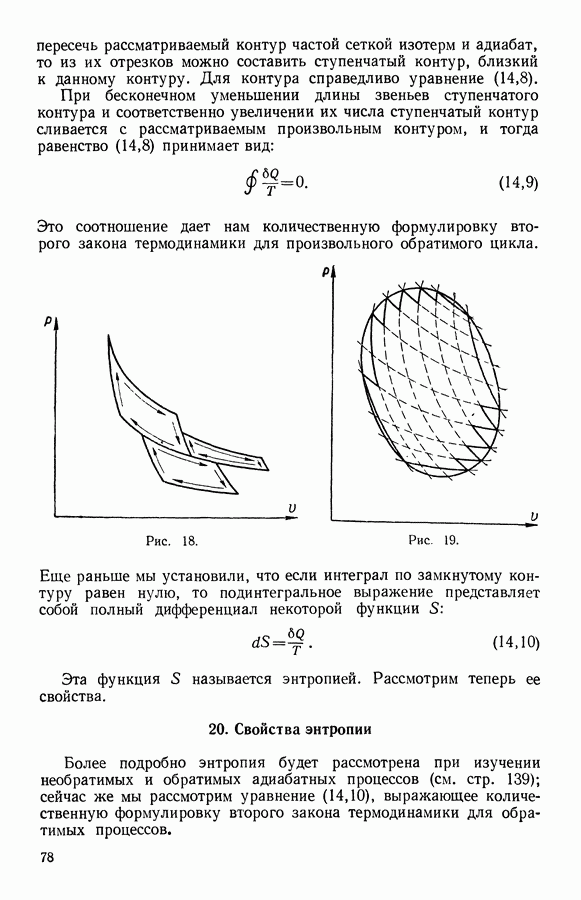
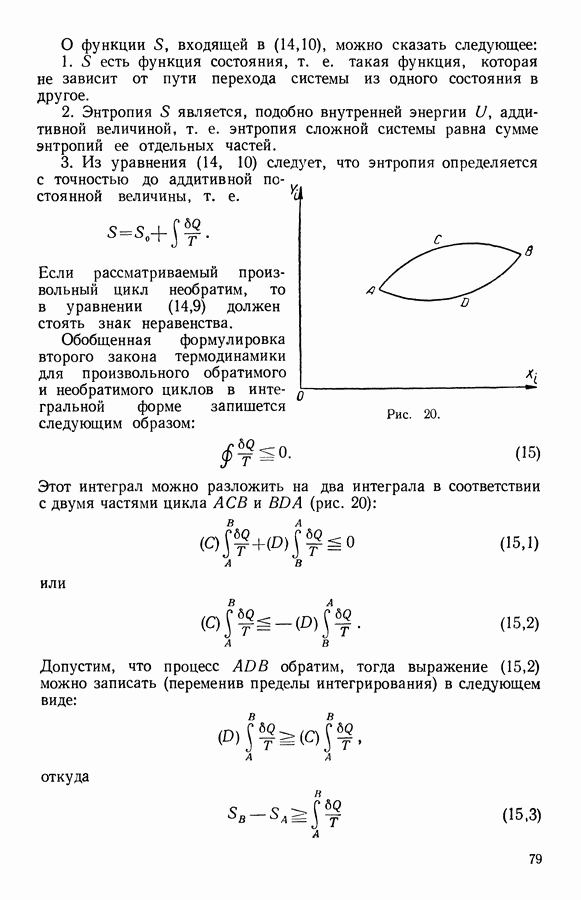
- 11. Количественная формулировка второго закона
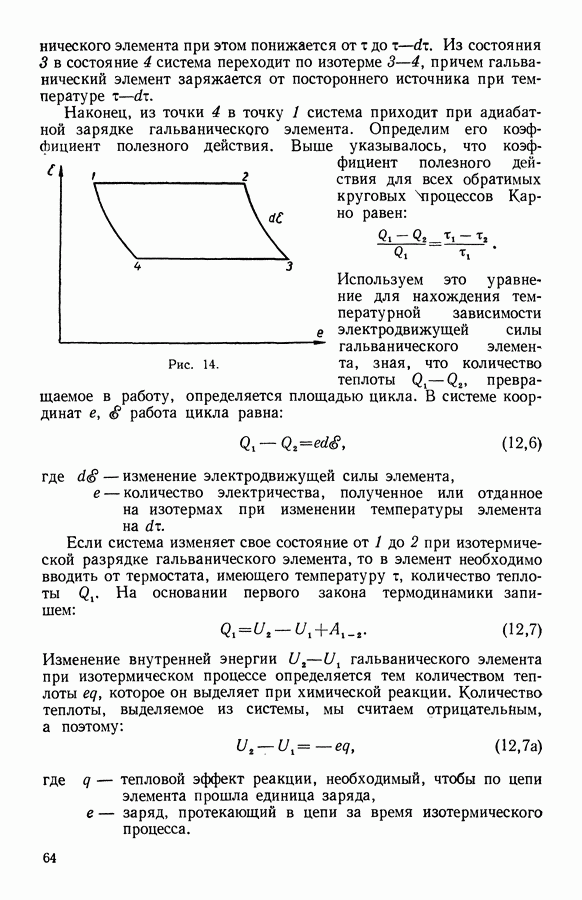
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
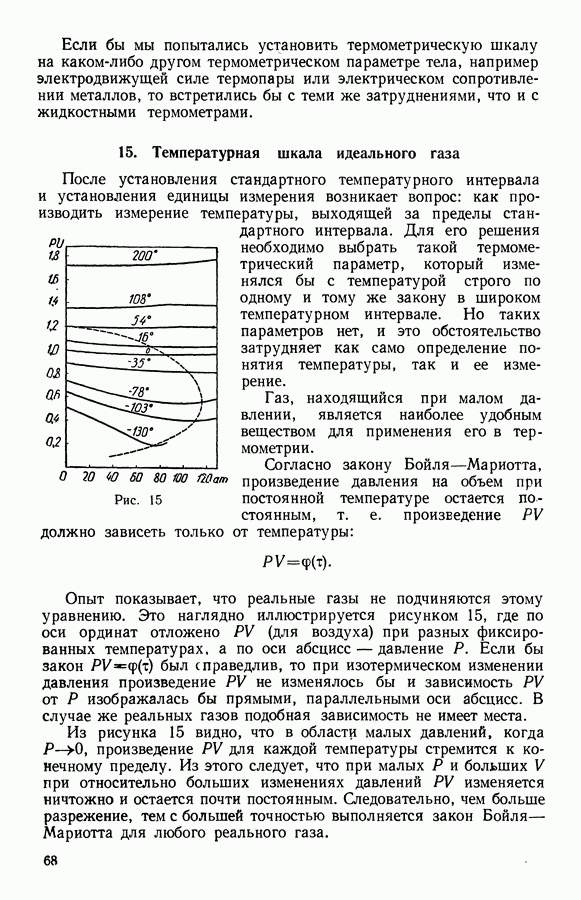
- 15. Температурная шкала идеального газа
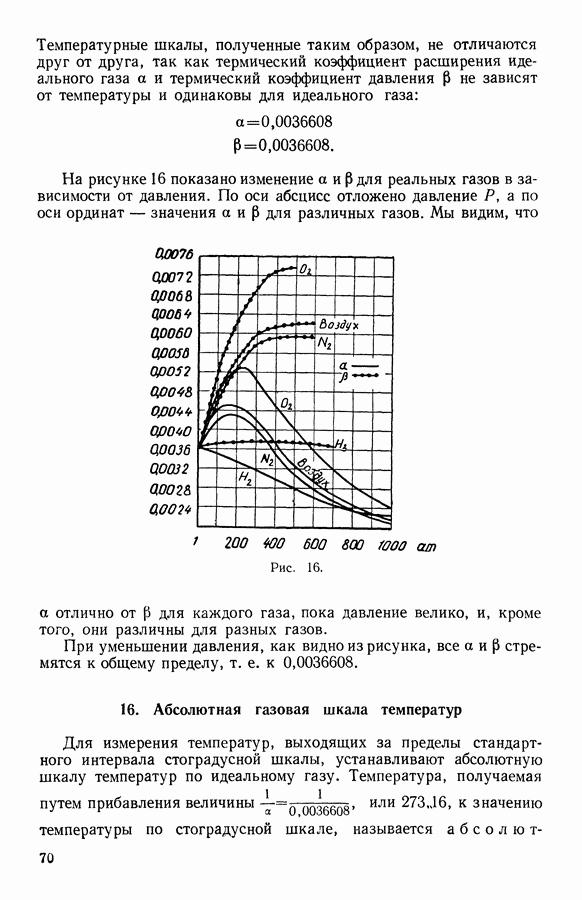
- 16. Абсолютная газовая шкала температур
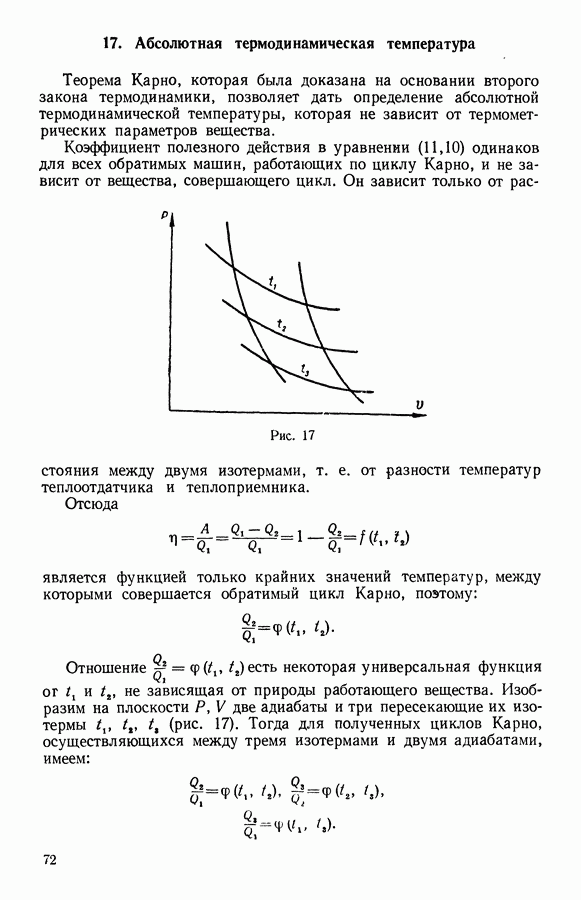
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
- 16. Возрастание энтропии при расширении газа в пустоту
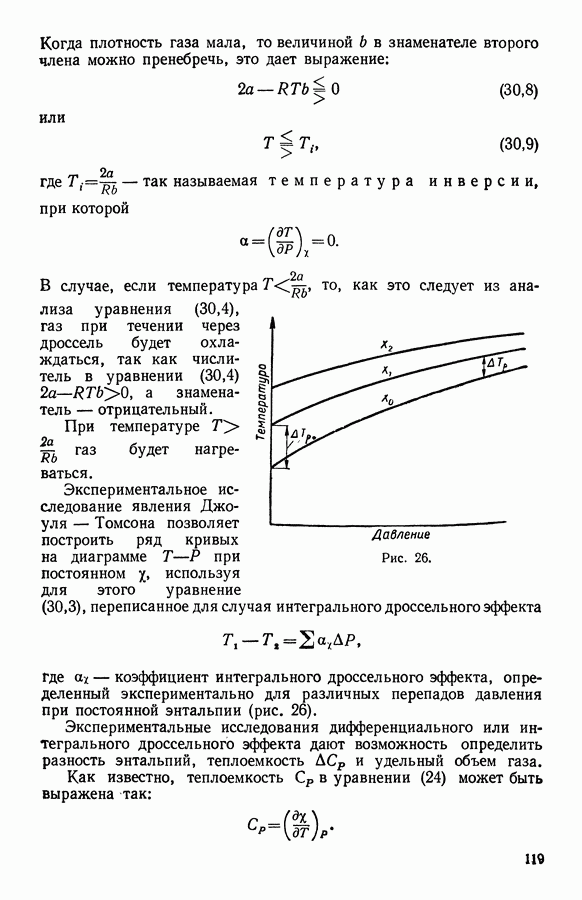
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- 1. Фазовые превращения в однокомпонентных системах
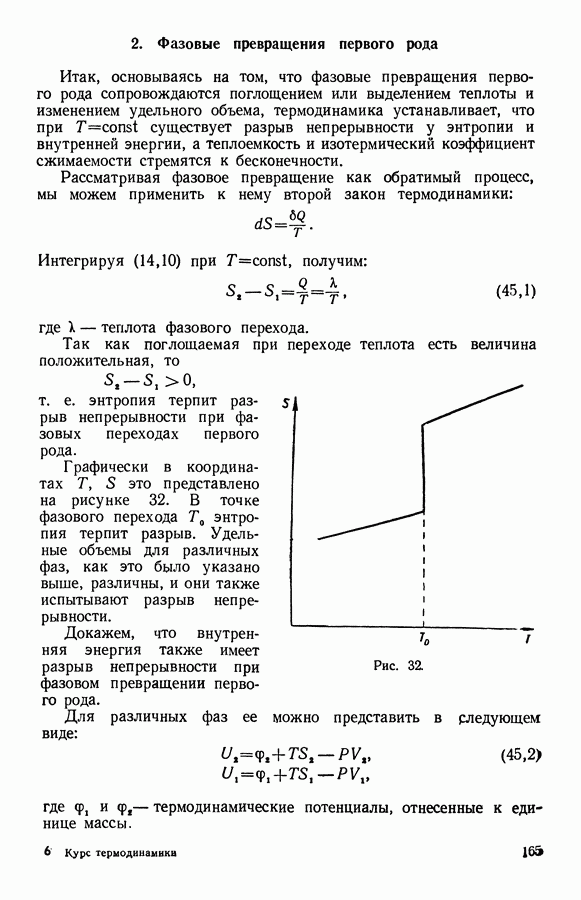
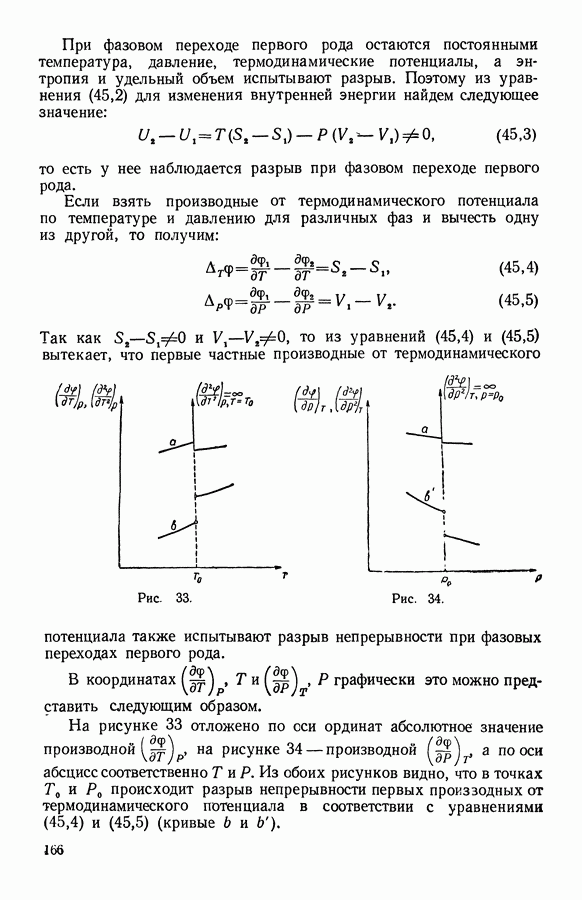
- 2. Фазовые превращения первого рода
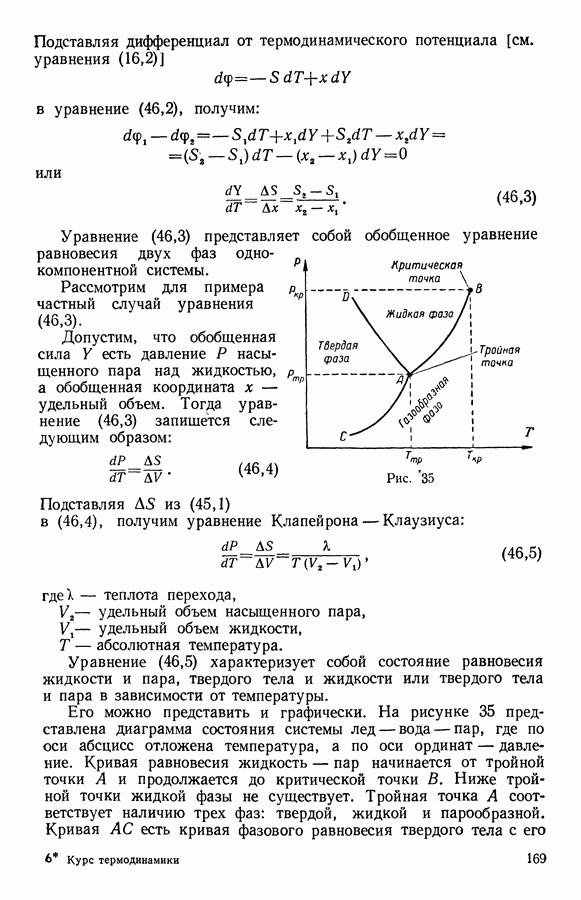
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
- 4. Фазовые превращения второго рода
- 5. Термодинамическая теория фазовых превращений второго рода
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
- 9. Сверхпроводящее состояние металлов
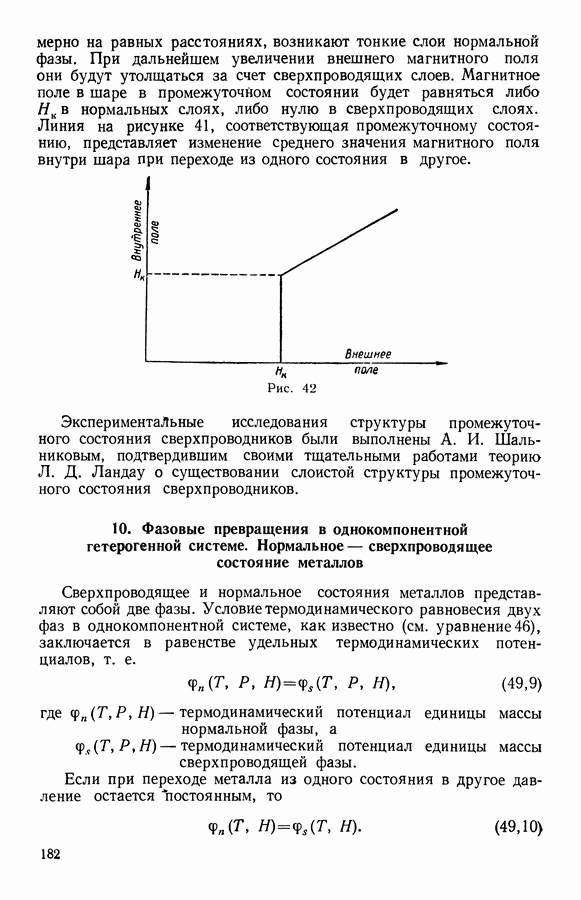
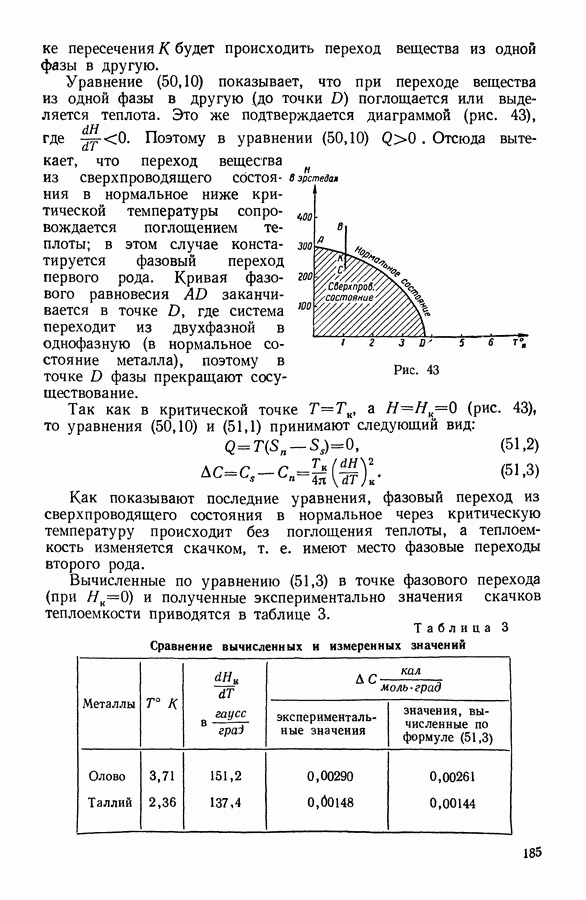
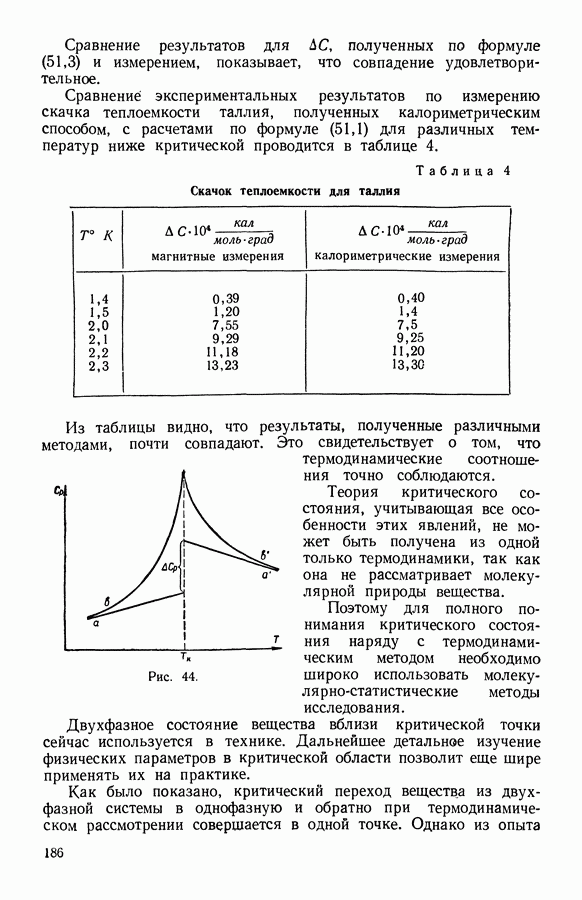
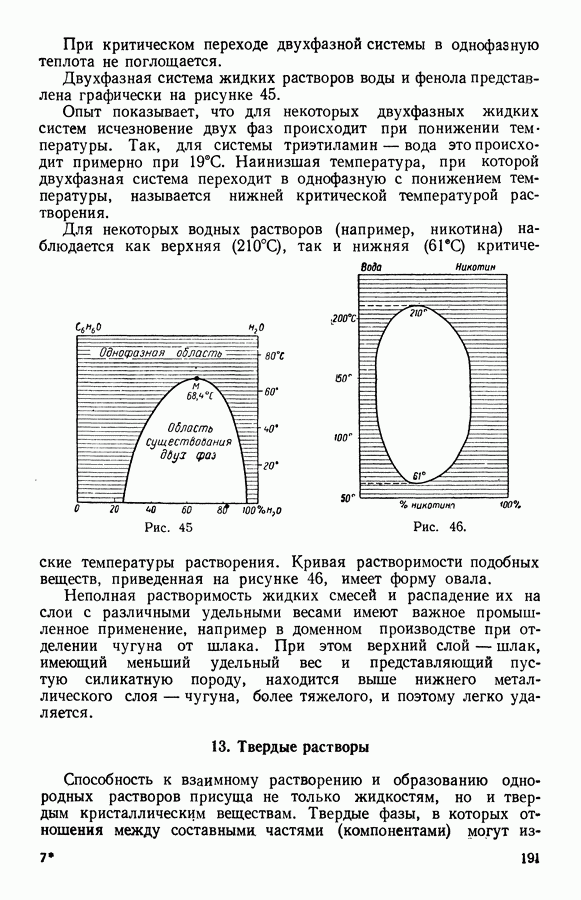
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
- 12. О взаимной растворимости жидкостей
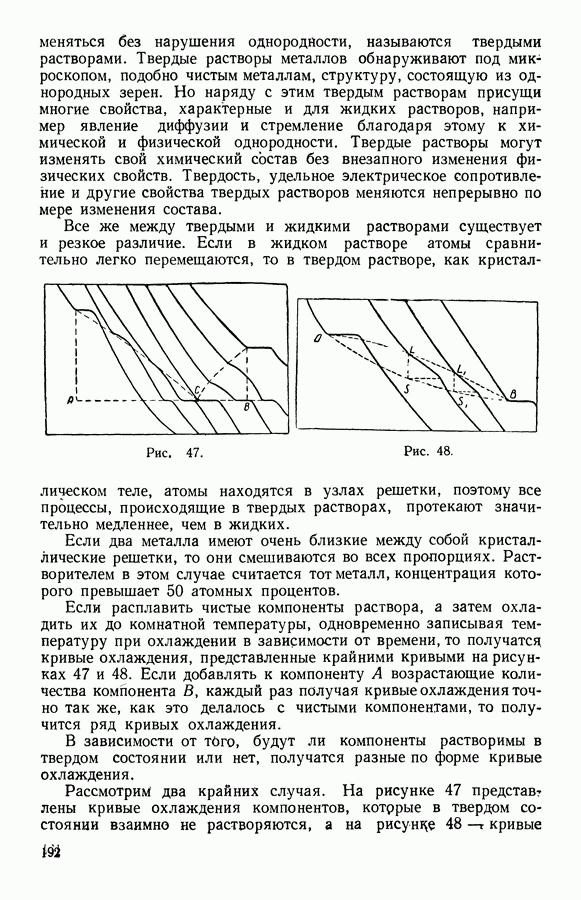
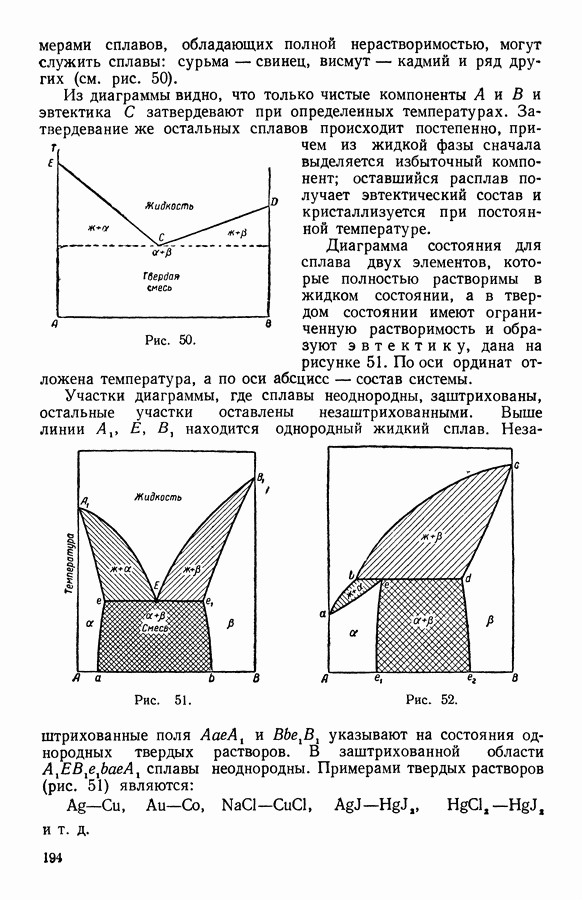
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
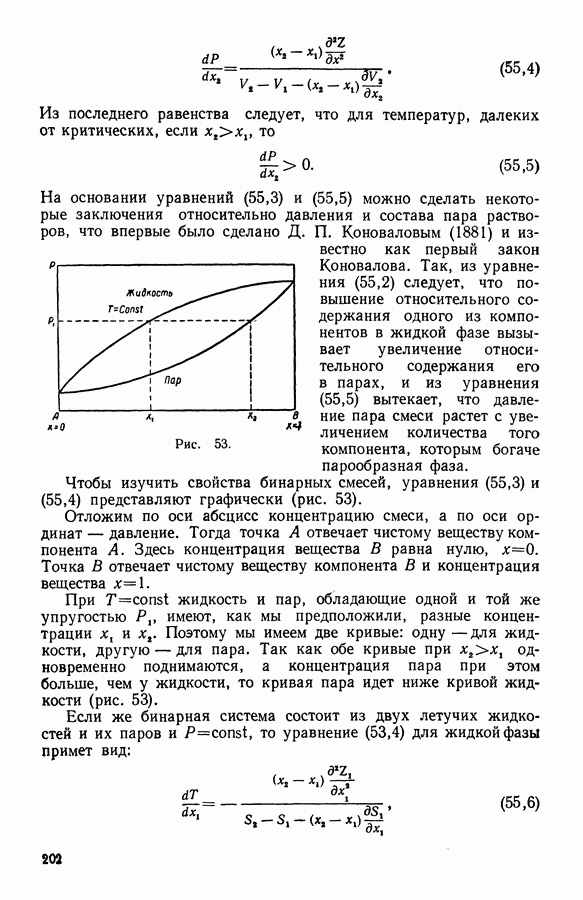
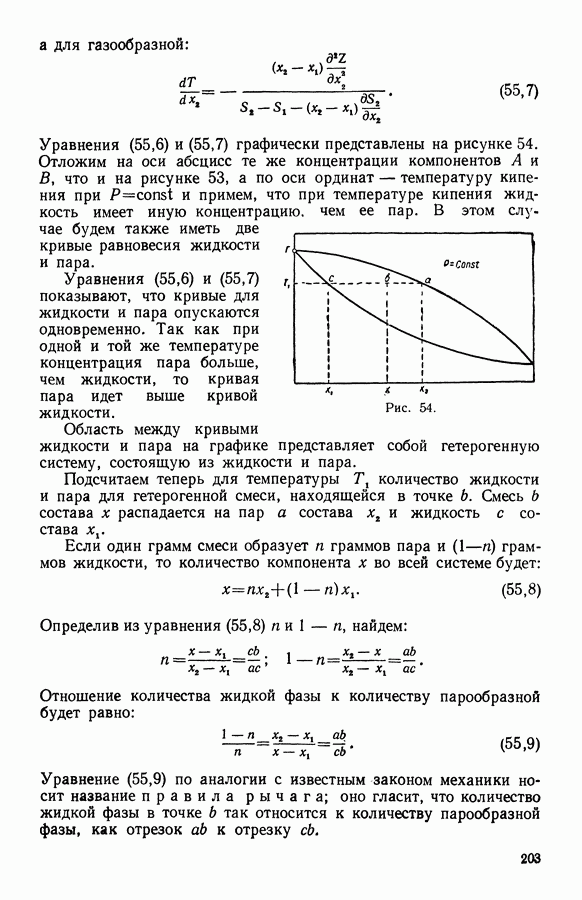
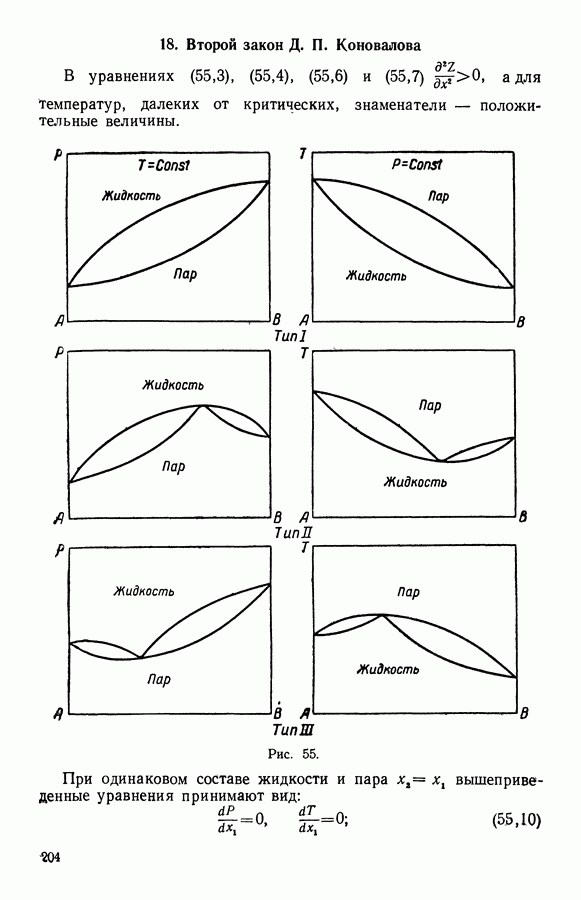
- 17. Первый закон Д. П. Коновалова
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
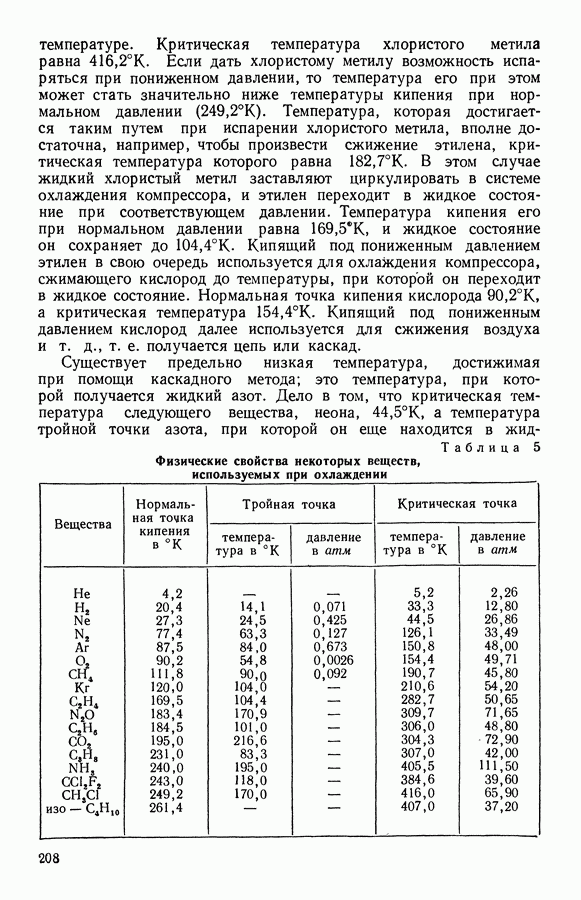
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
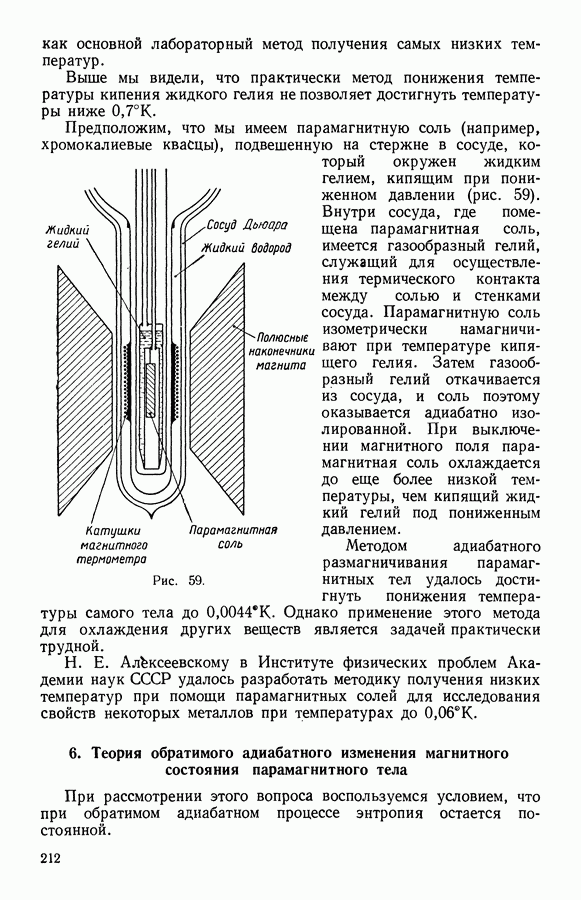
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса