| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
Если расширение газа при дросселировании происходит без отвода и поступления теплоты в систему, то такой процесс называется адиабатным дроссельным эффектом или явлением Джоуля — Томсона. Дроссельный эффект будет называться дифференциальным, если он представляет собой бесконечно малое изменение температуры газа в процессе его адиабатного дросселирования при бесконечно малом изменении давления.
Если изменение температуры вещества в процессе адиабатного дросселирования происходит при большом перепаде давлений, то такой процесс называется интегральным дроссельным эффектом. Если записать сказанное в виде формул, то при адиабатном дросселировании  и уравнение (29,8) принимает следующий вид
и уравнение (29,8) принимает следующий вид

а для бесконечно малого изменения давления:

Выше было выведено уравнение (23,10), напомним его:

Оно позволяет записать уравнение (30,2) в следующем виде:

или окончательно:

где  называется коэффициентом Джоуля — Томсона.
называется коэффициентом Джоуля — Томсона.
Если известно уравнение состояния и теплоемкость при постоянном давлении, то коэффициент Джоуля — Томсона вычисляется теоретически.
Продолжая рассуждения дальше и заменяя в (30,3) его значением из (26,7), получим:

Из уравнения (30,4) следует, что коэффициент Джоуля — Томсона имеет знак, противоположный знаку числителя, так как знаменатель  имеет всегда отрицательный знак.
имеет всегда отрицательный знак.
Для идеального газа уравнение (30,4) принимает следующий вид:

Отсюда следует, что при адиабатном дросселировании идеальный газ не дает эффекта Джоуля — Томсона, т. е. температура газа при дросселировании остается постоянной.
Рассмотрим эффект Джоуля — Томсона при дросселировании газа, подчиняющегося уравнению Ван-дер-Ваальса:

Найдем производные  и из Уравнения Ван-дер-Ваальса:
и из Уравнения Ван-дер-Ваальса:

Подставив данные (30,6) в уравнение (30,4) и сократив знаменатель, получим:

Когда плотность газа мала, то величиной  в знаменателе второго члена можно пренебречь, это дает выражение;
в знаменателе второго члена можно пренебречь, это дает выражение;

или

где  — так называемая температура инверсии, при которой
— так называемая температура инверсии, при которой

В случае, если температура  то, как это следует из анализа уравнения (30,4), газ при течении через дроссель будет охлаждаться, так как числитель в уравнении
то, как это следует из анализа уравнения (30,4), газ при течении через дроссель будет охлаждаться, так как числитель в уравнении  а знаменатель — отрицательный. При температуре
а знаменатель — отрицательный. При температуре  газ будет нагреваться.
газ будет нагреваться.
Экспериментальное исследование явления Джоуля — Томсона позволяет построить ряд кривых на диаграмме  при постоянном
при постоянном  используя для этого уравнение (30,3), переписанное для случая интегрального дроссельного эффекта
используя для этого уравнение (30,3), переписанное для случая интегрального дроссельного эффекта

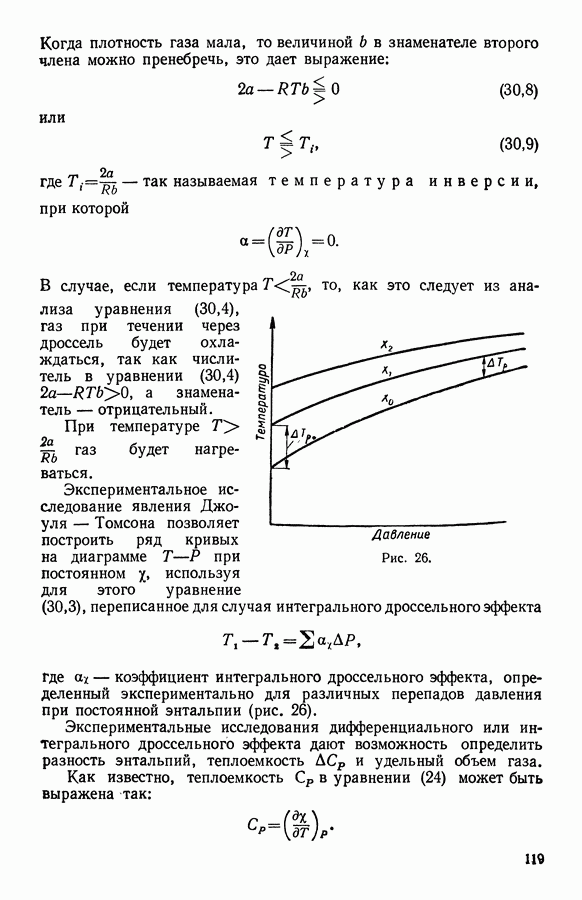
Где — коэффициент интегрального дроссельного эффекта, определенный экспериментально для различных перепадов давления при постоянной энтальпии (рис. 26).
Экспериментальные исследования дифференциального или интегрального дроссельного эффекта дают возможность определить разность энтальпий, теплоемкость  и удельный объем газа.
и удельный объем газа.
Как известно, теплоемкость  в уравнении (24) может быть выражена так:
в уравнении (24) может быть выражена так:


Рис. 26.
Из этого уравнения получаем:

Если при низком давлении теплоемкость известна как функция температуры, то, произвольно выбирая значение  можно определить энтальпию
можно определить энтальпию  из графика (рис. 26) для каждой точки, где кривая на диаграмме температур пересекает ось
из графика (рис. 26) для каждой точки, где кривая на диаграмме температур пересекает ось  . В небольшом температурном интервале уравнение (24) можно представить в виде:
. В небольшом температурном интервале уравнение (24) можно представить в виде:

где  представляет среднюю теплоемкость в данном интервале температур.
представляет среднюю теплоемкость в данном интервале температур.
Если использовать уравнение (31,1), то можно написать соотношение:

где  — известная теплоемкость
— известная теплоемкость  при малых давлениях. Величина изменения энтальпии
при малых давлениях. Величина изменения энтальпии  одинакова для всех точек между двумя линиями постоянного например
одинакова для всех точек между двумя линиями постоянного например  (рис. 26).
(рис. 26).
При таком условии уравнение (31,2) примет следующий вид:

где  определяются непосредственно из диаграммы (рис. 26).
определяются непосредственно из диаграммы (рис. 26).
Зная  из уравнения (31.3) легко отыщется
из уравнения (31.3) легко отыщется  для различных температур и давлений.
для различных температур и давлений.
Удельный объем газа определяется уравнением (30,3), если известны  как функции температуры и давления. В этом случае из уравнения (30,3) получаем:
как функции температуры и давления. В этом случае из уравнения (30,3) получаем:

Если же принять, что давление постоянно, то последнее уравнение выразится так:

или еще так:

Интегрируя вдоль изобары, получим:

где объем  должен быть известен для одной какой-либо температуры
должен быть известен для одной какой-либо температуры 
Заменив в уравнении  его значением из уравнения (24) при
его значением из уравнения (24) при  получим, что:
получим, что:

Если из эксперимента известны  как функции температуры и давления, то удельный объем можно без труда определить из уравнения (31,6).
как функции температуры и давления, то удельный объем можно без труда определить из уравнения (31,6).
Рассмотрим теперь несколько задач.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
- 11. Количественная формулировка второго закона
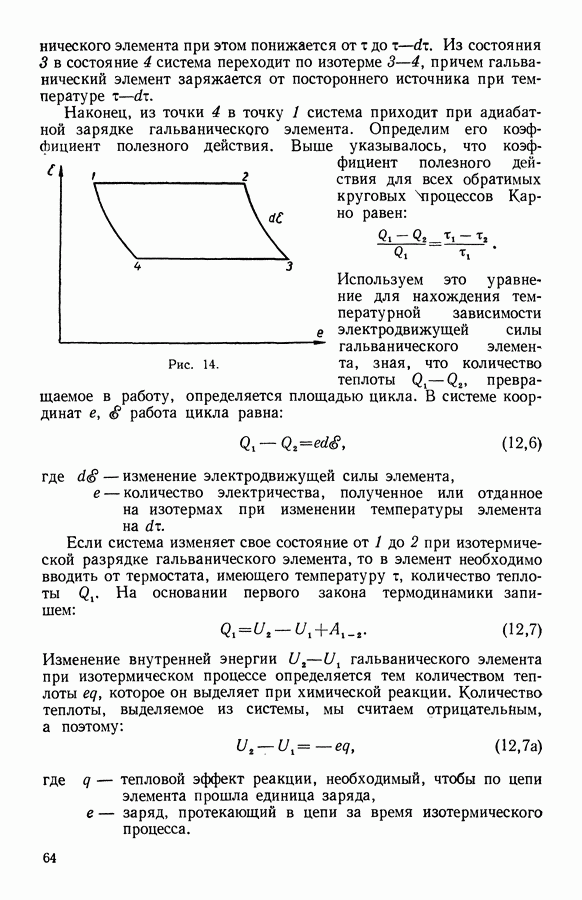
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
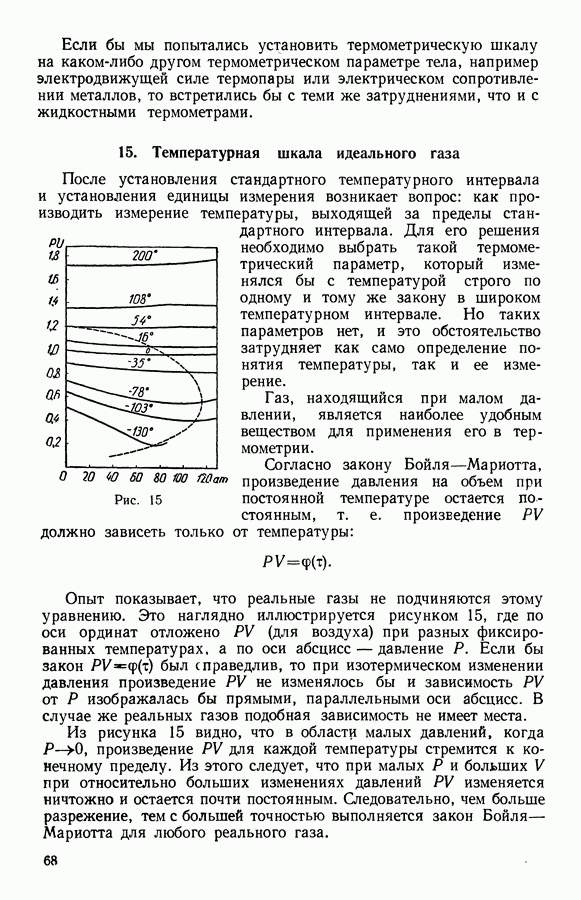
- 15. Температурная шкала идеального газа
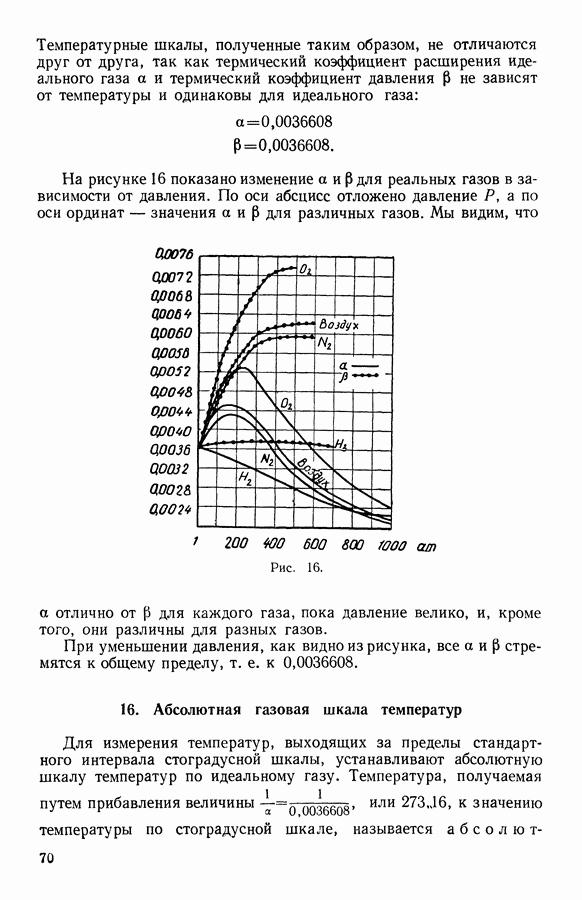
- 16. Абсолютная газовая шкала температур
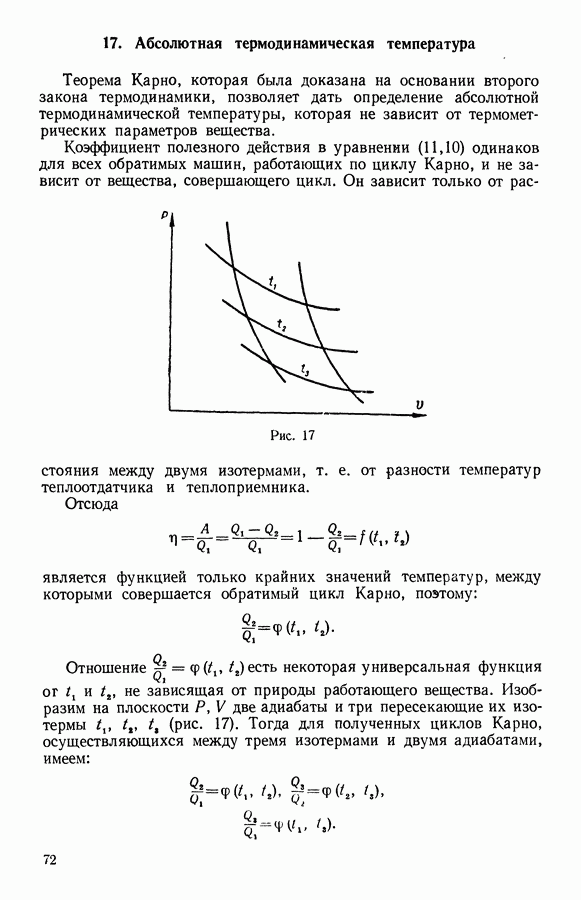
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
- 16. Возрастание энтропии при расширении газа в пустоту
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- 1. Фазовые превращения в однокомпонентных системах
- 2. Фазовые превращения первого рода
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
- 4. Фазовые превращения второго рода
- 5. Термодинамическая теория фазовых превращений второго рода
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
- 9. Сверхпроводящее состояние металлов
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
- 12. О взаимной растворимости жидкостей
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
- 17. Первый закон Д. П. Коновалова
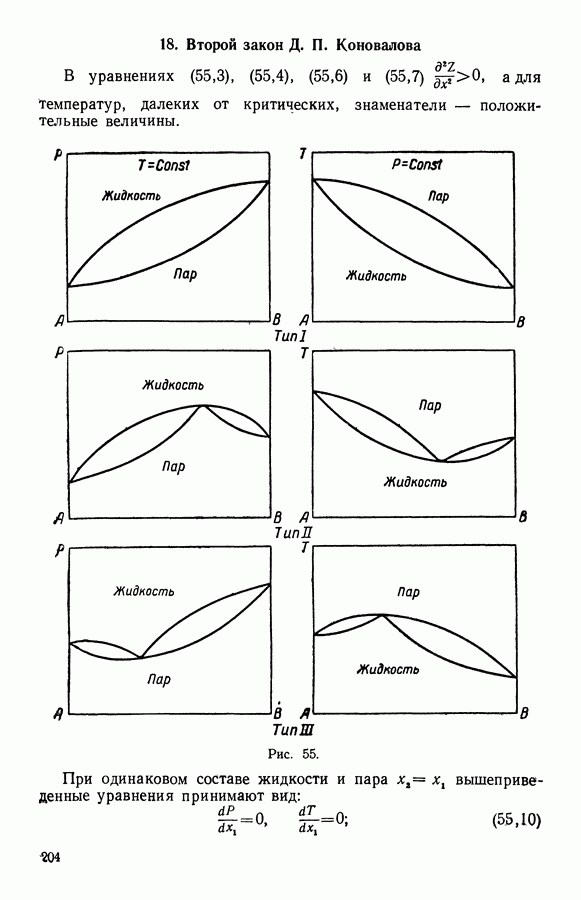
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
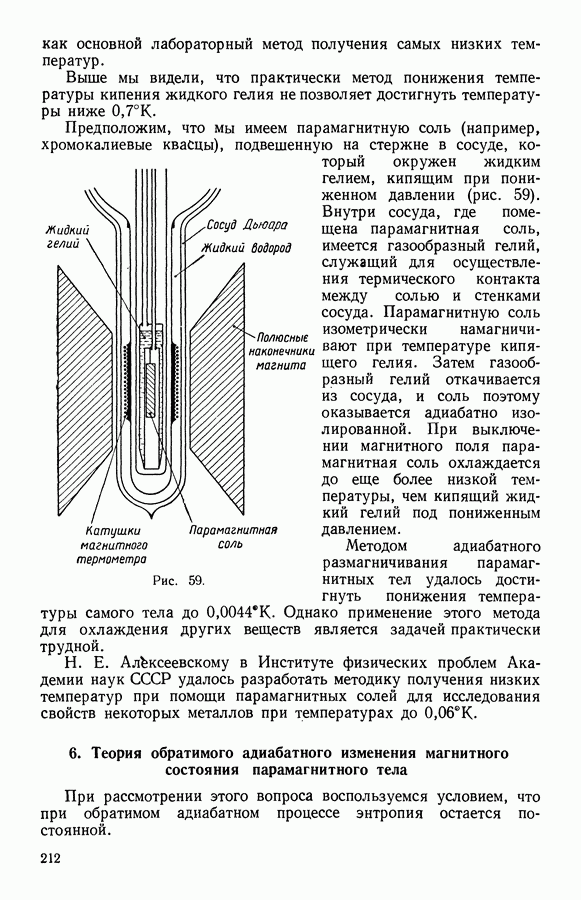
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса