| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
1. Характеристические функции
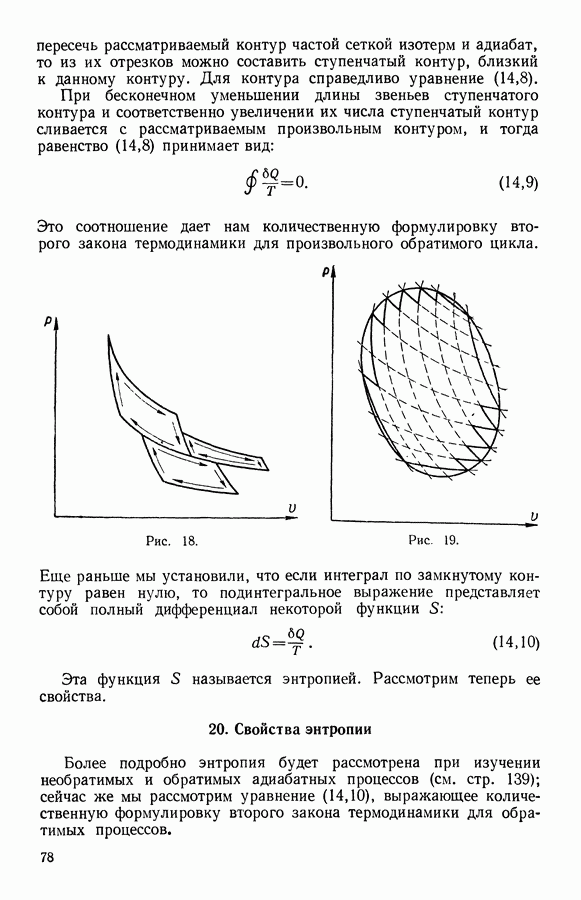
Применение второго закона термодинамики для решения любых конкретных задач, как это нами было рассмотрено выше, может быть использовано при анализе замкнутых циклов, совершаемых системой. Этим путем и была получена формула (12,10).
Однако применение второго закона более действенно при аналитическом методе исследования, основывающемся на рассмотрении особых функций состояния, называемых характеристическими функциями.
Исходя из количественной формулировки первого и второго законов термодинамики, можно получить уравнение, которое включает в себя оба закона.
Так, второе начало термодинамики для обратимого процесса в уравнении (14,10) имеет следующий вид:

где  энтропия,
энтропия,  абсолютная температура и
абсолютная температура и  количество теплоты.
количество теплоты.
Согласно первому закону термодинамики, мы имеем:

Подставив  в урайнение (14,10), получим:
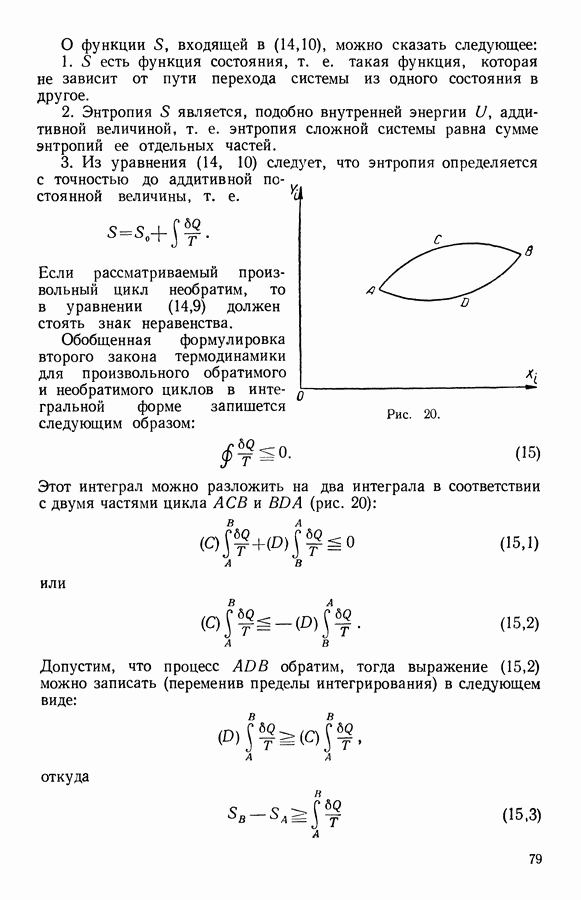
в урайнение (14,10), получим:

или

Это одно из самых общих уравнений термодинамики вытекает как следствие из первого и второго законов.
Если рассматривать термодинамическую систему, которая характеризуется параметрами Y (обобщенная сила), х (обобщенная координата) и Т (температура), то совершаемая работа

Подставив  в уравнение (15,5), получим:
в уравнение (15,5), получим:

Уравнение (15,6) связывает между собой пять переменных величин:  определяющих состояние системы. Если две из этих величин принять за независимые переменные, то уравнение (15,6) будет содержать три неизвестные величины. Для их определения, кроме уравнения (15,6), необходимы еще два независимых уравнения, которые должны связывать между собой те же переменные величины.
определяющих состояние системы. Если две из этих величин принять за независимые переменные, то уравнение (15,6) будет содержать три неизвестные величины. Для их определения, кроме уравнения (15,6), необходимы еще два независимых уравнения, которые должны связывать между собой те же переменные величины.
В качестве первого такого уравнения термодинамика использует уравнение состояния:

второе уравнение выражает зависимость внутренней энергии от температуры:

где  — фиксированное значение обобщенной координаты.
— фиксированное значение обобщенной координаты.
Зависимость внутренней энергии от обобщенной координаты или обобщенной силы, как это будет видно ниже, определяется из уравнения состояния, поэтому знание внутренней энергии в уравнении  как функции одной только температуры является достаточным.
как функции одной только температуры является достаточным.
Вот теперь-то, когда известны уравнения (15,6), (15,7) и (15,8), можно определить все термодинамические свойства системы.
Возможно также определить все свойства термодинамической системы и в том случае, когда известна одна из следующих характеристических функций: внутренняя энергия  энтальпия
энтальпия  свободная энергия
свободная энергия  термодинамический потенциал
термодинамический потенциал  Выбор той или иной характеристической функции при решении термодинамической задачи будет зависеть от выбора независимых параметров системы.
Выбор той или иной характеристической функции при решении термодинамической задачи будет зависеть от выбора независимых параметров системы.
Производные от характеристической функции по независимым параметрам системы дают (см. ниже) два независимых уравнения. Поэтому, чтобы иметь дополнительно к (15,6) еще два независимых уравнения, достаточно знать только одну характеристическую функцию.
Итак, функция состояния называется характеристической, если посредством нее или посредством ее
производных (разных порядков) могут быть выражены явно термодинамические свойства системы.
Из пяти неизвестных, содержащихся в уравнении (15,6), возможны десять различных парных комбинаций:  но только четыре из них соответствуют характеристическим функциям:
но только четыре из них соответствуют характеристическим функциям:

Вид характеристических функций может быть получен либо опытным путем, либо выведен при помощи молекулярно-кинетической теории так же, как и уравнение состояния.
Левая часть уравнения (15,6) есть полный дифференциал внутренней энергии как функции энтропии и обобщенной координаты. Функция  является характеристической.
является характеристической.
Если независимыми параметрами системы будут энтропия и обобщенная сила У, то внутренняя энергия не будет уже характеристической функцией; ею будет энтальпия, определяющаяся с помощью основного уравнения (15,6). Прибавив к правой и левой частям уравнения по  получим:
получим:

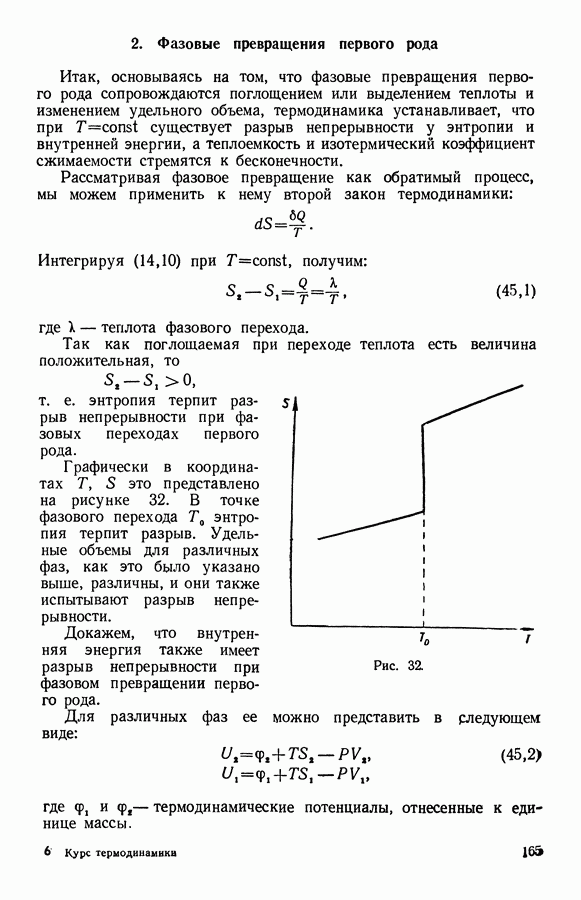
или

Левая часть уравнения (15,9) есть полный дифференциал функции  при переменных
при переменных  Энтальпия
Энтальпия  является характеристической функцией.
является характеристической функцией.
Если независимыми параметрами системы являются температура и обобщенная координата, то характеристической функцией будет свободная энергия. Она выводится также из уравнения (15,6). Вычитая из правой и левой частей его по  получаем:
получаем:

или

Левая часть уравнения (15,10) есть полный дифференциал функции  при переменных Тих.
при переменных Тих.  является характеристической функцией и называется свободной энергией.
является характеристической функцией и называется свободной энергией.
Свободная энергия имеет большое значение в различных отделах физики и в химической термодинамике. В дальнейшем будет показано, что направление химической реакции и химическое сродство именно и определяются разностью свободных энергий.
Продолжая дальше наши рассуждения, отметим, что при  уравнение (15,10) будет иметь вид:
уравнение (15,10) будет иметь вид:

или

где

т. е. при изотермическом процессе работа совершается за счет изменения свободной энергии.
Если независимыми параметрами системы будут температура и обобщенная сила У, то характеристической функцией будет термодинамический потенциал  Он может быть получен из уравнения (15,6) или, что гораздо удобнее, из эквивалентного ему уравнения (15,10). Прибавив к правой и левой частям уравнения по
Он может быть получен из уравнения (15,6) или, что гораздо удобнее, из эквивалентного ему уравнения (15,10). Прибавив к правой и левой частям уравнения по  получим:
получим:

или

Левая часть этого уравнения есть полный дифференциал функции  при независимых переменных
при независимых переменных  также является характеристической функцией и называется термодинамическим потенциалом. При помощи уравнений (15,6), (15,9), (15,10) и (16,2) можно решать задачи в различных отделах физики и физической химии.
также является характеристической функцией и называется термодинамическим потенциалом. При помощи уравнений (15,6), (15,9), (15,10) и (16,2) можно решать задачи в различных отделах физики и физической химии.
Применяя общие выражения дифференциалов от характеристических функций для конкретных систем, необходимо при этом всегда учитывать знак в выражении, показывающем работу. Мы условимся считать работу положительной, если система совершает работу над внешними телами, и, наоборот, отрицательной, если работа совершается внешними телами над конкретной системой.
Рассмотрим следующие термодинамические системы: 1. Система, параметрами которой являются давление, объем и температура. При этом 
Для нее дифференциалы от характеристических функций и сами функции запишутся в следующем виде:

2. Система — магнетик во внешнем магнитном поле. Параметры системы: напряженность магнитного поля  магнитный момент магнетика
магнитный момент магнетика  и температура
и температура  Если при намагничивании вещества объем и давление его остаются неизменными, то
Если при намагничивании вещества объем и давление его остаются неизменными, то  Дифференциалы от характеристических функций и сами функции в этой системе получат следующие значения:
Дифференциалы от характеристических функций и сами функции в этой системе получат следующие значения:

2a. Если же при намагничивании вещества объем и давление магнетика изменяются, то согласно уравнению (5,1)

и, значит,

или

В этом уравнении мы имеем семь переменных величин; если три из них принять за независимые переменные, то для определения четырех остальных необходимо, кроме (16,3), иметь еще три уравнения. Этими уравнениями могут быть магнитное уравнение состояния

термическое уравнение состояния

и уравнение

где  постоянное значение объема.
постоянное значение объема.
Все свойства системы могут быть также определены, если, кроме уравнения (16,3), будет известна одна из характеристических функций.
Внутренняя энергия в уравнении (16,3) является характеристической функцией трех переменных:  т. е.
т. е.  Частные производные от характеристической функции по трем независимым переменным дают три независимых уравнения. Поэтому знания характеристической функции в уравнении (16,3) достаточно для того, чтобы определить все величины термодинамической системы.
Частные производные от характеристической функции по трем независимым переменным дают три независимых уравнения. Поэтому знания характеристической функции в уравнении (16,3) достаточно для того, чтобы определить все величины термодинамической системы.
Если система имеет независимые переменные  то характеристической функцией будет энтальпия. Она может
то характеристической функцией будет энтальпия. Она может
быть получена из уравнения (16,3) следующим путем. Прибавив к правой и левой частям уравнения (16,3) по  получим:
получим:

или

где  и есть энтальпия.
и есть энтальпия.
При независимых переменных  характеристической функцией системы будет свободная энергия, выражение которой можно получить из уравнения (16,3). Вычитая из правой и левой частей уравнения по
характеристической функцией системы будет свободная энергия, выражение которой можно получить из уравнения (16,3). Вычитая из правой и левой частей уравнения по  мы найдем:
мы найдем:

или

где  свободная энергия. Поскольку
свободная энергия. Поскольку  есть полный дифференциал, то
есть полный дифференциал, то

Сравнение коэффициентов при дифференциалах  в уравнениях (16,5) и (16,6) дает равенства:
в уравнениях (16,5) и (16,6) дает равенства:

Из условия полного дифференциала  также следует, что
также следует, что

Если независимыми переменными являются  то характеристической функцией системы будет термодинамический потенциал. Он может быть получен также из уравнения (16,5). Прибавив к правой и левой частям этого равенства по
то характеристической функцией системы будет термодинамический потенциал. Он может быть получен также из уравнения (16,5). Прибавив к правой и левой частям этого равенства по  найдем:
найдем:

или

где  и есть термодинамический потенциал. Из условия, что
и есть термодинамический потенциал. Из условия, что  есть полный дифференциал, получим:
есть полный дифференциал, получим:

Соотношение  связывает измеримые величины. Величина
связывает измеримые величины. Величина  представляет собой относительное изменение объема вещества, вызванное магнитным полем, и называется объемной магнитострикцией.
представляет собой относительное изменение объема вещества, вызванное магнитным полем, и называется объемной магнитострикцией.
Член  выражает изменение полного магнитного момента, вызванное давлением.
выражает изменение полного магнитного момента, вызванное давлением.
3. Система — диэлектрик во внешнем электрическом поле. Параметры системы: напряженность электрического поля  момент поляризации и температура
момент поляризации и температура  Если при поляризации вещества во внешнем электрическом поле объем и давление его остаются неизменными, то
Если при поляризации вещества во внешнем электрическом поле объем и давление его остаются неизменными, то  т. е. получаем уравнение (2,4).
т. е. получаем уравнение (2,4).
Дифференциалы от характеристических функций и сами функции для этой системы принимают в таком случае следующие выражения:

3а. Система — та же. Объем и давление изменяются при поляризации вещества. Математическое выражение первого начала термодинамики для этого случая имеет вид:

Подставив  в выражение второго начала, находим:
в выражение второго начала, находим:

В этом уравнении внутренняя энергия как характеристическая функция имеет независимые переменные: энтропию, объем и момент поляризации диэлектрика, т. е.  . Энтальпия, свободная энергия, термодинамический потенциал и их дифференциалы могут быть получены из уравнения (17) таким же путем, как и для магнетика во внешнем магнитном поле, когда совершалась работа расширения (сжатия) вещества (пример 2а), т. е.
. Энтальпия, свободная энергия, термодинамический потенциал и их дифференциалы могут быть получены из уравнения (17) таким же путем, как и для магнетика во внешнем магнитном поле, когда совершалась работа расширения (сжатия) вещества (пример 2а), т. е.

где

где

и

4. Допустим, что имеется система, в которой происходит химическая реакция:

где  , соответственно — стехиометрические коэффициенты 1 веществ, вступающих в реакцию, и продуктов реакции. Работа в этой системе
, соответственно — стехиометрические коэффициенты 1 веществ, вступающих в реакцию, и продуктов реакции. Работа в этой системе  будет выражаться максимальной работой реакции
будет выражаться максимальной работой реакции  и работой расширения (сжатия) системы
и работой расширения (сжатия) системы  т. е.
т. е.

Подставив  в уравнение (15,5), получим:
в уравнение (15,5), получим:

Внутренняя энергия как характеристическая функция в этой системе зависит от  и изменяющейся массы входящих в систему веществ при химической реакции, т. е.
и изменяющейся массы входящих в систему веществ при химической реакции, т. е. 

где  соответственно массы всех входящих в систему веществ.
соответственно массы всех входящих в систему веществ.
Если независимыми переменными являются  то характеристической функцией их будет энтальпия. Прибавив к правой и левой частям уравнения (17,4) по
то характеристической функцией их будет энтальпия. Прибавив к правой и левой частям уравнения (17,4) по  находим:
находим:

где  энтальпия.
энтальпия.
При независимых параметрах системы  характеристической функцией будет свободная энергия:
характеристической функцией будет свободная энергия:

где  свободная энергия.
свободная энергия.
Если независимыми переменными системы являются  то характеристической функцией будет термодинамический потенциал, который может быть получен из уравнения (17,6) следующим образом: прибавив к правой и левой частям уравнения (17,6) по
то характеристической функцией будет термодинамический потенциал, который может быть получен из уравнения (17,6) следующим образом: прибавив к правой и левой частям уравнения (17,6) по  найдем:
найдем:

или

где  термодинамический потенциал.
термодинамический потенциал.
Если химическая реакция протекает при постоянных  то из уравнения (17,6) следует, что максимальная работа химической реакции равна разности свободных энергий в начальном и конечном ее состояниях:
то из уравнения (17,6) следует, что максимальная работа химической реакции равна разности свободных энергий в начальном и конечном ее состояниях:

или

где

При постоянных температуре и давлении максимальная работа химической реакции, как это видно из уравнения (17,7), равна разности термодинамических потенциалов в начальном и конечном состояниях системы:

или

где

Из уравнений (17,8) и (17,9) следует, что максимальную работу реакции можно определить, если известны разности свободных энергий или термодинамических потенциалов. Методы вычисления  и
и  будут рассмотрены ниже (глава VII).
будут рассмотрены ниже (глава VII).
5. Система — стержень, который растягивается внешней силой. Параметры системы: внешняя сила  длина стержня
длина стержня  и температура 7. Если при растяжении стержня под действием внешней силы объем и давление его остаются неизменными, то при этом
и температура 7. Если при растяжении стержня под действием внешней силы объем и давление его остаются неизменными, то при этом  [уравнение (1,4)].
[уравнение (1,4)].
Для этой системы дифференциалы от характеристических функций и сами функции принимают следующие выражения:

6. Система — стержень, который закручивается внешней силой. Параметры: момент вращающей силы  угол закручивания
угол закручивания  и температура
и температура  Если при закручивании стержня внешней силой объем и давление остаются неизменными, то при этом
Если при закручивании стержня внешней силой объем и давление остаются неизменными, то при этом 
[уравнение (1,5)]. Дифференциалы от характеристических функций и сами функцйи получают тогда следующие значения:

Дифференциалы характеристических функций и сами функции в группах II—V отличаются знаками в выражении элемента работы по сравнению со значениями дифференциалов и функций в I группе, а также знаками в функциях  Это различие получилось вследствие того, что в группе I работа была положительной, а во II—V группах уравнений — отрицательной.
Это различие получилось вследствие того, что в группе I работа была положительной, а во II—V группах уравнений — отрицательной.
Используя полученные общие соотношения для анализа конкретных систем, всегда необходимо учитывать знаки у дифференциалов от характеристических функций в конкретных системах.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
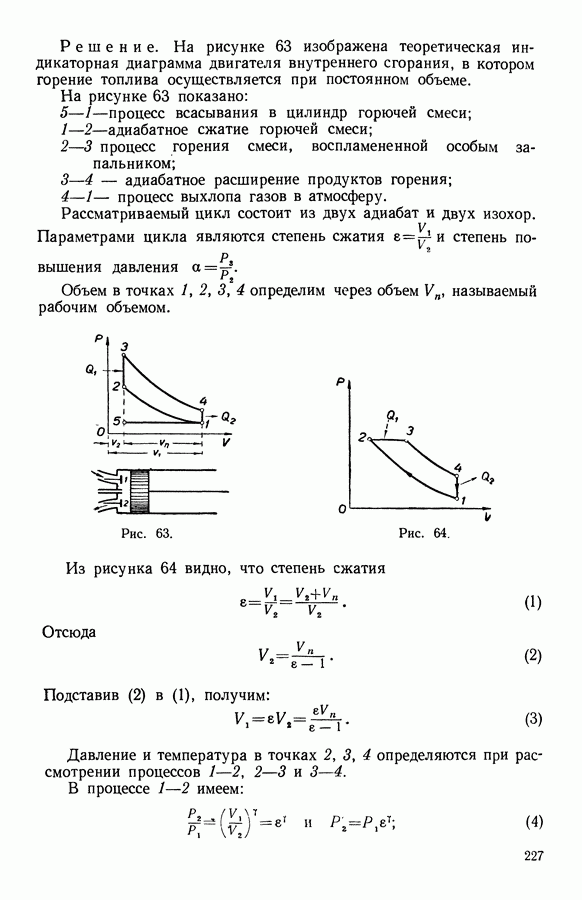
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
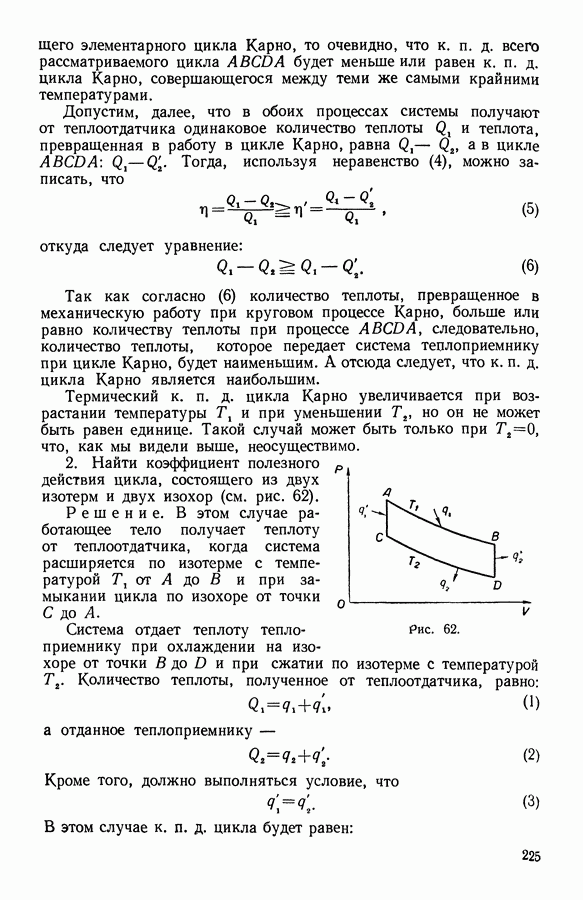
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
- 11. Количественная формулировка второго закона
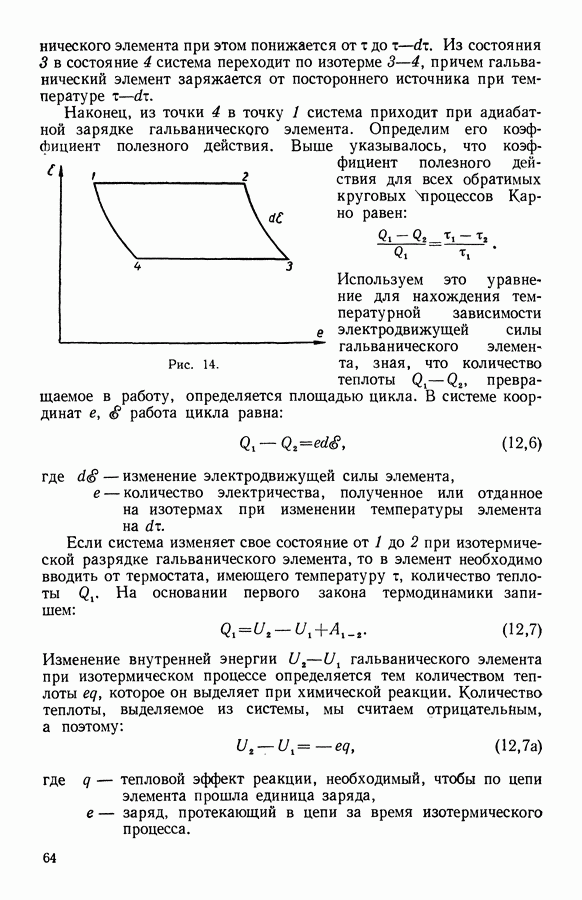
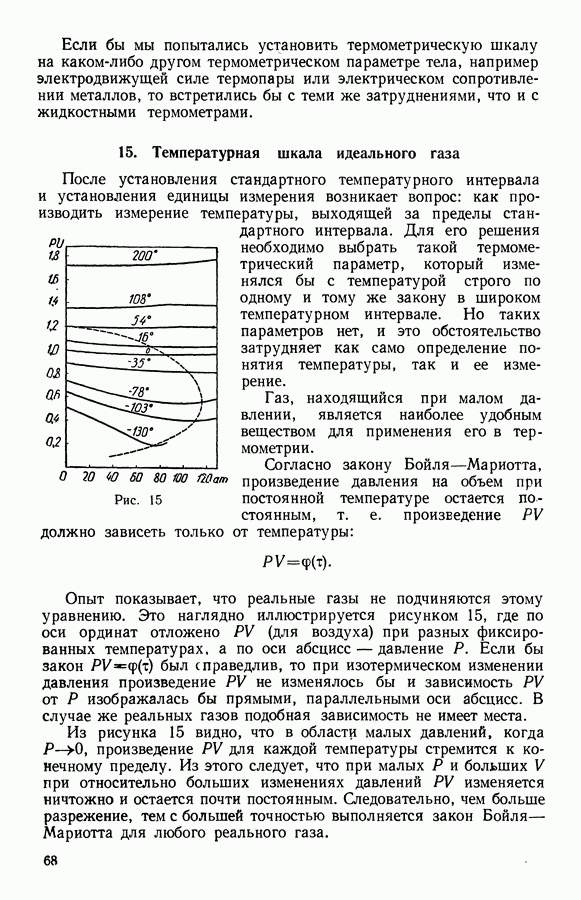
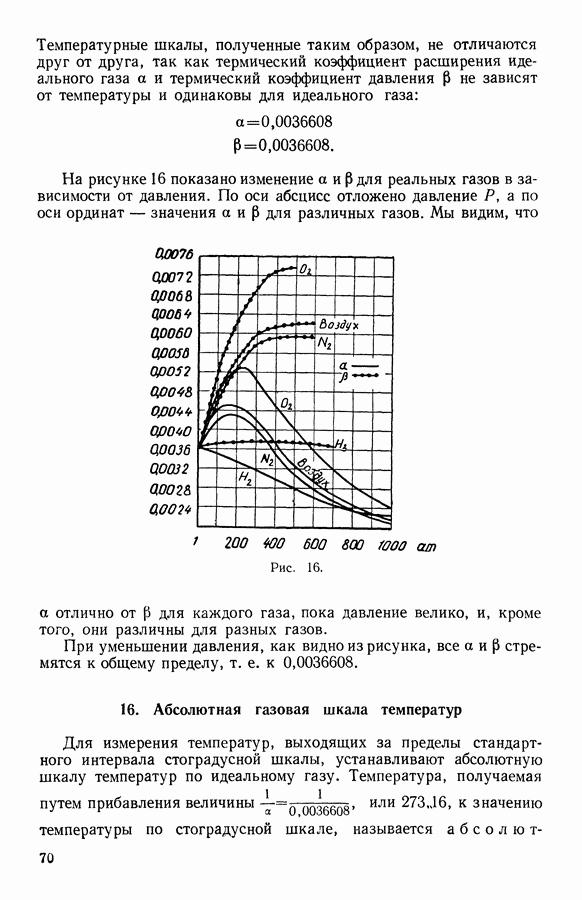
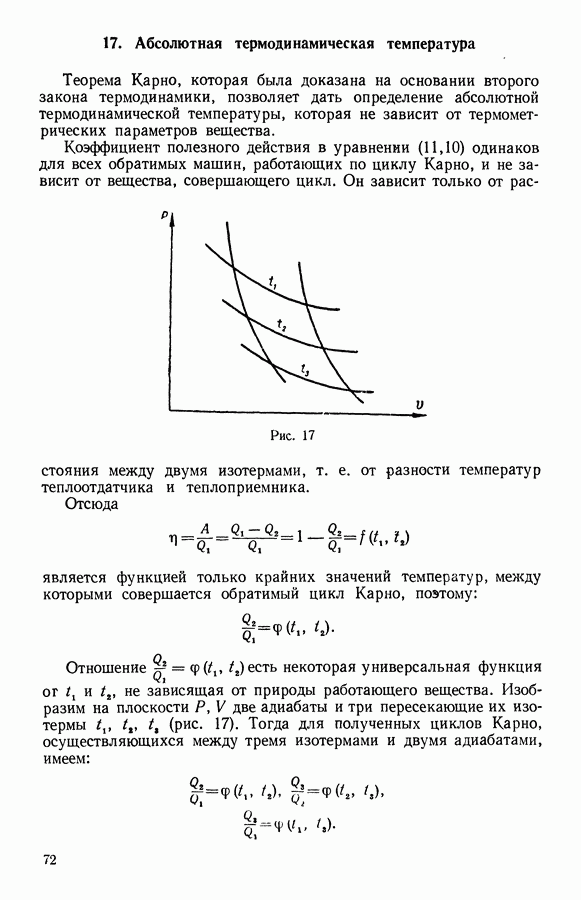
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
- 15. Температурная шкала идеального газа
- 16. Абсолютная газовая шкала температур
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
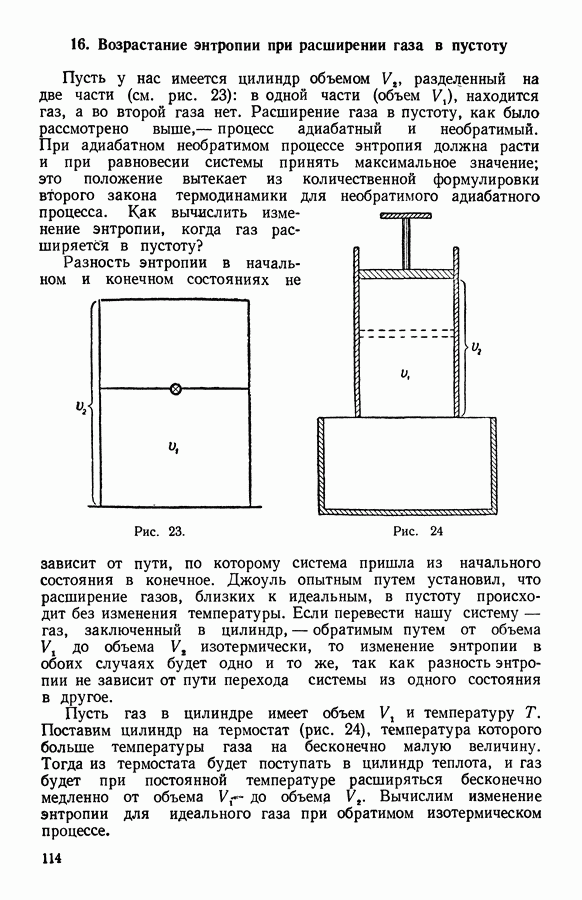
- 16. Возрастание энтропии при расширении газа в пустоту
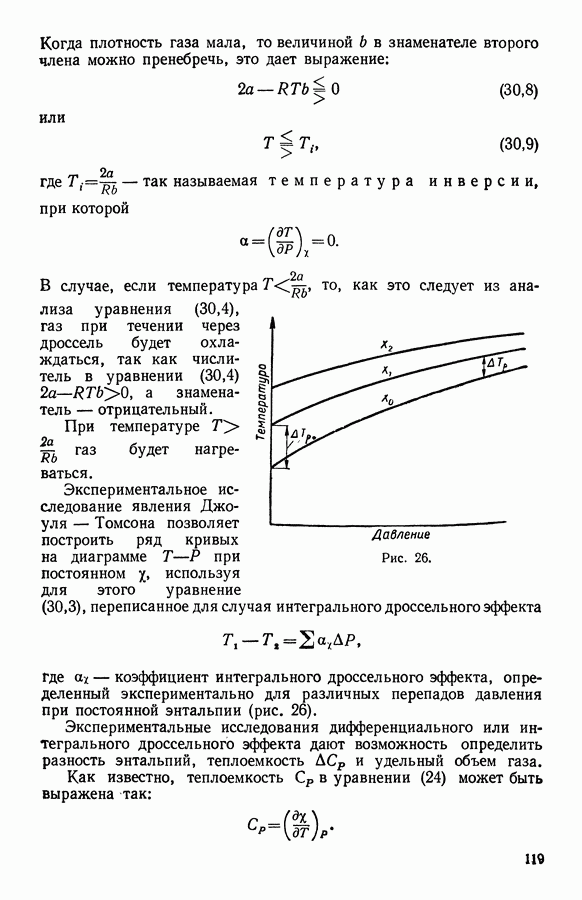
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
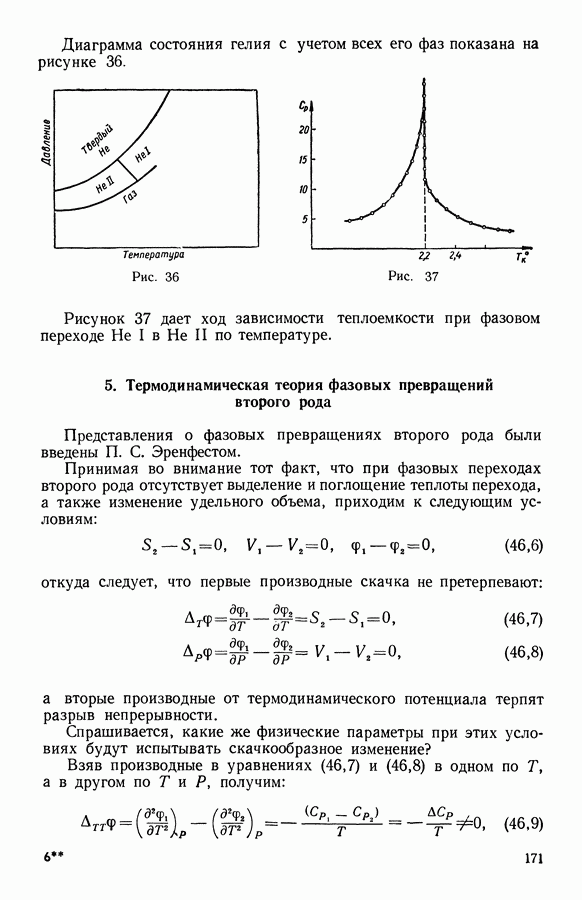
- 1. Фазовые превращения в однокомпонентных системах
- 2. Фазовые превращения первого рода
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
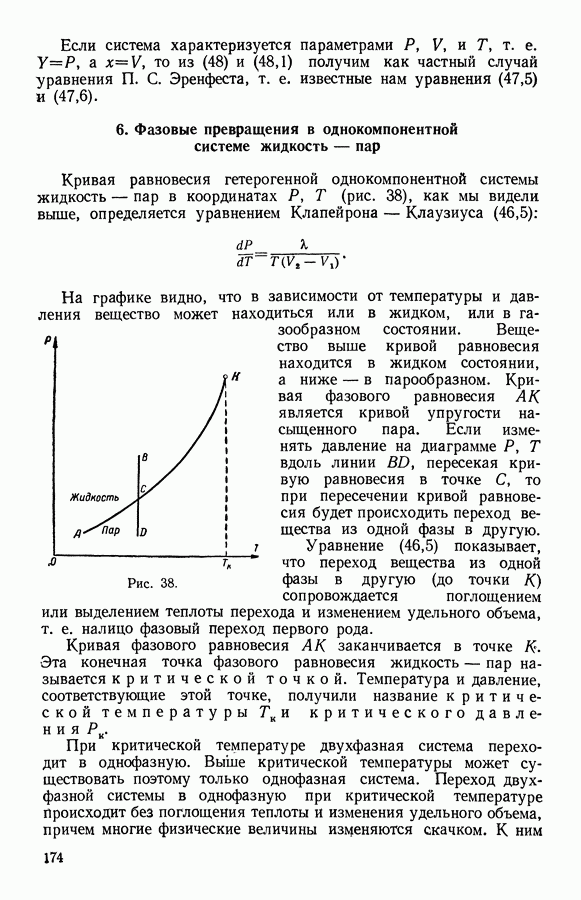
- 4. Фазовые превращения второго рода
- 5. Термодинамическая теория фазовых превращений второго рода
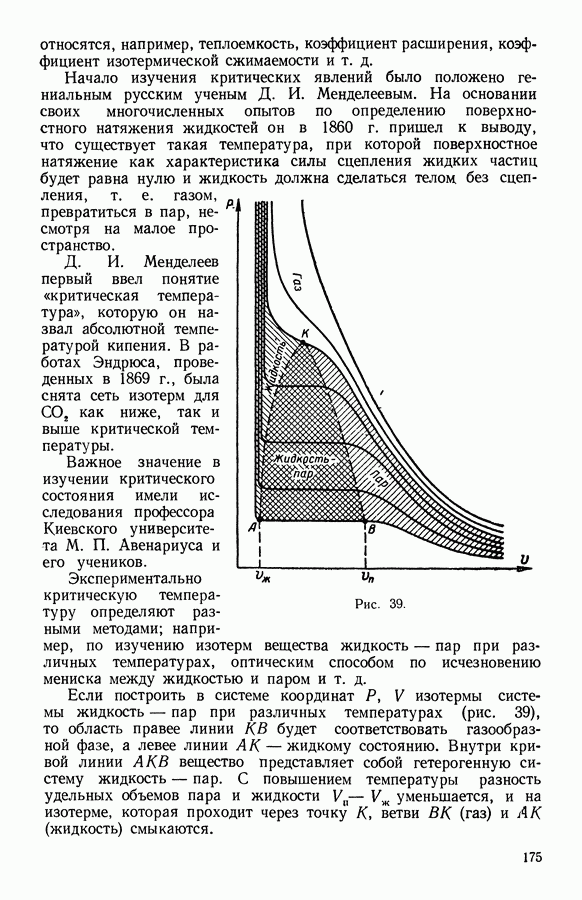
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
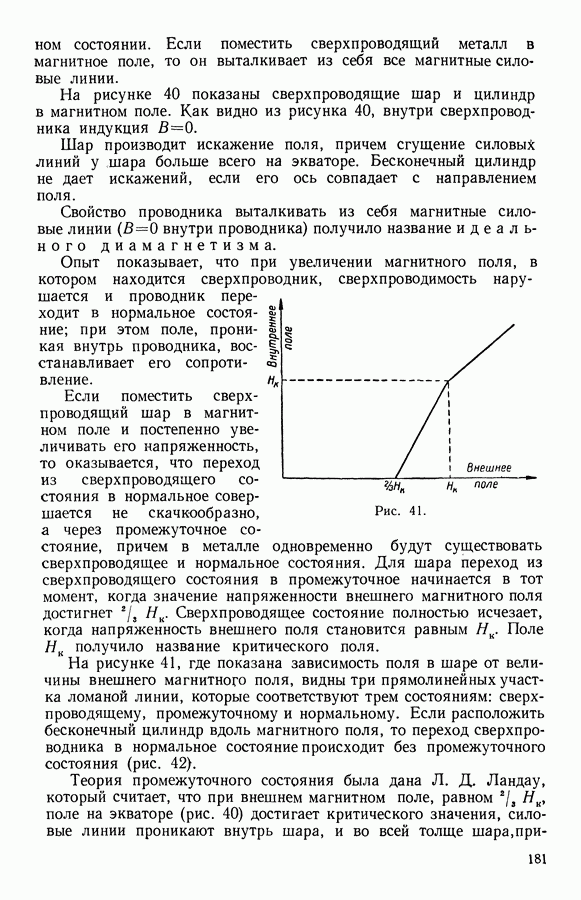
- 9. Сверхпроводящее состояние металлов
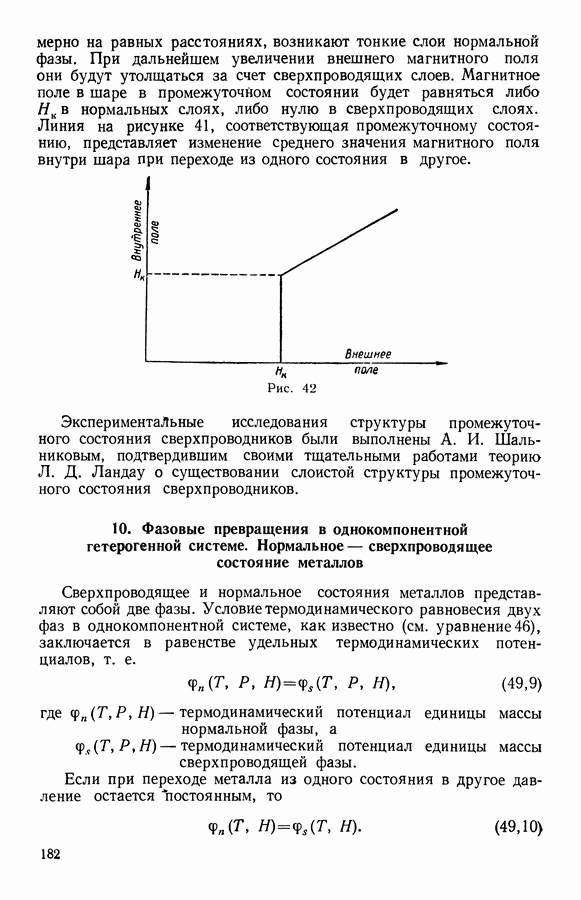
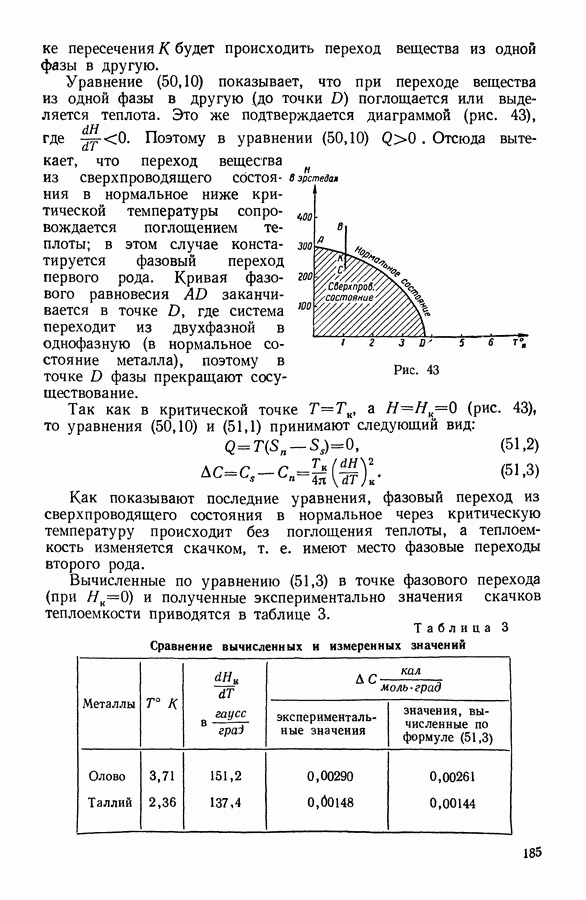
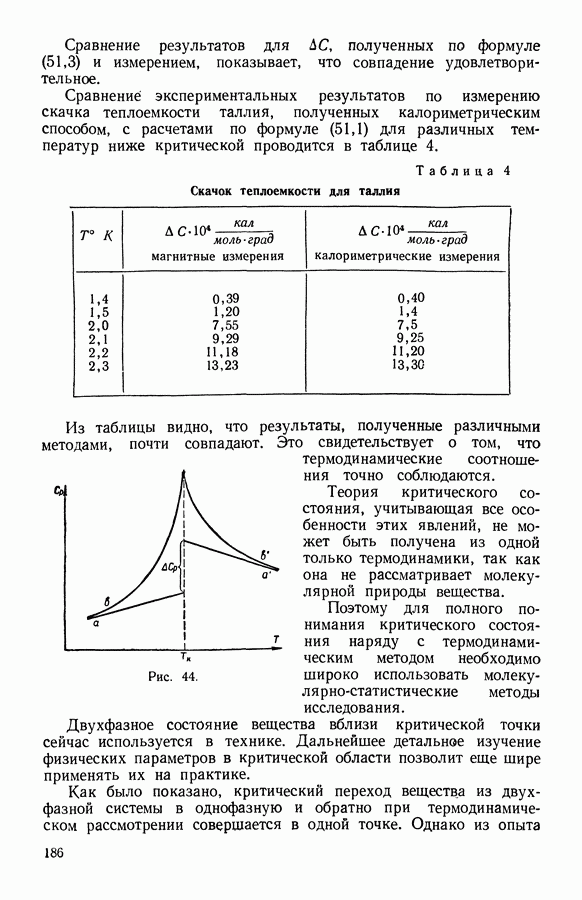
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
- 12. О взаимной растворимости жидкостей
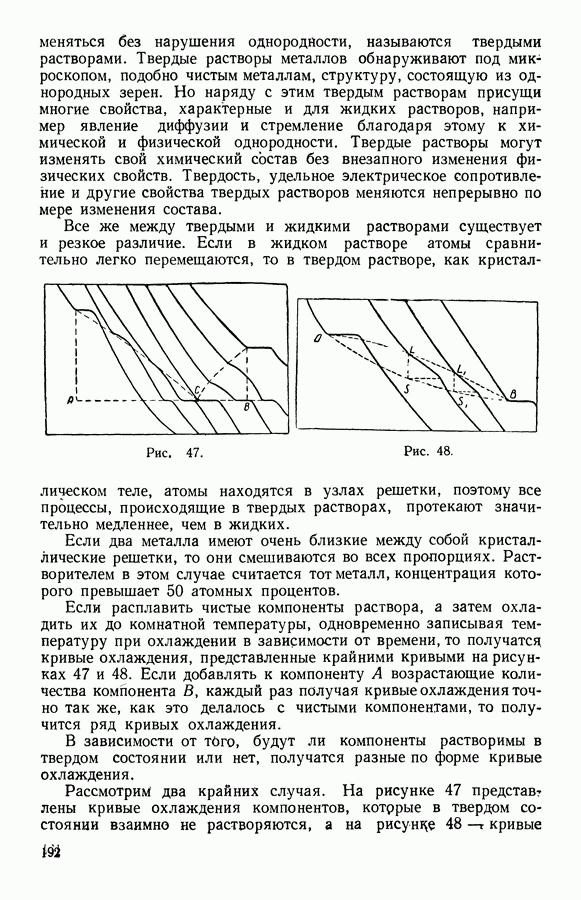
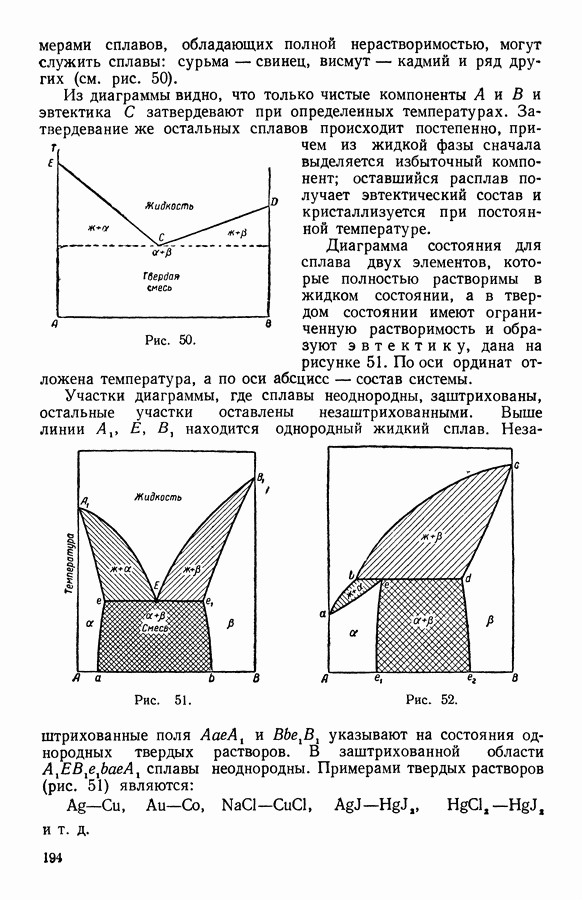
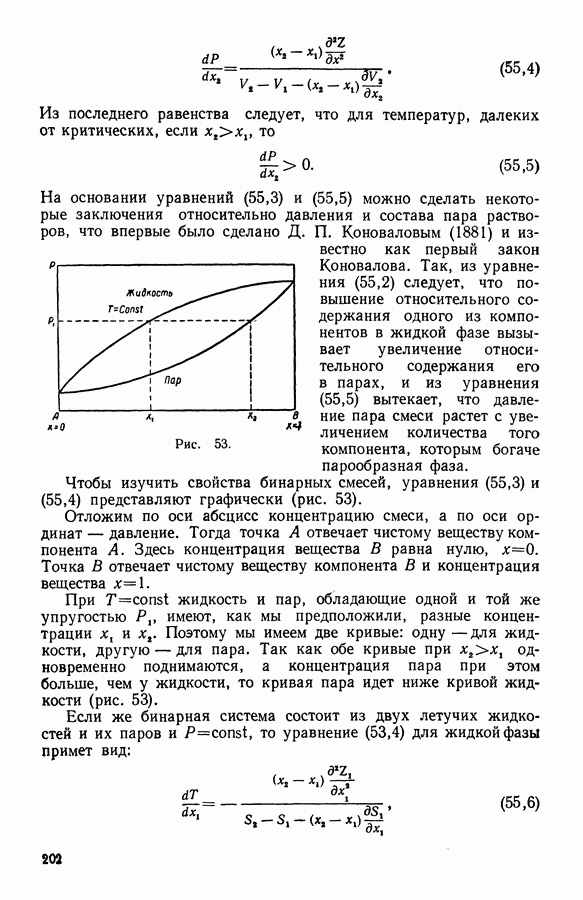
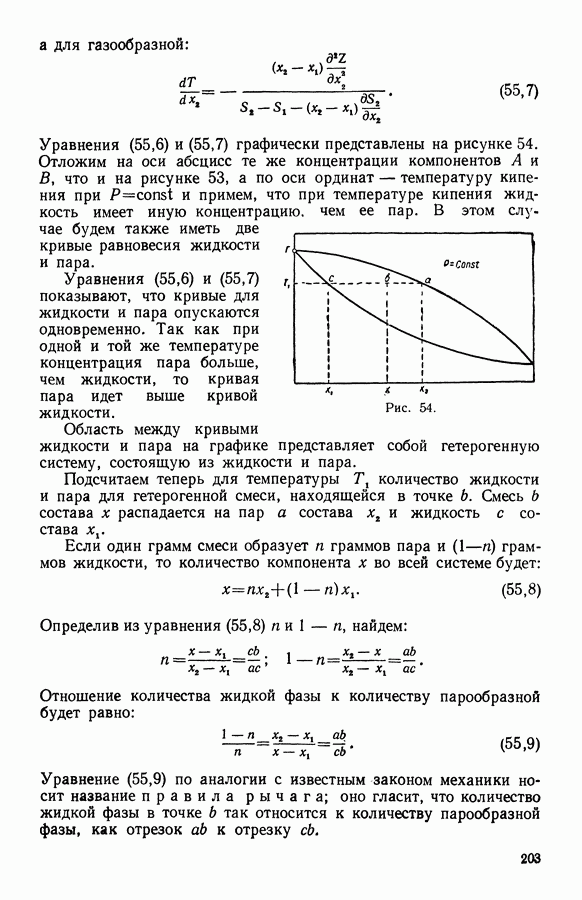
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
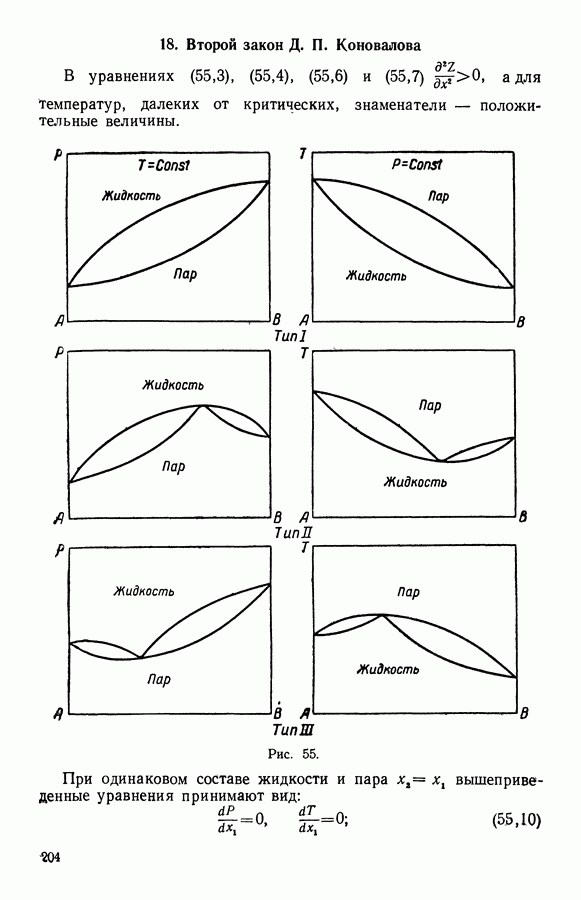
- 17. Первый закон Д. П. Коновалова
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
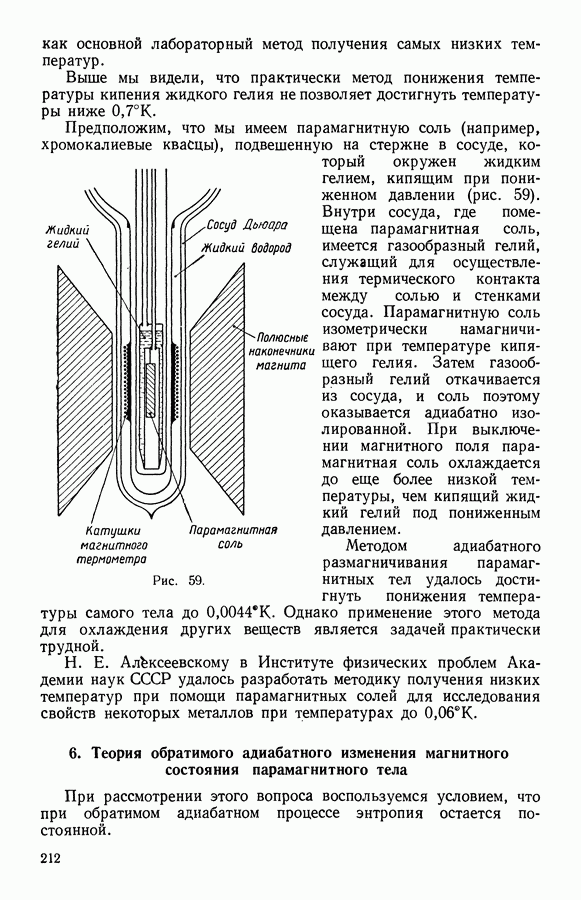
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
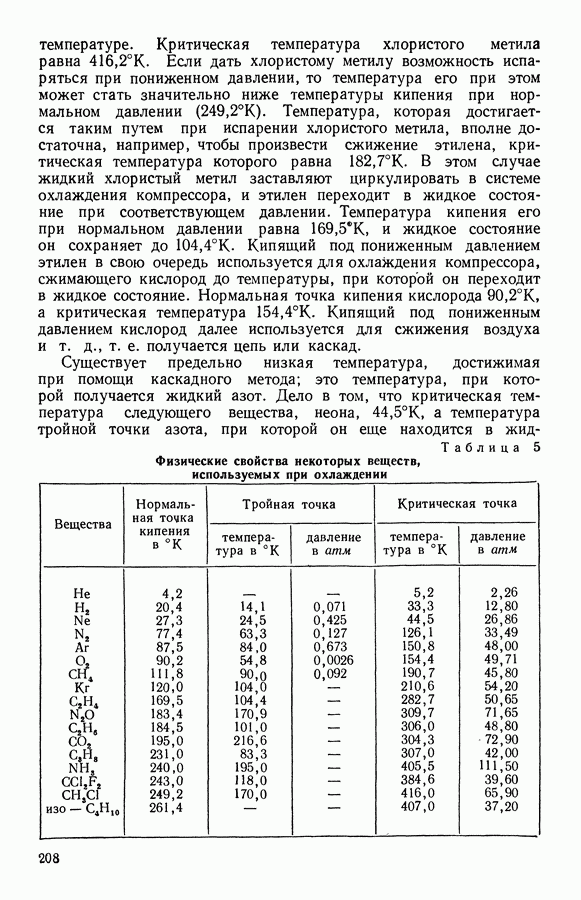
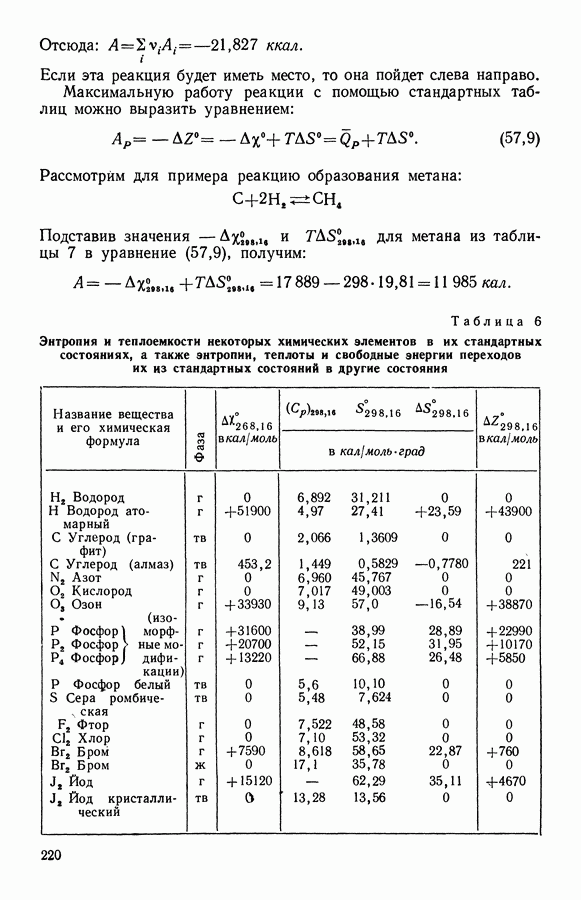
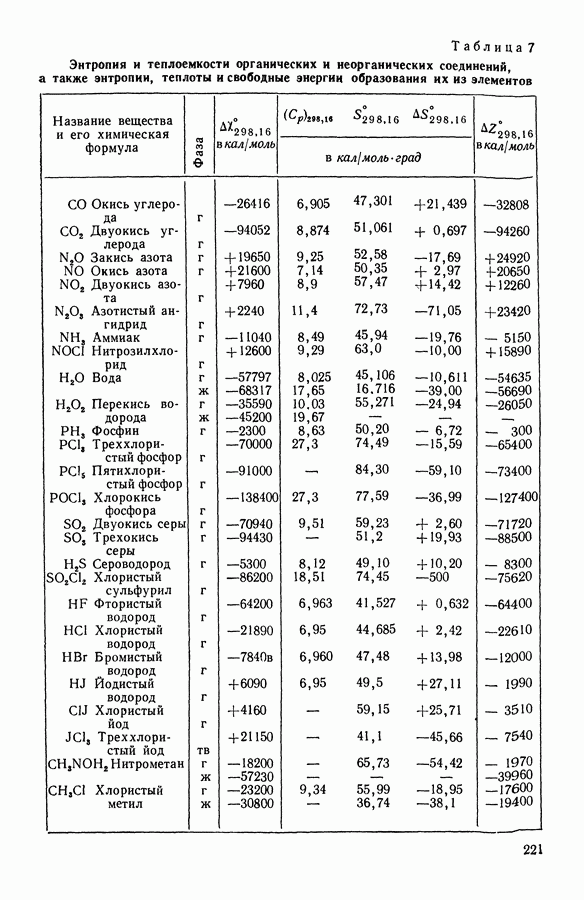
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса