| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
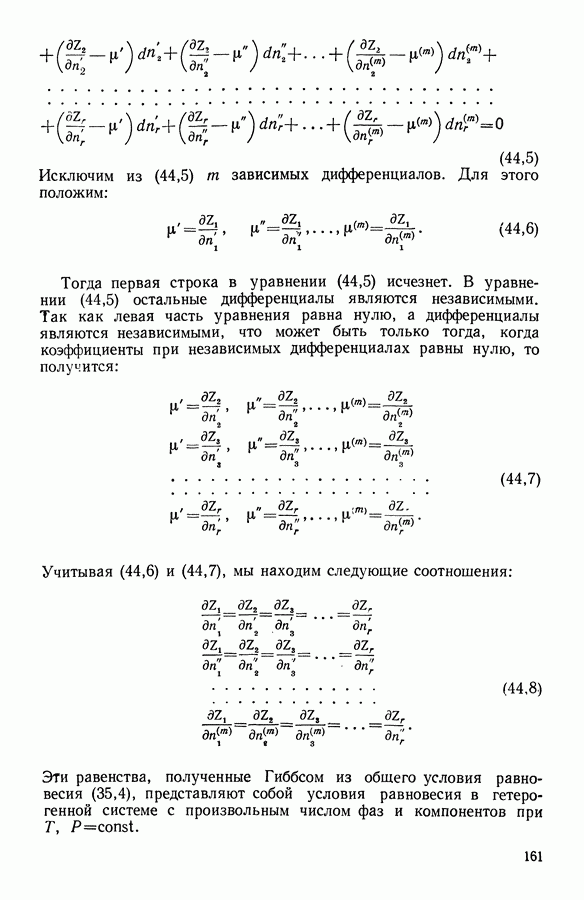
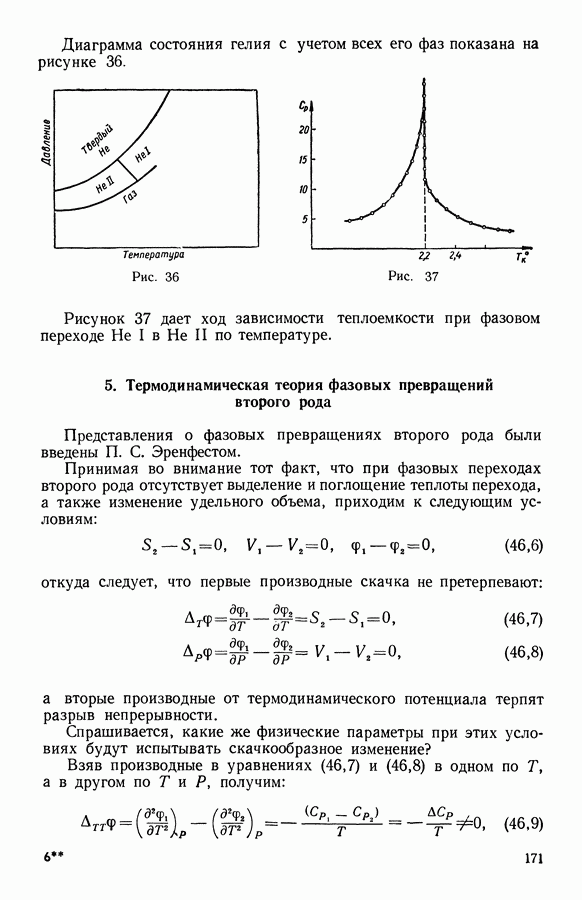
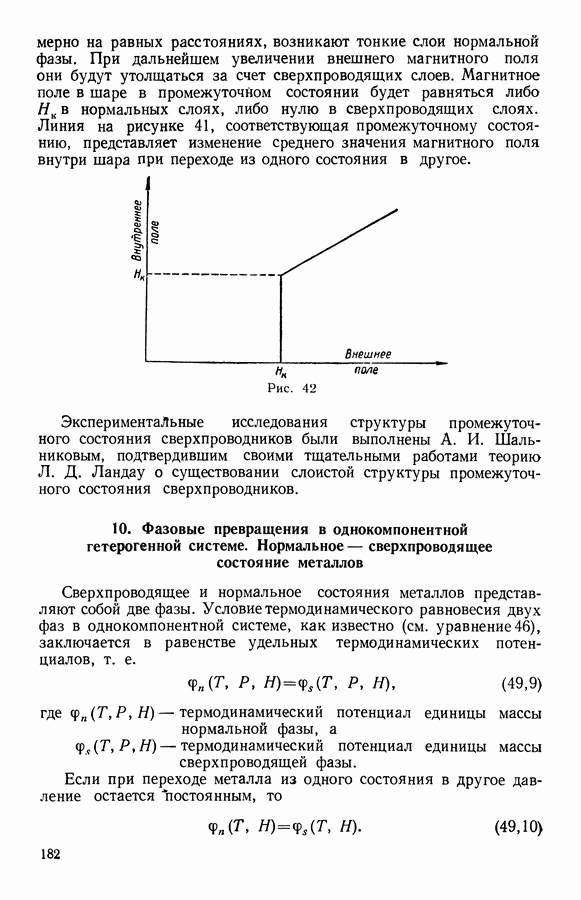
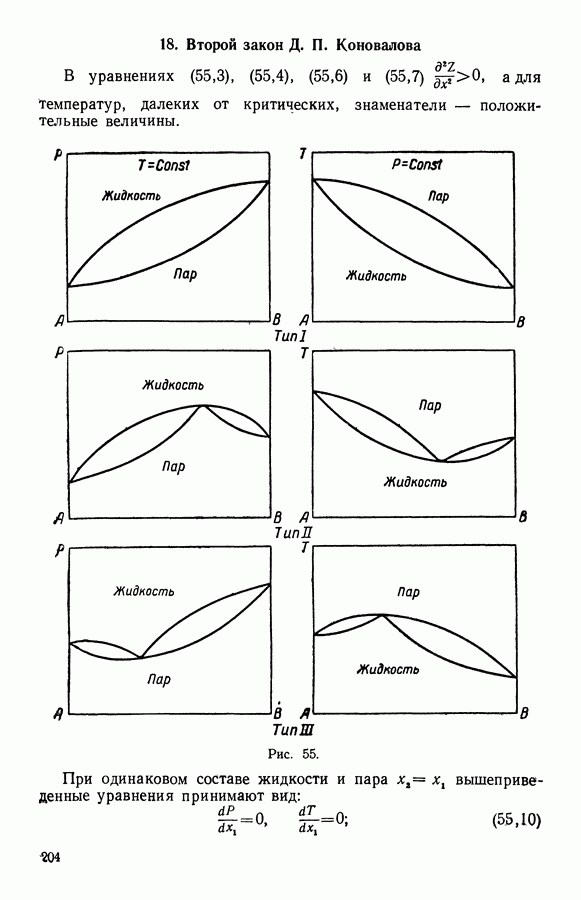
2. Фазовые превращения первого рода
Итак, основываясь на том, что фазовые превращения первого рода сопровождаются поглощением или выделением теплоты и изменением удельного объема, термодинамика устанавливает, что при  существует разрыв непрерывности у энтропии и внутренней энергии, а теплоемкость и изотермический коэффициент сжимаемости стремятся к бесконечности.
существует разрыв непрерывности у энтропии и внутренней энергии, а теплоемкость и изотермический коэффициент сжимаемости стремятся к бесконечности.
Рассматривая фазовое превращение как обратимый процесс, мы можем применить к нему второй закон термодинамики:

Интегрируя (14,10) при  получим:
получим:

где X — теплота фазового перехода.
Так как поглощаемая при переходе теплота есть величина положительная, то

т. е. энтропия терпит разрыв непрерывности при фазовых переходах первого рода.
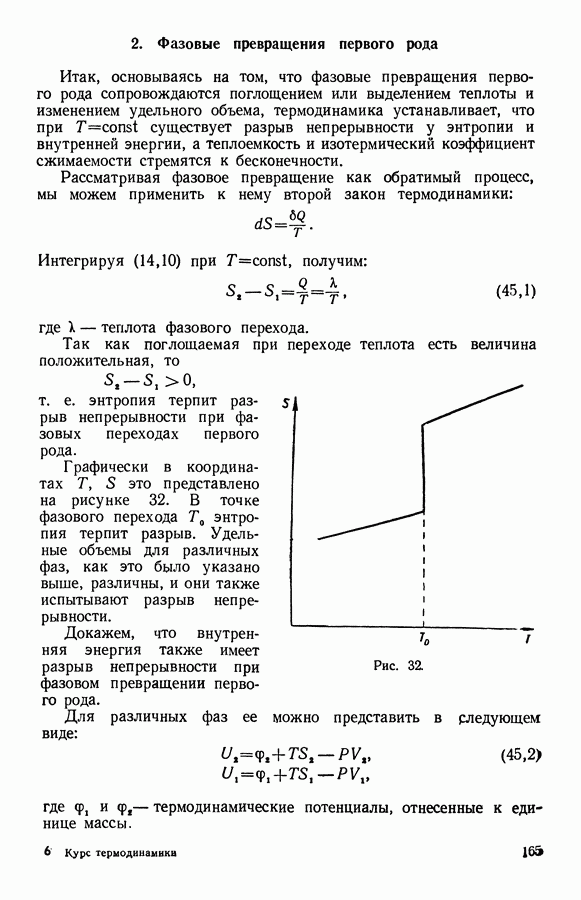
Графически в координатах  это представлено на рисунке 32. В точке фазового перехода
это представлено на рисунке 32. В точке фазового перехода  энтропия терпит разрыв. Удельные объемы для различных фаз, как это было указано выше, различны, и они также испытывают разрыв непрерывности.
энтропия терпит разрыв. Удельные объемы для различных фаз, как это было указано выше, различны, и они также испытывают разрыв непрерывности.
Докажем, что внутренняя энергия также имеет разрыв непрерывности при фазовом превращении первого рода.
Для различных фаз ее можно представить в рледующем виде:

где  термодинамические потенциалы, отнесенные к единице массы.
термодинамические потенциалы, отнесенные к единице массы.

Рис. 32.
При фазовом переходе первого рода остаются постоянными температура, давление, термодинамические потенциалы, а энтропия и удельный объем испытывают разрыв. Поэтому из уравнения (45,2) для изменения внутренней энергии найдем следующее значение:

то есть у нее наблюдается разрыв при фазовом переходе первого рода.
Если взять производные от термодинамического потенциала по температуре и давлению для различных фаз и вычесть одну из другой, то получим:

Так как  и
и  то из уравнений (45,4) и (45,5) вытекает, что первые частные производные от термодинамического потенциала также испытывают разрыв непрерывности при фазовых переходах первого рода.
то из уравнений (45,4) и (45,5) вытекает, что первые частные производные от термодинамического потенциала также испытывают разрыв непрерывности при фазовых переходах первого рода.

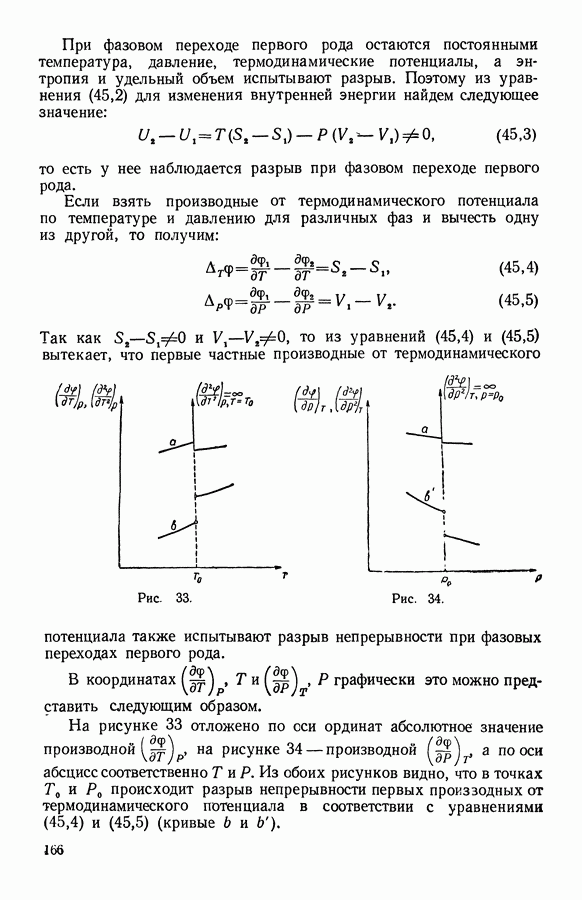
Рис. 33.

Рис. 34.
В координатах  графически это можно представить следующим образом.
графически это можно представить следующим образом.
На рисунке 33 отложено по оси ординат абсолютное значение производной, на рисунке 34 — производной а по оси абсцисс соответственно  Из обоих рисунков видно, что в точках
Из обоих рисунков видно, что в точках  происходит разрыв непрерывности первых произзодных от термодинамического потенциала в соответствии с уравнениями (45,4) и (45,5) (кривые
происходит разрыв непрерывности первых произзодных от термодинамического потенциала в соответствии с уравнениями (45,4) и (45,5) (кривые 
При фазовом переходе первого рода вторые производные от термодинамического потенциала по температуре и давлению обращаются в бесконечность (кривые  на рис. 33 и 34 изображают абсолютные значения вторых производных).
на рис. 33 и 34 изображают абсолютные значения вторых производных).
Из рисунков 33 и 34 видно, что абсолютные значения угловых коэффициентов касательных к кривым  в точках
в точках  стремятся к бесконечности, т. е.
стремятся к бесконечности, т. е.

Аналитическое выражение вторых производных от термодинамического потенциала по температуре и давлению можно представить в следующем виде:

Условия  и уравнения (45,6) и (45,7) подтверждают, что действительно при фазовых переходах первого рода теплоемкость
и уравнения (45,6) и (45,7) подтверждают, что действительно при фазовых переходах первого рода теплоемкость  и изотермический коэффициент сжимаемости
и изотермический коэффициент сжимаемости  стремятся к бесконечности: т. е.
стремятся к бесконечности: т. е.

Это обстоятельство объясняется поглощением или выделением теплоты превращения. Докажем, что это так. Из определения теплоемкости имеем:

Если при фазовом переходе поглощается или выделяется теплота (в этом случае  при
при  ), то и теплоемкость
), то и теплоемкость 
Подводя итог, можно дать фазовым превращениям следующее определение: фазовыми превращениями первого рода называются такие превращения, когда при переходе вещества из одной фазы в другую выделяется или поглощается теплота и изменяется удельный объем. При фазовом переходе первого рода испытывают разрыв непрерывности и внутренняя энергия, и энтропия, и первые производные от термодинамического потенциала по
температуре и давлению. В точке фазового превращения, как уже было сказано, теплоемкость  и изотермический коэффициент сжимаемости
и изотермический коэффициент сжимаемости  стремятся к бесконечности.
стремятся к бесконечности.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ ПОНЯТИЯ
- 1. Макроскопическая система
- 2. Состояние макроскопической система
- 3. Термодинамический процесс
- 4. Равновесное состояние
- 5. Функция состояния
- 6. Закон сохранения и превращения энергии
- 7. Внутренняя энергия системы
- 8. Количество теплоты
- 9. Температура
- 10. Работа
- 11. Условие полного дифференциала
- ГЛАВА ВТОРАЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Внутренняя энергия как функция состояния системы
- 2. Аддитивность внутренней энергии
- 3. Количественная формулировка первого закона для различных термодинамических систем
- 4. Определение теплоемкости
- 5. Применение первого закона термодинамики к некоторым простейшим процессам
- 6. Идеальный газ
- 7. Уравнение Майера для идеального газа
- 8. Адиабатный процесс
- 9. Уравнение адиабаты для идеального газа
- 10. Политропические процессы
- 11. Уравнение адиабаты для общего случая
- 12. Связь между модулями упругости и отношением теплоемкостей …
- 13. Связь отношения теплоемкостей со скоростью звука
- 14. Теплота процесса
- 15. Закон Гесса
- 16. Уравнение Кирхгофа
- ГЛАВА ТРЕТЬЯ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
- 1. Необратимые процессы
- 2. Равновесные (обратимые) процессы
- 3. Значение равновесных (обратимых) процессов
- 4. Формулировка Клаузиуса
- 5. Формулировка Томсона
- 6. Циклы
- 7. Обратимый цикл Карно
- 8. Обратимый цикл Карно с идеальным газом
- 9. Эквивалентность формулировок Клаузиуса и Томсона
- 10. Теорема Карно
- 11. Количественная формулировка второго закона
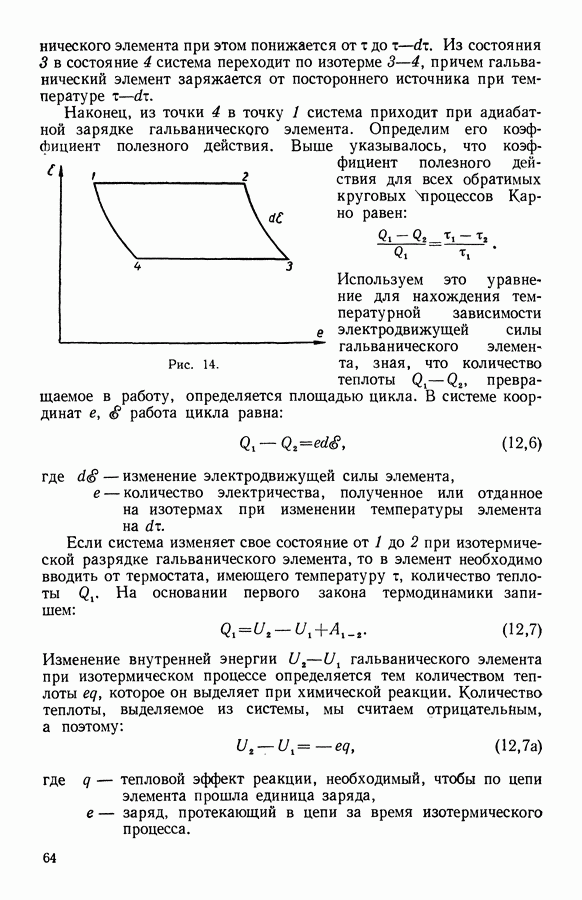
- 12. Зависимость электродвижущей силы гальванического элемента от температуры
- 13. Температурная шкала
- 14. Разнообразие шкал
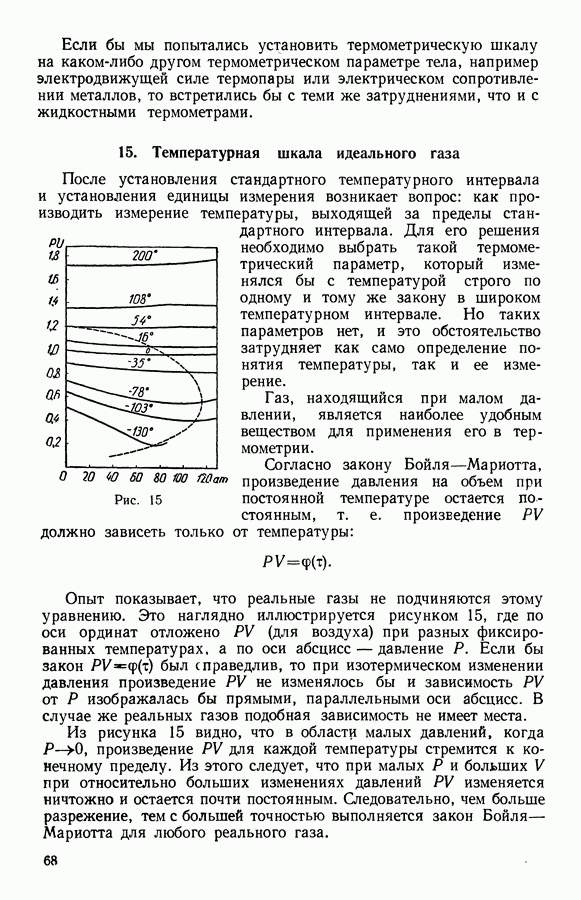
- 15. Температурная шкала идеального газа
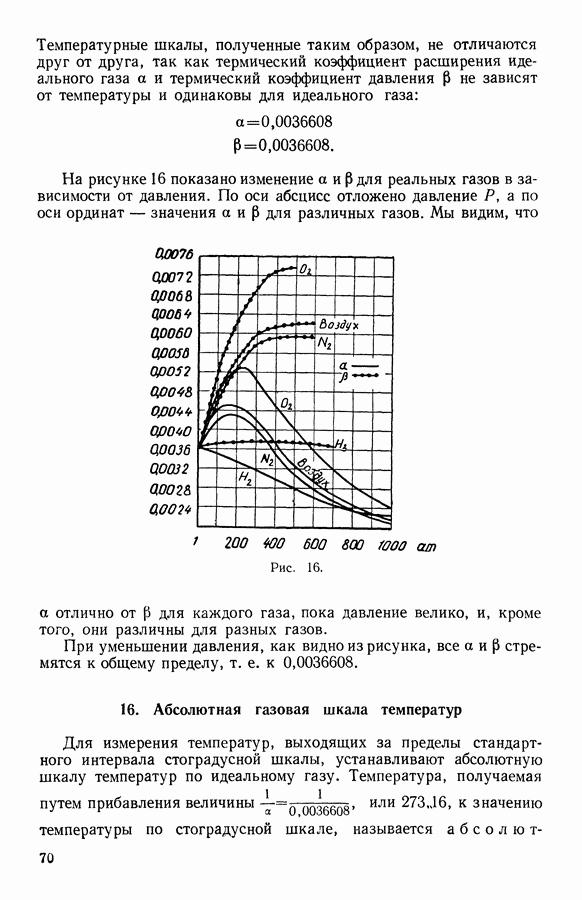
- 16. Абсолютная газовая шкала температур
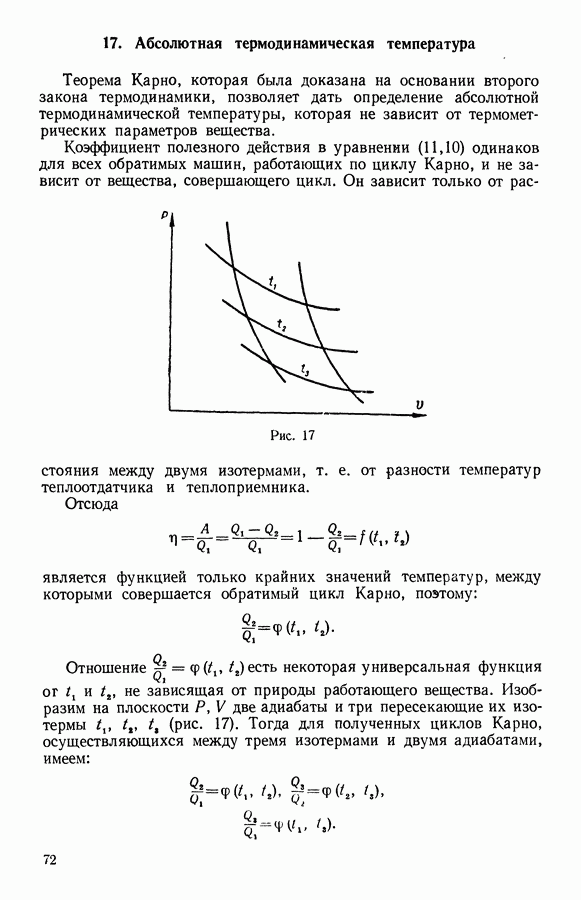
- 17. Абсолютная термодинамическая температура
- 18. Тождество шкалы идеального газа и газа, подчиняющегося уравнению Ван-дер-Ваальса, с термодинамической шкалой
- 19. Обобщение количественной формулировки второго закона термодинамики
- 20. Свойства энтропии
- 21. Аксиоматика второго закона термодинамики для равновесных (обратимых) процессов
- 22. Статистический характер второго закона термодинамики
- ГЛАВА ЧЕТВЕРТАЯ. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
- 2. Внутренняя энергия
- 3. Энтальпия
- 4. Свободная энергия
- 5. Термодинамический потенциал
- ГЛАВА ПЯТАЯ. РЕШЕНИЕ КОНКРЕТНЫХ ЗАДАЧ С ПОМОЩЬЮ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ
- 1. Вычисление энтропии при изменении агрегатного состояния при изотермическом процессе
- 2. Уравнение Клапейрона — Клаузиуса
- 3. Зависимость поверхностного натяжения от температуры
- 4. Энтропия как функция Т и x
- 5. Энтропия как функция T и Y
- 6. Энтропия как функция x и Y
- 7. Вычисление Cy-Cx
- 8. Связь теплоемкостей со скоростью звука
- 9. Зависимость Cv от объема
- 10. Зависимость Ср от давления
- 11. Изменение температуры в адиабатных системах
- 12. Уравнение адиабаты для газа, подчиняющегося уравнению Ван-дер-Ваальса
- 13. Уравнение Гиббса — Гельмгольца
- 14. Уравнение максимальной работы
- 15. Поверхностная энергия чистой жидкости
- 16. Возрастание энтропии при расширении газа в пустоту
- 17. Явление Джоуля — Томсона (дроссельный эффект)
- 18. Изотермическое дросселирование
- 19. Методы определения дифференциального и интегрального адиабатного дроссельного эффекта
- 20. Задачи
- ГЛАВА ШЕСТАЯ. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ
- 1. Тепловое излучение
- 2. Закон Кирхгофа
- 3. Световое давление
- 4. Закон Стефана — Больцмана
- 5. Формула и закон смещения Вина
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИЧЕСКОЕ УЧЕНИЕ О РАВНОВЕСИИ
- 2. Гетерогенная и гомогенная системы
- 3. Компоненты
- 4. Необратимые процессы и общие условия равновесия
- 5. Химический потенциал
- 6. Идеальные газовые смеси
- 7. Свободная энергия системы идеальных газов до смешения
- 8. Свободная энергия идеальных газов после смешения
- 9. Химический потенциал компонента идеального газа
- 10. Термодинамический вывод закона действующих масс
- 11. Термодинамический вывод уравнения работы химической реакции
- 12. Зависимость константы равновесия от температуры
- 13. Зависимость константы равновесия Ky от давления
- 14. Условие равновесия в гетерогенной системе
- 14. Правило фаз
- ГЛАВА ВОСЬМАЯ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
- 1. Фазовые превращения в однокомпонентных системах
- 2. Фазовые превращения первого рода
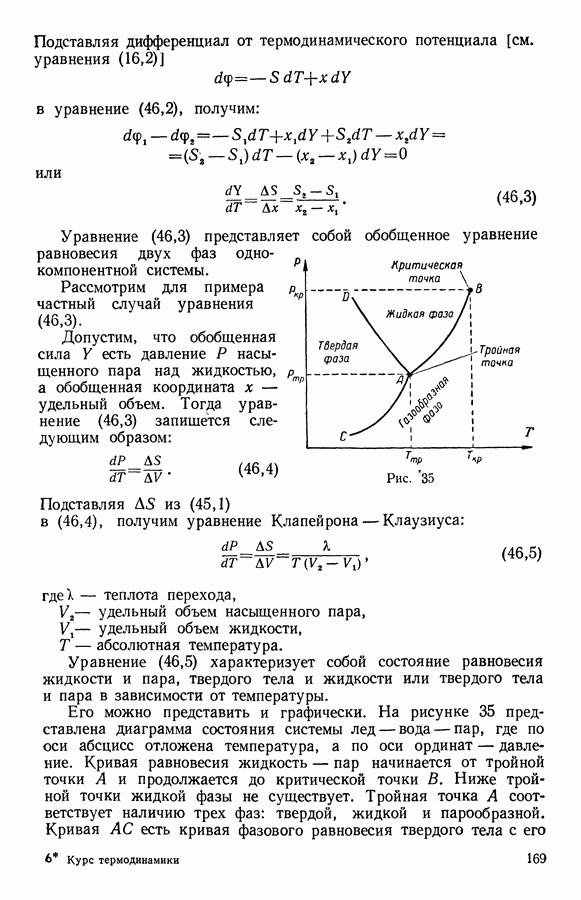
- 3. Общее уравнение равновесия двух фаз однокомпонентной системы
- 4. Фазовые превращения второго рода
- 5. Термодинамическая теория фазовых превращений второго рода
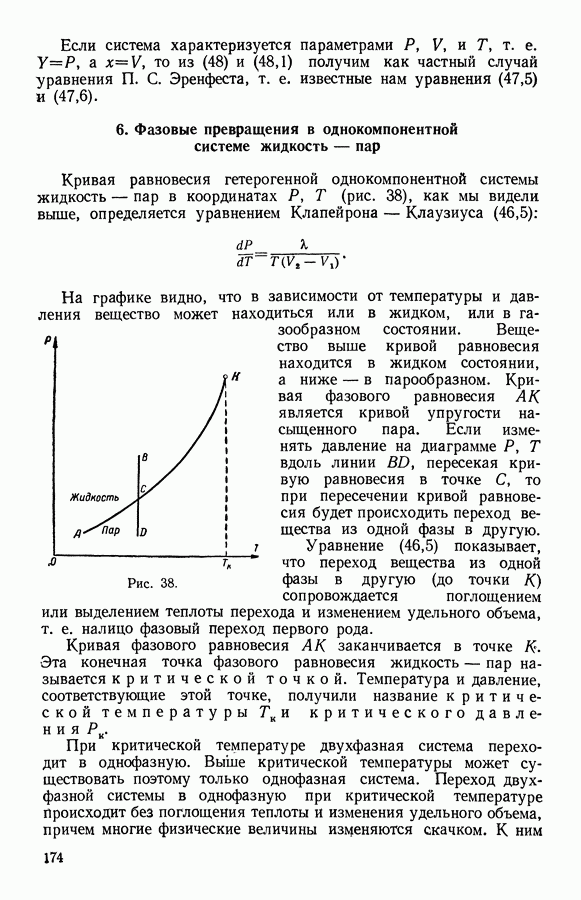
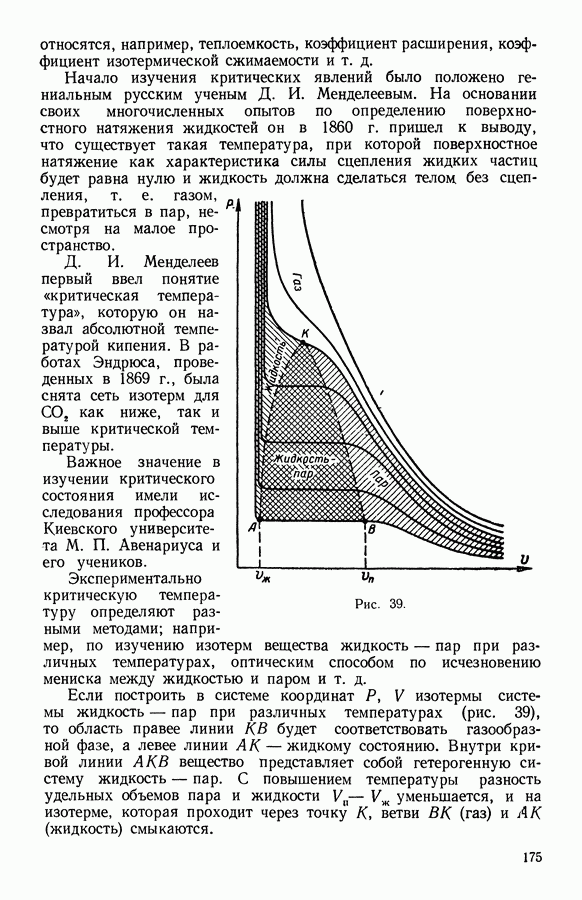
- 6. Фазовые превращения в однокомпонентной системе жидкость — пар
- 7. Термодинамическое условие равновесия системы жидкость — пар в критическом состоянии
- 8. Определение … из уравнения Ван-дер-Ваальса
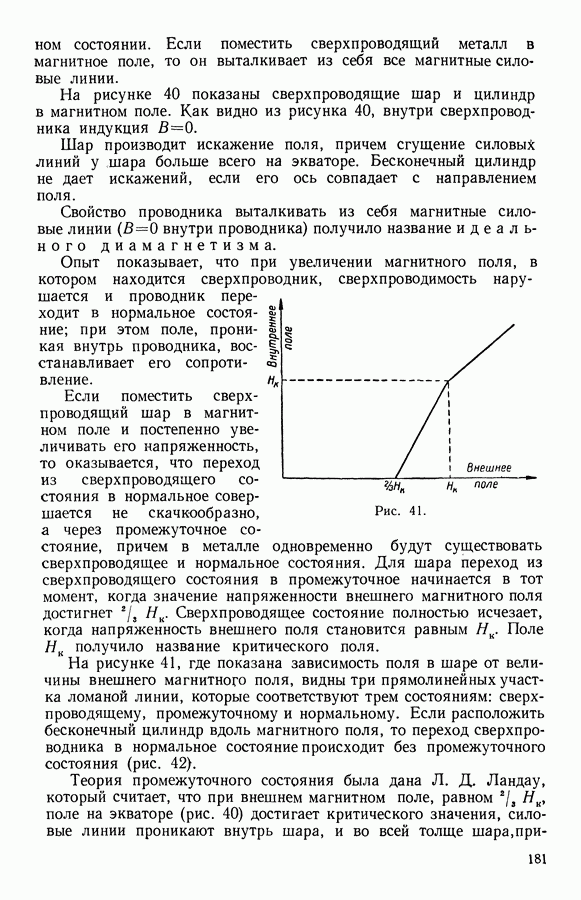
- 9. Сверхпроводящее состояние металлов
- 10. Фазовые превращения в однокомпонентной гетерогенной системе. Нормальное — сверхпроводящее состояние металлов
- 11. Бинарные системы
- 12. О взаимной растворимости жидкостей
- 13. Твердые растворы
- 14. Уравнение Ван-дер-Ваальса для бинарных смесей
- 15. Разбавленные растворы
- 16. Растворимость газа в жидкости
- 17. Первый закон Д. П. Коновалова
- 18. Второй закон Д. П. Коновалова
- 19. Температура кипения раствора и дистилляция двойных смесей
- ГЛАВА ДЕВЯТАЯ. НИЗКИЕ ТЕМПЕРАТУРЫ
- 1. Получение низких температур, их значение для техники и научных исследований
- 2. Каскадный метод
- 3. Метод дросселирования
- 4. Получение низких температур при расширении сжатого газа с отдачей внешней работы
- 5. Охлаждение методом адиабатного размагничивания
- 6. Теория обратимого адиабатного изменения магнитного состояния парамагнитного тела
- 7. Тепловая теорема Нернста
- 8. О третьем законе термодинамики
- 9. Свойства вещества вблизи абсолютного нуля
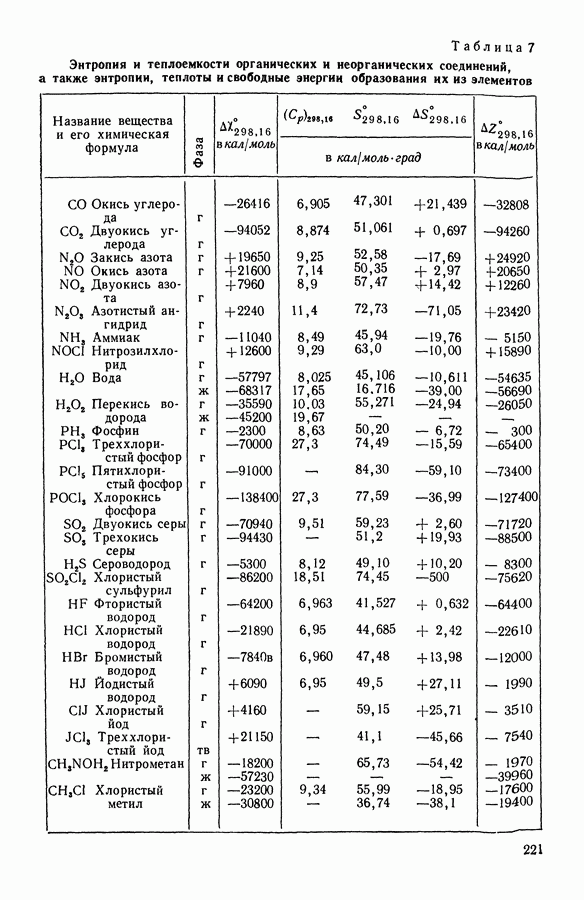
- 10. Стандартные таблицы термодинамических функций
- 11. Вычисление стандартных величин при изменении температуры
- 12. Вычисление стандартных величин при изменении давления
- 13. Применение стандартных таблиц
- 14. Вычисление стандартных величин
- 15. Задачи для всех разделов курса